Это копия, сохраненная 12 ноября 2023 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Также приветствуется обсуждения самого процесса изучения и учебников/задачников.
Анально модерируемый альтернативный тред для начинающих: https://2ch.hk/math/res/9338.html (
Обсуждение вузов и математического образования: https://2ch.hk/math/res/9453.html (
Мемасики сюда постите: https://2ch.hk/math/res/7199.html (
Список литературы от ОП-а, бывшего тут до меня. Был составлен на протяжении 13 тредов, к ознакомлению обязателен.
http://pastebin.com/4iMjfWAf
Если ты только зашел в тред и хочешь спросить, какую книжку прочитать, то ответ, скорее всего, будет в этих списках, анон.
Список от анона с dxdy. Довольно внушителен, тоже рекомендуется к прочтению. Является дополнением к списку старго ОП-а.
http://pastebin.com/YP1uaUyd
Goodbook.txt список книг с dxdy, рекомендованный тамошними обитателями.
http://pastebin.com/4FngRj6n
Литература - НМУ
https://docs.google.com/spreadsheets/d/1UWwIIAFwSwOQLK3m--LOaMOvHUivFDEz-JAnLa87i7Q/edit#gid=0
ОП-список 2. Составляйте список в реальном времени! Предлагайте в тред книги, критикуйте уже имеющиеся!
http://pastebin.com/szzZfkCM
Форчановский список, книги на английском.
http://4chan-science.wikia.com/wiki/Mathematics
Список с видеолекциями(в разработке):
http://pastebin.com/S3d7Jj6J
Качать книги тут:
http://libgen.io
А статьи тут(в разработке):
http://pastebin.com/3BfHPskz
Мемасы(в разработке):
http://pastebin.com/e38Yuj5V
Архивы тредов
http://pastebin.com/kiRZGVHW
http://arhivach.org/thread/233955/
Где можно прочитать про достижения математики прошлого? И я имею ввиду не времена гаусса-ньютона а реальную древность. Например из древней греции/египта/индии/китая.
Men of mathematics была такая книжка, но это научпоп про историю вообще, а тебе, видимо, надо искать пейперы, раз хочешь прям углубляться в это. Хотя вообще непонятно, во что там углубляться. Статьи на вики по теме точно недостаточно?
Мне интересно как они пришли, например, к выводам о площади круга, тупо меряли ирл или какие то логические уловки уровня теории множеств использовали.
Норм.
Типа такого? http://mathlets.org/mathlets/
Только не слушай коэффициенты Фурье в наушниках там.
Я послушал. Ничего страшного не произошло.
Да ладно, это я запаниковал слишком рано, оказалось, что я просто школьную программу позабыл. Пойду наворачивать выше по списку. Хотя с доказательствами у меня всегда были проблемы, непонятно вообще с чего начинать, за что цепляться и как развивать мысль дальше. Сложно это все.
Доказательство - вещь творческая всё-таки. Никаких алгоритмов в ней нет, поэтому без опыта ты и должен чувствовать себя дезориентированным. Читай учебники, разбирай и прорабатывай доказательства, которые в них приводятся, когда почувствуешь почву под ногами - можешь пытаться читать только формулировки теорем, а доказательства к ним придумывать самостоятельно. Твои доказательства будут громоздкими и уродливыми, но это поначалу - элегантность и чувство прекрасного постепенно придут. Ну и делай упражнения, конечно. Просто бегать глазами по строчками и кивать головой - непродуктивный способ изучения математики.
история математики в трех томах, том первый. И у Ван-дер-Ваардена была книга по истории древней математики.
А как они находили площади этих многоугольников? Разбивали многоугольник на треугольники равнобедренные?
Да, именно так.
 8 Кб, 1360x579
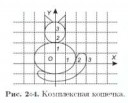
8 Кб, 1360x579аноны, помогите мне пожалуйста. Мне нужно решить задачу по теоретической механике, нужно найти уравнение движения точки M через угол ф, который изменяется по правилу ф=3\pi*t. Для этого же нужно спроецировать на оси х и у точку M(?). То есть, фактически это задача школьной геометрии, но что-то я не могу её решить. Может подскажете, как эти проекции найти? Или хотя бы подскажите, какие свойства, теоремы школьной геометрии мне нужно вспомнить. Или может тут можно составить уравнение движения точки как-то по-другому?
Недавно, кстати, поймал себя на мысли, что одних только польских математиков я знаю примерно столько же, сколько и женщин-ученых во всех областях
Почему ты так думаешь?
Первое я еще понимаю, но нет ли у вас житейского примера почему работает второе?
 5 Кб, 573x447
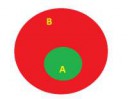
5 Кб, 573x447А содержится в В, поэтому их пересекая получается А.
По другому - AB = {x | A э x и B э х}[множество таких икс, что икс принадлежит А и В(обоим множествам]. Т.к. каждый элемет А лежит и в В, то их пересечение есть А.
Да никакой не надо, берешь сикп\конкрит матматикс\интро ту фп харриса и читаешь.
Спасибо.
Какие книжки по физике есть чтобы находились между школьным курсом и ланду-лившицем? А то школьные сильно простые, а ландау сразу начинает бросаться "ОЧЕВИДНО ЧТО КАК МОЖНО ЗАМЕТИТЬ ПОСЛЕ НЕБОЛЬШИХ ПРЕОБРАЗОВАНИЙ". Или скажите какой то другой курс физики по хардкору чтобы был, но понятный.
Любой курс общей физики. Сивухин или Иродов, например. Ландавшиц - это всё-таки теорфиз уже.
Пол Локхард «Плач математика»
Манифест Дьедонне
Некоторые посты Дмитрия Павлова на тифаретнике
Гротендик - Урожаи и Посевы
А в чем разница между обычным и теоритической?
Ведь по идее теоритическая лучше для знаний чем общая.
Спасибо
ЛОГИКА
Я в крайнем раздражении от доступных мне источников о логике предикатов.
Если конткретно: мне нужны примеры натуральной дедукции.
(Чтобы они были максимально точными и аккуратными.)
Что есть хорошего почитать по теме?
Просто сложилось впечатление, что доказывают как хотят, без всякого адекватного придерживания некоторой формальной системе. (На самом деле, просто пропускают очевидные для них вещи, которые мне не очевидны.)
Нашел что-то?
Вот коэффициент скорости роста меня интересует
Арнольд Что такое метематика. И другие статьи Арнольда.
>Просто сложилось впечатление, что доказывают как хотят, без всякого адекватного придерживания некоторой формальной системе.
Так, в общем-то, и есть. Настоящая база математики куда глубже формализма. О формальных системах вспоминают, когда нужно разрешить какие-то разногласия, или привлечь к делу компьютер.
А если не только тригонометрию, а вообще?
Для меня в своё время открытием был самый обычный курс матана в первом семестре. Когда всю школьную математику, которую я тогда воспринимал неким набором вычислительных рецептов, слабо связанных между собой, на моих глазах целиком построили буквально из грязи, из понятия натуральных чисел. Именно тогда я по-настоящему полюбил математику, ибо понял, что это такое на самом деле.
Аноны, что думаете про этот курс лекций Вавилова? Хочу вспомнить, что забыл из линейной алгебре примат и расширить свои знания по алгебре в целом.
 5 Кб, 288x234
5 Кб, 288x234>>2903
Посмотрел в целом по курсу, складывается впечатление, что собственно линейной алгебры будет не так уж и много, в отличие от высшей алгебры теории групп, колец, категорий и прочих гомологий.
Из минусов курса - некоторые вещи даются на семинарах и благополучно оставлены за кадром, без книжки в руках эти лекции мало чего дадут, разве что немаленький математический кругозор, потому как Николай Александрович очень любит забегать вперёд и распалять в студентах и зрителях любопытство.
Вообще, лучше бы рассматривать этот курс целиком, вместе с топологией и матанализом а в дальнейшем и с более продвинутыми курсами, ведь эти дисциплины очень уж плотно перекликаются. Но для этого его сперва надо осилить целиком.
А какие книги можешь посоветовать? Можно и на английском. но я не математик, поэтому можно и какие-то попроще.
Если тебе интересна конкретно линейная алгебра - есть книга Кострикина и Манина "Линейная алгебра и геометрия". Как не математику она может тебе показаться сложноватой и бросающей тебя сразу с ровного места в воду, так что читать её лучше будет после трехкнижия "Введение в алгебру" того же Кострикина. Будет много повторов, которые напомнят тебе подзабытые понятия, и и немного нового.
На английском особых книг именно по линейной алгебре не подскажу, благо у нас хватает авторов, разбирающихся в тематике.
 148 Кб, 923x465
148 Кб, 923x465Правильно ли я понял, что раз многочлен P(2) должен быть 0, то раз 2-1 дает 1, значит Q(2) должен быть нулем? Тогда почему именно от 2?
Я, наверное, слишком тупые вопросы задаю для этой доски, не бейте только сильно. Нужно как-то повторить школьный курс.
Общая физика больше о том, чтобы что-то конкратное рассчитать, ответить на вопрос в духе "если мы сделаем вот так и измерим вот это, то что мы увидим в результате". Она оперирует наглядными и интуитивными понятиями, её рассуждения легко визуализировать, нарисовать картинку. Поэтому изучать физику начинают именно с неё - она более "плотская" и осязаемая, позволяет выработать какое-то интуитивное ощущение физической реальности, и в то же время не требует серьёзной математической подготовки и привычки к абстрактному мышлению. Кроме того, её изложение больше соответствует тому, как наука развивалась исторически. Она не стесняется апеллировать к эксперименту и каким-то феноменологическим частным законам, вроде закона Ома.
Теорфиз же от конкретики намеренно дистанцируется - уже уровне используемых понятий и единиц. Чтобы конвертировать его выкладки в конкретные предсказания в конкретном эксперименте, нужно немало попотеть. С точки зрения философии теоретической физики, не так уж важно знать, как далеко полетит снаряд, если выстрелить им из пушки. Гораздо важнее понимать, как природа устроена в целом, на структурном уровне. Наглядность и интуитивность здесь только мешают, и их вытесняют математические выкладки (хоть и не всегда совершенно строгие), а изложение подчинено структуре материала, логическим связям между его частями.
Попробую пояснить эту разницу на примере электродинамики и специальной теории относительности.
Суть кинематики СТО, с точки зрения общей физики: время не является абсолютным, при разгоне оно замедляется, длины сокращаются вдоль направления движения, одновременность относительна, передавать сигналы быстрее скорости света нельзя. Есть преобразования Лоренца, которые связывают разные системы отсчёта.
Суть кинематики СТО, с точки зрения теорфиза: время и пространство не существуют по отдельности, а являются разными проявлениями единого объекта - пространства-времени. В нём существует метрика специального вида, и группа преобразований, которая эту метрику сохраняет. Отсюда само собой вытекает требование ковариантности. Все уравнения должны иметь лоренц-ковариантный вид, и все физически реальные сущности должны описываться ковариантными математическими объектами.
Суть электродинамики, с точки зрения общей физики: Существуют электрические и магнитные поля, которые порождаются зарядами и токами, и могут взаимно порождать друг друга, за счёт чего передаются на далёкие расстояния в виде волн, и даже переносят энергию.
Суть электродинамики, с точки зрения теорфиза: Электрическая и магнитная составляющие электромагнитного поля и не могли бы существовать по отдельности, без взаимосвязи друг с другом, поскольку описываются одним и тем же неделимым ковариантным объектом - электромагнитным векторным потенциалом. Магнитное поле можно в первом приближении рассматривать как релятивистскую поправку к электростатике - именно поэтому оно порождается движущимися электрическими зарядами, а не каким-то особым магнитным зарядом.
Взгляд на динамику, с точки зрения общей физики: Существуют уравнения движения (второй закон Ньютона, к примеру, или уравнения Максвелла), которые определяют всю динамику. Свободные тела двигаются равномерно и прямолинейно, а любые отклонения от этого режима определяются действующими силами - силой тяготения, силой реакции опоры, силой трения, и другими - всё, что мы привыкли встречать в обычной жизни. Бывают особые комбинации переменных, которые сохраняются во время движения при определённых условиях - вроде энергии и импульса. Это упрощает расчёты и анализ, и именно поэтому их и ввели. Ещё сохраняется масса, заряды и некоторые другие вещи - так уж нам повезло.
Взгляд на динамику, с точки зрения теорфиза: Вся динамика закодирована в особой величине, называемой лагранжианом, и другой связанной с ним величине - действии. Их вид неслучаен и зачастую может быть выведен из геометрических принципов или каких-то ещё соображений. Ключевое значение имеют симметрии - именно наличием симметрий определяется существование сохраняющихся величин (теорема Нётер). Так, энергия двойственна ко времени и её сохранение связано с однородностью времени, и точно так же импульс двойственен к пространству и его сохранение связано с его однородностью. Таким образом, энергия и импульс гораздо более фундаментальные вещи, чем сила, и, в отличие от неё, сохраняют свой смысл даже в квантовом мире. Единственная сила (читай - взаимодействие), существующая в СТО - это взаимодействие вещества с электромагнитным полем. Единственная сила (читай - взаимодействие), существующая в СТО - это взаимодействие вещества с электромагнитным полем, и оно тоже закодировано в лагранжиане. Другие законы сохранения также имеют соответствующие им симметрии. Таким образом, изучение устройства группы симметрий может многое рассказать о динамике.
Общая физика больше о том, чтобы что-то конкратное рассчитать, ответить на вопрос в духе "если мы сделаем вот так и измерим вот это, то что мы увидим в результате". Она оперирует наглядными и интуитивными понятиями, её рассуждения легко визуализировать, нарисовать картинку. Поэтому изучать физику начинают именно с неё - она более "плотская" и осязаемая, позволяет выработать какое-то интуитивное ощущение физической реальности, и в то же время не требует серьёзной математической подготовки и привычки к абстрактному мышлению. Кроме того, её изложение больше соответствует тому, как наука развивалась исторически. Она не стесняется апеллировать к эксперименту и каким-то феноменологическим частным законам, вроде закона Ома.
Теорфиз же от конкретики намеренно дистанцируется - уже уровне используемых понятий и единиц. Чтобы конвертировать его выкладки в конкретные предсказания в конкретном эксперименте, нужно немало попотеть. С точки зрения философии теоретической физики, не так уж важно знать, как далеко полетит снаряд, если выстрелить им из пушки. Гораздо важнее понимать, как природа устроена в целом, на структурном уровне. Наглядность и интуитивность здесь только мешают, и их вытесняют математические выкладки (хоть и не всегда совершенно строгие), а изложение подчинено структуре материала, логическим связям между его частями.
Попробую пояснить эту разницу на примере электродинамики и специальной теории относительности.
Суть кинематики СТО, с точки зрения общей физики: время не является абсолютным, при разгоне оно замедляется, длины сокращаются вдоль направления движения, одновременность относительна, передавать сигналы быстрее скорости света нельзя. Есть преобразования Лоренца, которые связывают разные системы отсчёта.
Суть кинематики СТО, с точки зрения теорфиза: время и пространство не существуют по отдельности, а являются разными проявлениями единого объекта - пространства-времени. В нём существует метрика специального вида, и группа преобразований, которая эту метрику сохраняет. Отсюда само собой вытекает требование ковариантности. Все уравнения должны иметь лоренц-ковариантный вид, и все физически реальные сущности должны описываться ковариантными математическими объектами.
Суть электродинамики, с точки зрения общей физики: Существуют электрические и магнитные поля, которые порождаются зарядами и токами, и могут взаимно порождать друг друга, за счёт чего передаются на далёкие расстояния в виде волн, и даже переносят энергию.
Суть электродинамики, с точки зрения теорфиза: Электрическая и магнитная составляющие электромагнитного поля и не могли бы существовать по отдельности, без взаимосвязи друг с другом, поскольку описываются одним и тем же неделимым ковариантным объектом - электромагнитным векторным потенциалом. Магнитное поле можно в первом приближении рассматривать как релятивистскую поправку к электростатике - именно поэтому оно порождается движущимися электрическими зарядами, а не каким-то особым магнитным зарядом.
Взгляд на динамику, с точки зрения общей физики: Существуют уравнения движения (второй закон Ньютона, к примеру, или уравнения Максвелла), которые определяют всю динамику. Свободные тела двигаются равномерно и прямолинейно, а любые отклонения от этого режима определяются действующими силами - силой тяготения, силой реакции опоры, силой трения, и другими - всё, что мы привыкли встречать в обычной жизни. Бывают особые комбинации переменных, которые сохраняются во время движения при определённых условиях - вроде энергии и импульса. Это упрощает расчёты и анализ, и именно поэтому их и ввели. Ещё сохраняется масса, заряды и некоторые другие вещи - так уж нам повезло.
Взгляд на динамику, с точки зрения теорфиза: Вся динамика закодирована в особой величине, называемой лагранжианом, и другой связанной с ним величине - действии. Их вид неслучаен и зачастую может быть выведен из геометрических принципов или каких-то ещё соображений. Ключевое значение имеют симметрии - именно наличием симметрий определяется существование сохраняющихся величин (теорема Нётер). Так, энергия двойственна ко времени и её сохранение связано с однородностью времени, и точно так же импульс двойственен к пространству и его сохранение связано с его однородностью. Таким образом, энергия и импульс гораздо более фундаментальные вещи, чем сила, и, в отличие от неё, сохраняют свой смысл даже в квантовом мире. Единственная сила (читай - взаимодействие), существующая в СТО - это взаимодействие вещества с электромагнитным полем. Единственная сила (читай - взаимодействие), существующая в СТО - это взаимодействие вещества с электромагнитным полем, и оно тоже закодировано в лагранжиане. Другие законы сохранения также имеют соответствующие им симметрии. Таким образом, изучение устройства группы симметрий может многое рассказать о динамике.
>Единственная сила (читай - взаимодействие), существующая в СТО - это взаимодействие вещества с электромагнитным полем. Единственная сила (читай - взаимодействие), существующая в СТО - это взаимодействие вещества с электромагнитным полем, и оно тоже закодировано в лагранжиане.
Зачем-то два раза скопипастил.
Есть классическая ошибка игрока, изучение которой гласит, что важно помнить о независимости испытаний от предыдущего исхода. Если пренебречь внешними факторами, монетке похер, сколько раз она там уже выпадала орлом или решкой, каждый раз она снова выпадает с вероятностью в 50%.
Но при этом есть и закон больших чисел. Который гласит, что при достаточно большой выборке, распределение будет приближаться к математически ожидаемому результату. Так вот, если монетка выпала 99 раз орлом, разве не логично предположить, что выборка достаточно большая, чтобы на сотом броске началось сдвижение в сторону ожидаемого 50/50, и вероятность выпадения решки была бы больше?
Закон больших чисел работает не так. У тебя конкретный исход кодируется строкой из 100 битов, причём все эти строки равновероятны. Вероятность появления (для n = 6) 000000, 111111, 110100, 010101, 011110 - одна и та же, они все после шести бросков выпадут с равной вероятностью. А закон больших чисел - это просто выражение того факта, что строк с примерно равным числом нулей и единиц намного больше, чем тех, где их число сильно отличается. Иными словами, всё дело в том, что мы забываем про порядок выпадения орлов и решек и считаем только их количество. На вероятность выпадения орла или решки в конкретном эксперименте закон больших чисел никак не влияет.
Значит общая физика это что то в духе "как это работает", а теоретическая "как работает общая физика"?
Другими словами, если обычному физику интересно как снять с коленвала в таких то условиях такой то крутящий момент, то физику-теоретику интересно почему крутящий момент вообще передается?
И наконец, даже если я начну учить ландау-лившица и над одной страницей пять дней сидеть до полного понимания сути написанного, это не сделает меня великим мастером снимания вращательного момента с коленвалов?
Опять же, другими словами, если я смогу в теоретическую физику я буду знать тайны устройства мироздания, но не смогу поменять розетку или выключатель в ванной?
Практический смысл я смогу из теоретической физики вынести? Или только если пойду работать в церн гонять протоны по кругу и доказывать гипотезу что под сабатон протон получает в 400 раз больше энергии?
Ты сам кто по образованию? А то так расписал со знанием. Или это паста?
Начала эвклида.
Почему площадь круга пи радиус квадрат, а площадь кругового сектора угол в радианах на радиус?
 150 Кб, 1360x579
150 Кб, 1360x579вот картинка, и мне нужно задать уравнение движения точки М данного механизма. Для этого мне нужно спроецировать на оси Х и У точку М, и длины отрезков, которые должны зависеть от угла /phi. Но у меня не получается выразить эти проекции через /phi. Помогите мне пожалуйста, может я что-то делаю не так? Там угол /alpha равен 30 градусам, а отрезок AM=0.1
>И наконец, даже если я начну учить ландау-лившица и над одной страницей пять дней сидеть до полного понимания сути написанного, это не сделает меня великим мастером снимания вращательного момента с коленвалов?
>Опять же, другими словами, если я смогу в теоретическую физику я буду знать тайны устройства мироздания, но не смогу поменять розетку или выключатель в ванной?
Ну, в общем случае так и выйдет, разве что ты какой-то там очень умный человек. Это как местная история с гомологами и ящиком. Вроде бы люди и математику знают, а такую простую прикладную задачу так долго решали. Хотя оптимизацию функции одной переменной преподают в любом односеместровом курсе высшей математики. А еще же и множители Лагранжа есть, например. Но они это не смогли увидеть.
Порядки роста?
Потому что это не так.
Ты думаешь если тебе обычная книжка не далась то дастся эта?
Разочарую, тебе и эта книжка будет не по зубам.
 332 Кб, 596x628
332 Кб, 596x628>формы (двумерные и трехмерные)
Лол блядь. Смотрел по диагонали и слегка прихуел от такого, прежде чем понял, что имеется в виду. Видимо, у меня уже математика головного мозга.
Примерно так, да. Хороший теоретик не обязан быть хорошим практиком, знание, как снимать вращательный момент с коленвала, не поможет тебе мастерски орудовать напильником, а если ты умеешь изготавливать великолепные шахматные фигуры из слоновой кости, это ещё не делает тебя великим шахматистом. Как и наоборот. Серебряной пули не существует, специализация возникла не просто так.
>Ты сам кто по образованию?
Я матфизик. Не тот, который краевые задачи решает, а в широком смысле.
Если ты даун, то видосики на khan academy должны хорошо зайти, заодно английский выучишь
Детки то, с синдромом Дауна, вовсю когомологии де Рама ебашут, а ты всё сидишь как сыч.
И что делать, если я больше на практику нацелен и хочу уметь искать разрывы в проводке с помощью радио настроенного на короткие волны? Читать сивухина/иродова а потом что?
Или этих знаний достаточно чтобы на коленке из двух магнитов и проволоки скрутить коллекторный электромотор?
Тебе тогда нужно что-нибудь техническое и инженерное. Тут я тебе ничего конкретного уже посоветовать не могу.
при поиске решения частных дифур, как уравнение волны или heat equation, допускают, что
u(x, t) = X(x)T(t)
фу-я может быть представленна как произведение фу-й. метод разделения переменных.
это вывод из вида дифура? как? или угадали?
Угадали. Это более-менее стандартная подстановка.
391
=
221 · 713
391 · 713
Всем привет! Откуда взялось число 713, никто не подскажет? А то я понять не могу.
Ты их с аутистами перепутал.
Блджад, я совсем запутался. Ладно, хуй с ними!
Учебник арифметики
Ты ебанулся? Кто тебе такое говорил?
Я свою племяшку учу всяким прикольным морфизмам одновременно с таблицей умножения. В школу она пока ещё не ходит.
У меня чувство, что в одном из предыдущих тредов ты (а может и не ты) эту задачу постил.
ну вроде бы в точке А скользящая заделка, хотя не знаю, а насчёт длины АЕ - наверное с помощью неё можно что-то выразить. Но к сожалению, у меня не выходит.
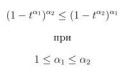 10 Кб, 538x337
10 Кб, 538x337Или, может его можно доказать самостоятельно?
(знак может быть в другую сторону, я запутался)
Учитывая, что написанное имеет смысл только при 0 < t < 1, неравенство почти очевидно. Достаточно сравнить выражения в скобках.
Ой, и правда всё просто. Спасибо.
Ну хорошо.
Что тогда посоветуешь по общей физике, кроме сивухина и иродова?
И да, расскажи кулстори как докатился до жизни такой? Почему матфизиком стал, какими проблемами занимаешься, почему и т.д.
 242 Кб, 1104x302
242 Кб, 1104x302 34 Кб, 500x366
34 Кб, 500x366Школьник, тут никто не будет разбираться в твоей глупой домашке, - тем более когда ты разговариваешь как унтерменш. Все вопросы задавай своей шараге.
Какая-то неведомая хуйня, вроде бы не произошло ничего страшного, но есть проблема, масштабы которой не пойму как оценить. Решать уравнения, неравенства и прочее могу, с параметрами, хуяметрами - не вопрос. Геометрию люблю всей душой, физику туда же. Так вот теперь к сути дела, я не могу никак научится воспринимать текстовые задачи и составлять исходя из условия точную модель ситуации, что в алгебре, что геометрии подобная лабудень. Самостоятельно не удается просто, я хуй знает, просто мозг отказывается воспринимать условия. Постоянно нуждаюсь в помощи.
Толи мозг кипит от этих всех формулировок дебильных или я тупой. С логикой какие-то проблемы что ль.
Пробовал решать олимпиадные задачи 7-8 класса - сосу хуй.
Было ли у кого подобное? Как лечили?
> и почти во многих требуется доказательство
Не только лишь во всех, надеюсь?
На мой взгляд, готовиться к конкретным вопросам, или тем более оценивать сложность экзамена по их количеству - верх уебанства. Я всегда просто читал конспект и повторял ключевые выкладки, чтобы быть уверенным, что воспроизведу их на экзамене. А список вопросов - это просто дополнительная опора для твоей памяти, когда ты их просматриваешь, поднимаешь материал в голове, и осознаёшь, что вот это ты помнишь, а вот это нужно ещё повторить. Не нужно пугаться их количества. Наоборот, чем они детализированнее, тем меньше шансов, что ты упустишь что-то важное. И да, тебе вовсе не обязательно воспроизводить лекции слово в слово. Если у какого-нибудь скалярного произведения выписано 20 свойств, от тебя никто не будет требовать их все. Если ты что-то упустишь, на это просто забьют хуй, или, если это было что-то реально важное, попросят написать прямо на месте. А если ты сдаёшь не лично лектору, то экзаменатор, скорее всего, вообще в душе не ебёт, что и как конкретно у вас было. За исключением старых пердунов, которые из 80 лет жизни 55 лет ходят принимать этот экзамен к этому лектору. Но это патологический случай. Вообще, чем моложе преподаватель, тем меньше он доёбывается до незначительной хуйни. Хотя если ты зафейлишь определение предела, то тебя это не спасёт.
>Не только лишь во всех, надеюсь?
Блджад, не проверил пост.
По матану у меня как раз "патологический случай", мда.
А есть смысл билеты писать по ходу семестра? И перечитывать их постоянно.
Есть.
Если ты понимаешь материал и можешь прочесть 3-4 раза за день до экзамена все конспекты, а после утром - заранее выписанные вопросы просмотреть за часик, то экзамен пролетает без проблем. Приходишь, пишешь, уходишь.
Ну и это, надеюсь, не надо объяснять, что подготовка к экзамену идёт с первого по последнее аудиторное занятие, а дальше - только повторение пройденного?
помогите пожалуйста, знаю надо было учиться, ходить на пары, но долбаеб
Вычислить меру Лебега множества:
V = { (x; y) : 0<y<1/(1+x^2), x<0} на плоскости
нихуя не знаю, заебался перечитывать определение меры в википедии, в статьях из гугла какая-то непонятная херь
Как это сделать? интеграл лебега и мера лебега это одно и то же? где найти прочитать, как просто решить это дерьмо?
пи пополам получил, а точно так, чот эт слишком просто, если я не накосячил. мне просто эту херню надо в курсач написать, серьезно просто обычный интеграл с первого курса?
величина, размер мерить, я хз. но просто она же называется Лебега. И я смог найти чтобы где-то говорилось что достаточно просто взять интеграл. я просто еще и к своему стыду понятия не имею что-такое интеграл, знаю только Ньютона-Лейбница
Ну, голубчик, вы бы взяли томик Зорича по матану, и так сказать провели бы ликбез. А после Зорича можно уже вещи по-серьезнее взять.
И да, не всегда можно взять интеграл, это зависит от множества, от того насколько оно замудренное.
Спасибо, ты мне помог, возможно, когда я этот сдам курсач и еще 6 долгов меня даже не отчислят
Перейти к полярным координатам или к обобщенным полярным координатам и вычислить двойной интеграл ∫∫dxdy
за заданной областью D
D: x^2+y^2<=x, x^2+y^2<=y
 897 Кб, 2656x1494
897 Кб, 2656x1494Со всем)))Дохожу до этого момента, а с построением графика и дальнейшим решением проблема. Зато есть ответ(в ответнике): p/8-1/8
ну можно посмотреть на уравнения области, даже нарисовать их, и сделать нормальную замену.
> p/8-1/8
Хм, что-то не то. Причем у вольфрам альфы тоже ответ вышел как у меня (я даже два интеграла отдельно взял для точности). Или я упоролся с областью интегрирования?
Тебе и этого хватит. Тот же Сивухин охватывает вообще всё, что тебе в принципе может когда-нибудь понадобиться с практической точки зрения. Хотя это всё ещё не инженерный курс, со всеми вытекающими.
>Почему матфизиком стал
Сложно сказать. Поступил на физфак, поскольку всегда любил физику. А математику полюбил уже в универе. Я восхищался её стройностью и цельностью, тем, как на моих глазах выстраивают и связывают воедино всё, что я ещё со школы знал какими-то обрывками заклинаний и рецептов. Выбор кафедры матфизики был для меня естественным в такой ситуации.
>какими проблемами занимаешься, почему и т.д.
Мой научник занимается спектральной теорией дифференциальных операторов - в частности, спектром оператора Шрёдингера с периодическим потенциалом. Это имеет самое прямое отношение к ФТТ, зонной теории проводимости и всему такому - периодические потенциалы характерны как раз для кристаллических решёток, а спектр оператора Шредингера - это, по сути, множество допустимых энергий для пробного электрона. В частности, изучаются всякие пороговые эффекты, переходы из связанного состояния в свободное, гомогенизации (предельные спектры при стремлении периода решётки к нулю) с получением довольно хороших - квадратичных - оценок погрешностей, и так далее. Пока что я изучаю всю эту науку.
Хотя вообще-то есть тема, которая меня занимает с того самого момента, как я узнал, что такое квантмех и как он работает. Это динамические теории коллапса. Мне никогда не нравилось, что понятия наблюдения и наблюдателя вносятся искусственно, на уровне постулатов, что в квантмехе два фактически несовместимых друг с другом динамических принципа. Я ещё на третьем курсе, не читая никаких статей, самостоятельно пришёл к выводу, что линейное детерминированное уравнение Шрёдингера должно быть всего лишь приближением реального закона, который должен приводить в известных предельных случаях к унитарной эволюции или коллапсу. Я пытался придумать альтернативу, но ничего разумного у меня не получилось, и я со временем оставил попытки. И только сравнительно недавно я с удивлением обнаружил, что люди в мире вообще-то занимаются этой проблемой, и есть ощутимые результаты, хотя у них хватает принципиальных проблем. Вот хочу найти время и разобраться в этой теме как следует.
>>3029
Какую ещё проблему?
Квантовые компьютеры к нечёткой логике отношение не имеют никакого.
>>3036
У тебя есть некое семейство объектов, как-то связанных между собой стрелками. Объекты занумерованы элементами частично упорядоченного множества, а стрелки идут или от меньшего к большему (прямой предел), или наоборот (обратный). Если в твоём частично упорядоченном множестве есть максимальный элемент, то предел будет равен ему. Если нет, то он как бы добавит его искусственно. Т.е. в первом случае у нас пределом будет объект, в который есть стрелки из любого другого объекта, согласованные со всеми остальными. Во втором, соответственно, наоборот. Скажем, если мы возьмём цепочку расширяющихся множеств
A1 -> A2 -> A3 -> ...
то её прямым пределом будет их объединение.
И наоборот, обратным пределом сужающейся цепочки множеств
B1 <- B2 <- B3 <- ...
будет их пересечение.
Все стрелки - естественные вложения множеств, само собой.
>и если сможете то расскажите также про то как п-адические числа построить с помощью обратного предела
Ну зададимся простым числом p, и будем рассматривать кольца вида Z/pk. По смыслу элемент этого кольца - это младшие k разрядов некоторого целого числа в p-ичной системе счисления. Между ними существуют естественные морфизмы проекции из больших k в меньшие, которые работают как отрезание лишних разрядов. Таким образом, получаем диаграмму
Z/p <- Z/p2 <- Z/p3 <- ...
Здесь у нас в роли частично упорядоченного множества выступает N, в котором максимального элемента нет. Пределом будет "искусственный максимальный элемент", т.е. некое кольцо Zp, которое можно было бы поставить в конец диаграммы
Z/p <- Z/p2 <- Z/p3 <- ... <- Z/pk <- ... <- Zp
Это значит, что от элемента x ∈ Zp можно при каждом k в каком-то смысле "отрезать" левую часть, чтобы получить k последних разрядов. Нетрудно понять, что это числа, бесконечные влево, т.е. целые p-адические числа.
Тебе и этого хватит. Тот же Сивухин охватывает вообще всё, что тебе в принципе может когда-нибудь понадобиться с практической точки зрения. Хотя это всё ещё не инженерный курс, со всеми вытекающими.
>Почему матфизиком стал
Сложно сказать. Поступил на физфак, поскольку всегда любил физику. А математику полюбил уже в универе. Я восхищался её стройностью и цельностью, тем, как на моих глазах выстраивают и связывают воедино всё, что я ещё со школы знал какими-то обрывками заклинаний и рецептов. Выбор кафедры матфизики был для меня естественным в такой ситуации.
>какими проблемами занимаешься, почему и т.д.
Мой научник занимается спектральной теорией дифференциальных операторов - в частности, спектром оператора Шрёдингера с периодическим потенциалом. Это имеет самое прямое отношение к ФТТ, зонной теории проводимости и всему такому - периодические потенциалы характерны как раз для кристаллических решёток, а спектр оператора Шредингера - это, по сути, множество допустимых энергий для пробного электрона. В частности, изучаются всякие пороговые эффекты, переходы из связанного состояния в свободное, гомогенизации (предельные спектры при стремлении периода решётки к нулю) с получением довольно хороших - квадратичных - оценок погрешностей, и так далее. Пока что я изучаю всю эту науку.
Хотя вообще-то есть тема, которая меня занимает с того самого момента, как я узнал, что такое квантмех и как он работает. Это динамические теории коллапса. Мне никогда не нравилось, что понятия наблюдения и наблюдателя вносятся искусственно, на уровне постулатов, что в квантмехе два фактически несовместимых друг с другом динамических принципа. Я ещё на третьем курсе, не читая никаких статей, самостоятельно пришёл к выводу, что линейное детерминированное уравнение Шрёдингера должно быть всего лишь приближением реального закона, который должен приводить в известных предельных случаях к унитарной эволюции или коллапсу. Я пытался придумать альтернативу, но ничего разумного у меня не получилось, и я со временем оставил попытки. И только сравнительно недавно я с удивлением обнаружил, что люди в мире вообще-то занимаются этой проблемой, и есть ощутимые результаты, хотя у них хватает принципиальных проблем. Вот хочу найти время и разобраться в этой теме как следует.
>>3029
Какую ещё проблему?
Квантовые компьютеры к нечёткой логике отношение не имеют никакого.
>>3036
У тебя есть некое семейство объектов, как-то связанных между собой стрелками. Объекты занумерованы элементами частично упорядоченного множества, а стрелки идут или от меньшего к большему (прямой предел), или наоборот (обратный). Если в твоём частично упорядоченном множестве есть максимальный элемент, то предел будет равен ему. Если нет, то он как бы добавит его искусственно. Т.е. в первом случае у нас пределом будет объект, в который есть стрелки из любого другого объекта, согласованные со всеми остальными. Во втором, соответственно, наоборот. Скажем, если мы возьмём цепочку расширяющихся множеств
A1 -> A2 -> A3 -> ...
то её прямым пределом будет их объединение.
И наоборот, обратным пределом сужающейся цепочки множеств
B1 <- B2 <- B3 <- ...
будет их пересечение.
Все стрелки - естественные вложения множеств, само собой.
>и если сможете то расскажите также про то как п-адические числа построить с помощью обратного предела
Ну зададимся простым числом p, и будем рассматривать кольца вида Z/pk. По смыслу элемент этого кольца - это младшие k разрядов некоторого целого числа в p-ичной системе счисления. Между ними существуют естественные морфизмы проекции из больших k в меньшие, которые работают как отрезание лишних разрядов. Таким образом, получаем диаграмму
Z/p <- Z/p2 <- Z/p3 <- ...
Здесь у нас в роли частично упорядоченного множества выступает N, в котором максимального элемента нет. Пределом будет "искусственный максимальный элемент", т.е. некое кольцо Zp, которое можно было бы поставить в конец диаграммы
Z/p <- Z/p2 <- Z/p3 <- ... <- Z/pk <- ... <- Zp
Это значит, что от элемента x ∈ Zp можно при каждом k в каком-то смысле "отрезать" левую часть, чтобы получить k последних разрядов. Нетрудно понять, что это числа, бесконечные влево, т.е. целые p-адические числа.
Интересно. А можешь посоветовать каких-то книг по математике, которые тебе понравились? Буду благодарен.
Однажды Ковалевская язвительно пошутила про скотов, с тех пор скоты не не любят Ковалевскую
>понятия наблюдения и наблюдателя вносятся искусственно, на уровне постулатов, что в квантмехе два фактически несовместимых друг с другом динамических принципа.
Не только это.
Самое дубовое что сталкивает квантмех с теорией эйнштейна это квантовая телепортация. Эйнштейн лично запретил чему бы то нибыло передаваться со скоростью света, а квантмех запутанные частицы передает чуть ли не черту на рога.
Хотя с другой стороны, эйнштейн сказал что скорость света это максимум, но не уточнил какая именно скорость света. Можно конечно с помощью максвела её вывести, но все же.
Я думал, раз "нечеткая логика" применяется в ситуациях когда ответ не очевиден, то наличие "квантового компьютера" даёт возможность "просчитать" вероятности для каждого из случаев. Буду благодарен если поправите.
просто вектор развития, который я для себя определил, "нечеткая логика-->нейронные сети.
>Мой научник занимается спектральной теорией дифференциальных операторов - в частности, спектром оператора Шрёдингера с периодическим потенциалом.
Как Сан Саныч поживает?
Рудин меня в своё время впечатлил. Если ты ньюфаг, можешь его почитать. Ещё сходу могу вспомнить Неструева, и книжку Хелемского по функциональному анализу.
>>3059
Нечёткая логика применяется к нечётким высказываниям - "на улице холодно" или "2 - маленькое число". А если утверждение на самом деле либо истинно, либо ложно, но мы просто не знаем этого наверняка - это не нечёткая логика, это байесовские вероятности. Квантовая суперпозиция имеет одинаково мало общего и с тем, и с другим.
И да, если квантовый компьютер имеет вероятностный фактор в своей работе, это ещё не значит, что он хорошо вычисляет вероятности.
>>3060
Лучше многомерным анализом, матрицами и графами займись. Для нейросетей это всяко полезнее нечёткой логики будет.
>>3064
Мимо. Тот Сан Саныч, которого я знаю, чем-то совсем другим занимается.
 17 Кб, 1091x130
17 Кб, 1091x130Записал параметрическое уравнение, проинтегрировал, но ответ не сходится. x=-/2cos(t), y=-/2sin(t), z=-/2?
При подстановке твоей параметризации в уравнения они оба должны превратиться в тождества. Проверяй.
Алсо, в задаче прямо-таки напрашивается формула Стокса.
Walter Rudin (May 2, 1921 – May 20, 2010)[2] was an Austrian-American mathematician and professor of Mathematics at the University of Wisconsin–Madison.[3]
In addition to his contributions to complex and harmonic analysis, Rudin was known for his mathematical analysis textbooks: Principles of Mathematical Analysis,[4] Real and Complex Analysis,[5] and Functional Analysis[6] (informally referred to by students as "Baby Rudin", "Papa Rudin", and "Grandpa Rudin", respectively).
> as "Baby Rudin", "Papa Rudin", and "Grandpa Rudin", re
А я думал это просто идиотский форчевский мемчик очередной.
У многих и к книгам ненависть появляется, из-за того, что марьванна заставляла Тургенева читать. Так что ж теперь? Их можно только пожалеть.
ХЗ, у меня в школе было полное безразличие к точным наукам вообще, а вот после вуза как понеслооо
Двачую на счет Евклида. Повторяю все с низов, учитывая, что в детстве ненавидел Геометрию из-за кучи теорем по сравнению с той же Алгеброй в школе. Как все это переваривать? Не беря в счет очевидные вещи, конечно же.
Лучше всего вот так http://aleph0.clarku.edu/~djoyce/java/elements/elements.html
Ещё лучше взять что-нибудь посовременнее
>Почему простые числа считаются такими важными?
Вопрос к профессорам из /math от завсегдатаев тупых вопрос треда из /b.
Простые числа образуют мультипликативный базис целых чисел. Свойства любого целого числа сводятся к свойствам простых сомножителей этого числа. Поэтому изучение целых чисел = изучение простых чисел.
Это как молекулярно-кинетическая теория в физике. Целые числа состоят из простых чисел так же, как физические тела состоят из атомов и молекул.
Охуеть. Мерси и дай Перельман тебе здоровья.
Вы ебанутые? Не лезь, она тебя сожрёт блядь! Загугли что такое движение, их классификацию. Всё! Дальше берешь линейную алгебру.
>А можно построить обучение математики так, чтобы возникали когнитивные диссонансы
Дык оно всегда такое, собственно. Интереснее построить обучение математике так, чтобы диссонансов не было.
А что дальше расписывать то? Это вторая производная, по-видимому от температуры, по х-координате. Определяет выпуклость/вогнутость температурного профиля. Давай конкретный пример, в общем, тогда и подскажем тебе чего-то поконкретнее.
Подмножество - это когда мы из множества берём часть элементов. Из любого множества можно взять ничего.
Каким образом? Если нам нечего брать, то мы не можем ничего доказать по определению, т.к. определение завязано именно на этом. Допустим, А – пустое множество, а так же А⊂В. Тогда ∀х (х∈А⇒х∈В). Но А=∅, ∄х∈А
В чем я неправ? Не понимаю.
Квантор всеобщности сам по себе не привязан ни к какому множеству. Для любого x - значит вообще для любого x. Всякий раз, когда какой-нибудь x принадлежит A, он принадлежит и B. Это выполнено для А=∅.
> Квантор всеобщности сам по себе не привязан ни к какому множеству.
Я понимаю, но он привязан к определению подмножества ведь. Через это подмножество определяется.
> Это выполнено для А=∅.
Можно понятнее как-то объяснить? Вообще не понимаю. Это ломает мне сознание.
> Всякий раз, когда какой-нибудь x принадлежит A, он принадлежит и B.
Но в нашем случае ∄х (х∈А⇒х∈В), следовательно, условие ведь не может выполняться.
>но он привязан к определению подмножества ведь
Нет. У тебя есть выражение, ∀х P(x). Ты не знаешь и не обязан знать, какая семантика у предиката P(x) и как он вообще устроен. Ты вообще можешь понятия не иметь, что у тебя есть какие-то A и B. У тебя есть чёрный ящик, который умеет принимать на вход какой-то объект и говорить в ответ "да" или "нет". И написанное выше означает просто, что чёрный ящик всегда скажет "да", что бы ты ему ни подсунул. Объект может быть абсолютно любым, который допускается твоей теорией. x = ∅, x = {∅}, x = π/1488!, x = Александр Гротендик. Всё что угодно. И всё это сработает, потому что если в импликации предпосылка ложна, то это автоматически делает всю импликацию истинной.
>>3129
>∄х (х∈А⇒х∈В)
Wrong.
∄х х∈А
но
∀х (х∈А⇒х∈В)
Второе, между прочим, следует из первого.
Все равно непанятна. Кстати, я так же не понимаю, почему импликация с ложной посылкой истинна и как этим можно обосновать истинное следствие из этой посылки, ведь если следствие ложно, то, опять же, импликация истинна.
> Wrong
Но каким образом? Почему?
> ∄х х∈А
> но
> ∀х (х∈А⇒х∈В)
Но такого не может быть, если не существует никакого х. Нечем просто. Ну вообще. Любые попытки представить себе это просто невозможны.
>Кстати, я так же не понимаю, почему импликация с ложной посылкой истинна
Потому что импликация всегда работает в связке с квантором всеобщности.
∀х (P(x)⇒Q(x))
Если бы импликация при ложной предпосылке была ложной, то все выражения такого вида были бы ложными, если только оба предиката не являются совсем уж тавтологиями. Кроме того, если ты попробуешь написать какую-то другую таблицу истинности для импликации, то очень быстро поймёшь, что так быть не может.
>не существует никакого х
Существует, вот он: x = ∅. Это как минимум. В твоей теории присутствует пустое множество, раз ты о нём рассуждаешь. А если у тебя есть ещё какие-то правила конструирования множеств из уже существующих, то иксов у тебя вообще целая куча. Правда, ни один из них не является элементом A, но это ничему не мешает.
> Если бы импликация при ложной предпосылке была ложной, то все выражения такого вида были бы ложными
И как этим можно обосновать использование импликации с ложной посылкой в качестве получения истинных утверждений?
> Кроме того, если ты попробуешь написать какую-то другую таблицу истинности для импликации, то очень быстро поймёшь, что так быть не может.
А нельзя просто избавиться от этих дурацких парадоксов, дав какое-то более качественное определение?
> Существует, вот он: x = ∅. Это как минимум.
Тогда х∈А⇒∅∈∅⇒∅={∅}, что противоречит аксиоме регулярности.
> то иксов у тебя вообще целая куча
Но мы же допускаем, что А=∅, значит их просто нет. Мы ничем не оперируем. Вообще.
>И как этим можно обосновать использование импликации с ложной посылкой в качестве получения истинных утверждений?
Понятия не имею, о чём ты.
>А нельзя просто избавиться от этих дурацких парадоксов, дав какое-то более качественное определение?
А ты попробуй, говорю же. Возьми и попробуй определить импликацию как-то по-другому. Вариантов-то всего 16, их легко перебрать и убедиться, что больше ни один из них импликацией быть не может.
> Тогда х∈А
Нет.
У тебя не написано ∀х (х∈А). Это неверно, причём не только для A = ∅. Множества A с таким свойством вообще не существует.
У тебя написано ∀х (х∈А => х∈В). Это совершенно разные вещи.
Но нету ведь такого х, чтобы было х∈А => х∈В. По сути х вообще не принадлежит А. Ибо в А вообще нет элементов. Ну не существует такого х, чтобы принадлежал А. Значит и не существует такого х, принадлежащего А, который принадлежал бы и В. Значит условие не выполняется для пустого множества.
>Но нету ведь такого х, чтобы было х∈А => х∈В
Абсолютно любой x, который ты в состоянии придумать. Например, x = ∅.
>По сути х вообще не принадлежит А
Кажется, до тебя начинает доходить. Осталось только осознать, что в выражении (х∈А => х∈В) ничего не говорится о том, что x должен принадлежать A.
> больше ни один из них импликацией быть не может
Мне кажется, что тебе промыли мозги, и любую самую интуитивно очевидную логику ты отрицаешь. Либо я в ∅ тупой. Т.е. импликация, которая содержит в себе суждения, которые связаны между собой, импликацией быть не может? А то некоторые доказательства таки даются в стиле "у меня большой пенис"→"я еб@л твою жену".
> Например, x = ∅.
В таком случае (х∈А => х∈В) – противоречит аксиоме регулярности, та БЛДЖАД.
> Осталось только осознать, что в выражении (х∈А => х∈В) ничего не говорится о том, что x должен принадлежать A.
Допусти, что он НЕ ПРИНАДЛЕЖИТ А, тогда бессмысленно говорить о подмножестве, т.к. его нет нихера.
А мне ничего не кажется. Я ясно вижу, что ты не понимаешь очевидных вещей. Это, однако, ещё не значит, что ты тупой, хоть и повышает вероятность подобного. И нет, когда я говорю "возьми и сделай", это не фигура речи. Я действительно предлагаю тебе убедиться самому. Разве так сложно нарисовать 16 вариантов таблицы 2x2, внимательно на них посмотреть и закрыть для себя этот вопрос раз и навсегда?
>тебе промыли мозги
Воу, палехчи. Сегодня ты пишешь, что мне промыли мозги кто и зачем, интересно?, а завтра разоблачаешь еврофашистский заговор оффициальной науки и рисуешь православные таблицы электроатомов русов. Аккуратнее с этим дерьмом.
>>3138
>противоречит аксиоме регулярности
Не противоречит. Нигде не утверждается, что ∅ ∈ ∅. Из (х∈А => х∈В) это никоим образом не вытекает.
>Допусти, что он НЕ ПРИНАДЛЕЖИТ А, тогда бессмысленно говорить о подмножестве
Для любого множества найдутся элементы, которые ему не принадлежат. Что ж теперь?
> Я ясно вижу, что ты не понимаешь очевидных вещей.
Мне кажется, что это совсем не очевидные вещи. Тут сознание уже крошится.
> И нет, когда я говорю "возьми и сделай", это не фигура речи. Я действительно предлагаю тебе убедиться самому.
То же самое с этой хуйнюшкой (х∈А => х∈В)? Да, я действительно не понимаю, как может образоваться подмножество из ничего. По твоей логике ∀х (х∈А⇒х∈В) – совсем не противоречит тому, что ∄х∈А. Но если ∄х∈А, то х∈А⇒х∈В неверно, только потому, что х∈А не выполняется никак. Не из чего составить множество. Значит не существует никакого х∈А. Не существует его. Это точно, 100%. Значит уже такая херня под определение не подходит, поскольку нарушается его целостность.
> Но если ∄х∈А, то х∈А⇒х∈В неверно, только потому, что х∈А не выполняется никак.
Ему и не обязательно выполняться, чтобы импликация была верной.
>Не из чего составить множество
Так в нём и нет элементов, всё правильно. На то оно и пустое.
Смысл в том, что, ЫЫЫААААА!!!!(эх), получается, что х(не принадлежит)А⇒х∈В. Это уже не определение подмножества, а что-то другое совершенно.
Это действительно совсем другое утверждение, и оно не имеет никакого отношения к нашей ситуации. Я тебе объясняю, что именно ИСХОДНАЯ импликация (х∈А⇒х∈В) истинна ровно потому, что x ∉ A, независимо от того, верно ли х∈В или нет. Ложность условия автоматически влечёт истинность импликации, всегда.
И да, я понимаю, что если ∄х∈А, то это еще не значит, что ∄х∈В. А так же я понимаю, что ∀х (х∈А⇒х∈В) при ∄х∈А не становится неверным, ибо В может включать в себя разные х(но может и не все), однако что-то мне интуитивно подсказывает, что в этом есть некоторые неточности, а может и противоречия. Выглядит как-то слишком странно, но никаким образом не могу объяснить внятно, что именно меня смущает. Я привык к точным определениям, а это какое то не такое. И даже не могу объяснить в достаточной степени, что меня смущает.
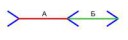 3 Кб, 620x201
3 Кб, 620x201Это обычное когнитивное искажение, вроде пикрелейтед. Человек, который до этого с таким не сталкивался, и не имеет математической культуры, будет убеждать окружающих, что красный отрезок длиннее. И сколько бы ты ни прикладывал линейку, его это не убедит. Пустое множество действительно устроено несколько шиворот-навыворот с точки зрения житейского здравого смысла, но с точки зрения логики здесь всё в порядке, никаких противоречий и неточностей нет. Похожие предрассудки многие века мешали людям придумать позиционные системы счисления - для этого нужна цифра ноль. Но ведь ноль - это "ничего", а как "ничего" может быть цифрой, т.е. "чем-то"? Ты про ноль знаешь с детства, поэтому у тебя он не вызывает такого диссонанса, как у людей в античности. А вот базовую теорию множеств в начальной школе не проходят, увы. Поэтому у многих проблемы с осознанием некоторых тривиальных вещей. Как это, чётных чисел столько же, сколько и всех натуральных чисел? Так не бывает, мне здравый смысл подсказывает. Ну и что, что биекция? Не убедительно! И только привычка позволяет перестать воспринимать подобные вещи в штыки, и выработать здравый смысл, адекватный математической реальности.
(А⊂В) = ∀х (х∈А⇒х∈В)
Больше всего проблема именно в том, что ∄х∈А.
> Как это, чётных чисел столько же, сколько и всех натуральных чисел? Так не бывает, мне здравый смысл подсказывает. Ну и что, что биекция? Не убедительно!
Это я сразу понял, без всяких проблем. Понял и запомнил. А тут ни с чем интуитивным связать не могу. Обычно связываю с чем-то таким, что может нести похожий смысл, а тут вообще беда.
Мне нужно какое-то более подробное доказательство, чтобы разжевывало на пальцах. Есть какая-то тавтология к ∀х (х∈А⇒х∈В)?
> Но ведь ноль - это "ничего", а как "ничего" может быть цифрой, т.е. "чем-то"?
Я могу согласиться с тем, что А/А=∅, но не совсем могу согласиться с тем, что пустое множество является подмножеством любого множества.
Пусть А не подмножество множества В, тогда в А есть элемент x, который не принадлежит B.
В пустом множестве нет элемента, который не принадлежал бы любому множеству. Тогда пустое множестве является подмножеством любого множества.
Пусть каждый элемент x, являющийся элементом множества A, является элементом множества B. Но если A пусто, то не существует такого x, что принадлежит A, и высказанное только что утверждение ложно. Что на это можно сказать?
Тут вся суть в том, что по определению подмножество какого-то множества является совокупностью объектов, которые находятся в этом каком-то множестве. Но если в подмножестве нет объектов? Вот этого я и не могу понять.
Ты заебал.
>Пусть каждый элемент x, являющийся элементом множества A, является элементом множества B.
Да, тогда А - подмножество В.
>Но если A пусто, то не существует такого x, что принадлежит A, и высказанное только что утверждение ложно.
Если в А нет такого х, тогда в В нет такого же х. Всё! Это не значит, что утверждение ложное.
>привести
Вернее, доказать, что контрпример существует.
А то попросят тебя контрпримеры к получающимся выбором утверждениям наприводить.
Ну это я и подразумевал под "можно".
Каждое утверждение об элементах пустого множества истинно.
Для любого предиката P каждый элемент пустого множества обладает свойством P. Множество всех автобусов на Марсе пусто. Поэтому каждый автобус на Марсе красный. Кроме того, каждый автобус на Марсе не красный. Каждый элемент пустого множества равен сам себе, а также не равен сам себе. Это называется vacuous truth.
Каждый элемент пустого множества принадлежит A. Кроме того, каждый элемент пустого множества не принадлежит A.
> Если в А нет такого х, тогда в В нет такого же х.
> каждый элемент x, являющийся элементом множества A, является элементом множества B.
Все равно что-то не дает мне покоя... Каждый элемент х, не являющийся элементом А, может являться элементом В тамщето, ты неправ.
> Для любого предиката P каждый элемент пустого множества обладает свойством P.
Это утверждение ложно, т.к. в пустом множестве нет элементов, это значит, что нет элементов, обладающих свойством Р. Дальше там ахинея пошла.
И хули?
>Если в В нет такого х, тогда в А нет такого же х.
Если А - пусто, то никакого противоречия тут нет, т.к. в А нет никакого элемента, который не принадлежал бы В.
1. Утверждение A→B равносильно утверждению ¬A ∨ B.
2. Отрицание утверждения A→B равносильно утверждению ¬(¬A ∨ B), что, в свою очередь, равносильно утверждению A ∧ ¬B.
3. Утверждение P∧Q→P - аксиома.
Рассмотрим утверждение ∀x(x∈M → P(x)).
Оно равносильно утверждению ∀x(¬x∈M ∨ P(x)).
Это утверждение ложно тогда и только тогда, когда ∃x(x∈M ∧ ¬P(x)).
Из этого утверждения следует, что ∃x(x∈M).
Пусть M = ∅. Это значит, что ¬∃x(x∈M).
Теорема. ∀x(x∈M → P(x)) для любого P.
Доказательство.
Предположим, что ¬∀x(x∈M → P(x)).
Значит, ∃x(x∈M ∧ ¬P(x)).
Значит, ∃x(x∈M).
Пришли к противоречию. Предположение ложно.
Значит, ∀x(x∈M → P(x)).
Воспользуюсь тем же
А пм В, если ∀x ∈ A -> x ∈ B - верно
Т.к. 0 -> 1 - верно, то пустое множество явл. подмножеством любого множества.
ТА СУКА, ТЫ СЛЕПОЙ. О подмножестве А можно сделать такие утверждения:
В А нет никакого элемента, который принадлежал бы В.
В А нет никакого элемента, который не принадлежал бы В.
Как ни крути, нет в них таких элементов.
Далее.
Если А включено в В, то каждый элемент А принадлежит В. Но если А не содержит в себе элементов, то В не принадлежат никакие элементы А, т.к. их там НЕТ. Можно сделать только один вывод: А не является подмножеством В.
Слышь блядь, ебало на ноль, пидор.
А - подмножество В, если каждый элем. А принадлежит В => А не подмножество В, если в А есть элемент, который не принадлежит В. Т.к. в пустом множестве нет элемента, который не принадлежит В, тогда пустое не является НЕ ПОДМНОЖЕСТВОМ. 3-тьего варианта есть, остается только ПОДМНОЖЕСТВО.
Т.е. то, что элементов нет – тебя это никак не волнует? Само понятие пустого множества противоречиво. Как и понятие множества, включающего все множества, которые не включают сами себя.
Если в А нет элементов, то утверждение: если х лежит в А, то х лежит в В, не будет ЛОЖНЫМ, оно будет ложным, только если х лежит в А, но х не лежит в В(1 → 0 | гугли импликацию)
>понятие пустого множества противоречиво
ПАШОЛ В ЖОПУ МУДАК!!1
ТЫВ ГГОВНО ГОВНО ОБДРИСЛЫЙ КАЛ ВОТ ТЫ КТО!!!1
Этот со своими абсрактными импликациями всякими с ума сходит. Это нужно доказывать с содержательной точки зрения, раз формально, как ты говоришь, шиворот навыворот определено
Как ты заебал, просто доебали твои ахуительные истории.
Множество - фигура на плоскости. Если фигура_1 лежит внутри фигуры_2, то множество_1 явл. подмножеством множества_2. Пустое множество это фигура из 0 точек. Она может находится внутри любой фигуры.
Я нихуя не говорю.
Определение быть подмножеством можно дать через не_быть подмножеством и через это определение не_быть подмножеством легко показать, что пустое множество - подмножество любого множества. Что я в общем-то выше и писал. Если хочешь строгости, то юзай импликацию.
Что за шизофрения)) и лучше было бы дать определение такое: если отрезок А лежит на прямой В, то множество точек А включено в В. Но как ноль точек может быть включено в множество? Ты что несешь? Чтобы множество было включено в другое, то оно должно из чего-то состоять, блядь. Это из определения следует.
Так вот в том и суть, что в двух определениях ничего не выходит. Я понимаю вашу точку зрения, но что делать с теми вот элементами в определении??
А - подмножество В, если каждый элем. А принадлежит В => А не подмножество В, если в А есть элемент, который не принадлежит В. Т.к. в пустом множестве нет элемента, который не принадлежит В, тогда пустое не является НЕ ПОДМНОЖЕСТВОМ. 3-тьего варианта нет, остается только ПОДМНОЖЕСТВО.
Где? Всё подходит.
>>3183
>Но как ноль точек может быть включено в множество? Ты что несешь?
Без задней мысли. Причем может включено даже в самого себя.
Я тебе теперь по начальному определению толкую, дура4ок.
Если А включено в В, то каждый элемент А принадлежит В. Но если А не содержит в себе элементов, то В не принадлежат никакие элементы А, т.к. их там НЕТ. Можно сделать только один вывод: А не является подмножеством В. И дальше ни о каких элементах речи идти не может.
Ладно, заебал. Смотри:
Пусть А - не_подмножество В. Добавим туда элемент из B. A+{b} будет подмножеством В? нет
Теперь представим, что 0(пустое) все же не подмножество А, добавим туда элемент из A: 0+{a}, тогда 0+{a} не должно быть подмножеством А, но оно подмножество А, тогда предположение, что 0 - не подмножество НЕ ВЕРНО.
Не, нихуя, я не про это толкую. Мы рассматриваем ситуацию не во времени, тут или/или, третьего/четвертого не дано. Аналогия с брадобреем. Брадобрей бреет всех, кто не бреет себя сам. Бреет ли брадобрей сам себя? Вы просто стараетесь упростить все формальным методом. Получается, что он в любом случае себя не побреет, потому что это нарушит его нерушимое правило. Но тут вне времени, он себя или бреет, или нет. Точно так же и тут. Порочный круг начинается на определении, на понятии элемента.
Здесь нет никаких проблем.
> А не подмножество В, если в А есть элемент, который не принадлежит В. Т.к. в пустом множестве нет элемента, который не принадлежит В, тогда пустое множество подмножество любого множества.
Ты смотри там, дальше, от равномощности квадрата и отрезка не охуей.
 1,2 Мб, 1080x1920
1,2 Мб, 1080x1920Какая-то методичка преподавателя по дискретке. Там задали прорешать несколько номеров, а вот как их делать (по диаграммам Вена / просто упрощать) не объяснили.
Меня тут смутило только умножение в 17 примере. Скорее всего это пересечение, но точно я не уверен. А ещё какие-то условия даны?
Нет, не даны. Задание гласит: "Упростите выражения.", не слова больше. Меня вот интересует одно, к пересечениям и объединениям можно применять те же упрощения, что и к логич. выражениями с дизъюнкцией, конъюнкцией?
Ой, всё. Если ты просишь объяснений, получаешь их, а потом игнорируешь и продолжаешь нести ту же самую хуйню по десятому кругу, то тебе здесь не место. Пиздуй в тред к предельному дебилу, вы с ним явно найдёте общий язык.
>Порочный круг начинается на определении, на понятии элемента.
А теперь приведи мне определение элемента. Я тебе несколько написал простым языком, почему пустое множество подмножество любого множества, но ты продолжаешь копротивлятся, не хотя поменять в своём манямирке определение быть подмножеством на эквивалентное не быть подмножеством, из которого легко получить обоснование твоего вопроса.
Кардинал множества натуральных равен кардиналу множества четных. Элементарно, 2=21, 4=22, 2n=2*n, ... Далее по индукции заключаем, что каждому четному числу можно сопоставить натуральное. С отрицательными - по аналогии.
Я мимо проходил, если что
f(n) = 2n - биекция.
> конкрит матматикс
Не слушай, не читай это говно. Книга очень сложная, но не своими концепциями (любой школьник эти концепции способен осилить, я не преувеличиваю), а тем, что:
1) написана как художественный текст, т е там нет нормального математического изложения в стиле "определение-теорема-доказательство", читать очень тяжело и неприятно;
2) это по сути сборник школьных (именно школьных) олимпиадных задач на определенную тематику. Если хочешь именно получить базу для изучения computer science, гугли mit mathematics for computer science. Задачи там реально для даунов погромистов, вся нужная теория есть и излагается намного лучше.
> сикп
Эх, щас бы на scheme писать в 2017...
Никогда не слушай тех, кто советует типа "классические" книги: Демидовича, Кнута, Рудина и т. д. Это люди с мышлением "деды говно жрали и мы будем". В 2017 году надо думать не о том как разорвать себе жопу олимпиадными задачами, а о том, как побыстрее изучить нужные и интересные разделы, потому что доступной информации слишком много и естественным состоянием для тебя должно быть "бля, я не успеваю изучить такие-то и такие-то штуки", а не "бля, я не могу решить пример номер 1488 из Демидовича".
>Никогда не слушай тех, кто советует типа "классические" книги: Демидовича, Кнута, Рудина и т. д.
А шо по анализу чтать??77
Ну зависит от целей. Если тебе нужен учебник для прикладников, то хз, не могу ничего подсказать. Если для математиков, то Pugh: Real Mathematical Analysis и Львовский: Лекции по математическому анализу. Львовский сложнее намного и упражения там очень хардкорные, советую их просматривать и пытаться решать, но отступаться от задачи, если не получилось решить за n минут.
Хотя, если ты ньюфаг и не привык по несколько дней думать над задачей , а потом все равно не решить, то можешь пытаться все подряд решать, чтобы жопу натренировать.
>>3210
>В 2017 году надо думать не о том как разорвать себе жопу олимпиадными задачами
Мань, олимпиады хорошо смекалочку развивают, в матеше без этого никак.
>а о том, как побыстрее изучить нужные и интересные разделы
Это какие? Гомологии? Топологии? Или что там популярно у школьников? Ах да, вспомнил, сейчас популярны модули на кольцами.
Может, перечислишь те разделы в которые надо вкатиться быстро, решительно?
> Гомологии? Топологии?
Как вариант.
> Может, перечислишь те разделы в которые надо вкатиться быстро, решительно?
"Надо" - это очень субъективное понятие, не хочу никому ничего навязывать. Если тебе надо круто решать олимпиады - дрочи Конкретную Математику, в этом плане книга хорошая, тут не поспоришь.
А счет для быдла. Математики выше этого. Интегралы это математический спид, топология это жопоебля, все в теорию множеств.
> математики не считают нихуя, а просто доказывают теоремы. А счет для быдла. Математики выше этого.
То есть ты это до сих пор не осознал?
Математики считают, ты просто лицемерный лжец.
Сигма_р и u - функции, которые надо найти.
h - известная функция.
А вот что значит d(sigma_r h)/dr не пойму. Это производная от двух функций или что? Никогда такого не видел.
>Мань, олимпиады хорошо смекалочку развивают, в матеше без этого никак.
Как же раньше без олимпиад смекалочку та развивали, и не понять!
Ты хочешь вернуться к образу жизни безолемпиадных дидов, ирод?!
Как скажешь. Теперь уёбывай.
спасибо
Так какова же она, идеальная система конспектирования в 2017 году? Какой workflow и сочетание инструментов обеспечит максимальное удобство?
Недостатки уже названы.
 13 Кб, 803x441
13 Кб, 803x441Я веду не конспекты, а дневник, в котором пишу все что меня удивило/показалось интересным, что вызвало сложности и т д. Каждое определение/теорему не вижу смысла записывать. Дневник в техе пишу.
> набирать текст сразу в LaTeX это пиздец,
Нет, почему? Придрочиться просто надо.
> к тому же иногда бывает удобно накорябать какой-нибудь рисунок от руки и т.п.
Рисую от руки -> фоткаю -> посылаю фотку сам себе в вк -> includegraphics.
Алсо, для скорости я стараюсь использовать слова вместо формул тогда, когда это возможно.
Еще я сейчас прочитал твой пост и подумал, что для удобства поиска в будущем можно ставить тэги в духе [гамалогии], [тапалогии] и т д. Пока что не ставлю, потому что не так давно начал и у меня пдфка страниц 50.
Пробовал писать конспекты - пришел к выводу, что это неоправданная трата времени. Обычно читаешь разные книги + википедию + math.stackexchange, обозначения везде разные, порядок изложения разный и получается так, что приводить все к своим обозначениям и своему порядку изложения - это слишком большая трата времени, которая точно не будет оправдана, если нет цели написать свой учебник. Запоминание должно происходить за счет обдумывания и решения задач, а не за счет того, что ты пишешь.
Без них и сейчас можно обойтись.
Да. Что открытые в открытые - очевидно, а пример открытого множества, прообраз которого не открыт, [0;pi). Открытого в индуцированной с R топологии, конечно.
> Что открытые в открытые - очевидно
Для меня это только геометрически очевидно. Но в принципе, формально я это доказывать не хочу, поэтому и попросил проверить. Спасибо.
Пикрелейтед 1 сейчас писал, 2 и 3 - старое с картинками. Утверждения на 2 и 3, конечно, не заслуживают, чтобы я их записывал, просто я хотел сохранить картинки, которые придумал для иллюстрации.
Кстати, я сейчас не могу понять, почему верно то, что я писал на пикрелейтед 2 и 3, вроде там хуйня какая-то.
Хотя не, все правильно.
А ящик все равно через вольфрам с маткадом решают.
Ну что ж, попытаюсь.
Компакт, конкретно здесь, в R - это замкнутое и ограниченное множество.
Пересечение произвольного набора замкнутых множест - замкнутое. (В силу правиладе моргана и топологического свойства, что произвольное объединение открытых - открыто.)
Значит прообраз _любого_ замкнутого множества - замкнут.
Значит прообраз _любого_ открытого множества - открыт.
Что является определением непрерывности f. Д-но.
Ок, я просто так хуйню сказал, чтобы выебнуться, я был не прав.
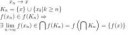 4 Кб, 379x105
4 Кб, 379x105Мог просто в отдельной вкладке пикчу открыть. Ну да ладно.
Открой в новой вкладке.
В стрелке на 3 строчке ошибка. Откуда следует, что предел существует? По твоему рассуждению получается, что для любой сходящейся последовательности {x_n} сходится {f(x_n)}.
Из того, что f(Kn) - это последовательность вложенных компактов, имеющая своим пересечением одну точку.
 21 Кб, 1117x172
21 Кб, 1117x172Найти площадь, ограниченную этими линиями
• y=7x-2x^2; x+y=7/2
Или то же задание, но функции такие:
• y=-x^2; y=2e^x; x=0; x=1 (тут у меня даже на графике ебучая фигура не получается, потому что -х^2 и 2е^х не пересекаются бляяяяять)
Не, все, я пожалел, что тебе ответил. Одно дело, если бы ты по невнимательности ошибку допустил, но ты же вообще хуйню пишешь.
Разница, по нормально вродеп дополнение называется.
A={1,2,3,4,5}
B={3,4,5,6,7}
A/B={1,2} Типа как откусили кусок общий от A.
> Нет, почему? Придрочиться просто надо.
А пишешь ты прямо в живом латехе, каким-нибудь емаксом? Даже без всяких щадящих обёрток типа маркдаун + MathJax?
В обычном текстовом редакторе пишу (sublime text), потом компилирую через консоль.
Спасибо большое
> Ну и катись со своей домашкой, мне-то что.
Ну я-то уже решил, захотел поделиться интересной задачей. Если никто не решит, через 3 дня запощу решение.
Чего там решать-то, она элементарная.
Тебе бы, прежде чем в непрерывные дроби лезть, с элементарной алгеброй разобраться. С тем, что такое деление, например.
Так и есть, это свойство в пятом классе проходят. Разделить на a/b - то же самое, что умножить на b/a.
Двачематики/таполаги/гамолаги/модульщики над кольцами, каждый век в истории человечества был веком какого то математика.
Например ньютон довил в 17 веке, эйлер в 18, гаусс в 19, в 20 сложно кого то выбрать, так как оттуда некоторые до сих пор шевелятся.
Так вот, стоит ли читать высеры этих величайших математиков? Сейчас они имеют какую то познавательную ценность? Или васян из международного института по строению и изучению ящиков для песка может в сто раз лучше написать?
>Сейчас они имеют какую то познавательную ценность?
Да
>Васютко из МИСИЯДП может в 100 раз лучше написать?
Да
Противопоставлять эти вопросы некорректно. 'Познавательная ценность' скорее историческая, ты можешь наблюдать за развитием науки и мотивировками, что подчас полезно для более глубокого понимания предмета. Использовать как учебники конечно же не стоит.
Это я про архаическое говно мамонта, а вот 20 век сюда приплетать не стоит
>Использовать как учебники конечно же не стоит.
На самом деле стоит. Тот же Фихтенгольц - пересказ Коши, только хуже.
http://rgho.st/8GXhPgjNz
Притом у Коши часть теорем неверна. На свалку истории. Хотя, можно Харди навернуть, он по чистой матеше угорал.
Примеры неверных теорем быстро, решительно.
Переведи в синусы косинусы pi/3, может поможет.
Чего так?
Жан Реле! Потому что пучки придумал! ВСЁ ПУЧКОМ! ПУЧК ПУЧК
Я не математик, я студент механик. Поэтому у меня есть некоторые сложности.
Я решаю задачи устойчивости систем. Не суть важно, что я там делаю, в механику посвящать не вижу смысла.
Суть решения сводится к получению некоторой системы уравнений. Эта система имеет бесконечно много решений. Решения я ищу, приравняв определитель матрицы уравнений к нулю.
Но мне нужен первый корень, то есть первая форма потери устройствости.
Функция root в маткаде и матлабе ищет корень на некотором промежутке. Но не ищет первый.
Короче, как всегда находить первый корень?
Желательно с примером.
Квадрипл, лол.
Внезапно, твой пост указывает на то, что все ЧЕСТЫИ МОТИРМОТИКИ угоряющие по АЛГУБРИОЧИСКАЙ ГОЕМЕТРИИ И ТЕПЛОГОИИ неправы, когда говорят, что математики не считают, и называя считающий людей инжинерами. Поскольку, инжинеры постоянно приходят к математикам для решение уравнений.
Математики считают, запомни это юнный ВРОТЕНДИК.
Первый попавшийся на глаза.
Первый в смысле первый. Да, наименьший.
Я не шарю в матлабе (дрочу на Mathematica), но, например, можно поискать нужную тебе функцию, которая найдет все корни. Например такая https://www.mathworks.com/help/symbolic/vpasolve.html
А потом отсортируешь корни
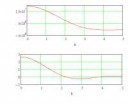 10 Кб, 507x414
10 Кб, 507x414Ну, я вот не понимаю откуда взялись все эти дискриминанты, 4ac и почему они вообще существуют и появились. И зачем нужны квадратные уравнения, собственно.
почитай Гашков "квадратный трехчлен для умственно отсталых"
Берешь первую производную.
В точках в которых эта производная превращается в ноль это точки минимума/максимума.
Берешь еще одну производную а точках в которой первая производная стала нулем, чтобы узнать это локальный или глобальный минимум/максимум и что это именно, минимум или максимум.
Задача уровня того же ящика.
Возьми значение, которое заведомо меньше, и начинай искать от него, постепенно сокращая отрезок.
Может, можно под твою задачу придумать что-то типа метода монте-карло, который выдаст самое низкоэнергетическое решение, но в общем случае - только так.
>>3351
Окружность с отрезком сначала перемножь, а потом подумай.
Это всё понятно. Мне как численно ловить.
>Окружность с отрезком сначала перемножь, а потом подумай.
Представил себе окружность в центре кординатной плоскости. Потом добавил ещё одну ось, которая представляет множество точек прямой. Умножил -- получил цилиндр. Подумал. Не получилось представить.
Бери отрезок и запускай решатель. Нашёлся корень - уменьшаешь отрезок. Не нашёлся - сдвигаешь вперёд. И так до победного.
Предлагаешь скрутить цилиндр, который получился в результате умножения окружности на прямую, так, что получится тор?
Короче, для моей задачи я тупо построил график по точкам. Посчитал пару десятков значений критической силы, и построил график. Не знаю, примет ли препод, лол. Зависимость всё равно явно видна.
Вот мне нужно найти синус угла 17 градусов, как мне его расссчитать без рисования треугольника/единичной окружности и без таблиц с калькулятором? Есть какой то финт ушами позволяющий хотя бы первые правильные пять знаков после запятой получить?
Ряд Тейлора есть, но оно того не стоит. Гугл всяко лучше.
На руках проще всего через треугольник.
Подскажите книги по терверу/матстату. Тервер читаю Ширяева сейчас, в теоретическом плане все устраивает, но слишком сухо что ли. Хотелось бы параллельно читать что-нибудь более наглядное, с интересными задачами и тп. По матстату вообще хз что читать. Можно на ангельском. Бэкграунд 3 курса мехмата.
Ты можешь надрочить только решение однотипных задач по однотимным алгоритмам. Так что нет.
А можно подробнее про уровни.
y=1/(t-t^3)
Нужно построить график этой параметрической функции. В условии не сказано, чем принадлежит t.
В школе так и делают
 2 Кб, 489x44
2 Кб, 489x44помогите пожалуйста, возможно ли исключить t из двух уравнений, задающих движение точки. Или во втором уравнении слишком много косинусов, синусов и корней и выразить из этой системы траекторию в явном виде невозможно?
что значит треугольная система? да, там ошибка, перед корнем там должна быть дробь 7/8
Это значит, что тебе не нужно выражать t из второго уравнения, чтобы его исключить из системы.
Вырази косинус и синус через x и y.
я понимаю, но у меня так не получается со вторым уравнением
первое можно переписать в виде:
cos(3\pi t)=40x-1;
и если удастся из второго уравнения выразить синус, то можно оба уравнения возвести в квадрат и сложить,
но второе уравнение в таком виде переписать у меня не выходит, и я не знаю, возможно ли его в принципе так переписать.
Так подставь выражение для косинуса во второе уравнение, а потом спокойно вырази из него синус.
 661 Кб, 744x800
661 Кб, 744x800Хочу познать азы геометрии за 7-9 класс, посоветуйте авторов или хороших книжек, и задачник к нему если можно. Обидно что нет в интернете таких кошерных учебников по геометрии как алгебра по Мордковичу.
Дайте задачник какой то, в котором бы пояснялся ход решения и почему правильный ответ такой как указанно.
Решебников мало, а вот задачников много. Просто китайцы прорешали ВСЕ здачи из Демидовича. Поэтому такой набор будет полным.
Бля, почему в 1 томе Кострикина издания 2000 и 2004 года столько опечаток? В остальных томах такого нет надеюсь?
А что за антидемидович? В поиске рядом с китайским решебником встречается.
Никто не смог решить задачу для 1 курса, пощу свое решение. B(x, eps) означает открытый шар радиуса eps с центром в x (метрика стандартная).
Я думаю, тебе рано изучать пространства, в которых не выполняется первая аксиома счетности. Ты программу 1 курса не осилил.
А может, просто ты не осилил моё доказательство. Подумай об этом, сынок.
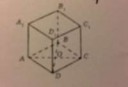 18 Кб, 604x415
18 Кб, 604x415 2 Кб, 402x83
2 Кб, 402x83А хотя, в принципе, тоже не очень интересно. Но уже что-то.
Пусть A - множество всех функций из R в R.
Топологическое пространство X - это множество A с топологией, порождённой базой {Uh(f)} со всевозможными f∈A и h: R -> R>, принимающих строго положительные значения во всех точках, кроме может быть счётного их числа.
Топологическое пространство Y - это тоже A, но с дискретной топологией.
Отображение φ: X -> Y работает как тождественное на A.
Ясно, что непрерывным оно не будет. Проверим условия задачи. Второй пункт очевидно выполнен, осталось проверить, что компакты переходят в компакты. В Y компактами являются конечные множества и только они. Докажем, что то же самое справедливо и для X. Пусть S ⊆ X - какое-то бесконечное множество. Предъявим его покрытие открытыми множествами, из которого нельзя выбрать конечное подпокрытие.
1) Пусть найдётся точка x ∈ R, такая что πx(S) - бесконечное множество. Тогда возьмём функцию h равной нулю в x и единице во всех остальных точках R, и Uh(f), f∈S, будет искомым покрытием.
2) Пусть такой точки не найдётся. Тогда возьмём h(x) равным половине минимального расстояния между двумя различными точками πx(S).
Контрпример построен.
Обращайся.
 7 Кб, 593x248
7 Кб, 593x248помогите пожалуйста доделать этот пример
после подстановки косинуса во второе уравнение и складывание у меня получается какое-то жуткое уравнение, которое равно отрицательному числу. Я правильно решаю или это уравнение траектории вообще, в принципе невозможно привести к нормальному виду? Или у меня ошибка? Проверьте пожалуйста.
Арифметику я проверять не буду, вольфрам проверит. Но в принципе что-то вроде этого и должно было получиться.
ничего, что вот это уравнение равно отрицательному числу? Напиши пожалуйста, как в вольфраме проверить, что написать?
Понятия не имею, зачем ты перенёс это число направо, но нет, ничего. То, что слева, может принимать и отрицательные значения.
Просто набираешь (выражение_для_косинуса)^2+(выражение_для_синуса)^2-1, и всё.
я просто знаю, что точка движется по эллипсу, и поэтому спрашиваю, ну тип это же радиус в правой части, и он не может быть отрицательным. Я не понимаю, как записать в вольфраме эти синусы и косинусы, объясни подробней пожалуйста и ещё, как построить в вольфраме график этого выражения, которое у меня получилось?
 79 Кб, 834x656
79 Кб, 834x656спасибо. Вот, получился эллипс. А можно в вольфраме как-нибудь это выражение упростить, чтобы по виду уравнения сразу было видно, что это эллипс, или же привести к виду y=f(x)? Или к более простому виду это выражение не привести?
Если оно похоже на эллипс - это ещё не значит, что это эллипс. Избавься от корня, после чего перенеси всё влево и попробуй заставить вольфрам это разложить на множители.
>или же привести к виду y=f(x)?
Эта запись подразумевает, что для любого x, существует единственный y, которые связаны функцией f. Уже на примере окружности видно, что нет такой f, ибо каждому x удовлетворяют два значения.
Любая функция хоть немножечко локально полином. Разность функции и ее немножечко полинома -остаточный член. Его можно выразить по-разному: через интеграл, через производную и т.д. Вот одна из форм (остаточного члена) и называется формой лагранжа
зачем раскладывать на множители?
Ранее неправильно была набрана формула, вот траектория. И там внизу wolfram написал solutions, это и есть упрощённое выражение , выражающее y через х?
 68 Кб, 950x877
68 Кб, 950x877Пусть f дифференцируема в точке x. Тогда
f(x + dx) = f(x) + f'(x)dx + o(dx).
Естественно задаться таким вопросом: можно ли с помощью производных получить более хорошее приближение? Например, найти a2 такое, что
f(x + dx) = f(x) + f'(x)dx + a2 (dx)2 + o(dx^2 ).
Может, можно бесконечно раскладывать? Продолжение мотивировки на пикрелейтед.
Что касается доказательств формулы Тейлора, то они все уродливые, тут ничего не поделаешь.
Ну покажи мне неуродливое. Вот самое нормальное, которое я знаю:
http://math.stackexchange.com/questions/481661/simplest-proof-of-taylors-theorem
>Список от анона с dxdy. Довольно внушителен, тоже рекомендуется к прочтению. Является дополнением к списку старго ОП-а.
http://pastebin.com/YP1uaUyd
Что из этого осваивать если нужны знания на уровне где-то между олимпиадой физтех-ОММО и вышка-всеросс? Может что-то, что зайдёт вместе с курсами фоксфорда (ну там на бесплатные курсы ещё заданий нет, поэтому я хуй знает что решать, кроме олимп прошлых лет и Шабунина, но этот задачник для подготовки чисто к физкеку, а это уже не актуально)? Там просто не рационально сразу все книги одновременно читать, а летом-то можно будет освоить и оставшееся да.
не знаю что там в списке и вообще долбоеб-неолимпиадник, но думаю будет полезно поучить что-то связанное с линалом, мат. логикой. А ещё что-нибудь типа "школьной математики с точки зрения высшей"
вообще, после семестра в среднем вузе на примате (читали курсы по дискретной математике (комбинаторика, мат. логика и немного графов было), мат. анализу, лин. ал), смог решить 4 или 5 заданий из олимпиады вышки по математике. понятно, что в вузе далеко выходящих за понимание школьника знаний мне не дали.
Список тот к олимпиадам имеет косвенное отношение. И вообще он недоделан, рандомен и преисполнен картофаном, лучше его нахуй убрать.
>знания на уровне где-то между олимпиадой физтех-ОММО и вышка-всеросс
Скилл тогда уж, а не знания, знаний для олимпиадок достаточно в объеме чуть превышающем школьную программу.
Если хочешь готовить к олимпиаде, то самое актуальное - это задачники Прасолова, почти все олимпиады (особенно мск) - это рандомный сет из этих задачников. Как правило, хотябы одна треть будет взята оттуда.
Другое дело, что и задач там овердохуя, все ты не прорешаешь.
>фоксфорд
и прочая поебота - это бесполезное наебало для выкручивания денег из доверчивых школяров
Олимпиадный фольклор со временем сильно меняется, если хочешь не просто тренировать ум, а чтоб задачки были наиболее близки к тем, что могут попасться, можешь еще порешать
>Элементы математики в задача: Через олимпиады и кружки к профессии
>Математика в задачах. Сборник материалов выездных школ
Бери что-нибудь из этого и дрочи все лето по 2 Grot в день.
сап матемач.
чем отличается математическая статистика от статистики финансов ?
статистику финансов знаю, там дисперсия, корреляция, регрессия, мода, анализы и тд.
в мат.статистики в принципе тоже самое ведь да ?
Очевидно, что статистика финансов - приложение мат.статистики к финансам.
Дайте простеньких книжек для вкатывания в матан, линал, теорвер, функан, комплан
Тебе в основания математики тред.
Есть, но там как только открываешь книжку на тебя гамалогеи с тапалогеямы вываливаются.
Мне для первого ознакомления, с прицелом на том что я нихуя не знаю в данных областях.
Ты всё сразу захотел? Без них никак. Учишь множества, категории, алгебру, топологию. Потом читаешь остальное.
Смотри, для начала можешь просмотреть Куранта Дифференциально и интегрально исчисление том 1. Параллельно учишь множества и читаешь Констрикина введение в алгебру. Всего Куранта читать не обязательно, прочти 300 страниц, их довольно просто читать, там много воды, чтобы получить интуицию и идёшь читать Зорича.
 460 Кб, 560x4638
460 Кб, 560x4638Бутузов Кадомцев 2005г. Планиметрия
У местных пучкистов то что не самое модное не математика.
Ну вот я и прошу поначалу. Я же писал, когда открываю книжки из оппоста меня тапалогеями гомеоморфно выворачивают на изнанку.
bump
>Я серьезно.
>Анализ... без топологии... топология... без множеств и категорий... линейная алгебра... без полей, колец, групп...
Но он только начинает учить. Ему ни то, ни другое сейчас не надо. Что ему надо, так это интуитивное понимание для начала. Ты же понимаешь, что подавляющему большинству людей от того, что у тебя на скринах становится скучно и они просто дропают обучение.
Если ему от этого скучно, то зачем он пытаются учить? Это бесполезно.
>>3541
Как ты выучишь топологию без знания множеств и линал без знаний по алгебре? НИКАК! Там много не надо, конкретно по множествам: множества, действия над ними(объединение, пересечение, разность, декартово произведение), отображения множеств, отношение эквивалентности, фактор-множества, упорядоченные множества(частино-, вполне-...).
>Если ему от этого скучно, то зачем он пытаются учить? Это бесполезно.
Есть много простых, интересных и полезных книг по математике. Нахера вы всем подряд своей ссаной теорией множеств тычете? Начинающий может отлично и без нее обходиться. А когда поймет, что дальше без нее нельзя продвигаться, то вот тогда и будет о ней читать.
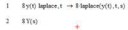 1 Кб, 256x62
1 Кб, 256x62>Начинающий может отлично и без нее обходиться.
>Дайте простеньких книжек для вкатывания в матан, линал, теорвер, функан, комплан
Чтобы вкатиться туда, куда он хочет, не может. Да и что в ней сложного, блядь? За день-два можно освоить необходимый минимум.
Ильин-Позняк есть по матану и, по-моему, по линалу. Для начала норм.
Для теорвера нужен матанализ, для функана матанализ и линал, для комлана нужен матанализ.
Вернешься когда выучишь матан и линал
Блять, помогите дауну, пожалуйста.
Не могу решить эту парашу.
Разложил, а дальше как действовать?
Нет. Лоран Шварц, Львовский будут в 100 раз лучше.
никак, избавься от иррациональности в знаменателе
Определения типа: A - это B. Они же работают в две стороны, т.е. A <=> B, так?.
спасибо
 12 Кб, 618x126
12 Кб, 618x126http://formylu.ru/geometriya/formuly-perimetra/dlina-ellipsa
Понятно, что проскользнула в мыслях какая-то аналогия с формулой длины окружности, но какая именно аналогия? Как это вообще можно написать в здравом уме?
Проиграл. Вспомнил что-то мем из тесача, где там пепельные упыри стилизованные под "мемчики)0))" из 2013, и типо написано "искал двемерскую головоломку месяц)))00)))"
классика, сам такого персонажа знаю, который месяц наиграл в морку не найдя головоломку
 28 Кб, 887x451
28 Кб, 887x451Только там по оси абсцисс не b, а b/2, если что. Я упоролся. Вот тут я пофиксил вроде бы. Давно с таблицами не работал, сорри.
Да пиши как хочешь, единственное, что важно — понимают тебя или нет.
Картинка? При чем тут картинка? Хотел спросить о математической индукции, но в результате стало совсем стыдно и... ДА Я НИ ЧЕРТА НЕ ПОНИМАЮ, у меня явная истерика. Какие-то аналогии непонятные, принцип домино понятный. Но доказательства математической индукции... домино мы взяли сколько надо изначально, установили и уже не манипулируем, не представляем домино на боку или еще что-то такое. А в математике, похоже это везде, какие-то символы не пойми откуда и по каким законам мы можем их взять, почему их вообще можно взять ни откуда и ПРОСТО ОЧЕВИДНО связать. У меня реакция первобытной обезьяны. В особенности из-за того, что это задачка для 8 класса. Все понимают, а я какой-то ущербный, пожалейте меня. Слезы просто.
Давай эти самые книжки/авторов пищущих такие книжки.
Ну почти любую математическую конструкцию можно натянуть на теорию множеств, даже определение числа 1, даже аллаха как элемент множества выдуманных персонажей, так что совсем без множеств даже на пальцах посчитать не получится. Дети спокойно считают в свои считалочки и без множеств, я о том что количество пальцев на рухак можно вполне легально втиснуть в множества из за их "резиновости", как например множество гвоздей в коробке
Без языка теории множеств....как бы это сказать так чтобы понятно было...вот чтобы описывали конструкции, например бесконечно малое/большое не многоходовочкой по множествам и подмножествам с расслоениями на пучках сечений модульных, афинно зависимых гиперпространственных проекций на гиперплоскость с неэвклидовой геометриией, а как последовательность чисел которая меньше наперед заданного числа, находящаяся между нулем и заданным числом/последовательности чисел которые больше заданного числа, и чтобы потом было подробное описание логической конструкции описывающей почему именно они бесконечные.
Не понятно наверное нихуя. Ну вот в множествах считают что ты уже знаешь определения и теоремы которые тебе потом будут подавать в виде множеств. А я их не знаю. И мне их нужно выучить не участвуя в множествах.
По мат.индукции анон в /b/ пояснял что если условие выполняется для двух случаев (например n и n+1), то смотрим выполняется ли данное условие к разности случаев, и если да, то всё нормально
>Слезы просто
ты тян? (ну просто тянки так обычно пишут) асечку писечку плз
Есть множество Х.
Если x_n обладает каким-то свойством и из этого следует, что x_(n+1) обладает таким же свойством, то все элементы в Х начиная с x_n обладают таким свойством.
Про домино.
Выстроили в ряд бесконечное кол-во доминошек. Если N-ая доминошка упадет, то(из этого следует что) упадет и следующая за ней N+1-ая доминошка. Т.к. первая доминошка упадет, то упадут и все за ней.
>гендерного равенства тред
>на пиках одни девушки
А вообще я хотел задать вопрос.
Что из математики нужно изучить после школьного курса чтобы понимать более 3/4 части всех документов arxiv.org?
>понимать более 3/4 части всех документов arxiv.org
Хуясе у тебя запросы. Может тебе еще царский путь в тапалогею нужен?
4*tg^2(x) + 3/cos^2(x) + 3 = 0
получается
cos(2x) = 4
где я мог ошибиться?
Для неё нужно немного алгебру знать. В первых же задачах используется билинейная симметричная форма.
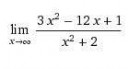 9 Кб, 139x75
9 Кб, 139x75 388 Кб, 687x680
388 Кб, 687x680только в них вообще не уверен, никак не могу понять
вроде решается все устно
1)2 вообще хз
2)2
3)4?
Куда именно? Не понял.
Если третья степень, то бесконечность (делим числитель и знаменатель на x3) это случаем не домашка с фоксфорда?
Ладно. Пересечение этого R с транспонированным R будет подмножеством диагонали того самого декартового квадрата?
Спасибо.
Ну и ещё вопрос. Антисимметричное отношение содержит диагональ множества, на котором оно определено?
Не обязательно. Хотя самый распространённый пример - это отношение порядка, а оно содержит.
Не вижу тапалогий! Ничем помочь не могу! Удачи!
С уважением, звук с 1:34 по 1:36 в песне Chicane – Come Tomorrow
В последней задаче некорректная постановка. Вторая тривиальна. В первой тангенс половинного угла.
Да определения то я знаю
Юамп
Разве что те, которые вышли в 19-м веке, или на крайняк в начале 20-го. Множества давно и прочно стали частью естественного математического языка. Требовать математику без теории множеств - это примерно как требовать художественных текстов без буквы "а", на том основании, что тебе сложно её писать. Нелепица полнейшая. Наоборот, матшкольников нынче стараются научить множествам как можно раньше, чтобы они у них не вызывали суеверного ужаса и не мешали интуиции, когда дело дойдёт до действительно сложных конструкций.
>Начиная со второй половины XX века представление о значении теории и её влияние на развитие математики заметно снизились за счёт осознания возможности получения достаточно общих результатов во многих областях математики и без явного использования её аппарата, в частности, с использованием теоретико-категорного инструментария (средствами которого в теории топосов обобщены практически все варианты теории множеств).
УРЕТЕ, ВАШИ ТОПАСЫ НЕ ТОПАСЫ, ПРУФЫ НЕ ПРУФЫ, А ТО ШТО КАЖДЫЕ ПОЛГОДА НОВУЮ ТЕОРИЮ МНОЖЕСТВ ПРИДЖУМЫВАЮТ ТАК ЭТО ФИЧА А НЕ БАГ
Речь не об аксиоматической теории множеств, ебло. Когда вы уже научитесь разделять формализм и содержание? Я говорю о множестве как понятии. Современная математика без него немыслима. Категории - это средство описания, не более того. Все осязаемые примеры категорий строятся из множеств. Собственно, без понятия класса ты категорию даже не определишь толком.
Разве что что-то подобное, да.
Векторный анализ - это всякие внешние дифференциалы роторы и дивергенции. Оно тебе пока не надо.
Тогда второй том Зорича к твоим услугам.
Осязаемость зависит от привычки. Я вот в последнее время стал сомневаться в существовании некоторых эзотерических конструкций вроде large cardinals, потому что не могу придумать для них категорного обоснуя.
Ну и категория прекрасно определяется чисто категорным языком без всяких классов, конечно.
Для меня реально то, что имеет категорный обоснуй.
Как бы ты ни определял категорию, это всё равно сущность, которая содержит другие сущности, в некотором смысле. От того, что ты не произносишь слова "класс", он отсюда никуда не девается. В теории категорий, самой по себе, ещё ниоткуда не следует, что хоть одна категория вообще есть на свете, и не существует способов конструирования новых категорий из существующих. И даже если какая-то категория дана тебе свыше самим Гротендиком, у тебя нет других способов выяснить, есть ли в ней какой-нибудь классификатор подобъектов или там декартовы квадраты, кроме как ковырять её теоретико-множественную реализацию. Этот язык слишком общий, чтобы говорить о конкретике каким-то замкнутым способом.
Потому что для людей, не знающих, что такое умножение, даже собака будет звучать убедительно.
А откуда следует, что множества есть? К ним все привыкли и они кажутся настолько убедительными, что вопрос об их существовании не ставится. Но ведь их существование, по сути, дело личной веры математика. Для меня ETCC и ETCS не менее убедительны, чем ZFC.
Это уже не смешно. Я биты три треда спрашиваю один и тот же вопрос и ни один таполаг с гамолагом не ответил.
Как вывести формулы интегралов без привлечения фокуса с обратными производными?
Давай серьёзно.
Есть пустое множество, и есть небольшой набор естественных операций. ZF их просто конкретизирует. Из этого строится всё что нужно. Я не сомневаюсь, что всё то же самое можно закодировать и на чисто категорном языке, но говорить, что здесь нет множеств и они не нужны - это лукавство, поиск лазеек в формулировках. Множества - естественный инструмент для конструирования объектов и изучения их внутренней структуры, категории - для изучения взаимосвязей с другими объектами.
>>3673
Никак. Тебе вообще никто не гарантирует существование каких бы то ни было "формул". Даже чтобы написать ряд тейлора для первообразной, тебе сначала надо понять, как интегрировать мономы.
Естественные операции? Кому вы рассказываете, в самом деле. Например, аксиома подстановки - это не естественная операция, а чуть ли не оккультизм.
спасибо уже решил, это одно из заданий которое будет на контрольной
>Нихуя ты загнул.
Что не так? Очень простая и доходчивая книга. Скачать то же 4 издание на либгене .
Интегралы основываются обычно на том что они обратные по значению от производных.
А юез обоснования этого, просто как площадь под графиком/предел суммы можно или нет?
это для физиков
Хотя там не везде книги есть, но вообще просто ищи X для физиков
По той же причине почему в школах не учат общению и взаимодействию с другими людьми.
По определению.
Да нет, что же в ней оккультного. Множество, по своей сути - это чёрный ящик, умеющий говорить "да" и "нет". От того, что мы к его выходу добавим ещё одну дополнительную проверку, это не перестанет быть чёрным ящиком, умеющим говорить "да" и "нет".
учат
у нас на физфаке книжки были по двум предметам сразу, в таком порядке, как в книжке и учишь
сложно на физфак попасть? Собираюсь туда идти, но олимпиады не затащил (но в принципе некоторые знания и умение работать имеются- спохватился слишком поздно что надо чуть-чуть выходить за школьный курс).
Так-то я бы на физтех пошёл, мне тупо 15 минут на элке ехать до него, а без олимпиад лапу сосать- самое обидное что в /un/ аноны ноют что "луче бы на физфак поступал патаму что там тёлочки гыгыг, а на физкеке тока суецид да суецид", а я, наученный ошибками социального взаимодействия, сейчас стремлюсь стать maximum dodik
>БГУ
это который BSU или BRGU???
У вас там есть что-то наподобие СУНЦа?
Мне просто кажется ещё что бОльшая часть СУНЦов после 11го у себя на родине останутся, в своём вузе тут есть вообще кто с физфака МГУ?
Аксиома говорит вот что. Пусть ф - правильно построенная формула языка теории множеств первого порядка, в которую буква B не входит свободно. Пусть p - её строчка параметров. Тогда для любого множества A и любого набора параметров p если ф функциональна относительно A, то существует множество B, состоящее в точности из таких элементов, которые являются ф-образами элементов A.
Эта аксиома является эзотерической потому, что позволяет легко доказывать существование множеств, о пустоте или непустоте которых в принципе ничего сказать нельзя.
Например, правильно построенной формулой является формула "мощность x строго больше алеф-0, но строго меньше континуума". Применив эту формулу к какому-нибудь кардиналу большему, чем континуум, мы получим множество кардиналов M, пустота которого равносильна континуум-гипотезе. Множество M существует, но его элементы никакими средствами не могут быть изучены. Нелепость какая-то.
А ведь ф - любая правильно построенная формула. Которая к тому же может зависеть от любого числа параметров. Это, если вдуматься, позволяет буквально доказать существование Ктулху.
В самом деле, доказательство сводится к точному теоретико-множественному описанию того, что мы понимаем под Ктулху. Если C(x) - утверждение, что множество x является Ктулху, то может быть построена формула f(x, y), которая функциональна по x и каждому иксу сопоставляет Ктулху. Применив эту формулу к какому-нибудь одноэлементному множеству, мы докажем, что существует множество, единственным элементом которого является Ктулху.
Более того, если считать, что мы имеем право перенумеровать Великих Древних ординалами, то мы можем доказать существование любого наперед заданного количества экземпляров Ктулху. Даже алефа с трансфинитным нумером различных ктулх.
Фтагн, фтагн.
Не хотите ли вы стать пропагандистом ктулху? Оплата по собеседованию, ставка плюс количество новообращенных.
8 не простое число. Простое число это такое число, что делиться только на себя и на единицу.
Бля, я прочитал жопой.
Тогда зачем это нужно? Я ведь тоже могу придумать свой одночлен, но почему его назовут моим именем? А есть такое, чтобы получались?
Насколько я знаю (я не специалист), нету такого чтобы получалось, но люди постоянно пытаются придумать.
Нашел еще какие-то числа Софи Жермен, но там приписка, что и для них не доказано бесконечность такого ряда. Что есть лучшим решением?
>Если задано 2^n - 1 , где n это простое число, на выходе получиться простое число?
Нет. Обратное утверждение верно.
Производная! Все учите производные! С помощью производной я доказал небесконечность вселенной!!!
>но его элементы никакими средствами не могут быть изучены.
Кажется, ты опять путаешь формальные теории и содержательные. ZF - это не священное писание, не 10 заповедей теории множеств. Это просто некий конкретный набор операций, которые над множествами можно делать. Они сформулированы в виде аксиом просто для того, чтобы не было разночтений в том, каких свойств мы ожидаем от множеств. Мир множеств на самом деле намного богаче, чем то, что из них выводимо. Вместо эзотерики вроде трансфинитных ординалов можно взять самые обычные натуральные числа и корни диофантовых уравнений. Уж это-то объект совершенно земной, и корни либо существуют, либо нет. А вот поди ж ты. Это говорит лишь о том, что наш инструментарий недостаточен для таких вещей.
посоветуйте что интересного можно почить про операционное исчисление, оригиналы?
в универе данную тему не дали..а самому въезжать сложна
Ну, к примеру, число 13492656777600 имеет 11520 делителей. Это довольно близко к максимуму.
>>3726
Википедия -> преобразование Лапласа. Там и теория, и свойства, и даже таблица изображений. Не хватит - смотришь раздел "библиография" и читаешь что приглянётся. Но вряд ли в этом будет нужда, на твоём уровне тема совершенно элементарная.
С такой точки зрения должна существовать некая единая вселенная множеств, а все формальные теории суть просто попытки описать эту гипотетическую единую вселенную. Единая вселенная существовала бы, даже если бы ни одной формальной теории не было.
> на твоём уровне тема совершенно элементарная
ага, когда препод так говорит, оказыввается всё наоборот
Для удовольствия.
Да, раздели 1 на 3, затем умножь на 3.
Системы счисления бывают только с целым основанием. Можно, конечно, придумать какой-нибудь изврат, но он будет абсолютно неюзабелен.
Но математики постоянно придумывают извраты. Не уж-то нет готового уже?
https://www.youtube.com/watch?v=494uupfgWSQ
Хуйню какую-то несешь, нужно просто понимать, а не "интуитивно". Ни разу еще не встречал человека, который захотел что-то конкретное понять, старался для этого, но все равно нихуя не понял. Остальные же только сидят и ноют, мол склад ума не тот, математику/физику только избранные понимают и прочие кукареки.
А я встречал. Старательный парень, не быдло, на все пары ходит, всё записывает, пытается разобраться, но вот просто мозгами природа обделила. И это не только в математике - у него во всём так, вплоть до ориентирования на местности. Поступил по квоте из Крыма.
> но все равно нихуя не понял
Я не говорил про нихуя, я говорил про то, что смысла не ловишь. Есть формула какая-то, я вроде понимаю как она получилась и как она работает и когда применять и прочее. Но если спросить меня почему так, я обосрусь, потому что НЕ ПОНИМАЮ почему так. Вот, например, биномиальные коэффициенты, разложение (1+x)^n, число e. Я только на днях понял, что это всё вытекает из треугольника Паскаля, а он из фундаментальных свойств чисел, из правил, по которым из единиц получаются все числа. И вот это только сейчас я понял, до этого это были разрозненные знания из нескольких областей математики, а сколько ещё мимо меня прошло? Да хуй знает. Провал, понимаешь? Это провал, я ебланище тугое, могу повторить, заучить грубо говоря, но смысла не увижу в большинстве случаев.
У меня вот слух абсолютный, могу мелодию из матрицы на слух наиграть, а играть не умею, и ебать мне слух режет, когда люди без слуха петь пытаются. Слуху нельзя обучиться, так и математическому слуху ты и за двадцать лет не научишься. А хочется почувствовать ту красоту и глубину связей,ту мистику, которую я на дгнях от треугольника Паскаля словил
> математическому слуху ты и за двадцать лет не научишься
У меня был знакомый из консерватории, он без нот играть не мог, вот я про что. Кнопки нажимает и получается музыка. Тут что-то вроде того, математические кнопки ты нажимать то можешь научиться, но слышать математику некоторые могут вообще не умея кнопки нажимать, а некоторые будут хуй сосать по жизни.
Или дальтоники те же, они ж не переходят на красный свет, понимают, что это красный, но не видят его таким, какой он на самом деле.
>Относительный слух, или интервальный слух, — способность помнить разницу в высоте звуков. Эта важнейшая составляющая музыкального слуха даёт музыканту возможность определять интервалы, — то есть частотные отношения между нотами в мелодии, гармонических интервалах и аккордах.
>Развитие относительного слуха входит в обязательную программу профессиональной подготовки музыканта, этим занимается дисциплина сольфеджио.
>Абсолютный слух — способность достаточно точно помнить высоту звука, позволяющая носителю определять и называть любые услышанные ноты без предварительного прослушивания заранее известных звуков
>Эта способность может формироваться в раннем детстве, а во взрослом возрасте её приобретение крайне затруднительно.
Это значит, что если и возможно, то крайне затруднительно, единичные случаи, да и то не факт, что эти люди не обладали им до этого, в то время как пыталось учиться этому и учить очень много людей.
100
В. Б. Брайнин
О НЕКОТОРЫХ ВОЗМОЖНОСТЯХ РАЗВИТИЯ АБСОЛЮТНОГО
СЛУХА1
Если читатель рассчитывает на сенсацию, его ждёт разочарование.
Развитие абсолютного слуха в тех случаях, когда предварительное
тестирование предрасположенности к нему не обнаружило, станет
возможным (или невозможным) лишь тогда, когда природа абсолютного
слуха прояснится. Из обилия публикаций на эту тему однозначной картины
пока что не складывается. Указывается на то, что целые народы могут
обладать абсолютным слухом, если с рождения говорят на так называемых
тональных языках (китайцы, вьетнамцы – мой опыт преподавания группе
вьетнамцев-немузыкантов это подтвердил). Есть сообщения о том, что все
младенцы имеют соответствующий потенциал, который закрепляется лишь
будучи востребованным. В нашей школе мы проводим эксперимент по
обучению малышей с 12-ти месяцев, но, во-первых, это уже не младенцы, а,
во-вторых, о результатах говорить пока преждевременно – эксперимент
сравнительно свежий.
http://www.brainin.org/Method/absolute_pitch_RU.pdf
>если с рождения говорят на так называемых
>тональных языках
кек, китайский, например, использует относительный слух
Короче, мне реально влом объяснять, но допустим, чтобы освоить X нужно затратить 10000 часов. Если у тебя талант, дели это на 2-10, если ты гений, то еще на 2-10. То, что у тебя таланта нету, говорит только о том, что придется больше времени убить. Поэтому рационально расходовать время на то, что тебе дается. Но люди иррациональны.
Да не о том же речь, я говорю о том, что в математике тоже существует похожая штука, интуитивное понимание, которое неясно как развивать и вообще возможно ли это во взрослом возрасте. Вспомни, тот же Гаусс в 15 лет себя проявил, да и у других, Римана, например, похожие истории были.
Понимаешь, некоторые вещи ты не осилишь сколько ты не потрать. Ты просто неверно будешь видеть, ну дело же не в упорстве и усердии, вот выше я пример писал про связь e,(1+x)^n и треугольник паскаля, я вообще на это случайно вышел, когда в б фракталы постили и я стал их гуглить. Я учился неплохо, вуз технический закончил, но только тогда разные факты из комбинаторики, матанализа, алгебры, теорвера получили настоящее объяснение и понимание почему так в голове, а не видимое.
Попал в ноту. Когда в следующий раз такое произойдёт и произойдёт ли вообще неясно, никак ты это не разовьёшь, а если вспомнить какой объём часов у нас был посвящён математике я 95% просто-напросто упустил. И ведь проблема в том, что упорство, 1000 часов это всё круто, но тут ты думаешь, что понимаешь, решаешь задачи, получаешь одобрение препода, сдаёшь экзамены с теорией и практикой, у тебя даже мысли не возникнет, что ты вообще нихуя не знаешь на самом деле.
Мне кажется вообще, что детям, рассказывая теоремы и доказательства, начиная с теоремы Пифагора, нужно ещё рассказывать то, как автор к этому пришёл, тогда мб не так всё хуёво будет. Потому что во взрослом возрасте это походу почти нереально развить.
> когда в б фракталы постили
https://ru.wikipedia.org/wiki/Треугольник_Серпинского
>Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные — в белый, то образуется треугольник Серпинского.
Забыл.
То есть если бы в б кто-то не запостил фракталы я бы никогда так и жил дальше, думая,что что-то знаю.
Именно, блядь! Потому и сгорел!Жил бы и жил себе, а так я типа приоткрыл дверцу, но понимаю, что никогда, блядь, никогда всей красоты не увижу. Я в жизни никогда никому не завидовал. А теперь зависть какая-то мерзкая гложет, злюсь на себя за это и горииит очаааг.
>Гаусс
> Уже в двухлетнем возрасте мальчик показал себя вундеркиндом. В три года он умел читать и писать, даже исправлял счётные ошибки отца. Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050
>Первый эффектный успех пришел к Гауссу, когда ему не было еще девятнадцати - доказательство того, что можно построить правильный 17 - угольник циркулем и линейкой.
>В 1796 году Карл Фридрих Гаусс, учащийся первого курса Геттингенского университета, решил задачу, перед которой математическая наука пасовала более двух с лишним тысяч лет. Несмотря на то, что еще древними греками были найдены способы построения с помощью только лишь циркуля и линейки правильных многоугольников с числом сторон 3, 4, 5, 15, а также с числом сторон, большим в 2 раза, в отношении прочих правильных многоугольников царила полная неизвестность. И вот именно в этот день будущий «король математиков» Гаусс догадался, как построить правильный 17-угольник, кстати, также, с помощью циркуля и линейки
2000 лет, анон. Чувак в школе изобрёл арифметическую прогрессию. Какие нахуй 10000 часов? Я, конечно, экстремальный пример привёл, но именно ту внутреннюю интуицию, только гораздо меньшей силы, я имею ввиду.
То есть как и со слухом отсутствие этой интуиции не помешает тебе стать математиком или просто хорошо усваивать материал
>Бытующим недоразумением является представление, что обладание абсолютным слухом — гарантия музыкальной гениальности[4]. Иногда родители, обнаружив это качество у ребёнка, заставляют его заниматься музыкой, даже если нет ни особых способностей, ни желания. Другая сторона этого же недоразумения — мнение, что без абсолютного слуха в музыке ничего серьёзного добиться нельзя (что опровергается хотя бы примерами П. И. Чайковского или Р. Вагнера).
>Абсолютный слух полезен для музыкальной деятельности, но, вопреки бытующему мнению, не приносит своему обладателю значительных преимуществ.
но без неё ты никогда полностью не увидишь всей красоты. Это нечестно.
математика нужны чтобы меньше думать.
Выглядит привлекательно, но я сомневаюсь, что могу как-то сосчитать, ввести какую-то формулу и прочая для этой картинки. Могу только смотреть, может даже любоваться.
Да он там такую хуйню творил в 12 лет написал какую то дисертацию что йоба ученые того времени не верили что аффтару этого талмуда 12 лет.
> Но если спросить меня почему так, я обосрусь, потому что НЕ ПОНИМАЮ почему так.
Потому что надо доказательства всех утверждений читать. Естественно, если быть быдлом и просто применять формулы, которые препод дал, не будешь ничего понимать. Это не только к математике относится, но и ко многим другим областям жизни.
Нужен icq как у хлебушка, чтобы верить в то, что существует некий набор знаний, которым должен обладать каждый "образованный" человек.
Такой набор знаний действительно существует. Уж по крайней мере математика по 6 класс включительно в него входит.
Согласен
Скорее даже не логику, а идеи.
Например, интегралы связаны общий идеей разбиения на бесконечно малые величины, которые затем суммируются. Уже по этому ты сможешь сперва кратко, а затем подробно восстановить у себя в голове ход доказательства.
> Такой набор знаний действительно существует. Уж по крайней мере математика по 6 класс включительно в него входит.
Очень интересно узнать, по каким критериям ты определяешь, что входит в этот набор, а что нет. Вот представь, что я тоже верю в существование такого набора. Допустим я считаю, что любой образованный человек должен знать определение хаусдорфова пространства. Попробуй оспорить.
Они именно в доказательствах, и их оттуда надо научиться вычленять. Сначала это будет непросто, и из-за этого надо будет возвращаться к ранее пройденному, чтобы вспоминать и закреплять эти идеи.
Выписывай леммы, теоремы и определения, записывай доказательства, следи за тем, как доказывают и из каких соображений вообще это нужно.
>>3808
Имхо, набор необходимых знаний не просто существует, а его ещё и расширять постоянно нужно.
Ой, оставь свою демагогию при себе. Ясно, что человек, не умеющий читать и писать, никак не может считаться образованным.
Не знаю. Вопрос был в том, как понять "почему так". Для меня "понять почему так" = "понять доказательство" = "разложить переходы между утверждениями, которые мне кажутся неочевидными, на последовательность маленьких очевидных переходов".
 221 Кб, 825x577
221 Кб, 825x577Так всё-таки, НА СКОЛЬКО?
Я думаю, что слово "образованный" не имеет никакого смысла, пока не зафиксируешь предметную область. Умение читать и писать - это грамотность. Неграмотный человек не может стать образованным ни в какой области, потому что у него нет доступа к информации. Поэтому его можно назвать необразованным. Человек, который не знает математику за 6 класс, все еще имеет доступ к очень большому количеству информации.
>Человек, который не знает математику за 6 класс, все еще имеет доступ к очень большому количеству информации.
Например?
Образованность - это предмет консенсуса. Ты образованный, если достаточное количество людей согласно тебя таковым признать, обладая точной информацией о твоих знаниях и навыках. Если ты убедишь большинство людей, что без хаусдорфовости жизни нет, то это немедленно станет обязательным условием, чтобы называться образованным человеком.
Я утверждаю, что в любой стране большинство (т е больше половины) людей не способны решить квадратное уравнение, потому что много лет этим не занимались. Следовательно, знание математики за 6 класс не является необходимым условием образованности.
В моё время квадратные уравнения были в седьмом классе. А шестой - это дроби.
Каждый сам для себя устанавливает уровень, на котором ему комфортно знать ту или иную область науки. Слишком много факторов имеется, в том числе и никак не зависящих от человека, которые человек учитывает, устанавливая этот уровень.
>Слишком много факторов имеется,
Чтобы бросаться такими словами как "каждый, должен, образованность" и прочими.
Ну и чё, в итоге походу наебались учёные и ведущий, лол. Я ещё думаю как так такие сооружения строили и на целых две сотых наёба.
А выходит вот: пикрелейтед равен 3.1416313. Второе число это 1-1/(золотое сечение), которое им точно было известно. Такие дела.
А 4/81 получается из того, что диаметр равен 9, радиус равен 9/2, в квадрате получается (9/2)^2= 81/4. Домножаем на pi, получаем 63.6172512352
63+2/(sqrt(5)+1) же равно 63.618034
Пишу потому что мало ли меня приглючило под ночь, лол и там ошибка какая-то бредовая.
>Египтяне предполагали, что площадь круга S диаметром d равна площади квадрата, сторона которого составляет 8/9 диаметра: Это правило соответствует приближению ≈ 3,1605 (погрешность менее 1 %)
https://ru.wikipedia.org/wiki/Математика_в_Древнем_Египте#.D0.92.D1.8B.D1.87.D0.B8.D1.81.D0.BB.D0.B5.D0.BD.D0.B8.D0.B5_.D0.BF.D0.BB.D0.BE.D1.89.D0.B0.D0.B4.D0.B5.D0.B9
Выходит, у египтян точность повыше то была, чем 1 %, лол.
 1 Кб, 498x339
1 Кб, 498x339>2/(sqrt(5)+1)
Охуеть, загуглил, и вот как это число представляется в виде цепной дроби. Нет, вы понимаете? АБСОЛЮТНАЯ ДРОБЬ, ОСКОЛОК ГЛАЗА ГОРА. Сакральненько.
>ОСКОЛОК ГЛАЗА ГОРА
>Сумма шести знаков, входящих в Уаджет, и приведенных к общему знаменателю: 32/64 + 16/64 + 8/64 + 4/64 + ²/64 + 1/64 = 63/64
Да ничего, просто думаю, что египтяне использовали более точное значение пи, чем об этом пишут.
Ну и в Индии, например,долгое время юзали pi=3.1416, с его помощью рассчитывали длину экватора и только на 100 км ошиблись. Показалось интересным, что в таком приближении золотое сечение всплывает, хотя считается, что между пи и золотым сечением явной связи нет.
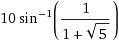 119x42
119x42Ну и ещё оттуда точное значение пи выводится, лол. Да хз, дело было ночью, смотрел передачу, услышал про то, что в Египте площадь квадрата со стороной 8 считали равной площади круга с диаметром 9 и чёт меня понесло. Сорян, что тред засрал.
90+
 49 Кб, 1132x162
49 Кб, 1132x162Нарисовал для себя, и по рисунку получилось так:
(a - MB) + (AC - PC) + MP
Если следовать правильному ответу, то можно AC заменить на a, ведь точки касания равноудалены от точки A? Но дальше я не знаю как сократить, чтобы вышло 2a.
Аноны, я в замешательстве. Множество людей в интернете говорит, что пи не может быть выражено через фи, так как пи трансцендентное число, а фи алгебраическое. Но почему тогда ответ получается верным в любой программе?
To start off, it's necessary to establish the following:
e and π are transcendental numbers (there does not exist a non-zero polynomial equation with rational coefficients of which either is a root)
phi (by which, I am assuming you mean the golden ratio) is not a transcendental number
So lets say you have a transcendental number a. Exponentiation of a to a rational power, addition of a rational constant to a, and multiplication of a with a rational, nonzero number would all result in a transcendental answer.
 121 Кб, 776x584
121 Кб, 776x584Но почему тогда пишут, что нельзя выразить и никакой связи между ними быть не может? Я тоже думаю, а как же arcsin(sqrt(3)/2)=pi/3, например?
Нельзя выразить алгебраическую связь. А синус и арксинус не являются алгебраическими функциями.
 79 Кб, 954x600
79 Кб, 954x600То есть это такая массовая путаница получается? Спрашивают же не просто об алгебраической связи, а вообще о хоть какой-нибудь.
>Is there any connection between the golden ratio
> Is there an identity that links π and ϕ (the golden ratio)?
>Can the golden ratio accurately be expressed in terms of e or π
>о хоть какой-нибудь
Это довольно бессмысленный вопрос. Для любых чисел x и y найдется функция, "выражающая одно через другое. Например,
f (t) = t + y - x => f (x) = y
Понятно, что если не ограничивать себя с выбором функции, можно подобрать и какую-нибудь существующую.
Ну ладно, спасибо. Да хотел поискать другие интересные соотношения между ними, загуглил
connection between pi and golden ratio а выдало кучу ссылок на форумы, ВиО и там больше половины ответов заплюсованных говорят о том, что нет связи и прочее.
что-то я проиграл в голос блять. Там на пи сокращается получается ведь кок раз алгебраическое значение ФИ-то
так ведь можно с чем угодно сделать, с e там и с другими
 5 Кб, 739x96
5 Кб, 739x96Мне нужно знать сколько заливать топлива чтобы хватило точно на определенное количество кругов и в какой максимально поздний момент включать гибридную установку.
Допустим мне нужно проехать 15 кругов с минимальным количеством топлива. Помимо двигателя в машине есть гибридная установка, которая за каждый круг подзаряжается на 4%. И при включении тратит 8% на круг, но сокращает расход топлива с 1.4 до 0.5.
Спасибо.
Нихуя не понял что тебе надо, но тебе скорее всего надо либо в /sci/ либо в /au/ в крайнем случае /vg/.
абсолютно тривиальная задача, решение которой является следствием теоремы Сосницкого
ну посмотри сколько там для конкретной машины уходит топлива/круг, потом умножаешь на кол-во кругов и заливаешь. Это если без гибридной установки. А гибридную установку в таком случае ты можешь включать в любой очень короткий момент до окончания гонки, т.е. dx. Но как я понял тебе надо так штобы допустим у тебя 15 кругов, и ты кароч допустим 13 проехал на топливе, а ещё 2 на установке. Тогда просто составь уравнение что кол-во топлива является m/(m+n), тогда убер-заряд это n(m+n). Ну и делай уравнение для n, когда за несколько кругов идёт заполнение, а потом в два раза быстрее тратишь. Может быть там ещё о мощности получается (1/m если на одном топливе, а 1/(m+n) если на топливе и убере)
Я слишком тупой вопрос задал?
Ну смотри, в предельном положении получается одна сторона равна 0, а две другие равны a. Остаётся только доказать, что ответ не зависит от положения касательной.
Прошу помощи для мотивации.
Я уже всех кого только можно заебал своим нытьём, но, испытаю шанс ещё раз.
В школе не учился (проф.спорт, травма, пропущенная школа). Теперь мне 24 года, год назад взахлёб прочитал книгу Колмогорова "профессия математик", теперь влюблён в эту науку по уши. Однако, мотивации поступать в университет в 25 нет. Старый, кругом будет вчерашняя школота, насмешки, предвзятое отношение и т.д. и т.п. Друзья! Помогите найти мотивацию, чтобы поступить в ВУЗ и заняться наукой. Или добейте до конца.)
 21 Кб, 600x445
21 Кб, 600x445Да ладно, я любя. А нафиг тебе мотивация? В плане, понимаю там мотивация по карьере лезть или учёбу подтягивать. Это ж не тот случай.
Ну, чтобы в 25 поступить в университет, где 99% группы - вчерашние школьники, нужна серьёзная мотивация. Чувствовать себя стариком-аутсайдером в конкуренции с более молодыми студентами в перспективе заняться наукой это не очень хорошо.
Доступ к вычислительным центрам, научным материалам и руководствам, ""корочка"", научный руководитель, работа в лаборатории и т.д. и т.п.
Сейчас быть ученым-одиночкой невозможно
>Сейчас быть ученым-одиночкой невозможно
Неправда. Я два часа назад сегодня доказал, что не существует нечётных совершенных чисел, лол.
Поздравляю
Анус пса))))))))00000000000
Ты хоть школьной программой владеешь? Может лучше тян найдёшь.
На доске элементарная логика для первокурсников. Если точнее - определение формальной теории первого порядка и сбоку, кажется, зайчатки моделей.
> насмешки, предвзятое отношение и т.д. и т.п.
На самом деле нет. В нормальном вузе всем будет плевать, особенно если ты не тупой. Мне сейчас 26, я второкурсник, нормально общаюсь с одногруппниками, никакого барьера из-за возраста нет. А в шарагу идти ради науки бессмысленно.
No fucking idea.
Поступал после школы, но как-то не пошло, забил на всё, отчислили. Предки устроили на завод в родной мухосрани. Я там поработал какое-то время, и понял, что провести вот так всю жизнь я не хочу. Подал заявку на егэ, как выпускник прошлых лет, набрал приличный балл, поступил, учусь. Собственно, вся кулстори.
>Это само егэ
Ну я про него и говорю же. Как-то 26 лет, второй курс, поступал в 24, в 21 писал егэ что ли?
Школу окончил в 2007, егэ писал в 2013, поступил в 2015, скопив достаточно денег.
Ага, тогда понятно.
Платно же только можно второе получать. Да и лучше подкопить, чтобы на работу не отвлекаться, наверное.
Это не второе высшее. Не имеет значения, сколько раз ты поступал, отчислялся и восстанавливался. Если у тебя нет законченного высшего - ты можешь претендовать на бюджет наравне со всеми. Приёмную комиссию интересуют только баллы егэ, а не твой возраст и предыстория.
>Платно же только можно второе получать
This. Хотя на всё время не хватит один хуй. Максимум до следующей зимы растяну. ДС всё-таки.
Второе-то да, но у тебя разве первое есть? Если ни один вуз не выдавал тебе диплом бакалавриата государственного образца, то на бюджет в разные места можно поступать без всяких проблем. Отчислили из одного вуза - можешь по тем же ЕГЭ поступать в другой или даже в этот же самый на этот же факультет (в таком случае даже сданные экзамены автоматически перезачтутся).
>но у тебя разве первое есть?
Ага, есть первое. Я чё и удивился, что егэ у тебя остался, у меня в прошлом вышел, 21 если что. А ты, оказывается, уже потом сдавал.
 152 Кб, 737x763
152 Кб, 737x763> Чтобы в этом убедиться
Поясните, что за преобразования, да и причем тут скалярное умножение?
Но тут ведь говорится про τ и dτ/ds. Потом какие-то не совсем понятные преобразования идут, вроде d(τ²)/ds= 2τ*dτ/ds. Последнее – это что такое и как? Почему не сразу 2τ?
 1,1 Мб, 384x1823
1,1 Мб, 384x1823Очень нужно ее понять. На каком уровне математики надо быть дабы понять эту статью?
Уровне /b
2-3.
Тоже эквидистанта, нет?
Матаны, посоветуйте годный курс по обыкновенным диффурам, только не Хартман и Арнольд. Можно на английском.
Там по урматам, мне обыкновенные нужны.
Понтрягин
Дифференциальные уравнения и вариационное исчисление. Автор: Эльсгольц Л.Э
Математика - любая деятельность, которую считают математикой математики.
Типа того.
Сейчас морфизмик появится, давай на функторах. Пучкнул тебя!
Наука, занимающаяся поиском инвариантов.
Планиметрия. Остальное - мутное гавно шизофреников.
 204 Кб, 484x592
204 Кб, 484x592Наука о землемерии.
Познание вечного бытия.
Числа правят миром через свойства геометрических фигур.
Наука о восполнении и противопоставлении.
Детка не рань меня, больше не рань.
Ну это когда ты типа кольца изучаешь, группы там абелевы, категории, а потом заходишь в тред и громко кричишь ПУЧК ПУЧК ПУЧК.
>Чайковского
Закончил вуз на ебучую службу, работал пол-года что ли.
Дропнул все нахуй и ушел лбом в музыку с нуля, тренировался играть на пианино с помощью нарисованными от руки клавишами.
Великий русский композитор если что.
Ну это такое направление в основаниях математики, что некий объект существует, только тогда когда есть алгоритм, его строющий. Конструктивист обвиняет всех в вере, поскольку мы не пользуемся такими алгоритмами.
Зашквар в форсе и обзывания всех верунами, причем, он сам верит в некоторые аксиомы.
А что такое модули и пучки в двух словах, в чём суть этого эпичного конфликта между старообрядцами и модернистами?
При этом существование алгоритма никак не определяется, лол.
Модуль эта такая хуйня, типа векторного пространства. А пучки невъёбно абстрактная херня для алгебраических геометров.
Суть конфликта в том, что местный форсер-дед начал продвигать идею о том, что математика это наука о модулях над кольцами. Очень жестко он это форсил, в результате появились Пыни-Пучкисты, которые не знали определение модуля, но кричали про их важность. Один из таких дебилов пытался форум создать, но у него ничего не вышло. Далее, мудульнику было определено место у параши и его адептов стали называть пучкистами. Вот и всё. Финита ля ПУЧК.
 11 Кб, 873x43
11 Кб, 873x43Модуль - это обобщение векторного пространства, когда вместо поля используется произвольное кольцо. У модулей появляются необычные свойства - например, не у всякого модуля есть базис.
Топологическим пространством называется множество, в котором выделено семейство подмножеств, замкнутое относительно произвольных объединений и конечных пересечений. Эти подмножества называются открытыми. Топологическое пространство формализует, что такое "быть близко расположенными друг к другу".
Категорией называется совокупность однотипных объектов такая, что для любых двух объектов указано множество морфизмов между ними. Обычно объекты - множества с какой-то математической структурой, морфизмы - сохраняющие эту структуру функции. Например, в категории групп объекты - группы, морфизмы - гомоморфизмы групп. В категории множеств объекты - множества, морфизмы - отображения. Для морфизмов введена ассоциативная операция композиции по аналогии с композицией функций. Причем для каждого объекта есть тождественный морфизм, нейтральный относительно композиции.
Пусть T - топологическое пространство, C - категория групп/колец/небес/Аллахов. Каждому открытому множеству U сопоставляем объект FU категории C. Требуем, чтобы для любого открытого подмножества V данного открытого подмножества U был бы указан морфизм склейки rVU = FU→FV. Причем rUU - тождественный морфизм U, и, кроме того, для любой тройки W⊂V⊂U выполняется равенство rWU = rWV rVU. Это называется предпучок.
Формальнее, рассмотрим категорию T, объектами которой являются открытые подмножества T, а морфизмами - обыкновенные отображения вложения. Предпучок - это контравариантный функтор из T в C.
Пучок - это способ ввести топологию на произвольной категории математических структур. Пусть есть предпучок категории T в категорию C. Мы говорим, что он является пучком, если для любого открытого покрытия произвольного открытого множества U предел функтора F над подкатегорией T, объектами которой являются элементы покрытия, изоморфен FU.
Если хорошо поломать мозг, то станет очевидно, что любую область человеческой деятельности можно рассматривать как теорию когомологий специально подобранных пучков. Но это юмор, а не серьёзный факт.
Модуль - это обобщение векторного пространства, когда вместо поля используется произвольное кольцо. У модулей появляются необычные свойства - например, не у всякого модуля есть базис.
Топологическим пространством называется множество, в котором выделено семейство подмножеств, замкнутое относительно произвольных объединений и конечных пересечений. Эти подмножества называются открытыми. Топологическое пространство формализует, что такое "быть близко расположенными друг к другу".
Категорией называется совокупность однотипных объектов такая, что для любых двух объектов указано множество морфизмов между ними. Обычно объекты - множества с какой-то математической структурой, морфизмы - сохраняющие эту структуру функции. Например, в категории групп объекты - группы, морфизмы - гомоморфизмы групп. В категории множеств объекты - множества, морфизмы - отображения. Для морфизмов введена ассоциативная операция композиции по аналогии с композицией функций. Причем для каждого объекта есть тождественный морфизм, нейтральный относительно композиции.
Пусть T - топологическое пространство, C - категория групп/колец/небес/Аллахов. Каждому открытому множеству U сопоставляем объект FU категории C. Требуем, чтобы для любого открытого подмножества V данного открытого подмножества U был бы указан морфизм склейки rVU = FU→FV. Причем rUU - тождественный морфизм U, и, кроме того, для любой тройки W⊂V⊂U выполняется равенство rWU = rWV rVU. Это называется предпучок.
Формальнее, рассмотрим категорию T, объектами которой являются открытые подмножества T, а морфизмами - обыкновенные отображения вложения. Предпучок - это контравариантный функтор из T в C.
Пучок - это способ ввести топологию на произвольной категории математических структур. Пусть есть предпучок категории T в категорию C. Мы говорим, что он является пучком, если для любого открытого покрытия произвольного открытого множества U предел функтора F над подкатегорией T, объектами которой являются элементы покрытия, изоморфен FU.
Если хорошо поломать мозг, то станет очевидно, что любую область человеческой деятельности можно рассматривать как теорию когомологий специально подобранных пучков. Но это юмор, а не серьёзный факт.
Тут главное с категорными понятиями разобраться. Особенно что такое предел функтора вдоль категории.
Спасибо, я думал что-то серьезное означает. Заодно ещё спрошу, так как нихуя не понял. Сейчас прочел про алгоритм Евклида, ну базовую вещь, что НОД находится с помощью a / b, b / r1 -> r1 / r2 и т.д. Дальше про коэффициенты Безу (расширенный алгоритм Евклида). Вот зачем они нужны? Просто ноль информации для понимания, а в заданиях меня просят порассуждать на эту тему.
Мошу ошибаться, но погугли про цепные дроби, вроде бы расширенный это оно и есть.
что? ссылки где?
У тебя есть какие-то ожидания, которые мешают тебе читать то, что написано. Вместо этого ты пытаешься прочитать то, что ждёшь увидеть; у тебя не получается.
No idea.
Нагуглил Gephi, но она отказывается запускаться с ошибкой "Can´t find the name of Intel ICD openGL driver".
Примеров больше читай, пока один не попадет в цель.
Лол, Михайлов драматург?
А зачем их помнить наизусть? Их суть легко запоминается, если их просто использовать.
Нет, это в корне неверный подход, определения, а также прочий символизм+формализм нужны лишь для того, чтобы как Диофант всё словами в несколько страниц не записывать. Мало того, даже доказательства никто не запоминает, однажды убедившись в истинности утверждения ты легко сможешь сам вывести доказательство.
>однажды убедившись в истинности утверждения ты легко сможешь сам
Лол, ну-ну. Отчасти это так, конечно, но в основном для простых теорем.
Да хуй знает, он очень странный чувак, мне временами кажется, что он на самом деле вообще никакой не математик, придумал себе несколько легенд и живёт несколько разных жизней, и зовут его совсем не так, короче типа дона Хуана.
https://www.youtube.com/watch?v=1FdY01KDfc0
https://www.youtube.com/watch?v=t28DwaZv4eQ
https://www.youtube.com/watch?v=_818e4Sbn7M
https://www.youtube.com/watch?v=jNeRYQSD6mE
>Но выглядеть более странным сошедший с ума матлогик не начинает.
Теорема Эскобара во всей красе.
Аксиома.
 5,1 Мб, webm,
5,1 Мб, webm,640x360
Манин, Доказуемое и недоказуемое. Клини. Мендельсон. Шенфилд. Для говноедов - Колмогоров, Драгалин.
 66 Кб, 480x800
66 Кб, 480x800> ни я, ни я
Окей, ты не сможешь помочь. Надеюсь, что на этой доске не только ты да я да мы с тобой
Следующий вопрос, ребята: Максима может выводить пошаговые решения? Интересует такая возможность как под ондроедом, так и под вендой
Аноны, помогите с задачей за 4 класс.
3 Бублика=6 батонам. Дополните задачу чтобы решить её.
Я придумал такое условие: всего за покупку заплатили 60 рублей.
А т.к батоны в 2 раза дешевле в рублях чем бублики, то выходит 40 и 20 заплатили за все по отдельность.
Теперь вопрос что будет если поделить 60/40? Мы найдем кол-во всех купленных бубликов?
Подпиши к числам единицы измерения, как в физике например, и узнаешь что у тебя получится.
Однако здесь symbolab.com предусмотрено пошаговое решение.
Есть среди вас действительно мощные математики?
Реквестирую формулу для нахождения N-ой цифры числа e.
Для числа Pi изи найти https://habrahabr.ru/post/179829/ , а вот для е почему-то нету :c
Выручайте ананасы!
Я понял почему местные таполаги не смогли ящик решить. Они читают книжки и на задачках из книжек только согласительно кивают и не решают их.
Сам такой был пока не решил решить всего демидовича и на первой же задачке обосрался.
Что тебе мешает решать задачи по тапалогиям и гамалогиям, игнорируя при этом прикладные задачи?
 84 Кб, 1127x674
84 Кб, 1127x674> Демидович - книга для математика а не для прикладника.
> Демидович - книга для математика
Мань, плиз...
Здравствуйте робяты. Дед на связи.
А о какой книге Демидовича вы говорите? У него их очень много:
Сборник задач и упражнений по математическому анализу
Задачи и упражнения по математическому анализу для ВТУЗов
Краткий курс высшей математики
Основы вычислительной математики
Дифференциальные уравнения
Лекции по математической теории устойчивости
Математические основы квантовой механики
Численные методы анализа
* Элементы теории множеств в курсе математического анализа
Берешь полярные координаты дроченые и вставляешь их в область точенную.
Ты же говоришь о мемасах, пучнутый.
ТАк же как и математики не считаю а устанавливают изоморфизмы.
Вконец уже ебанулись.
У тебя если только.
Возможно, но зачем нужна книга, где полезных задач процентов 10? Почему бы не читать книгу, где все задачи нормальные?
Типа вычисление интегралов это ненормально? Лол, твои слова да моей бы преподше в уши, я всё через вольфрам всегда решал, кек. Правда так нихуя и не помню по матеше, но пох.
Охуеть просто, он значит решает, что будет полезно другим только по себе.
Вот ты и обосрался. У тебя тупые придирки, но по факту ты не можешь сказать, почему Демидович книга не для математиков.
Сложно, конечно, понять, что полезность - это крайне субъективное понятие, но ты постарайся.
Если ты считаешь взятие интегралов полезным хоть для кого-то, например, для себя, то приведи пример ситуации, в которой тебе нельзя было пользоваться математическим по и знание кучи дедовских трюков по вычислению неопределенных интегралов тебе помогло.
Тогда зачем ты вообще упоминаешь субъективщину, когда мы тут объективно её оцениваем?
Спор был о том, для математиков это книга или нет, не пытайся сворачивать с темы. И как я вижу, у тебя нет не одного огрумента в свою пользу, кроме визжания о дидах и трюках.
Видимо ты из тех поехавших, для которых вычисления это не математика а инжинерное дело.
> Тогда зачем ты вообще упоминаешь субъективщину, когда мы тут объективно её оцениваем?
Ясно.
> И как я вижу, у тебя нет не одного огрумента в свою пользу, кроме визжания о дидах и трюках.
Вполне конкретный вопрос тебе задал. Пример ты привести не смог.
> Видимо ты из тех поехавших, для которых вычисления это не математика
Ааа, то есть ты с этим не согласен? Ну ясно, я-то думал, что ты не полный даун, а оказался полный.
>Ясно.
Мне вот категории не нужны, значит они бесполезны для математика? Всё, категории теперь - computer science а не часть алгебры.
>Вполне конкретный вопрос тебе задал. Пример ты привести не смог.
Ты не смог привести то, что устарело в Демидовиче, поскольку интегралы не устрели, манька.
>Ааа, то есть ты с этим не согласен? Ну ясно, я-то думал, что ты не полный даун, а оказался полный.
ПУЧК ПУЧК ПУЧК ТОЛЬКО МУДУЛИ НАД КОЛЬЦАМИ ИНТЕГРАЛЫ ДЛЯ ДИДОВ КОЛЬЦА КОГОМОЛОГИИ СИМПЛЕКСОВ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА ПУЧК
ДАУН СЧИТАЕТ ЧТО ВЫЧИСЛЕНИЕ НЕ ИНЖИНЕРНОЕ ДЕЛО НЕ НУ ВЫ ВИДЕЛИ ПУЧК? ЗА ТАКОЕ НА ТИФАРЕТИ УБИВАЮТ
Вообще чего ожидать от дегенерата, который считает, что умение считать не часть математики? Типичный мошеник, лжеч и урод, который только и делает, что вводит других людей в заблуждение. Лживая манька, пытается объявить всё что ей не нравится и что она не понимает не математикой.
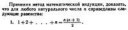 21 Кб, 458x112
21 Кб, 458x112>Мне вот категории не нужны, значит они бесполезны для математика? Всё, категории теперь - computer science а не часть алгебры.
Самое простое: категории нужны для топологии, топология нужна для много чего.
>>4083
>Сам такой был пока не решил решить всего демидовича и на первой же задачке обосрался.
Ты серьезно? Ты тот анон, который чуть ранее плакался, что не понимает мат. индукцию?
>Самое простое: категории нужны для топологии, топология нужна для много чего.
НУ ДЛЯ МИНЯ ЖЕ ОНИ БЕСПОСЛЕЗНЫ ЗНАЧИТ НЕ МАТЕМАТИКА РЯЯЯЯ КАТЕГОРИИ КОМПЬЮТЕР САЕНС А НЕ МАТЕМАТИКА
 151 Кб, 810x1080
151 Кб, 810x1080Метрический тензор иногде представляют как оператор из пространства в его сопряжённое. Видимо, это и имеется в виду.
С дискриминантным - хуй знает. Я не представляю, как он может не существовать, и при чём тут "заданный базис", если тензор - это по определению ковариантная вещь.
g_i,j = e_i * e_j
Нет.
sqrt(abs(x))
Чем он не подходит?
циклоиду гугли
>По себе людей не судят.
>теорию учат, хотя сами едва её понимают, а когда доходит дела до выёбонов на дваче, то просто переписывают определения из книги.
Так а при чём тут "для меня"? И при чём тут компьютер саенс? Речь вроде как была о том, что матпакеты давно считают интегралы лучше людей, поэтому с научной точки зрения это вопрос построения эффективного алгоритма, а не каких-то устаревших кустарных методов. Что такое в категориях компьютер умеет делать лучше человека? Он вообще в них хоть что-то может? Взятие интегралов сейчас - это примерно как строевая подготовка в современной армии. Вещь заведомо рудиментарная, остающаяся в программе в основном потому что "диды считали и мы будем", плюс если их убирать, то нужно их чем-то заменять, и переобучать легион 80-летних дедов, которые в своей жизни ничего кроме интегралов и водовки с картофаном не видели.
Я олимпиадник, так что интегралы считать умею, тут без этого далеко не уедешь. Но олимпиады - это всё-таки спорт, а не наука. Учёному важно уметь не СЧИТАТЬ интегралы, а исследовать их. Куча разных спецфункций определяются или могут быть выражены в интегральной форме, и из неё нужно как-то извлечь их свойства. Но на то это и спецфункции, что такие интегралы ПОСЧИТАТЬ не получится, хоть усрись.
 272 Кб, 1280x720
272 Кб, 1280x720Ну кто бы мог подумать.
Я бы, конечно, мог сдеанониться и предоставить пруфы, но не вижу смысла. Заблуждайся дальше, если хочешь.
Александр Шень
В редакцию журнала "Математическое просвещение"
Олимпиадный культ: основные принципы
1. Каждому школьнику ставится в соответствие некоторый элемент
линейно упорядоченного множества, называемый его олимпиадностью.
2. Каждой задаче ставится в соответствие некоторый элемент
линейно упорядоченного множества, называемый её олимпиадностью.
3. Значения О. школьников и задач не даны нам непосредственно в
ощущениях. О них можно судить по косвенным признакам:
а. О. школьника связана с умением решать задачи высокой О.
б. О. задачи связана с тем, насколько её решение коррелирует
с высокой О. школьника.
(Взаимная рекурсивность а и б приводит к интересным задачам в
области линейной алгебры)
4. Для применения критериев п.3 проводятся массовые ритуальные
жертвоприношения (олимпиады); О. школьника связана с числом О.,
в которых он участвовал, и с характером повреждений ("диплом",
"похвальная грамота" и др.)
5. Пройдя достаточное число ритуалов, участник О. посвящается в
сан Организатора О., имеющего дар судить об О. задач. Наиболее
просветлённые О. О. могут судить также об О. нерешённых ими
задач и незнакомых им школьников.
6. Признаком высокой О. школьника и задачи является её появление
на Вышестоящей О., независимо от обстоятельств такого появления.
Настоящие принципы открыты группой этнографов, в научных целях
принимавших участие в отправлении О. культа в течение ряда лет.
Ими установлено также, что
- нет статистически достоверных результатов о вреде О. культа
для участников О., хотя поклонники О. вовлекают в ритуалы
тысячи школьников; данные о вреде культа для О.О. более
достоверны, но также требуют уточнения;
- хотя поклонники О. и презирают не участвующих в нём, а также
отступников и лиц с малой О., они их не преследуют.
Тем самым нет оснований считать культ О. опасным и
препятствовать его отправлению; напротив, следует отметить
разнообразие и загадочность ритуалов, благодаря которым он
представляет несомненный интерес для этнографии.
Статья представлена 01.04.2002
Александр Шень
В редакцию журнала "Математическое просвещение"
Олимпиадный культ: основные принципы
1. Каждому школьнику ставится в соответствие некоторый элемент
линейно упорядоченного множества, называемый его олимпиадностью.
2. Каждой задаче ставится в соответствие некоторый элемент
линейно упорядоченного множества, называемый её олимпиадностью.
3. Значения О. школьников и задач не даны нам непосредственно в
ощущениях. О них можно судить по косвенным признакам:
а. О. школьника связана с умением решать задачи высокой О.
б. О. задачи связана с тем, насколько её решение коррелирует
с высокой О. школьника.
(Взаимная рекурсивность а и б приводит к интересным задачам в
области линейной алгебры)
4. Для применения критериев п.3 проводятся массовые ритуальные
жертвоприношения (олимпиады); О. школьника связана с числом О.,
в которых он участвовал, и с характером повреждений ("диплом",
"похвальная грамота" и др.)
5. Пройдя достаточное число ритуалов, участник О. посвящается в
сан Организатора О., имеющего дар судить об О. задач. Наиболее
просветлённые О. О. могут судить также об О. нерешённых ими
задач и незнакомых им школьников.
6. Признаком высокой О. школьника и задачи является её появление
на Вышестоящей О., независимо от обстоятельств такого появления.
Настоящие принципы открыты группой этнографов, в научных целях
принимавших участие в отправлении О. культа в течение ряда лет.
Ими установлено также, что
- нет статистически достоверных результатов о вреде О. культа
для участников О., хотя поклонники О. вовлекают в ритуалы
тысячи школьников; данные о вреде культа для О.О. более
достоверны, но также требуют уточнения;
- хотя поклонники О. и презирают не участвующих в нём, а также
отступников и лиц с малой О., они их не преследуют.
Тем самым нет оснований считать культ О. опасным и
препятствовать его отправлению; напротив, следует отметить
разнообразие и загадочность ритуалов, благодаря которым он
представляет несомненный интерес для этнографии.
Статья представлена 01.04.2002
Если попросишь его вычислить определённый интеграл, который Вольфрам не посчитает, он скажет, что это можно сделать на любом языке программирования, но он не какое-то быдлопрограммист, а тополог, если попросишь неопределённый скажет, что в неопределённых смысла нет, так как на практике всё считается только с конкретными значениями, а кроме практики нигде этот картофан под водовку не используется, в отличие от метафизическитеоретической топологии, пучков, категорий и что там ещё в википедии близко расположено. Это ж бред, зачем ты тратишь своё время?
Ездишь по стране (а иногда и за её пределами) за казённый счёт, решаешь интересные задачи, выигрываешь призы. В универе тебя за это любят, физру и всякие психологии с правоведениями закрывают автоматом, стипендию повышенную платят. Годно же.
Оставшиеся 330 дней в году, полагаю.
Это копия, сохраненная 12 ноября 2023 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.







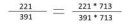
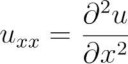
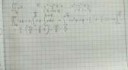
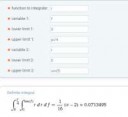
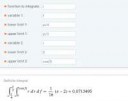


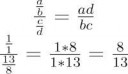




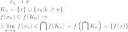
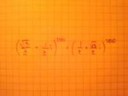




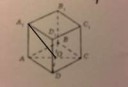





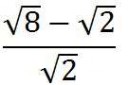
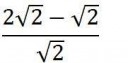
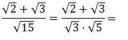



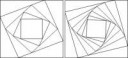
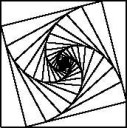
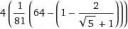
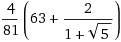


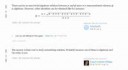
![0.48384400201240206589-3[1].jpg](/math/big/thumb/12775/14908255449440s.jpg)

