Криптовалют тред. - Криптовалюта

Этого треда уже нет.
Это копия, сохраненная 18 июня 2017 года.

Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее

Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

151 Кб, 800x474

Криптовалют тред. 02 Окт, 18:03 #150966 В конец треда | Веб

Есть walletgenerator.net, работающий локально.
И есть возможность выбрать валюту
для генерации адреса, после сбора энтропии.
И много там валют.
И возвращаются в результате, как правило два значения, приватный ключ и адрес кошелька.
И есть блокчейны для этих валют, и возможность просмотреть баланс по адресу.

Вопрос: возможно ли сформировать транзакции локально, и отправить их в соответствующую сеть с помощью приватного ключа?

Кто сколько знает криптовалют которые можно юзать без клиентов, онлайн через их блокчейны?

Ответы150983 151107 151178 151198 151604 151609

1103 Кб, 750x1334

03 Окт, 03:29 #2 #150983

>>150966 (OP)
Блокчейн это бд с данными. Она не умеет в создание транзакций, для этого процесс кошеля нужен, через который все операции и проводятся.

А так, оффлайново сгенерировать транзакцию, зная приватный ключ можно для практически любой монеты. И заслать ее потом через процесс кошелька.

Ответы150985

56 Кб, 1349x943

03 Окт, 08:29 #3 #150985

>>150983
Но блокчейн же вгружает блоки с децентрализованной сети, а значит - имеет с ней связь. Более того, на blockchain.info, при указании приватного ключа, кошелёк добавляется и можно совершать транзакции внутри блокчейна. Значит, блокчейн ещё и может отправлять данные в сеть на обработку, а не только просматривать.
Ясное дело, что и одиночный клиент может создавать транзакции и подписывая их своим приватным ключём - отправлять их в сеть напрямую, но нужна программа.
Мне же интересно приёмо-передача крипты исключительно онлайн, без этих всяких клиентов в десятки мегабайт, и их цепочек блоков в десятки гигабайт...

Вот был, когда-то brainwallet.org, но сейчас почему-то не работает.
Так вот, там было что-то наподобие пикрелейтед.

Ответы150993 151033 151098 151178 151185

03 Окт, 16:48 #4 #150993

>>150985

>блокчейн же вгружает блоки

Для особо тугих: блокчейн это бд с данными. Она ничего не умеет, она просто лежит на дисках.
Сайт блокчейн.инфо всё перечисленное умеет, но это сайт, работающий с блокчейном, а не сам блокчейн.

05 Окт, 00:06 #5 #151016

Коинососы, есть на примете годные краны? Ну что бы много платили и выплата была небольшой, с меня нихуя.

Ответы151018 151020

05 Окт, 00:14 #6 #151018

>>151016
Майни, ебанько.

05 Окт, 00:27 #7 #151020

>>151016
Ось мои любимые + краны с epay:
goo.gl/4Pocgp снизу слева
И вот 3 брата сатоши-выхрёбывателя, выплата после 6к, за раз 125 сатоши минимум
goo.gl/9VqF3j
goo.gl/WG05Zx
goo.gl/6NTMLC

Ответы151026 151037

05 Окт, 10:48 #8 #151026

>>151020
А они не хотят адблок. Больше уйдёт за трафик при загрузке рекламы, чем эти сатоши...

Ответы151035

05 Окт, 20:01 #9 #151033

>>150985
Ты вообще не понимаешь смысл слов, которые произносишь. Вообще, пиздец, поток бреда! Вали обратно в свою чечню!

Ответы151054

05 Окт, 20:52 #10 #151035

>>151026

>2016

>ограниченный трафик

Ответы151056

449 Кб, 286x119

35 Кб, 912x366

05 Окт, 20:59 #11 #151036

Локалбиткоинс ВСЁ?

Ответы151055

05 Окт, 21:35 #12 #151037

>>151020
Пасебо

06 Окт, 00:16 #13 #151054

>>151033
Во-первых, не произношу, а печатаю.
Во-вторых, понимаю.
В-третьих, ты что, читать не умеешь?
В-четвертых, смотри сам туда не свали.
В-пятых, блокчейн - дословно, цепочка блоков.
Блоки на диске. Речь идёт же идёт о blockchain.info и ему подобным сайтам для онлайн переводов имея лишь приватный ключ.

06 Окт, 00:18 #14 #151055

>>151036
Нет, не всё. На walletgenerator.net, помимо биткоина - есть ещё куча разных валют.
Интересует сама технология создания и подписи транзакций приватным ключем с возможностью отправить транзакцию в сеть.

Ответы151058

06 Окт, 00:23 #15 #151056

>>151035
А если я капчую морзянкой по радиоканалу через телефонный модем в 56кбит/сек, с батискафа в Тихом океане?

Ответы151097

06 Окт, 09:14 #16 #151058

>>151055
Так гугли формат транзакций и создание raw транзакций через консоль, хотя бы для биткоина. Берешь, создаешь и отправляешь любому узлу сети, дальше она рассылается сама и включается в блок.

Ответы151098

06 Окт, 19:10 #17 #151097

>>151056
Я вас помню, кстати...

06 Окт, 19:11 #18 #151098

>>151058
Ну так для консоли надо прогу ставить, а интересно онлайн, типа пикчи >>150985

07 Окт, 01:42 #19 #151107

>>150966 (OP)
Смотрите прикол.
http://directory.io/904625697166532776746648320380374280100293470930272690489102837043110636674

Как им удалось на одном сайте разместить
904625697166532776746648320380374280100293470930272690489102837043110636675 страниц?

Можете посчитать сами, сколько это в байтах...

Ответы151108 151124 151134 151606

07 Окт, 08:15 #20 #151108

>>151107
Никак, страницы генерируются на лету.

08 Окт, 16:29 #21 #151124

>>151107
Т. е. 904625697166532776746648320380374280100293470930272690489102837043110636674 всего лишь берется в качестве префикса для генерации приватных ключей?
Вижу в адрес ссылки каждого ключа входит
http://directory.io/warning:understand-how-this-works!/5Km2kuu7vtFDPpxywn4u3NLpbr5jKpTB3jsuDU2KYEqeXFitbFU

sage 09 Окт, 01:02 #22 #151134

>>151107
Ёбнутый, блядь.

10 Окт, 06:29 #23 #151148

чё за говно с рипплом?

48 Кб, 602x787

11 Окт, 19:55 #24 #151178

>>150985
Вот, нашёл.
http://wallet-2sx53n.sakurity.com/#converter
В правом нижнем углу - можно скачать в зипе JS.
Работает локально.

>>150966 (OP)
Вот есть, значит, ECDSA.
И есть пара ключей, приватный ключ и закрытый ключ.
И формат приватного ключа Base58Check.
И есть биткоин-адрес, полученный из открытого ключа по пикрелейтед схеме.
И не светится открытый ключ в адресе, а Ripemd160 его sha256-хеша.

Есть возможность подписать сообщение приватным ключем, и проверить подпись.

Вопрос. Можно ли использовать открытый и закрытый ключи для шифрования сообщений приватным ключем и расшифровки их публичным с помощью ECDSA?
И если да, то как?

Ответы151179 151185 151190

11 Окт, 20:08 #25 #151179

>>151178

>можно скачать в зипе JS. Работает локально.

Не-а. Closed Permanently

Вот, ещё тот старичёк brainwallet, на рыгхосте:
http://rgho.st/6LCyRbn5L

12 Окт, 10:03 #26 #151185

>>151178

>приватный ключ и закрытый ключ.

Это одно и то же. Более того, в ECDSA публичный ключ можно выдернуть из приватного.

>Можно ли использовать ... для шифрования сообщений

Нельзя, DSA алгоритмы могут только подписывать\валидировать подпись. Это не RSA.
>>150985
Обладая приватным ключем можно на любом ПК создать транзакцию и подписать её. Потом в виде json перенести транзакцию на онлайн тачку и транслировать в биткоин-сеть. Такой подход позволяет хранить ключи на машинах, вообще не подключенных к инету.

Ответы151190 151200

12 Окт, 21:05 #27 #151190

>>151185

>Это одно и то же. Более того, в ECDSA публичный ключ можно выдернуть из приватного.

Ну, давай, раз такое дело, зайдём на http://wallet-2sx53n.sakurity.com/#generator
и вобьём туда любой приватный ключ, например 5JBeeb8eAurr2w2LGVGp5Kh4Gph3RLDtYshUUcRmMLE4GmZNDNv,
и посмотрим соответствующий ему публичный ключ 0468ee4a73cc3dfb44f80fd33c22e97c1a458729dad2b924910d5b6c927afd36a3947d8033f36ef687b9c3456d2419739a5a4afcbb68f555d1fd7685ef84c650bb.

Теперь, проследуем в http://wallet-2sx53n.sakurity.com/#converter, и сконвертируем приватный ключ
с base64Check -> в hex, получая вот это 30820113020101042041020101a14403420004a34b99f22c790c4e36b2b3c2c3.
Итак, получилось 32 байта. А длина публичного ключа - 65 bytes.

А теперь, скажи, как из приватного ключа можно выдернуть публичный.
Алсо, на пике >>151178 ты можешь увидеть аж два 32-байтных числа, входящих в публичный ключ.
Такой вопрос напрашивается ещё...
Действительно ли публичный ключ единственный для конкретного приватного ключа.

Ответы151193 151249

13 Окт, 08:27 #28 #151193

>>151190
Ты такие вещи читать можешь?
https://en.bitcoin.it/wiki/Technical_background_of_version_1_Bitcoin_addresses
Наверняка у тебя в публичном только точка x, вместо (0x04,x,y). y вычисляется по x при заданной кривой.
Ключ единственен, адресов биткоин два.

Ответы151194 151196 151249 151341

13 Окт, 08:48 #29 #151194

>>151193
Таки-да. Но там не показано, как вычисляется x.

Поэтому, я тут в параллель, JS brainwallet'a всковырнул, и что я вижу?..
gen_pt = curve.getG().multiply(eckey.priv);

Pub же имеет два представления:
1. Uncompressed - константа 0x04 (признак полной записи),
+ два набора по 32 байта, которые описывают координаты точки x и y.
2. Compressed - координата x.
Поскольку x и уравнения кривой достаточно для восстановления координаты y и при восстановлении возникает неопределенность
в четности восстанавливаемой координаты y - в байтовом виде compressed-public содержит 33 байта,
первый из которых представляет собой одну из двух констант 0x02 или 0x03
(признак короткой записи и указание на четность),
за которым следуют 32 байта координаты x точки.

Ответы151341

13 Окт, 09:27 #30 #151196

>>151193

>Наверняка у тебя в публичном только точка x, вместо (0x04,x,y).

Я же его оставил, выше.

87 Кб, 385x257

13 Окт, 09:35 #31 #151198

>>150966 (OP)

>Кто сколько знает криптовалют

Просто оставлю это здесь:

42coin
Acoin
Alphacoin
Animecoin
Anoncoin
Apexcoin
Auroracoin
BBQcoin
Bitcoin
BitcoinDark
Birdcoin
Blackcoin
BlackJack
BunnyCoin
CanadaeCoin
CannabisCoin
Capricoin
CassubianDetk
CashCoin
Catcoin
Corgicoin
CryptoBullion
CryptoClub
Cryptoescudo
Dash
DeafDollars
Devcoin
Digitalcoin
Dogecoin
DogecoinDark
eGulden
eKrona
Emercoin
EnergyCoin
Fastcoin
Feathercoin
Fibre
Fluttercoin
Freicoin
FUDcoin
Fuelcoin
Fujicoin
GabenCoin
GlobalBoost
Goodcoin
GridcoinResearch
Gulden
Guncoin
HamRadioCoin
HTML5Coin
HyperStake
ImperiumCoin
IncognitoCoin
Influxcoin
IridiumCoin
iCash
iXcoin
Judgecoin
Jumbucks
Latium
Litecoin
LiteDoge
MagicInternetMoney
Magicoin
Marscoin
MarteXcoin
MasterDoge
Mazacoin
Megacoin
MobiusCoin
MonetaryUnit
Monocle
MoonCoin
Myriadcoin
NameCoin
Neoscoin
Novacoin
Nubits
Ocupy
Omnicoin
Onyxcoin
Paycoin
Pandacoin
ParkByte
Pesetacoin
PHCoin
PhoenixCoin
Peercoin
Potcoin
Primecoin
Quark
Reddcoin
Riecoin
Rimbit
Rubycoin
Sambacoin
SecKCoin
SibCoin
SongCoin
SpreadCoin
StealthCoin
Syscoin
Titcoin
TittieCoin
Topcoin
TransferCoin
TreasureHuntCoin
Unobtanium
USDe
Vertcoin
Viacoin
VikingCoin
W2Coin
WankCoin
WeAreSatoshiCoin
WorldCoin
Zetacoin

87 Кб, 385x257

13 Окт, 09:35 #31 #151198

>>150966 (OP)

>Кто сколько знает криптовалют

Показать весь текст

Ответы151199

60 Кб, 3840x2160

13 Окт, 09:38 #32 #151199

>>151198
И Ethereum ещё.

13 Окт, 10:03 #33 #151200

>>151185

>приватный ключ и закрытый ключ.

Имел в виду открытый. Паблик кей.

>Это одно и то же.

ok.

>>Обладая приватным ключем можно на любом ПК создать транзакцию и подписать её. Потом в виде json перенести транзакцию на онлайн тачку и транслировать в биткоин-сеть. Такой подход позволяет хранить ключи на машинах, вообще не подключенных к инету.

Ok.

>Более того, в ECDSA публичный ключ можно выдернуть из приватного.

ok. Через G.

>DSA алгоритмы могут только подписывать\валидировать подпись. Это не RSA.

Ok.
Однако ECIES (или ECDH) жи есть.
Могут ли эти фичи работать с ключами формата ECDSA?
priv - 32 byte, и pub(x, y) - по 256 bit.
Ну, чтоб в крайнем случае - просто выдернуть эти числа из ключей.

Ответы151204

13 Окт, 11:11 #34 #151204

>>151200
Вот, ещё нарыл инфы:
y^2 = x^3 + 7 mod P,
где P = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f, простое.
Gx = 55066263022277343669578718895168534326250603453777594175500187360389116729240,
Gy = 32670510020758816978083085130507043184471273380659243275938904335757337482424,
координаты G.
(Gx^3+7) mod p =
32748224938747404814623910738487752935528512903530129802856995983256684603122
(Gy^2) mod p =
32748224938747404814623910738487752935528512903530129802856995983256684603122

y = sqrt(x^3+7) (mod P) - два значения y1 и y0, положительное и отрицательное.
При этом, y1 = P - y0, и т. к. P - простое, нечётное, то один результатов нечётный, а другой - четный.
Указание чётности в первом байте compressed-адреса даёт возможность
однозначно восстановить y по x.

privatekeyG = publickey, вот тут что?!!

k G doesn't mean (k Gx, k Gy)
X=Gxpriv mod p
Y=Gypriv mod p
I understand '*' is this http://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication operation.
Взято отсюда, https://bitcointalk.org/index.php?topic=456737.0
но там непонятно нифига.

13 Окт, 11:11 #34 #151204

Показать весь текст

Ответы151205 151276

19 Кб, 460x360

13 Окт, 11:28 #35 #151205

>>151204
Точки эллиптической кривой над конечным полем представляют собой группу.
Для этой группы определена операция сложения.
Мы можем представить умножение числа k на точку G как G+G+..+G с k слагаемыми.
C=MG.
The way to do multiplication is "double and add".
You start with G and double it. That gives you 2G. You double again and get 4G and then 8G and so on.
You do this until you have 256 numbers.
A private key is just a number, and you multiply it by G.
If your private key was 25, then you would do it like this
25 = 11001 (in binary)
25 = 16 + 8 + 1
25 G = 16 G + 8 G + 1 * G
You can work out 16G, 8G and G by just doubling G over and over. You then add them together.
16G + 8G + G = 25G
Только вот, как это сделать, если имеется две координаты?..

Ответы151206 151240

13 Окт, 11:43 #36 #151206

>>151205
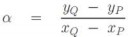
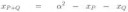
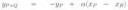
Запишем сложение двух точек в виде формулы: пик1.
Пусть координатами точки P будут (xp, yp), а координатами точки Q соответственно (xq, yq).
Вычислим пик2.
И тогда координаты точки P+Q будут равны: R(пик3, пик4).
Взято с хабра https://habrahabr.ru/post/188958/

Ну ок...
xp = xq = Gx
yp = yq = Gy
α = (Gy-Gy)/(Gx-Gx) = 0/0 (неопределённость).
Пускай будет ноль.

2G = G+G;
2G(-2Gx, -Gy)
Всё верно?

Ответы151993

14 Окт, 01:32 #37 #151240

>>151205

>25 = 11001 (in binary)

>25 = 16 + 8 + 1

>25 G = 16G + 8G + 1G

>16G + 8G + G = 25G

Короче, чтобы получить координаты точки pub(Xpub, Ypub) из priv,
priv бьётся по битам,
эти биты читаются с конца, и первый разряд - нулевой,
Там где бит 0 - ноль пропускается,
а там где бит 1 - приписывается 2^N, где N - номер разряда минус 1 (т. к. первый разряд нулевой),
и точка G удваивается N раз.
Максимум - 2^255, т. е. 255 удвоений точки G,
а потом суммирования всех этих удвоенных точек.
Потому что, 25 = 11001 (in binary) = 2^0 + 0^1 + 0^2 + 2^3 + 2^4 (с конца читаем бинарник).

Так как координату Ypub можно вычислить из P, значит можно её не учитывать в вычислениях, а оперировать только x-ом. Правильно?

Ответы151253

14 Окт, 09:18 #38 #151249

>>151190 >>151193
Охуеть, что случилось с моим /cc/? Двое людей знают матчасть, и ни один из них не я, то есть всего как минимум трое.
Исход трейдеропетушков явно пошёл на пользу.

Ответы151251

47 Кб, 640x430

14 Окт, 09:29 #39 #151251

>>151249

>как минимум трое

Может, чуток больше?

14 Окт, 11:27 #40 #151253

>>151240
Well, you have to start with "G". This point counts as the equivalent of 1.

This point is

Gx = 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
Gy = 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Double

You can double a point (x, y) using the doubling formula

p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

num = 3 x x mod p

dem = 2 y mod p

lambda = num modInverse(dem) mod p

Rx = (lambda lambda) - 2 x mod p
Ry = ((x - Rx) lambda) - y mod p

The result is (Rx, Ry)

Addition

You can add 2 points (x1, y1) and (x2, y2) using

p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

num = (y1 - y2) mod p

dem = (x1 - x2) mod p

lambda = num modInverse(dem) mod p

Rx = (lambda lambda) - x1 - x2 mod p
Ry = ((x1 - Rx) lambda) - y1 mod p

Multiplication

The way to do this is "double and add".

You start with G and double it. That gives you 2G. You double again and get 4G and then 8G and so on.

You do this until you have 256 numbers.

You add some of them together using the add formula. You only include numbers where that bit is one in the binary representation.

There is info on wikipedia, but the formalas are broken at the moment.

This page has the 2 formulas.

A private key is just a number, and you multiply it by G.

If your private key was 25, then you would do it like this

25 = 11001 (in binary)

25 = 16 + 8 + 1

25 G = 16 G + 8 G + 1 G

You can work out 16G, 8G and G by just doubling G over and over. You then add them together.

16G + 8G + G = 25G

Like I said, it is pretty complex and will take a while to actually compute. The modular inverse function is slow.

При Gx1 = Gx2 и Gy1=Gy2
Addition не равно Double и G+G не равно 2G,
так как лямбда нум и дем уходят в нуль.
Хрень какая-то...

14 Окт, 11:27 #40 #151253

Показать весь текст

Ответы151336 151339

14 Окт, 12:43 #41 #151259

Седня по первому каналу про криповалюты говорили в "добром утре"

Ответы151260

14 Окт, 13:08 #42 #151260

>>151259
Лучше бы говорили про манипуляции с точкой G, по эллиптической траэктории.

Ответы151262

14 Окт, 18:33 #43 #151262

>>151260
Годная шуточка, нужно запомнить.

1 Кб, 285x41

1 Кб, 306x42

15 Окт, 11:08 #44 #151276

>>151204

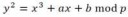
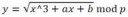
>y = sqrt(x^3+7) (mod P) - два значения y1 и y0, положительное и отрицательное.

При этом, y1 = P - y0, и т. к. P - простое, нечётное, то один результатов нечётный, а другой - четный.
Указание чётности в первом байте compressed-адреса даёт возможность
однозначно восстановить y по x.

А смотрите какая вилка:
1. y2 = (x3 + 8x + 5) mod 293 - уравнение кривой.
2. Точка на этой кривой.
3. Координаты точки x = 29; y = 127;
4. Точка принадлежит кривой:
(x3 + 8x + 5) mod 293 = 24626 mod 293 = y^2 mod 293 = 127^2 mod 293 = 16129 mod 293 = 14;

Однако, sqrt(x3 + 8x + 5) = ±156,92673449734433316074944334497 ≠ 127, а mod 293 ≠ 14 = 17 и 37(если округлить до 157);

В чём дело? Вопрос, возможно ли однозначно вычислить y по x, или нет?

Ответы151284 151285

16 Окт, 01:21 #45 #151284

>>151276

>sqrt(x3 + 8x + 5) = ±156,92673449734433316074944334497 ≠ 127

>В чём дело?

Проиграл. Добро пожаловать в увлекательный мир вычислений в полях классов вычетов по простому модулю.
Следи за пальцами:

x = 29
y = 127
x³ + 8x + 5 = 29³ + 8 x 29 + 5 = 24626 = 84 x 293 + 14 ≡ 14 mod 293
y² = 127² = 16129 = 55 x 293 + 14 ≡ 14 mod 293

Здесь нельзя просто так вычислить корень, а никаких округлений быть не может. Читай теорию чисел, лолка.

Ответы151285 151341

71 Кб, 710x710

16 Окт, 02:04 #46 #151285

>>151284
Ну, я так понимаю, чтобы получить реальную координату Y(127)
- надо не извлекать корень из вот этого кубического многочлена,
а вычислить с него модуль 293,
и прибавлять к этому модулю 293 до тех пор, пока не получится квадрат.
Корень из этого квадрата и есть Y,
при условии, что Y - натуральное число. (А если нет?)

И вот ещё, Y ≠ sqrt(x^3 + ax + b) (mod P),
т. к. уравнение проверки принадлежности точки эллиптической кривой - имеет вид:
Y^2 mod P = (x^3 + ax + b) mod P.

Y^2 mod 293 = (29^3 + 8X + 5) mod 293;
(29^3 + 8X + 5) mod 293 = 14;
Y^2 mod 293 = 14;
14+293 x 55 = 16129 - квадрат;
Y = корень из 16129 = {127, -127}

127^2 = 16129 mod 293 = 14;
16129 - 14/293 = 55 - количество прибавлений числа P к модулю кубического многочлена от P;

Да, это всё хорошо и прекрасно, но смущает число 55, т. е. количество прибавлений P к модулю в этом случае.
При условии работы с 256-битными числами - этих прибавлений может быть over9000,
и поиск Y таким образом, наверное, будет проще заменить его брутфорсом вероятностным, подобно 1-му пикрелейтед.

Алсо, почитал о Cipolla's algorithm и ваще... Мягко-сказать, запутался... Пришлось поднагадить вопросами на странице обсуждения этого алгоритма, в википедии.

Что ещё?.. А, вот!..
Y = корень из 16129 = {127, -127} пик 2.
Положительное и отрицательное. Оба - нечётные.
А должно быть четное и нечётное, ибо >>151276

>y1 = P - y0

Или этих игриков 4?..

71 Кб, 710x710

16 Окт, 02:04 #46 #151285

>y1 = P - y0

Или этих игриков 4?..

Показать весь текст

Ответы151286 151287 151341

24 Кб, 440x317

16 Окт, 02:05 #47 #151286

>>151285
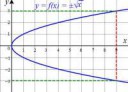
Пик2 отклеился.

16 Окт, 09:30 #48 #151287

>>151285

>Y = корень из 16129 = {127, -127} пик 2.

>Положительное и отрицательное. Оба - нечётные.

-127 ≡ 166 mod 293
А вообще, хуйню несёшь, хохол. Просто хуйню, полнейший бред, не имеющий связи с реальностью.
Я тебе сказал, читай теорию чисел, вычисление в полях классов вычетов по простому модулю.

Ответы151288 151341

16 Окт, 11:26 #49 #151288

>>151287
-127 ≡ 166 mod 293
Вот, теперь понятно. 166 - нечётное, 127 - четное.

-50 mod 11 = 5
Потому что -50 + 5 x 11 = 5 mod 11 = 5;
-50 mod 11 не равно -50/11 = 4 x (11) x [-6], потому, что кольцо. Хотя на калькуляторе - так.

Ну да ладно.

>читай теорию

Начто мне целая теория,
если стоит задача найти 256-битный Y,
по известному x, уравнению кривой, и a, b и P.

Вот, например, здесь: бит.ly / 2eiwbGq
Сообщение m, кодируется точкой Pm, которая имеет две координаты.
Код сообщения M может быть числом, являющимся координатой x.
Значит, надо вычислить y!

Ну и ещё вот, пример.
Есть публичный ключ биткоина, compressed, с одной координатой.
И есть его хеш, соответствующий одному из адресов.
Вычислив y - нужно получить второй адрес.
Как будешь поступать в случае 256-битных чисел,
с этой своей теорией чисел, холоп?

16 Окт, 11:26 #49 #151288

>читай теорию

Показать весь текст

Ответы151291

16 Окт, 13:58 #50 #151291

>>151288

>Как будешь поступать в случае 256-битных чисел, с этой своей теорией чисел, холоп?

Точно так же, как и с любыми другими, дурачок. Минимальная матчасть нужна, чтобы ты понимал, о чём говоришь, а не пытался брать корень привычным методом, оперировать с рациональными числами на множестве натуральных и не совершал другие подобные ошибки.
Когда заботаешь её, то бери любой биндинг к openssl и считай, дело пары часов при совсем кривых руках. Если у тебя аллергия на матан, можешь брать прямо сейчас: быстрее обосрёшься — быстрее сдашься. А ещё можешь попробовать заюзать какую-нибудь библиотеку непосредственно для биткоина.

Ответы151313

16 Окт, 19:27 #51 #151299

Кто-ниудь пытался искать коллизии в sha256?

16 Окт, 19:45 #52 #151302

Например дано 32 битное число, над ним производят операцию rotr 18 ^ rotr 7 ^ shr 3. Можно ли выполнить обратную операцию?

Ответы151309 151312

17 Окт, 00:32 #53 #151309

>>151302
Пошел нахуй пидор

Ответы151312

Аноним 17 Окт, 00:59 #54 #151310

Началось.

Ответы151311

17 Окт, 02:57 #55 #151311

>>151310
#altsbareback

17 Окт, 03:51 #56 #151312

>>151302
#define SHR(x,n) ((x & 0xFFFFFFFF) >> n)
#define ROTR(x,n) (SHR(x,n) | (x << (32 - n)))
После того, как обратишь - можешь прислушаться к этому: >>151309

Ответы151315

17 Окт, 03:58 #57 #151313

>>151291

>Минимальная матчасть нужна

>чтобы ты

>не пытался брать корень привычным методом

√a^2, он и в Африке {a, -a};

Как взять результат из отрицательного числа по модулю, я уже понял:
-a mod p = |(|a| mod P) - P|

>оперировать с рациональными числами на множестве натуральных

А это, где?

>в случае 256-битных чисел

Они, по определению, целые, положительные.

17 Окт, 07:56 #58 #151315

>>151312
Че ты мне реализацию написал, ты мне напиши обратную операцию или объясни почему этого нельзя сделать или расскажи сюрьекцтивна, биктивна или есть ли у нее взамиооднозначное соответствие между входом и выходом
__________________________________________
Еще раз для танкистов, дано 32 битное число x.
Сдвигаем x rotr 18, x rotr 7, x shr3. Ксорим между собой три получившихся числа. Получаем ответ. Вопрос: можно ли не зная исходного числа, только из ответа получить исходное число? То есть выполнить обратную оерацию.

Ответы151317 151319

17 Окт, 10:15 #59 #151317

>>151315
#define S0(x) (ROTR(x, 7) ^ ROTR(x,18) ^ SHR(x, 3))
#define S1(x) (ROTR(x,17) ^ ROTR(x,19) ^ SHR(x,10))

>Ксорим

>три

>числа

Уже нет, потому что надо знать на что идёт xor.
a xor b = c; прямая
c xor b = a; обратная для a
c xor a = b; обратная для b
А у тебя только c;

Ещё бы спросил, как получить e,f,g,h,x,K при известном
temp1 и его формуле:
temp1 = h + S3(e) + F1(e,f,g) + Kx;

Хеши - надо брутфорсить. Лол.

Ответы151423

17 Окт, 11:01 #60 #151319

>>151315
Обозначим биты x как b0, b1, ..., b31
После этих трех операций получится всего четыре числа, каждое из которых записывается через bi (например после rotr 1 будет b31b1b2...b30).
Далее ксорим все 4 числа и получаем новое a0a1a2...
Получается система вида bi xor bj xor bk xor bl = an, где an известны, а bi- нет. Каждое уравнение решается, только если известны все переменные, кроме одной, как и для обычных уравнений. Впринципе, мы имеем 32 уравнения и 32 неизвестных и все должно решаться, если нет вырожденных уравнений, т.е. когда одно типа a xor b xor c, а другое - b xor a xor c, потому что это одно и то же. Я думаю, проверка в лоб может показать, решается ли или нет.

Ответы151320 151321

17 Окт, 11:02 #61 #151320

>>151319
b31b0b1...b30 конечно же.

17 Окт, 11:19 #62 #151321

>>151319
Кстати 32 битное число реально просто сбрутить.

38 Кб, 1116x590

17 Окт, 11:34 #63 #151323

Вот я кратенько набросал чего хочу

Ответы151324 151327 151333 151334 151338 151423

17 Окт, 11:39 #64 #151324

>>151323

>биты результата

>6

>30

>17

>31

>32 байта в 256 битах

Просто оставлю здесь, для тебя
FF = 11111111 = 2^8 = 256;
Ну и... 2^256 заодно.

Ответы151325 151326 151327

17 Окт, 11:41 #65 #151325

>>151324

> разбить кусок на 16 слов длиной 32 бита

17 Окт, 11:44 #66 #151326

>>151324
К чему это вообще здесь, ты тип намекаешь на то что невозможно или что. Хоть объясняй

Ответы151330

17 Окт, 11:45 #67 #151327

>>151323
А ты не потерял 2, 1, 0 в начале shr3 или там нулевые значения в результирующем 32-битном слове?

>>151324
Сори, принял пронумерованные биты за байтовые значения.

Ответы151328

17 Окт, 11:46 #68 #151328

>>151327
Да там 0, их нет смысла писать x^0 = x
Я же написал

17 Окт, 11:56 #69 #151330

>>151326
256 бит = 2^256 комбинаций = 115792089237316195423570985008687907853269984665640564039457584007913129639935 вариантов = 37352286850747159814055156454415 MIPS-лет

Ответы151331

17 Окт, 11:57 #70 #151331

>>151330
А как это относится к моей задаче. Я же не буду в лоб перебирать, так как ты думаешь

13 Кб, 1119x165

17 Окт, 12:11 #71 #151332

Или например так

Ответы151346 151423

17 Окт, 12:18 #72 #151333

>>151323

>там нули

>при xor числа с одинаковой позицией дают 0

C чего взял?

>xor с нулём ничего не даёт

1 xor 0 = 1;

Ответы151344

17 Окт, 12:45 #73 #151334

>>151323
Должен, но слишком муторно. Решение системы, которую я описал выше, методом Гаусса по модулю 2, например, сработает всегда, и даст либо уникальное решение, либо бесконечный набор решений. Формулу для каждого бита может дать метод Крамера, но я не знаю, как его применять в случае модуля 2.

Ответы151335 151345

17 Окт, 13:09 #74 #151335

>>151334
Я так понимаю, ты хочешь вычислить все множества результатов при вполне определённых, конкретных битах на входах, верно?
При этом, прописав эти множества в виде формул и законов в своей проге, для однозначного определения конкретных бит, исходя из заданного результата, входящего в эти множества. Так?
Но, всё-равно - ты получишь только отдельные биты входного значения, а не результат.
Ведь, на вход sha256 может быть подан файл, а не строка.

Ответы151346

23 Кб, 400x313

17 Окт, 13:18 #75 #151336

>>151253

>P = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFF

пффффффф

Ответы151337

17 Окт, 13:25 #76 #151337

>>151336
http://coub.com/view/9aq9i

17 Окт, 13:33 #77 #151338

>>151323
Ты хочешь биткойны майнить sat-солвингом чтоле? Не взлетит, CNF на 4-5 раундов sha2 уже выжрет несколько терабайт.

Ответы151347

17 Окт, 13:53 #78 #151339

>>151253
дабл и адд - разные операции.
адд - только для точек с разными координатами.
Если точки одинаковые, то только дабл.

386 Кб, 844x600

17 Окт, 16:04 #79 #151341

>>151194

>восстанавливаемой координаты y

>>151193

>Наверняка у тебя в публичном только точка x, вместо (0x04,x,y). y вычисляется по x при заданной кривой.

>>151284

>Следи

>теорию чисел

>>151285

>поиск Y

>>151287

>вычисление в полях классов вычетов по простому модулю

>Cipolla's algorithm

>Решаем сравнение по модулю

>Если сравнение имеет решение – квадратичный вычет по mod p – , то имеются два значения y

>Символ Лежандра

>надо вычислить y!

>надо прибавлять P

>пока не получится квадрат

>Потом

>вычислить корень.

>в случае 256-битных чисел

>количество прибавлений

>Максимум

>2^256

>37352286850747159814055156454415 MIPS-лет

>ECDSA, ECIES, ECDH.

Ну, хорошо.
Пускай точки на эллиптической кривой получаются только путём операций с генераторной точкой.
Дабл и адд. К этим двум операциям, с применением мультипликативных и аддитивных инверсий по модулю - сводится умножение, суммирование, вычитание, получение координат обратной точки с координатой (x, -y mod P), и...Деление? Ведь a/b mod P = a x (b^-1 mod P) mod P.

И пускай, есть сообщение r, и соответствующая ей точка rP(x,y).
Задача - получить r из координат точки rP.
Это что? Надо разделить rP на P?? Что будет в результате? Число??? Или точка?!!
Это что, исходя из пикрелейтед надо каждый char кодировать? Или бит? А как декодировать?

Судя по исходникам, эти ваши ECIES и ECDH тупо юзают AES, а не ECC.

386 Кб, 844x600

17 Окт, 16:04 #79 #151341

>>151194

>восстанавливаемой координаты y

>>151193

>Наверняка у тебя в публичном только точка x, вместо (0x04,x,y). y вычисляется по x при заданной кривой.

>>151284

>Следи

>теорию чисел

>>151285

>поиск Y

>>151287

>вычисление в полях классов вычетов по простому модулю

>Cipolla's algorithm

>Решаем сравнение по модулю

>Если сравнение имеет решение – квадратичный вычет по mod p – , то имеются два значения y

>Символ Лежандра

>надо вычислить y!

>надо прибавлять P

>пока не получится квадрат

>Потом

>вычислить корень.

>в случае 256-битных чисел

>количество прибавлений

>Максимум

>2^256

>37352286850747159814055156454415 MIPS-лет

>ECDSA, ECIES, ECDH.

Показать весь текст

Ответы151342 151350 151353

363 Кб, 931x615

17 Окт, 16:51 #80 #151342

>>151341
Причём симметричный AES, где key - это sha256 от координат точки S полученной от ECDH.

17 Окт, 17:34 #81 #151343

Ньюфаг в треде. Подскажи где можно купить биткоины по выгодному курсу?

Ответы151348

17 Окт, 17:42 #82 #151344

>>151333
#31 = 6-й бит ^ 13-й бит ^ значение 0 = 6 бит ^ 13 бит

17 Окт, 17:43 #83 #151345

>>151334
Тыкни пожалуйста где ты написал

17 Окт, 17:57 #84 #151346

>>151335
Я хочу обратить операцию

>s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)

Из алгоритма хеширования
https://ru.wikipedia.org/wiki/SHA-2

Не более.
Вот здесь >>151332 таблица, числа 0, 1, 2...31 над чертой это порядковые номера бит получившегося s0, числа под чертой, например 7, 8, 9,... это порядковые номера бит w[i-15], т.е первая строка под чертой (rotr7 справа) это w[i-15] сдвинутая на 7, втроая строка - w[i-15] сдвинутая на 18, третья- w[i-15] сдвинутая на 3 (я замечу что shr и rotr отличные операции). Так вот получается чтобы получить бит с порядковым номером 0 у s0, нужно поксорить 7, 18 и 3 биты у w[i-15], чтобы получить 1 бит s0, нужно поксорить 8, 19 и 4 биты w[i-15] и т.д. Напомню что задача состоит в нахождении w[i-15] по известному s0. Так вот, можно записать #0 = 7 ^ 18 ^ 3 (# рядом с нулем обозначает что бит с этим порядковым номером принадлежит s0). Так вот теперь можно выразить 7 = #0 ^ 18 ^ 3. Теперь мне нужно так подставить числа, чтобы справа остались только числа с # - то есть выразить например 7 бит через биты s0. И так для всех бит w[i-15]

Ответы151364 151423

17 Окт, 18:03 #85 #151347

>>151338
Спасибо, почитаю по этой теме. Я хочу обратить sha256 хеш. То есть по хешу искать строку, хеш от которой есть исходный хеш. y = sha256(x), мне нужно найти x зная y. Суть в том, что размер хеша фиксирован и составляет 256 бит. А размер x может быть любым, то есть возможны коллизии

Ответы151349 151350

17 Окт, 18:14 #86 #151348

>>151343
btc-e.com

17 Окт, 18:48 #87 #151349

>>151347
Так и гугли сразу sha256 preimage attack, велосипедить-то зачем?

17 Окт, 18:57 #88 #151350

>>151341

>есть сообщение r, и соответствующая ей точка rP(x,y).

>Задача - получить r из координат точки rP.

Ебать ты молодец. Это вообще-то задача, на вычислительной сложности которой строятся криптосистемы на эллиптических кривых. k — приватный ключ, kG — публичный. Если бы можно было просто так вычислить k из kG, как думаешь, стали бы этот алгоритм использовать в битке?
>>151347

>Я хочу обратить sha256 хеш.

Впрочем, судя по всему, тут просто поехавших завезли. А я чёто сперва подумал, что это разговор только умных людей.
Деление для EC и обратных хеш им подавай, пиздец просто, охуительные истории.

Ответы151352 151353 151356

17 Окт, 19:09 #89 #151352

>>151350
Ну а вдруг у него получится и он сюда запостит. Можно будет резко продать квартиру - зашортить биток на все плечи, потом остров купить.

17 Окт, 19:11 #90 #151353

>>151350

>k — приватный ключ, kG — публичный.

Внатуре, только сейчас догнал это.

>Если бы можно было просто так вычислить k из kG, как думаешь, стали бы этот алгоритм использовать в битке?

Ну, публичный ключ не светится же в битке, а только: бейс -> рипемда -> ша -> его.

>Деление для EC

>им подавай

Ну, ты что, внатуре предлагаешь,
для реал ЕСС асимметричной - каждый бит с точкой ассоциировать,
чтоб закодить этими точками сообщение r
из пикрелейтед >>151341
и гнать эти точки по открытому каналу в виде шифротекста, а именно - 256-битных x-ов + 256-битных y-ов для каждого бита?
Или, раз уж на то пошло, может лучше уже сразу массивы байтовых комбинаций прописать в ассоциациях?
Ну а как, тогда, по-другому,
достать Бобу открытый текст, закодированный в точку на EC?

Ответы151354 151355 151363

17 Окт, 19:33 #91 #151354

>>151353

>публичный ключ не светится

Иногда светится, миллионы Сатоши лежат на p2pk адресах.

17 Окт, 19:46 #92 #151355

>>151353

>и гнать эти точки по открытому каналу в виде шифротекста

Тогда ничто не мешает вскрыть исходник и по таблице соответствий восстановить m.
Совсем другое дело - если rP шифруется, и получается в результате декрипта.
Тогда, имеет смысл прописывать соответствия rP значению бита/байта исходного текста r,
Чтобы его извлечь-таки из rP.
И раз уж открытый текст r - лишь множитель генераторной точки, а операция деления точки на точку отсутствует, то разумеется, этот множитель может быть связан с координатами кодируемой точки открытого текста rP - только ассоциативно.
Значит, нужно указать все возможные соответствия всех возможных результатов умножения открытого текста на P всем возможным входным значениям r (или их компонентам). Имеет ли это смысл при длине блока входящей инфы от Алисы в 256-бит?

17 Окт, 19:57 #93 #151356

>>151350
Что такое деление для ЕС

Ответы151357 151363

17 Окт, 20:01 #94 #151357

>>151356
Операция, обратная сложению удвоенных точек в порядке возрастания и в соответствии с битовой последовательностью числа-множителя в бинарном виде.

Ответы151358

17 Окт, 20:46 #95 #151358

>>151357
Бля, тебе за знаки что ли платят? Это умножением назыается.

Ответы151360

17 Окт, 21:13 #96 #151360

>>151358
Какие такие, знаки?

>Операция, обратная

Умножению точки на числовую константу.
Потому что точку на точку умножать неизвестно как.

324 Кб, 818x1854

18 Окт, 00:07 #97 #151363

>>151353

>публичный ключ не светится же в битке

Светится, при отправке ты его должен вписать в транзакцию, иначе её никто не сможет проверить.
>>151356

>Что такое деление для ЕС

Пикрелейтед. Операция, обратная умножению точки на число, ага. Преобразование (kG, G) -> k. Вычислительно сложное настолько, что не существует известных алгоритомов, позволяющих осуществить её быстрее, чем перебором всех возможных значений.
Наверное.

Ответы151369 151385

18 Окт, 00:21 #98 #151364

>>151346

> Я хочу обратить операцию

>s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)

Еще раз:
Исходное число: w32w31w30...w2w1
После rotr 7: w7w6...w1w32...w8
После rotr 18: w18w17...w1w32...w17
После shr 3: 000w32w31...w4
После xor пусть получается число a32a31a30...a2a1
где
a32 = w32 ^ w7 ^ w18
a31 = w31 ^ w6 ^ w17
...
a1 = w1 ^ w8 ^ w17 ^ w4

a32, a31, ..., a1 известны
w32, w31, ..., w1 - неизвестные, их надо найти, 32 переменных
Выше записано 32 уравнения. Если среди них нет зависимых, то система всегда решается и дает тебе ответ. Например, методом Гаусса со всеми операциями по модулю 2. Если есть зависимые, то будет набор решений. Полагаю, может быть и так, и так, зависит от w.

Ответы151365 151371 151417 151419 151423

18 Окт, 00:44 #99 #151365

>>151364
На простом примере:
надо обратить x xor (x ror 1), где x - 4битовый
Пусть x = 0101
x ror 1 = 1010
x xor (x ror 1) = 1111, это исходные данные.

Теперь x неизвестен.
x = x4x3x2x1
x ror 1 = x1x4x3x2
x xor (x ror 1) = 1111
1 = x4 ^ x1 (^ - xor для краткости)
1 = x3 ^ x4
1 = x2 ^ x3
1 = x1 ^ x2
В матричной форме:
1001|1
1100|1
0110|1
0011|1
Например, первая строка означает 1x4 ^ 0x3 ^ 0x2 ^ 1x1 = 1 (mod 2)
Одно зависимое, выкинем:
1100|1
0110|1
0011|1

x3 ^ x4 = 1
Либо x3 = 0, x4 =1, тогда решая дальше получим 0101
либо x3 = 1, x4 = 0, тогда получим 1010.
Оба ответа подходят для x xor (x ror 1) = 1111.

Следуя этой логики можно перейти к любой битности и любым хэшам. Только зачем, вот вопрос.

18 Окт, 00:44 #99 #151365

Показать весь текст

Ответы151366 151371 151376 151377 151379

18 Окт, 00:45 #100 #151366

>>151365

> логики

логике

18 Окт, 08:35 #101 #151369

>>151363

>ты его должен вписать

С чего бы это в ECDSA?

https://ru.wikipedia.org/wiki/ECDSA#.D0.92.D1.8B.D1.87.D0.B8.D1.81.D0.BB.D0.B5.D0.BD.D0.B8.D0.B5_.D1.86.D0.B8.D1.84.D1.80.D0.BE.D0.B2.D0.BE.D0.B9_.D0.BF.D0.BE.D0.B4.D0.BF.D0.B8.D1.81.D0.B8

Ответы151370

18 Окт, 08:38 #102 #151370

>>151369
Ой, сори, в следующем же разделе, не узрел открытого ключа Q.

18 Окт, 08:39 #103 #151371

>>151364
Да именно это, теперь можно пытаться решить подставляя одно уравнение в другое и пытаться найти зависимости, которые однозначно укажут как n-й бит w зависит от битов a. Ладно, можно попробовать не искать прямой ответ вида: wn = ax ^ ay ^ az ^ ... (где n, x, y - порядковые номера битов). Но что если найти множество уравнений вида: wn = ax ^ ay ^ az ^ ... ^ wj (где n, x, y, j - порядковые номера битов, где wj - один операнд с типом w. То есть после этого можно записать:
wn = res_a1 ^ wj ( где res_a = ax ^ ay ^ az ^ ... )
wn = res_a2 ^ w(j+1)mod32
...
wn = res_a32 ^ w(j+31)mod32

И так для n от 1 до 32.
А уже после их проанализировать и составить зависимости. Я например нашел некоторые зависимости, что мешает найти их большую часть и исключить неопределенность определения бита(то есть найти однозначную зависимость одного бита от другого как я написал выше)

>>151365
Как ты получил матричную форму? Как ты определил зависимое?

Ответы151372 151373

18 Окт, 09:08 #104 #151372

>>151371
Попробуй заполнить эти свои строки битов для ротра и шифта - единицами.
И пропустить потом, циклом через каждый бит первой строки - ноль, глядя на то, какие биты изменяется у шр3.
А потом, через каждый бит второй строки, третьей... Так?

Ответы151374

18 Окт, 09:22 #105 #151373

>>151371
Не надо пытаться подставлять, эта система всегда решается за 2 прохода. Другое дело, что уже на этапе одного такого преобразования возникают коллизии.

Зависимое есть, т.к. детерминант матрицы
1001
1100
0110
0011
равен 0.

8 Кб, 779x218

18 Окт, 09:36 #106 #151374

>>151372
В одном столбике не может быть нечетного числа нулей

Ответы151409 151423

18 Окт, 09:53 #107 #151375

Ладно, я понял, почитаю метод Гаусса

18 Окт, 10:03 #108 #151376

>>151365

>x xor (x rotr 1) = 1111

>x1 = 0101, x1 rotr 1 = 1010; 0101 xor 1010 = 1111

>x2 = 1010, x2 rotr 1 = 0101; 1010 xor 0101 = 1111

Это хотел сказать?

18 Окт, 10:53 #109 #151377

>>151365
x = 1100 = x3x2x1x0
x rotr1 = 0110
y = x ^ (x rotr1) = 1010 = y3y2y1y0

y3y2y1y0
---------
x3x2x1x0
x0x3x2x1

y0 = x0 ^ x1
y1 = x1 ^ x2
y2 = x2 ^ x3
y3 = x3 ^ x0
_____________

x0 = y0 ^ x1 = 0 ^ x1
x0 = y0 ^ y1 ^ x2 = 1 ^ x2
x0 = y0 ^ y1 ^ y2 ^ x3 = 1 ^ x3

x1 = y1 ^ x2 = 1 ^ x2
x1 = y1 ^ y2 ^ x3 = 1 ^ x3
x1 = y1 ^ y2 ^ y3 ^ x0 = 0 ^ x0

x2 = 0 ^ x3
x2 = 1 ^ x0
x2 = 1 ^ x1

x3 = 1 ^ x0
x3 = 1 ^ x1
x3 = 0 ^ x2

Пусть x2 = 0:
x3 = 0
x0 = 1
x1 = 1
x3x2x1x0 = 0011 - первый ответ

Пусть x2 = 1:
x3 = 1
x0 = 0
x1 = 0
x3x2x1x0 = 1100 - второй ответ

Оба удовлетворяют если подставить
1010 = 1100 ^ (1100 rotr1)
1010 = 0011 ^ (0011 rotr1)

18 Окт, 10:53 #109 #151377

Показать весь текст

Ответы151378

18 Окт, 11:38 #110 #151378

>>151377
А посмотри, что у меня:

31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0
0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1| x input

1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0| x1 rotr7
0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1| x2 rotr13
0|0|0|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0| x3 shr3

1|1|1|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1|0|1| output x1^x2^x3

Результат - побитово равен части x2;

Ответы151380 151382

18 Окт, 11:41 #111 #151379

>>151365
Я понял

>1x4 ^ 0x3 ^ 0x2 ^ 1x1 = 1 (mod 2)

гениально, нули же ничего не дают, то же что и x4 ^ x1

>Либо x3 = 0, x4 =1

Здесь достаточно взять x3 = 0 или 1, x4 получится "само"
Если x3 = 0, x4 = 1, x2 = 1, x1 = 0: получится 1010

>Следуя этой логики можно перейти к любой битности и любым хэшам. Только зачем, вот вопрос.

Вот здесь не понял вопроса, что значит перейти к любой битности, в твоем примере ты получаешь 2 ответа, это значит что для каких-то двух x, результат x xor (x ror 1) будет одинаковым, а значит функция сюръективна. Не факт что моя функция сюръективна

18 Окт, 11:42 #112 #151380

>>151378
31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|
1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|

1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|
1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|
0|0|0|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|

0|0|0|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|1|

__________________________________________________________________________________
31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|
0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|

0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|
0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|
0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|

0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|

Ответы151381 151382

18 Окт, 11:48 #113 #151381

>>151380
Однако, вот:
31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|

0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|1|1|1|0|0|0|0|0|0|0|0|0|

0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|1|1|1|0|0|
0|0|0|0|0|0|1|1|1|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|
0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|1|1|1|0|0|0|0|0|0|

0|0|0|0|0|0|1|1|1|0|0|0|0|0|0|0|0|0|0|0|0|0|0|1|1|1|0|1|1|1|0|0|

Ответы151382 151383

18 Окт, 11:50 #114 #151382

>>151378
>>151380
>>151381
Ну да, видно что-то, но к чему это?

Ответы151384

18 Окт, 11:54 #115 #151383

>>151381
31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|
1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|

1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|
0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|
0|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|

1|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|0|0|1|1|
__________________________________________________________________________________

18 Окт, 11:56 #116 #151384

>>151382
Чтобы ты увидел, это.

Ответы151386

18 Окт, 12:00 #117 #151385

>>151363
Ну, вот есть у тебя kG, и есть у тебя k.
Разве нельзя kG разелить на k/2 и получить 2G?

Ответы151398 151454

18 Окт, 12:01 #118 #151386

>>151384
Ну то что результат не особо отличается (а вернее он просто сдвинут) но задачу это не решает. Для "некрасивого" набора бит вида
0101 0010 0001 0101 0011 1010 1110 0110 не проследишь

Ответы151387 151401 151404

18 Окт, 12:02 #119 #151387

>>151386
Задай набор из 32-х бит, я прослежу.
Я уже и говнокод на пыхэпе настрочил для этого.

Ответы151388 151389 151401

18 Окт, 12:04 #120 #151388

>>151387
Да зачем, я тоже настрочил, а смысл, это бред. Нужно искать правила как один бит зависит от других

Ответы151391

18 Окт, 12:05 #121 #151389

>>151387
Ты мне обратную функцию найди

Ответы151393

18 Окт, 12:14 #122 #151391

>>151388

>как один бит зависит от других

А вот так вот:

a|b|c|a^b^c
0|0|0|1
0|0|1|1
0|1|0|1
0|1|1|0
1|0|0|1
1|0|1|0
1|1|0|0
1|1|1|1

Ответы151392 151409

18 Окт, 12:16 #123 #151392

>>151391

>0|0|0|1

Не правильно

Ответы151394

18 Окт, 12:18 #124 #151393

>>151389

>расскажи сюрьекцтивна, биктивна или есть ли у нее взамиооднозначное соответствие между входом и выходом

Функция, обратная тройному xor - многозначна? Очевидно же.
Через обратный shr и rotr ты можешь сузить количество её значений.

Ответы151395

18 Окт, 12:19 #125 #151394

>>151392
Да. Там 0.

18 Окт, 12:20 #126 #151395

>>151393
Так именно, суть в том что там 2 rotr и shr и им всем надо удовлетворить.

Ответы151397

18 Окт, 12:21 #127 #151396

Ладно, короче, буду решать по своему методу, никто не в силах

18 Окт, 12:26 #128 #151397

>>151395
ну так пропиши по 4 варианта входных значений для каждого бита результата тройного xor,
и сопоставь затем их так, чтобы если результат не накладывается при обратном rotr и shr - чтобы выбирался другой.

18 Окт, 12:39 #129 #151398

>>151385
Имелось в виду деление точки на числовую константу.

Если k не простое, разумеется...

18 Окт, 14:37 #130 #151401

>>151387 а вот же он: >>151386

>0101 0010 0001 0101 0011 1010 1110 0110

31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|
0|1|0|1|0|0|1|0|0|0|0|1|0|1|0|1|0|0|1|1|1|0|1|0|1|1|1|0|0|1|1|0|

1|1|0|0|1|1|0|0|1|0|1|0|0|1|0|0|0|0|1|0|1|0|1|0|0|1|1|1|0|1|0|1|
0|1|0|0|1|1|1|0|1|0|1|1|1|0|0|1|1|0|0|1|0|1|0|0|1|0|0|0|0|1|0|1|
0|0|0|0|1|0|1|0|0|1|0|0|0|0|1|0|1|0|1|0|0|1|1|1|0|1|0|1|1|1|0|0|

1|0|0|0|1|0|0|0|0|1|0|1|1|1|1|1|0|0|0|1|1|0|0|1|1|0|1|0|1|1|0|0|

Ответы151402 151406

18 Окт, 14:55 #131 #151402

>>151401
Поехавший

Ответы151403

18 Окт, 15:27 #132 #151403

>>151402
C чего бы это?

18 Окт, 16:12 #133 #151404

>>151386

> Для "некрасивого" набора бит вида

0101 0010 0001 0101 0011 1010 1110 0110 не проследишь
Это число является одним из прообразов:
11110101011110111000000010101100

Ответы151405 151406 151410 151412 151413

13 Кб, 924x498

18 Окт, 16:13 #134 #151405

>>151404

Ответы151406 151407 151410 151412 151414

18 Окт, 16:15 #135 #151406

>>151405
>>151404
Выведи 11110101011110111000000010101100 пожалуйста в виде таблицы
>>151401

>>151405
Что за язык

Ответы151410

18 Окт, 16:27 #136 #151407

>>151405
Нет, у меня не получается

1111 0101 0111 1011 1000 0000 1010 1100

1110 0000 0010 1011 0011 1101 0101 1110
1001 1110 1010 1111 0111 0000 0001 0101
0010 0111 0110 1110 1011 1010 0100 1010

0010 0111 0110 1110 1011 1010 0100 1010 не равно 1111 0101 0111 1011 1000 0000 1010 1100

Ответы151408 151410

18 Окт, 16:34 #137 #151408

>>151407
Поторопился
1111 0101 0111 1011 1000 0000 1010 1100

0101 1001 1110 1010 1111 0111 0000 0001
1110 0000 0010 1011 0011 1101 0101 1110
0001 1110 1010 1111 0111 0000 0001 0101

1010 0111 0110 1110 1011 1010 0100 1010

1010 0111 0110 1110 1011 1010 0100 1010 не равно 1111 0101 0111 1011 1000 0000 1010 1100

Ответы151410

18 Окт, 16:35 #138 #151409

>>151374
Давай, исходя из пикчи >>151374 и пофиксенноно нулём >>151391

рассмотрим бит N результата Y при значении 1.
Обратная функция двойного xor даёт 4 варианта значений, для N-го бита:
x1[N], x2[N], x3[N].
Эти значения - [1, 0, 0]; [0, 0, 1]; [0, 1, 0]; [1, 1, 1], соответственно.
Так вот, твоя задача - отобрать из всех таких вариантов те, и только те,
в которых значения удовлетворяют следующим условиям:
x1[N] = x2[(N-11) mod 32] = x3[(N+4) mod 32],
x2[N] = x1[(N+11) mod 32] = x3[(N-17) mod 32],
x3[N] = x1[(N-4) mod 32] = x2[(N+17) mod 32],
И так, по всем N.
Все результаты, не вписывающиеся в эти условия - удаляй с помощью unset,
и ты получишь непрерывную последовательность
сцепленных, таким образом троек бит.

Ответы151411

18 Окт, 16:45 #139 #151410

>>151404

>0101 0010 0001 0101 0011 1010 1110 0110

>11110101011110111000000010101100

Не оно.
>>151406
Этот >>151405 - не я.

>Что за язык

у меня - php;

>Выведи 11110101011110111000000010101100 пожалуйста в виде таблицы

На.
31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|
1|1|1|1|0|1|0|1|0|1|1|1|1|0|1|1|1|0|0|0|0|0|0|0|1|0|1|0|1|1|0|0| input

0|1|0|1|1|0|0|1|1|1|1|0|1|0|1|0|1|1|1|1|0|1|1|1|0|0|0|0|0|0|0|1| rotr7
1|1|1|0|0|0|0|0|0|0|1|0|1|0|1|1|0|0|1|1|1|1|0|1|0|1|0|1|1|1|1|0| rotr17
0|0|0|1|1|1|1|0|1|0|1|0|1|1|1|1|0|1|1|1|0|0|0|0|0|0|0|1|0|1|0|1| shr3

1|0|1|0|0|1|1|1|0|1|1|0|1|1|1|0|1|0|1|1|1|0|1|0|0|1|0|0|1|0|1|0| output

>>151407
А это - правильно?
Ой, ты ж не поксорил.
>>151408

>1010 0111 0110 1110 1011 1010 0100 1010

Да.

>не равно 1111 0101 0111 1011 1000 0000 1010 1100

Это же вход.

P.S.: Кто нибудь сможет поделить точку на число на эллиптической кривой?

18 Окт, 16:45 #139 #151410

>>151404

>0101 0010 0001 0101 0011 1010 1110 0110

>11110101011110111000000010101100

Не оно.
>>151406
Этот >>151405 - не я.

>Что за язык

у меня - php;

>Выведи 11110101011110111000000010101100 пожалуйста в виде таблицы

>1010 0111 0110 1110 1011 1010 0100 1010

Да.

>не равно 1111 0101 0111 1011 1000 0000 1010 1100

Это же вход.

P.S.: Кто нибудь сможет поделить точку на число на эллиптической кривой?

Показать весь текст

Ответы151412

18 Окт, 16:53 #140 #151411

>>151409
Там, в x3, ещё нули прописать надобно же.

18 Окт, 17:03 #141 #151412

>>151410
>>151405
>>151404
То есть, получается, работает. Как только я разберусь, я тебя похвалю

Ответы151413

18 Окт, 17:11 #142 #151413

>>151412
11110101011110111000000010101100 = x
01011001111010101111011100000001 = x rotr 7
11100000001010110011110101011110 = x rotr 18
00011110101011110111000000010101 = x shr 3
01010010000101010011101011100110 = xor этих четырех
Оно. >>151404

Ответы151416 151428

18 Окт, 17:12 #143 #151414

>>151405
Это матпакет wolfram mathematica. Заебался писать это и отлаживать.

Ответы151415

18 Окт, 17:17 #144 #151415

>>151414
А ты не можешь вкратции описать идею?

Ответы151417

18 Окт, 17:22 #145 #151416

>>151413

>rotr 18

Почему 18?

>xor этих четырех

Почему 4-х?
Ты что, тройной ксор врубил?

А ну, давай проверю:
11110101011110111000000010101100 xor
01011001111010101111011100000001 =
10101100100100010111011110101101 xor
11100000001010110011110101011110 =
01001100101110100100101011110011 xor
10101100100100010111011110101101 =
01010010000101010011101011100110. Да.

Ответы151428

18 Окт, 17:28 #146 #151417

>>151415
Без проблем.
>>151364

Ответы151418

18 Окт, 17:29 #147 #151418

>>151417
Метод Гаусса?

Ответы151421

18 Окт, 17:44 #148 #151419

>>151364
Нифига не соответствует намаляканным пикчам.

Ответы151420

18 Окт, 17:46 #149 #151420

>>151419
Каким пикчам? Конкретнее

Ответы151423

18 Окт, 17:52 #150 #151421

>>151418
LinearSolve, фиг его знает, чем он там решает. Все остальное - просто всякие переводы в нужные форматы, создание матрицы коэффициентов и проверка.

Ответы151424

18 Окт, 17:58 #151 #151423

>>151420

>a1 = w1 ^ w8 ^ w17 ^ w4

Вот это, отсюда: >>151364
не соответствует вот этому:

>s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)

отсюда: >>151346
этому

>#define S0(x) (ROTR(x, 7) ^ ROTR(x,18) ^ SHR(x, 3))

#define S1(x) (ROTR(x,17) ^ ROTR(x,19) ^ SHR(x,10))
отсюда: >>151317

и пикчам >>151323 >>151332 >>151374

эллиптический ОП-кун, с таблицами из палочек.

Ответы151424

18 Окт, 18:01 #152 #151424

>>151421
Спасибо, ты гений
>>151423

>a1 = w1 ^ w8 ^ w17 ^ w4

То видимо опечатка, естественно без w4

>#define S0(x) (ROTR(x, 7) ^ ROTR(x,18) ^ SHR(x, 3))

>s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)

Одно и тоже
Пикчи формируют образ

Ответы151425 151428

18 Окт, 18:02 #153 #151425

>>151424
Вернее
a1 = w8 ^ w19 ^ w4

Ответы151426

18 Окт, 18:04 #154 #151426

>>151425
Хотя да, тут криво как-то

>После xor пусть получается число a32a31a30...a2a1

где
a32 = w32 ^ w7 ^ w18
a31 = w31 ^ w6 ^ w17
...
a1 = w1 ^ w8 ^ w17 ^ w4

18 Окт, 18:04 #155 #151427

Ну суть ясна

18 Окт, 18:05 #156 #151428

>>151424

>То видимо опечатка, естественно без w4

>Пикчи формируют образ

В коде и пикчах - 3 значения и два xor'a,
а тут >>151413 >>151416
и тут:

>>a1 = w1 ^ w8 ^ w17 ^ w4

4 значения и 3 xor'a
[soiler], и сходится.[/spoiler]

Ответы151429 151433

18 Окт, 18:11 #157 #151429

>>151428
Ахаха крыша поехала

11110101011110111000000010101100 = x
--------------------------------------------------------
01011001111010101111011100000001 = x rotr 7
11100000001010110011110101011110 = x rotr 18
00011110101011110111000000010101 = x shr 3
--------------------------------------------------------
01010010000101010011101011100110 = xor этих четырех
--------------------------------------------------------
10100111011011101011101001011010 = (x rotr 7) ^ (x rotr 18) ^ (x shr 3)
--------------------------------------------------------
Действительно, нам-то нужен xor трех

Ответы151430 151431 151438

18 Окт, 18:14 #158 #151430

>>151429
НЕТ
Все совпадает, я ошибся в 5 бите там 0

18 Окт, 18:14 #159 #151431

>>151429
А, ну извините. Это я проебался, поксорив четыре. Но общей сути не меняет.

18 Окт, 18:18 #160 #151432

11110101011110111000000010101100 = x
01011001111010101111011100000001 = x rotr 7
11100000001010110011110101011110 = x rotr 18
00011110101011110111000000010101 = x shr 3
01010010000101010011101011100110 = xor этих четырех
10100111011011101011101001011010 = (x rotr 7) ^ (x rotr 18) ^ (x shr 3)

>некрасивое число 0101 0010 0001 0101 0011 1010 1110 0110

И что это, почему тройной ксор дает то что должен давать двойной ксор, ааааа

Ответы151442

18 Окт, 18:20 #161 #151433

>>151428

>сходится

Сходится в том плане, что:
x = 11110101011110111000000010101100;
y = ROTR(x, 7) ^ ROTR(x,18) ^ SHR(x, 3) =
10100111011011101011101001001010;

а y ^ ROTR(y, 7) ^ ROTR(y,18) ^ SHR(y, 3) =
11110101011110111000000010101100;

Но это - совпадение и наёбка, а не обратная функция.
Потому, что:
11010001100010111101000010110010 input
01100101101000110001011110100001 rotr8
11110100001011001011010001100010 rotr18
00011010001100010111101000010110 shr3
10001011101111101101100111010101 output
10101011000101110111110110110011 output_rotr8
10110110011101010110001011101111 output_rotr18
00010001011101111101101100111010 output_shr3

output ^ output_rotr8 ^ output_rotr18 ^ output_shr3
= 10000111101010110001110110110011
≠ 11010001100010111101000010110010

Тред, с криптовалют - плавно перетёк в ECC (что ещё куда не шло),
и в rotrы ебучие.

18 Окт, 18:20 #161 #151433

>>151428

>сходится

Показать весь текст

18 Окт, 18:24 #162 #151434

11101100111101110111100101001000 прообраз для 01010010000101010011101011100110 для функции (x rotr 7) ^ (x rotr 18) ^ (x shr 3)

Ответы151435 151436

18 Окт, 18:25 #163 #151435

>>151434
11101100111101110111100101001000 = x

10010001110110011110111011110010 = x rotr 7
11011110010100100011101100111101 = x rotr 18
00011101100111101110111100101001 = x shr 3

01010010000101010011101011100110 = xor этих трех

18 Окт, 18:25 #164 #151436

>>151434
А он один или их несколько?

Ответы151437

18 Окт, 18:26 #165 #151437

>>151436
Скорее всего, несколько.

18 Окт, 18:26 #166 #151438

>>151429
Хули ты пиздишь?

Ответы151439

18 Окт, 18:28 #167 #151439

>>151438
x ^ (x rotr 7) ^ (x rotr 18) ^ (x shr 3) дает такой же результат какой должен давать (x rotr 7) ^ (x rotr 18) ^ (x shr 3)

Ответы151442

18 Окт, 18:31 #168 #151440

Ладно, ВСЕ, анон с вольфрамом гений

Ответы151441

18 Окт, 18:40 #169 #151441

>>151440
http://freetexthost.com/eanerf40x6

18 Окт, 18:54 #170 #151442

>>151432

>И что это, почему тройной ксор дает то что должен давать двойной ксор, ааааа

>>151439

>x ^ (x rotr 7) ^ (x rotr 18) ^ (x shr 3) дает такой

>же результат какой должен давать

>(x rotr 7) ^ (x rotr 18) ^ (x shr 3)

А там же xor на результат предыдущего xor'a, вот и совпадение получилось.

Задолбали со своими ксорами. Обратить-то получилось?

И ваще, ITT, EC, ECC (ECDSA, ECIES и ECDH) и точка G обсасывается, а не эти всякие, брутфорсы хешей.
ОП

Ответы151443

18 Окт, 19:21 #171 #151443

>>151442
Непонятно как устроен вольфрамовый молот

Ответы151444

18 Окт, 19:30 #172 #151444

>>151443
http://peshera.org/khrono/Fotos-03/foto-281.jpg

18 Окт, 19:49 #173 #151445

dim = 32; //константа
ROR[x_, k_] := FromDigits[RotateRight[IntegerDigits[x, 2, dim], k], 2]; //функция сдвига
y = FromDigits["01010010000101010011101011100110", 2];
Em = IdentityMatrix[dim];//создаем квадратную матрицу 32х32
mtx = RotateRight[Em, 7] + RotateRight[Em, 18] +Transpose[RotateLeft[ReplacePart[Em, {{1}, {2}, {3}} -> ConstantArray[0, dim]], 3]]; //непонятно как можно сдвинуть матрицу. ReplacePart[Em, {{1}, {2}, {3}} -> ConstantArray[0, dim]] - заменить 1, 2, 3 столбец нулями и потом сдвинуть влево?Непонятно что делает transpose. Затем сложение ?
mtx = Mod[mtx, 2]; //представляем все числа внутри по модулю 2
BaseForm[y, 2] //выводим y в двоичной форме
ans = FromDigits[LinearSolve[mtx, IntegerDigits[y, 2, dim], Modulus -> 2], 2];//finds an x that solves the matrix equation m.x==b.
BaseForm[ans, 2] //выводим ответ
BaseForm[BitXor[ROR[ans, 7], ROR[ans, 18], BitShiftRight[ans, 3]], 2] //проверка

Ответы151446 151447

18 Окт, 19:53 #174 #151446

>>151445
Хотя понятно как сдвинуть, непонятно что внутри матрицы, после IdentityMatrix там единичная

18 Окт, 19:58 #175 #151447

>>151445
Так, вроде сдвиг ясен, после сложения в матрице появляются единички на тех местах, где нужно.
Что делает IntegerDigits[y, 2, dim]?

Ответы151448

18 Окт, 20:06 #176 #151448

>>151447

>Что делает IntegerDigits[y, 2, dim]?

Дополняет нулями до 32 бит слева, чтобы дать 32-битное значение.
IntegerDigits[n,b,len]
pads the list on the left with zeros to give a list of length len.

Ответы151449

18 Окт, 20:08 #177 #151449

>>151448
ponyal

Ответы151451

18 Окт, 20:18 #178 #151451

>>151449

>Непонятно что делает transpose.

https://reference.wolfram.com/language/ref/Transpose.html
Меняет уровни списка, короче.

>Затем сложение ?

>mtx

сложение к матрице
что-то вроде push;
А затем, mtx = Mod[mtx, 2]
ROR это ксор?

Ответы151452 151453

18 Окт, 20:23 #179 #151452

>>151451
ROR - функция циклического сдвига

>ROR[x_, k_] := FromDigits[RotateRight[IntegerDigits[x, 2, dim], k], 2];

IntegerDigits[x, 2, dim] - дополняет слева нулями до 32 бит, RotateRight[IntegerDigits[x, 2, dim], k] - циклически сдвигает вправо на k позиций, FromDigits[RotateRight[IntegerDigits[x, 2, dim], k], 2] - возвращает получившееся число в двоичном виде

7 Кб, 501x484

18 Окт, 20:30 #180 #151453

>>151451
ROR это rotr. Xor это BitXor[].
mtx после всего получается как на пике. Это просто матрица с 0 и 1, которая делается из двух сдвинутых единичных (зеленая и красная диагонали из 1) и еще одной сдвинутой, от которой отрезано 3 строки (ну, отрезаются столбцы, а потом транспонируется, так что все равно что строки).
Это все коэффициенты в системе уравнений, которая потом решается LinearSolve. Например, в 1й строке 1 стоят на 7 и 18 месте С КОНЦА (потому что первым битом принято считать самый правый, то есть нумерацию столбцов лучше делать справа налево). Это отвечает уравнению x7 ^ x18 = a32.

Ответы151455 151534

18 Окт, 20:31 #181 #151454

>>151385

>Разве нельзя kG разелить на k/2 и получить 2G

Можно. Тебе повторить, какая сложность у этой операции деления?

Ответы151458

18 Окт, 20:34 #182 #151455

>>151453
Можешь расписать всё это алгоритмом, в виде
1.
2.
3.?????
4. PROFIT!
или ссылку на онлайн вольфрам математика или exe под винду чтоб код вставить, не?

Ответы151456 151457

18 Окт, 20:36 #183 #151456

>>151455
https://rutracker.org/forum/viewtopic.php?t=4854855
Тоже думаю поставить, но сейчас времени нет

18 Окт, 20:36 #184 #151457

>>151455

> Можешь расписать всё это алгоритмом, в виде

Относительно x решается СЛАУ вида Mx=y, где y - образ (входное число), x - прообраз, а M - матрица с пика.

Ответы151483

18 Окт, 20:43 #185 #151458

>>151454

>какая сложность...

kG/(k/2) = kG × ((k/2)^-1 mod P) = 2G, не?

Деление точки на числовую константу с точкой в результате, а не деление точки на точку, для получения числовой константы.

Ответы151459

18 Окт, 21:41 #186 #151459

>>151458
А, ты там kG на k делить хочешь. Лол, это я тебе и без вычислений скажу: kG/k = G.
Только какой смысл в этом вычислении, если k тебе не известен, а известен только kG и G?

Ответы151460 151461

18 Окт, 23:26 #187 #151460

>>151459
Чтобы показать тебе, что операция деления жи есть.
Алсо, 150kG /k = 150G,
по идее должно быть.

Ответы151478

18 Окт, 23:33 #188 #151461

>>151459

>это я тебе и без вычислений скажу: kG/k = G.

А если замутить что-то вроде:
kG / ((x(kG)^3 + ax + b) mod P / (y(kG)^2) mod P)
даст ли это что-то интересное?

Ответы151462

18 Окт, 23:38 #189 #151462

>>151461

> ((x(kG)^3 + ax + b) mod P / (y(kG)^2) mod P)

Ой, тут походу единица будет.
А если y(G), взять или обратную ей?

Ответы151463

19 Окт, 03:59 #190 #151463

>>151462

> взять или обратную ей?

Не знаю, я вот беру пизду твоей мамаши шлюхи обычно.

Ответы151464 151465

19 Окт, 07:03 #191 #151464

>>151463

>обычно

>твоей

Ответы151465

19 Окт, 09:28 #192 #151465

>>151463
>>151464

>Не

>,

>обычно

>твоей

Пофиксил.

19 Окт, 22:50 #193 #151478

>>151460
Впрочем, тут уже я затупил: действительно, операция деления точки на число есть, но толку из этого никакого.

>x(kG)^3 + ax + b

Тут ты вообще точку в степень пытаешься возвести, а потом сложить с числом. Лолшто?

>y(G)

Кого-кого?

Ответы151484

20 Окт, 07:37 #194 #151483

>>151457

>Mx=y

М(32 столбца, 32 строки),
x(1 столбец, 32 строки),
y(1 столбец, 32 строки).

Там же, при умножении элементов строки на столбец, сложение идёт.
Взять строку 4, например, в ней - три единичных бита.
При совпадении единичных бит в столбце с единичными битами в 4-й строке матрицы:
1x1 + 1x1 + 1x1 уже = 3, а может быть в результате - 1 или 0.
Т. е. результат 3 представляется в бинарном виде как 11, записывается результат 1
и одна единица идёт вниз, прибавляясь к следующему результату, я правильно понимаю?

Также, интересна функция LinearSolve из wolfram mathematica (он же весит 6,5 гигов).
Eсть ли у неё аналоги на других языках программирования?

Ответы151485

20 Окт, 07:40 #195 #151484

>>151478

>x(kG)^3

имелась в виду координата x от точки kG;
kG(xkG, ykG);
xkG^3 mod P;
Короче, если с координатами поиграться, может получатся какие-то интересные точки.
Хотя... Забей...

20 Окт, 08:04 #196 #151485

>>151483

> Взять строку 4, например, в ней - три единичных бита.

1x32 + 1x15 + 1x4 = 4-му элементу y (mod 2)
Ничего вниз никуда не идет.

Ответы151486

20 Окт, 08:33 #197 #151486

>>151485
32+15+4 = 51 mod 2 = 1, так?
Откуда тогда цифры 32, 15, 4?

>LinearSolve

Я как понял, при M⋅x=y; x = (M^-1)⋅y,
где M^-1 - матрица, обратная матрице М.

22 Окт, 13:44 #198 #151534

>>151453
А как найти матрицу, обратную матрице на пикче?

Ответы151536

22 Окт, 16:39 #199 #151536

>>151534
Используя любой метод для обращения матриц. Только нужно не забывать делать все по модулю 2.
Да, вот такой код тоже сработает:
inv = Mod[Inverse[mtx]⋅Det[mtx], 2]
Mod[inv.IntegerDigits[y, 2, dim], 2]
Первый mod можно делать, можно не делать. Делать выгодно, чтобы inv содержал только 1 и 0. Вот эта матрица: http://freetexthost.com/ide12yhn11

Ответы151537 151539

22 Окт, 16:41 #200 #151537

>>151536
Если совсем упростить, то вот это обращает твой хэш http://textuploader.com/d5lrf

Ответы151539 151554

22 Окт, 19:22 #201 #151539

>>151536

>Вот эта матрица

Как искал? Методом Гаусса-Иордана?
>>151537
http://matrix.reshish.ru/inverse.php
Здесь, при попытке найти обратную матрицу вообще выдало вообще 5-ти значные отрицательные числа.

>это обращает твой хэш

Не хеш, а лишь один милипиздрический элемент его. Обратить хеш невозможно в принципе же , не?

Ответы151541 151543

22 Окт, 19:31 #202 #151541

>>151539

> Не хеш, а лишь один милипиздрический элемент его. Обратить хеш невозможно в принципе же , не?

Да.
Искал методом

> Inverse[mtx]

только там и есть отрицательные дробные значения. Нужно привести их к целым и взять по модулю 2.

> inv = Mod[Inverse[mtx]⋅Det[mtx], 2]

Ответы151554

22 Окт, 19:31 #203 #151543

>>151539

> Здесь,

Ты что, вбил туда 32*32 значения?

Ответы151544

22 Окт, 20:14 #204 #151544

>>151543

>Ты что, вбил туда 32*32 значения?

Нет, только единички.
А остальные ячейки нулями заполнил.
Там же кнопка есть. =)

22 Окт, 23:11 #205 #151554

>>151541

>Нужно привести их к целым и взять по модулю 2.

При умножении матрицы на столбец,
нужно брать модуль от 2 каждого слагаемого или всей суммы?

31|30|29|28|27|26|25|24|23|22|21|20|19|18|17|16|15|14|13|12|11|10|9|8|7|6|5|4|3|2|1|0|
0|1|0|1|0|0|1|0|0|0|0|1|0|1|0|1|0|0|1|1|1|0|1|0|1|1|1|0|0|1|1|0| input
1|1|0|0|1|1|0|0|1|0|1|0|0|1|0|0|0|0|1|0|1|0|1|0|0|1|1|1|0|1|0|1| rotr7
0|1|0|0|1|1|1|0|1|0|1|1|1|0|0|1|1|0|0|1|0|1|0|0|1|0|0|0|0|1|0|1| rotr18
0|0|0|0|1|0|1|0|0|1|0|0|0|0|1|0|1|0|1|0|0|1|1|1|0|1|0|1|1|1|0|0| shr3
1|0|0|0|1|0|0|0|0|1|0|1|1|1|1|1|0|0|0|1|1|0|0|1|1|0|1|0|1|1|0|0| output

в свою очередь:
M^-1 ⋅ 10001000010111110001100110101100 =
10010100100001010111111011100110 ≠
01010010000101010011101011100110,
хотя 10 последних бит совпадают.

M^-1 брал отсюда: >>151537
Каждый бит - считал так:
(0⋅0 + 1⋅1 + 2⋅2 + 3⋅3 + ... + 31⋅31) mod 2,
(32⋅0 + 33⋅1 + 34⋅2 + ... + 63⋅31) mod 2,
и т. д.

При этом, первый множитель в мономах - j-тый индекс столбца конкретной i-той строки матрицы, второй множитель - номер бита входного числа.

22 Окт, 23:30 #206 #151555

Что вообще эти ебанаты несут?

Ответы151562 151563 151564

22 Окт, 23:47 #207 #151562

>>151555
Зарепортил неврастеника.

22 Окт, 23:54 #208 #151563

>>151555
Здесь кружок занимательной математики.
Один начинающий ебанушка пытается что-то понять, полторы продвинутых ебанушки пытаются ему что-то объяснить, один ебанушка скрывает свой уровень и наблюдает.

22 Окт, 23:55 #209 #151564

>>151555
Почему матом ругаешься?

25 Окт, 19:32 #210 #151604

>>150966 (OP)
Как не качать все блоки блокчейна в тяжеловесном Qt-клиенте, а только блоки с определённого заданного?
У dogecoin их овер миллион - шизануться можно же. Тут и bootstrap.dat не радует.

25 Окт, 20:16 #211 #151606

>>151107
Тут получаются даже не зеттабайты, а YOBIбиты YOBAбайтов.

26 Окт, 00:45 #212 #151609

>>150966 (OP)
Как с блокчейна получить актуальный блок для брутфорса соли (майнинг)?
Откуда вообще берутся новые блоки, как они формируются, и где собираются транзакции в блоки?
Можно ли вообще как-то майнить в режиме соло через блокчейн без установки каких-либо программ и участия в пулах?

Ответы151613

26 Окт, 09:37 #213 #151613

>>151609

>для брутфорса соли (майнинг)

>майнить в режиме соло через блокчейн без установки каких-либо программ

Пиздос.

Ответы151618

26 Окт, 17:05 #214 #151618

>>151613
А если у меня петафлопсы?

Ответы151621 151625

23 Кб, 505x337

26 Окт, 20:42 #215 #151621

>>151618

Твои вопросы легко гуглятся.

>Как с блокчейна получить актуальный блок для брутфорса соли (майнинг)?

Скачать из сети, не?

>Откуда вообще берутся новые блоки

Создаются майнерами, не?

>как они формируются,

В Гугл.

>и где собираются транзакции в блоки?

Где, блядь, собираются? В блокчейне собираются.

>Можно ли вообще как-то майнить в режиме соло через блокчейн

Можно

>и участия в пулах?

это так и называется - соло-майнинг

>без установки каких-либо программ

Да, можешь считать хэш в уме, а последний блок качать через браузер.

23 Кб, 505x337

26 Окт, 20:42 #215 #151621

>>151618

Твои вопросы легко гуглятся.

>Как с блокчейна получить актуальный блок для брутфорса соли (майнинг)?

Скачать из сети, не?

>Откуда вообще берутся новые блоки

Создаются майнерами, не?

>как они формируются,

В Гугл.

>и где собираются транзакции в блоки?

Где, блядь, собираются? В блокчейне собираются.

>Можно ли вообще как-то майнить в режиме соло через блокчейн

Можно

>и участия в пулах?

это так и называется - соло-майнинг

>без установки каких-либо программ

Да, можешь считать хэш в уме, а последний блок качать через браузер.

Показать весь текст

Ответы151622

26 Окт, 22:08 #216 #151622

>>151621

>Скачать из сети, не?

Не. Не current block, а блок без nonce, к которому её надо подобрать.

>Создаются майнерами, не?

Где?

>как они формируются

Куда конкретно?

>В блокчейне собираются.

После того, как nonce подобрана, и блок готов, да. А до того?

>Можно

>майнить в режиме соло через блокчейн

blockchain.info - тут только пулы.

>это так и называется - соло-майнинг

Ок.
Я так понимаю, нужно скачать bitcoin-Qt,
слить все блоки (а их там много), врубить его в режим сервера, и на сервер включить майнер с параметрами:
-o http://localhost:8332 -u RPCUSER -p RPCPASS
Потому что последний актуальный блок, ещё не сгенерённый и свежие транзакции, прилетают в виде tcp-пакетов прямо в прогу из одноранговой p2p.
И чтобы это было, надо загрузить ВСЕ БЛОКИ, ВСЕ 45 ГИГОВ, нафиг_не_нужных_блоков.
И как же подключиться к blockchain.info для этого?

>можешь считать хэш в уме, а последний блок качать через браузер.

Зачем мне последний блок, если за его генерацию уже выплачены битки предыдущему майнеру?
Мне надо новый блок сгенерить, я же майнер, ёпт.

И к чему ты Турчина поцепил, он что тоже майнит биток через блокчейн?

sage 26 Окт, 23:45 #217 #151625

>>151618
Да хоть зетафлопсы, неграмотности это не оправдывает.

>как же подключиться к blockchain.info для этого?

Перестань называть этот сайт блокчейном. Блокчейн это база данных биткоина.
blockchain.info это отдельный сайт, просто показывающий тебе красивый интерфейс для просмотра этой базы.

Ответы151629 151631

27 Окт, 00:32 #218 #151629

>>151625
Есть ещё
https://blockexplorer.com/
и https://webbtc.com/
и antpool с его 295.29 PetaHashes/sec

Алсо, вижу 436042-й блок
https://blockchain.info/block/0000000000000000028603f405c303c1711f22ffa1c31ffee89397b90099cb42
С его Nonce 1106733466, которую можно было бы перебрать в соло за 6.14851926 секунд на моей видеокарте, у которой 180Мh/s

Так вот, блок 436042 уже сгенерён и вошёл в блокчейн.
А блок 436043 ещё нет. Как только соль к нему найдут майнеры - он будобавлен, как и другие последующие.
Этот блок, после генерации будет разослан по p2p-сети всем клиентам у которых bitcoin-Qt, и не только, верно?

Так вот, как и откуда его получить, чтобы начать искать nonce?

Ответы151630 151641

27 Окт, 00:33 #219 #151630

>>151629

>будобавлен

Будет добавлен.
самоfix

27 Окт, 01:06 #220 #151631

>>151625
Короче, blockchain.info- это парсер.
А block chain дословно блок цепь - цепочка блоков.
База в виде bootstrap.dat или blk*.dat.
Так легче в башке укладывается всё это.

sage 27 Окт, 11:58 #221 #151641

>>151629
Создай сам, тупица.

Ответы151648

27 Окт, 19:04 #222 #151648

>>151641
Ты имеешь в виду блок с одной транзакцией получения сгенерированных биткоинов?

Вот так вот, что-ли?
https://blockchain.info/block/000000000000000002eb076392586c5b034ba3826ff6adb459bc57db4191943e

Транзакции откуда берутся для следующего блока?

Ответы151656

27 Окт, 23:21 #223 #151656

>>151648
Да, так.

Из сети.

01 Ноя, 08:45 #224 #151993

>>151206

>α = (Gy-Gy)/(Gx-Gx) = 0/0 (неопределённость).

Там не нули.
Удвоение - это отдельная операция.
α = 3x^2/2y;

Интересно, есть ли операция, обратная удвоению?

Ответы151997

01 Ноя, 14:34 #225 #151997

>>151993
http://point-at-infinity.org/ecc/Prime_Curve_Standard_Projective_Coordinates.html

Тред утонул или удален.
Это копия, сохраненная 18 июня 2017 года.

Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее

Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.