Вы видите копию треда, сохраненную 5 сентября в 05:03.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 47 Кб, 354x251
47 Кб, 354x251А почему остальные 6 не решат? Я правильно понимаю. что эти задачи не шибко то и нужны капиталистам поэтому никто их не решает ибо всем похуй?
Да, капиталисты до сих пор не захватили всю галактику и не создали автономные корабли добывающие ресурсы с планет, только потому что это не выгодно.
А разве нет? Например, можно было бы с Луны тащить ресурсы, но это экономически невыгодно, проще на Земле по старинке добывать как диды.
Значит я прав что те оставшиеся 6 из 7 задач тысячелетия не решают просто потому что это не выгодно корячиться решать эти задачи ради всего лишь миллионной награды?
нон секвитур
Пока думаю начать с определения геометрической вероятности, вставить задачу из эгэ в качестве примера разобрать подводные применения теории вероятности к геометрии. Потом разобрать задачу с применением иглы бюффона для нахождения числа пи. И как я понимаю пиксельный метод это мой случай?
ну записи тригонометрических функций реально хрень. я это выписывание sin и cos по 50 раз за строчку решения еще в школе возненавидел. Поэтому на черновиках всегда синус обозначал за s косинус за с.
А я даже математические продвижения 2019 года до нашей эры не знаю
мимо хочу начать учить математику с самых школьных азов
 61 Кб, 1668x1094
61 Кб, 1668x1094На плоскости находится точка. Где-то ещё - прямая (точка не лежит на прямой). Нужно найти такую траекторию движения для точки, которая позволит определить, где находится прямая и при этом будет самой короткой.
Интуитивно понятно, что, вроде бы, это какая-то спираль типа изображённой на пике. Но как это доказать?
>Нужно найти такую траекторию движения для точки, которая позволит определить, где находится прямая и при этом будет самой короткой.
Перпендикуляр из точки к прямой.
Прямая перпендикулярна отрезку перпендикуляра, проведённого из точки. Находится на расстоянии длины отрезка.
>>03012
Анон, ты не вкурил условие задачи.
>>02992
Что-то на стыке стохастического анализа и вариационного исчисления. Может быть релевантна статья "A probabilistic deformation of calculus of variations with constraints", а также https://en.wikipedia.org/wiki/Onsager–Machlup_function.
есть мнение, что это возможно только когда радиус монотонно и неограниченно возрастает при возрастании угла
если тяжело, конечно, не надо
работа через силу едва ли имеет смысл
особенно учитывая, что учебников по линалу несчетное множество
но книга хорошая
>работа через силу едва ли имеет смысл
Не согласен. Лично мне только это и помогло однажды достигнуть просветления.
Я тут с анонами не раз спорил о том, что LADR как вводная книга для рандомного самообразователя - хуита. Её идёальная аудитория - это прикладные математики (таки да, в том числе андерграды), которые будут заниматься чем-то, связанным с функциональным анализом. В крайнем случае её могут полистать особо любознательные после того, как уже пройдут курс линала по другой книжке.
Все кричат о том, что "по гауссу" и матричный дроч - это плохо. Какой-нибудь Булдырев-Павлов - это ещё одна крайность. Акслер избегает прикладных рассуждений и в то же время пропускает многие важные теоретические конструкции.
Важен баланс. Нужно дать понять, почему матрицы полезны, что за ними кроется. Дроч систем линейных уравнений или пивотов а-ля странг этого не даст, но сухое абстрактное повествование этого тоже не добьётся (тут исключаю чистых математиков).
Я бы советовал линал (и вообще любую область) читать по крайней мере по двум, разнонаправденным, книжкам.
Вы, мне кажется, идиот. Весь интернет завален решениями LADR, для второго издания и вовсе есть официальный мануал от Акслера. Он также сделал accompanying видеолекции для книги. Можно также отыскать lecture notes курсов линейки из универов, вплотную идущих по LADR и не решать все подряд, а только то, что указано в problem set'ах этих самых готовых курсов.
Пиздеж.
Вопрос такой. Основываясь на теории алгебр Клиффорда, про мнимую единицу можно очень просто думать как об операторе поворота на $\frac{\pi}{2}$ в какой-то плоскости. К нам ещё давно на кафедру приходили ребята с теорфизики и показывали, как вообще весь электромагнетизм (и много чего ещё) можно строить без упоминания комплексных чисел - там естественным образом возникают псевдоскаляры, квадрат которых равен -1. То есть часто там, где используются комплексные числа, более фундаментальной является какая-то связь с поворотами и $SO(3)$, а точнее даже с $so(3)$. Ну ясное дело это всё изоморфно $\mathbb{C}$ или там $\mathbb{H}$, но суть в интерпретации. Это всё замечательно обобщается на н-мерное пространство, в частности становятся более очевидными всякие факты вроде того, что $SU(4)$ есть двойное накрытие $SO(6)$, если думать в терминах алгебр Клиффорда.
С другой стороны, комплексные числа - это алгебраическое замыкание $\mathbb{R}$.
Вопрос - как эти описания связаны? Есть ли какая-то фундаментальная причина связи поворотов с алгебраической замкнутостью? Что интересно, мне пару лет назад уже задавали вопрос про кажущуюся магической связь между $\Lambda^2(\mathbb{R^3})$ (грубо говоря, "площадями") и поворотами. Но там я, вроде как, сам понимаю всё хорошо.
Здесь же я студенту как-то помахал руками про фундаментальную теорему алгебры, но интуитивного объяснения я не дал. Есть ли оно?
>Вопрос - как эти описания связаны
В должны быть связаны? Кватернионы же тоже про повороты, но даже поле не образуют.
я, конечно, простой человек и не облдаю такими глубочайшими познаниями, как ты, но кажется очевидным, что если из прямой удалить точку, она развалится, а если из плоскости - у нас образуется гомотопический хаос,
в котором и обретает черты основная теорема алгебры. это топологический факт, а не алгебраический
>Кватернионы же тоже про повороты
Так кватернионы замечательно интерпретируются в этом же самом фреймвёрке - действительные спиноры в двух измерениях это $\mathbb{C}$, а в трёх - $\mathbb{H}$. Но поскольку повороты происходят в (двумерной) плоскости даже в $\mathbb{R^n}$, то комплексные числа сами собой естественным образом появляются, даже если работать чисто над $\mathbb{R}$.
Вопрос-то мой в другом.
Пока моё объяснение - это комбинация доказательства фундаментальной теоремы алгебры через индекс точки, плюс факт того, что замкнутость релевантна только для полиномов чётной степени. Но всё равно как-то грубо выходит.
>должны быть связаны?
Годы и годы занятия математикой меня научили одному: если я не вижу связи, это скорее всего значит, что я недостаточно глубоко копаю и чего-то не знаю. Ну кроме очевидных случаев, когда объекты вообще из разных, никак не связанных областей.
я считаю, что пусть учится каждый, кто хочет учиться,
но спиздануть про участников сво, из которых кто-то случайно убил бабушку или жену, это совсем в край ёбнуться надо
тупое говно, откуда вы повылазили
>>03121
>Её идёальная аудитория - это прикладные математики
довольно странное утверждение про эту книгу, учитывая, что основное вычислительное средство в ней даётся в самой последней голове, а всё изложение построено из категорического принципа, что это средство должно быть отложено как можно дальше
>Акслер избегает прикладных рассуждений и в то же время пропускает многие важные теоретические конструкции.
одно из хороших свойств этой книги - она короткая
в ней материала не очень много, а объём (небольшой) получается, более-менее исходя из того, что всё разжёвывается крайне подробно. кому важно поместить в один том "все важные теоретические конструкции", может потискать какого-нибудь алуффи, если заняться нечем
Типичный любитель порешать задачки и высерающий
>топология на множестве есть множество его открытых множеств
чтд мозгов нет нихуя
>довольно странное утверждение про эту книгу
Утверждение перестанет быть странным, если его дочитать до конца, а не цитировать, оборвав на половине.
я читал её всю, правда, давно и не помню уже деталей, кроме собственных моих впечатлений от неё (в частности, мне лично очень помогла)
мне непонятно, в каком месте можно посчитать, что "Её идёальная аудитория - это прикладные математики", по-моему, это чепуха
Анон, в оригинальном посте сказано - книга для прикладных математиков, связанных с функаном. Ты вырвал из контекста и прицепился к части утверждения, и это полностью исказило смысл. И даже во второй раз ты не понял, о чём речь.
Ну так-то конечно всё будет чепуха, если читать посты жопой. Как у тебя с русским вообще? "Если его дочитать до конца" очевидно относится к утверждению, а не к книге.
ну ок, я не особо представлаю себе, что такое прикладные математики, связанные с функаном, чем они разительно отличаются от остальных математиков, которых ты от них отделяешь, и чем книга якобы для одних идеальна, а для других типа нет. с учётом того ещё, что книга вообще для начинающих и её задача - не рассказать досконально материал, а произвести только введение в него, такое разделени выглядит ещё более странно. но ради бога
>я не особо представлаю себе
Раз не представляешь, то зачем так оживлённо спорить? Очевидно, что у тебя какое-то однобокое представление.
Функан и его приложения вроде матфизики - это самая естественная среда для понимания определителя в терминах спектра, как делает Акслер.
Собственно сам Акслер, да и другие математики, писавшие книги в том же ключе (Булдырев/Павлов, скажем) - все писали статьи про функан. Вот так совпадение! (нет)
Если чего-то себе не представляешь, то может лучше посидеть-подумать, почитать, поискать. Если ты правда не видишь разницы между подачей линала через матрицы и по гауссу, через функан-ориентированную линзу вроде Акслера и Булдырева-Павлова, и через общую алгебру и теорию модулей.
>Очевидно, что
если тебя кто-то не понимает или понимает как-то не так, это не значит априори, что он идиот
>все писали статьи про функан.
давать материал можно по-разному, однако я не могу солгаситься с тем, что подача одним образом более важна для какой-то специализации, как бы ты ее не называл, чем другая подача, коль скоро речь идет о вещах совершенно базовых и нужных для всех. из перечисленных тобой подходов они нужны все и всем (хотя модули я бы отложил), но это не значит, что они должны содержаться в одной книге, а если не содержатся, то книга не годится
>Если чего-то себе не представляешь, то может лучше
что за любовь все время поучать
>что за любовь все время поучать
Что за любовь нести ересь вроде
>коль скоро речь идет о вещах совершенно базовых и нужных для всех. из перечисленных тобой подходов они нужны все и всем
Линал используется инженерами, экономистами, социологами. Им совершенно не нужно знать, что такое кольцо эндомофризмов, для того, чтобы пользоваться матрицами. Им совершенно не нужно знать, что такое спектр оператора. Им просто нужно знать, как эти вещи используются для решения конкретных задач. Например, экономист может просто кликнуть в интерфейсе статпакета и получить результат критерия коинтеграции или стационарности в виде собственных чисел. Знать, что там за ними "реально" кроется - ненужная для них информация. Также, как для пользования смартфоном не нужно знать квантовой механики, которая используется под капотом.
А уж если мы сузим круг читателей до математиков, то тогда книга Акслера вызывает ещё больше вопросов, потому что внешней алгебры нет, а определитель не упоминается на протяжении почти всей книги.
>Что за любовь нести ересь
ересь говорит твой собеседник или нет - это твоё личное мнение о том, что ты от него слышишь. в то время как манера поучать - это явное свойство личности (твоей собственной). странно сравнивать одно с другим
>то тогда книга Акслера вызывает ещё больше вопросов, потому что внешней алгебры нет, а определитель не упоминается на протяжении почти всей книги.
это вводная книга для начинающих. про внешнюю алгебру (а заодно и более основательно про определитель) начинающий прочтёт в следующей книге
>это вводная книга для начинающих
>про внешнюю алгебру (а заодно и более основательно про определитель) начинающий прочтёт в следующей книге
А если и в той книге не будет, то начинающий прочтёт об этом в третьей книге...
может быть, и в третьей, а почему нет? вообще я нахожу это не особо умным - критиковать книгу за то, чего в ней нет, когда следовало бы обсудить, что в ней есть. у книги акслера не очень аккуратное название (понравилось оно ему), но в целом понятно (должно быть), что рассказать весь линал - это явно не ее цель. на самом деле она дает альтернативный подход к самым на базовым понятиям, стараясь раскрыть их геометрический смысл, и надо обладать весьма узким вглядом на вещи, чтобы считать, будто такой подход полезен только будущим специалистам по функану. ну, когда у человека в смартфоне под капотом используется квантовая механика (что правда лишь частично), такой его взгляд наверно можно понять
твой пост ушёл в сторону от изначальной критики анона
ну с подменой тезиса конечно легче спорить, что тут скажешь, это ж двощ
если кратко, его критика сводилась к тому, что эта книга полезна только будущих специалистов по функану, а для других не полезна, поскольку в ней нет внешнего произведения (чего ещё в ней нет, пояснено не было). По моему мнению (подробности см. выше) первое есть ерунда, а второе бессмыслица. Если я что-то важное упустил, можешь указать
ну то есть читаешь ты жопой, ясно понятно
в оригинальном посте ни слова про внешнее произведение не было, кстати
и то, что она ни для кого больше не полезна, тоже сказано не было
>ерунда
>бессмыслица
ну если самому придумывать себе утверждения, с которыми спорить, то таки да, всё будет ерундой и бессмыслицей
к нам ccс/сай/ что ли утекает
а ты настырный.
хорошо, я пройдусь по основному посту, хотя в ясности его не упрекнёшь (у автора свои собственные определения "прикладных математиков" и т.д.)
>LADR как вводная книга для рандомного самообразователя - хуита.
абсолютно прекрасна как вводная вводная книга для рандомного самообразователя: в ней ясно и подробно разжёвывается геометрическая природа линала, что в вводных книгах нечасто встретишь (здесь приходит на помощь преподаватель, которого у самозанятого обучающегося нет), это чудесно и очень помогает пониманию.
>Её идёальная аудитория - это прикладные математики
глупости, книга даёт альтернативный взгляд на вещи с акцентом на их геометрическую природу; это полезно всем, кто изучает предмет. кроме того, альтернативный взгляд на вещи особенно полезен математикам, которые доказывают теоремы (не будем вдаваться в детали терминологии "прикладные математики"); всегда здорово указать, как теоремы доказываются другими способами
>в то же время пропускает многие важные теоретические конструкции
(такие как внешнее произведение, было пояснено ниже)
это нестрашно для вводной книги
> Нужно дать понять, почему матрицы полезны, что за ними кроется
матрицы - это операторы, насколько я помню, в этой книге было сказано об этом. если нет (я уже не помню), то это недостаток, тут я соглашусь
и ещё
>Акслер избегает прикладных рассуждений
я не знаю, что такое "прикладные рассуждения"
Акслер даёт альтернативные рассуждения - тем, что более традиционны. это прекрасно; про традиционные рассуждения читатель прочтёт в другой книги. вообще, нет ничего плохого в том, чтобы читать разные книги (наоборот - хорошо)
Культ Карго какой-то?
>Типа чтоб заумней звучало
Как и половина научных словечек. Себя не похвалишь - никто не похвалит. Не выставишься умным - посчитают дураком.
>нет повышения мудрости
Ну это естественно же.
Вот ты собираешься решить задачу. Возможны два варианта:
1) ты либо знаешь как ее решить - и только зря тратишь время
2) ты не знаешь как ее решить - и ничего не решишь
Это на столько блядь очевидно... Как только удается задачаблядям засирать нубасам мозги.
 204 Кб, 785x1101
204 Кб, 785x1101А для меня они чет ЖОССССКИЕ (не все, но многие). Сам пока сижу вспоминаю чего учил в вузе по mathprofi
скажи честно, тебя с первого курса отчислили? или ты недобрая баллов на егэ, и тебя не взяли на матфак?
И теперь ты мстишь аноним за свою неудачную жизнь, как настоящий двачер. Теперь ты будешь неосилятор-петух
Прошу всех нормальных анонов запомнить; когда этот шиз снова влезет, можно будет применять. Предлагайте также свои варианты, если этот не очень
У безмозглой задачебляди подгорает от очевидных фактов.
ЕГЭ я не сдавал кстати потому что его еще тогда не придумали, малолетний отброс.
А, т.е. ты в том возрасте, когда мозги уже в принципе не соображают, особенно в том, что хоть немного отличается от того, к чему они привыкли, и потому не можешь решать задачи. Тебе больно даже читать их условия, не говоря уже о том, чтобы остановиться на какой-нибудь и подумать
Ты понимаешь, что уже никогда не восполнишь те знания, которые вовремя не осилил, не получишь уже образование и ничего уже не достигнешь, из-за этого страдаешь и мстишь анонам, которые только начинают. Из зависти и от бессилия
Нет, просто делюсь по доброте душевной своей житейской мудростью приобретенной и отшлифованной с годами, чтобы аноны хуйней не страдали.
Ты же, долбоебушка малолетний, можешь хоть за яйца себя подвешивать, мне не жалко.
ой, какие мы снисходительно щедрые
И как же анон определит, где «мудрость», а где больной шизобред, больше похожий на троллинг? Что ж, иногда полезно делать выбор самому. К тому же в случае неосилятора-петуха ответ, по-моему, очевиден
Ну да, те у кого есть мозги разберутся где "троллинг" а где очевидные вещи. Малолетние безмозглые ебанько вроде тебя пусть дальше головой об стену бьются, мне не жалко.
 25 Кб, 328x359
25 Кб, 328x359>с ним с большой вероятностью справится компьютер
Здесь же доска для ментатов, какие такие разумные машины?
несешь какую-то дичь
если компьютер не взял, то и ты не сможешь
Ещё, если интеграл расходится, то это обычно не очень трудно доказать, но это другая задача
Че с матмеха выперли?
Начни с трилогии Ромы Михайлова
В теорфизике интегралы компьютерами вообще не берутся, но физики их как-то берут
Физики крутые вообще, но они же физики, а не математики. Так что за ними не сюда
>В теорфизике интегралы компьютерами вообще не берутся
Монте-карло в помощь. Руками никто ничего не берёт. Если аналитически не берётся машиной, то он машиной берётся численно.
Умеют ли машины хорошо работать с обобщёнными функциями в интегралах?
Ключевое слово - теорфизика.
 432 Кб, 1920x1080
432 Кб, 1920x1080Даже с банальным преобразованием Фурье там надо что то подкрутить чтобы вольфрамальфа не срался под себя.
Тупорылый школотун тупорыл во всем. Народная мудрость.
Ищу книжки про разложение модулей через идемпотенты/инволюции в контексте алгебр Клиффорда и спиноров. Удивительно мало литературы об этом, в большинстве учебников про это вообще не говорится, или уходят не в ту степь (Book of Involutions). Пока самое релевантное, что я нашёл, это "Clifford Algebras and Spinors".
질문은 낱말안에 물어야 한다
Если на стандартном инженерном уровне, то обычный матанализ.
Если в контексте теорфизики, то нужно почитать про дифформы, а ещё лучше про алгебры Клиффорда.
https://www.youtube.com/watch?v=Aub2OgAfuhg
 5 Кб, 285x28
5 Кб, 285x28Анон, что это вообще за конструкция, если R это не кольцо, а поле, а R(fin) это не идеал, а кольцо? В этом контексте R это поле гипервещественных чисел, R(fin)- конечные гипервещественные числа.
Разметка подвела, R* поле, R(inf) кольцо.
Вероятно тебя просят указать размерность векторного пространства, так что $\mathbb{R}_{\ast}\mathbb{R}_{\text{fin}}$ нужно рассматривать как факторпространство по подпространству.
*$\mathbb{R}^{\ast}/\mathbb{R}_{\text{fin}$
Спасибо, в предыдущих примерах все объекты были кольцами, так что я и не подумал про факторпространства. Чем в таком случае будет R*/R(fin)? Очень похоже на R.
Читаю определения по матеше и нихуя не понимаю.
Подозреваю у себя СДВГ, по линии бабки была биполярка.
Даже если у меня СДВГ и внимание блуждает и я улетаю в фантазирование/ как мне это компенсировать то блядь??
Стараюсь высыпаться и прямо ощущаю огромный буст до уровня 50% от нормы (обычно 10-20).
Как не пытайся мне требуется МНОГО времени чтобы вникать в определения, что хотел сказать автор учебника.
Не имеет значение смотрю я ролик популярный на ютубе или это учебник. Все равно буду тупить.
Проходил тест на дискалькулию и выдало что у меня ее нет (7/50). СДВГ много баллов набираю в любом тесте.
У меня нет проблем с визуализацией объектов, но есть проблема с визуализацией концепций типа даже ебаных дробей чтобы интуитивно вырабатывать логику решения если я уже знаю как их вычитать.
Это какая-то трабла с рабочей памятью. Я не могу ее хакнуть. Даже если записывать что я недопонимаю то забуду что я делал в предыдущих шагах пока записывал. Даже сейчас проебал мысль пока писал предыдущее предложение. Вспоминаю... Вспоминаю... 3 minutes later... а вот мысль... что я даже эти вопросы не могу вовремя нормально сформулировать пока усваиваю материал. Оперативка мозга попросту перегружена.
Или читаю определение и вспоминаю каждое ебаное слово - что оно значит. Мозг еле подгружает. Могу даже на ебучем "знаменателе" затупить, вспоминать пару секунд что это и картина начинает трещать так как я забываю остальное где нахожусь пока усваиваю.
Я ощущаю математические концепции как "прозрачные", как какой-то хаос. Потому не могу их визуализировать. Проходил визуальные тесты и мой результат был до 10 объектов (восстанавливаешь порядок), то есть я вписывался в норму в 7 объектов. Спокойно могу визуализировать физические явления. С физикой проблем не было, кроме этих ебаных определений снова.
Таких проблем нет когда я уже знаю предмет. То есть ресурс мозга не уходит на бесполезные домыслы что подразумевалось.
Хули делать без фармы? Закладки и индусов не предлагать.
Читаю определения по матеше и нихуя не понимаю.
Подозреваю у себя СДВГ, по линии бабки была биполярка.
Даже если у меня СДВГ и внимание блуждает и я улетаю в фантазирование/ как мне это компенсировать то блядь??
Стараюсь высыпаться и прямо ощущаю огромный буст до уровня 50% от нормы (обычно 10-20).
Как не пытайся мне требуется МНОГО времени чтобы вникать в определения, что хотел сказать автор учебника.
Не имеет значение смотрю я ролик популярный на ютубе или это учебник. Все равно буду тупить.
Проходил тест на дискалькулию и выдало что у меня ее нет (7/50). СДВГ много баллов набираю в любом тесте.
У меня нет проблем с визуализацией объектов, но есть проблема с визуализацией концепций типа даже ебаных дробей чтобы интуитивно вырабатывать логику решения если я уже знаю как их вычитать.
Это какая-то трабла с рабочей памятью. Я не могу ее хакнуть. Даже если записывать что я недопонимаю то забуду что я делал в предыдущих шагах пока записывал. Даже сейчас проебал мысль пока писал предыдущее предложение. Вспоминаю... Вспоминаю... 3 minutes later... а вот мысль... что я даже эти вопросы не могу вовремя нормально сформулировать пока усваиваю материал. Оперативка мозга попросту перегружена.
Или читаю определение и вспоминаю каждое ебаное слово - что оно значит. Мозг еле подгружает. Могу даже на ебучем "знаменателе" затупить, вспоминать пару секунд что это и картина начинает трещать так как я забываю остальное где нахожусь пока усваиваю.
Я ощущаю математические концепции как "прозрачные", как какой-то хаос. Потому не могу их визуализировать. Проходил визуальные тесты и мой результат был до 10 объектов (восстанавливаешь порядок), то есть я вписывался в норму в 7 объектов. Спокойно могу визуализировать физические явления. С физикой проблем не было, кроме этих ебаных определений снова.
Таких проблем нет когда я уже знаю предмет. То есть ресурс мозга не уходит на бесполезные домыслы что подразумевалось.
Хули делать без фармы? Закладки и индусов не предлагать.
"Не шарить в математике" - это стильно, модно, молодёжно. Если сказать, что ты безграмотный, то на тебя косо посмотрят. Если сказать, что ты не знаешь, где Антарктида, то тоже в общем-то рукоплесканий не последует. А вот если сказать, что ты никогда не мог в математику, у тебя родители вообще художники, ну нет таланта, генетически хуёмоё, adhd, дискалькулия, то тебя соучуствующе похлопают по плечу, скажут, мол, у нас у всех также бро, кому она вообще нужна эта маняматика, мы творческие люди да ещё биполярОЧКА и нужна таблетОЧКА для адхд.
Десятилетиями непонимание математики обществом нормализовывалось. Всё скидывается на таинственную генетическую предрасположенность, "другой склад ума", ADHD, и прочие деструктивные мемы вроде "таланта". ADHD это вообще пик современной моды. "Я что-то читал на тилибоне а потом посмотрел в окно и отвлёкся, эх вот ADHD не даёт нам покоя ребзя правда?". "Я делал что-то долгое нудное джва часа подряд и устал, ну у меня точно ADHD же верно??".
Из моей личной практики преподавания, ровно 100% учеников и студентов, жалующихся, что они "никогда математики не понимали", просто-напросто проебали основы ещё в школе. Скажем, идёт тема производных, там примеры основаны на понятиях их тем предыдущих лет вроде функций, графиков, тригонометрии, алгебраических выражений, и т.д.
Школьная математика - крайне иерархичная вещь. В какой-нибудь истории или литературе можно проебать, Скажем, 7-8ой класс, и нормально закончить 9ый. В математике это не проходит. Во всяком случае в школе - например, ты можешь начать читать линейную алгебру и общую алгебру (кольца\модули, поля и теория Галуа), полностью пропустив весь курс матанализа.
Поэтому "помощь зала" следующая:
1) Хватит искать генетического козла отпущения. Если только у тебя буквально нет медицинской справки о серьёзных нарушениях деятельности головного мозга, то ты можешь понять когомологии и спектралки, можешь выучить китайский язык, можешь научиться играть на пианино, можешь научиться рисовать и программировать, коль скоро ты вложишь время и усилия.
2) Если тебе не понятны, скажем, дроби, то сформулируй точно - что именно тебе не понятно. Задавай вопросы как себе, так и кому можешь вокруг (преподаватели, сверстники). Качай рефлексию.
"Не шарить в математике" - это стильно, модно, молодёжно. Если сказать, что ты безграмотный, то на тебя косо посмотрят. Если сказать, что ты не знаешь, где Антарктида, то тоже в общем-то рукоплесканий не последует. А вот если сказать, что ты никогда не мог в математику, у тебя родители вообще художники, ну нет таланта, генетически хуёмоё, adhd, дискалькулия, то тебя соучуствующе похлопают по плечу, скажут, мол, у нас у всех также бро, кому она вообще нужна эта маняматика, мы творческие люди да ещё биполярОЧКА и нужна таблетОЧКА для адхд.
Десятилетиями непонимание математики обществом нормализовывалось. Всё скидывается на таинственную генетическую предрасположенность, "другой склад ума", ADHD, и прочие деструктивные мемы вроде "таланта". ADHD это вообще пик современной моды. "Я что-то читал на тилибоне а потом посмотрел в окно и отвлёкся, эх вот ADHD не даёт нам покоя ребзя правда?". "Я делал что-то долгое нудное джва часа подряд и устал, ну у меня точно ADHD же верно??".
Из моей личной практики преподавания, ровно 100% учеников и студентов, жалующихся, что они "никогда математики не понимали", просто-напросто проебали основы ещё в школе. Скажем, идёт тема производных, там примеры основаны на понятиях их тем предыдущих лет вроде функций, графиков, тригонометрии, алгебраических выражений, и т.д.
Школьная математика - крайне иерархичная вещь. В какой-нибудь истории или литературе можно проебать, Скажем, 7-8ой класс, и нормально закончить 9ый. В математике это не проходит. Во всяком случае в школе - например, ты можешь начать читать линейную алгебру и общую алгебру (кольца\модули, поля и теория Галуа), полностью пропустив весь курс матанализа.
Поэтому "помощь зала" следующая:
1) Хватит искать генетического козла отпущения. Если только у тебя буквально нет медицинской справки о серьёзных нарушениях деятельности головного мозга, то ты можешь понять когомологии и спектралки, можешь выучить китайский язык, можешь научиться играть на пианино, можешь научиться рисовать и программировать, коль скоро ты вложишь время и усилия.
2) Если тебе не понятны, скажем, дроби, то сформулируй точно - что именно тебе не понятно. Задавай вопросы как себе, так и кому можешь вокруг (преподаватели, сверстники). Качай рефлексию.
>Читаю определения по матеше и нихуя не понимаю.
Люди разные.
У некоторых людей есть эйдетическое воображение - очень детализированное и богатое. Например, воображая ёлку, такие люди могут пересчитать на ней все иголки. А у некоторых людей ситуация полностью противоположная - визуального воображения нет вообще. Такие люди в принципе не понимают, как это - вообразить визуально что-нибудь. Математические определения часто рассчитаны как раз на таких людей. На людей, у которых визуальное мышление либо в принципе отсутствует, либо может быть выключено произвольно, по желанию.
Это ярко проявляется при изучении общей топологии. Некоторые люди при слове "шар" не могут не воображать себе нечто вроде трёхмерного шарика для пинг-понга. И если таким людям предложить рассмотреть вложенную последовательность пятимерных шаров в пространстве с какой-нибудь хитрой метрикой - эти люди перегреются и поломаются. Они, читая текст со словом "шар", не могут не воображать шарик. У них это не отключается.
А людям, которые умеют при слове "шар" не воображать геометрическую картинку, но при этом вызывать в памяти все интуиции, связанные с понятием шара, изучать общую топологию будет очень легко. Ровно до тех пор, пока не понадобится построить какой-нибудь контрпример, хе-хе.
Возможно, чтобы тебе было проще работать с определениями, тебе стоит развить навык: при чтении текста отключать автогенерацию в воображении всяких ненужных ассоциаций. Визуальных и не только.
>У некоторых людей есть эйдетическое воображение
>А у некоторых людей ситуация полностью противоположная - визуального воображения нет вообще.
Эта "теория" была опровергнута ещё несколько десятилетий назад.
>На людей, у которых визуальное мышление либо в принципе отсутствует
Такого не существует, если только у тебя нет крупных отклонений, скажем дополнительной хромосомы, или опухоли мозга.
Тебе в обос/сай/ с такими "фактами".
>They found that 0.8% of the population was unable to form visual mental images, and 3.9% of the population was either unable to form mental images or had dim or vague mental imagery
Чего сказать то хотел?
Мне реально не понятно как можно что то "видеть в голове". Если все так умеют, то почему если попросить схематически нарисовать велосипед большинство людей рисуют невнятную поебень, ведь им достаточно было бы вызвать его образ в своем мысленном взоре и перерисовать.
присоединяюсь к анону выше, тебе с такой "наукой" в /sci/, там твои братья по разуму
А это не одни и те же люди?
Есть набор чисел (показания датчиков, которые должны быть равны между собой) (12,84; 12,99; 13,07; 13,1; 12,49; 12,56)
Каждое из этих значений является Х(допустим, X - среднее из набора)/Y(число в районе 10000 плюсминус пару десятков).
Цель минимум: определить Y для каждого из чисел набора
Цель максимум: определить Y для каждого из чисел набора на основании нескольких таких наборов чисел (срезов показаний датчиков).
 110 Кб, 1280x933
110 Кб, 1280x933Здравствуйте, перекачу свой пост из sci:
Читаю Челпанова логику, почему из 64 комбинаций силлогизмов он называет верными только 11, игнорируя IEO? Это глава XV "Силлогизм. Фигуры и модусы силлогизмов".
Пик1 - в экселе накидал таблицу, где сначала я закрасил темно-серым все комбинации которые противоречат восьми правилам силлогизмов. Потом зеленым закрасил те комбинации которые автор называет верными. Как результат IEO - остался не закрашенным, то есть он и ни одному правилу не противоречит, но и не приводится автором как верный.
Пик2 - фрагмент из учебника где перечисляется список верных силлогизмов.
Пик3 - доказательство того, что я не шиз и некий "Ratigan" на древнем форуме уже задавался этим вопросом, но ему так и не ответили
 299 Кб, 757x587
299 Кб, 757x587Отмена, он в той же главе объясняет почему не берется IEO хотя он говорит, что оно противоречит четверотому правилу, но я еще не понял почему
Просто почему-то уже после того как объяснил фигуры
Хорошо, что ты нашёл ответ сам, потому что никто бы тут не стал самостоятельно разбираться в твоих обозначениях и определениях, которые ты не предоставил (и даже если бы предоставил, то это всё равно это к тематике доски имело бы не большее отношение, чем шахматы, например, или лингвистика).
>>99999
>>100000
> Burbara, Celarent, ...
Учите блядь нормальную математическую логику по современным учебникам, нахуй вы в этом древнем говне ковыряетесь.
 74 Кб, 403x592
74 Кб, 403x592>Учите блядь нормальную математическую логику
Мир не ограничивается логикой предикатов, даже мир математики.
>нахуй вы в этом древнем говне ковыряетесь.
Я лично сейчас читаю свежее, прикл, пока ещё только в начале. Очень интересно как автор вводит различие на сущностные и не-сущностные термы, для того чтобы обосновать модальную силлогистику. Всё выглядит вполне понятно и ясно. Берётся знаки из aeio, берётся знак из XNQM, и вот у нас к примеру NXN силлогизм Barbara:
A aN B - Всё А необходимо принадлежат B
B aXC - Всё B принадлежат C
A aN C - Всё А необходимо принадлежат C
Значки Q и М обозначают это двухсторонняя возможность или односторонняя возможность. Берёшь два терма, формируешь копулу (связку) и ставишь два терма субъект и предикат. Тут самый сок в семантике которая обосновывает почему такая-то фигура работает, мне нравится.
Неее. Ну так модальность была у Аристотеля, но в новое время из-за падения схоластики уже закрепилась традиционная логика (которая суть урезанная силлогистика Аристотеля). Потом был Фрёге который срал Буля за отсутстиве кванторов и что его "запись в понятиях"(которые предикаты) через штрих (прикл3) гораздо удобней чем тупой закос под арифметику (прикл1), паралелльно разбирая насколько Пеано база (прикл 2). А уже потом после, сложилась традиция оформившая классическую математическую логику как пропозициональную и предикатную логику. И как-раз где-то в этот периуд началось создание "не-классических логик", хотя "Классическая логика" - на тот момент существовала совсем ничего. То-есть, S1-S3 модальные логики появились в 1930 годы, хотя ещё лет 30 назад Фрёге не получил никакого признания как и его исчисление (На лекции Фрёге было буквально 0 человек, то-есть, исчисление с предикатами нахуй никому не было нужно вплоть до начала 20 века когда Рассел подметил парадокс и началась движуха с аксиоматизацией). Крч, странно тыкать пальцем во всё что не является матлогикой и говорить что это что-то странное, когда сама матлогика взлетела из-за того что звезды так сложились.
Обпучкался с пикчи. Охуенно просто.
 22 Кб, 429x600
22 Кб, 429x600Мне не хотелось отдавать. Но вот случилось одно небезызвестное решение верховного суда, к сожалению.
 24 Кб, 528x474
24 Кб, 528x474@FORMAL_V
а
 249 Кб, 547x362
249 Кб, 547x362Матаны, а есть ли не вещественные математические константы? Если точно нет, то чем комплексные, кватернионы и прочие покемоны хуже?
Можно вспомнить и другие базисы, но почему так скудно то? Неужели на прямой больше интересных чисел с интересными свойствами чем на плоскости, например.
> Престиж математики в Китае был высок. Каждый чиновник, чтобы получить назначение на пост, сдавал, помимо прочих, и экзамен по математике, где обязан был показать умение решать задачи из классических сборников.
В I—V вв. н. э. китайцы уточняют число
�\pi — сначала как
10
{\sqrt {10}}, потом как 142/45 = 3,155…, а позже (V век) как 3,1415926, причём открывают для него известное рациональное приближение: 355/113.
В это время китайцам уже было известно многое, в том числе:
вся базовая арифметика (включая нахождение наибольшего общего делителя и наименьшего общего кратного);
действия с дробями и пропорции;
действия с отрицательными числами (фу), которые трактовали как долги;
решение квадратных уравнений.
Был даже разработан метод фан-чэн (方程) для решения систем произвольного числа линейных уравнений — аналог классического европейского метода Гаусса.[2] Численно решались уравнения любой степени — способом тянь-юань (天元术), напоминающим метод Руффини-Горнера для нахождения корней многочлена[3].
В области геометрии им были известны точные формулы для определения площади и объёма основных фигур и тел, теорема Пифагора и алгоритм подбора пифагоровых троек.
В III веке н. э., под давлением традиционной десятичной системы мер, появляются и десятичные дроби. Выходит «Математический трактат» Сунь-Цзы. В нём, помимо прочего, впервые появляется задача, которой позднее в Европе занимались крупнейшие математики, от Фибоначчи до Эйлера и Гаусса: найти число, которое при делении на 3, 5 и 7 даёт соответственно остатки 2, 3 и 2. Задачи такого типа нередки в теории календаря.
Другие темы исследования китайских математиков: алгоритмы интерполирования, суммирование рядов, триангуляция.
А я и не знал, что китайцы такими продвинутыми были/есть. Кто знает может и американские индейцы имели хоть какие-то представления о математике дальше арифметики.
нули зета-функции Римана
>были/есть
Только были. В конечном итоге только европейцы смогли непрерывно пронести научную традицию и развить современную науку в 18-19 веках.
Европейцы знали Евклида и маняфантазировали по образу Начал строить и другие разделы матеши. В итоге взлетело благодаря Лагранжу. А так европейская матеша ничем особо не выделялась до Нового времени.
нету никакого соглашения или традиции относительно того, как записывать слагаемые вида $1/x^k$, в виде дроби или в виде $x^{-k}$; если ты везде видишь дроби, это только оттого, что авторы выбирают такой способ записи
 8,9 Мб, 2736x2736
8,9 Мб, 2736x2736Которые знают и изучают такие науки как математика и физика?
https://www.youtube.com/watch?v=Zw5t6BTQYRU
https://www.youtube.com/watch?v=Zw5t6BTQYRU
Не серьезно? Разве такие в тиндерах ведутся?
В библиотеку идти и как додик пытаться их домогаться пока они заняты изучением науки? Так себе, по моему библиотека последнее место для этого.
Идти в университет и в столовой подкатывать? Охрана/полиция сразу прийдет, причем не обязательно потому что тянка с которой пытался знакомиться, а просто кто-то заметит что пытаешься в университете будучи не студентом знакомиться.
Так что где? Какие интересы у таких тянок? Разве что шахматный клуб? Что еще?
p.s. я sapiosexual, и были исследование которые показывали что у умных людей мозг более развит и больше wrinkles/folds in the brain, которое безусловно передастся потомкам.
не надо троллить, к тому же ты не умный тролль, ведь смог бы разузнать что это была ссылка на одну из самых простых тем на которую она преподает
>к тому же ты не умный тролль
не хочешь, получается, со мной размножаться? жаль
>ссылка на одну из самых простых тем на которую она преподает
не волнуйся, всё остальное тоже покрывается в школьной программе, ну или в пту каком-нибудь в крайнем случае
>Идти в университет и в столовой подкатывать? Охрана/полиция сразу прийдет
придет дружинник-студотрядовец с фсзкультурного факультета и объяснит, что так делать низя
я самопровозглашенный юморист, а свои амурные предметы продолжайте обсждать без меня
Университетские "nerd females" - это обычно пиздец.
Во-первых, у них охуевшее количество внимания даже по женским меркам, потому что тут их совсем меньшинство => завышенное ЧСВ и армия фанатов. Готов ли ты через это пробиваться?
Другая проблема - няшнотян тут еще меньше, остальные - серые мыши и/или шизухи. Недавно читал в чате общаги, как один парень жаловался, что соседка принципиально не смывает говно за собой.
P.S. - в тиндерах водятся.
 10 Кб, 480x360
10 Кб, 480x360>Ищу решебник по статистическим задачам всяким околоматематическим
Это как спросить, есть ли решебник по механике сплошных сред, задачам всяким околоматематическим. Ответом будет, собственно, сам учебник по механике сплошных сред. Необходимо, как в привиденном мной примере, так и в твоем случае, искать учебник а не решебник. Как вообще должен в твоем представлении, выглядеть решебник по разным статистическим задачам? Сам подумай, если это приложение теории (а чем иным может быть задача?), а тебе нужен некоторый решебник этих задачь (то-еесть решение приложений), то наверное тебе наверное здесь нужен прикладной учебник в интересующей тебя области приложения, где изложение статистики соседствует с решением типовых задачь из области приложения. Вот тебе и задачник и решебник одновременно. Если ты имел в виду под "околоматематическим" и "статистическим" нечто совершенно иное, то наверное стоило бы уточнить это иное, а не описывать свою проблему одним единственным предложением.
По школе есть решебники, должны быть и здесь. Только как и знания никто их давать не собирается. Я аутировать и сидеть не намерен. Это нецелесообразно в моей ситуации. Это предмет статистика.
 191 Кб, 830x436
191 Кб, 830x436>Только как и знания никто их давать не собирается. Я аутировать и сидеть не намерен. Это нецелесообразно в моей ситуации.
Может хватить демагогии? Я был в 2 школах, там только 1 парень хорошо учился, потому что не кушал говно и жил в средних условиях в рамках города, да еще и фамилия заканчивается на штейн, еще и отец программист старой закалки. А хуету мне собачью рассказывать не надо с детьми алкашей я обязательно стану умным.
Должны? Кому должны, тебе?
Решебники к университетским учебникам можно пересчитать по пальцам одной руки. Нет такого массового запроса, как в школе.
В лучшем случае в некоторых вузах студентота складирует свои решения для будущих поколений во всяких облаках, но туда левому человеку попасть почти нереально.
Да мне пох уже, не хотите не надо. Мигранты красавчики постепенно все ниши займут, местная диспора будет за бесплатно обучать.
Да-да, шиз, это не решебников не существует - это от тебя их ПРЯЧУТ и не хотят давать из вредности.
Но справедливости ради второй вариант это куча разных широко применимых идей и легко эти три книги можно навернуть за месяц. В то время как первый - это узко-специализированный дроч, причем минимум полгода надо чтобы нормально разобраться.
Нет никакой справедливости. Есть у кого бабло и репетиторы для них остальные шизы вот и все.
Ты шиз не потому что у тебя нет бабла, а потому что не понимаешь различия между школьным и университетским образованием, вместо этого считая что от тебя что-то СКРЫВАЮТ.
В школе мало учебников и есть унифицированная программа, поэтому там очень легко сделать решебники.
В универе полнейшая солянка - каждый препод вправе читать практически как захочет и активно этим пользуется. Даже в рамках одного факультета и одного предмета разные потоки могут учиться на разных задачниках. Более того, очень часто в универах учатся по своим собственным методичкам, которые являются сборником задач из десятка разных задачников, а то и придуманных из головы. Кто и как должен решебники делать в такой ситуации? И главное для кого - для сотни-другой студиков? Есть буквально пара общепризнанных учебников, у которых есть массовая аудитория, сравнимая со школьной - это например Демидович, для которого есть решебник. В остальных случаях, особенно если предмет узконаправленный, ни у кого нет просто ресурса и мотивации делать решебники.
Поэтому делают не решебники, а разборы типовых задач, что тебе и советовали уже выше.
Еще ты можешь загуглить записи семинаров по статистике.
Но ты, конечно же, предпочтешь загнать правацкую телегу про мигрантов.
Мимо без бабла и репетов, всю жизнь на бюджете
пидараха или блатняк вся суть
Ищу книжку по алгебре, в которой будет рассказано, как в произвольной ассоциативной алгебре искать подалгебры Ли через инволютивные антиавтоморфизмы. Общая картина понятна (если α
- такой морфизм, то ${a \in A: \alpha(a)=-a}$ образуют алгебру Ли), но хочется детально.
Ну и ещё вдогонку: есть ли где-то переводы (можно на англ) французских статей Арнольда? Особенно интересует "Sur la géométrie différentielle des groupes de Lie de dimension infinie et ses applications à l'hydrodynamique des fluides parfaits".
>inb4 французский там не сложный
Очень хорошо, значит точно кто-то уже перевёл.
>Особенно интересует
Перевода, скорее всего, нет, но по идее хотя бы часть материала должна быть в его книжке по топологическим методам в гидродинамике.
Даже и забыл, что у него такая книжка есть, спасибо анон!
Но французский в статье и правда не сложный, так что наверное прочту и её. Ещё нашёл блог пост Тао об уравнении Эйлера-Арнольда, там тоже много интересного.
>но хочется детально
Посмотри литературу/разделы учебников по классификации полупростых алгебр Ли, не совсем то, что ты спрашиваешь, но может что-то полезное найдешь.
>по классификации полупростых алгебр Ли
Видимо да. Вот буквально на днях прочитал ту самую статью Дынкина, "Структура полупростых алгебр Ли". Он там с ничего (ну, с линала) всё выводит, включая корневые системы и свои диаграммы. Очень занятно, и это он в 23 года написал. Но всё равно не то, что мне нужно - ну или по крайней мере я слишком тупой, чтобы понять, как это связано. Так что читаю сейчас про разложение Картана.
Ещё нашёл The Book of Involutions, там тоже много интересного.
А вообще конечно нужно просто взять и прочитать нормальный учебник. Взял плохую привычку таскать факты из разных мест, а потом над ними сидеть думать джва года.
Посмотри первую главу Xu, Representations of Lie Algebras and Partial Differential Equations.
 133 Кб, 1399x393
133 Кб, 1399x393Блин, случайно лишнее "не" написал…
Крч, правильно так:
Подскажите аналог формулы Бернулли, ту же хрень, но не для ровно m раз, а ДЛЯ m И БОЛЕЕ раз.
Какой же уебищный сука пидорас понасрал своих What is... говновидосов на все темы с абсолютно нулевым содержанием.
Вопрос, если что, про математику. Какая фундаментальная причина того, что преобразование Лежандра вообще полезно (в контексте теорфизики)? Фактически мы переходим от N диф уравнений 2-ого порядка на многообразии к 2N диф уравнениям 1-ого порядка на кокасательном расслоении.
То есть уже сразу есть два преимущества: ур-я 1ого порядка проще, и на кокасательном расслоении "богаче" структура.
Я вот долго думол, и мой ответ такой: переход к уравнениям 1ого порядка позволяет динамику интерпретировать как потоки/локальные группы диффеоморфизмов (симплектоморфизмов). И тут сразу вся геометрия возникает, группы/алгебры Ли, симплектическая геометрия, гамильтоновы потоки, скобка Пуассона, и т.д.
Ведь с системой ур-й 2-ого порядка такого не добиться, верно? Без конвертакции её в эквивалентную систему ур-й 1ого порядка.
про преобразование Лежандра я не помню ровным счётом ничего, но там была какая-то достойная геометрия за ним
попробуй посмотреть Ж. Лере, Лагранжев анализ и квантовая механика.
я не обещаю, что там будет, но возможно что-то и найдётся
Преобразование Лежандра устанавливает двойственность между формализмами Лагранжа (вариационное исчисление) и Гамильтона (симплектическая геометрия).
Смотри: Годбийон, Дифференциальная геометрия и аналитическая механика; Tulczyjew, The Legendre transformation; da Silva, Lectures on Symplectic Geometry; https://ncatlab.org/nlab/show/prequantized+Lagrangian+correspondence#HamiltonianTrajectoriesAndPrequantizedLagrangianCorrespondences
Был вопрос, почему преобразование Лежандра фундаментально полезно. Ответ - это преобразование устанавливает двойственность между двумя формализмами классической механики. Всё, что он написал, следует из этого, и подробно описано у того же Годбийона.
Нет
"Устанавливает двойственность" это на уровне чатжпт, который не понимает, что за двойственность, и что вообще за задача и предметная область, но просто где-то прочитал, что там двойственность
 107 Кб, 1788x284
107 Кб, 1788x284Круто, но я просто воспользовался формулировкой Годбийона.
По мне так вся эта симплектическая геометрия высосана из хуя.
>мы переходим от N диф уравнений 2-ого порядка на многообразии к 2N диф уравнениям 1-ого порядка
переход основан на потрясающем факте что производная 2ого порядка это производная 1го порядка от производно 1го порядка.
>преобразование Лежандра вообще полезно
думаю что то там со свойствами производных и как они изменяются при этом преобразовании, как например преобразования Фурье сводят дифференцирование к алгебраическим манипуляциям, возможно там что то похожее есть
>По мне так вся эта симплектическая геометрия высосана из хуя.
сильное утверждение. чувствуются глубокие основания под ним и знание предмета
>преобразования Фурье
совершенно другое. преобразование Фурье - чисто аналитическая вещь, существует только в $\mathbb{R}^n$ (есть попытки обобщить на римановы многообразия, но они выглядят ужасно)
преобразование Лежанра по сути своей геометрическое, оно вектора (элементы векторного расслоения) переводит в ковектора (элементы двойственного расслоения), которые действуют специальным образом
Хуй соси, губехой тряси, чмондель.
Two differentiable functions ... are said to be Legendre transforms of each other, if their derivatives are inverse functions of each other
https://ncatlab.org/nlab/show/Legendre+transformation
Какой с этого профит - хз
>А сколько будет i если его тоже числами написать?
в десятичной системе не представимо
>Хочу пароли крутые сделать. Типа из математических чисел.
Это слабые пароли.
>в десятичной системе не представимо
Мне в любой пойдет. Главное чтобы можно было цифрами напечатать>>13611
>Это слабые пароли.
Знаю. Фильтры на сайтах обычно просто цифры не разрешают как пароль использовать. Мне это туда где нужно цифры вводить. Типа пароль для разблокировки телефона или пин к приложению банка
Поздно маневрировать, говноглот.
Я аспер в хорошем месте, выступаю на конференциях, есть несколько статей с научруком. Но мой вклад в эти статьи 10-15%, и хоть все говорят что это норма, но я все равно чувствую себя тупым. Как от этого избавить блять
был на твоём месте, но не поборол синдром самозванца
но я вообще пребываю в тяжёлых комплексах всю жизнь
>Но мой вклад в эти статьи 10-15%
достаточно, если тебе в них 100% понятно
ещё не переставай любить свою работу и не переставай никогда учиться, стремиться узнавать новое. дальше будет видно
всё, что могу посоветовать
Чмондель, так ты ж реально тупой как дрова, какой нахуй синдром.
Возьмём в качестве A поле вещественных чисел, в качестве a -- любое ненулевое вещественное число, а в качестве b -- число 0. Тогда соотношение ab=b выполняется.
Условие, что ab=b, эквивалентно условию (a-1)b=0. Как тут без делителей нуля?
К примеру яблоко и груша, чья трактовка это еда или салат. В том смысле, что вычислять абстрактное какого-то яблока или же конкретность абстрактного того же яблока, что само есть абстрактное. (Еда как абстрактное, салат как блюдо, где блюдо есть конкретное еды, но абстрактное яблока).
Хм. Ну вообще, если говорить о том, что еда есть абстрактное яблока, а яблоко есть конкретное еды, то это можно воспринимать как множества. Ну думаю тут ясно, только правда есть одно но, у множества {яблоко, груша} есть название еда, и это тут тоже важно.
Но вообще как хочешь трактовать можно. Хоть равенством. Еда это яблоко, еда это груша, еда это еда, яблоко это груша, но груша не яблоко.
Так что я бы сказал бы, наверное, что это любое бинарное отношение. Вроде порядковым называлось.
Только правда есть условие, по сути, что абстрактное это логическое сложение, а конкретное это элемент логического сложения.
>>13685
Значит нужны структуры без вычитания.
Предлагаю покопать в сторону тропического полукольца.
Тут как раз под рукой бумажка, где наводят линейную алгебру над полукольцом (которое уже над R), так что ,в зависимости от определений, ответ найден
https://www.imprs-mis.mpg.de/fileadmin/imprs/imprs-ringvorlesung-2018_may-22.pdf
>>13685
Значит нужны структуры без вычитания.
Предлагаю покопать в сторону тропического полукольца.
Тут как раз под рукой бумажка, где наводят линейную алгебру над полукольцом (которое уже над R), так что ,в зависимости от определений, ответ найден
https://www.imprs-mis.mpg.de/fileadmin/imprs/imprs-ringvorlesung-2018_may-22.pdf
Каким образом тут появляется дизъюнкция
Равенство то там настоящее. Другой смысл у знака $\sum$, который понимается НЕ как предел частичных сумм. И то смысл не другой, а обобщенный. Ведь везде, где обычная сумма даст число, эта обобщенная сумма даст такое же число. Просто там, где привычный ряд скажет "не определено" обобщенный даст число
> Другой смысл у знака ∑ , который понимается НЕ как предел частичных сумм.
тогда вернее сказать, что другой смысл в принципе у всех сумм бесконечных последовательностей? Если в результате операции предельного перехода они дают конечное число - их можно привести к бытовому уровню понимания. Если не дают - то это абстрактная хрень, обращаться с которой нужно аккуратно. И числовое значение им можно присвоить не предельным переходом (который даёт в лучшем случае бесконечность), а другими операциями (которые в свою очередь могут включать в себя предельные переходы сходящихся рядов наверно).
> Просто там, где привычный ряд скажет "не определено" обобщенный даст число
так в том и >50% дела, что в этой сумме нет неопределённости, тут есть предел +бесконечность. Не определено - это +1-1+1-1..., например. А в этом выражении если впереди поставишь ещё число или поменяешь порядок конечного числа членов, оно поведёт себя совсем не как сумма, выдаст не те числа, что ожидаешь.
Тут есть определенность, если жить на $\mathbb{R}\cup\{+\infinity,-\infinity\}$, что делает матан гораздо более громоздким, да и вообще это не поле. Над обычным R проще жить, и там предела нет.
Перестановка конечного кол-ва элементов не изменит значение суммы ряда, ни в обычном, ни по Чезаро. Вероятно есть на этот счет теоремы и для любого обобщенного суммирования рядов, но сходу я ручаться не стану.
Да, от перестановки конечного кол-ва элементов ряд не поменяется в силу линейности взятия суммы ряда и того факта, что любой ряд с конечным колвом ненулевых элементов сходится.
Не понял, к чему ты это, таблица истинности импликации в этом контексте это про множества отображений между множествами с не более чем одним элементом.
-1/12 - это значение анал продолжения дзетафункции в -1, а если другая анал-функция в данной точке будет представима этим рядом, то может она дать другое значение? Или она будет тождественно равна первой в своей области определения?
-1/12 можно получить и по-другому, например разложив $\sum n\exp(-\alpha n)$ в нуле в ряд Лорана, и взять оттуда константу.
Что такое большие числа? Функция бобра от эквивалента одного мегабайта состояний это большое число?
Ничего удачнее пока предложить не могу, чем два варианта:
-числа, размер которых невозможно оценить без применения рекурсии типа стрелочной нотации и тд. Ну т.е. максимум разрешено перемножать степенные башни типа 10^10^10... Даже если тратить все ресурсы и всё время до тепловой смерти вселенной на постройку компьютера, который их считает и держит в памяти, нифига не приблизишься.
-перемножение самых маленьких вероятностей, связанных с реальными физическими параметрами и оценками, и взять обратное от этого числа. Что типа из флуктуаций возникнет не больцмановский мозг, а суперкластер галактик или юпитер вдруг полетит прямо к солнцу, туннелирует через него, вернётся на орбиту и покажет ему фак. На это ж всё не строго нулевая вероятность, верно? Опять же построить максимально большой комп, который не сделается черной дырой и пусть он считает максимальное время, которое отводят более-менее общепринятые физические теории (большой разрыв, тепловая смерть или что там ещё).
Если всё это для тебя звучит как хуйня, то тогда прямо и чисто произвольно: числа, бОльшие, чем число Грэма. Можно взять даже поменьше: там же 64 итерации со стрелками надо провести, пускай будем считать с 30 итерации. И допустим, постоянная Эйлера-Маскерони таки рациональна со знаменателем такого размера. Означает ли это, что доказать её рациональность тогда почти невозможно?
 455 Кб, 1438x1438
455 Кб, 1438x1438Тг: vronu
>Взамен могу предложить то же самое по программированию.
Полезность сомнительна. Математикам помощь в программировании чаще всего не требуется. Большинство, конечно, не знает, как правильно писать "корпоративный" код по шаблонам, или какие там самые новые фреймворки, но базовые вещи уж всяко известны (по крайней мере, двощерам), скажем написать скрипт в пейтоне, или поднять сервер.
Вообще, выросши на irc и форумах, никогда не понимал этого. "Вот мой тг", "вот дискорд". Ну ты же блядь вот сейчас сидишь на доске, ну хули не спрашивается-то? Зачем приплетать ещё какую-то мокрописку, для этого не предназначенную. Тут даже латех прикрутили.
Вообще, требуется. Но программисты такую помощь называют фрилансом и просят денег. Мне бы например один алгоритм по-нормальному на суперкудахтере бы запустить, а скилов не хватает.
Потому что:
1. Я засру доску, либо наоборот, мои сообщения утонут в ней
2. Доску не проверяют так часто, как мессенджеры
3. Обращение к человеку лично работает лучше, чем обращение к массе, потому что в последнем случае легко проигнорировать вопрос
4. Иногда хочется уйти немного в оффтоп или даже во что-то личное
5. Я пробовал и нихуя мне никто не ответил
Нет, я же сказал, помощь за помощь. Примерно как у друзей.
>Я засру доску, либо наоборот, мои сообщения утонут в ней
Скилл ишшью
>Доску не проверяют так часто, как мессенджеры
Если кто-то постоянно проверяет мессенджеры, то его умственные, в том числе математические, способности уже ставятся под сомнение.
>Обращение к человеку лично работает лучше, чем обращение к массе, потому что в последнем случае легко проигнорировать вопрос
Иди со своим НЛП куда пришёл.
>Иногда хочется уйти немного в оффтоп или даже во что-то личное
Ну естественно причина оказалась не в математике, а в социоблядских потребностях.
>Я пробовал и нихуя мне никто не ответил
Игнорировал правила борды, вопрос был тупой или скучный, мало ли причин.
Нуль бывает разный. Финансовое моделирование тоже. В какой-нибудь Renaissance Technologies отбирают людей из PhD по чистой математике, добившихся успехов в науке. У нас в универе финансовую математику преподают тем, кто раньше собирался теоретической физикой заниматься какой-нибудь. Но есть и намного проще пути, я уверен. И это не отдельные случаи, в квантах (quantitative finance) очень любят сильны математический бэкграунд и вроде бы он даже пригождается временами.
Самое важное, что нужно знать, насколько я понимаю, это статистические методы. Для этого нужно как-то первый курс мат.анализа понимать (ну или calculus, более приложения-ориентированная дисциплина), потом теорвер, потом уже собственно статистика. Ещё дифуры, кажется, нужны. Это примерно год учебной программы.
Ну и по классике дата анализ и машинка, это сейчас основные инструменты в области. Тут линейная алгебра сильно нужна.
Насколько нужно знать экономику и как её учить — вообще без понятия.
Алсо добавлю, что я описал, какие навыки нужны, слышал это от других людей, сам не занимаюсь этим. Другое дело, что для вката на рынок, возможно, нужна другая стратегия.
ПРошу объясните как дроби делить.
Эти знания мне нужны, чтобы опровергнуть доказтельства перельмана, думаю эта еврейская голова ошиблась, а кто проверял доказтельство сами не понимали что смотрят, и поэтому решили согласиться, чтобы сойти за умных
Через преобразование Фурье
Всё правильно, там во второй его публикации при устранении особенности к знаменателю общему приводит он неправильно, дальше всё ломается.
привет
>начал учить математику и не понимаю деление дробей. КАК ЭТО ДЕЛАТЬ??
нужно понять, что такое дроби и зачем они нужны
из натуральных и целых чисел мы знаем о делении нацело. встречается уравнение [math]a \cdot x = b[/math], при [math]a \neq 0[/math] оно может иметь относительно [math]x[/math] целочисленное решение [math]\frac{a}{b}[/math]
смысл дробей в добавлении таких дробных чисел, чтобы подобные уравнения всегда имели решение. дроби так и обозначаются - парой чисел: числителем и знаменателем
при этом можно определить операции [math]+[/math], [math]/cdot[/math] и [math]\colon[/math] так, что они согласуются с операциями над натуральными и целыми числами и обладают привычными свойствами.
по смыслу деления как обратного к умножению, для деления числа [math]a[/math] на дробь [math]frac{x}{y}[/math] следует умножить [math]a[/math] на знаменатель дроби и поделить на числитель. требует усилий, чтобы представить, но так и получается.
Любой здоровый человек, начинающий учить матешу, пошлёт тебя и будет прав. Точка зрения "чтобы решать уравнения" оправдана при переходе с действ до комплексных, но для новичка эта цель надуманная. И проблемы с дробями обычно из-за того, что не ясно, почему они складываются так как складываются, умножаются так как умножаются и делятся так как делятся.
>>15954
Пусть ты по лесу гуляя нашел две палочки $a$ одинаковой длины и три палочки $b$ одинаковой длины. Их длину ты можешь сверить просто приложив их к друг-другу, для этого не обязательно их измерять чем-нибудь.
Ты выложил две палочки $a$ друг за другом, и под ними три палочки $b$ так же друг за другом и оказалось, что $a+a$ по длине такая же, как и $b+b+b$. Это можно записать как $2a=3b$.
Теперь ты захотел измерить эти палочки. За меру длины ты можешь взять палочку $b$, тк она меньше, полагаем что $b=1$. Тогда сумма $a+a = b+b+b = 3$. Но палочку $a$ ты палочкой $b$ измерить не можешь, тк она не укладывается целое число раз. Тогда хорошо бы найти такую палочку $c$, что она укладывается целое число раз и в $a$ и в $b$.
Немного поразмыслив приходим к следующему вопросу: единственна ли такая палочка $c$? Допустим мы нашли такую палочку $c$ и она целое число раз укладывается в палочки и в $a$ и в $b$. Тогда если мы её разломаем пополам, то половина от $c$ так же будет укладываться целоые число раз. А так же и треть, четверть...
Тогда палочка $c$ не единственная. Но каждая следующая палочка получается из $c$ путем деления. Существует ли палочка $d$ такая, что она не равна ни сумме нескольких палочек $c$, тк $c$ может быть само какой-то частью от $d$, ни является частью от $c$ при делении нацело? Но оставим этот вопрос.
Теперь, пусть ты нашел палочку $e=a+a=b+b+b$. Тогда ты палочку $a$ можешь получить разломав палочку $e$ пополам, а палочку $b$ отломав треть. Если $c$ целое число раз укладывается и в $a$, и в $b$, то $c$ укладывается целое число раз и в $e$. Раз уж так, то $c$ можно получить отломив от $e$ какую-то часть. Посмотрим на то, как палочки ломаются.
Пусть мы поломаем $e$ сначала пополам, а затем обе части разломим на трети. Получим 6 одинаковых частей. Пусть теперь сделаем наоборот, сначала поломаем $e$ на трети, а затем каждую треть пополам. Получим так же 6 частей. Тогда в обоих случаях эти части одинаковые, а значит нет разницы, как ломать в первую очередь.
Поломаем $e$ пополам, получим $a$ и этой палочкй $a$ палочка $e$ измеряется целое число раз. Поломаем теперь $a$ на трети, этими третями $a$ измеряется целое число раз. Теперь поломаем $e$ сначала на трети, получим палочки $b$. Палочкой $b$ можно нацело измерить $e$. Теперь $b$ поломаем пополам, половинкой от $b$ можно нацело измерить $b$. Так как выше мы "доказали", что не разницы в каком порядке делить, получим одно и тоже, то в 1) случае получаем палочку, которой целое число раз можно измерить $a$, а во 2) случае которой можно измерить $b$ и эти последние палочки равны, и эта палочка $c$ равна $\frac{1}{6}$ от $e$. Символ $\frac{1}{6}$ означает поделить на 6 равных частей и взять одну. Символ $\frac{2}{6}$ значит поделить на 6 частей и взять 2 из них и тд.
Поделить палочку и взять её копию похожие операции, они обратные. Если мы возьмем палочку $2a=a+a$ и поделим пополам, то получим палочку $a$. Поступим наоборот, сначала поделим, а затем удвоим, тогда получим ту же самую палочку $a$. Тогда выражение "взять $\frac{2}{6}$ от $e$" можно истолковать как сначала поделить на 6, а затем сложить 2 копии, так и как сначала взять 2 копии, а затем поделить на 6. Порядок действий тут не важен. От сюда: пусть есть дробь $\frac{2}{6}$, если мы увеличим и числеть и знаменатель на одно и тоже число $p$, то дробь не изменится, то есть $\frac{2p}{6p}=\frac{2}{6}$. Так же $\frac{2}{6}=\frac{2}{2\cdot3}=\frac{1}{3}$. Теперь мы готовы определить операции над числами.
Дробь это пара чисел $\frac{a}{b}$. Пусть мы хотим сложить две дроби $\frac{a}{b}$ и $\frac{c}{d}$. Чтобы их сложить нужно найти общую меру, для дробей $\frac{1}{b}$ и $\frac{1}{d}$ это $\frac{1}{bd}$. $\frac{1}{bd}$ содержится $d$ раз в дроби $\frac{1}{b}$ и $b$ раз в дроби $\frac{1}{d}$. Тогда в дроби $\frac{a}{b}$ дробь $\frac{1}{bd}$ содержится $ad$ раз, иначе $\frac{a}{b}=\frac{ad}{bd}$, аналогично и для второй. Тогда их сумма равна $\frac{ad+bc}{bd}$
Этого же результата можно достичь воспользовавшись свойством, что числитель и знаменатель мы можем домножить на одно и то же число, дробь не изменится.
Умножение легко продемонстрировать так же, как умножение целых чисел. Возьмём квадрат $1x1$, разделим его стороны на $b$ и $d$ частей и возьмем на них $a$ и $c$ отрезочков и построим на них прямоугольник. Его площадь равна $\frac{ac}{bd}$ от площади квадрата.
Деление определим как операцию, обратную умножению. $(\frac{a}{b}:\frac{c}{d})\frac{c}{d}=\frac{a}{b}$. Умножение за скобкой делит число в скобках на $d$ частей и берет $c$ из них, чтобы вернуть изначальную дробь "на место". Тогда дробь, что делила, делала наоборот, увеличивало в $d$ раз и делило на $c$, то есть $\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{c}$
Любой здоровый человек, начинающий учить матешу, пошлёт тебя и будет прав. Точка зрения "чтобы решать уравнения" оправдана при переходе с действ до комплексных, но для новичка эта цель надуманная. И проблемы с дробями обычно из-за того, что не ясно, почему они складываются так как складываются, умножаются так как умножаются и делятся так как делятся.
>>15954
Пусть ты по лесу гуляя нашел две палочки $a$ одинаковой длины и три палочки $b$ одинаковой длины. Их длину ты можешь сверить просто приложив их к друг-другу, для этого не обязательно их измерять чем-нибудь.
Ты выложил две палочки $a$ друг за другом, и под ними три палочки $b$ так же друг за другом и оказалось, что $a+a$ по длине такая же, как и $b+b+b$. Это можно записать как $2a=3b$.
Теперь ты захотел измерить эти палочки. За меру длины ты можешь взять палочку $b$, тк она меньше, полагаем что $b=1$. Тогда сумма $a+a = b+b+b = 3$. Но палочку $a$ ты палочкой $b$ измерить не можешь, тк она не укладывается целое число раз. Тогда хорошо бы найти такую палочку $c$, что она укладывается целое число раз и в $a$ и в $b$.
Немного поразмыслив приходим к следующему вопросу: единственна ли такая палочка $c$? Допустим мы нашли такую палочку $c$ и она целое число раз укладывается в палочки и в $a$ и в $b$. Тогда если мы её разломаем пополам, то половина от $c$ так же будет укладываться целоые число раз. А так же и треть, четверть...
Тогда палочка $c$ не единственная. Но каждая следующая палочка получается из $c$ путем деления. Существует ли палочка $d$ такая, что она не равна ни сумме нескольких палочек $c$, тк $c$ может быть само какой-то частью от $d$, ни является частью от $c$ при делении нацело? Но оставим этот вопрос.
Теперь, пусть ты нашел палочку $e=a+a=b+b+b$. Тогда ты палочку $a$ можешь получить разломав палочку $e$ пополам, а палочку $b$ отломав треть. Если $c$ целое число раз укладывается и в $a$, и в $b$, то $c$ укладывается целое число раз и в $e$. Раз уж так, то $c$ можно получить отломив от $e$ какую-то часть. Посмотрим на то, как палочки ломаются.
Пусть мы поломаем $e$ сначала пополам, а затем обе части разломим на трети. Получим 6 одинаковых частей. Пусть теперь сделаем наоборот, сначала поломаем $e$ на трети, а затем каждую треть пополам. Получим так же 6 частей. Тогда в обоих случаях эти части одинаковые, а значит нет разницы, как ломать в первую очередь.
Поломаем $e$ пополам, получим $a$ и этой палочкй $a$ палочка $e$ измеряется целое число раз. Поломаем теперь $a$ на трети, этими третями $a$ измеряется целое число раз. Теперь поломаем $e$ сначала на трети, получим палочки $b$. Палочкой $b$ можно нацело измерить $e$. Теперь $b$ поломаем пополам, половинкой от $b$ можно нацело измерить $b$. Так как выше мы "доказали", что не разницы в каком порядке делить, получим одно и тоже, то в 1) случае получаем палочку, которой целое число раз можно измерить $a$, а во 2) случае которой можно измерить $b$ и эти последние палочки равны, и эта палочка $c$ равна $\frac{1}{6}$ от $e$. Символ $\frac{1}{6}$ означает поделить на 6 равных частей и взять одну. Символ $\frac{2}{6}$ значит поделить на 6 частей и взять 2 из них и тд.
Поделить палочку и взять её копию похожие операции, они обратные. Если мы возьмем палочку $2a=a+a$ и поделим пополам, то получим палочку $a$. Поступим наоборот, сначала поделим, а затем удвоим, тогда получим ту же самую палочку $a$. Тогда выражение "взять $\frac{2}{6}$ от $e$" можно истолковать как сначала поделить на 6, а затем сложить 2 копии, так и как сначала взять 2 копии, а затем поделить на 6. Порядок действий тут не важен. От сюда: пусть есть дробь $\frac{2}{6}$, если мы увеличим и числеть и знаменатель на одно и тоже число $p$, то дробь не изменится, то есть $\frac{2p}{6p}=\frac{2}{6}$. Так же $\frac{2}{6}=\frac{2}{2\cdot3}=\frac{1}{3}$. Теперь мы готовы определить операции над числами.
Дробь это пара чисел $\frac{a}{b}$. Пусть мы хотим сложить две дроби $\frac{a}{b}$ и $\frac{c}{d}$. Чтобы их сложить нужно найти общую меру, для дробей $\frac{1}{b}$ и $\frac{1}{d}$ это $\frac{1}{bd}$. $\frac{1}{bd}$ содержится $d$ раз в дроби $\frac{1}{b}$ и $b$ раз в дроби $\frac{1}{d}$. Тогда в дроби $\frac{a}{b}$ дробь $\frac{1}{bd}$ содержится $ad$ раз, иначе $\frac{a}{b}=\frac{ad}{bd}$, аналогично и для второй. Тогда их сумма равна $\frac{ad+bc}{bd}$
Этого же результата можно достичь воспользовавшись свойством, что числитель и знаменатель мы можем домножить на одно и то же число, дробь не изменится.
Умножение легко продемонстрировать так же, как умножение целых чисел. Возьмём квадрат $1x1$, разделим его стороны на $b$ и $d$ частей и возьмем на них $a$ и $c$ отрезочков и построим на них прямоугольник. Его площадь равна $\frac{ac}{bd}$ от площади квадрата.
Деление определим как операцию, обратную умножению. $(\frac{a}{b}:\frac{c}{d})\frac{c}{d}=\frac{a}{b}$. Умножение за скобкой делит число в скобках на $d$ частей и берет $c$ из них, чтобы вернуть изначальную дробь "на место". Тогда дробь, что делила, делала наоборот, увеличивало в $d$ раз и делило на $c$, то есть $\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{c}$
>Любой здоровый человек, начинающий учить матешу, пошлёт тебя и будет прав.
здоровый грубиян, начинающий учить матешу, и то не любой
>Точка зрения "чтобы решать уравнения" оправдана при переходе с действ до комплексных, но для новичка эта цель надуманная.
здоровый грубиян и новичок в математике, не понимающий, причем тут уравнения... тоже не всегда пошлет
>Тогда сумма a+a=b+b+b=3. Но палочку a ты палочкой b измерить не можешь, тк она не укладывается целое число раз. Тогда хорошо бы найти такую палочку c, что она укладывается целое число раз и в a и в b.
речь идет о решении системы уравнений [math](2a = 3b) \& (kc = a) \& (lc = b)[/math] относительно [math]c[/math], [math]l[/math] и [math]k[/math]
Потребность в дробях возникает безо всяких уравнений. Комплексные числа можно мотивировать уравнениями, но всё что до них имеет более понятные и приземленные мотивировки для вкатунов.
У греков, кстати, дроби хоть и были, но только в виде пропорций. Они не воспринимали дроби как деление целого на части.
>речь идет о решении системы уравнений
Я думал так изначально написать, типа пусть $c$ общая мера и $a=k_{1}c$, $b=k_{2}c$, то $2k_{1}c=3k_{2}c$, от сюда легко подобрать, что $k_{1}=3$, а $k_{2}=3$, но интересно было придумать как обойтись без буквенной алгебры, ведь она в общем возникла после изобретения дробей.
наверное, наш спор о словах
все, что ты пишешь - я в этом вижу рассмотрение уравнений, для чего производится расширение числовой системы
палочки и яблочки это не математика
уравнения — это математика
Все правильно, складывают не цифры, а люди! Математики подсунули нам вместо складывания сЛОЖение, нужно вернуться к истокам и все переосмыслить!
>целочисленное решение [math]\frac{a}{b}[/math]
[math]\frac{b}{a}[/math]
>определить операции [math]+[/math], [math]/cdot[/math] и [math]\colon[/math]
[math]+[/math], [math]\cdot[/math], [math]\colon[/math]
> тех я тебе дам
> превью я тебе не дам
100 процентная гарантия безостановочных веселых обсеров.
петух-неосилятор, ты сам двух слов не можешь связать, чтобы получилось что-то осмысленное, и потому тебе это непонятно, однако называть опечатки "обсерами" уныло и тупо
и определение топологии у Вербицкого правильное, кстати
Причина внезапного анального подрыва, чмоха?
>и определение топологии у Вербицкого правильное, кстати
похоже годы ежедневных преобразований Фурье взяли над мелкочмохой свое.
почитал интервью этого вербицкого. вот как он может заниматься интеллектуальной деятельностью, тем более математикой?
он ведь в общественных ввпросах совсем инфантильный экстремист, которому, судя по всему, не хватает самообладания, чтобы отвлечься от эмоций и постараться выработать хотя бы сколь-либо беспрестрассную и интеллектуально добросовестную позицию.
а в математике сдержанность нужна. ведь с одной стороны, тут как: одна ошибка и ты ошибся. а с другой стороны, так и вовсе: в том и состоит удовлетворение математическое, чтобы сделать аккуратно, тоненько, в т. ч. и особенно там, где по неряшливости можно было бы оплошать.
ну какой это математик?
У тебя просто стереотип, что математики это какие-то сверхрациональные люди. Избавляйся от стереотипов.
>У тебя просто стереотип, что математики это какие-то сверхрациональные люди.
наверное, ты прав.
>Избавляйся от стереотипов.
желательно кнч пошире мыслить. но в данном случае... даж хз как
>может заниматься интеллектуальной деятельностью
>в общественных ввпросах совсем инфантильный экстремист, которому
противоречия никакого
>не хватает самообладания, чтобы отвлечься от эмоций и постараться выработать хотя бы сколь-либо беспрестрассную позицию.
скорее, желания, чем самообладания: таки такую позицию вырабатывать для чего? он не политик
можно обратить ещё внимание, что при всей своей позиции он практически ни с кем не ссорится (в отличии от некоторых). недавние обвинения от бывшей студентки это что-то совсем ему несвойственное (в том смысле, что до того никто его ни в чём реальном не обвинял)
>интеллектуально добросовестную
непонятно вообще что это
Список заблуждений о математиках и математике:
математик как следует разберется в любом вопрос или по крайней мере не будет пиздеть хуйни
<---- вы находитесь здесь
по крайней мере об этой своей математике не будет
или здесь
если математик что то знает как следует то он это и сможет объяснить как следует
чтобы разобраться в математике как следует надо посмотреть что делает хороший математик и повторять за ним
 473 Кб, 1280x1600
473 Кб, 1280x1600Можно няшиться в попчан с другими маняматиками
Сколько в процентах агонии, а сколько экстаза?
Согласно англ. вики:
>If the key is random and is at least as long as the message, the XOR cipher is much more secure than when there is key repetition within a message.[4] When the keystream is generated by a pseudo-random number generator, the result is a stream cipher. With a key that is truly random, the result is a one-time pad, which is unbreakable in theory.
Спасибо, получается различается только генератором случайных / псевдослучайных чисел
Нет.
я не от мира математики, и профессионально выражаться не умею, ищу способ визуализировать простые числа, да и всего
бамп тиме
конечно, когда у тебя есть какое-то множество, ты можешь из него выкинуть отдельно взятый элемент, никто тебя в этом упрекать не будет
однако, если говорить о декартовом произведении, то множество, которое получится из него выкидыванием элемента, декартовом произведением уже лучше не называть. дело в том, что декартово произведение возможно не только на множествах: например, возьмём декартово произведение двух векторных пространств; на таком произведении есть естественная структура векторного пространства, т.е. прямое произведение двух векторных пространств - это снова векторное пространство. а теперь давай из этого произведение один элемент выкинем. тогда это уже не будет векторное пространство, а будет просто какое-то множество. но тогда и давать ему название, которое намекает на его естественность в контексте векторных пространств, уже не стоит
более точно, декартово произведение есть категорная операция, определённая в категориях; в этом смысле она к множествам уже вообще отношения не имеет, а является более абстрактной
говорить о множестве каких-то пар элементов и даже рассматривать его как подмножество декартова произведения всегда можно. но с следует быть названиями аккуратнее, чтобы не создавать у читателя ложных ассоциаций и впечатлений
Спасибо, но тут я имею ввиду именно что множества и декартово умножений множеств, так что получается всё не плохо.
>мы бы говорили бы о всех парах без этого элемента, что было бы тем же самым, как если бы мы сразу говорили бы о создании всех пар без данного элемента?
Да. Этот фрагмент понятен и выражаемое им утверждение справедливо.
Разве? Всё же у тебя точка то одна выколота.
- чем отличается tag и brach в git?
- чем отличается процесс и поток?
Бесит, пиздец!
Что на это можно ответить с позиции математической или общенаучной логики?
Вот прям как в рассказе "Срезал" ?
Нужно достать дихлофос и гасить тараканов
DooM!
 262 Кб, 1080x720
262 Кб, 1080x720Типа срыв покровов.
https://www.youtube.com/watch?v=7Ufspa60zd8
Ну всяко было больше анонов с хотя бы базовым математическим образованием, алгем там, топология. Достаточно почитать старые треды про условную алгебру, и сравнить их с типичными обсуждениями в 2024 (про какие-нибудь основания), или с говновбросами в новичковом треде.
И я имею в виду старые, а не 5 лет назад.
Про Картье наверное большинство знают из-за дивизора Картье, но он вообще много какие идеи продвинул, например определение спектра через простые идеалы, а не максимальные. В физике космические группы Галуа тоже его идея.
Вот замечательная статья самого Картье:
A mad day’s work: from Grothendieck to Connes and Kontsevich. The evolution of concepts of space and symmetry
В догонку: пару недель назад за Картье ушёл и Гамильтон. Поток Риччи, гипотеза Тёрстона о геометризации, вот это всё.
Функциональные уравнения это треш, потому что каждое решается каким-то трюком. Почти нигде это не встречается в математике. Существует преимущественно в олимпиадах.
>>17994
>>17993
Очень уныло и жалко гнать анона, который принёс задачу, которую ты не можешь решить
Олимпиадная она или нет, интересна тебе лично или нет, это чисто математическая задача, сформированная в математических терминах (пусть и не совсем строго). Так что либо решай, либо заткнись, если не петух
>если в задаче есть символы, которые встречаются в математике, то это математика
В книгах по кулинарии пропорции используются, наверное это тоже математика?
>решается каким-то трюком
Вся математика состоит из трюков. Те, которые используются чаще других, называются леммами.
Нет, это не так. Бывает конечно теорему доказывают трюком, но спустя время её докажут описательно.
Как элементарный пример - формула Кардано. Кардано её вывел трюком. Но её же можно вывести с помощью резольвент Лагранжа, которые получаются не трюком, а описанием.
Вся олимпиадная "математика" это трюки. Вся продуктивная математика описательна.
там еще номера страниц есть, а это числа, т.е. математика
если задача сформулирована полностью на языке математике и предполагает соответствующее решение, то это математическая задача. это чисто объективный критерий, независящий от того, какие эмоции она вызывает у двачеров
>>17999
выдели из книги по кулинарии задачу на пропорции, и это будет безусловно математика. а почему, собственно, нет? просто такие задачи решены уже очень давно
>Вся олимпиадная "математика" это трюки. Вся продуктивная математика описательна.
А вот этот аргумент целиком состоит из собственных предпочтений и эмоций, обусловленных только личностью автора, и больше ничего. автор такого аргумента может сколько угодно жарко спорить о том, что именно это его видение настоящее, правильное, "содержательное" и "продуктивное", а какое-то другое видение только наоборот, но это всё равно останется только его видением, сформированным из его личностных особенностей
это же тебе (или вам) сраку рвёт - увидел задачу, которую сделать не в силах, и сразу в крики НИНУЖНААА
а ведь мог просто промолчать, лол
>постит заведомо трюковую дристню
>всех, кто не хочет есть дерьмо, обвиняет в том, что ниасилели
не я постил
я только вступил в спор и выразил своё мнение, почему тебя так рвёт и ты тратишься на личные оскорбления, твоё личное дело
семен не пизди
>из собственных предпочтений и эмоций, обусловленных только личностью автора, и больше ничего
Чел, нужно разбиратсья в сортах, иначе можно жизнь потратить на какое-то говно типа теории графов и логики. А некоторые и вовсе всю жизнь олимпиадки решают, а потом других этим заражают.
>>18012
>это же тебе (или вам) сраку рвёт - увидел задачу, которую сделать не в силах, и сразу в крики НИНУЖНААА
Опять же, не нужно стремиться уметь и знать всё. Это невозможно. Потому нужно тратить время только на интересные и базовые вещи. Функциональные уравнения к ним не относятся.
Ладно, беру свои слова назад, математики ведь ебанутые двачеры поголовно.
Во время рисёрча приходится решать любые задачи, которые встречаются на пути к цели. Да, область и подходы сильно меняют пропорции, какие именно задачи ты будешь решать. Но даже если ты там когомологии в inf-категориях считаешь, иногда может понадобиться и комбинаторика.
>>18023
Откуда ты взял эту задачу, все ли условия ты написал и уверен ли ты, что у неё есть решение?
Сам придумал сам попытался решить. Не получилось, но стало интересно решение, вот и задал тут вопрос.
 85 Кб, 1063x233
85 Кб, 1063x233Не все функциональные уравнения имеют решение в виде элементарных функций. Вот, например: https://en.wikipedia.org/wiki/Half-exponential_function
Так что я не уверен, что у твоей задачки есть разумное решение. Более того, иногда вообще никакого решения не существует.
http://yaroslavvb.com/papers/rice-when.pdf
Под iterative roots тут имеется в виду решения функциональных уравнений вида $\smash{\underbrace{f(f(...f(x))...)}_\text{$r$ раз}}=g$ для $r\geq 2$
Ну терь буду знать, спасибо.
>Чел, нужно разбиратсья в сортах, иначе можно жизнь потратить на какое-то говно типа теории графов и логики.
так ты изучай математику, там и разберёшься, что тебе нравится. кто-то и графами занимается и очень доволен, хули тебя это беспокоит? у них и приложения какие-то есть, полезные людям
>Опять же, не нужно стремиться уметь и знать всё. Это невозможно.
я тебе предлагал стремиться уметь и знать всё?
однако расширять кругозор и быть открытым новому всегда полезно, у тебя не получится меня переубедить
ты увидел задачу, которую не хочешь решать - так и не решай, кто тебя заставляет? но если ты останавливаешься, отвечаешь на соответствующий пост, и ответ твой состоит исключительно из криков НИНУЖНААА, это наводит на мысли. конечно, ты можешь веровать, что такие крики и есть полезное, но как-то очень самонадеянно, мягко говоря, особенно для анонима с двача
потому либо решай задачу, либо иди мимо
тот, кто задачу спросил, он не обращался лично к тебе
Честно говоря, я примерно так же считаю
я лично считаю, программирование это вообще не та профессия, которую следует изучать в вузе. это чисто прикладное занятие, в то время как вуз даёт фундаментальные знания
that being said, абсолютно неважно, чему учить студентов на специальности "программирование", потому как такой специальности в вузе быть не должно вообще
так что функан такой программе отлично подходит, очень приятная наука на самом деле.
есть же компьютер сайенс
Ну знаешь. Смотрю какой-нибудь лекториф фпми, где приходит чел из Яндекса и читает курс по корутинам с семинарами. А нам, собственно, читали какую-то бесполезную фигню под названием "параллельное программирование", за которую всем поставили просто так оценки за посещение лекций.
Я бы ещё понял, если бы вместо этого читали алгебру, теорвер и матстат в удвоенном объеме, а не как у нас какую-то базу, которую я уже забыл без должной практики.
А так абсолютно непонятно, зачем мне функан. В следующем семестре будет матфизика, к слову.
>А так абсолютно непонятно, зачем мне функан.
тебе и корочка твоего вуза совершенно незачем, разве что впечатлить работодателя, к которому ты придёшь на собеседование
программирование значительно лучше изучать на практике, чем в рамках высшего образования.
это моё имхо, конечно
так-то не математика
Так вам функан дадут урезанный в виде обрывков из 19 века. Это не функан.
>теорвер и матстат
я могу ошибаться, но ведь эти науки строятся более менее вменяемо с использованием теории меры(тервер) и функана(statistical learning theory), мб знающие могут подтвердить?
по-хорошему да: на основе адекватного им курса функана (в рамках которого и базовую теорию меры можно пояснить) эти разделы получаются более естественно
>эти разделы получаются более естественно
Что тут значит "естественность"? Такое изложение нахуй почти никому не нужно, в большинстве случаев даже математикам.
нормально учат, хоть бы и программист
>А так абсолютно непонятно, зачем мне функан. В следующем семестре будет матфизика, к слову.
1) Функан - аппарат современной матфизики
2) Если ты на каком-нибудь ПМИ - то это не "учеба на программиста", лел.
То, что одебилевшие студенты после ПМИ все поголовно прогерами работают, не значит что это учеба на прогера. Ебучее когнитивное искажение, из-за которого айтишники толпами прут на ПМИ, а в итоге 2/3 к выпуску отваливаются, потому что О ШОК на программе с названием прикладная математика и информатика оказывается ебут математикой, а не 4 года учат жисончики перекладывать.
>в итоге 2/3 к выпуску отваливаются
В большинстве программ со словом "математика" в названии 2/3 отваливается, дело не в программистах и ПМИ.
Как тут уже сказали выше, это не функан. Дадут обрывки, ну условно чтобы ты понимал, что такое $L_1$/$L_2$ норма в машинном обучении\регрессии. Если что-нибудь расскажут из вариационного исчисления - тоже неплохо. И матфизика тоже может быть полезна, в машинном обучении много чего взято из физики по аналогии (гамильтонов MCMC например).
вероятность будет 1/2: либо выпадет, либо нет
Это стандартная задача, погугли её лучше. Решается через производящую функцию, например.
>>18728
Мнение?:
from math import comb
# Параметры задачи
n_dice = 100 # Число кубиков
target_sum = 346 # Целевая сумма
sides = 6 # Число граней на кубике
# Вычисляем коэффициент при x^346 в разложении производящей функции
total_ways = 0 # Коэффициент для нужной суммы
# Число полных шагов для коэффициентов кратных 6 (k)
for k in range((target_sum - n_dice) // sides + 1):
sign = (-1) k # Чередующийся знак
ways = comb(n_dice, k) comb(target_sum - sides k - 1, n_dice - 1)
total_ways += sign * ways
# Общая вероятность
total_outcomes = sides n_dice # Общее число исходов
probability = total_ways / total_outcomes
total_ways, probability
 128 Кб, 1080x1037
128 Кб, 1080x1037Есть формула
g^x=b mod(p), где p - простое, g∈{2,...,p-1}
При x∈{1,...,p-1} получается полный цикл остатков b всех чисел из множества {1,...,p-1}
При этом каждый x имеет свой уникальный b, но не всегда. Это зависит от выбранного примитивного корня g. Но вот какого именно g?
Например p=7, получаем такой набор остатков
b₂ -> {2,4,1,2,4,1}
b₃ -> {3,2,6,4,5,1}
b₄ -> {4,2,1,4,2,1}
b₅ -> {5,4,6,2,3,1}
b₆ -> {6,1,6,1,6,1}
Здесь g={3,5} - являются примитивными остатками
При p=11, g={2,6,7,8}
При p=13, g={2,6,7,11}
При p=17, g={3,5,6,7,10,11,12,14}
И тд
Еще известно, что количество примитивных корней можно вычислить по формуле fi(p-1), где fi - функция Эйлера(на фото)
Так вот, во-первых, есть ли способ проверки конкретного g на примитивность, исключая метод полного перебора x?
Во-вторых, возможно ли найти все g для конкретного p, исключая полный перебор и проверку каждого g в диапозоне {2,...,p-1}?
 128 Кб, 1080x1037
128 Кб, 1080x1037Есть формула
g^x=b mod(p), где p - простое, g∈{2,...,p-1}
При x∈{1,...,p-1} получается полный цикл остатков b всех чисел из множества {1,...,p-1}
При этом каждый x имеет свой уникальный b, но не всегда. Это зависит от выбранного примитивного корня g. Но вот какого именно g?
Например p=7, получаем такой набор остатков
b₂ -> {2,4,1,2,4,1}
b₃ -> {3,2,6,4,5,1}
b₄ -> {4,2,1,4,2,1}
b₅ -> {5,4,6,2,3,1}
b₆ -> {6,1,6,1,6,1}
Здесь g={3,5} - являются примитивными остатками
При p=11, g={2,6,7,8}
При p=13, g={2,6,7,11}
При p=17, g={3,5,6,7,10,11,12,14}
И тд
Еще известно, что количество примитивных корней можно вычислить по формуле fi(p-1), где fi - функция Эйлера(на фото)
Так вот, во-первых, есть ли способ проверки конкретного g на примитивность, исключая метод полного перебора x?
Во-вторых, возможно ли найти все g для конкретного p, исключая полный перебор и проверку каждого g в диапозоне {2,...,p-1}?
>b₂ -> {2,4,1,2,4,1}
>b₃ -> {3,2,6,4,5,1}
>b₄ -> {4,2,1,4,2,1}
>b₅ -> {5,4,6,2,3,1}
>b₆ -> {6,1,6,1,6,1}
Только здесь опечатка, вместо b будет g
Примитивный корень = образующая мультипликативной группы. Можно посмотреть на порядок мультпликативной группы ($n-1$ или в твоём случае $p-1$, видимо), посмотреть на делители этого чилса, показать, что порядок $g$ не равен ни одному из делителей (кроме самого n-1). Это проще, чем полный перебор, кажется. Наверняка ещё из каких-нибудь групповых соображений можно это упростить.
g для фиксированного p тоже из подобных соображений ищутся, но это не прям кардинально дело упрощает.
Мало того, что монотонно бубнит свой конспект, практически не дает никаких примеров и нихуя не мотивирует определения, так еще и лекции тратит на какую-то хуйню. Два часа показывали, что существуют прямые и проективные пределы колец, а нахуя? Чтобы один раз упомянуть их в доказательстве существования алг. замыкания. Зато теорем Силова нет. Охуенно.
>что существуют прямые и проективные пределы колец
Это полезнее, чем теоремы Силова, честно говоря. Группа Прюфера и профинитные дополнения мне хоть иногда встречались. Поработали с пределами — уже хорошо. Остальное звучит не очень хорошо.
>Так они бесполезные.
>>19046
>Это полезнее, чем теоремы Силова
В любой ситуации, где нам нужна какая-то классификация конечных групп и/или подгрупп какой-то конечной группы, нам нужны теоремы Силова. Мне интересна область, где часто рассматриваются действия конечных групп, поэтому теоремы мне кажутся довольно полезными.
>>19046
>Поработали с пределами — уже хорошо.
Я не против работы с пределами, но нам не рассказали ничего про категорные (ко)пределы, только про прямые и проективные колец, потратили два часа, чтобы показать, что на пределе будет структура кольца (про коуравнители и копроизведения тоже ничего не рассказали), и из приложений показали только построение p-адических целых чисел. Я уверен, что это и близко не самый лучший способ ввести пределы.
Окей, мб тогда они тебе пригодятся. Правда мне однажды нужно было описать представления коненой p-группы, даже там не пригодились.
Некатегорное построение руками — это как раз полезно. Но да, судя по остальному, что ты рассказываешь, курс у вас так себе.
>В любой ситуации, где нам нужна какая-то классификация конечных групп и/или подгрупп какой-то конечной группы, нам нужны теоремы Силова
Такая ситуация возникает редко. И более того, обычно можно какими-то другими аргументами понять, что за подгруппы.
Теоремы Силова пихают в учебники не потому, что они полезные в (математической) практике, а потому, что они (могут быть) полезны педагогически. Например, илююстрация того, как можно использовать действия групп, или илююстрация того, как можно подойти к классификации объектов.
>Теоремы Силова пихают в учебники не потому, что они полезные в (математической) практике
То есть Серр использует теоремы Силова в учебниках по локальным полям, когомологии Галуа и конечным группам просто по приколу, как и авторы учебников по теории модулярных представлений? Как-то сложно в это поверить, но ладно.
Если ты не пездюк-второкур, который пришёл ныть на двощ про плохих преподов с плохим курсом алгебры, а уже занимаешься исследованиями в перечисленных темах, то ознакомиться с теоремами Силова и их доказательством - это дело от силы на один вечер. Противоречия никакого нет.
>то ознакомиться с теоремами Силова и их доказательством - это дело от силы на один вечер.
Для меня действительно не проблема ознакомиться с теоремами Силова и их доказательством за один вечер - собственно, я это и сделал. Но странно, как мы перешли от "теоремы Силова не нужны" к "если они тебе нужны, то выучи сам". Я-то выучу, а нахуй университет и доценты вообще тогда нужны, если я на один из базовых результатов в теории конечных групп должен и сам наткнуться и сам выучить?
че ты такой душный? не нравятся тебе лекции твоего препода - не ходи на них. тебя заставляют?
Я тебе открою страшную тайну. В принципе на любой стадии обучения математика (ну может кроме первого курса) значительная часть знаний о математике - если даже не большинство - из самообучения, чтения книг, и решения задач/доказательств. Иначе ты не будешь знать вообще ничего.
А можно вообще сесть под дерево и как Будда за 40 дней высрать из головы всю математику от Пифагора до наших дней. Хули мелочиться.
Реалии таковы, что таких вот "базовых результатов" очень много, а времени очень мало. И нужно делать выбор. Я не утверждаю, что вот в твоём курсе этот выбор сделан правильно. Но теоремы Силова - это точно не какой-то фундаментальный результат, без которого типичный математик не обойдётся.
Классика. В целом, ничего страшного.
>>19096
>This story really highlights, to me, the poor job which humans do of documenting modern mathematics. There appear to be so many things which are “known to the experts” but not correctly documented.
>For me, this is just one of many reasons why humans might want to consider getting mathematics written down properly, i.e. in a formal system, where the chances of error are orders of magnitude smaller.
Так это практически в каждой дисциплине так. Эксперты знают недосказанные интуитивные детали, а документируется всё с учётом ограниченного времени, и ограниченного места в монографии\статьях. Из моего личного опыта: так же с изучением музыкальных инструментов, и изучением языков. Есть куча деталей, которые нигде не написаны, но "подразумеваются".
Другое дело, что погромисты хотят поиграть в математиков, и поэтому формально нужно задокументировать именно её. Ну или просто оставить математику математикам, которые эти детали поймут и без формализации - да не, бред какой-то.
Нет уж, это тебе в /pr/.
>Другое дело, что погромисты хотят поиграть в математиков, и поэтому формально нужно задокументировать именно её.
Если что, формализацией в этом случае занимаются довольно неплохие и относительно именитые алг. геометры/теоретики чисел, а не погромисты.
Ну и бтв, не уверен, что ты понимаешь, что в этом контексте значит быть "экспертом". Обычно "экспертов" в подобласти математики в лучшем случае около дюжины, и они знают не "недосказанные интуитивные детали", а вещи для которых нужно среди этой самой дюжины экспертов крутится.
выписаны в программисты
Еще есть подозрение, что это должно обобщаться для классификации к.п. модулей над областями главных идеалов и как-то связано с тороидами, но тут я вообще потерян.
аксиоматика Колмогорова, более менее, есть назначение некоторых ограничений на объекты из теории меры, разделом которой теория вероятностей является. так что теория вероятностей это вполне адекватная математическая наука, пусть и с ограниченным (внутри самой математики) кругом применения
 95 Кб, 962x1280
95 Кб, 962x1280Планирую пройти все учебники Мордковича с 7го класса. Есть идеи какой подход использовать к упражнениям? А то их там дохуя слишком и если все делать, то это пизец времени займет? Хочется и не упустить ничего и лишнее не делать.
Может кто уже делал нечто подобное, как подходили к этому вопросу?
>Моя основная проблема что я долго считаю очень
Это дело наживное, по мере того, как что-то решаешь у тебя в голове образуются некие ассоциации, которые позволяют тебе всё это делать быстрее.
>туплю пиздец хуже всех
А тебе есть куда спешить? Сиди и осмысляй потихоньку.
Можно идти по каждой десятой например, особенно если видишь что они однотипные, со звездочкой решать
>у тебя в голове образуются некие ассоциации, которые позволяют тебе всё это делать быстрее
Пока не достигаешь потолка (по глубине и по охвату), кототрый, возможно, уже и не сможешь пробить своими куцыми интеллектуальными способностями. Чем больше я изучаю математику, тем хуже мне становится.
мимо
Смотришь на упражнение, и если сразу готов дать правильный ответ и/или понимаешь, как решать (насколько я помню, у Мордковича слишком много однотипных), то пропускай. Но вообще от понимания той или иной темы отталкивайся. Если прорешал 10 задач и не допустил ни одной ошибки, то можно приступать к следующей темке. Через неделю-две можешь проверить, насколько твои знания сохранились (выбери из пройденых тем по паре задач и реши).
По терверу можешь взять Вентцель, Гнеденко, Феллера, Ширяева. У последнего задачник есть.
Можешь взять в рот.
Этого не знаю. Может, Рома объяснит: он, наверно, понял
Гёдель. Не совсем шизофрения правда, параноидальное расстройство. Но заболевания связанные. Так что, возможно, он тоже мог бы срать в треде оснований на поздней стадии болезни.
 1,7 Мб, 1280x793
1,7 Мб, 1280x793вспоминаешь 9*3=27?
видишь что до 200 от 180 нужно 20, потом 90-20 и 200+70
или например 8+9=17 ->270? Я например не помню что 8+9=17 и кажется даже если запомню это не будет так органично в голове складываться как например, 8+2 или 5+3, как кубики.
Я помню что 9+9=18 следовательно 8+9=17
но вот все эти алгоритмы всплывают в голове одновременно когда примеры типа 18+9 и я не знаю какой применять
Есть какие годные видосы про устный счет? Я никогда не заморачивался и вот заморочился
Не только. Симплициальные множества как предпучки, например, определяются. А через них всякая inf-категорная фигня, например, и не только, это довольно хороший объект.
Выходит предпучки в том числе нужны чтобы классифицировать какие-то объекты(определять т.е). А то я думал у них какой-то более сакральный смысл как у пучков с сечениями.
Ну, это сам по себе достаточно общий и хороший объект с универсальным свойством.
Но именно геометрического смысла у него, наверное, явного нет, как раз из-за вот такой вот общности, хотя вот алгебротопологические трактовки мб и есть, не знаю.
>пространство модулей это
Это контравариантный функтор (т.е. "предпучок") из категории схем в категорию множеств. Какая-то схема ("параметры") это аргумент функтора, и значение функтора на этой схеме это множество классов эквивалентности семейств параметризованных этой схемой.
Ну вроде понял, спасибо.
Ты сам понял, что спросил? Как определение чего-либо может определять противоречивость или непротиворечивость какой-либо аксиоматики
>определять
Ну ладно, тогда давай скажу что не определять, а выводить или приводить к противоречиям. Хотя в таком случае ответ очевиден, спасибо!
0)Элементом множества может быть всё что угодно
1)Элементом множества может быть само же это множество
.
.
.
Это не определения
ты тупой
Хз, конечно, но по идее нетривиальные автоморфизмы кольца индуцируют автоморфизмы алгебры, которым не найдётся соответствия среди автоморфизмов проективного пространства.
ищи мой пучок у себя в расслоении
Скажите, как решать рекуррентную последовательность для, скажем, вот такого случая:
$x_{n+1}=\frac{x_n}{n+1}$
хуита говно
$x_{n+1} = \frac{x_n}{n+1} \Leftrightarrow x_{n+1} - \frac{1}{n+1}x_n = 0 \Rightarrow \chi(x) = x - \frac{1}{n+1} \Rightarrow x = \frac{1}{n+1} \Rightarrow \frac{1}{(n+1)^n}$ - частное решение.
сказочный долбоеб
А есть что-нибудь среднее между Хатчером и Спеньером?
Хатчер да, весь такой, хотя там есть полезные инсайты (так говорят). Книжек по топологии множество, у меня лично любимой нет
Большинство математических "учебников" можно читать только если уже знаешь все что в них написано. Потому что они полное говно.
Чем громче массы кукарекают какой охуенный "учебник" тем он как правило говеннее.
tom Dieck.
По-моему, Хатчер хорош чисто как база; то есть строго главы про гомологии и гомотопии, а все приложения это бля какая-то солянка без задач.
Зависит от теории множеств.
А вот физики и инженеры (тоже, вроде бы, технари) - наоборот, успешные гигачеды.
ИМХО, увлечение виртуальными несуществующими мирами до добра не доводит, человек даже с недюжинным интеллектом теряет навыки, необходимые для реального мира.
>Вы замечали, что маняматики и программистишки (настоящие) - жалкие, никчемные омеганы?
многих ты математиков знаешь помимо Перельмана? можешь не отвечать
Перельмана ты тоже не знаешь, очевидно
Стоит отметить, что, кажется, по отзывам сотрудников он действительно временами инженерит чуть ли не до сих пор.
A priori не верил, но некоторые источники почти меня убедили.
Только в отсталом совке (на который надрачивают большинство маняматиков) инженер = жалкий нищук, который не может купить машину. Маск и Эдисон - примеры всем известных американских инженеров, а миллиардер Говард Хьюз вообще стал архетипом в массовой культуре, породив образы Бэтмена, Тони Старка, Лекса Лютора...
>>21578
Многих. Опущенного дырявого петуха Вербицкого, например. Или 15-рублевого лахтовика Савватеева. А вот ни одного успешного советского или российского маняматика не знаю. Из физиков, например, гигачедом был Ландау (хотя был и куколд Сахаров, не все так однозначно). Из программистов успешными стали только уехавшие эмигранты.
>>21579
Дешевый графоман-фантаст, аналог нашего Лукьяненки или Головачева, пример успешного человека? Вот Хаббард, например, был миллионером и основал целую собственную религию.
Он держит связь с двумя женщинами: одна смотрит за его квартирой на набережной реки Мойки, где случилось убийство, а с другой у преступника общие интересы. Избранница расчленителя преподает историю и посылает ему литературу. Именно на последней Соколов и планирует жениться.
«Мне Олег сказал: «Мама, она мне делает столько добра, что даже не знаю, как это произошло». Он хочет жениться. Она тоже историк, любительница этого дела, — сообщает мать историка.
https://www.starhit.ru/life/ona-tozhe-istorik-oleg-sokolov-raschlenivshii-studentku-sobiraetsya-sygrat-svadbu-v-tyurme-902580/
Гуманитарии - чеды, поэтому жалкие программистишки и маняматики им так завидуют.
А вы продолжайте дрочить на лолей и бояться взрослых женщин, как Льюис Кэрролл (профессор Доджсон, для А. Лиделл - дядюшка Додо, которому ее родители запретили встречаться с девочкой, узнав об обнаженных фотоснимках).
 881 Кб, 643x764
881 Кб, 643x764>А вот ни одного успешного советского или российского маняматика не знаю.
Вспомнил таки сабж. Но его вряд ли можно назвать маняматиком. Ведь он занимался не научной деятельностью, а сугубо прагматичным обуванием гоев. В советское время торговал импортными компьютерами. С математикой его связывает только полученный диплом.
Есть Березовский, Дерипаска, много их.
кушать кал полезнее
Была какая-то книжка про логарифмы, из библиотечки квант или типа того. Короткая, там и про число Непера, и про геометрическую последовательность.
А вообще в тред для новичков с таким.
>Как интуитивно понять операции возведения в степень и логарифмы?
А че тут непонятного? Я сам недоматематик, но это школа, а тут все должно быть понятно.
$n^x = \underbrace{n \cdot n \cdot n \cdot n \cdot n... }_{x}$
$\log_{a} b = p; a^p = b$
Что значит n раз умножить число?
Гротендик - нормис который в молодости нализался клиторов и женских анусов и поехал кукухой на старости.
он вовсе не поехал кукухой, просто ему всё остопиздело (и его можно понять)
при этом уже в глубокой старости к нему захаживала восторженная молодая тяночка, с которой он радостно проводил время. Гротендик крутой
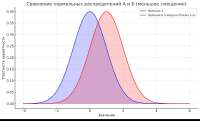 165 Кб, 1080x654
165 Кб, 1080x654Моя шиза на тему ИИ, типо щас все коупят, что ии не может их заменить, потому что у этой хуйни нет разума, сознания сколь либо аналогичного человеческому или отдельным его аспектам и т.д, ведь она просто является стохастической моделью приспособленная к прикладной деятельности (что безусловно так)опустим аспект возможного обретения эмерджентных свойств сложной системой, дело даже не в этом.
Но я тут подумал, а почему аргумент что это штука просто статистика и угадывание, должен противоречить тому что она через какое то время доработки станет способна делать вообще все, что делает человек эффективнее его и как следствие "заместить" нас?
Ведь ирл в природе постоянно встречается нормальное распределение, и всю деятельность каждого отдельного человека в той или иной сфере, групп людей, да и всего человечества можно представить как статистическую модель где опять же будет угадываться нормальное распределение. В нем нижний левый сегмент "колокола" - это типо наши проебы и ошибки, когда мы условно выполняем работу ниже какого-то адекватного уровня эффективности - проще говоря факапимся, потому что у всех без исключения людей бывают ошибки и неудачные испытания в жизни. Правый нижний сегмент - это типо все случаи когда мы были на пределе своей эффективности, делали что то сверх необходимого или сверх ожидаемого и т.д. Ну а середина - это середина, то есть наша рутинная деятельность когда мы делаем что-то просто в пределах условной нормы, просто выдаем результат из категории - "пойдет".
И тогда получается, что аргумент про незаменимость человека из-за его разумности нерелевантен, потому что нейронки не нужно быть разумной. Аргумент про "это просто статистический попугай" не имеет смысла потому что ей не нужна разумность деятельности, чтобы нас превзойти, ей нужна более эффективная статистика, выдавать рандомный буллшит могут и люди и нейронка, но она просто будет за счет доработки модели (новые архитектуры, узкая специализация, объединения несколько специализированных агентов в "коллективы" которые будут заняты фактчекингом друг-друга чтобы имитировать контроль на "здравый смысл" в ответах, и прочее над чем уже работают) статистически все реже и реже выдавать кал, все чаще и чаще более удобоваримый результат и чаще выплевывать "гениальные" решения и концепты которые можно принять за прорыв который человек в аналогичной ситуации бы не сделал, пока в какой то момент её нормальное распределение эффективной деятельности (которую мы ей поручили), не станет смещено более вправо относительно НР бедолаги который пытается с ней конкурировать на этом поприще (в некоторых областях это уже можно считать произошло, например в переводе с языка на язык. Думаете живые переводчики-синхронисты, даже если они с высочайшим опытом и уровнем знания языков иногда не оговариваются, ошибаются, нераспознают контекст, забывают слово?). И таким образом просто тупая игра с вероятностями, и без всякого разума и самосознания, прекрасно замещая человека, достигая КПД, которое он чисто физически выдать не способен.
Пикрил сделан на отъебись чисто для наглядной визуализации, типо Б - это условный AGI, который нихуя не будет разумен, но просто его объявят таковым, сделав очередную подмену понятий как это с самим термином AI уже произошло на хайпе
 165 Кб, 1080x654
165 Кб, 1080x654Моя шиза на тему ИИ, типо щас все коупят, что ии не может их заменить, потому что у этой хуйни нет разума, сознания сколь либо аналогичного человеческому или отдельным его аспектам и т.д, ведь она просто является стохастической моделью приспособленная к прикладной деятельности (что безусловно так)опустим аспект возможного обретения эмерджентных свойств сложной системой, дело даже не в этом.
Но я тут подумал, а почему аргумент что это штука просто статистика и угадывание, должен противоречить тому что она через какое то время доработки станет способна делать вообще все, что делает человек эффективнее его и как следствие "заместить" нас?
Ведь ирл в природе постоянно встречается нормальное распределение, и всю деятельность каждого отдельного человека в той или иной сфере, групп людей, да и всего человечества можно представить как статистическую модель где опять же будет угадываться нормальное распределение. В нем нижний левый сегмент "колокола" - это типо наши проебы и ошибки, когда мы условно выполняем работу ниже какого-то адекватного уровня эффективности - проще говоря факапимся, потому что у всех без исключения людей бывают ошибки и неудачные испытания в жизни. Правый нижний сегмент - это типо все случаи когда мы были на пределе своей эффективности, делали что то сверх необходимого или сверх ожидаемого и т.д. Ну а середина - это середина, то есть наша рутинная деятельность когда мы делаем что-то просто в пределах условной нормы, просто выдаем результат из категории - "пойдет".
И тогда получается, что аргумент про незаменимость человека из-за его разумности нерелевантен, потому что нейронки не нужно быть разумной. Аргумент про "это просто статистический попугай" не имеет смысла потому что ей не нужна разумность деятельности, чтобы нас превзойти, ей нужна более эффективная статистика, выдавать рандомный буллшит могут и люди и нейронка, но она просто будет за счет доработки модели (новые архитектуры, узкая специализация, объединения несколько специализированных агентов в "коллективы" которые будут заняты фактчекингом друг-друга чтобы имитировать контроль на "здравый смысл" в ответах, и прочее над чем уже работают) статистически все реже и реже выдавать кал, все чаще и чаще более удобоваримый результат и чаще выплевывать "гениальные" решения и концепты которые можно принять за прорыв который человек в аналогичной ситуации бы не сделал, пока в какой то момент её нормальное распределение эффективной деятельности (которую мы ей поручили), не станет смещено более вправо относительно НР бедолаги который пытается с ней конкурировать на этом поприще (в некоторых областях это уже можно считать произошло, например в переводе с языка на язык. Думаете живые переводчики-синхронисты, даже если они с высочайшим опытом и уровнем знания языков иногда не оговариваются, ошибаются, нераспознают контекст, забывают слово?). И таким образом просто тупая игра с вероятностями, и без всякого разума и самосознания, прекрасно замещая человека, достигая КПД, которое он чисто физически выдать не способен.
Пикрил сделан на отъебись чисто для наглядной визуализации, типо Б - это условный AGI, который нихуя не будет разумен, но просто его объявят таковым, сделав очередную подмену понятий как это с самим термином AI уже произошло на хайпе
>Переформулирую про интерпретацию графика
А - деятельность ведет человек, Б - деятельность поручили нейронке
От -4 до - 2 пусть будет тупизм, "провал" в широком смысле слова, неудачное испытание при попытки эффективно осуществлять какую-либо деятельность.
0 - рутинная посредственность
От 2 - сверхуспех (реализация низких, но самых благоприятных вероятностей, условно: самое оптимальное решение из всех возможных, генерация прорывов, оптимизация деятельности, и т.д что даже трудно вообразить и сформулировать)
Даже так? Т.е сам пост просто никто не будет читать.
Я все таки ожидал разъеба моего профанного подхода к математической статистике, каких нибудь подводных и т.д, которые гуманитарию поверхностно понимающему теорию вероятностей неовевидны и т.д
Это не математика, попробуй /sci/.
Если сможешь выцедить из этой воды конкретный вопрос по математике - приходи, поможем.
> не математика
Все разделы современной математики перечислены в MSC2020 от AMS, кукарекая что-то другое, ты просто признаешь себя колхозником.
таракан, спок
Философия - раздел математики
Мой оптимизм основан на нескольких наблюдениях. Во-первых, теория категорий — сокровищница чрезвычайно полезных идей программирования. Haskell-программисты черпали из нее уже долгое время, и эти идеи медленно просачиваются в другие языки, но этот процесс идет слишком медленно. Нам нужно его ускорить.
Во-вторых, есть много различных видов математики, и все они предназначены для разных аудиторий. У вас может быть аллергия на математический анализ или алгебру, но это не означает, что вам не понравится теория категорий. Не побоюсь утверждать, что теория категорий — это именно тот вид математики, который особенно хорошо подходит для мышления программистов. Это потому, что теория категорий вместо того, чтобы иметь дело с деталями, оперирует структурой. Она оперирует такими понятиями, которые делают программы компонуемыми.
Композиция в самой основе теории категорий, она — часть самого определения категории. И я утверждаю, что композиция — суть программирования. Мы комбинировали вещи уже очень давно, задолго до того, как какой-то великий инженер придумал подпрограммы. Некоторое время назад принципы структурного программирования произвели революцию в программировании, — они сделали блоки кода комбинируемыми. Потом пришло объектно-ориентированное программирование, суть которого в комбинировании объектов. Функциональное программирование не только о комбинировании функций и алгебраических структур данных, еще оно делает параллелизм компонуемым, что практически невозможно с другими парадигмами.
В-третьих, у меня есть секретное оружие, нож мясника, которым я буду кромсать математику, чтобы сделать ее понятнее для программистов. Когда вы профессиональный математик, вы должны быть очень осторожны, чтобы определить все ваши предположения точно, выписать каждое выражение должным образом, и строить все свои доказательства строго. Это делает математические статьи и книги чрезвычайно трудными для чтения непосвященными. Я по образованию физик, и в физике мы добились удивительных успехов, используя неформальные рассуждения. Математики смеялись над дельта-функцией Дирака, которая была придумана великим физиком, П. А. М. Дираком, чтобы решить некоторые дифференциальные уравнения. Они перестали смеяться, когда придумали совершенно новую отрасль анализа, формализующую идеи Дирака и названую теорией распределений.
Конечно, с помощью размахивания руками вы рискуете сказать что-то откровенно неверное, поэтому я постараюсь убедиться, что позади неформальных аргументов в этой книге есть твердая математическая теория. У меня есть потертая копия книги Сандерса МакЛейна «Теория категорий для математиков» на моей тумбочке.
Мой оптимизм основан на нескольких наблюдениях. Во-первых, теория категорий — сокровищница чрезвычайно полезных идей программирования. Haskell-программисты черпали из нее уже долгое время, и эти идеи медленно просачиваются в другие языки, но этот процесс идет слишком медленно. Нам нужно его ускорить.
Во-вторых, есть много различных видов математики, и все они предназначены для разных аудиторий. У вас может быть аллергия на математический анализ или алгебру, но это не означает, что вам не понравится теория категорий. Не побоюсь утверждать, что теория категорий — это именно тот вид математики, который особенно хорошо подходит для мышления программистов. Это потому, что теория категорий вместо того, чтобы иметь дело с деталями, оперирует структурой. Она оперирует такими понятиями, которые делают программы компонуемыми.
Композиция в самой основе теории категорий, она — часть самого определения категории. И я утверждаю, что композиция — суть программирования. Мы комбинировали вещи уже очень давно, задолго до того, как какой-то великий инженер придумал подпрограммы. Некоторое время назад принципы структурного программирования произвели революцию в программировании, — они сделали блоки кода комбинируемыми. Потом пришло объектно-ориентированное программирование, суть которого в комбинировании объектов. Функциональное программирование не только о комбинировании функций и алгебраических структур данных, еще оно делает параллелизм компонуемым, что практически невозможно с другими парадигмами.
В-третьих, у меня есть секретное оружие, нож мясника, которым я буду кромсать математику, чтобы сделать ее понятнее для программистов. Когда вы профессиональный математик, вы должны быть очень осторожны, чтобы определить все ваши предположения точно, выписать каждое выражение должным образом, и строить все свои доказательства строго. Это делает математические статьи и книги чрезвычайно трудными для чтения непосвященными. Я по образованию физик, и в физике мы добились удивительных успехов, используя неформальные рассуждения. Математики смеялись над дельта-функцией Дирака, которая была придумана великим физиком, П. А. М. Дираком, чтобы решить некоторые дифференциальные уравнения. Они перестали смеяться, когда придумали совершенно новую отрасль анализа, формализующую идеи Дирака и названую теорией распределений.
Конечно, с помощью размахивания руками вы рискуете сказать что-то откровенно неверное, поэтому я постараюсь убедиться, что позади неформальных аргументов в этой книге есть твердая математическая теория. У меня есть потертая копия книги Сандерса МакЛейна «Теория категорий для математиков» на моей тумбочке.
>Дираком
Дураком? Судя по количеству элементарных частиц в фищике говноед на говноеде и говноедом погоняет.
>Не побоюсь утверждать, что теория категорий — это именно тот вид математики, который особенно хорошо подходит для мышления программистов. Это потому, что теория категорий вместо того, чтобы иметь дело с деталями, оперирует структурой.
Очень странный отрывок, конечно.
У тараканов такое встречается. Они сами толком ничего не знают, но им может вдруг ударить в голову, что НАДО НАПИСАТЬ КНИГУ. В книге должно быть очень много воды и очень много местоимений "я" (в отличии от книг по математике, где авторы редко пишут "я"). Назвать книгу можно "Библия/Философия [вставить нужное]" или, например, "Учебник по математике" (помните, был такой? его автор ещё про проституток писал). В общем, обычное дело
 84 Кб, 225x225
84 Кб, 225x225Ну и обратных вопрос - сколько sum-free множеств (https://en.wikipedia.org/wiki/Sum-free_set ) ? Искал - не нашел, а самому, как вы помните, впадлу.
>Короче, господа аноны, призываю вас
А зачем же нас призывать? У тебя уже есть отличный помощник -
>Чатгпт говорит
ты из любого множества можешь образовать свободную группу, которая будет включать это множество как строгое подмножество, так что количество всех групп не меньше, чем количество всех множеств; очевидно, и не меньше тоже, так что их ровно столько же
Меня интересует другой вопрос: сколько множеств $A$, для которых $\forall a, b, c \in A, a + b = c$, при $A \subseteq \mathbb{N}$? Самое простое решение - это $aleph_0 aleph_0$, т.е. $aleph_0 ^2$. Но это, очевидно, не все множества.
Как принять то, что тебе математиком не стать? Читаю все эти учебники, формулы, посты на матемаче и т.д. и осознаю себя дегродом. Она мне нравится, но это равно как долбиться в стену - никакого профита, а только боль.
>никакого профита
А какой тебе профит нужно? Вкатывайся туда где сразу можно пощупать результат.
>думали что юрист это как мошенник
Ебать у макаки с юридическим дипломом, питающейся дошиком, копиум пошел про юрист как ремесленник.
Обязательны к прочтению "Введение в оркскую гойметрию" и "Исчисление малых пидорашек"
Арсений, тебя кто отвязал?
Это скорее всего его выблядок с ником что-то вроде syphilys который срёт хохлошизой в математических ТГ каналах из которых его наверное пидорнули и он пришёл срать сюда.
 235 Кб, 1212x1486
235 Кб, 1212x1486блин, этого стоило ожидать
не хватает только геополитику начать обсуждать с точки зрения "Category Theory" и "Homotopy Theory"
всё остальное, кажется, с этой позиции уже рассмотрели
Вы видите копию треда, сохраненную 5 сентября в 05:03.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

































