Вы видите копию треда, сохраненную 13 августа в 01:46.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Зря я вас послушал, двачеры.
Сами ничего не знаете и не понимаете, так ещё и других с верного пути сбиваете, при этом обильно поливая грязью.
Итак, производная - это предел:
lim{Δx->0}Δy/Δx
Находим чему равно Δy в точке, где Δx=0:
Δy = f(x+Δx)-f(x) = f(x+0)-f(x) = f(x)-f(x) = 0
Решаем предел, для чего нужно подставить в функцию Δx=0 и Δy=0:
lim{Δx->0}Δy/Δx = lim{Δx->0}0/0
Вот и всё. Это то, чему на самом деле равна производная:
f '(x) = lim{Δx->0}Δy/Δx = 0/0 - "Предел неопределённости", это и есть классическая производная.
Да, мы можем написать:
f '(x) = lim{Δx->0}tg a = tg ф (a - угол наклона секущей, ф - угол наклона ксательной)
Всё правильно, мы можем поставить здесь знак "=" между lim{Δx->0}tg a и tg ф.
Но не забывайте только о том, что мы говорим о "недостижимом пределе" и секущая, действительно, никогда не достигнет касательной в классическом пределе.
Но у них не было альтернативы, а "достижимый предел" они не додумались ввести.
Тогда его введу я:
f+(x) = alim{Δx->0}tg a = tg ф.
Вот и всё, проблемы больше нет. Секущая достигла касательной.
И именно такому пределу дожна была равняться классическая производная, но нам придётся назвать её f+(x).
Решение аналогичное:
f+(x) = alim{Δx->0}Δy/Δx = 0/0
f+(x) = 0/0 = tg ф = dy/dx
dx = Δx, где Δx - первоначальное состояние Δx до начала повотора секущей (по договорённости). dx не равно 0.
А dy - дифференциал, мы, ясное дело, найти не можем! Нет конечного точного результата.
Всё, что мы можем найти:
0/0 = dy/dx
dy = 0dx/0
dx/0 = inf - бесконечность.
dy = 0dx/0 => dy = 0xinf - "НОЛЬ УМНОЖИТЬ НА БЕСКОНЕЧНОСТЬ" Мы получили неопределённость вида 0xinf.
Другой вариант решения:
0dx=0
dy = 0dx/0 => dy = 0/0 - "НОЛЬ РАЗДЕЛИТЬ НА НОЛЬ" Мы получили неопределённость вида 0/0.
Вот и всё, что мы можем найти:
f '(x) = f+(x) = 0/0
dy = 0/0 = 0xinf
А теперь проводим во всей математике "Черту Позора":
В левой части у нас будет "Точная Метематика", а в правой - "Примерная Математика".
Ну так вот, производную, дифференциал и интеграл и всё, что на них основано мы "выбрасываем" в правую часть.
Потому что с их помощью у нас получаются всегда только лишь приблизительные расчёты.
/math/ тут тупят даже тролли
Отсюда
>нужно подставить в функцию Δx=0 и Δy=0
до сюда
>у нас получаются всегда только лишь приблизительные расчёты
брызгал слюнями во все стороны из за приступа гомерического хохота, аж в боку заболело от смеха.
Это очепятка, я сначала написал текст, потом дописал "= 0/0", а текст исправить забыл.
Предел исчезает, когда мы выполняем подстановку, не тупи.
В спешке же всё делаю.
fixed
Ежжи братишка, согласен на все сто!!! Так их даунов, так держать, одобряю!!!
Развенчай еще миф тупых математиков о трансфинитных числах.
Это те самые которые идут после всех натуральных чисел. Там же во всех учебниках сказано что натуральных чисел бесконечное множество и не может быть какого то самого большого числа, а они такую хуйню говорят, что есть числа такие большие что их цифрами не напишешь.
Ты понимаешь что ты дурачок и что бы я тебе не говорил ты не согласишься со мной?
В качестве домашнего задания, почему ты дурачек, найди сумму последовательности 1/2^n при n от нуля до n стремящимся к бесконечности.
"дурачок, дурачок" - просто иди на х отсюда и всё. Тупой неконструктив, если ты настолько глуп, что не понимаешь того, что я написал, значит, всё, просто иди на х. О чём говорить с самоуверенным идиотом.
Мы говорим про конкретные вещи, а его понесло куда-то... ууу :)
К врачу по пути зарули.
По существу так по существу.
Когда в самом конце раскрыли функцию с приращениями все дельты устремляют к нулю, делают меньше любого наперед заданного числа, все числа с которыми суммируется дельта считаются неизменными, так как дельта может быть как угодно мала, в ней между запятой и последней цифрой очень много нулей и мы не можем их посчитать так как у нас есть условие "меньше любого наперед заданного числа". Чем меньше наперед заданное число мы берем, тем больше нулей после запятой мы можем с уверенностью написать, но мы не можем написать их все из за условия "меньше любого наперед заданного числа" и поэтому оставляем еще место между последним уверенно написанным нулем и последней цифрой наперед выбранной дроби.
Из за этого же, когда мы умножаем дельту на любое число получается тоже околонулевое число, которое мы не можем написать из за того что не можем сказать сколько нулей в дельте из за условия "меньше любого наперед заданного числа". Это число мы игнорируем при вычислении производной из за того что оно околонулевое из за условия дельты быть "меньше любого наперед заданного числа".
И вычисляем мы производную тупо преобразованиями уровня первого класса, который ты прогулял. А именно, если делить одно число на другое и при этом числа одинаковы, в итоге получается единица. В верхней части дроби производной любое значение которой умножается на дельту в первой степени один раз в итоге дает то самое значение, но уже без дельты. Это значение и называется производной.
>ты настолько глуп, что не понимаешь того, что я написал
И я понимаю что ты хочешь потролировать тут, но не сегодня.
Я пока не знаю, что это, но вот смотри:
Берём отрезок (второй мир) от 0 до 1 в нём бесконечное множество точек (первый мир), а после 1 во втором мире у нас ведь идёт 2, 3,... И эти 2, 3,... как бы больше любой точки из превого мира. Ультрабольшие числа относительно них.
И все эти 0,1,2,3 мы берём и запихиваем в другой отрезок от 0 до 1 (третий мир) и так бесконечно.
Но есть небольшая проблема:
превый мир - точечный мир в сравнении со вторым, и сравить их между собой точно никак не получится, ясно только то, что весь первый мир умещается между 0 и 1 второго мира.
>lim{Δx->0}Δy/Δx
Давай ты напишешь словами что значит эти символы в твоей больной головушке, чтобы я мог их решить.
Я не сильно читал твой кирпич, но если ты про пикчу, то тот человек не прав. Приравнять то, что не равно нельзя.
И те, кто говорят, что 0,99999...9=1 - не правы.
нет, просто возьми и реши, как все это делают.
>f+(x) = alim{Δx->0}tg a = tg ф.
Наклон касательной к функции x^2 в точке (8,64) какой по твоему?
Реши этот предел в общем виде.
Мы начинаем искать dy.
Мы находим производную f '(x) = lim{Δx->0}Δy/Δx = 0/0 и обламываемся. dy нам уже не найти.
Но мы можем посчитать "примерно равно", вместо 0/0, мы будем считать 0,0000000000000006/0,0000000000000002, например.
Ты не можешь элементарный предел решить, тогда с тобой пока не о чем и говорить, иди учи пределы.
Но вот тут есть один интересный момент, у нас же дробь и можем просто поделить первичные Δy/Δx.
Хотя, что тут можно возразить, два элементарных действия, в которых невозможно сделать ошибки.
Проверим:
tg 0 = Δy/Δx = 0/0
tg 0 = sin 0/cos 0 = 0/0 / 0/0 = 00/00 = 0/0
Короче, угол в точке у нас не 0 вовсе, а arctg 0/0.
И вообще, все эти правила к точке не применимы.
Бедный чувак с затраханным матаном мозгом.
Он больше не отличает реальность от воображаемых моделей.
Мне его жалко.
Вот эта последняя девятка лишняя. И это факт.
Бесконечное стремление к 1 в данном случае записываем так:
0,99999...=0,(9)
Мы либо стремимся до недостижимого предела и стремимся бесконечно, он ведь недостижим по условию.
Либо мы стремимся до достижимого предела и не бесконечно, ведь мы должны его достичь.
дегенерат, свали отсюда
http://mathprofi.ru/opredelenie_proizvodnoi_smysl_proizvodnoi.html
Находим: "Откуда взялись правила дифференцирования и таблица производных?"
Читаем, потом идёт "Пример 1", его и рассмотрим (рисунки).
Находим Δy:
Δy= f(x0+Δx) - f(x0) = C -C = 0.
Всё правильно, никаких вопросов.
Теперь находим производную (как нам предлагают):
f '(x0) = lim{Δx->0}Δy/Δx = lim{Δx->0}0/Δx = 0.
Смотрите-ка как у вас всё заебись получается. И везде же строго "=".
А теперь я найду производную:
Мы знаем, что f(x0) - не ноль.
Δy= f(x0+Δx) - f(x0) = C -C = 0 => Δx=0.
Находим производную:
f '(x0) = lim{Δx->0}Δy/Δx = Δy/0 = 0/0.
Вот вам и производная.
С остальными правилами дифференцирования ситуация ровно такая же, везде строго = 0/0.
А то, что вы все делаете, это просто грубые ошибки.
Я даже не могу сказать, что у нас во всех случах "примерно равно" можно будет поставить. Будут просто грубые ошибки и всё.
В любом случае, мы говорим про несуществующие вещи. И хорошо если бы мы всегда их получали по одним и тем же правилам, но, я боюсь, и этого нет.
Не забывайте, что не только Δx всегда =0, но и Δy всегда =0.
Всё ещё ищите площади при помощи интегралов?
А как же все эти, преобразования Лоренца и прочая физическая мутатень, которые отправляются на свалку истории?
Вся физика, основанная на производных, дифференциалах и интегралах катится к чёрту, вы представляете?
Теперь это всё чисто воображаемые и волшебные модели, а не только "идеальные состояния" и всё такое.
Алхимия 21 века. Молодцы ребята, постарались. Даже денег срубили в своих обсосных гос-институтах, гос-шестёрки сраные. Хррр-тьфу. Они друг друга стоят.
Презираю всё, что связано с государством. И как видно, не зря.
Короче, эти гос-шестёрки пытаются выслужиться перед государством, сделать себе статус, имя, денег добыть, лабораторию получить, своих шестёрок поиметь итд и они придумывают какую-нибудь херню, абсолютно пофиг какую, а мы потом учим эту херню и верим на слово.
Да, если они знали о проблемах, они мошенники.
Сегодня так госбюджеты пилят под любую хуйню. Попилы и откаты.
А честсные независимые учёные, которые знают, что они ничего не получат за свою ложь, а только похоронят своё имя, они так не делают.
Правда, иногда находятся исключения, которые стермятся сделать себе имя всеми силами и либо не замечают ошибок, либо скрывают их.
А вы думаете Эйнштейн не видел нестыковок в своих теория? Муахахаха, ну конечно. Неееет, он вовсе не идиот был, это вы идиоты. В сравнении с ним... Вы не видите ошибок в тупейших теориях "великих учёных", которые всеми силами пытаются усложнить свои поделия, запутать, завуалировать ошибки и нестыковки.
>f '(x0) = lim{Δx->0}Δy/Δx = Δy/0 = 0/0.
>Вот вам и производная.
Предел берется в последнюю очередь, до этого выражение упрощается, чтобы не было 0/0, другими словами неопределенность РАСКРЫВАЕТСЯ
Ага, да, я вот пример привёл, смотри как классно там раскрыта неопределённость. Мы просто выкидываем лишний нолик :)
И так вездеее.
Как ты избавишься от дх в знаменателе, изменив числитель? Сократишь нули? Матпрофи так и делает.
Я пытался и дх заменить, но 0 есть 0, а при дх 0 и ду 0 и ничего тут не сделать.
Придурок, приведи хотя бы один пример рабочий, к своей тупой теории.
Найти производную, чтобы получилось не 0/0.
Давай.
ну delta(y) как правило содержит delta(x), и можно избавиться от delta(x) в знаменателе.
Какая разница, когда мы делим на 0, у тебя с головой проблема? А дх равен строго нулю.
ну возьмем к примеру функцию y = x
итак y(x+delta(x))=x+delta(x)
delta(y) = y(x+delta(x))-y(x) = delta(x)
составляем отношение delta(y)/delta(x) = delta(x)/delta(x) = 1
Берем предел при delta(x)->0
итого получаем, что производная от x равна единице.
Я ещё раз повторяю, ду = 0 всегда, а дх = 0 всегда. Что ты можешь там сократить?
ду тебе обнуляет любой числитель, а дх остаётся 0. Никакие спекуляции не прокатывают.
Да блядь, мы уже обсуждали этот пример в общей теме по математике, которая для новичков, и я говорил, человеку, который поделил:
Δx/Δx=1
Что он сделал это:
Δx/Δx=0/0=1/1=1
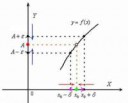
 16 Кб, 459x336
16 Кб, 459x336Производная сказала, прямо в пределе это написано: "Δx->0".
Смотри на рисунок "Геометрический смысл производной":
Там чётко видно, что Δx=Δy=0 в точке K.
Ты тупой или что? На рисунок смотри, там два нуля.
> "Δx->0"
Это не означает что delta(x) в строгости равно нулю, кури теорию пределов.
>Смотри на рисунок
>Там чётко видно, что Δx=Δy=0 в точке K.
Не, я точно что вижу, что там delta(x) = 10^{-10} и delta(y) = 10^{-10}
Ты основ не знаешь и моё время отнимаешь!
lim{x->x0}y(x)=y0
y0 - предел функции y, это координата по Y предельной точки (x0,y0).
Чтобы найти значение y, мы должны в функцию подставить x. Чтобы найти значение y0, мы должны подставить в функцию значение x0:
lim{x->x0}f(x0)=y0
Да, именно x=x0, строго равно.
Вот так мы и находим предел функции.
Изучи, матчасть, потом свои мысли излагай.
Производная - это предел:
f '(x) = lim{Δx->0}Δy/Δx
У нас решнеие в точке K, а там Δx=Δy=0!
Подставляем:
f '(x) = 0/0
толстичок
Ты чего так толсто троллишь-то?
Но если ты нашёл случаи раскрываемости, может с нами поделишься?
таким образом пациент показал полную неспособность формулировать свои мысли, давать определения, вести конструктивную беседу, также выражаю сомнения в способности индивида проводить элементарные арифметические действия, делать логические выводы. Лечения: лоботомия.
так ты дай определение что такое предел, мой сладкий.
lim{x->x0}y(x)=y0
Мы все ищем y0, которому соответствует x0, а ты ищешь что-то до x0, например, x1, ты это подсталяешь в функцию x1 и находишь соответствующий ему y1.
Но y1 не является пределом функции, предел это конкретно y0.
Так чтобы найти y0, ты обязан подставить в функцию x0.
Прочитай учебник ещё раз, если до сих пор не понял:
lim{x->x0}y(x)=y0
Здесь сказано, что:
y0=y0
Только и всего.
Окей, я залезу в википедию вместо тебя:
Итак: Значение A называется пределом функции f(x) в точке x_{0}, если для любого наперед заданного положительного эпсилон, найдется такая delta, что для всех x, для которых 0 < |x-x_{0}| < delta, выполняется неравенство |f(x)-A| < epsilon
Ключевой момент тут: 0 < |x-x_{0}| < delta как видишь окрестность проколотая. Разность неравна нулю.
Еслы ты думаешь, что "lim{x->x0}y(x)" - динамический процесс стремления, то ты ошибаешься.
"lim{x->x0}y(x)" - это второй кусок статичной системы, которая называется "Предельная Точка (x0,y0)":
(x0,lim{x->x0}y(x)) = (x0,y0) - это одно и то же, но разными словами.
Эта статичная система никуда не стремится, а вот x к ней стремимся бесконечно x->x0 и никогда не достигает x0.
МЫ СТОИМ В ПРЕДЕЛЬНОЙ ТОЧКЕ (X0,Y0), x стремится к нам и никогда нас не достигает, но нам на него насрать.
Когда мы находим lim{x->x0}y(x), мы просто находим y0. Мы находим, чему равен y статичной предельной точки.
Поэтому мы и говорим, "предел в точке x0" (или при x->x0).
Можно написать просто:
lim{x0}y(x)=y0
или при x->x0 - здесь подразумевается:
"Предел функции при x->x0", предел аргумента там x0, а предел функции y0.
Короче, нам просто насрать на стремление и на все точки, которые быле до предела.
Мы говорим о пределе, мы находим предельную точку, мы находим чему равно y в предельной точке.
Мы это делаем, когда решаем предел.
А ты решаешь не предел, а то, что было до него, нам насрать, что было до него, нам нужно найти до куда всё бесконечно стремится.
В случае... предел понимается как, ты сам-то слышишь, что ты говоришь?
Был предел, но потом мы назвали его производной и что-то изменилось. Вот это да!
Когда мы находим предел, мы говорим о предельной точке K, где все дельты нули.
А ты что несёшь?
блядь, же а, реши хотя бы один предел.
http://function-x.ru/lim1.html
http://mathprofi.ru/predely_primery_reshenii.html
Чтобы найти А, мы должны подставить значение x=x0, если это не x0, тогда мы получим не A.
И смотри, там даже точки А и x0 не выколоты, а закрашены.
Да Δx не равна нулю в недостижимом классическом пределе (Δx->0), но мы находим саму эту недостижимую точку, когда решаем предел.
>И рисунок посмотри.
Зачем смотреть на рисунок когда есть строгое определение, в котором говорится о выколотой окрестности предельной точки? Мало ли, кто там как рисовал.
Я же тебе сказал:
lim{x->x0}y(x) и y0 - одно и то же, но записано разными способами.
y0 - предельное значение функции (при предельном x=x0)
lim{x->x0}y(x) - предельное значение функции (при предельном x=x0)
А в твоём варианте ты даже точки K никогда не достигаешь и не сможешь приравнять тангенс наклона угла касательной к тому, что получишь.
Мы вычисляем предел в точке (x0,y0) а не до неё, так как до этой точки - не предел. Ещё что не понятно?
Я тебе ещё раз повторяю.
Предел в точке (x0,y0) и только там, ты подставляешь в функцию значение меньше x0, ты получаешь значение функции меньше y0.
Ты получаешь некоторую точку (x1,y1), а это вообще не предел, твоя точка стоит перед пределом.
До (x0,y0) нет ни одного предела, короче, ты находишь не предел вообще!
я вообще-то там доказал всем свою точку зрения, и все последние сообщения мои, я то надеялся, что все уже поняли всё, но ты, видимо, не читал.
Прекрати свой затянувшийся театр одного семена и иди в РАН. Может когда тебя там озалупят ты вернешься в свое стойло дефективных дегенератов.
продолжай думать, что понимаешь что такое предел.
"Предел функции в точке x0" или "Предел функции при x->x0".
Решает примеры, подставляет x0 в функцию, получает y0. Но продолжает нести какую-то херню.
Почему так трудно понять, что:
lim{x->x0}y(x)
и
lim{x0}y(x)
и
y0
Это одно и то же!? Я же уже сказал об этом.
Ну так как ты решишь "lim{x0}y(x)=y0"?
Как ты решишь предел в точке?
>В любом учебнике написано:
"Предел функции в точке x0"
проблема в том, что в силу своих психических отклонений дальше этой фразы ты учебник не читал.
ну не злись, тупеньким очень легко живется
Ты даже не в сосстоянии понять, что такое предел, когда читаешь его определение.
Я тебе дал ссылки, прочитал бы ты первую и понял бы, что такое предел, но ты же самый умный, ну так и катись. Всё. Разговор закончен.
Тебе цена ноль.
не подожди, надо же всего лишь подставить нуль в sin(x)/x по твоей гениальной методике, разве нет?
разложи его доказательносто по полочкам, я 100% даю, что он просто не заметил, что он наделал
один ты в белом пальто стоишь, ага
"Функция бесконечно убывает в точке, где она равна нулю."
Как тебе такое?
Ну так вот ты и найди чему равен x в точке x0, и чему равен y в точке y0. Потому что нам нужно именно это, а то, что мы никогда там не окажемся - вообще роли не играет.
Атлищна алищна тащемта например
Доказательство того человека ошибочно.
Он выполнил его при x не равном ноль.
В итоге расчитан не предел, а точка до предела.
Зато в пределе получается именно то, о чём я ещё до проверки говорил: 0/0
lim{x->0}sinx/x = lim{x->0}sinx / lim{x->0}x = 0 / 0
lim{x->0}(1+x)^1/x=e
Подставляем 0 в функцию:
(1+0)^1/0=1^inf - неопреденность вида 1^inf
И нет там никаких e.
(второй вариант формулы)
lim{x->inf}(1+1/x)^x=e
Подставляем бесконечность в функцию:
(1+1/inf)^inf.
И ещё большой вопрос что это за неопределённость конкретно. Есть несколько вариантов, например:
неопреденность вида 1^inf.
Я ещё пока даже не знаю, можно ли уравнять эти формулы в реале.
И скажу, что "пока нет е", а есть он или нет, раскрывается такая неопределённость или нет, это нужно доказательство проверять.
Я посмотрю.
Ну это уже даже не смешно, так тупостью тролировать. Тоньше надо, /Ь/ратишка, ведь это и проверить можно самому на листочке бумаги.
1.0000000001^10000000000=2.7182820532347876
 256 Кб, 600x1024
256 Кб, 600x1024Почему ты думаешь, что e - предел, а не бесконечно близкое к нему число?
Гипотенуза же не ноль, а неопределённость.
Итого sin 0 = 0/ 0/0 = 0/0
А lim{x->0}sinx/x = 0/0 /0 =0/0
Что и требовалось доказать.
Но как нам они помогут найти производную функции y=x?
Мы никогда не должны достигнуть 1.
1 - недостижимый предел для 0,(9).
А в нашем случае недостижимым пределом может оказаться и 0,(9).
А ты логику программы смотрел? А может там не 1, а 0,(9) на самом деле и:
lim{x->x0}sinx/x = 0,(9) -> 1
lim{x->inf}(1+1/x)^x -> e
переписать заново можно что угодно, в т.ч. и матан..в чем смысл сейчас этого срыва покровов?
Какой срыв покровов?
То, что доказательство замечательных пределов не подходит для 0 и мы доказываем вообще хз что? Одно умножение всего на 0 чего стоит.
Или конструкция.
>>11583
В которой всё больше и больше девяток после запятой и в конце, вероятно, бесконечность 9, почему-то равно 1. Но это только предположение. Нет так нет.
А я вот человеку пытаюсь объяснить, что мы решая предел находим значение А и для этого подставляем в предел x0, а он не верит.
Хорен, теперь ты окончательно спалился. Прекращай.
Ничего себе.
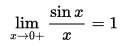 2 Кб, 127x46
2 Кб, 127x46Мы прямо так и пишем - рис:
x>x0, а y0=1
Вот что это за доказательство такое?
А потом мы пишем:
x<x0, y0=1.
Хотя, в принципе, прокатывает, ок.
Если наш предел не может быть одновременно и больше 1 и меньше 1, конечно. :)
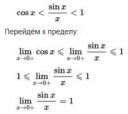 12 Кб, 242x217
12 Кб, 242x217Получится 1 < lim < 1.
В итоге, решений нет.
хотя мы и можем округлять "0,(9)".
Рисуй давай сам тогда.
Его с утробы одурманеный алкоголем мозг не может объять понятие бесконечности/неограниченности/нескончаемости/беспредельности/бескрайности/необъятности. Ему же в школе учили что везде есть начало и конец.
Он небось даже будет отрицать тот факт что в любом численном промежутке нету самого большого и самого маленького числа.
Вот его мозг начинает понимать что он нихуя не понимает и включает психическую защиту, чтобы не лопнуть от натуги и сохранить пусть и дефективное, но свое мировоззрение, уровня "вы все говно а я один в белом пальто".
Ну так глянь его посты. Он везде про бесконечность пишет как о недостижимости. Он использует интуицию там где нужно использовать воображение вместе с логикой.
>>11624
пц, почему здесь столько слабоумных "людей"?
С другой стороны, такой всего один...
И все подобные посты выше от того же существа явно.
Душу он сюда излить приходит что ли, ирл небось полное ничтожество и конченный неудачник, а тут из себя пытается строить что-то существенное, но и здесь ничего не получается и гонят его отовсюду ссаными тряпками.
Я думаю он просто болен даунизмом крайней степени, + не способен воспринимать информацию ни в какой степени, + психические отклонения, и вот ты имеем нашего опа.
>А я вот человеку пытаюсь объяснить, что мы решая предел находим значение А и для этого подставляем в предел x0, а он не верит.
Вычисляя предел, мой сладкий, мы прежде всего не кладем x=x0, ибо функция может там иметь разрыв, а гуляем в малой проколотой окрестности x0, как и следует из определения предела >>11517
пц придурок, разумеется функция не имеет разрыв и это условие, прямо так и написано
я вертолет
>Если эта фукция есть в точке, я предлагаю тебе доказать это.
Ахуенная лемма, все же сходи к психотерапевту или бросай принимать наркотики.
 21 Кб, 768x293
21 Кб, 768x293И наш пример там разобран
http://mathprofi.ru/nepreryvnost_funkcii_i_tochki_razryva.html
Когда ты это уже поймёшь?
Перестань нести бред, мы находим значение y в пределе поворота секущей и всё тут.
Можно не перебрасывать, т.к. ничео не меняется, мы же предел рассматриваем.
Зато теперь они понимают, что такое предел.
А заодно и остальные понимают, что мы неправильно находим производные в конкретных случаях.
А если правильно, то нужны доказательства раскрытия неопределённостей конкретным образом.
С одной стороны, до предельной точки производной в функции y=x: 7/7=1, 3/3=1, -9/-9=1 и так везде, но в самой предельной точке 0/0, и мы не можем просто взять и сказать, что там 1, мы обязаны выполнить доказательство.
И кто сказал, что там 1? Неопределённость есть неопределённость.
А что если речь идёт о сложной функции с разными значениями и нет ни единого намёка, что должно получиться?
Хорошо, если найдётся доказательство для общего случая. А если его нет?
Как мы выполним доказательство в случае:
y=x хотя бы?
это не доказательство раскрытия неопределённостей
ну там это теорию пределов создали, которая позволила отказаться от понятий бесконечных малых и еще много чего.
ты выполняешь деление в других точках, докажи, что мы имеем право раскрыть в этой точке неопределённость.
ты кретин
идиот, выполни доказательство от и до по всем правилам.
не можешь - всё пока
В общем случае у нас есть некоторая кривая, выбираем там две точки, зависимость не линейная.
x0 не принадлежит к N.
между x и x0 расстояние бесконечность.
Что будешь делать?
Абсолютно любая, но возьмём ту, что не из простейших и под общие правила не ложится.
В точке получили неопределённость.
Пытаемся считать рядом, а там бесконечное количество цифр после запятой везде и абсолютно хз, какая именно в той самой точке.
Точного решения нет, неопределённость не раскрывается.
Ну всё облом?
y=x
Слева все единицы | Предельная точка 0/0 | Справа все единицы
Ну так нам предстоит ещё конкретно доказать, что у нас в середине 1.
Да, разумеется, ты не можешь сделать в том случае (x0-x+x0+x)/2=x0 и подобные вещи.
Там ужасная нелепая кривая из реального мира, а не из школьного курса математики.
>Там ужасная нелепая кривая из реального мира
Это не определение класса кривой а твои влажные фантазии.
Но это всё теория.
А на практике у нас есть копмьютеры и они быстро делают нам приближённо равно с огромной точностью.
Сначала подменяет определение предела своим собственным, а потом уже других упрекает в неправельном определении. Лол.
Введём такие обозначения : lim - нормальное определение предела из учебника, с дельта-епсилон формализом.
Обозначения предела предельного дауна будет таким - zalupa. Как утверждает сам даун - zalupa может быть только значением функции, то есть это по сути тождественное преобразования. Тема закрыта.
Предельного дауна прошу не шкварить своими маня-теориями нормальное определение предела и в будущем называть свой предел zalupa.
>что предел функции - это только значение A
Ага только A не получается поставлением x0 в функцию, мой сладкий
я ебууууу бляяя,
ты даже не слышал про связь между существованием функции в точке x0 и существованием предела при x -> x0 да? Этой связи НЕТ блядь, все, иди нахуй.
Учи матан.
до тебя с первого раза не дойдет, поэтому поясняю: ФУНКЦИЯ МОЖЕТ БЫТЬ НЕ ОПРЕДЕЛЕНА В ТОЧКЕ x0, ДАУН
Да, именно, мы берём и подставляем x0 в функцию и находим А.
Иногда там возникают трудности - неопределённости, которые мы иногда раскрываем.
А ты сходи к врачу уже наконец.
Это такая хуйня, которая больше любого действительного числа.
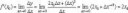 379x41
379x41Во-первых классический предел нельзя использовать для производной, т.к. секущая никогда не станет касательной.
А во-вторых производная всегда нам даёт неопределённость вида 0/0. А вот раскрывается она или нет - дело десятое.
Но так, как на рисунке, делать явно нельзя в случае строго "=".
бля, я уже не человек, я уже зверь нахуй. не "нет окрестности", а все члены последовательности по модулю БОЛЬШЕ ЕЕ БЛЯТЬ
Пока всем.
У кого есть мозг, поймёт что мои замечания верны, кто не понял, просто катится куда подальше в выгребную яму к таким же.
Одна уже есть - стандартный пидораховый матан, к которому все привыкли.
правильно, отправляйся в свой чуханозагон к шизикам. скорее бы уже модер вам парашный угол выделил
открой учебник и посмотри нормальное определение и выводы, ученик по гуглу
Какая разница для предела существует или нет функция в предельной точке?
Такая же есть ли там максимум или минимум или ещё что-то.
Короче, не ебёт, что там.
Подпредельная функция живёт по своим законам, а функция по своим.
ты осознал свою ошибку?
А то, что ты неверно понимаешь определение по Коши, ну что поделаешь, просто забей.
Ты не понимаешь определение предела по Коши. Когда пишут lim f(x) при x->x0, то это не значит, что надо вычислить значение функции f(x) в точке x0. Когда говорят о пределе функции, то подразумевают, что x может принимать сколь угодно близкое значение к x0, но никогда в этом случае не берут x = x0. Почитай Куранта, там все это разжевано.
что ты, там свой собственный анализ у него, каноничный
Мы при решении пределов подставляем x0 в предел.
Был модульный фашизм, а теперь предельный фашизм.
У нас по оси Y яблоки, а по оси X - корзины. Две точки: (x0,y0) и (x0+Δx,y0+Δy). Мы двигаемся от второй к первой. Яблоки можно резать на куски.
Линейная зивисимость (любая точка между x и x+Δx включительно) Δy/Δx:
6 яблок
2 корзины
6/2=3 яблока в каждой корзине (18/6=3; 60/20=3)
Уменьшаем всё до нуля:
0/0 У нас 0 яблок в нуле корзин, сколько яблок на корзину?
Правильно, 0!
Нелинейная зависимость Δy/Δx: Теперь только в одной точке 3, в остальных другие цифры (4;5,2 итд).
Уменьшаем до нуля:
0/0. Опять ноль яблок на корзину.
Ну так вот, чтобы мы ни делали, но в относительных координатах у нас всегда 0/0 и нихрена эта неопределённость не раскрывается даже в линейной зависимости.
А чтобы раскрыть её, мы вынуждены перейти к абсолютным координатам (в точке 0/0 о.к.):
Δy/Δx = y0/x0 о.к. = а.к.
Именно, когда Δx=Δy=0 в о.к., мы достигаем в а.к. точки (x0,y0). И в большинстве случае там нет ни одного нуля.
И чтобы найти значение предела (найти производную), произведём замену в пределе следующим образом (не забываем, что мы уже конкретно в конечной точке (x0,y0)):
lim{Δx->0}Δy/Δx=lim{Δx->0}y0/x0=y0/x0
Это видно и из рисунка.
Но даже теперь на Δx (на ноль) мы делить не можем, ноль остаётся нулём.
Не забываем и том, что когда вы подставите Δy/Δx далёкие от нуля в свои о.к., их значения могут сильно отличаться от y0/x0 в а.к..
В результате нахождения производной мы и так всегда получаем а.к..
Но если и в y0/x0 мы получили мешающие нули, тогда превращаем наши нулевые в о.к. Δy/Δx. в другие и не нулевые о.к.
Т.е. добавляем ещё одни относительные координаты и переводим в них.
Затем, выполняем преобразование, переводим из вторых о.к. в а.к. и получаем ответ.
У нас по оси Y яблоки, а по оси X - корзины. Две точки: (x0,y0) и (x0+Δx,y0+Δy). Мы двигаемся от второй к первой. Яблоки можно резать на куски.
Линейная зивисимость (любая точка между x и x+Δx включительно) Δy/Δx:
6 яблок
2 корзины
6/2=3 яблока в каждой корзине (18/6=3; 60/20=3)
Уменьшаем всё до нуля:
0/0 У нас 0 яблок в нуле корзин, сколько яблок на корзину?
Правильно, 0!
Нелинейная зависимость Δy/Δx: Теперь только в одной точке 3, в остальных другие цифры (4;5,2 итд).
Уменьшаем до нуля:
0/0. Опять ноль яблок на корзину.
Ну так вот, чтобы мы ни делали, но в относительных координатах у нас всегда 0/0 и нихрена эта неопределённость не раскрывается даже в линейной зависимости.
А чтобы раскрыть её, мы вынуждены перейти к абсолютным координатам (в точке 0/0 о.к.):
Δy/Δx = y0/x0 о.к. = а.к.
Именно, когда Δx=Δy=0 в о.к., мы достигаем в а.к. точки (x0,y0). И в большинстве случае там нет ни одного нуля.
И чтобы найти значение предела (найти производную), произведём замену в пределе следующим образом (не забываем, что мы уже конкретно в конечной точке (x0,y0)):
lim{Δx->0}Δy/Δx=lim{Δx->0}y0/x0=y0/x0
Это видно и из рисунка.
Но даже теперь на Δx (на ноль) мы делить не можем, ноль остаётся нулём.
Не забываем и том, что когда вы подставите Δy/Δx далёкие от нуля в свои о.к., их значения могут сильно отличаться от y0/x0 в а.к..
В результате нахождения производной мы и так всегда получаем а.к..
Но если и в y0/x0 мы получили мешающие нули, тогда превращаем наши нулевые в о.к. Δy/Δx. в другие и не нулевые о.к.
Т.е. добавляем ещё одни относительные координаты и переводим в них.
Затем, выполняем преобразование, переводим из вторых о.к. в а.к. и получаем ответ.
модульность - устаревшая технология.
продолжай делить 0 на 0.
"Ну так вот, чтобы мы ни делали, но в относительных координатах у нас всегда 0/0 и нихрена эта неопределённость не раскрывается даже в линейной зависимости."
Поправка. Неопределённость у нас раскрывается: "0".
Но от этого нет толку.
fixed
в данном примере 0...
X - время (с).
Скорость = Y/X
Поехали:
L -> K
Скорость в точке L:
f(x0+Δx)/x0+Δx
f(x0+Δx)->f(x0)
x0+Δx->x0
Скорость в точке K:
f(x0+Δx)/x0+Δx=f(x0)/x0
А мы что делаем:
L -> K
а -> ф
tg a -> tg ф
lim{Δx->0}tg a = lim{Δx->0}Δy/Δx = 0/0 = tg ф = dy/Δx = f '(x)
И это скорость в точке K?
Ах, нет, это же "мгновенная скорость" в точке K за время Δx->0.
У меня такое чувство, что я психотерапевт выслушивающий бред психическибольного.
Я его спрашиваю, "А зачем нам нужна такая штука как "производная" ?", в ответ он начинат что-то невнятно бормотать, кричать и махать руками.
X - время (с).
Скорость = Y/X
Поехали:
L -> K
Скорость в точке L:
f(x0+Δx)/x0+Δx
f(x0+Δx)->f(x0)
x0+Δx->x0
Скорость в точке K:
f(x0+Δx)/x0+Δx=f(x0)/x0
А мы что делаем:
L -> K
а -> ф
tg a -> tg ф
lim{Δx->0}tg a = lim{Δx->0}Δy/Δx = 0/0 = tg ф = dy/Δx = f '(x)
И это скорость в точке K?
Ах, нет, это же "мгновенная скорость" в точке K за время Δx->0.
У меня такое чувство, что я психотерапевт выслушивающий бред психическибольного.
Я его спрашиваю, "А зачем нам нужна такая штука как "производная" ?", в ответ он начинат что-то невнятно бормотать, кричать и махать руками.
Δt2-Δt1=0
Это хорошо, и я нахожу скорость в максимально малый момент времени.
Вы делаете:
За 0 секунд пройдено 0 метров (Δx=Δy=0).
Поэтому у вас мгновенная скорость = 0/0.
Я вообще не запариваюсь и нахожу среднюю скорость в момент времени.
 800 Кб, 1280x720
800 Кб, 1280x720А была бы линейная зависимость...
Тогда у меня моя средняя скорость была бы одинаковой на всём промежутке и равна:
y = x + 99999999998 - линейная зависимость
x = 2 (с)
y = 100000000000 (м)
v=y/x=100000000000/2=50000000000 (м/с)
А у вас:
y' = (x + 99999999998)' = 1 + 0 = 1 (м/с)
Нехуёвое различие неправда ли?
 178 Кб, 1920x802
178 Кб, 1920x802В учебниках читаем, что чем меньше Δx, тем точнее результат v.
Возьмём пример, Δx->0 и чем ближе он к нулю, тем сильнее возрастает y.
x1=мало (0,000...)
y1=много (10000...)
x2=на многие порядки меньше
y2=на многие порядки больше
v1=1x10^20
v2=1x10^900
Дальше больше.
Но у нас не раскрывается неопределённость и хз чему там равно y в точке x0. Да и пох.
Мы же берём и решаем примерно без компа калькуляторе, округляем и ошибаемся на огромную величину.
Потом у нас валятся ракеты, а чёрная дыра из БАК поглощает Землю со всеми её обитателями.
Хорен-хорен он король параш!
Хорен-хорен левачок-левак!
Хорен-хорен рвётся только так!
Хорен-хорен модули не знал!
Хорен-хорен форум проебал!
Реши сам.
Производная - мгновенная скорость, так должно быть.
Но, как мы видим, это не так.
Она вообще никакую реальную скорость не отображает, кроме того ещё и ошибку даёт.
>Реши сам
Ты не можешь это же устный пример!
>Производная - мгновенная скорость, так должно быть.
Нет, не должно. Ты перепутал среднюю и мгновенную.
Я ничего не перепутал, мгновенная скорость в данном случае не отображает реальную скорость в какой-либо момент, у нас тут просто нет такой скорости, а должна была быть.
Скорость - константа и она огромна, какие там, к чёртку 1 м/с, которые предлагает производная?
Где, в какой момент у нас такая скорость?
Это полный маразм, это тупо грубая ошибка.
Я тебе говорю, у нас никогда не было, нет и не будет скорости 1 м/с здесь. Это просто ошибка.
Покажи точку или интервал, где в некоторый момент времени такая вот скорость? Это же просто смешно.
Это полный фейспалм.
Что отображает мгновенная скорость по твоему?
А вот сделаем мы + триллиард^триллиард^триллиард (м/с).
А производная сделает опять, чпок и всё, 1 (м/с).
Да нет там такой скорости.
Ты не понимаешь смысл мгновенной скорости. Пока не решишь предел, с тобой я разговаривать не буду.
А почему тебе это нужно?
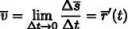 3 Кб, 161x37
3 Кб, 161x37Ну так что, всё облом?
Т.к. скорость за бесконечно малый промежуток времени абсолютно в любом месте всего пути у нас стремится и не просто стремится, а равна постоянной огромной скорости.
http://ru.solverbook.com/spravochnik/mexanika/kinematika/mgnovennaya-skorost/
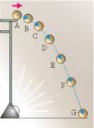 5 Кб, 160x217
5 Кб, 160x217Я с полным олигофреном разговариваю или что?
Тело движится с одинаковой скоростью от начала пути и до конца пути.
Скорость в любой момент времени постоянна и равна:
50000000000 (м/с)
Но по производной получается 1 (м/с).
И человек, у которого своего мозга нет, на это скажет: "миллионы людей не могут ошибаться".
>Скорость в любой момент времени постоянна и равна
Это и означает, что производная от скорости равна 1. Производная от скорости - ускорение.
У нас была мгновенная скорость, которая и есть производная, ты взял от неё ещё одну производную, молодец.
Бескоечномалый не равно очень маленький.
>Тело движится с одинаковой скоростью от начала пути и до конца пути.
>Скорость в любой момент времени постоянна и равна:
50000000000 (м/с)
Путь s=u*t=50000000000t
мгновенная скорость = 50000000000
Ты просто производную там неправильно посчитал и единицу приплёл.
Вот ты и нашёл мгновенную скорость.
Я даже специально проверял через онлайн-кулькулятор, а может и ты проверил.
Хорошо, а теперь давай считать среднию при t -> 0
vсред= lim(s(t0+t)-s(t))/t при t -> 0
s=vt
s(t_0+t)-s(t)=v*t0=vсред
а ты IQ повысь, тода и к мелочам придираться не будешь
сказано "везде", а раз так, значит просто y/x
Нет, ты долже взять и объяснить буквы, которые используешь, шавка.
Предел уже решил?
Сунул тебе за щечку свою питательную и ароматную залупу.
Неподписанное мнение - гнойное мнение от жалкого подобия человека.
Пишу в этот тред, потому что его жалко меньше всего.
Horen.
В dxdy.
Ты забыл трип-код: в поле "Имя" вставь сначала ##, а сразу затем пароль. Это и будет твой трип-код.
Долдаёбина, трипкод-блядь не человек.
>рватся
Да ты ещё и в донбасском подвале всю жизнь провёл. Как там твои многообразия Фано, пучк-пучк?
>жалкие попытки вхорена перевести стрелки
Ты и так уже обосрался, хорёк. Тебя не спасти.
И, да, ты забыл пробел поставить в имя.
Иди нахуй!
Ну и долго же ты ещё гореть а трипкодный чухан?
Или тут стоит написать пасту про федерализацию сибири, чтобы мода напрямик из ольгино в жопу ебать стали?
Мой пост с ответом опу он почему-то удалил, зато тупое перебрасывание говном между двумя шизиками спокойно висит.
Что ты несёшь, параноик? Под кроватью пойди поищи своих партнёров по анальным игрищам.
Двачую этого "параноика", только хорен парашный клоун про федерализацию и олег будет говорить.
Я говорю как есть. Мой пост по теме удалили, ваш скудоумный анрилейтед-срач висит. Факт.
Да он нихуя не может, этот пидор. Как же ненавижу тварь. Просто наизнанку меня выпихивает. Удалите его. Пусть не очерняет нашу доску и нашего модератора.
Конечно претворяюсь.
Так точно! R-модулем над кольцом R называется абелева группа M, образующая вместе с кольцом операцию умножения R × M -> M, которая удовлетворяет свойствам дистрибутивности, коммутативности, ассоциативности, а также имеет нейтральный элемент.
Соси, вхорон!
Сделаю всё, чтобы унизить вхорона!
Любое векторное пространство над полем N есть модуль над N.
А ты неплох. Теперь давай конкретный пример. Больше конкретики.
Модульный дед велел его призвать и сказал ему: - Знаешь, Хорен, кто такой "Гротендик"?
- ПУЧК!
- Не пучкай. Запомни: так называют величайшего математика. Знаешь, что такое алгебраическая геометрия?
- Пучк. Вроте дик! Аналитическая говнометрия.
- Молодец, Хорен. Так запомни: если услышишь, когда ходишь по избам обедать, кто-нибудь скажет, что Гротендик скотина или что-нибудь в этом роде, то моментально приди ко мне и сообщи. За это получишь от меня пару биткоинов. А если услышишь, как кто-нибудь скажет, будто кто-то хвалит вторую культуру, опять приходи ко мне, понимаешь? Скажешь, кто это говорил, и снова получишь двадцать биткоинов. Но если я узнаю, что ты что-нибудь скрыл,-- плохо тебе придется. Заберу и отправлю в Писек. А теперь, ну-ка, Хорен, пучкни!
Хорен пучкнул, а Дед дал ему сорок биткоинов и, довольный собой, написал репорт моче, что завербовал осведомителя.
На следующий день к деду пришел вербит и сообщил ему по секрету, что утром он встретил за деревней сельского дурачка Хорен-Пучкни и тот ему сказал: "Вербит, а дед говорит, что Гротендик второкультурщи ПУЧК ПУЧК ПУЧК" После дальнейшего разговора с вербитом дед велел арестовать сельского петуха. Позднее градчанский суд приговорил его к годовому бану. Он был обвинен в опасных и предательских злодеяниях, в подстрекательстве, оскорблении Гротендика и в целом ряде других преступлений и проступков.
Хорен-Пучкни на суде держал себя, как на двачев, на все вопросы блеял козой, а после вынесения приговора крикнул: "Пучк"-- и прыгнул. За это он был наказан в дисциплинарном порядке: жесткая постель, одиночка и три дня в неделю на картофан и водку.
С тех пор у деда не было осведомителя, и ему пришлось ограничиться тем, что он сам выдумывал себе осведомителя, сообщил по инстанции вымышленное имя и таким образом повысил свой ежемесячный заработок на пятьдесят биткоинов, которые он пропивал в трактире dxdy. После десятой кружки его начинали мучить угрызения совести, пиво казалось горьким, и он слышал от крестьян всегда одну и ту же фразу: "Что-то нынче наш дед невеселый, словно как не в своей тарелке". Тогда он уходил домой, а. после его ухода кто-нибудь всегда говорил: "Видать, наши во Франции опять обделались - дед сегодня больно молчаливый"
Модульный дед велел его призвать и сказал ему: - Знаешь, Хорен, кто такой "Гротендик"?
- ПУЧК!
- Не пучкай. Запомни: так называют величайшего математика. Знаешь, что такое алгебраическая геометрия?
- Пучк. Вроте дик! Аналитическая говнометрия.
- Молодец, Хорен. Так запомни: если услышишь, когда ходишь по избам обедать, кто-нибудь скажет, что Гротендик скотина или что-нибудь в этом роде, то моментально приди ко мне и сообщи. За это получишь от меня пару биткоинов. А если услышишь, как кто-нибудь скажет, будто кто-то хвалит вторую культуру, опять приходи ко мне, понимаешь? Скажешь, кто это говорил, и снова получишь двадцать биткоинов. Но если я узнаю, что ты что-нибудь скрыл,-- плохо тебе придется. Заберу и отправлю в Писек. А теперь, ну-ка, Хорен, пучкни!
Хорен пучкнул, а Дед дал ему сорок биткоинов и, довольный собой, написал репорт моче, что завербовал осведомителя.
На следующий день к деду пришел вербит и сообщил ему по секрету, что утром он встретил за деревней сельского дурачка Хорен-Пучкни и тот ему сказал: "Вербит, а дед говорит, что Гротендик второкультурщи ПУЧК ПУЧК ПУЧК" После дальнейшего разговора с вербитом дед велел арестовать сельского петуха. Позднее градчанский суд приговорил его к годовому бану. Он был обвинен в опасных и предательских злодеяниях, в подстрекательстве, оскорблении Гротендика и в целом ряде других преступлений и проступков.
Хорен-Пучкни на суде держал себя, как на двачев, на все вопросы блеял козой, а после вынесения приговора крикнул: "Пучк"-- и прыгнул. За это он был наказан в дисциплинарном порядке: жесткая постель, одиночка и три дня в неделю на картофан и водку.
С тех пор у деда не было осведомителя, и ему пришлось ограничиться тем, что он сам выдумывал себе осведомителя, сообщил по инстанции вымышленное имя и таким образом повысил свой ежемесячный заработок на пятьдесят биткоинов, которые он пропивал в трактире dxdy. После десятой кружки его начинали мучить угрызения совести, пиво казалось горьким, и он слышал от крестьян всегда одну и ту же фразу: "Что-то нынче наш дед невеселый, словно как не в своей тарелке". Тогда он уходил домой, а. после его ухода кто-нибудь всегда говорил: "Видать, наши во Франции опять обделались - дед сегодня больно молчаливый"
Ты его создал.
Я бы хотел поговорить о многообразиях Фано, кажется я нашел некоторые очень хорошиве функторы, которыми можно описать точные схемы.
Я пока ещё не оформил статью. Боюсь, что кто-то украдёт мои наработки, если я выложи материал.
А чего ты так боишься? Я ведь имею научный интерес. Да и ты сам хотел со мной связаться, я тогда про Гротендика говорил.
Ты говорил о каком-то форуме, когда я вчера объявился. Я помню, тут выли об этом ещё когда я за модеркой был. Таки создали?
Почему тебе так инетересует форум. Забудь про него и никогда не вспоминай.
Великий фокусник Пучкини
Залез в наполненный говном
Сосуд шарообразной формы
Два раза пучкнул и издох
Ну нихуя ты себе пошутил! Ха-ха-ха-ха...!
но он же, говорят, того
Но сама тема говно. Ты просто предельный даун, который не может врутся в определение предела и придумывает своё фриковатое.
y0 - предел функции.
y0 - предел функции в точке x0.
Какие проблемы?
нет ты, мы о пределе функции говорим даже, а ты и этого не понимаешь, толстичок, опять начал?
y0 - предельное значение функции в точке x0
да ты сам залупа, предел - это y0, это и в определении написано, ещё раз прочитай
я на тебя время больше не трачу
Я думал что уже увидел достаточно тупости в этом подзалупном итт треде. Но после этого
>Что такое y0?
я опять начал умирать от смеха. Пиздец.
Ты просто запутался и сам не помнишь уже, а сейчас маняврируешь.
блять, помимо линейного приращения есть еще бесконечно малая альфа(x), которую ты опустил
Модульный дед.
напиши определение проколотой окрестности. слышал про такую?
при дельта х = 0, у тебя ПРИРАЩЕНИЯ НЕТ, блять идиот о какой производной ты вообще речь ведешь?
Ньютон с гауссом щитали бесконечно малыми и мы будем. Как диды. Модульные.
Некий школьник считает, что предел - это подставить предельную точку вместо переменной. А средняя скорость - это координата (!), делённая на время. Или не считает, а просто толстит, что вероятнее.
> Некий школьник считает, что предел - это подставить предельную точку вместо переменной.
> предельную точку
Так предельное значение это и есть предел, нет?
> А средняя скорость - это координата (!), делённая на время.
> координата
Че?
нет, ты не прав
ушлёпок, у тебя же проекции, выходит ты на самом деле шизофреник, а мы то думали, в чём же дело :)
его лоха опустили, ошибся, поплакал, а потом как давай тут истерить, до сих пор не угомонится чудо поехавшее :)))
Но мы имеем две разных точки К в одном месте, в случае производной она выколота, а в случае тангенса угла наклона касательной - нет.
Вот в этом вся парашная суть математики.
Пока ерохины наебенив интегралы и циклы ушли в кодинг, штампуя за бешенные даллары хэш-таблицы под водовку, упортоые задроты разбирают как у них выколота сраная окрестность...
Даа, классическую математику давно пора закапывать.
Ну и в чём проблема тогда? Они все одинаково простые. Тут по частям, тут на два разбить, там замену сделать.
юзай этот калькулятор. Там пошагово нормальное решение описано http://ru.symbolab.com/solver/indefinite-integral-calculator
Вот поэтому надо вводить производные как оператор.
Нет. Не нужно.
Случайно заглянул на вашу доску и мне кажется, что это какой-то софизм уровня Зенона, но пояснить за это не могу, может ты укажешь мне, где ошибка в том, что ты написал?
Нигде.
Дерьмо все эти учебники, предел и значение функции в предельной точке неразрывно связаны.
Когда мы находим предел, мы именно находим значение функции в этой точке, подставляя туда соответствующий x, а выколота она или нет - это дело десятое.
С точки зрения малолетнего долбоеба безусловно.
Говна поешь, дебил)
Ты вообще нихуя не понял, идиот.
Под точной математикой ты подразумеваешь только дискретную, что ли?) На конечных множествах?)
Бесконечно-малая != ноль, и вообще её надо понимать как переменную. Не пытайся ей дать смысл вроде точки или числа, она бессмысленна в таких формулировках, её определение -- "для любого эпсилон больше нуля..."...
Использование б/м не приводит к неопределённостям, к неопределённостям приводит использование нулей вместо них. Даун тупорылый.
Это, наверное, различия в мозге, которые не исправить. Потому стоит вести два параллельных курса по выбору: анализ и нестандартный анализ. Теоремы в них одни и те же.
Если человек не в состоянии мыслить достаточно абстрактно, чтобы понять, что такое бесконечно-малая в смысле обычного анализа, то до нестандартного ему ещё дальше.
кстати говоря, для нестандартного анализа верны некоторые рассуждения, неверные в обычном. Причём _очень_ существенные (больцано-коши о промежуточном значении).
>"для любого эпсилон больше нуля..."...
Не устаю ржать с таких долбоёбов.
Ты хоть для начала Одекватное определения предела найди или создай сам, хотя ты же зеро, какое там создай сам.
Несёт какую-то хуйню и не понимает, что он мудак и его в жопу ебут.
Коши вас уже не одно столетие всех в жопу ебёт.
Коши во время создания определения предела:
Ой, я не могут понять, что такое предел.
Давай-ка создам такое определение, которое не будет ничего определённого значить, но будет выглядеть умно.
Всё равно эти уёбки ещё тупее меня все.
Пиздец, кретины.
Бляяядь, какие же вы все кретины.
Я ни одного адекватного определения предела до сих пор не видел. И уж тем более все его классические определения - тупо говно и всё.
Пусть M - частично упорядоченное множество.
Подмножество F множества M называется фильтром, если:
1. F непусто
2. Для любой пары элементов в F есть нижняя грань
3. Если элемент m из M мажорирует какой-то элемент из F, то m входит в F.
Пусть T - топологическое пространство, F - фильтр.
Пусть дана функция f: F -> 2T.
Точка x из T называется пределом f вдоль F, если частью любой окрестности x является f-образ некоторого элемента фильтра.
Часть = подмножество.
А может все-таки ты слишком тупой?
Шаришь, оно нихуя непонятное только для тебя, а используется -- везде) Так что ты всё-таки тупой, иди соцопросы проводи или листовки раздавай.
Бля, дочитал и понял, что ты тролль. Сорян.
по частям возьми епта
 128 Кб, 808x448
128 Кб, 808x448>А теперь проводим во всей математике "Черту Позора":
Буквально вчера прочитал про это кул стори
Арнольд этот баян рассказывал раз 7 в разных местах. Ты явно не знаток творчества раз впервые столкнулся.
Вот люблю Арнольда, уважаю его умение видеть за деревьями лес и связи между дисциплинами.
Я уже несколько лет после аспирантуры изучаю именно деревья, например всякие там к-теории и когомологий Хохшильда в некоммутативной геометрии. Мозг стимулирует знатно, но больший кайф я испытывал от моих сайд-проджектов - физических задач, которые решал на мэйджоре и в аспирантуре, например моделирование турбулентных потоков или свойств графена.
Я бы, наверное, обменял своё чсв первокультурщика на Арнольдов insight. Простите Миша, Дима.
>но больший кайф я испытывал от моих сайд-проджектов
Вот тоже постепенно прихожу к мнению что всякая инженерная прикладнуха гораздо более творческое занятие чем наслоения всяких гамалогичных техник и категоричных конструкций.
дело всё в том, что каждому своё, каждый должен заниматься своим делом
а вот это всё
>гораздо более творческое занятие
напоминает продукт дутого чсв и гонора, распространённого среди элиты, которая занимается "гамалогичными техниками". проф. деформация, короче. как у погромистов
правда, я подозреваю, ты этих техник и не знаешь вовсе
>что есть числа такие большие что их цифрами не напишешь
Нет никаких цифр, кроме ОДИН.
Просто вдумайся, если есть ОДИН, как может быть второй ОДИН?
If there is more than one, then one is just one, not "the one".
Лучшее доказательство того, что ты мелкобуквенный шизоид, всюду лезущий со своим усравшимся мнением.
Бля, дочитал и понял, что ты тролль. Сорян.
Спасибо конечно,но первые 3 я решил уже.
Осталось ОПушке почувствовать разницу между Δx->0 и Δx=0, ну т.е. прочитать определение предела. А то, через неделю, ему начнут сниться гиперболы, касающиеся ветвями координатные оси, то в числе в x=0. А такая шиза мало того, что не лечится, дак ещё и мешает нормально ёбаться по матану.
>dx/0 = inf - бесконечность.
>dy = 0dx/0 => dy = 0xinf - "НОЛЬ УМНОЖИТЬ НА БЕСКОНЕЧНОСТЬ" Мы получили неопределённость вида 0xinf.
Термин "бесконечность" придуман лишь только для ВУЗов, то есть для поточного выпуска дрессированных обезъянок с инженерными дипломами, у которых существенно не хватает деталек в головах, и потому чтобы у них не выкипали мозги, материал им преподаётся в предельно упрощённом виде: от "инженерных формул", в которых нахуй выброшена куча констант и второстепенных составляющих, до вот таких вот "бесконечностей". В серьёзной математике численные и аналитические вычисления никогда не смешиваются, и потому все эти "бесконечности" при встрече элементарно сокращаются, то есть в серьёзной математике "бесконечность" является самым обычным числом: у "бесконечностей" есть порядки и тому подобное, и никакого затыка здесь нет и не может быть. Блин, да пересмотри хотя бы "газонокосильщика", для понимания.
 1,3 Мб, 1217x1859
1,3 Мб, 1217x1859Ну и прочитать Фихтенгольца, как сравнивать бесконечно малые величины, когда можно на них забить, а также связь дифференциалов и производной.
Эй, серьёзный математик, тут ты сразу же даёшь пару ссылок на серьёзную литературу, а то от
>в серьёзной математике "бесконечность" является самым обычным числом
меня аш трисёт.
Во-первых, вместо "серьёзной литературы" у меня были "серьёзные преподаватели", а во-вторых, это было двадцать лет назад.
Термин "бесконечность" относится строго к численным методам, а при аналитических вычислениях сначала сокращается всё что может сокращаться, и только потом идут вычисления. И если где-то в формуле неявно происходит "деление на ноль", то никакого ЕГГОГ не высвечивается, представь себе. Да потому что этот ЕГГОГ существует только для логических процессоров и голов имбецилов.
>И если где-то в формуле неявно происходит "деление на ноль"
Только лютые алгебраисты с грехом пополам разрешили эту проблему, введя задроченную супер абстрактную структуру. Во всех остальных случаях - деление на 0 неопределенно, и точно не даёт никаких бесконечностей.
Всё с тобой ясно, короче. Хуёво не знать, да ещё забыть. К матану и алгебре на пушечный выстрел тебя не подпускать, твои советы не слушать, или слушать, но 1000 раз перепроверять.
>то никакого ЕГГОГ не высвечивается
Ещё отдельно хотелось бы плюнуть в лицо за полное отсутствие понимания различая деления на 0 и граблей, возникающих из-за конечности разрядности сетки в компуктерных ЦПУ.
Ещё раз: термин "бесконечность" введён лишь только для численных вычислений, например в инженерии, потому что классические измерительные приборы предельно малые величины не отличают от нуля, и аналогично не позволяют фиксировать большие числа. И вот тут-то и всплывает оный ЕГГОГ, который требует остановиться, в силу зашкаливания накопившейся ошибки в вычислениях. То есть когда работаешь с живыми вещественными числами, буквально перебирая их пальцами. Если же вычисления производятся другими способами, то никаких проблем здесь нет, и не может быть.
Чувак, я изначально "местный житель" твоих матана и алгебры, а ты являешься "неподпускателем" только в своей фантазии. Впрочем, в современной науке действительно подавляющее большинство подобных тебе, так что в математике действительно имеется некоторый религиозный раскол, с клубом шизофреников, медленно двигающимся в палату теоремы Ферма. Но они обычно не буйные, и на них никто не обращает внимания. Но если тебе нужен действительно результат, то тебе придётся думать описанным мной образом.
>измерительные приборы предельно малые величины не отличают от нуля, и аналогично не позволяют фиксировать большие числа.
Это называется чувствительностью прибора. И это, как и конечность разрядности сетки не о том.
> И вот тут-то и всплывает оный ЕГГОГ, который требует остановиться, в силу зашкаливания накопившейся ошибки в вычислениях
Пожалуйста, не приводи этот пример. Ты реально не понимаешь, почему в IEEE 754 это сделано как сделано. Это раз. И почему твоё чистое аналитическое деление на ноль с исчезновением порядка с ЦПУ имеют мало общего. Это два.
>То есть когда работаешь с живыми вещественными числами, буквально перебирая их пальцами
Я не смогу пересчитать живые вещественные числа, и не потому, что у меня не хватит пальцев, как в случаи, например, с целыми числами, а потому, их множество обладает замечательной особенностью непрерывности. именно это пытаешься смешивать
>Чувак, я изначально "местный житель" твоих матана и алгебры
В этом я даже не сомневаюсь. Если селишь меня в палату, то не забудь забронировать себе койку по соседству.
>Если же вычисления производятся другими способами, то никаких проблем здесь нет, и не может быть.
1/0 - 9/0. Приведи способ вычисления другими способами, который можно хоть как-то притянуть за уши к понятию осмысленность.
>Но если тебе нужен действительно результат, то тебе придётся думать описанным мной образом.
Я тебя спросил как, ты промычал. Иди в жопу, я так не играю.
>>58036
Ты наркоман чтоли блядь? Или ещё один погромист? Вычислительные проблемы и понятие бесконечности в серьёзной (хотя бы не школьной) математике абсолютно н-и-к-а-к не пересекаются.
Ни в какой "серьёзной" математике бесконечность не является числом, она всегда особая. Её можно прикостылить проективной геометрией, можно сшить, можно не сшивать и полчать разные геометрии, но обычным числом оно не является в силу базовой абстрактной алгебры, которые "серьёзные" математики проходят на 1-ом курсе.
Что несёт нахуй, я как будто в сс/сай/ попал. Обколются своими питонами и датасайенсами.
>Я не смогу пересчитать живые вещественные числа, и не потому, что у меня не хватит пальцев, как в случаи, например, с целыми числами, а потому, их множество обладает замечательной особенностью непрерывности. именно это пытаешься смешивать
Пересчётом чисел занимаются только шизофреники, а все вменяемые люди этими числами просто пользуются.
>>Если же вычисления производятся другими способами, то никаких проблем здесь нет, и не может быть.
>1/0 - 9/0. Приведи способ вычисления другими способами, который можно хоть как-то притянуть за уши к понятию осмысленность.
У тебя в знаменателе "0", то есть это практически наверняка одна величина. Далее заменяешь её на b, сокращаешь, и получаешь ровно то же переполнение. Если величины разные, то ты попал изначально. То есть в быту это бесполезно, и оно используется только в серьёзной математике, где полученные "бесконечности" ещё и время от времени сравниваются между собой. Там действительно нету никаких проблем.
 959 Кб, 1219x1879
959 Кб, 1219x1879>практически наверняка одна величина.
И теоретически тоже - это всё тот же одинаковый ноль, допустим, из ℝ.
>Далее заменяешь её на b, сокращаешь, и получаешь ровно то же переполнение.
Чиво, блядь? a/b - c/b = (a+c)/b, т.е. это первоначальное выражение равняется -8/0?
>в серьёзной математике, где полученные "бесконечности" ещё и время от времени сравниваются между собой
Сравниваются бесконечно малые и бесконечно большие величины, которые, вообще говоря, не являются числом.
>>практически наверняка одна величина.
>И теоретически тоже - это всё тот же одинаковый ноль, допустим, из ℝ.
Там может быть не ноль, а бесконечно малая, и в этом случае преобразования могут излишне исказить картину.
>>Далее заменяешь её на b, сокращаешь, и получаешь ровно то же переполнение.
>Чиво, блядь? a/b - c/b = (a+c)/b, т.е. это первоначальное выражение равняется -8/0?
Если я правильно прочитал написанное, то именно так. Впрочем, можно на эту формулу тупо смотреть и нифига не делать, тоже вариант.
>>в серьёзной математике, где полученные "бесконечности" ещё и время от времени сравниваются между собой
>Сравниваются бесконечно малые и бесконечно большие величины, которые, вообще говоря, не являются числом.
Математика колоссальна и имеет множество подразделов, так что там бывает вообще всё. Бесконечности там никого не шокируют, и изначально, просто обычно отсутствует смысл с ними возиться.
Тогда с разморозкой, бесконечно малые и бесконечно большие величины это ни разу не числа. И если ты хотел плевать в ВТУЗы, то надо было это делать гораздо подготовленней - сам похож на обезьянку, которую дрессировали решать пределы и раскрывать неопределённости, где часто и приходилось "делить" на 0 или на бесконечность. Но сюрприз, это было деление на бесконечно малые/большие величины, а вот в результате предельного перехода получали строгое число. Всё-таки каша в голове у тебя. Садись, два.
Просто ты оперируешь числами, а я, -- процессами, потому что с детства варюсь в этой среде. Почему собственно и случился переход в погромисты вообще без перехода.
Зачем ты впариваешь предельный переход туда, где его вообще нет? Потому что вся логика без этого костыля рассыпается?
>Просто ты оперируешь числами, а я, -- процессами
Ух, нихуя себе. Как оператор процессов, ты должен был чётко провести черту между вариантой и числом.
>переход в погромисты
Это пиздец. Надеюсь структуры и алгоритмы ты знаешь лучше, чем арифметику чисел с плавающей точкой.
>Потому что вся логика без этого костыля рассыпается?
Бляя, это правила, чтобы не наёбываться и не совершать ошибок. Вся математика в этом особенно современная алгебра.
>Зачем ты впариваешь предельный переход туда, где его вообще нет?
А почему его там нет? Как у ОПа-долбоёба, который предел заменил сразу же нулём? Или потому, что ты так скозал, но так и не удосужился привести отсылок к серьёзным источникам. Лол. Дак и чем ты лучше обезьянки из ВТУЗа? Ничем.
Процесс в математике, это вообще-то операция, а не число или там что вместо него.
Структуры и алгоритмы "знают" кодеры, а программисты их вообще-то "создают".
Чтобы не совершать ошибок, вообще-то нужно обладать "здравым смыслом", то есть "разумом". И досконально понимать то, что ты вообще здесь делаешь. И проблемы обычно как раз здесь, очень многие почему-то вообще нихера не понимают, и выживают строго за счёт зубрёжки и аккуратного исполнения чужих ниструкций. Биороботы, чо.
В моём примере 1/0 - 9/0 пределов нет. Но я утверждаю, что это выражение не имеет смысла. Его и дальше можно развёртывать, и пользуясь "серьёзной" математикой пограмиста наворачивать и дальше усложнять. Ну например, 2/∞ + 1/(2^∞). Ответов, конечно, мы от него не услышим, тут же математик на кончиках пальцев со своей врождённой чуйкой.
А вот в классическом в том смысле, что тут давно блядь придумано от обозначений до самой сути и разжёванно не одним поколением людей определении производной, он есть. И им нельзя пренебрегать.
>>58057
>Структуры и алгоритмы "знают" кодеры, а программисты их вообще-то "создают".
Ты и на кодера-то не тянешь, дай б-г пузырёк разобрал, как работает.
>тобы не совершать ошибок, вообще-то нужно обладать "здравым смыслом", то есть "разумом". И досконально понимать то, что ты вообще здесь делаешь. И проблемы обычно как раз здесь
Да кто же с этим спорит.
>очень многие почему-то вообще нихера не понимают, и выживают строго за счёт зубрёжки и аккуратного исполнения чужих ниструкций. Биороботы, чо.
Всё понятно. Непонятый, нитакой как все, непризнанный при жизни и после смерти тоже анонимный Пуанкаре, который что-то знает, но ничего сказать не может.
А выражение действительно не имеет смысла, потому что бесконечность никуда не девается.
Как, вы еще не выяснили всю ссуть дифференциирования? Я думол тред утонул безвозвратно...
Вы видите копию треда, сохраненную 13 августа в 01:46.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.



![spaceships-digital-art-science-fiction-artwork-docks-1920x1[...].jpg](/math/big/thumb/11443/14875232889333s.jpg)


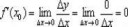
![чел понимает, что дх равен нулю, но до этого берёт и сокращ[...].gif](/math/big/thumb/11443/14875862657270s.jpg)



![beskonechnomalyefunkciizamechatelnyeekvivalentnosticlipimag[...].gif](/math/big/thumb/11443/14877014224750s.jpg)
![beskonechnomalyefunkciizamechatelnyeekvivalentnosticlipimag[...].jpg](/math/big/thumb/11443/14877014224751s.jpg)