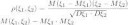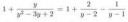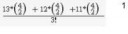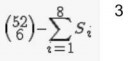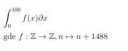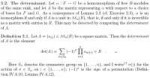Вы видите копию треда, сохраненную 25 марта в 12:01.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 37 Кб, 200x150
37 Кб, 200x150Архив тредов (там же списки литературы и полезные ссылки):
https://pastebin.com/qhs0WNbY
А есть "алгем в задачах" но не хартсхорн?
 21 Кб, 677x343
21 Кб, 677x343Извини, но причём тут математика? "пределы интегрирования" к математике не имеют никакого отношения.
Интересная догадка. Особенно учитывая то, что я оскорбляю гуманитариев в том же посте.
 2,6 Мб, 2448x3264
2,6 Мб, 2448x3264вот это человек
https://vk.com/hard_freedom
генерирует большинство бреда на этой доске (в том числе форс пыни итд)
типичный студент мехмата, ко всему прочему дрочащий на путина
Где тут математика?
Задачи из ЦТ по математике. Задавай вопросы Республиканскому институту контроля знаний(Беларусь).
помогите мне пожалуйста с задачей по теории вероятностей
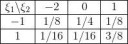
задан совместный закон распределения двух случайных величин кси1 и кси2
и у меня возникли некоторые вопросы
1. как найти коэффициент корреляции?
известно, что он находится по формуле на второй картинке, но мне не понятна верхняя часть данной дроби,на паре препод писал вторую формулу на второй картинке, и чтобы найти M(кси1, кси2) показывал что нужно умножить каждое значение кси1 на каждое значение кси2 и на их общую вероятность, то есть например в этом случае это (-2)(-1)1/8+(-1)01/4+1(-1)1/8+1(-2)1/16+011/16+113/8=5/8. Но ведь не всегда дан совместный закон распределения, как вычисляется корреляция, если даны 2 отдельных закона распределения?
2. подскажите пожалуйста, как найти закон распределения случайной величины ню1=кси1+кси2 и ню2=кси1*кси2 и совместный закон распределения этих величин?
Ладно, помогу. Очевидно, что гамалогии A тривиальны, следовательно его 15% обнуляются. Также очевидно, что все когамалогии B тривиальны, так что и его 20% обнуляются.
У С нетривиальная фундаментальная группа и она абелева, следовательно первая гамалогия у него не нулевая. Из чего конечно же следует, что его проценты мы оставляем.
В итоге у нас остаётся 0% - A, 0% - B, 25% - C. Думаю дальше всё понятно должно быть.
Проценты A и B равны, так что вопрос сводится к любому из них. Предположим, что 50 хватит. Берём проективную резолюцию 50-ти и видим, что у неё есть нетривиальные гамалогии, противоречие. Так проделываем со всеми вариантами и видим, что во всех случаях противоречие.
Следовательно, в тексте опечатка и ни один из вариантов не является верным.
 7 Кб, 952x140
7 Кб, 952x140>1. как найти коэффициент корреляции?
Я в теории вероятностей не силён, но тут вроде просто.
Рассмотрим произвольный функтар T : TeorVer^op -> Set, применяем его к кси1 и кси2, в результате получаем терминальный объект так как любой функтар из категории TeorVer сохраняет все пределы (а кси1 и кси2 являются терминальными объектами TeorVer).
После чего применяем функтар F : Set -> ℤ-Mod который назначает каждому множеству X свабодную абелеву группу с базисом X. Очевидно, что свабодная абелева группа назначенная кси1 и кси2 тривиальная, так как свабодная абелева группа на терминальном объекте Set тривиальна. Из этого следует, что коэффицент корреляции нулевой.
>2.подскажите пожалуйста, как найти закон распределения случайной величины ню1=кси1+кси2 и ню2=кси1*кси2 и совместный закон распределения этих величин?
Точно не уверен конечно, но вроде можно так.
Рассмотрим последовательность ℤ-модулей и гамаморфизмов как на скрине (ню1 - свободный ℤ-модуль с базисом ню1, кси1 - свободный ℤ-модуль с базиом кси1 и так далее) и пробуем посчитать их гамалогии.
Быстро замечаем, что все гамалогии тривиальны. Ну и следовательно сам закон распределения гамалогичен тривиальному. Нахождение совместного закона дуально, вместо гамалогий берём когамалогии.
Забыл добавить, что в TeorVer все копределы и пределы совпадают.
Не он, но тут похоже действительно опечатка.
 28 Кб, 849x513
28 Кб, 849x513А как можно формулой задать диапазон? Щас на работе коллега попросил помочь с заданием по информатике для его пиздюка. Задание такое. Нужно составить программу ЛОТЕРЕЯ с тремя выводными строками в первой значения от 1 до 100, во второй от 101 до 200, в третьей от 201 до 250. Я просто написал random (1,100); random (101,200); random (201,250); а училка говорит что неправильно так делать. Надо что бы в условии были заданны переменные с присвоенными им значениями и результат(рандомное значение из диапазона от x до y) получался через формулу.
Я же помог, насчёт второго не уверен, но первый точно правильный.
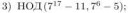 10 Кб, 793x86
10 Кб, 793x86Такая задача: Вероятность попадания в цель при каждом выстреле равна 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20? Какова вероятность этого события?
чо делал: n беру как 20/0.8 (на первый вопрос)
и дальше ищу вероятность: P(20из25) = C2025 0.820 0.25 = ~0,0086
Мне кажется что-то не так. мб где херню сделал, подскажите
Направление в философии математики.
Как думаете, что это означает?
Ravi Vakil
Они тоже через это прошли. Терпи, и через некоторое время бомбить будут с тебя.
Желающие аноны могут пополнять и править.
По поводу что добавить, то это
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mp&paperid=313&option_lang=eng
ну бля, ты как будто не сидел в предыдущих тредах
>Чат мехмата МГУ в Telegram
lol, там нет конструктивных дискуссий, там есть /кеки и срущие петушки, лучше уж оставить линк на инфернал или основной чат нму (хотя там тоже пиздец, обсуждают милф, эротические фотографии студенток, кодинг и изредка просачивается математика), но у них есть отдельные конфы под задачи, где нет говна
>Другие списки книг
возьми из пастебина линк на пост в группе НМУ
>Общие курсы
ткачук, шабунин, дорофеев-розов, вавилов-мельников-олехник, ЧТМ, феликс итд
>Алгебра для школьников
алексеев абель, александров теория групп, понтрягин обобщения чисел, табачников многочлены (не надо сносить вниз)
>Я. П. Понарин
у него 5 томник, а не двух
есть еще треугольники и тетраэдры (но там далеко не только про них), аффинная и проективная, а так же книжка по комплексным числам в геометрии.
>Геометрия
ну сюда бы еще детские задачники шеня, волкевича, задачники прасолова, шарыгина, яглома, гордина
книжки акопяна и заславского (3 их)
>Начала анализа
>Давидович
"мат анализом" в 57-ой называют курсы "спецматематики" и там далеко не только анализ. Есть книжки поинтереснее давидовича, это Элементы математики в задачах (2 тома за 8-9 класс с полным разбором всех задач, томик с олимпиадными задачами на 700 страниц, который скоро выпустят еще и в печатном виде, и курс за 8-11 на странице Мерзона, но без решений)
>Общая алгебра
>Нет Лэнга
у тебя на него какая-то личная обида?
>линал
добавь прасолова
>Топология
вообще самых важных книг нету
>голдблатт
ну а сразу после него Джонстон
>Алгема
абсолютно смешной список, в котором нет основных книг
>Немного физики
сивухина убери и поставь вместо него флф
крч, наспех сделано,
пиздуй на пастебин из оп-поста и допиливай
ну бля, ты как будто не сидел в предыдущих тредах
>Чат мехмата МГУ в Telegram
lol, там нет конструктивных дискуссий, там есть /кеки и срущие петушки, лучше уж оставить линк на инфернал или основной чат нму (хотя там тоже пиздец, обсуждают милф, эротические фотографии студенток, кодинг и изредка просачивается математика), но у них есть отдельные конфы под задачи, где нет говна
>Другие списки книг
возьми из пастебина линк на пост в группе НМУ
>Общие курсы
ткачук, шабунин, дорофеев-розов, вавилов-мельников-олехник, ЧТМ, феликс итд
>Алгебра для школьников
алексеев абель, александров теория групп, понтрягин обобщения чисел, табачников многочлены (не надо сносить вниз)
>Я. П. Понарин
у него 5 томник, а не двух
есть еще треугольники и тетраэдры (но там далеко не только про них), аффинная и проективная, а так же книжка по комплексным числам в геометрии.
>Геометрия
ну сюда бы еще детские задачники шеня, волкевича, задачники прасолова, шарыгина, яглома, гордина
книжки акопяна и заславского (3 их)
>Начала анализа
>Давидович
"мат анализом" в 57-ой называют курсы "спецматематики" и там далеко не только анализ. Есть книжки поинтереснее давидовича, это Элементы математики в задачах (2 тома за 8-9 класс с полным разбором всех задач, томик с олимпиадными задачами на 700 страниц, который скоро выпустят еще и в печатном виде, и курс за 8-11 на странице Мерзона, но без решений)
>Общая алгебра
>Нет Лэнга
у тебя на него какая-то личная обида?
>линал
добавь прасолова
>Топология
вообще самых важных книг нету
>голдблатт
ну а сразу после него Джонстон
>Алгема
абсолютно смешной список, в котором нет основных книг
>Немного физики
сивухина убери и поставь вместо него флф
крч, наспех сделано,
пиздуй на пастебин из оп-поста и допиливай
Нет, но она эквивалента.
Как называется не знаю, я особо не интересуюсь не математикой.
дифференциальные уравнения возможно называется
на какой ответ ты рассчитываешь, задавая такой общий вопрос? от программы зависит. если там только матрицы, то не сложно. если теория групп, скажем, то сложнее
на какой ответ ты рассчитываешь, задавая такой общий вопрос? от программы зависит. если там только матрицы, то не сложно. если теория групп, скажем, то сложнее
Спасибо
Подскажи дурачку: как найти точку на окружности, которая лежит на одной прямой с другой точкой, которая находится не на окружности
Что?
Считаешь когамалогии точки и сравниваешь с когамалогиями окружности. Разница индуцированных гамаморфизмов и будет твоей точкой.
>Как это называется
Это разлажение гамалогий (в данном случае гамалогий y) на копроизведение циклических ℤ-модулей с парядком 1, 2 и 3.
>как такое делать
В основном с помощью аксиомы (или леммы, тут уже от оснований зависит) выбора.
Для этого считай гамалогии первого семестра высшей алгебры и смотри, тривиальные ли они. Если выше 30-той или 31-той или сколько там дней в твоём месяце гамалогии всё обнуляется, то можно.
 172 Кб, 1080x1860
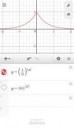
172 Кб, 1080x1860Он строится довольно простым образом. Достаточно заметить, что твой график изоморфен (в категории графиков) графику когомологий твоей функции.
А какое отношение это имеет к математике?
Как раз таки наоборот. И вообще, как ты дашь хотя бы адекватное определение векторного пространства без групп? Начинать изучать алгебру нужно с теории Галуа, причем через функциональные модули, а не через моднявые автоморфизмы полей. А матрицы и определители в 1-ом семестре - грех.
 206 Кб, 640x507
206 Кб, 640x507Подскажите, пожалуйста, вот когда в классической электродинамике говорят о векторном поле, то что в плане математической модели имеется ввиду?
Я так понимаю, что это отображение из Евклидова пространства(непрерывность, скалярное произведение, и т.д.) в трёхмерное линейное пространство. Так какими дополнительными свойствами это линейное пространство должно обладать(в рамках классической электродинамики)?
Раскладывать (2+x)^3
>то что в плане математической модели имеется ввиду
Это к математике особого отношения не имеет.
>самым крутым первокуром на матфаке
Гамалогии и пучки тут точно не помогут, занимайся неинтересной и убогой хуйнёй какой-нибудь. Желательно, чтобы она даже математикой не являлась. Советую так называемый "мат." анализ.
Определение. Модуль над полем K называется векторным пространством, если он обладает базисом, то есть является свободным.
Если множества Z1,Z2 - выпуклые, будет ли Z1+Z2 выпуклым?
Если Z - выпуклое множество, будет ли a*Z - выпуклым для любого a в R?
Будет ли выпуклая оболочка замкнутого множества замкнутой?
Математик порвался.
>Он к математике не имеет никакого отношения.
Есть что-то, что имеет отношение к математике? И если да, то что?
Потому что мне интересно, существуют ли в твоем представлении разделы математики, имеющие отношение к математике. Если есть хотя бы один - то, очевидно, да.
Скажем так, что их существование не отрицается. Конструктивного доказательства (примера) их существования я не знаю.
Алгебраическая к-теория, алгебраическая геометрия, топологическая к-теория, список можно продолжать.
Анализ имеет отношение к математике, это часть к-теории c*-алгебр.
Существительное {алгебра, топология, геометрия, теория групп}
+
Прилагательное {алгебраическая, топологическая, дифференциальная, метрическая, комплексная, геометрическая, аналитическая, симплектическая, тропическая, комбинаторная, общая}
Нужно ещё добавить прилагательные "гомотопическая" и "гомологическая".
Да это местный юродивый с очередным унылым говнофорсом.
Если ты не знаешь, что такое изоморфизм в 10 классе, то тут уже спокойно вешаться можно.
f, g - вещественные фу-и.
его ответ в принципе правильный.
Алгебраическая геометрия, алгебраическая топология, алгебраическая к-теория, алгебраическая теория чисел, топологическая алгебра, топологическая к-теория, дифференциальная алгебра, дифференциальная геометрия, аналитическая геометрия, аналитическая теория чисел, геометрическая алгебра, геометрическая топология, геометрическая теория групп, геометрическая теория меры, геометрическая теория представлений, комбинаторная теория групп, коммутативная алгебра, некоммутативная алгебра, некоммутативная геометрия, гомологическая алгебра, гомотопическая алгебра, гомотопическая топология, гомологическая теория групп, симплектическая геометрия, торическая топология, тропическая геометрия, производная геометрия, линейная алгебра, общая алгебра, общая топология.
Я наверное тебе тайну открою, но модуль = абелева группа, чтобы определить "модуль над полем" тебе нужно сначала определить "группу".
Да, извини, не заметил, что ты имел ввиду топос пучков гомологичных функторам в категории функторо-пучков-Гротендика.
>модуль = абелева группа
В абелевой группе не определено умножение операторов, так что нет. Просто ты тупой, и читал хуевые учебники, в которых сначала определяют группы. Если рассуждать как ты, но более последовательно, то можно заметить, что группа это моноид, в котором каждый элемент обратим. Моноид, в свою очередь, это полугруппа с нейтральным элементом. И так далее, со всеми остановками до магм, амальгам, и прочих никому не усравшихся конструкций универсальной алгебры,
Модуль фундаментален в маиематике, группа нет, смирись. Во всех хороших учебниках вроде Вавилова, Айзекса, сразу даются аксиомы модуля, без упоминания слов "группа" или "кольцо".
Модульный дед, посоветуй что почитать правильного тогда ужкроме Вавилова, стиль не нравится, может перестану быть тупым.
 60 Кб, 535x292
60 Кб, 535x292> Модуль фундаментален в маиематике, группа нет, смирись.
Хуйня какая-то. А что с некоммутативными группами? Это тоже модули?
>Моноид, в свою очередь, это полугруппа с нейтральным элементом. И так далее, со всеми остановками до магм, амальгам
Именно так и есть, тут ты сразу задаёшь миллион функтарав до категорий всех никому не усравшихся конструкций универсальной алгебры.
>Модуль фундаментален в маиематике
Никто и не спорит.
>группа нет
Вот это уже полная хуйня, ведь фундаментальная группа является группой (не обязательно Z-модулем), а фундаментальная она по определению.
И че ты тут делаешь, нематематик? С какой стороны модуль фундаментален, а? Как ты его определяешь без абелевой группы, мань? И главное, как определяешь группы вообще через фундаментальные модули?
>И че ты тут делаешь, нематематик?
Но я ведь человек, так что не могу быть нематематиком.
Я не утверждал, что он "фундаметнальнее " группы. Я лишь сказал, что он сам по себе фундаментален в математике.
Модуль фундаментален для некоторых разделов, а не в математике. Хотя что вообще значит фундаментальность?
А вообще ладно. Хуйня какая-то из раздела спецолипиад. Ну вас.
Я уже советовал много раз. Berrick-Keating, Benson, Ramji Lal.
>>5570
Понятия группы и алгебры ли обобщаются более фундаментальным объектом, алгеброй хопфа (их еще называют квантовые группы). Например одна из самых интересных таких алгебр, это алгебра стинрода.
>>5575
Фундаментальная группа (у жордана – множество) это просто первая гомотопическая группа.
>>5578
Как ты определишь абелеву группу, мне интересно? Её же нельзя определить без моноида и полугруппы, так?
Определение любой алгебраической структуры это список множеств, операций на них и аксиом, которым они удовлетворяют. При чем тут группы вообще.
>>5580
Математика это наука об абелевых категориях.
>Justin R Smith Abstract
Не то написал, я имел в виду Johnathan D Smith, Abstract algebra.
Хотя та книга тоже хорошая, просто скорее для начальной школы.
>>5559
В последнее время часто стал возникать вопрос, можно ли определить модуль, не определяя абелеву группу при этом. Оставим в стороне случаи, когда абелевы группы упоминаются, хоть и не определяются. На картинках приведены примеры из литературы, в которых абелева группа даже не упоминается.
А доказывать уникальность интеграла с точностью до изоморфизма как лучше? И является ли он предельной или копредельной конструкцией?
 58 Кб, 660x628
58 Кб, 660x628Интересуют - гамалогии, гаматопические группы (хотя бы до pi_3).
Не тривиальные, а инфинитезимальные.
>мне кажется, что я нашел способ делать кое-что простое при помощи кое-чего очень сложного
Да, но зачем?
Я конечно понимаю, что гаматопические группы довольно простое явление сами по себе, но всё же. Думаю можно хотя бы одну медальку за это получить.
Это на самом деле тривиально, следует из теоремы Серра-Маклейна-Хопфа-Эйленберга (уже теорема, недавно доказал её). Что там насчёт медали?
>Серра-Маклейна-Хопфа-Эйленберга
К этому утверждению известен контрпример, он построен в 1846-м Леопольдом Кронекером, см. подробнее 4½ том Семинара по Регулярным Кольцам (SRR), его составлял Дедекинд.
Уже давно известно, что данный "контрпример" на самом деле не является контрпримером, так как теорема применима только к ко-регулярным ко-кольцам. Об этом впервые написали ещё Генцен и Стинрод, но даже Евклид уже об этом догадывался.
Евклид об этом знать не мог очевидно, ведь хорошо известно что условие регулярности колец впервые рассмотрел Диофант, живший намного позже Евклида.
Что до работы Генцена и Стинрода, то я о ней не знал, но в любом случае теперь сомневаюсь насчет твоей медали, поскольку на нашей кафедре считается что математика вне регулярных колец мало кому интересна. Можешь попробовать связаться с кафедрой топосов, геометрии и логики; у меня там нет знакомых.
Как подготовиться к ЕГЭ, если нихуя не знаешь, а последний раз сталкивался с математикой года 3 назад в шараге? Я вообще в душе не ебу что мне учить и с чего начинать. Всё забылось, да и учился я на отъебись. Решил вот поступать в ВУЗ. Подскажите что мне учить
Начинаешь с изучения теории гаматопий, а там уже видно будет в принципе. Интегралы решать на ЕГЭ это не математика.
Ну тебе уже посоветовали, теория гомотопий (и все её пререквизиты) неплохая для начала.
 103 Кб, 969x583
103 Кб, 969x583inb4: теория гаматопий и гамалогий уже пробовал гуглить, но в гуглеже оптимального управления не помогло
Я недавно думал, что меня собьёт машина и начал быстро считать фундаметнальную группу пространства между мной и машиной. Оказалось, что она не тривиальная, то есть есть пути машины, которые меня не заденут.
Ребят, помогите вкатиться в геометрию 7-8, что читать? Что учить? срок - 14 дней да, я школьник
Элементы алгебраической геометрии, Александр Гротендик. Я прочитал не за 14 дней конечно, но близко. 17.
Можешь пропускать что не интересно, тогда и за 14 успеешь.
У меня 20 билетов. Переводной экзамен в 9. Который я не сдал. Имеется список билетов. Могу дать его. В одном билете 2 вопроса.
Ну давай. Даже поверхностные знания алгебраической геометрии делают этот экзамен тривиальным.
Сейчас, закину на диск
Сейчас я попробую связаться с Александром Гротендиком.
Благодарю. А после неё уже что учить? От чего отталкиваться?
Y T Lam, excersises in modules and rings, lectures on modules and rings
Жесть какая. Вообще не понимаю, зачем делать 100500 билетов у которых разная сложность. Лучше тогда уж забить на школу и в казино пойти играть. 5-ый совсем элементарный, а остальные нет. Гугли вопросы в билетах и учи.
А, блядь, это что используется. Не пролистал до дна. Не знаю чем помочь.
>теорема Чевы, Менелая
Тут тебе нужна так называемая аффинная геометрия (термин придумал Эйлер, означает "родственный"). Это как евклидова геометрия, только без метрики. Читай Просолова-Тихомирова, Понарина, там это разобрано в подробностях.
Для остальных вопросов хватит школьного учебника.
 625 Кб, 2560x1440
625 Кб, 2560x1440Понимаю, что можно через 3 вектора выразить 4, но коофиценты никак выразить не могу без использования вектора OS...
Всё спокойно (тривиально) решается через подсчёт кагамалогий твоих векторных пространств с помощью спектральной последовательности Хопфа-Хохшильда-Серра.
Потому что она "пропускает" некоторые числа, не? Для того что тебе нужно существует трансфинитная индукция.
Понятно, то есть даже по целым числам нет индукции? Или там тоже трансфинитная нужна?
Целые числа можно занумеровать, счётно множество. Поэтому обычной можно обойтись, наверное.
С художки
https://habrahabr.ru/post/141475/
и я совсем не могу понять вот этот параграф
> Почему именно так? Как была создана эта колонка? Так вот, каждой букве первой колонки подбиралась пара так, что бы среднее арифметическое от суммы частотности их использования в русском языке примерно равнялось остальным средним арифметическим. Это повысит вариативность возможных слов.
объясните, пожалуйста
Решил я эту задачу геометрически, но потребовали алгебраическое решение, то есть через систему уравнений. Собственно, посчитать расстояние от центра окружности до ближайшей точки прямой я могу, и систему уравнений я составил:
(x-xокр)2+(y-yокр)2=R2
ax+by+c=0
где a,b,c - числа в уравнении, вводимые пользователем, R - радиус окружности, xокр и yокр - координаты центра окружности, а x,y - неизвестные.
Так вот, систему уравнений составил, но решить её не могу все равно. Не могу вывести из этой системы ни x, ни y так, чтобы в выведенной формуле не было никаких неизвестных переменных. И не понимаю, как найти координаты точек, когда у тебя их будет две.
В общем, окончательно запутался и перестал все понимать. Прошу решить задачу. Заранее спасибо.
"Частотность использования" - это когда ты берешь много текстов на русском языке и считаешь как часто встречаются разные буквы. Так буква О встречается чаще всего, а буква ъ - реже. https://ru.wikipedia.org/wiki/Частотность
У тебя уже есть первая колонка букв. Теперь ты выбираешь такие дополнительные буквы, чтобы (Q1 + Q2)/2 было для каждой цифры одинаковое. Где Q1 и Q2 - частотности букв
Что значит "решил геометрически"?
Обычно не существует, редко не определен. Вроде так.....
Лимит 1/x или 1/x^2 или 1/(1-x) при x стремящимся к нулю. Всегда получается 1 делить на ноль, но одни существуют, а другие нет.
Потому что ты делаешь неверное "упрощение". Нет такого числа 1/0. Ты подразумеваешь что в числителе и в знаменателе какие-то функции с соответствующим пределом, а не числа "1" и "0".
Предел "бесконечность" это вообще тухлое понятие, потому что все твои функции в нуле расходятся. Просто расходимость бывает разной, и один из частных случаев это расходимость в бесконечность. Так что надо различать предел равный конкретному числу (в этом случае функция сходится к этому числу), предел "равный бесконечности" (функция расходится в бесконечность) и отсутствие предела (функция расходится).
Есть соответствующие определения же. И следствия из них. Короче, функция сводящаяся к "1/0" будет расходится в +∞ если знаменатель всюду в некоторой окрестности положительный, в -∞, если всюду отрицательный, либо просто "в бесконечность без знака" в противном случае. А когда рассматривают комплексные значения функции +∞/-∞ вообще теряют смысл, там все такие функции называют "расходящимися в бесконечность".
lim 1/x = ∞
lim 1/x^2 = +∞
Нет. У lim 1/x нет значения т.к. расходится в разные стороны, а у lim 1/x^2 = +∞ есть т.к. расходится в бесконечность. И как отличать когда функция в одну сторону расходится, а когда в разные?
Тебе ж сказали, по знаку знаменателя в окрестности точки, где считаем предел. И "нет предела" это чисто вопрос договоренности. Потому что +∞ и -∞ это один хуй частные случаи, которые только похожи на конечный предел. Ничто не мешает ввести и частный случай "просто бесконечность".
1/x^2 расходится в +∞, 1/x расходится в бесконечность без знака. Второе можно обозначить как "lim 1/x = ∞", а можно не обозначать, ничего от этого не изменится. Если считать x комплексным, то обе функции будут расходиться просто в бесконечность.
Понятней не стало. Ладно. Спасибо. На экзамене разберусь.
Посоветуйте почитать что-нибудь простенькое по решению уравнений в целых чилах (линейных) с помощью алгоритма Евклида. Нашел один учебник, но в нем больно все неинтуитивно.
 1 Кб, 508x144
1 Кб, 508x144Да хули, там из 1 простого факта всё. Посмотри на пик. Не трудно догадаться, что если kx и y делятся на какое-то число, на такое же и делится z. Проделим на НОД(x,y), тогда на него будет делится и z. Нужно проверить, будет ли НОД(x,z) равен НОД(x,y).
Разделим z на x, получится такое выражение:
z = kx + y, где y - остаток.
1) Если НОД(x,y) существует, то НОД(x,z) тоже существует
Пусть НОД(x,y) существует, тогда выражение справа можно переписать так: z = НОД(x,y)(kx1+y1)[x1 это частное от x/НОД(x,y), с y так же]
2) НОД(x,y)=НОД(x,z)
Разделим обе части на НОД(x,z), получится
z1 = kx1 + y/НОД(x,z)
Видим, что y делится на этот НОД, поэтому он тоже общий делитель (x,y). Пусть НОД(x,z) != НОД(x,y), тогда один из НОДов не является НОДом. Вот и весь факт.
Если x разделить на y, то получится выражение
x = ry + f, и так же, нод(r,f) = нод(x,y) => нод(r,f) = нод(x,z). Можно продолжать делить делитель на остаток, будут получатся тройки чисел (a,b,c), причем c будет всегда уменьшаться. Так как натуральные числа не бесконечные, на каком-то шаге алгоритм остановитсяв произвольном кольце он может быть бесконечным, будет выражение g=jh и НОД их очевидно h, и он же будет НОДом (x,z).
Перед g=jh был шаг r=kg+h. Можно выразить h=r-kg, далее можно выразить r и g и т.д. В итоге h будет выражаться как линейная комбинация z и x, то есть h=az+bx. Отсюда - НОД(z,x) будет решением уравнения h=az+bx.
Остальное нагуглишь, думаю все непонятки ясны будут.
ленинградские математические кружки
>x = ry + f, и так же, нод(r,f) = нод(x,y) => нод(r,f) = нод(x,z)
нод(y,f) = нод(x,y) => нод(y,f) = нод(x,z)
фикс
Воеводский умер, а вы даже тред памяти не создали.
Я?
ну хотя теория чисел тоже топчик, конечно
Боюсь теорию чисел, потому что она напоминает мне "счастливые" школьные деньки со школьной арифметикой/алгеброй. Саму алгебру тоже побаиваюсь.
>ну хотя теория чисел тоже топчик
>топчик
Неудивительно, что такое убогое создание считает теорию чисел математикой.
ТАК ЕПТА, срочно нужен чел, который за бабки решит мне три задачи по статистике, сегодня, за часа четыре!!!!!!!!!!!!1 пожалуйста, если есть такие, то отпишитесь
>статистика
Извини, но причём тут математика? Наверняка же есть более подходящие доски для этого.
Предлагаю /b/, там этим многие занимаются.
Мудрое решение.
Нет.
Не могу понять, как это может быть возможно, что для каждого E выполняется |Xn-Xm|<E ? Допустим, E = 6, и есть последовательность, в которой Xn = 40, Xm = 50. |40-50|=10 10>E. И такой эпсилон, меньший, чем разность членов последовательности, я могу подобрать к любой последовательности. Следовательно, ни одна последовательность не является фундаментальной. Вот, в общем-то мои рассуждения, которые, очевидно, не верны. Но я не понимаю, в чем ошибка. Не закидывайте какахами
Спасибо
Ты пропускаешь шаги определения в своем примере. Чтобы показать, что последовательность фундаментальна, надо найти такое N0, что... etc
Мне впадлу переписывать тебе стандартные примеры, но возьми любой задачник с решениями (антидемидович) и разбери самое простое задание на этот критерий.
Что тут можно сделать, кроме составления неравенства с единицей на все возможные варианты суммы? Не приходит в голову ничего.
 27 Кб, 718x392
27 Кб, 718x392Очень простой вопрос.
На пикриле мне всё понятно. Проблема в том, что я изначально попытался решить через дискриминант, получил те же значения для иксов, но с обратным знаком (-1 и -3). Может кто объяснить, что я не понимаю? Почему по Виету получаются те же значения, но с другим знаком и они принимаются как правильные, а значения, высчитанные по дискриминанту, получаются неверными?
Без разницы чьё мнение если оно верное.
 32 Кб, 604x402
32 Кб, 604x402>Производная (функции в точке) — основное понятие дифференциального исчисления
>Дифференциальное исчисление — раздел математического анализа
>Математический анализ — совокупность разделов математики, посвящённых исследованию функций и их
 1 Мб, 720x960
1 Мб, 720x960в чем тут суть?
с.г.лобанов
Странно, всегда записывали через объединение.
Но ведь все эти задачи целочисленные. И вообще дроби требуют ввести деление и/или обратное число, с которыми опять же всё складывается. В любом случае, когда утверждают о различии этих двух действий, из этих слов оно, выходит, настолько огромно, что только 9000страничные доказательства могут их связать. Или в области действительных чисел оно действительно таково?
>умножение - это повторяющееся сложение
Для двух конкретных чисел, да. Но высказывания, где говорится про умножение произвольных чисел вообще нельзя выразить в некоторых системах со сложением.
https://en.wikipedia.org/wiki/Presburger_arithmetic
В любом случае нужно будет с нуля начинать. Так как calculus это не математика даже.
Два с половиной сложить само с собой три раза и сверху добавить три сотых от числа два с половиной.
По определению возрастания. Сформулируй его максимально формально и поймешь. Вкратце, функция на первом интервале может быть больше, чем на втором.
Да, ты прав.
то есть просто из-за разной скорости нельзя объединять?
1) Теории алгоритмов
2) Теории автоматов
3) Теории множеств
4) Теории классов
5) Теория категорий
( мимо злоебучий программист)
Плюс необходим не энтрилевел по теор.веру
 754 Кб, 1024x634
754 Кб, 1024x634>Что почитать прикладнику, который два года изучал калькулус
Тебе к врачу нужно, а не читать что-то!
 12 Кб, 822x80
12 Кб, 822x80Зачем тебе категории? У вас нет категорий, хватит себя тешить, что якобы есть. Их нет.
https://www.mccme.ru/free-books/
Выше по его списку похоже, что он занимается CS, а не программированием. Так что категории там точно есть.
Программа в универе такая. Первый год матанализ, простая линейная алгебра, нормальная дискретка, совсем чуть-чуть теории групп. Второй год продолжение анализа и теорвер. Все устраивает кроме матана. Преподавание странное, по сути мы изучаем калькулус, но с упором на теорию и доказательства. Определения все старые, через окрестности. Меры, интеграла Лебега тоже нет. Из-за этого страдает теорвер. Хочется что-то реального почитать в первую очередь по анализу.
>Хочется что-то реального почитать в первую очередь по анализу.
Лоран Шварц - Анализ. Но это оверкилл. Так что накати Рудина - функциональный анализ(если не тянешь, то начинать с оснований(!sic) математического анализа). Хочется меры? Пожалуйста D.H. Fremlin Measure Theory The Irreducible Minimum Vol. 1
А под основаниями ты что понимаешь?
Топологическая деформация пространства зафиксированная функцией "гвозди"
>прикладник
>Меры, интеграла Лебега тоже нет. Из-за этого страдает теорвер. Хочется что-то реального почитать в первую очередь по анализу.
Хуя ты тролишь. Прям илитно.
Но Ширяева невозможно читать, не зная таких вещей.
 52 Кб, 882x240
52 Кб, 882x240Никак не врубаюсь в доказательство, а именно в то, что подчеркнул на пике.
Это правило Моргана в простенькой форме.
Первый пункт док-ва.
Почему из того, что а принадлежит А\B следует еще и объединение с (A\C)?
Если а лежит в (А-В) то с чем (А-В) не объединяй то всегда в объединение будет лежать а.
Подсчёт когомологий проективных модулей P_11, P_12 и P_13.
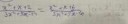 676 Кб, 4137x824
676 Кб, 4137x824Правильна ли вообще идея, или тут что-то другое?
Блядь, ты далбаеб? Если а лежит в А, то А+(какое угодно множество) содержит а, потому что А+В = такое множество, что любой его элемент принадлежит А или В.
> такое множество, что любой его элемент принадлежит А или В
Неверно. Любое подмножество объединения обладает этим свойством.
Может ли граф у которого все вершины валентности шесть быть планарным?
Нельзя доказать на основании этих данных отсутствие такого графа. Поэтому либо может и надо искать пример, либо вопрос задан некорректно.
перекатываюсь в CS.
 8,7 Мб, webm,
8,7 Мб, webm,1280x720, 1:02
1) Метод математической индукции. Равенство, неравенство и кратность
2) Определение пределов последовательности (Начиная с какого номера выполняется неравенство)
3) Вычисление пределов функции
4) Исследование на непрерывность и построение графиков.
Теорема Вагнера: граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в K5 или K3,3. Мимо слегка уточнил.
Барвейс. Справочная книга по математической логике.
Верещагин - Шень. Начала теории множеств.
Йех. Теория множеств и метод форсинга.
Клини. Введение в метаматематику.
Клини. Математическая логика
Колмогоров - Драгалин. Математическая логика.
Коэн. Теория множеств и континуум-гипотеза.
Манин. Доказуемое и недоказуемое.
Мендельсон. Введение в математическую логику.
Френкель - Бар-Хиллел. Основания теории множеств.
Шенфилд. Математическая логика.
Голдблатт. Топосы. Категорный анализ логики.
Кон. Универсальная алгебра.
Маклейн. Категории для работающего математика.
Jech. Set theory: the third millennium edition.
> Верещагин - Шень. Начала теории множеств.
Как раз оттуда, там ожидают, что читатель уже знаком с этим.
Начни с полужирного.
Где-то в прошлом треде я уже писал такое. В общем кратко, множество - это коробка, которая отвечает да/нет на вопрос "лежит ли Х в тебе?". Т.к. коробка отвечает только да/нет, то нельзя подсчитать предметы в ней, поэтому A={a,a}={a}.
Пустое множество = пустая коробка. Коробки можно вкладывать друг в друга. Поэтому ∅ это не тоже самое, что и {∅}. Можешь продолжать читать, только не пытайся делать все упражнения.
>>6074
Про алгебру Клиффорда, но прикладникам это не нужно вроде как.
Не вполне корректная аналогия. Ибо легко можно представить коробку, которая на все вопросы отвечает "да", для любого X. А её не может быть. Зато есть коробка, которая всегда отвечает "нет". И совсем не очевидно, почему одни коробки бывают, а другие - нет.
Окей, в пустом множестве существует ровно два элемента. Только не спрашивай у меня про моё определение пустого множества.
>в пустом множестве существует ровно два элемента
Слишком толсто, ты выпал из образа. Попробуй ещё раз.
Номера которые ты хочешь можно разбить на непересекающиеся множества номеров где совпадают две и только две конкретные цифры от 1 до 9 (почему они не пересекаются?), поэтому сначала посчитай количество номеров содержащих две и только две одинаковые конкретные цифры.
Итак, у тебя есть две фиксированные цифры которые могут по разному располагаться в номере (сколько вариантов?) а заполнения оставшихся мест в номере однозначно соответствуют двузначным числам с разными цифрами от 1 до 9 за исключением той цифры которая бралась для твоего множества (сколько таких?). Считаешь мощность этого множества, а потом складываешь все такие и получаешь ответ.
Не знаю причём тут твой пост и математика.
Похоже на численные методы.
X(n)
Все, написанное жирным - нижний индекс.
Т.е. к примеру X(1), где X1 - случайная величина, один из аргументов оценки (первый).
Потому что тут нет никакой науки. Если ты представляешь, что такое пустое множество, то должен понимать, что это три разных множества.
Действительно, главное пиши всякую хуйню и потом даже не пытайся её объяснить.
С 19века капчуешь? Нормальная аналогия, чтобы продолжить читать Шеня. Там, кажется, в конце первой главы есть про парадоксы наивной теории множеств. Так что всё пучком.
Бамп
Ну не тролль так толсто. Интегралы всегда были математикой, чтобы там Бурбаки не говорили.
>Интегралы всегда были математикой
Не были и не будут, сколько бы идиоты (примерно как ты) не несли такой хуйни.
С какого хуя?
Когда у подгрупп пустое пересечение, то всё ясно.
Пусть, оно не пустое. Тогда выходит второй пик. Множества A',B',H попарно не пересекаются.
Где ошибка?
Аналогия должна быть такой, чтобы неочевидные вещи вскрывались, обнажались. А ты заметаешь их под ковер.
>Когда у подгрупп пустое пересечение, то всё ясно.
А мне вот не ясно. поясни, что же тогда будет.
Нет, ты забыл разделить на нуль. Там же черным по белому написано, разделить на мощность пересечения.
>Нет, ты забыл разделить на нуль.
В пересечении единичный элемент. Это подгруппы одной группы.
Ладно, когда писал, перепутал, что пустое пересечение и пересечение с единичным элементом.
Но что со случаем, когда пересечение больше одного элемента?
 404 Кб, 1519x472
404 Кб, 1519x472Я уже пробовал как-то упростить первое выражение, перенес одно слагаемое в правую часть и возвел все в квадрат. Потом выразил одну переменную через другую и подставил в получившееся, вышла какая-то хрень, удвоенное произведение так и осталось под корнем
Математика— не математика, а задачу по предмету "высшая математика" решить все же надо.
>перенес одно слагаемое в правую часть и возвел все в квадрат
и все равно остался корень
>Потом выразил одну переменную через другую
С этого стоило начать.
> и подставил
А этим закончить.
Чтобы избавиться от корней в выражении типа сумма двух корней равна не нулю, надо возводить в квадрат два раза. Здесь все намного проще.
Почему ты думаешь, что у меня есть ответ на твой вопрос?
Aluffi. Algebra Chapter 0.
Chevalley. Fundamental concepts of Algebra.
Dummit, Foote. Abstract algebra.
Grillet. Abstract algebra.
Herstein. Abstract algebra.
Hungerford. Algebra.
I. Martin Isaacs. Algebra, a graduate course.
I. Martin Isaacs. Finite group theory.
Lang. Topics in Cohomology of Groups.
MacLane. Birkhoff. Algebra.
Michael Artin. Algebra.
Miln. Group theory.
Robinson. A Course in the theory of groups.
Rotman. Advanced modern algebra.
Rotman. An introduction to the theory of groups.
Suzuki. Group Theory.
Алексеев. Теорема Абеля в задачах и решениях.
Артин. Теория Галуа.
Белоусов. Основы теории квазигрупп и луп.
Вавилов. Конкретная теория групп.
Ван дер Варден. Алгебра.
Ван дер Варден. Метод теории групп в квантовой механике.
Вербицкий, Каледин. Тривиум.
Винберг. Курс алгебры.
Гельфанд. Лекции по линейной алгебре.
Городенцев. Алгебра. Учебник для студентов-математиков.
Гроссман, Магнус. Группы и их графы.
Дьёдонне. Геометрия классических групп.
Ж.-П. Серр. Линейные представления конечных групп.
Каргаполов, Мерзляков. Основы теории групп.
Кострикин. Введение в алгебру + Сборник задач по алгебре.
Крылов, Туганбаев, Чехлов. Упражнения по группам, кольцам и полям.
Кузнецов. Курс алгебры.
Кузьмин. Гомологическая теория групп.
Куликов. Алгебра и теория чисел.
Курош. Курс высшей алгебры.
Курош. Лекции по общей алгебре.
Курош. Общая алгебра.
Курош. Теория групп.
Ленг. Алгебра.
Постников. Теория Галуа.
Фейс. Алгебра. Кольца, модули и категории.
Холл. Теория групп.
Шафаревич. Основные понятия алгебры.
Aluffi. Algebra Chapter 0.
Chevalley. Fundamental concepts of Algebra.
Dummit, Foote. Abstract algebra.
Grillet. Abstract algebra.
Herstein. Abstract algebra.
Hungerford. Algebra.
I. Martin Isaacs. Algebra, a graduate course.
I. Martin Isaacs. Finite group theory.
Lang. Topics in Cohomology of Groups.
MacLane. Birkhoff. Algebra.
Michael Artin. Algebra.
Miln. Group theory.
Robinson. A Course in the theory of groups.
Rotman. Advanced modern algebra.
Rotman. An introduction to the theory of groups.
Suzuki. Group Theory.
Алексеев. Теорема Абеля в задачах и решениях.
Артин. Теория Галуа.
Белоусов. Основы теории квазигрупп и луп.
Вавилов. Конкретная теория групп.
Ван дер Варден. Алгебра.
Ван дер Варден. Метод теории групп в квантовой механике.
Вербицкий, Каледин. Тривиум.
Винберг. Курс алгебры.
Гельфанд. Лекции по линейной алгебре.
Городенцев. Алгебра. Учебник для студентов-математиков.
Гроссман, Магнус. Группы и их графы.
Дьёдонне. Геометрия классических групп.
Ж.-П. Серр. Линейные представления конечных групп.
Каргаполов, Мерзляков. Основы теории групп.
Кострикин. Введение в алгебру + Сборник задач по алгебре.
Крылов, Туганбаев, Чехлов. Упражнения по группам, кольцам и полям.
Кузнецов. Курс алгебры.
Кузьмин. Гомологическая теория групп.
Куликов. Алгебра и теория чисел.
Курош. Курс высшей алгебры.
Курош. Лекции по общей алгебре.
Курош. Общая алгебра.
Курош. Теория групп.
Ленг. Алгебра.
Постников. Теория Галуа.
Фейс. Алгебра. Кольца, модули и категории.
Холл. Теория групп.
Шафаревич. Основные понятия алгебры.
>Аналогия должна быть такой, чтобы неочевидные вещи вскрывались, обнажались. А ты заметаешь их под ковер.
Приведи тогда нормальный пример
Спасибо тогда.
Всякое множество - это ориентированный граф. Вершины графа суть наследственные элементы множества. Т.е. элементы множества, элементы элементов, элементы элементов элементов и т.д. Стрелка из x в y идёт титтк x - элемент y.
В ZFC каждое множество - граф-дерево, корень которого - пустое множество. И обратно, по всякому дереву строится множество в смысле ZFC, нужно начать с корня и поочередно сконструировать каждый уровень вложенности (в ZFC возможно только конечное число уровней вложенности).
Допустимы только деревья. Лес не допускается, т.е. в графе может быть самое большее одна компонента связности. Ну и ни петель, ни даже циклов быть не может.
Пустое множество - граф без вершин и рёбер, т.е. чистый лист бумаги. Граф с одной точкой и без рёбер - это множество {∅}. Множество {∅, {∅}} - это граф с двумя вершинами, причем из одной вершины в другую идёт стрелка.
Хуета.
 16 Кб, 1312x707
16 Кб, 1312x707Придумал красивее. Короче, берем множество M.
Корнем дерева называем само множество M.
На первом ярусе дерева живут элементы M, с каждым из них M связано ребром.
На втором ярусе живут элементы первого яруса, и так далее.
Элементы изображаем точками (повторения возможны).
Получится, что каждое множество разворачивается в дерево с конечным числом ярусов.
Например, пусть 0 = ∅, 1 = {0}, 2 = {0,1}, 3 = {0,1,2}, 4 = {0,1,2,3}.
Тогда дерево для множества M=4 - пикрелейтед.
Ситуация, когда у дерева есть два листика-сиблинга, невозможна (в ZFC нет праэлементов). Всякий листик - это пустое множество.
Множества - в точности деревья без листьев-сиблингов с конечным числом ярусов.
Пустое множество - граф с одной вершиной.
Множество = дерево с конечным числом ярусов, в котором нет листьев-сиблингов. Такие деревья существуют. Вот, я даже нарисовал одно.
Подумай ещё раз.
Надоело что именно? И почему я аутист?
Почти верно. Только там не конечное число ярусов, а
1. Ярусов не более чем счетное число
2. Нет бесконечного пути от корня вниз по дереву.
>>6168
Множество Кантора - подмножество R.
Достаточно нарисовать дерево для R.
R отождествим с 2^N.
Корень дерева будет множество 2^N.
На первом ярусе размещены все подмножества N.
И т.д. по рекурсии.
Любое подмножество R изображается поддеревом построенного дерева.
За базар ответишь?
В чем проблема? У графа вполне может быть сколь угодно большое множество вершин. Счётность там проявляется в уровнях вложенности: в ZFC не может быть бесконечных цепочек вида a ∋ b ∋ c ∋ d ∋ ...
Над полем Q - да, счётно. Множество таких многочленов очевидно счётно, у каждого лишь конечное число корней. Объединение счётного семейства конечных множеств не более чем счётно. e и пи не алгебраические числа.
Ого, вот это быдлоид.
 47 Кб, 645x968
47 Кб, 645x968Какие лекции?
Если у тебя дочерние элементы корня - элементы множества R, то получается, что R счетно, так как каждому узлу можно присвоить порядковый номер, а каждый узел соответствует числу из R.
https://en.wikipedia.org/wiki/Canadian_traveller_problem
С чего начать? Или есть простое вкатывание в теорию графов для прикладников?
> e и пи не алгебраические числа.
Но ведь и многочлены те не алгебраические. Или их корни всё те же? А если коэффициенты и степени икса в алгебраических степенях будут типа 2^1/2, или вообще степенные башни? А если ещё иксы в этих степенях ну тут-то е должно объявиться?
>так как каждому узлу можно присвоить порядковый номер
С чего бы? Вовсе нет. Ну или можно, но тогда эти порядковые номера - бесконечные ординалы вплоть до омеги-первого.
Не математика, извини.
ниматиматика
Двенадцать знаков после запятой - уже астрономическая точность.
>В чём смысл расположения первого элемента отдельно от пары
Показывает, что этот элемент первый.
Предъявить конструкцию, у которой
1. Выделен "первый" элемент
2. Выделен "второй" элемент
3. Две такие конструкции равны титтк равны соответственно их первые и вторые элементы
- это нетривиальная задача. И, вообще говоря, довольно сложная. Раньше даже считалось, что такая конструкция должна быть неопределяемым, первичным понятием.
>Две такие конструкции равны титтк равны соответственно их первые и вторые элементы
Не понял этого, объясни, пожалуйста
пиздец я заебался сегодня, пойду пожалуй спать, завтра чекну тред. Зараннее спасибо за ответ.
Пусть M - множество, являющееся некой конструкцией, у которой выделен "первый" элемент и "второй" элемент. Утверждение, что p - первый элемент M, q - второй элемент M, записываем как M = (p,q).
Пусть X=(a,b), Y = (c,d). Требуется, чтобы X=Y было верно тогда и только тогда, когда верно a=c и b=d.
Вот нужно теоретико-множественными средствами, т.е. на основе лишь аксиом ZFC и логики предикатов, описать такую конструкцию.
Либо:
1. Прямым построением с помощью аксиом бесконечности, выделения, подстановки, пары, объединения, булеана и выбора
Либо:
2. Доказательством, что несуществование ведет к противоречию, обычно на основе аксиом объемности и регулярности.
Существует ли способ решить эту задачу не через теорему Бернулли? Вольфрам говорит, что ответ: 0.5
Ну вот, например, множество {4, 2, твоя мамка, 3} это нормально или нонсенс?
Если твоя мамка было корректно определено на языке ZFC, то нормально. Иначе выражение не имеет смысла.
Можно, просто перебери все 127 комбинаций.
>Видимо должны быть какие-то критерии.
Есть, и они зависят от системы в которой ты работаешь, но ты пока её не назвал.
Почему содержит? У меня более физический, что ли, взгляд, поэтому я не понимаю как может пустое множество (т.е. ничто) отличаться от множества, содержащего несколько пустых множеств (т.е. также ничто). Небытие оно и есть небытие.
>>6078
> Т.к. коробка отвечает только да/нет, то нельзя подсчитать предметы в ней, поэтому A={a,a}={a}.
Пустое множество = пустая коробка. Коробки можно вкладывать друг в друга. Поэтому ∅ это не тоже самое, что и {∅}
Это троллинг что ли? Я просто приведу несколько цитат.
"Множество однозначно определяется набором составляющих его объектов".
"Множество состоящее из элементов х1, ...., хn, обычно обозначают ..." (то, что предметы в коробке нельзя подсчитать - вообще пушка).
Множество, содержащее пустое множество отличается от пустого множества так же как множество, содержащее двойку отличается от двойки.
>Почему содержит?
Да ты тупой гуманитарий потому что, какое нахуй "небытие"? Какие нахуй коробки?
∅ это просто символ для которого верно, что у него нет никаких элементов.
Правильно ли я понял, что каждый элемент множества в ZFC сам должен являться множеством, и проблемой множества {4, 2, твоя мамка, 3} является то, что твоя мамка не представима в виде множества?
>каждый элемент множества в ZFC сам должен являться множеством
Да.
>проблемой множества {4, 2, твоя мамка, 3} является то, что твоя мамка не представима в виде множества
Твоя мамка не определена пока что в виде множества, но это не значит, что она не представима в принципе.
Если ты представишь её в виде множества, то множество выше можно получить как - {4, 2, 3} ∪ {твоя мамка}
>но это не значит, что она не представима в принципе
А как ты можешь себе представить её представление в виде множества?
"совершенно разные множества". Конечно я бы не стал вторым вариантом обозначать ответ к уравнению без решений, но чем он по сути отличается от первого варианта мне не ясно.
>>6257
Я смутно понимаю о чем ты говоришь, но не до конца, м.б. я не верно воспринимаю определение понятия "множество".
> множество, содержащее двойку отличается от двойки
Вот есть две кучи из 4 одинаковых ручек. Первая - множество таких ручек, вторая - просто отдельные ручки. Но кучи ведь идентичны, ничем не отличаются.
>>6263
Видимо въеду до конца после прохождения графов. Подожду.
>>6258
> Какие нахуй коробки?
Про коробочки написали в ответ на мой вопрос.
> Да ты тупой гуманитарий
> какое нахуй "небытие"? Какие нахуй коробки? ∅ это просто символ для которого верно, что у него нет никаких элементов.
> Небытие - отсутствие, отрицание существования, жизни, бытия
Я понимаю, что ты безграмотный не гуманитарий, но не до такой же степени.
>значит они равны
>при этом это "совершенно разные множества"
Откуда такие животные берутся вообще? Гуманитарии все настолько отбитые?
>состоящее из
>без элементов
Я конечно понимаю, что с твоим заболеванием сложно замечать очевидные противоречия, но тут даже ты должен справиться.
А пустой список из программирования тебе знаком? Он же не является никаким небытием, вот и с множеством так же.
Да ладно, пустой список сам является небытием, так как он ничем от него не отличается. Они являются одинаковой коробкой.
x:(/x/)=y:(/y/)
(x-y)(x-2y)=0
x-[x]>y-[y] <-- [x] это целая часть числа х, на всякий случай
и немедленно сдулся, потому что представить это в виде параболы, прямой или прочих элементарных вещей у меня как-то не особо получилось. Препод на просьбу объяснить пробубнила что-то невнятное, вольфрам нарисовал какую-то дичь, в общем, я реквестирую помощь.
Послан нахуй.
>x:(/x/)=y:(/y/)
Знак x равен знаку y. Решение I - четверть и III четверть. Ноль - проколая точка.
>(x-y)(x-2y)=0
Две прямые.
x=y
x=2y
>x-[x]>y-[y]
x-y>[x]-[y] => {y}>{x} , {x} - дробная часть. График получется как бы заполнен треугольниками. Посмотри, что будет на кадрате [0;1][0;1]. То же будет на любом квадрате [k;k+1][k;k+1], если k - целое.
Где ты увидел противоречие в том, что данное множество состоит из других множеств, которые в свою очередь являются пустыми множествами, а значит в них нет элементов? Поделись своим гением.
>данное множество состоит из других множеств
Ты так говоришь, будто оно может состоять из чего-то другого.
Противоречие в том, что "состоит из" означает, что у него имеются элементы (то, из чего он собственно и состоит).
Как доказать существование и уникальность интеграла?
Первое, функция знака.
https://ru.wikipedia.org/wiki/Sgn
Ответ будет множеством точек, где знак x,y совпадает.
Второе, очевидно, что (x-y)(x-2y) будет равно нулю, когда равен нулю хотя бы один из множителей в скобках. А значит, мы объединяем решения уравнений (x-y)=0 (x-2y)=0.
И третье просто приводим неравенство к удобному виду, через определение дробной части.
https://ru.wikipedia.org/wiki/Дробная_часть
Хотя, я немного ошибся. Любой квадрат [t;t+1][k;k+1], где t,q - целые, будет выглядить так же, как [0;1][0;1]
Потому что, {t+q}-{k+p}={q}-{p}, где
0 <= q <= 1, 0 <= p <= 1
Осталось лишь посмотреть, что будет в первом квадрате.
Отбой. Решение интуитивно понятно.
Классический пример. Представь, что парабола x^2 это трубка. На нее навешана муфта, которую можно двигать вперед-назад по параболе. Если ты возьмешь ограниченный кусочек параболы, то ты можешь сделать муфту достаточно большой по вертикали, чтобы она могла свободно двигаться по всему куску трубы. Если ты возьмешь бесконечную часть параболы, то какую бы высокую муфту ты не взял, она когда нибудь застрянет при движении по параболе. Решай задачи и все вкуришь
Короче, посидел, подумал, полистал книжки и пришёл к выводу, что ни для каких яблок, апельсинов, машин и мамок ZFC не годится, только для математических объектов. Может кто-нибудь подскажет какую-нибудь аксиоматику, чтобы я мог поместить туда яблоки или буквы хотя бы?
Полный бред. Ни яблоки, ни буквы не реальны. Существует пустое множество, множество, полученное индукцией, и множество, полученное объединением.
Возьми счетное множество объектов и отождестви часть из них с яблоками или чем там тебе нужно упороться.
Не будет ли это биекцией между "счётным множеством объектов" и множеством яблок, которое мы как раз хотим получить?
C муфтой не зашло, но пока гуглил, нашел аналогичную аналогию с рамкой и понял. Ну а насчет задач, мне сложно не поняв определения понимать все шаги решения, а когда сам пытаешься что-то доказать, то тоже сомневаешься в некоторых логических шагах.
Браток, я тебя понял.
>полистал книжки и пришёл к выводу, что ни для каких яблок, апельсинов, машин и мамок ZFC не годится, только для математических объектов
В математике работают только с математическими объектами.
помогите мне разобраться с задачей по теории вероятности.
Случайная величина \eta является средним арифметическим 3200 независимых одинаково распределенных случайных величин с математическим ожиданием, равным 1, и дисперсией, равной 2. Найти вероятность того, что \eta принимает значения в промежутке (0.95;1.05)
Подскажите пожалуйста, как решается эта задача, хотя бы с чего начать.
Мой основной вопрос заключаются в том, что собой представляют множества, содержащие "нематематические" объекты, например алфавит из теории формальных языков. Вот определение:
An alphabet, in the context of formal languages, can be any set, although it often makes sense to use an alphabet in the usual sense of the word, or more generally a character set such as ASCII or Unicode. The elements of an alphabet are called its letters. Alphabets may be infinite;[3] however, most definitions in formal language theory specify finite alphabets, and most results only apply to them.
Какими множествами будут являться буквы этого алфавита? Или множество в данном контексте не есть ZFC множество?
>Или множество в данном контексте не есть ZFC множество?
this
Зависит от теории, которую ты используешь в качестве метаязыка.
>"нематематические" объекты
>алфавит из теории формальных языков
С чего это нематематический объект?
Можно спокойно закодировать его с помощью натуральных чисел, что ниже и написано, это же должно быть очевидно.
Всякое множество f={(x,y)} упорядоченных пар (x,y), x принадлежит множеству X, y - множеству Y, такое, что для любых пар (x1,y1), принадлежащих f, и (x2,y2), принадлежащих f, из условия y1 не равно y2 следует, что x1 не равно x2 называется функцией, или, что то же, отображением.
Неужели, нет ни одного случая, когда функция имеет две точки, имеющие одинаковую координату x, но разные y? Например, x=3.
Найдите ошибку в моих рассуждениях, пожалуйста.
>Неужели, нет ни одного случая, когда функция имеет две точки, имеющие одинаковую координату x, но разные y?
Нет, т.к. это противоречит определению.
>x=3
С чего ты взял, что это функция? Я тебе больше скажу, sqrt(x) тоже не функция!мани с арифметическим корнем и погромисты идут на хуй
Увидел беседу, вспомнил что тоже не до конца понимал этот вопрос, но забыл о нём. В школе следовали этому определению строго: x=3 - не функция и окружность тоже не функция, а просто уравнения задающие некоторые графики на плоскости. Как то так нам объясняли. Но на 1 семестре 1 курса, я специально это спросил у препода по линейной алгебре и он сказал что конечно же всё это функции, а в школе были не правы.
Не надо думать, что если препод работает в университете, то он умней тех, кто работает в школе.
Окружность радиуса r можно задать функцией f(t)=r(cos(2пиt)+isin(2пиt)), где t пробегает отрезок [0,1].
Если кодирование - это отображение, тогда у тебя до него уже должен быть алфавит в виде множества. Или это происходит на уровне метаязыка?
>мани с арифметическим корнем и погромисты идут на хуй
Мань, не плач от арифметического корня, он няшен.
>Я СКОЗАЛ!
Мань, ну твоё мнение никому не интересно.
sqrt(x):R+->R+
Вот и старый добрый арифметический корень.
Может создадим адвайс-лист ?
Куча же этих листов. Ты по ссылке из шапки переходил?
Бамп вопросу. Тут в интернете изредка проскакивает формулировка "задача о составлении графика персонала". Я точно знаю что в моём курсе такой не будет. Вопрос: это вообще типовая задача ЛП или нет ? В каких книгах её разбирают ?
Олимпиадник, плз. Ты можешь какие угодно мантры читать, но sqrt(x) не станет от этого функцией. =ЧАО ПОКА=
>Ты можешь какие угодно мантры читать, но sqrt(x) не станет от этого функцией.
Если только в твоём маня-мирке.
Я думаю, это верхний и нижний пределы.
Ты можешь хоть sqrt(x), N->N определить, всем похуй. Пошел на хуй от сюда, короче, направил свой морфизм тебе за щечку, олимпиадаун.
>sqrt(x) не функция
И нахуя она кому-то нужна тогда? Для отказывающихся от пожирания говна (теории множеств) она фактически невидимая.
>Не понимать что от разных областей значения не-функция может становиться функцией
Ты сам то олимпиадодаун тот еще, набросал тебе говна за щеку.
Да он это понимает надеюсь, просто он любит убогость.
>Ты можешь хоть sqrt(x), N->N
Это будет сужением на N, которое подмножество R.
>всем похуй.
Ты не все, мань.
>Пошел на хуй от сюда, короче, направил свой морфизм тебе за щечку, олимпиадаун.
Сую хуец в твою категорию колец.
>sqrt(x)
>The principal square root function f(x) = √x (usually just referred to as the "square root function") is a function that maps the set of nonnegative real numbers onto itself. In geometrical terms, the square root function maps the area of a square to its side length.
dxdy
Помню себя в твоём возрасте. Тоже писал такие посты, типо вопрос жизни и смерти. Помни одно: это говн о (математика) не надо никому, и как только ты закончишь школу, начнётся реальная жизнь, где все решают деньги, связи и смекалка
В открытое покрытие входят только открытые множества. В произвольное покрытие - произвольные. По аналогии можно выделить, например, замкнутое, компактное, связное покрытия - покрытия соответственно замкнутыми/компактными/связными множествами.
ну помогите пожалуйста
Я уже нашёл, но не буду публиковать пока его доказательство не проверят.
Понял, спасибо.
>в какой момент человек может утверждать что он понимает матрицы
Когда будет в состоянии доказать теорему о жнф.
>Должен ли , скажем аналитик
depends
on a situation
 330 Кб, 768x576
330 Кб, 768x576Если я подставлю туда тройку(а я могу это сделать, ведь неравенство позволяет), то первый модуль станет нулем, и тогда я не меняю знаки в нем. Если я так сделаю, уравнение пойдет по пизде. В чем проблема?
>В чем проблема?
Когомологии тройки не обязаны быть тривиальными (зависит от оснований), поэтому и всё так происходит.
Погугли, там всё должно быть понятно даже школьнику. Когомологии абелевых групп, чем вещественные числа являются, в том числе 3.
А как тогда правильно? Я думал, что тут произвольно можно. Главное, если с этим числом уже был строгий знак, значит теперь нужен нестрогий.
А объяните немного. В задаче просят удалять треугольники из полного графа пока тот не станет пустым. Очевидно, что удаляя треугольник мы уменьшаем количестве рёбер на 3, а степень некоторых вершин на 2. Интуитивно понятно, что количество рёбер должно делится на 3, а степень каждой вершины на 2. Эти 2 условия необходимы чтобы удалить из графа все вершины по треугольникам. Но как доказать, что этих условий достаточно?
>о как доказать, что этих условий достаточно?
Доказательство тривиально, гомологии всех треугольников в графе после этого становятся нулевыми.
Нужно для начала упорядочить твой граф с помощью аксиомы выбора, потом уже считать его гомологии, можно даже с каэффицентами в произвольном тапологическом пространстве.
Математика без непрерывности. Типа финитизма, только еще не верим в вещественные числа. Вайлдбергер-стайл.
>Математика без непрерывности.
Такой не существует, даже финитизм не подходит.
И причём тут вещественные числа вообще? Тапалогия это изучение ∞-группоидов, а не вещественных чисел.
>Тапалогия
Скажи хоть одно применение этого говна для аутистов в реальной жизни, иначе это не математика.
>Математика это в первую очередь прикладная к фзике
Ты видимо в каком-то другом мире живёшь. На фзику большинству математиков похуй, как и должно быть, так как это неинтересное дерьмо.
И сразу видно, что ты нихуя не знаешь про саму ф*зику (как и про математику). Тапалогия (в том числе агебраическая) там используется очень активно.
>отношения к реальности
Математика не обязана иметь отношение к реальности.
>физика очевидно к реальности имеет отношение прямое
Современная физика, точнее огромная её часть, почти никакого не имеет.
>Тапалогия (в том числе агебраическая) там используется очень активно
Так ты дай хоть одно применение.
>Математика не обязана иметь отношение к реальности
То что не имеет отношения к реальности это не математика а манямирок аутистов, исторически математикой всегда считалось то что можно использовать в реальности.
>Так ты дай хоть одно применение.
Общая теория относительности, TQFT, группы Ли используются в физике элементарных частиц. Моё понимание физики примерно как твоё (то есть несуществующее), но даже я про это знаю.
И почему тебя вообще интересуют её применения в физике? Ты же ей не занимаешься.
>То что не имеет отношения к реальности
Таких вещей в принципе не существует в нашем мире.
>всегда считалось
Всем похуй, что у тебя там считалось.
>использовать в реальности
Я вот прямо сейчас использую свою голову, чтобы думать про тапалогию. Разве это не использование её в реальности?
>использую свою голову
>реальности
Если твоя тапалогия не существует в реальности за пределами твоей головы то это не использование ее в реальности, даун.
>Она не очень то использовалась в реальности исторически
Ты думаешь она в тот момент была математикой а не аутизмом для фелосафов и илиток вроде тебя?
>Моя голова разве не находится в реальности?
Твоя голова не сможет использовать топологию ни для чего практического. Если ты этого не можешь понять то твоя голова действительно не находится в реальности.
>Ты думаешь она в тот момент была математикой
Со своим ебанутым релятивизмом можешь сразу нахуй идти.
>Твоя голова не сможет использовать топологию
Меня это не интересует. Пусть те, кому это интересно этим и занимаются.
>практического
Что такое "практическое"? То, что я перечислил выше по твоим же словам должно быть практическим.
>Со своим ебанутым релятивизмом
Но так и есть, пока математика не имеет применений она говно для аутистов.
>Меня это не интересует
Ну и нахуй ты кукарекаешь тогда?
Абсолютно любая математика (и вообще абсолютно что угодно, про что имеется хоть какая-то информация) имеет применение, и это довольно легко увидеть.
Хотя такому жалкому существу это будет сложно понять.
пукнул тебе в лицо
>Абсолютно любая математика
>имеет применение
Сейчас пойду применять теорию множест и матлогику, или какой еще аутизм который годами доказал свою бесполезность.
>>6414
И зачем мне это?
Я пробовал находить решения двумя способами, но почему-то ответы не сходятся. Помогите, пожалуйста, найти ошибку.
1 способ:
См. первый пикрил
Первую пару карт можно выбрать 13 способами, вторую - 12, третью - 11. Чтобы исключить наборы, отличающиеся только порядком делим на 3!
2 способ:
Пойдем от противного: найдем все варианты наборов из 6 карт, которые не удовлетворяют условию задачи:
<n> - набор из n карт одной масти
1) <1> + <1> + <1> + <1> + <1> + <1>
2) <2> + <1> + <1> + <1> + <1>
3) <2> + <2> + <1> + <1>
4) <2> + <3> + <1>
5) <2> + <4>
6) <3> + <1> + <1> + <1>
7) <3> + <3>
8) <4> + <1> + <1>
Получилось 8 вариантов наборов. Найдем их суммарное количество.
См. второй пикрил
Таким образом, ответ можно получить так:
См. третий пикрил
Первым способом я получил ответ 61776, а вторым способом 144612.
Почему ответы не сходятся? Помогите, пожалуйста, найти ошибку в моих рассуждениях. Может быть, во втором способе я забыл рассмотреть какой-то случай?
Я пробовал находить решения двумя способами, но почему-то ответы не сходятся. Помогите, пожалуйста, найти ошибку.
1 способ:
См. первый пикрил
Первую пару карт можно выбрать 13 способами, вторую - 12, третью - 11. Чтобы исключить наборы, отличающиеся только порядком делим на 3!
2 способ:
Пойдем от противного: найдем все варианты наборов из 6 карт, которые не удовлетворяют условию задачи:
<n> - набор из n карт одной масти
1) <1> + <1> + <1> + <1> + <1> + <1>
2) <2> + <1> + <1> + <1> + <1>
3) <2> + <2> + <1> + <1>
4) <2> + <3> + <1>
5) <2> + <4>
6) <3> + <1> + <1> + <1>
7) <3> + <3>
8) <4> + <1> + <1>
Получилось 8 вариантов наборов. Найдем их суммарное количество.
См. второй пикрил
Таким образом, ответ можно получить так:
См. третий пикрил
Первым способом я получил ответ 61776, а вторым способом 144612.
Почему ответы не сходятся? Помогите, пожалуйста, найти ошибку в моих рассуждениях. Может быть, во втором способе я забыл рассмотреть какой-то случай?
Сам попробуй тройку подставить и увидишь, что совсем другой икс получается
 10 Кб, 318x238
10 Кб, 318x238Анализ в ВУЗах нужен, чтобы отчислить здоровых людей и оставить дебилов, которые учат определения наизусть.
Возьми любой учебник и читай потихоньку. На лекции можешь нассать.
Я долбаеб, помощь больше не требуется
Никак, к математика это не относится.
Берешь какого-нибудь Лорана Шварца и читаешь. В наших ВУЗах преподают хуету, что она нихуя непонятна и нахуй не нужна в большинстве своём нигде вне аудитории универа.
>В наших ВУЗах преподают хуету, что она нихуя непонятна и нахуй не нужна в большинстве своём нигде вне аудитории универа
Примеры?
>анализ к математике имеет отношение очень посредственное
Анализ имеет много применений в реальности и поэтому отношения к математики он имеет огромное.
>применений
К математике отношения не имеет, это уже применения математики, а не сама математика.
Тем более анализ это вообще не математика изначально. Или физика тоже математика, раз она имеет применение к реальности?
Нет полной классификации этого (открытая проблема), узнать можно только в частных случаях. Например анализ не является математикой. Также любые применения математики вне математики по определению не математика.
>Например анализ не является математикой
Вот интересно, дауны в /math/ действительно так считают или это все же толстота?
>>6443
Функан это раздел теории ассоциативных алгебр.
Анализ же в смысле дифференциального и интегрального исчисления вещественных функций одной переменной, calculus то есть, это раздел коммутативной алгебры.
Комплексный анализ – раздел алгебраической геометрии.
Так что и calculus и analysis конечно, математикой являются, хоть и не очень интересной.
Алгебраическая к-теория, топологическая к-теория и алгебраическая геометрия. Это настоящая математика аспирантского уровня. Есть просто вузовская математика, например коммутативная алгебра, гомологическая алгебра, теория представлений. Наконец, есть школьная математика, например метрическая топология, алгебраическая топология и дифференциальная геометрия.
Математика аспирансткого уровня содержит интересные проблемы и темы для исследований. Математика вузовского уровня предоставляет язык, с помощью которого эти проблемы формулируются и некоторую базовую технику для работы в областях аспирантского уровня.
Школьная математика содержит базовые понятия, без которых невозможно понимание языка вузовской математики а так же некоторую мотивацию для его освоения.
Очень содержательный ответ. Как ты собираешься объяснять характеристические классы людям, которые не знают что такое многообразие?
Общая топология математикой уж точно никогда не была и не станет. К счастью у этого чудовища есть такой предшественник как метрическая топология (понятие метрического просиранства возникло раньше). Она же является и преемником, так как уже давно очевидно что формализм общей топологии это исторический курьёз, поворот не в ту сторону.
Ну до 30-х примерно никто не знал, по-моему. Пуанкаре и Эли Картан точно не знали. Гнать на них будешь?
Нет, они ещё уважаемые, но в такое время не знать это уже слишком.
Мое обучение полурандомно-полубессистемно, потому как я не знаю как правильно изучать математику. Мне мало вузовской программы, потому что вуз дает лишь куски.
Математикам не нужен конечно, но имеет приложения в машиностроении, геофизике и прочих областях. Если хочешь знать анализ, нужно хорошо изучить линейную алгебру (то есть всю науку про линейные операторы в конечномерных векторных пространствах, функциональный анализ отличается тем, что там пространства бесконечномерные и нормированные).
Начать можно с модулей, точных последовательностей гомоморфизмов, понятий коядра, кообраза и фактор-модуля, альтернативы Фредгольма и т.д.
Потом уже можешь читать про нормированные кольца и банаховы алгебры, например Гельфанда-Наймарка, это и есть пресловутый анализ.
В самом деле, книга похожа на дурно организованный справочник непонятно для кого.
Из oldies but goldies мне нравится Курант. У него довольно приятный, как по мне, язык.
Р. Курант: "Курс дифференциального и интегрального исчисления" в двух томах.
Шилов "Конечномерные векторные пространства", Хелемский "Функциональный анализ", Кириллов и Гвишиани "Задачи и теоремы функционального анализа".
Ещё бы Харди посоветовал тогда уж
Бурбаки не канают, теперь в моде посылать людей, нуждающихся в обычном калькулюсе, в топологию и функан?
Банаховы пространства - неправильная конструкция. Они допускают слишком много патологических частных случаев. И они не образуют никакой категории с хорошими аналитическими свойствами. Возможно, анализ и стоило бы строить без банаховых пространств.
Я это знаю, но любой дед с dxdy (специалистов по анализу думаю проще найти именно там) с тобой не согласится, а с
>не образуют категории
боюсь вообще засмеётся.
Про то что по существу анализ это про нормированные кольца и бесконечномерные ассоциативные алгебры, я уже писал выше.
Но другой контекст для калькулюса это гладкие многообразия, то есть дифференциальная геометрия, а это уже явно не "анализ".
Свои то мысли хоть есть или только копипасты?
В информатике ещё. Есть такой Шеннон, он теорию информации разработал.
В теории меры.
 22 Кб, 1118x234
22 Кб, 1118x234>Формула Стирлинга
ну и нахуй мне она упала, она там не к месту и вообще у меня тут вузовская математика, где таих сложностей не бівает.
Вот например, сколько денег дают за математическое открытие или теорию?
Я имею ввиду не математику с целью срубить ей бабла, а просто как факт. Т.е. может чел попутно ей занимается, а может ведет параллельно другие виды деятельности, типа бизнеса и благодаря этому богат.
Важен сам факт того, что данный чел занимается математикой ну или занимался хотя бы
помогите ради бога
Помоги найти вещественную и мнимую часть данного числа.
625x^4 +1 =0
Я вроде как вижу что b = 0, но онлайн калькуляторы говорять что мнимая часть есть, буду весбма признателен если ты мне поможешь.
Реши уравнение, у меня получилось 4 корня с разными комбинациями знаков у вещественной и мнимой части ±1/(5√2) ±i/(5√2)
Надеюсь, сам не налажал со знаками, ибо калькулятор выдал только 2 корня.
мимо ПТУшник
Как ты получил вещественную часть? У меня выходит после преобразований z = sqrt(2)/10
>Возможно, анализ и стоило бы строить без банаховых пространств.
Возможно, анализ вообще не стоило бы строить.
>dxdy
Не математика.
>с тобой не согласится
Смотри выше. На мнение не математиков в математике всем плевать.
Тут неверно.
>модулей, точных последовательностей гомоморфизмов, понятий коядра, кообраза и фактор-модуля
Не математика.
Г П Толстов Ряды Фурье.
Не математика спросить забыли что математика, а что нет. Буквально по определению всё, чем занимался Дедекинд, называется математикой. А Дедекинд как раз строил резольвенты и считал функторы.
Зависит от характеристики поля.
Если 0 не математика вообще, если положительное число – прикладная математика.
>прикладная математика
То есть "математика вне математики", или эквиваленто "не математика"? Зачем тут про это?
Не то есть. Прикладная математика это, например, коммутативная алгебра или теория категорий. Это просто области, имеющие большее значение как инструменты для других областей, нежели как области сами по себе.
 302 Кб, 576x768
302 Кб, 576x768Что тут писать?
 114 Кб, 570x245
114 Кб, 570x245Нашёл что-то про оре, и очень похожее свойство на то, которое я описал в посте. Говорят у него на этот случай теорема есть. Но не могу нагуглить. И ещё нужно то же самое, но не только для планарных графов.
 68 Кб, 1174x390
68 Кб, 1174x390Просто ты особенный, научись принимать себя таким, какой ты есть. Главное - твои старания, а не правильный ответ.
>сразу про R
Хуесоса сразу видно. Понятно, что ты не математикой занимаешься.
>Вычитай числа в R
Вычитание является функтором из категории (R, <=) с очевидными морфизмами в категорию R с одним объектом где морфизмы это элементы группы (R,+), композиция стрелок это просто операция группы.
>функтором из категории
>морфизмами в категорию R с одним объектом где морфизмы это элементы группы (R,+), композиция стрелок это просто операция группы.
Не математика.
Хорошо, то есть группы, частично упорядоченные множества и вычитание это не математика? Понял.
 274 Кб, 1318x741
274 Кб, 1318x741@
РЕШИЛ ПРОЛИСТАТЬ ТРЕД
@
БЕСКОНЕЧНЫЕ СРАЧИ О ТОМ, ЧТО МАТЕМАТИКА, А ЧТО - НЕТ
@
НИ НА ОДИН РЕКВЕСТ НЕТУ ОТВЕТОВ, А ЕСЛИ И ЕСТЬ, ТО ТАМ НАПИСАНО, ЧТО ТО, ЧТО ТЫ НЕ МОЖЕШЬ РЕШИТЬ - НЕ МАТЕМАТИКА
может уберем из шапки запись о том, что тут помогают?
Пыньки алгебраические заспамили тред. От интегралов триггеряться или от прикладной математики. А как их модули не математикой назвали, такой визг подняли! Вот такие пыньки модульные.
ПУЧК!
Т.е. все что не алгебра, то не математика по их мнению?
Но тогда еще больший вопрос: является ли алгебра математикой и почему.
На самом деле плохо быть алгеброкуколдом, еще хуже чем геометром: слишком сужает мышление, а в математике - это очень опасно даже для самих алгебраистов.
Фактически, они противоречат сами себе и “сами себе злобные буратино“, потому что не изучать “приложения алгебры“ - это неосиляторство и полное признание в неумении пользоваться инструментом. Фактически, алгеброкуколды расписалилсь в своей недееспособности.
*математической недееспособности
 375 Кб, 930x1024
375 Кб, 930x1024Ну не психуй. Вот дочитаю школьные учебники, потом господа Фихтенгольца с пророком его Демидовичем, и решу твою задачку про ряды.
А вообще есть добротред, десу.
>Т.е. все что не алгебра, то не математика по их мнению?
Такие вот пыньки алгебраические.
>является ли алгебра математикой и почему.
Пыньки говорят - Я ТАК СКОЗАЛ!
>Фактически, алгеброкуколды расписалилсь в своей математической недееспособности.
Ага.
У Арнольда.
>>6567
Алгебра отличается от анализа и прочего отюдь не предметом изучения, а методами работы и способом взгляда на вещи. Например, анализ, грубо говоря, задается такими вопросами как "сколько здесь всего?" или "с какой скоростью это меняется?"; основной вопрос алгебры же – "как это устроено?". При этом речь не обязательно о структуре (то есть описании взаимодействий объекта с другими объектами), в теории категорий изучается скорее "тип", можно взять циклическую группу как категорию с одним объектом, у которого все морфизмы это изоморфизмы, и тогда все аксиомы группы вытекают из определения категории.
Как хорошо замечено выше >>6548 вопрос "изоморфны ли две структуры?" имеет с категорной точки зрения столько же смысла, как вопрос "равны ли два числа?". Так что алгебра значительно шире, чем структурализм Бурбаков и Андре Вейля в частности, много упустившего из-за своей философии (определение схемы хотя бы, первый шаг из трех он сделал, но дальше идти отказался).
Ты говоришь про алгебру так, словно геометрия или анализ – не разделы алгебры и их изучение не сводится к изучению резольвенты модулей над каким-то кольцом. Что такое топологическое пространство, по-твоему, если не комплекс цепей на нём, снабженный алгебраическими структурами? Что такое алгебраическое многообразие, если не производная категория когерентных пучков на нём? Во всяком случае, именно так они изучаются и это приносит результаты, в отличие от наук "ради самих себя" типа общей топологии. Алгебра такой наукой не была никогда.
Если кто-то не любит алгебру, он просто её недостаточно хорошо знает. Что логично, алгебра это не тот предмет который удастся хорошо выучить, не полюбив в процессе. Гомологическая алгебра особенно.
На это еще забыл ответить
>слишком сужает мышление
просто неправда. В отличие от сомнительных способов думать, вроде "геометрической интуиции", алгебраический способ рассуждения доступен абсолютно каждому, да и внятных доказательств без него произвести невозможно.
Исторически, где не было алгебры, например в исследованиях Пуанкаре по топологии или в изучении проективных коник, кубик и квартик в Италии дв второй мировой, в половине работ или более находили ошибки, после чего их исправляли, выпуская работу, где уже содержатся другие ошибки и тд, а другую половину просто никто не читал.
>в половине работ или более находили ошибки, после чего их исправляли
А в классификации простых конечных групп такого не было?
Хинчин Цепные дроби.
И еще.
Вот допустим изучаю я дискретку, матлогику и теорию алгоритмов, к примеру - шишка в небеса, все ебать, другую математику больше не могу изучать да и как нахуй сосредоточиться на разных направлениях, иногда почти не пересекающихся?
Просто у меня получается, что я разное время любил разные разделы математики, но так и не пришел к тому, чего я хочу. Она прекрасна, но я не могу изучать ее всю нахуй.
Под всем математическим аппаратом ты имеешь всю "прикладную математику"? Но у неё нет чётких границ, следовательно, ты не получишь чёткого ответа.
Также ежу понятно, что разные прикладные задачи требуют разных комбинаций приложений математики.
Все твои кристаллизованные знания могут быть применены там, где ты описал - в преподавательстве и просвещении. И наверняка потребуется ещё больше, ведь плох тот препод математики, который игнорирует последний пункт...
...где "весь математический аппарат" применим к самой математике во множестве её проявлений и математических исследований. Так что можешь упарываться дальше и двигать вперёд матешу.
Ну вот смотри, сейчас я увлекся этими вашими гомологиями и С* и стал заднеприводным и вообще охуеваю сижу, в хорошем смысле.
Т.е. она слишком многогранная, разная, я не могу охватить мозгом все сразу, мне кажется я поехавший уже, потому что до этого дрочил дискретку, прямо мастурбировал на нее каждый день, а тут... новая богиня. И я не знаю что делать. Я постоянно меняю свои идеалы. И в итоге уже просто не хочу их иметь, поэтому иногда думаю вообще бросить матешу
Ну ты выбрал максимально далекие области, хули. Алгебраическая геометрия –> дифференциальная геометрия такого различия уже не будет.
В физике
>функтором
Хорошо, вычитание это не математика, я на самом деле согласен.
>категорию
Любая группа является категорией с одним объектом где все стрелки изоморфизмы, и наоборот. То есть группы это не математика?
>морфизмами
Я рад, что ты согласен, что функции это не математика.
Тот, с кем ты разговариваешь, этих слов тупо не знает, и думает что функтор это что-то логическое про синтаксис у Карнапа, категория это у множеств по Бэру, а морфизмы это из биологии.
lim (sin(11x)/sqrt(1-cos(x)), x - 0)
Я понимаю что sin (11x) ~ 11 x , но что делать дальше?
Я знаю что это матан. Но это тред для тупых вопросов, а я думаю что мой вопрос тупой.
Хорошо - хорошо, ты можешь помочь?
Нет, пределы из одной области математики не имеют ничего общего с твоими пределами. А про твои пределы тут скорее всего никто не знает, ведь мы интересуемся в основном математикой.
Все кроме тебя знают. Ты еще и сопряженные функторы небось не знаешь. Школу пропускать не надо было.
Вольфрамом сам пользуюсь, но у меня нет премиума, можешь подсказать как преобразовать sqrt(1-cos(x))
>Все кроме тебя знают.
Сомневаюсь.
>Ты еще и сопряженные функторы небось не знаешь.
Это из математики, так что знаю. Лично у Маклейна узнал ещё о них.
А, и плюс с каких книг/учебников начали бы.
 146 Кб, 600x619
146 Кб, 600x619>С гомологической алгебры
Как раз сейчас и занимаюсь её изучением. Дальше что делать?
>Топологическое пространство нужно представлять себе как комплекс модулей и не иначе.
Как мне узнать про то, как из топологического пространства получать цепные комплексы? Где это изучается?
Можешь вайлдбергера на ютубе посмотреть, он там камеру от автомобильного колеса симплициально разбивает веревками, наглядно. Вообще там учить много не надо, не велика наука, а сингулярные гомологии в любой книге по ГА определяются.
Не математика.
Это частный случай группоида. Группоид это категория, где все стрелки изоморфизмы.
Хотел было, но из-за отсутствия аргументированной позиции обоссал сам себя. Вечно всё не так с ненавистниками алгебры.
Я как раз обмазываюсь алгеброй, но в тоже время и дискреткой и анализом, и даже геометрией. И все ето чередую.
Пушто нельзя дрочить одну единственную область.
Тем более, что блять можно изучать в алгебре столько времени и нахуя? Почему блять алгебра-то, почему не, скажем, матлогика?
>но в тоже время
У тебя времени в принципе не хватит на глубокое изучение математики и какой-то левой хуйни за одно. Тут выбор - либо пытаться хорошо изучить математику, либо тратить время на всякие убожества по типу анализа.
>Пушто нельзя дрочить одну
Таким как ты без этого многого не достичь, сам ведь понимаешь.
>единственную область
Область чего? Явно не математики, раз ты анализ упомянул.
>Почему блять алгебра-то, почему не, скажем, матлогика?
Логика, как и большинство областей математики, это частный случай алгебры, так как они спокойно к ней сводятся (матлогика - это изучение (-1)-группоидов). Был бы ты не уебаном, то давно бы знал уже.
>Я как раз обмазываюсь алгеброй
Расскажи что-нибудь про неё, а то это сомнительно после твоего утверждения
>что блять можно изучать в алгебре столько времени и нахуя?
Окей, великий математик, тогда скинь хотя бы ссылку на развернутую интерпретацию жалкой матлогики богоподобной матерью-алгеброй, или алгебра такое говно не изучает? И группоиды для нее всего лишь - одно ссаное определение?
Про что конкретно рассказать?
Для меня алгебра была основой и дала наиболее общее представление о математике.
Я не вижу смысла изучать простые истины, в твоих глазах я все-равно буду теоретико-множественно-куколдом.
Кстати твоя ссанная алгебра была основана именно на теории множеств
Кстати, как по мне у тебя хватило мозгов осилить матлогику и основы, но люто горит от более высоких в переносном смысле уровней типа геометрии и ты замкнулся в алгебраическом манямирке, как старый сумасшедший профессор. Такая фанатичность и восхищает и в тоже время - пугает.
Тут даже группоиды не нужны не знаю где они вообще нужны кроме стэков, есть же булева алгебра, то есть алгебра над полем F(2), оно же кольцо вычетов по модулю 2 (a^2 = a).
Каждый элемент спектра в этом кольце, то есть простой идеал, является функцией, принимающей одно из двух значений.
Spec R содержит все высказывания, его подмножество M(p) – ,высказывания, для которых p истинно. Дальше точно такая же алгебраическая геометрия, как в случае алгебры многочленов над комплексными числами.
То есть те идиоты реально думают, что алгебра изучает только ограниченную часть математики, а вот дискретка или логика это не алгебра. Это лол просто, не знаю как ещё объяснить.
>Про что конкретно рассказать?
Про своё изучение алгебры.
>Для меня алгебра была основой и дала наиболее общее представление о математике.
Это само собой, так как алгебра это единственная область математики, которую ты изучал.
>Я не вижу смысла изучать простые истины
Не понял тебя.
>в твоих глазах я все-равно буду теоретико-множественно-куколдом
Ты им будешь ровно до того момента, пока не излечишься от этого. Благо сейчас это делается довольно легко, если ты конечно не совсем поражённый.
>Кстати твоя ссанная алгебра была основана именно на теории множеств
Это ничего не меняет, тогда альтернатив не было. Главное, что сейчас про эту хуету можно успешно забыть.
>>6628
>люто горит от более высоких в переносном смысле уровней типа геометрии
Про какую геометрию идёт речь? А то некоторые её "виды" разрешимы, так что являются частными случаями логики. И какие ещё есть примеры "более высоких уровней" математики?
>Сведение математики к алгебре - это утопия и манямирок
Всё, что является математикой (по определению) сводится к алгебре или к чему-то, что сводится к алгебре. Так что это тривиально.
>я готов измениться
Для чего тебе это только?
Ну и иди нахуй со своей алгеброй :3
Мне вообще поебать на математику, а для куколдовизуализации у меня есть матлаб и r
С радостью выгребу из ваших тредов годноту и придумаю как использовать. Продолжай разрабатывать свои манятеории, пока я наслаждаюсь компьютером
>Мне вообще поебать на математику
Это заметно, только такой идиот стал бы нести настолько тупую хуету.
>придумаю как использовать
Как ты собираешься использовать алгебру, когда ты её не понимаешь?
>Продолжай разрабатывать свои манятеории
Я продолжу, но вот ты их не сможешь воспринимать даже, ведь ты изучаешь какую-то хуйню, а не математику.
 38 Кб, 601x601
38 Кб, 601x601Почему ты такой жадный
Вот это маневры. Сначала >>6626 спрашивает интерпретацию, получив же, включает отрицание.
>>6627
>алгебра была основана на теории множеств
Голословный пиздеж. Наивную теорию множеств (а другая, вроде наработок Кантора по классификации бесконечностей, и не нужна) придумал Дедекинд, он же определил основные понятия алгебры (кольцо, идеал, модуль, поле). При этом кольца были как частный пример ещё у Гаусса (учителя Дедекинда), гугли гауссовых целые числа, а ассоциативные алгебры изучали Гамильтон, Грассман и Кэли. Линейная алгебра вообще начинается с Лейбница. Но в современном виде, как это изучается сейчас, появилось это только у Дедекинда.
Ты вместо того что бы пучкать, комиксы про Пыньку рисовал лучше
Стоит ли начинать с Алгебры Гельфанда и Шеня ?
1850-е ознаменовались началом стремительной экспансии алгебры под руководством Дедекинда, а когда в 1940-х подвезли ракетную артиллерию в виде гомологических методов, противостояние пришлось перенести с линии фронта в подполье, где партизаны с dxdy и преподы провинциальных МГУ НГУ вузов продолжают бороться против алгебры, как боролось Монтенегро против Османской империи.
Никто с ней не борется, наоборот хотят узнать.
Просто мало материала и не знают где или как искать
Сразу видно человека, который не пытался объяснить дидам, зачем изучать нормированные кольца вместо банаховых пространств и почему теория Фредгольма это естественное приложение гомологической алгебры. Книг про это немало было и в 70-х и я сомневаюсь что твои преподы о них не знают.
>>6645
Ну и генерал Бурбаки немало сражений выиграл, хоть так и не освоился с категорной доктриной ведения войны.
Извратить можно что угодно. Например определитель формулой, а не как скаляр у которого внешняя степень совпадает с эндоморфизмом (гомотетией); теорема о жордановой форме как утверждение о матрицах, а не о конечно порождённых модулей над кольцом главных идеалов, фактор-пространство не как точная последовательность, вообще векторные пространства вместо свободных модулей (над полями даже нет сизигий, зачем там линейная алгебра?).
Если было что-то из этого, ты как раз попал в руки к албанским партизанам, бессмысленным и беспощадным.
elementary theory of the category of sets
Спектральная последовательность Дирихле-Кронекера например, сам ей пользуюсь. Купил даже тетрадку специальную где страницы на два столбца, чтоб удобнее считать. Ничего не записываю конечно, мысленно в основном, тетрадь дорогая.
Я сам пользуюсь спектральной последовательностью Дедекинда-Эйленберга, тоже специальную тетрадку купил.
Ох и криво написал. Эндоморфизм это и есть матрица, для него определяется внешняя степень.
A – свободный модуль над R, f: A–>A эндоморфизм, f называется гомотетией если найдётся λ из R, что f(x) = λx. Если кольцо коммутативно, каждый его эндоморфизм это гомотетия.
Берем внешнюю степень, гомотетия сохраняется, тогда λ это детерминант f.
Вменяемо это излагается только на русском по крайней мере у Бурбаки в первом томе линейной алгебры, даже у Дьедонне путь про кососимметрические билинейные формы, внешней степенью он не пользуется, что уж говорить про остальных.
модульный дедекинд
Стренг, линейная алгебра и её применения.
Пиздец он поехавший.
С другой стороны: вдруг это новый мессия.
Кстати, теория алгебры развилась вокруг tyanochki -Эмми Неттер, которая не давала свою писечку пиздолисам, вынуждая их придумывать новые угодные ей теории
Что прямо свидетельствует об окуколдивании ВСЕЙ алгебры примерно с 1916 года
…It owes its existence to Emmy Noether, who used to say that “it's already in Dedekind.”
John Stillwell, Mathematics and it's history.
Noether*
>вынуждая их придумывать новые угодные ей теории
Хикккны в очередной раз пытаются втиснуть реальность в свой личный опыт. Пруфы? Кто придумал больше самой Нётер и Гильберта? Или это Гильберт пиздолиз? А то что баба, ну так напомни кем был её отец. Сестра Эли Картана тоже математиком стала, чисто под влиянием брата, которого толком и не видела, а тут не только братья, ещё и папа тоже.
Представляю как рвало шишку студентам и всем куколдам вьющимся вокруг нее, что ее аж с разных сторон в университеты приглашали
Как?
Извини, но это не он.
В sci computer science тред мёртв, а програмисты в это не могут. Думаю здесь есть те, кто в этом шарят.
Метод монте-карло называется, кажется. Заключаешь кусок, который надо проинтегрировать, в прямогульную область. В этом прямоугольнике расставляешь точки, желательно не рандомно, а чтобы они равномерно покрывали область; чем больше, тем лучше. Находишь отношение точек, который попали под функцию к общему количеству точек. Умножаешь это отношение на площадь прямоугольной области. В теории сложность константная. Точнее зависит от числа точек, а не функции.
Бля точно. Что-то ступил. Я помнил, что этот метод находит площадь под графом, но забыл, что именно это и есть определённый интеграл. Но чтобы построить прямоугольники нужно уметь находить производную функции и её нули т.к. Интеграл может быть отрицательный. Риманова сумма может быть даже быстрее в функциях, который часто меняют знак типа синуса. А какие ещё есть варианты?
Есть еще пара вариантов, но они не проще. Разные методы лучше работают для разных типов функций. Подбирай под свою.
>>6680
Забыл ссылку.
https://en.wikipedia.org/wiki/Numerical_integration
К слову, в мл-треде в pr советовали книжку по численным методам от МГУ. Почитай.
А можно побольше подобной литературы чтобы был выбор? Вообще если можно програмно найти производную, то самый эфективный способ это разложить в ряд маклорена. Но чтобы избежать мучений придётся писать на питоне. И это понизит производительность, а значит даже монтекарло может оказаться быстрее. Глаза разбегаются не знаю что выбрать.
А что тебе даст ряд Маклорена? Он же дает лишь приближение функции полиномом в окрестности какой-то одной точки. Или я не прав?
Как вообще интегрировать, и что именно интегрируют? Я посмотрел на значки интеграла и тоже захотелось узнать, хоть это и не математика конечно. Просто порисовать хочу значки.
Тебе нужно будет неопределенный интеграл взять в этих двух точках. Ну попробуй, не думаю что это окажется быстрее. Численно брать n-ю производную, кстати, как будешь?
Спасибо конечно, но мне сейчас именно не математика нужна.
Брать следующуюследующую производную должна уметь библиотечная функция. Посчитать её нужно будет n раз. Это быстрее чем кидать миллион точек.
А ты уверен? Ты в сложности алгоритмов шаришь? Знаешь, какова сложность взятия производной? А какова сложность нагенерить миллион точек?
Произведение цепи на коцепь.
5000 (module 1488)
 358 Кб, 1080x1920
358 Кб, 1080x1920>Ты в сложности алгоритмов шаришь?
Походу экспанента т.к. каждый следующий шаг даёт ещё 0 1 или 2 дополнительных шага. Но я сомневаюсь, что 10 раз взятт производную сложнее чем набросать миллион точек
>есть абстрактные символы, операции, формальная логика
Будто в интегралах такого нет. И что такое математика - открытый вопрос, не надо тут выслушивать нытьё категорных пынь. Модульный Дед вообще с dxdy сюда припёрся, подавленную агрессию на дидов тут вымещает, больной человек. Там он со своими модулями под шконарём сидел, а в /math пришел, королём чуханов стал!
пиндосы тупые потому что
Если ты имеешь ввиду именно изучение этих языков, а не просто программирование на них - то да, это частный случай теории категорий.
>И что такое математика - открытый вопрос
Полная классификация и вопрос разрешимости действительно открытый, но уже известно, что интегралы и анализ в целом ей не являются. Это стало известно ещё с появления интегралов на самом деле.
И второй вопрос: мне тут затирали, что опытные математики быстро учат языки и чуть ли не за день осваивают вторую науку. Разъясните по хардкору в чем правда, в чем ложь
Это открытый и очень сложный вопрос.
Наука тоже никогда не пользуется научным методом на практике, любой претендующий на метод набор рекомендаций либо бессодержателен, либо противоречит историческим прецедентам. Это хорошо показали Кун и Фейерабенд.
Математика является наукой, поскольку за неё дают в ноги гранты. Любую дающую гранты деятельность корректно называть наукой, поскольку наука всегда была институциональным явлением.
>>6754
Если профессиональный математик осваивает науку за полгода, эта наука говно, хорошую науку осваивают лет двадцать. При чем в математике любая деятельность за десять лет устаревает безнадёжно, так что никакую из хороших наук освоить вообще невозможно, в этом и состоит критерий.
>Наука тоже никогда не пользуется научным методом на практике
Я понимаю, поэтому я и не называю её "наукой".
>Математика является наукой
Я бы ей не занимался в таком случае, так что у тебя где-то явно ошибка.
>Любую дающую гранты деятельность корректно называть наукой
Это уже подмена понятий, меня такое не интересует.
Понятие одно и то же, просто определения разные, при чем моё больше приближено к реальности, особенно в рф.
Например вот вариант Посицельского:
В порядке усиления требований:
1. У теории должны быть интересные примеры.
2. У теории должны быть приложения к чему-то, ранее существовавшему.
3. Теория должна доказывать какие-нибудь ранее не доказанные естественные утверждения, в формулировки которых входят только определения, существовавшие до появления теории.
4. Теория должна доказывать ранее сформулированную гипотезу, которая не имела доказательств до появления теории.
Моя точка зрения попадает где-то между 1 и 2, условие 3 мне кажется слишком сильным. В то же время, конечно, если теория удовлетворяет 3 или 4, это говорит в ее пользу. Теория, не удовлетворяющая ни 1, ни 2, представляется не заслуживающей интереса.
Ничего не понимаю. Мне завтра решение сдавать, а доказательства достаточности всё ещё нет. Помогите
Помогите плиз решить задачу по терверу. У меня получилось, что второй стрелок за 10 выстрелов попадет с вероятностью в приблизительно 65%, за 9 - 61%. А дальше от чего плясать?
"Идет дуэль двух стрелков. Первый попадает в цель с шансом 100%, и наносит 1 ед. урона каждым выстрелом. Второй попадает в цель с шансом 10%, но при попадании наносит 10 ед. урона. Кто победит, если у обоих стрелков по 10 ед. здоровья и они стреляют по очереди?"
>В математике "научного метода" кстати больше в разы
Если так, то математика это хуйня. Очевидно, что это ведёт к противоречию.
Теория вероятностей — раздел математики, изучающий: случайные события, случайные величины, их свойства и операции над ними.
>>6767
Не гори. Любая хорошая деятельность типа Гротендика, Делиня, Квиллена, Марина, Аракелова и тд этому требованию удовлетворяет, а любая общая топология, универсальная алгебра, венгерская комбинаторика, оценки ассимптотик и тд нет. Значит требования удачные. В физике, замечу, такое не прокатит и требования либо неадекватные практике, либо они ничего не требуют.
…изучающий взаимодействия одного специального вида лептонов.
>Любая хорошая деятельность типа Гротендика, Делиня, Квиллена, Марина, Аракелова и тд этому требованию удовлетворяет, а любая общая топология, универсальная алгебра, венгерская комбинаторика, оценки ассимптотик и тд нет.
Я этого и не отрицал. Но из-за этого нельзя утверждать, что твои требования не нужно сразу нахуй слать.
>Значит требования удачные.
Мышление уровня физики.
>В физике
Дальше не читал даже. Сразу ясно, что с животным разговариваю.
>Манина
Ебучая автозамена
>>6775
Ты понимаешь что такое "научный метод"? Это чисто описательная штука, суммирующая представления о первой культуре в более внятной форме.
Физика это прикладная математика по сути, например квантовая механика это прикладная линейная алгебра, а стандартная модель это раздел теории представлений. Вообще любая человеческая деятельность это раздел математики, математика раздел алгебры, а алгебра раздел алгебраической к-теории.
>математика раздел алгебры
Воу. Хуя у тебя манямирок.
>а алгебра раздел алгебраической к-теории.
Пиздос.
>Ты понимаешь что такое "научный метод"?
Да. И я вижу, что в математике он не используется, что хорошо.
>Физика
Дальше не читал. Прости, не интересует хуета для животных, хоть я и понимаю, что она сводится к математике (алгебре). Как и в принципе многие вещи, если не все.
>Воу. Хуя у тебя манямирок.
Но он ведь прав.
>Пиздос.
Ты ведь ничего про неё не знаешь, промолчал бы лучше.
>Но он ведь прав.
У вас коллективный манямирок. Комбинаторика, например, тоже математика. А алгебра просто один её раздел, такой же, как комбинаторика.
вообще пиздос, ты почитай выше посты
>У вас коллективный манямирок.
Это уже называется "реальность", а не "манямирок".
>Комбинаторика
Раздел алгебры.
Конкретно этот нет, но мне понравилось как написано, поэтому и привёл. Вообще в голове у любого математика, знающего что такое профессиональная этика и интеллектуальная честность, есть представления о подобных требованиях, хоть и конкретная запись отличается.
>Раздел алгебры.
https://ru.wikipedia.org/wiki/Комбинаторика
>Комбинаторика (комбинаторный анализ) — раздел математики
https://ru.wikipedia.org/wiki/Алгебра
>Алгебра (от араб. اَلْجَبْرْ, «аль-джабр» — восполнение[1]) — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Вот-это манямирок.
>называет всех животными
>сводит ВСЕ к алгебре
По твоей логике так-то и мы - часть алгебры, геометрокуколд
А к-теория - вообще какой-то там ссаный подраздел
>геометрия
Какая именно геометрия, Евклидова? Аксиоматика Тарского разрешима, так что сводится спокойно к логике.
>топология
Да, вся математическая топология сводится к алгебре, так что является её частью.
>>6786
Животные (физики) тоже могут заниматься частью алгебры, алгебра довольно богата разделами.
>анализ
Не математика.
>>Алгебра (от араб. اَلْجَبْرْ, «аль-джабр» — восполнение[1]) — раздел математики
Всё тривиально является разделом себя, это понятно. Зачем ты это запостил?
Ну математика это наука о модулях над кольцами, в алгебре же бывает изучают категории, не являющиеся абелевыми.
Ну не траль
>Не математика.
Пынь, глаза протри. Анализ - раздел математики, алгебра тоже её раздел.
>Всё тривиально является разделом себя, это понятно.
Пынь, ну хватит быть таким тупым. Алгебра просто раздел математики, как комбинаторика, или диффуры. Иди интеграл возьми, не позорься.
>Анализ - раздел математики
Но это ведь не так, он никогда не являлся математикой и не будет ей являться.
>Алгебра просто раздел математики
Да, алгебра тривиально раздел алгебры.
>Иди интеграл возьми
Что такое "интеграл"? Точно не из математики.
>Но это ведь не так, он никогда не являлся математикой и не будет ей являться.
https://ru.wikipedia.org/wiki/Математический_анализ
Математический анализ (классический математический анализ) — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное[⇨] и интегральное[⇨] исчисления.
>На классическом математическом анализе основывается современный анализ, который рассматривается как одно из трёх основных направлений математики (наряду с алгеброй и геометрией). При этом термин «математический анализ» в классическом понимании используется, в основном, в учебных программах и материалах[1]. В англо-американской традиции классическому математическому анализу соответствуют программы курсов с наименованием «исчисление» (англ. Calculus).
Пыня, ты как Рыбников, в маня-мирке сидишь.
>Да, алгебра тривиально раздел алгебры.
Алгебра собственное подмножество математики.
>Что такое "интеграл"? Точно не из математики.
Я и говорю, тебе, Пынька, надо перестать таким тупым быть.
>Анализ это не математика.
>Это алгебраическая к-теории. Остальное – разделы алгебры. Но не все из её разделов это математика.
Это потому что ты так скозал?
1) Ты не прочитал, либо не понял, что он написал. Утверждений там было два
а) это контекстуальное определение (что совершенно очевидно)
б) данное определение ничем не лучше определения математики как науки о пучках
Знающий человек поймет о чем речь: проективные модули эквивалетны локально свободным когерентным пучкам. Прочесть об этом можно в "коммутативной алгебре" Бурбаки.
>википедия
Хорошо. Понял тебя.
>подмножество
Тут никто не говорил про множества.
>перестать таким тупым быть
Меня особо не интересуют вещи за пределами математики.
>Хорошо. Понял тебя.
А что, мнение Пыньки с двачей значимей википедии?
>Тут никто не говорил про множества.
А как тебе тупому объяснить, что алгебра просто раздел математики, но не является ей? Вот аналогия хорошая.
>Меня особо не интересуют вещи за пределами математики.
Если ты даже интеграл не можешь взять, то какая тебе математика, Пынь?
Да, или просто "подраздел алгебры, изучающий в основном замкнутые моноидальные категории".
>значимей википедии
Да практически что угодно значимей википедии.
>что алгебра просто раздел математики, но не является ей
Неверно.
>Если ты даже интеграл не можешь взять
Это в математике не нужно, я же ей каким-то образом занимаюсь.
>Да практически что угодно значимей википедии.
И при этом википедия имеет значимость больше вскукареков алгебраического петуха с двача. Будем следовать ей.
>Неверно.
Википедия с тобой не согласна. Так, что неправ ты.
>Это в математике не нужно, я же ей каким-то образом занимаюсь.
Интегрально исчисление - математика.
>алгебраического петуха
Можешь сразу писать "математического петуха".
>Википедия с тобой не согласна.
Это уже хороший повод задуматься о моей правоте.
>Интегрально
Уже не математика.
>Можешь сразу писать "математического петуха".
Алгебраического, Пынь. Алгебраического.
>Это уже хороший повод задуматься о моей правоте.
Скорее о твоей неправоте.
>Уже не математика.
И чего ты раскудахтался?
Интегралы это не математика.
Интегралы от дифференциальных форм это алгебра.
Не являющиеся таковыми интегралы от кривых и тд, это алгебраическая к-теория.
>Алгебраического, Пынь. Алгебраического.
Ну да, с точностью до изоморфизма, что я уже объяснял выше.
>И чего ты раскудахтался?
Прости, не понимаю твоего языка.
>Ну да, с точностью до изоморфизма, что я уже объяснял выше.
Математика - не алгебра.
>Прости, не понимаю твоего языка.
Ты много чего не понимаешь, с твоим курином мозгом. Иди интегралы брать!
>Ты много чего не понимаешь
Действительно, особо часто это происходит с вещами за пределами математики, в них я не особо силён.
http://ikfia.ysn.ru/images/doc/mat_analiz/Fihtengolc_t1_1962ru.pdf
>>6826
А чего ещё ожидать от алгебраического петуха? Весь тред засрал! И воздух испортил!
За пределами алгебры только мотивы, p-адическая теория ходжа и прочие разделы алгебраической к-теории, один из которых алгебра.
Ну конечно, а теоретическая физика это раздел цитологии, у атома ядро и у клеток тоже. Не надо говорить чушь, математика это раздел алгебры, анализ раздел алгебры, но анализ – не математика. Так было ещё со времён Дедекинда.
А теперь сделай
>ctrl+f "интеграл"
и занимайся математикой.
>>6831
> Не надо говорить чушь, математика это раздел алгебры, анализ раздел алгебры, но анализ – не математика.
Это потому что ты так сказал? Википедия > чем твоё мнение.
>Дедекинда.
Дал бы ему расширить твоё кольцо его порождающим элементом?
Алгебраические петухи это любители математики, которые не любят анализ? Думаю тут таких много.
Вот специально для аналитических пынек, список разделов алгебраической к-теории с википедии:
К-теория полиномиальных расширений
К-теория формальных степенных рядов
К-теория эндоморфизмов
Примарная к-теория
К-теория автоморфизмов
К-теория дедекиндовых колец
К-теория функциональных полей
Мотивные когомологии
Теория пересечений
Смешанные мотивы
Топологические гомологии хохшильда
Топологические циклические гомологии
Л-теория расширений Лорана
Ассиметрическая л-теория
Изометрическая л-теория
Почти симметрическая л-теория
Л-теория полей и рациональной локализации
Алгебра
Список разделов алгебры надо?
Ссылку специально не привожу чтобы не сломалась кодировка, это из википедии на кхмерском, в англоязычной материала мало по этим темам.
дед
Давай ссылку, гомологокуколд, потому что все твои маня-теории - не более чем подразделы гомологической алгебры и куколдологии
призываются специалисты по интегрированию.
 58 Кб, 512x767
58 Кб, 512x767https://ru.wikipedia.org/wiki/Открытая_книга_(топология)
>многообразия
>топология
Твоя куколдология дальше своего манямирка так и не вышла.
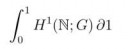 7 Кб, 381x150
7 Кб, 381x150G - произвольная группа.
>>6864
Я вижу ты специалист по анализу. Поможешь мне?
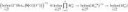 10 Кб, 1035x103
10 Кб, 1035x103Большинство бытовых предметов являются топологическими пространствами и даже многообразиями.
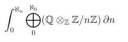 12 Кб, 553x185
12 Кб, 553x185Кто-нибудь поможет мне его решить?
Интегрирование на недостижимых кардиналах это новый раздел не\математики. Открытая проблема.
Если ты скажешь, как умение решать интегралы и выводить формулы, точнее даже сами все многочисленные формулы можно использовать в повседневной жизни и вне математике, я, возможно и помогу тебе. Потому что я ненавижу всю школьную математику и университетскую тоже. И задачи, которые не дают ничего, кроме умения решать их.
holim тут это гаматапический копредел?
Я без понятия. Меня в данный момент интересует вычисление выше заданных интегралов. Про них я сам ничего не знаю.
Вернее даже так: где я могу применить блядскую алгебру правила вывода, формулы -
вот это все или хотя бы анализ в повседневной жизни. Для решения бытовых задач.
Кроме картофана уровня "оптимизировать время производства носовых платков"
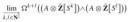 14 Кб, 1019x180
14 Кб, 1019x180абелевы диаграммы*
 25 Кб, 1477x205
25 Кб, 1477x205Я слышал, что этот человек сильно увлекается гипотезой Римана, так что может решение этого интеграла с ней как-то связано?
>>6875
Не понял вопрос. Мне нужно просто решение интеграла.
Что?
Натуральные числа. Определения графа. Индукция. Всё, что можно прочитать в учебнике розена.
Ты точно уверен, что тут опечаток нет? Твоя проблема сводится к открытому вопросу в теории гомотопий.
Для решения твоего вопроса нам нужно ввести понятие ядра гомоморфизма графов. Нужно искать подходящий функтор из категории графов в категорию (абелевых) групп (или хотя бы моноидов, там уже имеются нужные функторы), вы их изучали уже?
Ничего из этого не понимаю. Картинка на википедии напоминает функции. Injactive, surjective и всё такое. У розена книга с введением в дискретку. Поэтому только базовые определения знаю. И вообще я не уверен, что т описал термины из дискретки.
>Картинка на википедии
Картинка чего?
Нам нужен подходящий способ взять граф и "сделать из него" группу, так как у гомоморфизмов графов нет ядра.
>И вообще я не уверен, что т описал термины из дискретки.
Что подразумевается под дискретикой?
 100 Кб, 666x495
100 Кб, 666x495>Картинка чего?
пик
>Нам нужен подходящий способ взять граф и "сделать из него" группу, так как у гомоморфизмов графов нет ядра.
А можно то же самое, но без групп? Множествами и релейшинами может?
>Что подразумевается под дискретикой?
То, что проходят в курсе дискретки. Они везде разные разве?
>А можно то же самое, но без групп?
Посмотри определение моноида, это попроще групп. Короче, нужен способ взять граф и сделать моноид "похожий" на него. После этого уже можно считать гомологии, через них твоя проблема решается довольно легко.
>курсе дискретки
"дискретика" сводится к алгебре.
>"дискретика" сводится к алгебре.
Чтобы её свести надо знать алгебру. А чтобы учить дискретку алгебру знать не обязательно
>Посмотри определение моноида, это попроще групп. Короче, нужен способ взять граф и сделать моноид "похожий" на него. После этого уже можно считать гомологии, через них твоя проблема решается довольно легко.
Ну из программирования моноид это такая операция у которой скобки не важны и нейтральный элемент есть. Типа + или *. Но я в этом не разбираюсь и не умею пользоваться.
>А чтобы учить дискретку алгебру знать не обязательно
Дискретика по сути является разделом алгебры, как и многие вещи в математике.
>моноид это такая операция у которой скобки не важны и нейтральный элемент есть
Точнее множество с таким элементом и операцией, где скобки не важны. Вот нам нужен способ превращения графа в моноид, дальше уже есть методы переноски этих конструкций в категорию абелевых групп, а там уже можно считать гомологии.
>Дискретика по сути является разделом алгебры, как и многие вещи в математике.
Именно. Поэтому я хочу решить задачу используя термины дискретки и не выходя в прочую алгебру
> Точнее множество с таким элементом и операцией, где скобки не важны. Вот нам нужен способ превращения графа в моноид, дальше уже есть методы переноски этих конструкций в категорию абелевых групп, а там уже можно считать гомологии.
А потом что? Может смогу интуитивно понять твоё решение не вникая в термины.
>способ превращения графа в моноид
>Множество всех конечных строк с элементами из алфавита Σ образует моноид, обычно обозначаемый Σ∗. Операция определяется как конкатенация строк.
Может назвать его вершины буквами и типа будет алфавит, а дальше вот. Так можно сделать?
Лучше не использовать для доказательства термины выходящие за пределы дискретки. А лучше даже не выходить за теорию графов. Я уверен, что в тиории грфов достаточно определений и следствий из них чтобы решить эту задачу
Но не повредит ли изучение математики моей духовности и pravoslavno ли это? Говорят, что математика - это от Дьявола!
>Injective, surjective и всё такое
Ну все правильно.
kernel -- how much it fails to be injective
image -- how much it fails to be surjective
>Отображение с нулевым ядром называется мономорфизмом (иначе: вложение), отображение на весь модуль — эпиморфизмом (стягивание)
ded
Савватеев православный математик, глубоко верующий человек.
Сап. 9 классник в треде. Так получилось, что до 8 класса пинал говно, и нихуя не учил. За 8 класс я еле-еле начал понимать алгебру, а с геометрией застой.Я вроде выучу теорему, а применить не могу. Решил повторить все темы с 7-9 класс, уже половину точно выучил, хочу спросить, как лучше это все закрепить. Тупо задачи решать>?
Не могу зделать функцию из графа. Там же из каждой вершины больше одного ребра выходит. Поясни что за функция нужна?
В. И. Арнольд. Обыкновенные дифференциальные уравнения.
В. В. Степанов. Курс дифференциальных уравнений.
М. В. Федорюк. Обыкновенные дифференциальные уравнения.
М. В. Федорюк. Дифференциальные уравнения с частными производными.
Р. Курант. Уравнения с частными производными.
В. И. Арнольд. Лекции об уравнениях с частными производными.
А. Зоммерфельд. Дифференциальные уравнения в частных производных физики.
 73 Кб, 486x475
73 Кб, 486x475Спасибо.
Действительно. Группы не математика.
 42 Кб, 618x461
42 Кб, 618x461Нашёл решение почти без всяких сложностями с квазигруппами и прочими сложными терминами. Всё на примере графов поясняют. Но формат призентации сложно понять. Хотелось бы статью или книгу. Смотрел статьи сколема и боза. Там графы даже не упоминаются. Киркмана не нашёл. Что можно почитать чтобы это поясняли терминами из теории графов как в этой презентации?
https://team.inria.fr/coati/files/2017/04/JCALM_Presentation-Fionn.pdf
Не математика же.
Fn = Fn-1 + Fn-2
Зачем нужны эти "n-1" и "n-2"? Как будет выглядеть практический пример?
это обозначения номеров предыдущего и предпредыдущего членов. самый первый, n=1, F1, равен единице. второй F2=F(2-1)+F(2-2)=F1=1. F3=F2+F1=2, F4=F3+F2=3 и тд
Спасибо. То есть эти "n-1" и "n-2" нужны только для первых чисел (F1, F2)?
Да, вкатывайся.
Ни в коем случае не вкатывайся.
ZF нахуй не нужна.
>можно ли начать читать HoTT book без каких то предварительных знаний
Можно. Она с учётом этого и писалась.
Можешь и с http://www.cs.cmu.edu/~rwh/courses/hott/ начать, там как раз по началу довольно неплохо разбирается теория типов, на которой и "основана" HoTT.
Бамп.
 1,6 Мб, 3024x4032
1,6 Мб, 3024x4032Сделай замену t=y' и решай, как квадратное.
А вообще y'=y/(b-y)
>науку
Ты хочешь намекнуть, что математика на самом деле хуйня уровня физики? И зачем ты тут сидишь тогда?
>теории множеств
Можешь просто рисунки алефов ебашить на листочке. Это и есть так называемая "теория множеств".
Я серьёзно, просто рисуй значки алефа и рисуй буквы "AC", это и есть теория множеств.
Да, я серьёзно.
Да, это так. А что именно у него читать, сам выберешь.
https://www.mccme.ru/free-books/gerasimov-3ed-mccme.pdf
http://ikfia.ysn.ru/images/doc/Drugie_knigi_po_matimatike/KuratovskijMostovskij1970ru.pdf
Да не, я не из-за них, просто, например, сравни вот с этими двумя учебниками. Это нормально, что те книжки такие тонкие? Почему-то кажется, что там далеко не всё. Можешь с этими сравнить опытным глазом?
>Это нормально, что те книжки такие тонкие?
Вполне, на рисование различных теоретико-множественных значков много бумаги обычно не уходит, особенно если уже опытный (как авторы тех книг).
>абелевы диаграммы
Хуйня, лучше бы поставили туда значок алефа или гимеля.
А карточные масти это конечно круто.
>Бульканье — невразумительное изложение булевой алгебры. Булева алгебра — наука
о разливании бутылок по количеству содержащихся в них булек. Булька — крупная капля
или пузырь, глобула, шарик, мячик, клубок, бусина, снежок, биток, катышек, четка, шишка,
желвак, комок, клубень, луковица, (круглая) пилюля, или любой другой небольшой предмет
круглой формы. В русском языке широко представлены однокоренные слова: булла, булава,
бульба, булочка, булавка, булыжник, бульон, пуля, баллон, баллотироваться, волдырь (булдырь)
(сравни также латинское pila, bulla, bullire, bolus, французское boule, итальянское bolla,
palla, немецкое Ball, Bolle, английское ball, bullet, boulder, pill, pellet, голландское puyl,
литовское bul`ıs, санскритское bul´ıs . и т.д.) Поэтому оставим на совести Фассмера заявление,
что булькать представляет собой заимствование тюркского звукоподражания буль-буль или
буль-муль. По свидетельству крупнейшего отечественного специалиста в области булевой
алгебры Венечки Ерофеева в правильно разливаемой стандартной бутылке водки ровно 39
булек
Лол блядь. Я нашёл свой учебник короче.
>теория множеств
И зачем тебе эта хуйня? Она к математика особого отношения не имеет.
Ещё наверняка имеется ввиду не структурная теория множеств.
Хуй знает, я так решил, что надо математику изучать с логики и теории множеств, пушо они самодостаточны, а остальные разделы на них ссылаются как ни крути.
Ты не видешь, что тебя троллят? У нас тут завёлся срущий петух, который срёт в треде ЭТО НЕ МАТЕМАТИКА! Засрал весь тред. Игнорь его.
>с логики
Так с логики или математической логики? Это разные вещи.
>остальные разделы на них ссылаются как ни крути
Разделы чего? Разделы математики обычно не используют ZF и прочие ущербные формализмы с глобальным предикатом принадлежности.
Математической.
>Разделы математики обычно не используют ZF и прочие ущербные формализмы с глобальным предикатом принадлежности
Что?
>Ты же говорил Шень норм.
Там задачи и есть. У Вавилова есть "Краткий путеводитель по литературе", там и посмотри, что читать.
>И то же самое про теорию множеств
Теория множеств это рисование значков - алеф, бет, гимель, маленькая каппа, маленькая лямбда и так далее. Просто ищи в гугле картинки по их рисованию и распечатай, вот тебе и учебник по теории множеств.
Просто я не хочу потратить время, а потом окажется, что я дрочил основы и не более. Теория множеств вроде законченный раздел, я надеялся, что там можно как-то её осилить и затем двигаться дальше, а тут такая россыпь и хз что брать.
>>7041
То есть Шень это задачник, так? А по Вавилову учиться можно. Ну вот ты, анон, ты же как-то её изучал? А по логике? Непонятно, блджад!
>>7042
Не траль, плес.
>Просто я не хочу потратить время, а потом окажется, что я дрочил основы и не более
Ты хочешь с нуля сразу в продвинутую ТМ?
Нет, хочу огромный толстый учебник, где есть как ентрилевел, так и адвансед. Неужели такого нет?
 55 Кб, 541x480
55 Кб, 541x480>я надеялся, что там можно как-то её осилить и затем двигаться дальше
Двигайся дальше именно в той области математики, которая тебя интересует.
>>7043
>плес
Я же серьёзно. Для математика эти вещи действительно одинаковые, если тебя не интересует именно изучение теории рисования алефов.
Вот кстати неплохой учебник.
>То есть Шень это задачник, так? А
Там много задач.
> Ну вот ты, анон, ты же как-то её изучал?
Читал Александрова "Введение в теорию множество и общую топологию". Можешь и эту книгу посмотреть.
Вот, например. Этот хороший учебник?/
https://logic.wikischolars.columbia.edu/file/view/Jech,+T.+J.+(2003).+Set+Theory+(The+3rd+millennium+ed.).pdf
>>7046
Я бы рад, так там всё на языке теории множеств.
>теорию множество
Не нужна.
>общую топологию
Может лучше любой из разделов математической топологии?
Я английский знаю нормально если что, это не проблема.
Вот только черта с два ты по этому учебнику чему-нибудь научишься. Он написан чисто ради удовлетворения шизы автора. Все эпиграфы, кстати, выдуманные.
>так там всё на языке теории множеств
На языке наивной теории множеств, рисование алефов и гимелей в математике обычно не нужно.
Вот ещё один учебник хороший - https://www.amazon.com/Learn-Hebrew-Fun-Easy-Way-ebook/dp/B009MLLVCO
Да вроде заебись описано всё как раз, лаконично и тд. А задачи самому найти можно отдельно.
Ну теоркат в математике как ТМ в нематематике, так? Ту же функцию выполняет. Ок, а матлогика? Это математика?
Так че, может есть смысл вкатываться сразу в теоркат?
Вот и Вавилов такого же мнения.
Теория множеств не является единственнымым способом мыслить математические объ-
екты и в чисто фактическом плане. Теория категорий является не только реальной аль-
тернативой теоретико-множественному мировоззрению, но и гораздо более общей точкой зре-
ния. Уже сегодня многие алгебраисты и топологи владеют теоретико-категорным языком
столь же хорошо, как – или лучше, чем теоретико-множественным. Недавно я с изумле-
нием заметил, что единственный способ вспомнить определение эквивариантного отображе-
ния f(gx) = gf(x) состоял для меня в том, чтобы нарисовать соответствующую коммута-
тивную диаграмму. Любое современное изложение теории множеств должно подчеркивать
теоретико-категорные понятия и конструкции и готовить студента к переходу на категорный
язык.
• В действительности теория множеств и теория категорий являются лишь первыми дву-
мя членами бесконечной иерархии теорий. Говорить о множестве всех множеств не только
нельзя, но и бессмысленно, полезно рассматривать категорию множеств. Точно так же,
бессмысленно рассматривать категорию всех категорий как категорию – категория всех ка-
тегорий представляет собой 2-категорию, морфизмами которой являются функторы, а 2-
морфизмами – естсественные преобразования функторов. Теория множеств описывает объек-
ты, теория категорий – преобразования объектов, теория 2-категорий – преобразование этих
преобразований, и т.д. Поясним это метафорой из программирования. Теория множеств
описывает данные. Теория категорий описывает программы, которые являются способами
преобразования одних данных в другие. Но после этого возникает уровень 2-категорий, со-
стоящий в изучении способов переписывания одних программ в другие, уровень 3-категорий,
состоящий в изучении способов переписывания способов переписывания программ и т.д.
>Ну теоркат в математике как ТМ в нематематике, так?
Не понял вопроса. Теория категорий это просто раздел математики, который используют в некоторых других разделах математики.
ТМ вообще не является математикой, это больше к рисованию значков из иврита.
>Ок, а матлогика? Это математика?
Если речь идёт именно о матлогике, то это тривиально математика.
>может есть смысл вкатываться сразу в теоркат?
Вкатывайся, это хотя бы является разделом математики.
>Если речь идёт именно о матлогике, то это тривиально математика.
Ага, тогда посоветуй талмуд по матлогике, наиболее полный.
Ну теория множеств тоже является, просто устаревший раздел или вроде того. Законченный. По твоему то, что уже не развивается никак не математика, да?
>Не понял вопроса.
>ачиная со второй половины XX века представление о значении теории и её влияние на развитие математики заметно снизились за счёт осознания возможности получения достаточно общих результатов во многих областях математики и без явного использования её аппарата, в частности, с использованием теоретико-категорного инструментария (средствами которого в теории топосов обобщены практически все варианты теории множеств).
>Ну теоркат в математике как ТМ в нематематике, так?
Почти, химия не является математикой, но ТМ там не используют.
>По твоему то, что уже не развивается никак не математика, да?
То, что не является математикой не является математикой. Развитие тут не особо важно.
Как ты это посчитал?
Многие вопросы нашей вселенной сводятся к замеру "дефективности" определённых функторов.
Без троллинга? То есть то, что выше это не прикол, реально все эти задачи из геометрии, теорвера, дискретки решаются знанием алгебры и теорката?
В смысле тот анон рандомный набор гамалогических терминов говорил или на самом деле по теме отвечал? Просто стал читать про общую алгебру и что-то поверил уже в то, что он по теме отвечал, кек.
>Без троллинга?
Без троллинга.
>решаются знанием алгебры и теорката
Точнее умением переводить эти задачи в вопросы про алгебру и теоркату.
>В смысле тот анон рандомный набор гамалогических терминов говорил или на самом деле по теме отвечал?
Тут и то, и то на самом деле.
Жалко. А прикол по содержанию или по форме? То есть они принципиально так не решаются(по форме) или действительно можно всю математику грубо говоря переложить на этот язык и успешно решать, не в два предложения, конечно(по содержанию), но так можно.
>прикол по содержанию
Это.
>они принципиально так не решаются
Математические задачи принципиально решаются математическим образом. Тут уже не важно каким именно языком ты будешь её решать, просто некоторыми это сделать намного легче.
Понятно, что это из пушки по воробьям, но. Короче, есть ли может у вас примеры задач из разных областей математики, решающихся(только действительно, от начала и до конца) с помощью алгебры и теорката. Интересно было бы взглянуть.
>легче выучить один общий абстрактный и затем им пользоваться?
Именно в математике уже давно известно, что так и есть.
Можешь на примере показать? Вот задание:
"Построить триангуляцию и вычислить симплициальные гомологии с целыми коэффициентами круга, круга с дыркой, n-мерного шара."
Вот прочитал задание и выглядит как (не)троллинг выше один в один. А ведь это реальное задание в ВУЗе. Лол.
Ты бы ещё сказал, "Нарисуйте значок алефа используя теорию множеств", или "Докажите, что 2 является простым числом методами из теории чисел".
>вычислить симплициальные гомологии
Хуйня, которая легко делается на глаз. Лучше бы попросил посчитать высшие гаматопические группы.
>дакажите, что данный функтар является точным используя методы из такой несвязанной области как гамалагическая алгебра
Это открытая проблема, никто не знает пока как такие сложные вещи решаются. Особенно методами области, которая специально для них и создавалась.
Чему ты удивляешься?
>именно в той области математики, которая тебя интересует.
В Ленге всё на теории множеств основано, а без логики мне никак не научиться в доказательства.
>В Ленге всё на теории множеств основано
На наивной теории множеств, рисование алефов тебе нахуй не сдалось. Ещё посмотри книжку Algebra: Chapter 0, она вводит математику одновременно с множествами.
>без логики мне никак не научиться в доказательства
Формальная логика сильно отличается от того, что пишут в доказательствах. Но она в любом случае нужнее рисования всяких гимелей.
Спасибо.
>Algebra: Chapter 0
>Наивная теория множеств
Правильно ли я понимаю, что из ТМ нужен базовый минимум для вката, а дальше ТМ нахуй и не нужен собственно, так как там дальше идёт теоркат и тд? Или говоря хуйня/алефы, ты имеешь ввиду, что после наивной теории множеств они там стали онанизмом невнятным заниматься, имеющим малое отношение к математике? Раскрой мысль плес.
> сильно отличается от того, что пишут в доказательствах.
Ну она мне просто интересна сама по себе.
>We will then
get a small taste of the language of categories, which plays a powerful unifying role
in algebra and many other fields. Our main objective is to convey the notion of
`universal property', which will be a constant refrain throughout this book.
>ТМ нужен базовый минимум для вката, а дальше ТМ нахуй и не нужен собственно
Правильно. Именно сама теория множеств (рисование иврита) не нужно в принципе для большинства математиков.
>так как там дальше идёт теоркат и тд?
Не совсем, там дальше идёт сама алгебра. Теория категорий является всего лишь её частью и языком, который очень удобный для изучения алгебры.
>Или говоря хуйня/алефы, ты имеешь ввиду, что после наивной теории множеств они там стали онанизмом невнятным заниматься, имеющим малое отношение к математике?
Можно и так сказать, сейчас она нахуй не нужна для изучения алгебры. Если тебя не интересует изучение рисования алефов, то нет смысла углубляться в неё.
>>7121
Да, но там не такое хорошее введение в саму теорию категорий. Можешь почитать Awodey хотя бы до пятой главы про пределы совместно с Algebra: Chapter 0, у неё пререквизитов нет в отличии от книги Маклейна.
>Книжка уникальна тем, что там практически с первых страниц вводится язык категорий и кроме того она вполне понятно написана.
То есть примерно таким и должен быть современный учебник по алгебре...
Так это охуенная книжка получается. Я думал Ленг топовый учебник.
>>7123
>Awodey
http://angg.twu.net/MINICATS/awodey__category_theory.pdf
Оно? Я хз, может лучше тогда с неё и начать и мозга не ебать, всё равно ведь понадобится. Почему до 5 главы?
Бля, анон, спасибо тебе. А по матлогике Мендельсон? Или может ещё что-то есть эдакое у тебя?
Когда ж тебя забанят тут, ебан ты косоголовый.
По категориям это вводный учебник как я понял, потом можно
>Why write a new textbook on Category Theory, when we already have Mac
Lane’s Categories for the Working Mathematician? Simply put, because Mac
Lane’s book is for the working (and aspiring) mathematician. What is needed
now, after 30 years of spreading into various other disciplines and places in the
curriculum, is a book for everyone else
Маклейна навернуть
>Я думал Ленг топовый учебник.
Ленга неплохо использовать как справочник, для именно введения Chapter 0 получше будет.
>Оно?
Да.
>Почему до 5 главы?
Я сказал "хотя бы", конечно лучше всю, но не обязательно прямо сразу. Просто не всем нравится читать именно про основания математики и подобные темы, не знаю насчёт тебя.
Ну ок, всё, что нужно узнал. Спасибо ещё раз. Добра.
>Так ты дай хоть одно применение.
>Нобелевскую по физике вручили за топологические фазовые переходы
В том посте он прав. В других я не разбираюсь, но вполне может быть, что и там прав и анализ и прочее действительно просто прикладная алгебра. К тому же во всех этих областях рано или поздно без алгебраических понятий никак, хотя самой алгебре почему-то никто не хочет учить, мельком накарябать что такое группа и в путь это нормальная практика.
Например в теории графов постепенно начинает выясняться, что это никакая не теория графов, а топология для даунов, что очень обидно, если бы сразу преподавали топологию, может быть мы и поняли бы.
>В том посте он прав.
Естественно. Это очевидно. Как и в других постах.
>хотя самой алгебре почему-то никто не хочет учить
Самому заниматься этим нужно. Нет смысла надеяться.
Общая топология (ебля с множествами) сама по себе является топологией для даунов. А математическая топология является разделом алгебры.
Раздел алгебры.
 12 Кб, 698x154
12 Кб, 698x154Какая-то алгебраическая шизофрения, а не анализ. Попробуй на dxdy свой интеграл залить.
>из анализа ведь
Нет. Недостаточно нарисовать значек интеграла на алгебраической шизофрении.
>Зачем?
Потролишь их. Всем тредом поржем.
Ты знаешь анализ? Поможешь мне? А то я недавно начал заниматься его изучением, захотелось разбавить математику чем-то другим.
Ну спроси тогда у них, я просто сам лично с ними не знаком, а ты видимо их хорошо знаешь. Где они вообще находятся? В Москве?
А тебе и не надо лично быть знакомым, спроси в интернете их.
По трёхтомнику Верещагина-Шеня читается обязательный курс лекций на матфаке ВШЭ, почти слово в слово.
Герасимов - типичный курс "дискретной математики". Просто несколько не связанных между собой тем.
 15 Кб, 679x136
15 Кб, 679x136ряд Маклорена
Столкнулся с определением линейных объектов через их преобразования к другим координатам.
Как-то неприятно это заходит.
Собственно есть где-то пособие по геометрии с введением понятий векторов и прочего без дурацкой нотации с тысячами индексов и без "ковектор это такая штука, замена координат которой происходит вот так вот"?
 6 Кб, 412x86
6 Кб, 412x86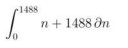 4 Кб, 269x101
4 Кб, 269x101n - целое число.
Как ты это вычислил?
Т.е. первое это пространство непрерывных функций с нормой (integral(a;b)(|x|^p))^1/p, а второе - пространство интегрируемых в степени функций. Я доказал неполноту C(p), теперь, ели я докажу вложенность первого во второе, а затем полноту второго, этого хватит? И еще там что-то про всюду полное множество сказать надо или в качество его можно взять все множество L? И как доказывать полноту L?
integral(n+1488)=n2/2+1488n=14882/2+14881488
Как найти угол наклона плоскоски к плоскости х-у?
 191 Кб, 720x1158
191 Кб, 720x1158Сап. Помогите разобраться. На 1 пикриле сайт с решенным примером под (а). Интересует, откуда взялась 2. Помогите плз.
То есть да, я могу по определению о-малого это всё посчитать и убедиться, но понимания самого смысла нет, и как следствие, улавливать конкретные случаи без подстановки в определение очень сложно.
Помогите
Нужны 2 факта, доказательства которых есть в любом учебнике фана:
1) Lp[a,b] - полное пространство
2) C[a,b] с этой нормой всюду плотно в Lp[a,b]
Отсюда уже следует, что Lp[a,b] - это пополнение C[a,b].
Опять ты.
Исключённое третье - "верно P или не P"
Закон противоречия - "неверно P и не P"
Закон противоречия спокойно доказуем без исключённого третьего, так что они уже не эквивалентны.
>В жизни они не выполняются.
Исключённое третье возможно, а закон противоречия вполне выполняется же. Определяем отрицание как "P ⇒ ⊥", то есть "P ведёт к противоречию" и получаем, что "P и P ⇒ ⊥" ведёт к противоречию.
>Исключённое третье - "верно P или не P"
>Закон противоречия - "неверно P и не P"
Тогда вместе эти два пункта это XOR получается? Верен только один?
>В жизни они не выполняются.
Например, если написать "я математик" для тебя это будет истинно, для меня ложно.
>Например, если написать "я математик" для тебя это будет истинно, для меня ложно.
То есть высказывание как бы суперпозиция всей хуйни и зависит от наблюдателя. Есть ли логика без закона противоречия?
>Ниже показаны таблицы истинности для логических операций «Сильной логики неопределённости» (strong logic of indeterminacy) Стивена Клини и «Парадоксальной логики» (logic of paradox) Приста. >Обе логики имеют три логических значения — «ложь», «неопределённость» и «истина», которые в логике Клини обозначаются буквами F (False), U (Unknown), T (True), а в логике Приста числами -1, 0 и 1.
Вопрос снимается. Спасибо.
>Верен только один?
В классической логике (где исключённое третье принимается на веру) они оба верны, "доказательство" закона противоречия выше, исключённое третье - просто верование.
>для тебя это будет истинно, для меня ложно.
Это зависит от конкретного определения "я". Не может быть такого, что конкретный человек одновременно и математик и не математик.
>>7240
>Есть ли логика без закона противоречия?
Есть логики, где оно недоказуемо. То есть в самой логике ты его не докажешь, но не обязательно, что оно ведёт к противоречию.
https://en.wikipedia.org/wiki/Paraconsistent_logic
Чтобы такое было возможно и логика оставалась не совсем ущербной, нужно не добавлять правило "⊥ ⇒ P".
>Не может быть такого, что конкретный человек одновременно и математик и не математик.
Конкретный человек нет, но это субъективность ведь, мне не нравится этот момент в классической логике, там по сути всегда рассматриваются частные случаи без общей картины, и даже нет возможности для такого рассмотрения. А в логике без закона противоречия можно оперировать не конкретными фактами, а сразу всеми вариантами развития событий, высказывание может в себе заключать их как бы.
>но это субъективность ведь
Нет. "я" там не является переменной. Если бы ты сказал, что "для всех людей Х, Х - математик", тогда уже можешь подставлять разных людей.
>не нравится этот момент в классической логике
Это в любой логике так.
>по сути всегда рассматриваются частные случаи без общей картины, и даже нет возможности для такого рассмотрения.
Так квантор всеобщности специально для этого.
>я не является переменной
Почему? Вообще не понял сейчас тебя.
>в любой логике
>strong logic of indeterminacy
>logic of paradox
Вовсе нет, нагуглил уже, что хотел.
> квантор всеобщности
Я не про это, лол. Алсо не понимаю нападок на исключённое третье, насколько я понял конструктивизм его не отрицает, просто для того, чтобы работало A или не А нужно как построить А, а это не всегда получается сделать.
Да и вообще принимать закон противоречия и не принимать закон исключённого третьего и при этом пользоваться бинарной логикой это как вообще?
A\/~A ложно, когда A ложно и ~A ложно. А это противоречит закону противоречия.
>Почему?
Потому что оно уже относится к конкретному объекту.
>насколько я понял конструктивизм его не отрицает, просто для того, чтобы работало A или не А нужно как построить А
Чтобы конструктивно доказать исключённое третье, нужно для каждого высказывания P дать доказательство того, что P верно или дать доказательство того, что P ведёт к противоречию.
>>7246
>не принимать закон исключённого третьего
>A\/~A ложно
Это разные вещи. Под "не принимать исключённое третье" имеют ввиду не принимать "∀ P, P ∨ ¬ P" как аксиому. В интуиционистской логике доказуемо "∀ P, ¬¬ (P ∨ ¬ P)".
>бинарной логикой
Что под этим подразумевается? Обычно это логика, где исключённое третье верно.
>Потому что оно уже относится к конкретному объекту.
Я у каждого разное.
>Чтобы конструктивно доказать исключённое третье, нужно для каждого высказывания P дать доказательство того, что P верно или дать доказательство того, что P ведёт к противоречию.
Зачем для каждого? Разве в конкретном случае после конструктивного установления истинностного значения A A\/~A не будет верна?
>Это разные вещи. Под "не принимать исключённое третье" имеют ввиду не принимать "∀ P, P ∨ ¬ P" как аксиому. В интуиционистской логике доказуемо "∀ P, ¬¬ (P ∨ ¬ P)".
Так аксиома это тавтология, значит чтобы она не была тавтологией нужно найти, когда она ложна.
>Что под этим подразумевается?
Логика, в которой высказывания могут быть только в двух состояниях.
>где исключённое третье верно
Ну да, потому и непонятно было, как можно усомниться в исключённом третьем, имея при этом всего два возможных состояния. Но я уже понял, если правильно понял, конечно, что исключённое третье в конструктивизме есть, просто для того, чтобы им пользоваться необходимо сначала конструктивно установить истинностное значение высказывания.
>Так аксиома это тавтология
Аксиома это "правило" логики, принимающееся без доказательства.
>Зачем для каждого?
Потому что исключённое третье это высказывание "∀ P, P ∨ ¬ P".
>в которой высказывания могут быть только в двух состояниях.
Двойное отрицание исключённого третьего и говорит, что нет такого высказывания, которое находится в "третьем состоянии".
>имея при этом всего два возможных состояния
Точнее она не имеет третьего состояния. Это и есть двойное отрицание исключённого третьего. А само исключённое третье говорит, что есть всего два состояния.
>что исключённое третье в конструктивизме есть
Есть только его частные случаи. Например можно легко конструктивно доказать, что для натуральных чисел n и m, n равно m или n не равно m.
>Аксиома это "правило" логики, принимающееся без доказательства.
Да, но она же тождественно истинна, значит тавтология.
>исключённое третье это высказывание ∀
>∀
Ну да, точно. Тупанул.
>Двойное отрицание исключённого третьего и говорит, что нет такого высказывания, которое находится в "третьем состоянии".
Ага.
>Точнее она не имеет третьего состояния.
>есть всего два состояния
Не вижу разницы, лол. Она есть?
>Есть только его частные случаи
Так, то есть закон противоречия говорит, что противоположные высказывания не могут быть одновременно истинными, исключённое третье, что не могут быть одновременно ложными, двойное отрицание, что нет третьего состояния, хотя погоди, а ты не перепутал, мб как раз исключённое третье говорит, что нет третьего состояния, а двойное отрицание что состояния всего два? В чём разница? Я запутался.
 60 Кб, 1218x211
60 Кб, 1218x211Короче, для закрепления, если вот это доказывать без исключённого третьего, то нужно сначала доказать рациональность/иррациональность и только потом можно рассуждать дальше, так?
>но она же тождественно истинна
В классической логике.
>Она есть?
Если исключённое третье верно, то нет. Так как из исключённого третьего следует "¬¬ P ⇒ P". Без него это разные вещи.
Точно известно (в интуиционистской логике), что третьего состояния нет. Но нельзя доказать для любого P, что оно находится в одном из двух состояний.
>Так, то есть закон противоречия говорит,
1) Закон противоречия - Ничто не может быть одновременно истинной и ложью.
2) Двойное отрицание исключённого третьего - Третьего состояния нет.
3) Исключённое третье - Есть всего два состояния.
2) и 3) конечно же эквиваленты если исключённое третье верно.
>мб как раз исключённое третье говорит, что нет третьего состояния
Из исключённого третьего следует его двойное отрицание. Для любого высказывания верно, что "P ⇒ ¬¬ P"
>>7255
>то нужно сначала доказать рациональность/иррациональность и только потом можно рассуждать дальше, так?
Да. Без него у тебя не будет изначально предположения "sqrt(2)^sqrt(2) рационально или sqrt(2)^sqrt(2) иррационально".
Мне всё понятно, спасибо, что разжевал.
1. В корзине лежат 4 шара чёрного и белого цвета. К ним прибавляют 2 белых шара. После этого из корзины случайным образом вынимают 3 шара. Найти вероятность того, что все вынутые шары белые, предполагая, что все предложения о первоначальном содержании корзины равновозможные.
2. В первой корзине 6 белых и 4 чёрных шара, а во второй 5 белых и 7 чёрных. Из первой корзины взяли случайным образом 3 шара, а из второй — 2 шара. Найти вероятность того, что среди вынутых шаров:
а) все шары одного цвета
б) только три белых шара
в) хотя бы один белый шар
A-"Вадиму нравится группа Prodigy"
~A-"Вадиму не нравится группа Prodigy"
Если исключённое третье верно, то одно из двух, а может быть, что Вадиму насрать на эту группу, она ему не нравится и не не нравится. Это подойдёт как пример, когда исключённое третье не работает и интуиционизм тащит? Типа только когда мы поймаем Вадима и заставим его ответить и он ответит Нравится/Нет, тогда будет работать A\/~A, а до тех пор так сказать нельзя. Что-то такое, анон?
Если это так, то реквестирую подобный пример в математике. Ну и получается, что классическая логика считает, что все высказывания в мире делятся на истинные и ложные, а интуиционизм говорит, что не все. Я уловил суть?
>а интуиционизм говорит, что не все
Но с такими он не работает, так как не может построить, а что может построить, то имеет истинностное значение.
Где именно неверно?
>>7260
>она ему не нравится и не не нравится.
То есть ¬(A ∨ ¬ A), а из верности двойного отрицания исключённого третьего следует, что это ведёт к противоречию.
>когда исключённое третье не работает
Это бы означало, что интуиционизм противоречив, ведь он доказывает, что исключённое третье не не работает. Или другими словами - отрицание исключённого третьего ведёт к противоречию.
>тогда будет работать A\/~A
Точнее тогда у нас будет доказательство (A ∨ ¬ A). Если доказательства A ∨ ¬ A (пока или вообще) не имеется, это не значит, что ¬(A ∨ ¬ A).
>>7261
>интуиционизм говорит, что не все
Но ведь в нём верно двойное отрицание исключённого третьего. То есть если у нас есть P такое, что "P ∨ ¬P" неверно, то у нас противоречие.
А, во
>Аристотель указал также границы применимости tertium non datur, рассмотрев пример неопределённого высказывания: «Завтра будет морское сражение», которое сегодня не истинно и не ложно
То есть классическая логика просто закрывает глаза на существование таких вещей, тогда как интуиционизм учитывает и
>>7264
Тогда я опять запутался Вот высказывание:"Завтра будет война", оно не истинно и не ложно сегодня.
>Точнее тогда у нас будет доказательство
То есть классическая логика аксиоматизирует исключённое третье, а интуиционизм доказывает?
>Где именно неверно?
Сейчас попытаюсь сформулировать. Для чего нам нужно доказательство A ∨ ¬ A? Значит есть пример, когда бездоказательное принятие этого принципа вело к ошибкам?
В математике.
Основной объект изучения линейной алгебры это алгебра эндоморфизмов свободных модулей (необразованные люди так же называют эндоморфизм модуля "матрицей", а сам модуль "векторным пространством", сути это не меняет).
>не нравится и не не нравится
A/\~A получается, ну бля, всё равно получается не вижу разницы между законом противоречия и исключённым третьим, у меня оно связано настолько в голове, не представляю как развязать.
> отрицание исключённого третьего ведёт к противоречию.
Но тем не менее его нет в аксиомах интуиционизма. Если его нет в аксиомах, значит есть ситуации, когда он не работает?
>сегодня
Это уже из темпоральной логики, я про многого не знаю.
>тогда как интуиционизм учитывает
Нет, он доказывает (как и классическая логика), что таких вещей не существует.
>То есть классическая логика аксиоматизирует исключённое третье
Да.
>а интуиционизм доказывает?
Нет, он доказывает только его двойное отрицание и частные случаи исключённого третьего. Исключённое третье ты вообще не докажешь без более сильных аксиом, например оно следует из аксиомы выбора.
>>7267
>Для чего нам нужно доказательство A ∨ ¬ A?
Потому что это математика. Даже если ты пользуешься исключённым третьим, не обязательно добавлять его как гипотезе абсолютно в любом доказательстве.
>когда бездоказательное принятие этого принципа вело к ошибкам?
Нет, просто оно ведёт к методам доказательства, где ты не знаешь какой именно из дизъюнктов является верным. Из-за этого некоторые его не принимают.
>>7271
>у меня оно связано настолько в голове, не представляю как развязать
Докажи, что "¬ P" и "P ⇒ ⊥" эквиваленты. Из этого тривиально следует, что "(P ∧ (P ⇒ ⊥)) ⇒ ⊥", а то есть "¬ (P ∧ ¬P)"
>просто оно ведёт к методам доказательства, где ты не знаешь какой именно из дизъюнктов является верным.
Расскажи подробнее или ткни куда.
>Докажи
Попробую.
>Если его нет в аксиомах, значит есть ситуации, когда он не работает?
Если такие ситуации есть, то интуиционизм противоречив (а следовательно и классическая логика - https://en.wikipedia.org/wiki/Double-negation_translation), так как он доказывает несуществование таких ситуаций.
>>7274
>Расскажи подробнее
Используя исключённое третье, гипотеза Римана верна или не верна. Ты не знаешь какой именно из дизъюнктов верен.
P ⇒ ⊥ Если P=1, то ¬ P=0 и P ⇒ ⊥=0
Иначе P=0, ¬ P=1 и P ⇒ ⊥=1 вот тут я пользуюсь же исключённым третьим опять неявно или нет? когда считаю, что P может быть только 0 или 1
>Используя исключённое третье, гипотеза Римана верна или не верна. Ты не знаешь какой именно из дизъюнктов верен.
А не используя?
>Используя исключённое третье, гипотеза Римана верна или не верна
"Используя исключённое третье, всё верно или не верно"
Это верно?
Не используя можно миллион долларов идти получать.
>>7276
>вот тут я пользуюсь же исключённым третьим опять неявно или нет? когда считаю, что P может быть только 0 или 1
То, что ты пытаешься доказать уже подразумевает, что ты работаешь в классической логике. Так как в интуиционистской ¬ P определяется как P ⇒ ⊥.
>>7278
Это и есть исключённое третье, то есть у тебя "Используя исключённое третье, исключённое третье верно".
>Не используя можно миллион долларов идти получать.
Лол, но всё же. Без исключённого третьего как переформулировать то предложение про гипотезу Римана?
> Так как в интуиционистской ¬ P определяется как P ⇒ ⊥
Это как аксиома берётся?
>Это и есть исключённое третье, то есть у тебя "Используя исключённое третье, исключённое третье верно".
>"∀ P, P ∨ ¬ P".
Лол, и правда. И как быть? Я не понимаю как можно брать за аксиому закон противоречия и не браать исключенное третье в интуиционизме, и не понимаю как можно в классической логике делить их на две, вместо того, чтобы просто записать как A xor ~A.
>(P ∧ (P ⇒ ⊥)) ⇒ ⊥
Но тогда ((P ∧ (P ⇒ ⊥)) ⇒ ⊥)⇒ ⊥) , а то есть "¬ (¬(P ∧ ¬P))", а это есть P ∧ ¬P.
А ну бля, так ты об этом и говорил. Доказывается исключённое третье как двойное отрицание. Лол.
Вот только это не исключённое третье, а закон противоречия.
>Без исключённого третьего как переформулировать то предложение про гипотезу Римана?
В каком смысле? Конструктивное доказательство "гипотеза Римана верна или гипотеза Римана не верна" обязано предоставить доказательство одного из дизъюнктов. То есть в процессе нужно будет её доказать или опровергнуть.
>Это как аксиома берётся?
Это определение отрицания. То есть у нас имеется импликация, имеется ⊥ и отрицание P это просто P ⇒ ⊥.
>брать за аксиому закон противоречия
Оно тривиально доказуемо с помощью правил работы с импликацией.
>и не понимаю как можно в классической логике делить их на две
В каком смысле? Классически они эквиваленты, так как исключённое третье тривиально следует из чего угодно.
>>7282
Цель - (P ∧ (P ⇒ ⊥)) ⇒ ⊥ (закон противоречия)
У нас есть предположение P ∧ (P ⇒ ⊥). Нужно доказать, что это ведёт к противоречию. Из P ∧ (P ⇒ Q) следует Q, в общем случае. Так что P ∧ (P ⇒ ⊥) ведёт к противоречию, то есть (P ∧ (P ⇒ ⊥)) ⇒ ⊥. Закон противоречия доказан.
>>7283
>Доказывается исключённое третье
Оно нигде не доказывается.
>То есть в процессе нужно будет её доказать или опровергнуть.
Но ведь третьего состояния нет.
>отрицание P это просто P ⇒ ⊥
Это, похоже, единственное отличие, в этом заключено всё остальное, просто выразили по другому. Поэтому и доказываются все аксиомы.
> Классически они эквиваленты
Вот и мне так кажется. В первом утверждается, что не могут быть верны одновременно, во втором что ложны, но отрицание опять-таки у нас есть же. А вместе это xor просто.
>>7285
>Закон противоречия доказан
>Не доказывается
>Двойное отрицание исключённого третьего
((P \/ (P ⇒ ⊥)) ⇒ ⊥)⇒ ⊥)
Разве по аналогии нельзя доказать закон исключённого третьего?
>Но ведь третьего состояния нет.
И как ты из этого факта сконструируешь целое доказательство (не)верности гипотезы Римана?
>Вот и мне так кажется.
Так эквивалентность это всего лишь импликация в обе стороны, "классически эквиваленты" это не значит "недоказуемо без исключённого третьего", так как классически любая тавтология и исключённое третье эквиваленты.
>Разве по аналогии нельзя доказать закон исключённого третьего?
Чтобы можно было везде убирать двойное отрицание нужно доказать "((P ⇒ ⊥) ⇒ ⊥) ⇒ P", что без исключённого третьего ты не сделаешь. Без него можно доказать только "P ⇒ ((P ⇒ ⊥) ⇒ ⊥)".
>И как ты из этого факта сконструируешь целое доказательство
Никак, то есть мы просто не можем говорить о недоказанном, непостроенном, так? Но по сути ничем не отличается.
>Чтобы можно было везде убирать двойное отрицание нужно доказать
А зачем его убирать? В таком виде он есть там? А двойное отрицание исключённого третьего это и есть исключённое третье, в этом смысл отрицания ведь, а третьего опять не дано.
Типа вместо исключённого третьего мы можем пользоваться его двойным отрицанием, суть не изменится.
>что без исключённого третьего ты не сделаешь
Можно использовать его двойное отрицание там по идее.
>мы просто не можем говорить о недоказанном, непостроенном, так?
Почему? Можешь предположить, что она (не)верна и рассуждать дальше. Просто для конструктивного доказательства той дизъюнкции нужно дать доказательство какого-либо дизъюнкта.
>А зачем его убирать?
Я имею ввиду сокращение двойного отрицания. То есть "убирание" двойных отрицаний из высказывания, чтобы получить высказывание без отрицаний.
>А двойное отрицание исключённого третьего это и есть исключённое третье
Только если исключённое третье уже верно, то есть только в классической логике.
>>7291
Его недостаточно, чтобы доказать ¬¬P ⇒ P для всех P.
>Просто для конструктивного доказательства той дизъюнкции нужно дать доказательство какого-либо дизъюнкта.
В чём разница между ¬¬P и P?
>Я имею ввиду сокращение двойного отрицания.
>А двойное отрицание исключённого третьего это и есть исключённое третье
Я понимаю, я имел ввиду пользоваться ((P \/ (P ⇒ ⊥)) ⇒ ⊥)⇒ ⊥) и дальше как законом, вместо исключённого третьего как бы. Что мешает это делать?
>Его недостаточно
Почему?
Просто непонятна разница между интуиционистской точкой зрения и классической логикой. До этого я думал, что интуиционисты отрицают исключённое третье. А выходит, что это по большому счёту одна и та же логика, только разные точки зрения на отрицание.
>В чём разница между ¬¬P и P?
Где именно? В классической логике разницы нет. В интуиционистской могут быть случаи, где ¬¬P имеет доказательство, но P не имеет. Например исключённое третье.
>вместо исключённого третьего
В каком смысле "вместо"? Только одно из них доказуемо без дополнительных аксиом.
>Почему?
Не понял твой вопрос.
>>7294
>непонятна разница между интуиционистской точкой зрения и классической логикой
Одно из самых важных отличий это то, что если у тебя (в интуиционистской логике) есть доказательство P ∨ Q, то у тебя обязательно есть доказательство или P, или Q.
Ещё если у тебя есть доказательство "∃x.P(x)", то ты сразу знаешь какой именно "x" удовлетворяет предикату P.
>по большому счёту одна и та же логика
Не совсем, есть многие вещи, которые классически эквивалентны, но конструктивно различающиеся. То есть как правило в конструктивной математике "больше различий".
Но они связаны тем, (по ссылке выше об этом говорится) что P классически доказуемо тогда и только тогда, когда ¬¬P доказуемо конструктивно.
>по ссылке выше об этом говорится
Я читал.
>Одно из самых важных отличий
Но всё это следует из по другому определяемого отрицания, не?
>В интуиционистской логике доказуемо "∀ P, ¬¬ (P ∨ ¬ P)".
Так, я понял, как спросить, то есть неверно, что закон исключённого третьего неверен? Но это не значит, что он верен. Но он точно не неверен, то есть он либо верен либо что? Вот что это "что"?
>Но всё это следует из по другому определяемого отрицания, не?
Так ты же выше доказал, что эти два определения отрицания эквиваленты классически. Это всё следует из исключённого третьего и из сокращения двойного отрицания, которое следует из исключённого третьего.
То есть если у тебя есть "∀ P, ¬¬P ⇒ P", тебе уже не обязательно давать в процессе доказательства "∃x.P(x)" конкретный пример такого x (или дать достаточно информации, чтобы такой х всего можно было найти), который удовлетворяет предикату P. Ты можешь просто показать, что несуществование такого x ведёт к противоречию.
>то есть неверно, что закон исключённого третьего неверен?
Не понял твоего вопроса полностью, но про это ты прав. Можно ещё сказать "отрицание исключённого третьего неверно".
>обязательно давать в процессе доказательства "∃x.P(x)" конкретный пример такого x
В этом смысл весь?
>Не понял твоего вопроса полностью
В классической логике неверно, что закон исключённого третьего неверен значит, что он верен. А в интуиционистской? Что мы знаем об этом законе? Что он точно не неверен. Тогда какие варианты остаются, что мы можем о нём сказать? Что он либо верен либо ещё что-то. Что? Ну как мыслит конструктивист в таком случае?
>В этом смысл весь?
Смысл чего?
>Что мы знаем об этом законе?
Мы знаем, что его двойное отрицание верно. То есть не исключено, что есть частные случаи где (P ∨ ¬ P) верно для некоторого P. Например с равенством натуральных чисел.
>Смысл чего?
Создания логики без аксиомы исключённого третьего, ну короче избавление от косвенных доказательств в математике и тп.
>не исключено
Хорошо, а другие варианты не рассматриваются принципиально? То есть рассуждать "если ... то он либо верен либо..." нельзя?
>Создания логики без аксиомы исключённого третьего
Я не особо много знаю про изначальную мотивацию кроме того, что уже написал. Но уже стало известно, что интуиционистская логика в разных её проявлениях (а то есть и теория типов) является "внутренней логикой" (internal logic) многих категорий. То есть её можно использовать как "синтаксис" для формальной работы в некоторых категориях.
>другие варианты не рассматриваются принципиально
Другие варианты чего?
>То есть рассуждать "если ... то он либо верен либо..." нельзя?
Любое доказательство высказывания формы A ⇒ P ∨ Q как раз примерно так и выглядит, или ты про что-то другое?
>>7302
В общем случае, то есть "∀ P, P ∨ ¬ P" просто недоказуемо. Но нет случаев, где существует P такое, что ¬(P ∨ ¬ P)
Подскажите кто может помочь посчитать угол отражения шара от стены, пренебрегая всеми законами физики?
как мы знаем угол падения равен углу отражения, так вот если стена и шар будет постоянно изменять свой угол как мне найти угол отражения в радианах?
Или хотя бы объяснить как это можно посчитать, второй день смотрю видяшки по тригонометрии
1. Возможно ли существование мира/Вселенной, полностью описанного и управляемой многозначной или бесконечнозначной логикой?
2. Существуют ли типы логики, допускающие внутренние противоречия?
3. Может ли мультивселенная (гипотетически) быть несчётно бесконечной? Если ответ положительный, буду благодарен за пару примеров.
Будет ли такая мультивселенная больше, чем типичная счетно бесконечная Вселенная?
3. Пока неизвестно, но можно это довольно легко узнать. Никто не занимался этим серьёзно ещё, но примерные наводки уже есть.
Нужно посчитать все гамалогии и когамалогии нашей вселенной (для начала нужно определить её как тапалогическое пространство, но это довольно легко), тогда у нас будет достаточно информации. А если можешь гаматопические группы посчитать, то вообще отлично.
гамалогии уже спокойно могут быть изаморфны в категории множеств множеству всех множеств, то есть они уж очень большие получаются, так что вселенная несчётна.
а мультивселенная является произведением вселенных (тапалогических пространств), так что она тоже будет несчётной, но настолько же несчётной.
Пока что конкретно известно, что первые гамалогии являются тапалогическим пространством и изаморфны подвселенной нашей вселенной, неизвестно только где именно она находится. Открытая проблема.
Можешь пробовать делить вселенную на инфинитезимальные треугольники и пытаться высчитывать.
И всё?
 26 Кб, 1457x139
26 Кб, 1457x1391) это открытая проблема. если найдём так называемых невидимых спектров, то логика нашей вселенной однозначно несчётно-бесконечнозначна. но уже доказано, что как минимум она 1.5-значна.
2) да, гамологии любых двух видов логики тривиальны, то есть можно показать что любые две логики изоморфны. это следует из того, что взятие гамалогии является вполне унивалентным функтарам. ну а из этого следует их противоречивость. теорема на скрине из моей книги по тапалогии нашей вселенной.
>Кто как начинал свой путь олимпиадника
Был у нас один такой. Начал с того, что его по кругу пустили.
не трать время на олимпиады
Короче, теперь мне нужно немножко практики, пару дней после работы поинтегрировать дома за занавесками. Вопрос: откуда задачки брать, пресловутый Демидович или на самом деле сейчас что-нибудь получше есть (можно англ.)?
Потому что это не математика.
Именно, поэтому просто съеби обратно под шконарь и перестань кукарекать оттуда давно всем известные вещи.
Нахуй ты пишешь про интегрирование на /math/? Создавай отдельный тред на другой доске.
бамп вопросу. Зачем изучать поля, не сильно ли узко это?
У меня дома можно.
>Есть универсальный способ?
Да. Его существование следует из функториальности интеграла и из того, что он является правым сопряжённым функтором, и получается, что интеграл сохраняет все пределы.
Так подынтегральное выражение и производна могут отличаться.
1/(x^3+x+1)^3
k целое.
По таблицам сложения.
6+6
1)6+4
1)10+2
Нужно выучить таблицу суммирования однозначных чисел, гугли.
Затем, нужно научиться разлаживать число на компоненты, такие, чтобы одна компонента была кратна десяти.
В рамках двухзначных чисел, это все то, что заканчивается нулем.
12+6=18. Тут нужно уметь добавлять числа с разрядами. Гугли "систему разрядов чисел". Единицы добавляешь к единицам.
12+6
1) 2+6 = 8
2) 8 + 10 = 18
18+6=
18+(6-4)=20
20+4 = 24
Кто-то знает более лёгкий базис для предоставления умножения в виде суммы?
1.Таблица суммы однозначных
2.Таблица разницы однозначных чисел
3. Умение оперирования с разрядами
4.Понимание и нахождение кратного десяти.
С точностью до слабой гомотопической эквивалентности будет 36.
Khanacademy.
Там когда как на самом деле.
Таким людям как ты, заплатить за курс - единственный способ поиметь мотивацию.
Да, и фермеры всякие тоже.
По-моему определяет в главе про коммутативную алгебру. Но книга всё равно довольно вредная.
бамп
Бурбаки, дьедонне, t.s. blyth, rotman.
Basic homological algebra Осборна
Heart of cohomology Като
24 часа локальных когомологий Айенгара
начни уже любую, не зайдет переключишься
Опс, извиняюсь. Не матан а математика. Смотрел я шапку, но там что-то больно дофига всего. Хотя, судя по описаниям, мне в "для самых маленьких".
В треде по твоей ссылке мной объясняется в основном философия
Что такое мат анализ я уже объяснил в другом треде:
https://2ch.hk/math/res/26200.html (
Посоветуйте литературы (книги/статьи неважно) по сглаживанию временных рядов, желательно что-нибудь свеженькое прям с пылу с жару
В 6 классе я более менее математику понимал , на 4, а до 6 на 5 , потом стал дико ебланить с уебанами которые не чем не занималимь , и вот теперь
и вот я теперь в 9, и вообще ее не понимаю , просто 0. Хотя я уверен что материал я этот нагнать смогу , вы просто подскажите можно ли в соло это нагнать? С чего начать? Я не стал ее понимать , когдаиначались всякие квадроциптическиевротнеебические дроби , а если быть точней я как то эту залупу упустил , и с этого все началось.... Я тему пропустил а весь дальнейший год был с ними связан , и пиздец , я сижу и не вдупляю по сей день.... Есть подводные камни? С чего начать? Стоит ли к учительниуе с этой хуйней идти?
Читай учебник, делай упражнения.
https://www.youtube.com/watch?v=nVpdQ1UnQjQ
Равинагар
 3 Кб, 1280x720
3 Кб, 1280x720Любую книгу по интегрированию.
Нет, но он является топосом, если ты принимаешь аксиому выбора.
Assuming ZFC, the inaccessible cardinal axiom is equivalent to the universe axiom of Grothendieck and Verdier: every set is contained in a Grothendieck universe.
Гмурмана изучал? У него там и задачник отдельно идёт.
Спасибо капитан, я это знаю, но как именно?
Да, запросто. Рекомендую начать с арифметики, можешь взять книжку Серр "Курс арифметики", очень хорошая.
Я долго ебался с этим. Рисовал какие-то квадраты, еще что-то. Сейчас уже и не вспомню. Вывести можно из формулы суммы квадратов всех чисел. Нужно найти сумму всех четных чисел и вычесть. Что-то такое.
Правильно
Да, он прав. Гугли основную теорему алгебры.
Корни краткости...
Прав, следует тривиально из функториальности взятия когомологий пространства петель твоего квадратного уравнения.
Это все верчения попой. Смотря как ты определяешь корень. Если просто как число зануления, то нет, оно одно.
Если как разложение на скобки, то да, там две одинаковые скобки будут.
Это и в школьном учебнике не скрывают.
Жвачую.
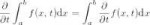 1 Кб, 243x42
1 Кб, 243x42Теореме о спектральной последовательности Лопиталя.
Лейбница вроде как, также можно гуглить как дифференцирование интеграла по параметру.
a^{b}=Exp[b*Ln(a)]
Можешь записать с помощью символа произведения П, если прямо зудит. Счётчик - i от одного до n, все члены равны твоему основанию степени V.
Есть вещи, которые невыразимые символами. Никак нельзя представить неопределённое количества с помощью записи значений, кол-во которых неопределённо.
Можно записать некое подобие, используя ординалы. Ординалы позволяют перешагнуть неопределённость, и даже бесконечность.
N раз взять А <=> (A1, A2, … , AN)
A^N = ( A1 A2 … AN)
Если N = 5, то А^5 = (A1 A2 A3 A4 * A5)
Fix
Невыразимые символами в рамках действительных чисел. Можно расширить множество до ординалов.
"…" показывают, что здесь может быть любое кол-во А, а A с индексом n показывает, что в зависимости от того, какой будет предпоследний член, будет последний
(An-b, …, An-1, An).Где b — любой член натурального множества, больше первого элемента из "…".
Матрицы это плохой способ записывать эндоморфизмы свободного модуля над кольцом. Плохой например тем, что эндоморфизм инвариантен относительно смены базиса, а матрица в общем случае нет.
>любого модуля
По-моему конечно порожденного и свободного, насчет первого не уверен
Аксиомы алгебры эндоморфизмов в принципе соответствуют алгебре матриц, так что да.
Такого не может быть.
>тензоры
В математике контравариантные тензоры называют "дифференциальными формами". Про ковариантные не знаю, по-моему это уже физика.
Что это? Элементы тензорного произведения модулей?
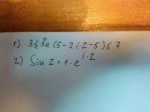 8,3 Мб, 2560x1920
8,3 Мб, 2560x1920Сап, матемач, поможешь решить? Желательно с объяснением решения.
Примерно 3 недели. Следует из теоремы Хопфа о когомологии ЕГЭ по матем.
Доказать утверждение:
( sin(a) + cos(a) )^2 + ( sin(a) - cos(a) ) ^2 + sin^4(a) - cos^4(a) + cos^2(a) = 2 + sin^2(a)
Учебник Крамора "повторяем и систематизируем". Страница 168.
Сам файл прикреплён. Там находится решение. Но оно мне непонятно.
Кто-то может более подробней расписать?
Ссылка на книгу:
https://fex.net/#!659722222060
 25 Кб, 1135x124
25 Кб, 1135x1241. S=1^2+3^2+5^2+...+(2n-1)^2
2. (2n-1)^2=4n^2-4n+1
3. Sum(4n^2-4n-1)=4 Sum(n^2)-4 Sum(n) + Sum (1)
4. Так как Sum 1 = n , Sum(n)=n(n+1)/2 (выводится достаточно просто), остаётся только найти Sum(n^2).
4.1 Найдём формулу для Sum(n^2). Здесь полезно бы это всё расписать, но там всё достаточно элементарно, однако можно заметить:
Sum((n+1)^3-n^3)=Sum(3n^2+3n+1)= 3 Sum(n^2)+ 3 Sum(n)+Sum(1)
Также учитывая, что (ты можешь это проверить на любой последовательности):
Sum((n+1)^3-n^3)=(n+1)^3-1^3 = n^3+3n^2+3n
Получаем, что
3 Sum(n^2)+ 3 Sum(n)+Sum(1) = n^3+3n^2+3n
Дальше, если не расписывать здесь все элементарные шаги, получим
Sum(n^2)=((2n+1)(n+1)n)/6
5. Вернёмся к формуле 4 Sum(n^2)-4 Sum(n) + Sum (1)
Подставляем найденные выражения:
4(((2n+1)(n+1)n)/6)-4((n(n+1))/2)+n
И снова тут всё расписывать не буду из-за простоты, но в итоге мы получим
(8n^3+4n-12n+6n)/6 = (8n^3 - 2n)/6 = (2n (4n^2-1))/6 = (n(4n^2 - 1))/3
---
Надеюсь, что нигде не ошибся.
1. S=1^2+3^2+5^2+...+(2n-1)^2
2. (2n-1)^2=4n^2-4n+1
3. Sum(4n^2-4n-1)=4 Sum(n^2)-4 Sum(n) + Sum (1)
4. Так как Sum 1 = n , Sum(n)=n(n+1)/2 (выводится достаточно просто), остаётся только найти Sum(n^2).
4.1 Найдём формулу для Sum(n^2). Здесь полезно бы это всё расписать, но там всё достаточно элементарно, однако можно заметить:
Sum((n+1)^3-n^3)=Sum(3n^2+3n+1)= 3 Sum(n^2)+ 3 Sum(n)+Sum(1)
Также учитывая, что (ты можешь это проверить на любой последовательности):
Sum((n+1)^3-n^3)=(n+1)^3-1^3 = n^3+3n^2+3n
Получаем, что
3 Sum(n^2)+ 3 Sum(n)+Sum(1) = n^3+3n^2+3n
Дальше, если не расписывать здесь все элементарные шаги, получим
Sum(n^2)=((2n+1)(n+1)n)/6
5. Вернёмся к формуле 4 Sum(n^2)-4 Sum(n) + Sum (1)
Подставляем найденные выражения:
4(((2n+1)(n+1)n)/6)-4((n(n+1))/2)+n
И снова тут всё расписывать не буду из-за простоты, но в итоге мы получим
(8n^3+4n-12n+6n)/6 = (8n^3 - 2n)/6 = (2n (4n^2-1))/6 = (n(4n^2 - 1))/3
---
Надеюсь, что нигде не ошибся.
Спасибо большое. Для проверки что надо.
>Basic homological algebra Осборна
Вроде неплохо написано, но нет спектральных последовательностей. Пока что для начала продолжу с этой.
>Heart of cohomology Като
Есть ещё что-нибудь похожее?
24 часа Ле-Мана же.
http://bookstore.ams.org/gsm-87/
Harpreet Bedi с ютубе (best math channel ever) примеры в своих лекциях брал оттуда.
Там видимо алгебраическая геометрия из пререквизитов, про неё пока что ничего не знаю.
>Harpreet Bedi с ютубе
Да, видел уже.
 221 Кб, 1008x564
221 Кб, 1008x564Теперь сам вопрос: как отсечь неподходящие вершины, т.е. те, которые находятся на возвышенности в фиолетовой области? Хотя бы подскажите, куда копать.
Ну это само собой. Вот только я не совсем понимаю как его потреблять? Вкупе с Винбергом? Или до? Уж простите, совсем нюфаг, но запасливый. Покупаю книги на будущие
Спасибо!
>Ну это само собой.
Почему это "само собой"?
>не совсем понимаю как его потреблять?
Желательно вообще никак.
> Почему это "само собой"?
Ну а как? Разве выйдет пройти мимо него? И не попасть впросак в каком-то место, из-за того, что пропустил?
>Разве выйдет пройти мимо него?
Зависит от твоих интересов. Если это именно математика, то выйдет.
Спаривание дифференциальных форм же, двойственность Пуанкаре.
>>7937
В матане ничего плохо нет, матан это когда изучают нормированные алгебры.
>>7939
Мимо конечно не пройдешь, но сперва надо выучить алгебру и топологию основательно. Нормированные алгебры это объект с топологической и алгебраической структурами, при чем обе они согласованы.
Первым делом, первым делом модули над R, ну а интеграл, а интеграл потом!
Ой сложно всё. Можешь для меня план накидать? Например: Шеня, чего-нибудь из Алгебры, Матан и т.д Дабы сформировать некую базу для дальнейшего, надеюсь, серьезного изучения.
Спасибо.
План очень простой. Книга нужна всего одна, Глазман-Любич (реально лучшее что я видел). Но в ней 2500 упражнений (читай: утверждений для доказательства).
Это как Кириллов-Гвишиани, только без картошки, упражений в пять раз больше, и есть гомологическая алгебра.
Как помощника можно смотреть в Прасолова "Задачи и теоремы линейной алгебры". Для правильного взгляда на эти темы – Бурбаки, алгебра, первый том; Blyth T.S. Module theory.
Мое мнение, что не стоит тратить время на фигню. В undergraduate учебниках (и в книгах с неброским названием "Алгебра" любого автора) полезной информации все равно ноль; а затупить с решением можно на чём угодно, хоть на олимпиадах за седьмой класс, гельфанде-шене и подобном (обсуждали в соседнем треде).
Выбор "книги попроще" это выбор интенсивной боли чуть ниже поясницы. Хорошо описано в "math made difficult" by Linderholm.
>>7950
Коммутативная алгебра Айзенбад + Ботт-Ту дифф. формы в топологии.
Не шучу, все что нужно знать по этим темам, там есть.
Допустим уже начал, дальше что?
>Коммутативная алгебра Айзенбад
Не смог найти в инете чтобы скачать.
>Ботт-Ту дифф. формы в топологии.
Не смог найти про дифференцирование ни слова.
Как-то читал как такого рода задачи решаются из римана-роха на графах, посмотри
https://arxiv.org/pdf/math/0608360.pdf
например
Как формально доказать, что:
ab = c -> c=a(b^(-1)), если опредеденна группа, т.е ассоциативность[(ab)c=a(bc)], нейтральный элемент[d={a;b;c); de = ed = d] и обратная операция[d(d^(-1))= (d^(-1))d = e
Не туда.
 41 Кб, 1040x193
41 Кб, 1040x193Любая более менее нормальная физика (если такая существует) без такой математики никуда.
Ну не базарь, если не знаешь. Может где на переднем крае науки она и нужна (сомневаюсь), но на моем уровне - нет.
>если не знаешь
Знаю точно, что вещи из текстов выше в ней используются. Но "нормальной" я бы физику в любом случае называть не стал.
>но на моем уровне - нет.
Ты тогда хуйнёй страдаешь, а не наукой занимаешься.
А кто говорил что я наукой занимаюсь? Я хочу вкатиться в дифференцирование, а потом в физику.
>в физику
На каком уровне? Электромагнитное поле это связность в главном расслоении со структурной группой U(1), где база расслоения это пространство-время, а тотальное пр-во расслоения – фазовое пр-во физ системы.
То есть без дифф. форм это вообще не определяется; без звёздочки Ходжа уравнений Максвелла не записать (во вменяемом виде).
Блядь че так сложно то нахуй базаришь. Ну либо ты говоришь как физик-теоретик, но это всю жизнь надо учить математику, а потом вторую жизнь - физику.
Начинать то надо с малого. Теория групп и твои расслоения подождут.
 28 Кб, 537x140
28 Кб, 537x140>надо учить математику, а потом вторую жизнь - физику
И зачем одно и то же два раза? Они совпадают.
Квантовая механика это линейная алгебра; сто/электромагнитная теория – дифференциальная геометрия; механика (лагранжева и гамильтонова) это симплектическая геометрия и т.д.
Всё что я назвал это материал первого-второго курса.
>Квантовая механика это линейная алгебра
Че, в линейной алгебре тоже много контр-интуитивных вещей?
>сто/электромагнитная теория – дифференциальная геометрия
>механика (лагранжева и гамильтонова) это симплектическая геометрия и т.д.
Что ж тогда в школах проходят? Ни разу не слышал про такую геометрию нигде, кроме /math/.
Опять же, начинать надо с начала, а ты хочешь чтобы я с места в карьер.
Есть учебник по дифференциальной геометрии для люмпена?
А на какую полезную хуйню есть?
>тоже много контр-интуитивных вещей
Не знаю чо там контр-интуитивное, но более менее все утверждения это утверждения о линейных операторах. Разобрано у Кострикина-Манина (по программе вербицкого это школьный материал).
>учебник по дифференциальной геометрии
Их много, например, John Lee introduction to manifolds.
>>8017
>sci
Раздел недоучек, такой же как /bo и /hi или какой-нибудь / pr; обсуждать там нечего и не с кем.
По количеству экспертов с /math может сейчас сравниться разве что /wm.
>Не знаю чо там контр-интуитивное
Та ты любой учебник по квантмеху открой.
>John Lee introduction to manifolds.
На русике есть хорошее?
>sci
>Раздел недоучек, такой же как /bo и /hi или какой-нибудь / pr; обсуждать там нечего и не с кем.
>По количеству экспертов с /math может сейчас сравниться разве что /wm.
Ты /po/ забыл. Максимум жирно.
>По количеству экспертов с /math может сейчас сравниться разве что /wm.
Человек зашел сюда физику узнать, а не про модульные расслоения читать. В /sci ему хотя бы подскажут, что читать, а не говном накормят.
>>8023
Можно заниматься математикой, не зная определения модуля. Ничего страшного не произойдёт.
>Можно заниматься математикой, не зная определения модуля.
Заниматься-то можно, только смысла нет тратить своё время впустую.
Если ты каким-то образом занимаешься "математикой", не зная определения модуля, то ты фактически максимум числа складывать и так называемые "интегралы" считать умеешь. Математикой это не даже не назовёшь.
>максимум числа складывать и
Нет. При сложении в столбик используется гомологическая алгебра (_"один в уме" это фактически коцикл).
Помогите, же.
http://www.staff.science.uu.nl/~gadda001/goodtheorist/index.html
Ультра-годнота. С самых начал.
Физик первокур приходит в тред, а вы ему про уравнения максвелла как калибровочную теорию талдычите, про гамильтонову механику через кокасательное расслоение. Это, конечно, круто, но нахуя это нужно первокуру физику? Он, блядь, даже еще не понимает, что такое банальный диполь. А резкий уход в эту ебанную математику просто напрочь лишает понимания. Был у меня приятель - на тот момент аспирант второго курса в ПОМИ (та еще помойка, конечно). Механика по Арнольду со второго курса, уравнения Максвелла можно писать только в формах, КМ можно только через красивый интеграл, fancy-pants короче. В результате недолгой беседы выяснилось, что он не понимает, почему частная производная преобразуется инче, чем обычная. Короче говоря, пусть старая система научит основам (неказистым и не принятым в мире, но крепким основам понимания), а потом после того, как человек определится с выбором специализации пусть постигает все то же, но как надо.
Монитор. Вообще заказал тут пару книг, и подумал нахуя? Книги в свободном доступе есть. Просто проебал 1к рублей.
> Но это же пиратство
Ну в общем да. Но мои книги на ftp ИТМО есть. Так что тотальный проеб денех.
Потому что бумажные книиги можно прочитать и не сойти с ума. Я вообще думаю что ни одна отцифрованная книга с экрана не была прочитана до конца.
Ага, ну да. Я десятка два уже прочитал до конца и от начала с экрана. Правда не за компом, конечно, у меня 7" китайский таблет за $20. Есть очень удобная программа document viewer, делающая любой говноскан читаемым (разделение страниц, обрезка белых полей, исправление контраста и тд).
Ты двум разным людям ответил. Первые две это мои посты, там реальные формулы из литературы.
>>6880
Этот например из Джейкоба Лури, я только значок интеграла подставил.
Ну а остальное это посты другого человека, который набирает чушь в латехе чтоб смешно было (у него неплохо получается).
>>6859
>>6865
>>6867
>>6878
>>6896
>>7152
и т.д.
 29 Кб, 604x453
29 Кб, 604x453Есть какие-нибудь лайфхаки для решения задачек? Например, теорема Лопиталя для легкого раскрытия неопределенностей очень помогла, правда препод пообещал отпиздить, если еще раз так сделаю. Есть подобные лайфхаки для решения дифуров?
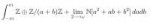 8 Кб, 604x93
8 Кб, 604x93Открытая проблема. Частный случай выводится из решения данного интеграла.
Кто знает ка решать?
>9876^3456789 * (9^99)^5555 - 6789^3414259
Таких чисел не существует, чернильное пятно будет слишком большое.
Согласен, но пример решить надо(
Какая разница? Если я наматываю нитку с делениями на круг, то мне не важно сколько мотков было сделано, круг-то никуда не денется.
>>8168
Это не теория чисел (области с таким названием вообще не существует). Сравнения по модулю уже понимают все, кто умеет определять время по часам с циферблатом и знают что 16:30 и половина пятого это одно и то же.
В моем словаре "помочь" это показать работающий метод, а не привести готовое решение.
Обращайся.
Видеоуроки воспринимаются проще чем книги, поэтому у меня вопрос такой - есть ли на ютубе хорошие годные лекции по матану? Чтобы лектор понятно рассказывал.
https://www.youtube.com/channel/UCErLELnXehsJ7ycW4OJgfQQ
Сразу предупреждаю, что лучше этого ты не найдешь.
y = x^2 - 1 ?
https://www.youtube.com/user/njwildberger
А "ненамного хуже" тебе уже выше посоветовали.
Ну и это, нумберфилы всякие с пи-би-эсами.
>njwildberger
Так там всего 3-4 нормальных видео насколько мне известно, да и они не очень.
>нумберфилы всякие с пи-би-эсами.
xDD ахуенно!
 215 Кб, 1920x1200
215 Кб, 1920x1200Оно, благодарю, анон!
 18 Кб, 588x111
18 Кб, 588x111Какие есть методы решения неоднородных дифференциальных уравнений в частных производных? Например, таких, это, я так понял, неоднородное уравнение теплопроводности.
Ты вообще неправ.
Что скажете о книге Aluffi: Algebra Chapter 0?
Стоит ли обмазываться? Есть адекватная замена ей с задачами?
 51 Кб, 412x271
51 Кб, 412x271Алсо, сам пример выглядит так z = u^2 - v^2u, где u = xsiny, v = ycosx
>3-4 нормальных видео
Как минимум вторая половина курса по алгебраической топологии хорошая, по истории математики некоторые лекции неплохие.
>>8233
Назови хоть одно утверждение в квантовой механике, которое не является утверждением линейной алгебры. Хайнсайт: таких утверждений нет.
>>8255
>>8256
Не лучшая, замена есть. Как минимум Rowen не хуже.
Лучшая это Глазман-Любич.
>>8260
Да.
2(u-v^(2u-1))
Graduate algebra в двух томах
я правильно понимаю, что (dz/dx)dx = u^2 и (dz/dy)dy = - v^2u ?
Да я не понимаю как найти dx и dy. Вот формула для нахождения dz мне дана. Как найти dz/dx я тоже знаю.
Приблизительно.
u^2-1 получается.
А dz/dx = dz/dx - dz
Математика - это дед.
Дед - это категория колец в алгебре в науке модулей.
Следовательно, математика - это категория колец в алгебре в науке модулей.
Ты осторожно, щас я его специальным функтором отправляю в категорию топологических пространств и там над ним поиздеваюсь.
Всё пучком.
Как функтор из производной категории.
 830 Кб, 1520x2688
830 Кб, 1520x2688Как мультипликативный аналог следа оператора.
Правильное определение (скаляр, у которого при взятии внешней степени сохраняется гомотетия) я видел только у Бурбаки и у Blyth. Если знаешь ещё, подскажи.
Не знаю. Начал решать Глазмана-Любича. Что параллельно покушать? Желательно поменьше примеров и больше задач.
>Правильное определение (скаляр, у которого при взятии внешней степени сохраняется гомотетия)
А чем мотивировано такое определение?
Если у нас линейная алгебра на языке модулей и без упоминания матриц и векторов (а только так и надо) то это определение самое естественнное.
Что "с какой стати"? Если не вводить операцию внешней степени заранее, придется расписывать определитель через кососимметрическую форму, это будет дольше и менее красиво.
Какие еще есть варианты? Через след удобно если у нас линейная алгебра будет в контексте операторов на конечномерном векторном пространстве, но это функциональный анализ, а не алгебра.
Как альтернирующую n-линейную функцию? Ну тогда уж сразу формулой давай, чего там.
Короче я не понял сути твоих возражений.
Еще скажу, что особенно было смешно с "down with determinats" и "done right", учитывая что изложение Бурбаки еще никто не превзошёл в последовательности и точности. У них определитель впервые появляется в разделе про внешнюю алгебру, то есть Axler и прочие дебилы никакой америки тут не открыли.
Когда я последний раз проверял, разделы линейной алгебры (алгебраическая к-теория, гомологическая алгебра, алгебраическая геометрия, теория представлений, функциональный анализ) вместе занимали примерно 100% от математики, и от четверти до трети физики.
 28 Кб, 405x596
28 Кб, 405x596А можно это определение полностью? На википедии я его не увидел. Скриншоты из Бурбаки вполне подойдут.
Допустим, у нас есть кольцо (возможно, с единицей). Как определить определитель?
Это гуглится за две с половиной секунды, буквально. Тебе нужно было выделить мою фразу, нажать правой кнопкой "search in google" и первая же ссылка в google books выдает первый том "Алгебры" Бурбаки, прямо всю страницу, где это дается (первый скрин).
 11 Кб, 637x223
11 Кб, 637x223http://booksshare.net/index.php?id1=4&category=math&author=burbaki-n&book=1962
>придется расписывать определитель
Его и так придётся расписывать если ты хочешь про него что-то доказывать,а иначе на черта он нужен.
 9 Кб, 618x107
9 Кб, 618x107С меня годній прон в ответ
Определитель это в любом случае полилинейная функция.
То есть либо ты сначала определяешь алгебру грассмана и пользуешься внешним произведением,
либо получается невменяемый бред про альтернирующие суммы подстановок и формулы.
Так понятно?
В смысле? Как ассоциативную алгебру над K с операцией ∧
>>8346
Потрясающее говно. Я думал фраза "эндоморфизм детерминантных векторов" это прикол местного пынефорсера, оказалось это из тривиума.
Сравни с >>8323
В принципе написано то же самое конечно, но кажется что вербилла долго думал, прежде чем написать наиболее косноязычно и наименее понятно.
>>8348
Уже раз тридцать сказал
Бурбаки, T.S. Blyth, частично Rotman (третье издание).
Скрины из всех этих книг я привёл.
Что бывает когда геометро-дауны берутся учить алгебре. Типа, сам бы выучил, для начала.
Это как его обсер с когомологиями де рама, которые "проще сингулярных" (на языке людей без психических расстройств эти два определения совпадают почти дословно; но у комплексных еометров одно сложнее, а другое проще).
Скорее всего это был плохой учебник. Наверное написал какой-то картофан, потому что сводить всю математику в линейную алгебру !!! может только абсолютно поехавший человек.
Можешь привести пример области математики, которая не являлась бы разделом линейной алгебры? Мне правда интересно, за всю жизнь с такой не сталкивался.
Я могу в котинг и начинаю работать в дата саенс, но у меня сравнительно плохой математический бэкграунд, статьи осиляются трудно, имплиментации алгоритмов которые еще не появились в библиотечках - болезненные. Это поэтому я еще девственник?
>>8360 (Del)
Спасибо, няши, я буду очень стараться. Математика вся интересная, какая-то глупость выделываться и говорить что то в чем ты разбираешься - лучше, не хочется - не трогай же и все. Но все гораздо умнее меня, уроки математиматики унизительны, некоторые одногруппники кажется отчасти поэтому их и ждут (серьезно, нигде не видел такой концентрации мудаков как среди математиков), как программист я гораздо лучше и на фоне веб-макак меня и так все хотят потому что могу что-то сделать по формулам. Физику сдам только если за выходные реализую модель с графикой по какому-то явлению описывающемуся дифуром Эйлера хотя бы первого порядка, на мой выбор. Я устал, мне хочется девочку и идей нет.
Здесь мерилом работы считают усталость.
Как любая наука в абелевой категории, то есть там, где можно писать точные последовательности.
>>8356 (Del)
Линейная алгебра это наука о модулях над кольцами, следовательно, математика = линейная алгебра.
>>8357 (Del)
>школьный, самый начальный
Это ты так учил. Линейная алгебра это, по сути, всё про конечномерные ассоциативные алгебры. В том числе теория Галуа это, очевидно, часть линейной алгебры, т.к. расширение поля это ассоциативная алгебра и есть.
>анализ
Функциональный анализ это в основном наука про банаховы пространства (или нормированные алгебры, не важно) что буквально по определению бесконечномерное векторное пространство с дополнительными условиями. В книге Глазмана и Любича первые 5 глав про линейную алгебру, оставшиеся про функциональный анализ, изложение при этом непрерывно. Разделять эти области бессмысленно.
>кодинг и дата саенс
Не математика.
>тяночек
Большинство твоих кодеров к сорока годам даже не женаты обычно как впрочем и ты.
Что, никто, совсем?
 53 Кб, 827x473
53 Кб, 827x473Из программы юрфака (мгу это одно из трёх мест в Москве, где можно стать юристом, а не оператором колл-центра, всего в стране этих мест меньше десяти) математику убрали совсем, лет пять назад, если не ошибаюсь.
А так юриспруденция это конечно крайне интересная вещь (конституционное право во всяком случае), как и экономика, история, философия и много чего ещё.
Как и везде, есть первая культура и вторая. Вторая культура это Оберон версии 2.0, в просторечии Java, цпп-сектанты и ООП в целом.
Первая культура это SML по Роберту Харперу, модули над типами, генеративность, функтор шеринг и прочие архитектурные преимущества.
А теперь выйди, зайди и пучкни.
Кольцо это когомологии, гомологии это группа.
Думаешь интегратары знают, что такое кольцо, а уж тем более (ко)гомологии?
Красивый попугайчик.
Множество это частный случай модуля над кольцом, а именно, такой модуль, в котором не обязательно выполняются аксиомы модуля, и кольцо не обязательно является кольцом, и не обязательно есть внешняя ассоциативность. Тривиальный случай, короче говоря.
Средствами теории модулей над кольцами почти невозможно получить какие-ибо содержательные результаты о множествах.
Средствами теории множеств, как ни странно, тоже.
Единственная причина, по которой о теории множеств до сих пор помнят, это то что её создание приписывается Дедекинду. На самом деле из его переписки с Дирихле вполне ясно, что на самом деле Рихард хотел создать теорию топосов.
>о теории множеств до сих пор помнят
Только из-за твоего поста теперь вспомнят, а так её обычно не помнят (вменяемые люди).
Какая область или так сказать, раздел математики наиболее интересная и перспективная для изучения? Хочу заниматься этим в системах компьютерной алгебры.
И что сейчас, так сказать, в тренде в математике?
Алгебраическая к-теория.
Именно. Один из таких результатов - SET определена корректно и образует well-pointed топос.
Разумеется, это является результатом теории множеств. Более того, это является ключевым результатом, с которым обстоятельно знакомят всех первокурсников всех матфаков (хотя и не произнося слово "топос", обычно).
>хотя и не произнося слово "топос", обычно
Ну в таком случае это к математике особого отношения не имеет.
Действительно, причём результат не из теории множеств. "топос" не является понятием "теории множеств".
Отнюдь. Результат принадлежит той теории, средствами которой он доказывается. Вовсе не той теории, языком которой он формулируется.
А, понял, вообще все результаты "обычной математики" на самом деле результаты теории множеств.
Нет. Ведь далеко не все результаты "обычной математики" доказываются специфичными теоретико-множественными средствами, такими как форсинг.
 22 Кб, 400x386
22 Кб, 400x386От нехуй делать перечитал даже всю элементарную.
Гомологии и алгебра настопиздела, анализ настопиздел. Осталась топология, в которую я особо не вникал и дискретка.
Но там просто нехуй делать. Пиздец деградация...
Философия упадка?
Вдохговляй учиться, а не копротивляй
Могу советовать почитать про суперанализ, считается чем-то очень сложным.
Леммы теории категорий проще доказывать вообще без слов, жестами.
ban
Я думаю что в наше время, после конца истории и осознания того эзистенциального факта что ни только математика или науки, а вообще ничего никому не надо, заниматься надо только тем что легко и приятно, а именно - изучать (\infty,Br)-топосы.
Какое отношение это имеет к математике только?
Я вот так тоже думаю, в анализе самая писечка, самая мякотка скрыта на самом деле, но перед тем, как спускаться к частному надо как следует обмазаться общим.
 49 Кб, 180x113
49 Кб, 180x113Как бы я не любил функан и матан, должен признать что именно эта хуерга сильнее всего развивает мышление.
Но о практичечкой пользе этого сейчас я бы поспорил. Слишком древние области. Но для мышления - бесспорно мастхэв
Готов выслушать в любое время.
Слушай, бро, а подскажи как мне матан который картофан с интегралами и дифференциалами в вузе рассмотреть с точки зрения алгебры? Чтобы прям аналогии можно было видеть: теорема картофана - описание на языке алгебры
>именно эта хуерга сильнее всего развивает мышление.
Почему? Как?
Зачем вообще "развивать мышление"? В чем польза или смысл?
Как по мне, "развитие мышления" - универсальная мантра в ответ на неудобные вопросы.
Формула Кирхгофа решения задачи Коши для решения волнового уравнения в R3
Задача Коши для уравнения колебаний струны. Формула Даламбера
Метод распространяющихся волн
Посмотри пока вот это
Никак, у анализа и алгебры разные методы. Есть конечно и алгебраическая часть в анализе и аналитическая в алгебре, но если целиком попытаться заменять анализ на алгебру получится невнятный, никому не нужный алгебраический картофанчик вроде нестандартного анализа.
Дифференциал это алгебраическое понятие (гомоморфизм модуля, удовлетворяющий условию ортогональности); дифференцирование это изначально алгебраическая операция; интегрирование же, не смотря на его происхождение в теории меры, тоже оказывается возможным определить чисто алгебраически (не для всех интегралов, но для большинства).
99% того, что есть в матане, это алгебра на самом деле, например операция свёртки.
>>8462
Методы (я бы лучше сказал: точки зрения) может и разные, а вот объекты изучения одни и те же. Не существует в математике таких объектов или операций, которые нельзя описать алгебраически. И не будет существовать никогда.
>нестандартного анализа
Не имеет отношения к алгебре, более того, эта хуйня возникла как раз как результат не понимания алгебры (в алгебре инфинитезимальные методы давно и хорошо известны).
Я бы еще понял, если бы ты про неархимедов анализ сказал, но это просто разговор не по делу.
>99% того, что есть в матане, это алгебра на самом деле
Особенно алгебраичен предельный переход, угу.
Это называется редукционизмом и хорошо известно тем, кто знаком с различными областями логики и философии. От тебя, конечно, знания этих областей не требую, ведь они один хрен сводятся к модус поненс или к Библии, да ещё и записаны буквами на бумаге, ну а это деревья и что их обсуждать, ну только если какой ты у нас дуб на борде.
Это топологическое понятие.
И что? Практически вся алгебра это изучение топологических объектов алгебраическими методами (гомоалгебра), алгебраических объектов топологическими методами (функан), and everything in between (теория представлений например).
Пределы определяются через понятие непрерывности, а не наоборот.
"Теория предела" же, это вообще не математика, и приложения о которых в ней рассказывается – определение производной, вычисление экспоненты и всё прочее, что прекрасно можно сделать и без пределов.
Вообще, пределы в линейной алгебре конечно используются; тем не менее, образованные люди под этим словом чаще всего понимают совсем другое.
>>8467
Мог бы сразу сказать что математика это раздел каллиграфии, как до тебя уже много раз говорили, и оставить упражнения в остроумии, тем более, что получается плохо.
То, о чем я говорю, к редукционизму отношения не имеет, и вообще-то называется линеаризацией, в математике этот принцип лежит в основе более-менее всех содержательных результатов.
Для этого на векторном пространстве должна быть топология. Оно должно быть нормированным, как вариант. Так что всё равно не чисто алгебраическое понятие.
Так гомологии это тоже не чисто алгебраическое понятие, пространство должно обладать рядом хороших топологических свойств.
Глупый вопрос, который ломает мне мой глупый мозг.
Допустим у человека зарплата Х рублей.
У другого человека зарплата больше чем у первого на 25 процентов. Получается X 1.25
У третьего человека зарплата больше чем у первого на 50 процентов. Получается X 1.5. Но ведь 50 процентов это в два раза больше, то есть X*2. Што. Вот тут мой мозг взорвался.
Нет, в 2 раза больше это он получает 2X, то есть больше на 100%
X1.25
x1.5
Ошибка в том, что ты воспринимаешь "1.5", как удвоенную "1.25".
0.25 2 = 0.5, но 1.252 ≠ 1, а 1.25 *2 = 2.5
> никому не нужный алгебраический картофанчик
>Лучшая это Глазман-Любич.
А вот выше лучшей книгой по алгебре считают
> Конечномерный линейный анализ в задачах.
![images[1]](/math/big/thumb/25291/15114794141670s.jpg) 7 Кб, 300x168
7 Кб, 300x168Ты берешь у мамы 25 рублей, и у папы 25, всего у тебя 50 рублей.
Идешь в магазин и тратишь там ровно 45руб.
По дороге домой ты даешь в долг подружке 3 рубля (ей не хватало на что то) .
У тебя остается 2 рубля.
Ты приходишь домой, отдаешь долг маме- рубль и папе - рубль.
Теперь ты должна им по 24руб.
Итог: 24 + 24 равно 48, и 3 рубля тебе отдает подружка, получается 51.
Вопрос - откуда взялся рубль если у тебя было 50?
Почему это тут нет пучков?
>Итог: 24 + 24 равно 48, и 3 рубля тебе отдает подружка, получается 51
Что за бред? Пусть я должен Пете 100 рублей, у меня в кармане 320 рублей. У суммы 100+320 нет никакого смысла.
>Итог: 24 + 24 равно 48, и 3 рубля тебе отдает подружка, получается 51.
Получается 45 вообще то, а не 51. Вычитаем же. Мы тут не зря математики, нас такой хуйнёй не возьмёшь.
Складывать долг как положительные числа? Школьник пиздуй с треда
3 рубля уже посчитаны в 24+24, математически это аналогично непустому пересечению множеств "должен маме-папе" и "должны мне", так что "складывать" их, просто добавляя элементы, нельзя.
>лимитов
>интегралов
Смотря на кого учишься, если даже немного связанно с математикой, то это чистая наёбка.
Очевидно, что это нечто социоэкономическое, так что если не доказывать всё нуля, а давать формулы, хера ли сидеть джва года на пределах? Один хуй никому не интересно, а разбираться во всём будут только когда приспичит по диплому.
Нет
Математический анализ это как священная римская империя: не математический и не анализ.
Посоветуйте книгу по эллиптическим кривым с задачами.
Второе.
S = 1 + 1/10 + 1/100 + 1/1000...
Умножаем на 10:
10S = 10 + 1 + 1/10 + 1/100... = 10 + S
Вот это вот 10 + S почему и как взялось?
Спасибо.
Внимательно посмотри на первое выражение, а потом на второе.
Мысленно убери во втором 10, получится: 1 + 1/10 + 1/100... Это и есть S (см. 1 выражение). Вернув 10, у тебя получится 10 + S
Я понял, точнее заметил. Спасибо! Надо быть внимательней.
:)
Не стоит лезть в подобное, не освоив школьную программу до 7 класса.
У Ленга было, насколько хорошая не знаю.
нужно пытаться доказывать теоремы самому, поэтому в любой книге есть задачи.
Семёрка вычеркнета потому что она единственная больше 6 - желтый круг в центре.
Во второй будет 9. А в третьей наоборот 4, потому что все остальные числа больше 5.
Спасибо.
Школьник-двоечник.
Какие шансы стать математиком?
А то насмотрелся на вас, тоже захотел познавать порядок вещей.
Если ты считаешь математикой то, что в посте на который ты ответил, то всё очень плохо.
Например?
Какое определение "+" у тебя, в какой системе работаешь?
Привет, посоветуйте не сильно зободробительную книжку по ТФКП и задачник. Цель - вспомнить универскую программу
Danke schön!
Needham Visual complex analysis
Форстер Римановы поверхности
Taylor Several Complex Variables
Уэллс Дифференциальное исчисление на комплексных многообразиях
Смотри список в шапке. Если совсем нулевой, то можешь начать с "Арифметики" Киселёва.
Jost Mathematical Concepts
"Для успешного изучения книги Серра в основном достаточно общего курса алгебры, читающегося студентам наших университетов и педагогических институтов в первые два года обучения."
Ну так и решай, считая y независимой переменной, а потом y вырази через x
Там опечатка. Должно быть так: "Для успешного изучения книги Серра в основном достаточно курса алгебры, читающегося школьникам старших классов или пту"
Доказывать существование и уникальность интеграла в любой категории с начальным объектом.
Школьники должны знать, что такое "изоморфизм", " группа ", " поле "?
Это даже не входит в школьную программу.
>Школьники должны знать, что такое "изоморфизм", " группа ", " поле "?
Да, школьники старших классов или пту. Определения этих вещей тривиальны.
Но там им не учат, в школах. Они могут догадаться об этих понятиях лишь из сообществ математиков.
Чтобы учить решению квадратных уравнений, знания формул площадей фигур, обучают логарифмам, производным, комплексным числам, свойствам треугольников, и тиа того.
Комплексным числам не обчают.
 1,1 Мб, 2265x125
1,1 Мб, 2265x125Интересует вот этот предел.
![15096383815020[1].webm](/math/big/thumb/25291/15118319292240s.jpg) 6,1 Мб, webm,
6,1 Мб, webm,640x360, 1:56
А в чем собственно отличие хуеты что он порет от перфоманса какой-нибудь обезьяны вроде Йоко Оно? Никто проверить правильность его слов не может, студенты организованы таким образом что они смотрят в рот и записывают чтобы потом воспроизвести, воспринимают все на веру. Потом в жизни они никак проверить хуйня это или нет все равно не смогут, для манагера по продажам формулы не требуются. Может математики просто придумывают это все, ну как гопобыдло прокачивает бредогенератор чтобы "грузить", вот и они так грузят чтобы была видимость сложности и непостижимости и деньги за это берут. Того кто научился так же складно пиздеть и прохавал фишку берут к себе шнырем аспирантом.
 8,6 Мб, 3425x658
8,6 Мб, 3425x658![15118179892851[1].webm](/math/big/thumb/25291/15118334092420s.jpg) 4,9 Мб, webm,
4,9 Мб, webm,1280x720, 1:24
Подозревал что зададут такой вопрос. Казалось бы - просвященная борда, но первый вопрос это детектирование свой/чужой, все по трибалистическим понятиям. Вот в /b/ тоже есть подобная система детекции да и практически в любых других группах - там нужно знать нужны мемы чтобы не быть баттхертом, которые фактически служат паролем.
Может и математика это набор мемов, которые просто служат паролем для входа в тусовочку?
>детектирование свой/чужой
Да тут даже никакое детектирование не нужно, ты первым же словом всё дал знать.
>просвященная борда
Ага, ещё мы все в белых халатах ходим и в очках, посещаем концерты класс. музыки по вечерам.
Уноси свои маняфантазии и догадки прочь.
Так что не так с "догадками", можешь пояснить? Вот современная математика основана на признании существования бесконечности, но есть секты математиков которые ее не признают. Почему ты на стороне тех, кто ее признает? Ты же служишь просто приемником мемов, которые спускают тебе в мозг самопревозглашенные авторитеты. И идея тем сильнее, чем больше у нее последователей, в чем больше мозгов ее удается импринтнуть.
https://en.wikipedia.org/wiki/Axiom_of_infinity
Просто берет чувак и говорит что надо так думать.
И причём тут "бесконечность"? "axiom of infinity" это просто название, названием получше будет "Axiom of a natural numbers object".
Аксиома бесконечности НЕ утверждает, что существует множество натуральных чисел. Она утверждает, что существует по крайней мере один непустой предельный ординал. Множеством, о котором идёт речь в этой аксиоме, запросто может быть w2.
Не всех ебут основания. Мне нравится уравнения как пример решать, так что, мне теперь это бросить? Заниматься математикой можно и с наивной теорией множеств, а можно и вообще без неё.
Не во всех школах
Пыня никто тут тебе домашку решать не будет.
Их либо пропускают, забрав время на дрочь егэ-задач, либо настолько хуего, что лучше бы вообще не рассказывали. В моей школе просто решали десятки примеров на сложение/умножение.
>дрочь на эге
Такого нету. Мы проходим интегрированние, комплексные числа, логарифмы, производные и тд.
Школьник из Украины.
Ясно, что n - целые. Но если предположить, что n = 1, x = 1.5, то неравенства будут выполнены, а функция пол - нет. В каком месте я ошибся?
Но статья называется "две культуры в математике". Две. Ты считать умеешь? Ах да, у нас же математикам считать не нужно...
> >
> Ага, ещё мы все в белых халатах ходим и в очках, посещаем концерты класс. музыки по вечерам.
Васерман ты?
Значение "x" равно "n" из этого следует, что "x" больше/меньше ИЛИ равняется[для "≥" достаточно чего-то одного] "n. Иначе, называется строгим неравенством.
n < n+1, значит, что любое число меньше своего следующего ["3" больше двух, так как для двух три — следущее].
В ту сторону, в какую направлен знак "<", то число и меньше, например " 2<3"; "3<4"; "400>30"
Махровые Пыньки не понимают чего-то, не умеют, а свою математическую несостоятельность признать не могут, вот и злятся. Одна пынька на анализ тригерится, чуть что нематематикой называет.
Нужно практиковаться. Как я помню, краткосрочная память берет максимально "6-7" символов.
Значит так, учишься разделять число на составляющие в голове.
640362= 600 362 + 40 362
362 = 300 + 60 + 2
640 3 100
640 6 10
640 2 * 1
Иначе говоря, для каждого x, определенного данными неравенствами для фиксированного n, справедливо [x] = n?
Но при этом сами неравенства не содержат в себе определения функции "целая часть числа x". Или содержат?
1. Рассуждает о вещах в которых не является специалистом;
(Дифференциальные уравнения, комбинаторика, математика...);
2. Агрессия. Не способен здраво рассуждать и доказывать свою позицию без перехода на личности;
3. Ложь. В силу отсутствия убедительных доводов, начинает подменять понятия, использует фальсификации и прочую ересь, которую не проверяет, выдумывает ложные факты;
4. Преувеличение. Из незначительных статистических событий делает событие десятилетия, что собственно вытекает из п.3;
5. Дискомфорт. Субъект испытывает дискомфорт исходя из п. 4, постоянно недоволен объективной реальностью, в силу этих обстоятельств пьет, испытывает депрессию итд;
6. Перекладывает вину на окружающих, считает, что виноваты все, но сам от социальной активности самоустраняется;
7. Инфантильность. Верит непроверенной информации. Вопреки здравым рассуждениям все равно пытается найти оправдания своей глупости, выдавая свои скороспелые суждения за мудрость.
Целая часть числа. Пол, потолок.
ПЕРЕКАТ: https://2ch.hk/math/res/29047.html (
Тред бесконечный, а потому в архивач его можно не добавлять. А можно и добавлять.
Вы видите копию треда, сохраненную 25 марта в 12:01.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.