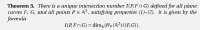52 Кб, 500x500
52 Кб, 500x500Основные списки литературы:
http://pastebin.com/raw/4iMjfWAf - classic
http://pastebin.com/raw/4FngRj6n - dxdy
Архив тредов (там же остальные списки литературы и полезные ссылки):
https://pastebin.com/raw/qhs0WNbY
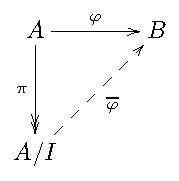
Ну короче судя по отсутствию реакции я делаю вывод, что все согласны со мной: такой нотации нет. Не могут квадратные скобки означать дельтирование, никак. Блядь ёбаное днище, ошибка в формуле в толстенном англоязычном учебнике издательства prentice hall.
Контекст не понятен, что за $\Delta$ вообще? Там четыре индекса в формуле, откуда нам знать, что означает эта разность (и разность ли это вообще)? К тому же в одной формуле есть верхние индексы, в другой нет.
Кидай название книг и страницу в каждом.
 67 Кб, 779x646
67 Кб, 779x646Вот обложка книги. Тебе придётся именно англояз версию скачать. Первая формула (4.39) на стр. 170. Вторая (4.47) на стр. 175.
Чтобы ты быстрее въехал к контекст поясню. Верхние индексы там сути дела не меняют. По смыслу это одна и та же формула. Ну короче жду с нетерпением вашего заключения.
>дельтирование
в математике такого термина нет
в математике квадратные скобки ставят иногда вместо круглых для лучшей читаемости
нейросети - это не математика
>в математике такого термина нет
Знаю
>в математике квадратные скобки ставят иногда вместо круглых для лучшей читаемости
Тоже знаю. Почему и говорю, что ошибка в формуле.
>нейросети - это не математика
Ну не стукай, а куда мне ещё идти? в /ai/ ретарды сидят.
Посмотрел. Вторая формула верна в предположении $w_{ij}^{(l)}(n-2)=0$. Из контекста не похоже, что это выполняется, так что это просто очепятка. Совершенно обычная вещь для текстов с формулами.
Среди математиков вообще нередко опечатки (и их поиск) рассматриваются как упражнения. Так что причина твоего недовольства на кучу постов не очень ясна, особенно в ключе
> учебнике издательства prentice hall.
Ты ведь этот учебник издательства prentice hall очевидно своровал в тырнете.
Гран мерси бро!
>Ты ведь этот учебник издательства prentice hall очевидно своровал в тырнете.
Не совсем. У меня таки есть русскоязычное бумажное издание аж 2020 года за 6 килорушлей. Я надеялся, что там опечаток не будет. Напрасно...
Если не нравится копаться в очепятках, то есть ещё один вариант - просто гугли список опечаток. На англ это называется errata. Для твоей книжки тоже есть, первая ссылка в гугле.
Не, нету. Первая ссыль это для книжки Neural Networks and Machine Learning, но это не та
Бля, точняк. Тогда придётся искать где спиздить теперь эту книгу. Ладно, спасибки ищо раз всем. Мб ещё приду.
Ты споришь с человеком, который не понимает, как определяется равномощность множеств и чем ⇔отличается от ⇒. Зачем ты это с собой делаешь?
Вкатывабсь в математику, сколько водки должен выпивать труматематик? Пока остановился на 0.7
>который не понимает, как определяется равномощность множеств и чем ⇔отличается от ⇒
О, так ты же дофига понимающий.
Уточни, знаток, почему множество натуральных чисел равномощно множеству чётных, натуральных? И в догонку, почему по такой логике множества {1, 2} и {2, 4, 6} нет?
А по поводу сопоставления тождества (эквиваленции) со следованием (импликацией) ты проебался, ведь в спорном утверждении не было эквиваленции. Да и попытка свести высказывание к булевой логике потешна, что предсказуемо от фантазёров-идиотов.
>>1348
>поэтому не думал
Да ты вообще лишён мышления, ёбаный сектант. Нарекаю тебя и таких как ты мат-петухами.
Можете дальше кукарекать и фантазировать, сучата.
зависит от специализации
если мат.анализ, то 0.7 будет явно мало; если диффуры, обязательно нужно заедать картофаном, однако 0.7 может и хватить; если ты занимаешься гомологической алгеброй, нужно неправильно жить, принимать разные препараты, и один раз в таком неправильном состоянии увидишь среду, такую, бурляющую, которая скажет "задавай мне любые вопросы", здесь ты на верном пути; если занимаешься гиперболическими многообразиями, нужно трахать себя в зад резиновым членом (ощущения интересные); наконец, если это алгебраическая геометрия, то здесь нет однозначного ответа.. можно измазывать говном стены в туалете гарвардского университета
>почему множество натуральных чисел равномощно множеству чётных, натуральных
потому что можно установить биекцию?
спор выше не читал
Очевидно что четных чисел меньше чем натуральных, ведь мы берем натуральные числа и выбрасываем из них половину. При этом мы не можем выбросить пловину четных чисел и получить натуральные. То что там какая то биекция-хуекция это вообще не имеет никакого отношения к вопросу. Это шиза просто какая то. Не удивительно что Кантор из психушки не вылезал.
Современная математика это подвид дрессуры поэтому никто не видит никаких странностей во всем этом шизойдном бреде. Как какое то время назад строили сто лет т.н. "итальянскую школу" алгебраической геометрии и всем было заебись пока все совсем не развалилось.
тоже мимокрок
У нас два множества: N и 2N. Для любого элемента из 2N существует элемент из N. Два разных элемента из N имеют разные образы в 2N.
Т.е. получается отображение из N в 2N покрывает полностью множество 2N, и кроме того, отображение идёт один-к-одному. Ну вот и всё, равномощные множества.
спасибо, есть к чему стремиться
>Очевидно что четных чисел меньше чем натуральных, ведь мы берем натуральные числа и выбрасываем из них половину.
из бесконечности половину выбрасываем?
дальше читать не стал
 3 Кб, 836x490
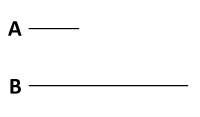
3 Кб, 836x490Так это, скажи мне тогда, 2N должно быть больше или меньше N? N в смысле множество натуральных чисел. А я посплю и почитаю что ты ответишь.
>потому что можно установить биекцию?
Она у вас довольно избирательная получается. Для конечных множеств, значит, работает, а для бесконечных нет. Фантастика, ебать.
>шестикласснику
можно и святые писания объяснить и что Пыпа самый лучший в мире вождь и какую угодно хуйню. Нахуй ты с сажей пишешь в закрепленном треде еще объясни, хуесоска.
Залетные дебики с зекача и как вкатиться в математику в хх лет - это база треда
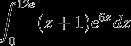 1 Кб, 131x46
1 Кб, 131x46Без телефонов, компов, нейронок и прочих калькуляторов
Листок бумаги и ручка, по времени не дольше 10 минут
За 10 минут он в уме берётся, лол
>И что тебя смутило
меня ничего не смутило, тупой вонючий кусок говна; наоборот, всё стало отлично ясно
>>1360
так и получается: для бесконечных множеств возможно, что имеется биекция между множеством и его собственным подмножеством, а для конечных такого не бывает (в случае натуральных и чётных чисел такая биекция даётся явной формулой, т.е. её буквально можно видеть). от твоих психических проблем этот факт никак не зависит
>>1365
это элементарное вычисление
Такие потешные проекции долбоебки. Или это ты реально про себя написал?
>от твоих психических проблем
Это ещё большой вопрос кто тут ёбнулся. Человек, отрицающий очевидное, в угоду принятому, поражает больше.
>являющиеся определениями в теории множеств
Мат-петух, ты так можешь в определении принять что Земля плоская, а под плоскостью киты да слоны находятся. Как тебя это оправдает?
ты не только несёшь чушь, но и демонстрируешь полнейшее невежество в предмете, о котором споришь
да, в математике допустимо в качестве определений и аксиом принимать абсолютно всё что угодно (что имеет формальный смысл в выбранной системе).
потому, если ты хочешь устроить действительно содержательную дискуссию про натуральные числа, следует сначала условиться, в какой системе аксиом эта дискуссия будет иметь место.
но такой разговор вряд ли будет уже тебе по силам, вонючий тупой кусок говна
>вряд ли будет уже тебе по силам
Согласен. Мне не по силам заниматься шизовой практикой для любителей спекулятивного мышления, самонаёбщиков. Лучше траву потрогать, а не курить её.
Продолжай и дальше, мат-петух.
нет ничего априори очевидного, если ты не петух
утверждение истинно, если оно осмысленно и его можно доказать
>нет ничего априори очевидного, если ты не петух
Начались наркоманские манёвры. "априори" сформировано опытом. Живи теперь с этим.
>утверждение истинно, если оно осмысленно
Истинно, если проверено.
>ты так можешь в определении принять что Земля плоская, а под плоскостью киты да слоны находятся
Земля, киты и слоны это не математические объекты, и, следовательно, никаких содержательных допущений о Земле, китах и слонах математики не делают. Ты вряд ли понимаешь, какого рода допущения математики действительно делают и почему.
Еще замечу, что ты продолжаешь не понимать, что мощность множество это не единственная мера "размера" множества, и есть достаточно инвариантов, которые различают, например, между "размером" натуральных чисел и "размером" четных натуральных чисел.
>>1384
>Пусть практика не отрывается от теории.
Математика, со всеми ее допущениями, пока сделала для "практики", что бы под этим не подразумевалось, и для понимания вещей, встречаемых в опыте, больше, чем все, кого эти допущения продолжительно корежат.
>Математика пока сделала больше, чем все, кого эти допущения продолжительно корежат.
Это уже даже не смешно. Казалось бы, люди делают открытия, но...
Знать недостатки отвлечённого подхода тоже нужно, а не петушиться математизацией всего, как истиной. Я закончил.
>Знать недостатки отвлечённого подхода тоже нужно, а не петушиться математизацией всего, как истиной
примени это на практике и расскажи, как из множества натуральных чисел выкинуть половину и получить меньшее множество, лол
>да, в математике допустимо в качестве определений и аксиом принимать абсолютно всё что угодно (что имеет формальный смысл в выбранной системе).
Это потешный копиум. Если бы это действительно было бы так то к математикам было бы такое же отношение как к долбоебам которые в 30 лет играют в солдатиков. Их бы обоссывали с порога все кому не лень.
Напомнило интервью с Эмилюшкой Ахмедовым. Он типа физик. Его спросили - что такое время. Так у него так же пердак воспламенился от этого вопроса и он так же начал нести известную хуиту - мол физики вообще никак этим вопросом не занимаются, а физики просто ставят эксперименты и записывают их результаты. Представляю какой бы был ор если бы физики пришли клянчить деньги на очередной коллайдер с таким то питчем - "да мы просто построим коллайдер, там будем сталкивать хуиту и записывать результаты. Все. А что еще нужно?" На самом деле они там такие наверняка охуительные истории расписывают как они пенетрируют в тайны Вселенной и change everything. Иначе бы захлебнулись бы в потоках урины.
>Если бы это действительно было бы так
просто ты очень тупой и не понимаешь, о чём речь
тебе уже предлагали выше пойти поучиться, потом затевать свои глубокомысленные шизо-дискуссии
Мелкочмоха, я же тебя спросил что тебя смущает, ты только жопой повилял и был закономерно обоссан. Чего тебе еще нужно? Еще струю урины? Ты когда нибудь про треугольник Серпинского слышал интересно? Иди почитай, тебе там так чердак снесет - ведь там выбрасывают бесконечное количество точек да еще бесконечное количество раз между прочим - в себя уже никогда не сможешь прийти.
петух, который написал вот это
>Очевидно что четных чисел меньше чем натуральных, ведь мы берем натуральные числа и выбрасываем из них половину.
будет мне рассказывать про треугольник Серпинского
А вдруг дауненок чего то сможет понять и станет меньше срать своей тупостью? Попытка не пытка же. Написал бы от чего тебе все сраку рвет, может бы чего тебе еще объяснил, я сегодня добрый.
Не понимаю, модуль же никогда не может быть отрицательным — по определению он всегда >= 0, поэтому например уравнение вида |a|= -7 не должно иметь решений
> Не понимаю, модуль же никогда не может быть отрицательным — по определению он всегда >= 0, поэтому например уравнение вида |a|= -7 не должно иметь решений
Кто тебе сказал, что модуль отрицательный?
Если ты берешь a=-7, то |a| чему равен? Правильно, он равен -a, то есть -(-7)=7
Спасибо, стало понятнее
>Ого.
Чего? Земля, киты и слоны это не математические объекты - они не определяются в формальной системе, о них не доказывают теоремы. Множества, функции, группы, числа, последовательности это математические объекты.
И ты продолжаешь игнорировать наличие инвариантов различающих размер натуральных чисел и четных натуральных чисел.
>>1387
Почему ты обрезал часть моего ответа, где я говорю, что математика сделала для практики больше, чем те, кого допущения в математике корежат? Это банальный факт - математика сделала больший вклад в улучшение повседневной жизни среднего человека и понимание мира, чем те, кого ее "допущения" корежат, потому что у последних обычно недостаточно умственных способностей, чтобы сделать хоть какой-то вклад хоть в какой-то области.
>Знать недостатки отвлечённого подхода тоже нужно
Ок, но равномощность множества натуральных чисел и четных натуральных чисел и наличие "актуальной бесконечности" это не недостатки "отвлеченного" подхода, и никакого вреда "практике" эти "допущения" пока не принесли.
 772 Кб, 666x561
772 Кб, 666x561>Земля, киты и слоны это не математические объекты
>о них не доказывают теоремы
>продолжаешь игнорировать наличие инвариантов различающих размер натуральных чисел и четных натуральных чисел.
Это же клиническая дурка.
>я говорю, что математика сделала для практики
Только в голове совсем больного человека направление что-то там делает, а не учёные. А ещё сама математика обогащена физиками и что?
>это не недостатки "отвлеченного" подхода, и никакого вреда "практике" эти "допущения" пока не принесли.
Ну как же? Внимание переведено на разработку и изучение ложных представлений, вместо того чтобы заниматься действительно полезными делами. А ещё внедрился явный догмат, что можно наблюдать на примере мат-петухов, как вот этот>>1402 шнырь, да и тебя.
>то к математикам было бы такое же отношение
Или как к выблядкам, которые отрабатывают гостовские задачи.
>нужно трахать себя в зад резиновым членом (ощущения интересные)
Правда ли, что только таким образом можно окончить НМУ?
На вес коммутативных диаграмм.
таких нет
>Почему модуль числа всегда равен положительному числу
Просто по определению и всё. Я же ведь могу договориться со своим сообщником вместо слова "хуй" говорить "банановое желе" чтобы враги не догадались? Могу. И теперь в нашей речи "банановое желе" всегда будет означать "хуй". Просто по определению. Так и просто потому что мы определяем модуль целого числа X, если X<0, как X*(-1), то | -6 | = 6. И всё. Никакой метафизики тут нет.
А я накатал пост, где хотел пояснить за всю хуйню, а потом просто закрыл браузер и всё. И сразу так спокойно на душе стало. Самое лучшее я уже получил, отрефлексировал и вербализировал свои знания, а спорить с воинствующей необучаемостью никакого смысла нет. В конце-концов, школьный учитель - это одна из самых худших работ.
Плохо, что ли? Хорошо! А учителям стоит помнить простую вещь: в реальности их задача состоит в том, чтобы помочь тем, кто хочет научиться. Тратить время на остальных смысла ноль.
 207 Кб, 640x640
207 Кб, 640x640Как ваши пучки?
Я аспер, бодро приближаюсь к защите диссера. По внутренним ощущениям мой вклад в него ну 10%, от силы 15-20%. Это норма? Чувствую себя каким-то лохом, тильт короче.
Там же они общие, у каждой науки своя специфика, и по ощущениям большая часть там только стремящиеся. А тут точно сидят несколько кфмн математиков.
среди всех моих знакомых, с кем я поступал в аспирантуру, защитился я один. так что норма, согласно моему опыту, это когда до защиты человек не добирается вовсе. мне известна также диссертация, вклад автора в которую 0% (она была сделана другими людьми). свою диссертацию я практически целиком сделал сам, поскольку мой научник не слишком хорошо знал тему, с которой я работал; местами он даже препятствовал моей работе, когда не верил, что я всё делаю правильно (мне было очень трудно спорить, поскольку я доверял авторитету); всё же в целом он очень внимательно отнёсся к моей работе, указывал на пробелы, которые стоит лучше прояснить, и т.д., так что я ему благодарен. очень важный момент, в котором не было никакого моего вклада, - это постановка задачи. задача была поставлена мне извне.
я не могу сказать, что моя работа была какая-то глубокая и сложная. скорее, требовалось хорошо разобраться в теме и применить известные техники нужным образом
несмотря на то, что в диссертацию я вложился сильно и многому научился, работая с ней сам, науку я в итоге бросил, ушёл в другую профессию, в которой больше денег. ныне по вечерам, бывает, попучкаю по чуть-чуть, но в основном сил на это нет, да и задумываться об этом я уже почти перестал
в целом, я считаю, неважно, какой у тебя вклад в твою диссертацию и насколько интересная задача, которую ты там сделал. главное - это то, чему ты научился, и сколько у тебя сил и возможностей продолжать идти по этому пути дальше. так что держись и удачи тебе
Я ктн, защищался десять лет назад. Можешь любые вопросы задавать. Я свой дисер полностью сам сделал, т.к. мой научник был старым дементным совком, и толку с него было как с козла молока. Но тебя за твою ситуацию не осуждаю. Главное, чтобы плагиата не было и чтобы всё то, что вложили в твой дисер другие, ты понимал очень хорошо. Просто пойми простую вещь, научная среда весьма честолюбива. В течении 10ти лет после защиты на тебя можно по положению ВАКа писать заяву о лишении степени. Твой дисер будет валяться в открытом доступе и ВООБЩЕ любой обрыган (например просто твой хейтер) может написать заяву, чтобы тебя лишили степени, имей это ввиду. Я знаю как случаи заявлений диссернета за плагиат - там человека лишили степени. И знаю случаи заяв по причине интриг и ненависти преподов между собой. Грубо говоря твоего научника ненавидят, и чтобы ему насрать, накатают заяву на тебя. Я знаю два таких случая минимум (но там степени сохранили - заявителя ВАК послал нахуй). В этом случае ВАК с вероятностью 90% вызовет тебя в ДС и там будут тебя щипать за разные места. Если они там заподозрят, что ты в своём дисере нихуя не шаришь, тебе пиздос. Там сидят монстры науки, которым лапшу на уши не повесишь. В общем учти, ВАК - контора серьёзная. Даже магистерский диплом по сравнению с кандидатской - это хуйня подзалупная в плане серьёзности, как могут выебать.
>так что держись и удачи тебе
Спасибо за ответ, анон. Добра.
>>1427
Тебе тоже спасибо, но я вовсе не о плагиате, тут все чисто. У меня научрук как раз не дементный дед, а кайнда мастодонт, который меня раздолба тащит. Я вот про что - выпустили мы статью, как она делалась? Во время обсуждения он мне накидывает схему того, что должно получиться, и говорит проверить самому что все будет действительно так. Я проверяю. Если в какой-то теореме затык с доказательством, он еще дает подсказку как надо делать. Короче постоянно ведет за руку, а иногда и за уши тащит. С одной стороны вроде понятно, тема довольно сложная, не из разряда "об одном частном решении частного случая уравнения хуева-пиздуева", но с другой стороны не хватает ощущения сопричастности что ли, будто это все и не я делаю. Много раз слышал байку, что докторская получается хуже кандидатской, потому что из кандидатской всегда торчат уши научрука, а докторскую делаешь сам. Но я не понимаю, до какой степени эти уши должны торчать.
Видимо, в процессе сообщения кинетической энергии на Луне тело получает большую энергию.
Выглядит бессмысленно. Контекст?
А я не понял, ответ неверный?
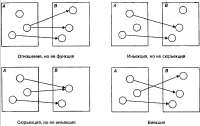
>3. Если запырку отравить, то она сразу начнет пускать пузыри.
>a. если запырка пускает пузыри, то она была отравлена;
>b. если запырку не отравить, то она не будет пускать пузыри;
>c. если запырка не пускает пузыри, то она не отравлена.
Да, если её отравить, она запузыриться. А может она так же запузыриться, если её уебать по животу с ноги.
а) Нет, её могли уебать с ноги
б) Нет, она может пускать пузыри и в ином случае. Нет гарании, что если мы её не отравим, она точно не будет пускать пузыри
с) Да, потому что иначе она бы пузырилась.
мимо другой анон
Вообще не употребляю. А ты в Москве с какой регулярностью ешь? Нравится? Сорта различаешь?
>А может она так же запузыриться, если её уебать по животу с ноги.
А если запырка - это космический объект по объёму на уровне планеты?
Ну и что? Может быть другой фактор, отчего она пузыриться может. В черную дыру влетит и запузырится.
Если известно что да, только отравление пузырение вызывает и болше ничего, то все 3 варианта подходят получается.
>Если известно что да
А если известно только то что указано, то зачем строить ещё предположения?
Если в воду добавить серной кислоты, вода нагреется. Добавление серной кислоты это единственная возможная причина нагревания воды? А теперь просто съеби.
>Если в воду добавить серной кислоты, вода нагреется.
О, стандартная логическая ошибка смены объекта обсуждения. Тупица, там речь шла о воде? И ты ещё, пиздаглазая мразь, будешь мне что-то за логику рассказывать? Ты бы сам отсюда съебал быстро, мат-петух.
>если кто-то из вас в это неспособен
Если ты посторонний уебан, которого не спрашивали, влезаешь в обсуждение, то идёшь на хуй и заваливаешь ебало, мат-петух.
во-первых, это не обсуждение
во-вторых, нахуй следует идти тебе, порватка, ты здесь на доске посторонний
>Если ты посторонний уебан, которого не спрашивали, влезаешь в обсуждение, то идёшь на хуй
>Туши свой синдром вахтёра
у вас тут двойные стандарты отклеились
>у вас тут двойные стандарты отклеились
>во-вторых, нахуй следует идти тебе, порватка, ты здесь на доске посторонний
Не тебе об этом сообщать, полудурок.
доска посвящена математике, а ты занимаешься исключительно бессодержательным срачем
причём в заглавном треде, посвящённом вопросам начинающих
само собой, тебе здесь не место
Вопрос изначально касался логического высказывания. Пока ты, мат-петух, не стал выставлять своё ЧСВ и включать вахтёра, всё было в рамках обсуждения. Само собой тебе следует завалить ебало.
>Вопрос изначально касался логического высказывания
вот я и высказался насчёт этого вопроса: переводи высказывание в логику первого порядка, и вопрос решён
но ты быстро перешёл на срач, что ясно указывает на тот факт, что никакой математический вопрос тебе не интересен и ты не намерен его обсуждать. твой ответ на моё замечание также подтверждает это. я вежливо рекомендую тебе зашить жопу и отдохнуть от интернетов года 3-4. можно посвятить их образованию, чтобы не быть дебилом
Результат аффинных преобразований x и y обычно обозначают x' и y' (икс/игрек штрих). Как этот штрих звучит в английской терминологии x prime? Всех чмоки в этом чатике.
Короче да, напишу нормально - мысль всего лишь подтверждает, больше ничего. И что? Такая же штука. Значит и документ документом не проверяют к примеру.
>но ты быстро перешёл на срач, что ясно указывает на тот факт, что никакой математический вопрос тебе не интерес
Когда мы касаемся логики, то она не замыкается только на логике предикатов, тупой идиот, что подтверждается парадоксами в речевых оборотах, а потому, вполне возможно, находясь в контексте, я могу давать обоснование и вне неё. Вахтёрская попытка увязать в удобненьких границах не прокатит.
>я вежливо рекомендую тебе зашить жопу и отдохнуть от интернетов года 3-4. можно посвятить их образованию, чтобы не быть дебилом
Вежливо тебе порекомендую пойти на хуй. Снова, ведь ты, по-умолчанию, являешься тупым, раз не понял с первого раза
Суп, /math/!
Как всякий уважающий себя гумусонитарий после журфака (по специальности которого один хер не работаешь) решил сесть и разобраться в математике. Есть год времени 2-3 часа по вечерам, профильный ЕГЭ по матеше сданный лет 9 назад на 90 баллов.
Цель: подготовитсья к нормальному курсу от The Open University по терверу/статистике на undergraduate сертификат.
Проблема: я нихуя не понимаю математику. В школе я тупо задрочил ЕГЭ (и даже последние задачи) по принципу робота (видишь паттерн - хуярь алгоритм). В вузе ходил в кружок дата сайенса и корпусной лингвистики, там это прикладывание формул продолжилось.
Предполагаемое решение: освоить программу "Матшкольник", и лекции НМУ по общей алгебре и анализу одной переменной, а также терверу. И от этого уже плясать на статистику. Параллельно с чтением литературы найденной в чат жопате и решением задач, читаю How To Prove It за авторством Daniel J. Velleman.
Анон, подскажи проверенной русской и английской литературы по:
1. Элементарной теории чисел (делимость, кольца вычетов, смежные простые, теоремы Эйлера и Бернулли).
2. Полиномам.
Наверное, утверждение "что-то ощущается" Вы посчитаете менее притязательным и необоснованным. Разве что вопрос вызовет значение слова "ощущается".
То же самое и с изначальным вопросом: откуда мы знаем, что существуем? Вопрос к слову "мы".
>>1469
Понимание математики и намечаемые Вами темы очень удалены друг от друга. Начать, конечно, следует с понимания.
>>1469
Сначала критика, потом совет.
>Предполагаемое решение: освоить программу "Матшкольник", и лекции НМУ по общей алгебре и анализу одной переменной, а также терверу. И от этого уже плясать на статистику. Параллельно с чтением литературы найденной в чат жопате и решением задач, читаю How To Prove It за авторством Daniel J. Velleman.
Заблуждаетесь. Все это либо не направлено общее на понимание математики, либо только увеличит прикладывание формул.
Советую посмотреть серию книг «Энциклопедия элементарной математики». Особенно продвинутого материала в них не будет, они концентрируются на привитии понимания.
 69 Кб, 502x361
69 Кб, 502x361любой уважающий себя начинающий обязан освоить линейную алгебру и анализ одной переменной. конкертных книг я не подскажу (их миллион и это отдельная дискуссия), но это обязательные предметы. и на самом деле единственно нужные, если ты не намерен погружаться глубоко
после них изучение статистики и тервера не составит никакого труда
Этот шарит.
Интегралы и дифференциалы 100% нужны для инженерных направлений
Го делить на ноль!
Опять на связь выходишь?
Начинай читать Винберга, там первые главые как раз про это. Легко не будет, в начале точно.
А ты тоже любишь пучкать?
если люди не могут согласиться на справедливости какой-то логической связки, то это наилучший способ разрешить их спор
а у меня мат. логика в университете была (как и у всех, кто учился в университете)
>наилучший способ
Наилучший способ - это установить положения в споре, мат-петух. А пока таковых не было, каждый волен полагать наиболее разумное. Но вот только фантасты любят придумывать неуказанное, а потому и неразумное. Запомнил?
Мы никогда не знаем, может наш мозг взломали. это если без полиции которая нас защищает и такого не допустит, описания обычной мирной жизни и прочих пап-мам.
Допустим, вы захотели поставить хак защиту (достаточную) на мозг, чтобы не было фейка у вас в башке, и вам таковая доступна (супер элемент 300 на сайте защита ру, вам бесплатно потому что вы студент универа электроники энного города). Но вы до этого еще родились задолго, и раньше еще некие более быстро развивающиеся люди поставили вам умный бэкдор с контролем и прочими плюшками, и вам никогда не поставить эту крутую штуку, хоть и вам будет казаться что поставили.
На самом деле это может происходить с вами сейчас. И вы не можете это проверить, нечем, там фейк один в этой ситуации.
Как Билл Гейтс тогда сможет может забрать 100$, которые он якобы выиграл в споре на доказательство что он существует, где он привел слова Декарта "я мыслю-я существую", то есть проверять что он существует ему нечем- там фейк всегда будет.
Вы не представляете себе как математика прочистила мои мозги в школе, поэтому и пишу, вопрос-то не по науке прям какой. Имею право, хоть и не по математике, но по логике-может сильнейшей составляющей математики.
>то это наилучший способ
Зачем тогда свой ёбаный догмат пишешь по нашему спорному вопросу, блядота петушиная?
 11 Кб, 242x350
11 Кб, 242x350Братан, тебе что тяжело? Тут логика лучше, ответ на вопрос-интересует. Что мне делать? Зря на сайт пришел? Странно ты добра сайту желаешь! Отпугнешь же!
как же тебя корёжит
То местный нематиматикопетух, у него все что не пожоже на хуй негра не является математикой, не обращай на него внимание, или шли на хуй
Да все ок, спасибо. Парень/девушка просто слишком старательно чистит треды.
>Если шизику засунуть хуй в жопу, шизик завизжит.
А если засунуть тебе, ты будешь радоваться и смеяться?
мем "не математика" здесь был, когда ты ещё под стол пешком ходил и про двачи не слыхивал. забавно наблюдать, как тебя от него триггерит теперь, залётыш
Ты не ввёл первоначальных определений, мат-петух.
Ввожу определение. Мат-петухом нарекается любой, кто подпадает под положение фанатика, строго придерживающего какой-то системы идей, не подвергая их сомнению, в рамках нашего контекста.
Теперь на понятном тебе языке
{\displaystyle \forall }x : МП(x).
>Этот шизик
Не доказано.
>уже визжит.
Не доказано.
>Если шизику засунуть хуй в жопу, шизик завизжит.
Дополняю. Мат-петух, по-умолчанию, шизик, исходя из строгой приверженности своим идеям, но его особая разновидность обязывает от подобного получать удовольствие, что подтверждается мыслями о данном процессе вообще.
Думайте.
>полное неумение в элементарный TeX
я всё понимаю, но надо же так палиться
если тебе нечего сказать, зачем так усиленно пытаться из себя что-то выжать?
уж лучше с адресацией, чем с ТеХом, пытаясь изобразить из себя знающего человека, лол.
это уже полный зашквар
>пытаясь изобразить из себя знающего
Кто тебе это сообщил, мат-петух? Опять расщепление в башке?
Но меня радует что ты принял свою пидорскую и сектантскую сущность.
А зачем пытаться что-то насрать в ТеХе, если ты этого никогда не делал? чтобы что?
на вопрос можешь не отвечать
рассмотрим куб со стороной $1$ и сферу с радиусом $r$, где $4\pi r^2 = 6$. площади поверхности этих двух фигур одинаковые, однако объёмы разные: у куба это $1$, у сферы - $4/3\pi r^3$, где $r$ выражено выше
а происходит так, потому что кривизна, но это уже сложнее объяснить
ещё один занимательный эффект, имеющий к этому отношение: при деформации куба в сферу, кратчайшие расстояния между точками поверхности будут меняться
Молодчина. Хорошо что ты не сопротивляешься своей пидарской сущности, мат-петух. Теперь можешь вытереть лицо от жёлтых пятен.
Расщепление башки довело тебя до восприятия себя в третьем лице. Ха.
Здесь утверждается что если площадь всей поверхности 108, то при изменении формы куба на другую форму, например на сплюснутый куб без изменения площади поверхности будет совсем другой объем. Как по мне это не возможно.
Ты без проблем можешь построить объект с бесконечной площадью поверхности и конечным объёмом. Самый простой пример - рог Гавриила.
>>1521
Буквально возьми кусок пластилина и поиграйся с ним, стараясь сохранять площадь поверхности и меняя объем. Или буквально построй два прямоугольных параллелепипеда с одной и той же площадью поверхности и разными объемами.
>>1524
Ты тот же идиот, у которого $2\mathbb{N}$ и $\mathbb{N}$ не равномощны? То, что у объекта с небольшим объемом может быть очень большая площадь поверхности, буквально используется на практике в реальности. Есть такая штука, активированный уголь, например, может слышал.
>Есть такая штука, активированный уголь, например, может слышал
Слышал, у него внутри маленькие пещеры, так что там все нормально с площадью.
>Буквально возьми кусок пластилина и поиграйся с ним, стараясь сохранять площадь поверхности и меняя объем
Поигрался, площадь и обьем взаимозависимы
Это физика
Это задача по математике в рамках моего курса Algebra 2.
 52 Кб, 1106x769
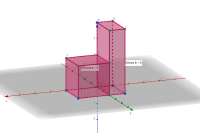
52 Кб, 1106x769Книга пиздит, у фигур одинаковая площадь всех плоскостей и объема, но разная форма.
Ты считать не умеешь. У куба ребро 2, площадь всех граней 6 х 2 х 2 = 24. У кирпича ребра 1, 2, 4, площадь всех граней 2 х 2 х 4 + 2 х 1 х 4 + 2 х 1 х 2 = 28.
 661 Кб, 1200x800
661 Кб, 1200x800Представь, как заполняются почтовые конверты. Изначально они довольно плоские.
всем привет!
Тундра или Столичная?
если ты хочешь учиться именно математике, то на приличный заработок не стоит надеяться, уж точно во время обучения. цель будет другая - поступление в аспирантуру или на постдок за границу. совмещать работу и учёбу без ущерба последней едва ли будет возможно (точно не будет). если хорошо учиться и суметь быстро скооперироваться с научником, можно попасть к нему на грант; это не будут совсем небольшие деньги, но что-то
если что, я не учился в топовых вузах, но думаю, нигде не ошибся
не, работа - это не главное. скорее просто показатель нагрузки в вузе. поступать на математику хочу именно из-за крутого образования, а не из-за профессии или научной карьеры
> поэтому математика слабая относительно крутых московских школ. готовлюсь к олимпиадам, но особо не рассчитываю, т.к. не ботал с 3 лет.
Так ботай, хули сидишь? Даже если бви на мкн не выбьешь по олимпиаде (а туда вроде почти что только всеросов набирают), то все равно есть шанс получить бви хоть куда то в качестве подстраховки или сотку по профилю. Тоже хорошо
> расскажите пж выпускники/студенты упомянутых мест о том как проходит обучение, насколько сложно учиться и возможно ли совмещать учебу со стажировкой или работой (на последних курсах, очев не 1-2)
Сложно. У нас люди понимали, что попали не туда уже на первой недели, некотоыре на второй отчислялись уже. Если к концу года осталась половина студентов, это норм. Если на первых курсах совмещать крайне не рекомендуется, то ближе к последним ровно наоборот. Ты просто без каких то активностей выходящих за простое прослушивание лекций диплом не получишь. У тебя диплом должен быть посвящен какой то рабочей хуйне, а для этого, очевидно, нужно работать, либо какой то научной дрочи под руководством какого то крутого чела в какой нибудь лабе. Сам понимаешь, что второе гораздо сложнее и реже выходит.
про слабую программу я имел в виду что нас не задрачивают на олимпиады ну и математика интересна 4-5 людям из класса, поэтому глубоко не копают на уроках и приходится самому этим заниматься. просто вопрос был скорее про то реально ли учиться на математике людям, которые сунц не оканчивали и всерос не брали. понятно 100500 примеров будет где чел из церковно-приходской школы мехмат оканчивал.
>просто вопрос был скорее про то реально ли учиться на математике людям, которые сунц не оканчивали и всерос не брали
реально, хотя поначалу будет трудновато
>совмещать учебу
Я реально не понимаю как нормиблядям это удается. Вот допустим во вторник у тебя будет очень важный предмет на который ты ОБЯЗАН приходить (вроде физкультуры или второго иностранного языка). Т.к. добираться до любого места в Моске или любом большом городе минимум час - можно считать что весь день у тебя занят. А может таких предметов будет два или три и ты не сможешь их перенести на один день. Тогда ты скажешь РАБотодателю так и так буду приходить не пять раз в неделю а три. А он скажет конечно ололоша ведь ты самый незаменимый сотрудник. Нет. Он пошлет тебя нахуй и в пизду с порога. Это уж не говоря про сессии с которыми надо будет несколько недель крутиться как сумасшедший. А уж если к ним еще и реально готовится надо... А тебе еще и на РАБоте мозги ебут на всю катушку параллельно...
Реально конечно. Можешь взять дефолт учебники университетского уровня, например Зорич-Виндберг-КострикинМанин и попробовать их почитать. В реальности может оказаться всё ещё проще, например в МФТИ вместо КострикинМанином тебя накормят Беклемешивым, который гораздо менее абстрактен.
Чтобы олимпиады тащить не нужно их решать с 5 лет. Если на всерос или межнар метишь, то возможно это так, если не утрировать. Но есть куча других олимпиад, более простых, и которые котируют ВУЗы. Можешь их сам нагуглить, у каждого ВУЗа свой список.
Я сам не олимпиадник, всё моё олимпиадничество закончилось где-то на 3/4 ЛенМатКружков в своё время. Но мне кажется возможно к ним за полгода подготовиться, особенно если с репетом. Поищи какие-нибудь сообщества, может там лучше ответят. Я знаю только о Поступашках.
Ну и не думай, что олимпиады = математика. Многие олимпиадники, покушав настоящей, разочаровываются и съебывают в программисты.
Ещё, если ты проваливашься, то не расстраивайся. Поступай в МухГУ и пробуй перевестись. Не получится, то закончи и пробуй поступить в магу в другое место, куда ты хочешь.
Так просто бери Сканави и читай+решай. Можешь параллельно ютуб смотреть, по школьной математике видосов тонна, на любой вкус.
Например?
водка
Это ты очень хорошо сделал, что конкретизировал своб цель. Изучение школьной математики и изучение математики - это совершенно разные вещи.
По школьной математике тебе нужны школьные учебники Виленкин и др. по алгебре и началам анализа и Атанасян и др. по геометрии. Только при условии их внимательного изучения можно прибавить руководства по подготовке к ЕГЭ.
>>1618
>Так просто бери Сканави и читай+решай. Можешь параллельно ютуб смотреть, по школьной математике видосов тонна, на любой вкус.
Я считаю твой совет спорным. Теорию следует предпочитать перед практикой.
>>1035 (Del)
Полагаю, математика занимается разработкой методологии, а не построением научной картины.
>Теорию следует предпочитать перед практикой.
Зависит от цели. Если у анона цель просто сдать ЕГЭ, то реальной необходимости в дрочеве теории нет. К тому же у Сканави не только задачники, да и там вроде теория немножко есть.
Я ваще в первой половине дня думать не могу нормально, когда заканчиваются занятия и начинается сессия переворачиваю режим полностью. Ложусь спать часов в 8-9 утра, просыпаюсь около 4-5, где-то до 6 на раздуплиться, потом часов до 10 занимаюсь, потом созвон с одногруппниками, обсуждение всякого что разобрали, что прорешали, объясняем друг другу какие-то моменты, часов до 12/до часу, и потом где-то до 5-6 утра занимаюсь, кушаю и укладываюсь спать.
Дневной сон тема, если б с учебы приходила не в 6 вечера часик бы выделяла, а так я уже не встану если лягу(
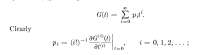 33 Кб, 1153x320
33 Кб, 1153x320это формула Тейлора
ты лучше меня, вот что
а я сидел чет нихуя не вдуплял довольно продолжительное время (ну я и не учился нигде, и не очень часто на математику смотрю, но все равно позор сука)
 202 Кб, 1301x694
202 Кб, 1301x694Я кстати вот еще подумал что чтобы дифференцировать ряд желательно чтобы он сходился равномерно. В противном случае нет гарантии что не получится херня.
Но думаю что если книга не учебник по матану - где особенно любят ебать мозг разными контр-примерами - то автор скорее всего даже сам не задумывался над подобным.
если степенной ряд сходится на каком-то интервале, то он сходится равномерно (и представляет собой ряд Тейлора функции, к которой он сходится)
это хорошо известные факты из базового курса матана
Ах вон оно как. Надо будет как-нибудь матан освежить/подтянуть.
Не бывает цели просто сдать ЕГЭ. А что дальше? Нужно шарить.
Можно было бы посоветовать литературу дополнительно, для большей подкованности. Но считаю, что начать полагается со школьных учебников.
А Я И НЕ СПЛЮ
если у тебя есть научные интересы, это значит, ты над какой-то проблемой работаешь, в которой у тебя интерес, иначе это не интересы, а праздное любопытство в лучшем случае
если ты работаешь над научной проблемой, ясно, что ты как минимум основное не забываешь
>это значит, ты над какой-то проблемой работаешь
Не значит. Ты выдумал определение "научному интересу", а речь не об этом.
Если бы я работал над интересной мне научной проблемой, то такой вопрос бы вообще не стоял.
Жаль, что ты душный дурачок, как и большинство российских технарей и мне приходится объяснять такие простые вещи.
>Он пошлет тебя нахуй и в пизду с порога
Если ты не греча с завода - всегда есть возможность договориться на 30/25/20 часов в неделю за 0,7/0,6/0,5 ставки. Работодатель - тоже человек, сычуш, а ты в унике ещё и квалификацию себе повышаешь, чтобы ему же потом больше денег приносить.
>мехмат мгу
Выебут в душу
>матфак вшаночки
Выебут в жопу
>шызтех с райгородом и шабатеевым
Выебут в мозг
Выбирай
ты не понимаешь значения слов. термин "научные интересы" обозначет область, в которой работающий учёный проводит исследования, а вовсе не "что мне интересно в науке". если ты не работающий учёный, то говорить о "научных интересах" бессмысленно. я полагаю, термин "праздное любопытство" более точно отражает верное положение вещей. можно убрать "праздное", если тебе так обидно, хотя смысл немного потеряется
пусть будет "хобби" вместо "любопытство", смысл тот же: ты либо проводишь исследования, либо нет
На физтехе сейчас есть лаборатории Цфасмана и Бондала (вторая правда без бака пока вроде, но там же на фопфе есть маткафедра другая).
Увлечение. Что за хобот? Совсем уже поехали кукухой, слоняры.
 1,8 Мб, 1024x1536
1,8 Мб, 1024x1536Всех чмоки в этом чатике, кто то пользуется программами для доказательства теорем (theorem prover)? Хочу научиться матдоказательствам, стоит ли рассматривать такой софт как помощник в обучении? Какая его область применения?
Я с дивана. Сам не пользовался. Только читал об этом.
>Хочу научиться матдоказательствам, стоит ли рассматривать такой софт как помощник в обучении?
Есть Xena project, цель обучение андеградов док-во с помощью Lean. Я не знаю, насколько это отличается от традиционных доказательств. Я не пробовал пройти ни один урок из этого. Соответственно я не знаю, может ли это служить заменой/помощником в обучении.
>Какая его область применения?
Теоремы становятся большими и сложными. Ни у кого нет времени каждую статью тщательно проверять, потому люди сразу пользуются результатами и строят на их основе уже свои теоремы. И часто бывает что в каких-то статьях есть ошибки, которые десятилетиями никто не замечал.
Пруверы помогают сразу проверить правильность док-ва, найти в нём ошибки.
Но есть у них минусы. Чтобы запрограммировать док-во нужно потратить огромное кол-во времени. Недавно какую-то статью Шольце проверили с помощью Lean. Чтобы перевести его человеческий текст в программу, потребовалась группа математиков и полгода времени. Потому мне кажется пока, а может и всегда, это тупиковый путь, потому что вбивать каждую лемму в прувер будет занимать. Можно было бы использовать нейросети, которые текст переводят в программу, но как проверить, что она не добавила что-то от себя, не знаю есть ли возможость.
Мне кажется, нужно отдельную специальность в вузах ввести "формализация доказательств". Типа учить как обычных математиков, но с прицелом на формализацию.
И по итогу одни будут обычным образом доказывать, а другие брать готовое и формализовать. Ясное дело, что нужно понимать, что формализуешь, но немного в меньшей степени, чем самому придумывать.
Под санкциями.
Возможно, это как-то связанно с посредственным iq.
 104 Кб, 729x368
104 Кб, 729x368Что знающие аноны по этому поводу думают?
Для меня индукция оч. долго как шизотрюк выглядела, пока изучал её на примерах "доказать правильность формулы" которыми школьников кормят.
Это ощущение ушло, когда столкнулся с более живыми примерами. Там она как-то "естественно" возникает и никакой попаболи при этом.
Незнание определения функции никак не мешает изучать анализ. Классических анализ появился и полностью развился и без ТМ, и определение функции тоже дали довольно поздно. Вообще в анализе ТМ нужна для двух теорем: несчетность R, существование трансцендентных чисел. Обе эти теоремы не особо и важны на начальном этапе, можно жить без них. Логика, кванторы и вовсе бесполезная хуета. Вторую, кстати, можно и без ТМ доказать.
Вообще определения нужны, чтобы конструкции с одних примеров переносить на другие. Например у функций нет "длины", а у векторов, как направл отрезков, есть. С помощью формализаций, можно перенести понятие "длина" на векторные пространства, с помощью скалярного произведения, а затем уже будет легко это определить для функций. Школьникам ничего подобного делать не придется, потому спокойно можно воспринимать функцию как зависимость пути от времени.
идея в том, что нужно доказать импликацию $P(k) \Rightarrow P(k+1)$, т.е. доказать $P(k+1)$ в предположении, что верно $P(k)$ (иначе говоря, при доказательстве этим предположением можно пользоваться). особых здесь правил нет. изредка бывает проще доказывать $P(k)$ в предположении, что верно $P(k-1)$, это то же самое
А если я кассир, то что? Я раньше думал что американцы тупые с их системой мер, но оказывается, это европейцы тупые с их десятеричной. Насильно навязанный неудообный калыч
Суть индукции, которая теряется за формализацией, скорее обратная. Тебе нужно не доказать $k+1$, исходя из $k$, а правильнее было бы сказать тебе нужно свести случай $k+1$ к случаю $k$.
Если из верности утверждения для некоего произвольного k логически следует верность утверждения для "следующего" значение, т.е. для k + 1, значит, высказывание верно для всех значений k, ну и всё по идее
Фу мясоед! Я у таких на поводу не иду. Пересядь на пирожки с капустой и можно будет поговорить.
Область применения - верификация по
 1,2 Мб, 1211x663
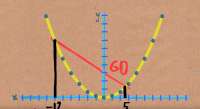
1,2 Мб, 1211x663Гугли пучки и когомологии.
В шапке она, конечно, есть, но отдельно её как будто бы не выделяли в треде.
И хуле? Зачем греки это придумали? Какое практическое применение этим формам? Поржать чисто что так можно? У меня аж жопа подорвалась что нигде нет конкретики по применению этой йобы, везде бесполезные нейрокалычные сайты под копирку либо заблоченые чебурнетом сайты.
"44" это 4 умножить на 4, двач сломал текст
 20 Кб, 697x735
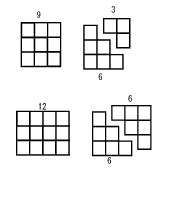
20 Кб, 697x735Вот тут третье квадратное число это 3х3=9, внутри него третье треугольное число 1+2+3=6. Если 9-6=3, то остаётся прошлое (второе) по порядку треугольное число, т.е. 1+2=3. Если прибавить к квадрату длину одной стороны, т.е. 9+3=12, будет прямоугольник. В прямоугольник влезет уже 2 одинаковых треугольника, у которых сторона равна короткой стороне прямоугольника, т.е. 6+6. Как применение у этого? Зачем это придумали? Это абстрактное дрочево или это можно где-то применить?
Хотел блеснуть своими познаниями в семиотике, но потом осёкся и подумал, нахуй оно вообще кому надо. Можешь почитать вот эту статью http://ec-dejavu.ru/e/Eisenstein.html Неудивительно, что вся эта хуйня имеет отношения к кинематографу больше, чем к современной математике.
Я ничего не понял из статьи. Как это относится к тому, что греки зачем-то придумали представлять числа в виде фигур?
Да там вода какая-то и словесный понос как у панасенкова и невзорова, неинтересно. Я про квадратики спрашивал а не про культуру азии.
Ты можешь так же найти для любого действительного числа любое натуральное число, но эти множества не считаются равномощными по какой-то причине.
Выбираешь любое случайное число из действительных чисел, ставишь ему в соответствие 1, потом выбираешь любое следующее случайное действительное число, ставишь 2, и так далее до бесконечности. Важно сделать так, чтобы выбранные случайные числа не повторялись. Нетрудно видеть, что каждому действительному числу можно найти натуральное соответствие.
Ты не указал никакой функции, ебанько. В случае с чётными и натуральными задаётся функция f, такая что f(n) = 2*n, где n - это, собственно, натуральное число. Почему f является биекцией? Да потому что для f существует обратная функция t, такая что t(2n) = n. t(f(n)) = n.
 173 Кб, 620x370
173 Кб, 620x370>Важно сделать так, чтобы выбранные случайные числа не повторялись
вот с этим поподробнее пожалуйста :D
Смотришь их в списке, если повтор случился во время случайного выбора, то не записываешь. ЧЯДНТ?
то, что ты таким образом не перечислишь все действительные числа. иначе: при любом их перечислении найдётся такое, которое в перечисление не входит. это в точности и есть то утверждение, которое доказывается в диагональном методе Кантора (в нём явно указывается такое лишнее число для любого заданного перечисления)
Разве бесконечность не означает, что оно уже содержит это число, которое Кантор пытается вывести при помощи диагонального метода? Кантор смещает каждую цифру каждого следующего числа прибавлением на 1, но, дело в том, что оно уже должно оказаваться в списке бесконечно выписанных/натурально пронумерованных действительных чисел по определению бесконечности.
Я знаю, что такое функция, и это не обязательно линейное уравнение. Это любое правило, по которому мы задаём отношения между двумя множествами или объектами которые им принадлежат. Оно может быть логическим (как у меня), а не только через квадратное, линейное и т. д. уравнения.
А может кто нормально ответить в чем я неправ?
Кантор говорит буквально: пусть задано произвольное соответствие между натуральными и действительными числами иначе говоря,пусть имеется набор действительных чисел перенумерованных как первое, второе, и т.д. (на языке функций, речь идёт об области значений любой функции $\mathbb{N} \to \mathbb{R}$) Тогда, утверждает Кантор, существует действительное число, которого в этом наборе нет, в доказательство чего явно указывает такое число для заданного набора
Если этот набор бесконечный, то там есть все действительные числа, перенумерованные как первое, второе и т. д. Я не понимаю, почему его доказательство верно, потому что вне зависимости от того, как много единиц прибавить, ты никогда не достигнешь момента «вот, это число, которого здесь нет», потому что их бесчисленное количество, которые там есть. И не стоит обзываться, я действительно хочу понять, что здесь не так, это не должно быть так интуитивно понятно, поскольку от этого доказательства плевались даже такие люди, как Креникер и Пуанкаре.
>Если этот набор бесконечный, то там есть все действительные числа
именно это и опровергается Кантором
причём отсутствующее число указывается явно
я не обзываюсь, это другой анон (его можно понять)
Как это опровергается?? Разве бесконечность не означает, что там есть все пронумерованные действительные числа, а это значит, что невозможно найти число, которого там нет? Кантор берет число, которое там есть, и утверждает, что его там нет. Но ты не можешь взять такое число, так как там бесчисленное количество этих чисел. Оно всегда где-то повторяется по закону бесконечности.
>Разве бесконечность не означает, что там есть все пронумерованные действительные числа
там есть все пронумерованные числа, но это не означает, что там есть вообще все числа
>Кантор берет число, которое там есть
нет, он предъявляет число, которого там нет
>по закону бесконечности
мне неизвестно, что это такое
Функция - это множество упорядоченных пар. А с помощью правила это множество определяется. Можно и просто перечислением задать функцию, например, в табличном виде. Но в итоге ты никакого правила-то не задал, которое бы определяло множество, которое бы подпадало под определение функции. Просто кукарекнул, нахрукнул какую-то хуйню и всё.
> там есть все пронумерованные числа, но это не означает, что там есть вообще все числа
Не понял... Разве бесконечный случайный выбор всех чисел из R не выбирает все числа из R? Потом мы их просто нумеруем по порядку, в котором они нам выпали, вот и все.
>>1777
Ну, ты и задаешь функцию данной логической цепочкой: рандомный выбор из R, нумерация, если это число из R не находится в списке (пока что).
>Не понял... Разве бесконечный случайный выбор всех чисел из R не выбирает все числа из R?
определись аккуратно, что именно ты утверждаешь и что именно ты хочешь доказать
Я хочу понять, что R и N это неравномощные множества, но я не могу, на том основании, что, поскольку ты можешь бесконечно выбирать рандомные числа из R и нумеровать их, доказательство Кантора кажется несостоятельным. Если ты можешь выбирать их бесконечно, и, таким образом, поскольку ты это сделал, они все должны быть записаны, что мешает их пронумеровать в этом бесконечном списке?
 196 Кб, 982x620
196 Кб, 982x620>Ну, ты и задаешь функцию данной логической цепочкой: рандомный выбор из R, нумерация, если это число из R не находится в списке (пока что).
Поэтому я и говорю, что ты не смог выучить определение термина "функция", неосилил. Функция - это не рандомный выбор. Если у тебя f - это функция, то если f(x)=y и f(x)=z, то y=z. Никакого рандома тут не может быть.
Может быть, тебя смущает, что там у Кантора написано. Так вот, Кантор не имеет в виду какую-то конкретную функцию. У Кантора в рассуждении присутствует ПЕРЕМЕННАЯ и тип этой переменной - функция. И эта переменная связана квантором.
По логической форме у Кантора типичное доказательство от противного: Предположим, что существует какая-то функция, такая что ... . И дальше это сводится к противоречию.
равномощность $\mathbb R$ и $\mathbb N$ означает возможность построить функцию $\mathbb{N} \to \mathbb{R}$, которая является биекцией. в силу метода Кантора, любая функция $\mathbb{N} \to \mathbb{R}$ биекцией не является, поскольку не является сюръективной
выражая это на твоём (неаккуратном) языке, выбирать числа из $\mathbb R$ ты можешь сколько угодно, но выбрать все никаким образом не получится; для любого такого выбора найдётся число, которого в нём нет
>поскольку ты можешь бесконечно выбирать рандомные числа из R и нумеровать их, доказательство Кантора кажется несостоятельным
А, опять эта дегенеративная хуйня от малолетних дебилов! Никакой ситуации, что во времени происходит процесс, что кто-то или что-то сидит и выписывает пары натуральных и вещественных чисел, нет. Это ты сам эту хуйню придумал потому что не осилил несколько банальных определений.
Даже если я выбираю бесконечное количество чисел из R, там все равно остаётся бесконечно количество чисел, верно? Как так выходит? Не понимаю.
Пуанкаре тоже не осилил получается, если называл теорему Кантора психической болезнью.
если ты определил фунцию $\mathbb{N} \to \mathbb{R}$, то обязательно найдётся хотя бы одно число, которое не лежит в её области определения. справедливо и то, что таких чисел будет на самом деле бесконечно много (их несчётное число), но это уже другое утверждение
Я думаю, что они просто не понимали его теорию и теорему. И если такие светлые умы не понимали, то что от новичка в математике вы хотите чтобы он сразу понял? Я поэтому сюда и пришел, потому что тема сложная.
Я пока только выбор порядковый определил, но потом мы просто нумеруем этот выбор, когда расположили бесконечное количество чисел по порядку. Не означает ли это, что в этом списке должны быть все действительные числа?
наличие функции $\mathbb{N} \to \mathbb{R}$ означает, что у тебя каждому номеру $n \in \mathbb{N}$ сопоставлено число из $\mathbb{R}$, которое этому номеру соответствует. по Кантору, при любой нумерации найдётся число, которое ни к какому номеру не приписано
никакого
>расположили бесконечное количество чисел по порядку
нет и быть не может. у тебя либо определена функция между двумя множествами, либо нет
 34 Кб, 685x277
34 Кб, 685x277Ну, рандомный выбор и нумерация точки из него это и есть функция.
А что непонятного? "Число Кантора" отличается от первого "посчитанного" вещественного числа своим первым разрядом, от второго "посчитанного" вещественного числа своим вторым разрядом, от третьего "посчитанного" вещественного числа своим третьим разрядом, от энтого "посчитанного" вещественного числа своим энтым разрядом и так до бесконечности.
Имеется в виду не какой-то конкретный ряд вещественных чисел, а любой ряд вещественных чисел, и для него строится своё "число Кантора" по вот этому "диагональному алгоритму".
>мне стало скучно, закрыл книгу. Я не создан для математики?
вероятно, да
чтобы заниматься математикой, это должно быть интересно
А что если этот ряд вещественных чисел бесконечен? Ты ведь будешь просто до бесконечности считать число Кантора.
>А что если этот ряд вещественных чисел бесконечен?
С этого и начинается рассуждение. Что натуральных чисел бесконечно. Затем "начинается" "счёт" вещественных чисел:
первое вещественное число,
второе вещественное число,
третье вещественное число и так далее.
И для каждого следующего разряда каждого следующего вещественного числа этой последовательности в "числе Кантора" будет отличие.
>Ты ведь будешь просто до бесконечности считать число Кантора.
Суть в том, что ни на каком шаге это "число Кантора" не будет "посчитано". Каждый шаг оно будет отличаться потому что так задан "диагональный алгоритм". А шагов и есть бесконечное количество, то есть квантор всеобщности всю бесконечность натуральных чисел "учитывает".
Ты просто получаешь череду бесконечных бессмысленных операций в таком случае, а не число, которого нет в списке. Потому что там уже вся бесконечность бесконечно пронумерованных действительных чисел.
"Число Кантора" отличается от каждого энтого числа из списка своим энтым разрядом. Поэтому его не может быть в списке.
Там нет числа, там операция, чтобы получить это гипотетическое число, которого может и не быть, в виду того, что там бесконечное число этих чисел, так что ты просто бесконечно меняешь число, но оно никогда не становится новым оригинальным числом.
А, опять эта дегенеративная хуйня от малолетних дебилов! Никакой ситуации, что во времени происходит процесс, что кто-то или что-то сидит и выписывает пары натуральных и вещественных чисел, нет. Это ты сам эту хуйню придумал потому что не осилил несколько банальных определений.
Никто не говорил, что во времени происходит процесс. Он происходит моментально, если хотите. Не это главное, а то, что всякий раз, когда ты меняешь число, там находится ещё бесконечное количество чисел, для которых нужно изменить твое число так, чтобы оно отличалось от твоего, пока не получаешь новое число, чего никогда не происходит, потому что бесконечность чисел уже там выбрана.
>Он происходит моментально, если хотите.
Тогда и "число Кантора" строится моментально. "Построился" список пронумерованных чисел, "построилось" и вещественное "число Кантора", которое отличается от любого из вещественных чисел в списке.
>чего никогда не происходит
Почему? На каждом шаге эн оно отличается от энтого вещественного числа в списке. Оно не совпадает ни с одним вещественным числом из списка.
Где оно отличается? Оно отличается до тех пор, пока ты не находишь ещё одно число в этом бесконечном списке, которое совпадает с твоим только что измененным числом, и так до бесконечности. Это просто бесконечная итерация поиска, но не новое число.
>пока ты не находишь ещё одно число в этом бесконечном списке
От вещественного числа номер n+1 оно будет отличаться в разряде n+1.
>и так до бесконечности
В этом и смысл, у вещественного числа счётная бесконечность разрядов, и каждый из них отличается.
Но их все ещё бесконечность, поэтому ты делаешь это до бесконечности, никогда не находя нужное отличное число.
>никогда
Никто не говорил, что во времени происходит процесс. Он происходит моментально, если хотите.
Список строится "моментально", и "число Кантора" тоже строится "моментально".
А если ты апеллируешь к тому, что сам список никогда не может быть построен потому что он бесконечный, то просто вернись к началу диалога.
Но число Кантора не строится, потому что ты строишь его вечно? Бесконечность означает, что сколько бы ты итераций и изменений не провел, всегда будет ещё одно n, где тебе нужно будет провести операцию для своего числа в этом n-ном разряде, чтобы оно отличалось от данного числа, нет?
Оно и записывается, и строится бесконечно. Что это за число такое, для которого, сколько бы ты изменений в нем не провел, всегда будет ещё одно n, где тебе нужно будет провести модификацию для своего числа в этом n-ном разряде, чтобы оно отличалось от данного числа?
а число $\pi$ тебя не смущает?
чтобы его правильно записать, надо произвести бесконечное количество вычислений
здесь то же самое: ты не изменения в числе проводишь во времени, а просто считаешь его с возрастающей точностью. при этом задано оно уже полностью, как только задана полностью функция $\mathbb{N} \to \mathbb{R}$
> Это просто бесконечная итерация поиска
В /pr или в жж Кравецкого съеби. У тебя мышление убито программированием, тебя не спасти, к сожалению.
>Оно и записывается, и строится бесконечно.
У всякого вещественного числа счётная бесконечность разрядов. Столько же, сколько и натуральных чисел.
>Что это за число такое, для которого, сколько бы ты изменений в нем не провел, всегда будет ещё одно n, где тебе нужно будет провести модификацию для своего числа в этом n-ном разряде
Потому что это не число, блядь, это функция. Аргументом этой функции является функция из N в R, а значением вещественное число, не какое-то конкретное число, а именно что в зависимости от аргумента. Функция от функции. Есть запись вида a(b(c)), то есть композиция функций, а здесь сама функция, то есть всё множество упорядоченных пар, является аргументом другой функции.
Платонизм и математика несовместимы, кстати. Платонисты не верят в отношения, то есть они верят в предикаты формы P(x), то есть свойства, а вот в P(x, y) они уже не верят.
Поясни.
Ты хочешь доказать, или опровергнуть, что числа из R можно пронумеровать. ВСЕ числа.
>но я не могу, на том основании, что, поскольку ты можешь бесконечно выбирать рандомные числа из R и нумеровать их, доказательство Кантора кажется несостоятельным
Да, ты можешь. Но это не доказывает, что ты их всех пронумеруешь. Просто доказывает, что какое-то подмножество R ты пронумеруешь. Ты можешь бесконечно выбирать целые отрицательные {0, -1, -2, ...}.
> Если ты можешь выбирать их бесконечно, и, таким образом, поскольку ты это сделал, они все должны быть записаны, что мешает их пронумеровать в этом бесконечном списке?
У тебя здесь ошибка и прыжок к неверному заключению.
>Если ты можешь выбирать их бесконечно, и, таким образом, поскольку ты это сделал, они все должны быть записаны
Из первого второго не следует. Я могу из R выбирать одни положительные целые {0, 1, 2, ...} бесконечно. Очевидно я записал не все числа из R.
Док-во Кантора в этом и состоит. Что каким образом ты не выписывай, ты не выпишешь все. Представим что мы не знаем ответ на неё. У нас есть 2 пути её доказать или опровергнуть.
1(доказать). найти явно нумерацию, покрывающую весь R, формулу или описать алгоритм.
2(доказать). доказать что номерация из 1. хотя бы существует, не выписывая её явно.
3(опровергнуть). доказать что нумерации не существует.
Если ты вместо R возьмешь Q, то ты можешь доказать 1. явной формулой(проще всего если допустить повторы чисел) или 2. как следствие счетности прямого произведения множеств.
У нас есть основания полагать, что всё же R несчетно, потому что оно непрерывно. Ты можешь ирл подсчитать яблочки, но подсчитать воду, саму воду, а не объем или прочие дискретные величины, не можешь, это даже звучит бессмысленно.
Дальше Кантор использует док-во от противного, которое в математике очень распространенно. Он допускает, что нумерация всё же существует и выводит из этого противоречия.
>Я пока только выбор порядковый определил, но потом мы просто нумеруем этот выбор, когда расположили бесконечное количество чисел по порядку. Не означает ли это, что в этом списке должны быть все действительные числа?
Все натуральные числа будут израсходованы, но действительные числа не будут пронумерованы. Это говоря образно.
Диагональный аргумент показывает, что любая нумерация действительных чисел не учитывает те или другие из них.
На деле же, без образности, все рассматриваемые пошаговые процессы являются конечными. Поэтому не может быть законченного бесконечного произвольного выбора действительных чисел одного за другим.
Вместо этого выбор совершается согласно какой-нибудь придуманной формуле - конечной сама по себе,ставящей в соответствие данному натуральному числу определенное действительное число.
При этом сами по себе не существуют ни натуральные числа, ни действительные. Они получаются только в результате их рассмотрения или разговора о них, задания аксиом и формул.
Поэтому все конкретно рассматриваемые в некоем разговоре натуральные и действительные числа, а также формулы - конечны по количеству. Формулы перечисления действительных чисел конечны, выбранные натуральные числа конечны, действительные числа под такими номерами тоже конечны. И для каждой формулы рассматривается только одно ею неперечисленное действительное число, хотя теоретически таких чисел бесконечно.
Попробую доказать: если число нечётное, то количество повторений будет тоже нечётное. Например 7х7. Нечётное умноженное на 2 становится чётным. 7х2=14. Но если оно нечётное, то количество повторов тоже будет нечётным, т.е. чётность перекроется последним добавлением нечётного числа 42+7=49. И всё. И приехали. Я прав?
>При этом сами по себе не существуют ни натуральные числа, ни действительные. Они получаются только в результате их рассмотрения или разговора о них, задания аксиом и формул.
Это надо в закреп добавить или в шапку треда.
>Поделил его пополам на два прямоугольных треугольника и понял что можно тут же найти площадь
Какая площадь у этих прямоугольных треугольников? Как ты ее запишешь не используя корень из трех?
это так здорово, когда твой незамутнённый ум, вообще никак не осведомлённый ни о каком опыте человечества, вдруг сталкивается с проблемой, которая волновала людей несколько тысяч лет назад
Найти половину а, найти h теоремой пифагора, корень стороны можно перевести в нормальное число видрил формулой:
https://www.youtube.com/watch?v=MXveVqBxFow
h x a будет площадь треугольника, потому что их два одинаковых.
Уже ведь придумали всё, зачем упоротые числа использовать, я не понимаю...
А может ты? Я спросил прямо: нахуя придумывать упоротые формулы с несуществующими числами, когда можно без них обойтись. В ответ ты пукаешь с умным видом.
>h x a будет площадь треугольника
Пересчитай.
>>1833
>нахуя придумывать упоротые формулы с несуществующими числами, когда можно без них обойтись
Ты без них не обошелся, ты посчитал площадь используя "упоротые" числа и потом нашел рациональное число которое достаточно близко к "упоротому" корню из трех. Многие люди используют для подобного так называемые "калькуляторы", но ты можешь также пользоваться методом из видео.
узнаю почерк Вавилова, лол
А тебе кто-то обещал профит?
 499 Кб, 1748x561
499 Кб, 1748x561В переменную?
только в часть
Правда, что в Москве преимущественно говорят действительные а в Петербургу вещественные числа?
Пределы последовательностей рациональных чисел это функции которые принимают на вход натуральное число n и возвращают рациональное с n знаками после запятой
более точно сказать, это элементы пополнения множества рациональных чисел, снабжённого стандартной метрикой
зачем ты порвался?
Но не интуитивно, и человек продолжит не верить.
Только я придумал что в тком случае делать с длинами сторон треугольников. Можно сказать, что не все измеряемые, но некрасиво выходит
НЕ придумал
Многие греческие учёные были в Египте. Разве нет? Прасолов что-то писал в своей книге по истории математики. На счёт каких-то Тотов неизвестно.
Если заменить дуб на эквивалентный по весу объём ели, общий вес не изменится. Для получения веса дуба, выраженного в елях, сделаем $(6+\frac{1}{2}) \cdot (1+\frac{1}{3})$
Прибавим $2 + \frac{2}{5}$. Это количество кубических метров ели, которое весит $6 + \frac{16}{25}$ тонн
Соответственно чтобы узнать вес одного кубического метра ели, делим общий вес на общее количество метров. $(6 + \frac{16}{25}) :(((6+\frac{1}{2}) \cdot (1+\frac{1}{3})) + (2 + \frac{2}{5})) = \frac{3}{5}$ тонны весит кубический метр ели. Дуб соответственно по условию $\frac{3}{5} \cdot (1 + \frac{1}{3}) = \frac{4}{5}$
$n \cdot n = n_1 + n_2 + n_3 + \cdots + n_n$
$n+n = n \cdot 2 = 2n mod 2 = 0$
Если $n$ - нечетное, то $n_1 + n_2 + n_3 + \cdots + n_n = n \cdot (n-1) + n = n^2 mod 2 \neq 0$
Следовательно, $n^2$ - нечетное.
P.S. И нахуя я это написал.
>>1868
Дядя с таким уверенным ебалом шпарит, но на самом деле несёт хуйню. Есть очень большая разница между рецептурным знанием и научным. Научное знание отвечает на вопрос "почему?", оно строит какие-то теории, доказательства и итд. А рецептурное знание - это по сути те же танцы с бубном. Мы знаем, что у треугольник со сторонами 3, 4, 5 является прямоугольным. Почему? В Древнем Египте такой вопрос не задавался. А в Древней Греции такой вопрос задали и придумали геометрию как дедуктивную систему аксиом и доказательств. Это как в том анекдоте, в результате многолетних исследований муравейников в Московской области было установлено, что отношение длины окружности любого муравейника к его диаметру - величина постоянная, приблизительно равная 3.
Спасибо.
Квадрат нечётного - произведение квадратов всех его простых множителей. Нет простого множителя из N, в квадрате дающего 2, квадрата двойки тоже нет, потому что двойки не было. Потому квадрат нечётного - нечётный. Всё, хуле там доказывать-то?
 209 Кб, webm,
209 Кб, webm,460x412, 0:05
Читаю, разбираюсь, потом забываю. Как фиксить, памагите111
>Читаю, разбираюсь, потом забываю.
это норма, если не пользоваться новым знанием регулярно
делай конспекты - но обязательно такие, чтобы легко они легко и быстро читались (тобой)
тогда восстанавливать будет легче
У меня со всякими квантовыми механиками и ядерными физиками так же. Интересно пиздец как, а через год-другой забываю, ибо нафиг в жизни не нужно. В голове только чувство охуевания от красоты устройства нашего мира. Раз пять всё это по новой перечитывал. Конечно же научпоп.
аугментировать знания в текст - решения задач, схемки, рисунки, скетчи, идеи, математический дневник - все во внешнее персонализированное хранилище. spaced repetition, преподавание изученного, отвечание на стэке, перечитывание при необходимости.
уходи
>аугментировать знания в текст - решения задач, схемки, рисунки, скетчи, идеи, математический дневник
так и зделою, достал тетрадку, буду рисовать всякое
>>1890
>Интересно пиздец как, а через год-другой забываю, ибо нафиг в жизни не нужно
Ну это такое, вон Онотоле Вассерман всякой хуйни не нужной помнит и ему норм, при чем он не самый крутой. Человек может много всего запомнить, нужно как то мнемотехнику прокачивать.
Я хочу понимать как это всё работает, а не просто задрочить алгоритм.
Исходя из твоего описания, тебе нужен матан для математических факультетов.
x^2 = -4
извлекаю квадратный корень из обоих частей уравнения
sqrt(x^2) = sqrt(-4)
получаю
|x| = +- 2i
в итоге, у меня модуль равен комплексному числу, чего быть не может, так как модуль и комплексного, и вещественного числа это вещественное число, по определению, или расстояние, в геометрическом смысле. Какая операция тут была неверной?
придумали божков по своему подобию, а потом, после каких то открытий, ноют, что бог оказывается так вообще не задумывал
Ты сам-то понимаешь, откуда ты модуль получил? Гугли арифметический корень. Это лишь соглашение, в комплексном случае оно не используется.
Какой предмет и объем ты подразумеваешь под матаном?
Приведи пример: где ты встретил матан, что было не разжевано, также что ты считаешь разжеваным?
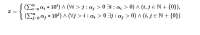 9 Кб, 600x107
9 Кб, 600x107вот нахуя ты знак конъюнкции между суммой и логическим выражением ебанул
сам-то понял, что написал?
Математики доказали абсолютную теорему?
да, пиво без водки - денги на ветер
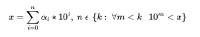 4 Кб, 436x81
4 Кб, 436x81>>1912
>Читаю, разбираюсь, потом забываю. Как фиксить, памагите111
1. Мнемоника. Читай любую книгу по этой тематике, ну или это статью:
https://deru.abcdef.wiki/wiki/Merkspruch
Если сложно "дворцы" создавать, используй карты из игр, журналы про жильё, инженерные кады или sims.
2. Mind maps. Очень полезная вещь.
3. Быстрое чтение.
4. Спорт. И здоровое питание. Очень помогает мозгу. Ещё хорошо мозг развивает жонглирование, и новые хобби.
сдохни сам, анонимное говно
 26 Кб, 1050x700
26 Кб, 1050x700>Когда эта жидовская чурка сдохнет?
чот пучкнул
Я тебя не понял. Изучи язык первого порядка и пиши на нем. Почему вы думаете, что логический язык - это стенография и пишите без определенных правил? Ну, понятно, в ВУЗе так учат. Ой, бли-ин...
Это Дробышевский?
Какой же он жид? Он сто процентов ортодоксальный христианин.
Здесь два вопроса в одном.
Для дегенератов и на уровне так называемых "причинно-следственных связей".
Любой курс мат анализа строится как последовательность теорем, поэтому нет никакой проблемы всё это освоить по шагам.
Но для этого надо немного шарить в логике, а это отдельная дисциплина, и невозможно всё это объединять, поэтому логика живёт отдельно где-то на философских факультетах, а мат анализ отдельно.
Как вы вообще себе представляете, что на математическом форуме вдруг начнётся спор об универсалиях? И там выступит Савватеет
 207 Кб, 640x640
207 Кб, 640x640Дочитал книгу до третьей главы и заблудился, при том материал первых двух уже плохо помню. Решил не продолжать чтение, а начать с начала ведя конспекты и прорешивая все задания, ответы на которые я в основном подсматривал, план такой, смотрю и прорабатываю решение, потом через какое то время пытаюсь его повторить по памяти. Я молодец?
Не владеешь интуитивным пониманием темы. Не знаешь поставленные задачи и мотивацию теории.
Можно ли считать точку вектором? Получается тогда, что вектор образованный между точками, есть разность векторов, а вычитание точки из точки фигня какая то. Каков положняк?
Гугли что такое афинное пространство, там с участием векторного пространства.
От афинного пространства можно обратно к векторному перейти. Точку можно считать вектором, если в афинном пространстве выбрать точку отсчёта, откуда проводить вектора до любой точки.
А можешь мне объяснить почему в алггеоме исследуют вроде бы афинные пространства, хотя про вектора как то там в курсах ни слова?
в алггеоме используются афинные пространства, потому что именно в афинном пространстве удобно изучать нули многочленов. в афинном пространстве нет выделенной точки (нуля), к которой привязана его геометрия, и это удобно, поскольку геометрия нулей многочленов тоже не привязана ни к какой выделенной точке
>в афинном пространстве нет выделенной точки (нуля)
Разве в алггеоме не будет такой выделенной точкой 0=(0,0,...,0)?
Я просто пытаюсь понять как связаны определение афинного пространства по определению с векторами и то "А" которое в алггеоме используется и я не вижу ничего общего.
А как в твоих книжках опреляется афинное пространство и его точки?
В некоторых книжках вполне себе говорят при первом определении про подлежащее векторное. В других говорят просто, что
афинное пространство размерности n -- это набор кортежей вида $(a_1,...,a_n)$, что напоминает определение векторного пространства $k^n$, не так ли (мы только о линейной структуре тут не говорим)? А где-то авторы считают, что это уже очевидный и хорошо известный с разных сторон объект.
Одна из эквивалентных интерпретаций такая: если давать определение афинного пространство через множество точек и векторное пространство, то ты когда координаты точки записываешь, ты выбираешь точку отсчёта и на самом деле в некотором смысле работаешь в векторном пространстве уже. И полиномы вычисляешь в конкретной системе координат, и нули там же ищешь. Полиномы можно трактовать как элементы симметрической алгебры $SV^{\times}$, построенной на подлежащем векторном прострастве $V$.
Другое дело, что нас в афинном алгеме обычно интересует лишь множество решений, поэтому линейная структура нам не особо интересна, поэтому "туповатое" опредление через кортежи чаще всего нас тоже устроит. И ещё мы хотим менять не только базисы, но и систему координат, поэтому не ограничиваемся только действительно линейными (без констанстных членов) преобразованиями. Собсна, другое определение афинного пространства -- это как раз векторное пространство, но с более широким набором преобразований.
она не нужна. ты можешь сделать замену координат, в которой она станет $(1,1,\dotsc,1)$, при этом множество нулей твоего многочлена останется тем же
вообще говоря, нам хотелось бы понимать нули многочленов как своего рода многообразия, которые определены абскратно, уже безо всяких координат. и для них в качестве карт как раз удобно рассматривать афинные пространства, потому как афинные преобразования укладываются в то, что удобно считать морфизмами таких многообразей
у тебя тут есть анон, который пишет подробнее, пусть он рассказывает
>В других говорят просто, что
>афинное пространство размерности n -- это набор кортежей вида (a1,...,an)
Ну да, литерали так и определяется. Без охуительных историй про отсутствие выделенной точки. Поэтому мне и не понятно откуда они берутся.
афинное пространство - это множество, на котором задано свободное и транзитивное действие векторного пространства
Ну, потому что для большинства теоретических построений достаточно проделать всё в выбранной системе координат с выделенным началом по сути, отождествляя точки со множеством радиус-векторов. И/или как можно быстрее перейти от замкнутых подмножеств афинного пространства к идеалам.
Но скорее всего в твоей книжке всё равно есть какие-нибудь конкретные примеры, где что-то про выбор системы координат сказано вскользь. Если да, то это уже какая-то дополнительная структура на твоём множестве кортежей (если только это тоже не с алгебраической точки зрения объясняют).
Напомню, что алгебраическая геометрия -- это не только изучение колец и их идеалов, а также когомологий пучков, но и про свойства фигур, которые иногда мы даже можем нарисовать. Странно было бы, если бы мы не могли менять выделенную точку и рассуждения, которые годились бы для кривой, не подошли бы для смещённой кривой.
Это примерно то же самое, что считать, что векторное пространство определяется не просто набором векторов, но там ещё и фиксирован базис всегда, а к другому базису мы переходим через изоморфизм.
>не припомню чтобы где то явно что то куда то смещалось хоть в одной теореме алггеома
В теоремах про свойства локальных колец в точке любят обычно предполагать для простоты выкладок, что эта точка в начале координат лежит.
Т.е. можно начать просто с множества кортежей без каких-либо операций, а потом сказать, какие морфизмы мы в этой категории рассматриваем. При необходимости аффинную и векторную структуру мы из автоморфизмов восстановить, кажется, можем (например, автомофризм (f(x)=x+p, g(y)=y+c) можно трактовать как сложение с вектором (p, c), и так для любого вектора).
Так что в принципе однохуёственно, кажется, мы же не в изоляции на множества эти смотрим.
>но есть-то и другие автоморфизмы.
какие другие?
>Т.е. можно начать просто с множества кортежей без каких-либо операций, а потом сказать, какие морфизмы мы в этой категории рассматриваем.
на этом множестве, а не в категории
получится афинное пространство с выбранной системой координат
>какие другие?
Треугольные автоморфизмы, например. Для аффинной плоскости это теорема Юнга или как-то так.
>на этом множестве, а не в категории
Я имел в виду, когда проделаем обычную машинерию по определению аффинных многообразий (кажется, её можно проделать просто с множествами кортежей без доп.структуры a priori) и скажем, какие морфизмы хотим рассматривать в целом, то тогда и с афтоморфизмами кокнретного множества будет всё понятно.
>получится афинное пространство с выбранной системой координат
Ну да, о том и речь.
* Для аффинной плоскости это теорема Юнга или как-то так.
В том смысле, что полное описание автоморфизмов даёт, если вдруг интересно. Можно просто привести пример, который не является афинным преобразованием, конечно: $(x, y) \mapsto (x+y^2, y)$.
>из автоморфизмов восстановить
Из подмножества эндоморфизмов всё же, на ноль тоже надо уметь умножать.
Можешь показать?
>>1983
То что ты как всегда бессвязную хуйню несешь, мелкочмонь. Ну вот взял и вынудил меня раскрыть все карты. Надеюсь не приключится очередной срач на несколько сотен постов.
>>1984
Не улавливаю твой ход мысли.
Но вот я думаю тут должно быть что то совершенно очевидное, что лежит прямо на поверхности. Потом когда я откопаю это и напишу тут, наверняка какой нибудь умник мне напишет - а ну это же очевидно. Бывало такое уже и не раз.
Ну вот, к примеру.
Если перейти к алгебраическому описанию, то выбор системы координат можно трактовать как выбор образующих в алгебре. 4 пик примерно в таких терминах рассуждает.
Ну да, очевидно: если мы рассматриваем кортежи как аффинные многообразия, то аффинная и векторные структуры на них есть, но мы это отдельно не проговариваем, так как интересуемся более общими свойствами. Когда мы рассматриваем , например, R^n как гладкое многообразие, то мы обычно тоже не говорим о том, что это ещё и аффинное многообразие, хотя записываем координаты тоже в виде кортежей и при необходимости алгеброгеометрическую структуру восстановить можем (аффинные эндоморфизмы гладкие естественно).
петух-неосилятор, давно не виделись! ты решил с картофана перейти на первую культуру? сильное решение. жаль, опять полный провал, потому что хуйню несёшь ты (тоже опять). но всё же удачи в этом начинании, я поддерживаю
Страдаю шизой, которая требует от меня ИДЕАЛЬНЫХ конспектов, из-за чего я трачу овердохуя времени и сил на эту хуйню. Из-за этого также не способен сесть и чисто по фану послушать лекцию, ведь "мне нужно это записать это ВАЖНО!!".
Первые два курса уника лечился похуизмом: забивал хуй на конспекты, и соответственно на предметы. Но сейчас хочу изучать все нормально. Как научиться отпускать перфекционизм?
можно делать всё, что угодно, если это для тебя работает
можно вообще ничего не слушать, а сразу решать задачи
А зачем конспект вообще нужен (за пределами экзамена), если есть учебники и, чаще всего, готовые заметки лекций от лектора/одногруппников? Мне кажется, имеет смысл своими заметками только дополнять проблемные/интересные места.
На мой вкус анализ это трюки и картинки, доказательства оттуда не запоминаются, а откладываются в виде "какой-то ебанутый трюк с нормами и неравенствами, дающий нужную оценку" или "неявная функция+чейн рул", а детали всегда трудновато восстановить сходу. Я внятно понимаю только теоремки где инварианты топологические пресервятся. Чтобы понять глубже и запомнить надо свои картинки рисовать, расписывать интуиции свои, а переписывать учебник и слова лектора кажется хуетой какой-то.
Какие-то фишки из этих методичек мб зайдут:
https://docs.google.com/document/d/1BLme5o6AQ3i2m5nK76QJcBPZzH5NDV19g4wlkHNS53A/edit?tab=t.0
https://pi.math.cornell.edu/~zakh/homeworkguide.pdf
 33 Кб, 751x131
33 Кб, 751x131Что не смеетесь?! Не смешно?!!
Тогда уж $k^n$-торсор.
 182 Кб, 640x738
182 Кб, 640x738Помогите упорядочить
 2,8 Мб, 2016x4592
2,8 Мб, 2016x459242
Парни, я знаю, что это очень простое задание, но я реально не справляюсь, помогите, пожалуйста.
Спасибо!
открой книжку манина и попробуй поглядеть, как оно тебе заходит
ты что конкретно собрался в ней делать? если просто изучать, то ничего сложного. Всё то, что и в любой другой теме. Никто за тобой не бежит, и экзамена в конце жизни нет, умрёшь с тем, что успел постичь, а дальше уже не важно будет
>ты что конкретно собрался в ней делать?
Понимать, уметь что-то. Люблю аутично копаться в числах, вот и заинтересовался.
И что там трудного?
И ещё слегка связанный вопрос: есть ли какой-то класс алгебр Ли, которые можно представить как алгебры дифференцирований?
И ещё вопрос: есть какое-то обобщение теоремы Адо кстати как правильно - Адо или адО? на бесконечномерные алгебры Ли?
 119 Кб, 1792x828
119 Кб, 1792x828 574 Кб, 736x471
574 Кб, 736x471а является элементом {a}, и элементом {a, b}.
{a} это подмножество {a, b}.
Если оставить только {a, b}, то потеряется порядок, так как в множествах он не важен: {a, b} = {b, a}. Из-за чего упорядоченная пара не смогла бы сохранять порядок: (a, b) = {a, b} = {b, a} = (b, a).
 1,6 Мб, 1536x1024
1,6 Мб, 1536x1024Небольшая тонкость, но хотя тут верное определение, мне кажется, лучше начать с другого: (a, b) = {{a}, {a,b}}.
Мне кажется, это более понятное, но ещё и эквивалентное тому, что написано на доске.
 685 Кб, 828x1685
685 Кб, 828x1685Мы ведь уже знаем, что в 2 |G|=n, а до этого в предложении доказали, что |Aut|<=n
А блядь сорри я дебил жопочтец
в теореме формулируются три утверждения, автор их доказывает по схеме 1) => 2) => 3) => 1)
текст, мягко говоря, недружелюбный
>>2057
алгебра Ли векторных полей тебя устроит в качестве алгебры дифференцирований?
алгебру Ли всегда можно представить как подалгебру эндоморфизмов какого-то бесконечномерного векторного пространства (независимо от её размерности), в каком-то смысле это аналог теоремы Адо. но не очень полезный: если мы говорим о бесконечномерном случае, мы, наверное, хотим также наделить наши пространства топологией и чтобы все представления топологию уважали (т.е. чтобы гомоморфизмы между алгебрами были непрерывными). а это вопрос значительно более трудный, его можно ставить для различных видов топологических векторных пространств, и мне в этом направлении ничего неизвестно. что-нибудь должно быть, надо полагать
Мы с тобой играем в игру: я называю число или даю определение некоего числа, а ты должен сказать его порядковый номер в своём списке. Если ты сумел отбиться три раза, ты победил, иначе ты у меня сосёшь хуй.
- 12341324184581358931858513298,41235135441234, - начинаю я.
- Это рациональное число у меня есть под номером 31809123482194801248120380129380129301293801238012380313809124809124, - отвечаешь ты. Список действительно очень длинный.
- Отношение диаметра окружности к её длине, - делаю я ход поинтереснее.
- 1, - ловко парируешь ты. Все козырные константы ты выписал первыми.
- Такое число, которое отличается от первого числа в твоём списке первой цифрой на единицу, от второго - второй цифрой, и так далее, ну ты понял, - вбрасываю я определение.
- Но это не число!
- С хуя бы? Я дал чёткое определение, как это число вывести с произвольной точностью до любого знака. Список прямо у тебя в руках. Давай, ищи его у себя там.
Ну и ты кароч у меня хуй сосёшь.
Кстати, угорал с таких книг, где сначала так определяется упорядоченная, а потом в какой-то момент рассматривается множество и автор наивно полагает, что среди его элементом можно различить однерки, пары, тройки и т. п. Хотя все эти элементы - всего лишь множества, допускающие двоякое толкование.
>>2061
К тому же, аккуратнее, и позволяет обойти некоторые моменты, как описанны выше, но не все.
>Как элемент может принадлежать вложенному множеству и при этом быть вне него одновременно?
В смысле, "вне него"? Он внутри него. Но при этом также и внутри еще одного множества. Элемент может одновременно принадлежать различным множествам.
Есть два элемента a и b, получается множество {a, b}. Это такое множество, что при любом x выполняется x ∈ {a, b} тогда и только тогда, когда или x = a, или x = b.
Теперь по той же схеме берем a и {a, b}, получается {a, {a, b}}. Для любого x x ∈ {a, {a, b}} тогда и только тогда, когда x = a или x = {a, b}.
 567 Кб, 1200x1688
567 Кб, 1200x1688>>2059
Мне запись {{a}, {a, b}} кажется нелогичной, избыточной. У нас и так есть множество {a, b}, мы как бы говорим "множество, в которое входит множество, в которое входит a и b, и еще в него входит множество, в которое входит a". Мы тут повторяемся. Анон >>2059 любезно пояснил что, тем что мы дублируем a мы показываем что она первая в паре, но это как-то странно, я не понимаю как из ее повторения следует то, что она первая
тебе нужно на двух элементах $a,b$ образовать такое множество $P(a,b)$, изоморфное $\{a,b\}$, при этом чтобы $P(a,b) \neq P(b,a)$
тебе также хочется писать $a \in P(a,b)$, вместо этого следует писать $\varphi(a) \in P(a)$, где $\varphi\colon \{a,b\} \to P$ - указанный выше изоморфизм.
таким образом получается полная анология с "наивным" определением упорядоченной пары: $(a,b)$ это такой набор, что $a,b \in (a,b)$ и $(a,b) \neq (b,a)$
подобных конструкций с $P$ можно придумать сколько угодно, и {{a}, {a, b}} есть одна из наиболее простых. никакого инсайта никакая из этих конструкций не даёт, просто указывает на то, что термин "упорядоченная пара" можно определить в теоретико-множественных терминах (и допускает строгое определение, если зафиксирована аксиоматика). на практике об упорядоченной паре можно думать наивно, ничего при этом не потеряешь
>как из ее повторения следует то, что она первая
Это условность: считать, что множество, устроенное как {a, {a, b}}, представляет собою упорядоченную пару (a, b).
Зная эту условность, можно различать, что a поставлено на первое место, а b - на второе.
Как заметил Коллега >>2072, не следует искать скрытой логики в выборе именно такой или другой конструкции для обозначения пары, потому что только ее пригодность играет роль.
Мне кажется, интуитивно это можно воспринимать так:
Какие нам нужные данные для определения упорядоченной пары? Первая порция данных — это собственно два элемента, вторая порция — указание на то, какой из них мы считаем первым.
Давайте, петросяны, ваш выход. Объясните, чем занят этот математик?
>>2059
>>2061
>>2069
>>2071
>>2072
>>2074
>>2075
Я тоже обо всём об этом думал и пришёл к следующему выводу: упорядоченная пара является базовым термином, на основании которого потом определяется всё остальное. То есть если человек изначально не обладает концепцией упорядоченной пары, он попросту не сможет воспринять весь текст выше. Что конкретно я имею в виду? Не касаясь нечётких множеств, рассмотрим высказывание "мой батя лысый". Его логическая форма P(x). Вместо икс подставляется "мой батя", вместо предиката Р подставляется предикат "быть лысым". Вот это предикат "быть лысым", это термин, понятие. И оно даже обозначает что-то в реальности, то есть это не пустое множество. А в частности это множество лысых людей, причём это множество именно в математическом, в канторовском смысле. Теперь рассмотрим высказывание "мой батя поехал на лошади", и вот теперь логическая форма P(x, y), то есть отношение. То есть x - батя, y - лошадь, предикат P - поехал. Здесь две переменные. И это именно что упорядоченная пара, то есть поехал именно батя на лошади, а не лошадь на бате. Вот эта концепция отношения P(x, y) - и есть база, и есть та стартовая точка, через которую мы можем определить функции, а через функции всё остальное.
Концепция множества на самом деле является абстракцией, в частности если мы запишем список из трёх элементов как
a, b, c
a, c, b
b, c, a
и так далее, то у нас всё равное будет получаться какая-то упорядоченность. И только поигравшись с примитивной комбинаторикой, мы сможем отделить саму структуру и элементы, которые её составляют. В реальном мире мы можем столкнуться только с какой-то формой, а сами элементы как таковые - это всегда абстракция. Например, конструктор лего какую-то форму всё равно имеет, даже если он просто свален в кучу. И только составляя из него разные фигуры, ребёнок сможет запомнить, какие у него детали есть вообще в наличии, то есть образует концепцию множества деталей конструктора в своей голове, множества в математическом смысле.
А почему тогда вся эта хуйня начинается именно со множеств? А ни по чему, просто для математики в современном смысле слова используется дедуктивный метод познания, поэтому свои интуиции относительно натуральных чисел необходимо смоделировать в виде каких-то базовых высказываний. Чтобы дальше с ними можно было вести какую-то работу.
В аксиомах Пеано мы имеем счёт: 1, последователь единицы s(1), последователь последователя s(s(1)), s(s(s(1))), и так далее
Или то же самое в другой нотации: 1, 1+1, 1+1+1, 1+1+1+1....
А в теории множеств:
{}
{ {} }
{ {}, { {} } }
{ {}, { {} }, { {}, { {} } }
...
Но на самом деле всё это просто самая примитивная палочковая запись натуральных чисел, палочковый счёт:
I, II, III, IIII, IIIII, IIIIII ...
А римские цифры - это палочковый счёт с сокращениями:
I, II, III, IV, V, VI ....
Суть этого всего одна и та же. Просто математики уже всё это знают, а потом выбирают способ как свои знания закодировать в виде дедуктивной системы высказываний и определений. А человек, который только начинает всё это изучать, он нихуя не знает, поэтому ему сложно всё это понять. Но вопрос преподавания не является вопросом какие аксиомы и определения нам выбрать, а почему-то они каким-то образом в один вопрос сливаются, и на выходе получается хуй знает что. То что Савватеев рассказывает для других математиков то что они и так знают, причём непоследовательно, перескакивая с темы на тему.
>>2059
>>2061
>>2069
>>2071
>>2072
>>2074
>>2075
Я тоже обо всём об этом думал и пришёл к следующему выводу: упорядоченная пара является базовым термином, на основании которого потом определяется всё остальное. То есть если человек изначально не обладает концепцией упорядоченной пары, он попросту не сможет воспринять весь текст выше. Что конкретно я имею в виду? Не касаясь нечётких множеств, рассмотрим высказывание "мой батя лысый". Его логическая форма P(x). Вместо икс подставляется "мой батя", вместо предиката Р подставляется предикат "быть лысым". Вот это предикат "быть лысым", это термин, понятие. И оно даже обозначает что-то в реальности, то есть это не пустое множество. А в частности это множество лысых людей, причём это множество именно в математическом, в канторовском смысле. Теперь рассмотрим высказывание "мой батя поехал на лошади", и вот теперь логическая форма P(x, y), то есть отношение. То есть x - батя, y - лошадь, предикат P - поехал. Здесь две переменные. И это именно что упорядоченная пара, то есть поехал именно батя на лошади, а не лошадь на бате. Вот эта концепция отношения P(x, y) - и есть база, и есть та стартовая точка, через которую мы можем определить функции, а через функции всё остальное.
Концепция множества на самом деле является абстракцией, в частности если мы запишем список из трёх элементов как
a, b, c
a, c, b
b, c, a
и так далее, то у нас всё равное будет получаться какая-то упорядоченность. И только поигравшись с примитивной комбинаторикой, мы сможем отделить саму структуру и элементы, которые её составляют. В реальном мире мы можем столкнуться только с какой-то формой, а сами элементы как таковые - это всегда абстракция. Например, конструктор лего какую-то форму всё равно имеет, даже если он просто свален в кучу. И только составляя из него разные фигуры, ребёнок сможет запомнить, какие у него детали есть вообще в наличии, то есть образует концепцию множества деталей конструктора в своей голове, множества в математическом смысле.
А почему тогда вся эта хуйня начинается именно со множеств? А ни по чему, просто для математики в современном смысле слова используется дедуктивный метод познания, поэтому свои интуиции относительно натуральных чисел необходимо смоделировать в виде каких-то базовых высказываний. Чтобы дальше с ними можно было вести какую-то работу.
В аксиомах Пеано мы имеем счёт: 1, последователь единицы s(1), последователь последователя s(s(1)), s(s(s(1))), и так далее
Или то же самое в другой нотации: 1, 1+1, 1+1+1, 1+1+1+1....
А в теории множеств:
{}
{ {} }
{ {}, { {} } }
{ {}, { {} }, { {}, { {} } }
...
Но на самом деле всё это просто самая примитивная палочковая запись натуральных чисел, палочковый счёт:
I, II, III, IIII, IIIII, IIIIII ...
А римские цифры - это палочковый счёт с сокращениями:
I, II, III, IV, V, VI ....
Суть этого всего одна и та же. Просто математики уже всё это знают, а потом выбирают способ как свои знания закодировать в виде дедуктивной системы высказываний и определений. А человек, который только начинает всё это изучать, он нихуя не знает, поэтому ему сложно всё это понять. Но вопрос преподавания не является вопросом какие аксиомы и определения нам выбрать, а почему-то они каким-то образом в один вопрос сливаются, и на выходе получается хуй знает что. То что Савватеев рассказывает для других математиков то что они и так знают, причём непоследовательно, перескакивая с темы на тему.
>То что Савватеев рассказывает для других математиков то что они и так знают, причём непоследовательно, перескакивая с темы на тему.
То, что рассказывает Савватеев, он рассказывает только для других математиков, которые и так уже это всё знают, а не для обучающихся. Причём рассказывает он сумбурно, непоследовательно, перескакивая с темы на тему. Но математики его и так поймут и согласятся - потому что они уже это всё знают.
Ну если ты баба, то да, иначе у тебя девиация и тебя нужно обоссать.
>>2072
Ок, спасибо. Ну раз мне представление через множества не нужно на данном этапе, остановлюсь на интуитивном понимании, что упорядоченная пара это множество из двух элементов с доп атрибутом в виде порядкового номера.
>>2081
Спасибо, анон. То, что множество это абстракция и в физическом мире его нет потому что все находится на разных координатах в пространстве, я понимаю. Благодарю за пример с порядком аргументов в предложении с лысым батей и деконструкцию римских цифр.
Отождестви алгебру эндоморфизмов с алгеброй $n \times n$ матриц. Если ты превратишь ее в алгебру Ли, то ты получишь касательное пространство в единице группы Ли GL_n($\mathbb{R}$). Элемент алгебры тогда естественно рассматривать как касательный вектор, а результат экспоненцирования как кривую в GL_n($\mathbb{R}$) через единицу, для которой этот элемент это вектор скорости этой кривой в единице. Но ты по идее и так всё это должен знать, так что вопрос мне не очень понятен.
>есть ли какой-то класс алгебр Ли, которые можно представить как алгебры дифференцирований?
Из теоремы Вейля следует, что любая полупростая алгебра Ли g изоморфна алгебре дифференцирований g. По теореме Адо, любая конечномерная алгебра Ли g изоморфна подалгебре алгебры дифференцирований.
>есть какое-то обобщение теоремы Адо
Любая алгебра Ли g изоморфна подалгебре End(U(g)).
Почему природа не любит целые числа?
Потому что вероятность выбрать целое число среди всех действительных чисел равна нулю. Не приблизительно нулю, не «бесконечно малой величине», а строго нулю. Даже несмотря на то, что среди действительных чисел есть целые, да.
Сука, что ты наделал, у меня перед глазами весь день этот еблан теперь кривляется.
интересненько
Вот хорошая лекция, не Савватеев, по упорядоченным парам в теории множеств https://www.youtube.com/watch?v=1Mlv8QBb8xQ&t=3416s
Ну ничего, вы справитесь занюхнуть.