Вы видите копию треда, сохраненную 13 августа в 10:46.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
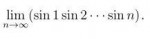 4 Кб, 217x57
4 Кб, 217x57Предлагаю в этом треде решить её, а также, может быть, и остальные 99
Что?
>>35179 (OP)
Нуль хуле. Модуль каждого синуса меньше 1 при натуральных N. Дальше элементарно доказать, что такая последовать носить стремится к 0.
Не знаю. Откуда?
Из этого ничего не следует, повторюсь. Попробуй посчитать предел у произведения e^{-1/n^2}. Они тоже все строго меньше единицы.
>>35357
Рассмотри sin(n). Эта последовательность плотна на [-1,1] (это все знают). Следовательно, для любого \eps будет существовать N, такое что |sin(N)|< \eps. Отсюда, |sin(1) sin(2) ... sin(N)|<\eps. Следовательно, предел 0.
Забавное задание, кстати. Скинь еще чего-нибудь.
Если бы для каждого 0 < d < 1 в интервале (-d,d) было бы лишь конечное множество членов последовательности {sin n}, то было бы |sin n| -> 1, что, как легко проверить, неправда. Поэтому для некоторого d имеем |sin n_k| < d < 1, для некоторой подпоследовательности {n_k } натурального ряда. Дальше просто:
|sin1...sin n| < |sin n_1 ... sin n_k| < d^k -> 0
Тут k - любое, такое что n_k < n
>Рассмотри sin(n). Эта последовательность плотна на [-1,1]
Я вот не знал, пытаюсь доказать теперь.
Это не тривиальный факт. Вот объяснение: http://www.mathstat.concordia.ca/faculty/pgora/m364/Density.pdf
здорово, спасибо. красивое решение
>Из этого ничего не следует, повторюсь.
Из этого следует, что каждый следующий член меньше предыдущего(последовательность убывает). Но убывать до бесконечности она не может, ограничение 0.
С чего ты взял, что 0 - это самое нижнее ограничение? Я привел тебе пример: рассмотри последовательность таких произведений
e^{-1} e^{-1/2^2} e^{-1/3^2} ... e^{-1/n^2}. В ней каждый следующий член меньше предыдущего и ограничение снизу 0. Но предел равен e^{-\pi ^2 /6}
Ты прав.
sin(pin)=0; [10^npi]->10^npi при n->infinity; [10^npi] \in N; из всего этого следует, что последовательность sin([10^npi])->0 при n->infinity; обозначим через {Xk} исходную последовательность без членов вида [10^npi]; так как для любого x sin(x) \in [-1, 1], то она ограничена, т.к. sin([10^npi])->0 при n->infinity, она бесконечно малая, исходная последовательность есть произведение {Xk} и sin([10^npi]), произведение б/м на ограниченную -- б/м => предел исходной последовательности 0. Вы вообще тупые бараны?
Сука, звёздочки превращают текст в курсив. Не знал. Ну, думаю, и так всё понятно. В выражениях 10^npi между n и pi умножение, и естественно с обычным приоритетом (не в степени npi, а десять в степени n умножить на pi)
Надеюсь, это троллинг. Между n и pi всегда ставь умножение, лол. Или тебе доказательство не понятно? Где конкретно? Да и если оно тебе непонятно, то советую открыть учебник, хотя бы самый простой.
В квадратных скобках обозначается целая часть.
Смысл в том, что последовательность [10^npi] приближает последовательность 10^npi, а так как для синуса похуй, что 10^npi, что pi, то sin([10^npi]) приближается к sin(pi) при n->infinity, при этом [10^npi] всё-равно остаётся в N.
net, не правильно, вообще. перерешаю щас.
>В квадратных скобках обозначается целая часть.
это надо пояснять. почему читатели должны догадываться?
>[10^npi]->10^npi при n->infinity;
эта запись -- бессмыслица
>Смысл в том, что последовательность [10^npi] приближает последовательность 10^npi
Что это значит?
>синуса похуй, что 10^npi, что pi
что-то осмысленное
>sin([10^npi]) приближается к sin(pi) при n->infinity
Почему?
Короче, из последовательности натуральных чисел можно выделить такую подпоследовательность {Xn}, что для любого e>0 существует N: для любого n>N => (Xn/pi-[Xn/pi])<e. То есть, существует такая подпоследовательность последовательности натуральных чисел, что разность между kPi для некоторого k (его существование очевидно) и Xn стремится к нулю. Дальше всё как в предыдущей попытке. Вот это точно верно.
Конечно, стоит обосновать, что такая {Xn} существует, но это тривиально следует из того, что Pi содержит все возможные конечные цепочки цифр, включая цепочки нулей, тогда {Xn}={10^Rn}, где Rn -- количество цифр после запятой до первой цепочки из n нулей, но большее, чем R(n-1). Это свойство числа Pi опять же нужно доказать, но я оставлю его как известную теорему, потому что можно обойтись и без этого свойства, но тогда доказательство существования {Xn} будет длиннее.
1. О чём догадываться? Это общепринятое обозначение.
2. Для любого e>0 существует N: для любого n>N =>
([10^npi]-10^npi)<e, действительно, надо было в фигурные скобки брать. Да и это не правильно оказалось.
3. В пункте 2.
4. ))
5. Опять же, признаю неправоту. В следующем посте исправленная версия.
>>36017
>1. О чём догадываться? Это общепринятое обозначение.
Общепринятое обозначение -- это число \pi. А операция взятия целой части встречается слишком редко, чтобы для неё было общепринятое обозначение, кроме того, квадратные скобки "общеприняты" для множества других вещей. Поэтому таки приходится догадываться.
>В следующем посте исправленная версия.
Там тоже непонятно. Во-первых, утверждение
>существует такая подпоследовательность последовательности натуральных чисел, что разность между kPi для некоторого k (его существование очевидно) и Xn стремится к нулю.
очевидно неверно, т.к. kPi = const (если формально читать, что написано)
Во-вторых, сомнительное утверждение
>из последовательности натуральных чисел можно выделить такую подпоследовательность {Xn}, что для любого e>0 существует N: для любого n>N => (Xn/pi-[Xn/pi])<e.
требует тщательной проверки.
>Это свойство числа Pi опять же нужно доказать, но я оставлю его как известную теорему
Пожалуйста, ссылку, если можно
Простите, что лезу со своим сельским умом в /math, но я хочу спросить. sin(360+πn)=0 не может послужить тут обоснованием того, что пределом будет 0?
Тут до тебя уже два решения выложили, так-то.
блин, мечтаю понимать, как такое решать. Или хотя бы понимать, что там перемножается
блин, гениально. Я аж проиграл от того, как же это очевидно, чёрт возьми. И какой страшной эта задача казалась
Предел произведения можно делить на пределы множителей, если они конечны. Там может неопределённость получается. В целом, твоё рассуждение - подчасть доказателства.
Также не понял.
 42 Кб, 720x1280
42 Кб, 720x1280Вероятность равна нулю.
Если 9 из 10 на своих местах, то последнему письму негде оказаться, кроме как в своем конверте.
Верно.
 3 Кб, 306x182
3 Кб, 306x182>>36260
Нуебанаврот, из строгого убывания же очевидно.
Ладно, давайте поиграем в формализм.
Построим систему из интервалов (a_n, b_n), пикрелейтед. По лемме о вложенных интервалах из первого семестра матана следует, что существует единственная лямбда, удовлетворяющая всем интервалам. И она, очевидно, строго меньше ебиницы. Промажорируем наше произведение синусов степенью этой чиселки. По скольку она фиксированна и строго меньше единицы, ее предельная степень это ноль. чтд
Ты про беспорядки, говоришь. Но здесь по другому. Вначале тоже про них подумал.
Интересно какое обобщение графиков?
Блять, вот тебе ебучая последовательность, которая тоже строго убывает, положительна и к нулю не стремится: 1488 + 1/n.
В твоем втором решении нихера не очевидно, что лямбда меньше единицы (на самом деле, она РАВНА единице, потому что синусы натуральных плотны на отрезке [-1, 1])
Мне очевидно только то, что ты обосрался. Дважды.
Лямбда нихуя не равна единице, поскольку она принадлежит объединению интервалов. Она строго меньше единицы.
Говорит что лямбда равна 1 равносильно утверждению, что 0.(9) = 1
Пизда.
А нельзя сказать просто что она во-первых убывает, а во-вторых имеет бесконечное число положительных и отрицательных знаков, поэтому ноль?
Ну и к тому же имеет предел по какому-нибудь признаку.
Если ты имел в виду "убывает по модулю", то нельзя. Вот контрпример: (-1)^n + (-1)^n/n.
Там выше два решения лежат.
У тебя правый конец закреплен, так что ты не доказал, что /lambla строго меньше единицы.
Для любого L < 1 найдется такое n, что sin(n) > L, т.к. sin(n) плотен на отрезке [-1;1]
Класс! Про плотность не додумался.
Из-за Арнольда.
если гора это фрактал Коха, то нет
Очевидный ноль же.
Синус имеет модуль, близкий к единице, с периодом pi. А аргумент в задаче меняется с шагом 1 < pi. То есть, из двух соседних множителей один будет заведомо меньше C < 1 (считать точное значение C влом). Отсюда, модуль произведения ограничен С^(n/2), то есть стремится к нулю.
Еще разок, ты утверждаешь
>C < 1 (считать точное значение C влом). Отсюда, модуль произведения ограничен С^(n/2)
Поясни, почему это не работает для
П(e^{-1/n^2})
Потому что для e^... нет такой константы, меньшей единицы. А для синуса (одного из двух соседних) в задаче есть, я хз 0,9 это или сколько там, но факт, что меньше единицы.
Вообще-то константа есть и это единица,
>нет такой константы, меньшей единицы
>Вообще-то константа есть и это единица
Ясно. Иди мамку свою потралируй перед сном.
Существует. Возьмем горизонтальную прямую ниже окружности и будем поднимать ее до тех пор, пока количество отмеченных точек под прямой и на ней не станет равно миллиону или больше (1000000 + K). При этом на прямой окажется K + M отмеченных точек, (а то мы бы остановились раньше). Если K = 0, достаточно поднять прямую еще на децл, чтобы на ней не было отмеченных точек. Если K > 0, возьмем за центр любую точку между K и K + 1 слева и чуток повернем прямую против часовой стрелки, чтобы на ней не было отмеченных точек и она не пересекла такие точки при повороте. Поскольку отмеченных точек конечное число, всегда можно подобрать достаточно малый угол для этого.
99.
Пусть с вероятностью p первый загадывает 10 (с вероятностью 1-p -- 20). Аналогично второй с вероятностью q пытается угадать 10. Тогда сумма, получаемая вторым игроком:
S = 10pq + 20(1-p)(1-q) - 15p(1-q) - 15q(1-p) = 20-35p-35q+60pq
Сумма линейна по q с коэффициентом -35+60p. То есть, если -35+60p > 0, то максимум S достигается при q=1 и равен -15+25p, если -35+60p < 0 -- при q=0 и равен 20-35p. Если -35+60p=0 (p=7/12), то S = 20-35p = -5/12 независимо от q.
При -35+60p < 0 S растет с уменьшением p, что невыгодно первому игроку. При -35+60p > 0 S растет с увеличением p (причем при p=7/12+eps S=-5/12-eps). В итоге, p = 7/12 наиболее выгодна для первога игрока.
Ответ: игра нячэсная, первый игрок получает в среднем 5/12 коп. за партию, если загадывает 10 копеек с вероятностью 7/12. Стратегия второго игрока при этом неважна.
Кстати, можно проще. Проведем все возможные прямые через каждые две отмеченные точки. Их дохуя, но все же конечное число. Так что можно построить прямую X, которая не параллельна ни одной из них. Теперь можно найти прямую Y параллельную X, удовлятворяющую требованию, поскольку на любой прямой параллельной X лежит не более одной отмеченной точки.
Ноль. При отрицательном x все слагаемые кроме -4x^2 положительны. То есть, |4x^2| должен быть больше суммы модулей всех остальных слагаемых, а значит и больше каждого. из |4x^2| > |4| следует, что |x| > 1 (x < -1). Но тогда |5x^3| > |4x^2|, то есть отрицательных корней нет.
>>но я уже нассал... Что делать, бро?
Известна площадь поверхности ящика (вроде без крышки). Нужно найти a b c, при которых объем будет максимален.
86) Единственная фановая задача среди всего этого говна тип ПОЩЕТАЙТЕ ПЛОЩАДЬ ГИПЕРСФЕРЫ) ПОЩЕТАЙТЕ 100 ПРОИЗВОДНУЮ. Что я придумал.
Лемма. Пусть f это гладкая функция на кубе (на котором гладкая структура индуцирована из S^2) такая, что
а) она регулярна (= имеет конечное число крит. точек)
б) она инвариантна относительно группы вращений куба
тогда её глобальный экстремум точно достигается либо в вершине куба, либо в центре грани.
Пруф.
1) Выпишем размер орбиты для каждого класса точек, относительно группы вращения куба
a) (!) центр грани - 6
б) общая точка грани - 6х4
в) (!) центр ребра - 12
г) общая точка ребра - 12х2
д) (!) вершина - 8
теперь вспомним теорию морса
Макс - Седл + Мин = Хар.Эйлера(S^2) = 2
теперь у нас чисто комбинаторная задача: решить уравнение
А - Б + С = 2
где А,Б,C \in {6(!),6x4,12(!),12x2,8(!)} (восклицательным знаком обозначены числа которые мы можем брать только один раз)
немного попердев в лужу можно увидеть что есть ровно два решения (с точностью до добавления/вычитания 24)
(6+k24,12+k24 + l24,8 + l24)
(8+k24,12+k24 + l24,6 + l24)
k,l \in N_0
откуда следует, что либо минимум в вершине, а максимум в центре ребра, либо наоборот (хотя наличие других минимумов и максимумов не исключается) ЧТД
Так как функция из задачи 86 удовлетворяет условиям леммы, то достаточно посчитать на прямой проходящей через центр грани и на прямой проходящей через вершину, сравнить что больше и сказать, что одно из них минимум, а другое максимум. Точно так же можно проанализировать и другие многогранники с богатой группой симметрии.
86) Единственная фановая задача среди всего этого говна тип ПОЩЕТАЙТЕ ПЛОЩАДЬ ГИПЕРСФЕРЫ) ПОЩЕТАЙТЕ 100 ПРОИЗВОДНУЮ. Что я придумал.
Лемма. Пусть f это гладкая функция на кубе (на котором гладкая структура индуцирована из S^2) такая, что
а) она регулярна (= имеет конечное число крит. точек)
б) она инвариантна относительно группы вращений куба
тогда её глобальный экстремум точно достигается либо в вершине куба, либо в центре грани.
Пруф.
1) Выпишем размер орбиты для каждого класса точек, относительно группы вращения куба
a) (!) центр грани - 6
б) общая точка грани - 6х4
в) (!) центр ребра - 12
г) общая точка ребра - 12х2
д) (!) вершина - 8
теперь вспомним теорию морса
Макс - Седл + Мин = Хар.Эйлера(S^2) = 2
теперь у нас чисто комбинаторная задача: решить уравнение
А - Б + С = 2
где А,Б,C \in {6(!),6x4,12(!),12x2,8(!)} (восклицательным знаком обозначены числа которые мы можем брать только один раз)
немного попердев в лужу можно увидеть что есть ровно два решения (с точностью до добавления/вычитания 24)
(6+k24,12+k24 + l24,8 + l24)
(8+k24,12+k24 + l24,6 + l24)
k,l \in N_0
откуда следует, что либо минимум в вершине, а максимум в центре ребра, либо наоборот (хотя наличие других минимумов и максимумов не исключается) ЧТД
Так как функция из задачи 86 удовлетворяет условиям леммы, то достаточно посчитать на прямой проходящей через центр грани и на прямой проходящей через вершину, сравнить что больше и сказать, что одно из них минимум, а другое максимум. Точно так же можно проанализировать и другие многогранники с богатой группой симметрии.
это открытая олимпиада по топологии, так что хуй тебе на ворот а не солюшн. но могу дать подсказку: "расслоение" диска на отрезки - это "расслоение" границы диска (окружности) на пары точек. при этом не абы какое - а хорошим образом. подумай, как это можно использовать
Неосилятор
1) диффеоморфизм f открытого квадрата на открытый круг продолжается до гомеоморфизма g топологических многообразий с границей
2) гомеоморфизм топологических многообразий обязательно переводит границу в границу, поэтому наш исходный диффеоморфизм f порождает гомоеоморфизм h, действующий из S^1 (которую гомеоморфно отождествляем с границей исходного квадрата) на S^1 (граница исходного круга)
3) для любого гомеоморфизма S^1 -> S^1 можно найти пару противоположных точек на первой окружности, которая переводится этим гомеоморфизмом в пару противоположных точек на второй окружности.
4) итак, на границе квадрата есть пара точек, которые c помощью h перейдут в противоположные точки на границе исходного круга. эти противоположные точки будут соединяться некоторой кривой вида f(x \times I). Эта кривая не может быть длины меньше двух, т.к. наименьшая кривая между противоположными точками -- диаметр.
Ну примерно так, таким же образом можно найти и замкнутую кривую на сфере, которая разбивает её на два куска равной площади, только у меня из этого сходу никакой оценки снизу на её длину дать не получилось (если получится дать оценку снизу на длину - то дать оценку снизу на минимальную поверхность, ограниченную кривой такой длины - дело техники).
Вернее можно даже найти слой, который делит шар на два куска равного объема, но опять же как высрать из этого оценку на его площадь - хуй знаит.
Кстати если совсем уж приедаться то то что ты нашел две диаметрально противоположные точки ещё ни о чем не говорит у тебя же "слой" по определению это ведь не образ любой кривой соединяющей две любые (или, далее, диаметрально противоположные) точки на границе?
если приедаться, то вот ошибка: ниоткуда не следует, что найденные точки на границе квадрата, которые перейдут в противоположные на границе круга, должны вдруг иметь одинаковую координату x; совсем не должны. значит, их образы не обязаны соединяться кривой вида f(x \times I)
надо говорить правильные вещи, но чтобы как можно менее понятно, тогда такие люди будут встречаться нередко
взять логарифм после чего задача сведётся к \sum 1/n^2 = pi^2/6. Это оч клоссическое тождество, https://www.youtube.com/watch?v=d-o3eB9sfls&t=5s даже на ютубчеке есть
вся доска подохла, забей хуй
Это, видимо, своеобразная /math-ематическа ирония, потому как взять градиент суммы квадратов расстояний до прямой, задаваемой вектором u, и проще, и результативнее. А именно, grad_u {sum_{v - вектор вершины правильного многогранника} (v,v)^2 - (u,v)^2} = - sum_{v} 2(u,v)v = f(u). Я утверждаю, что последнее выражение есть коллинеарный u вектор. Действительно, это выражение есть некоторое линейное преобразование вектора u, при этом для каждой вершины v' нашего многогранника оно отображает v' в коллинеарный вектор (рассмотрим базис из v' и d-1 вершины многогранника и движение многогранника, сохраняющее v', но меняющее всё подпространство, натянутое на оставшемся d-1 векторе, кроме 0; такое движение найдётся вроде бы всегда, для трёхмерных многогранников можно проверить ручками; рассматриваемая сумма при движении не меняется, значит она коллинеарна v'). При этом f(v') = kv', то из симметрии для всех остальных вершин коэффициент тот же. Значит f(u) = ku, то есть градиент ортогонален единичной сфере, а значит значение sum_{v} (v,v)^2 - (u,v)^2 на ней постоянно, а
это сумма квадратов расстояний до вершин.
Чёт я нихуя не понял, для двумерного случая твои аргументы прокатывают? Просто сумма расстояний от вершин единичного квадрата до его диагонали - это sqrt(2), а до его средней линии - это 2. Как функция f(u) связана с функцией из задачи, если она вообще векторная а?
если проверить что эта функция является функцией морса - а это не очень сложно, гессиан там выписать, такое вот.
Че это блять за значки
твоя мама с твоим отцом пидорасом там перемножаются гуманитарный гандон
Вы видите копию треда, сохраненную 13 августа в 10:46.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.