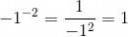Вы видите копию треда, сохраненную 25 декабря 2022 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 146 Кб, 1200x900
146 Кб, 1200x900Также приветствуется обсуждения самого процесса изучения и учебников/задачников
Архивы тредов
http://pastebin.com/kiRZGVHW
ВНИМАНИЕ! ВНИМАНИЕ!! ВНИМАНИЕ!!!
On-line LaTex. Формулы пишем в нём, а после прикрепляем картинками к посту
http://www.codecogs.com/latex/eqneditor.php
Львовский Набор и вёрстка в системе latex
http://www.mccme.ru/free-books/llang/newllang.pdf
Если ты только зашел в тред и хочешь спросить, какую книжку прочитать, то ответ, скорее всего, будет в этих списках, анон.
Список от ОП-а, бывшего тут до меня. Был составлен на протяжении 13 тредов, к ознакомлению обязателен.
http://pastebin.com/4iMjfWAf
Список от анона с dxdy. Довольно внушителен, тоже рекомендуется к прочтению. Является дополнением к списку старго ОП-а.
http://pastebin.com/YP1uaUyd
Goodbook.txt список книг с dxdy, рекомендованный тамошними обитателями.
http://pastebin.com/4FngRj6n
Литература - НМУ
https://docs.google.com/spreadsheets/d/1UWwIIAFwSwOQLK3m--LOaMOvHUivFDEz-JAnLa87i7Q/edit#gid=0
ОП-список 2. Составляйте список в реальном времени! Предлагайте в тред книги, критикуйте уже имеющиеся!
http://pastebin.com/szzZfkCM
Форчановский список, книги на английском.
http://4chan-science.wikia.com/wiki/Mathematics
Список с видеолекциями(в разработке):
http://pastebin.com/S3d7Jj6J
Качать книги тут:
http://libgen.io
А статьи тут(в разработке):
http://pastebin.com/3BfHPskz
Мемасы(в разработке):
http://pastebin.com/e38Yuj5V
СПИСКИ В РАЗРАБОТКЕ, НУЖНА ПОМОЩЬ АНОНА, ПОЖЕЛАНИЯ ОСТАВЛЯЕМ В ТРЭДЕ
Реквестируется логика/ключевые моменты и контекст, перспективы изучения математики в одном посте в двух предложениях лол - ничего лишнего, ни воды, ни неба, ни самой математики. Только суть.
Мне понравилось. Хорошо сделали.
Недавно составляли мою психологическую характеристику, и там отметили, что у меня низкий уровень абстрактного мышления и плохая математическая интуиция. Там надо было продолжить числовые ряды и решить несколько "стандартных" задач. На всё отводилось определённое время. Я очень долго думал над задачами, и поэтому прошёл тест хуёво. Я всегда знал, что сосу в математике, хотя она мне и нравится (в школе вроде легко справлялся со всеми задачами), но этот тест окончательно добил меня.
Это значит, что у меня хуёвые способности и это не лечится вообще, или практика всё таки поможет?
Пиздец, я из-за этой хуйни уже две недели в глубокой депрессии, постоянно рыдаю, как шлюшка, даже к врачу обратился. Он сказал, что я дебил, и выписал мне антидепрессанты.
Вот этот тест http://psytest24.ru/amthauer/
Задачи пикрилейтед, чуть видоизменённые. Все остальные субтесты хорошо прошёл, а вот здесь тормозил люто.
 37 Кб, 618x388
37 Кб, 618x388А, этот тест. Я его в психаче проходил. Так как плохо считаю, то ели-ели справился с немногими задачами из первого листка. Я там ещё невнимательно задания прочитал в одном месте и сильно затупил на словах. Даже тебе пикчу скину. Там и видно, на каких тестах ступил.
Эти задания, особенно первый листок, имеют мало общего с математикой. Они скорее инженерные-физические. Вторые, правда, более абстрактные, но всё равно. Бурбаки бы этот тест не прошли бы.
Так, что можно сделать вывод, о том, что численными методами тебе не стоит занимаеться. Ка и мне, лол. Можешь топологиями обмазаться.
Спасибо, антоша. Буду продолжать копротивляться, может в конце концов окажется, что я не такой уж хуй.Хотя из-за этого теста я всё равно ещё недели две истерить буду, потому что у меня что-то вроде психотравмы по этому поводу, лол.
Даны матрица A размером 30к*10 и вектор b, элементы матрицы и вектора целые положительные числа. x -- некоторое решение уравнения Ax = b в целых неотрицательных числах. Естественно, вектор x будет состоять в основном из нулей.
Дан функционал F(x) = номер последнего ненулевого элемента x.
Нужно минимизировать {F(x) | Ax = b}. Не обязательно находить точное решение, сойдет и какой-нибудь относительно маленький (понятие "относительно маленький" сложно определить) локальный минимум.
В голову приходит лишь найти какое-нибудь хорошее приближение F(x) функционалом типа c^{t}x, получившуюся задачу линейного программирования скормить комплуктеру (есть пакеты, умеющие решать ЗЛП в целых числах). Но пока получается не очень годно, проблемы в том, как бы получше найти вектор c.
У кого-нибудь есть идеи, как решать данную задачу?
Методом тыка нашел решение min ~ 10к. Но это много, хтелось бы поменьше.
 148 Кб, 810x1080
148 Кб, 810x1080Так вот,мне необходимо УГАДЫВАТЬ формулу последовательности членов.
Но вот возникает вопрос,можно ли использовать что-то кроме сложения/умножения?
препод ничего не сказал, просто необходимо прорешать 30 задач такого типа.
 69 Кб, 500x352
69 Кб, 500x352Линейная алгебра, комбинаторика, может какие-нибудь интегральные преобразования, но большинство тем матана тебе вряд ли при пригодятся.
 87 Кб, 651x436
87 Кб, 651x436Сэнькью
Поясните дебилу-дошкольнику, что такое e+.
И делится ли число 111...1 (100 единиц) на число 1111111 без остатка?
Добрый день, посоветуйте годные книги по мат.статистике, Теории вероятностей и че-нить про сплайны и т.д
e+ означает *10^. Мантисса и порядок.
111..1 = 1111111 + 1111111x10^7 + 1111111x10^14 + ... + 11x10^91 + 11x98^100
Машинное обучение/игры.
project euler
Да, как и любой expression-based язык. Типы и чистота тоже весьма математичны. И в коммунити есть немного интересующихся математикой людей.
 332 Кб, 720x1280
332 Кб, 720x1280одного из них. Источники расположены на главной оптической оси линзы. Расстояние между ними
составляет = 48 см. Каково фокусное расстояние линзы, если изображения источников находятся
в одной точке?
Можете объяснить как решать? Подгоном получено верное числовое значение, но не уверен что в формульном виде правильно решил.
После подсчета в вольфрам|альфа получается хуйня полная
*рисунке
Производящие функции, сочетания, эллептические интегралы и сферические функции. Также полезными будут знания аналитической геометрии.
Иди ботай диффуры, интегралы и комбинаторику.
1. Признак Д'Аламбера.
2. Радикальный признак. Во всех трёх точках сходится абсолютно.
3. Условие Коши-Римана.
Пиздос блять, в рот ебал, оказывается в задании на АВ силой трения пренебрегаем, а без нее я уже все решил 20 часов назад.
У тебя ещё на третьем пике во втором уравнении перед Rz плюс стоит, хотя сила против движения направлена.
сука бл, хули нет ни одной книги по теории вероятностей в шапке?
Ну это только там опечатка, далее я это учитывал, там потом сумма сил и перед ними минус, но почему с прогой не совпадает все равно, хоть можно и без этого.
Mathprofi, khan Academy
 1,7 Мб, 2560x1920
1,7 Мб, 2560x1920Сначала учить наизусть, потом пытаться понять до тех пор, пока не дойдет. И решать много-много задач по теме.
Не думать про обучаемость. Человек не способен сам оценить свою обучаемость, он способить только недооценить (не понимаю что вообще надо делать) или переоценить (читаю знакомые слова значит знаю). Хороший рецепт это работать и оценивать реальный показатель, именно время потраченное на что-то. Если человек 100 часов читает материал по теме, все более простой и простой и до него не дойдет, вот это реальная необучаемость.
 681 Кб, 4160x1156
681 Кб, 4160x1156Как блять догадаться каким способом решать эту хуиту??? Там же дохуя методов, Антон, как найти нужный? Прикрепляю задание для примера (10)
типовой способ это замена переменных для упрощения алгебраической ебли. например x+y=a, xy=b. Но прежде чем это делать, надо преобразовать выражении, чтобы оно зависело только от этих переменных. Для этого надо прежде всего "избавиться" от степеней.
в примере 10 моя первая идея была выделить (x^2-y^2)^2 из первого уравнения, потом разложить это на (x+y)^2(x-y)^2, а потом представить как (x+y)^2(x^2-2xy+y^2), и далее как (x+y)^2((x^2+2xy+y^2)-4xy), а после уже сделать замену на a и b.
Можно ли дойти до похожего? С геометрии я все забыл.
Отбросить, как ненужное.
Marco Taboga, Lectures on Probability Theory
and Mathematical Statistics
Если надо вероятность освежить, посмотри что там всякие мехматы выкладывают, вроде
http://www.nsu.ru/mmf/tvims/lotov/MMF.pdf
Можно, но скорее будешь как Рыбников, а не Паскаль.
есть манга книги по всем темам, целая серия
здесь периодически мелькают
http://nnmclub.to/forum/viewtopic.php?t=993281
Единственный плюс таких учебников - можно подрачивать прямо в процессе обучения
Вот наапример возьмем плоскость. Рисуем на ней координатную сетку, задаем векторное уравнение, допустим икс это тэ, игрек это тэ квадрат. Рисуем линии, все замечательно.
Но вот только вектор это же, грубо говоря, стрелочка. В какую сторону она должна быть направленна в моем случа, если я захочу изобразить все направленными стрелочками для наглядности??
>векторные пространства.
>Рисуем на ней координатную сетку
Ты мальца перепутал. Векторные пространства без координатных сеток, с сетками аффинные.
>задаем векторное уравнение, допустим икс это тэ, игрек это тэ квадрат
>Но вот только вектор это же, грубо говоря, стрелочка. В какую сторону она должна быть направленна в моем случа, если я захочу изобразить все направленными стрелочками для наглядности??
Можешь выбрать положительное направление на кривой, при t -> бесконечности.
Большая окружность?
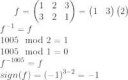 2 Кб, 246x154
2 Кб, 246x1541.Раскладываем в циклы
2.Возводить надо в отрицательную степень,поэтому ищем обратную перестановку
3.Любые циклы в степени своей длины - единичные перестановки, так что достаточно взять степени по модулю длины
4.Вычисляем знак
В другом задании аналогично,только надо ещё проделать ту же муть для h и перемножить.
В идеале, хотелось бы что-нибудь типа аналога фихтенгольца или кострикина, то есть несколько томиков с максимальным уровнем разжевывания, покрывающих большую часть университетского курса геометрии, и так, чтобы я, для начала, мог как минимум пролистнуть всю эту хуйню по диагонали и просто понять, из каких разделов она блядь вообще состоит.
Да, вполне.
Шеститомник? Я только у него помню учебник по аналу с исользованием групп.
Спасибо
Школьная математика: http://pastebin.com/Yn8DSzga
Копипаста: heller.ru/blog/2010/12/math-topics-list/, heller. ru/blog/2013/05/math-plan/
Книги: drive.google.com/folderview?id=0B47MUz8iO65LfnkzWUxGdXFqZXByUDVOb0xhNmp1Z1h5aWttb25CaEVJS3hrblpZdFN3N1E&usp=drive_web
Копипаста: imperium.lenin.ru/~verbit/MATH/programma.html, ium.mccme. ru/f04/experimental.html
Книги: drive.google.com/folderview?id=0B47MUz8iO65LfkhMdGt0RTlxUnZkOU9SUjdGUjNIWXRxdmhRWjloWlE2bi01ZGxYNkVxbXc&usp=drive_web
http://lj.rossia.org/users/dmitri_pavlov/
Книги: drive.google.com/folderview?id=0B47MUz8iO65LflZSWGZxcjlvdnRnZzhQczNPYzFtZnFZZENlemlmNklDclg5RmdJNVNsTjA&usp=drive_web
http://verbit.ru/Job/HSE/Curriculum/all.txt
Есть всё кроме:
Цфасман, Влэдуц, Ногин - Алгеброгеометрические коды. Основные понятия
Я. Элиашберг, Л. Трейнор - Лекции по симплектической геометрии и топологии
M. Gromov - Carnot-Caratheodory spaces seen from within
Книги:https://yadi.sk/d/XA0kQ40L37bPdy
Список НМУ
Книги: http://pastebin.com/At2vbyFN
Копипаста: http://pastebin.com/cH7HDf4U
Список: http://pastebin.com/PQ6nsAQj
Книги: https://yadi.sk/d/cMT8z8UBvyEyN
Ссылки:
https://sites.google.com/site/scienceandmathguide/subjects/mathematics
http://freebookcentre.net/SpecialCat/Free-Mathematics-Books-Download.html
Школьная математика: http://pastebin.com/Yn8DSzga
Копипаста: heller.ru/blog/2010/12/math-topics-list/, heller. ru/blog/2013/05/math-plan/
Книги: drive.google.com/folderview?id=0B47MUz8iO65LfnkzWUxGdXFqZXByUDVOb0xhNmp1Z1h5aWttb25CaEVJS3hrblpZdFN3N1E&usp=drive_web
Копипаста: imperium.lenin.ru/~verbit/MATH/programma.html, ium.mccme. ru/f04/experimental.html
Книги: drive.google.com/folderview?id=0B47MUz8iO65LfkhMdGt0RTlxUnZkOU9SUjdGUjNIWXRxdmhRWjloWlE2bi01ZGxYNkVxbXc&usp=drive_web
http://lj.rossia.org/users/dmitri_pavlov/
Книги: drive.google.com/folderview?id=0B47MUz8iO65LflZSWGZxcjlvdnRnZzhQczNPYzFtZnFZZENlemlmNklDclg5RmdJNVNsTjA&usp=drive_web
http://verbit.ru/Job/HSE/Curriculum/all.txt
Есть всё кроме:
Цфасман, Влэдуц, Ногин - Алгеброгеометрические коды. Основные понятия
Я. Элиашберг, Л. Трейнор - Лекции по симплектической геометрии и топологии
M. Gromov - Carnot-Caratheodory spaces seen from within
Книги:https://yadi.sk/d/XA0kQ40L37bPdy
Список НМУ
Книги: http://pastebin.com/At2vbyFN
Копипаста: http://pastebin.com/cH7HDf4U
Список: http://pastebin.com/PQ6nsAQj
Книги: https://yadi.sk/d/cMT8z8UBvyEyN
Ссылки:
https://sites.google.com/site/scienceandmathguide/subjects/mathematics
http://freebookcentre.net/SpecialCat/Free-Mathematics-Books-Download.html
Шапку составляет оп, а не модер.
Откуда все это?
Твоя работа?
Тi кто будешь?
>Алгеброгеометрические коды
Охуеть! С 2003 так никто и не отсканировал?!
Ну тогда я могу исправить эту несправедливость, в ближайшее время ждите от меня pdf-ку
Большое спасибо, анон
>Carnot-Caratheodory spaces seen from within
Ну вот же:
http://gen.lib.rus.ec/book/index.php?md5=4CEF95CF8A5F2DA286E9008771D26C65
Матпрофи.
 171 Кб, 1220x800
171 Кб, 1220x800Помогите, пожалуйста, разобраться в этих страшных зверях полному чайнику.
Что они из себя представляют на самом деле простым языком, желательно с картинками, но можно и на пальцах.
Можно объяснять как ребёнку.
Мне бы самое главное понять какие именно элементарные математические операции выполняются при их помощи? Это самый главный вопрос.
поправил, сорьки.
mathprofi
с меня как всегда
Ага, я уже позднее нашёл и добавил.
>>7358
Просто хобби, собирать интересные книги по спискам
>>7367
В свое время при сдаче очень помогла книга Фихтенгольца (1 том), учитывая архаичность образования в рахе.
В матрицах до сих не могу запомнить определений, если бы всё было так просто, как у Арнольда: "Определитель матрицы – это (ориентированный) объём параллелепипеда, рёбра которого – её столбцы. Если сообщить студентам эту тайну (тщательно скрываемую в выхолощенном алгебраическом преподавании), то вся теория детерминантов становится понятной главой теории полилинейных форм. Если же определять детерминанты иначе, то у каждого разумного человека на всю жизнь останется отвращение и к определителям, и к якобианам, и к теореме о неявной функции."
Тобишь общепринятого способа обозначать направление нету?
А то я в книжке смотрю на нарисованные стрелочками векторные картинки и понять не могу почему стрелочка туда или сюданаправленна.
инб4 гамалогея и тапалогея для жоаполазов
Арнольда очень сложно читать на самом деле, потому что он предполагает, что ты уже многое знаешь.
Закатыватся с него не стоит.
 213 Кб, 2468x1215
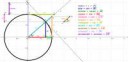
213 Кб, 2468x1215Длины (со знаком) отрезков вокруг угла и описанной единичной окружности.
Смотри, точки окружности - (cos(t);sin(t)). Положительное направление движения на оркужности - это изменение t от 0 до 2пи. Если будет прибавлять параметр t, то точка будет двигатся против часовой стрелки. Ясно?
 278 Кб, 1024x600
278 Кб, 1024x600Не могу найти картинку попроще, поэтому возьму вот эту.
Почекму в тридэ варианте по оси зэд горбы?
В прямоугольном треугольнике прилежащего катета к гипотенузе - косинус, противолежащего к гипотенузе - синус, противолежащего к прилежащему - тангенс. Такой треугольник на картинке с окружностью можно углядеть и там в силу единичности гипотенузы они приобретают удобное гееометрическое представление.
Потому что числа можно делать бесконечно.
Ни одна религия не запрещает любое число поделить на десять.
Диагональный метод лишь для счётных множеств, а как ты собрался перечислять трансцендентные числа?
да я просто не пойму. в чем там противоречие, например вот мы можем записать множество рациональных чисел и выписать в ряд идя по диагоналям. и у этого ряда установить биекцию с множеством натуральных все ок. но почему когда мы вещественные выписываем это не подходит? какое там противоречие, может кто объяснить? я просто студент первак я вот реально не могу понять
Да.
Я не очень понял это место.
Как угол альфа вдруг превратился в фи, а длина LN в длину MN (рис. 3), а точнее ниже...
Дельта x не поменялся, а вот дельта y превратился в маленькую dy, а у него в формулах "=" стоит:
Производная функции равна тангенсу фи (4 рис.), хотя до этого сказано, что производная функции равна отношению катетов, которые дают тангенс альфа (2 рис.).
Но достаточно взглянуть на рис. 1 и становится понятно, что углы альфа и фи не равны и LM не равен MN.
>Дельта x не поменялся, а вот дельта y превратился в маленькую dy, а у него в формулах "=" стоит:
Вот это вот самое мерзкое, паскудное, подлое, самое гадкое и отвратительное, что случалось со мной в моей сознательной жизни, в которой я имел несчастье учиться в третьесортном "математическом" универе. До слёз, до боли в груди, до дрожи в пальцах я ненавижу всю эту гнусность, этих мудил, которые давали мне это на лекциях. Которые спрашивали это на экзаменах. Я ненавижу школу, где мне объясняли "геометрический смысл производной", и это единственное, что я мог что-то понять (как мне казалось) в понятии предело. Они гады, уроды, садисты, они сломали мне жизнь, они сделали из меня овощ, они посадили меня в комнату 101, к крысам. Я не забуду, что я чувствовал, когда на 5м курсе уже я почему-то решил, что не хочу быть ебаным кодером, а хочу заниматься наукой, и сел себя насиловать опять, открыл старые лекции и стал пытаться понять, что такое этот ебаный dx, в который вдруг превращается дельта, потому что никогда не понимал. О, мерзость! Как же я ненавижу себя за это. Я хочу умереть, пусть меня переедед поезд, обольёт кислотой, оторвёт мне руку и ногу, да так, чтобы я жил ещё 1,5 часа, корчась от боли и перебирая свои кишки
Я читаю теперь всех этих долбаных вербитов, его последователей, всех этих матшкольников и студентов вышки, где они обсуждают, насколько это вредно, рашисткое мат. образование. Я читаю, как они жалуются на что-то плохое в нму или в вышке, я читаю то публичное письмо студентов матфака, где они призывают что-то поменять и предлагают свою программу. Я рыдаю. Слёзы обжигают мне щёки. Они, успешные, понаписавшие статей, понаехавшие в универы и на конференции, постигающие высокую науку, так, на досуге, немного возмущаются, что какие-то старпёры занимаются хуйнёй и убивают студентов. Меня убили.
Дорогой анон, пожалуйста, выбрось эти картинки и не старайся их понять. Возьми J. Lee - Introduction to smooth manifolds. Возьми что-нибудь ещё по многообразиям. Я не знаю, что там нужно по калкульсу, возьми Рудина, блядь. Открой math.stackexhange, там всё это тысячу раз и спрошено и разжёвано. Пойми, что производная - это такая функция, которая 1) линейная (т.е. в одномерном случае это умножение на число), 2) отличается от исходной функции на о малое первого порядка. И это всё, что нужно об определении. Разберись, что такое касательное и кокасательные расслоения. Пойми, что кокасательное расслоение над прямой есть одномерное векторное простарнство (над точкой), поэтому все дифф. формы отличаются умножением на число, и именно она и есть производная (в точке). Выучи, что дифференцирование это гомоморфизм модуля в себя, который удовлетворяет правилу Лейбница. И что, кроме производных, в алгебре гладких функцих на гладком многообразии других дифференцирований нет. Анон, учи нормальную математику, выкини это говно. Ради меня. Ради всех нас, кого уничтожили эти ебаные террористы
>Дельта x не поменялся, а вот дельта y превратился в маленькую dy, а у него в формулах "=" стоит:
Вот это вот самое мерзкое, паскудное, подлое, самое гадкое и отвратительное, что случалось со мной в моей сознательной жизни, в которой я имел несчастье учиться в третьесортном "математическом" универе. До слёз, до боли в груди, до дрожи в пальцах я ненавижу всю эту гнусность, этих мудил, которые давали мне это на лекциях. Которые спрашивали это на экзаменах. Я ненавижу школу, где мне объясняли "геометрический смысл производной", и это единственное, что я мог что-то понять (как мне казалось) в понятии предело. Они гады, уроды, садисты, они сломали мне жизнь, они сделали из меня овощ, они посадили меня в комнату 101, к крысам. Я не забуду, что я чувствовал, когда на 5м курсе уже я почему-то решил, что не хочу быть ебаным кодером, а хочу заниматься наукой, и сел себя насиловать опять, открыл старые лекции и стал пытаться понять, что такое этот ебаный dx, в который вдруг превращается дельта, потому что никогда не понимал. О, мерзость! Как же я ненавижу себя за это. Я хочу умереть, пусть меня переедед поезд, обольёт кислотой, оторвёт мне руку и ногу, да так, чтобы я жил ещё 1,5 часа, корчась от боли и перебирая свои кишки
Я читаю теперь всех этих долбаных вербитов, его последователей, всех этих матшкольников и студентов вышки, где они обсуждают, насколько это вредно, рашисткое мат. образование. Я читаю, как они жалуются на что-то плохое в нму или в вышке, я читаю то публичное письмо студентов матфака, где они призывают что-то поменять и предлагают свою программу. Я рыдаю. Слёзы обжигают мне щёки. Они, успешные, понаписавшие статей, понаехавшие в универы и на конференции, постигающие высокую науку, так, на досуге, немного возмущаются, что какие-то старпёры занимаются хуйнёй и убивают студентов. Меня убили.
Дорогой анон, пожалуйста, выбрось эти картинки и не старайся их понять. Возьми J. Lee - Introduction to smooth manifolds. Возьми что-нибудь ещё по многообразиям. Я не знаю, что там нужно по калкульсу, возьми Рудина, блядь. Открой math.stackexhange, там всё это тысячу раз и спрошено и разжёвано. Пойми, что производная - это такая функция, которая 1) линейная (т.е. в одномерном случае это умножение на число), 2) отличается от исходной функции на о малое первого порядка. И это всё, что нужно об определении. Разберись, что такое касательное и кокасательные расслоения. Пойми, что кокасательное расслоение над прямой есть одномерное векторное простарнство (над точкой), поэтому все дифф. формы отличаются умножением на число, и именно она и есть производная (в точке). Выучи, что дифференцирование это гомоморфизм модуля в себя, который удовлетворяет правилу Лейбница. И что, кроме производных, в алгебре гладких функцих на гладком многообразии других дифференцирований нет. Анон, учи нормальную математику, выкини это говно. Ради меня. Ради всех нас, кого уничтожили эти ебаные террористы
ок, разобрался
пиздец сообщение само отправилось
ок, разобрался https://www.youtube.com/watch?v=wYzc4F9GPGQ
Что насчёт матпрофи, он не умеет ни учить, не объяснять, пытается как проще вроде, но при этом приплетает сразу же кучу ненужной сложной хуйни с кучей вложенных скобок, вот тако вот типа правильней, да мне по хуй как првильней бля, мне понять надо тему, а не дерьмовые поучительные идеи выслушивать по улучшению мира, вместо дельта эф везде сука расписывает динное выражение и всё больше и больше нагромождает, проблема с логикой изложения, не делает акценты из-за чего я начал думать, что тангенгенс равен не пределу, а самому выражению, куча лишнего мусора и тупых словечек, улыбки дебильные итд, признак слабоумия.
А в пределах у него куча вычислительных ошибок, он делает несколько действий в голове, хуяк, а дробь забывает перевернуть или ещё подобные вещи.
Ищем другой сайт для изучения математики.
https://www.youtube.com/watch?v=wYzc4F9GPGQ
Если чисто логически прикинуть.
Если дельта x получает значение не достигая нуля, пусть даже и очень маленькое, но не равное нулю.
Тогда дельта икс уже не стремится к нулю, а угол альфа не стремится к углу бета и тангенс угла альфа не стремится к тангенсу угла бета, и производная равная тангенсу бета больше не равна пределу (дельта f)/(дельта x).
Но разница может быть настолько мала, что мы её даже не заметим.
В ОП-посте же есть списки.
> Вот это вот самое мерзкое, паскудное, подлое, самое гадкое и отвратительное
Так ведь там не определение dy, а его "геометрический смысл".
Значения функции по этой оси откладываются, куда их ещё-то пихать, если x и y - аргументы?
Если чисто логически прикинуть то нужно читать несколько разных учебников.
А по вопросу, если оставаться в поле вещественных чисел то разница будет числена, но ей можно будет пренебречь.
А если перейти в грань бесконечно малых, то разница так же будет бесконечно малой, но малой высшего порядка, тобишь быстрее будет становится малой.
С хуёв оно параметрическое-то? Там же координаты напрямую участвуют. Взяли, скажем, х и y по корню из 2, получили z=f(x,y)=-2e^-2
Но ведь каждый отдельный член в уравнении не зависит от другого.
Вот взять уравнение окружности икс квадрат плюс игрек квадрат равняется эр квадрат. Тут все связанно, уменьшился икс увеличился игрек, результат тот же.
В параметрической форме это все будет в виде икс эр косинус тэ, игрек эр синус тэ. ВРоде зависимости нету, а она есть
Да
Там говорится о том, как дельта превращается в d. Вот это самое ужасное во всей этой школьной конструкции. Это ложь, не превращается оно, d не имеет ничего общего с приращениями! это обозначение для ковекторов, а не "приращения в пределе" или как там объясняется
Нету у производной никакого геометрического смысла, кроме того смысла, что производная - это линейное приближение функции. То, что производная совпадает с наклоном касательной, - так это отражение (интуитивного ясного) того факта, что касательная есть линейное приближение прямой. Вся эта мерзость с предельными секущими - это ложь, пытки и изнасилования, и массовые убийства.
>мерзость с предельными секущими
Так, падажжи ебана.
Вот у нас есть точка a.
Вот у нас производная f в a существует и равна f'(a).
Это значит, что f(a+h) - f(a) = f'(a)h + o(h).
Это значит, что lim (f(a+h) - f(a))/h = f'(a), h -> 0.
Вот у нас есть определение предела по Гейне.
Берем последовательность h1, h2, h3, ... , сходящуюся к нулю.
Строим последовательность f(a+h1)/h1, f(a+h2)/h2, f(a+h3)/h3, ...
Она сходится к f'(a).
Что тут не так?
Да он не про это. Он бомбалирует, что дифференциал пределом приращения называют, что, в общем-то, пиздёж и есть.
Ограниченное множество вещественных чисел имеет супремум и инфимум по аксиоме.
Можно ли привести себя в порядок?
Какие доказательства тебе нужны?
Что сумма интегралов двух одинаковых функций от а до с и от с до б равны сумме интегралов? Очевидно из самого определения интеграла.
Что парабола это линия у которой разница расстояний до выбранной прямой и точке равно константе? Очевидно.
Что неэвклидовые пространства могут содержать треугольники с суммой углов больше 180 градусов? Очевидно из определения неэвклидового пространства.
Ты просто слушал, но не слышал. Чуть менее чем все доказательства в математике это доказательства уровня "2+2-4. А теперь докажем это на примере тапалагических прасранств"
Имеет место банальная терминологическая путаница. Тот кун называет дифференциалом линейную функцию D такую, что f(a+h)-f(h) = D(h) + o(h). Это современное понимание.
В классическом анализе (до революции Коши) дифференциалами называются прообразы и образы функции D. То есть если D - функция из пространства X в пространство Y, то вектор x из X обозначается как dx, вектор y из Y обозначается как dy - то есть просто пишется буковка d перед символом. Можно рисовать черточку со стрелочкой, можно писать d.
В одномерном случае функция D просто умножает свой аргумент на некоторое число, а именно на производную.
Поэтому, окончательно:
Пусть f дифференцируема в точке x, D - её дифференциал, f'(x) - её производная.
Запись dy = f'(x)dx означает всего-навсего, что y = D(x).
Сама функция D при классическом подходе не называется никак.
В учебниках матана сначала следуют современному подходу и дифференциалом называют функцию D, а потом, в объяснении геометрического смысла, внезапно начинают следовать классическому подходу и дифференциалами называют прообразы и образы D.
Когда говорят, что дифференциал - главная линейная часть приращения функции, имеют в виду классический подход.
>f(a+h)-f(h) = D(h)+ o(h)
>Запись dy = f'(x)dx означает всего-навсего, что y = D(x).
Может, f(a+h)-f(a) = D(h)+ o(h) и dy=D(x)?
У тебя на пике определение пустого множества, а не единицы. "Тот объект, которому не не не принадлежит тот объект, который ему не не принадлежит". Несколько "не" подряд появляются из-за кванторов. Если их аннигилировать, то у тебя на картинке написано всего-навсего, что пустое множество - это "тот объект, которому не принадлежит тот объект, который ему принадлежит".
Если хочешь пиздеть про нестандартный анализ, то потрудись пролистать хотя бы одну книгу про него. Ты охуеешь. Тени чисел, каждое множество содержит нестандартный элемент, регулярные по Слейтеру программы - вот что такое этот анализ. Нестандартный анализ - наркомания похлеще той, что несёт местный любитель Мартин-Лёфа. О нестандартном анализе нельзя думать как об анализе, в котором есть актуальные бесконечно-малые, поскольку а) на самом деле их там нет и б) это не анализ, это беспощадная теоретико-множественная наркомания.
Стремление к нулю - не есть ноль так же, как и стремление к супербольшому числу не есть супербольшоечисло, стремление к нулю - это супермаленькое число, но оно чисто мнимое, как и супербольшое.
Бесконечность и бесконечно малое - это направление стремления, а не конкретное число.
Это мой ИМХО. Докажешь обратное?
Тем более если там абсолютно точно получается не ноль, а число большее нуля, тогда вообще о чём разговор?.
Всем привет. Подскажите где посмотреть, как решаются подобные задачи.
Построить граф и график соответствия 8 между множествами X и Y. Указать упорядоченные пары соответствия.
X = {1,10,11,15} Y ={2,8,10,16},S X<=Y
>>7509
А вот я лично считаю, что 0,00000000000000...00000000000000001 - это не 0, ты же утверждаешь, что это ноль, как сам думаешь кто из нас прав?
Почти равно, т.е. примерно равно или равно - это абсолютно разные вещи.
Разумеется, если дельта икс не равна нулю, тогда производная - чисто примерная штука и чем больше дельта икс, тем больше погрешность. И настанет время, когда из-за этого кто-то сильно пострадает, а может это будет глобальная катастрафа и только после этого людишки начнут разбираться в чём проблема, но они 100% её не найдут и свалят всё на первого попавшегося. А не найдут они её, потому что они попросту идиоты.
Я тебя не спрашиваю, что пишут люди в своих книгах, которые не способны думать, а способны лишь передавать информацию дальше тем, кто на это способен. Я спрашиваю у тебя твоё личное мнение. Ты, видимо, полагаешь, что миллиарды людей не могут ошибаться, но поверь, они ошибаются. Они ошибаются каждую секунду, они ошибаются каждое мгновение, они ошибаются прямо сейчас.
И десятки млрд и сотни млрд людей тоже будут ошибаться и тебе несказанно повезёт, если ты найдёшь реально думающих людей среди всего этого сброда. Это как иголку найти в стоге сена.
Что такое предел понятно из одного только названия. У вас в голове не каша? Если вы не в состоянии 3-4 простейших логических шага проделать хотя бы на листочке?
пульс и координата квантовой частицы
Почему? Почему не работает коммутативность?
Векторное произведение не коммутативно в принципе.
потому что операторы в общем случае не обязаны быть коммутативными.
Я знаю, что когда у обеих последовательностей пределы конечные числа, то надо воспользоваться свойством модулей, а тут что делать?
Ну почитай как L4 доказывали и другие проекты.
Так то там какой-нибудь Coq небось использовали. По Coq есть годная книженция Software Foundations.
Если сам принцип: формализуют язык реализации, в пруверах типа Coq/Agda/Lean доказывают, что всё норм и опционально генерят код из доказательства.
 800 Кб, 2560x1600
800 Кб, 2560x1600И что посоветуете?
Почему именно Джава? Если ты хочешь изучать конкретно математику, то тебе не стоит распылять свои силы ещё на программирование, потому что много времени будет уходить на велосипеды. Используй математические пакеты (MatLab, Wolfram Mathematica). Если ты хочешь всё и сразу, то лучше Python тогда.
Еще же Арнольд, да и Вербит говорили, что эти задачи/тесты хуйня, чем больше у человека мат. бэкграунд тем сложнее ему решать подобные задачи, если это не его сфера интереса.
Есть ссылки?
А Maple что?
Ну и говно, особенно вопрос про города. При чём здесь интеллект вообще?
Основная теорема алгебры.
> они посадили меня в комнату 101
>101
Так бы и сказал, что К.О.З.У в Убежище на инженера сдал. То же мне, ОДИНОКИЙ СТРАННИК.
Гугл тебе на что?
Изучаю понятие полного дифференциала функции нескольких переменных. Вопрос почему f'x(x0 + Odx, y0 + dy, z0 + dz) = f'x(x0,y0,z0) + alpha
Куда пропали дельта приращении??
Задачник Бермана полистай, там много прикладных задач после вычислительных примеров бывает. А без пределов ты далеко не уплывёшь в дифференциальном и интегральном исчислении. Применение сами пределы имеют как минимум в определениях и несобственных интегралах.
Построить граф и график соответствия 8 между множествами X и Y. Указать упорядоченные пары соответствия.
X = {1,10,11,15} Y ={2,8,10,16},S X<=Y
f'x(x0 + Odx, y0 + dy, z0 + dz)
и
f'x(x0,y0,z0)
— просто два числа.
Когда есть два числа x и y, всегда можно написать x=y+c, где c — какое-то число (это называется разность).
Бери x=y-Δx и не парься.
Почему предел считается описываемым значение функции в месте где значение функции неопределено?
Фикс
Читаю 5 томник, П. С. Александров, А. И. Маркушевич, А. Я. Хинчин - Энциклопедия элементарной математики
Люто доставляет элементарность объяснений, хотя не всегда очевидно.
Спасибо. И что, в самом деле понятно?
>Нужно обязательно получать высшее образование?
Да.
>Доступ к вычислительной технике
Это вообще последнее, что тебя должно волновать при изучении математики.
>Да.
Т.е. концепция "ученого одиночки", каким был Пьер Ферма, например, который не был математиком, а работал гос. служащим, или Декарт и множество других математиков, примеры научного пути которых были описаны в книге Белла "Творцы математики" умерла?
В смысле, невозможность заниматься математикой как наукой не имея высшего образования упирается во что? В бумажку, статус, или современную сложность вычислений и необходимости в дорогом оборудовании для этих вычислений?
Посмотри годы их жизни.
Надеюсь, после этого придет понимание абсолютной тупости твоего вопроса.
>понимание абсолютной тупости твоего вопроса.
Скорее на меня накатывает понимание тупости твоего ответа.
Во что упирается необходимость получения ВО для математика? Прочти книгу Белла "Творцы математики" где как раз и рассказывается, что сотни математиков не имели ни то, что высшего, а вообще никакого университетского образования, где попутно расписывались их биографии.
Сейчас же я спрашиваю о современном положении математика и во что упираются его проф. возможности
Вижу, с тобой бесполезно вести дискуссию.
Ты задал вопрос с целью получения конкретного ответа.
Если ты так уверен в своих силах, то вот тебе либген, скайхаб, вот оверфлоу - пиздуй и учись.
Ты ограничен только уровнем своего интеллекта.
Если ты охуенно умён, а ты должен быть таким для того, что бы заниматься математикой на высшем уровне, то получение ВО, если оно вообще нужно, для тебя не будет проблемой.
И это весьма очевидно.
Ничего против этих ребят не имею, но это, видимо, не то, к чему ты стремишься
и фермаисты :)
>Ты ограничен только уровнем своего интеллекта.
Пфффф, а кто же не ограничен?
Или ты о том секретном способе, для достижения >2 Grot?
Звучит, как "Мы те, кто мы есть на самом деле!"
Нет, нельзя. Тебе для входа в исследовательскую деятельность нужны будут, во-первых, преподаватели, которые направят твои усилия в нужное русло и дадут базовые (не все, а только базовые!) знания предмета, а во-вторых - материалы, над которыми надо работать. Ты не можешь с потолка взять и решить какую-нибудь проблему, потому что ты банально не знаешь, что решать. За сложные же задачи браться сходу - путь либо в никуда, либо к научному фричеству.
Чтобы заниматься математикой, строго говоря, формальное образование не нужно. Но есть две большие проблемы. Первое, если не иметь подходящих дипломов получать деньги за занятие математикой (и наукой вообще) очень сложно. Второе, стать нормальным математиком в изоляции от других математиков, судя по всему, просто невозможно; завязывание же таких контактов в процессе получения нормального математического образование происходит довольно естественно.
Подводя итого, технически возможно (я даже знаю один живой пример), но по большому счету это метод создать массу дополнительных проблем самому себе.
>я даже знаю один живой пример
Гельфанд, Рамануджан?
>этот метод создать массу дополнительных проблем
Мягко говоря, а на деле это, как осознанное самобичевание. Нахуя изолировать себя, когда в коллективе и с научруком куда проще и лучше?!
Школьник под впечатлением от попсовой книжки решил наебать системутм и стать математиком самостоятельно. Не он первый, не он последний
Только зачем здесь так много развернутых ответов? Достаточно всего двух слов: "Не выйдет."
в сумме?*
>Нахуя изолировать себя, когда в коллективе и с научруком куда проще и лучше?!
А форумов и этой доски хватит? Просто далеко не школоло или студота уже, работаю, и второе формальное образование получать некогда. Математика интересует в разрезе computer science - теория типов, теория категорий, матлогика и прочая абстрактная поебень.
Почему Принстон называют цыганскими подвалами?
Прочитать их доказательства
Что вольфрам показывает? Вообще, что ты как маленький, каждое действие посмотри отдельно и всё.
>Что вольфрам показывает?
http://www.wolframalpha.com/input/?i=diff(asin((1-x^2)/(1+x^2))+2*x/17,x)
>Гельфанд, Рамануджан?
Я же говорю живой (вроде ему слегка за 40). И не то, чтобы человек очень выдающийся, но вполне компетентный.
>Нахуя изолировать себя, когда в коллективе и с научруком куда проще и лучше?!
Ну я и сказал, что в изоляции стать математиком невозможно, что означает, что ходить на научные семинары и фактически иметь научного руководителя/руководителей нужно будет в любом случае.
>>7814
>А форумов и этой доски хватит?
Нет.
Если вопрос, на который ты отвечаешь, вообще имел какой-то смысл, то он, вероятно, подразумевал следующее:
Возможно ли в ходе самостоятельных занятий (без университета) выйти на тот уровень, когда тебе уже понадобится
>ходить на научные семинары и фактически иметь научного руководителя
Ответ к данной формулировке вполне очевиден: да.
Бамп вопросу.
Почему все что дальше прикрепленного треда представляет из себя помойку из вхоренов, тапалогий и петушений на ЛЖР?
Потому что проще пиздеть про тусовочку, чем изучать и обсуждать математику.
у тебя есть плоскость, берешь нормаль, решаешь
 2 Кб, 316x70
2 Кб, 316x702 года назад влюбился в математику.
Понимаю, что о математической научной карьере в 26 лет можно забыть. Но, появилось лютое желание стать преподавателем математики, чтобы так сказать вовремя направить школьё или студентоту на путь истинный (если у таковой имеется интерес к математике).
Кто как считает, сильный ли зашквар будет в 26 лет поступать в университет учиться на педагога по математике и информатике?
>Какая разница, в каком возрасте начинать карьеру?
Есть ведь такие понятия, как "молодой ученый", "соискатель", которые сильно зависимы от возраста. Да и в карьерном росте больше питают надежд, перспектив и симпатий к молодым специалистам.
> Есть ведь такие понятия, как "молодой ученый"
Есть еще понятие как "просто ученый". Возраст - оправдание.
lim h->0 (g(x+h)-g(x))/h
Можно значит выразить разницу значений функции:
g(x+h)-g(x)=(d(g(x))/dx)*h+o(h), h->0
что означает о малое и зачем она нужна?
По бурбакам математик становится слишком старым после достижения 50 лет. У тебя есть 24 года, пиздуй учить.
Без паники.
Да, время упущено. Ты не будешь столь же эффективен, как если бы в 14 пошел в матшколу и дальше без перерывов занимался бы математикой (получив степень как раз примерно в свои 26). То есть, скажем, получить медаль Филдса надежд нет.
Но это не означает, что все безнадежно. Знаю несколько человек, которые перешли в математику заметно за 20. Надо признать, что звезд с неба они не хватают. Но при этом они весьма мотивированы и способны делать вполне содержательную работу. Я бы сказал, что они заметно лучше той части математиков, которые в какой-то момент, по-существу, потеряли интерес к математике, но почему-то не сменили карьеру.
Ну до Филдса у него еще 14 лет есть. Сложно конечно думаю вообще без шансов, без вузовской базы что-то там пытаться. Но после время будет, кто его знает, вдруг.
> а ещё и огромное удовлетворение от занятия математикой
Это самое главное. А медали, награды, премии, это все наживное, и от возраста я думаю не зависит, но не особо.
что такое о малое зачем его пишут? разве диффернециал не будет больше разницы функций всегда зачем там что то прибавлять
 9 Кб, 388x522
9 Кб, 388x522Пикрелейтед. Я совсем не понял как это произошло. Я бы понял если бы в знаменателе осталось 2-х, но тут я совсем в непонятках. Объясните пожалуйста.
Вот пидоры, я тут мозг сломал, дело в том, что у них она и дальше там в решении идет. Думал может там какое деление хитрое на -1/2.
Чтобы было верное равенство?
Что значит зачем, раздели всё на h, устреми h к нулю и получи тот предел, что у тебя в начале написан. Что тебе не понятно?
"Теория множеств" (Николя Бурбаки).
Учебник за 9 класс
Афлутова-Устинов и Гашков
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс
Р. Курант, Г. Роббинс: “Что такое математика?”
П. С. Александров: “Введение в теорию групп“
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”
Д. Пойа: “Как решать задачу“
Д. Пойа: “Математическое открытие“
Н. Я. Виленкин: "Рассказы о множествах"
>26 лет, высшего образования нет.
>2 года назад влюбился в математику.
>Понимаю, что о математической научной карьере в 26 лет можно забыть. Но, появилось лютое желание стать преподавателем математики, чтобы так сказать вовремя направить школьё или студентоту на путь истинный (если у таковой имеется интерес к математике).
>Кто как считает, сильный ли зашквар будет в 26 лет поступать в университет учиться на педагога по математике и информатике?
Такая же телега. Только я хочу и матаном заняться, и финансами. В смысле и рыбку съесть и косточкой не подавиться. Но мотивации нет настолько, что уже трижды учинял попытку суицида). Старый, ещё и поступать в 25 на 1 курс со вчерашними школьниками. Гордость и амбиции, ага.
Хеллер также в НМУ шел, с ним на одном курсе 10-классник был, и нормально всё.
>>7897
Ебать вы закомплексованные, ишь какие, со школьниками учиться не хотят. Тут не надо ни о чём волноваться, когда вы начинаете заниматься математикой, вы обнуляете свой возраст и перерождаетесь подобно фениксу. Тот, кем вы были до занятия математикой и то существо, каким вы стали после - это два совершенно разных организма, не имеющие ничего общего друг с другом, бренное тело и его возраст перестаёт что-либо значить, только сознание истинно.
Я не он. Но вот действительно, хоть институт уже и закончил правда специальность - не чистый математик.
Занимаюсь самообразованием, и вот чувствую какое-то ощущение - что вот это(некоторые вещи для младшекурсников) мне трудно читать и прорешивать,а есть юди, которые это ПИСАЛИ. (хотя, конечно, понятно, что это работа несколько иного толка - компиляция источников, выбор лучшиъ эпизодов и связывание это в одну сюжетную нить)
Есть такая штука что, ВРОДЕ БЫ, я просто тупо быстрее устаю из-за разных не особо серьёзных, но мешающих болезней - и получается медленнее,чем возможно, хотя время сейчас есть "в избытке"(на самом деле его всегда мало... именно из-за того, что медленный). Это только я или многие так?
> мне трудно читать и прорешивать,а есть юди, которые это ПИСАЛИ
Таки разбираться в чужом сложнее, чем писать самому.
Используя аксиому выбора.
Вникать в определения. Математика – наука о семантике/содержании понятий, а не о манипуляциях с символами.
почему в лемме ферма когда рассматривают односторонние пределы стоит нестрогое неравенство, там ведь должно быть просто равенство нулю, нет?
Я хочу увидеть полное доказательство. Что бы буквально была доказана невозможность построить такой гомеоморфизм.
 26 Кб, 513x268
26 Кб, 513x268реально объясните чего я не догоняю.
правосторонний и левосторонний пределы должны быть строго равны, только тогда существует предел, предел это ведь просто характеристика. почему в доказательстве какие то неравенства, односторонние производные в точке совпадают -> производная существует и равна им. там в док-ве левосторонний и правосторонние пределы равны это даже можно в вольфраме проверить или самому решить и увидеть. откуда неравенства
> там ведь должно быть просто равенство нулю
> правосторонний и левосторонний пределы должны быть строго равны
Это то, что нужно доказать.
Неравенства получаются из того, что f(x_0) максимум и знака (x-x_0).
Ребят, сюда несколько раз вбрасывали список тип
с темами которые должны изучаться в школе и на 1 2 3 4 5 курсах
Забыл фамилию составителя, киньте его пожалуйста
Так само значение в обоих этих равносторонних пределах будет 0. Значение правостороннего и левостороннего предела 0, это не надо доказывать мы же можем это просто посчитать. Какая разница с какой стороны подбираться, значение предела будет одно и то же. Понятно, что там слева во всех точках кроме максимума значение производной больше нуля, а справа меньше. Но если рассматривать конкретный предел с стремлением икса к максимуму неважно ведь с какой стороны подбираться значение будет одинаковым, почему именно в односторонних пределах стоит неравенство?
Странное исследование. Понятно же, что поп-музыка будет отвлекать. Там же много слов, всяких "ах-ух-трибиух".
Еще один. Попробуй в программе "курс" прочитать как "этап обучения" а "мат школьник" как минимальный набор основ, необходимых для развития культуры. Смысл не изменится.
Как скажешь, бро.
я кажется понял что имелось ввиду, именно в процессе изменения дельты которая зависит от эпсилона знаменатель будет меньше нуля в первом пределе, числитель понятно больше. Конечная левосторонняя производная конечно будет равно 0. Но нам надо зафиксировать как то тот факт что изменяется значение производной и поэтому поставили неравенства, это конечно правильно но запутывает, лучше бы придумали какой нибудь эпсилон сдвиг конечного предела и написали там строгое неравенство.
Спасибо за 3-ю ссыль, не видел её раньше.
Прочитал "Бурбаки" - Архитектура математики, сейчас читаю несколько книг, Голблатта - Топосы; Элементарную энциклопедию Александрова; Ван дер Вардена; Ленга - Алгебру; Прасолов - Геометрия. Позднее постараюсь перейти на англоязычную литературу. Пока теоремы не доказываю. Можете расписать, как лучше шагать от алгебры к другим областям?
Ван дер Варден и Ленг сразу? Читай лучше Ротмана или Роуэна/Айзексона.
>как лучше шагать от алгебры
Зачем тебе к другим областям? 98% математики это алгебра.
>Голблатта - Топосы
Не_нужно.
>Зачем тебе к другим областям? 98% математики это алгебра.
поддерживаю
именно поэтому не учу матан и функан
да хуйня это все, завтра ещё ебучая сессия по топологии
мне вообще кажется что матан функан комбинаторику и теовер стоит вырезать из математики, это лженауки
>Позднее постараюсь перейти на англоязычную литературу.
Нет. Переходи сейчас. Иначе потом будет поздно.
>Пока теоремы не доказываю.
Нужно доказывать с самого начала. Доказательство - главное в математике, что отличает её от всего остального в этом мире.
>Голблатта - Топосы.
Если только тебе сносит крышу с них в хорошем смысле.
>Можете расписать, как лучше шагать от алгебры к другим областям?
Другие области не нужны.
>Прочитал "Бурбаки" - Архитектура математики.
Умница. Продолжай их читать.
...и в итоге приходим, что самым главным является знак. А так как доказательство в математике строится на допущении их перемещать, приходим к первоначальному выводу.
 87 Кб, 1024x768
87 Кб, 1024x768На этой борде сидят реальные математики?
Или только студенты 1-2(3) курса?
>Гротендика не читали, Манина хоть почитайте
Первый, я так понял, обсуждаемые вопросы затрагивает в Récoltes et semailles, а у Манина где читать то? А то я французского ещё не знаю.
Математика как метафора.
math.ru/lib/files/pdf/manin.pdf
Можешь еще про мистицизм почитать у вербита, в конце треда о топологии ссылка.
В третий раз буду его читать и попутно решать задачки из него и демидовича.
После третьего раза я смогу вкатится в ландау-лившица или нужно еще что то для погружения в математику?
Всем привет, надо понять фильтр калмана. Нужно для оценки величины параметра, зависящего косвенно от двух других величин. Интересует сигма точечный фильтр калмана(Unscented Kalman filter).
Кто что может посоветовать почитать, или пояснить?
Это перевод, или на русском выходит первой?
>На этой борде сидят реальные математики?
>Или только студенты 1-2(3) курса?
В какую из этих двух категорий попадет человек, если он по возрасту приват-доцент или профессор, а по уровню знаний – второкурсник в смысле вербицкого?
Ты понимаешь, что это идиотский вопрос, в принципе?
Лучьше ответь про фильтры калмана плиз, а не на вопросы какого то еблана.
>Нужно ли уметь находить интегралы вручную
Да.
>Дрочить всю эту таблицу, приемы, если есть ПО которое это делает намного лучше?
Есть ПО, но лучше таблицу дрочить конечно.
>Как они вообще устроены
Кто они?
>Я про неопределенные, также как и человек решают или есть какой-то универсальный топорный алгоритм, который сложен для человека, но прост для компа?
Алгоритм Риша.
Что мне известно:
На пациента идет ток, я могу его регулировать и я знаю сколько тока идет на него.
Я знаю диапазон сопротивлений пациента от 50 до 1000 ом
Что я не знаю:
Напряжение которое идет на пациента
Что мне нужно найти:
Мощность идущую на пациента.
Может быть можно как то приблизительно определить без непосредственного измерения напряжения?
 212 Кб, 1920x1080
212 Кб, 1920x1080Что конкретно надо читать, чтобы смочь в нейронные сети и прочее?
на пик - хайкин, нейронные сети, полный курс. Нихуя не понятно
Вам же целый номерной тред сделали https://2ch.hk/pr/res/900102.html (
>то советую начать с анализа Шварца
Ты там не охул ли а щенок? Сам-то с чего начинал? Небось, како-нибудь Ильина-Поздника.
> А про дважды прочитанный полтора тысячный текст
Повторение мать учения. По-хорошему, учебник через месяц-два, после того, как прочитал, следует ещё раз прочитать, по ходу доказывая теоремы. Базарю, результат будет хороший, да и после первого чтения можно многое упустить.
>анализа Шварца
Хорошо пошутил, молодец. Когда закончишь ебаться в жопу тапалогиями покажешь мне где в физике применяются теории множеств
Если бы я начинал с говна, то я был бы только рад, если бы мне на это указали и подсунули что-нибудь хорошее взамен. И где было написано, что повторять изученный материал --- плохо?
Ящик посчитал?
Не очень.
Про множества там страничек двадцать-тридцать, типа что такое отображение, фактормножество и мощность. Топология в Шварце тоже не экзотическая, самые основные понятия и десяток важных теорем. И даже такие базовые понятия находят применение в физике. Например физическое пространство в квантовых масштабах имеет неархимедову метрику. Метрика -- отображение. Для ее определения необходимо определить множество действительных чисел, мощность которых континуальна, а сами они являются классами эквивалентости последовательностей коши рациональных чисел.
Собственно можешь дальше перечитывать талмуды калькулуса для студентов технических специальностей, но это малополезно.
Нахуя мне квантовая метрика, если ученые подкопченые в говне моченые до сих пор не разобрались какая интерпретация самая правильная и для разных ситуаций применяют кардинально отличающиеся?
Блядь, да они даже с физикой ядра не разобрались какую модель применять и для каждой подзалупной хуйни свою дичную модуль придумали. Оболочечная модель, капельная, статистическая, сверхтекучая, хуясекучая. Только электричество более менее проработали, и то, на основаниях термодинамики и химии, что считается смежными дисциплинами.
Это я к тому что разъяснение нахуй не нужной хуйни шварцем через три пизды колено о приращении функции мне не нужно.
Ну и потом, если бы вся физика стояла на математике получалась бы теория супер-пупер струн, а не физика.
 449 Кб, 1102x1960
449 Кб, 1102x1960Нельзя понять теорию относительности, не зная, что такое риманово многообразие, ассоциированная с метрикой связность, тензор кривизны, касательное пространство и еще кучу разъяснений Шварца.
Последовательность имеет предел тогда и только тогда, когда она фундаментальна.
Бамп поцаны, погибаю ваще, как переложить википедию на практические вещи? хеелп
Зачем она мне нужна, если для того чтобы применить её на практике нужно оборудование которое в гараже не соберешь?
Да, приборы которые нужны для измерения всяких расщеплений сверхтонкой структуры можно собрать на токарном станке с помощью кузьмича, но прибор этот больше ни на что не сгодится.
>>8102
Уже все теории старой математики доказал чтобы в множества вкатится?
Какие еще теории старой математики? Теория множеств меня не интересует. Ты меня с кем-то перепутал.
Это тебе не нужно, то тебе не нужно. Ладно, расскажи, зачем тебе нужно прочесть Ландау-Лифшица.
Зависит от области, причём очень сильно.
Чистая математика -- матфак ВШЭ, однако только 3 или сколько-то там направлений, если интересных тебе среди них нет, то МехМат МГУ.
Прикладная -- МФТИ (все факультеты сильные и заточены под математику, но под разную; но наиболее ориентированный на математику факультет -- ФУПМ, ну или ФОПФ, кафедра проблем теорфиза, но там больше абстрактной математики), СПбАУ, ВМК МГУ
Прикладная экономическая -- совместный бакалавриат ВШЭ и РЭШ. Очень сильный факультет, не подумай, что экономика -- штука гуманитарная.
Ну и не учись нахуй, еблан. Пиздец теперь, может вообще физику не учить никому, пока сам Господь Бог с небес не спустится и не скажет, что за закон двигал им, когда он творил вселенную? Интерпретации -- это блядь физический смысл, для прикладных задач, в которых используется квантмех, вообще поебать, сколько там миров и существует ли близкодействие и прямые причинно-следственные связи.
Значит, нужен только теормех, электричество да термодинамика? Без остального проживём? Только вот нахуй тебе теормех, электричество да термодинамика, если ты всем этим сразу в гараже одновременно не займёшься? Надо что-то одно выбрать.
Когда это матан и функан стали разделами алгебры? Определения тебе не завозили?
Матан (в широком смысле, то бишь включая функан, инфинитезимальный анализ и блабла) -- такой же самостоятельный раздел математики, как геометрия (включая топологию), алгебра, матлог и дискретка (и то, комбинаторика с теорией графов тоже самостоятельные области). Все они изучают математические объекты и связи между ними, и все объекты разной природы.
Кстати, очень интересно, что же за 98%? Считаем как алкоголь -- по объёму? Так зайди на arxiv.org.
По важности и глубине открытий? Так уже давно алгебраическая геометрия является доминирующей темой, ибо нужна одновременно (правда, в разных областях) в теорфизе и робототехнике. Да и премии последние годы дают геометрам в основном.
>И где было написано, что повторять изученный материал --- плохо?
>А про дважды прочитанный полтора тысячный текст для умственно бессильных
А какие конкретно направления есть на матфаке ? Что-то мне не найти. Сайт у них конечно не очень дружелюбный
>>8121
Чтобы все охуели как я могу из двух ржавых железок и мотка медного провода собрать магнитогидродинамический генератор на парах цезия питаемый дедовской буржуйкой 18 века.
Как можно показать небольшими преобразованиями, очевидно что мне в хуй не уперлись множества и квантмех. Разве что соберусь собрать фузор чтобы показать тянучке какой я умный, радиацию обуздал.
>>8120
Да и математику можно не учить уже. Компютеры же есть, они все посчитают.
Пруф ми вронг.
 266 Кб, 2153x1204
266 Кб, 2153x1204Опоздал, ну да ладно.
Хз где спрашивать. Какой сейчас самый норм учебник по логике на русском который можно купить в бумажном виде? вообще логике, не только математической.
колмогоров-драгалин
бамп
>А про дважды прочитанный полтора тысячный текст для умственно бессильных
>для умственно бессильных
Ну тогда ты понимаешь, что тебе нахуй не нужно читать некоторую часть томов? И что весь этот срач, только от того, что ты толком не можешь объяснить, что тебе от нас нужно?
Поэтому можешь показать своей тянучке этот тред, чтобы она охуела от твоей тупости.
Ты дурачок?
>Я прочитал калькулус томаса второй раз.
>В третий раз буду его читать и попутно решать задачки из него и демидовича.
>После третьего раза я смогу вкатится в ландау-лившица или нужно еще что то для погружения в математику?
 167 Кб, 757x648
167 Кб, 757x648>мне в хуй не уперлись множества
Ты наглухо отбитый? Посмотри содержание главы про множества в этой книге, чего ты к ним так приебался? Как можно этого не знать? Эта глава читается за максимум час-два.
И это мне говорит человек который на вопрос "мне хватит таких знаний чтобы понять такой то учебник" простой вопрос на который есть два ответа "да, хватит" и "нет, не хватит. нужно еще знать Х " взрывается говняной бомбой с криками "*ШТО ЗА ХУЙНЮ ТЫ ЧИТАЕШЬ??????? ЧИТАЙ НАРМАЛЬНОЕ"
А что может значить ответ "твой учебник --- говно"? Только то, что не можешь ты нихуя понять физику.
>этот раздел ты не поймешь, ты говоришь что он тебе не нужен
Нужно быть пинкертоном чтобы понять что мне не нужно читать том про квантмех, после того как я сказал что том про квантмех я читать не буду?
Выяснили уже, что квантмех без теории множеств и топологий я не пойму, я сказал что он мне не нужен. Сказать хватит или не хватит томаса для всего остального так сложно?
Давай напишешь мне в каких условиях существуют гладкие решения уравнений навье-стокса, раз ты физику знаешь.
>без теории множеств
Блядь, ты про главу в Шварце? Без нее ты не поймешь, что такое действительное число.
Почему ты такой необразованный и при этом агрессивный? Ты даже не знаешь, что наивная теория множеств это считай логика, как ты собрался думать о любой физике без логики?
>>8131
>Чтобы все охуели как я могу из двух ржавых железок
Ясно, физика и математика тебе не нужны. Пиздуй в какой-нибудь слесарный раздел.
>>8131
>Да и математику можно не учить уже.
Верно, тебе можно не учить.
Мне тоже интересно.
Ну с другой стороны у этой агрессии имеются основания, все таки мы разрушаем чью-то мечту. Это область еще неизведанной природы великовозрастных превозмогающих личностей, пытающихся заняться математикой. Кто все эти люди, которые толпятся на вводных лекциях в нму? К чему они стремятся? Имеются ли подобные явления в других областях науки и в других странах?
Это не мешает им быть в книжке томаса.
Плюс я векторы/тензоры дополнительно читаю у беклемишева и еще пары авторов, чтобы посмотреть на них со всех возможных сторон.
Эти понятия, очевидно, я не смогу применить на практике. Знать их мне сейчас не нужно. Может потом когда я смогу запускать ракеты в космос.
>>8163
Логика это не математика, так же как физика это не математика. Математика изъясняется языком логики, физика изъясняется языком математики, но это не означает что принцип изъяснений это сама суть изъясняемого.
Если ты считаешь иначе, реши тогда с помощью математики логическую задачку у которой только ОДИН правильный ответ,который ты должен обосновать
Если почесать угубку за ухом, он начнет довольно шипеть. Если угубок довольно зашипит, то молоко поблизости скиснет.
a. если не чесать угубка за ухом, то молоко поблизости не скиснет;
b. если почесать угубка за ухом, молоко поблизости скиснет;
c. молоко вдалеке никогда не скисает от чесания угубков.
>>8160
Вот из за этого я и не хочу теорию множеств даже километровой палкой трогать.
Июо она задается тупейшими вопросами уровня "почему слово лес не звучит как собтвенно лес, скопление большого количества рядом растущих деревьев?"
>Логика это не математика, так же как физика это не математика.
Верно, физика это умение склеивать две ржавых железки, тебе не нужна математика, иди в слесарный раздел.
Ландау-Лившица не читай, там задаются тупейшими вопросами о том как найти экстремумы функционалов, симметриями каким-то и прочей бесполезной абстракщиной, просто заучи законы ньютона и формулы для расчёта электрических цепей, т.е. школьной физики тебе хватит.
Атлищная аргументация моей неправоты. Все так понятно и обоснованно разложил по полочкам.
Немного срочно пишу, поэтому (уж извините ФАГи не читал)
Кто знает годный материал по вычислению интегралов с помощью вычетов?
В гугле не забанен, но из более-менее годного находил лишь скучные лекции какого то советского профессора из которых ничего не понятно.
студент средней тупости, раздолбай, завтра экзамен
 52 Кб, 542x520
52 Кб, 542x520>завтра экзамен
удачи
>Кто знает годный материал по вычислению интегралов с помощью вычетов?
Первые несколько ссылок в гугле ведут на сайт(где есть примеры) и на форум какого-то вуза, где рассматриваются более сложные случаи
>не хочу теорию множеств даже километровой палкой трогать
>Июо она задается тупейшими вопросами
Ты не знаешь какими вопросами она задается.
В Ландау-Лифшица после Томаса не вкатится.
Хех, не помешает
mathhelpplanet вроде норм, все по полочкам. Но это скорее справочник, там самое нужное без примеров и подробностей
А я искал скорее гайд
 325 Кб, 1280x720
325 Кб, 1280x720совсем забыл. Можете кинуть решение с объяснением?
Я тебе совет даю по твоему оригинальному вопросу.
Ты хочешь клеить ржавые железки, Л-Л это курс теоретической физики. Зачем тебе он/его кусок? Просто иди клеить ржавые железки в гараже, формулы по ходу гуглить будешь.
Если ты настаиваешь, что тебе нужен первый том Л-Л, то можешь читать. Вывод уравнений Лагранжа (и, наверное, ряд других результатов) придётся принять на веру не то чтобы он там давал сколь-либо полные выводы anyway, потому что там нужно знать вариационное исчисление, которое опирается на понятие функциональных пространств богомерзские МНОЖЕСТВА пробрались и сюда и близости точек в таких пространствах о боже, почему свитой Ландау не защитил нас от ереси ТОПОЛОГИИ. Не дай бох ещё придётся вникать в основы функционального анализа глубже, там уже палка никакой длинны не поможет. Может даже Шварца придётся полистать.
Получится, что ты вместо заучивание законов Ньютона заучишь уравнения Лагранжа и узнаешь какие бывают дифуры с произвольным лагранжианом для каких-то базовых ситуаций классической теоретической механики. Лично мне не понятно зачем это тебе для склеивания двух ржавых железок.
>Ты не знаешь какими вопросами она задается.
Опять обоснование моей неправоты на высоте.
Гомер и Аристотель плачут кровавыми слезами, и не от того что ебут друг друга в жопу, а от твоей аргументации.
Блесни умом что ли, покажи и распиши как распределятся импульсы между двумя телами, если одно из тел имеет несравненно меньшую массу чем другое в случае их столкновения.
>>8176
Тобишь по твоему нужно каждому обязательно вшивать в мозг при рождении теорию множеств с топологией, а теорию бесконечно малых и объяснение производной как "скорости" изменения значения функции печатать на латыни в книжках о истории темных веков?
К чему я это? Ты уверен на все сто, что предмет изучения топологии с множествами нельзя, ну вот совсем нельзя, от слова никак, выразить через другие понятия? Калькулус томаса и стюарта тогда что такое и для чего придуманы? Тупым инженерам проектирующим дамбы, дома и ядерные реакторы?
Или если объясняют математику доступным языком то это уже не математика?
И множества ваши я трогать не хочу из за вас долбоебов. Ибо все кто хоть как то знают множества ведут и себя и поступают как имбецилы с синдромом дауна. Тот же ящик ебучий посчитать не могли три треда с помощью вольфрама.
И да, ты можешь что то другое кроме курса ландау-лившица предложить?
>Опять обоснование моей неправоты на высоте.
Там над выделенной тобой строчкой есть еще одна, в ней написана причина. Вот еще раз. >не хочу теорию множеств даже километровой палкой трогать
Как ты можешь знать что-то о теории множеств, если ты не можешь осилить элементарнейшие ее определения? Пересечение, объединение, биекция, классы эквивалентности, мощность. Там в той главе материал посильный ученику начальной школы.
 6 Кб, 642x139
6 Кб, 642x139>Тот же ящик ебучий посчитать не могли три треда с помощью вольфрама.
Это связано с тем, что это выдуманная тобой процедура, несуществующая в природе.
>Калькулус томаса и стюарта тогда что такое и для чего придуманы?
А в ведении что-нибудь про это написано?
>предмет изучения топологии с множествами
Давай еще раз про множества. Разберемся с ними, хотя с топологией почти то же самое. Есть какие-то общие определения, которые включаются в вводные главы почти всех учебников для младшекурсников, это просто базовые понятия алгебры, геометрии и анализа. Иногда в введении упоминается, что предполагается, что читатель знаком с ними. Все люди писавшие учебники математики последние лет сто знают эти определения. И Ландау знали их, и Лифшиц знал их.
>все кто хоть как то знают множества ведут и себя и поступают как имбецилы с синдромом дауна
Поэтому это не настоящая причина твоего нежелания пробежать глазами тридцать страниц элементарного текста.
>И да, ты можешь что то другое кроме курса ландау-лившица предложить?
Тебе не нужно знать ни математику, ни физику, чтобы просто применять готовые формулы. Просто задайся целью сконструировать в своем гараже конкретный аппарат. А дальше по-ходу разберешься. Вот чем тебе знание
>как распределятся импульсы между двумя телами, если одно из тел имеет несравненно меньшую массу чем другое в случае их столкновения
поможет примотать скотчем друг к другу две железяки?
 9,9 Мб, 3442x2456
9,9 Мб, 3442x2456Бамп вопросу!
Я не понимаю почему теория множеств у тебя вызывает такой ужас и почему ты её ставишь в один ряд с топологией. Ничего сложного в ней нет и она возникает естественным образом как только ты начинаешь заниматься математикой.
>Или если объясняют математику доступным языком то это уже не математика?
>выразить через другие понятия
Без теории множеств? Нет, нельзя, она неявно используется и в книжках по калькулюсу.
И в книжках по калькулюсу не объясняют математику. В книжках по калькулюсу учать... считать, что неудивительно, ведь с латыни это именно так и переводится — "расчёт". Ты читаешь гайд по расчётам, принимаешь всё сказанное там на веру и применяешь как тебе хочется. Если ты хочешь убедиться, что всё действительно так или получить общее виденье предмета вместо коллекций трюков по расчётам, то тебе нужно доказывать теоремы. И тут уже нужно явно говорить о множествах.
>Ты уверен на все сто, что предмет изучения топологии с множествами нельзя, ну вот совсем нельзя, от слова никак, выразить через другие понятия
Во-первых, топология довольно естественная наука, говорит она о том, что такое "близко", "окрестность точки". Т.к. это центральные понятия анализа — топология сразу же полезна тут. Можно использовать эпсилон-делта формализм как завещали прадеды, но даже тут тебя ожидают страшная теория множеств и квантор существования/всеобщности.
Во-вторых, отвечу в общем: есть два пути. Первый это построить башню определений, в которых твои утверждения будут достаточно простыми. Второй это использовать "доступный язык" и простые определения, но все утверждения будут со всё возрастающей сложностью. Определения это способ прятать сложность и делать рассуждения доступными для мозга человека.
>И да, ты можешь что то другое кроме курса ландау-лившица предложить?
Для каких целей конкретно? Для общего понимания классической физики? Или всё таки чтобы научиться строить шлоебень в гараже?
Немного википедии, немного разговоров из тредов, немного из дхду.
Ну и сообразить что между нулем и единицей бесконечно много чисел труда не составляет. Так же как и сообразить что между нулем и двойкой чисел тоже бесконечно много, но их ровно в два раза больше чем в первом случае.
Но это заслуга не калькулюса а учебников лузина.
>>8181
>A great discovery solves a great problem but there is a grain of discovery in the solution of any problem. Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery.
Ты не ответил на вопрос и ушел в демагогию и в то что всем все очевидно. Если всем все так очевидно, почему до сих пор преподают и выпускают учебники в дедовских стилях, с приращениями, пределами и т.д.
Ведь если все реально так просто, нужно с прогрессивных множеств все начинать преподавать всем и везде.
Ну раз ты знаешь лучше меня какая у меня причина, то не буду переубеждать.
В приматывании скотчем ничем. А для определения ударной вязкости какого то сплава ниобия с танталом очень даже. Плюс, формулы иногда после небольших преобразований, реально небольших, могут сильно облегчить вычислять ту же ударную вязкость.
>>8184
Если она так естественно возникает, почему арнольд от нее плевался? Или это тут врётё в тредах было? Не то чтобы я сильно арнольда знал, но описание на вики и профильных ресурсах прочитать смог.
Где там в том же томасе все на веру заставляют принимать? Там есть доказательства с примерами, без всяких хитровыебаных виляний.
А если на веру все заставляют принимать, то почему растянули все на тыщу страниц?
Ну и как множества помогут доказать что два плюс два, таки да, четыре?
Учти, я не говорю что теория множеств хуита. Может даже я не прав и она таки да для успешных стильных и молодежных математиков, но она слишком сложна для того чтобы доказать что два плюс два равно четыре. Это все равно что пытаться промышленным гидравлическим прессом забить в доме гвоздь для вешалки. Можно конечно, но зачем?
Так то получается что топология прям везде применяется, раз она такая базовая и вообще изобретение покруче чем изобретение умножения. Даже два плюс два без топологии нельзя посчитать. Или можно?
И при чем тут пути?
Для практического применения знаний, я же уже писал.
Немного википедии, немного разговоров из тредов, немного из дхду.
Ну и сообразить что между нулем и единицей бесконечно много чисел труда не составляет. Так же как и сообразить что между нулем и двойкой чисел тоже бесконечно много, но их ровно в два раза больше чем в первом случае.
Но это заслуга не калькулюса а учебников лузина.
>>8181
>A great discovery solves a great problem but there is a grain of discovery in the solution of any problem. Your problem may be modest; but if it challenges your curiosity and brings into play your inventive faculties, and if you solve it by your own means, you may experience the tension and enjoy the triumph of discovery.
Ты не ответил на вопрос и ушел в демагогию и в то что всем все очевидно. Если всем все так очевидно, почему до сих пор преподают и выпускают учебники в дедовских стилях, с приращениями, пределами и т.д.
Ведь если все реально так просто, нужно с прогрессивных множеств все начинать преподавать всем и везде.
Ну раз ты знаешь лучше меня какая у меня причина, то не буду переубеждать.
В приматывании скотчем ничем. А для определения ударной вязкости какого то сплава ниобия с танталом очень даже. Плюс, формулы иногда после небольших преобразований, реально небольших, могут сильно облегчить вычислять ту же ударную вязкость.
>>8184
Если она так естественно возникает, почему арнольд от нее плевался? Или это тут врётё в тредах было? Не то чтобы я сильно арнольда знал, но описание на вики и профильных ресурсах прочитать смог.
Где там в том же томасе все на веру заставляют принимать? Там есть доказательства с примерами, без всяких хитровыебаных виляний.
А если на веру все заставляют принимать, то почему растянули все на тыщу страниц?
Ну и как множества помогут доказать что два плюс два, таки да, четыре?
Учти, я не говорю что теория множеств хуита. Может даже я не прав и она таки да для успешных стильных и молодежных математиков, но она слишком сложна для того чтобы доказать что два плюс два равно четыре. Это все равно что пытаться промышленным гидравлическим прессом забить в доме гвоздь для вешалки. Можно конечно, но зачем?
Так то получается что топология прям везде применяется, раз она такая базовая и вообще изобретение покруче чем изобретение умножения. Даже два плюс два без топологии нельзя посчитать. Или можно?
И при чем тут пути?
Для практического применения знаний, я же уже писал.
>с прогрессивных множеств
Теории множеств уже сто с лишним лет. Более того 1 том Зорича по Матану начинается именно что с наивной теории множеств.
> почему арнольд от нее плевался?
Арнольд плевался от Бурбаков, а это совершенно другое.
>топология прям везде применяется
Почти везде, другое дело, что это порой нелегко заметить.
>Даже два плюс два
Ну два плюс два это больше к алгебре
>Для практического применения знаний
Для практического применения знаний надо было в ПТУ идти, там научат как балки скреплять и прочую залупу. Ну или на инженегрофак.
>сообразить что между нулем и единицей бесконечно много чисел труда не составляет. Так же как и сообразить что между нулем и двойкой чисел тоже бесконечно много, но их ровно в два раза больше чем в первом случае.
Во-первых, нет, действительных чисел там одинаковое число. Во-вторых, речь про главу в Шварце, про тридцать страниц, а не про то, чтобы бы глубоко разбираться в тонкостях теории множеств. Можешь про это пояснить? Почему все имеющие отношения к физике и математике люди знают содержание этой главы, а ты не хочешь? Три десятка страниц элементарных понятий, которые позволят тебе не ходить под себя на таких элементарных вопросах, как количество действительных чисел между нулем и единицей, и нулем и двойкой.
Непейвода
>Ты не ответил на вопрос и ушел в демагогию и в то что всем все очевидно.
Он не в демагогию ушёл, он тебе как раз пояснил ситуацию очень просто. "Страшная" теория множеств даётся в первых главах учебников для первокурсников. И применяется она для всего. Как что-то можно доказать не зная теорию множеств я себе слабо представляю. И как в Томасе выглядят доказательства без теории множеств боюсь себе представить.
>Ну и как множества помогут доказать что два плюс два, таки да, четыре?
Какой-то ебанутый пример. Множества помогут доказать, что для каждого действительного числа d, существует такое e, что выполняются такие-то условия и тем самым определить предел, производную и т.п. Сразу становится понятно, что же такое предел. Понятие функции тоже определяется через теорию множеств и сразу же проясняет суть этого понятия в том числе и в расчётно-прикладных контекстах.
>Если она так естественно возникает, почему арнольд от нее плевался?
Владимир Игоревич Арнольд (12 июня 1937, Одесса — 3 июня 2010, Париж[4]) — советский и российский математик, автор работ в области топологии, теории дифференциальных уравнений, теории особенностей гладких отображений и теоретической механики. Один из крупнейших математиков XX века.
>Или это тут врётё в тредах было?
Не воспринимай слишком близко к сердцу культурные споры, тут много тонкостей в контекстах. Арнольд, конечно, прекрасно знал математику, и не был просто калькулятором интегралов.
> Даже два плюс два без топологии нельзя посчитать
Калькулюс для этого тоже не нужен.
>И при чем тут пути?
Я объяснил зачем нужны определения, которые тебе кажутся сложными.
>Для практического применения знаний, я же уже писал.
Не читай Л-Л, читай гайды по сборке шлоебеней в гараже и по физике (механике) конденсированных сред, термодинамике, химии, электротехнике и всём том, что тебе посоветуют на профильной слесарной доске/форуме.
>Ну и сообразить что между нулем и единицей бесконечно много чисел труда не составляет. Так же как и сообразить что между нулем и двойкой чисел тоже бесконечно много, но их ровно в два раза больше чем в первом случае.
Потрясающе, дальше можно и не разговаривать.
изоморфизм моделей поищи
x=0
 153 Кб, 640x320
153 Кб, 640x320Смотреть первые ссылки в гугле по запросу "влияние пива и сметаны на аппетит пиявок pdf"?
Или есть получше методы?
Сейчас вот ищу нормальный учебник по линейному погромированию (оптимизация, симплекс-метод, вот эта хуйня).
На английском тоже подойдут.
Но не могу читать древние учебники с хуёвыми сканами, да и вообще со СКАНАМИ
Гугли определитель матрицы.
Лучше спроси у знающих людей, которые занимаются этим. Зайди на dxdy, mathoverflow.
Николай Вавилов
В разделе же куча списков платиновых учебников в шапках.
Васильева двухтомник.
 64 Кб, 850x476
64 Кб, 850x476Несколько вопросов касающихся использования терминологии.
1. Как только в математическом тексте встречается слово "норма" или "скалярное произведение", то это значит что речь идёт о каком-то векторном(линейном) поле?
(то есть есть какое-то поле скаляров и множество векторов)
И нет другого использования этих слов?
(кроме неверного)
2. Какие свойства(упорядоченность, непрерывность, ...), если можно так сказать, используются для определения функции SIN? То есть её можно определить на произвольном множестве? И что в ней такого особенного?
Заранее спасибо.
Надеюсь больше стану понимать благодаря вашим ответам.
1) Да.
2) Разложение в ряд тейлора. Это наиболее общее определения, позволяющее взять синус о матрицы, например. Это функция тесно свзянна с комплексными числами, от сюда идут корни её геометрического и матанного смысла.
Платиновый ответ.
Алсо, когда мне не нравится скан, я его сам допиливаю в scantailor'е, нихуя сложного, зато глазам приятно.
Благодарю.
Небольшое уточнение по 1) пункту:
Но при этом не обязательно это векторное пространство будет на R(действительными числами)?
По 2) пункту не могу ничего уточнить, так как мало понимаю. Спасибо за направление.
>Но при этом не обязательно это векторное пространство будет на R(действительными числами)?
Да.
Это при том, что "норма" и "скалярное произведение" вещественно-значные функции.
 11 Кб, 605x182
11 Кб, 605x182Вроде бы очень простой вопрос, но я могу понять, какой ответ правильный
А что тут понимать то? Просто если а из R, то a может быть = 1, 1 - действительное число
Получается ответ AБВ?
Сорян, просто завтра на экзамене вообще ни разу нельзя ошибиться, поэтому чет параною
Ответ АВ.
Б не подходит, так как 2*1=2, ок? Что такое подпространство, вспомни, какое условия должны выполняться?
Но ты не будешь отрицать что математика и там и там применяется?
>>8193
Зачем мне доказывать то что и так очевидно? Зачем доказывать что интеграл это площадь под кривой бесконечно большого количества бесконечно малых трапеций?
И вы так и не обосновали существование калькулусов без теории множеств.
Не могу дорешать уже больше месяца эту очень простую задачу, из за того, что не могу понять, как найти базис пересечения подпространств
В интернете есть несколько примеров решений, но мой препод отвергает их
До уравнения
a1x1 + a2x2 + a3x3- b1y1 - b1y2 = 0
[Из которого по совету препода я получил
a1x1 + a2x2 + a3x3- b1y1 = b1y2
И расширенную матрицу (x1 x2 x3 b1 | b2)]
Все правильно, дальше не понимаю что делать, прочитал уж е все что можно, с остальными темами в алгебре и матане все отлично
На скринах мое последнее решение, но оно врядли правильное
Что такое d1, d2, d3?
Вектор, который лежит в пересечении ты обозначил как a1x1+a2x2+a3x3, он же равен b1y1+b2y2.
Вот ты получил систему уравнений
>a1x1 + a2x2 + a3x3- b1y1 - b1y2 = 0
Как её решать? Да всё тем же ступенчатым методом, собственно, так ты и начал. После этого тебе нужно просто посчитать этот самый a1x1+a2x2+a3x3 и всё.
>Зачем мне доказывать то что и так очевидно
Во-первых, "очевидно" не значит верно. Во-вторых, не всё очевидно и вообще это субъективное понятие. В-третьих, уточнения понятий и доказательства теорем углубляет понимание.
>И вы так и не обосновали существование калькулусов без теории множеств.
Калькулюсы — гайды по тому как считать определённые вещи. И то там ТМ используется явно и неявно. Потому что это базовая вещь.
 60 Кб, 801x181
60 Кб, 801x181Свой провал ты комментировать не собираешься?
>Ну и сообразить что между нулем и единицей бесконечно много чисел труда не составляет. Так же как и сообразить что между нулем и двойкой чисел тоже бесконечно много, но их ровно в два раза больше чем в первом случае.
Кстати, вот снимок третьей страницы одиннадцатого издания.
Страница номер три. Назови номер своего уникального издания калькулуса, в котором этого нет.
Альтернативные помогают глубже взглянуть на десятичную
Ну хорошо, вот докажи мне что объем конуса одни треть высоты на площадь основания.
>>8265
Не собираюсь. Что там еще комментировать если неправильно?
Вот эта книжка.
http://www.aazea.com/book/calculus-early-transcendentals-8th-edition/
Написана просто и понятно с обсасыванием.
Хуйни уровня "сечение множества верхнего класса содержит число меньшее чем числа сечения множества нижнего класс" тут просто нету. Как и нету того что читаешь, вроде все понятно, а потом постепенно непонятнее и непонятнее, пока совсем станет нихуя не понятно, даже если пять раз перечитать две страницы.
Альтернативные это какие? Двоичные восьмеричные?
Так у человека то пальцев на которых удобно считать десять а если вспомнить про суставы, то можно даже до шестидесяти досчитать двумя руками и не сбится. Дальше сам.
Не ебу, что такое сечение множеств, что такое верхний, нижний класс и подобная ебола. В Шварце этого нет. Что ты на это скажешь?
По твоей ссылке нужно регистрироваться для скачивания и чтения, я этого делать не буду.
На скрине из прочитанного тобой дважды учебника выписаны определения теории множеств, как ты это можешь прокомментировать?
>Ну хорошо, вот докажи мне что объем конуса одни треть высоты на площадь основания.
Это называется посчитать объём конуса и с чего я тебе буду что-то доказывать или считать? Тебе уже выдали советов, иди читай книги, не испытывай терпение.
 78 Кб, 857x875
78 Кб, 857x875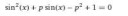 1 Кб, 231x31
1 Кб, 231x31У меня там вроде бы как квадратное тригонометрическое уравнение с параметром, но я, решая это уравнение, каждый раз получаю новый ответ. В общем, я уже запутался и не знаю, что со мной не так.
Я не прошу решить это задание, я прошу натолкнуть меня на верный ход мыслей.
Условие такое: при каких p уравнение имеет корни?
При попытке прочитать происходит переход на вредоносный сайт, но я нашел шестое издание.
http://www.vnua.edu.vn/khoa/fita/wp-content/uploads/2014/10/stewart.pdf.Chuvien.gui_.pdf
Вот что было в аппендиксе (скрин 1). Это все вынесено в конец, чтобы слабые студенты (ты) могли себе помочь, что указано в самом начале книги (скрин 2). Можешь еще поискать в этом документе cartesian product, one-to-one correspondence может там еще что-нибудь есть из теории множеств. Ну ладно, собственно я трачу на все это силы в надежде, что ты выдашь какой-нибудь перл уровня >>8194
Но вряд ли это уже произойдет, так что вот еще кое-что. Детей десятилетия травят в школе математикой, которая им не нужна. Такие курсы калькулуса, которые ты показываешь --- это дальнейшее продолжение этого процесса. Детям на пальцах объясняют то, к чему они в жизни более никогда не притронутся. Такое вот объяснение. Там в аппендиксах имеется глава с доказательствами на одиннадцать страниц. То есть меньше процента книги занимают доказательства, остальное время детишек приучают считать. Причем эти доказательства уровня упражнений в обычных учебниках математического анализа.
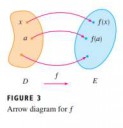 18 Кб, 293x303
18 Кб, 293x303Второй скрин не про этот аппендикс, но ссылка на него есть на 12 странице, там же противные для тебя теоретико-множественные картиночки есть, они там повсюду. Зачем я трачу на это время?
Картинка дебильная абсолютно. Современная математика делится примерно на:
1) Арифметику и миксование арифметических структур с другими (гипотезы Вейля, программа Ленглендса, теоремы Делиня, ...)
2) Геометрию и геометризацию (пучки, гомологии, кобордизмы, геометрическая логика, ...)
3) Схематизацию и отчищение от догм теоретико-множественного мышления (группоиды, категории, схемы, топосы. мотивы, ...)
4) Деформацию и квантование (нелинейность, некоммутативность, квантовость, q-объекты, ...)
5) Рефлексию теорий над самими собой (классификационные теории, неподвижные точки, монструозные модели, элементарные/неэлементарные классы, ...)
1. Как геометрически (в координатах y,p) выглядят решения уравнения y^2 +py-p^2 + 1= 0?
2. а если y = sin(x)? (т.е. -1 <= y <= 1)?
А есть текст поподробнее на эту тему?
Хотя бы второй уровень классификации подробнее или чтобы гуглилось, а то в 4) как-то совсем абстрактно получилось: "деформация", "нелинейность"?
4 вполне конкретные вещи: noncommutative topology/geometry/probability/functional analysis/homotopy/differential geometry, quantum groups, тысячи их - но дух у них примерно один и тот же, взять коммутативную теорию и попытаться сделать её некоммутативный аналог, за некоторые из этих наук люди филдса пополучали.
Про второй уровень не понял вообще - это геометрия не гуглится что ли?
Да твой пост не особо лучше.
Гипотезы вейля, этальные когомологии и геометрический ленглендс это не "миксование арифметических структур", что бы ты под этим не понимал, скорее наука про автоморфные пучки и зеркальную симметрию
>пучки, гомологии, кобордизмы
Чего здесь общего? "Топосы, когомологии, к-теория", пиздец, у тебя каша в голове, что ли
>отчищение от догм теоретико-множественного мышления
Отчищение, ага. Ты в курсе, что в теории категорий используется теория множеств, вообще-то? На, почитай
https://ncatlab.org/nlab/show/ETCS
>схемы, топосы. мотивы
Что ты этим хочешь сказать, снова? Мотивы имеют отношение разве что к алгебраической к-теории, которую ты даже не упомянул в своей классификации. По сути наука о линеаризации категории топологических пространств.
>группоиды
Это h-spaces имеются в виду?
В общем, глупость, как по мне. Свою версию классификации я уже давал. Математика это:
а) циклические гомологии, "некоммутативная геометрия", аддитивная к-теория
б) этальные когомологии, гипотезы Вейля, геометрический Ленглендс
в) спектральная геометрия Лури и эллиптические когомологии
г) когомологии Галуа и мотивы воеводского
д) кристаллические когомологии и p-адическая теория Ходжа
>>8297
Ты теперь у всех спрашивать будешь?
Половина слов - тотальное непонимание всего на свете - уровня "что общего у топосов и когомологий", другая половина - какие-то передёргивания уровня /б/ вида "статья на ncatlab о ETCS доказывает, что теория множеств нужна для категорий". Даже шквариться о дальнейший разговор с тобой не хочу.
Ну я-то могу тебе объяснить, что такое когомологии, если спросишь более вежливо. Просто перебирание терминов в духе "слон, стол, соль" выглядит не особенно умно.
>передёргивания уровня /б/ вида
Кто что передергивал? Ты здесь пишешь глубокосмысленные фразы про "избавление от догматов теории множеств", между тем, как только дурачок-первокурсник может сказать, что теория множеств там не нужна. Не нравится статья, читай книгу Sets for mathematicians от создателей теории категорий, например.
Намиксовал слов на википедии типа умный, и баттхертит. Не шкварься об разговоры, пожалуйста.
Обращайся еще, эксперт с мировым именем, связывающий разные области по наличию в их описании слова "квантовый", всегда рад ответить. Только если ты не зашкваришь его излишне глупым вопросом, тогда не ответит.
Достаточно общие.
Ты неправ. При a=b=1 уже неверно.
Список от опа из шапки глянь.
 210 Кб, 1024x770
210 Кб, 1024x770> Не собираюсь. Что там еще комментировать если неправильно?
Не прав ты или неправы математики?
>>8321
Нет, это не так интересно.
Ктонибудь читал хеллерское поделие? Не совсем догоняю, что от меня требуется в упражнении 1.2
Выведите формулу для эквиваленции:
a <-> b = 1 + a + b
Напильник для ААА проектов, не нужен
В чём проблема? Главное центром приложить к той точке от которой будешь угол откладывать
 45 Кб, 500x407
45 Кб, 500x407Есть ли книги по вышей математики которые логично объяснены и понятно иллюстрированные. Вот пример книги которую я ищу https://rutracker.org/forum/viewtopic.php?t=5228801 только по вышей и дискретной математики, где все с первого раза стает понятно.
Все остальные книги которые я скачивал их было около 50-70 штук были написаны дегенератами которые ничего сами не понимают, веди если ты не можешь ПОНЯТНО объяснить материл, так чтобы это понял 5 ребенок значит ты сам ни черта не знаешь.
>Все остальные книги которые я скачивал их было около 50-70 штук были написаны дегенератами которые ничего сами не понимают, веди если ты не можешь ПОНЯТНО объяснить материл, так чтобы это понял 5 ребенок значит ты сам ни черта не знаешь.
Такое может прокатить с грёбанной физикой, но не с математикой. Потому что, у большинства математических понятий не физического смысла, а значит нет и простого объяснения.
Пошел на хуй, ленивый пидор.
>Потому что, у большинства математических понятий не физического смысла
Непизди, все можно свести к реальному миру и объяснить на простых элементарных примерах, и математика не исключения. Так что иди ты нахуй.
>дегенератами которые ничего сами не понимают
Ты типичный воинствующий невежда (человек, который винит в своём незнании плохих учетелей, а не свою лень), научно-популярная экспозиция материала не даёт понимания, как бы этого не хотел, это всегда упрощение материала, которые привносит неточности. Фейнман, которого ты тут цитируешь, тоже самое говорил.
Так что либо ты читаешь научно-популярные тексты и получаешь просто какое-то представление о предмете. Либо ты читаешь книги и разбираешься в сути. Научно-популярных учебников не существует, тем более по "высшей математике".
>если ты не можешь ПОНЯТНО объяснить материл, так чтобы это понял 5 ребенок значит ты сам ни черта не знаешь
Доказательства этого утверждения имеются?
>человек, который винит в своём незнании плохих учетелей, а не свою лень
Я знаю очем говорю, я пытался вникнуть но иза этих некомпетентных людей которые только и могут что кидаться умными словами а пользы от них нулевая, нихрена непонятно.
>Доказательства этого утверждения имеются?
Я предоставил ссылку на книгу, это единственная найденная мною книга где ПОНЯТНЫМ языком описывается элементарная математика, так чтобы было интересно и понятно.
Ну о каких 50-70 книгах идет речь? Ты открывал Зорича или Шварца? На какой странице стало непонятно?
Это доказывает, что если человек не может объяснить материал так, чтобы это понял пятилетний ребенок, то он сам ничего не знает? Да или нет?
Вот я открыл Зорича, Математический анализ. С 22 страницы уже пошла непонятная ересь. Книга дно.
Нет, просто ты тупой и ничего не понимаешь. Тебе не стоит заниматься математикой, иди вон, как местный клован делай из жравых железок приборы, чтобы впечатлить шкур.
Мне даже тебе доказывать ненужно ведь все и так очевидно, открой любой учебник и посмотри что там написано, легче китайский выучить чем это понять.
Мудила, ты не можешь это сделатб потому что, эти вещи не связаны с физикой и у них нет физического смысла, ну по крайней мере у второго точно нет.
 211 Кб, 1366x768
211 Кб, 1366x768Какая строчка непонятна? Если не это издание, то сделай скрин, разберемся.
Очевидно, что ты тупой. Зачем ты вообще паришся о матеше и лезешь в эту область?
Дело в том, что доказательств у этого утверждения нет.
Кстати, у тебя очень хорошие ПРОЕКЦИИ! Давно я таких не видел, честно. Ты чувствуешь себя тупым дегенератом, но не осознаешь это, и переносишь эти чувства на авторов учебников, типа это не я кретин, а они такие ебланы мне объяснить не могут.
>Я знаю очем говорю
Нет, не знаешь. Я понимаю, что ты этого не понимаешь, иначе ты бы не был воинствующим невеждой.
И так, как я уже сказал — не существует учебников с цветными картинками про "высшую математику". Огромная куча не самых умных людей разбирается с математикой по книжкам без картинок. Если тебе это не под силу, то очевидно, что дело в тебе.
Читай это:
Математическая грамотность:
https://www.amazon.com/Mathematical-Proofs-Transition-Advanced-Mathematics/dp/0321797094/
https://www.amazon.com/Naive-Set-Theory-Paul-Halmos/dp/1781394660/
Velleman "How to prove it"
Сам калькулюс:
https://www.coursera.org/learn/single-variable-calculus
Зельдович Я.Б., Яглом И.М. "Высшая математика для начинающих физиков и техников"
Если ты проявишь упорство и после долгих раздумий и рефлексии над материалом тебе будет непонятен Зельдович, то просто смирись и забей. Это учебник для ПТУшников.
до дискретке ничего не посоветую, разве что книжку по алогритмам Кормэна "Алгоритмы: построение и анализ"
 290 Кб, 1900x943
290 Кб, 1900x943Вот обвел красным. Сразу пошли сложные примеры, не объяснено почему это так и зачем, нету графических примеров с картинками, просто в книге влепили что нибудь и разбирайся почему где и зачем.
Проиграл в голос.
>Математическая грамотность:
>https://www.amazon.com/Mathematical-Proofs-Transition-Advanced-Mathematics/dp/0321797094/
>https://www.amazon.com/Naive-Set-Theory-Paul-Halmos/dp/1781394660/
>Velleman "How to prove it"
Вот тут расскажут про этот язык.
>Ты чувствуешь себя тупым дегенератом
Раньше чувствовал. Но после того как посмотрел видео с этого сайта http://interneturok.ru/algebra/7-klass и как понятно объясняют. Я понял что не я тупой дегенерат а тупые те кто не может понятно объяснить.
В первом прямоугольнике выделены утверждения, первое из которых доказывается далее по тексту. Тебе понятно, что означает первое утверждение? Дополнение объединения равно пересечению дополнений.
Выдели теперь импликацию во втором прямоугольнике, которая тебе не понятна.
Нет, как раз, это ты тупой дегенерат. Нормальные люди читают без дополнительных разъяснений и жвачки для мозгов. И если тебе надо такое разъеснение, как на сайте, то ты либо быдло, либо школьник.
Если тебе не хватает базовых знаний для того, чтобы что-то понять, то это не значит, что авторы учебников тупы.
Я словами так не могу воспринять информацию, мозг отказывается так воспринимать, только графически с картинками могу понять. Ведь непонятно с какимы сущностными работают множества с примеров 2 - 3- 4, если с числами, то почему в книге ради примера не написано и графически не отображено.
Нет мне 25. Но в школе учился на 2. Сейчас захотел немного понять. Так ка занимаюсь программирование хотелось бы вкатится в игровую разработку а не делания сайтов.
Там в картинках простые примеры, я это понимаю. Но там где сложные выражения, без картинок и числовых массивов.
 89 Кб, 900x800
89 Кб, 900x800Эта картинка не теряет своей актуальности.
В Зориче кратко написано про множества, и предполагается, что ты их знаешь.
 65 Кб, 487x854
65 Кб, 487x854Ладно, давай так, на каком конкретно шаге у тебя возникает непонимание? Доказательство же совершенно элементарное.
 77 Кб, 1032x781
77 Кб, 1032x781В книге есть математические элементы которые мне незнакомы.
Вот еще пример деграданского образования, проходил на сайте https://stepik.org/course/Дискретные-структуры-83/syllabus но на задании застопорился и было попыток 20 сразу пошли сложные задания.
Здесь более наглядный пример чем в книге. Красным обвел то что я считаю правильным, но на сайте не принимает такой ответ.
Кстати, этот человек с оп-пика начал публиковать свою книгу. Он кстати во многом прав. Называя свою область деятельности взрослой, он как бы противопоставляет себя гротендиковскому детскому видению. В содержании книги указаны основные главы дифференциального и интегрального исчисления, дифференциальные уравнения, можно будет отсылать к этой книги две-железяки-дибилов и картинко-даунов.
Нахождения кратчайшего пути, чтобы боты небыли тупыми и адаптировались к условиям боя, а я так понял что нужно знать теорию графов, но чтобы знать теорию графов нужно знать множества и сопутствующие материалы.
Просто забей на все это, это не твое. Есть же какие-то видео-уроки по математики в видео-играх. Там конкретные примеры, все наглядно. У юнити и унриал точно такие есть. Тебе лучше в /gd сходить. Зачем тебе вся эта муть? Людям чтящим строгость в рассуждениях сложно понять ответ "В книге есть математические элементы которые мне незнакомы" на вопрос "на каком конкретно шаге у тебя возникает непонимание?".
Нужно просто поискать на хабре темы про это, гуглить незнакомые слова. Математика тебе почти не нужна, особенно доказательства.
>хабр
За такие советы пора вводить уголовную ответственность. Нормального человека туда вообще пускать не стоит.
Для людей, не способных самостоятельно доказать законы де Моргана, статьи на хабре могут оказаться полезны.
>Нормального человека туда вообще пускать не стоит.
>Нормального человека
Поэтому тебя туда и посылают.
Я так правильно понял? что такие алгоритмы не строятся на математических понятиях а используется программная логика.
Какое еще подмножество? Ебать. Давай объясню. Смотри. Есть множества. Есть их дополнения. Пересечение этих дополнений -- то, что нам нужно. Ты сейчас слишком занят? Можешь пройти тестик http://ru.iq-test.cc/ там всего 30 вопросов.
 35 Кб, 750x548
35 Кб, 750x548Что в ней можно изменить? Изначально предполагалось, что вы будете принимать в составлении разных списков участие, в частности в списке мемов. Но движуха быстро утихла. Особенно спискосрач. Стоит ли вообще шевелить тему списков? По теме книг, скорее всего нет. Хотя, если кто-то хочет, чтобы я добавил книги в текущий список, я это сделаю.
Дальше, вместо списка статей оставлю ссылку на scihub.
Список с видеолекциями тоже стоит убрать, поскольку никто не предлагает лекций, да и сам список никто не смотрит, если верить статистике на пастебине. Хотя, если кто-то накидает список видеолекций, то он останется.
Далее, в шапку стоит добавить пошаговые калькуляторы.
С мемасами дело обстоит так, я могу заняться созданием pdf-файла, но не смогу самолично описать все мемы. Нужна помощь в материале по ним. Даже если кто-то из вас напишет небольшую статью с каким-то мемом, то это будет хорошая наработка для дальнейшего pdf-файла.
Также жду предложений по шапке, может чего-то не хватает?
Под конец, думаю, стоит сделать единый список сохранённых тредов /math, где будут лежать все заархивированные треды раздела с датами их создания/завершения.
Эту проблему можно решить, созданием faq с часто задаваемыми ньюфажными вопросами.
>Можно предложить мем для оп-пика?
Да. Хорошо сделал.
>Что в ней можно изменить?
Добавить минималистичный список по наивной теории множеств, логике и доказательствам (математической граматности, если угодно) (типа такого >>8374).
Почему минималистичный (буквально 3-5 книг)? Чтобы нубы не обсыкались от огромных списков и не впадали в ментальный ступор.
По лекциям, можно добавить такое: https://www.youtube.com/watch?v=ihoATq9jSlQ&list=PLgqZ7cC8KvvZcMjXYLP53SaXCG35hF_E8
Алсо, в какой-нибудь список, где есть про теорию категорий можно всунуть https://arxiv.org/abs/1612.09375 . Я не читал, но Баез вроде рекомендует.
>Какое еще подмножество?
Подмножество которое содержится в пересечении множеств.
Прошел тест. IQ 97.
>Качать книги тут:
Кстати, где-то была ссылка с торрентом из книг. Так же кто-то кидал сайт с множеством книг. Найду, добавлю.
Смотри, у нас есть какое-то множество, в котором мы рассматриваем подмножества. пусть это будет R, тогда дополнение A это R/A, т.е. все числа, не содрежащиеся в A, но содержащиеся в R. Ясно?
Т.е. пересечение дополнений множеств -- это подмножество, которое содержится в пересечении множеств?
списки оставь, с пдфкой погоди, сейчас паренек допилит форум, обещал прилепить вики, там и будем работать
что за форум?
да
Половина теста сложна.
Головные боли.
Нужно занять чем-то детей, чтобы они меньше всякой хуйни вытворяли. Вот чем может себя занять человек с iq 97?
Или чтобы перегрузить мозги и отключить критическое мышления чтобы сделать народ покорным перед властью.
iq не показатель человек существо ситуативное, есть области в которых человек лучше всего подходит и наоборот, главное найти то к чему есть талант.
Ладно, меня заебали эти игры в пятнашки, я думал, что ты сообразишь в конце, что пересечение дополнений множеств и дополнение их объединений -- это одно и то же, а это и есть доказываемое у Зорича утверждение. Но ты чересчур туп. ари ви дер чи ))))
А что такое "неузкоспециализированное знание"? Химия 7го класса узкоспециализирована? А физика 6го?
Для 99% людей нужно только, 5 класса математики, 4 класса русского языка, 5 класса географии, ну и по мелочи музыкалка физра и т.д, все больше среднему человеку и ненужно.
>Химия 7го класса узкоспециализирована? А физика 6го?
Да это тоже узкоспециализировано и в реальной жизни обычными людьми не используется.
Я тоже так думаю, тогда непонятно, почему притензии именно к математике 9го-11го класса, а не ко всему комплексу знаний выше 5го.
Охуеваю с этого пацана, даже для 7-ми классника он чересчур туповат
 44 Кб, 600x320
44 Кб, 600x320Покажешь что знаешь стереометрию, или интегралы, и как важны доказательства.
>>8294
И опять возвращаемся к вопросу о доказательствах и смысла существования таких учебников.
Если уйти в доказательства то уйдешь в бесконечный цикл в котором нужно все доказывать и доказывать. Одно доказательство стоит на другом, другое на третьем, и так до бесконечности. Это показано у бурбаков.
Учат считать ты так говоришь будто это что то плохое.
И опять же, если множества так просты и элементарны и фундаментальны, почему их не разжевывают в учебниках типа этого?
И вопрос такой для вас обоих, почему в учебниках по математике все прячут за сложной и непонятной аксиоматикой без пояснения этих аксиом? Взять хотя бы того же фихтенгольца. У него сразу же на 12 страничке идет про сечения множеств на классы, хотя до этого определялись операции сложения/умножения/деление/отнимания.
И это не только проблема учебников этого еврейчика. У всех что я качал такая хуйня. Складывается такое чувство что сами авторы слабо шарят в теме и прячутся за сложными терминами чтобы звучало по умному и вызывало уважение.
>>8320
Неправ я, представляешь. Я думал что так, а оно не так. Охуеть вообще, да?!
>не существует учебников с цветными картинками про "высшую математику"
Are you fucking kiddin me?
Так там вроде анон хотел вики на своем хостинге поднимать. Может дождаться его, да заливать туда? Лично я на пастебинех.ком вообще никогда ничего не читаю, например. Юзайте https://notehub.org/new , пожалуйста. Алсо, было бы лучше иметь не просто списки, а пошаговую инструкцию по выбору книжки. Ну или хотя бы какое-то подобие туториала.
Вообще, вики надо, конечно.
Пиздарики, тред для НАЧИНАЮЩИХ захватили олдпердуны которые требуют сделать из треда пристанище для гауссов, лобачевских и римманов.
Надо про треды и модерацию, кстати, в факе пояснить, а то тут недавно два дня объяснял одному нытику, что ему нехуй делать в треде про топологию.
Какие еще платиновые вопросы есть?
- пошаговый калькулятор
- книги по школьной математике
- мне эн лет, поздно ли вкатываться
- не могу в логику\матнотацию, посоветуйте
- а как вы понимаете это а вам правда нравится а удовольствие получаете
Что еще?
Тоже верно. И так-то вообще обсуждать шапку надо не в этом треде, а в отдельном. А тут для вопросов типа. бля не репортуйте мой пост, жалко ж, если потрут
Вот про это тоже в фак надо написать?
Сомневаюсь.
Подразумевалось что ты настолько умный чтобы понять школьны курс, но настолько туп чтобы не понять учебник по вышмату.
Может нарезкой про гомотопический хаос на это отвечать? Ну или пояснять кратенько за философию математики, мол мы тут идеальные миры исследуем, цыц.
>Если уйти в доказательства то уйдешь в бесконечный цикл в котором нужно все доказывать и доказывать. Одно доказательство стоит на другом, другое на третьем, и так до бесконечности
нет
>Это показано у бурбаков.
нет
>И опять же, если множества так просты и элементарны и фундаментальны, почему их не разжевывают в учебниках типа этого?
Потому что существуют люди типа тебя с iq 97, не способные понять простейших вещей по физиологическим причинам.
>сложной и непонятной
Мне было легко и понятно.
>без пояснения
Мне пояснений было достаточно.
>сложными терминами
У меня термины не вызывали сложностей.
>это не только проблема учебников
это исключительно проблема тупых неосиляторов
>Неправ я
Во многом, ты неизлечимо туп.
Да я мимо проходил. Сейчас учу последовательно, где-то в 7 классе уже почти. Хоть и блеск озарениями бывает, но все-же скучновато. Хотелось бы, вообще, что-то вроде как дети изучают с помощью игры обучаются.
Заходим на вики и зрим что
>Логика (др.-греч. λογική — «Философский термин», «способность к рассуждению» от др.-греч. λόγος — «рассуждение», «мысль», «разум») — раздел философии, нормативная[1] наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка...... Кроме философии, логика также является подразделом математики, а булева алгебра одной из основ информатики.
Заходим в математическую логику и, о ужас
>Математическая логика (теоретическая логика, символическая логика[1]) — раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики[2]. В более широком смысле рассматривается как математизированная ветвь формальной логики[3] — «логика по предмету, математика по методу»[4], «логика, развиваемая с помощью математических методов»[5].
Так что с помощью математической логики из двух посылок "Сокрта - человек" и "Все люди смертны" нельзя вывести следствие "Следовательно Сократ смертен".
Переходим на личности, мм, /Ь/ратишка?
Поясни тогда, почему мне очевидно когда тянучку нужно идти ебать тепленькую, а ты поясняешь на сосачах дурачкам типа меня что то про множества и отрицание замкнутости петли доказательств, которые основываются на субъективном чувственном опыте понятия числа?
Абстрагируйся от этого. Математическая логика может это вывести, ведь она оперирует отношениями.
Вообще-то я сам начинающий и Шварца еще не дочитал. Просто есть люди, которые и не притронутся к математике, а в тред придут срать о том, чего знать не знают.
Конечно, нельзя. Математическая логика это дурацкое название, люди путаются. Более удачное – "логика математики". Типа "какая в ваших рассуждениях логика?". Метадисциплина такая, обсуждает методы, что в математике допустимо и корректно, а что нет.
Да путаюсь постоянно. Да еще и только сегодня вспомнил и запомнил, какие углы есть прямые, острые и тупые. Я учился в 7 классе как-то не стараясь вникать в суть.
Ты умственно отсталый. Ты не способен понимать математику, тебе это не нужно, и ты пришел сюда срать.
Ладно, нужно дать себе слово, что я больше не буду здесь появляться со следующего треда, эта доска отнимает слишком много сил.
Это из-за меня?
Блять, самое несправедливое, что после всего этого ты будешь считать, что ты прав. Типа ты настолько туп, что обосрался на простейшем теоретико множественном утверждении, что учебники твои написаны для даунят, которые математикой после последнего сданного экзамена заниматься не будут, что физические законы останутся для тебя не познаваемыми, после прочтения этого говна, но прав ты, потому что дурака называть дураком грубо.
This
Пиздец там вопросов
Мне очень важно твое мнение. Держи меня в курсе.
>>8484
>учебники твои написаны для даунят, которые математикой после последнего сданного экзамена заниматься не будут,
Сильное утверждение. Доказывать ты его конечно же не будешь, ведь это ОЧЕВИДНО КАК МОЖНО ПОКАЗАТЬ ПОСЛЕ НЕБОЛЬШИХ ПРЕОБРАЗОВАНИЙ ЧТО И ТРЕБОВАЛОСЬ ДОКАЗАТЬ!?
И да, я прав. Понятные и просто написанные учебники нужны и важны. Учебники в духе "очевидных небольших преобразований", которых сейчас ебаное большинство, можно использовать только с тем кто уже знает курс учебника.
Ну и ты так и не показал мне почему я не прав, хотя я и согласиля что я не прав в непрерывности чисел между нулем и двойкой
>И да, я прав. Понятные и просто написанные учебники нужны и важны. Учебники в духе "очевидных небольших преобразований", которых сейчас ебаное большинство, можно использовать только с тем кто уже знает курс учебника.
Дело в том, что нормальным людям эти учебники понятны и доступны. Просто ты особый случай, пытаешься изучать то, к чему твой мозг не приспособлен.
А потом из-за ущемлёного чувства достоинства проецируешь свои чувства по отношению к себе на авторов учебников. ЭТО НЕ Я ДАУН, ЭТО АВТОРЫ ТУПЫЕ НИЧЕГО МНЕ ОБЪЯСНИТЬ НЕ МОГУТ, ВЕДЬ НУЖНО ПОНЯТНО, ЧТОБЫ КАРТИНКИ БЫЛИ, А ТО ДЕГЕНЕРАТЫ НЕ ПОНИМАЮТ, КАК ДЕЛАТЬ, ДОКАЗАТЕЛЬСТВА ТАМ КАКИЕ-ТО)))
Но в глубине души, ты осознаешь, что ты тупой даун и не можешь понять, то что на самом деле ОЧЕВИДНО.
1.Кибернетические системы. Входные и выходные воздействия.
2. Основные определения алгебры логики. Двоичный набор. Функция алгебры логики. Фиктивные аргументы и метод их выявления.
3.Структура системы. Элементы систем. Оператор системы. Векторы входных и выходных сигналов. Возмущающие воздействия. Отрицательная обратная связь. Задачи исследования систем
4. Элементарные функции алгебры логики.
5.Элементы теории множеств. Диаграммы Эйлера-Венна. События. Разность событий. Объединение и пересечение событий.
6. Таблица функции двух переменных.
7.Элементы функционального анализа. Расстояние. Метрические пространства. Евклидова метрика.
8. Аналитическая запись логических функций. Характеристическая функция единицы.
9.Евклидовы пространства . Образ шара.
10. Дизъюнктивное представление логической функции.
11.Пространства Гильберта
12.Условные понятия степени аргумента логической функции. Использование дизъюнкции, конъюнкции для описания функций алгебры логики.
13.Скалярное произведение векторов в Евклидовом пространстве . Расстояние между элементами данного пространства.
14. Таблица соответствия для выходных слов и внутренних состояний конечных автоматов (последовательных схем). Глубина памяти. Стохастические автоматы.
15.Иллюстрация понятия расстояния в пространствах .
16. Законы алгебры логики. Формулы Де-Моргана.
17.Ортонормированный базис линейного пространства. Базис пространства, ортогональность векторов.
18. Свойства конъюнкции и дизъюнкции. Сочетательный, переместительный и распределительный законы.
19.Расстояние между векторами в пространстве Гильберта в . Норма вектора. Скалярные произведения векторов в . Ортогональный базис.
20.Условные понятия степени аргумента логической функции. Использование дизъюнкции, конъюнкции для описания функций алгебры логики.
21.Обобщенный спектральный анализ в пространстве Гильберта. Ряд Фурье по ортогональной системе.
22. Геометрическая интерпретация логической функции двух аргументов с примерами раскраски вершин единичного куба.
23. Построение ортонормированного базиса методом Грамма-Шмидта.
24. Задание функции алгебры логики. Таблица истинности и покрытие нулевых и единичных вершин единичного куба дизъюнкциями и конъюнкциями.
25.Основные понятия математической логики. Высказывания, предикаты, алгоритмы, конечные автоматы.
26. Таблица функции двух переменных.
27.Конечные автоматы. Входной и выходной алфавит. Таблица соответствия для выходных слов. Комбинационная схема.
28. Полные системы функций в классе R. и Mn. Полная система в базисе И-ИЛИ-НЕ.
29. Таблица соответствия для выходных слов и внутренних состояний конечных автоматов (последовательных схем). Глубина памяти. Стохастические автоматы.
30.Минимизация логических функций методом покрытия нулевых вершин и рёбер куба дизъюнкциями.
1.Кибернетические системы. Входные и выходные воздействия.
2. Основные определения алгебры логики. Двоичный набор. Функция алгебры логики. Фиктивные аргументы и метод их выявления.
3.Структура системы. Элементы систем. Оператор системы. Векторы входных и выходных сигналов. Возмущающие воздействия. Отрицательная обратная связь. Задачи исследования систем
4. Элементарные функции алгебры логики.
5.Элементы теории множеств. Диаграммы Эйлера-Венна. События. Разность событий. Объединение и пересечение событий.
6. Таблица функции двух переменных.
7.Элементы функционального анализа. Расстояние. Метрические пространства. Евклидова метрика.
8. Аналитическая запись логических функций. Характеристическая функция единицы.
9.Евклидовы пространства . Образ шара.
10. Дизъюнктивное представление логической функции.
11.Пространства Гильберта
12.Условные понятия степени аргумента логической функции. Использование дизъюнкции, конъюнкции для описания функций алгебры логики.
13.Скалярное произведение векторов в Евклидовом пространстве . Расстояние между элементами данного пространства.
14. Таблица соответствия для выходных слов и внутренних состояний конечных автоматов (последовательных схем). Глубина памяти. Стохастические автоматы.
15.Иллюстрация понятия расстояния в пространствах .
16. Законы алгебры логики. Формулы Де-Моргана.
17.Ортонормированный базис линейного пространства. Базис пространства, ортогональность векторов.
18. Свойства конъюнкции и дизъюнкции. Сочетательный, переместительный и распределительный законы.
19.Расстояние между векторами в пространстве Гильберта в . Норма вектора. Скалярные произведения векторов в . Ортогональный базис.
20.Условные понятия степени аргумента логической функции. Использование дизъюнкции, конъюнкции для описания функций алгебры логики.
21.Обобщенный спектральный анализ в пространстве Гильберта. Ряд Фурье по ортогональной системе.
22. Геометрическая интерпретация логической функции двух аргументов с примерами раскраски вершин единичного куба.
23. Построение ортонормированного базиса методом Грамма-Шмидта.
24. Задание функции алгебры логики. Таблица истинности и покрытие нулевых и единичных вершин единичного куба дизъюнкциями и конъюнкциями.
25.Основные понятия математической логики. Высказывания, предикаты, алгоритмы, конечные автоматы.
26. Таблица функции двух переменных.
27.Конечные автоматы. Входной и выходной алфавит. Таблица соответствия для выходных слов. Комбинационная схема.
28. Полные системы функций в классе R. и Mn. Полная система в базисе И-ИЛИ-НЕ.
29. Таблица соответствия для выходных слов и внутренних состояний конечных автоматов (последовательных схем). Глубина памяти. Стохастические автоматы.
30.Минимизация логических функций методом покрытия нулевых вершин и рёбер куба дизъюнкциями.
>10. Дизъюнктивное представление логической функции.
Вот про это как раз вчера читал у шлюхоеба. Легкотня.
недоучка-кун
>3.Структура системы. Элементы систем. Оператор системы. Векторы входных и выходных сигналов. Возмущающие воздействия. Отрицательная обратная связь. Задачи исследования систем
>Элементы систем
Осколки империи элементы систем.
И тот кто был всем - тот станет никем.
Вообще трэш и угар какой-то. Формулы де Моргана, спектральная теория оператора на гильбертовом пространстве и конечные автоматы в одном билете.
Нужно было ещё добавить что-то про нётеровы схемы, представления конечных групп, ракетостроение и лечение ЗППП подорожником.
И джаваскрипт, без него сегодня никуда
Скажи еще что вот ему
>>8541
тоже
>Дело в том, что нормальным людям эти учебники понятны и доступны. Просто ты особый случай, пытаешься изучать то, к чему твой мозг не приспособлен.
>А потом из-за ущемлёного чувства достоинства проецируешь свои чувства по отношению к себе на авторов учебников. ЭТО НЕ Я ДАУН, ЭТО АВТОРЫ ТУПЫЕ НИЧЕГО МНЕ ОБЪЯСНИТЬ НЕ МОГУТ, ВЕДЬ НУЖНО ПОНЯТНО, ЧТОБЫ КАРТИНКИ БЫЛИ, А ТО ДЕГЕНЕРАТЫ НЕ ПОНИМАЮТ, КАК ДЕЛАТЬ, ДОКАЗАТЕЛЬСТВА ТАМ КАКИЕ-ТО)))
>Но в глубине души, ты осознаешь, что ты тупой даун и не можешь понять, то что на самом деле ОЧЕВИДНО.
Тебе помогли сразу же и очень терпеливо потом разжовывали что не так ты делаешь. До тебя не дошло и ты продолжал ныть про картиночки — справедливо получил хуев за воротник.
Ты сам начал обкладывать авторов учебников, это во первых. Во вторых, тебе помогли. Тебе сказали, что ты слишком тупой, чтобы понимать нормальные учебники и что виноваты не авторы, а лично ты. Так что либо развиваешь свой интелект, чтобы ботать нормальные книги, либо идёшь нахуй. Специально для таких умственно отсталых как ты не будут писаться книги по математике отдельно, это того не стоит.
>>8549
У него и у тебя разные вопросы и отвечать на них следует по разному. Расписывать все билеты я не буду, пусть у одногруппников материал спросит, большу толку будет.
Плохой тест. Я ИРЛ гений, а тест показал что я идиет
 428 Кб, 1600x900
428 Кб, 1600x900>Это по твоему нормально?
Да. Как по твоему должна выглядить построика действительных чисел в курсе матана?
>Или все кто не понял с наскока, без подготовки, умственно отсталые?
А сколька у тебя времени было, чтобы переварить это? За два дня, что тыт тут ноешь, можно было въехать.
Повторяю: тебе сразу помогли и сказали что делать, если ты не понимаешь математику и не хочешь разбираться. Сказали что делать, если ты не понимаешь и хочешь разбираться.
Какие ещё вопросы у тебя?
Хорошо, почему тогда теория о бесконечно малых преподаваемая на основании теории множеств представляет из себя переусложненное изложение того, что написано в книжке лузина на первых 80 страничках?
>теория о бесконечно малых
Ору.
>на основании теории множеств
Что тебя смущает в множествах?
>из себя переусложненное изложение того, что написано в книжке лузина на первых 80 страничках?
Что за книга? И что там конкретно написанно?
Я не знаю, что там писал Лузин на своих страничках.
Лена, иди читай книги, хватит сюда писать хуйню.
http://www.vixri.ru/?p=236
Сайт конечно хуевенький, но у меня регистрации не просит чтобы прочитать.
У Фихтенгольца правда ебанутый и старый способ определение действительных чисел, который был придуман ещё до множеств. У Зорича они определяются так же, как и в Лузине.
У Зорича, насколько я понял, аксиоматически они определены. А есть явные конструкции действительных чисел из рациональных, или там из геометрии, прости господи.
Как тут выяснили, множества появились в 19 веке, а фихтенгольц родился в 1888 году. Он просто не мог не знать множества.
Что значит явные?
Зорич доказывает, что точки на прямой изоморны полю действительных чисел - вот и твоя явная интерпритация.
До множеств один из способов определение действительных чисел через сечения и классы. Потом на этот способ натянули множества, назвав классы множествами, лол. У Харди такой способ определения, без множеств, но с классами.
Значит как в современных учебниках, вроде Аман-Эшера. То как делает Зорич имхо даже вредная хуита, т.к. не имеет формального смысла, только "напальцевый".
Где он говорит о формальном смысле? Он просто предлагает поверить в аксиоматику, мол умные дяди обо всём позаботились.
У тебя в корне неправльное представление о математике, она часто работает с аксиоматически методом. И математики им пользуются. Ты только что назвал дохуища математиков, в том числе Бурбаков и Гилберта инженерами. Молодец.
Объясни, как явное построение позволяет лучше понимать объект. То же сечение Дедикинда просто архаичный мусор, который бесполезен для математика.
*Дедекинда
>У тебя в корне неправльное представление о математике, она часто работает с аксиоматически методом.
Я в курсе, спасибо. Не знать конкретно конструкцию действительных чисел для математика зашквар. И Гильберт, и Бурбаки её знали.
> архаичный мусор
Я понял твою точку зрения, во мне понимания ты не найдёшь.
>Объясни, как явное построение позволяет лучше понимать объект.
>И Гильберт, и Бурбаки её знали.
Я говорил про аксиомы, знали ли они её или нет имеет связи с тем, что я сказал. Я говорил про аксиоматический методв целом.
>Не знать конкретно конструкцию действительных чисел для математика зашквар.
Чем конструкция с аксиомами хуже?
>Я понял твою точку зрения, во мне понимания ты не найдёшь.
Тогда скажи, где она применяется кроме определения действительных чисел? Какая от неё польза в самом анализе или за его пределами?
>сечение Дедикинда просто архаичный мусор
А не пошел бы ты нахуй, собака.
Дедекинд это величайший математик в истории после Гаусса, такой Андре Вейль (и Ленглендс, в одном лице) 19-го века. Среди его изобретений, помимо идеала и модуля
-римановы поверхности в современном определении
-дедекиндовы сечения
-канторовская теория множеств
-аксиоматика пеано
И все это, согласно задумке Дедекинда, должно было объединить математику.
>где она применяется кроме определения действительных чисел
Того, что эта удивительная по красоте конструкция в некотором смысле аналогична модулю над кольцом, уже не достаточно что ли?
Ты охуел совсем, я посмотрю.
Если ты не понимаешь дополнительной ценности в явной конструкции математического объекта, я тебе ничем помочь не могу.
Это же не значит, что все, что он сделал имеет одинаковую ценность. Те же сечения отвратительны и бесполезны.
>>8597
Нет, сечения не красивы. Совсем. Если для тебе этот мусор красивый, то это значит, что у тебя дурной вкус. Вот последовательности Коши. Да хорошая вещь.
>>8598
Я действительно не понимаю, объясни мне.
Зельдович математика для техников и инженеров
>Дедекинд это величайший математик в истории после Гаусса
Святая толстота.
Давай посмотрим, в честь дедекинда назвали йоба пушку, кратер на луне и график нормального распределения?
Еще
Способен судить только по названиям? Открою секрет, теорема Гаусса-Бонне не имеет никакого отношения ни к Гауссу, ни Бонне.
Дедекинд просто сильно недооценен, в отличие от какого-нибудь Галуа, который дохуя переоценен.
Я тебе тоже открою секрет.Гаусс не имеет никакого отнощение к кратеру имени себя и к пушке имени себя.
Но из за того каким он был человеком ему все высказывают уважение в такой манере.
Теперь давай посмотрим на твоего декаденса. Что он сделал значительного чтобы в его честь назвать астероид какой то?
>Дедекинд просто сильно недооценен,
Действительно, ведь сечения Q такая полезная вещь! Встречается в математике на каждом углу. Без неё не топологию не построить, в алгбре без неё никак, в геометрии тоже. Сам удивляюсь, как в анализе без неё обходятся и отправили такую вещь на свалку истории. Эх. Что-что? Явное построение? Ох, без него никуда! Мнение парочки коструктивистов очень важно, а значит эти сечения должны быть не в специализорованный литературе по математической логике и основаниям а в книге анализа, правильно, нечего веровать в аксиоматику, веру плодить себя губить. Да, как же можно заниматся анализом не зная, что такое сечение, даже в Демидовиче на первых страницах задачи с сечениями, ух, всё по Фихтенгольцу.
Тепепь это ненависти к Дедекинду тред.
Как же я проиграл с Рехорда.
>>8629
Я уже понял, что ты не математик, и знаешь о Гауссе только по рельсогану. Перечислишь реальные достижения Гаусса?
>>8619
>>8624
>что он сделал значительного
>кривляется про сечения
1. Понятие идеала и модуля, nuff said, наука о модулях это и есть определение математики
2. Риманова поверхность как поле функий, понятие связавшее комплексный анализ и комбинаторную топологию
3. Теория множеств, которую спиздил Кантор (Дедекинд был настолько хорошим человеком, в отличие от Гаусса, что не стал претендовать на приоритет, хотя публиковал работы; вместо этого он стал пропогандировать работы Кантора. Гаусс же только умел ссылаться на неопубликованные результаты, за что его м хуесосили)
4. Аксиоматика Пеано до Пеано уже была у Дедекинда.
Все? Или еще надо обосать?
Я ещё раз говорю, если он сделал полезные вещи, не значит, что всё, что делал полезно. Сечения Q - мусор, просто признай это, и место этому архаизму в книге Харди и Фихтенгольце.
1) Спорно, Вербиту не понравилось, он сказал, что это определение, как сепульки.
3) Пруфов не будет?
>Вербиту не понравилось
Причём тут ваще Вербит? Если тебе так важно мнение Вербита иди спроси у него нужно ли студентов учить явной конструкции действительных чисел.
Обоснованную. Еще раз: почему у действительных чисел именно такая аксиоматика? Почему она полна и непротиворечива?
Ты даже не видел его критику, а уже агришся. Вне математике, фраза модуль над кольцом не имеет смысла. А теперь смотри, давая определение математики через неё саму, мы даём определение, понятиям входящих в неё, через самих себя.
Тогда зачем ты продолжаешь говорить, что математика наука о модулях над кольцами, эти приводит к порочному кручу.
1) Ты не прочитал, либо не понял, что он написал. Утверждений там было два
а) это контекстуальное определение (что совершенно очевидно)
б) данное определение ничем не лучше определения математики как науки о пучках
Знающий человек поймет о чем речь: проективные модули эквивалетны локально свободным когерентным пучкам. Прочесть об этом можно в "коммутативной алгебре" Бурбаки.
2) Любая книга по истории математики второй половины XIX века:
Dedekind's more foundational work in mathematics is also widely known, at least in parts. Often acknowledged in that connection are: his analysis of the notion of continuity, his introduction of the real numbers by means of Dedekind cuts, his formulation of the Dedekind-Peano axioms for the natural numbers, his proof of the categoricity of these axioms, and his contributions to the early development of set theory (Grattan-Guinness 1980, Ferreirós 1996, 1999, 2016b, Jahnke 2003).
What happens in Was sind und was sollen die Zahlen?, in the context of Dedekind's logicist reconstruction of the natural numbers, is that the adoption of set-theoretic techniques is raised to a new level of clarity and explicitness. Dedekind not only presents set-theoretic definitions of various mathematical notions, he also adds a systematic reflection on the means used thereby (and he expands that use in certain respects). Consequently, the essay constitutes an important step in the rise of modern set theory. We already saw that Dedekind presents the notion of set, together with those of object and function, as fundamental for human thought. Here an object is anything for which it is determinate how to reason about it, including having definite criteria of identity (Tait 1997). Sets are a kind of objects about which we reason by considering their elements, and this is all that matters about them. In other words, sets are to be identified extensionally, as Dedekind is one of the first to emphasize. (Even as important a contributor to set theory as Bertrand Russell struggles with this point well into the twentieth century.) Dedekind is also among the first to consider, not just sets of numbers, but sets of various other objects as well.
1) Ты не прочитал, либо не понял, что он написал. Утверждений там было два
а) это контекстуальное определение (что совершенно очевидно)
б) данное определение ничем не лучше определения математики как науки о пучках
Знающий человек поймет о чем речь: проективные модули эквивалетны локально свободным когерентным пучкам. Прочесть об этом можно в "коммутативной алгебре" Бурбаки.
2) Любая книга по истории математики второй половины XIX века:
Dedekind's more foundational work in mathematics is also widely known, at least in parts. Often acknowledged in that connection are: his analysis of the notion of continuity, his introduction of the real numbers by means of Dedekind cuts, his formulation of the Dedekind-Peano axioms for the natural numbers, his proof of the categoricity of these axioms, and his contributions to the early development of set theory (Grattan-Guinness 1980, Ferreirós 1996, 1999, 2016b, Jahnke 2003).
What happens in Was sind und was sollen die Zahlen?, in the context of Dedekind's logicist reconstruction of the natural numbers, is that the adoption of set-theoretic techniques is raised to a new level of clarity and explicitness. Dedekind not only presents set-theoretic definitions of various mathematical notions, he also adds a systematic reflection on the means used thereby (and he expands that use in certain respects). Consequently, the essay constitutes an important step in the rise of modern set theory. We already saw that Dedekind presents the notion of set, together with those of object and function, as fundamental for human thought. Here an object is anything for which it is determinate how to reason about it, including having definite criteria of identity (Tait 1997). Sets are a kind of objects about which we reason by considering their elements, and this is all that matters about them. In other words, sets are to be identified extensionally, as Dedekind is one of the first to emphasize. (Even as important a contributor to set theory as Bertrand Russell struggles with this point well into the twentieth century.) Dedekind is also among the first to consider, not just sets of numbers, but sets of various other objects as well.
*кругу
Это не я говорю, я другой анон.
Я на минуту подумал, что ты тот поехавший, которому конструкция R не нужна.
Дружище, я вообще тут ни к месту, я просто мемы клепаю.
>>8640
Какой порочный круг, ты тупой? Определения бывают разными, это – контекстуальное. А сказав про пучки, тифарет по сути согласился со мной, смотри выше.
>>8643
Про ненужность R это я набрасывал, а не он. Про мистику и эзотерику тоже я.
Я не говорил, что конструкция R не нужна. Просто есть фундаментальные последовательности, которые гораздо лучше, чем дедекиндский мусор.
В маттредах sci до создания этого раздела.
Определение Кантора несколько более громоздко, чем определение Дедекинда, когда дело доходит до определения элементарных функций. Например, возведение в степень по Дедекинду определяется в несколько слов. А знаешь ли ты, как определить возведение в степень с помощью фундаментальных последовательностей?
 86 Кб, 1920x1080
86 Кб, 1920x1080Вот такие должны быть учебники на простых элементарных примерах, как на картинке, где обычный человек видит и начинает понимать что к чему и в голове уже сопоставляются логические связи. Даже обезьяна поймет тот пример который я нарисовал.
Учебники должны делаться для того чтобы люди поняли и усвоили материал, а не для того чтобы автор книги увеличивал свое чсв что он умную непонятную книгу написал.
>666
>а не для того чтобы автор книги увеличивал свое чсв что он умную непонятную книгу написал.
Ну тебе, конечно, виднее, для чего ученые и люди знаний пишут книги, дьявол.
Они для этого и делаются, просто ты тупой и тебе нужны ОСОБЫЕ учебники для умственно одарённых.
Почему ты решил, что обычный человек не может понять конкретно выделенное тобой утверждение без простого примера?
>Я не обязан знать все на свете.
Правильно. А ещё ты не обязан знать математику.
>Людям нужны понятные разжеванные учебники а не инопланетное чтиво.
Тот же Зорич или Фихтенгольц, особенно последний, понятно разжёванные учебники. Если разжёвывать материал в твоём даунском стиле, то учебники будут неподъёмными, все будет засранно тривиальными объяснениями и картинками. По таким учебникам ты ничего не выучишь, хотя бы из-за того, что колиство страниц станет гиганским.
>Я его не понял значит и другой человек не поймет
Ложное следствие. По твоему, если я понял, значит и другой поймёт? Я не говорю за всех, но особо одарённым нужны примеры, чтобы понять.
>но большинству нужно примеры чтобы понять.
Никто не запрещает тебе придумывать примеры самостоятельно. Можешь ещё и картиночки к каждой теореме рисовать.
>большинству
Большинству обычных людей нужен пример, чтобы понять дистрибутивность пересечения множеств относительно объединения?
Скачал и посмотрел Фихтенгольца и Зорича, это непонятное дно.
>Если разжёвывать материал в твоём даунском стиле, то учебники будут неподъёмными, все будет засранно тривиальными объяснениями и картинками. По таким учебникам ты ничего не выучишь, хотя бы из-за того, что колиство страниц станет гиганским.
Лучше потерять время и нормально изучить на простых примерах и понять, нежели потерять время расшифровывая "китайскую грамоту" и ничего не выучить.
>По твоему, если я понял, значит и другой поймёт?
Есть сопредельный процент людей, кто может понят, и той процент очень мал.
>Никто не запрещает тебе придумывать примеры самостоятельно. Можешь ещё и картиночки к каждой теореме рисовать.
Я могу нарисовать, но не факт что я пойму материал правильно и не ошибусь в самом начале.
Иза таких некомпетентных авторов книг и учителей вузов, в мире не повляются гении типа эйнштейн, теслы, гаусса и т.д.
В книге даже не объясняется что такое дистрибутивность.
>Большинству обычных людей нужен пример, чтобы понять дистрибутивность пересечения множеств относительно объединения?
Да нужен пример, не только на это но на все выражения в книге. Тогда это будет полноценный качественный учебник.
Ты считаешь, что большинству обычных людей нужен пример, чтобы понять дистрибутивность пересечения множеств относительно объединения. Никто кроме тебя здесь так не считает. Как ты можешь это прокомментировать?
Да я так считаю.
>Никто кроме тебя здесь так не считает.
Ты что у каждого спрашивал и проводил опрос?
>Скачал и посмотрел Фихтенгольца и Зорича, это непонятное дно.
Прекращай проецировать, дно ты раз не можешь понять Фихтенгольца, который создавался для ниженеров. По чему ты не признаёшь того, что ты тупой?
>Лучше потерять время и нормально изучить на простых примерах и понять, нежели потерять время расшифровывая "китайскую грамоту" и ничего не выучить.
Не факт. Учёба не бывает простой, это тебе не лекции для семиклассников и не научпоп. И есть мнение, что как раз при такой расшифровке ты и учишся чему-то.
>Есть сопредельный процент людей, кто может понят, и той процент очень мал.
Понимаешь, процент людей, занимающихся математикой очень мал и они не собираются все расписывать для того, чтобы, чтобы тупой, понял то, что умному очевидно. Тебе ясно?
>Иза таких некомпетентных авторов книг и учителей вузов, в мире не повляются гении типа эйнштейн, теслы, гаусса и т.д.
Во первых, это не так. Эти люди могли понять то, во что ты не врубаешься.
Ты первый, кто за 70+ тредов начал ныть о таком и назвал авторов учебников дегенератами. Так, что да. Никто кроме тебя так не считает.
Опроса не было, но все ответы на твои сообщения содержат несогласие с твоими суждениями. Но предположим, что ты считаешь так, а я считаю по-другому. Доказательств у тебя нет и у меня нет. Тогда к чему эти вбросы?
>По чему ты не признаёшь того, что ты тупой?
Потому что я не тупой, я тоже могу написать книгу в которой ты ничего не поймешь и будешь тоже тупой.
>И есть мнение, что как раз при такой расшифровке ты и учишся чему-то.
Расшифровка информации только тратит время, заместо объяснений.
>Понимаешь, процент людей, занимающихся математикой очень мал
Потому и мал что книги пишутся некомпетентными людьми.
>Эти люди могли понять то, во что ты не врубаешься.
Не спорю есть уникумы на свете.
>>8689
>Тогда к чему эти вбросы?
Чтобы открыть людям глаза на то, что не они виноваты в том что не понимают математику и остальные предметы, а виновны авторы учебников, учителя вузов и система образования.
Расскрой по определению произведения результирующее множество слева и справа равенства. Убедись, что получилось одно и то же выражение.
Госпади, какой же ты еблан. Это не авторы учебников виноваты, а именно ты, кретин. Глаза он собрался открывать.
Госпади, это самый тупой посетитель /math.
>Потому что я не тупой, я тоже могу написать книгу в которой ты ничего не поймешь и будешь тоже тупой.
Смотри, люди понимают учебник, а ты особенный тебе нужен специальный учебник для даунов. Ты не можешь учится по нормальным, потому что они слишком сложны для тебя. Суть - ты тупой. ТУПОЙ.
>Расшифровка информации только тратит время, заместо объяснений.
Какой информации? Что ты говоришь, кретин. То, что для нормальных людей ОЧЕВИДНО, то для тебя нет. Тебе нужны дополнительные объяснения.
>Потому и мал что книги пишутся некомпетентными людьми.
Объясни с чего это вдруг они некомпетентные? Ты ведь понимаешь, что у тебя проблеммы с логикой - в твоей невозможности осилить учебники элементарного анализа виновать ты, а не их авторы. Если ты не был тупый, то понял. С такой логикой тебе не стоит приблежатся к математике вообще.
>Не спорю есть уникумы на свете.
Эти уникумы обычные люди.
А то что тренды по матеше) тянутся на 70 трендов тебя не настораживает?
Ведь если бы были простые учебники, которые можно было бы сделать универсальным ответом на любой вопрос "что посмотреть из аниме? боко но пику", "двач я покакал, что делать? сделай бочку/сосни хуйцов", почему никто до сих пор не постил на вопросы о гауSSе-боннне какого то штурма или рому михайлова?
Или тут с первого же треда обсуждают теорию хаоса и вычисляют как взмах бабочки на одном континенте вызывает ураган на другом?
>>8699
>Чтобы открыть людям глаза на то, что не они виноваты в том что не понимают математику и остальные предметы, а виновны авторы учебников, учителя вузов и система образования.
Нет, виновато наследие совка. Сравни классический учебник по математике на русском языке и на английском. Дам подсказку, у саксонцев это томас, а у нас ебаный демидович.
Да, это сборник задач. Есть у демидовича еще и краткое вкатывание в вышмат, но не про него сейчас.
Давай скажи тогда, что сейчас считается Ъ учебником по вышмату в МГУ, МГИМО, МФТИ, т.д.
>тянутся на 70 трендов тебя не настораживает?
Потому что мимокрокодилы приходят.
По анализу/калькулюсу есть уже устоявшийся ответ: Зельдович (для ПТУшников), Зорич (для обычных пацанов), Шварц (для умняш или знакомых в целом с другой математикой или второго знакомства с анализом)
Так выражения получаются разные.
Смотри, пусть A = {1,2}, B = {a,b}, C = {x,y}.
AxB = {(1,a), ... }
(AxB)xC = { ((1,a),x), ... }
BxC = {(a,x), ...}
Ax(BxC) = {(1,(a,x)), ... }
Пара ((1,a),x) не равна паре (1,(a,x)). Множества (AxB)xC и Ax(BxC) не могут быть равны.
>Давай скажи тогда, что сейчас считается Ъ учебником по вышмату в МГУ, МГИМО, МФТИ, т.д.
ФихтенгольцИльин-Позняк
Тогда почему ты ведешься на провокацию, как ты утверждаешь, и не советуешь
>Зельдович (для ПТУшников), Зорич (для обычных пацанов), Шварц (для умняш или знакомых в целом с другой математикой или второго знакомства с анализом)
?
Тебе больше нечем заняться, кроме как на сосачах двачевать? Ты чувствуешь себя мессией от лобаческого? Ты хочешь популярности уровня матх? К чему вся эта энтропия?
А еще более другой анон который зашел на огонек.
Я прямо сейчас могу назвать как минимум 4 способа понять "непонятный" учебник:
1) просмотр/посещение лекций по предмету;
2) приведение примеров для данного определения - отличный метод, кстати;
3) конспектировать, перечитывать на свежую голову - понимание станет глубже;
4) посмотреть в другом учебнике или ином источнике, авось иной стиль изложения поможет понять.
Думаю, этот список с лёгкостью можно продолжить.
Зельдович Я.Б., Яглом И.М. "Высшая математика для начинающих физиков и техников"
Халмош Теория меры
Ну охуеть теперь.
>В чём проблема выебать тян? Можно быть сколь угодно глупым человеком, но если не нашёл способа, при котором не можешь выебать тянку - это край, и ВОЗ ввела для таких как ты стату инвалида. А если не искал способа поебаться - какого дьявола надо об этом ныть на борде?
>Я прямо сейчас могу назвать как минимум 4 способа выебать тян:
>1) просмотр/посещение кино с тян;
>2) приведение тянки в ресторан- отличный метод, кстати;
>3) конспектировать, перечитывать переписку с тянкой на свежую голову - понимание станет глубже;
>4) посмотреть в ютубе или ином источнике пикап видео, авось иной стиль изложения поможет понять.
>
>Думаю, этот список с лёгкостью можно продолжить.
Посыл понял или нет?
Если нет, то скажи почему одним нужно таскать штангу на триста кило чтобы накачать мускул на пол сантиметра а у других мышцы от онанизма растут?
Почему у восьми людей на земле половина денег всего земного шара, а другие умирают от голода в гнусной халупе?
Почему у одних больных спидом в крови осталось полтора лейкоцита, но они не подхватывают даже простуду, а у полностью здоровых людей нос постоянно течет на ниагара?
Вот и всё. Ты сам ответил на свой вопрос, ты тупой и не способен заниматся математикой. Не трать время на картинки и поиск простых учебников. Уходи.
 60 Кб, 720x951
60 Кб, 720x951Ты так ничего и не понял и хочешь продолжать кидаться какашками.
Правильный ответ, потому что все люди разные.
Если ты будешь продолжать судить всех по себе ты нихуя не понял а я все понял значит ты дурак и не сможешь становится на чужое место ты так и будешь продолжать кидаться какашками в отстойниках типа сосачей.
 158 Кб, 998x913
158 Кб, 998x913Вот нашел книгу где есть элементарные минимальные примеры, скрин прилагается. Не понимаю зачем вы дрочите на ущербное совкове образования и книги.
Ты конченый или окончательно конченый? Я тебе прямо указал на фатальные недостатки твоих же слов.
Долбаёбище, ты начал кидаться говно в авторов учебников. Причём, ты называл их тупыми дегенератами и после этого ты привел пример с тяночками. Это же пример показывает, что ты кретин и тебе не надо даже близко подходить к матеше, пусть этим займутся местные альфачи, а ты дрочи свои картинки в кулачок.
http://discretetext.oscarlevin.com/pdfs/dmoi-tablet.pdf
Вот еще, есть же элементарные примеры, зачем себе мозги задрачивать и терять попусту время.
Тогда почему ты до сих пор не мистер олимпия с заработком 300к в секунду и с напомаженной венерой вместо девушки? Ведь есть куча книг про успех, атлетизм и пикап в которых все разжевано до состояния каши?
Отлично.
Ответь тогда на один последний вопрос, почему учебники по вышмату продолжают упорно выпускать тысячи авторов по всему миру, если достаточно один раз написать мега учебник в котором будет все обо всем и про всех?
Потому что
>куча книг про успех, атлетизм и пикап
наебалово на деньги. Говорю как прочитавший несколько книг об атлетике, и каждая гласила своё.
Какие новые математические теоремы открыли за прошлый год, из за которых стоило бы переписывать абсолютно все учебники по математике за позапрошлый год?
Дело тут скорей в технологическом прогрессе. Нахуй нужен учебник в котором все упражнения решаются через wolframalpha? Чему он научит человека?
Почему тогда математика это не наебалово на деньги? Потому что её можно проверить, так?!
Что тогда тебе мешает проверить врут или нет про то что за 10 недель можно увеличить количество подтягиваний с нуля до пятидесяти?
Зачем тогда вообще нужна математика если все компьютер в маткаде посчитать может? Чему она научит человека, если сборище кремния, меди и пластика может сделать то же самое но гораздо быстрее и качественее?
Потому что на результатах математики и областей, её использующих, держится нынешняя человеческая среда обитания, не? Ты какой-то ебанутый.
Алсо, проверял - за 10 недель не достичь.
Тогда зачем тебе её учить? Зачем человеку делать игры, если тоже самое может сделать компуктер гораздо быстрее и качественее?
>Смотри, люди понимают учебник, а ты особенный тебе нужен специальный учебник для даунов. Ты не можешь учится по нормальным, потому что они слишком сложны для тебя. Суть - ты тупой. ТУПОЙ.
>Какой информации? Что ты говоришь, кретин. То, что для нормальных людей ОЧЕВИДНО, то для тебя нет. Тебе нужны дополнительные объяснения.
Я не хочу тратить время, задрачивая инопланетянские иероглифы и терять зрения и приобретать головные боли от перенапряжения, так само другие люди не хотят, информацию можно подать более простым способом постепенно увеличивая сложность, а не сразу с 10 страницы выдавать несуразную хуету.
>Объясни с чего это вдруг они некомпетентные?
Не могут подать информацию на элементарных примерах хотя бы числовыми массивами, или объектами из мира.
>Эти уникумы обычные люди.
Бетховен и Моцарт тоже обычные и без задней мысли вот так просто и начали сочинять музыку, да?
Математика не учит считать, а учит понимать. Каждый второкурсник должен понимать доказательство теоремы Ферма, а не то, как считать интеграл.
>Бетховен и Моцарт тоже обычные и без задней мысли вот так просто и начали сочинять музыку, да?
https://en.wikipedia.org/wiki/Category:18th-century_classical_composers
просто без задней мысли посвятили музыке всю свою жизнь.
Много людей посвящает музыке жизнь но не все добиваются успеха, есть же особый талант, генетика.
Да, но суть ассоциативности не в равномощности, а в равенстве.
Почему тогда в учебниках пишут, что декартово произведение ассоциативно?
Не на математике, на моделях использующих математику. Если скажешь что нет, то найди мне в природе закон кулона/всемирного тяготения/любой другой.
Ну и кому ты врешь? Почему я за два с половиной года научился подтягиваться на одной руке с поддержкой, а ты не смог в элементарные обычные подтягивания?
>>8757
Зачем человеку вообще что то делать если найдется кто то кто сделает что то лучше быстрее и качественнее чем он?
>>8759
И какой прок с теоремы ферма? Что ты будешь с ней делать? Показывать богу/пришельцам чтобы они охуели как мы можем? Прекращай толстить, я начинаю терять интерес к этой дискуссии, которая на самом деле не дискуссия, а дебаты.
>Бетховен и Моцарт тоже обычные и без задней мысли вот так просто и начали сочинять музыку, да?
Почему ты приводишь в пример гениев? Разне нужно быть гением, чтобы по Фихтенгольцу вкактиться в матан? Нет.
>Не могут подать информацию на элементарных примерах хотя бы числовыми массивами, или объектами из мира.
У тебя наивное предстваление о математике. Я ещё раз спрашиваю, зачем тебе вообще заниматься матешей, если ты ничего не понимаешь без примеров, там где можно без них обойтись?
>Я не хочу тратить время, задрачивая инопланетянские иероглифы и терять зрения и приобретать головные боли от перенапряжения, так само другие люди не хотят, информацию можно подать более простым способом постепенно увеличивая сложность, а не сразу с 10 страницы выдавать несуразную хуету.
У тебя нет знаний, чтобы вкатиться в матан? Если для тебя написанная человеческим языком вводная часть - несуразная хуета, то ты даун.
>>8761
А теперь ссылку на пруфы, что есть ген с понимаем математике. А хотя, постой. Я понел, у тебя плохая генеита, лишняя хромосома все дела. Я тебе не завидую.
>Зачем человеку вообще что то делать если найдется кто то кто сделает что то лучше быстрее и качественнее чем он?
Вот и не занимайся матешей. Всё просто. Уходи от сюда. И не возвращайся.
>Если скажешь что нет, то найди мне в природе закон кулона/всемирного тяготения/любой другой.
Проведение соотвестующего экспермента.
>И какой прок с теоремы ферма? Что ты будешь с ней делать?
Это не раздел для инженеров, уебывай. Открой, например, arxiv.org, почитай чем занимаются математики.
В учебниках в принципе не отражено ничего из того, в чем были совершены открытия в прошлом году. Никакие открытия в науке не могут изменить эти учебники. Следовательно, все эти учебники - говно мамонта.
Я тебе в отцы гожусь, чёрт малой. Пиздуй от сюда смотреть лекции для семиклассников.
И он даст тебе какие то данные. И ты эти данные будешь использовать для того чтобы предсказать некие явления.
Но самого закона ампера/кулона/т.д. в мире нет. Есть только математический образ того что мы называем законом ампера/кулона/т.д.
Ясно.
>>8769
Молодец, довел до абсурда и рад что не понял сути той мысли которую я пытался до тебя донести.
>>8770
Тебе 55? Потому что меньше чем в 15 лет мало кто может поднять свой писюн силой мысли, а еще меньше сможет вставить этот писюн в нужное место чтобы дети были.
К чему я это? Надоели вы мне. Пойду я спать.
В норме учебник - это компиляция свежих и интересных статей, дополненная справочной информацией, такой как общеизвестные определения и обозначения. Учебник по общей топологии должен меняться каждые два-три года, например.
Ну и расскажи, что должно быть в учебнике 2017. Изложение через локали?
В общей топологии уж лет 40 ничего не происходит.
Должен быть обзор всех тех идей, которыми пользовались авторы https://arxiv.org/list/math.GN/16
Или хотя бы самых перспективных из них.
Можно наверное назвать это абузом нотации. Типа чтобы не писать каждый раз "есть биекция между (a, b, c), ((a, b), c) и (a, (b, c))". А в каких учебниках пишут, что ассоциативно? Открыл Мункресову Топологию, так такого нет. На википедии тоже явно сказано, что не ассоциативно.
Два тела притягиваются друг к другу с силой прямо пропорциональной массам тел и обратно пропорциональной квадрату расстояния между ними. Это называется законом всемирного притяжения.
Этот закон основывается на трех законах кеплера
-каждая планета вращается по эллипсу в одном из фокусов находится солнце
-за равные промежутки времени радиус вектор ометает одинаковые площади эллипса
-квадраты периодов обращения планет относятся как кубы больших полуосей орбит
Законы кеплера основываются на многолетних наблюдениях браге выполненных со всей возможной точностью деревянных визиров и телескопов циклопических размеров собранных вручную и скрупулезной записью всех наблюдений в специальную книжку с записью времени.
Теперь найди момент в который появилось то что мы называем законом всемирного притяжения.
Да, Моцарт в пять лет без задней мысли внезапно взял и начал писать музыку. Ты бы сперва хоть немного узнал про тех, чьи фамилии употребляешь.
ассоциативно для равных множеств.
>Разне нужно быть гением, чтобы по Фихтенгольцу вкактиться в матан? Нет.
Даун это ты, не понимаешь что от качества изложения материала зависит качество знаний и усвояемости информации, это все люди понимают кроме такого дебила как ты.
> Я ещё раз спрашиваю, зачем тебе вообще заниматься матешей, если ты ничего не понимаешь без примеров, там где можно без них обойтись?
Может я хочу программировать AI для игр, но нужно наличия знаний в теории графов.
>А теперь ссылку на пруфы, что есть ген с понимаем математике. А хотя, постой. Я понел, у тебя плохая генеита, лишняя хромосома все дела. Я тебе не завидую.
http://www.nat-geo.ru/science/47520-obnaruzhen-gen-otvechayushchiy-za-genialnost/
Учебник - это не научная статья. Учебник ставит своей целью научить, а не просто сообщить информацию.
К сожалению эти авторы пользуются идеями, которые есть в каждом учебнике по топологии: у них они даже в референсах.
Вот тебе аналогия с машиной: ты хочешь собрать гоночный болид. Тебе нужно идти на формулу-1? Нет, тебе прежде всего надо знать на зубок аэродинамику, механику, устройство ДВС... А потом уже ты сможешь приступать к современной науке.
Научить ставит своей целью ученик. Мне, например, показался дебильным учебник Зорича и я начал читать Шварца. А учебник Лэнга мне показался слишком сложным и я пользовался сразу несколькими дополнительными источниками, чтобы лучше усвоить материал.
>http://www.nat-geo.ru/science/47520-obnaruzhen-gen-otvechayushchiy-za-genialnost/
Я говорил про ген с понимаем математики а не гениальности. Но ты кретин и ничего так и не понял.
>Даун это ты, не понимаешь что от качества изложения материала зависит качество знаний и усвояемости информации, это все люди понимают кроме такого дебила как ты.
Еблан, плиз. В том-то и дело, что качество изложения хорошее. Просто ты тупой и не можешь въехать.
>Может я хочу программировать AI для игр, но нужно наличия знаний в теории графов.
Даже не думай, тебе столько придёться испытать боли тогда.
У каждого дискурса есть свой уровень сложности. Есть самый сложный уровень, обозначим его филдс-0. Есть уровень на 1 меньше самого сложного, филдс-1. Есть уровень на 2 меньше самого сложного, филдс-2. И так далее до уровня детсада.
Очевидно, что учебник может поднять уровень дискурса читателя самое большее на единицу. Учебник не может поднять уровень сразу на десяток ступеней. Нельзя написать учебник на языке дошкольников, превращающий читателя в филдсовского лауреата.
Если мы готовим учебники для филдсовских лауреатов, то они должны быть написаны на языке филдс-1. Уже филдс-2 будет недостаточно выразительным.
>Может я хочу программировать AI для игр, но нужно наличия знаний в теории графов.
Бери учебник по AI: в одном из них стопудово есть необходимые данные по теории графов. Можешь взять книгу "Оре Теория графов" и прочитать оттуда где-то 5-7 глав, тебе хватит с головой.
Если ты не можешь сменить учителя, то ты виноват именно ты. Учитель ничего не должен, он просто объект этого мира.
Это значит, что хайлевельный учебник и должен выглядеть очень сложным. Это нормально. Он же хайлевельный.
Чего блядь? Ты выше написал, что "научить ставит своей целью ученик". Я тебя поправил: учитель, а не ученик.
Но вузовский учебник не может быть хайлевельным по определению. Это раз. Называть дураками всех, кто в данный момент находится ниже филдса-эн - ошиюка и провокация. Это два.
Хайлевельный - понятие относительное. Если уровень твоего дискурса филдс-n, то хайлевельные дискурсы - это дискурсы с номерами меньше чем n-1. Для филдс-50 уже филдс-48 будет хайлевельным.
Может. И что у тебя за определение такое? Это раз.
Называть аторов учебников дегенератами и дебилами потому что ты ничего не понял - это ошибка и провокация. Это два.
Ну так ученик здесь выступает в качестве учителя, просто процесс замкнут на себя. Понятия все равно разные.
Нет, эн-хайлевельные дискурсы - те, что лежат в эн-окрестности филдса-ноль. А ты говоришь об хайер-вен-левельных дискурсах.
Не ври. Процитируй.
Суть в том, что если вузовские учебники кажутся тебе сложными, то уровень твоего дискурса отстоит от филдс-вузик как минимум на две ступени.
Сложный и непонятный, впрочем, разные вещи. Как и дурак - нуб.
>Я говорил про ген с понимаем математики а не гениальности. Но ты кретин и ничего так и не понял.
Ты тупой, я говорил про ген который хорошо помогает в усваивании информации мозгом, а не математики.
>Еблан, плиз. В том-то и дело, что качество изложения хорошее. Просто ты тупой и не можешь въехать.
Какое должно быть качество изложения материала как минимум я предоставлял пример выше, идиота ты кусок.
>Даже не думай, тебе столько придёться испытать боли тогда.
Почему?
Предлагаю лично тебе забить на этого >>8789 хуесоса и заняться тем дерьмом что и я. Вводить понятие минимального понимания материала для тот кто не знаком с какой либо "предыдущей" матчастью всё понял (либо, если тут я зафейлился) просто какую-то минимальную единицу понимания, которой будет достаточно.
Ибо усложнить может каждый ебаный пидрила на этой планетке
А теперь, ленивая жопа, пили перекат.
Потому что длина предельной кривой неравна пределу длин кривых.
 27 Кб, 1024x684
27 Кб, 1024x684>Не на математике, на моделях использующих математику.
Когда читать научишься, мудила? Я написал чётко и ясно - на результатах математики и областей, её использующих. Если ты, дегенерат, не способен дойти до того, что матмодели входят в это всё - то неудивительно, что ты не в силах осилить простенькие классические учебники.
>за два с половиной года научился подтягиваться
>10 недель
>2,5 месяца
>2,5 года
Ты реально тупой.
По построению предел длиный этой кривой не стремится к длинне окружности.
Погугли "square pi = 4".
Бамп
А вот и реформатор подъехал!
Кто-нибудь из людей, думающих так же как и ты, понимает уравнения общей теории относительности?
Всё правильно, математика постоянно модернизирует свой язык. Например, анализ перевели на язык топологии, соеденив огромные математические области вместе. Теперь не нужно дрочить эпсилон-дельта и решать интегральчики 5 лет, теперь можно прочитать Шварца, а интегральчики компухтер посчитает.
То, на что умнейшие люди тратили десятки лет занятий с дорогим персональным учителем, который рисовал картинки и простые примеры, можно изучить, прочитав 200 страниц Шварца.
Во первых, когда она создавалась не было того формального языка, а почти всё было написанно с картинками и объяснено ими, по образу начал Евклида. Ты не знаешь, о чём говоришь, самый тупой посетитель /math.
Нет, пища же.
Блять, меня заебало, вот с Лощининым я никогда не пререкаюсь, а тут все анонимно и я не могу остановиться. Может прикреплять айди к постерам и менять его раз в тред?
В учебнике по топологии Вербицкого доказывается эквивалентность леммы Цорна, аксиомы выбора и теоремы Цермело. Еще там есть теорема Кантора и теорема Кантора-Бернштейна.
Вербицкого? Я чет очкую, он же поехавший, считающий, что восьмиклассники должны теорию Галуа знать. Что-нибудь энтри левела есть?
>Посмотрел я шварца нету там простых примеров, значит книга устаревшая и неактуальна.
Да, верно их там нет. Как раз потому что она относительно свежая. Хотелось бы, чтобы была такая же, но на языке модулей над кольцом.
А простые примеры Евклид давал, вот он как раз устарел. Возвращаться к такому регресс и деградация. А деграданты всегда могут пойти в сантехники и неплохо зарабатывать. Интеллект же не высшее благо для всех, сантехники тоже нужны и должны быть уважаемы в обществе.
Там есть пару опечаток, но в целом читабельно. Если задачи некому показывать, то не советую сильно увлекаться, а то это может растянутся на месяцы.
>Я не знаю таких людей.
Умелый маневр. Ну то есть так же как и ты думают только малообразованные слабые в математике личности или такие мысли приходили в голову и ученым-математикам?
Опчик, ты на что-то можешь повлиять в техническом плане? Ну скажем система лайков как в апачане тут была бы замечательной.
Извиняюсь, что немного, хм, коснусь, если так можно выразиться вашей с тем требующим пояснений аноном, дискуссии, но судя по тому, как ты с ним разговариваешь, сколько брани, направленной злобы ты на него льёшь, ты сам ни чуть не лучше. И хотя я согласен с тем тезисом, что пишутся учебники для математиков, кто хочет и понимать и заниматься математикой, тогда, если взглянуть и на твоём замечание о ничтожно малом кол-ве математиков от всего кол-ва людей на этой земле, и то, что ты говоришь "нормальные люди понимают математику, учась по этим учебникам", тогда кого ты имеешь в виду? Нормальные это те, кто учится математике, чтобы стать математиком или те, кто не хочет быть математиком, но некоторые математические методы ему требуются для решения его локальных задач, в его науке? Потому что первых - очень мало, как ты заметил, а вторых куда больше, но, вот незадача, им тоже ненужна значительная часть знаний, предоставляемых математикой, отчасти потому что они не могут понять их, или из-за каких-то иных причин, но это не делает их плохими специалистами в своей области, не делает их, как ты говоришь, тупыми, они тоже НОРМАЛЬНЫЕ люди. Или по-твоему они должны быть признаны ненормальными, потому что не поняли (или для них есть проблемы с пониманием) какую-то часть анализа, но вот какой-то другой раздел им дался лучше, и они вполне себе хорошие научные сотрудники. Ты всё еще будешь считать их ненормальными? Потому как, ты уж извини, подавляющее число людей на этой земле вполне здоровые психически и физически, следовательно, нормальные люди, но вот математику они не изучают дальше high school+колледж/университет (какой-то базовый уровень университетской математики и всё, на этом всё, дальше только специализированные мат.методы и разделы, но это куда меньше чем то, что осваивает и должен освоить математик). Причем я взял сразу как людей, изучающих какие-нибудь arts, humanities, social sciences так и людей которые связаны с natural sciences (коме математиков). Многие 1-ой категорий лиц могут тебе сказать, что они либо не понимают математику, либо очень многое не понимают, кроме некоторых методов, которые и используют в своих исследованиях, но они что... тупые? Слишком смелое заявление, правда? И ведь на этой планете куда больше чем самих математиков, их - тех самых нормальных людей.
Может ты и классный математик, может ты просто с математическим умом человек, но общение с тобой - наказание для человека. И ты очень груб и озлоблен, чего кстати, о других анонах из треда я не скажу. Извини, что вмешался в диалог.
Извиняюсь, что немного, хм, коснусь, если так можно выразиться вашей с тем требующим пояснений аноном, дискуссии, но судя по тому, как ты с ним разговариваешь, сколько брани, направленной злобы ты на него льёшь, ты сам ни чуть не лучше. И хотя я согласен с тем тезисом, что пишутся учебники для математиков, кто хочет и понимать и заниматься математикой, тогда, если взглянуть и на твоём замечание о ничтожно малом кол-ве математиков от всего кол-ва людей на этой земле, и то, что ты говоришь "нормальные люди понимают математику, учась по этим учебникам", тогда кого ты имеешь в виду? Нормальные это те, кто учится математике, чтобы стать математиком или те, кто не хочет быть математиком, но некоторые математические методы ему требуются для решения его локальных задач, в его науке? Потому что первых - очень мало, как ты заметил, а вторых куда больше, но, вот незадача, им тоже ненужна значительная часть знаний, предоставляемых математикой, отчасти потому что они не могут понять их, или из-за каких-то иных причин, но это не делает их плохими специалистами в своей области, не делает их, как ты говоришь, тупыми, они тоже НОРМАЛЬНЫЕ люди. Или по-твоему они должны быть признаны ненормальными, потому что не поняли (или для них есть проблемы с пониманием) какую-то часть анализа, но вот какой-то другой раздел им дался лучше, и они вполне себе хорошие научные сотрудники. Ты всё еще будешь считать их ненормальными? Потому как, ты уж извини, подавляющее число людей на этой земле вполне здоровые психически и физически, следовательно, нормальные люди, но вот математику они не изучают дальше high school+колледж/университет (какой-то базовый уровень университетской математики и всё, на этом всё, дальше только специализированные мат.методы и разделы, но это куда меньше чем то, что осваивает и должен освоить математик). Причем я взял сразу как людей, изучающих какие-нибудь arts, humanities, social sciences так и людей которые связаны с natural sciences (коме математиков). Многие 1-ой категорий лиц могут тебе сказать, что они либо не понимают математику, либо очень многое не понимают, кроме некоторых методов, которые и используют в своих исследованиях, но они что... тупые? Слишком смелое заявление, правда? И ведь на этой планете куда больше чем самих математиков, их - тех самых нормальных людей.
Может ты и классный математик, может ты просто с математическим умом человек, но общение с тобой - наказание для человека. И ты очень груб и озлоблен, чего кстати, о других анонах из треда я не скажу. Извини, что вмешался в диалог.
>Возвращаться к такому регресс и деградация.
Да неужели, вот тут ты ошибаешься, посмотри на скрины и увидишь что это намного быстрее помогает понять и усвоить информацию чем текстовая писанина.
>>8881
Я в голову им не лазил и мысли не читал.
Вы все ошибаетесь, вы некомпетентные неучи. Я скинул пруфы смотрите, можно приставить математические понятия простым языком и объяснениями. Какой же у вас манямирок сильный что не хотите видеть очевидные вещи.
Квадрипл говорит правду.
Я просто бомбанул из-за того, что он стал наезжать на авторов учебников и называть их тупыми деградантами.
Гет.
Ну я не видел, чтобы кто-нибудь из людей, понимающих, например, общую теорию относительности, утверждал то же что и ты, напротив, они пишут статьи и книги без таких вот картинок. И ты таких людей назвать не можешь. Почему при этом прав должен быть ты?
По такому учебнику я бы учился раз в 10 дольше, чем по нормальному. Как раз как в древние времена. Сколько цветастой хуеты перед глазами и непонятно, где главные идеи. Зато написано, что + это плюс. Ахуеть, спасибо, что потратили моё время.
А где на первой картинке объяснено, что такое число пи? Там просто под ним написано, что вот три значащие цифры, а более точное значение можно посмотреть в калькуляторе. Это по-твоему удовлетворительное объяснение?
Пусть есть число 0,6541651.
Как можно найти целое делимое и делитель, которые при делении дадут частное, равное этому числу?
>>8897
>>8898
Ничего не пойму.
Алгоритм бабушкина:
Алгоритм™ архивации таков: любой файл представляет собой HEX-последовательность символов, переводим этот HEX в DEC, получаем неебически-большое число, дописываем перед этим число 0, — получаем число в диапазоне от 0 до 1 с огромным числом знаков после запятой, а дальше всё просто — подбираем 2 таких целочисленных числа, частное которых даст нам искомое число в диапазоне от 0 до 1 с точностью совпадений до последнего знака. Беда в подборе чисел, которое может идти и 2 часа, а может идти и 2 недели. Есть опытные образцы и работающая программа, и всё это работает.
Пусть:
1. hex = 63D153
2. в dec = 6541651
3. 0 спереди = 0,6541651 (получилось число от 0 до 1).
4. умножить на 10000000 = 6541651 = dec = hex.
5. Получается, делимое 6541651, делитель 1, ну или кратные им числа.
В чём тогда суть архивации?
Делимое = 6541651, делитель = 10000000. И это блядь просто десятичная дробь. Бабушкин поехавший.
>кто-нибудь из людей, понимающих, например, общую теорию относительности, утверждал то же что и ты, напротив, они пишут статьи и книги без таких вот картинок.
Значит они пишут книги не с целю научить, а для таких самых ученых как и они.
>>8893
>По такому учебнику я бы учился раз в 10 дольше, чем по нормальному.
Значит ты тупой, эту книгу как раз писали для детей. Так как логически и доходчиво все объяснено, читать интересно и увлекательно.
Смотри скрин с книги зорича, там нихуя непонятно, про что написано где логическая цепочка и примеры, голова болит чтобы разобрать про что написано и сопоставить для себя логику, уйдет много драгоценного времени, хуета одна, такую книгу может и обезьяна нацарапать на дереве.
>>8894
>А где на первой картинке объяснено, что такое число пи?
>Это по-твоему удовлетворительное объяснение?
Скачай книгу и прочитай.
Усложнять материал нужно маленькими шагами и только постепенно увеличивая сложность, для начала и такого объяснения хватит, не перегружая мозг лишней информацией.
>Скачай книгу и прочитай
Я уже скачивал две книги, в которых как мне утверждали отсутствует теория множеств, а она там есть. Так что давай скрин определения числа пи из этого волшебного учебника.
>Значит они пишут книги не с целю научить, а для таких самых ученых как и они.
Учебники по математике, применяющейся в теории относительно, написаны для студентов.
А ты не иначе как дежуришь тут. Нормальный человек за то время, пока ты тут срёшь, уже осилил бы треть "Теоремы Абеля в задачах и решениях".
>Значит они пишут книги не с целю научить, а для таких самых ученых как и они.
А как они сами изучили теорию относительности?
>Значит ты тупой, эту книгу как раз писали для детей.
Верно, книги для детей должны читать дети. Книги для взрослых взрослые.
Вот ты — интеллектуальный ребёнок и тебе нужны картинки, сам их ты нарисовать не способен.
Как человек с коэффициентом интеллекта 97 сможет написать хороший искусственный интеллект?
>сможет написать хороший искусственный интеллект?
А где твой искусственны интеллект? И толку с того что у тебя IQ чуть больше 97, если ты не можешь его применить.
Ага, главное чтоб тут перестал срать.
Так ведь правда говно.
>А как они сами изучили теорию относительности?
На это влияет много факторов, может им родители нанимали репетиторов которые доходчиво и с картинками им объясняли, или родители тоже были учеными, может когда учились и были студентами собирались группами и расшифровывали учебники.
Да, либо это, либо это ты глупый. Ну, если не ученые единомышленники, то хотя бы просто сторонники твоих идей относительно учебников имеются? Кто эти люди?
А как эти репетиторы и родители-ученые изучили теорию относительности?
>Верно, книги для детей должны читать дети. Книги для взрослых взрослые.
Учебники пишутся с целю НАУЧИТЬ. Книгу которую я скидывал поймет и ребенок и взрослый, книги которые мне рекомендовали, не каждый взрослый поймет.
Взрослому детские книги плохо читать. Много воды, рассказывают не всё и не точно. Скучно, очень долго и некрасиво. Взрослому хочется от такого блевать и он начинает ненавидеть предмет. Это как смотреть телепузиков, когда тебе 25. Очень хочется блевать.
>"ты тупой", "ты дебил", "учебники пишут дураки", хочется знать эти все люди вообще понимают что пишут и являются ли они представителями математического сообщества.
Конкретно картинкоблядь — не математик. Он веб-макака, которая хочет в гейм-дев (как и все ментальные подростки)
Есть задокументированные свидетельства присутствия тут настоящих ученых, но вряд ли они участвуют в этих срачах. Я для развлечения тут. Вкидываю совершенно абсурдные и оскорбительно нелепые сообщения и наслаждаюсь.
Смотри.
Окружность -- множество точек на плоскости, равноудаленных от данной, называемой центром. Расстояние от центра до любой точки окружности называется радиусом. Диаметр -- максимальное расстояние между точками окружности. Пи -- это отношение длины окружности к диаметру.
На усвоение этого уходит одна условная единица времени. Сколько тебе потребуется таких условных единиц, чтобы усвоить приведенный тобой оборот?
Ну тогда многие из веб-дева и геймдев индустрии ментальные подростки, которые, мягко говоря, не дружат с рациональным "само я" и очень засоряют свою технологическую сферу крайне не оптимизированными, дурными решениями. Потому что так оно в сфере IT и происходит. Конкретно тот, о котором ты говоришь, соглашусь, парень немного странноватый и назойливый, но все его посты можно объединить одним вопросом, я думаю, "где есть математика в в нашем, человеческом мире?" В этих вот немного неумелых стараниях в треде он пытается увидеть математическую сущность того, что читает, что пытается изучить, и как-то связать её со своим разумом. Может все эти вопросы от того, что как-то не выработана какая-то научная интуиция, чувство поиска прекрасного и поразительного в явлениях, структурах, системах?
>>8930
А, спасибо, понял. Энтузиаст и шутник?
Ты не ответил на вопрос, ты болен, раз считаешь совковые учебники годными по сравнению с пиндосскими?
Посыл, характеризующийся этой фразой про учебники был впервые упомянут в этом треде двежелезяки-дебилом. Если учитывать контекст, то ее суть в том, что переведенный советским издательством на русский язык анализ Шварца или тот же Зорич хуже ежегодного переиздания пиндосского Томаса или Стеорта. Я так не считаю. Но в совке выходило картафанное говно, да, с этим никто спорить тут не собирается.
>На усвоение этого уходит одна условная единица времени.
Тому кто первый раз это читает нужно раз десять прочитать и время чтобы понять, как минимум 100 единиц времени.
А взгляд на картинку ты сразу воспринимаешь информацию без чтения мгновенно. Займет это 0.01 единиц времени.
То есть получается, ты оцениваешь две строчки в 100 единиц времени, а эти две страницы -- в 0.01 единицы времени. То есть в десять тысяч раз легче? Ты считаешь себя глупым человеком?
>Взрослому детские книги плохо читать. Много воды, рассказывают не всё и не точно.
Именно ту книгу которою я скидывал, там мало воды и все конкретно написано что помогает усвоить и осознать материал.
>Взрослому хочется от такого блевать и он начинает ненавидеть предмет.
Мне 25 лет и мне хочется блевать от книг зорича, шварца и иже сними, и ненавидеть предмет.
Те две строчки не дают ту полноту информации чем те две страницы.
>Ты считаешь себя глупым человеком?
Нет не считаю.
>Мне 25 лет и мне хочется блевать от книг зорича, шварца и иже сними, и ненавидеть предмет.
Это и не удивительно, ты в 25 лет дошел до уровня седьмого класса.
>Мне 25 лет и мне хочется блевать от книг зорича, шварца и иже сними, и ненавидеть предмет.
Всё верно, потому что ты интеллектуальный ребёнок. 5-классник в теле 25-ти летнего жлоба.
>Те две строчки не дают ту полноту информации чем те две страницы.
То есть эти две строчки сложнее более чем в десять тысяч раз? Ведь из них нужно выводить и додумывать всякие вещи, которые понятны только гениальным детям? Так?
Вас (местных дол бой обов) просто жирно троллят. То ли еще веснгой будет - обос трение, все дела.
Это когда два мужика друг друга в жопу ебут.
>В плане математики ты глупый человек?
Математика понятия растяжимое, смотря какая математика, есть области в которых я глупый и незнающий, а есть в которых что то знаю. Зависит от качества пояснений и от сложности самого предмета.
>>8944
>То есть эти две строчки сложнее более чем в десять тысяч раз?
Да, так как взгляд на картинку сразу воспринимаю информацию, а эти строчки еще нужно прочитать, обдумать представить нарисовать на бумаге.
В каких областях математики, выходящих за пределы школьного курса, ты что-то знаешь?
 11 Кб, 619x86
11 Кб, 619x86Такой существенный разрыв в более чем десять тысяч раз может свидетельствовать о проявлении некоторой умственной болезни?
Пиздец, как же я туп. Спасибо.
Ага, а че? Там же просто если эту 2016-производную в ручную считать без ряда Тейлора получится какая-то комбинаторная мишура. Но 812+602+602=2016 и в разложении синуса в ряд тейлора почти все зануляется.
Основы множеств.
Немного знаю, отношения между множествами и операции множеств.
О декартовом произведения имею смутное представления.
Далее идет уже неразбериха.
Не может, так как разная подача информации.
Ты ведь понимаешь, что по сути, ты почти ничего из теории множеств и не знаешь. Даже разбиения на классы эквивалентности не написал.
Яж говорю учебники идут зашифрованные, там хер поймешь о чем они дальше, то что мог расшифровать я уже сказал.
Нужно перечитывать учебники, хотя бы бегло, через долгое время, примерно несколько недель. Прочитал, повтори через неделю две, а потом ещё раз по такой же схеме. Можешь ещё в перерывах между чтением решать задачи для закрепления знаний.
С чего ты взял, что они зашифрованны? Подразумевая такое, получается, что изначально математические знания были в простой форме, понятной семикласснику, а потом злые авторы учебников зашифровали их, чтобы никто кроме них ничего не понял!
А ведь здравая мысль
Объясни мне эти темы максимально заумно по-твоему мнению, чтобы было сложнее в десятки тысяч раз, чем взглянуть на картинку. Вот как в том примере с числом пи, но только максимально заумно. Но при этом хочу напомнить, что в том же Шварце, например, имеются определения всех терминов, в которых формулируются теоремы, они могут казаться тебе непонятными, но они есть. Так что определи максимально непонятно основы множеств, можно начать с определения множества и так далее.
Смотри, если предположить, что изначально математические знания понятны семикласснику, то для шифрования в сложный учебник авторы затратят гораздо больше времени и сил, чем просто печатая, как есть. Поэтому аргумент с ленью отпадает.
Эти знания по умолчанию зашифрованы, это как скульптор высекает из камня скульптуру, только авторы учебников ленятся высекать суть из общего.
Ну на самом деле тут есть что-то логичное, вот скажем я, изучив подробное доказательство какой-нибудь теоремы, пересказываю ее в свой конспект максимально кратко, т.к. писать лень. Получается мало понятно посторонним людям.
Предположим, что это так. Тогда, если бы они были однажды расшифрованны, то не надо было бы каждый раз пасать учебник с зашифрованными знаниями, был бы учебник с расшифрованными, т.к. это принесло бы больше профита. И учебники с зашифрованными знаниями перестали бы существовать.
Опять противоречие с твоими словами.
На расшифровывания более сложных знаний нужно затратить больше усилий, чтобы простые люди поняли, нужно иметь способность к простому объяснению материала и не лениться. Можно подать материал в котором человек ничего не поймет, а можно подать так что все станет понятно с первого раза.
Например, английски учебник по математик и алгебре, там расшифровка знаний 10 из 10, учебник зорича это дно дна, 0 из 10.
Всё сходится. Тебе нравится детский учебник и не нравится взрослый. Следовательно ты ребёнок. Это норма.
Тебе нравятся учебники, где понятно для твоего уровня объясняется материал. Если тебе нравятся детские учебники, значит ты ребёнок.
Простые люди и от логарифмов ноют, им это все не нужно. Им бы лишь сдачу в магазине считать.
>На расшифровывания более сложных знаний нужно затратить больше усилий,
Если знание в учебнике, то значит его кто-то понял и расшифровал, тогда зачем ему писать зашифрованное знание?
Значит, ты неправ и знания никто не шифрует.
>чтобы простые люди поняли, нужно иметь способность к простому объяснению материала и не лениться.
В математику нет царских дорог. Простые люди ленивые, как ты, и вместо чтобы сидеть и разбирать смысл понятий, ты ленишся и ищешь учебник, где всё разжеванно, как для детей. Ты ленивый.
>Можно подать материал в котором человек ничего не поймет, а можно подать так что все станет понятно с первого раза.
Если ты не можешь понять с первого раза вводную часть со множествами, то у тебя не университетский уровень, а школьный, тебе надо пройти школьный материал, чтобы встать на ступень выше. Ну или ты ленивый ребёнок.
>>8991
Гомалогчую.
Записаться в маткружок 15 лет назад, например.
Много читать, думать над прочитанным и решать упражнения. Если что-то непонятно можно погуглить, открыть другой учебник или спросить на каком-нибудь форуме смысл какого-то определения или доказательства.
Только трудом можно достигнуть просветления.
После 1000
Помочь ей завершить процесс. Очевидно же.
Ну лол, то есть мне каждый раз уточнять как оно называется, с чем его едят и подобные вопросы? Я же вроде не роботами разговариваю.
В будущем хочу заняться бизнесом и наукой
Бизнес планирую развивать консалтинговый в области финансов и IT
Научную деятельность хотелось бы связать с компьютерными науками/математикой и их непосредственным применениям в бизнесе.
Встал вопрос с выбором специальности
"прикладная математика" или "финансовая математика"
Что можете посоветовать неопределившейся школоте?
Врачём будешь, инфа 70%
aleph_0 x aleph_k = aleph_k верно для любого кардинала. В том числе и для кардинала <2^aleph0. Что полностью решает.
Докажите это, молю.
Это общий факт. Леммой цорна 4 раза.
Не более чем счётное объединение не более чем счётных множеств не более, чем счётно. Следовательно, если в твоём разбиении не будет множества мощности континуум, его будет можно пересчитать.
идти в ВШЭ на любую специальность.
Ну вот и я о том же.
Есть шестиугольник со стороной "а", с центром диагоналей находящейся в начале координат, при чем одна из диагоналей находится на оси иксов. Найти координаты вершин шестиугольника?
Это понятно, так можно получить координаты вершин шестиугольника с единичной стороной. А что дальше?
Знаешь, как найти гипотенузу, зная катеты?
ну и поверни его.
Инженер колдует с рулеткой и логарифмической линейкой, после чего уверенно объявляет результат: "3,99".
Программист обратился в службу технической поддержки, поставил численный эксперимент на компьютере и доложил: "между 3,98 и 4,02".
Математик посмотрел в потолок, подумал и сказал, что точного ответа он не знает, но зато может доказать, что этот ответ существует.
Логик попросил более точно определить, что такое "дважды два".
Философ полчаса рассуждал о том, что "дважды два" можно понимать совершенно по-разному.
Хакер предложил взломать защиту секретной сети Пентагона и заставить все компьютеры решать эту проблему.
Наконец, бухгалтер сказал: "Закройте все двери и окна, а теперь ответьте - а сколько вы хотите получить?"
Философ порассуждал, примерился, помедитировал, потом махнул рукой, авось повезет и прыгнул. Не повезло.
Физик поднял палец, померил скорость ветра, просчитал несколько вариантов, прыгнул и попал точно в середину бассейна.
Математик построил модель, написал программу, вычислил траекторию полета, построил график разбега. Разбежался, прыгнул и... Стрелой унесся вверх!!! Ошибка в вычислениях, противоположный знак результата!
- Скажите, пожалуйста, где мы сейчас находимся?
Человек на холме долго думает, после чего отвечает:
- На воздушном шаре.
Более пожилой и, следовательно более умудренный опытом воздухоплаватель говорит другому:
- Этот человек на холме - математик.
- Почему же?
- Он долго раздумывал над простым вопросом, после чего дал абсолютно точный и совершенно бесполезный ответ...
Этим математиком был Альберт Галуа-Гротендик.
>Может все эти вопросы от того, что как-то не выработана какая-то научная интуиция, чувство поиска прекрасного и поразительного в явлениях, структурах, системах?
Возможно мой мозг не настолько приспособленный чтобы воспринимать высокий уровень математической абстракции.
>>8982
>Объясни мне эти темы максимально заумно по-твоему мнению
Открой книгу зорича и шварца и увидешь заумное объяснения, без примеров, это все равно что я попытаюсь тебе словами описать как выглядит динозавра, так ты будешь очень долго в голове представлять как он выглядит и то неправильно себе представишь, а взглянувши на картинку ты сразу составишь для себя целостную картину.
>>8993
Охуеная логика, если тебе нравятся игры значит ты ребенок а взрослые дяди в игры не играют они зарабатывают деньги и ебут тян.
 322 Кб, 1362x745
322 Кб, 1362x745Это в Зориче-то всё заумно и без примеров? Там к каждому определению по 10 штук примеров с детальным разжёвыванием каждого. Ты ещё литературы без примеров не читал, я погляжу.
Я не учил в школе шестиугольники и не знаю их свойств.
Предыдущая задачка была на нахождение углов квадрата обе диагонали которого совпадают с осями и проходят через начало координат, и равностороннего треугольника, одна сторона которого на оси иксов с одним углом в начале координат.
Их я решил, для квадрата ответ +/-корень(а^2/2) для треугольника координаты второго угла (а,0) третьего (а/2, корень(а^2-a^2/4))
Летят шерлок холмс и доктор ватсон на воздушном шаре...Унесло их, и не знают, где они сейчас... Пролетают мимо холма, на котором сидит человек и пасет овец. Храбрые воздухоплаватели спрашивают его:
- Скажите, пожалуйста, где мы сейчас находимся?
Человек на холме долго думает, после чего отвечает:
- На воздушном шаре.
Шерлок холмс говорит ватсону
- Этот человек на холме - математик.
- Почему же?
- Он долго раздумывал над простым вопросом, после чего дал абсолютно точный и совершенно бесполезный ответ.
Еще несколько подумав он говорит
- Я точно уверен что мы в России
- Но почему?
- Где еще вы сможете увидеть математика пасущего овец?
Вот теперь правильно.
>Охуеная логика, если тебе нравятся игры значит ты ребенок а взрослые дяди в игры не играют они зарабатывают деньги и ебут тян.
Совсем не так. Если тебя нравятся детские игры, то ты ментальный ребенок. Вот скажем игры про Дашу путешественницу могут вызвать искреннее удовольствие только у человека, который прибывает в состоянии детского мышления или является ребенком. Так же и с учебниками. Если ребенку нравится изучать дифференциальные формы на гладких многообразиях, то он ментальный взрослый.
>Открой книгу зорича и шварца и увидешь заумное объяснения
Я там не увижу твоих заумных объяснений. Поставь себя на место авторов учебников, с чувством собственной важности выплескивающих заумные определения. Начни с множества, объединения и пересечения, например. Представь, что тебе лень разжевывать и выдай все максимально зашифровано.
ну я тебе подсказал гарантированное: через корни из единицы и поворот плоскости. А так вполне вероятно, что надо просто какие-то треугольники другие посчитать.
Веселее будет "скорее всего мы в Дагестане".
А зачем поворачивать, если вершина лежит на абсциссе? И как от единицы перейти к произвольной стороне?
Я не читал далее "шестиугольник", может и не надо никуда поворачивать.
>как от единицы перейти к произвольной стороне
Что будет если корень из единицы умножить на a?
Посмотрел видео этой тематики [Математическая модель и текстовые задачи] и просто прозрел. Что еще можно посмотреть и почитать [кроме этого сайта естественно] дабы так же прозреть? Но учтите, что я сейчас нахожусь в 7 классе по своим знаниям[, а может и ниже, так как сейчас пытаюсь вспомнить пропорции].
Это другой анон, почини свою логику, я раньше скидывал эту ссылку.
Для делания сайтов математика ненужна, неук ты.
Еще есть это https://stepik.org/explore/courses но там похеровей, мало объяснений и сложные задания.
Еще вот это недавно нашел https://allbesta.net/torrent/15022-matematika-7-11-klass.html
Как-то подозрительно куда-то пропал две-железяки-дебил и появился картинко-дебил делающий сайты с iq 97 и уровнем знаний семиклассника. Это один и тот же человек.
Можешь прочитать учебники Алимова 7,8,9, 10-11 класс, там даже множества есть с картинками.
И поэтому ты втыкаешь в учебники по математическому анализу?
Во-первых - это не учебник по теории множеств и математической грамотности, когда ты учишь анализ то предполагается, с исчислением кванторов первого порядка и с базовой теорией множеств. Зорич лишь сделал главу для беглого повторения твоих знаний.
Во-вторых половина ответов на твои вопросы на этой же странице и написана, другая половина была написана раннее. Не очень понятно как ты читал. Я по Зоричу на первом курсе в математику вкатывался, мне было (после некоторых усилий) всё понятно.
В-третьих с таким подходом ты точно вообще ничего не изучишь. Не только в математике. Когда что-то непонятно - то нужно пытаться выяснить - искать доп. материалы, спрашивать, пытаться самому строить примеры; а не сидеть ровно и жаловаться на то, что учебники не заточены специально под тебя.
Ты, к слову, вообще хоть представляешь что значит написать учебник? Понимаешь, что учебник по анализу в себе должен содержать довольно большое количество информации и при этом не должен быть на 3к страниц? Знаешь, что иногда нужно выбирать, на чём нужно акцентировать внимание, а на чём нет (не только из-за объёма, но ещё из-за того, что если акцентировать внимание на всём, читатель просто устанет и не составит для себя никакой big picture)?
Нет не оставляли, да закончил. По математике всегда была оценка 2, от 6 класса и выше.
>>9100
Синтаксис хорошо знаю и умею программировать, но алгоритмы не учил.
Я хотел узнать по какой логике работают графы чтобы не из книг брать готовый программный код, а самому написать, я предположил что лучше изучить теорию графов, чтобы в этом теме без проблем ориентироваться и обрести полное понимания.
>По математике всегда была оценка 2, от 6 класса и выше.
>Синтаксис хорошо знаю и умею программировать, но алгоритмы не учил.
> но алгоритмы не учил.
>умею программировать
О, быдломакака, а вот и ты.
Не везде и не всегда так строго, я живу на Украине и смутно помню только один случай где оставляли на второй год. Хотя были люди которые учились похуже меня, такое предписания нигде не выполняется про которое ты говоришь, и я мог спокойно забивать болт на уроки и уходит не дождавшись окончания всех уроков.
Никаких предпосылок к самостоятельной разработке ии и даже понимания готовых программных кодов я пока у тебя не увидел. Почему бы тебе не копипастить все решения и алгоритмы из хабра и обучающих видео на ютюбе? Ориентироваться ни в чем математическом ты к 25 годам не в состоянии, даже выдавить из себя пару строчек о теории множеств не можешь. Ты же собираешься заниматься геймдевом в свободное от работы время? Или ты мечтаешь о работе в рокстар? Или индиигры для телефончиков?
А после школы чем занимался? 9 классов, пту, офис? Так примерно выглядела твоя жизнь?
>Почему бы тебе не копипастить все решения и алгоритмы из хабра и обучающих видео на ютюбе?
Могу и скопипастить, но как я добьюсь гибкости в разработки без понимания сути происходящего в этих алгоритмов, и я подумал что дискретная математика мне поможет понять.
>Ты же собираешься заниматься геймдевом в свободное от работы время?
Если добюсь понимания этих алгоритмов то может и перейду в геймдев.
>Или ты мечтаешь о работе в рокстар? Или индиигры для телефончиков?
Я не особо фанатичен к деньгам чтобы так сильно напрягаться, чтобы устроится в крупную компанию, мне нужно чтобы хватало на жилье и на хавку, меня интересует удовольствие от процесса разработки, возможно геймдев это то что мне нужно.
>>9107
>А после школы чем занимался? 9 классов, пту, офис? Так примерно выглядела твоя жизнь?
Было пту, но там еще больше напрягали по учебе чем в школе. После учился на программиста, а после немного работал на дому.
То есть тебе отчисли из пту, потом ты пошел на курсы программиста и теперь верстаешь в конструкторе сайтики?
>меня интересует удовольствие от процесса разработки, возможно геймдев это то что мне нужно.
Ты думаешь это такое весёлое дело от которого ты будешь получать удовольствие? Я вот занимался подобным и скажу, что это довольно нудно, особенно вылавливание багов. Если у тебя не хватает сообразительности для того, чтобы осилить определения из Зорича, то как ты будешь выискивать где ошибка? Ты же будешь так сильно тупить и проклинать создателей движка, библиотек и т.д. из-за того, что они не объяснили с примерами, что и как делается. Ты ленивый и не хочешь разбираться с определениями, то можешь даже и не мечтать о создании ИИ, сам же потом забросишь, не трать время.
Я серьезно, организовал бы лучше семинар в своем университете, пересказывали бы там друг другу любимые теоремы. Тут мало чему можно научится.
>То есть тебе отчисли из пту, потом ты пошел на курсы программиста и теперь верстаешь в конструкторе сайтики?
Неоткуда меня не вычисляли, да и сайты я особо не делал, делал парсеры на С# под заказ, а жил на свою инвалидность проблемы со спиною были, хорошо знаю С#, сейчас учу js и node.js, чтобы вкатится в бекенд.
>>9112
>Ты думаешь это такое весёлое дело от которого ты будешь получать удовольствие?
Может будет интересно не знаю.
>Если у тебя не хватает сообразительности для того, чтобы осилить определения из Зорича, то как ты будешь выискивать где ошибка?
Человек существо ситуативное, некоторые области я плохо знаю, некоторые знаю хорошо.
>то можешь даже и не мечтать о создании ИИ
То есть написать ии для ботов, чтобы боты знали как обходить игрока и атаковать, искали оптимальные укрытия и не лезли на рожон. Ты считаешь что это неподъемная задача?
>чтобы боты знали как обходить игрока и атаковать, искали оптимальные укрытия и не лезли на рожон. Ты считаешь что это неподъемная задача?
Это элементарная задача и для этого не нужно даже знать графы и множества, особенно читать все эти ублюдские учебники для задротов. Скачай юнити, братан. Там куча видеоуроков, подробная документация с примерами. Код можно писать на нескольких языках, в том числе и на си шарпе.
Спасибо за совет, попробую unity.
Откуда ты взял корень из единицы?
Там же если считать треугольниками получится что угол на оси иксов находится на расстоянии а и -а соответственно.
Нихуя не понял. Ты из тех, кто слова "зачем" и "почему" путает или это мем какой-то?
Если считать треугольниками, то получается что ответ из предыдущего задания, про треугольник с вершиной в начале координат и стороной на оси, нужно просто взять четыре раза с разными знаками.
Смотри как все должно быть.
Стоит бот. Тут из за угла ГЕЙмер.
Бот должен сперва определить друг перед ним или враг.
Если друг, стоять дальше.
Если враг узнать какой враг.
Узнать какое у него шмотье, увидел ли он бота или нет, как он себя ведет, куда смотрит.
Потом решить стоит атаковать сейчас или отступить, если атаковать то как и откуда, если отступить то куда и как.
А это все решается по опыту. Как бы ты йобко не сделал ии, опыт ты ему не запрограмируешь.
Он тупой даже по меркам треда для начинающих. Сколько ещё человек гнали на авторов учебников, называя их тупыми дегенератами, которые сами ничего не понимают из того, что пишут?
далее находим первообразные корни: (1+-sqrt(3)i)/2, выделяем мнимую и реальную часть, ответ готов.
Этих терминов не существует в природе, что значит считать треугольниками? Что такое расстояние до угла?
и иди посчитай своими треугольниками, например, 17-угольник, сторона которого лежит на одной оси, а одним из углов он касается другой оси.
Смысл? Скрин можно нарисовать в фотошопе.
Объясните по-простому, пожалуйста, почему булеан является множеством всем подмножеств. И какой смысл заложен в его записи типа 2^X. А если X - множество отображений плоскости в себя, то как 2 в его степень возводить?
Слово "булеан" значит "множество всех подмножеств" по определению.
Символом YX обозначается множество всех существующих функций из X в Y. В арифметике кардиналов это действительно соответствует возведению в степень, но это неважно для понимания дальнейшего.
Символом 2 обозначается множество {0,1}, где 0 и 1 - два каких-нибудь неравных объекта. Символом 2X обозначается множество всех существующих функций из X в 2.
Функция из множества X во множество 2 называется характеристической. Между подмножествами X и характеристическими функциями на X есть биекция. Она такова.
Пусть f - какая-нибудь характеристическая функция. Определим множество M как множество всех таких x из X, что f(x) = 1. То есть если f(x) = 1, то мы считаем, что x входит в M. Если f(x)=0, то мы считаем, что x не входит в M. Таким образом, каждой характеристической функции сопоставлено подмножество X. Причем инъективно.
Обратно, пусть M - какое-нибудь подмножество в X. Определим характеристическую функцию f, положив f(x)=1, если x входит в M, и f(x)=0 в противном случае. Таким образом, каждому подмножеству X сопоставлена характеристическая функция. Причем инъективно.
В силу теоремы Кантора-Бернштейна, между множеством всех подмножеств X и множеством всех функций из X в 2 есть биекция. Поэтому-то булеан и обозначается 2X.
При чем тут комплексные числа, если задание дано в декартовых координатах?
>>9135
Считать треугольниками значит упростить шестиугольник до треугольников.
Расстояния от начала координат до угла.
>>9136
Давай мне ты почитаешь координаты углов семнадцатиугольника, покажи что ты не какой то лох-начинающий.
Спасибо за ответ. Суть понял. Но если не трудно, разъясни, пожалуйста, пару моментов.
>Символом 2 обозначается множество {0,1}, где 0 и 1 - два каких-нибудь неравных объекта.
В данном случае что это за объекты? Принадлежность x к M, и не принадлежность?
>Между подмножествами X и характеристическими функциями на X есть биекция.
Биекция - это же 1-1 соответствие, нет? Характеристических функций ведь много, а подмножеств - 2: M и его дополнение в X.
В данном случае это ординалы. 0 - пустое множество, 1 - множество {0}.
Каждой характеристической функции f соответствует одно конкретное подмножество X, а именно {x∈X | f(x)=1}.
Это соответствие биективно.
Спасибо.
spaced repetition, например
Неожиданно неплохой сайт
Минимальный
Возможно стоит попробовать каналы на ютубе.
Автор не тупой, он просто преподавать не умеет.
Попробуй сам рассказать кому то как на велосипеде кататься.
А на каком велосипеде? Цирковой с квадратными колесами? Эт я умею.
Умение ездить на велосипеде - неявное знание по Полани. Рассказать об этом в принципе невозможно.
Мимо-проходил.
Нет. В этом и суть. Неявное знание можно получить только самостоятельно. Окружающие могут только дать совет и надеяться, что он поможет.
Если он умеет держать равновесие, то легко
Потому, что неявное знание неформализуемо и может быть получено только при непосредственном контакте с ним. Так, например, словами нельзя нельзя рассказать как правильно плавать, кататься на велосипеде, невозможно объяснить что такое красный цвет, если человек его никогда не видел. Почитай статьи Майкла Полани. Так-то это одна из основополагающих статей современной теории познания.
Но ведь посмотрев на картинку можно понять как плавать, кататься на велосипеде. Или там видео + картинки + схемы, еще что. Ты можешь стать великим теоретиком по этим делам даже не пытаясь. Или вот, люди могут вызывать эйдетические образы и запускать механизмы прямо перед собой. Еще почему-то мне хочеться приплести к этому синестезию, но это, наверное, не совсем верно.
Глухие люди учаться распознавать красный цвет по звуку, например. Тебе могут сказать, что красный цвет обозначает опасность, кровь и так далее. Ты можешь построить с этим ассоциацию. И прибор будет видеть красный цвет, а передавать тебе звуком.
мимо
Это все не не верно. Зная что нужно делать, кататься на велосипеде ты не научишься. Теория может лишь помочь двигаться в верном направлении, но пока не сформируется мышечная память ничего не выйдет.
Я так и подумал, но для порядку надо было уточнить.
О таком я не слышал, но судя по описанию это - простая замена визуального образа слуховым. Понятия о красном цвете таким образом получить невозможно, слепой человек может только узнать присутствует этот цвет в окружении или нет.
А теперь докажи, что тот гештальт, который формируется у слепого и ассоциируется со звуком, отличается от того, что мы называем "красным цветом".
Не ударяйся в платонизм. Рациональное мышление построено на материалистических началах. В рамках теории научного познания подобные рассуждения неправомочны. Человек рождается без представлений об окружающем мире, соответственно без представлений о красном цвете, и сформироваться эти представления могут только напрямую под влиянием этого цвета и никак иначе. Дальнейшие мудрствования уводят в область идеализма и солипсизма.
Рассмотрим множество A
всех множеств X таких, что X не является элементом X. Будет ли A
принадлежать A? Если A не принадлежит A, то A должно быть своим
элементом. То есть формальным следствием A /∈ A является A ∈ A.
Должен, так как в любом случае он или бреется сам, или не бреется сам и бреется как брадобрей.
Бреет себя -> не должен брить себя (так как брадобрей бреет всех, кто не бреет себя)
Не бреет себя -> должен брить себя (так как браадобрей бреет всех, кто не бреет себя)
Твоё рассуждения не понял. И не очень хочу.
Брадобрей бреет себя либо как тот кто бреет себя сам, либо не бреется сам и бреет себя как брадобрей, который бреет тех кто не бреет себя сам, что тут не понятного?
Ноль функции f, это такая точка x из области определения f, что f(x) = 0.
>Я словно обмазываюсь всеми этими аксиомами, плаваю в мире ощущая полет фантазии и состояние эйфории.
По этому поводу я бы не беспокоился - конечно из твоего описания не до конца ясно, что ты имеешь ввиду, но в целом люди которые любят математику часто испытывают положительные эмоции по её поводу.
>Все ощущения удивительным образом переплелись, я могу слышать увиденное, чувствую запах звука, математика становиться как переплетения цвета у импрессионистов
Я вовсе не психолог, но насколько я могу судить это ненормально. В норме математика воспринимается в визуальных и вербальных терминах. Хотя, насколько я помню из чтения чего-то популярного по психологии, незначительная ассоциация одного вида сенсорных ощущений с другим находится в пределах нормы, но когда этот эффект становится существенным это уже ненормально. Впрочем, ничего не могу сказать, касательно того, может ли это являться симптомом более существенной проблемы или нет.
Попробуй из них
1) Васильев В. А. - Топология для младекурсников
2) Сидней А. Моррис - Топология без слёз
3) В. Г. Болтянский, В. А. Ефремович - Наглядная топология
4) В. В. Прасолов - Наглядная топология
5) Стинрод Н., Чинн У. - Первые понятия топологии
Брадобрей либо бреет себя, либо не бреет себя. Никаких модальных связок вида "бреет себя как тот, кто себя сам", "бреет себя как брадобрей", "бреет как Николай II" в этой задаче не может быть. Когда ты их вводишь - ты решаешь другую задачу.
Зачем ты мне это скидываешь?
Не угадал мудак, это другой анон, я тот.
Пиздеть насчет iq каждый может, пройди тест сняв этот процесс на видео, и сбрось сюда результат, хуеплет.
>Брадобрей бреет всех, кто не бреет самого себя. Должен ли брадобрей брить сам себя?
Да-да, видел такую формулировку этого парадокса. Мне не понятна связь между ними. В терминах множеств для меня это не имеет смысла. Начиная хотя бы с того, как могут быть "все" множества X. X - либо одно множество, либо множеств много и тогда они X1, ..., Xn, а не просто X. И так далее. Вообще для меня такая формулировка - просто набор не связанных семантически слов.
> могут только напрямую под влиянием
Редукционист, ты психическую деятельность мозга к восприятию длин волн сетчаткой глаза не приравнивай, угумс? Начнем с того, что "красный цвет" - понятие настолько абстрактное и размытое, что нет, наверное, даже двух человек, у которых оно сформировалось бы под действием одних и тех же раздражителей. Я даже не заикаюсь про лингвистическую сторону вопроса, я о более простых вещах говорю.
>Редукционист
Лол, значение знаешь?
>нет, наверное, даже двух человек, у которых оно сформировалось бы под действием одних и тех же раздражителей
Почему ты приравниваешь единичную сущность к классу сущностей? Красный цвет в человеческой культуре воспринимается исключительно как класс раздражителей во всем многообразии их подтипов. Ты бы хоть учебник по эпистемологии открыл прежде чем позориться.
А можно ссылку?
Ну у меня в том тесте был результат 140, и это по-моему максимальный результат этого теста. Давай я запарюсь и сниму видео с прохождением для тебя, если ты воспроизведешь действия заумных авторов и распишешь максимально непонятно все, что знаешь про множества, уже который пост тебя прошу. Ты же говорил, что это легче, чем объяснять с примерами и картинками, чего же ты этого не сделаешь?
>рациональное мышление построено на материалистических началах
Рационалист выискался, поглядите. До Полани добрался, но до Фейерабенда ещё нет?
Назвать какую-то процедуру или точку зрения объективной (объективно истинной) — значит утверждать, что она верна независимо от человеческих ожиданий, идей, позиций, желаний. Однако сама идея объективности гораздо старше, чем наука, и не связана с ней. Она появляется тогда, когда какой-то народ, племя или цивилизация отождествляет свой образ жизни с законами мироздания (физическими и нравственными).
Второй идеей, играющей важную роль в защите западной цивилизации, является идея Разума (с большой буквы),
или рациональности. Как и понятие объективности, эта идея имеет материальный и формальный варианты. Быть рациональным в материальном смысле — значит избегать одних идей и признавать другие идеи.
> значение знаешь
То же самое хотел спросить по поводу не к месту вспомненного тобой платонизма.
> Почему ты приравниваешь
Тебе показалось. А еще ты упустил контекст и совершенно не уловил мой поинт. Я даже не знаю, что тут можно сделать; если тебе хочется специальной олимпиады вместо обсуждения - увольте, давай как-нибудь сам.
Условие задачи помечено жёлтым, остальное не надо, данные предоставил и примерное решение аналогичной задачи, очень надеюсь на вашу помощь, если кто-то добрый вдруг возьмётся, прошу, отпишите.
> https://allbesta.net/torrent/15022-matematika-7-11-klass.html
Как это скачать? Скачивается экзешник с амигой.
Это ни разу не матан. Но попытаюсь разобраться (как у вас там назывется каждое из чисел в кружках я не знаю буду называть по позиции).
Значит так.
Обозначения: В левой верхней графе кружечка находится его номер в остальных 3 графах другие данные. Как они у вас называются спросить у согрупников.
I) Составление схемы.
1) Определяем номер который не встречается как последний аргумент в таблице - это начало схемы в данном случае - это номер 1.
2) Слева вверху схемы рисуем первый кружокк. Кружок делим на 4 графы. В левой верхней графе пишем номер 1.
3) В правом нижнем углу схемы рисуем кружок с тем номером который не встречается в таблице в качестве первого аргумента. В данном случае это кружок номер 10. Опять в левой углу кружка пишем его номер т.е. 10.
4) Аналогично рисуем кружки с номерами от 2 до 9. Анон расставляй их широко я не знаю правил расстановки, но думаю что их нет. В левой верхней графе каждого кружка пишем номер кружка.
5) Теперь нужно соединить кружки стрелками. Смотрим таблицу и русуем стрелки:
Т(1,2) означает что нам нужно на схеме провести стрелку от кружка 1 к кружку 2 и написать число 13 над стрелкой. Когда все стрелки нарисованы у нас есть схема для анализа.
II) Анализ схемы "вперед"
1) В кружке 1 пишем три нуля в отставшиеся 3 графы.
2) Идем "волной" с первого кружка по направлению стрелок.
Складываем число на стрелке с числом записанным справа вверху в том кружке откуда стрелка выходит. Получаем числа-кандидаты. Если в кружок заходит одна стрелка - сразу пишем число в графу справа вверху в том кружке куда стрелка зашла. Если в кружок зашло более одной стрелки определям максиамльное из чисел кандидатов и пишем туда же.
3) Повторяем так до тех пор пока не заполним графу во всех кружках.
III) Анализ схемы "назад"
1) В кружке 10 переписываем число из правой верхней графы в правую нижнюю
2) Идем волной против направления стрелок от последнего кружка - кружка 10. Вычитаем из числа записанного справа внизу в том кружке куда стрелка заходит число записанное на стрелке. Это число-кандидат. Если из кружка выходит одна стрелка - сразу пишем число справа внизу. Если из кружка вышло более одной стрелки определям минимальное из чисел и пишем туда же.
3) Повторяем так до тех пор пока не заполним графу во всех кружках.
IV) Определние критического пути и прочей хуеты
1) В каждой кружке вычитаем из нижней правой графы верхнюю правую. И пишем результат в нижнюю левую графу. Кружки с нулевыми значениями этой графы образуют цепочку - критический путь. Ненулевые значения указывают запас.
Это ни разу не матан. Но попытаюсь разобраться (как у вас там назывется каждое из чисел в кружках я не знаю буду называть по позиции).
Значит так.
Обозначения: В левой верхней графе кружечка находится его номер в остальных 3 графах другие данные. Как они у вас называются спросить у согрупников.
I) Составление схемы.
1) Определяем номер который не встречается как последний аргумент в таблице - это начало схемы в данном случае - это номер 1.
2) Слева вверху схемы рисуем первый кружокк. Кружок делим на 4 графы. В левой верхней графе пишем номер 1.
3) В правом нижнем углу схемы рисуем кружок с тем номером который не встречается в таблице в качестве первого аргумента. В данном случае это кружок номер 10. Опять в левой углу кружка пишем его номер т.е. 10.
4) Аналогично рисуем кружки с номерами от 2 до 9. Анон расставляй их широко я не знаю правил расстановки, но думаю что их нет. В левой верхней графе каждого кружка пишем номер кружка.
5) Теперь нужно соединить кружки стрелками. Смотрим таблицу и русуем стрелки:
Т(1,2) означает что нам нужно на схеме провести стрелку от кружка 1 к кружку 2 и написать число 13 над стрелкой. Когда все стрелки нарисованы у нас есть схема для анализа.
II) Анализ схемы "вперед"
1) В кружке 1 пишем три нуля в отставшиеся 3 графы.
2) Идем "волной" с первого кружка по направлению стрелок.
Складываем число на стрелке с числом записанным справа вверху в том кружке откуда стрелка выходит. Получаем числа-кандидаты. Если в кружок заходит одна стрелка - сразу пишем число в графу справа вверху в том кружке куда стрелка зашла. Если в кружок зашло более одной стрелки определям максиамльное из чисел кандидатов и пишем туда же.
3) Повторяем так до тех пор пока не заполним графу во всех кружках.
III) Анализ схемы "назад"
1) В кружке 10 переписываем число из правой верхней графы в правую нижнюю
2) Идем волной против направления стрелок от последнего кружка - кружка 10. Вычитаем из числа записанного справа внизу в том кружке куда стрелка заходит число записанное на стрелке. Это число-кандидат. Если из кружка выходит одна стрелка - сразу пишем число справа внизу. Если из кружка вышло более одной стрелки определям минимальное из чисел и пишем туда же.
3) Повторяем так до тех пор пока не заполним графу во всех кружках.
IV) Определние критического пути и прочей хуеты
1) В каждой кружке вычитаем из нижней правой графы верхнюю правую. И пишем результат в нижнюю левую графу. Кружки с нулевыми значениями этой графы образуют цепочку - критический путь. Ненулевые значения указывают запас.
Дружище, спасибо тебе большое, к сожалению я уже решил, но ты всё равно хорош!
У меня на 7 ссылки не открывает.
Определим формулу P(X) как P(X) ⇔ X ∉ X.
Рассмотрим класс K, определенный как K = {x | P(x)}.
Предположим, что K - множество.
Тогда либо K∈K, либо K∉K.
Предположим, что K∈K. Тогда P(K). Тогда K∉K.
Предположим, что K∉K. Тогда P(K). Тогда K∈K.
В обоих случаях имеем противоречие.
Значит, K не является множеством.
Нужно найти обратную функцию к функции y=х^4+x^2.
В предыдущем задании была линейна функция и она легко прошла, делом то, плюс минус и корень из степени сделать.
А тут я не знаю как быть.
https://www.youtube.com/watch?v=ysGdt9ZLiQQ
Бамп
![47c2cf8605ee9ddd07411bb1ef89a4edbf0e34.pngsrz39339385220.50[...].png](/math/big/thumb/6879/14851783420270s.jpg) 103 Кб, 393x393
103 Кб, 393x393Нагуглил какую-то "ментальную арифметику" и эйдетизм.
Суть в том, что сначала берут устройство типа пикрелейтед под названием абакус. Что-то похожее на счеты. Учат с ними работать.
Потом как-то постепенно перемещают процесс такого счета с реального предмета в ум.
Но я таки не нашел материалов для самостоятельного развития. Да и говорят, мол это лишь детям до 12 лет.
Ну, вот. Заблокировали в гугле.
Ты хочешь сказать, что я фиолетовая стрелка?
Доказывают.
Нет, просто видел там детей, которые складывали большие числа, перебирая пальцами по воображаемым счётам. Выглядело это глупо.
Набор действий чтобы однозначно получить из одних чисел другие.
Обратная когда из других получают одни.
Это скорее понятие алгоритма.
Тривиальный вопрос:
как определяется кольцо целых чисел Z[\sqrt(-1)]?
Ну через эти, всякие категорные конструкции.
Это двумерный модуль над целыми числами - ок.
Но там ещё определено умножение... Вот что-то меня беспокоит... Как определяете?
Кольцо остатков от деления на x^2+1. Всегда ли это кольцо?
Факторкольцо...
Факторизовать можно на идеал, вроде. Значит идеал у нас - это многочлены, делящиеся на x^2+1. Главный идеал, так как умножение многочленов коммутативно. (Я чего-то очень торможу.)
>>9268
Функция это такое подмножество декартового произведения двух множеств AxB, что все a из A встречаются один и только один раз в нём.
Т.е. функция это множество пар (x, f(x)), где f(x) значение функции, которое мы выбрали для данного х. И в этом множестве каждое конкретное х встречается только один раз.
Пусть дана функция f и предположим существование обратной функции g для этой f. Тогда должно выполнятся тождество g(f(x)) = x по определению обратной функции.
Очевидный способ получить обратную функцию из множества пар (x, f(x)) это построить множество пар (f(x), x) (взять кажду пару из определения f и поменять местами компоненты пары). Покажи теперь, что для функции f(x) = x^2 определённой на всех (в т.ч. отрицательных) действительных числах это не сработает. В частности, т.к. нарушится условие уникальности первой компоненты в множестве пар (f(x), x).
Если всё ещё непонятно: заметь, что f(-2) = f(2), чем должно быть ровно g(f(-2)) и g(f(2))? -2 и 2? Но ведь f(-2) = f(2), а значит по определению функции g(f(-2)) = g(f(2)), -2 = 2?!??!??!
Требуется найти параметрическое уравнение кривой получающейся при качения точки на окружности s по S в случае
если s внутри S
если s снаружи S
Поясните как тут нужно действовать. Я могу понять что будет какая то кривая где то между R и R+r|R-r, но я не могу понять как взять синус с косинусом чтобы получить то что требуется.
Если говорить в терминах композиции функций, то g ∘ f = Id, где Id(x) = x. Id в алгебраическом смысле "единица".
С чего стоит начать? C 7 класса общеобразовательной?
>Список от ОП-а, бывшего тут до меня. Был составлен на протяжении 13 тредов, к ознакомлению обязателен.
>>9278
 85 Кб, 1451x799
85 Кб, 1451x799Есть ли в природе обратные интерполяторые? Как они называются? Называются ли они как-то?
>Ну через эти, всякие категорные конструкции.
Честно-говоря не очень понимаю, как с разумными категорными конструкциями может быть ясно, что это двумерный модуль, но не ясно, что это кольцо (скорее вопрос будет о том, как доказать двумерность). Если не вдаваться в излишнюю общность, то я бы определял примерно так. Рассмотрим категорию колец и категорию колец с константой i в которых имеет место тождество i^2=-1. Естественным образом есть забывающий функтор из второй категории в первую P. У него есть левый сопряженный F. Искомое Z[\sqrt(-1)] - это просто P(F(Z)). Притом, кольцом оно будет просто в силу своего определения. Единственное остается вопрос, почему у P есть левый сопряженный, но здесь либо нужно сослаться на общие факты, либо доказать в конкретном случае, например в духе >>9271.
С тем остаточным набором знаний, которые я еще не проебал, я могу надеяться только на какую-нибудь специальность, где придется что-то считать первые пару курсов, знания лишними не будут.
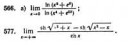 19 Кб, 645x230
19 Кб, 645x230Во втором всё вроде идёт ровно, пока не остаётся дробь с кошинусами в числителе и знаменателе, в которых хуй знает, как доказать, что бесконечности одного порядка.
В тематический тред ступай, брат.
От нас уже успел форум отпочковаться.
В числителе вынести за скобку e^x, в знаменателе e^2x. получится нечто вроде
[1+ln(1+x^2 exp(-x))]/[2 + ln(1 + x^4 exp(-2x)]
Теперь вспомнить, что ln(1+x) ~ x. такие же примеры всегда по одному и тому же шаблону делаются, ну
[1+ln(1+x^2 exp(-x))]/[2 + ln(1 + x^4 exp(-2x)]
простой подстановкой x=0.
То есть нужно не получить правильный ответ, а проебать своё время строго определенным способом. Ничем не отличается от покраски травы, в принципе.
Кафедра матанализа в нашем ВУЗике достаточно консервативная.
Погугли по архивачу. Если коротко: был хорен, потом хорена пидорнули.
в лоб решается производной сложной функции, вместо того, чтобы просто вынести экспоненту и получить ответ. Весьма рационально.
во втором разность синухов можно в произведение преобразовать и дальше по тексту
Ведь по идее мы находим объем тела ограниченного осями, пределами интегрирования и криволинейной поверхностью.
Я сейчас прям конкретно не вспомню, но вот в качестве примера функция хе^y.
Интегрируем по икс, получаем x^2e^y/2, интегрируем по игрек, получаем xe^y.
Вот я и спрашиваю, для нахождения полного интеграла их надо умножить? Или полный интеграл интеграл по икс и по игрек одновременно я выдумал пока читал книжку?
ЧТО ОТ МЕНЯ ТРЕБУЮТ?!!
Доказать, что рациональные числа - упорядоченное поле, в котором аксиома Дедекинда не выполняется.
 18 Кб, 578x270
18 Кб, 578x270Не уверен, что с этим прям сюда.
Но точно не к лингвистам.
По ссылке : http://taweb.aichi-u.ac.jp/tmgross/DG.html , коротко о Dependency grammars и две схемы для наглядности. ,
Я не могу уловить принцип по которому слова в схемах объединены именно так, а не иначе.
Объясните пожалуйста.
Что? Я интересовался анти интерполяцией, которая позволила бы получить обратно этот квадрат который потрачен при обработке. Но не учёл тот факт что в звуке не бывает отдельных квадратов, там слишком много частот, а что делать если они рядом - наверное никто толком и не знает. тут по крайней мере
Так ведь там написано, в чем принцип. Или тебе нужен полный алгоритм синтаксического разбора?
В будущем хочу посвятить себя научной карьере в области математики и информатики.
Но, учиться на очном не могу, нужно как-то зарабатывать на жизнь. Скажите, если сперва отучиться ЗАОЧНО на бакалавра, а уже потом перейти в магистратуру на очное, можно ли таким образом построить профессиональную карьеру в науке? Или обязательно нужно учиться на очном?
Ну я провел аналогию, раз у дифффуров есть такое, то по закону бабкина-няньского и у интегралов должно быть что то такое.
Хорошо, где почитать про кратные интегралы чтобы я понял или ты объясни.
Это невозможно. Через 8 точек можно провести бесконечно много графиков, как и через 10/300/100(500) и никто не дает гарантию что график получившийся даже после 100(500) точек будет в точности повторять исходный.
Поэтому интерполяция Интерполяция(от лат. inter–polis — «разглаженный, подновлённый, обновлённый; преобразованный») так и называется, что может примерно сказать какой график будет.
Сомнительно, что ты сможешь получить хорошее образование, посвящая весь день работе. Но очно учится, конечно, необязательно - по идее, заочно даже лучше, можешь двигаться быстрее.
Што? В вольфрам введи.
Всё, разобрался. Формулу половинного аргумента не проходили ещё, вот и не мог решить.
гельфанд тригонометрия
 69 Кб, 638x741
69 Кб, 638x741Ну вот косяки интерполяции и возникли от того, что интерполировали не непрерывную функцию.
Если тебе нужно убрать эти косяки лишь для того, чтобы получить обратно этот сигнал по типу меандр, то могу предположить, что тебе надо добавлять отсутствующие нечетные гармоники высших порядков
![n5H3ShMXBF0[1].jpg](/math/big/thumb/6879/14853544046070s.jpg) 18 Кб, 947x130
18 Кб, 947x130Объясни настолько сложно, насколько можешь. Меня интересует твое объяснение, сделанное тобой. Меня интересует не объяснение, а твое объяснение твоими словами, сделанное тобой. Ну чтобы ты объяснил. И автором объяснений был ты. И объяснения были сделаны тобой. И то, что ты объяснял, было бы сделанным тобой твое объяснение. Что бы ты объяснял. Твое собственное определение множества, сделанное тобой. Ну там и связанные определения данные тобой в твоем объяснении.
Изи, школьная программа вообще мизерная.
что-то по гомологической алгебре, ротман, вайбель там
можете не расписывать, и можете дать соус из соответствующей литературы
Кормен "Алгоритмы: построение и анализ". Сам изучал по этой книге. Многие курсы и статьи также по этой книге пилятся, это что-то типа стандарта
>раз у дифффуров есть такое
Снова-здорова. Диффуры это уравнения, содержащие производные.
>Хорошо, где почитать про кратные интегралы чтобы я понял
Сначала хорошо всосать, что такое первообразная и определённый интеграл особенно второе.
Книг, таких, чтобы "кратные интегральны for dummies" я не встречал. Единственное хочу сказать, что кратные интегралы охуенно раскрываются с своих приложениях по нахождению квадратур площадей и кубатур объёмов фигур. Попробуй Фихтенгольца 2ой том X главу.
На пальцах, кратные интегралы - это такое дерьмо, когда подынтегральная функция последовательно интегрируется по разным переменным.
Кстати, может тредж для программинг лангуадж энтузиастов и прочих комплюктер сциенсов запилить? Ну типа тоже математика же, хули.
А вроде был в сцы, но можно свой запилить.
То есть,
1^2 = 1
2^2 = 1+3
3^2 = 1+3+5
4^2 = 1+3+5+7
и т.д.
У этого есть какое-нибудь название?
Это всё можно математизировать?
сумма последовательных нечетных чисел. Очень просто выводится, если знаешь просто сумму последовательных чисел (1+2+3...). Также нетрудно заметить это геометрически: пирамидку из кубиков можно всегда перестроить в квадрат.
>Теория типов одна из альтернатив мат. логики в основаниях математики.
Яйцо как альтернатива курице: звучит как бред.
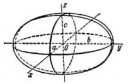 9 Кб, 356x236
9 Кб, 356x236Пытался влоб — не осилил. Ответ вроде интуитивно прост, но не всплывает. Я так понял надо аффинные преобразования курить, чего стоить читануть по этому поводу?
1)Найти угол между a и а-b: 90 (pi/2) градусов. Тут проблем нет.
2)Найти угол между b и a+b, здесь сложности, что это за HEX a+b, как это представить, в чем различие a-b и a+b в данном треугольнике. (0.3333 радиана). Спасибо.
Я дам тебе её координаты, если ты мне поможешь
Забыл добавить, это начало изучения векторов, и решение опирается на тригонометрию и простую алгебру.
Ну производная и интеграл взаимно обратимы, же.
>подынтегральная функция последовательно интегрируется по разным переменным
Это я и так понял по самому тексту.
Короче, такой интеграл можно самому вывести из обычного или нет?
Что вы думайте о статье и о сайте.
Годно ли начать изучение рядов с этого сайта?
надо сделать так (поворотом), чтобы векторы плоскости стали новыми осями. Останется одна неизвестная z.
неясен вопрос. угол между векторами это скалярное произведение векторов делить на произведение модулей. Берешь и считаешь по формулам.
если геометрически, то полезно знать
a-b=a+(-b)
и правило параллелограмма.
В ИТМО когда учился - физика с первого семестра, вместе с лабораторными. В другом ВУЗе, но тоже в примате, был только термех со второго курса. А вообще, такие вопросы скорее в /un.
лоран шварц
Завтра свободен. Жду тебя на Петровско-разумовской, я буду в центре зала с красной розой.
http://dedbotan.com/
Ты охуел тут спамить? Зарепортил
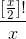 26x39
26x39Да, так и есть. Вопрос в том, что делать, если у меня X больше 1,000,000. Вообще, мне нужно взять синус от этой дроби, умноженной на пи, соответственно целая часть мне не нужна, поэтому я пытаюсь найти формулу в общем виде для дробной части.
Даже не буду спрашивать в каком ты классе. Держи.
ПЕРЕКАТ
https://2ch.hk/math/res/9479.html (
https://2ch.hk/math/res/9479.html (
https://2ch.hk/math/res/9479.html (
Вы видите копию треда, сохраненную 25 декабря 2022 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.







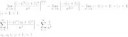


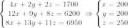

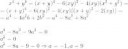



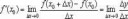
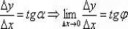
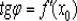



































![6ec[1].jpg](/math/big/thumb/6879/14849202787470s.jpg)



![14851121701010[1].jpg](/math/big/thumb/6879/14851130001890s.jpg)
![14851121701021[1].jpg](/math/big/thumb/6879/14851130001901s.jpg)
![14851121701032[1].jpg](/math/big/thumb/6879/14851130001912s.jpg)
![14851121701073[1].jpg](/math/big/thumb/6879/14851130001973s.jpg)
![103726160largePR20121203140916[1].JPG](/math/big/thumb/6879/14851793004630s.jpg)