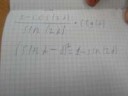Что такое трансфинитные числа?

Натуральные числа - это 0, 1, 2, 3, 4, 5, ... и так далее. Самого большого натурального числа нет. Однако за всеми натуральными числами идёт первое трансфинитное число ω0. С него начинается как бы новый натуральный ряд. ω0+1, ω0+2, ω0+3, ... и так далее. Потом идёт число ω0+ω0, за ним ω0+ω0+1, ω0+ω0+2, ω0+ω0+3, ... и так далее - ещё один натуральный ряд. Этот процесс продолжается неограниченно. За далью даль, за каждым рядом - ещё один такой же ряд.

Дело в том, что каждое число - это множество всех предыдущих чисел. 0 - это пустое множество, 1 - это множество {0}, 2 - это множество {0,1}, 3 - это множество {0,1,2}, и т.д. Так вот, ω0 - это множество всех натуральных чисел, ω0+1 - это множество, содержащее все натуральные числа а также число ω0. А число ω0+ω0 - это множество, содержащее все натуральные числа и все числа вида ω0+n, n - натуральное.

Числа, о которых я говорю, называются "ординалы". Натуральные числа - конечные ординалы, все остальные ординалы - бесконечные. Ординалы, у которых есть предшественники, называются непредельными. Остальные называются предельными. ω-числа - типичные предельные ординалы. Каждый предельный ординал есть не более чем множество предыдущих ординалов.

Каждый ординал - это множество. У множеств есть мощность, поэтому у ординалов она тоже есть. ω0 - счетный ординал, ω0+ω0 и другие подобные тоже являются счетными. Первый несчетный ординал называется ω1, все последующие ординалы также несчетны. Для каждого множества ординалов существует ещё больший ординал. Самого большого ординала нет.

Формально ординалы определяются с помощью конструкции фон Неймана. Её я не приводил. Сказанное выше - просто пояснения.

>>403033

Охуенный анончик из /сци пояснил по хардкору. Вот тебе и статья в вики, епт.

>>9483
В обычной вики да и вообще везде разве не то же самое написано?

>>9484
Конечные порядковые (и кардинальные) числа представляют собой числа натурального ряда: 0, 1, 2, …, поскольку два любых полных упорядочения конечного множества изоморфны с сохранением порядка. Наименьшее бесконечно большое порядковое число ω {\displaystyle \omega } \omega отождествляется с кардинальным числом ℵ 0 {\displaystyle \aleph _{0}} \aleph_0. Однако в случае трансфинитных чисел, больших ω {\displaystyle \omega } \omega , ординалы — по сравнению с кардинальными числами — позволяют выразить более тонкую классификацию множеств, основанную на информации об их упорядоченности. В то время как все счетные множества описываются одним кардинальным числом, равным ℵ 0 {\displaystyle \aleph _{0}} \aleph_0, число счетных ординалов бесконечно велико и притом несчетно:

Почувствуй разницу.

>>9487
Не обязательно читать только первый абзац.

>>9488
Ну так я о том и говорю: текста больше, а смысла столько же. По-моему анончик понятно и простым языком ответил на вопрос, и поэтому охуенен. Если вики поднимут, полюбому надо запилить фак в таком же стиле, не согласен?

Смысла, конечно, тоже больше, если ты не захотел разбираться в терминологии и можешь воспринимать только "рассуждения на пальцах" - то это твои проблемы, но не следует исходя только из этого упрекать какие-то тексты в отсутствии смысла.

По поводу согласен или нет - ничего не скажу, так как считаю эту вики невероятно тупой затеей. Мне очевидно, что качественный педагогический материал могут предоставить только высококвалифицированные математики, а не группа анонимных хуй-пойми-кого с двачей, 95% которых являются, скорее всего, второкурами с какой-нибудь вшэшэчки.

Ищу околоолимпиадного математика для того, чтобы помог мне подготовится к поступлению этим летом в ШАД. Сам 3 курс ВШЭ, минимальный математические знания есть, но без наставника и четкого плана действий, чувствую, что не успею подготовится. Цену обсудим. ДС.
alqZwequarANUSyaIh/ndexPUNCTUMrXC1u

>>9490
Не, ты не понял, я вообще не про это говорю. Я не имею в виду, что вики хуже анончика с двощей или еще что-то в таком духе. Я говорю, что было бы охуенно иметь список вот таких простых, написанных понятным языков ответов на всякие частозадаваемые вопросы, чтобы в шапку этого треда добавить.

Что до вики - ну, блядь. Ты опять перегибаешь палку. Какой еще педагогический материал? Просто сейчас все списки\факи\пасты\смешные картинки и прочее раскиданы по шапкам тредов, а тут они будут в одном месте, и их можно будет удобно редактировать. Ну очевидно же лучше того, что сейчас. Это же не вузовский учебник должен получиться, это такой малюсенький луркмор про /матх. Лично меня беспокоит только ебанутый ленивый админ, который сподобился эту вику поднять.

Алсо, ты говоришь "второкур из вшэ" как будто это что-то плохое. По-моему писание факов и ответов полезно и второкуру из вшэ, и остальным, кто будет потом это читать, так что сплошные профиты.

И вообще, мы дохуя далеко от темы ушли. Создам сам тред про вику, есди хорен продолжит слоупочить.

кто-нибудь читал структуру пространства-времени осипова? можете рецензировать, плис?
знаю, тут есть пацаны из спбгу

>>9495
Он же ёбнутый наглухо

>>9498
а вот с этого момента, пожалуйста, поподробней

Поставили синдром Арнольда-Киари 1. Это может быть оправданием того, что я не знаю и не хочу знать математику?

>>9505
Оправданием перед кем?

>>9506
Перед собой.

>>9479 (OP)
Скидывал в прошлый тред все почти книги из литературы НМУ, а ты даже не добавил.

Подготовка к НМУ
https://yadi.sk/d/PKJKMreqshMQo

НМУ Алгебра
https://yadi.sk/d/8WCKbNCPshN7M

НМУ Анализ
https://yadi.sk/d/WcJwF_kZshN8P

НМУ Геометрия
https://yadi.sk/d/QSflY0WDvyEfA

Красное – мои решения. Есть решения для остального?

>>9509
7-7/7 например.

>>9510
И правда, как же я не догадался то.

>>9509
Еще 4 + 4/sqrt(4).

Это не противоречит правилам, поскольку ты не дописываешь никаких цифр.

>>9509
9 - sqrt(9)*sqrt(9).

>>9512
степени слишком имбово
можно
x - x + x^требуемой

>>9515
Нельзя, в таком случае ты дописываешь число, а если это просто квадратный корень, то все норм.

>>9509
(sqrt(8 + 8/8))!

>>9510
>>9512
>>9514
>>9517
Вот, дорешал, требую свое законное спасибо.

>>9518
Спасибо, вот только девятку я не понял, там же ноль будет.

>>9519
Всегда пожалуйста.

>там же ноль будет

С чего это?
8/8 = 1
8 + 1 = 9
sqrt(9) = 3
3! = 6

>>9519
А, стоп, я тупенький. Забыл в 9-ке еще один корень.

9 - sqrt(sqrt(9)*sqrt(9))

>>9519
Кстати, с пятеркой ты что-то больно мощно выебнулся. 5 + 5/5 же.

>>9523
Я обычно вечером это решаю, простые решения теряю часто.

> 9 - sqrt(sqrt(9)*sqrt(9))

Теперь сошлось, спасибо.

>>9509
((¡)'! + (¡)'! + (¡)'!)!
Для всех i от 0 до 9

>>9528
Думал об этом, но отбросил. Слишком жирно.

>>9479 (OP)

Пикрелейтед - фраза из википедии.

"Аксиома регулярности эквивалентна эпсилон-индукции"

Звучит хорошо! Надо доказать!

В качестве P - выбрал аксиому регулярности.

До которой по номеру закрывающей стрелки распространяется действие квантора "forall y"?
https://en.wikipedia.org/wiki/Epsilon-induction
Я думаю, что до первой закрывающей.Да,конечно это так.

Так вот, подставил, пытаюсь контрапозицию применить, заменяю кванторы на сопряженные (не для всех А <=> для некоторого не А)

И чего-то пока к тавтологии не прийти никак

>>9508
Ты не мне скидывал, опа прошлого треда походу на районе поймали пацаны и заставили решать интегралы, так что мы его потеряли((

Давай если вику так и не поднимут через пару дней, то я перепилю как-нибудь шапку, добавлю туда все и кину репорт, чтоб обновили, вот. Ну или до следующего треда можно подождать.

>>403123

Бампану вопрос сюда

>>9544
Лол, я ещё и кретин

В чем подводные поступать на факультеты прикладной математики/информатики? Куда можно будет пойти работать с этой специальностью?

>>9548
Работать онли программистом, подвох в том, что нужно будет учить тонны ненужной, тупой, антиэстетической хуйни, от которой блевать хочется, вроде "численных методов мат. физики", "мат. моделирования" и ещё каких-то совершенно тупых курсов с претензией на полезность, но на самом деле в которых рассказывается анализ невероятно хуёвого качества.
мимо-кун-прикладной-математик-сто-раз-об-этом-пожалевший

>>9550
Np, bro. Спрашивай ещё, если какие-то конкретные аспекты интересны, мне пока всё равно нехуй делать.

>>9551
Так, а если пойти на прикладную математику И информатику мне пизда?

>>9552
Отличаются они довольно слабо, если посмотреть на список изучаемых дисциплин то там
1) 90% совпадений
2) Невозможно определить, где "и информатика", а где нет.
Ну вообще это от конкретного вузика зависит, конечно, но не сильно.

Вообще, если трезво смотреть, то все специальности в рамках одного факультета довольно слабо отличается, как по фактическому содержанию курсов, так и по дальнейшим перспективам. Не следует фантазировать, будто для "информатиков" подготовлены специальные места в роботостроительных компаниях, а для "програмной инженерии" специальные позиции софтвар девелоперов в Гугле. "Информатик" и "програмный инженер" - вещи тупо взаимозаменяемые. Единственное что, следует идти на самую понтовую специальность чисто ради интеллектуального климата, а вовсе не из-за каких-то секретных талантов специализации, как в каком-нибудь WoWе, которые тебе, якобы, может она предоставить.

>>9553
Хм, ну вроде простому смертному по силам. Еще чаю?

>>9548
>>9549
Двачую этого куна - сам тоже раз 100 жалел, только благодаря железным яйцам получил высшее.

Однако есть те, кому норм, но это именно фапающие на то, что они ИНЖЕНЕРЫ, а не МАТЕМАТИКИ.
Очень разные вещи! Не дай названию "прикладная математика" тебя одурачить - это инженеры.

>>9538
Кст, Начинайкин в Испании живет, вроде в Мадриде (не запомнил точно)

>>9560
А он не гей случаем?

>>9565
Гей.

Отмеченные моменты прокомментируйте пожалуйста, или поподробней как-то сокращение объясните, не могу въехать.

>>9567
sqrt(n)/sqrt(m) = sqrt(n/m)

Посоветуйте справочник по математике школьного уровня. Именно справочник. Пожалуйста.

>>9567
Синее - приведи к общему знаменателю.
Красное - ты наркоман штоле блядь? Вычти четыре из двух нахуй.

И, честно говоря, решал долбоёб: ну ты возьми в числителе и перемножь число за скобочкой и разность в скобочках. Всё сокращается же, дистрибутивность умножения относительно сложения, нет?
И кто нахуй запятыми отделяет десятичную часть?

>>9479 (OP)
Подскажите туториалы или литературу, по прочтению которых, в течении двух недель, можно будет освоить пределы на этапе первого курса университета.

>>9567
Нахуй тебе это нужно, даун? Это не математика.

Пиздец.

Где Горен вообще?

по моему скромному мнению - тут как раз пролегает тонкая грань между искусством и средством для быстрого, простого и эффектного заработка денег...

Тут уже вопрос в лично твоих моральных качествах и, даже больше - в твоём вкусе. Ошибешься - страдания обеспечены. И не стоит приспосабливаться, если этого не требуют твои моральные императивы(мало ли, у родного человека - рак?) Прожить можно и без развлечений, которые дают деньги, зато - по совести и с пользой.

>>9571
В. Е. Епихин - Алгебра и теория пределов

Антош помоги с матаном

>>9571
Курсы по калькулюсу на курсере.

>>9569
Ну так есть же всякие сайты по подготовке к егэ для школьников, матхпрофи или что там еще.

>>9577
Что тебе непонятно? Где застрял? Или иди читай учебник, или расписывай сам, как понимаешь.

>>9580
Вообще не шарю

>>9581
Бро, вот тебе лучший совет, который ты когда-либо уносил с двачей: ты можешь бегать к старосте\тянке\двачам каждый раз, когда у тебя возникает проблема, или ты можешь с их помощью научиться решать такие проблемы. Что будешь делать на следующей сессии, также бегать по форумам? Задачка - школьная хуйня, а понятие ряда Фурье - лёгкое, интересное, и полезное!

Так и не нашел нормального ресурса или справочника по все разделам вузовского вышмата. Либо говно по частям, либо папирусы на 700 листов с охуительными доказательствами

>>9595
Может быть математическая кафедра твоего учебного заведения выпускает какие-нибудь брошюры типа конспектов лекций?

Поцыки, халп. Где этот больной ублюдок использует это чёртово неравенство Бернулли и как? Что вообще происходит в примере 13? Несколько часов уже сука интерферирую над этим дерьмом, пытаясь восстановить ход мысли блядского автора.

>>9601
проебал все материалы спустя 2 года после окончания вуза, теперь пытаюсь судорожно вспоминать по интернету...

>>9604
Ну в смысле, посмотри на знак меньше или равно после слов "покажем, что...убывающая". Там же как раз то самое неравенство с одним лишним множителем. Не обращай внимания на множитель, он с обоих сторон и на неравенство не влияет. Посмотри, вот у тебя слева альфа, а справа - альфа помноженная на эн, видишь эн в числителе?

>>9595
"Вышмат" - довольно расплывчатое понятие. Тебе для чего это надо-то, к каким-то экзаменам готовиться?

>>9607
Я всё равно не понимаю, что он хотел этим всем показать. Зачем он вытащил это дурацкое неравенство? Почему последовательность y_n убывающая? Сама по себе x_n = (1 + 1/n)ⁿ нихуя не убывает же.

>>9608
нет, просто мне бомбануло когда я обмазался основаниями и мат. логикой и я осознал что ничего не знаю

>>9611
y(n) убывает, потому что y(n-1)/y(n) > 1 (что он доказывает на второй страничке). x(n) не убывает, но так как x(n) - это не y(n), то противоречия никакого нету.

>>9611
Он хочет показать, что yn убывает, для этого ему и нужно неравенство Бернулли, затем он показывает, что пределы xn и yn равны.

>>9612
Так зачем для матлогики и оснований тебе справочник по вышмату? Вышмат - это обычно основы анализа, линейки и прочей дискретки для гуманитарных специальностей. Возьми лучше книжки из шапочного списка для начинающих.

>>9613>>9616
Кажется, начинаю немного въезжать. Довольно неожиданно, что простой инкремент показателя степени может так радикально изменить свойства последовательности. Спасибо, что натолкнули на эту мысль, хотя там как бы вычисления перед носом, пусть и не очень прозрачные. Иногда стоит всё-таки верить своим глазам.
Но всё же изуверские выкладки у него.

>>9620
Позже ты сможешь доказать Бернулли гораздо более простым способом (через ряды тейлора).
А убывание функции (1+1/x)^(x+1) ещё более простым (через знак производной).

Зачему нужен анализ последовательностей? Какой самый подробный гайд по классическому анализу или какие вопросы туда должны входить? Нахуя половину книги описывать теорию множеств?

>>9625
Возьми учебник анализа Шварца там теории множеств страничек тридцать. Я бы еще посоветовал знать теорему Кантора-Бернштейна и лемму Цорна.

>>9626
мне кажется я уже поехал. такое чувство, что в универе просто объебали с материалом, но я учился на прикладной

http://www.kokch.kts.ru/math/

А вы сможете пройти тест по математике здесь? Я уже на 4 классе начал валить.

Если кто-то хочет, то может пройти и тест на IQ от них
http://www.aplusclick.com/iqtest.htm У меня говорит, что меньше 100.

Ультрахардкор

Из города A в город B выехали Женя, Коля и Антон с одинаковой скоростью. Через 40% пути Женя поехал не туда, и ему потребовалось x минут, чтобы снова выехать на нужную дорогу, уже в другом месте. До города B ему осталось еще 70% дороги, поэтому дальше он поехал со скоростью в три раза большей начальной. Когда Коля проехал в 6 раз больше, чем ему осталось, у него отвалилось колесо, и он вынужден был остановиться на 15 минут, после чего поехал со скоростью в два раза больше начальной. Чему равно x, если известно, что с Антоном ничего не приключилось и все три мальчика приехали в город В одновременно.

В таблице 10x9 расставлены натуральные числа так, что числа в клетках, имеющих общую сторону или угол, различны. Какое наименьшее значение может принимать сумма чисел во всей таблице?

>>9658
215

Из города A в город B выехали Женя, Коля и Антон с одинаковой скоростью. Через 40% пути Женя поехал не туда, и ему потребовалось x минут, чтобы снова выехать на нужную дорогу, уже в другом месте. До города B ему осталось еще 70% дороги, поэтому дальше он поехал со скоростью в три раза большей начальной. Когда Коля проехал в 6 раз больше, чем ему осталось, у него отвалилось колесо, и он вынужден был остановиться на 15 минут, после чего поехал со скоростью в два раза больше начальной. Чему равно x, если известно, что с Антоном ничего не приключилось и все три мальчика приехали в город В одновременно.

>>9660

>>9662
Ну-с?

>>9663
Тебе не надоело сюда срать, четвероклассник?

>>9664
Извините.

Как взять интеграл от этой хуйни?

Поясните пруф Кантора-Кокоши. Понятно, что a_m меньше или равно b_n. Но какого хуя с будет между a_n и b_n, и как из этого следует, что оно всем множествам последовательности принадлежит?

>>9685

>/math/

>не уметь пользоваться вольфрамом

Мда.

>>9677
Заходишь вот сюда: http://math24.biz/integral
и вбиваешь вот это: sqrt((x-1)/(x+1))1/x

Получишь полноценное решение от начала до конца.

>>9686
Спасибо. Мне не приходилось им пользоваться. Надо мануал почитать будет.

>>9684

>с будет между a_n и b_n

https://ru.wikipedia.org/wiki/Непрерывность_множества_действительных_чисел

>всем множествам последовательности принадлежит

Принадлежит любому = принадлежит всем.

>>9684
По определению, множество вещественных чисел M является отрезком, если существуют два таких числа a и b, что x∈M ⇔ a≤x ∧ x≤b.

В списках вроде не нашёл теорию вероятности и мат. стат. Посоветуйте что почитать.

>>9692
А возможно из них выделить лучшие-понятные для начинающего?

>>9693
Шень/Тюрин - самые азы азов для школоты
Колмогоров/Гнеденко более серьезные
Томас-Рурке-Мостеллер классика
Ну и Ширяева если углубляться

>>9699
а есть че с более современным изложением?

>>9703
В ютубе можешь поискать видеозаписи лекций Михаила Громова.

https://olymp.hse.ru/data/2016/11/30/1112641412/010-011_Математика, Математическая физика.pdf

Задача 3. Кто-нибудь знает чисто линейно-алгебраическое решение? Я смог только через анализ и всякие производные.

>>9686
Как канонiчно сумму Дирихле вбить? Пробовал "n sum n^(s)^-1"

Матаны, посмотрите, пожалуйста, кто-нибудь сможет сказать, какая это книга, автор? Мб кто-то из вас решал. Спасибо

>>9688
Но почему? Я так понял, что ан и бм это фактически константы, а вот ам и бн могут двигаться как угодно между ними. Получается что с это ан, так как в таком случае оно подойдет для всех значений ам и бн включая предельный случай когда ам = ан = бн.

Но в таком случае достаточно взять любой непредельный случай и следующий интервал с ао > ан и тогда с уже не попадет в этот интервал ао бо.

>>9690
Ну чего ты тявкаешь тут, петух? И так это понятно блядь, иди отсюда, даун лысый.

>>9684
да нарисуй ты на листочке r^1. они ВЛОЖЕНЫ

>>9721
предположу что сканави, там тоже нумерация дебильная

>>9708
ну первая идея это сжать эллипсоид

>>9723
забыл прикрепить

>>9726
То что задачу можно свести к следующей: "все эллипсоиды вписанные в единичный куб имеют один и тот же объём" это понятно, но никакого продвижения это не даёт.

>>9479 (OP)
Ребята, вот вы используете логику первого порядка.
А помните ли вы как она определяется или просто вот практикой приучились так мыслить?
Она - загадочная очень вещь! Мне кажется все выучиваются её использовать, без понимания всяких подоплёк с основаниями, верно? (ну, кроме логиков)

Где конкретно про сабж можно почитать на русском(шоб понятнее было)?

Саб матач, помогите решить, с меня нихуя.

>>9754
В учебнике логики?

>>9754

> Она - загадочная очень вещь!

А то. Все что написано на логике первого порядка - потенциально невычислимо. Потому, когда дело доходит до практики, нормальные люди стараются няшиться на уровне пропозиционной логики (которая полна и непротиворечива), или какой-нибудь модальной (где, например, жонглируя модальностями можно выбрать удобный для задачи "порог вычислимости", скажем, добиться того, что даже в худшем случае алгоритм будет рекурсивно перечислим)
Первые две главы Ю.Г. Карпов "теория автоматов". А вообще на инглиш переходи.

>>9756
1-cos(2a)=2sin^2(a)
sin(2a)=2sin(a)cos(a)

>>9763
Пролистал Карпова, там всё достаточно стандартно и по-вузовски. Мне очень понравился Elliott Mendelson, последние главы.

Где читать про "порог вычислимости"? Модальные логики - это красиво, но я пока не видел явно полезного применения, а то, про что ты говоришь звучит интересно.

>>9772
Так это всё та же теория автоматов (теория вычислимости). В двух словах, мы ограничиваем функционал машины тьюринга чтобы избежать проблему остановки.
Например, если лишить машину тьюринга памяти, то это будет конечный автомат, он эквивалентен пропозиционной логике, со всеми её плюсами и минусами. (Например, лишаемся возможности сравнивать). Хочется больше экспрессии, оставаясь в рамках конечной разрешимости? Добро пожаловать в мир бесконтекстной грамматики (он же автомат со стековой памятью). Вот охуительные лекции на эту тему (инглиш) https://www.youtube.com/playlist?list=PLK_sH5jbkYciCyOTllsGyHVcHErHhtnZZ

Про модальную логику все советуют Modal logic for open minds. Ну вот мое мнение, что это гибкий фреймворк для конструирования систем. С теорией автоматов они друг друга отлично дополняют. А если ещё навернуть сверху теорию трансформации графов...

Сап матач поясните пожалуйста почему так скобки раскрываются ?
Что это за хуйня сверху? Это уравнение третьей степени?

Что думаете об учебнике "Ультраматематика"? Недавно обновился, новые главы появились, все дела.

Чтобы быть ТруЪ Демидовича всего прорешать надо ?
Или можно только половину?

>>9780
Один из лучших учебников по математике.

Бля.
>>9779
>>9781

>>9780
80%

>>9777
Подставляешь 1 в числитель и знаменатель, видишь, что 0. Значит, и тот, и другой делится на x-1 в столбик. Если не знаешь, что такое деление многочленов в столбик - загугли.

Заключение

С каждым годом появляются все новые математические технологии, ориентирующиеся на современные процессоры и компьютерные сети. Поэтому ультраматематика – не статичная наука. Она всегда остается на острие развития науки и техники. К тому моменту, как вы прочитаете эту книгу, многое уже устареет. Поэтому ультраматематику нельзя изучить по устаревшим книгам, а надо регулярно мониторить интернет, читать последние статьи на форумах типа Хабра, и особенно полезен собственный опыт, свои наработки в ходе выполнения современных математических проектов.

Читаю я эту ультраматематику. Он сам себе противоречит. То он говорит, что с лишь с помощью компуктера можно решать максимально точно любую задачу, потом, что в ультраматематике можно решать задачу как угодно глупо и приближенно. Всю жизнь обсирал метод деления отрезка пополам и говорил, что люди без расстройств психики его не используют, но что же я вижу?
"Простой пример. Решите уравнение sin x + x = 0,8. Это трансцендентное уравнение, и нет НИКАКОГО аналитического метода точного решения этого уравнения.
Единственный способ аналитически его решить – грубые приближения. Например, можно считать, что х мал, поэтому sin x = x, тогда x + x = 0,8, откуда x = 0,4.
Но при этом допускается ошибка порядка 10 %. Еще есть вариант аналитического решения: можно разложить синус в ряд и ограничиться первыми двумя слагаемыми, тогда уравнение примет вид: x – x3/3! + x = 0,8. Получается кубическое уравнение, которое можно решить аналитически (правда на это уйдет целый вечер). При этом решение тоже будет не точное, ошибка будет порядка 5 %.
То есть аналитические методы в принципе не являются точными. А вот численными методами, например методом деления отрезка пополам, можно решить это уравнение ТОЧНО – с любой необходимой степенью точности – хоть до двадцати значащих цифр. При этом решение производится за очень короткое время: метод деления отрезка пополам программируется за 5 минут, а само уравнение компьютер решает за 0,0001 с. "

>>9788
Пиздец, копируешь из книги, а там табуляции, ёбтваюмать

>>9788

>Решите уравнение sin x + x = 0,8. Это трансцендентное уравнение, и нет НИКАКОГО аналитического метода точного решения этого уравнения.

А его правда нет? В каких-нибудь неэлементарных функциях точно же есть аналитические решение?

http://dxdy.ru/topic41666.html
Вот здесь обсуждают решение (c^x)-x=0 и у этого уравнение есть аналитическое решение. А с sin x + x = 0,8 такое прокатит?

>>9780
нужно прорешать всего хартсхорна.

как доказать что из (a+b)+c = a+(b+c) следует что, в принципе
a1 + a2 + ... an не будет зависеть от расстановки скобок?

>>9794
по индукции же.

>>9777
схема хорнера

Сап, анон. Намедни прочитал одну поистине прекрасную книгу - "Истина и красота. Всемирная история симметрии". Я даже не удивлен, что этой книги нет в ваших гайдах - аннотация книги составлена таким хитровыебанным способом, что понять о чем она, и что она вообще имеет отношение к математике, очень сложно. Я математикой не увлекаюсь, и от книги ждал вовсе не этого. Но дропнуть её не смог. Она прекрасна, мой внутренний гуманитарий пищал от счастья. Серьезно, эта книга маст рид любому гуманитарию, кто хочет ознакомится с математикой. Блять, я наконец-то понял что такое квадратное уравнение и нахуя оно вообще блять нужно!
Собственно, нахуя я это написал. Посоветуйте мне, пожалуйста, подобных книг. Чтобы пояснялась какая-то тема (не так уж и важна какая), но чтоб осмысленно, чтоб было понятно для чего это нужно, а не какая-то абстрактная хуйня уровня "а+б дает с, ясно? м?"

>>9788

> ограничиться первыми двумя слагаемыми

Пиздец, а первые двадцать им религия запрещает взять?

>>9811

> я наконец-то понял что такое квадратное уравнения

Лол, в голосину.

> Посоветуйте

"Гедель, эшер, бах"

>>9832

>"Гедель, эшер, бах"

Двачую. Ещё "Путь к реальности" Пенроуза

Помогите аутисту решить задачу. "Грузы связаны нитью, перекинутой через невесомый блок. Груз массой 2 кг находится на наклонной плоскости, образующей угол 45 градусов с горизонтом. Коэффициент трения между грузом и плоскостью равен 0.15. При какой максимальной массе вертикально висящего груза он будет подниматься вверх?".
Понимаю, что нужно вводить ось и прописывать проекции и как-то использовать синус 45, но в моей школе мы такое еще не проходили, хотя задача моего класса. Вроде не слишком трудно, но не могу понять с чего начать. Помогите, с меня как обычно. Алсо, подскажите сайтов и учебников по этой тематике, как научится решать такие задачи, ну где проекции сил, синусы, коэффициент трения.

>>9861
Пикрил, кстати, к задаче

Аноны, помогите разобраться как считается D-итое в квадрате.
для конкретного примера
X это массив из трех чисел [1,2,3]
X1 это массив из трех чисел [4,5,6]

Матемач помоги решить , A B C D каждая послед цифра больше на +1 а X такие же цифры но в разброс как найти A B C D

>>9861
Сила действующая на груз 2х9.8=19.6 ньютон. Реакция опоры равна 19.6 умножить на синус 45, 19.6хкорень2/2.
Трение равно .15 значит нужно умножить 19.6х(корень2/2)х0.15=2.94х(корень2/2).
Вес при котором груз будет двигаться равен 2.94х(корень2/2)/9.8

Аноны, вопрос не расистский а сугубо математический.
Эта агитка борцов с расистами была высмеяна и интерпретирована как "50% белых умнее чем 80% черных".
Чет не могу понять, это уничижительно звучит для негров с тз цифр или нет. Можно еще сказать "50% белых не умнее чем 80% черных". Следует ли из всех этих высказываний что "белые умнее чем черные"? Нужно ли знать общее число тех и других? Если че, в США белых 64% а черных 12%
Рассмотрю только серьезные математические ответы без мемасиков.

t. негр стремящийся к знаниям

>>9991
платиново тупой вопрос
из пикчи действительно следует, что остальные 80% негров ⩽ половины белых
общее количество роли не играет

>>9999
Вообще-то не следует. Остальные 80% могут иметь в среднем такой же уровень интеллекта, как и остальные 50% белых. А 20% черных умнее другой половины белых. То есть черные в целом будут умнее, но нажо смотреть на общее количество, чтобы увидеть кто выиграл по абсолютной величине.

>>9999

> 80% негров ⩽ половины белых

и что? и что блядь? я спрашиваю, следует ли из этого утверждения, что в целом черные тупее белых, или нет.

32% от общего населения одновременно белы и тупы, а 2.4% от общего населения черны и умны. Это хорошо или плохо? Решай сам.

>>10014

>хорошо или плохо

>раздел математики

И сразу с разбегу выйграл, сделал моё утро

>>9479 (OP)
Помню тут как то обсуждались всякие препараты чтобы достичь производительности в несколько гротендиков/день.
Что это были за препараты?

не понимаю пикрелейтед.

так как Hom({},{1}) = {{}} и Hom({},{2}), то их пересечение непустое. но это не значит, что в обоих множествах есть одна и та же функция, верно?

хотя если определять функции, например, так f = (график функции, domain, codomain), то все получается правильно.

>>10031
Амфик

>>10032
Функции обязательно определяются как тройки.

>>10032

>их пересечение непустое

Пустое

>если определять функции, например, так

А как ещё определять?

Ответьте кому не впадлу, посоны (тут, там, мне похуй в целом)

https://www.reddit.com/r/mathematics/comments/5rlzcx/please_tell_me_where_can_i_find_answers_to_this/

>>10037
угу, ясно
>>10038
я думал так

>>10031
легальный вариант - какой-нибудь ноотроп, по типу фенибута
почитай статью на лурке

>>10039
Дополню на всякий похуй
Дополню на всякий случай. Это типа продолжение ХУУУЙ знает когда заданного вопроса про построение метасистемы для каждого иррационального уравнения не могу его даже тут нагуглить. (а я нихуя не математик, если чо, но вот приходится изучать, а тут такой пиздец, сразу какой-то косяк идёт в самом начале. Софисты, как известно - идут нахуй. А я философ, и чо? И как мне их тут послать нахуй?)

>>10044

>иррационального

Парадоксального (не знаю есть ли разница)

>>10043
Не стоит тратить на такое время

>>10043
Удваиваю >>10043, это недоказательная хуйня. Из рабочих - только люди с альцгеймером, но они, блядь, больны. А так можешь попробовать мемантин (вроде бы частичный антагонист NMDAR, вроде глика/кетамина/PCP, только легально). Ноотропы -- хуйня.

>>10040

>я думал так

Denoted, а не defined же.

Здравствуйте, уважаемые форумчане. Нет ли, случаем, у кого
A. K. Cline, C. B. Moler, G. W. Stewart and J. H. Wilkinson "An Estimate for the Condition Number of a Matrix", SIAM Journal on Numerical Analysis
Vol. 16, No. 2 (Apr., 1979), pp. 368-375?

>>10051
лови
http://rgho.st/7HG7m7bVf

>>10043
>>10049
НЕ, там был обстоятельный пост, со всякими витаминами, глизином каким то, т.д.

И что, фенибут мне в аптеке не достать?

Как это получилось или какие формулы нужно использовать для результата?

>>10077
внизу квадрат разности разложить и все.

>>10039
Стыдно за тебя.

>>10105
По делу блядь ответь, ну ёбаный стыд. Стыдно ему блядь

>>10105
Ткни в википедию и я отъебусь. Я никого из себя не строю, уёбище. Как вы заебали уже, я вообще охуеваю.

>>10105
Мне стыдно в одной стране с таким людьми находиться, где им стыдно блядь, где я пидор, где ещё какая-то срань, кто по делу отвечать будет, кто делать будет-то вообще? Я спрашивал твоё мнение стыдно тебе или нет? Я спрашивал как ты поебал мою мамку? Нет, вы всё сообщите, что не спрашивал, что спрашивал - похуй. Главное не вникать и нихуя не делать.

Объясните ньюфагу. В геометрии есть условные знаки принадлежности, пересечения и т.д. Это же действия над множествами? Получается, что геометрические фигуры - это множества?
Глупость сказал, да?

>>10129
Да, множества точек, удовлетворяющих уравнению.

>>10129
Да, действия над множествами. Геометрическая фигура - множество точек.

>>10140
Спасибо.

>>10145
И тебе спасибо. Получается, что и плоскость имеет уравнение. Пойду дальше разбираться.

>>10148
В пространствах размерности больше двух - конечно имеет.

>>10119
Ебать у тебя бомбануло, лол. На что тебя в википедию тыкать? Твои вопросы показывают отсутствие малейшего понимания того, какой должен быть ход мысли. Википедией тут не отделаешься, нужно просто брать и заниматься, начиная со школьного курса. А конкретно на твои вопросы тебе на реддите ответили первым же постом.

Есть уравнение (1). Есть уравнение (2), являющееся частным случаем (1). Есть утверждение A, делающееся относительно этих уравнений (например, относительно их решений).

(1) <= (2)

Правильно?

A(1) => A(2)

Правильно?

>>10119
У тебя iq 97? Опять выходишь на связь?

>>10140
Напиши мне уравнение треугольника с вершинами (x1,y1), (x2,y2), (x3,y3).

>>10172
Возьми и напиши сам, ты чего?

>>10174
Треугольник фигура? Фигура. Фигуру можно задать уравнением. Напиши мне его.

>>10175
Вы параметрические уравнения прямой не проходили еще, или что?

>>10176
Просто напиши уравнение треугольника с заданными вершинами.

>>10177
Сперва скажи "пожалуйста".

>>10177
Вот скажем три вершины A=(xa, ya), B=(xb, yb), C=(xc, yc).
Треугольник с такими вершинами задается точками X=aA+bB+c*C, где коэффициенты a,b,c принимают значения от 0 до 1 и их сумма a+b+c равна 1.

>>10014
я же не про хорошо или плохо спрашивал.
есть две группы А и Б. 20% из Б умнее 50% из A. Следует ли из этого что группа А в целом умнее? Или недостаточно информации?

>>9479 (OP)
Изучаю пределы и то как их решать.
Так как я туповатый то я соотвественно не могу решить все пределы, мне нужно пояснение как их решать.
Заебывать всех в ИТТ не хочу, а учителя под ругой у меня нет.

Потому посоветуйте какой то сборник задач где есть решения с пояснением как это решалось. Я буду смотреть в ответы после того как не смогу решить сам.
Алсо я буду рад если предложите какую то другую методику самообучения.
Демидовича не предлагать, хуй найдешь на него ответы.

>>10192
schaums?

>>10192

>Демидовича не предлагать, хуй найдешь на него ответы.

Ты туповатый? Гугли "антидемидович". Там и ответы, и решения.

>>10197
Честно написал что я туповатый.
Антидемидович похоже больше на какое то справочное пособие, но спасибо.

Господа, нужна помощь. Теория чисел. Задача такая, требуется найти НОД двух чисел в квадратичном поле Q(sqrt(17))
Применяю обычный алгоритм Евклида с округлением до целых, но в один прекрасный момент он зацикливается. Что я делаю не так?

>>10165
Эй, ну что же вы, математики, молчите...

Почему интеграл называется интегралом?
Он, видимо, что-то интегрирует. А что значит "интегрировать"? Откуда это слово взялось и что оно обозначает, и почему именно оно?
На вики ничего нет

>>10191
Тебе же написали все >>10005 >>10014 что тебе еще неясно

>>10211
от частных к целому. Куча маленьких частей обобщается в интеграл.

>>10165
Что именно ты понимаешь под (1) <= (2) и "уравнение является частным случаем другого"

>>10165
Судя по постановке задачи:
1 => 2, 2 => 1, значит 1 = 2.
Поэтому A(1) = A(2), а значит A(1) => A(2)

>>10220
А интегральная схема - это тоже обобщённые маленькие части?

>>10227
да, все на одном кристалле.

Анон, поясни за дескриптивную теорию множеств. Что в ней происходит?

>>10098
А дальше? У меня не получается сократить к тому, что на картинке.

>>10253
скобки раскрыть не выходит?

>>10258

2ab-4b-a^2+2ab-8ab+2ab+4b
_________________________ =
(a-2b)(a+2b)

-a^2-2ab
=__________
(a-2b)(a+2b)

>>10262
верхняя часть это -a(a+2b).

>>10263
Спасибо!

Создана ли внятная логика для оперирования временем, временными отношениями и так далее?

>>10270
Тоже интересно

Анон помоги советом.
Во время учебы или подготовки какой-либо дисциплины, для себя или для сдачи сессии - неважно, довожу себя до задроченного состояния, когда начинает болеть голова, потеть руки и ноги от зубрежки. Причем инфу достаточно средне запоминаю, просто как ебанутый загон. После того как все сдам, прихожу в себя неделю и хожу как олух туплю.
Как перестать нервничать и нормально готовиться? Как перестать съедать свою психику из-за всякой хуйни? Это же говно, вот так себя дрочить: эффективность-то к нулю стремится...

>>10270
Что такое "оперирование временем" и "временные отношения"?
Для чего, по-твоему, уже создана внятная логика?

>>10281
Есть обычная логика. Есть нечеткая логика как аналог обычной, только про НЕУВЕРЕННОСТЬ. Есть линейная как аналог обычной только про РЕСУРСЫ. Тот анон, видимо, спрашивает про что-то аналогичное, что можно интерпретировать в духе "аналог обычной, только про ИЗМЕНЧИВОСТЬ".

>>10270
Я погуглил за тебя и нашел "темпоральная логика".

>>10280
Модафинил
В Рашке запрещён
В цивилизованном мире - нет

>>10280
Попробуй фенибут (ноотроп, обладающий седативным действием), ибо модафинил в России не достать и не факт, что тебе нужно именно такое воздействие.

https://www.youtube.com/watch?v=lyZQPjUT5B4 вот сортировка пузырьком, которая объясняется с помощью танцев. Что, вообще, есть такого для математики дабы задействовало и правое полушарие, в том числе?

>>10287
Ээээ, осторожней с этим фенибутом. Он не такой-то и седативный. И на разных людей может действовать оооочень по-разному. Мозги не сожжешь себе, конечно, и страшного ничего не случится, но далеко не факт, что результат будет как ожидается.

>>10292
Многие ноотропы действуют на разных людей по-разному. Тот же фенотропил некоторых усыпляет. Да даже амфетамин на некоторых людей действует усыпляюще. Осторожнее надо быть со всем.

Понимаю, что это физика, но мне больше некуда идти. Как решить эти задачи и научиться решать подобные? Помогите

1. "Найти сопротивление между точками А и B. Сопротивление каждого резистора равно 120 Ом." Пикрил 1

2. "Найти сопротивление между точками А и B. Сопротивление каждого резистора равно 15 Ом." Пикрил 2

Помогите, ЯННП.

Сап котаны, я к вам из /spc/. Есть у нас такая формула, формула Циолковского, достаточно серьезная хуета, для очень серьезных расчетов, но крайне элегантная как некоторые физмат формулы и короткая. И глядя на неё у меня появился вопрос, почему так много в нашем мире завязанно на е и на натуральный логарифм? Золотое сечение там, фракталы, хуе-мое. Почему такие уникальные числа как е и пи, являют собой бесконечные непериодические дроби? Неужели десятиричная система была ошикой и работая с системой по основанию не 10, а 2.7 мир был бы намного понятнее?

>>10303
/ra/ и /sci/

Ну или например множество Мандельброта, это пиздос же, я козявки из носа длинне достаю, чем запись этой формулы, а она описывает бесконечный мир. Ваще охуеть короче. Странно, что у вас нет треда по математической философии. Надеюсь хоть на часть вопросов усшать ответы.

Суп матанач, я тут впервые. За плечами школа, шарага и заочка института. Восхищён возможностями математики и хочу просто немного подковать себя в этой дисциплине, но в исключительно прикладном аспекте.
Считаю самой большой проблемой учителей\преподавателей, что они не объясняют природу происходящего в математических уравнениях и законах на физических примерах, как это было в первые классы "У Васи одно яблоко, у Пети два...", в итоге из-за этого так все вайнять на интегралы и дифференциалы "зачем они нам нужны, не пригодятся в жизни...", в итоге только недавно узнал на примере как выглядит дифференциал и интеграл, и это было охуенно, как когда узнаешь что-то новое. Вот, есть ли такая литература для даунов, которая может не только показывать формулы и говорить в каких случаях ими надо считать, но и хотя бы намекнёт, что за процессы какого рода происходят в конкретной функции.
Учусь на автоматизацию, поэтому сейчас строим всякие частотные характеристики, но я даже понятия не имею как называется этот раздел математики, хотел бы тоже немного поднатореть, в будущем планирую (точнее уже начал) в программирование, хочу чтобы знания полученные не были бесполезными.

Получаю истинный экстаз, когда понимаю как что-то работает, вот матрица, например, для меня являлась набором цифр, захуй они нужны? Откуда эти цифры берутся и куда деваются? Мне может и было интересно, но ответ я понял случайно, когда преподавали ТАУ в колледже и рассматривали систему на устойчивость.
Т.е. матрица если проецировать на рассчитываемую систему автоматического управления это совокупность всех измеряемых величин, всех возможных вариантов их взаимодейсвтия и на выходе получается некая величина характеризующая выходной сигнал. Т.е. своего рода предсказание возможного будущего? Поправьте меня.

В общем такие маленькие открытия доставляют мне массу удовольствия, это реально круто. Вот хотелось бы почитать что-нибудь эдакое.

>>10306

>Странно, что у вас нет треда по математической философии.

Не нужно, потому что каждый тред в неё скатывается.

Поясните за двоично-десятичную систему счисления. И эт, это можно типа "изобрести" в качестве троллейбуса из буханки хлеба любую систему счисления, типа "троично-десятичная", "128-ричная-десятичная" и тд?
Я не говорю о их практичном применении. Двоично-десятичная может хоть в калькуляторах использоваться.

>>10312
Шумеры изпользовали 60-ти ричноую. А римляне вообще безсистемную.

>>10304
Бампец

>>10304
Как ты сделаешь систему счисления с дробным основанием?

>>10316
Никак, потому что два числа могут математически обозначать одно и то же.

1/7 и 2/14, например.

>>10304
Функции экспоненцирования и логарифмирования ничем принципиально не отличаются от других функций, вроде умножения и сложения. Почему тебя не удивляет, что почти во всех физических формулах используется операция умножения?

Это не особенность мира, а особенность используемого нами набора инструментов. У нас есть набор функций, с помощью этого набора мы описываем мир. Никакой мистики. Какой молоток есть, таким гвозди и забиваем.

Многим кажется, что раз периодическая бесконечная дробь, то есть какая-то нестрогость. Это заблуждение. Бесконечная непериодическая дробь не является чем-то плохим. Вещественные числа в принципе не являются десятичными дробями - просто из вещественных чисел в десятичные дроби есть каноническая инъекция. И число пи, и число e определены вполне точно, и у математиков не возникает никаких проблем при работе с ними.

В системе счисления, основание которой - иррациональное число, есть свои подводные камни. Например, в большинстве случаев обычные целые числа должны в такой системе записываться бесконечными дробями. Есть, впрочем, системы вроде https://habrahabr.ru/post/302178/ , но они неудобны для практических нужд.

>>10316
Это нетрудно. Более того, основанием системы счисления может быть даже комплексное число.

>>10310
Попробуй лекции В. Босса (настоящая фамилия Опойцев). Это сотрудник Академии наук, физико-математический доктор.

>>10312
ты охуеешь когда узнаешь что есть системы счисления с отрицательным основанием.
Называется нега позиционная система счисления.

>>9797
Спасибо, но как узнать на какой многочлен нужно делить?

>>10310
В английский можешь?

>>10318
Спасибо, пояснил аки бог

другой анон

>>10304
На самом деле, >>10318 - анон, конечно, много полезного сказал, но на вопрос не ответил. По крайней мере, мне бы его ответ не помог в школе\университете (но я медленный).

Ответ копается из следующего сооюражения - логарифм и экспонента (основание не важно, просто вылезут коэффициенты) естественным образом возникают, когда мы изучаем скорость изменения чего-либо. А скорость изменения мы изучаем в 99% случаев, от цены опционов в экономике и роста популяции в биологии до передачи тепла в физике и абстрактных производных Ли в математике.

Мне кажется, ключ к начальному пониманию - определение числа е через предел и интерпретации в терминах выплат %% или роста популции какой-нибудь бактерии. Более глубокое понимание приходит из дифгеомерии, дифуров, абстрактной алгебры.

>>10331 отклеилось
Допустим, я знаю математику с первого по 11 класс школьный. Что надо изучить чтобы понять пикрилейтеды?

>>10332
КраКурВышМат.

Нужны тесты по начальной математики (10-11 класс), именно в электронном варианте.

>>10334
Пиздуй в /un.

>>10329
>>10318
Спачибо, котики.
>>10318

>У нас есть набор функций, с помощью этого набора мы описываем мир.

То есть даже наше абсолютно строгое математическое описание мира не является полностью правильным?

>>10336
Я считаю что да. Ведь абсолютно везде есть погрешности

>>10336
Есть философский подход, который называется "карта и местность". Согласно этому подходу, научные теории описывают реальность так же, как карты описывают местность. Наука занимается построением всё более полезных, интересных карт. Притом ценность имеют лишь неточные карты, никто не стремится построить карту, которая была бы абсолютно точной.

>Льюис Кэрролл в «Сильви и Бруно» (1889) даёт юмористическое описание вымышленной карты, у которой «масштаб миля к миле». Персонаж в произведении описывает некоторые практические сложности при использовании подобной карты и заключает, что «теперь мы используем саму страну в качестве её собственной карты, и я уверяю вас, она столь же хороша».

Абсолютно точной картой реальности является лишь сама реальность. Все созданные человеком научные теории обязаны быть неточными картами. Научный прогресс - это непрекращающееся улучшение имеющихся карт. Новые карты не обязательно точнее - они просто лучше.

https://ru.wikipedia.org/wiki/Соотношение_карты_и_территории

>>9479 (OP)
Хочу понимать теорию динамических систем, теорию хаоса и околообласти. Что нужно понимать, чтобы можно было приступать к изучению данных разделов? Есть вышка технарская мухгу, общий предмет был высшая математика, там основ по чуть-чуть было от анализа, вероятности , линала, ну основы самые.

>>10347
http://ium.mccme.ru/f16/f16-analiz1.html
http://ium.mccme.ru/f16/f16-algebra-1.html
http://ium.mccme.ru/s16/topology1.html
Для начала попробуй прорешать листочки для первокурсников.

Где я накосячил?

https://stepik.org/lesson/Предел-последовательности-9519/step/6

Отсюда

>>10352
В самом верху где -(2n+4), когда переносишь хуйню в общий знаменатель проебываешь минус у четверки.

Почитываю тут Алгебру Шеня и внезапно нагрянуло 76.
В чем суть? Это метафора? Проверка на внимательность? Не понимаю.

есть 12 точек на окружности. сколько треугольников можно составить с вершинами в этих точках?
правилен ли пикрил?

Есть ли смысл читать Эвклида, Аль-Хорезми и прочих весьма древних авторов?

>>10355
Спасибо анон за то что ты существуешь, отсосал бы тебе.

>>10360
да

>>10359
(a+b)^2 и a^2+b^2. Сумма квадрата и квадрат суммы. Сын отца и отец сына.

>>10361
Евклида стоит, он вполне актуален.
http://jemmybutton.livejournal.com/8502.html

остальных, только если интересуешься историей того или иного предмета.

Как такую задачу решать? Какой закон применить?

Тесты по темам: Основы молекулярно-кинетической теории; Температура. Энергия теплового движения.
Нужны формулы к каждой задаче, название формул и обозначения.

>>10367
Не понимаю.

>>10332
Савельева.

>>10372
пусть sq - функция "квадрата", а sum - функция суммы, определенные как
sum(a,b,...,x)=a+b+....+x; т.е. sum(a,b)=a+b
sq(a)=a^2
Тогда квадрат суммы это sq(sum(a,b))=sq(a+b)=(a+b)^2
а сумма квадратов это sum(sq(a),sq(b))=sum(a^2,b^2)=a^2+b^2.

Теперь пусть father() функция отца, а son() функция сына... Тогда father(son(a)) это отец сына а, т.е. дедушка а, а son(father(a)) это сын отца а, т.е. либо а, либо его брат.

>>10374
Так сын отца и отец сына это одно и тоже или нет?

И зачем это там нужно?

>>10376
Не, ну ты непробиваемый даун, сорян. Похоже алгебра это не твое.

>>10379
Я таки не могу понять какая связь между этой задачей и алгеброй, конкретно даже теми формулами. С бытовой точки зрения это как-то слишком очевидно, но тут это может значит не пойми что.

Маша в день рождения напекла пирожков. В гости пришли два привидения, три поросёнка и волк. Поросята съели по пирожку, волк — съел поросят, и стал приставать к привидениям. Приехала полиция и доела 25 оставшихся пирожков. Сколько пирожков было вначале?

>>10387
28

>>10319
Лекции видео или сборник лекций?
>>10325
Могу, но научный язык боюсь будет даваться тяжело. Не тот уровень.

>>10319
Ну да не важно, домой попаду загуглю.

Так а построение графиков частотных характеристик это какая область математики? Анализ?

>>10389
Книги, их шестнадцать штук. Большую часть написали литературные негры из молодых ученых.

>>10389
Ну так-то технический английский наоборот проще публицистического\разговорного\литературного же