Двач.hk прислал битые данные.
Вы видите копию треда, сохраненную 2 января 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Вы видите копию треда, сохраненную 2 января 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

65 Кб, 547x493
Начну с себя,
Билли Бонс положил в сундук некоторое количество золотых монет. На второй год он вынул из сундука сколько-то монет. Начиная с третьего года, он добавлял столько монет, сколько было в сундуке два года назад.
Требуется написать программу, которая определит, сколько монет было в сундуке в первый и во второй года, если в X-м году там оказалось ровно Y монет.
Входные данные
Входной файл содержит натуральные числа X и Y (3 ≤ X≤20, 1≤Y≤32767).
Выходные данные
В выходной файл выведите через пробел количество монет в первый и второй года. Гарантируется, что решение задачи всегда существует.
Как ее решить?В душе не чаю.
Билли Бонс положил в сундук некоторое количество золотых монет. На второй год он вынул из сундука сколько-то монет. Начиная с третьего года, он добавлял столько монет, сколько было в сундуке два года назад.
Требуется написать программу, которая определит, сколько монет было в сундуке в первый и во второй года, если в X-м году там оказалось ровно Y монет.
Входные данные
Входной файл содержит натуральные числа X и Y (3 ≤ X≤20, 1≤Y≤32767).
Выходные данные
В выходной файл выведите через пробел количество монет в первый и второй года. Гарантируется, что решение задачи всегда существует.
Как ее решить?В душе не чаю.
1. Положил: С монет (1C-0x)
2. Вытащил - Х монет. (стало 1С-1X)
3. Положил C монет. (стало 2С-1X)
4. Положил С-X монет. (стало 3C-2х)
5. Положил 2С-Х монет (стало 5С-3х)
6. Положил 3с-2х монет. ( стало 8С - 5Х монет)
7. Положил 5С-3х монет. ( стало 13С - 8Х монет)
Очевидно что коэффициенты у чисел равны числам фибоначчи:
Число монет в год N равно F(x) Положил - F(x-1) Взял.
Таким образом, тебе надо решить уравнение AX - BY = Z, в котором A и B известны, и при этом Y < X, а также известно что значения - целочисленные.
Дальше, я думаю, сможешь посчитать сам.
2. Вытащил - Х монет. (стало 1С-1X)
3. Положил C монет. (стало 2С-1X)
4. Положил С-X монет. (стало 3C-2х)
5. Положил 2С-Х монет (стало 5С-3х)
6. Положил 3с-2х монет. ( стало 8С - 5Х монет)
7. Положил 5С-3х монет. ( стало 13С - 8Х монет)
Очевидно что коэффициенты у чисел равны числам фибоначчи:
Число монет в год N равно F(x) Положил - F(x-1) Взял.
Таким образом, тебе надо решить уравнение AX - BY = Z, в котором A и B известны, и при этом Y < X, а также известно что значения - целочисленные.
Дальше, я думаю, сможешь посчитать сам.
>>582242
Спасибо
Спасибо
Если решений несколько, нужны все или любое? А так-то легко.
Пусть в первый год положили N монет, а во второй год вытащили m монет.
В год X в сундуке Y=(N-m + (X-2)N) монет.
m = N(X-1) - Y ≤ N
Пусть m≥1. Тогда берёшь любое натуральное N из промежутка от (Y+1)/(X-1) до Y/(X-2) и по нему считаешь m. Если m может быть равно нулю, то промежуток надо брать от Y/(X-1) до Y/(X-2)
Пусть в первый год положили N монет, а во второй год вытащили m монет.
В год X в сундуке Y=(N-m + (X-2)N) монет.
m = N(X-1) - Y ≤ N
Пусть m≥1. Тогда берёшь любое натуральное N из промежутка от (Y+1)/(X-1) до Y/(X-2) и по нему считаешь m. Если m может быть равно нулю, то промежуток надо брать от Y/(X-1) до Y/(X-2)
>>582262
Хотя я неправильно условие понял, забудь.
Хотя я неправильно условие понял, забудь.
>Начиная с третьего года, он добавлял столько монет, сколько было в сундуке два года назад.
Сколько было после того как он забрал монеты, или столько, сколько он положил в первый год?
>>582242
это считается элементарным; вся суть задачи в поиске этих самых коэффициентов. циклом по времени не проходит. возможно бинарный поиск
это считается элементарным; вся суть задачи в поиске этих самых коэффициентов. циклом по времени не проходит. возможно бинарный поиск
Дан массив n целых положительных (>0) чисел и число k <= n. Нужно разбить массив на k (возможно пустых) частей так, чтобы минимизировать максимальную сумму внутри частей.
Например:
4 2 -1 5, k = 2
Видим, что оптимальное разбиение это 4 + 2 - 1 и 5, т.е. max(5, 5) = 5, в остальных случаях максимум больше.
Найти минимальную максимальную сумму, само разбиение находить не надо.
Время: O(kn)
Память: O(k + n)
задачка с собеседования в американский яндекс
Например:
4 2 -1 5, k = 2
Видим, что оптимальное разбиение это 4 + 2 - 1 и 5, т.е. max(5, 5) = 5, в остальных случаях максимум больше.
Найти минимальную максимальную сумму, само разбиение находить не надо.
Время: O(kn)
Память: O(k + n)
задачка с собеседования в американский яндекс
>>587591
Вот обосрался с примером. Если числа отрицательные, то только O(k * n^2)
Вот правильный пример:
4 2 1 5, k = 2
4 + 2 и 1 + 5, ответ 6.
Вот обосрался с примером. Если числа отрицательные, то только O(k * n^2)
Вот правильный пример:
4 2 1 5, k = 2
4 + 2 и 1 + 5, ответ 6.
Это оффициальный тред? Тут теперь спрашивать помощь по решению олимпиадных задач?
>>587586
Бин поиск по ответу + жадность. Ответ надо искать в промежутке от 1 до суммы всех чисел. Выбрав какую-то сумму s идем по последовательности и в текущую подпоследовательность пихаем столько элементов, сколько можем.
Бин поиск по ответу + жадность. Ответ надо искать в промежутке от 1 до суммы всех чисел. Выбрав какую-то сумму s идем по последовательности и в текущую подпоследовательность пихаем столько элементов, сколько можем.
>>588072
Только тут время n log(sum a_i), что меньше o(nk) для маленьких k. Ща еще подумаю.
Только тут время n log(sum a_i), что меньше o(nk) для маленьких k. Ща еще подумаю.
Кстати в наукаче есть тред про Computer Science. Говорят и с олимпиадными задачами к ним можно. Поэтому если в этот тред будут заходить только полтора умеющих решать задачки анона, то можно к ним перекатиться.
>>588072
вот это ты хотел сказать.
Оригинально. Я просто через SMAWK решил т.к. матрица получается строго монотонная.
>для больших k
вот это ты хотел сказать.
Оригинально. Я просто через SMAWK решил т.к. матрица получается строго монотонная.
Дан массив uint64_t, найти непрерывный подмассив с максимальным xor-ом. Т.е. подмассив l1, l2, ... lk такой, что l1 ^ l2 ^ ... lk максимально.
>>588333
На самом деле бин поиск по ответу - это стандартный асмовский прием, я его десятки раз писал. А про SWAMK первый раз слышу.
> Оригинально
На самом деле бин поиск по ответу - это стандартный асмовский прием, я его десятки раз писал. А про SWAMK первый раз слышу.
Лол, оп, задача в твоём посте очень простая, решил буквально за 3 минуты полным перебором, думал словлю таймлимит, но нихуя. Вот как я рассуждал. Во первых, сразу бери листочек и ручку и начинай придумывать примеры, я вот взял числа 6 и 30 и сразу увидел, что снизу вверх можно собрать уравнение, а потом перебором найти коэффициенты. Вот код, если интересно. http://pastebin.com/sRYe7kUz
>>582265
Гарантируют, что оно ЕСТЬ. Учись читать условия.
Гарантируют, что оно ЕСТЬ. Учись читать условия.
>>588823
Ну SMAWK это тоже в некотором смысле "олимпиадный приём".
Есть матрица nxn с таким свойством. Если a[r1][c1] >= a[r1][c2], то для всех r > r1 a[r][c1] >= a[r][c2]
Найти в данной матрице минимальный элемент в каждой строчке за O(n)
Это и есть SMAWK
Ну SMAWK это тоже в некотором смысле "олимпиадный приём".
Есть матрица nxn с таким свойством. Если a[r1][c1] >= a[r1][c2], то для всех r > r1 a[r][c1] >= a[r][c2]
Найти в данной матрице минимальный элемент в каждой строчке за O(n)
Это и есть SMAWK
>>588384
>>589366
То есть нужно модифицировать "Поиск подотрезка с максимальной суммой" вот в этой статье
http://e-maxx.ru/algo/segment_tree
>>589366
То есть нужно модифицировать "Поиск подотрезка с максимальной суммой" вот в этой статье
http://e-maxx.ru/algo/segment_tree
>>589368
Ну а для тупых есть вариант с trie. Запихиваем все частичные xor-ы в trie, а после этого нам нужно для каждого частичного xor-а найти такой частичный xor, который бы при xor-е дал максимальный результат, т.е. в trie стараемся идти в 0 когда в исходном числе 1 и в 1, когда в исходном числе 0.
Ну а для тупых есть вариант с trie. Запихиваем все частичные xor-ы в trie, а после этого нам нужно для каждого частичного xor-а найти такой частичный xor, который бы при xor-е дал максимальный результат, т.е. в trie стараемся идти в 0 когда в исходном числе 1 и в 1, когда в исходном числе 0.
Блядь, какое-то торжество олимпидодаунов, и их ещё не обоссали? Что ж! Я буду первым! Открывайте рот пошире, чтобы не пропустить ни капли!

73 Кб, 704x864
Чет никто не вбрасывает. Тогда я вброшу такую задачу с опенкапа недавнего. Это обобщение загадки о волке, козе и капусте на случай, когда животных много.
Кстати можно где-нибудь получить сертификат что я мастер алгоритмов? Как к нему готовиться?
только начал
только начал

181 Кб, 600x600
>>590762
ЧО ЗА ГРАФЫ ТАКИЕ?
@
КРУЖКИ РИСУЕШЬ ЧТО ЛИ?
@
РАСКРАСКИ? КАКИЕ РАСКРАСКИ?
@
БЛЯ У МЕНЯ У ПЛЕМЯННИКА ТОЖИ РАСКРАСКИ ЕСТЬ))0
@
А ТЕБЕ-ТО 20 ЛЕТ, КАКИЕ РАСКРАСКИ, ТЫ ЧО ЕПТ))0
@
А ДЕВУШКУ СВОЮ ТЫ ГРАФАМИ БУДЕШЬ ЗАЩИЩАТЬ?)))0
ЧО ЗА ГРАФЫ ТАКИЕ?
@
КРУЖКИ РИСУЕШЬ ЧТО ЛИ?
@
РАСКРАСКИ? КАКИЕ РАСКРАСКИ?
@
БЛЯ У МЕНЯ У ПЛЕМЯННИКА ТОЖИ РАСКРАСКИ ЕСТЬ))0
@
А ТЕБЕ-ТО 20 ЛЕТ, КАКИЕ РАСКРАСКИ, ТЫ ЧО ЕПТ))0
@
А ДЕВУШКУ СВОЮ ТЫ ГРАФАМИ БУДЕШЬ ЗАЩИЩАТЬ?)))0
>>590787
Это учит мыслить out of the box. Современная архитектура, кстати, уже подгнивает. Индустрии требуется языки шестого поколения, потому что предыдущие уже не справляются с нагрузкой комплексностью.
Изобретать же новые инструменты будут не дрочители паттернов, а те кто смогут выйти за пределы текущей парадигмы.
Это учит мыслить out of the box. Современная архитектура, кстати, уже подгнивает. Индустрии требуется языки шестого поколения, потому что предыдущие уже не справляются с нагрузкой комплексностью.
Изобретать же новые инструменты будут не дрочители паттернов, а те кто смогут выйти за пределы текущей парадигмы.
>>590787
Ты просто быдло. Я не знаю как объяснить. Ты музыку слушаешь? Тебе музыка как-то поможет деньги заработать, если ты не профессиональный музыкант?
Ты просто быдло. Я не знаю как объяснить. Ты музыку слушаешь? Тебе музыка как-то поможет деньги заработать, если ты не профессиональный музыкант?
>>590828
Ну ладно. Тогда я профессиональный математик, занимаюсь теорией графов, в своей команде по acm отвечаю за всякие графы и деревья.
Ну ладно. Тогда я профессиональный математик, занимаюсь теорией графов, в своей команде по acm отвечаю за всякие графы и деревья.
>>590848
А я Иван, сосу кукан))
А я Иван, сосу кукан))
>>590855
Спасибо.
Спасибо.
Даунята не в курсе, что на собеседовании в любую нормальную компанию сейчас дают решать олимпиадные задачи, и спрашивают про математику и алгоритмы.
Энтри левел. Дано n (очень большое) и m, найдите n-е число Фибоначчи по модулю m.
>>591181
Можно использовать формулу Бине (с корнями из 5) и быстрое возведение в степень. Если m и n взаимно простые, то по теореме Эклера можно найти обратный элемент. Время работы O(log n + log m).
Можно использовать формулу Бине (с корнями из 5) и быстрое возведение в степень. Если m и n взаимно простые, то по теореме Эклера можно найти обратный элемент. Время работы O(log n + log m).
>>591384
m влазит в инт, ну как минимум линейное от номера числа.
m влазит в инт, ну как минимум линейное от номера числа.

54 Кб, 1194x660
>>591390
Какой обратный элемент, что ты несёшь? Быстрое возведение в степень по модулю, ты хотел сказать?
>теореме Эклера
Какой обратный элемент, что ты несёшь? Быстрое возведение в степень по модулю, ты хотел сказать?
>>591420
Ну в формуле Бине надо в конце делить на 2^n. А чтобы поделить на 2^n в кольце вычетов по модулю m, нужно найти обратный элемент, нельзя просто делить. А его проще всего найти по теореме Эклера (но если n и m не взаимно простые, то не получится).
Наверное, более простой вариант, последовательно вычислять числа по модулю m, пока пары чисел не начнут повторяться. Дальше просто находим период. Назовем его T. Ответ - это число с номером n mod T. Пары чисел начнут повторяться через O(m^2) вычисленных чисел, потому что есть m^2 / 2 различных пар элементов в Z_m. У меня есть подозрение, что они раньше начнут повторяться, но я хз как доказать.
Ну в формуле Бине надо в конце делить на 2^n. А чтобы поделить на 2^n в кольце вычетов по модулю m, нужно найти обратный элемент, нельзя просто делить. А его проще всего найти по теореме Эклера (но если n и m не взаимно простые, то не получится).
Наверное, более простой вариант, последовательно вычислять числа по модулю m, пока пары чисел не начнут повторяться. Дальше просто находим период. Назовем его T. Ответ - это число с номером n mod T. Пары чисел начнут повторяться через O(m^2) вычисленных чисел, потому что есть m^2 / 2 различных пар элементов в Z_m. У меня есть подозрение, что они раньше начнут повторяться, но я хз как доказать.
>>591430
Фикс: 2^n и m не взаимно простые естественно. То есть m должно быть хотя бы нечетным.
> но если n и m не взаимно простые, то не получится
Фикс: 2^n и m не взаимно простые естественно. То есть m должно быть хотя бы нечетным.
http://ideone.com/0TGSWI а как же вариант через матрицы, который за O(log(n)) работает через школьную арифметику..
>>591439
Ебать, оказывается это еще и назвали в честь кого-то, хотя этот результат придумывается за 5 минут любым асмщиком.
Ебать, оказывается это еще и назвали в честь кого-то, хотя этот результат придумывается за 5 минут любым асмщиком.
>>591458
Бляяя, точно, чет не подумал.
Бляяя, точно, чет не подумал.
Пожалуй, продолжу. Задачка из facebook задавал индус
Кузнечик находится в (0, 0). После этого он делает n шагов. Шаг это - (+1, 0), (-1, 0), (0, +1) или (0, -1).
Рассмотрим множество всех его возможных путей. Их 4^n. Будем считать два пути различными, если множество посещённых координат различается.
Сколько всего уникальных путей у кузнечика, если он делает n шагов?
Нужно быстрее чем за O(n) и без преподсчёта.
Кузнечик находится в (0, 0). После этого он делает n шагов. Шаг это - (+1, 0), (-1, 0), (0, +1) или (0, -1).
Рассмотрим множество всех его возможных путей. Их 4^n. Будем считать два пути различными, если множество посещённых координат различается.
Сколько всего уникальных путей у кузнечика, если он делает n шагов?
Нужно быстрее чем за O(n) и без преподсчёта.
20 Кб, 703x313
>>591464
Чет хуй знает пока что. Я спать пойду.
Чет хуй знает пока что. Я спать пойду.
>>591516
Некоторые пути одинаковые по определению "различных путей". Например влево - влево - враво - влево и влево - вправо - влево - влево.
Некоторые пути одинаковые по определению "различных путей". Например влево - влево - враво - влево и влево - вправо - влево - влево.
>>591514
Я так подумал, это тоже не правильно. Нужно на каждом шаге (от 1 до n) высчитать количество путей которые не пересекаются сами с собой, и проссумировать.
Я так подумал, это тоже не правильно. Нужно на каждом шаге (от 1 до n) высчитать количество путей которые не пересекаются сами с собой, и проссумировать.
>>591521
Ох блядь, там еще нужно учесть пути соприкасающиеся с началом. Вот же индус.
Ох блядь, там еще нужно учесть пути соприкасающиеся с началом. Вот же индус.
>>591464
Хуйня кокая-то.
для n=2 путей 16 но уникальных только 12, ибо путь (1 -1 1) образует подмножество пути (1 1 1). И так 4 раза.
Т.е наверно нужно учитывать только самы длинные пути, ибо у них самы сильные множества.
>Будем считать два пути различными, если множество посещённых координат различается.
Хуйня кокая-то.
для n=2 путей 16 но уникальных только 12, ибо путь (1 -1 1) образует подмножество пути (1 1 1). И так 4 раза.
Т.е наверно нужно учитывать только самы длинные пути, ибо у них самы сильные множества.
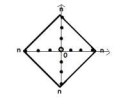
Лол, походу задача сводится к поику площади прямоугольника с вершинами {n,n}{n,-n}{-n,n}{-n,-n}.
Ну сами посудите: любая крайняя клетка(принадлежит периметру) может быть достигнута за n шагов, любая внутреняя клетка не является уникальным путем, ибо ее координаты точно войдут в путь до края или станут конечными в путе-цикле(путь с повторами шаг - вперед шаг назад).
цыфры вроде сходятся.
Кароч формула: (4n) + 4 sum(1, n - 1)
Ну сами посудите: любая крайняя клетка(принадлежит периметру) может быть достигнута за n шагов, любая внутреняя клетка не является уникальным путем, ибо ее координаты точно войдут в путь до края или станут конечными в путе-цикле(путь с повторами шаг - вперед шаг назад).
цыфры вроде сходятся.
Кароч формула: (4n) + 4 sum(1, n - 1)

92 Кб, 1323x320
>>591512
>>591530
>>591532
по фразе "Нужно быстрее чем за O(n) и без преподсчёта." наверное можно понять что формулы там нихуя нет и надо писать алгоритм.
>>591529
какие из слов "множества посещенных координат" тебе непонятны?
>>591530
>>591532
по фразе "Нужно быстрее чем за O(n) и без преподсчёта." наверное можно понять что формулы там нихуя нет и надо писать алгоритм.
>>591529
>для n=2 путей 16 но уникальных только 12, ибо путь (1 -1 1) образует подмножество пути (1 1 1).
какие из слов "множества посещенных координат" тебе непонятны?
Нужен учебник олимпиадным задачам. Не алгоритмам, а именно задачам.
>>591675
Я сегодня уже думал out of the box, когда твою мамку на секс разводил. Уже лимит думанья out of the box превышен.
Я сегодня уже думал out of the box, когда твою мамку на секс разводил. Уже лимит думанья out of the box превышен.

33 Кб, 557x350
Поясните за функцию эйлера. Как этот код и формула связаны? В формуле от 1 отнимают единицу деленную на простое число что меньше единицы и это перемножают с другими результатами которые меньше единицы. Получается какое-то маленькое число которое умножают на n. И при чём тут этот код?
>>591844
Скобочки начни раскрывать слева.
Скобочки начни раскрывать слева.
>>591844
Функция эйлера - это количество чисел меньше n, взаимно простых с n. Несложно доказать, что она мультиплакитивна. А какой-то арифметической формулы для нее нет. Код который ты привел вычисляет функцию Эйлера перебором. А что это за формулы - хуй знает.
Функция эйлера - это количество чисел меньше n, взаимно простых с n. Несложно доказать, что она мультиплакитивна. А какой-то арифметической формулы для нее нет. Код который ты привел вычисляет функцию Эйлера перебором. А что это за формулы - хуй знает.
>>591844
А нет, падажжи, я понял. В той формуле сверху пэ это простые делители, а альфа - их кратность. Но один хуй в коде вычисляется не по этой формуле.
А нет, падажжи, я понял. В той формуле сверху пэ это простые делители, а альфа - их кратность. Но один хуй в коде вычисляется не по этой формуле.
>>592906
Во первых, там нихуя не полный перебор, а перебор с учётом формулы. Во вторых, того что она мультипликативна достаточно для вывода формул выше.
>>591844
Следи за рукой:
n(1-1/p1)...(1-1/pk) = (n - n/p1)(1-1/p2)...(1 - 1/pk) и так далее последовательным раскрытие скобок. Код делает то же самое - находит простой делитель n и раскрывает для этого делителя его скобку, а само n делит пока оно не станет взаимно просто с этим делителем.
Во первых, там нихуя не полный перебор, а перебор с учётом формулы. Во вторых, того что она мультипликативна достаточно для вывода формул выше.
>>591844
Следи за рукой:
n(1-1/p1)...(1-1/pk) = (n - n/p1)(1-1/p2)...(1 - 1/pk) и так далее последовательным раскрытие скобок. Код делает то же самое - находит простой делитель n и раскрывает для этого делителя его скобку, а само n делит пока оно не станет взаимно просто с этим делителем.
>>591464
Ну дак че, как решать?
Ну дак че, как решать?

171 Кб, 1347x493
Как без массива решать? С решение в лоб меньше половины тестов проходит.
>>594919
dl.gsu.by Ссылка не дам т.к. нужна регистрация она без инвайтов, но всё равно всем лень и так проще.
dl.gsu.by Ссылка не дам т.к. нужна регистрация она без инвайтов, но всё равно всем лень и так проще.
>>595138
Пожалуйста.
Пожалуйста.
>>595466
Ну хуй знает. Можно такой тупой алгоритм: рассмотрим каждую строчку. Возьмём наш прямоугольник RxC и будем двигать его слева направо и считать количество деревьев в нём. Для каждого отдельно взятого прямоугольника линия будет иметь вид / --- \ (то есть, три фазы- рост, константность, падение). Заметим, что скорость роста - константна, падения - тоже. Теперь у нас задача - есть 100 таких линий, нужно их сложить, а потом найти точку минимума.
Вот так примерно выглядит линия для одного прямоугольника:
0 0 0 10 20 30 30 30 30 30 30 30 20 10 0 0 0
Представим, что это - линия, имеющая в x=0 значение 0, в x =1 значение 0, в x=2 значение 0, потом между x=2 и x=3 она идёт вверх с производной 10, в x=3 достигает значения 10, в x=4 - значения 20, итд. Теперь возьмём производную от этой линии. она будет представлять из себя 3 отрезка - со значением 10 на отрезке [2, 5], со значением 0 на отрезке [5, 11] и со значением -10 на [11, 14]
Нас интересуют точки, где производная либо меняет знак с - на +, либо равна 0 (ну, будем считать, что меняет знак с - на + включает переход из 0 в положительное значение). То есть изначально интересные точки - [2, 5, 11, 14]. В точке 2 производная набирает 10 очков, в точке 5 их теряет, в точке 11 теряет ещё 10 очков, а в точке 14 набирает 10 очков. (очки - скорость роста).
Значит, таких линий всего может быть 100. Пройдёмся сканлайном по их интересным точкам,и найдём минимальное значение количества деревьев. Проглядеть минимум мы не могли так как он находится только в интересных точках. Сканлайн нужен, чтобы мы могли, зная значение производной, предсказать сколько же будет деревьев в следующей интересной точке.
Итого на строчку уходит 400 log(400) на сортировку интересных точек + 400 на проход по ним + 400 на заполнение массива перед сортировкой.
Получаем 400 (log(400) + 2) 10^5 = 4000 10^5 = 4 10^8.
Ну хуй знает.
И тут возникает идея - нам по сути можно перенести идею с производными на двумерное пространство.
Тогда нужно всего-лишь понять, какое множество точек для парка является интересным. Нарисуй в 3D как оно будет выглядеть - я вижу, что сверху, слева, внизу, справа это будут тупо плоскости наклонные, (как раскрытая коробка), а вот по углам контур интересных точек я не могу представить. нужна бумага уже.
Тогда идея такая - у каждого парка будет 10^5 20 интересных точек. Каждую из них можно проверить за 100 (тупо пересекаем со всеми парками и смотрим сколько деревьев), получается 10^5 20 100 = 2 * 10^8.
Мб как-то можно сократить множество проверяемых парков какими-нибудь тупыми корзинками по координатам.
Ну хуй знает. Можно такой тупой алгоритм: рассмотрим каждую строчку. Возьмём наш прямоугольник RxC и будем двигать его слева направо и считать количество деревьев в нём. Для каждого отдельно взятого прямоугольника линия будет иметь вид / --- \ (то есть, три фазы- рост, константность, падение). Заметим, что скорость роста - константна, падения - тоже. Теперь у нас задача - есть 100 таких линий, нужно их сложить, а потом найти точку минимума.
Вот так примерно выглядит линия для одного прямоугольника:
0 0 0 10 20 30 30 30 30 30 30 30 20 10 0 0 0
Представим, что это - линия, имеющая в x=0 значение 0, в x =1 значение 0, в x=2 значение 0, потом между x=2 и x=3 она идёт вверх с производной 10, в x=3 достигает значения 10, в x=4 - значения 20, итд. Теперь возьмём производную от этой линии. она будет представлять из себя 3 отрезка - со значением 10 на отрезке [2, 5], со значением 0 на отрезке [5, 11] и со значением -10 на [11, 14]
Нас интересуют точки, где производная либо меняет знак с - на +, либо равна 0 (ну, будем считать, что меняет знак с - на + включает переход из 0 в положительное значение). То есть изначально интересные точки - [2, 5, 11, 14]. В точке 2 производная набирает 10 очков, в точке 5 их теряет, в точке 11 теряет ещё 10 очков, а в точке 14 набирает 10 очков. (очки - скорость роста).
Значит, таких линий всего может быть 100. Пройдёмся сканлайном по их интересным точкам,и найдём минимальное значение количества деревьев. Проглядеть минимум мы не могли так как он находится только в интересных точках. Сканлайн нужен, чтобы мы могли, зная значение производной, предсказать сколько же будет деревьев в следующей интересной точке.
Итого на строчку уходит 400 log(400) на сортировку интересных точек + 400 на проход по ним + 400 на заполнение массива перед сортировкой.
Получаем 400 (log(400) + 2) 10^5 = 4000 10^5 = 4 10^8.
Ну хуй знает.
И тут возникает идея - нам по сути можно перенести идею с производными на двумерное пространство.
Тогда нужно всего-лишь понять, какое множество точек для парка является интересным. Нарисуй в 3D как оно будет выглядеть - я вижу, что сверху, слева, внизу, справа это будут тупо плоскости наклонные, (как раскрытая коробка), а вот по углам контур интересных точек я не могу представить. нужна бумага уже.
Тогда идея такая - у каждого парка будет 10^5 20 интересных точек. Каждую из них можно проверить за 100 (тупо пересекаем со всеми парками и смотрим сколько деревьев), получается 10^5 20 100 = 2 * 10^8.
Мб как-то можно сократить множество проверяемых парков какими-нибудь тупыми корзинками по координатам.
>>595466
Ну хуй знает. Можно такой тупой алгоритм: рассмотрим каждую строчку. Возьмём наш прямоугольник RxC и будем двигать его слева направо и считать количество деревьев в нём. Для каждого отдельно взятого прямоугольника линия будет иметь вид / --- \ (то есть, три фазы- рост, константность, падение). Заметим, что скорость роста - константна, падения - тоже. Теперь у нас задача - есть 100 таких линий, нужно их сложить, а потом найти точку минимума.
Вот так примерно выглядит линия для одного прямоугольника:
0 0 0 10 20 30 30 30 30 30 30 30 20 10 0 0 0
Представим, что это - линия, имеющая в x=0 значение 0, в x =1 значение 0, в x=2 значение 0, потом между x=2 и x=3 она идёт вверх с производной 10, в x=3 достигает значения 10, в x=4 - значения 20, итд. Теперь возьмём производную от этой линии. она будет представлять из себя 3 отрезка - со значением 10 на отрезке [2, 5], со значением 0 на отрезке [5, 11] и со значением -10 на [11, 14]
Нас интересуют точки, где производная либо меняет знак с - на +, либо равна 0 (ну, будем считать, что меняет знак с - на + включает переход из 0 в положительное значение). То есть изначально интересные точки - [2, 5, 11, 14]. В точке 2 производная набирает 10 очков, в точке 5 их теряет, в точке 11 теряет ещё 10 очков, а в точке 14 набирает 10 очков. (очки - скорость роста).
Значит, таких линий всего может быть 100. Пройдёмся сканлайном по их интересным точкам,и найдём минимальное значение количества деревьев. Проглядеть минимум мы не могли так как он находится только в интересных точках. Сканлайн нужен, чтобы мы могли, зная значение производной, предсказать сколько же будет деревьев в следующей интересной точке.
Итого на строчку уходит 400 log(400) на сортировку интересных точек + 400 на проход по ним + 400 на заполнение массива перед сортировкой.
Получаем 400 (log(400) + 2) 10^5 = 4000 10^5 = 4 10^8.
Ну хуй знает.
И тут возникает идея - нам по сути можно перенести идею с производными на двумерное пространство.
Тогда нужно всего-лишь понять, какое множество точек для парка является интересным. Нарисуй в 3D как оно будет выглядеть - я вижу, что сверху, слева, внизу, справа это будут тупо плоскости наклонные, (как раскрытая коробка), а вот по углам контур интересных точек я не могу представить. нужна бумага уже.
Тогда идея такая - у каждого парка будет 10^5 20 интересных точек. Каждую из них можно проверить за 100 (тупо пересекаем со всеми парками и смотрим сколько деревьев), получается 10^5 20 100 = 2 * 10^8.
Мб как-то можно сократить множество проверяемых парков какими-нибудь тупыми корзинками по координатам.
Ну хуй знает. Можно такой тупой алгоритм: рассмотрим каждую строчку. Возьмём наш прямоугольник RxC и будем двигать его слева направо и считать количество деревьев в нём. Для каждого отдельно взятого прямоугольника линия будет иметь вид / --- \ (то есть, три фазы- рост, константность, падение). Заметим, что скорость роста - константна, падения - тоже. Теперь у нас задача - есть 100 таких линий, нужно их сложить, а потом найти точку минимума.
Вот так примерно выглядит линия для одного прямоугольника:
0 0 0 10 20 30 30 30 30 30 30 30 20 10 0 0 0
Представим, что это - линия, имеющая в x=0 значение 0, в x =1 значение 0, в x=2 значение 0, потом между x=2 и x=3 она идёт вверх с производной 10, в x=3 достигает значения 10, в x=4 - значения 20, итд. Теперь возьмём производную от этой линии. она будет представлять из себя 3 отрезка - со значением 10 на отрезке [2, 5], со значением 0 на отрезке [5, 11] и со значением -10 на [11, 14]
Нас интересуют точки, где производная либо меняет знак с - на +, либо равна 0 (ну, будем считать, что меняет знак с - на + включает переход из 0 в положительное значение). То есть изначально интересные точки - [2, 5, 11, 14]. В точке 2 производная набирает 10 очков, в точке 5 их теряет, в точке 11 теряет ещё 10 очков, а в точке 14 набирает 10 очков. (очки - скорость роста).
Значит, таких линий всего может быть 100. Пройдёмся сканлайном по их интересным точкам,и найдём минимальное значение количества деревьев. Проглядеть минимум мы не могли так как он находится только в интересных точках. Сканлайн нужен, чтобы мы могли, зная значение производной, предсказать сколько же будет деревьев в следующей интересной точке.
Итого на строчку уходит 400 log(400) на сортировку интересных точек + 400 на проход по ним + 400 на заполнение массива перед сортировкой.
Получаем 400 (log(400) + 2) 10^5 = 4000 10^5 = 4 10^8.
Ну хуй знает.
И тут возникает идея - нам по сути можно перенести идею с производными на двумерное пространство.
Тогда нужно всего-лишь понять, какое множество точек для парка является интересным. Нарисуй в 3D как оно будет выглядеть - я вижу, что сверху, слева, внизу, справа это будут тупо плоскости наклонные, (как раскрытая коробка), а вот по углам контур интересных точек я не могу представить. нужна бумага уже.
Тогда идея такая - у каждого парка будет 10^5 20 интересных точек. Каждую из них можно проверить за 100 (тупо пересекаем со всеми парками и смотрим сколько деревьев), получается 10^5 20 100 = 2 * 10^8.
Мб как-то можно сократить множество проверяемых парков какими-нибудь тупыми корзинками по координатам.
>>596141
Хотя, 100 миллионов это слишком дохуя для OJ, есть подозрение, что тут нужно что-то более хитровыебанное, либо тебе повезёт и на их тестах оно пройдёт. Хотелось бы увидеть правильное решение, ну ты попробуй, вдруг прокатит.
Хотя, 100 миллионов это слишком дохуя для OJ, есть подозрение, что тут нужно что-то более хитровыебанное, либо тебе повезёт и на их тестах оно пройдёт. Хотелось бы увидеть правильное решение, ну ты попробуй, вдруг прокатит.
Кажись, придумал решение, которое влезает всегда в TL.
Забудь про вторую идею с коробкой. Итак, для каждой строчки у нас есть набор интересных точек, их не более 400. Объединим интересные точки всех строчек. Их опять будет 400. Бинго! То есть мы можем из 10^5 столбцов оставить 400.
Теперь проведём такой же финт, но со строчками. Теперь у нас матрица 400 на 400.
После этого нам только нужно быстро уметь находить количество деревьев в данной точке. Просто для каждого прямоугольника проставляем правильное значение производной для каждой интересной точки - 400, а потом сканлайн за 400.
Получается, каждую строчку мы пробегаем за 800, строчек 400 - ответ за 320,000. Должно влезать в любой таймлимит теперь.
Забудь про вторую идею с коробкой. Итак, для каждой строчки у нас есть набор интересных точек, их не более 400. Объединим интересные точки всех строчек. Их опять будет 400. Бинго! То есть мы можем из 10^5 столбцов оставить 400.
Теперь проведём такой же финт, но со строчками. Теперь у нас матрица 400 на 400.
После этого нам только нужно быстро уметь находить количество деревьев в данной точке. Просто для каждого прямоугольника проставляем правильное значение производной для каждой интересной точки - 400, а потом сканлайн за 400.
Получается, каждую строчку мы пробегаем за 800, строчек 400 - ответ за 320,000. Должно влезать в любой таймлимит теперь.
>>596323
Оставил подсчёт количества деревьев через производные. Выкинул перебор ненужных 10^5 строчек, оставив только 400.
Вот код на питоне
http://ideone.com/b17P6I
По крайней мере на вариантах до 100 ответ совпадает с тупым перебором.
Оставил подсчёт количества деревьев через производные. Выкинул перебор ненужных 10^5 строчек, оставив только 400.
Вот код на питоне
http://ideone.com/b17P6I
По крайней мере на вариантах до 100 ответ совпадает с тупым перебором.
>>596389
Ого даже код написал. Спасибо. Щас сам попробую.
Ого даже код написал. Спасибо. Щас сам попробую.
Пацаны, кто-то следил за полуфиналом? Вот standings:
http://neerc.ifmo.ru/information/standings.html
А как понять, кто прошел в финал?
http://neerc.ifmo.ru/information/standings.html
А как понять, кто прошел в финал?
Пусть A = {1, 2, ..., n}. Найти максимальное по мощности A' ⊂ A такое, что A' не содержит x и y таких, что x = 2y.
>>598530
Забыл еще:
Если максимальных по мощности подмножеств несколько, вывести любое из них.
Время полиномиальное.
Забыл еще:
Если максимальных по мощности подмножеств несколько, вывести любое из них.
Время полиномиальное.
>>598533
Ну давай подумаем в двоичной системе.
Если есть число XXXX, то нельзя чтобы было число XXXX0, при этом XXXX00 можно.
То есть для любого числа XXX мы выводим XXX XXX00 XXX0000, удваивая число нулей на конце. при этом начинать с XXX0 не имеет смысла так как, если начать с XXX, мы получим больше чисел - раньше вылезем за N.
Значит, алгоритм такой: для каждого нечётного числа выводим x, x 4, x 16, x * 64, ...
Так как каждое число мы просмотрим максимум один раз, сложность O(n)
http://ideone.com/BWwyTO
Ну давай подумаем в двоичной системе.
Если есть число XXXX, то нельзя чтобы было число XXXX0, при этом XXXX00 можно.
То есть для любого числа XXX мы выводим XXX XXX00 XXX0000, удваивая число нулей на конце. при этом начинать с XXX0 не имеет смысла так как, если начать с XXX, мы получим больше чисел - раньше вылезем за N.
Значит, алгоритм такой: для каждого нечётного числа выводим x, x 4, x 16, x * 64, ...
Так как каждое число мы просмотрим максимум один раз, сложность O(n)
http://ideone.com/BWwyTO
>>598557
Да, я так же решил.
Да, я так же решил.
Дано дерево, у каждого ребра некоторый вес. Поступают запросы
1) Изменить вес ребра между u и v
2) Найти максимальное ребро на кратчайшем пути между вершинами u и v.
Давайте представим, что про HLD мы не знаем.
1) Изменить вес ребра между u и v
2) Найти максимальное ребро на кратчайшем пути между вершинами u и v.
Давайте представим, что про HLD мы не знаем.
Есть какой-нибудь учебник по олимпиадным задачам?
бамп
Двач.hk прислал битые данные.
Вы видите копию треда, сохраненную 2 января 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Вы видите копию треда, сохраненную 2 января 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.