Вы видите копию треда, сохраненную 13 февраля 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Предыдущий попал под знаменатель тут
https://2ch.hk/sci/res/320047.html (
Википедию, например.
Зачем же ты так сильно приложил впискоанона)))
Здравствуйте. Я задал этот вопрос в соответствующем треде, но там никого нет, может тут кто ответит.
А почему решили, что время это целое измерение, а не дробное? 0,14 например.

>едЕницей
Такого обосрамса маттред еще не видел. Унижайте ОПа, насмехайтесь над ним, гоните его ссаными тряпками.
Математически дробные мерности возможны. Почитай Хаусдорфа по этому поводу. Но топологическая метрика, используемая в физике, чуть ли не постулирует, что мерность пространств может быть только натуральной.
А почему ты решил что дробное? Плюс это физический вопрос а не математический.
ну да теперь я вижу
Если мы будем строить точки на отрезке от 0 до 1 по правилу: для двух соседних точек отмечаем "сумму двоечника" (складываем числители с числителями и знаменатели со знаменателями); то в пределе мы получим все рациональные точки? Это очевидно?
Если вас чарует геометрия, вам вполне могут быть близки огромные тексты, написанные красивым языком. Геометрия - власть закона, там правят юристы.
Топология - это пространство под ЛСД. У него все было хорошо и стройно, но тут началось. Его инфецировали и начали размазывать шизоидные бхуты. Оно больше не пространство, а текст. Пытаешься увидеть у него кривизну, а бхуты ржут - для понимания кривизны надо преобразовать текст обратно в жесткое пространство, а это не так просто.
У нас говорят "мы в город не ходим". Городом правят юристы, они нас посадят в тюрьмы за неприятие гармонии и могущества.
Хочу ли я, чтобы у нас в стране полиция была честной, не коррумпированной, строго выполняющей закон? Нет, не хочу. Почему? Тогда закон будет идеально работать. А я его даже не читал, в нем могут быть такие бездны, что самый большой беспредел покажется сладкой сказкой. Этот закон составляли люди другого разума, мы попадем к ним во власть целиком. Мы должны будем жить и мыслить в их парадигмах, а если нет, может найтись ход, чтобы нас ликвидировать. Пока нет. А чтобы сказать "да", надо сначала изучить закон, найти ходы (стать юристом по-сути), на это надо отдать много лет, а этих многих лет нету, поэтому пока "нет".
Анализ занимается непрерывными переходами, работой на гладкой бесконечности, нежным контролем регулярно тянущихся объектов, в анализе мало сложных понятий, дорожки рассуждений сотканы из комбинаций стандартных замен-подстановок, там сложность спрятана в очень плотных пространствах, которые можно переносить туда-сюда, там работа с пакетами энергий, можно направленно открывать краники со струями, корректировать систему подачи воды на всей земле. Попросите оклеить обои во всех домах мира - вас не поймут.
Юнг малось залип на простом графическом эффекте: многие перед приступом эпилепсии видят мандалу. Не интересно, почему многие люди разного опыта и восприятия под одинаковыми галлюциногенами видят схожие орнаменты, рисуемые внутри глаза в схожем ритме?
А вот, что. Есть набор универсальных принципов, следуя которым, Природа создает сложность. Сколько их? 108, 1008 или 16108 - не так важно, они есть. И об этом я постараюсь подробно рассказать в конце января, если.
Алгебра очень разная. Есть круг идей, проникаясь которыми, становишься по-сути ограниченным лингвистом, а не математиком - играешь с буквами без привязки к остальному миру.
Но вот что меня восхитило в последние месяцы. Есть целое подобщество в алгебре, теории групп, которое считает, что если у нас есть более-менее естественное и просто формулируемое чистое утверждение о группах, которое доказывается сложным методом, с применением инородной науки (будь то топология или гомологии), то есть и простой прямой метод, как это показать. И я чаще всего сильно и активно согласен с ними. Новые теории чаще всего создаются (увы) ради расширения плоскости игры, а не ради создания новых методов решения старых задач. Но вот, периодически сталкиваюсь с феноменальным, и это феноменальное позволяет высматривать новую сложность. Да, я увидел утверждение, простое, лаконичное, про буквы и слова, то, которое я как профессионал должен выводить стандартными методами за пару минут работы, но не смог это сделать и за неделю, и не знаю, как это сделать и сейчас, но имею при этом хитрое гомологическое док-во. Удивительно.
Есть вопрос о том, где спрятана природная сложность, как она закодирована человеком. Человек кладет сложность в разные коробки, переставляет их, смотрит, как сложность изменилась. Или не так.
Да неважно, как что называется, как что метится. Важно, как пакуется сложность. Вот, есть альтернатива Титса, конструкция Рипса или свойство Артина-Риса. Вы выводите дорожку рассуждений, более-менее очевидных, подводите их к применению готовой формы и то, что получаете дальше - сложное утверждение. Сделать дорожку к готовой форме. Вы пробовали доказывать нелинейность каких-нибудь групп? Крайне неприятное занятие. Есть готовая форма - "ядовитая группа", которая обнаруживается в разных автоморфизмах, надо нащупать место, где она может лежать, вложить и получить нелинейность. Фигня, но приятно. Можно ходить на разные научные доклады, задаваясь одним единственным внутренним вопросом (его лучше не произносить вслух, это вопрос не докладчику, а слушателю): куда они прячут сложность? Если в одну-две готовые формы - ясно, если в десяток готовых форм - ну, молодцы, а если там минимум готовых форм и сложность раскрыта по-новому - это интересно и ценно. Искусство упаковывать сложность и затем работать с этой упаковкой. Дальше, есть то, что дается Природой - природная сложность. Она упакована в малых формах, очень компактна, она как атомная бомба - маленькая, но взрывается люто. Природная сложность организуется в разных областях, видимо, схожим образом. Но распознавание этих соответствий и структур сложности - жуткое дело. Люди, которые берутся за описание структуры обычно не знают математики. А если люди серьезно проработали внутри математики лет 20, весь их ум туда утек, они как правило очень наивно и беспомощно судят об остальном мире. И у тех, и у других выходит научпоповская фигня.
Простите, если что.
https://www.youtube.com/watch?v=6c3sMIGaimw
Если вас чарует геометрия, вам вполне могут быть близки огромные тексты, написанные красивым языком. Геометрия - власть закона, там правят юристы.
Топология - это пространство под ЛСД. У него все было хорошо и стройно, но тут началось. Его инфецировали и начали размазывать шизоидные бхуты. Оно больше не пространство, а текст. Пытаешься увидеть у него кривизну, а бхуты ржут - для понимания кривизны надо преобразовать текст обратно в жесткое пространство, а это не так просто.
У нас говорят "мы в город не ходим". Городом правят юристы, они нас посадят в тюрьмы за неприятие гармонии и могущества.
Хочу ли я, чтобы у нас в стране полиция была честной, не коррумпированной, строго выполняющей закон? Нет, не хочу. Почему? Тогда закон будет идеально работать. А я его даже не читал, в нем могут быть такие бездны, что самый большой беспредел покажется сладкой сказкой. Этот закон составляли люди другого разума, мы попадем к ним во власть целиком. Мы должны будем жить и мыслить в их парадигмах, а если нет, может найтись ход, чтобы нас ликвидировать. Пока нет. А чтобы сказать "да", надо сначала изучить закон, найти ходы (стать юристом по-сути), на это надо отдать много лет, а этих многих лет нету, поэтому пока "нет".
Анализ занимается непрерывными переходами, работой на гладкой бесконечности, нежным контролем регулярно тянущихся объектов, в анализе мало сложных понятий, дорожки рассуждений сотканы из комбинаций стандартных замен-подстановок, там сложность спрятана в очень плотных пространствах, которые можно переносить туда-сюда, там работа с пакетами энергий, можно направленно открывать краники со струями, корректировать систему подачи воды на всей земле. Попросите оклеить обои во всех домах мира - вас не поймут.
Юнг малось залип на простом графическом эффекте: многие перед приступом эпилепсии видят мандалу. Не интересно, почему многие люди разного опыта и восприятия под одинаковыми галлюциногенами видят схожие орнаменты, рисуемые внутри глаза в схожем ритме?
А вот, что. Есть набор универсальных принципов, следуя которым, Природа создает сложность. Сколько их? 108, 1008 или 16108 - не так важно, они есть. И об этом я постараюсь подробно рассказать в конце января, если.
Алгебра очень разная. Есть круг идей, проникаясь которыми, становишься по-сути ограниченным лингвистом, а не математиком - играешь с буквами без привязки к остальному миру.
Но вот что меня восхитило в последние месяцы. Есть целое подобщество в алгебре, теории групп, которое считает, что если у нас есть более-менее естественное и просто формулируемое чистое утверждение о группах, которое доказывается сложным методом, с применением инородной науки (будь то топология или гомологии), то есть и простой прямой метод, как это показать. И я чаще всего сильно и активно согласен с ними. Новые теории чаще всего создаются (увы) ради расширения плоскости игры, а не ради создания новых методов решения старых задач. Но вот, периодически сталкиваюсь с феноменальным, и это феноменальное позволяет высматривать новую сложность. Да, я увидел утверждение, простое, лаконичное, про буквы и слова, то, которое я как профессионал должен выводить стандартными методами за пару минут работы, но не смог это сделать и за неделю, и не знаю, как это сделать и сейчас, но имею при этом хитрое гомологическое док-во. Удивительно.
Есть вопрос о том, где спрятана природная сложность, как она закодирована человеком. Человек кладет сложность в разные коробки, переставляет их, смотрит, как сложность изменилась. Или не так.
Да неважно, как что называется, как что метится. Важно, как пакуется сложность. Вот, есть альтернатива Титса, конструкция Рипса или свойство Артина-Риса. Вы выводите дорожку рассуждений, более-менее очевидных, подводите их к применению готовой формы и то, что получаете дальше - сложное утверждение. Сделать дорожку к готовой форме. Вы пробовали доказывать нелинейность каких-нибудь групп? Крайне неприятное занятие. Есть готовая форма - "ядовитая группа", которая обнаруживается в разных автоморфизмах, надо нащупать место, где она может лежать, вложить и получить нелинейность. Фигня, но приятно. Можно ходить на разные научные доклады, задаваясь одним единственным внутренним вопросом (его лучше не произносить вслух, это вопрос не докладчику, а слушателю): куда они прячут сложность? Если в одну-две готовые формы - ясно, если в десяток готовых форм - ну, молодцы, а если там минимум готовых форм и сложность раскрыта по-новому - это интересно и ценно. Искусство упаковывать сложность и затем работать с этой упаковкой. Дальше, есть то, что дается Природой - природная сложность. Она упакована в малых формах, очень компактна, она как атомная бомба - маленькая, но взрывается люто. Природная сложность организуется в разных областях, видимо, схожим образом. Но распознавание этих соответствий и структур сложности - жуткое дело. Люди, которые берутся за описание структуры обычно не знают математики. А если люди серьезно проработали внутри математики лет 20, весь их ум туда утек, они как правило очень наивно и беспомощно судят об остальном мире. И у тех, и у других выходит научпоповская фигня.
Простите, если что.
https://www.youtube.com/watch?v=6c3sMIGaimw
Что сказать то хотел?
Вопрос имею. А что из себя топологически представляет человек = большой взрыв, все дела, зарождение жизни, человек+женщина+сперма, следующий человек.
ладно просто человек. или никто не рассматривал человека как топологический объект. Я встечал только пример, как человек может развязаться с соедиенными в кольцо пальцами. Ну, и да, если в качестве топологии учитывать, родителей, в чем тут тосионщина?
бамп
В долине ущербная луна сияет мертвенно и тускло, концами
своего неровного серпа касаясь губительной листвы гигантских
анчаров. В глубине долины полно уголков, где царит вечный мрак, и
те, кто там обитает, надежно скрыты от постороннего взора. Среди
дворцовых руин, разбросанных по заросшим травой и кустарником
склонам, стелются ползучие лозы и побеги вьющихся растений -
цепко оплетая надломленные колонны и зловещие монолиты, они
взбираются на мраморные мостовые, выложенные руками неведомых
зодчих. В ветвях исполинских деревьев, что высятся среди
запущенных дворов, резвятся обезьянки, а из глубоких подземелий,
где спрятаны несметные сокровища, выползают ядовитые змеи и
чешуйчатые твари, не имеющие названия.
Громадные каменные глыбы спят мертвым сном под одеянием из
сырого мха - это все, что осталось от могучих стен. Когда-то эти
стены воздвигались на века - и, по правде сказать, по сей день
еще служат благородной цели, ибо черная жаба нашла себе под ними
приют.
А по самому дну долины несет свои вязкие, мутные воды река
Век. Неизвестно, где берет она начало и в какие гроты впадает, и
даже сам Демон Долины не ведает, куда струятся ее воды и отчего у
них такой красный цвет.
Однажды Джин, пребывающий в лучах Луны, обратился к Демону
Долины с такой речью: "Я стар и многого не помню. Скажи мне, как
выглядели, что совершили и как называли себя те, кто воздвиг эти
сооружения из Камня?" И Демон отвечал: "Я - Память, и знаю о
минувшем больше, нежели ты. Но и я слишком стар, чтобы помнить
все. Те, о ком ты спрашиваешь, были столь же загадочны и
непостижимы, как воды реки Век. Деяний их я не помню, ибо они
продолжались лишь мгновение. Их внешность я припоминаю смутно и
думаю, что они чем-то походили вон на ту обезьянку в ветвях. И
только имя запомнилось мне навсегда, ибо оно было созвучно
названию реки. Человек - так звали этих созданий, безвозвратно
канувших в прошлое".
Получив такой ответ, Джин вернулся к себе на Луну, а Демон
еще долго вглядывался в маленькую обезьянку, резвившуюся в ветвях
исполинского дерева, что одиноко высилось посреди запущенного
двора.
В долине ущербная луна сияет мертвенно и тускло, концами
своего неровного серпа касаясь губительной листвы гигантских
анчаров. В глубине долины полно уголков, где царит вечный мрак, и
те, кто там обитает, надежно скрыты от постороннего взора. Среди
дворцовых руин, разбросанных по заросшим травой и кустарником
склонам, стелются ползучие лозы и побеги вьющихся растений -
цепко оплетая надломленные колонны и зловещие монолиты, они
взбираются на мраморные мостовые, выложенные руками неведомых
зодчих. В ветвях исполинских деревьев, что высятся среди
запущенных дворов, резвятся обезьянки, а из глубоких подземелий,
где спрятаны несметные сокровища, выползают ядовитые змеи и
чешуйчатые твари, не имеющие названия.
Громадные каменные глыбы спят мертвым сном под одеянием из
сырого мха - это все, что осталось от могучих стен. Когда-то эти
стены воздвигались на века - и, по правде сказать, по сей день
еще служат благородной цели, ибо черная жаба нашла себе под ними
приют.
А по самому дну долины несет свои вязкие, мутные воды река
Век. Неизвестно, где берет она начало и в какие гроты впадает, и
даже сам Демон Долины не ведает, куда струятся ее воды и отчего у
них такой красный цвет.
Однажды Джин, пребывающий в лучах Луны, обратился к Демону
Долины с такой речью: "Я стар и многого не помню. Скажи мне, как
выглядели, что совершили и как называли себя те, кто воздвиг эти
сооружения из Камня?" И Демон отвечал: "Я - Память, и знаю о
минувшем больше, нежели ты. Но и я слишком стар, чтобы помнить
все. Те, о ком ты спрашиваешь, были столь же загадочны и
непостижимы, как воды реки Век. Деяний их я не помню, ибо они
продолжались лишь мгновение. Их внешность я припоминаю смутно и
думаю, что они чем-то походили вон на ту обезьянку в ветвях. И
только имя запомнилось мне навсегда, ибо оно было созвучно
названию реки. Человек - так звали этих созданий, безвозвратно
канувших в прошлое".
Получив такой ответ, Джин вернулся к себе на Луну, а Демон
еще долго вглядывался в маленькую обезьянку, резвившуюся в ветвях
исполинского дерева, что одиноко высилось посреди запущенного
двора.
Рефлексивность это свойство не "объектов", а отношений https://ru.wikipedia.org/wiki/%D0%9E%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_%28%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%29.
Равенство - это отношение, оно обладает свойством рефлексивности, т.е. a=a.
Нестрогое неравенство - тоже отношение, оно обладает свойством рефлексивности a<=a.
Строгое равенство - отношение, оно свойством рефлексивности НЕ обладает, т.е. неверно что a<a.
У меня такое чувство, что он спрашивал про другое, но я не могу толком сформулировать.
Ну вот например в ООП у нас один и тот же объект может быть не равен себе в смысле значения. Есть ли еще примеры таких штук, где с равенством все непросто?
Ведь логичнее было бы назвать их некоммутативными, потому что композиция отображений некоммутативна, а ребра этих диаграмма направленные. Вместо употребления слова "коммутативность" можно было бы сказать "карач идем по стрелочкам и независимо от пути попадает из одного объекта в другой"
>>323581
>Ну вот например в ООП у нас один и тот же объект может быть не равен себе в смысле значения
Потому что ООП для даунов, а программирование - говно. Убожество программирования в том, что хорошую идею положили на убогую основу электронных цепей.
>Потому что ООП для даунов
Если ты не заметил, я в своем посте не утверждал, что ООП хорошее, и не предлагал обсуждать ни ООП, ни программирование. Я не знаю, к чему тут этот твой пассаж.
Коммутативность — независимость от порядка.
ab=ba — сначала сделать a, потом b = сначала сделать b, потом — a.
[тут должна быть коммутативная диаграмма] — сначала пройти по одному пути, потом — по другому = ну ты понел.
Ассоциативность, кстати, тоже — независимость от порядка. Эти два понятия (должны быть) близко связаны.
Ну верна)) И чё?))
Про отношения я понимаю (по крайней мере надеюсь, что не так туп), но вопрос о другом. Есть ли такие объекты (вещественные числа, многочлены, группы, что угодно), сравнение которых с собой не дает привычного для бытовой логики результата? Например 3=/=3. Или, например, а(1)=а(2), но а(2)=/=а(1), при том, что а(1) и а(2) - один и тот же элемент. Ну или при умножении элемента на его обратный элемент не получается нейтральный элемент.
Да это вопрос обозначений даже больше, значком = обозначают именно определённое отношение, которое рефлексивное по определению.
Не совсем понял, что значит "в смысле значения". Два разных объекта одного типа? Ну, естественно, в любой категории в которой больше одного объекта, можно взять два разных объекта который будут иметь типа один "тип". Как два разных множества, и.т.п. Но в чём тут сложность, я не понимаю.
Ну, как я и написал выше, это вопрос обозначения. Отношение равенства, обратный элемент и.т.д. это по определению что-то такое что выполняется X, поэтому найти такое что-то для которого X не выполняется не получится. Назовём "хорошими" прямыми прямые, которые не пересекаются. Тогда не получится найти пересекающихся хороших прямых, по определению.
Почему же тогда рефлексивность постулируют вместе с коммутативностью, ассоциативностью и дистрибутивностью? Помню в школе особо подчеркивали, что число равно само себе. С тех пор примеров объектов, которые "себе не равны" я не встречал, но не просто же так это оговаривается?
"Число равно само себе" и рефлексивность - это про разное, сказали ведь уже. Рефлексивность - это свойство отношения "равно", а не свойство чисел.
Вангую, что аксиомы навроде a=a вводят формальности ради, чтобы сложную ёбу можно было свести к a=a, которое по определение истинно, чтд.
о хоспаде, посмотри в сторону комплексных чисел, а особенно в то, что у них не производные, а вычеты.
>Чего ты к языку придираешься?
Эм, я не к языку придираюсь, а к содержанию. Просто тебе выше объяснили, ты вроде сказал, что понимаешь это, а тут опять путаешь - ну, или мне так показалось.
Нерефлексивное отношение
Точно? Но это означает, что любая окружность имеет "размерность", "мерность" 3 + 0,14.
Да, так и есть. Диаметр умножаем на пи и получаем длинну окружности. Такие дела.
не представляет интереса
Я не математик, но хочу в своем исследовании запилить математическую модель. Я ее пилил на линейном пространстве, но потом нагуглил, что есть абелевы группы, и они мне больше подходят, так как мне достаточно только натуральных чисел и сложения.
Правомерно ли будет использовать понятия линейного пространства, такие как вектор, размерность и линейная зависимость к абелевой группе?
Я так понял, что у тебя только свободные абелевые группы, т.е. просто сумма n копий Z. Т.е. как векторное пространство размерности n только не над R или C, а над Z, там никаких сложностей с размерностью нет. Вообще говоря, в абелевой группе, даже конечно порождённой, базиса нет, поэтому и размерность тоже не определить.
Это новый уровень опредления N?
Я просто тупой и мне кажется, что любой объект можно описать, как имеющий окружность, в том числе и время, которое как все знают, род пространства. (И вообще, кроме пространства ничего и нет больше). И это пространство имеет 3 целых измерения и бесконечное множество дробного. Время дробное измерение, линия Коха или что-то такое.
Наполовину правомерно. Идеология линейной алгебры тут применима, но Z — не поле, поэтому получается не линейное пространство, а модуль.
зачем?
не дегенераты, в смысле, а особого рода комрьютеры, которые ничего не понимают кроме символов, а чито эти символы означают, мозгов понять нету.
Топология?
с ручкой и без.
Расскажи. Чем интереснее?
Расскажи. Чем интереснее?
>как векторное пространство размерности n только не над R или C, а над Z
Верно.
>в абелевой группе, даже конечно порождённой, базиса нет, поэтому и размерность тоже не определить
Мне нужно различать линейную зависимость между векторами. Если есть линейно независимые, то должен быть и базис.
>>323758
В общем, можно ли в абелевой группе различать линейно зависимые векторы и линейно независимые? И правомерно ли вообще называть эти объекты векторами?

> Если есть линейно независимые, то должен быть и базис.
Это не так и это одно из первых отличий модулей от векторных пространств. Если, например, ты рассмотришь рациональные числа как модуль над целыми, то существуют сколь угодно большие по мощности множества линейно независимых векторов. Однако базиса, т.е. линейно независимой системы, через которую всё выражается найти нельзя.
Но мне не понятно, нужно это тебе или нет, т.к., повторюсь, в свободных абелевых группах-то всё норм.
> линейно зависимые векторы и линейно независимые? И правомерно ли вообще называть эти объекты векторами?
Понятие линейной зависимости имеет смысл для модулей вообще. Хотя тут тоже есть разночтения, например пикрил пассаж из книжки Вавилова. Если хочешь, векторами можно называть что угодно.
Так и надо. Математикам похуй что это за числа и они могут даже векторную массу получить. Ибо их стезя числа и действия над ними.
Спасибо. Буду переваривать.
Потому что событие может никогда не наступить, даже если вероятность его наступления ненулевая.
Т.е. если мы бросим кубик с желанием получить двойку неограниченное количество раз, всегда есть шанс того, что мы получим событие с вероятность 5/6? Такая логика рассуждений?

хуйню написал какую-то
Покупать шесть близлежащих в самом начале и качать их до максимума.
Ну может так и выгоднее, но шанс, что у кого-то 2 раза подряд будет 7, все равно очень маленький.

Скорее всего это мегатупой вопрос, но все-таки.
Везде пишут, что простых чисел бесконечное множество, тут все предельно понятно, доказательство найти легко.
Но почему так сказано именно про простые числа, разве с составными не аналогичная ситуация? Гугл по запросу "бесконечное множество составных чисел" ничего годного не выдает. Существование бесконечного множества простых чисел подразумевает и бесконечно множество составных?
Чтобы этот ответ не казался таким тупым, представьте, что его автору 10 лет (и он умственно отсталый).
Да, потому что всё очевидно с составными.
точняк, если P - множество простых, то 2P вложено во множество составных и имеет ту же мощность, что и P.
Кстати, я тут мимоходом, а как доказывается, что множество простых счётно? Чёт не вижу простого доказательства.
ну вроде бы если множество счетно(а множество натуральных счетно), то его подмножество счетно и подавно. а простые это подмножество натуральных
Множество простых счётно, потому что, во-первых, оно не более чем счётно, т.к. множество натуральных счётно и, во-вторых, бесконечно.
К чему тут твой вопрос? 2 - простое число. 2x3x5+1 = 31, простое число. А ты - некультурный и глупый уебок.
Ты просил доказать, что оно счетно, и тот анон дал совершенно правильное доказательство. А ты - некультурный и глупый уебок.
Ты просил про счётность, как будто бесконечность тебе уже ясна. Чел выше всё правильно сказал про доказательство бесконечности - берёшь сумму простых и прибавляешь единицу - новое простое, опа ай тыдымдым тым дым дай. Ты просто забыл ещё с двойкой перемножить.
>>323941
васюк, я просил доказать, что множество простых чисел бесконечно. То, что оно не более чем счётно - очевидно. Вероятно, что и доказательство того, что не менее чем счётно тоже школьное, но я его не смог придумать, поэтому и спросил. То, что ты выдаёшь за доказательство бесконечности - какая-то несуразная хуита.
> берёшь сумму простых и прибавляешь единицу - новое простое
вот это докажи тогда мне, пока про это речи не было
> Кстати, я тут мимоходом, а как доказывается, что множество простых счётно? Чёт не вижу простого доказательства.
>васюк, я просил доказать, что множество простых чисел бесконечно.
> Кстати, я тут мимоходом, а как доказывается, что множество простых счётно? Чёт не вижу простого доказательства.
>>323943
> То, что ты выдаёшь за доказательство бесконечности - какая-то несуразная хуита.
Если тебе не хватает мозгов додумать до конца - это твои проблемы. Я тебе дал идею доказательства, не можешь додуматься сам - спроси у гугла. И уебывай отсюда, кстати.
Так ты тут самообразовываться пришёл или выёбываться? Это стандартное доказательство, смотри википедию например. Если ты не хочешь для себя проделывать даже этого, то пшёл отсюда пёс, не лезь к господам с перегаром люмпен.
Даже дураку вроде тебя должно быть очевидно, что он опечатался, и вместо суммы там должно быть написано "произведение".
анус себе зарепорть, пидор
Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор. Противоречие.
Такое док-во никто даже близко не обозначил, только тявканье было какое-то.
Ну слава богу, хоть в википедию слазил. Не всё потеряно, может в Саров возьмут какой-нибудь или конструкторское бюро, квадратурные формулы для интегральчиков программировать.
>ты пропердел только то, что при перемножении простых и добавлении единицы получаем простое
Процитируй.
Почитай Хамфри.
>пик
Ну бред же! Никогда в книгах по программированию такого не было. Обычно наоборот книги пишутся американскими специалистами по вбиванию информации в тупые головы. Там наоборот всё просто обычно.
нравится жевать чужое дерьмецо, не имея собственного мнения, сраное чмо?
Как раз по теории вероятности, вероятность выпадения 7 шагов два раза подряд максимальна, а именно (1/6)*(1/6) все остальные меньше.
Открывай ротик, братишка.
упорок, я нихуя не пойму тебя. тебе надо бесконечность доказать? для любого натурального числа можно поставить в соответствие число+1. для любого. поэтому оно бесконечно. про счетность уже все отписали. чего спрашивается раскудахтался?
В Монополии бросают два шестигранных кубика. Всего элементарных исходов 36. буду обозначать исход, когда на первом кубике выпало a, на втором b, как a.b.
Рассмотрим вероятности выпадения чисел от 1 до 12.
1 = {}, пустое множество
2 = {1.1}
3 = {1.2, 2.1}
4 = {1.3, 2.2, 3.1}
5 = {1.4, 2.3, 3.2, 4.1}
6 = {1.5, 2.4, 3.3, 4.2, 5.1}
7 = {1.6, 2.5, 3.4, 4.3, 5.2, 6.1}
8 = {2.6, 3.5, 4.4, 5.3, 6.2}
9 = {3.6, 4.5, 5.4, 6.3}
10 = {4.6, 5.5, 6.4}
11 = {5.6, 6.5}
12 = {6.6}
Соответственно,
P(1) = 0,
P(2) = 1/36
P(3) = 2/36
P(4) = 3/36
P(5) = 4/36
P(6) = 5/36
P(7) = 6/36
P(8) = 5/36
P(9) = 4/36
P(10) = 3/36
P(11) = 2/36
P(12) = 1/36
Так что и правда, 7 наиболее вероятно.
В Монополии бросают два шестигранных кубика. Всего элементарных исходов 36. буду обозначать исход, когда на первом кубике выпало a, на втором b, как a.b.
Рассмотрим вероятности выпадения чисел от 1 до 12.
1 = {}, пустое множество
2 = {1.1}
3 = {1.2, 2.1}
4 = {1.3, 2.2, 3.1}
5 = {1.4, 2.3, 3.2, 4.1}
6 = {1.5, 2.4, 3.3, 4.2, 5.1}
7 = {1.6, 2.5, 3.4, 4.3, 5.2, 6.1}
8 = {2.6, 3.5, 4.4, 5.3, 6.2}
9 = {3.6, 4.5, 5.4, 6.3}
10 = {4.6, 5.5, 6.4}
11 = {5.6, 6.5}
12 = {6.6}
Соответственно,
P(1) = 0,
P(2) = 1/36
P(3) = 2/36
P(4) = 3/36
P(5) = 4/36
P(6) = 5/36
P(7) = 6/36
P(8) = 5/36
P(9) = 4/36
P(10) = 3/36
P(11) = 2/36
P(12) = 1/36
Так что и правда, 7 наиболее вероятно.
Хуйню написал.
Для кубиков это так, а для монополии нет. Ведь там еще развитие идет, цена домиков деревянных, набигать на них можно и платить.
Так ведь наиболее вероятно, что попадать будут на каждое седьмое поле, значит покупать поля данного цвета наиболее выгодно.
Домики развиваются только если куплены три в ряд из одной секции одного цвета. Такие правила.
В самом начале домики самые дешевые, самые выгодные на первом повороте после старта, самые йобы до старта, но у них цена заоблачная.
так я в смысле поддвачиваю, а не опровергаю) просто судя по срачу выше анон не понял что надо перемножать ВСЕ простые числа до определенного, а не от пизды выбранные на удачу)
Ты что, N цИпленка не узнал?
Я это к тому написал, что если у тебя простые числа начинаются с 3 и 5, с присутствующей еденицей, то ты пропустил двойку. Короче, хуевый пример ты привел. Намного лучше сито платона/сократ/как там блядьего звали, на котором уголкой на воске все числа сократимые зачеркиваются.
Давайте. Я считаю, что определяют.
Вероятность выпадения семи и любого другого числа, кроме семи, больше, чем вероятность выпадения семи и семи.
1) уже всё доказали. 2)следование верное т.к. простые только подмножество натуральных. если бесконечна часть, то целое ясен красен бесконечно. 3) заебал уже, фурри модера натравить на тебя надо

>простые только подмножество натуральных. если бесконечна часть, то целое ясен красен бесконечно.
> Если натуральных бесконечно, то и простых бесконечно.
> если бесконечна часть, то целое ясен красен бесконечно.
> Если натуральных бесконечно, то и простых бесконечно.
Перечитай пост, на который ты отвечаешь.
Действительно. Спасибо, анон.
Неравенство отсюда.
http://research-journal.org/physics-mathematics/trigonomericheskoe-otobrazhenie-dejstvitelnyx-chisel-elementarnoe-dokazatelstvo-poslednej-velikoj-teoremy-p-ferma/
Похоже я тупой слишком, раз меня элементарное озадачивает. В общем, предлагаю умному анону найти ошибку в статье.
Ошибка в формуле 4. Произвольное c не равно a2+b2.
Верное. Если B - истинное высказывание и A - любое высказывание, то импликация "A -> B" истинна.
https://ru.wikipedia.org/wiki/%D0%98%D0%BC%D0%BF%D0%BB%D0%B8%D0%BA%D0%B0%D1%86%D0%B8%D1%8F
> Не следует путать импликацию (→) и логическое следование (⇒). Импликация как логическое выражение может сама принимать значения истины или лжи. Логическое же следование A ⇒ B утверждает, что во всех случаях, когда формула A истинна, B также будет истинно.
> Неверное следование.
> Верное.
Еще вопросы?
Теорема о логическом следовании.
Формула B является логическим следствием формулы A тогда и только тогда, когда импликация "A->B" истинна.
А хотя хрен с вами, докажу.
Напомню таблицу истинности для импликации.
0->0 истинно
0->1 истинно
1->0 ложно
1->1 истинно
Доказательство.
Пусть импликация A->B истинна.
Пусть A истинно.
Значит, B истинно, иначе импликация была бы ложной.
Поэтому если импликация истинна, верно, что во всех случаях, когда A истинно, B тоже истинно.
Т.е. если импликация истинна, верно, что B является логическим следствием A.
Пусть B является логическим следствием A.
Тогда во всех случаях, когда A истинно, B тоже истинно.
Импликация ложна только когда истина влечёт ложь, поэтому импликация A->B не может быть ложной.
Т.е. если B является логическим следствием A, то импликация A->B истинна.
Формула B является логическим следствием формулы A <=> во всех случаях, когда A истинно, B тоже истинно.
Короче, мне надоело этой хуйней страдать. Доказательство анона выше верно, если не заморачиваться логическими изъебствами. Если тебе правда интересно, то определи, что такое простое число для данной модели натуральных чисел, там операции всякие и прочее прочее.
https://en.wikipedia.org/wiki/Logical_consequence почитай уже и не "страдай хуйней", ага.
>>324165
>там операции всякие и прочее прочее.
Лол.
Ты и я.
Определение, которое я дал, вполне корректно, я взял его из учебников матлогики. Укажи на недостаток в нём или объясни, чем оно неадекватно обсуждаемым нами вещам, какой аспект обсуждаемого в нём не отражён.
Не могу понять, почему алгебра и сигма-алгебра - не одно и то же.
Допустим, я по свойству алгебры возьму два элемента и объединю их. Их объединение будет лежать в этой алгебре. Почему я не могу добавлять к этому элементу еще счетное количество элементов? Оно, ведь, тоже будет лежать в алгебре.
Я хз про что ты, но когда пишут АUВ, то подразумевают конечное число сложений. А когда счетное и несчетное U a из Г (Aa), где Г счетное или несчетное.
Просто приведи несколько примеров алгебр, не являющихся сигма-алгебрами.
Например, рассмотрим множество M всевозможных конечных подмножеств ℝ и их дополнений.
Т.е. если m∈M, то m либо конечно, либо является дополнением конечного.
Легко проверить, что M - алгебра (в смысле, алгебра множеств).
Заметим, что дополнение конечного множества в ℝ - несчётное множество.
Поэтому M не содержит ни одного счётного множества.
Например, M содержит множества {1}, {2}, {3}, {4}, {5} и так далее.
То есть каждое множество вида {n}, где n - натуральное число, является элементом M.
Таких множеств счётное количество.
Объединение этих одноэлементных множеств есть ℕ.
Но ℕ счётно и потому не есть элемент M.
То есть M - алгебра, но не сигма-алгебра.
> Не могу понять, почему алгебра и сигма-алгебра - не одно и то же.
http://lmgtfy.com/?q=algebra+that+is+not+a+sigma-algebra
Ты его взял из вагины своей мамаши, уебок. Ввел два понятия с одинаковыми определениями а потом доказывает что они эквивалентны. Поссал на твое лицо.
мимо
Понял, Анон. Благодарю.
Недавно осознал что ни одной такой нет у меня (хотя, возможно, это нормально).
один математический вопрос, связанный с производными.
поясните почему y''(x)= 0.5d/dyy'(x)^2
Я действовал так:
y''(x) = d2y/dx2 = [d(dy)]/(dx)^2 , домножим и разделим на dy, тогда
d(dy)(dy)/[(dy)(dx)^2] и это равно d/dy*(dy/dx)^2
почему там ещё надо на двойку делить?
Нету. Я что, дурак, что ли?
Я не ебу, ты или не ты, но какой-то хуй говорил, что если у него хуй маленький, то у всех хуй маленький.
короче я разобрался.
Блядь, так выше и сказали про то, что импликация != логическое следование, школотрон.


>между шумерами и количестом градусов в круге
Хочешь знать то, чего не знаем мы?
Ну попробуй.
Мы уже давно вычисляем числовые поля, через вычисления и можем кое что сказать по этой теме. Но не все сразу
Более того, у меня нет ни одной книги, которую я читал более менее последовательно начиная с начала, кроме совсем уж ентрилевела вроде фихтенгольца. И то, только для экзаменов.
Ты дебил? "Импликация" и "логическое следование" равносильны.
A→B истинно тогда и только тогда, когда A⊧B.
Все очевидно. Шумеры пользовались шестидесятиричной системой счисления, ибо дроби у них еще не изобрели. Ихнеё сто равнялось нашим трехсотшестидесяти. А дальше все совсем очевидно, круг они делили на 360 кусочков, это себе забрали египтяне, потом у египтян греки, и гдето между греками и нынешним временем все начали считать что у круга 360 градусов.
У меня только одна (возможно, это потому, что я математикой заинтересовался год назад).
Sheldon Axler: Linear Algebra Done Right
Прочитал все, решил все упражнения кроме одного.
Читать книгу начал год назад. По ощущениям в сумме ушло часов 300-400.
Дебил, у тебя по определению логическое следование = импликации, и ты доказываешь, что логическое следование = импликации. Блядь, что за ебаный тред, позор какой-то нахуй, почитай хотя бы википедию, я даже не говорю про учебники про матлогу, просто блядь обычное введение для гуманитарных специальностей, блядь, да на первой же лекции в любом вузе этот вопрос разбирается, иди нахуй короче.
Ты ебанутый? Я тебе определение принёс, доказательство принёс, хули ты кукарекаешь вообще? Или у тебя какое-то особенное логическое следствие? В таком случае определи, что означает значок ⊧. Я определение, в отличие от тебя, дал.
Давай я тебе вслух прочитаю, что там написано.
Formula A is a semantic consequence within some formal system FS of a set of statements Г, if and only if there is no model I in which all members of Г are true and A is false.
Формула X является логическим следствием множества формул Г тогда и только тогда, когда во всех случаях, когда каждая из формул из Г истинна, формула X также истинна.
Прекрати свой цирк с конями. Тут уже все поняли что ты школяр бунтующий против пеано, имплификации, сети, и т.д.
В бе пройдись, там ты найдешь дискуссоров своего уровня. Смотри балет, короче.
петух_у_параши.пнг
Ты можешь сказать что-то конкретное? Я тебе учебники матлогики пересказываю, а ты про каких-то коней вещаешь. Небось даже слова "теорема о логическом следствии" не слышал ни разу.
Хули ещё ждать от /sci/, впрочем.
Теорема о логическом следствии ошибочна?
Если она при этом непрерывна, то это константа, вроде бы. Но как доказать?
А что если она разрывна? или непрерывна только с одной стороны?
UPD по поводу непрерывной: если она дифференцируема на всём промежутке, то понятно, что там f' = 0 и это константа, а вот если у неё есть точки, в которых она не дифференцируема?
Если вспомнить отпределение синуса, то это сколько раз влезает гипотенуза в противолежащий катет треугольника. Поясните мне, что это должен быть за треугольник, чтобы синус равнялся единице? Получается у него должен быть один угол почти равным девяноста градусам, а другой стремится к нулю. Тобишь треугольник должен вырождаться в прямую. Я все рпавильно понял или нет?
А как получаются экспоненту из пределов? В википедии написано на уровне "вот тут доказываем что снизу ограничена двойкой, вот тут тройкой, а потом чики-брыки и экспонента равна 2.7год рождениятолстого два раза"
это
lim (1+1/x)^x x->+inf
Если подставить вместо x 1000 то ты получишь уже похожее на экспоненту число.
Сперва докажем, что последовательность (1 + 1/n)^n возрастает и ограничена, а значит имеет супремум, который по определению назовём "е". Рассмотрим f(x) = (1 + 1/x)^x. Оценим сверху:
(1 + 1/x)^x <= (1 + 1/n)^n {где n -- целая часть x} = (1 + 1/n)(1+1/n)^n <= (1+1/n)e <= (1+ 1/(x-1))e = x/(x-1) e.
Потом снизу:
e <= (1+1/(n+1))^(n+2) <= (1+1/x)^2 (1+1/x)^x.
Потом по теореме о милиционерах получаем, что f(x) -> e.
Математика предстала передо мной напрочь оторванным от реальности продуктом мышления, жалкую часть которого порой как-то удаётся связать с жизнью. Чаще всего от апологетов я слышу что-то про математическую красоту и про развитие ума, но это звучит как-то неубедительно.
Слишком много вопросов накопилось: Какое право математика имеет на истинность? Почему математики тратят столько времени на совершенно бесполезную и непродуктивную деятельность, когда представители других фундаментальных наук занимаются реальными делами? Нельзя ли найти более эффективного инструмента для описания мира, чем математика?
От многих слышал, что если с детства математикой не занимаешься, то все попытки её изучения будут тщетны - не понравится, не поймешь, будешь плеваться. Так ли это? Может, книжек каких почитать, или уже всё потеряно?
>у неё есть точки, в которых она не дифференцируема
тогда она не сможет иметь экстремум в каждой своей точке
АТВИЧАЮ, БЛЯ БУДУ
Ничего. Никакого. Просто так. Пока не удалось, да и зачем. Ну такое. Перестала нравиться математика - иди в кодеры.
Далеко не все свойства тел, которые изучает физика, когда-либо будут востребованы рынком.
Далеко не все вещества, которые синтезирует химия, когда-либо будут востребованы рынком.
Далеко не все абстрактные объекты, которые изучает математика, когда-либо будут востребованы рынком.
Но это не значит, что все эти науки бесполезны. Математики изучают абстрактные объекты (по сути, наборы свойств). Изучение заключается в систематизации, в установлении теорем и в доказательстве эквивалентности. Мы берём множество с какой-то структурой и изучаем эту структуру. Мы выдвигаем гипотезы о ней и затем пытаемся решить, правдивы ли они. Чувство, которое нами движет, - любопытство. Мы очень хотим знать, к примеру, является ли топологическое пространство с аксиомой T3.5 пространством с аксиомой T2 или же всё-таки нет. Мы готовы не спать ночами, зарываться в литературу и от корки до корки исписывать тетради, лишь бы понять, является ли оно или же не является.
Если у тебя нет чувства научного любопытства, то тебе, пожалуй, не нужно заниматься наукой. Чувство научного любопытства похоже на раскалённое шило в заднице. О нём нельзя просто забыть. Оно постоянно жаждет ответов.
И нет, более эффективного инструмента найти нельзя, потому что математикой становится любое достаточно далеко зашедшее исследование абстрактных объектов.
Ну во первых математика имеет приложения практически во всех науках. Интегральное исчисление и дифференциальные уравнения продвинули физику, мат статистика нужна для анализа экспериментальных данных. Дискретная математика нужна для исследования алгоритмов.
Топология активно применяется в химии. Плюс еще и интеллект развивает, человек с наивысшим iq в мире математик: https://ru.m.wikipedia.org/wiki/%D0%A2%D0%B0%D0%BE,_%D0%A2%D0%B5%D1%80%D0%B5%D0%BD%D1%81
Ещё раз бамп. Хорош обсуждать хуйню, диванные философы, лучше подсобите с тривиальной задачей.
Чтобы точка x была экстремумом функции f, по определению нужно, чтобы функция f была определена в точке x.
Если функция имеет экстремум в каждой точке, то функция определена в каждой точке.
И что? это не отменяет того, что она может не дифференцироваться в какой-то точке.
Он взял милиион, или сколько там полагается за решение проблемы, и переехал работать на запад, как ему предлагали?
> Он взял милиион
Про пирамиду потребностей маслоу слышал что-то? Очевидно что Перельман находится на самом высшем уровне, где "потребность в самовыражении" и для него выразить свое мнение было намного значимей чем миллион. Ясно что тебе-то со второго-третего уровня это кажется тупостью, так как у тебя таких потребностей нет. Но это не делает Перельмана дауном.
Нахуя ему деньги, если он умеет управлять вселенной: http://so-l.ru/news/show/perelman_priznalsya_chto_umeet_upravlyat_vselennoy
Эта статья - выдумка и бред. Причём за неё до сих пор никто не извинился.
>Перестала нравиться математика - иди в кодеры.
А я то же самое хотел посоветовать, но как раз чтоб вернуть\привить эту самую "любовь к математике". Занятно.
>И нет, более эффективного инструмента найти нельзя, потому что математикой становится любое достаточно далеко зашедшее исследование абстрактных объектов.
Попахивает недальновидным шовинизмом и очень портит в остальном блестящий пост.
Ему 40, а выглядит он на 18. Математика еще и омолаживает, так-то!
Все там нормально, любое исследование абстрактных объектов-математика по определению.
Не видит в этом нужды, нахуя просторная трешка, если твое призвание-решать математические задачи. Ты бы еще спросил, почему у него нет тян.
чувство эстетичности!= Интеллект
Интеллект нужен для того, чтобы эффективно достичь своей цели, но он не определяет цель.
буду особливо рад чему-нибудь буржуйскому, но на русском тоже покатит
П.С.Александров. Введение в теорию групп.
Философия, например, бывает не только математической. Поэты и композиторы тоже исследуют абстрактные объекты. Но я вообще не об этом говорил.
>>324595
Я же процитировал, где. Если быть еще точнее, вот здесь:
> нет, более эффективного инструмента найти нельзя
Это из разряда "ньютоновской физикой можно описать все". Знаем, проходили.
>до сих пор живет с мамкой в тесной однушке и ходит в одежде от кутурье бомж михалыч
И тем не менее, наверняка, всякий завсегдатай мат. тредов хотел быть на его месте. Шёл бы ты отсюда.
Так ведь любая теория об абстрактных объектах, автоматически становится математической, философия не в счет, там больше рассуждений без доказательств, ИМХИ так сказать, а единственный способ установить истинность абстрактного утверждени-математическое доказательство(конечно можно считать, что в будущем мы найдем другие способы, но это все рано, что называть людей научного склада мышления шовинистами из-за того, что возможно существуют какие-то иные методы познания)Вроде если ты выдвинешь теория какой-нибудь наука_неймлогии оперирующей абстрактными объектами, то это все ровно будет математика. Квантовая физика , тоже ведь физика. Также как и алгебра и высшая алгебра обе являются разделами математики.
Алсо, в силу строгости математических доказательств-предыдущие результаты не могут быть опровергнуты, как в физике. Не возможно опровергнуть, что квадрат гипотенузы не равен сумме квадратов катетов,ибо это строго доказано.В физике можно например показать эффекты не вписывающиеся в классическую картину в эксперименте, потому физика потенциально может серьезно меняться, а математика может только развиваться ибо невозможно опровергнуть уже доказанные теоремы.
То, что математическое доказательство вообще является способом установить истинность абстрактного утверждения, а также то, что истинность абстрактного утверждения вообще осмысленное понятие - это наивный взгляд на вещи, мне кажется. Всё так или иначе сводится к тому, как ты интерпретируешь некоторые абстрактные термины образами из реального, или не очень, мира. Тот треугольник, который выпуклая оболочках трёх афинно-независимых точек в трёхмерном евклидовом пространстве и тот треугольник, который получается в твоей голове как абстрагирование зрительных образов контуров реальных объектов - вообще говоря разные треугольники.
>Так ведь любая теория об абстрактных объектах, автоматически становится математической
Кстати, в физике очень хорошо прослеживается следующий сюжет: некоторая абстрактная сущность есть, как она ведёт в частных случаях более-менее понятно, а нормального математического формализма нету. Пример: интегралы Фейнмана по траекториям. Вот ещё один наглядный пример науки об абстрактных объектах, которая не математика.
Разве нет строгого определения?
Ок, пример не очень удачный, т.к. теорема Пифагора есть по сути определение евклидовой метрики, но что например с теоремами теории множеств(Кантора-Бернштейна например, неужели по вашему мнению оно субъективно)
Разве можно представить понятие множества по разному. Алсо, в чем существенная разница описанных тобой представлений треугольника в соответствующей метрике
А почему если множества, то сразу ZFC? Есть NF, в которой теорема Кантора-Бернштейна не выполняется.
>>324644
Потому что одно - математический формализм, грубо говоря - конечная строка построенная по некоторым изощрённым правилам, а другое - голая абстракция прямиком из пещеры Платона.

Тут нужно кое-что уточнить. Несмотря на мощное лобби логиков, математики не думают о своих объектах как о строчках символов, о чём и ты сам когда-то говорил. Математический объект не сводится к его определению, определение само по себе почти ничего не стоит. Важен смысл понятия; важны его мотивировка, аллюзии, интуитивный смысл, примеры, история эволюции, равносильные формулировки, основные свойства, а также контексты, в которых оно используется, и даже инфа о математических школах, которые его употребляют. Математическое понятие - это "психологический объём", некоторое количество "когнитивной материи", поименованная клика мыслеобразов. Вовсе не строка символов.
Ну это как и в любой нормальной сфере человеческой деятельности - человек не становится рабом того, что он напридумал, наоборот он изменяет и управляет тем что создал.
Гм, либо я не понял коммент kaledin'а (я не знаю его контекста...), либо ещё чего, но из него может сложиться впечатление, что программистам на удобство плевать. А на самом деле именно в программировании почти все нововведения появляются для повышения удобства (и "концептуальной правильности", если я правильно понимаю этот туманный термин). Потому что обычно самая критичная вещь - скорость работы кодера и часто ещё чтобы его код могли понять другие.
Не поверишь, но такой пример это тоже математика, просто хуевая в некотором смысле. У итальянских геометров конца 19го века та же хуйня было с их занятиями алгебраическкой геометрией. Дошли до того, что доказывали противоречащие друг другу факты и спорили, кто правее. До тех пор пока всякие Гротендики наконец не формализовали это все.
Ты же не собираешься назвать алгебраическую геометрию не матетической наукой?
А суть в том, что математика та же естественная наука (изучает абстрактные объекты), просто роль эксперимента, подтверждающего теорию, играет доказательство. Поэтому работа с объектами без нормальных доказательств и определений подобна работе в физике с теорией, которая еще не подтверждена экспериментами, но часто помогает.
>>324673
Каледин разумеется не прав, так как имел в виду былдлокодера, для которого не важно, как именно писать, а важно только то, что в итоге делает программа. Разумеется, в программировании очень важно удобство и читаемость кода, которые как раз достигаются за счет повышени уровня абстрактности (всякое ООП, функциональщина). Прямо как в математике.

А ну все, понял. Это график f(x), а теорема Ролля для F(x)
Математические объекты, не обсуждая вопрос об их существовании, не доступны прямому наблюдению. Мы можем иметь интуиции на их счет, но единственный способ устанавливать знание в математике, принимаемое математическим сообществом, как таковое - это подробные математические доказательства. После последних существенных поправок, т.е. выделения формальных теорий и установления стандарта использования аксиоматической теории множеств по умолчанию, этот способ не давал принципиальных осечек - не известно двух, действительно хорошо проверенных, подробных доказательств дающих противоречивые результаты. Тем самым отождествление математической истины с существованием подробного и безошибочного доказательства единственный видный на текущий момент способ получить не субъективное понятие математической истины.
>Разумеется, в программировании очень важно удобство и читаемость кода, которые как раз достигаются за счет повышени уровня абстрактности (всякое ООП, функциональщина). Прямо как в математике.
Угу, именно так. Ну и даже быдлокодеры тоже стремятся к удобству в меру своих возможностей, иначе они бы все писали на ассемблере.
Так я про то и говорю, что абстракция и математическая формализация этой абстракции - вещи не тождественные, а теоремы, они всё-таки о втором, а не о первом, поэтому я бы не говорил, что математическое доказательство - это: "...способ установить истинность абстрактного утверждения...", - а уж тем более единственный. Приведу простой пример, вот у нас есть арифметика (аксиомы ZFC, если угодно), берём какой-нибудь многочлен p(x1,x2,x3,...,xn) от многих переменных с коэффициентами в целых числах такой, что ZFC не доказывает то, что у этого многочлена есть целочисленный корень и что его нет тоже не доказывает. Однако мы-то понимаем, что это значит только то, что корня на самом-то деле нет (по модулю того, что мы верим в то, что аксиомы ZFC непротиворечивы), потому что если бы он был, мы бы подставили его в многочлен и получили бы тем самым доказательство существования корня, а мы знаем, что его не существует по условию выбора многочлена p. Более того, мы можем даже присоединить аксиому о том, что такой корень существует и получить новую теорию, которая, безусловно недостаточно адекватно отражает утилитарную абстрактную концепцию: "многочлен нескольких переменных с коэффициентами в целых числах", которая имеется у всякого чуть ли не a priori, однако в этой теории мы точно так же можем "математически доказать", что у многочлена p корень есть (при том в одну строчку). Поэтому, мне кажется, в ХХI веке неправильно возводить математическое доказательство в абсолют и считать его непоколебимой истиной. Хотя, тут опять же всё упирается в то, что понимать под "непоколебимой истиной" и под "абстрактным утверждением", очередной спор об определениях и категориях, короче.
>>324684
Ну так можно дойти до того, что философия - это тоже математика, просто хуёвая в некотором смысле, а математика - это тоже философия, просто хуёвая в другом смысле. И что такое "абстрактный объект"?
Я не хочу тебя обидеть, но мне видится вполне вероятным, что твое недоумение вызвано банальным недостатком релевантных знаний.
>>324627
>истинность
define истинность.
> но это все рано, что называть людей научного склада мышления шовинистами из-за того, что возможно существуют какие-то иные методы познания
Ты путаешь точку зрения "математика полезна" с "нет ничего полезней математики".
>>324632
>В физике можно например показать эффекты не вписывающиеся в классическую картину в эксперименте
Ньютоновская физика неверна, хе-хе. Надеюсь, ты уловил суть рассуждения.
>>324633
>Всё так или иначе сводится к тому, как ты интерпретируешь некоторые абстрактные термины образами из реального
Неверно по сути, на мой взгляд. Интерпретация - удел физиков.
>>324656
Не согласен с его трактовкой понятия "программист".
>>324684
>А суть в том, что математика та же естественная наука
Принципиально не согласен. Мировое научное сообщество меня, кстати, поддерживает в этом.
>Неверно по сути, на мой взгляд. Интерпретация - удел физиков.
Пример ещё проще: ZF+{Аксиома выбора} доказывает утверждение: "Измеримые по Лебегу множества существуют", а ZF+{Аксиома детерменированности} доказывает утверждение: "Измеримые по Лебегу множества не существуют". Так что мне ответить человеку, который у меня спросит: "Существуют ли измеримые по Лебегу множества?"? И о какой тогда "абсолютной истине" и "единственном способе выяснения природы абстрактных объектов" может идти речь?
Так это вроде бы подкрепляет высказанную мной точку зрения, а не опровергает ее, нет?
>Ньютоновская физика неверна.
Да, но ты никогда не сможешь опровергнуть топологию и теорию Галуа т.к. они строго доказаны.
Видимо спутал. Зачем бы мне на свой же пост понадобилось бы отвечать?
Но это все равно не то. Я-то начал эту дискуссию с гораздо более радикального утверждения, ежели кто не заметил.
Возьмем тех же комплюктер сцайенистов. Возгласы "cs - не наука, cs'еры - не математики" прошу приберечь для следующей итерации. В доброй половине пейперов цель, гхм, работы формулируется примерно как "возьмем вот эту штуку и посмотрим, насколько будет удобно с ее помощью что-нибудь делать". Я потому и не согласился со словами kaledin: все, как мне кажется, наоборот. А за его высказываниями о "концептуальной правильности" так и сквозит еще одно понятие: эстетика.
>неправильно возводить математическое доказательство в абсолют и считать его непоколебимой истиной.
В твоем примере, что в первом случае, что во втором (с дополнительной аксиомой) - с доказательствами всё в порядке, они будут безукоризненно правильными. И при условии, что теории - ZFC и ZFC+аксиома - непротиворечивы, оба доказательства имеет место быть.
Можно посчитать два эти доказательства непоколебимой истиной, если так уж хочется использовать слово "истина". Ну а вообще, по-моему, оно здесь лишнее.
Теперь уловил, извиняюсь.
С формальными доказательствами всё в порядке, но ведь все понимают, что многочлен p на самом деле корней не имеет, а доказательство, что в первом, что во втором случае, это доказательство, грубо говоря, не о самом многочлене, а об его образе сквозь призму ZFC и ZFC+{p имеет корень}.
Вообще говоря отвечаю, в меру своих возможностей, я просто на саентач зашёл первый раз за 10 дней, и тут в конце ветки дискуссия была околофилософскоо характера, а вопросов не было. А ещё я на math.stackexchange всяких активен достаточно.
>все понимают, что многочлен p на самом деле корней не имеет
Это "самое дело" зависит от модели теории, которая выбрана именно таким образом, что многочлен не имеет корней. Но, вообще говоря, нет никаких математических оснований отдавать предпочтение одной модели и считать такую интерпретацию единственно верной.
Не думаю что мой ответ тебе понравится, и заранее предупреждаю, что я плохо разбираюсь.
Ну во-первых давай вопрос чуть структурируем, я буду отвечать только про изометрии плоскости и пространства, т.е. Iso(2,R) и Iso(3,R).
1) Тебя интересует классификация подгрупп в этих группах (Iso(2,R) и Iso(3,R)).
У этих двух групп помимо структуры группы есть ещё структура многообразия, что превращает эти группы в так называемые "группы Ли" и сразу же я отвечу тебе на второй вопрос, фундаментальное отличие группы симметрий диска от группы симметрий многоугольника ни в том, что первая бесконечна, а вторая конечна, например группа симметрий Z^2 ("целочисленная решётка") тоже бесконечна, однако она не "непрерывная" как группа симметрий диска. Фундаментальное отличие как раз в том, что группа симметрий диска - является подгруппой Ли (которая называется O(2,R)) у Iso(2,R) а группа симметрий многоугольника или Z^2 - являются дискретными группами (у них топология, индуцированная из Iso(2,R) - дискретная).
Не дискретные и не подгруппы Ли тоже существуют - например все повороты на рациональный угол образуют некоторую подгруппу, но они, вроде бы, никому не интересны.
C конечными группами всё совсем просто, любая конечная группа у Iso(2,R) сохраняет точку, поэтому является подгруппой О(2,R), а любая конечная подгруппа у О(2,R) является либо диэдрической группой, либо циклической группой.
Любая бесконечная дискретная подгруппа у Iso(2,R) порождает так называемые "решётки", которые более-менее все расклассифицированы: https://en.wikipedia.org/wiki/Frieze_group https://en.wikipedia.org/wiki/Wallpaper_group
Структура подгрупп Ли ещё проще: есть подгруппа чётных симметрий, которая не включает в себя отражений, эта чётная подгруппа распадается в прямое произведение группы параллельных переносов и группы поворотов SO(2,R), есть подгруппа симметрий диска O(2,R) и больше там вроде ничего нет. Но насчёт этого я точно не уверен. Посмотри ещё https://www.math.ucdavis.edu/~mathclub/cheat_sheets/notes.150B.pdf
У Iso(3,R) всё точно так же, только конечные группы включают в себя ещё подгруппы платоновых тел, "wallpaper groups" заменяются на кристаллографические группы (https://en.wikipedia.org/wiki/Crystallographic_group) по поводу классификаций подгрупп Ли у Iso(3,R) я мало что знаю, можешь посмотреть тут http://homepages.math.uic.edu/~kauffman/FiniteRot.pdf
2) По поводу "условий на множество", вряд ли можно сказать что-то глубже, чем "множество имеет такую-то группу симметрий", представь шестиугольник и какую-нибудь шестиугольную снежинку. Воспринимай это наоборот - считай, что группы симметрий это правильный язык для формулировки этих самых условий на множество.
3) Ну, кроме того, что мы у одной группы симметрий нашли "цепочку" подгрупп, то есть выяснили, что D_3 < D_4 < D_5 < ... < O(2,R), где D_n - диэдрические подгруппы, вроде бы никакой.
>>324822
В том-то и дело, что логическими средствами "адекватные модели" от "неадекватных моделей" отличить либо нельзя, либо очень сложно. Однако с точки зрения обычного здравого смысла p не имеет корня, и это ни от какой модели не зависит, то есть, как минимум, есть некоторые модели которые более "концептуально правильные", чем другие. Тут дело вот в чём, в моделях, где у р есть корень есть так называемые "нестандартные натуральные числа" одно из которых и является корнем многочлена р, которые от "стандартных" первопорядковыми средствами отличить невозможно, но с точки зрения нашего интуитивного ощущения такого объекта как "многочлен с коэффициентами в целых числах" нам бы очень хотелось работать в модели, в которой если многочлен р имеет корень, то этот корень - стандартное число, так как "нестандартные числа" не имеют отношения к нашей интуиции числа вообще. Программист, который условно пишет программу для управления ядерным реактором, который взорвётся если p имеет корень (из-за ошибки деления на ноль, например) интересуется не ответом "в зависимости от модели" а ответом в конкретной "стандартной модели", а то что существуют нестандартные модели арифметики в которых р имеет корень - его не волнует.
Не думаю что мой ответ тебе понравится, и заранее предупреждаю, что я плохо разбираюсь.
Ну во-первых давай вопрос чуть структурируем, я буду отвечать только про изометрии плоскости и пространства, т.е. Iso(2,R) и Iso(3,R).
1) Тебя интересует классификация подгрупп в этих группах (Iso(2,R) и Iso(3,R)).
У этих двух групп помимо структуры группы есть ещё структура многообразия, что превращает эти группы в так называемые "группы Ли" и сразу же я отвечу тебе на второй вопрос, фундаментальное отличие группы симметрий диска от группы симметрий многоугольника ни в том, что первая бесконечна, а вторая конечна, например группа симметрий Z^2 ("целочисленная решётка") тоже бесконечна, однако она не "непрерывная" как группа симметрий диска. Фундаментальное отличие как раз в том, что группа симметрий диска - является подгруппой Ли (которая называется O(2,R)) у Iso(2,R) а группа симметрий многоугольника или Z^2 - являются дискретными группами (у них топология, индуцированная из Iso(2,R) - дискретная).
Не дискретные и не подгруппы Ли тоже существуют - например все повороты на рациональный угол образуют некоторую подгруппу, но они, вроде бы, никому не интересны.
C конечными группами всё совсем просто, любая конечная группа у Iso(2,R) сохраняет точку, поэтому является подгруппой О(2,R), а любая конечная подгруппа у О(2,R) является либо диэдрической группой, либо циклической группой.
Любая бесконечная дискретная подгруппа у Iso(2,R) порождает так называемые "решётки", которые более-менее все расклассифицированы: https://en.wikipedia.org/wiki/Frieze_group https://en.wikipedia.org/wiki/Wallpaper_group
Структура подгрупп Ли ещё проще: есть подгруппа чётных симметрий, которая не включает в себя отражений, эта чётная подгруппа распадается в прямое произведение группы параллельных переносов и группы поворотов SO(2,R), есть подгруппа симметрий диска O(2,R) и больше там вроде ничего нет. Но насчёт этого я точно не уверен. Посмотри ещё https://www.math.ucdavis.edu/~mathclub/cheat_sheets/notes.150B.pdf
У Iso(3,R) всё точно так же, только конечные группы включают в себя ещё подгруппы платоновых тел, "wallpaper groups" заменяются на кристаллографические группы (https://en.wikipedia.org/wiki/Crystallographic_group) по поводу классификаций подгрупп Ли у Iso(3,R) я мало что знаю, можешь посмотреть тут http://homepages.math.uic.edu/~kauffman/FiniteRot.pdf
2) По поводу "условий на множество", вряд ли можно сказать что-то глубже, чем "множество имеет такую-то группу симметрий", представь шестиугольник и какую-нибудь шестиугольную снежинку. Воспринимай это наоборот - считай, что группы симметрий это правильный язык для формулировки этих самых условий на множество.
3) Ну, кроме того, что мы у одной группы симметрий нашли "цепочку" подгрупп, то есть выяснили, что D_3 < D_4 < D_5 < ... < O(2,R), где D_n - диэдрические подгруппы, вроде бы никакой.
>>324822
В том-то и дело, что логическими средствами "адекватные модели" от "неадекватных моделей" отличить либо нельзя, либо очень сложно. Однако с точки зрения обычного здравого смысла p не имеет корня, и это ни от какой модели не зависит, то есть, как минимум, есть некоторые модели которые более "концептуально правильные", чем другие. Тут дело вот в чём, в моделях, где у р есть корень есть так называемые "нестандартные натуральные числа" одно из которых и является корнем многочлена р, которые от "стандартных" первопорядковыми средствами отличить невозможно, но с точки зрения нашего интуитивного ощущения такого объекта как "многочлен с коэффициентами в целых числах" нам бы очень хотелось работать в модели, в которой если многочлен р имеет корень, то этот корень - стандартное число, так как "нестандартные числа" не имеют отношения к нашей интуиции числа вообще. Программист, который условно пишет программу для управления ядерным реактором, который взорвётся если p имеет корень (из-за ошибки деления на ноль, например) интересуется не ответом "в зависимости от модели" а ответом в конкретной "стандартной модели", а то что существуют нестандартные модели арифметики в которых р имеет корень - его не волнует.
1.) нам известны некоторые её точки s(10)=2, s(120)=5
2.) некоторые свойства этой функции в стиле s(a)=s(2a)-1
Требуется найти аналитический вид этой функции или приближение.
Вообщем вопрос: в какой раздел математики с этим обращаться.
Слишком общий вопрос.
Вроде как этим занимается вычислительная математика.
http://matlab.exponenta.ru/spline/book1/10.php
http://lib.alnam.ru/book_ced.php?id=39
Что-то в этом роде?
Просто современная математическая философия, предложенная ещё Гильбертом, недостаточно сильна, и за её бортом остаются часто используемые понятия "здравый смысл" и "на самом деле". Это - повод дорабатывать философию.
Правильнее, адекватнее, интуитивнее - субъективные оценки для конкретных нужд. То, что какая-то модель пригодна для описания определенного процесса программистом или физиком, не делает её непоколебимой истиной, в математическом смысле.
Мне кажется тут есть доля лукавства, я уверен что и ты чувствуешь то, что стандартные натуральные числа гораздо "выделеннее", чем нестандартные, то что это не делает её непоколебимой истиной в математическом смысле повод изменить математический смысл определения "непоколебимой истины".
А вот у Куздры с известного ресурса есть очень большой зуб на идею, что аксиомы Пеано чем-то выделеннее, чем их конкуренты, и даже есть глубокое сомнение в том, что аксиомы Пеано адекватны идее натуральных чисел. Но, во-первых, Куздра не пишет о своих мыслях подробно, а во-вторых, если мы продолжим это обсуждать, в тред засуммонится N-петух.
Что-то ты горячее с мягким мешаешь, доколе тут аксиомы Пеано, если мы говорим о моделях?
>стандартные натуральные числа гораздо "выделеннее", чем нестандартные
Я вот про это. Подумалось, что стандартные числа - это то, что определяется аксиомами Пеано. В любом случае, инфу про Куздру я вбросил, дискуссию закругляю.
Это всё равно. Пусть делает. Только тогда непоколебимых истин будет много, и все они будут зависеть от конкретных моделей.
Это скорее повод задуматься о том, что слово "истина", - в том смысле как его понимают его философы, - в математике лишнее.
Аксиомам Пеано удовлетворяет много неизоморфных моделей, надобно бы знать, коль уже в такой дискасс вступаешь.
>>324915
Философы его понимают по разному, а вот считать, что корень p у многочлена может существовать или не существовать в зависимости от модели - это как раз лукавство. То есть по сути ты считаешь, что какая-то конкретная программа на С с одним и тем же исходным кодом может остановится и не остановится в зависимости от того, какую модель ты там себе мыслишь, тебе это не кажется неадекватным?
Лол, да нет, я просто представил стереотипного Перельмана, громогласно вопрошающего: "Доколе? ДОКОЛЕ ТУТ АКСИОМЫ ПЕАНО?!"Нужно посмотреть что-нибудь из Пайтона.
>а вот считать, что корень p у многочлена может существовать или не существовать в зависимости от модели - это как раз лукавство. То есть по сути ты считаешь, что какая-то конкретная программа на С с одним и тем же исходным кодом может остановится и не остановится в зависимости от того, какую модель ты там себе мыслишь, тебе это не кажется неадекватным?
Я другой анон, но тем не менее. Программа на идеализированном (без ограничений на объем адресуемой памяти) C может остановиться за сколь угодно большое время. Несложно написать программу на таком языке, которая, что можно обосновать средствами слабой метатеории, остановится, если определено значение A(10,10) за время порядка A(10,10) (здесь A(x,y) функция Аккермана). Но в природе нет числа A(10,10), ни одно реальное вычислительное устройство за обозримый период времени не сможет довести эту программу до завершения. На мой взгляд это явно указывает, что вопрос о завершаемости работы этой программы зависит от теории в которой мы работаем.
Спасибо.
Но меня интересует в общем-то такой вопрос: какие из этих подгрупп реализуются как группы ВСЕХ симметрий какого-то множества?
Можно для циклической группы найти такое множество, что она является группой всех его изометрий?
Почему не дискретная подгруппа должна быть подгруппой Ли?
Не могу говорить о программировании - не разбираюсь в этом.
Можно привести простой математический пример того, как разные модели реализации одной теории, обладают прямо противоположными свойствами. Возьмем две группы - группу (Z,+) и группу диэдра D_3. Обе структуры являются моделями теории групп (аксиом теории групп), но - для первой справедливо утверждение x@y=y@x, а для второй - его отрицание (@ - групповая операция).
Отсюда очевидно, что одинаковые выражения, в зависимости от того, какую модель ты рассматриваешь, могут иметь разные значения истинности.
a это какая-то конкретная точка или равенство должно выполняться для любой точки?
Если конкретная, то например, можно взять полиномчик с достаточным количеством параметров (достаточной степени), подставить туда твои точки и получить систему линейных уравнений для коэффициентов полиномчика. Это самый простой способ, совсем неэффективный со многих точек зрения, но тем не менее.
Если равенство должно держаться для любой точки то это сложный прекол. Такие равенства называются функциональными уравнениями, и основную сложность тут представляет именно найти их решения. Я бы посоветовал гуглить конкретно твоё уравнение, или полистать книжку посвященную функ.равенствам, - твои линейные зависимости выглядят довольно просто, должны быть решены. А дальше уже для этих решений, которые видимо от параметров должны зависеть, подставляешь свои числа и решаешь какие-там равенства на них возникнут.
Спасибо, я знаю что такое модель теории, но мне также очевидно, что целые числа - они одни и если теоретико-множественный + теоретико-модельный формализм не умеет выделять "настоящие числа" среди всех прочих моделей - тем хуже для них.
>>324952
>Но меня интересует в общем-то такой вопрос: какие из этих подгрупп реализуются как группы ВСЕХ симметрий какого-то множества?
Любая.
>Можно для циклической группы найти такое множество, что она является группой всех его изометрий?
Фашистская свастика - это Z/4Z, например
>Почему не дискретная подгруппа должна быть подгруппой Ли?
Я этого не говорил, а говорил ровно обратное - если взять точку и повернуть её на все возможные рациональные углы вокруг начала координат, то получим, вообще говоря, подгруппу на которой нету естественной гладкой структуры.
>Фашистская свастика - это Z/4Z, например
А, а для Z/nZ вообще n-свастики это будут?
Да, я пропустил пассаж этот пассаж про группу рациональных углов. Ясно, спасибо.
Вместимость грузовика и объем груза на каждой точке так же известны.
>А, а для Z/nZ вообще n-свастики это будут?
Да.
>А её зеркальное отражение?
Её зеркальное отражение тоже Z/4Z. Вообще если взять достаточно сложный рисунок (в случае со свастикой - это "буква Г") и взять его орбиту относительно поворота 2pi/n, то получим множество, группа симметрий которого как раз Z/nZ.
похоже на это
https://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5#.D0.A2.D1.80.D0.B0.D0.BD.D1.81.D0.BF.D0.BE.D1.80.D1.82.D0.BD.D0.B0.D1.8F_.D0.B7.D0.B0.D0.B4.D0.B0.D1.87.D0.B0
что-то такое может быть в учебниках а-ля "линейное программирование для экономистов" (никакого собственно программирования там нет, не пугайся названия)
Хелпани тогда, что ли. Я что-то не вижу тут транспортной задачи. Весь груз вывозится в одно место, оптимизировать нужно именно порядок объезда точек.
И как выделять "настоящие числа"? Математика - не эмпирическая наука, эксперимент поставить нельзя, поэтому всё, что не приводит к противоречиям - имеет место быть. Да и никто не отнимает никакие числа. В общем, всё это пустой разговор. Как говаривал Рома Михайлов - "правильно то, что вас качает".
В том-то моя мысль и состояла, что логическими средствами их никак не выделить, потому следует различать "абстракции" и "математическая формализация абстракции", и так как математическое доказательство - это некоторый факт о втором, а не о первом, то говорить, что математика - это способ установления абсолютно истинных и непоколебимых фактов об абстрактных сущностях - несколько опрометчиво. Весь двач - это один пустой разговор, на самом деле, так что в пустом разговоре нет ничего страшного.
Если бы не заполняемость машины - то конечно да. А так, загнал я все точки в алгоритм, итерируюсь по пути, который он выдал, и считаю общий объем груза, приближаюсь к объему машины - и надо увозить груз в сборник, который в ебенях. В оптимальный маршрут получается искусственно вклиниваем какую-то левую точку. О какой оптимальности тут речь?
>Ну так можно дойти до того, что философия - это тоже математика, просто хуёвая в некотором смысле, а математика - это тоже философия, просто хуёвая в другом смысле.
Ну, я считаю, что хорошая философия это действительно сильно извращенная математика. Если бы философы изучали серьезно математику, то было бы у них все гораздо понятнее (ну, или если бы математики старались разбираться в работах философов, чтобы изложить их по-человечески). Рассел являет собой прекрасный пример, в его учебнике внятно изложена даже самая ебанутая хуйня, которая в оригинале представляет собой казалось бы обычный трип-репорт.
Собственно, примеры итальянских геометров и некоторых философов показывают (а также, наверное, некоторых матфизиков) показывают, что даже в отсутствии строгих в современном смысле слова доказательств и определений математика не так уж сильно искажается.
>Что делать, если совсем потерял интерес к математике?
Отдохни от этого дерьма. Ты устал. Возьми в руки книжку по биологии, купи микроскап и восторгайся.
>Какое право математика имеет на истинность?
Никакого. Математика исследует наши самые фундаментальные представления о мире, и только. Наши представления.
>Почему математики тратят столько времени на совершенно бесполезную и непродуктивную деятельность, когда представители других фундаментальных наук занимаются реальными делами?
Кому-то это доставляет. Кто-то больше ничем заниматься и не может.
>Нельзя ли найти более эффективного инструмента для описания мира, чем математика?
Математика не является инструментом описания мира, смотри выше. Эти самые фундаментальные представления потом используются во всех науках.
>От многих слышал, что если с детства математикой не занимаешься, то все попытки её изучения будут тщетны - не понравится, не поймешь, будешь плеваться. Так ли это? Может, книжек каких почитать, или уже всё потеряно?
Гонево. Математикой заниматься просто.
Для начала прочти Адамара "ИССЛЕДОВАНИЕ ПСИХОЛОГИИ ПРОЦЕССА ИЗОБРЕТЕНИЯ В ОБЛАСТИ МАТЕМАТИКИ", из первых рук поймёшь, чего тебе ждать от математики в плане творчества.
Пойми: все эти уравнения, символы и запутанные словеса - ничто иное, как средства выражения математических идей. Это просто язык, который надо выучить, и потом уже на нём говорить.
На мой взгляд, самое сложное в математике - усвоение фундаментальных понятий. Потом из них без каких-либо сложностей получится конструировать более сложные объекты - определения, теоремы, доказательства и т.д. Но сейчас, в самом начале пути, мы сталкиваемся с проблемой - нам нужно понять идею которая, казалось бы, не находит вещественного отражения в реальном мире. Что делать?
Самое ошибочное, что здесь можно сделать - это попробовать начать их осозновать. Это бесполезно. Ты врятли сможешь родить эти идеи из ничего.
Здесь самое важное - понять, что все математические идеи УЖЕ заложены в твоём разуме. Ты уже знаешь, что такое "множество", когда впервые обобщаешь несколько предметов. Банан, апельсин, лимон - фрукты. Ты уже знаешь, что такое "пресечение множеств", когда идёшь покупать зелёные яблоки. Когда ты считаешь мелочь в кармане ты уже знаешь, что такое "число". Видишь сколь Она многогранна и сколь всеобъемлюща? Видишь, сколь глубокие корни имеет Она в твоём разуме? Математика - это не просто сухая умозрительная наука. Она глубже - гораздо глубже, чем психология - исследует законы человеческого мышления. Но как истинная первооснова, Она видится не столь явно.
Нужно учиться видеть её в окружающих тебя вещах. Форма этого автобуса - параллелепипед. Как красиво легли кривые на оконном стекле. Это яблоко весит столькоже, сколько вон та гроздь винограда и мандарин вместе взятые. Как мне нарисовать вот этот прекрасный геометрический орнамент на стене мечети, используя только циркуль и линейку? Если поставить яйцо на острый конец - то не важно, как мы его повернём - его внешний вид всё равно не изменится. А вот с пирамидой Хеопса такой номер не пройдёт, и не тоько потому, что она тяжёлая, как мамаша Оп-а.
Полезно решать различные головоломки, основанные на математике. Могу порекомендовать Мартина Гарднера, Генри Дьюдени, Якова Перельмана - последнего особенно. Его труды по математике далеко не исчерпываются "Занимательной" серией. Взять хотя бы его "Живую математику".
И последнее. Математика - это не монастырь. Не закрывайся в Математике. Отвлекайся от Неё: хоть пожинай Её плоды в физике, химии, астрономии, хоть изучай биологию, палеоантологию, хоть просто выбирайся на природу, хоть в картинные галереи. Ты не сможешь забыть о Ней - ибо ты видишь Её везде, куда падает твой взгляд. Только теперь ты будешь это осознавать.
>Что делать, если совсем потерял интерес к математике?
Отдохни от этого дерьма. Ты устал. Возьми в руки книжку по биологии, купи микроскап и восторгайся.
>Какое право математика имеет на истинность?
Никакого. Математика исследует наши самые фундаментальные представления о мире, и только. Наши представления.
>Почему математики тратят столько времени на совершенно бесполезную и непродуктивную деятельность, когда представители других фундаментальных наук занимаются реальными делами?
Кому-то это доставляет. Кто-то больше ничем заниматься и не может.
>Нельзя ли найти более эффективного инструмента для описания мира, чем математика?
Математика не является инструментом описания мира, смотри выше. Эти самые фундаментальные представления потом используются во всех науках.
>От многих слышал, что если с детства математикой не занимаешься, то все попытки её изучения будут тщетны - не понравится, не поймешь, будешь плеваться. Так ли это? Может, книжек каких почитать, или уже всё потеряно?
Гонево. Математикой заниматься просто.
Для начала прочти Адамара "ИССЛЕДОВАНИЕ ПСИХОЛОГИИ ПРОЦЕССА ИЗОБРЕТЕНИЯ В ОБЛАСТИ МАТЕМАТИКИ", из первых рук поймёшь, чего тебе ждать от математики в плане творчества.
Пойми: все эти уравнения, символы и запутанные словеса - ничто иное, как средства выражения математических идей. Это просто язык, который надо выучить, и потом уже на нём говорить.
На мой взгляд, самое сложное в математике - усвоение фундаментальных понятий. Потом из них без каких-либо сложностей получится конструировать более сложные объекты - определения, теоремы, доказательства и т.д. Но сейчас, в самом начале пути, мы сталкиваемся с проблемой - нам нужно понять идею которая, казалось бы, не находит вещественного отражения в реальном мире. Что делать?
Самое ошибочное, что здесь можно сделать - это попробовать начать их осозновать. Это бесполезно. Ты врятли сможешь родить эти идеи из ничего.
Здесь самое важное - понять, что все математические идеи УЖЕ заложены в твоём разуме. Ты уже знаешь, что такое "множество", когда впервые обобщаешь несколько предметов. Банан, апельсин, лимон - фрукты. Ты уже знаешь, что такое "пресечение множеств", когда идёшь покупать зелёные яблоки. Когда ты считаешь мелочь в кармане ты уже знаешь, что такое "число". Видишь сколь Она многогранна и сколь всеобъемлюща? Видишь, сколь глубокие корни имеет Она в твоём разуме? Математика - это не просто сухая умозрительная наука. Она глубже - гораздо глубже, чем психология - исследует законы человеческого мышления. Но как истинная первооснова, Она видится не столь явно.
Нужно учиться видеть её в окружающих тебя вещах. Форма этого автобуса - параллелепипед. Как красиво легли кривые на оконном стекле. Это яблоко весит столькоже, сколько вон та гроздь винограда и мандарин вместе взятые. Как мне нарисовать вот этот прекрасный геометрический орнамент на стене мечети, используя только циркуль и линейку? Если поставить яйцо на острый конец - то не важно, как мы его повернём - его внешний вид всё равно не изменится. А вот с пирамидой Хеопса такой номер не пройдёт, и не тоько потому, что она тяжёлая, как мамаша Оп-а.
Полезно решать различные головоломки, основанные на математике. Могу порекомендовать Мартина Гарднера, Генри Дьюдени, Якова Перельмана - последнего особенно. Его труды по математике далеко не исчерпываются "Занимательной" серией. Взять хотя бы его "Живую математику".
И последнее. Математика - это не монастырь. Не закрывайся в Математике. Отвлекайся от Неё: хоть пожинай Её плоды в физике, химии, астрономии, хоть изучай биологию, палеоантологию, хоть просто выбирайся на природу, хоть в картинные галереи. Ты не сможешь забыть о Ней - ибо ты видишь Её везде, куда падает твой взгляд. Только теперь ты будешь это осознавать.
Ну пускай даже так. Я уже точно не помню, то ли связанно это с ихней системой счилени, то ли с астрономическими наблюдениями круглогодичными земля крутиться за 365.2459 дней, но глазки шумеров могли зафиксировать только 360 дней
Вот даун. Вместо того чтобы на практике начать знания применять, он начинает про первичность математики загонять.
Иди пососи у своего Канта, мудила.
>Вот даун. Вместо того чтобы на практике начать знания применять, он начинает про первичность математики загонять.
>Иди пососи у своего Канта, мудила.
Читающие жопой в треде, я спокоен.
Так суть-то в решение нестандартных задач, а не понимании абстрактных моделей. Нет понимать это тоже хорошо, читать книги по математике с огромным количеством определений, но суть то не в этом. Математическое творчество заключается в выдумывании новых способов решения задач, в нешаблонности мышления.
Математическое творчество состоит в наблюдении связей между математическими понятиями, что невозможно без понимания. Одним из продуктов этого творчества и является нахождение путей решения задач.
>Докажите с помощью метода математической индукции
>метода математической индукции
Ты рэтард? Написано же как доказывать.
Выложи своё доказательство.
>четыре последовательных натуральных числа с равным количеством натуральных делителей.
Ты где-то описался.
Если я правильно тебя понял - нет.
Это не ты описался, это я жопой читал.
Точно, извиняюсь.
Существует ли четыре последовательных натуральных числа с равным количеством простых делителей.
ладно. я думаю мне лучше по больше прочесть лекций по линейной алгебре. там как раз и про линейный оператор было.. но сначалааа...решения дохуя задач из практикума!
Я и сам не нашел, я подумал: у кого-нибудь будут идеи доказательства.
мне надо объяснение для идиотов)
Всё нравится.
Детерминант - это такая функция от n векторов (столбцов матрицы), которая меняет знак при перемене аргументов местами и полилинейна, т.е. линейна по каждому из n векторов. Если ты ещё и нормируешь, т.е. требуешь чтобы на, например, наборе столбцов единичной матрицы значение было единицей, то такая функция единственна.
Геометрически это имеет смысл коэффициент растяжения ориентированного объёма при действии этой матрицей как линейным преобразованием. Т.е. если ты возьмёшь, например, обычный ортонормированный базис и подействуешь оператором, то объём параллелограмма, натянутого на получившиеся вектора - и есть детерминант.
вот. спасибо. вобщем, разберусь с типовиками, которые я решаю, чтобы подготовиться к экзамену. после практики сразу буду читать теорию и разберусь с половиной понятий, которые мне не совсем хорошо знакомы... в том числе про линейный оператор.
это и так я знаю. я хочу разобраться в другом.
Кстати, есть люди которым обычный курс линейной алгебры через определители не очень нравится.
http://www.axler.net/DwD.html
а у меня по сути и не курс линейной алгебры. просто в перовом семестре на математике проходим)) дело то хорошее. таки юзается во всяких OpenGL и всё такое. и вообще...здоровски это.
4) При раскрытии скобок в левой части получится сумма геометрической прогрессии от 1 до q^(2^(n+1) - 1) включительно. Понять это очень просто - если раскрыть все скобки слева, то получится сумма нескольких слагаемых, каждое из, которых - это q в какой-то степени. Чтобы сформировать хоть какое-то слагаемое q^x, мы должны в i ой скобке выбрать либо 1, либо q^(2^i) и домножить на то, что выбрали, то есть по сути мы либо "включаем" i-ый бит в x, либо его выключаем.
3) Если представить сумму справа как функцию F(q) от q, то получим соотношение:
F(0) = 1
1 + Integral (0..q) F(x) dx = 1 + q + q^2 + q^3 + ... + q^n
1 + Integral (0..q) F(x) dx = (1 - q^(n+1))/(1-q)
после дифференцирования по q получим
F(q) = d/dq (1 - q^(n+1))/(1-q)
что даёт как раз то, что нужно ( http://www.wolframalpha.com/input/?i=d%2Fdq+%281+-+q%5E%28n%2B1%29%29%2F%281-q%29 ).
Кристаллографический.
Проиграл с этого завистливого ничтожества. Наверно, бугуртишь оттого, что твое абстрактное кукарекание никому нахуй не надо, а быдлокодеры просто берут и фармят бабло, испытывая отвращение к математике? На самом деле ты не математик, а хуесос. Такие как ты придумывают наукообразные исследования и говнотеории типа теорвера на группах и сингулярных случайных величин для получения докторских званий. Вы не ученые. Вы бизнесмены и говно. Всех дегенератов, штампующих далекие от реальности и практики теории, которые никогда не найдут применение, надо выгонять нахуй из науки. На двачи. Поэтому ты здесь и сидишь, говно.
Или тебе нужно, чтобы сумма степеней в факторизации была одинаковая? Тогда 602 603 604 605.
Какой-то искусственный абсолютно вопрос. Непонятно как он мог возникнуть.
Что я такого сказал?
>быдлокодеры просто берут и фармят бабло, испытывая отвращение к математике
Мсье забыл про /pr и computer science thread? Это как те места, где можно выразить свое, безусловно, важное мнение по данному вопросу.
У четырех два простых делителя.
Вот верный пример, спасибо.
извините, если глупый вопрос
Ну максимальная последовательность из последовательных чисел с двумя простыми делителями три(четыре не может быть, ибо одно из них тогда делится на четыре). Предположил, что для чисел с тремя простыми делителями максимальная последовательность имеет длину 7(ибо 8 минимальное число с тремя простыми делителями). Запилил программу, она показала что от 1 до 10000 таких нет(видать неверная программа)

>функция непрерывная ваще)
Тип "на множестве" значит везде? Нихуя не понял. А если функция определена только на отрезке? Отсюда отрезок = множество. Или нет?
Функция непрерывная на отрезке - это функция непрерывная на множестве, где в данном случае множество это отрезок.
Нет. Множество это когда МНОГА, а отрезок по определению не может быть МНОГА
Попизди мне тут. На отрезке R столько же точек, сколько и во всем R, так что иди умойся)
Моча какая-та. Я тут просто теорему Кантора не могу проанализировать. Типа если функция непрерывна на отрезке, то она равномерна непрерывна на нем. А про множество такого типа не скажешь. Ебанулся короче.
Множества бывают разные - синие, зеленые, красные
Но всем постоянно хочется с отрезками заморочится
Ну не писюнами же меряться, в sci.
Хуйня ваш iq, вот от чего зависит интеллект(пикрелайтед), ну и от времени реакции.
Как уменьшить время реакции?
Ну, все-таки нет. Интеллект и образованность - разные, несвязанные понятия - как впрочем и интеллект и навык.



1) Что такое p_ij с индексом (n) наверху на первой пикче? Вероятность перехода из состояния i в состояние j за n шагов? Но ведь там написано, что это вероятность перехода в состояние j при условии, что мы находимся в состоянии i. Что означает индекс (n)?
2) Из чего состоит матрица переходов цепи Маркова? Чем нумеруются строки и столбцы этой матрицы? При нумеровании можно адресовать каждую ячейку парой индексов i, j. Что подразумевается под этими индексами и что находится в ячейке?
3) В доказательстве теоремы солидарности мне непонятна стройка, где применяется формула полной вероятности. Мы рассматриваем какое-то p_kk (N + M + n) и говорим, что это равно двойной сумме произведений p_kl (N), p_ls (n) и p_sk (M). Что означают индексы? Почему добавляется буква s в нижних индексах? Это значит, что система выходит из состояния k и через промежуточное состояние s снова попадает в k?
Определение p_ij дано на третьей пикче. Это вероятность перехода из начального состояния i в состояние j.
Похоже, в понимании всего этого проблема исключительно языковая, потому что язык изложения настолько уебищный, насколько это вообще возможно, чтобы сделать информацию трудно воспринимаемой.
Что такое образованность? Что такое интелект? У нас тут вообще нучная борда или как? What is love, baby don't hurt me...
Утилитарист хуже н петуха
Посмотрел на пик меня почему-то охватила глубокая экзистенциальная тоска. Зачем так жить?
извините, ребятЖ, но еще в 7 классе для всех функций указывали область определения. мне показалось потому что функция это инструмент который отлично работает в одном месте и не так отлично в другом. не кажется ли вам, господа, что наука и знание - инструмент с точно такой же областью определения. и возвращают корректные результаты только там где применимы?
Теорема о равномерной непрерывности справедлива для компактных множеств. Отрезок это компактное множество, поэтому она справедлива для него. Но есть и некомпактные множества.
Между любыми двумя точками на R несчётное множество точек. Хочешь поспорить?
Бамп, кстати.
Ты просто гуманитарий. Там понимать нечего, даже деревянные счёты разберутся. Чисто логическое мышление, буквы можешь не читать, они только мешают. Анализируешь, сравниваешь, делаешь выводы.
>Ты просто гуманитарий
Ты просто пидораха. За рубежом нет деления на гуманитариев и технарей. Там есть специалисты, охуенные в своем деле. В том же Гарварде успешным людям дают навыки для самореализации в интересной им сфере со значительным вкладом в нее. Даже чтобы попасть в Гарвард, надо быть охуенным еще со школы и участвовать в крупных олимпиадках или занимать в коллективе ведущую роль, показывая, что это ты охуенный, это тебя надо выбрать из тысячи желающих. Поэтому студенты там уже на втором курсе работают во всяких микрософтах и гуглах, а экономисты и управленцы рубят тонны бабла, потому что сократить затраты предприятия и максимизировать прибыль это тебе не на книжки дрочить. Ну а парашка состоит из соснувших в разных сферах борщехлебов, которые утешают себя мыслями о принадлежности к воображаемым технарям, не вынимая хуй изо рта.
Ну так пиздуй в Гарвард, гуманитарий. Хотя кому ты там нужен такой тупой. Я тебе сказал как разобраться, а ты начал заливать всё своей попоболью. Не можешь осилить - зубри.
Въеби путинки, рашкован. Будешь зарабатывать контрольными, дипломными работами и репетиторством с даунами, не вынимая хуй изо рта. По сравнению с программированием математика это ебаное говно, где простые идеи выражаются максимально запутанно. Разбираться в этой залупе несколько часов, чтобы увидеть, как на самом деле все тривиально, это занятие долбоебов. Когда вам уже нормальный язык завезут?
Мне не интересны твои гадания, гуманитарий. Съеби уже в программирование, Гарвард, хоть куда, лишь бы не засирать своим нытьём тут всё.
>Чисто логическое мышление
Вот тут обосрался. Ведь это именно среди техноблядков больше всего шизанутых долбоебов, которые не ищут истину, пусть даже истина принесет им попаболь, а отстаивают свое мнение, не отличают причину от следствия и во всех рассуждениях видят лишь самую поверхность. Мощно выссался на однополушарных унтерменшей. Ебаные половинчатые мрази.
Но ведь страдаешь здесь только ты, оттого что твоя алгебраическая геометрия - говно без задач, в рашке от таких как ты дрочеров на иероглифы ожидают практическую пользу, которую ты не даешь, а сам ты нищеброд, не способный в кодинг ни по способностям, ни по интересам.
>алгебраическая геометрия - говно без задач
Вот это вы, батенька, загнули.
мимошелсрачнечиталвасвсехпоразабанить
>Вас что сегодня из макдаков выперли на мороз?
Сказал даун, осевший на кафедре, чтобы переводить на русский статьи зарубежных математиков, потому что больше ни на что не способен) Иди подработай в ПТУ и в каком-нибудь лицее для маняматиков, а то все деньги только за проезд в автобусе отдаешь)
Тютю, какие мы грозные, правда знаний тебе это не прибавит, так и останешься глупеньким.
Не рой яму другому не то сам в неё попадёшь!
> Гарвард
Расхайпованное дерьмецо для богатых идиотов - родителей. Дальше этот манямирок рекламных лозунгов не читал.
в твоей формулировке "просто непрерывная" функция это гораздо более общее понятие чем "на отрезке"
функция непрерывна тогда и только тогда когда прообраз каждого открытого множества открыт
то есть она бывает непрерывана на множествах в которых вообще нет никакого отношения порядка (больше-меньше)
отрезок подразумевает упорядоченность
Верно ли что если у группы только одномерные представления, то она абелева?
Ну как, все еще сидишь?
Как посчитать произведение всех значений f(x) на определенном участке? знаю что практически всегда стремится к бесконечности мне интересно это произведение в областях еденицы
Пардон за сажу - непроизвольно получилось
Здесь есть логики? Как доказать, что множество чисел в записи которых есть "99" вычислимо, в десятичной СИ? ТО есть нужно построить вычислимую характеристическую функцию этого множества.
>в десятичной СИ
в _Системе _Счисления с основанием 10
в десятеричной СС
Ага, великий, могучий и ебанутый.
Чому? Как минимум произведение вида (1+x)(1+2x)...(1+nx) при x->0 стремится к бесконечности, (1-x)(1-2x)...(1-nx) при x->0 к стремится к 0, а (1+x)(1-x)(1+2x)(1-2x)...(1+nx)(1-n*x) при x->0 равно 1.
https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
http://www.inf1.info/book/export/html/200
http://dic.academic.ru/dic.nsf/ruwiki/4992
http://www.gmcit.murmansk.ru/text/information_science/base/logic/materials/material2.htm
Наисчислял тебе на лицо
При чем тут либерализм? Под "исчислением" обычно понимают кое-что другое. СИ - общепринятое обозначение для международной системы единиц.
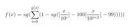
Логикоебы как всегда. Как о какой-то хуйне затирать так весь тред засрут, как помочь решить задачку так нет никого. Кому интересно ответ на пике. Вроде верный.
{
x = 2cost
y = 4sint
}
И нужно найти уравнения касательной к кривой в точке t0=pi/4
Можете подкинуть решение или где его искать?
У тебя счётное количество множителей.
"Вы, конечно, шутите, мистер Фейнман"
Сколько времени нужно, чтобы выбивать 1600 на кодфорсес?
Есть 2-3 часа в день,после пар и сессии
ну он прав допустимто, всё именно так.
Примерчик.
Пишу с пирамиды Пернатого Змия, ну что там у православных? Как там, до ацтекских язычкников с их двадцатиричной системой счисления они уже доросли?
Они, епта, отрицательные числа не признают. Автор настолько ебнутый, что называет себя православным, исповедуя языческие славянские культы, смешанные с извращенным содержанием Библии, русских народных сказок и словаря великорусского языка Даля. Углы он называет "гостями", а степень числа - "репкой".

>Углы он называет "гостями", а степень числа - "репкой".
Опуская вопрос "что делает понятие угла в арифметике" стоит отметить, что хотя бы такие понятия там есть. Далеко продвинулись.
Там не только арифметика. Точнее автор называет арифметикой алгебру, геометрию, тригонометрию, теорию чисел, космогонию, грамматику (причем неверную) дореволюционного русского языка, и многое другое.
Попробуй dxdy.

Да есть куча разных фриков и что? Вытаскивание очередных сумашетшовых от псевдонауки тип смотрити как прикольна и иронична)) это какой-то 2009.
Это не псевдонаука. Это вообще к науке отношения не имеет. А вопрос я в первом посте сформулировал.
Рыбников штоле? Этот не просто поехал, он приехал уже. Помню как орал с его "опровержений" Ньютона и "доказательств", что свет имеет нулевую скорость. Хотя над больными и грешно смеяться.
Странно, а Эйнштейн опроверг Ньютона (доказал неполноту и частность его теории) и доказал, что в системе отсчёта, связанной с фотоном, нет времени (вырожденный параметр). И никто с него не "орал".
Умел бы ты читать ещё, лалка.
Впискоблядок, плиз
Ну, где её "прошарили в математике", конечно.

Определение компланорности векторов: Три вектора называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.
Хорошо, представим, что вектор С раскладывается так с=xa+yb, как видно система будет лин. зависима. Почему тогда система векторов с, а, b является компланарной? Ведь все таки по чертежу вектор с не лежит в плоскости, в которой находятся а и б. Почему же мы называем их компланарными, это из-за того, что я спутал определение комплонарности?
Заранее благодарствую.
Два вектора называются компланарными, если
лежат в одной плоскости
У тебя фиолетовый вектор на с, а, б расскладывается
А вектор с линейно независим от а и б
То есть С не можем разложить xa+yb, только фиолетовый.
То есть я правильно думаю, что система с, а, б некомлпнарны из определения. Че-то запутался уже. фмолетовый вектор пусть будет d. d=xa+yb+zc. Вектор d линейно выражается через все остальные, то есть система векторов d,a,b,c компланарна верно.
Компланарность она о двух векторах,
с, а и б у тебя по определению образуют
трёхмерное декартовое пространство,
разумеется они линейнонезависимы, но каждая пара а и б или а и с - компланарна
>Компланарность она о двух векторах
Нет, о трёх и более.
>с, а и б у тебя по определению образуют трёхмерное декартовое пространство
Нихуя неправда.
Векторы называются компланарными, если, будучи приведёнными к общему началу, лежат в одной плоскости. Любые два вектора компланарны, поэтому понятие компланарности не имеет смысла для 2 векторов, только для 3 и более
>>327249
>Вектор d линейно выражается через все остальные
Да.
>то есть система векторов d,a,b,c компланарна верно
Нет.
Занимается в области теории управления. Об успехах не в курсе.
>Странно, а Эйнштейн опроверг Ньютона (доказал неполноту и частность его теории)
Показать частность – не значит опровергнуть.
>в системе отсчёта, связанной с фотоном,
Такой системы отсчёта не существует.
>>3) Ну, кроме того, что мы у одной группы симметрий нашли "цепочку" подгрупп, то есть выяснили, что D_3 < D_4 < D_5 < ... < O(2,R), где D_n - диэдрические подгруппы, вроде бы никакой.
А разве не возникает тут какой-нибудь категорный предел-копредел? Или что-то другое в духе свободного объекта только, наверное, не нужно требовать единственность отображения из "большой группы" в малую.
Вроде это как раз и будет проективный предел если я не в конец не соображаю.
А ответ на вопрос про "является ли любая группа группами симметрий некоторого геометрического объекта" вроде бы положительный, причём обратное тоже верно (слышал утверждение где-то).
Любая группа - фактор некоторой свободной группы.
Значит, нужно посмотреть реализацию объекта, группу симметрий которого составляет свободная группа. А потом посмотреть, что эти самые соотношения, по которым факторизуешь, меняют в этом объекте.
Ну или посмотреть на представления этой группы.
> Показать частность – не значит опровергнуть.
Это уже политический вопрос, но твою позицию я понял.
> Такой системы отсчёта не существует.
Действительно, систем отсчёта не существует в реальности, их выдумывает учёный, строя свои умозаключения. Нужно лишь описать формализм преобразований из выбранной точки отсчёта в нулевую (связанную с самим учёным, например).
Она училась (ну или по крайней мере числилась) на мехмате МГУ на механике, научрук Садовничий. Все работы в соавторстве с ним же. Так что блестящим математиком она явно не является. Точнее сказать сложно.
>научрук Садовничий. Все работы в соавторстве с ним же
Кек, это уже какой-то вложенный уровень зашквара, так как у самого Садовничего все работы в соавторстве.
Садовничий - это носитель зашквара. Всё, с чем он в соавторстве, зашкварено пожизненно.
>Действительно, систем отсчёта не существует в реальности...
Не поэтому. Не существует системы отсчёта относительно которой фотон находится в покое, поскольку у фотона нет массы покоя, а значит нет фактора позволяющего определить СО.

И в самом деле.

В целях самообразования решил начать задрачивать тему исключительно для себя. Поэтому прошу какой-нибудь учебник для чайников или видеокурс от А до Я, знакомящий человека с матаном, чтобы с объяснием тех или иных понятий и их значении в жизни. Вот нахуя людям нужен тот же интеграл? Я не знаю, но мне интересно. Ведь не из пальца же высосано. А вдруг лучше начну этот мир понимать
Перелопатил ютюб и трекеры, но там абсолютное большинство всех уроков уже рассчитаны на хорошее понимание школьного курса, а на школьные учебники у меня фобия.
Никому не интересно писать книги, популяризирующие науку среди всратых гуманитариев. Поэтому лучшее, на что ты можешь рассчитывать, - статьи в википедии. Се ля ви.
Репетитора найми. Сейчас по скайпу можно заниматься.
Самый простой и легко проверяемый аргумент - открыть гуглсколар и найди его статью без соавторства. Будет исключительно туфта уровня "Высшее образование России. Доступность. Качество. Конкурентоспособность" и "Знание и мудрость в глобализирующемся мире"
Вы видите копию треда, сохраненную 13 февраля 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.






