Вы видите копию треда, сохраненную 29 февраля 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Пикрелейтед - показатель "разброса".
Желаю удачи и даю напутствие на чистую математическую дискуссию.
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
> динамических систем, задаваемых функциями аналогичного рода
с чего можно начать изучать (в расчете на первокура, матан не оче, с алгеброй немного получше)?
С перехода в /un
Двоеточие - вообще не часть языка предикатов, если уж придираться. Можно его не ставить вообще.
А где есть строгое фундаментальное изложение языка предикатов, кстати? Под строгостью я понимаю изложение на русском языке некой метатетории и уже в этой метатеории определение предикатов. Я видел определения предикатов с использованием теории множеств, но ведь сама теория множеств использует язык предикатов, поэтому следствия, извлечённые из такого определения, не кажутся мне фундаментальными.
я серьёзно спрашиваю, прошу не путать с теми, кто ракует про N
Почему я не смогу?
У них нет понятия "предикат", к тому же они пользуются эпсилон-оператором, который в логике до сих пор не нашёл признания. В философии Бурбаки εx"x - столица России" - вполне корректное имя одного конкретного предмета, являющегося столицей России (но совершенно не известно, какого из них, если таких предметов несколько), или же бессмыслица, если предмета, способного именоваться этим именем, не существует. В нормальной логике такой конструкции просто нет.
Ну ок. Как насчет исчисления предикатов, например Гильбертовского типа?
Нет.
Ты лох.
Гильберт не формализовал предикаты, к сожалению. Кроме того, эпсилон-оператор - это его изобретение.
Жополаза ответ.
Математика -- для была. Тупого была. Ноудискасс.
>спрашивает, для чего нужны мнимые числа
>рассказываю ему про тахионы
>возникает лютый бугурт и слышны мольбы, сквозь слёзы, больше не приходить сюда
Очень интересно!
Зарепортил дауна.

Почему у быдла так печет от Банаха-Тарского? Это же совершенно очевидно, что для произвольных подмножеств R^n хуй определишь функцию объема.
Потому что физикам, которых ты называешь быдлом, охуительные маняистории маняматиков НЕ НУ ЖНЫ
Будто что то плохое что первокурсник хочет разобраться с комплексными числами.
Это уже за меня сделали. А так хотелось тебя говном накормить чтобы ты мне пояснил за комплексные числа.
Физикам математика нужна априори. Математикам физика полезна в их профессиональной деятельности только если они хотят заниматься вопросами с физической мотивацией или иными словами в некоторой степени стать физиками. Но физика - это всего-лишь одна из множества областей, где применяется математика. Многими областями математики, которые не имеют отношения к физике можно успешно заниматься совершенно не касаясь оной.
Это, впрочем, не отменяет того, что из общих соображений знакомства с достижениями человеческой культуры познакомиться с физикой стоит.

АААААААААААААААААА СУКА БЛЯДЬ СЪЕБИ ОТСЮДА СУКАААААААААААААААААААААААААААААААААААААААААААА
АААААААААААААААААААААААААААААААААААААААААААААА
но ты даже не пытался искать, иначе был бы более конкретный вопрос
поэтому иди нахуй
А было тут любят! Заходит, присаживайся. Чай будешь?
Спасибо.
>>332011
А может мне кто-нибудь по-простому объяснить, почему дальше кватернионов чисел нет?
а) типа эквивалентности (симметрично-транзитивное)
б) типа порядка (антисимметрично-транзитивное) здесь понятно, частично-упорядоченное множество
в) антисимметрично-антитранзитивное-в-узком-смысле (антитранзитивность понимается, как (aZb)&(bZc)->(cZa))
Желательно, чтобы книга не требовала предварительного знакомства с пост-Галуа алгеброй - и весь необходимый для своего понимания математический аппарат вводила по мере изложения (и необходимости).
Языки: английский или русской, если совсем без этого никак - тогда со скрипом ещё французский.
доказал тебе за щечку, проверяй
>>332028
Только хотел написать что реквест слишком общий и вряд ли кто-то вообще писал книгу только по отношениям, ан нет, нагуглил обсуждение http://math.stackexchange.com/questions/100256/branch-of-math-studying-relations
и нашёл таки две книжки
http://www.amazon.com/dp/0444505423/?tag=stackoverfl08-20
http://www.jstor.org/stable/2268577?seq=1#page_scan_tab_contents
ну и там несколько статей ещё упоминается.
Правда в свободном доступе их не нашёл.
Вообще-то есть. Октавы например (или алгебра кэли).
https://ru.wikipedia.org/wiki/Алгебра_Кэли
Есть и еще дальше, более того можно идти бесконечно дальше. Правда, "дальше" октав операция деления уже будет неопределена.
Есть книжка на эту тему: Гиперкомплексные числа (Кантор, Солодовников).
Но ведь физики не быдло и отлично понимают суть этого парадокса. Зачем ты называешь мамкиных технарей из 7Б физиками?
Комплексные числа применяются для вычисления токов в узлах электрической цепи.
Как именно они применяются?
Удвой мне тогда яблоко, физик двощевский.
Нужны они затем, чтобы у уравнения n-ного порядка было ровно n корней, а не как бык поссал.
Ещё они нужны затем, что когда у уравнения третьего порядка таки честно есть три действительных корня, по формуле Кардана, для их нахождения придётся - сюрприз-сюрприз - извлекать квадратные корни из отрицательных чисел, иначе хуй тебе, а не какие-либо корни (в случае, когда действительный корень в уравнении третьего порядка только один, он формулой Кардана извлекается на ура безо всяких квадраных коней отрицательных чисел). Всё это, скажем так, мягко, но верно натолкнуло математиков ковырявшихся в уравнениях (и не только) на мысль о том, что жизнь очень сильно упрощается, если допустить существовании каких-то там сущностей, которые, будучи возведёнными в квадрат, давали бы отлицательное число, а также всевозможных продуктов ебли этих сущностей с числами действительными путём элементарных арифметических действий.
>квадратных корней
>отрицательное число
>элементарных арифметических операций
фиксы, может ещё чего пропустил, похуй
кривой*
Спасибо.
Спасибо.
нет
Отвратительно, ну и мразь же ты.
А какого хуя производная определяется как скорость изменения функции и как тангенс угла в быранной точке?
потому что это одно и тоже
То есть как это разное? С чего вдруг? Одинаковое же.
Функция f называется линейной, если f(x+y) = f(x) + f(y) и f(ax) = af(x).
>A linear function is a polynomial function in which the variable x has degree at most one, which means it is of the form f(x) = ax + b.
https://en.wikipedia.org/wiki/Linear_function_(calculus)
Теперь если мы возьмем функцию f(x) = 3 (как в моем вопросе) по определению в твоем посте она нелинейная, по этому определению - линейная.
2π + 1
Очевидно, потому что значения слов не закреплены жёстко, а определяются в контексте. В анализе изучают как при малых значениях чего-то ростёт там что-то, линейная ф-я + константа в этом смысле от строго говоря линейного отображения ничем не отличается. А всякие жёсткие "сохранения структуры" важны только для маняматиков-алгебраистов.

Это ты ещё алгебру множеств не пытался осмыслить.
Имелось в виду, что предположение от противного, что Z следует из A т.е. A → Z, после чего приходим к тому, что истинность этой импликации противоречит.
Делаю все так
1/(х+Δ)^2-1/x^2
1/(x^2+2xΔ+Δ^2) - 1/x^2
(x^2 - x^2+2xΔ+Δ^2)/(x^4+2x^3Δ+x^2Δ^2)
2xΔ+Δ^2/(x^4+2x^3Δ+x^2Δ^2)
А дальше не знаю что делать.
Где, в каком месте ошибка?
То есть если я читаю какой-нибудь пейпер, то все понятно: я знаю, что мне надо, записываю кейпойнты, чтоб потом пробежаться и все мгновенно вспомнить, схороняю ссылки, ну как обычно, короче. Если я прохожу какой-нибудь курс, то тоже понятно: там будет экзамен, вот список вопросов, мне их нужно все задрочить в любом случае.
А что делать, если я читаю книжку для себя, и притом не ради каких-то конкретных результатов, а ради общего, фундаментального развития, что ли? Просто черкаться от руки по ходу чтения? Делать полноценные конспекты? Устраивать себе самому экзамены по главам? Что-то я в сомнениях. Поделитесь, как вы это делаете.
Я понял, что я узнаю новое только когда удивляюсь. Поэтому прежде чем прочитать очередной параграф, я явно составляю, а иногда и записываю в тетрадке, мои ожидания, мои гипотезы о том, что именно будет там написано. Иногда книге не удаётся меня удивить, но чаще всего я бываю удивлён. Ну и да, я читаю с тетрадками в руках, веду конспекты, рисую схемы зависимости понятий, составляю список теорем.
Противоречие надо получить, в процессе доказательства.
l2
>>332294
>пейпер
>кейпойнты
>список вопросов
>конспекты
>схемы зависимости понятий
Какие-то вы аутисты. Хотя так, наверное, даже полезно делать. Но среди математиков таких не встречал, в основном, все хуярят абы как.
Я просто читаю и делаю упражнения. Просто по дороге я интересуюсь, сам себе вопросы задаю. Иногда начинаешь думать и бросаешь учебник надолго, сам че-то гуглишь и выясняешь. А иногда никаких таких мыслей не возникает. Хз короче.
Читаю по абзацам, в конце абзаца – осмысливаю, конспектирую, делаю упражнения.
>>332294
> я явно составляю, а иногда и записываю в тетрадке, мои ожидания, мои гипотезы о том, что именно будет там написано
А ведь это интересно, да! Спасибо.
А по поводу конспектов - ну, ты их старательно ведешь, потом повторяешь, заучиваешь формулировки? Или просто по ходу дела записываешь, что хочется записать, без особой структуры?
>>332301
Разумеется, но я ведь не о том спрашивал, согласись?
>>332347
Лол, а "пейпер"-то тебе чем не угодило?!
>>332361
Вот да, с одной стороны - это лучше всего, так все, что нужно, запоминается само, потому что интересно же. С другой - я заметил, что так тратится очень много времени, если ты плохо разбираешься в теме. То есть ты вроде бы ищешь, читаешь, сравниваешь, все дела, а в итоге понимаешь, что вместо этого достаточно было последовательно прочитать следующий параграф, и та же информация усвоилась бы за полчаса, а не за полдня.
>>332363
Тот же вопрос: конспект - подробный, чтоб как к экзамену готовиться, или просто черкание по ходу чтения для вовлечения нейронов?
Вообще, спасибо за отзывы.
>Тот же вопрос: конспект - подробный, чтоб как к экзамену готовиться, или просто черкание по ходу чтения для вовлечения нейронов?
Стараюсь уложить мысль в несколько "буллетов".
Круче только факапы с дедлайнами.
Натыкаясь на очередную thиорем откладываю текстбук и трай ту пруф ит майселф дринкая смусси под чизкейк. Кто круче?
Upon encountering another theorem, I'm putting the textbook away and trying to prove it by myself drinking coffee and eating muffins (yes, smoothie and cheesecakes – blow ass).
RUSSIAN, MOTHERFUCKER, DO YOU SPEAK IT?
Во-первых, когда я читаю текстбук, я пишу ноутс. Когда я встречаю дефинишн, я пытаюсь придумать юз кейсы, где соответствующий объект будет использоваться. Когда я встречаю пропозишн, я тоже сначала пытаюсь написать скетч пруфа, а если не получается, читаю тот, что в текстбуке.
таутолоджи
Хуейшн и пиздинг.
Ошибка в разделе. Уходи в /un
Все приличные люди говорят вообще-то. Дифференциал это линейное приближение функции просто по определению.
В одномерном пространстве две: отрезок.
В двумерном - три: треугольник.
Но сколько в трёхмерном?
Тобишь
f(x2)~f(x1)+f`(x2)(x2-x1)
для википедии слишком сложно? Или там приличных людей нету?
Кстати, насколько растет ошибка в результате вычисления функций, например 1.5678....^2, если начинать вычислять с самого последнего, самого самого правого, доступного разряда числа?
Или по определению к нулю стремится?
>Максимум сколько точек можно соединить прямыми линиями каждая с каждой так, что бы линии не пересекались?
Сам то понял что сказал? По определению пересекаться будут.
Я попробовал посмотреть, но мои волосы встали, выпали и ушли.
Может быть есть готовые фигуры или способы их генерации для n точек?
И всё же меня терзают сомнения, что в трёхмерно пространстве можно соединить прямыми линиями друг с другом бесконечно много точек и линии не будут пересекаться. Может я криво написал в моём первом посте и ты не так понял?
>>332758
Три точки: если соединить каждую с каждой, то линии не пересекаются - всё ок.
Четыре точки: если соединить каждую с каждой, то лини пересекутся и нет возможности расположить точки так что бы они не пересеклись.
>>332761
Возможно я не слишком понятно выразился. Соединяем каждую точку с каждой другой прямыми линиями. Линии не должны пересекаться. Какое максимальное количество точек, соединённых друг с другом подобным образом, можно разместить в n-мерном пространстве?
Или например: полный граф на n вершинах вкладывается в трехмерное пространство, при том ребра переходят в отрезки прямых. Возьми точки вида Ai=(xi,(xi)^2,(xi)^3), xi \in N. Два отрезка между точками будут пересекаться тогда и только тогда, когда 4 точки (края отрезков) компланарны. Посчитай мешаное произведение (Ai-Am,Ai-An,Ai-Ak), будет что-нибудь в стиле (xi-xm)(xi-xn)(xi-xk)(xm-xn)(xm-xk)(xn-xk) (c точностю до знака), что не равно нулю.
Немного наврал про "и только тогда", но оно и не нужно.
>Может быть есть готовые фигуры или способы их генерации для n точек?
Это верно для n точек общего положения. Скажем, если фиксировать n и каждую из n точек брать случайным образом из куба [0,1]3 (относительно равномерного распределения), то с вероятностью 1 это будет пример.
Дополню, явный пример для любого конечного n тоже легко строится. Пусть есть пример для n. Построим пример для n+1. Рассмотрим все пары из точки и прямой вне её из нашего примера. Для всех таких пар рассмотрим плоскость проходящую через точку и прямую. В качестве n+1-ой точки возьмём любую, не лежащую ни на одной из этих плоскостей. Несложно доказать, что никаких запрещённых пересечений не появится.
Ну и такое построение, как-ни странно, действует для континуального количества точек и пространства любой размерности.
Смущает меня то, что я не слушал "классических" курсов, которые слушают все математики на 1-4 курсе: дифуры, ТФКП, функциональный анализ, теоретическая механика и т. д. Во-первых, мне кажется, что эти курсы содержат в себе какой-то чудовищный объем информации, во-вторых, мне они неинтересны. Мне нравится алгебра (хорошо ориентируюсь в линейной алгебре, всякие группы/кольца/поля изучал совсем поверхностно в курсе криптографии), недавно начал изучать общую топологию.
Какие реально знания нужны, чтобы учиться в магистратуре? Нужен весь этот картофан? Что стоит изучить до осени?
Какие у меня вообще перспективы? Не окажется ли так, что студенты матфака - это вообще god tier и Рудина они прочитали еще в 9 классе?
Я больше про красивые фигуры, а не случайные.
Смотрел в сторону визуализации графов, но они не гнушаются пересечением линий. Да и в полных графах особо нечего визуализировать.
Но вот за идею генерировать случайно - спасибо. Что-то сам не додумался. Попробую подобрать правила так, что бы выглядело хорошо.
И тебе >>332772 спасибо. Так же попробую твою фигуру.
>>332780
Охуенно. Теперь я вижу почему их бесконечно много.
Реализовал твою идею. Выглядит забавно, но на глаз не видно, что они не пересекаются. Могу код скинуть - сам поиграешься в блендере.

Пикча потерялась.
Что начинающему лучше первым изучать: линейную или абстрактную алгебру?
>Не получится так, что я туда приду и не буду понимать курсы, потому что не знаю предыдущего материала?
Получится, но это норма, научишься короч.
> студенты матфака - это вообще god tier
Такие в меньшинстве.
Да, точно.
Ну погоди. Ты можешь поместить внутри треугольника точку и соединить с вершинами, не пересечется
>>332794
А какие темы изучать-то? Если что, я спрашиваю, что нужно, чтобы дальше понимать курсы, а не как поступить. Выборочно надрачивать темы из вступительных экзаменов я не собираюсь. В конце концов, можно поступить не во ВШЭ а в более слабое место либо подождать, пока мой уровень вырастет.
Я пока еще не знаю, чем хочу заниматься, но пацаны говорят, что интересные области сейчас - это алгебраическая топология, алгебраическая геометрия и другие. Ниже напишу, что я изучил (знаю определения, ознакомился с доказательствами результатов, которые использую, решал задачи) и что планирую изучать дальше. Надеюсь, что аноны, которые занимаются интересными разделами математики, меня направят.
1) Непрерывность, компактность и связность (это все в метрическом пространстве). Числовые ряды и их сходимость. Дифференцирование. Интеграл Римана. Всякие несложные интегралы вычислять умею. Дальше планирую изучать многомерный матан, дифференциальные формы. Потом теорию меры.
2) Топологические пространства и непрерывные функции по Munkres: Topology. Связность и компактность пока только в метрическом пространстве изучал, сейчас буду изучать в топологическом. Дальше хз что. Очень часто встречал словосочетание "фундаментальная группа". Вот надо будет разобраться, что это такое.
3) Конечномерные векторные пространства. Пространства со скалярным произведением. Диагонализуемость нормальных операторов на комплексном векторном пространстве и самосопряженных на вещественном. Форма Жордана. Насколько я понял, бесконечномерные векторные пространства изучаются в функциональном анализе. Дальше планирую его изучать, но я хз насколько надо углубляться, потому что, вроде как, это очень обширная тема.
4) Всякие группы/кольца/поля знаю только на уровне определений. В общем, воьсмиклассники в матшколе знают больше меня. Планирую Винберга навернуть.
5) Более-менее ориентируюсь в разделах, связанных с CS, потому что я у мамы погромист. Еще в численных методах немного ориентируюсь.
6) Совсем не знаю дифуры и физику. И не планирую знать в ближайшем будущем.
7) Совсем не знаю ТФКП. Знаю только результаты о комплексных числах уровня 18 века типа формулы Эйлера и формулы Муавра. Хз, что оттуда надо изучать. Планирую прочитать Rudin: Real and Complex Analysis.
>>332794
А какие темы изучать-то? Если что, я спрашиваю, что нужно, чтобы дальше понимать курсы, а не как поступить. Выборочно надрачивать темы из вступительных экзаменов я не собираюсь. В конце концов, можно поступить не во ВШЭ а в более слабое место либо подождать, пока мой уровень вырастет.
Я пока еще не знаю, чем хочу заниматься, но пацаны говорят, что интересные области сейчас - это алгебраическая топология, алгебраическая геометрия и другие. Ниже напишу, что я изучил (знаю определения, ознакомился с доказательствами результатов, которые использую, решал задачи) и что планирую изучать дальше. Надеюсь, что аноны, которые занимаются интересными разделами математики, меня направят.
1) Непрерывность, компактность и связность (это все в метрическом пространстве). Числовые ряды и их сходимость. Дифференцирование. Интеграл Римана. Всякие несложные интегралы вычислять умею. Дальше планирую изучать многомерный матан, дифференциальные формы. Потом теорию меры.
2) Топологические пространства и непрерывные функции по Munkres: Topology. Связность и компактность пока только в метрическом пространстве изучал, сейчас буду изучать в топологическом. Дальше хз что. Очень часто встречал словосочетание "фундаментальная группа". Вот надо будет разобраться, что это такое.
3) Конечномерные векторные пространства. Пространства со скалярным произведением. Диагонализуемость нормальных операторов на комплексном векторном пространстве и самосопряженных на вещественном. Форма Жордана. Насколько я понял, бесконечномерные векторные пространства изучаются в функциональном анализе. Дальше планирую его изучать, но я хз насколько надо углубляться, потому что, вроде как, это очень обширная тема.
4) Всякие группы/кольца/поля знаю только на уровне определений. В общем, воьсмиклассники в матшколе знают больше меня. Планирую Винберга навернуть.
5) Более-менее ориентируюсь в разделах, связанных с CS, потому что я у мамы погромист. Еще в численных методах немного ориентируюсь.
6) Совсем не знаю дифуры и физику. И не планирую знать в ближайшем будущем.
7) Совсем не знаю ТФКП. Знаю только результаты о комплексных числах уровня 18 века типа формулы Эйлера и формулы Муавра. Хз, что оттуда надо изучать. Планирую прочитать Rudin: Real and Complex Analysis.
>А какие темы изучать-то?
Если ориентироваться на то, чтобы стать математиком в будущем, то важно определиться с тем, чем будешь заниматься. Чтобы определиться наиболее информированным образом лучше познакомиться с разными областями. Я бы конечно мог предложить свой вариант программы, исходящий из моих вкусов, но думаю будет честнее просто отослать к разумной существующей программе, скажем, программе бакалавриата того же матфака. Если в целом следовать порядку, то проблем в основном быть не должно.
Кроме того хочу заметить, что у тебя сейчас знания более-менее на уровне среднего выпускника хорошей матшколы (ну может чуть выше). Если это возможно, то я бы на твоем месте особенно не торопился бы. Если ты из Москвы, то можно было бы пока походить в НМУ - курсы второго семестра должны скоро там начаться (если еще не начались).
>>332798
Если что, это называется скрученная кубика. Очень важный пример кривой в алгебраической геометрии.
>>332829
Наверни примерно первые два курса НМУ, видеозаписей разных годов дохуя, можешь на свой вкус выбрать лекторов. Это действительно база, после которой уже можно не испытывать баттхерта от своей неграмотности и посещать очень большое количество приличных курсов и семинаров. Соответственно, функан, диффуры и физика не первостепенно важны.
В магистратуру поступай, конечно. Уверяю, что там средний уровень не сильно лучше чем у бакалавриата (ибо хорошие студенты уезжают заграницу часто), хотя есть и godlike. А еще она вроде не так уж популярна.
> знания более-менее на уровне среднего выпускника хорошей матшколы
Это если бы на дворе был какой-нибудь 80й год.
>>332855
Например в 57 курс примерно соответствует этой книге
http://www.mccme.ru/free-books/57/davidovich.pdf
Средний выпускник, разумеется, усваивает не все, но из-за необходимости устно сдавать задачки большая часть усваивается.
В общем, посмотри лекции/листочки. Если понравится какой-то курс, то можешь сказать, возможно, опишу подводные камни. Например Сосинский и Скопенков это что-то совершенно невразумительное. Алсо, вообще можешь задавать вопросы как по математике, так и про матфак.
Ах, да. Разумеется, смотреть лекции и решать лекции не единственный путь.
По книгам Львовского (если все еще хардкорно, то Зорич), Винберга (еще рекомендую Алуффи, когда освоишься), Хатчера (или Фоменко-Фукса) и чего-то рандомного по комплану должно быть достаточно.
> Если понравится какой-то курс, то можешь сказать, возможно, опишу подводные камни.
Ну я открыл лекции Левина по алгебре, собираюсь смотреть и листки решать. Там правда у лекций качество звука хуевое и рассинхрон звука с изображением, но, вроде, воспринимать можно. Есть еще лекции алгебры-1 за осень 2015 года, но листки к ним почему-то еще не выложили. Или ты можешь посоветовать алгебру-1 за какой-то конкретный год?
Читать собираюсь Винберга.
> еще рекомендую Алуффи, когда освоишься
Я его листал, мне показалось, что там материала больше чем в Винберге. Может после Винберга прочитаю когда-нибудь.
Что можешь посоветовать по комплану? Пока планирую какой-нибудь курс НМУ навернуть. Углубляться не хочется, потому что я пока не представляю, где реально комплексные числа нужны. Я знаю фундаментальную теорему алгебры, знаю мелкие трюки уровня 18 века (типа как вывести матрицу поворота через комплексные числа, как вывести тригонометрические формулы), но я пока не понимаю, где без комплексных чисел прям не обойтись. При этом их почему-то везде суют, поэтому как-то обзорно освоить надо.
>>332906
Я вообще не понимаю. Почему, например, основная теорема теории Галуа у Левина в конце алгебры-2, а у Шабата в середине алгебры-1?
Почему на дваче нет фака с годными книгами по каждой мат. дисциплине.
По тому же, почему нет фака с годными книгами по русскому, английскому и другим языкам.
По каждой дисциплине есть много учебников и многие из них не являются строго худшими какого-то другого, в том смысле, что они будут лучшими для людей с определенным бэкграундом и целями. Хороший FAQ должен это отражать и для каждого предмета требует от автора хорошего знакомства с основной массой литературы по этому предмету и адекватности. По понятным причинам такое здесь сделать затруднительно.
Какой-то FAQ написать несложно. Но чем его советы будут лучше, чем информацию, которую можно почерпнуть из интернета за 3 минуты гугления?
Ищешь на math.stackexchange вопросы типа "%subject-name% book recommendation". Скачиваешь несколько книг из верхних постов, листаешь оглавление, выбираешь то, что нравится.
Наверняка, на двоще есть люди, способные написать годный фак, просто никто не берется.
Долбоёбы, хуле.
Так вот, реквестирую у местных мастеров рекомендуемый порядок, в котором стоит дрочить книги и материалы со спецкурсов, чтобы градус нарастал постепенно. Тому що сейчас, например, стал смотреть по теоркату - вот здесь http://komar.bitcheese.net/files/Учебник.pdf все разжевано как для сосницких, и чувствуется, что очень многое осталось за бортом, а у Маклейна, наоборот, сразу используется дохуя понятий из областей, которые мне пока неведомы.
Помогите, посоны, расскажите, в каком порядке и какие вы читали книжки.
Ну да, самые основы, вместе с линалом и ангемом. Группы, кольца, поля, изоморфизмы-гомоморфизмы, простейшие выводы всякие.
Что скажете, дегенераты?
Потому что я ненавижу сумасшедших и закомплексованных любого сорта.

Ты знаешь, что надо делать.
Ничего первые не строят, точно так же пытаются хоть как-то доказать своё засохшее говно, точно так же как вторые.
У Шабата, судя по программе и листкам, несколько всратый и сильно хардкорный курс. У Левина вроде наоборот лайтовый.
Рекомендовать не берусь, так как реально вкусовщина. У Городенцева вроде хороший курс был из недавних, но я вот его, например, совершенно не перевариваю.
>Я его листал, мне показалось, что там материала больше чем в Винберге. Может после Винберга прочитаю когда-нибудь.
Правильно, его надо просто посмотреть уже после какого-то курса алгебры, чтобы взлянуть еще раз на те же вещи в чуть более правильном свете (ну, и гомологическую алгебру можно там будет начать учить).
>Что можешь посоветовать по комплану?
Тут у меня четких предпочтений нет, так как нахватался из разных мест и больше устноъ. Лекции Домрина вроде все читают
>где реально комплексные числа нужны
Что значит нужны? Это фундаментальный объект с кучей интересных свойств. При этом гораздо более приятный и удобный, чем R, во многих отношениях. С ним банально проще работать обычно (хотя бы из-за свойства алгебраической замкнутости).
>>332909
Потому что разные преподы с разными представлениями о том, как должен быть устроен курс алгебры.

А по современным разделам математики нет не только годных книг, но и вообще хоть каких-нибудь книг. Только статьи в журналах.
Временная разница между собственно статьями с действительно важными результатами, если они не слишком техничны, и их появлением в учебниках по моему опыту в среднем лет 10-15. За этот период перекраиваются во что-то совершенно другое лишь малая часть областей. В большинстве случаев учить раздел по книге вышедшей в последние 10 лет и потом читать актуальные статьи вполне здраво.
> У Шабата, судя по программе и листкам, несколько всратый и сильно хардкорный курс.
почему хардкорность я кажись понял (превышена средняя плотность новых понятий которые надо усвоить)
а в чем всратость?
Почему?
Ну допустим я есть. Объясни, чем тебя не устраивают существующие факи? Та же программа Вербицкого, например.
>Объясни, чем тебя не устраивают существующие факи?
Я имел ввиду, что на дваче нет своего фака.
И не надо.
Подборку книг, видео, сайтов к основным (и не только) дисциплинам с указаниями плюсов и минусов. Оптимальный порядок, в котором это стоит изучать.
Слишком субъективно получится. Как на той глупой картинке, где политику советуют изучать по Макиавелли.
Ну так для этого и нужно указывать различные источники и их преимущества и недостатки.
А что такое "дисциплина"? Просто я вот под этим понимаю вещи типа гомологической алгебры и общей топологии, а кто-то может считать дисциплинами аналитическую геометрию и дискретную математику.
>а кто-то может считать дисциплинами аналитическую геометрию и дискретную математику
Я из этих.
Хуякт.
Взял с википедии, возможно, тут многого нет.
Математический анализ
Алгебра
Аналитическая геометрия
Линейная алгебра и геометрия
Дискретная математика
Математическая логика
Дифференциальные уравнения
Дифференциальная геометрия
Топология
Функциональный анализ и интегральные уравнения
Теория функций комплексного переменного
Уравнения с частными производными (вместо этого курса физикам читаются Методы математической физики)
Теория вероятностей
Математическая статистика
Теория случайных процессов
Вариационное исчисление и методы оптимизации
Методы вычислений, то есть численные методы
Теория чисел
Хорошо. Я читал некоторое количество книг и смогу составить описание. Только уточни, чем различаются алгебра, линейная алгебра и геометрия и аналитическая геометрия?
Наверное, так лучше: общая алгебра, линейная алгебра, аналитическая геометрия.
А с чего ты решил, что именно твои книги должны быть включены, и именно ты должен что-то там составлять?
Я?!.jpg
Я принципиально не стал включать сюда более новые книги. Перечисленные книги адекватны математической программе большинства современных российских вузов.
Математический анализ
1. Фихтенгольц. "Курс дифференциального и интегрального исчисления" в трёх томах.
Это очень старый учебник, написанный ещё до появления топологии как науки и даже до установления современной терминологии теории множеств. Изложение ведётся в стиле девятнадцатого века, с явным акцентом на практические приёмы вычислений. В учебнике используется нестандартная терминология: так, последовательность названа "варианта". Первый том содержит классический анализ вплоть до понятия неявной функции и матрицы Якоби. Фихтенгольц особо не скрывал, что образцом для первого тома послужил курс Коши, написанный ещё в 1821 году. Второй том - неопределённый и определённый интеграл, а также ряды. Есть много сравнительно экзотических вещей: признаки Раабе, Куммера и Ермакова, например. Третий том - криволинейные, двойные, поверхностные и тройные интегралы, а также ряды Фурье. Общей теории интеграла Римана, опирающейся на меру Жордана, книга Фихтенгольца не содержит, несмотря на свою объёмность.
2. Кудрявцев, "Курс математического анализа" в трёх томах. Книга, видимо, задумана как современная версия Фихтенгольца. Книга весьма странная. Например, в ней не определяются выражения вроде "индекс пробегает множество", зато определяются выражения вроде "число элементов множества равно единице" - предполагается, видимо, что второе непонятнее первого. В книге есть упражнения, в которых читателю предлагается доказать утверждения, для доказательства которых материала книги в принципе недостаточно, и такие упражнения никак особо не отмечены. Для учебника это странно.
Первый том содержит элементы теории множеств, элементы комбинаторики (перестановки, сочетания, биномиальный коэффициент), последовательности, пределы, дифференциальное и интегральное исчисления для функций R->R. Второй том содержит ряды, дифференциальное и интегральное исчисление на R^n (мера Жордана определяется явно), а также элементы теории поля (вплоть до потенциальных и соленоидальных полей). Третий том - ряды Фурье и интеграл Фурье, функциональные пространства, обобщённые функции. В приложении к третьему тому изложено определение предела вдоль фильтра. Многообразий в курсе нет.
3. Ильин, Позняк, "Основы математического анализа" в двух томах. По сути, это Кудрявцев для бедных. Изложение, несмотря на свою объёмность, весьма странное. Так, все концептуально важные замечания о непрерывности R вынесены в приложение к первому тому, зато эволюта и эвольвента удостоились места в основном тексте. Второй том, однако же, содержит определение интеграла Лебега и пространства Гильберта.
4. Архипов, Садовничий, Чубариков, "Лекции по математическому анализу". Одна объёмная книжка. Изложение изобилует странными заявлениями вроде "множество есть неопределяемое понятие". Вещественные числа определяются как бесконечные десятичные дроби, что ведёт к ожидаемым проблемам с определением арифметических операций. Многие теоремы, например теорема Вейерштрасса, оставлены без доказательств. Книга состоит из четырёх частей. Интеграл Римана и интеграл Лебега определяются, - ну, вернее, описываются, - явно, без умолчаний, с опорой на соответствующие меры. Изложение стандартное, заканчивается обобщённой формулой Стокса.
5. Демидович, "Сборник задач и упражнений по математическому анализу". Nuff said.
6. Виноградова, Олехник, Садовничий. "Задачи и упражнения по математическому анализу" в двух томах. Задач больше, чем в Демидовиче. Есть задачи весьма унылые, есть и сравнительно интересные.
Алгебра
1. Курош, "Курс высшей алгебры". Несмотря на название, курс в основном посвящён многочленам и тривиальным вычислительным аспектам линейной алгебры, специфических абстрактных объектов в нём нет. Группы определяются лишь в последней, четырнадцатой главе.
2. Курош, "Общая алгебра". Курош сумел создать собственную научную школу, в заметной степени обособленную от остальной математики. Школа Куроша занимается изучением, по сути, самой себя. Фундамент школы образован вещами, которые интересовали лично Куроша. Так как Курош был человек увлекающийся, фундамент получился чрезвычайно эклектичным: универсальные алгебры, лупы Муфанг, мультиоператорные группы и почему-то нормированные кольца. Книжечка меметична тем, что образует ядро школы Куроша, будучи при этом малоизвестной. В ней даны определения основным понятиям, интересовавшим Куроша.
3. Курош, "Лекции по общей алгебре". Не следует путать с книжкой с похожим названием. В лекциях систематически, последовательно излагается более-менее вменяемая общая алгебра, начиная с понятия бинарного отношения, заканчивая основной теоремой теории Галуа. При этом, конечно, Курош пользуется своим стилем и своей терминологией - например, упорно использует омега-группы - но в целом это не критично. Из всех книг Куроша эта, пожалуй, самая ценная.
4. Курош, "Теория групп". Magnum Opus Куроша, его величайшая книга, сборник просто огромного количества теорем и малоизвестных определений. К сожалению, теоремы сведены в этот сборник механически, а не доказаны единым образом в какой-то общей парадигме. У книги есть несколько изданий, сильно различающихся между собой. В книге нашлось место операциям - книга писалась полвека назад, и тогда это ещё были операции - Ext, Hom, Tor и многим другим вещам, всё ещё сохраняющим актуальность.
5. Постников, "Теория Галуа". Дополнение к вышеперечисленным книгам, написанное откровенным фанатом Куроша. Любовь автора к Курошу проявляется с первых же страниц, когда Постников объявляет, что слово Курс - именно так, с большой буквы, - обозначает "Курс высшей алгебры". Книга выдержана в том же стиле, что и творчество Куроша, сходство просто удивительное. Книжка состоит из трёх частей. В первой части определяются штуки вроде композита полей, во второй части доказывается теорема Абеля о неразрешимости в радикалах, в третьей части технические аспекты и приложения - вычисление группы Галуа, построение циркулем и линейкой и прочие луночки Гиппократа.
Я принципиально не стал включать сюда более новые книги. Перечисленные книги адекватны математической программе большинства современных российских вузов.
Математический анализ
1. Фихтенгольц. "Курс дифференциального и интегрального исчисления" в трёх томах.
Это очень старый учебник, написанный ещё до появления топологии как науки и даже до установления современной терминологии теории множеств. Изложение ведётся в стиле девятнадцатого века, с явным акцентом на практические приёмы вычислений. В учебнике используется нестандартная терминология: так, последовательность названа "варианта". Первый том содержит классический анализ вплоть до понятия неявной функции и матрицы Якоби. Фихтенгольц особо не скрывал, что образцом для первого тома послужил курс Коши, написанный ещё в 1821 году. Второй том - неопределённый и определённый интеграл, а также ряды. Есть много сравнительно экзотических вещей: признаки Раабе, Куммера и Ермакова, например. Третий том - криволинейные, двойные, поверхностные и тройные интегралы, а также ряды Фурье. Общей теории интеграла Римана, опирающейся на меру Жордана, книга Фихтенгольца не содержит, несмотря на свою объёмность.
2. Кудрявцев, "Курс математического анализа" в трёх томах. Книга, видимо, задумана как современная версия Фихтенгольца. Книга весьма странная. Например, в ней не определяются выражения вроде "индекс пробегает множество", зато определяются выражения вроде "число элементов множества равно единице" - предполагается, видимо, что второе непонятнее первого. В книге есть упражнения, в которых читателю предлагается доказать утверждения, для доказательства которых материала книги в принципе недостаточно, и такие упражнения никак особо не отмечены. Для учебника это странно.
Первый том содержит элементы теории множеств, элементы комбинаторики (перестановки, сочетания, биномиальный коэффициент), последовательности, пределы, дифференциальное и интегральное исчисления для функций R->R. Второй том содержит ряды, дифференциальное и интегральное исчисление на R^n (мера Жордана определяется явно), а также элементы теории поля (вплоть до потенциальных и соленоидальных полей). Третий том - ряды Фурье и интеграл Фурье, функциональные пространства, обобщённые функции. В приложении к третьему тому изложено определение предела вдоль фильтра. Многообразий в курсе нет.
3. Ильин, Позняк, "Основы математического анализа" в двух томах. По сути, это Кудрявцев для бедных. Изложение, несмотря на свою объёмность, весьма странное. Так, все концептуально важные замечания о непрерывности R вынесены в приложение к первому тому, зато эволюта и эвольвента удостоились места в основном тексте. Второй том, однако же, содержит определение интеграла Лебега и пространства Гильберта.
4. Архипов, Садовничий, Чубариков, "Лекции по математическому анализу". Одна объёмная книжка. Изложение изобилует странными заявлениями вроде "множество есть неопределяемое понятие". Вещественные числа определяются как бесконечные десятичные дроби, что ведёт к ожидаемым проблемам с определением арифметических операций. Многие теоремы, например теорема Вейерштрасса, оставлены без доказательств. Книга состоит из четырёх частей. Интеграл Римана и интеграл Лебега определяются, - ну, вернее, описываются, - явно, без умолчаний, с опорой на соответствующие меры. Изложение стандартное, заканчивается обобщённой формулой Стокса.
5. Демидович, "Сборник задач и упражнений по математическому анализу". Nuff said.
6. Виноградова, Олехник, Садовничий. "Задачи и упражнения по математическому анализу" в двух томах. Задач больше, чем в Демидовиче. Есть задачи весьма унылые, есть и сравнительно интересные.
Алгебра
1. Курош, "Курс высшей алгебры". Несмотря на название, курс в основном посвящён многочленам и тривиальным вычислительным аспектам линейной алгебры, специфических абстрактных объектов в нём нет. Группы определяются лишь в последней, четырнадцатой главе.
2. Курош, "Общая алгебра". Курош сумел создать собственную научную школу, в заметной степени обособленную от остальной математики. Школа Куроша занимается изучением, по сути, самой себя. Фундамент школы образован вещами, которые интересовали лично Куроша. Так как Курош был человек увлекающийся, фундамент получился чрезвычайно эклектичным: универсальные алгебры, лупы Муфанг, мультиоператорные группы и почему-то нормированные кольца. Книжечка меметична тем, что образует ядро школы Куроша, будучи при этом малоизвестной. В ней даны определения основным понятиям, интересовавшим Куроша.
3. Курош, "Лекции по общей алгебре". Не следует путать с книжкой с похожим названием. В лекциях систематически, последовательно излагается более-менее вменяемая общая алгебра, начиная с понятия бинарного отношения, заканчивая основной теоремой теории Галуа. При этом, конечно, Курош пользуется своим стилем и своей терминологией - например, упорно использует омега-группы - но в целом это не критично. Из всех книг Куроша эта, пожалуй, самая ценная.
4. Курош, "Теория групп". Magnum Opus Куроша, его величайшая книга, сборник просто огромного количества теорем и малоизвестных определений. К сожалению, теоремы сведены в этот сборник механически, а не доказаны единым образом в какой-то общей парадигме. У книги есть несколько изданий, сильно различающихся между собой. В книге нашлось место операциям - книга писалась полвека назад, и тогда это ещё были операции - Ext, Hom, Tor и многим другим вещам, всё ещё сохраняющим актуальность.
5. Постников, "Теория Галуа". Дополнение к вышеперечисленным книгам, написанное откровенным фанатом Куроша. Любовь автора к Курошу проявляется с первых же страниц, когда Постников объявляет, что слово Курс - именно так, с большой буквы, - обозначает "Курс высшей алгебры". Книга выдержана в том же стиле, что и творчество Куроша, сходство просто удивительное. Книжка состоит из трёх частей. В первой части определяются штуки вроде композита полей, во второй части доказывается теорема Абеля о неразрешимости в радикалах, в третьей части технические аспекты и приложения - вычисление группы Галуа, построение циркулем и линейкой и прочие луночки Гиппократа.
вот тут на вики дают типа интуицию
https://en.wikipedia.org/wiki/Simplicial_set#Intuition
> Formally, a simplicial set X is a collection of sets Xn, n=0,1,2,..., together with certain maps between these sets: the face maps dn,i:Xn→Xn-1 (n=1,2,3,... and 0≤i≤n) and degeneracy maps sn,i:Xn→Xn+1 (n=0,1,2,... and 0≤i≤n). We think of the elements of Xn as the n-simplices of X. The map dn,i assigns to each such n-simplex its i-th face, the face "opposite to" (i.e. not containing) the i-th vertex. The map sn,i assigns to each n-simplex the degenerate (n+1)-simplex which arises from the given one by duplicating the i-th vertex. This description implicitly requires certain consistency relations among the maps dn,i and sn,i. Rather than requiring these simplicial identities explicitly as part of the definition, the short and elegant modern definition uses the language of category theory.
конкретно вот эту вот фразу
> We think of the elements of Xn as the n-simplices of X
что такое симплекс в этом контексте?
Линейная алгебра
1. Ильин, Позняк. "Линейная алгебра". Архетипичный учебник линейной алгебры. Главы таковы: матрицы, линейные пространства, системы линейных уравнений, евклидовы пространства, линейные операторы, итерационные методы, билинейные и квадратичные формы, тензоры, элементы теории групп. Несмотря на отсутствие явного разделения алгебры на линейную и полилинейную, книга выдержана в довольно чётком стиле.
2. Гельфанд, "Лекции по линейной алгебре". Эта книжка действительно является лекциями. В ней углубленно изучаются некоторые вещи, например, нормальная форма линейного оператора. Основным учебником эта книга служить не может.
3. Воеводин, "Линейная алгебра". Тот же Ильин-Позняк, только труба пониже, дым пожиже. Есть сложение направленных отрезков.
4. Проскуряков, "Сборник задач по линейной алгебре". Nuff said.
Аналитическая геометрия
1. Александров, "Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры". Учебник примечателен тем, что геометрия здесь излагается поначалу независимо от теории множеств. Вводится самостоятельная система понятий (не аксиоматическая), описывающая прямую и отрезок на ней. Вектор сперва вводится как направленный отрезок. В учебнике есть чудесный привет из восемнадцатого века: параграф "Пропорциональность пар чисел". Абстрактные векторные пространства вводятся только в двенадцатой главе.
2. Ильин, Позняк. "Аналитическая геометрия". По сравнению с предыдущей книжкой выглядит современнее, но гораздо бледнее. По сути, эта книга - учебник линейной алгебры, к которому приделали координаты и в котором переобозвали некоторые понятия, а потом использовали для описания кривых и поверхностей второго порядка.
3. Беклемишев, "Курс аналитической геометрии и линейной алгебры". Кривые и поверхности второго порядка изучаются в третьей главе, последующие главы - кое-какая теория аффинных пространств, последняя глава - тензоры.
4. Ефимов, Розендорн, "Линейная алгебра и многомерная геометрия". Первые десять глав - стандартны, дальше начинается любопытное заигрывание с поливекторами и внешними формами. Последняя глава - проективное пространство.
5. Оболенский, "Лекции по аналитической геометрии". Учебник позиционируется как бы для программистов, однако содержит алгебры Грассмана и симплектическую геометрию. Автор игрив, его язык шутлив.
Линейная алгебра
1. Ильин, Позняк. "Линейная алгебра". Архетипичный учебник линейной алгебры. Главы таковы: матрицы, линейные пространства, системы линейных уравнений, евклидовы пространства, линейные операторы, итерационные методы, билинейные и квадратичные формы, тензоры, элементы теории групп. Несмотря на отсутствие явного разделения алгебры на линейную и полилинейную, книга выдержана в довольно чётком стиле.
2. Гельфанд, "Лекции по линейной алгебре". Эта книжка действительно является лекциями. В ней углубленно изучаются некоторые вещи, например, нормальная форма линейного оператора. Основным учебником эта книга служить не может.
3. Воеводин, "Линейная алгебра". Тот же Ильин-Позняк, только труба пониже, дым пожиже. Есть сложение направленных отрезков.
4. Проскуряков, "Сборник задач по линейной алгебре". Nuff said.
Аналитическая геометрия
1. Александров, "Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры". Учебник примечателен тем, что геометрия здесь излагается поначалу независимо от теории множеств. Вводится самостоятельная система понятий (не аксиоматическая), описывающая прямую и отрезок на ней. Вектор сперва вводится как направленный отрезок. В учебнике есть чудесный привет из восемнадцатого века: параграф "Пропорциональность пар чисел". Абстрактные векторные пространства вводятся только в двенадцатой главе.
2. Ильин, Позняк. "Аналитическая геометрия". По сравнению с предыдущей книжкой выглядит современнее, но гораздо бледнее. По сути, эта книга - учебник линейной алгебры, к которому приделали координаты и в котором переобозвали некоторые понятия, а потом использовали для описания кривых и поверхностей второго порядка.
3. Беклемишев, "Курс аналитической геометрии и линейной алгебры". Кривые и поверхности второго порядка изучаются в третьей главе, последующие главы - кое-какая теория аффинных пространств, последняя глава - тензоры.
4. Ефимов, Розендорн, "Линейная алгебра и многомерная геометрия". Первые десять глав - стандартны, дальше начинается любопытное заигрывание с поливекторами и внешними формами. Последняя глава - проективное пространство.
5. Оболенский, "Лекции по аналитической геометрии". Учебник позиционируется как бы для программистов, однако содержит алгебры Грассмана и симплектическую геометрию. Автор игрив, его язык шутлив.
Я прочитал много книг и выбрал среди них сравнительно приличные. Мой опыт нужно сохранить для потомков.
min(f_1(x), f_2(x), ..., f_n(x)) -> max,
где f_i - полином n переменных,
x = (x_1, ..., x_k), 0 <= x_j <= 1
Может есть метод специально для полиномов или максимизации минимума?
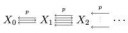
>что такое симплекс в этом контексте?
Примерно такая конструкция. Стрелки влево - face maps, стрелки вправо - degeneracy maps. Элемент такой конструкции - последовательность - это n-симплекс.
Бля, чет я слепой
Может банально, но нельзя сделать сетку, а потом из каждой точки сделать градиентный спуск и сравнить?
Если нужно точное решение, то хз.
> У Левина вроде наоборот лайтовый.
Вот я его выбрал, потому что хочу большое количество материала изучить побыстрей. И еще у него в листках нет чисел. Я вообще боюсь чисел и не люблю их.
Кортеж: x = (x_1, ..., x_k)
Просто поленился полностью переменные записать. Наверное правильнее и понятнее будет так:
min(f_1(x_1, x_2, ..., x_k), f_2(x_1, x_2, ..., x_k), ..., f_n(x_1, x_2, ..., x_k)) -> max
где f_i - полином k переменных
Еще можешь попробовать с генетическими алгоритмами как-нибудь скомбинировать.
Это сейчас реализую, но результат будет близок к точному решению если шаг сетки будет мал, а при больших k его маленьким не сделаешь:
d^k, где d - число точек на каждой из k осей
Даже если всего пять точек на каждой из осей брать и 30 мерное пространство:
5^30 = 931322574615478515625
В общем как в случае любого другого брутфорса: наблюдай числа отдалённо напоминающие правильные или запасайся эликсирами вечной жизни.
Клевая проблема, можно попробовать через тензорные методы. Если степень полиномов не слишком высокая, получится тензор малого ранга. Его моожно записать в пиздатенький формат и запустить blackbox-approximation (хз как по-русски)
Ищи работы L. Grasedyck, Espig, Hackbusch (наставник первых двух), Kolda.
У них солидные разработки по этой теме. Но не факт что именно такую проблему можно решить тензорами. Поиск максимума в тензоре нихуюво сложная проблема.
Hackbusch таки наверно по этой теме сам не писал.
Еще есть какой-то хмырь в Сколоково, который тоже типо тензорами занимается.
Чему равно контактное число в евклидовых пространствах с размерностью n>4.
Всякая ли бесконечная непериодическая непрерывная дробь с ограниченными членами — трансцендентна?
Давай трахаться.
Не верю в это утверждение
> Всякая бесконечная непериодическая непрерывная дробь с ограниченными членами трансцендентна
и в его отрицание тоже не верю.
f'(x)=lim(x треуг ->0) f(x+x треуг) -f(x)/ x треуг
Ну не знаю. Че так сразу что ли? Мы еще в парке не гуляли, цветов ты мне еще не дарил.
>цветы
>парки
>прогулки
Так это же всё для быдла! Мы вместе будем открытые математические проблемы решать!
>>333554
>>333573
Уж не очередная ли это инкарнация N-обиженного? Всех уже "победил", можно и поглумиться? ОТВЕЧАЙ, МРАЗЬ!
А по-хорошему репортните этого экспата с параши - мне в лом. МОЧЕ, хватит это терпеть!
Есть два варианта: либо ты предоставляешь мне корректное определение множества N, либо сосёшь хуй.
Сейчас ты сосёшь хуй.
Ну как так? Если я буду встречаться с мужчиной, то он должен меня обеспечивать! Настоящего мужчину даже просить не надо, если он настоящий. Он по факту обязан.
Это ложь! Настоящей любви нет преград!
Мне вообще похуй на то, что я - мужчина!
С водовкой! И со шкварочками.
>>333357
Логика
1. Игошин, "Математическая логика и теория алгоритмов".
Типичное введение в логику, книжка для первого знакомства. В ней содержится много исторических и философских отступлений, даётся толкование аристотелевских фигур и модусов в терминах современной логики. К сожалению, есть заметное количество опечаток.
2. Колмогоров, Драгалин. "Математическая логика". Более подробное, по сравнению с Игошиным, исследование различий между синтаксисом и семантикой. Во второй главе предпринимается попытка построить некую формальную теорию (многосортные термы, атомы, кванторные приставки, формальные подстановки). Книга заканчивается "теорией алгорифмов".
3. Ершов, Палютин. "Математическая логика". Материал примерно тот же, что в предыдущей книжке, но используется чуть более современная терминология (алгоритм вместо алгорифм, например). Есть явная глава про теорию моделей.
4. Кейслер, Чэн. "Теория моделей". Не следует путать с книжкой тех же авторов про непрерывные модели. Здесь изложена, собственно, теория моделей. Первая глава - про синтаксис, начинается алфавитами, заканчивается элиминацией кванторов. Вторая глава - собственно теория моделей. Последующие главы - ультрапроизведения, насыщенные и специальные модели.
Опа, это уже для N-петуха.
А как вообще изучать мат. литературу? Конспект обязателен?
Да, нужно прочтя главу выписать, по возможности не подглядывая, с пониманием, все теоремы с доказательствами, ну и упражнения, разумеется. Да и чуть не забыл, обязательно в ТеХе, иначе совсем не усвоить материал.
У всех по-разному. Сильно по-разному.

Нет, это пост с книгами, которые можно рекомендовать в качестве учебников ширнармассам, не специализирующимся на современной математике. Думаю, тебе пригодятся первые несколько глав Игошина.
Что с ними не так?
Просто берешь и без всякой задней мысли читаешь. При этом не забывай рычать и двигать тазом, как будто ты уже изучил всю математику.
Ну я пишу конспект без доказательств. Много времени не занимает.
Если ты такой умный, то подскажи мне книжечку по алгебраическим кривым с прицелом на приложения в алгебре.
Эх Игошин, забавный мужичок, логику у меня вел на первом курсе
Лекции у него и правда неплохие
Есть еще тетрадь рабочая по мат.логике, не знаю реально ли найти её в электронном виде, но если найдете, то советую посмотреть
Если тебе для общения, а не матана, то почитай учебник логики для юристов и что-нибудь по риторике.
Ну рассмотри 2 случая и ответь на свой вопрос.
А как ты при этом на простые числа смотришь? Они у тебя на потолке что ли или ты в левой руке листок с числами держишь?
Я вот, например, прихожу домой, задергиваю шторы, открываю oeis.org и понеслась...
Я делаю вид, что читаю учебник по тригонометрии, а на самом деле читаю про простые числа.
Потому что это building blocks, из которых строятся другие числа.
Кроме того, они имеют прикладное значение для криптографии. Одна из главных причин криптостойкости существующих алгоритмов в том, что задача факторизации числа сложная.
Потому что это building blocks, из которых строятся другие числа.
Кроме того, они имеют прикладное значение для криптографии. Одна из главных причин криптостойкости существующих алгоритмов в том, что задача факторизации числа сложная.
Есть ли в треде люди, которые будучи студентами публиковались?
Сложно ли это, какие советы вы бы дали? Поделитесь инфой пожалуйста
Тащем-та ничего сверхъестественного тут нет - просто берёшь и публикуешься.
Что за ебанутый вопрос такой? Идёшь на кафедру с текстом, просишь соавтора, соавтор какой-нибудь водяной хуйнёй допиливает, и публикуетесь. Возможно, засчёт вуза. Но вероятнее всего нет.
>>333765
окей, спасибо за ответ
вопрос некорректно сформулировал.
в моём понимании публикация - это когда ты что-нибудь новенькое придумал или вроде того.
поэтому, если придумать что нибудь эдакое затруднительно, то как в этом случае происходит процесс. например, идешь к научнику своему и он тебя за красивые глаза вписывает в соавторы или даёт какие нибудь темы возможные и т.д.
Обычно так, да. Хотя какой у бакалавра научник, лол? Но мы же сейчас говорим о том, что ты такой с новой идеей приходишь, и научник просто становится твоим соавтором, потому что в противном случае система не даст опубликоваться. Такие дела.
Когда я был студентом было примерно так: научрук дал задачу, я ее решил, дальше записал, научрук дал ряд советов по тексту и указал журнал в который подать статью, примерно через полтора года после подачи ее опубликовали.
Касательно публикаций без собственных математических идей, это по моему опыту происходит не так часто.
Но ведь ты его вводишь в заблуждение, не указывая, что опубликовался в говножурнале, где публикуются статьи, не подкреплённые авторитетом.
а может он в анналах публиковался
Че в /un/-то, это нормальная задача.
latex он имел в виду, погугли
Определяете множество N?
В Математическом Сборнике, если указывать явно. Для математического журнала на русском он вполне неплох.
Пусть дано одномерное векторное пространство V над k. Докажите, что End V естественно изоморфно k.
Хочешь задачку посложнее? Ответь тогда, почему средний "разброс" простых чисел приближается к экспоненте?
Я в заголовке удаленного поста написал, что моя задача элементарна, после условия я привел решение. Все, что мне было нужно, это красиво построить предложение. Вопрос в невероятной степени ньюфажеский >>333892 , но я еще даже не учусь в университете. Но вот ответ на твой вопрос был к примеру озвучен в каком-то научпопе для профанов простая одержимость. Ты правда мод? Что вообще произошло? Какие правила я нарушил?
Потому что их задал не ты. Устраивает такой ответ?
Что долдке знать математик-алгебраист?
В совершенстве линейную и гомологическую алгебру, достаточно общей алгебры, околоентри-левел теорию групп, ассоциативных алгебр, колец и их представлений, функциональный анализ, вокруг теоремы о индексе, функции бесселя, марковские процессы и интеграл римана.
Нужен.
Он получает новое знание. То есть это один из немногих людей на планете, кто по-настоящему нужен.
А какая реальная практическая польза от алгебры? Ну кроме криптографии и способности алгебраиков чрезмерно раздувать чсв?
Он исключительно теоретик и трудится на благо науки или есть какие-либо промышленные применения?
А какая польза от Вселенной?
Ну не совсем. Короч это такое говнецо ни нашим, ни вашим.
Не все. Аналитики получают не знание, а только очередные признаки сходимости рядов, например. Уже сами забыли, сколько признаков открыли, но продолжают открывать.
> только очередные признаки сходимости рядов
Хуета какая.
Не говоря уже о том, что даже если бы это было так, то новые признаки сходимости вполне себе новое знание, ничуть не хуже алгебраических.
Решение уравнений.
Все в названии чего есть слово "алгебра".
Ну так ответит кто нибудь?
Он пытается определить определение N. Пока эта проблема тысячелетия не решится не будет новой математики.
Он охуел. Как и ты.
Как минимум чтобы определить «направление» кривой. Также при помощи касательных можно построить её линейное приближение.
https://en.m.wikipedia.org/wiki/Tangent

Что за направление? Я думал намного лучше будет
Ссылка мне не дала ответа, только всякие определения, двойные точки касания, т.д.
Плюс, насколько я понял, ты говоришь о обратной задаче, типа "у нас есть касательная с уравнением у=три_пизды_колено_х, найти уравнение функции".
Например что пропало?
>Что за направление?
Направление движения точки по кривой.
>Ссылка мне не дала ответа, только всякие определения, двойные точки касания, т.д.
Читай внимательней.
>Плюс, насколько я понял, ты говоришь о обратной задаче
Нет.
f'(x) = lim_{t -> x} (f(t) - f(x)) / (t - x).
А потом я читаю, что из определения производной следует, что
f(t) - f(x) = f'(x)(t - x) + eps(t),
где
eps(t) / (t - x) -> 0 при t -> x.
Как это получилось? Интуитивно это понятно, если посмотреть на картинку, но что-то я не могу придумать доказательство. Я вижу только, что из определения следует, что
f(t) - f(x) = f'(x)(t - x)
при t -> x.
Отвечу сам на свой вопрос.
f(t) - f(x) = (t - x)f'(x) + f(t) - f(x) - (t - x)f'(x)
Обозначим последние 3 слагаемых как g(t).
При t -> x
g(t) / (t - x) = f'(x) - f'(x) = 0.
Те из книг, которые читал, были люто годными. Добра тебе!
Было бы охуенно, если бы ты запилил моар. Особенно хотет рекомендаций вводных книжек в топологию, дифгем и вот это все, что касается переката от стандартного двухгодичного курса математики к высоким материям.
Математики они такие. Даже очевидную единицу обосновывают что это единица.
Ты сейчас в треде математики проигрываешь с общепринятого в математике метода познания. Ты не очень умный.
Если ты задаешься таким вопросом, значит тебе она не нужна.
Я проигрываю с тебя, тупой уебан. Зачем нужно доказательство я хорошо представляю, только вот точно не для
>Чтобы установить его истинность.
Ведь истинность чего-либо установить невозможно.
> Ведь истинность чего-либо установить невозможно.
Ой бля, может ты в какой-нибудь тред философии съебешь?
>Ведь истинность чего-либо установить невозможно.
Дебил, невозможно установить истинность естественноначной теории, а не математической.
Это я спрашивал, зачем доказывать очевидное. И я имел в виду, что там доказательство очевидно геометрически, на уровне картинки, и потому ставил под сомнение необходимость формального вывода.
> там доказательство очевидно геометрически, на уровне картинки
А ты результаты из теории множеств через круги Эйлера доказываешь?
Короче ты походу чистый математик, всё с тобой понятно.
Вброшу мысль, которая почему-то ясна не всем. Доказательство с помощью кругов Эйлера является строгим доказательством.
Для того, чтобы это было строгим доказательством, нужно как минимум формализовать понятие кругов Эйлера.
Мне кажется, графический язык кругов ничем не хуже других формализмов.
Отнюдь. Круги Эйлера относятся к метаязыку и нуждаются в формализации не больше, чем понятия "символ" и "строка символов". Если ты испытываешь какие-то сомнения, то заметь, что с помощью кругов Эйлера нельзя доказать ничего, что нельзя было бы доказать с помощью строк символов.
> с помощью кругов Эйлера нельзя доказать ничего, что нельзя было бы доказать с помощью строк символов.
И нет ничего, что можно было бы доказать с помощью кргуов Эйлера, но нельзя было бы доказать с помощью букв. Зачем мне расширять метаязык, если это не дает никаких дополнительных возможностей, но дает риск возникновения какой-то хуйни?
Это упрощает доказательства.
>если это не дает никаких дополнительных возможностей
Мне задачки в уме легче решать с помощью наглядных представлений, а не греческой крупы.
И если ты спросишь "Что за топосы и категорный анализ логики? Как это? Хотел прочесть книгу, но не смог(", тебя пошлют к мамке с пером в заднице.
Не нужно проецировать на математику свойства местного сообщества. Опознание "свой-чужой" капчующие школьники производят вне зависимости от темы обсуждения.
Ну, не знаю. Мне вот все математики ИРЛ попадались (молодые, про возрастных ничего не знаю) и все на один были как ёбаные нервные уроды. Совпадение?
Согласен, качественный ебаный нервный урод.
Только дурак и истеричка - все верно.
Я, вообще говоря, исключение. Я - суть не нервного математика.
Хотя я знаю несколько высокомерны математиков (не молодых) у которых запросто ничего не спросишь, но это скорее исключение. Касательно распознавания уровня знаний, если идет предметное обсуждение - как иначе, ведь хочется донести до собеседника содержательную информацию, а не что-то для него тривиальное или же недоступно сложное.
Впрочем, эти рассуждения напомнили мне одну известную книгу:
>Дух презрения, проникший в математический мир, постепенно распространялся, чтобы в конце концов охватить его целиком. Но в те годы я еще ничего не замечал, с легким сердцем продолжая называть волшебным именем «математического сообщества» свой, неумолимо преображавшийся, мир. Не то, чтобы он менялся сам по себе: все мы, его обитатели, принимали в этом участие. И мою собственную роль мне бы хотелось определить поточнее - с тем я и начал этот разговор. К чему-то я уже пришел, но до окончательного ответа еще не добрался; грех прерываться на полпути. Да и потом, заглянув из моего теперешнего угла в страну большой математики, что еще, кроме вопросов и ответов, я мог бы предложить людям, которых знал и любил? Когда-то я ушел из их мира и потерял с ними связь. Сегодня я внутренне готов прервать долгое молчание. Это - не возвращение, но всего лишь новая попытка высказать то, что накопилось в душе.
>Думаю, я должен прежде всего разобраться в том, как складывались мои отношения с «сильными» и «слабыми» мира математики - в те времена, когда я сам был одним из его обитателей.
>Сейчас, размышляя об этом, я не устаю удивляться одному странному обстоятельству. Выходит так, что весьма существенной части этого мира я (неизвестно, почему) просто не замечал. Между тем, ее составляли люди, с которыми я сталкивался достаточно регулярно. Вероятно, я воспринимал ее, как некое «болото»: в чем его предназначение, и вообще что там внутри него происходит, мне было неясно. В лучшем случае, я мог бы приписать ему роль пресловутого «резонатора» - для скрипки, на которой играют мастера. В моих глазах это была серая, безликая масса, на всех семинарах и коллоквиумах неизменно заполнявшая задние ряды. Эти люди были словно созданы затем, чтобы сидеть в тени, пуще всего опасаясь случайно привлечь к себе внимание. Они почти никогда ни о чем не спрашивали докладчика - из страха, что вопрос окажется неуместным (более того, создавалось впечатление, будто они заранее были в этом уверены).
Хотя я знаю несколько высокомерны математиков (не молодых) у которых запросто ничего не спросишь, но это скорее исключение. Касательно распознавания уровня знаний, если идет предметное обсуждение - как иначе, ведь хочется донести до собеседника содержательную информацию, а не что-то для него тривиальное или же недоступно сложное.
Впрочем, эти рассуждения напомнили мне одну известную книгу:
>Дух презрения, проникший в математический мир, постепенно распространялся, чтобы в конце концов охватить его целиком. Но в те годы я еще ничего не замечал, с легким сердцем продолжая называть волшебным именем «математического сообщества» свой, неумолимо преображавшийся, мир. Не то, чтобы он менялся сам по себе: все мы, его обитатели, принимали в этом участие. И мою собственную роль мне бы хотелось определить поточнее - с тем я и начал этот разговор. К чему-то я уже пришел, но до окончательного ответа еще не добрался; грех прерываться на полпути. Да и потом, заглянув из моего теперешнего угла в страну большой математики, что еще, кроме вопросов и ответов, я мог бы предложить людям, которых знал и любил? Когда-то я ушел из их мира и потерял с ними связь. Сегодня я внутренне готов прервать долгое молчание. Это - не возвращение, но всего лишь новая попытка высказать то, что накопилось в душе.
>Думаю, я должен прежде всего разобраться в том, как складывались мои отношения с «сильными» и «слабыми» мира математики - в те времена, когда я сам был одним из его обитателей.
>Сейчас, размышляя об этом, я не устаю удивляться одному странному обстоятельству. Выходит так, что весьма существенной части этого мира я (неизвестно, почему) просто не замечал. Между тем, ее составляли люди, с которыми я сталкивался достаточно регулярно. Вероятно, я воспринимал ее, как некое «болото»: в чем его предназначение, и вообще что там внутри него происходит, мне было неясно. В лучшем случае, я мог бы приписать ему роль пресловутого «резонатора» - для скрипки, на которой играют мастера. В моих глазах это была серая, безликая масса, на всех семинарах и коллоквиумах неизменно заполнявшая задние ряды. Эти люди были словно созданы затем, чтобы сидеть в тени, пуще всего опасаясь случайно привлечь к себе внимание. Они почти никогда ни о чем не спрашивали докладчика - из страха, что вопрос окажется неуместным (более того, создавалось впечатление, будто они заранее были в этом уверены).
>Если же они все-таки решались обратиться с вопросом к кому-нибудь из нас, «признанных специалистов» в соответствующей области, то не иначе, как в кулуарах (предварительно убедившись, что «светила науки» не подают признаков желания сию минуту побеседовать между собой). Им было как будто совестно отнимать драгоценное время у таких важных особ, как мы. Иногда вопрос действительно бывал «не из той оперы»; тогда, если человек обращался ко мне, я (как мне кажется) всегда старался в нескольких словах объяснить, почему. Довольно часто, однако, вопрос оказывался дельным, и я, в свою очередь, старался как можно лучше на него ответить. И в том и в другом случае разговор чаще всего на этом заканчивался: мой собеседник явно чувствовал себя стесненно и, получив ответ, обыкновенно не решался углубиться в дальнейшие детали.
>Быть может, нам, людям из первых рядов математических аудиторий, и впрямь слишком недоставало времени? При этом мы как будто не напускали на себя чрезмерно занятого вида; но было ли у нас время задуматься над тем, почему нас боятся? По сути, мы оказывались не в силах что-либо предпринять для того, чтобы прогнать, рассеять этот нелепый страх; а ведь настоящее общение при таких обстоятельствах невозможно. Само собою, в ходе разговора я, как и мой собеседник, ощущал всю неестественность ситуации. Но я даже не пытался, хоть бы и для себя, выразить это чувство словами. Мой собеседник, я уверен, также не особенно размышлял об этом; наше взаимное чувство неловкости оставалось безотчетным. Одного из нас сжимала в тисках тревога, другой смутно чувствовал ее и рад был бы рассеять. И все же, словно бы сговорившись, мы оба старательно делали вид, будто ничего этого нет - ив разговоре топтались на месте, как некие странные автоматы. Там, где мы стояли, ощущалось напряжение; как если бы на этом самом месте материализовалась частица мучительного беспокойства, пронизывавшего общую атмосферу в научных кругах. Это чувствовали все, не только мы вдвоем - и все до одного предпочитали не замечать.
>Если же они все-таки решались обратиться с вопросом к кому-нибудь из нас, «признанных специалистов» в соответствующей области, то не иначе, как в кулуарах (предварительно убедившись, что «светила науки» не подают признаков желания сию минуту побеседовать между собой). Им было как будто совестно отнимать драгоценное время у таких важных особ, как мы. Иногда вопрос действительно бывал «не из той оперы»; тогда, если человек обращался ко мне, я (как мне кажется) всегда старался в нескольких словах объяснить, почему. Довольно часто, однако, вопрос оказывался дельным, и я, в свою очередь, старался как можно лучше на него ответить. И в том и в другом случае разговор чаще всего на этом заканчивался: мой собеседник явно чувствовал себя стесненно и, получив ответ, обыкновенно не решался углубиться в дальнейшие детали.
>Быть может, нам, людям из первых рядов математических аудиторий, и впрямь слишком недоставало времени? При этом мы как будто не напускали на себя чрезмерно занятого вида; но было ли у нас время задуматься над тем, почему нас боятся? По сути, мы оказывались не в силах что-либо предпринять для того, чтобы прогнать, рассеять этот нелепый страх; а ведь настоящее общение при таких обстоятельствах невозможно. Само собою, в ходе разговора я, как и мой собеседник, ощущал всю неестественность ситуации. Но я даже не пытался, хоть бы и для себя, выразить это чувство словами. Мой собеседник, я уверен, также не особенно размышлял об этом; наше взаимное чувство неловкости оставалось безотчетным. Одного из нас сжимала в тисках тревога, другой смутно чувствовал ее и рад был бы рассеять. И все же, словно бы сговорившись, мы оба старательно делали вид, будто ничего этого нет - ив разговоре топтались на месте, как некие странные автоматы. Там, где мы стояли, ощущалось напряжение; как если бы на этом самом месте материализовалась частица мучительного беспокойства, пронизывавшего общую атмосферу в научных кругах. Это чувствовали все, не только мы вдвоем - и все до одного предпочитали не замечать.
Так и знал, что цитата из этого «плача Ярославны» от математики.
интимных
Это проблема математических средств, например. Вот работа по теме недостаточности аналитических техник необходимых для решения ураванений навье-стокса. http://arxiv.org/pdf/1402.0290v2.pdf
Не "аналитических техник" вообще, а только тех, что использовали обычно до сегодняшнего дня.
Нет? А вот смотрите: у меня было одно яблоко, мне дали ещё одно. Но разве выражение 1 + 1 говорит, сколько у меня теперь яблок? Как вообще можно ответить с помощью абстрактного мира, сколько у меня яблок? Что вообще значит этот вопрос: сколько у меня яблок? Зачем он нам и зачем нам математика?
Можно другой пример привести. У тебя есть сфера, её объем V=3/4пR^3 -- по сути её физическая информация. Но разве формула даёт какое-либо наглядное или алгоритмическое представление о структуре фигуры?
Двачую этого философа. А физики не поймут сути вопроса.
"Смотрите, какой я умный, я сейчас задам вопрос самому Энштейну! Видите, я пожал руку Энштейну, а это что-то да значит! Трепещите, твари, я поднялся до уровня бога! Но... тут скучно, тут нет безудержного веселья и похоти, в чём суть? Ладно, потерплю немного этого яйцеголового, потом расскажу всем, что из себя представляет наука. Уверен, все кругом завидуют ему, но не понимают, как он печален, как он одинок. Лишь мне хватило моей природной чувственности и интуиции увидеть это. Уверен, такое не опишешь формулой."
Почему?
Это вопрос не математики, а тех, кто ее применяет. Такие люди помимо аксиоматики задействуют еще здравый смысл.
И в чём же состоит здравый смысл, когда мы "вычисляем" количество реального через абстрактное?
Все правильно сделали, там твоим мечтам и место.
Реально ли такое сопоставление? Или всего лишь абстракция реальности?
Хотелось бы увидеть подобное по теории вероятностей и мат. статистике.
>будем ИТТ делать
ИТТ - не будем.
Ибо быдлу - вроде тебя в частности и всех вас в общем - не положено
^_^
И какова замена?
Иди статью на хабру пиши, пизденок :3
Почему не имеет смысла сопоставить одному яблоку число 1, если мне требуется посчитать количество яблок?
Короче, не хочу это обсуждать. Этими вопросами математика не занимается.
Нельзя быть математиком, не будучи превосходным философом.
Сопоставление числа "1" яблоку не имеет смысла, как таковое, ведь оно не описывает яблоко. В таком ключе вопрос "сколько?" вообще не имеет смысла.
Да и зачем тебе знать, сколько у тебя яблок, если это ни толики не даёт?
Как совместить наглядность для человека и полное описание фигуры? Какого характера должна быть общая аппроксимация?
Больная тема.
Забавно, когда зверюшка в мат. треде с пеной изо рта сначала говорит, что я увлекаюсь радиологией и затем называет быдлом. Давно у тебя так?
>сделал уроки на понедельник
>заходишь в /sci в мат. тред с ебанутой радиологией на руках
>пишешь в серийный тред с сажей
Оттуда
H — нормальна, если xH=Hx для всех x. Нужно это, чтобы перемножать смежные классы:
xHyH=xyHH=xyH
>Нахрена вообще так перемножать?
Так коммутирует с умножением.
gx(g^-1) gy(g^-1) = gxy(g^-1)
Посередине сокращаются.
То есть сопрягнуть потом умножить = умножить потом сопрягнуть. Получается не просто отображение в себя, а гомоморфизм в себя.
Наверное то, что интеграл по контуру, то есть ничего.

куда вторая H делась?
>>334831
А зачем ghg^-1? Почему нельзя просто gh или g^-1h написать? Для чего обратный элемент с другой стороны?
Угодно. Спасибо.
Однажды академика Владимира Игоревича Арнольда переехал грузовик. После этого Владимир Игоревич приобрёл привычку рассказывать про Изумрудную Скрижаль и Гермеса Трисмегиста. По мнению уважаемого академика, Гермес Трисмегист был Бог Тот, изобрётший натуральные числа. Также Владимир Игоревич осознал, что должен начать войну с бурбакизмом и калькуляторами.
И начал.
При каком-то большом n уже не будет разницы, прибавил ли ты эту(очень малую) дробь или нет - следовательно до какого-то большого n твоя сумма будет расти более-менее ощутимо - а следовательно ее ты можешь посчитать.
e всегда вычисляется с некоторой погрешностью. Каждая следующая точная цифра в e вычисляется со всё большим трудом. e иррационально, поэтому точное значение e не известно никому.
>куда вторая H делась?
Она сократилась.
HH=H
Слева — множество всех попарных произведений элементов H.
В H есть 1.
Когда 1 зафиксирована, а справа пробегаются все элементы H — покрывается всё:
1H=H
С другой стороны, HH не выходит за пределы H.
Поэтому они равны.
>А зачем ghg^-1? Почему нельзя просто gh или g^-1h написать? Для чего обратный элемент с другой стороны?
Потому что
gxgy не обязательно равно gxy
То есть, если рассматривать умножение на фиксированный g слева как отображение g: G —> G, то
g(x)g(y) не равно g(xy)
Со скобками может быть понятнее?
То есть это — не гомоморфизм.
В 1 томе Зорича точно было объяснение. Хотя, по-моему, не очень простое.
>С другой стороны, HH не выходит за пределы H.
Разве произведение элемента группы на самого себя обязано принадлежать этой группе? Групповая аксиома же о перемножении разных элементов говорит, а тут один и тот же получается.
>gxgy не обязательно равно gxy
А оно вообще может быть равно, кроме случая g=1? Честно говоря, не понял твоей мысли. В чем вообще смысл существования сопряженных элементов?

Подставляешь вместо n охуительно большое число и считаешь.
Если хочешь ПАНЯТЬ как он УСТРОЕНА начинаешь с n=1 и увеличивая n на единицу с каждым шагом идешь вперед, бесконечность не предел Когда в оригинале звучит "To infinity and beyond/ бесконечность и еще дальше"
>Разве произведение элемента группы на самого себя обязано принадлежать этой группе? Групповая аксиома же о перемножении разных элементов говорит, а тут один и тот же получается.
Во-первых, не на самого себя. AB, где A и B — подмножества чего-то, где можно умножать, означает множество всего, что можно получить умножая что-то из A на что-то из B однократно, важен только порядок. То есть всё вида ab, где a принадлежит A, а b принадлежит B.
То, что буквы HH одинаковые не означает, что можно перемножать только одинаковые элементы! Это множество любых парных произведений элементов из H.
Оно содержит произведения вида 1h, значит, и всё H. Оно не выходит за пределы H, так как в группе что не перемножай, за пределы не выйдешь, умножение в группе сопоставляет каждой упорядоченной паре элементов группы единственный элемент той же группы.
Во-вторых, групповая аксиома говорит о перемножении любых элементов, не обязательно разных. То, что буквы разные не означает, что обозначаемые ими элементы множеств разные!
>А оно вообще может быть равно, кроме случая g=1?
Рассмотрим это как уравнение:
gxgy=gxy
В группах можно сокращать с краёв (следует из наличия обратных).
Сокращаем слева g, справа y:
xg=x
Ну и x сокращается.
То есть да, это верно только для g=1.
>В чем вообще смысл существования сопряженных элементов?
Замечательный просто вопрос. Объяснить «смысл существования» математических понятий трудно, так как этих смыслов очень много. Геометрическая картинка:
g — переворачивание треугольника.
h — прокрутка треугольника
gh(g^-1) — перевернул, прокрутил, затем перевернул обратно.
В геометрии сопряжение очень часто отвечает ситуациям «смена координат», «смена
базисов». Поменял координаты, сделал что-то, потом поменял обратно. Нечто, сделанное во вторых координатах выражается в первых координатах.
Чтобы лучше общаться (звуками или символами) и считать.
Соус?
Для получения количественной информации с последующим её анализом, получением решения и прогнозированием.
Это не доказательство. Используй индукцию, ну же.
>Оно содержит произведения вида 1h, значит, и всё H
Чому?
>групповая аксиома говорит о перемножении любых элементов, не обязательно разных. То, что буквы разные не означает, что обозначаемые ими элементы множеств разные
Во! Только вот теперь другой вопрос появился, как можно умножать элемент сам на себя, если в группе он только в одном количестве? И если взять две одинаковые группы и перемножить идентичные элементы в них, как можно утверждать нахождение результирующего элемента в этой же группе, если группа замкнута относительно операции между своими элементами, а тут элементы двух (хоть и одинаковых) групп?
>То есть да, это верно только для g=1.
Круто, только к чему был этот пример? Что он был призван доказать?
>В геометрии сопряжение очень часто отвечает ситуациям «смена координат», «смена базисов».
Хоть я и не про это говорил, но спасибо за интересный пример. Меня интересует почему в отвлеченной от геометрии алгебре в отдельный объект вынесено перемножение элемента "внутри единицы". Что значит термин "сопряжение"? Соответственно не могу понять что значит если подгруппа инвариантна относительно сопряжений. И то, что результат такого внутриединичного умножения лежит в ней же самой мне ничего, увы, не говорит.
Сейчас самый важный вопрос в математике - дать корректное определение тупого ничтожества и множества N.
>Чому?
Потому что произведения 1 на все элементы и все элементы — одно и то же.
Содержит — плохое слово, так как можно содержать как элемент и содержать как подмножество.
Содержать H как подмножество = содержать все элементы h из H как элементы.
Может, это было не ясно?
>Во! Только вот теперь другой вопрос появился, как можно умножать элемент сам на себя, если в группе он только в одном количестве? И если взять две одинаковые группы и перемножить идентичные элементы в них, как можно утверждать нахождение результирующего элемента в этой же группе, если группа замкнута относительно операции между своими элементами, а тут элементы двух (хоть и одинаковых) групп?
Двух (хоть и одинаковых) объектов не может существовать. По крайней мере в рамках теоретико-множественной идеологии.
По этой идеологии умножение в группе строится так:
Берётся множество G.
Формируется множество всевозможных упорядоченных пар элементов из G, обозначается GxG (прямое произведение множества на себя). Это множество содержит все упорядоченные пары, включая пары с одинаковой первой и второй координатами.
Каждой паре из GxG сопостовляется элемент G.
Этим полность определяется «умножение».
Выражение ab=c означает:
образ пары (a, b) равен c.
Хотя, чего это я тут объясняю. Ты 2 на 2 не можешь умножить? Это же разные двойки, значит должны принадлежать разных натуральным числам, по твоей логике, и, значит, никто не гарантирует, что получится натуральное число.
Почему именно они?
Если что, я хочу знать математику только чтобы понимать о чем физики шушукаются.
>Что от меня хотят в этом упражнении?
Хотят, чтобы ты понял, что такое производная и интеграл с геометрической точки зрения.
А, ну тогда хз.
То упражнение я посоветовал не делать, потому что там предполагается, что ты примерно измеришь чему равна производная в нескольких точках и соединишь их плавной кривой. Наверное, это упражнение задумывалось как упражнение на геометрический смысл производной, но по-моему оно такое себе.
А как решить то? Это идт после параграфа о касательных к графикам и их нахождении через производные.
По логике я должен применить эти знания для решения, но я не могу понять как их применить.
Ну производная в геометрическом смысле это угловой кожфииент в уравнении прямой, которая является касательной к некой функции в некой точке.
>Может, это было не ясно?
Туплю, другое хотел спросить. "HH=H
Слева — множество всех попарных произведений элементов H.
В H есть 1.
Когда 1 зафиксирована, а справа пробегаются все элементы H — покрывается всё:
1H=H
С другой стороны, HH не выходит за пределы H"
Что тут значит H зафиксирована? А что если она не зафиксирована? Такой подход вообще законен?
>Ты 2 на 2 не можешь умножить? Это же разные двойки, значит должны принадлежать разных натуральным числам, по твоей логике, и, значит, никто не гарантирует, что получится натуральное число.
Вообще говоря, мне такой подход кажется очевидным. Я бы именно так математику развивал. Не понимаю почему это не верно.
Она совпадает с тангенсом угла, но не в коем случае не определяется как он.
Но ведь тангенс этот определяется как игрек минус игрек нулевое делить на икс минус икс нулевое. Плюс функция икса.
Картинка, кстати, идиотская.
>>335015
Производная функции - предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Как правильно говорит википедия.
А все эти коэффициенты и тангенсы угла наклона касательной ЧИСЛЕННО СОВПАДАЮТ со значением производной, но не являются определением.
Тобишь произодная это "скорость изменения" функции в точке.
Что значит не являются определением? Определением касательной? Но ведь СОВПАДЕНИЕ это не из пальца высасывали. Или высосали из пальца в процессе развития бесонечно малых? Как гаусс с средним распределением простых чисел и экспонентой.
Не знаю уж откуда приплели касательные. Наверняка не просто так. Скорее всего откуда-то это следует. Но строго определить производную функции можно только через предел отношения приращений.
Хреново автор написал, да, бывает. Может он и не со зла, а просто от невнимательности или отсутствия способностей грамотного обращения с русским языком.
Ну так это математическая формулировка, а про тангенсы графическая.
Так же как интегралы это сумма бесконечно малых членов последовательности для математики и площадь подинтегральной ривой для геометрии.
Не путай теплое с мягким. Площадь под кривой - не определение, а геометрическая интерпретация. интеграл - не площадь под кривой, а предел интегральной суммы. Так же и с производными. Одно дело определение, а совсем другое дело интерпретации для более простой визуализации и расчетов.
>Oрдинатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y в прямоугольной системе координат.
Это ты так толстишь?
2. Обычнокун. Просто сычую в общаге. Читаю литературу. Грущу.
3. Тян для отношений. Либо же тян для секса без обязательств. Либо красивых кунов, для погулять. Побухать. Не знаю чем там люди занимаются, просто вытащите меня на улицу.
4. http://vk.com/desperate_cat
Ну хорошо, оттолкнулся от точек пересечения Ох. У меня есть точки 0, 4.5 и 6.5, при Оу=0. Что мне с ними дальше делать?
Так какими программами? Вот, например, у меня сотня точек в объёме, я хочу посмотреть как они выглядят в 3д и желательно что бы график можно было покрутить.
Что бы понять как выглядит f(x,y) можно построить z = f(x,y)
>>335045
До x=2.1(примерно) производная меньше нуля, затем производная становится больше нуля;
в точке x=5.5(примерно) производная становится меньше нуля и больше нуля на графике быть не должна
А точки пересечения, что я говорил выше, здесь вроде ни на что не влияют. Как ведет себя график сказать не могу, т.к. не знаю.
Хотя, если ты говорил, что глава была о касательных, то производную можно через тангенс выразить вроде, но и то, что я написал тоже нужно

Мы тут, блядь, математикой занимаемся. Иди в соц или поищи вконтактике себе тяночку тянучку
2. Ищу интересных людей для походов куда либо, интересного общения, обменом полезной инфы. Причем сойдет как и брутальный тип (для певаса и кулсторей с глумом), так и домашняя няша (прикосновение ее тени@шопот ее имени). Главное чтоб человек был интересным и адекватным. Реальным.
3. Мир вокруг. Научная картина мира. Исскуство. Качественный контент. Меломан. Психология. Социальные тренды. Социология. Опенмайнд. Не враг тусануть.
4. "F'sexfake0101ANUSLxLmailPUNCTUMr !3u
Вот тебе задача. Всем известно, что гомоморфный образ группы до победы коммунизма изоморфен факторгруппе по ядру гомоморфизма. Но вот вопрос, что будет ПОСЛЕ победы коммунизма. С выкладками, если можно.
Нет, "до".
https://ru.wikipedia.org/wiki/Факторгруппа
Хотя "в честь" тоже встречал, но значительно реже. Кроме того, коммунизм, как известно, еще не побеждал, поэтому логически "в честь" быть не может.
Все корректно. Именно поэтому требуется уточнение в виде "будущего события", если событие еще не произошло.
Требуется, именно поэтому ты, сам того не понимая, уточнил.
"=" - символ смысловой идентичности для данного контекста.
Я слышал, что в музаче модер сосет, а тут, вроде бы, все ок.
>Требуется, именно поэтому ты, сам того не понимая, уточнил.
Нет. Уточнение подразумевается, но не необходимо для записи. Таким образом "в честь победы" корректная конструкция не требующая "будущей", но подразумевая её. Синтаксически и семантически конструкция "в честь" не требует свершившегося факта.
>"=" - символ смысловой идентичности для данного контекста.
Используется "–". Которое грамматически верно, и используется в более широком смысле. Символ "=" – требует строгого определения – ты его не привёл.
У меня нет нихуя. Нихуя. И не будет нихуя.
Какой вайп? Ты ёбнутый?
ссылки на работы с таким - было бы хорошо.
Вы видите копию треда, сохраненную 29 февраля 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.