Вы видите копию треда, сохраненную 29 июня 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


Скорее, вера в то, что за ограниченным конечным количеством чисел, есть нечто куда большее.
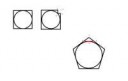
2. А тут что не так?
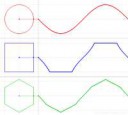
То есть если последовательность кривых стремится к другой кривой, не означает, что последовательности длин стремятся к предельной длине. (Чтобы это выполнялось, нужно ещё добавить условие на то, чтобы производные почти всюду стремились.
> число не стремится
Какое число? И что ты вообще понимаешь под "число [не] стремится"? В общепринятой математике такого понятия нет.
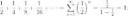
То, что на первом и втором п ке используется один и тот же метод (предел), а потому они либо оба неверны, либо оба верны.
>>352790
За щекой грамм тебе капнул, проверяй.
Покажи мне предел с первого пика. Для второго у тебя есть красивая формула. Тебе нужна такая-же формула для первого пика - тоесть ряд с неизвестной переменной которая будет стремиться к бесконечности. Также тебе нужно показать что предел этого ряда (при неизвестной стремящейся к бесконечности) равен 4. Также ты должен показать что этот ряд при неизвестной стремящейся к бесконечности также превращается в окружность - тоесть аналитическая формула ряда должна превращаться в какую-то из формул окружности. А до тех времен первая картинка это просто пук в лужу. То что линия очень похожа на окружность еще не значит что она является окружностью. Можно нарисовать бесконечно большое количество фигур не отличимых на взгляд от заданой окружности, с любой длиной (большей от заданой окружности), в том числе с бесконечной.
А зачем? Зачем мне переменные, если всё на картинке вполне конкретные числа? Переменной тут можно назвать только разве что разницу между геометрической фигурой и окружностью, и уже формулой доказать что разница нулевая. Но я могу просто заявить, что она нулевая, так как я провернул эти срезания углов бесконечное кол-во раз.
И вот уже ты как бы и не сможешь доказать, что разница не нулевая, т.к. тогда нужно будет определить где она наблюдаема, хотя бы на каком масштабе. (то есть нигде)
Ты либо можешь доказать неверность этого утверждения, либо не можешь. В чём проблема, ЧСВшник?
Формулирую: периметр окружности и квадрата равны. На картинке сокращаем разницу до нулевой между фигурами. Ну и "проблемс?" пишем в конце, как изюминку на торте.
>На картинке сокращаем разницу до нулевой между фигурами.
Не понимаю этого набора слов - математики так не говорят, так что утверждения у тебя нету.
Окей, корчи из себя дурачка, вот тебе поточнее: Создаю геометрическую фигуру, равную данному квадрату, такую, что она имеет большее число общих точек с данной окружностью(это когда углы внутрь вогнули). Из полученной фигуры создаю следующую такую, чтобы она удовлетворяла данным условиям (то бишь ещё больше общих точек с кругом и тот же периметр). И продолжаю это делать до бесконечности, таким образом периметр полученной фигуры будет равен 4м, тогда как все точки окружности будут общими с точками полученной фигуры.
>Окей, корчи из себя дурачка
Дурачок тут только один, который не разу в руках книжки по математике не держал, но с умным видом рассуждает о том, чего не знает.
>И продолжаю это делать до бесконечности
Так математики тоже говорят и в учебниках по математики не пишут, что этот набор слов значит?
>Дурачок тут только один, который не разу в руках книжки по математике не держал, но с умным видом рассуждает о том, чего не знает.
Я делаю утверждение вполне чёткое, это ты даже не решаешься его опровергать.
Тогда пойдём от обратного: Ряд на второй пикче сходится?
>Я делаю утверждение вполне чёткое
Вот я же и говорю, представление о "вполне чётких утверждениях" на уровне детского сада, а виноваты все, кроме тебя.
>Тогда пойдём от обратного: Ряд на второй пикче сходится?
Да.
Раз ряд сходится, то как ты получаешь единицу, ведь при каждом сложении ты имеешь определённую разницу между единицей? Каким образом сложение бесконечного количества дробей в итоге дают нам ответ в единицу?
Как ты это доказываешь?
>все точки окружности будут общими с точками полученной фигуры
Это не возможно. В данном примере (рисунок 1) разница между фигурами сокращается путем последовательного повторения операции которую мы назвем "созданием углов" (так как после этой операции вместо одного угла получается три). Для "создания угла" на фигуре выбирается подходящий угол С (не все углы фигуры подходящи, но это не важно) который образован двумя перпендикулярными отрезками a и b. На этих отрезках выбираются две точки A и B в результате чего получается угол ACB. Для "создания угла" строится точка D которая симметрична точке C отсносительно центра отрезка AB. После чего из фигуры удаляются отрезки AC и BC, и добавляются отрезки AD и BD. Очевидно что отрезок AC = BD а BC = AD, тоесть общий периметр фигуры не меняется. В результате такой операции фигура теряет два отрезка и один угол и получает два отрезка и три угла. Следствием из того что после каждой операции фигура получает два новых отрезка является верность утверждения: "После любого количества операций создания угла получившаяся фигура имеет как минимум три точки лежащие на одной прямой" - так как любой ненулевой отрезок состоит как минимум из трех точек. А так как фигура (после любого, даже бесконечного, количества операций "создания угла") всегда будет иметь как минимум три точки лежащих на одной прямой она не может быть идентична окружности, так как окружность не имеет трех точек лежащих на одной прямой. Следователно разница между фигурой образованой из квадрата путем совершения бесконечного количества операций "создания угла" и окружностью которую он описывает не может быть равна нулю.
>А так как фигура (после любого, даже бесконечного, количества операций "создания угла")
Вот опять это "бесконечное число операций", у меня уже несколько научных статей по математике, но я не понимаю, что это значит. Погуглил - тоже ничего не написано, объяснить мне никто этого в этом треде не хочет, зато всем очевидно, что после этого "бесконечного числа операций" должно сохранятся, а что нет.
Если тебе сложно то в данной фразе "бесконечного" можно выбросить и дальше по тексту "бесконечного" заменить на "любого".
Выражение "1/2+1/4+1/8+...=1" это просто кароткая запись следующего утверждения: для любого eps>0 существует некоторый номер N (конечный) что |1/2+1/4+...+1/2^N - 1| < eps. Это вполне очевидно всем, кто понимал программу 11го класса.
>>352827
То есть ты хотел сказать, что квадратик после любого количества такого вот отрезания углов будет иметь как минимум три точки, лежащие на одной прямой? Содержательно. И что?
Очевидная вещь здесь заключается в том, что если последовательность фигур стремится к какой-то фигуре тактично умолчим о том, что мы вообще-то не знаем, что это такое: "последовательность фигур стремится к ..."; предположим, что мы смогли придать этим словам строгий смысл, то их периметры не обязаны стремиться к периметру предельной фигуры. То есть неявное утверждение с пика о том, что периметр тоже должен равняться 4, из пизды взято, и требует доказательства. Ну а сам пик демонстрирует, что доказать это утверждение не удастся, т.к. оно неверно.
Всё правильно написал.
>Раз ряд сходится, то как ты получаешь единицу, ведь при каждом сложении ты имеешь определённую разницу между единицей?
Сумма ряда - это не складывание чего-то там с чем-то там, а предел последовательности его частичных сумм. О каком сложении ты говоришь, да еще сложении бесконечного количества (что это значит)?
А то, что утверждается что предел - это и есть сумма бесконечного количества этих дробей, потому оно именно равно единице, а не стремится к нему. Навряли меня учил кривой математик, но в любом случае я сюда пришёл немного за другим: я тип опровергаю бесконечность как число впринципе, ну и как возможность такого пиздеца в реальности (как следствие). Суть в том, что с бесконечностью нельзя работать, ни умножать, ни делить, складывать или вычитать, но матан со мной не согласен в общем-то, вот и пришёл, чтобы мне разрулили.
Лол. Матан (классический) то с тобой полностью согласен. Бесконечность - не число, попытка сделать его числом обречена на провал (в аксиоматике чисел, которая принята в мат. анализе), так как вызывает противоречия.
>что предел - это и есть сумма бесконечного количества этих дробей
Не утверждается.
>Навряли меня учил кривой математик
Да, скорее всего - ты плохо усвоил курс.
>о в любом случае я сюда пришёл немного за другим: я тип опровергаю бесконечность как число впринципе, ну и как возможность такого пиздеца в реальности (как следствие)
Сменку в понедельник взять не забудь, опровергун.
Бесконечность - это на самом-то деле удобное обозначение в матане, которое заменяет достаточно длинное выражение, которое похоже на определение предела.
Вот это кстати близко, мне в /б/ ебали мозг час прежде чем пришли к этому же.
Тогда я продолжу: у окружности не может быть 3 точки, принадлежащие ей и лежащие на одной прямой. И вот это утверждение я считаю не верно. Мне нужно определение окружности по матану чтобы разобратся, но, насколько я помню, оно аксиоматично и противоречиво, сейчас приведу:
Окружность это множество равноудалённых от центра всех возможных точек. Подразумевается из этого, что у него не может быть углов, но ведь невозможно создать изгиб прямой так, чтобы не было точки, на которой создаётся угол. То есть даже если я возьму 3 ближайшие точки на окружности - я же всё равно смогу провести 2 прямые, образующие угол.
Вариант, что эти отрезки не принадлежат полностью окружности тоже будет ошибочно: ведь вся окружность состоит из точек и только из них.
Так где ошибка?
>попытка сделать его числом обречена на провал
Это не так.
https://ru.wikipedia.org/wiki/Расширенная_числовая_прямая
Я говорю не о том, что фигура стремится стать окружностью. У меня более наглое утверждение: то что фигура в пределе в итоге становится окружностью и ничем иным.
>Так где ошибка?
Здесь:
>Вариант, что эти отрезки не принадлежат полностью окружности тоже будет ошибочно: ведь вся окружность состоит из точек и только из них.
У тебя в этих двух отрезках только три точки будут удовлетворять определению точек окружности.
К счастью, в математике вопросы решаются не при помощи /б/, а чуть по-другому. В частности - всё что написано в посте >>352825 - бред, индуцированный непониманием.
> То есть даже если я возьму 3 ближайшие точки на окружности - я же всё равно смогу провести 2 прямые, образующие угол.
Ближайших точек нету.
Я не зря расставлял упоминание о классическом матане, о принятой в классическом матане аксиоматике чисел.
Любые 3 ближайшие точки на окружности могут так, ведь они ближайшие. В итоге из них и можно построить окружность как из лего же.
Каким образом? Их бесконечное количество?
Получается вся концепция строится по типу "Бесконечность есть потому что есть окружность итд...Окружность существует, потому что она состоит из бесконечного кол-ва...." Ну ты понел.
Вот ты и попался.
>ближайшие
Не бывает таких. Возьми любые два различных числа (любые две точки) и между ними найдётся ещё одно число, которое не будет равняться этим двум.
>Их бесконечное количество?
Разумеется.
> "Бесконечность есть потому что есть окружность итд...Окружность существует, потому что она состоит из бесконечного кол-ва...."
Нет, не по этому принципу. То что бесконечные множества есть в математике постулируется (аксиома бесконечности, утверждающая по сути, что натуральные числа существуют) после чего с помощью некоторых технических тонкостей из натуральных строятся вещественные. А окружность - это множество пар вещественных чисел, удовлетворяющих уравнению x^2+y^2=1.
Ты не поверишь, но это не семёнство. Просто >>352860 мыслит в правильном направлении. То есть у нас в пределе получится фигура, которая похожа на окружность, но имеет углы только в некотором счётном (это важно!) количестве точек.
Решать в правильном или нет - будут не школьники, а математики - специалисты в подобных вопросах.
>То есть у нас в пределе получится фигура, которая похожа на окружность, но имеет углы только в некотором счётном (это важно!) количестве точек.
Ты можешь настаивать на своём непонимании, как не очень умный человек, а можешь попробовать разобраться, при помощи шарящих в этом людей - как люди поумнее. Хотя, судя по духу всего треда, твой выбор уже очевиден.
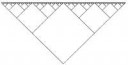
Сформулирую по другому: невозможно представить изгиб без наличия угла. Одна точка, соендинённая с другой - отрезок. На окружности, как следствие, не должно быть ни единой возможности чтобы были 3 точки, которые можно соендинить одной прямой. Получается когда я провожу прямую через 3 точки, я получаю ломанную, и мне приходится сокращать в итоге этот отрезок. Я же могу его точно так же сокращать до бесконечности, то есть бесконечно-малый отрезок, и в итоге 2 таких отрезка я смогу найти, ведь при увеличении (так как нет углов же, она на прямую будет походить) я всё равно буду получать угол с помощью 2х отрезков.
В конце концов всё сводится к тому, что бесконечность и "изгиб без углов" взаимосвязанны, они на себе зацикленны. Одно доказывается через другое и наоборот, а это не логично.
У тебя какой-то свой манямир с непонятными лингвистическими конструктами и самобытной терминологией, в котором лично я разбираться не хочу. Что можно сказать наверняка, так это то, что к математике и к тому, как там что-либо доказывается это никакого отношения не имеет.
Да нет, я оперирую математическими ткрминами вообще то. Ещё раз:
>В конце концов всё сводится к тому, что бесконечность и "изгиб без углов" взаимосвязанны, они на себе зацикленны. Одно доказывается через другое и наоборот, а это не логично.
Подразумевается, что существует бесконечное количество точек. Это же можно и опровергнуть, ведь на множестве будут вполне себе конкретные точки, сознающие изгиб. И при увеличении мы получаем всё более подобную прямой линию, и нельзя просто так утверждать, что что изгиб на ней порождён не углом. Доказываем: я могу создать многоугольник с бесконечным количеством углов (в матане же можно, хули), такой, что между ним и окружностью не будет не общих точек. Как теперь доказать, что общих точек нет? Ведь отрезки то бесконечно малые, они, считай, состоят из стольки же точек, из скольки состоит окружность.
Давай, как ты создашь изгиб на отрезке так, чтобы там точно не было угла?
>я могу создать многоугольник с бесконечным количеством углов (в матане же можно, хули)
нельзя
Можно. Бесконечное количество точек=бесконечное количество отрезков=бес-ное количество углов. Давай нормально сформулируй уж.
>что бесконечность и "изгиб без углов" взаимосвязанны, они на себе зацикленны
Есть у нас число 1, есть число 2 = 1 + 1, есть число 3 = 2 + 1 и так мы можем продолжать "до бесконечности", то есть у нас появляется бесконечное множество натуральных чисел. А теперь вопрос: где тут изгибы, углы и окружности?
Ноу проблем, только я и кун >>352879 вроде бы, были единственными людьми которые кое-как тебе пытались что-то объяснить. Впрочем, если этот тред потонет - будет только лучше. Удачи, бесконечно тупой хуесос поверхность мозга которого не содержит изгибов.
Ты не с того конца решаешь задачку, это ничего не доказывает, но и не опровергает.
Смотри, давай на точках сосредоточимся (кек): Любые 3 точки либо будут проводить прямую, либо создавать угол, третьего вроде как не дано. Каким образом в окружности 3 точки творят такие чудеса?
Не кажется тебе это нелогичным?
Если это называется обьяснением, то я лучше сам подумаю своими услиями. Твоя хуйня =/=доказательство.
>А то, что утверждается что предел - это и есть сумма бесконечного количества этих дробей, потому оно именно равно единице, а не стремится к нему.
Предел не может к чему-то стремиться, предел - это число (если мы о вещественной прямой говорим). Перевернутая восьмерка - это такая форма записи того, что последовательность стремится к бесконечности, и вот эта фраза - "последовательность стремится к бесконечности" - это неделимый математический термин (и его определение довольно сильно отличается от определения стремления к какому-то числу), т.е. нет никакой бесконечности самой по себе, а есть только эта фраза целиком. Впрочем, это все на вещественной прямой и на уровне матана 1го курса. Иногда, если захотеть, можно сделать "бесконечность" полноправным объектом (например, на проективной плоскости есть бесконечно удаленная точка, бесконечно удаленная прямая, и они ничем не отличаются от "нормальных" точек и прямых, только у них формулы более странные). Но в любом случае понятие "бесконечность" по дефолту не определено и требует определения (хотя суть обычно ясна и без него).
>я тип опровергаю бесконечность как число впринципе
Это и не число. Это вообще ничто, даже самостоятельного термина такого нет (применительно к пределам последовательностей). Однако при желании можно соорудить множество, состоящее из вещественных чисел и объекта "бесконечность" (а можно из чисел и из плюс и минус бесконечностей). Нормальное полноценное множество. Вопрос только в том, насколько оно тебя устраивает или не устраивает.
>ну и как возможность такого пиздеца в реальности (как следствие)
Если честно, меня не особо колышет, что там есть или нет в реальности. Чисел в реальности тоже нет, потому что числа (натуральные) - это лишь выдуманная человеками система знаков для описания такой характеристики группы объектов, как количество. Можно количество описывать не числами, а хуями, например. Суть, конечно, не изменится, но это уже другая история. Однако если ты не веришь в существование бесконечности в реальности, то иди упади в черную дыру, например. Как упадешь, отпишись. Всегда было интересно, че там.
>Суть в том, что с бесконечностью нельзя работать, ни умножать, ни делить, складывать или вычитать
Ну и что? Много чего нельзя делать не только с бесконечностью. Нельзя на ноль делить, нельзя ноль в нулевую степень возводить, в вещественных числах нельзя корень из отрицательного числа брать, в рациональных числах корень вообще практически ни из чего нельзя брать, в целых много на что нельзя делить, в натуральных много чего нельзя вычитать. И ничего. Это норма.
Хотя, собственно, поэтому бесконечность в отдельный объект и не выделяют в курсе матана. Ибо толку с этого ноль, ничего нетривиального ты с ним не научишься считать, а вот нормальными строгими определениями пользоваться отучишься, а значит, будешь постоянно обсираться, натыкаясь на что-то неочевидное.
А если ты думаешь, что матан учит, например, прибавлять бесконечность, то ты глубоко ошибаешься, и скорее всего, запомнил правильное математическое утверждение в упрощенной быдлоформе, а теперь пытаешься этим упрощением всерьез оперировать, отсюда и все твои проблемы. А матан - это вообще не о бесконечностях, матан - это о поисках пределов и их применениях.
>А то, что утверждается что предел - это и есть сумма бесконечного количества этих дробей, потому оно именно равно единице, а не стремится к нему.
Предел не может к чему-то стремиться, предел - это число (если мы о вещественной прямой говорим). Перевернутая восьмерка - это такая форма записи того, что последовательность стремится к бесконечности, и вот эта фраза - "последовательность стремится к бесконечности" - это неделимый математический термин (и его определение довольно сильно отличается от определения стремления к какому-то числу), т.е. нет никакой бесконечности самой по себе, а есть только эта фраза целиком. Впрочем, это все на вещественной прямой и на уровне матана 1го курса. Иногда, если захотеть, можно сделать "бесконечность" полноправным объектом (например, на проективной плоскости есть бесконечно удаленная точка, бесконечно удаленная прямая, и они ничем не отличаются от "нормальных" точек и прямых, только у них формулы более странные). Но в любом случае понятие "бесконечность" по дефолту не определено и требует определения (хотя суть обычно ясна и без него).
>я тип опровергаю бесконечность как число впринципе
Это и не число. Это вообще ничто, даже самостоятельного термина такого нет (применительно к пределам последовательностей). Однако при желании можно соорудить множество, состоящее из вещественных чисел и объекта "бесконечность" (а можно из чисел и из плюс и минус бесконечностей). Нормальное полноценное множество. Вопрос только в том, насколько оно тебя устраивает или не устраивает.
>ну и как возможность такого пиздеца в реальности (как следствие)
Если честно, меня не особо колышет, что там есть или нет в реальности. Чисел в реальности тоже нет, потому что числа (натуральные) - это лишь выдуманная человеками система знаков для описания такой характеристики группы объектов, как количество. Можно количество описывать не числами, а хуями, например. Суть, конечно, не изменится, но это уже другая история. Однако если ты не веришь в существование бесконечности в реальности, то иди упади в черную дыру, например. Как упадешь, отпишись. Всегда было интересно, че там.
>Суть в том, что с бесконечностью нельзя работать, ни умножать, ни делить, складывать или вычитать
Ну и что? Много чего нельзя делать не только с бесконечностью. Нельзя на ноль делить, нельзя ноль в нулевую степень возводить, в вещественных числах нельзя корень из отрицательного числа брать, в рациональных числах корень вообще практически ни из чего нельзя брать, в целых много на что нельзя делить, в натуральных много чего нельзя вычитать. И ничего. Это норма.
Хотя, собственно, поэтому бесконечность в отдельный объект и не выделяют в курсе матана. Ибо толку с этого ноль, ничего нетривиального ты с ним не научишься считать, а вот нормальными строгими определениями пользоваться отучишься, а значит, будешь постоянно обсираться, натыкаясь на что-то неочевидное.
А если ты думаешь, что матан учит, например, прибавлять бесконечность, то ты глубоко ошибаешься, и скорее всего, запомнил правильное математическое утверждение в упрощенной быдлоформе, а теперь пытаешься этим упрощением всерьез оперировать, отсюда и все твои проблемы. А матан - это вообще не о бесконечностях, матан - это о поисках пределов и их применениях.
Окружность определяется не тремя точками. Более того любой отрезок, проведённый между любыми (как бы близко они не находились) двумя не совпадающими точками окружности не будет полностью лежать на окружности.
Это утверждения всё у тебя, не доказательство их. Это уже слишал, плавали блин.
Выделяю: Любые 3 точки либо будут проводить прямую, либо создавать угол, третьего вроде как не дано.
Как создаётся изгиб и не создаётся угол? Каким образом это доказывается? Я даже уверен почти наверняка, что всё это аксиоматические утверждения.
Ну например в физике это говорит о том, что ни пространство ни время не бесконечны. Из этого мы уже можем начинать строить выводы и физическую модель уточнять, то есть мой вопрос имеет смысл для меня, такие дела.
Любые три точки - это любые три точки, они не проводят прямую, они не создают угол. Они сами по себе. Изгиб создаётся не тремя точками, а бесконечным набором точек (отрезок кстати тоже).
Ну раз время не бесконечно, то прыгай в черную дыру, чего ж ты ждешь, мы хотим фоточек оттуда.
Ты понял, что я имею ввиду, угол можно построить с помощью 3х точек, Изгиб без угла - нет, ибо я могу разделять его точно так же до бесконечности, что с этого меняется?
Концепция, которая не работает в математике, очевидно и в физике не должна работать, лол.
Я туда не упаду только для наблюдателя. Как раз таки внутрь я попаду, что опять же не в пользу бесконечности говорит.
>угол можно построить с помощью 3х точек
Окружность можно построить с помощью двух точек и что с того. Весь вопрос в том КАК строить те или иные фигуры. А фигуры - это бесконечные наборы точек.
Нет же, время кончится, и ты придешь оттуда с фоточками.
Теперь нужно не заниматься словоблудием, а формализовать это самое КАК. И тут тебе на помощь приходит понятие функции. С помощью функций ты можешь описать, какие точки будут принадлежать нашей фигуре. И с помощью матана и понятия гладкости (существование производной функции) ты сможешь ответить на вопрос: а есть ли углы у нашей фигуры.
>И с помощью матана и понятия гладкости (существование производной функции) ты сможешь ответить на вопрос: а есть ли углы у нашей фигуры.
И каким образом?
В угле происходит разрыв производной. Если ты запишешь функцию окружности (вернее полуокружности) и возьмёшь её производную, то увидишь, что производная всюду существует, а значит окружность - гладкое множество.
>бесконечные наборы точек.
Понимаешь ты хоть на секунду как это звучит то?
Смотри: какие бы ты изгибы и окружности не взял, у тебя в любом случае на них найдутся такие 3 точки, с помошью которых я смогу построить либо угол (хоть и бесконечно малый, как угодно), либо прямую. Потому что с тремя точками невозможно сделать что-либо ещё. А теперь ты рассматриваешь окружность (лучше для простоты дугу), и строишь её с помощью точек. Но не образуя углов и не создавая прямую ты какой-то магией добиваешься изгиба, понимаешь?
>В угле происходит разрыв производной
Не обязательно, это не доказательство, а скорее следствие из наблюдений.

Я в курсе, я просто не знаю где за это деньги платят. Мне это по большей части в физике нужнее было, но так я нигде особо не учусь и не работаю: просто самодроч на тему какой я у мамы умный
Наработки действительно серьезную, ну и на физику можно выйти опять же через этот приём. Мы показываем, что график любой волновой функции - это просто объединение некоторого количества инфенитизимальных отрезков, откуда сразу же следует, что пространство на самом деле дискретно, ведь если бы оно было непрерывно, то тогда мы смогли бы построить эдакую "квантовую окружность" в которой не было бы отрезков, а из наших наблюдений следует, что такого быть не может. Что думаешь?
>>352914
Ну и не уверен прав ли я само собой. Сейчас главная проблема в сходимости и расходимости рядов, ведь если одни сходятся (как на втором пике), а в другом расходятся (например в случае с первой пикчей может быть вполне), то всё это всё таки можно будет выбросить в помойку а я буду лах и опозорившимся. Но пока больше проблем не вижу.
Да, всё так. Следует это всё из невозможности теоретически создать какое либо искривление на прямой, только угол, других способов не вижу, и очень похоже на то, что это и невозможно.
На самом деле почти очевидно, что они сходятся, в первом случае получится "многоугольник с бесконечным количеством углов", а во втором - "единица с бесконечным количеством углов слева" (ведь мы как бы подбираемся к единице слева в этом ряду, и опять теми же инфинитиземальными отрезками).
>>352914
Исследования, кстати, лучше держать в секрете, иначе идею могут спотхватить и нажиться на ней (нормальная практика в научном сообществе). Думаю лучше писать сразу в Стекловку или в MIT или заведения такого уровня, остальные просто отшутятся и не поймут.
Не особо важно. Мне бы знать лучше, что тут ошибок нет, за матан крайне хуёво платят жи.
Крайне хуёво у нас платят, в Европке - очень неплохо, ну и плюс ЧСВ потешить. Ошибок я не увидел, единственно, нам же нужно как-то обосновать, что в этом дискретном физическом пространстве мы не можем провести инфинитезимальный отрезок "между точек"? Пока что я не вижу каких-то путей для исправления этой ситуации. Может если перестроить К-теоретические методы под твои идеи (в цикле Ботта теперь ведь тоже могут быть только инфинитезимальные отрезки), в общем, ты подумай над этим, а так-то всё хорошо выглядит.
Я собираюсь снять видеоматериал с уже чёткосформулированными утверждениями и строгими доказательствами (не то, что я сюда и в /б/ вбросил), ну и опять вбросить в оба места, посмотреть на результат. Сложно будет спиздить идею и оформить её так, как будто она была раньше моей видеозаписи, но даже если возможно ( и если сделают) то как то похуй, если кому то это настолько нужно будет, то пох,и это ещё не вся работа во вторых.
А по поводу самих доказательств: 2 аксиомы опровергаются подряд, не в курсе я особо, но в роде в матане в них принято "верить", так что и принятие работы будет наверняка со срачем, ну а так как я ноунейм то и помимо аргументов уверен будет просто тонна хуйни по типу "сперва математиком стань". В общем посмотреть будет позже на что я думаю.
Удачи, будем следить за твоей деятельностью всем саентачём!
Да не пацаны, это мамкин любознатик в треде, я просто встрял неудачно в ваш диалог (или триалог). Не знаю может вы и тролите, но мне доставляет. Читаю вас, и мотивация у меня че-нить понять хотя мало чего понимаю лол.


>>352925
Ну звучало это так, как будто я клоуном выгляжу просто, не пойми неправильно, но фраза "всем саентачем!" прямо орёт о том, что что-то тут не так. Без обид, просто не пугай так больше.
>>352926
Да у меня тоже, просто я привык сратся с людьми. Вдруг так внезапно согласились со мной, аж жутко стало.
Всмысле реальный или математический?
Если матан - то точка, а в реальности не знаю вещи, так как физики сочинили целую балладу про сингулярность.
Хотя-бы на единицу.
>Не обязательно
Обязательно. Существование производной - это определение гладкости функции. Почему гладкость функции в математическом смысле означает гладкость графика функции в обывательском смысле (отсутствие углов) становится интуитивно понятным после внимательного рассмотрения понятия производной и того предельного перехода, который возникает при этом.
Всё понял, что ты хочешь донести. Возьмём три близкие точки на окружности, проведём некоторый угол. А теперь приблизим две крайние точки и угол станет больше. Последовательно приближая точки мы будем приближать угол между отрезками к 180 градусам. Продолжая отрезки в бесконечность мы получим пару лучей, которые выходят из угловой точки. А вот дальше идёт МАГИЯ. Уменьшая расстояние мы получаем последовательность углов, а ПРЕДЕЛОМ этой последовательности будет 180 градусов, и в ПРЕДЕЛЬНОМ случае эти два луча будут образовывать прямую, которая будет являться КАСАТЕЛЬНОЙ к нашей "угловой" точке, тангенс угла наклона которой будет являться ПРОИЗВОДНОЙ функции, которая задаёт множество точек, образующих окружность. И проделав такое в каждой точке окружности мы получим существование КАСАТЕЛЬНОЙ и ПРОИЗВОДНОЙ в каждой точке окружности, то есть её ГЛАДКОСТЬ. А теперь возьмём квадрат, в нём самое интересное происходит в углах этого квадрата. Возьмём три точки, одна из которых совпадает с угловой и проделаем те же операции бесконечного приближения. Там угол между этими тремя точками будет всегда 90 градусов, сколь бы близко они не находились, и лучи НИКОГДА не превратятся в прямую, то есть эти лучи НИКОГДА НЕ СМОГУТ ОБРАЗОВАТЬ КАСАТЕЛЬНУЮ В УГЛЕ и следовательно ПРОИЗВОДНОЙ В УГЛЕ НЕ СУЩЕСТВУЕТ ТАКЖЕ КАК И НЕ СУЩЕСТВУЕТ КАСАТЕЛЬНОЙ.
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
2 × 3 = 8
Определение=/=доказательство.
То, что это интуитивно понятно ещё не означает, что в концепции нет ошибки. Само доказательство основывается на том, что между любыми 2мя точками бесконечное их количество. И из этого уже следует, что у окружности нет углов, и только из этого. И всё это построение можно считать верным только если бесконечность принимать за аксиому и не искать в ней противоречий. Вот простые, даже "интуитивно" понятные: в какой из данных отрезков точек больше? И что тогда будет, если вычесть одно кол-во точек из другого?
Плюс к этому в свою очередь я могу утверждать абсолютно точно таким же методом об многоугольнике, в котором их будет бесконечное количество. И в действительности ты не найдёшь разницу между ним и окружностью никаким методом, ведь единственная теоретическая разница между ними - это наличие углов в "многоугольнике" и абсолютная гладкость другого. И если даже не спорить с "гладкостью" (что не факт, ибо это не доказывается логически, это скорее эмпирический результат), то при любом приближении, при любом измерении ты никогда не сможешь выделить то место, в котором будет видна разница. Доказываю от обратного: Если ты такой находишь эту разницу, ты увидишь угол на каком либо этапе, имея 1 угол многоугольника с равными углами ты сможешь вычислить их количество (потому что в равностороннем многоугольнике с равными углами они все подобны, имея 1 ты получаешь считай все). Получив все углы ты уже не сможешь утверждать, что их бесконечное количество, ведь их теперь возможно сосчитать. Вывод простой- многоугольник и есть окружность. Возможно ли найти здесь противоречие?

>в какой из данных отрезков точек больше? И что тогда будет, если вычесть одно кол-во точек из другого?
Вот пик
То есть не существует касательной ни к какому углу или что? СЛОЖНА для меня, а если я допущу, что у меня бесконечно малый угол, прямо как такой, который был бы в окружности если бы там был угол? Будет ли между ними какая-то принципиальная разница?
Фига себе ты пригорел, вот сразу видно верующего, прям как метку на лбу нарисовать.

>>352914
>>352915
>>352916
>>352917
>>352918
>>352919
>>352920
>>352921
>>352922
>>352923
>>352924
>>352925
>>352927
Очень интересный диалог. Оп, а ты не думал об обобщениях теоремы Атьи-Зингера при помощи инфинитезимальных отрезков? Ведь тогда получится новый, "отрезочный индекс", который равен двум остальным, что может полностью перевернуть алгебраическую геометрию.

Я об Атьи-Зингера понятия не имею, а об инфинитезимальных отрезках у меня представление только из вики и вот этой гифки. Так что молчу.
Бесконечно малые - это способ, которым я пытался показать почему бесконечность не работает и каким образом при помощи неё мы можем привести 2 противоречащих друг другу вывода. То есть в таких вещах как теорема Атьи-Зингера я ничего толком не знаю, просто пытаюсь разобратся в противоречиях выводов Евклидовой геометрии.
Это наверное потому, что пользуясь бесконечно-малыми величинами ты получаешь бесконечно-малые выводы, которые несовместимы с обычными. Возможно следует просто категоризировать (все выводы расставить по своим размерам)?
Можно провести касательную к углу, но нельзя провести ЕДИНСТВЕННУЮ касательную к углу.
>Определение=/=доказательство.
Определение гладкости в математике конкретное и не требует никаких доказательств. Можно доказать, что геометрическая конструкция типа "угол" не подпадает под определение гладкости, так как касательная в двух точках, сколь угодно близких к угловой, но лежащих по разные стороны от угла имеют совершенно разные углы наклона, а значит производная в точке угла претерпевает разрыв (производная справа не равна производной слева), а следовательно не определена, а следовательно угол не является гладким. В то время как функция, описывающая окружность известна и можно по определению найти производную этой функции и она не претерпевает разрыв. Ничего эмпирического здесь нет, можно все доказательства выразить формулами.
>Само доказательство основывается на том, что между любыми 2мя точками бесконечное их количество.
Именно. И если я не ошибаюсь, это утверждение является аксиомой.
В них "одинаковое" количество точек, так как я могу построить простейшее изоморфное отображение одного отрезка в другой.
Сейчас долго писать, но если коротко: при нынешней геометрии получается именно отрезки о должны быть определяющими всё, о размерностях их я не буду ничего говорить потому что не уверен в этом.
Я тут вещь поинтереснее обнаружил: нельзя утверждать о какой либо длине окружности, ведь точки в ней между собой ничем не соендинены. То есть как вообще можно предположить что есть такое длина окружности, если ВООБЩЕ нельзя провести между абсолютно любыми 2мя её точками ни одного отрезка? Только эмпирически, логикой геометрии это не обоснуешь
Очень интересный вывод, не следует ли из этого, что в физическом пространстве нету окружностей и что Бог на самом деле создал недоделанный мир?
Лол, нет, окружности то в реальности существуют. Её геометрическое определение неправильно, точнее оно не точное и требует доработки. Решая эту задачу можно будет и до решения её длины добратся, но пока множества точек между собой не связанны - геометрической фигурой "это" называть нельзя.
Может реальные окружности в реальности и связаны как раз этими бесконечно-малыми отрезками?
Идеальная окружность - да, по идее так. Альтернативы пока не вижу, не точками же.
Окружность - это множество точек, равноудалённых от конкретной заданной точки (центр). Координаты точек окружности радиуса R, с центром в точке с координатами (x0, y0) удовлетворяют следующему уравнению: (x - x0)^2 + (y - y0)^2 = R^2
И где здесь ошибка, или противоречие, или неточность?
А что насчёт реальных окружностей?
>точки же не соендинены на самом деле
Гугли математическое определение непрерывности.
>то откуда ты возьмёшь длину?
Википедия тебе в помощь: https://ru.wikipedia.org/wiki/Длина_кривой
Окружность не может быть задана функцией в декартовых координатах, но полуокружность может. Для верхней единичной полуокружности с центром в точке (0, 0) это функция: f(x) = (1 - x^2)^(1/2). Тогда длина этой полуокружности вычисляется как интеграл от -1 до 1 (1-(df(x)/dx)^2)^(1/2).
Кстати, а ты не думал обобщить отрезки на отрезки слов? Тогда можно будет перенести некоторые твои результаты на лингвистику.
> как возможно соединить точки кроме как отрезком
Любой непрерывной кривой которая содержит эти точки.
А что такое длина отрезка?
>Это не доказательство, это термины и утверждения.
Ой насмешил. Это математическое доказательство с формулами и выкладками. Мне лень доказывать непрерывность и гладкость функции, описывающей полуокружность, так как нужно возиться с формулами и пределами, но ты можешь это проверить (хотя нет, не можешь, знаний не хватит, но это уже не моя проблема).
>Функция твоя не геометрическая фигура.
График функции (множество точек с координатами (x, f(x)) является геометрической фигурой. Ты можешь взять мою функцию, вставить её в любую программу построения графиков и получить полуокружность.
А что такое "эталон" и "выражаемая численно характеристика"?
Расстояние между точкой с координатами (x1, y1) и точкой с координатами (x2, y2) есть d = ((x1 - x2)^2 + (y1-y2)^2)^1/2.
Если точка (x1, y1) - задана, и задано положительное число R, то все точки (x2, y2), для которых выполняется уравнение R = ((x1 - x2)^2 + (y1-y2)^2)^1/2 будут образовывать окружность радиуса R с центром в точке (x1, y1).
Блять, я же тебе все формулы написал, отправил в гугол за определениями. Но ты видимо хочешь строгого математического доказательства, которому ты всё равно не поверишь, так как слишком сложно, слишком много букв и формул. Это долго, бесполезно (всё равно что обучать мартышку чтению), мне лень, да и вообще в учебнике Фихтенгольца по матану всё уже давно написано, все доказательства приведены.
У тебя бесконечно-малый отрезок порвался, маня, всё от недостатка изгибов.
>функция=\=геометрическая фигура
>>353018
>График функции (множество точек с координатами (x, f(x)) является геометрической фигурой.
Этот школьник порвался, несите нового.
Лол, их не нужно соединять, они уже соединены. Длина (мера) каждой точки = 0, но длина всех точек не 0, так как этих точек бесконечно много. Когда я говорю, что их бесконечно много, то я имею ввиду не счётную бесконечность, а континуум. Тогда длина этого бесконечного континуального множества точек будет не нулевой, хотя длина каждой точки 0 и никаких отрезков их соединяющих нет. Я знаю, что это контринтуитивно, это трудно понять, но существуют разные виды бесконечных множеств с разными, порой удивительными и "парадоксальными" свойствами.
Кстати, а ты никак с N-петухом не связан? Интересно просто.
Неверно. Не всякая функция - это фигура и не всякая фигура - это функция. Функция может быть разрывной и не образовывать фигуру, а образовывать просто кучу или облако несвязанных точек. И не каждая фигура представляется в виде функции в декартовых координатах по понятным причинам.
>то ни одну её точку нельзя соединить отрезком с другой
Схуяли? Берём и без задней мысли соединяем. Правда этот отрезок не лежит на окружности.
>каким образом находится длина окружности
Берём близкие точки, соединяем отрезком, таким образом строим фигуру из отрезков, которая близка к окружности, но не является ей, постоянно (бесконечно) уменьшая максимальную длину отрезка мы получаем бесконечную последовательность длин фигур из отрезков, которые похожи на окружность, но всё же не являются ей. ПРЕДЕЛОМ этой бесконечной последовательности будет являться длина окружности.
>Между точками не должно быть расстояния, на котором не будет находится любая другая точка, которая так же принадлежит этой окружности. НО ПРИ ЭТОМ БЛЯДЬ ОНИ НЕ КАСАЮТСЯ НИ ОДНА ДРУГУЮ.
Между любыми двумя точками на окружности, сколь бы близко они не находились, найдётся ещё БЕСКОНЕЧНОЕ НЕСЧЁТНОЕ множество точек на той же окружности, которые лежат между этими двумя.
Где ты увидел противоречие?
>окружностью доказывается что есть бесконечность
Нет, бесконечность с окружностью никак не связана.
>Каким образом окружность является геометрической фигурой при том, что ни одна точка не контактирует с другой впринципе?
Таким образом, что мысленно взглянув на континуальное множество точек в микроскоп ты не увидишь дырок в нём, СКОЛЬ БЫ СИЛЬНЫМ УВЕЛИЧЕНИЕМ НЕ ОБЛАДАЛ БЫ МИКРОСКОП.
>Окружность - это бесконечное количество точек равноудалённых от центра, ещё как связана.
Да, но бесконечность не определяется через окружность, это окружность определяется через бесконечное множество точек.
>Ни одна из её точек не связана с другой и принципиально не может быть связанно, это множество точек и никак иначе.
Точки связаны, только не отрезком как ты думаешь, а некоторым уравнением (ограничением на координаты этих точек). Я его ранее выписывал. Более того, окружность - не единственное такое множество точек. Есть ещё отрезок. Это тоже бесконечное континуальное множество точек на плоскости. Для него тоже можно выписать уравнение (ограничение), которое однозначно определяет координаты этих точек.
Так как между любыми двумя точками найдётся ещё хотя бы одна (вернее целое бесконечное множество точек) точка.
>Расстояние между точками конкретное, либо же нулевое ( и тогда это одна и та же точка).
Задай любую точку на окружности или отрезке (это тоже множество точек ничем принципиально, кроме уравнения не отличающееся от окружности), задай ЛЮБОЕ НЕНУЛЕВОЕ, СКОЛЬ УГОДНО МАЛОЕ РАССТОЯНИЕ и можно будет найти точку, которая лежит на таком расстоянии от этой заданной точки. В этом то и заключается непрерывность.
>каким образом геометрическая фигура состоит только лишь из точек
Любая фигура, линия, кривая состоит только из точек. Даже твой любимый отрезок тоже состоит из точек.
>Это и есть противоречие, ведь ты сейчас ноль (длина точки) умножаешь на бесконечность (количество всех точек в окружности) и получаешь не ноль.
Вот ты и попался, дружок. 0 умножить на бесконечность - это не ноль, это не бесконечность, это неопределённость.
>>353063
Причём существует несколько видов неопределённостей:
https://ru.wikipedia.org/wiki/Раскрытие_неопределённостей
Очень просто: бесконечность - не число и никогда (в классическом анализе) не ведёт себя как число. Ведь бесконечность + 5 = бесконечности - это уже поведение совершенно не как у числа.
Отрезок состоит из точек и прямая кстати тоже. И любая фигура тоже, раз на то пошло. Возьми любую точку на плоскости и ты сможешь точно сказать принадлежит ли она отрезку/прямой/окружности/заданному множеству точек или нет.
Это для тебя нет смысла.
>ведь символ бесконечности у тебя не ведёт себя в соответствии с математической логикой
Вот тут ты ошибаешься. Символ бесконечности ведёт себя не как число (так как не является числом), но это не значит, что он не подчиняется математической логике, это лишь значит, что он не подчиняется аксиоматике чисел.
>Таким образом оно не применимо в реальности
Иррациональных чисел в реальности не существует так как у них бесконечное количество цифр после запятой и их тупо нельзя записать на бумаге. В реальности не существует 10000 мерных пространств. Но все эти объекты существуют в математике.
>Там бесконечность минус бесконечность = бесконечность, в этом нет смысла.
Бесконечность не число.
>В окружности я не могу сделать этого по определению.
Зато можно провести дугу окружности, сколь угодно малую. Вот тебе и связь.
Нет не применяю. Я применяю её как характеристику мощности множества. А множество можно задать через операцию принадлежности объекта к множеству, то есть никаких ограничений на количество объектов в множестве нет (то есть бывают бесконечные множества).
>Сможешь ли ты построить такую малую дугу окружности, которая будет состоять только лишь из 2х определяющих её точках? Нет. Сможешь ли ты определить её 5ю точками? Миллиардом? Нет. Тебе нужно бесконечное их количество, каждая из которых равна по длине нулю, и никаких возможных соендинений между ними нет, но при этом дуга будет иметь длину.
Сможешь ли ты построить такой малый отрезок, который будет состоять только лишь из 2х точек? Нет. Почему нет, да потому что если у тебя есть только две точки, то тебе совершенно неизвестно как ведут себя все остальные точки. Чтобы тебе стало это известно тебе нужно дополнительно сказать, что эти две точки задают отрезок. Но ты также можешь сказать, что эти две точки задаю не отрезок, а скажем квадрат или дугу окружности.
Относится, но это не делает бесконечность числом. Более того ответ "бесконечность" не является полным ответом на вопрос "сколько", так как есть различные виды бесконечностей.
Есть только один геометрический примитив - это точка, всё остальное является тем или иным конечным, счётным или континуальным множеством точек. Даже отрезок - это континуальное множество точек. То что ты его задаёшь двумя точками никак не выделяет это множество точек перед другими множествами точек, такими как окружности или квадрат или что-то ещё.
>точки счётны
И вот ты опять попался. Множество точек, как и множество действительных чисел не счётно.
https://ru.wikipedia.org/wiki/Счётное_множество
https://ru.wikipedia.org/wiki/Вещественное_число
https://ru.wikipedia.org/wiki/Непрерывность_множества_действительных_чисел
https://ru.wikipedia.org/wiki/Мощность_множества
>Множество точек, как и множество действительных чисел не счётно.
Так как каждая точка взаимно однозначно задаётся парой вещественных чисел x и y (координат).
Точки существую, просто их настолько много, что их даже пронумеровать нельзя.
>Если относится, то как раз таки значит что ты применяешь его как число.
Оно чем-то похоже на число, но это не число, так как нарушаются аксиомы, которые приняты для чисел. Ты можешь поменять эти аксиомы так, чтобы бесконечность их не нарушала, но это будет уже другая математика и другие числа с другими свойствами, и все известные теоремы придётся также изменять и доказывать заново.
>Доказать логически, что существует какая либо ещё точка тогда нельзя никак.
Можно. Возьмём вещественные числа. Их несчётное количество. Возьмём два любых вещественных числа a и b. Тогда можно найти новое число c = (a + b) / 2, которое лежит между a и b. Точно также происходит с точками окружности, так как их можно взаимно однозначно отобразить на отрезок числовой прямой.
>Беру и за бесконечное количество времени с бесконечной скоростью нумерую бесконечное количество точек.
Точки изоморфны паре своих координат (x, y). Координаты вещественны. Множество вещественных чисел не счётно, то есть его нельзя пронумеровать, то есть оно не изоморфно множеству натуральных чисел. А теперь покажи мне схему, по которой будешь нумеровать вещественные числа.
Мне неочевидно, какое отношение все твои словесные пассажи в духе Фомы Аквинского, имеют к математике. А ещё мне жаль, что совсем уж упоротых долбоёбов типа тебя тут не ебашут банхаммером. Парочка таких как ты - и интеллектуальный климат на саентаче понижается в два-три раза.
Весели нас дальше, дружок. И свой ютуб-канал обязательно не забудь сюда закинуть, и как филдсовскую премию получишь - отпишись.
Шизик-школьник претендует на лавры Рыбникова, первокуры пытаются ему что-то объяснить - не выходит, остальные лолируют и подтралливают. В принципе всё.
У Марь.Ивановны на переменке спроси.
Ебать ты тралл)) А канал на ютубе всё же скинь - чисто поржать.
Окей, великих тебе свершений, критически мыслящий.
ОК ВОПРОС, ПОЧЕМУ КОНСТАНТЫ БЕСКОНЕЧНЫЕ ?
> делаю вывод, что точки в окружности не контактируют, все и каждая
Тогда бы существовало такое вещественное число k что такая точка окружности что она была бы удалена от всех остальных точек окружности на величину равную или больше k. К примеру если взять любые две непересекающихся фигуры, с легкостью можно обнаружить такую точку на одной фигуре, и такое число k что все точки другой фигуры удалены от выбранной точки на первой фигуре на число равное или больше k. Для точки на окружности этого нельзя сделать - какую бы мы точку окружности не взяли, и какое-бы число k не выбрали - всегда будет как минимум еще одна точка окружности на меньшем расстоянии. Следовательно все точки окружности контактируют.
Те, у которых бесконечное количество углов.
Ну, если у точки бесконечное количество углов, то она может касаться другой точки бесконечно малым отрезком - всё очевидно ведь.
как можна поделить на чесло меньше единицы?
ну смари делешь на два - получается в двое меньшее число, делишь на один - само это число, но как можно паделить на чесло меньше одного?
Какое такое обратное? Для умножения не надо никакого обратнова. Обясни, как можно сразу преставить себе деление на число мнньшее единицы, как это можно сделать с умножением и с делением на два.
Так канешна можно, но панимаишь, правела дробей, они ета, эээ... для пидаров кароч. Так что давай для нормальных пацанов по быстрому разложи все как есть епте.
Ебать ты ученый в гавне маченый, по нормальному без пидорских дробей не можеш, лох! Мы тут с пасанами открыли, что чем меньше делитель, тем больше частное епту блядь, а чего дабился ты, мальчек?
Ну падели сразу 1 на 0,5 без преобразованея драбей, что сложна что ли?
Ебать дщебил. Ну смари бирешь такой и делишь 1 на две части, получается 0,5. А как можно 1 разделить на 0,5 частей?
>Пи не бесконечна, она имеет конкретное значение
Хорошо если пи конечна, назови мне последние число?. Все константы бесконечные. С бесконечно, малым остатком, но бесконечным.
> больше 3х, меньше 4х
А еще есть положительный нуль, и отрицательный ноль. как смешно
Вы теоретики, всегда ими и останетесь
Всё, в говнемоченый слился, нобелевка наебнулась. Можно конечно представить себе деление как число вложений в делимое делителей, но это грех. А по нормальному представить себе деление нельзя. Поэтому деление - это операция мразь, операция гной, операция пидор.
вот тебе первые 10 миллионов знаков пи.
http://pi.karmona.com/
в инете есть архивы на 10 и 40 терабайт Пи
Если ты не знаком с бесконечными константами, то мне тебя очень жаль.
а ты знал что делить и умножать можно бесконечно? угу?
Учитесь, у доктора. Наук, дети. И не несите чушь
Я тоже считаю что все замкнуто но как технически доказать это? когда в числе пи будет число пи? замкнутое?
Вот тебе простой пример.
При бесконечном делении один на два
остаток результата будет всегда 125 и 625
кроме первых двух результатов.
>>353189
Зашивайся, лолка. При сложении и умножении не бывает никаких остатков и прочего говна и эти операции интуитивно понятны. А вот деление - отдельная совершенно хуйня, которая просто так сложна для понимания. Надо принять, что изначально доступны для понимания только натуральные числа, сложение и умножение. Всё остальное - абстрактная херота, для понимания которой надо уже включать воображение и выводить новые объекты из предыдущих.

По-моему ты просто жонглируешь терминами. Если нечто неограниченно, если мы не можем сосчитать конечное количество элементов множества — разве это не бесконечность? Бесконечность и есть.
Какой у тебя бэкграунд математический? Что изучал, о чем можешь рассказать?
Это правильно. Мне кажется двач хорошее место тренироваться идеи высказывать. Срач помогает лучше в предмет вникнуть!
Ну с другой стороны он же пытается разобраться. Может и не шарага. Много ли таких как он в шарагах, кто стал бы анализ осмысливать? Мне интересно, есть ли смысл в таких упражнениях, стимулируют ли они развитие, или это только срач ради срача получается.
Так я согласен с тобой.
Это другой анон
ВОТ КАК БЫ 22 ТЕРАБАЙТА ЧИСЛА ПИ
https://geektimes.ru/post/101210/
И БУДЕТ ХОТЬ ТРИЛЛИОН ТЕРАБАЙТ, ЭТО КОНСТАНТА МАНЯ. А КОНСТАНТЫ БЕСКОНЕЧНЫЕ, ЕСЛИ ОТРЕЗОК НЕ ЦЕЛЫЙ
"Пытается разобраться", - это читать учебники, задавать вопросы на math.stackexchange или dxdy и получать ответы. А это я называю бредом сверхценной идеи, который индуцирован глупостью помноженой на высокомерие.
ИМЕЮЩИЙ ТОЛЬКО КРУГЛЫЕ ЧИСЛА.
Ну так вот тебе единственно возможный правильный ответ: ты не можешь указывать на ошибки в математике, так как не понимаешь, что математика утверждает и что такое "логика" и как она понимается в современном смысле - тоже не понимаешь, так как у тебя серьезные пробелы в образовании. Единственное, что можно сделать в этом случае: отложить вопросы в ящик на год и заняться устранением этих пробелов, после этого, если вопросы ещё остануться (что очень навряд ли), ты, по крайней мере, сможешь их адекватно задать. Все твои реплики - детский лепет, это скажет любой студент-математик, и даже мат.школьник. А если ты считаешь, что всё математическое сообщество глупее тебя - то это и есть высокомерие и бред сверхценной идеи. У меня всё.
>слова имеют конкретное значение, двояко их сложно понять
Ну вот ты и математики их понимают по-разному. По крайней мере, ты не понимаешь, что в математике называют "числом", "точкой", "фигурой", "множеством", "бесконечным множеством", "пределом", "кривой", "отрезком", "плоскостью". Более того, ты не понимаешь даже, что такое "определение" и "доказательство". То есть с тобой тупо невозможно общаться, из-за того что ты не знаешь слов. (Я тебя дико удивлю - но преамбулы на википедии, это не математические определения, а математические определения - в учебниках по математике для математиков).
>А вот здесь не согласен полностью, я понимаю логику получше многих
Пусть так, тогда ты не знаешь, что математики понимают под "логикой", то есть опять же, математикам с тобой общаться невозможно - быть может стоит сначала выучить, что математики понимают под логикой, чтобы хотя бы донести им, что они не правы?
>это моё увлечение с детства, и логические ошибки как раз скорее будут у кого либо ещтё, чем у меня.
И неужто это основание считать себя умнее всего человечества? Какое ребячество.
>Есть претензия к моему логическому методу или где-то в суждениях найдена ошибка?
С точки зрения математиков, ни одного (математического) суждения среди твоих реплик нет - поэтому опять же, понять тебя математикам невозможно, а тебе - понять их.
ОК
>>Постарайся брать строгие определения, а не хуйню из головы блядь. "Круглые" числа не бывает, есть множество натуральных чисел, раз уж на то пошло.
ПРОСТОЙ ПРИМЕР
10, 100, 1000, 1000
>Под логикой я понимаю вполне конкретную методологию доказательства и аргументации. Нет никакой "другой" логики у математиков, есть только противоречия.
Пусть даже так, и существует единственная правильная логика, которую знаешь только ты. Но может ВСЁ ЖЕ тебе стоит потратить годик-другой и узнать, что математики понимают под логикой, раз ты уж собрался учить математиков тому, как им жить и устраивать научные революции?
>Википедия не пишет правды и определение, взятое с её преамбулы - зашквар что-ли? Серьёзно?
Во-первых в самой википедии написано, что там не всегда правда. Во-вторых, в преамбуле определения энциклопедические, а не математические - то, что ты не видишь разницу между этими двумя понятиями, как минимум уже огромный барьер между тобой и математиками. В-третьих, могу ещё больше удивить: определения "числа" в математике нету. Есть определение "натуральных чисел", "целых чисел", "вещественных чисел" и даже целых классов числовых систем "поля", "кольца", но определения "просто числа" - нету. Ровно такая же ситуация с определением понятия "фигура", есть "компактные множества", "измеримые множества", "квадрируемые множества" и куча других классов объектов, но в математике нету единого специфицированного определения "фигуры".
>Опять же - делаешь вывод о том, что я ЧСВшный уебан. С чего это?
Ну ты напрямую заявляешь, что тысячи великих умов не знали логики и сделали хуйню, а ты, такой умный, за вечер всё переделаешь. Что это, как не ЧСВ?
>С точки зрения математики их аксиоматическое утверждение - истина и оспаривать её не имеет смысла.
Вот опять, говоришь о математике, хотя её не знаешь. Это неправда и математики так не считают.
> утверждения формулируются словами, слова имеют конкретное значение
Утверждения должны быть формализованы, потому как естественный язык так или иначе подразумевает множественность трактовок, и, следовательно, неполное понимание.

Множество I называется индуктивным, если:
1. Пустое множество является элементом I
2. Если множество M является элементом I, то и множество M' является элементом I.
Седьмая аксиома ZFC: существует хотя бы одно индуктивное множество.
Множество называется бесконечным, если оно равномощно своему собственному подмножеству.
Нетрудно доказать, что индуктивное множество бесконечно. Для этого достаточно рассмотреть функцию f из I в I такую, что f(M) = M'.
Таким образом, существование индуктивного множества гарантируется седьмой аксиомой Цермело-Френкеля, а его бесконечность тривиально доказывается.
И в чём проблема, господа?
> M∪{M}
Почему такое множество существует в ZFC и какая формула его описывает (напомню, что \{\} - это синтаксический сахар)?
Непустое множество Z называется неупорядоченной парой множеств X и Y, если для любого p из того, что p является элементом Z, следует, что p=X или p=Y. Неупорядоченная пара множеств X и Y обозначается как {X,Y}.
Существование неупорядоченной пары любых двух множеств доказывается сравнительно просто, для этого нужны третья и четвёртая аксиомы.
Четвёртая аксиома ZFC утверждает, что для любых двух X и Y, не обязательно различных, существует такое множество M, что X является элементом M и Y является элементом M. Я обозначу это множество как [X,Y]. Множество [X,Y] не обязательно является неупорядоченной парой X и Y - оно может являться её собственным надмножеством. Чтобы выделить из [X,Y] пару {X,Y}, нужно воспользоваться аксиомой выделения.
Третья аксиома ZFC, аксиома выделения, утверждает, между всем прочим, что если P - одноместный предикат, то для любого множества A существует множество B такое, что для любого множества x утверждение "x - элемент B" равносильно утверждению "x - элемент A и выполняется P(x)".
Если применить эту аксиому ко множеству [X,Y] и к высказыванию "x=X или x=Y", то она гарантирует нам существование множества, которое и будет являться {X,Y}.
Символом {M} обозначается неупорядоченная пара множеств X и Y в случае, когда X=Y=M. Существование множества {M} для множества M вытекает из существования неупорядоченной пары для любых двух множеств.
Далее, символом ∪M я обозначу такое множество, что утверждение "m - элемент ∪M" равносильно утверждению "существует такое множество X∈M, что m∈X". Множество ∪M называется объединением множества M. Если M = {X,Y}, то объединение M я буду обозначать как X∪Y.
Пятая аксиома ZFC утверждает, что для любого множества существует объединение.
Пусть M существует. Тогда, по теореме о существовании неупорядоченной пары, существует {M}. Тогда, по этой же теореме, существует {M, {M}}. Тогда, по пятой аксиоме, существует ∪{M, {M}}, которое я обозначаю как M∪{M}.
Ась?

Что не нравится?
>последовательность кривых стремится к другой кривой, не означает, что последовательности длин стремятся к предельной длине
А в чем же тогда заключается суть понятия "последовательность кривых стремится к другой кривой"
>существует единственная правильная логика, которую знаешь только ты.
"Доказывай что это так и покажи что по другому быть не может".
Вот тебе великая тайна и открылась, кот выллез из мешка, мозайка стала картиной итд. Всё остальное в логике строится именно на этом принципе, причина-следствие, дедукция, индукция итд. Она не моя, никакого патента на логику не имею.
>определения "числа" в математике нету
Нумерация, в любом случае я работал конкретно в сещ. числами, так что определение числа "строго" мне и не было нужно, не его я обрабатывал.
>Ну ты напрямую заявляешь, что тысячи великих умов не знали логики и сделали хуйню, а ты, такой умный, за вечер всё переделаешь. Что это, как не ЧСВ?
Я строил заявление на проверке одной из аксиом. Была придумана и построена модель с использованием нескольких аксиом и с помощью неё выводилось всё остальное. Тысячи великих не проверяли саму аксиому, во первых потому что не было возможности без доработанной модели, а во вторых потому что конфликт между аксиомами впринципе не очевиден.
Я сейчас раскажу о схожем событии в истории физики, где не менее именитый учёный подверг сомнению именно аксиоматическое знание, про Эйнштейна сейчас речь. У физиков были данные, и их проверка и перепроверка вела к тому, что смысла во всём полученном не было, не работал принцип сложения скоростей, тогда как в других случаях он прекрасно выполнялся (подобно тому, как у математиков в одном месте бесконечность применяется одним способом, а в другом другим и делается это "потому что"). Так вот, загадка этого так и не была бы решена если бы под сомнение не попали именно константы на примере времени и пространства. Вся модель физического мира теперь такая именно вследствие довольно наглого предположения Эйнштейна о том, что физики нихуя не знают что такое время и пространство и поэтому о том как оно должно работать у них тоже ложное представления. Вот тебе прямая связь между моими рассуждениями и доказанной практикой в науке "по соседству".
>Вот опять, говоришь о математике, хотя её не знаешь. Это неправда и математики так не считают.
Именно так и считают, это их точка отсчета, те первичные параметры из которых они строят систему. С этим они не могут сказать "как хочу так и ворочу", они с этим вынуждены работать и подводить одно к другому.
>существует единственная правильная логика, которую знаешь только ты.
"Доказывай что это так и покажи что по другому быть не может".
Вот тебе великая тайна и открылась, кот выллез из мешка, мозайка стала картиной итд. Всё остальное в логике строится именно на этом принципе, причина-следствие, дедукция, индукция итд. Она не моя, никакого патента на логику не имею.
>определения "числа" в математике нету
Нумерация, в любом случае я работал конкретно в сещ. числами, так что определение числа "строго" мне и не было нужно, не его я обрабатывал.
>Ну ты напрямую заявляешь, что тысячи великих умов не знали логики и сделали хуйню, а ты, такой умный, за вечер всё переделаешь. Что это, как не ЧСВ?
Я строил заявление на проверке одной из аксиом. Была придумана и построена модель с использованием нескольких аксиом и с помощью неё выводилось всё остальное. Тысячи великих не проверяли саму аксиому, во первых потому что не было возможности без доработанной модели, а во вторых потому что конфликт между аксиомами впринципе не очевиден.
Я сейчас раскажу о схожем событии в истории физики, где не менее именитый учёный подверг сомнению именно аксиоматическое знание, про Эйнштейна сейчас речь. У физиков были данные, и их проверка и перепроверка вела к тому, что смысла во всём полученном не было, не работал принцип сложения скоростей, тогда как в других случаях он прекрасно выполнялся (подобно тому, как у математиков в одном месте бесконечность применяется одним способом, а в другом другим и делается это "потому что"). Так вот, загадка этого так и не была бы решена если бы под сомнение не попали именно константы на примере времени и пространства. Вся модель физического мира теперь такая именно вследствие довольно наглого предположения Эйнштейна о том, что физики нихуя не знают что такое время и пространство и поэтому о том как оно должно работать у них тоже ложное представления. Вот тебе прямая связь между моими рассуждениями и доказанной практикой в науке "по соседству".
>Вот опять, говоришь о математике, хотя её не знаешь. Это неправда и математики так не считают.
Именно так и считают, это их точка отсчета, те первичные параметры из которых они строят систему. С этим они не могут сказать "как хочу так и ворочу", они с этим вынуждены работать и подводить одно к другому.
>Вот тебе великая тайна и открылась, кот выллез из мешка, мозайка стала картиной итд. Всё остальное в логике строится именно на этом принципе, причина-следствие, дедукция, индукция итд. Она не моя, никакого патента на логику не имею.
>Я строил заявление на проверке одной из аксиом. Была придумана и построена модель с использованием нескольких аксиом и с помощью неё выводилось всё остальное. Тысячи великих не проверяли саму аксиому, во первых потому что не было возможности без доработанной модели, а во вторых потому что конфликт между аксиомами впринципе не очевиден.
Как я уже говорил - бред сверхценной идеи, индуцированный глупостью, помноженной на ЧСВ. Разговариват с тобой не имеет никакого смысла по той простой причине - что слушать ты не хочешь, заткнул уши и начинаешь заливать своё "ля-ля", с таким подходом ты сыщешь себе только славу Рыбникова или Катющика, - фрика, над которым ржёт весь интернет (сейчас над тобой ржёт только весь саентач).
Кстати, ещё: на этом моменте я скрываю тред, поэтому тратить свои силы на ответ - бесполезно.
он и так не пустует.
А отрезок это что, не множество точек лежащих на одной прямой между двумя заданными точками? Токая же хрень, как и окружность.
Его ты можешь ограничить 2мя крайними точками и обозвать это длинной. Дугу без деформаций ты никак не сможешь представить как отрезки, не говоря уже о том, что из-за бесконечного количества точек ты не сможешь описать где и в каких местах происходит изгиб - главное отличие дуги от прямой и отрезка. Каждая последующая точка должна быть ниже (или выше) предыдущей принадлежащей этой прямой, но тут такое дело, что никакой "следующей" по порядку точки, потому что между любыми 2мя найдётся ещё точка по определению.
Да я знаю, просто не удержался и, не дочитав тред, ответил
Ну для него специальные правила и придумали, так что это тоже "ОСОБОЕ" число. Тебе же нельзя делить на ноль, и предположить не сложно чтобы получалось, если б разрешали. В остальном пустое множество ни на что больше так не влияет, в сумме или разности как будто бы и не делал его.
>Но ведь нуль - это, тоже, бесконечность.
У вас тут в треде просто одна история охуительнее другой.
Да, одна ахуительнее другой просто. Разбиратся всё равно надо, что из этого неправда, а что "неправдоподобно".
Пи - это константа, о чём ты?
PS. В соседнем треде мне поясняли за существование бесконечно малых отрезков через какое то пиздатое множество и его подмножество, здесь писали что бесконечно малых отрезков не может быть. Я хуею если честно.
В смысле? Это я тут через хитровыебанные квадраты пытаюсь доказать всякое разное нехорошее, в действительности даже эмпирически пи ж никак не будет равно 4м.
Погугли taxi cab distance. Суть в том что расстояния можно мерить не по пифагору а зигзагами под прямым углами, как такси по улицам ездит. И как раз вроде получается как на твоей первой картинке.
Ну так это измерение и называют тут некорректным. А корректного измерения окружности я так и не нашёл, только интегрирование, пределы и в общем все изьёбства, что дают возможность говорить о каких либо отрезках в которых длина и измеряется (а значит о длине), либо же не дает этой возможности, но тогда возникает вопрос что отличает окружность (точнее её сегмент - дугу) от прямой и ломанной.
Методы измерения дающие разные результаты - это уже отдельная головная боль, мне бы просто евклидову геометрию разрулить адекватно.
Поэтому в данной ситуации нужно применять правильный многоугольник и привести его к бесконечному количеству углов, в этом случае длина каждой стороны будет равна расстоянию между точками, так как каждая сторона этого многоугольника будет лежать на окружности.
>Расстояние между ближайшими двумя точками
Без обид, парень, но иди пока из этого треда.
Для того, чтобы иметь возможность предположить парадокс в матане нужно его для начала знать, сорян.
>>354306
Ладно, предположим это оговорка и ты не имел на полном серьёзе "ближайшие" точки. В любом случае весь смысл "repeat to infinity" в том, что когда я УЖЕ сделал это бесконечное приближение, тогда то и разницы между фигурами нельзя будет обнаружить ни на каком масштабе. Это для тебя очевидно сейчас, что само строение фигуры с углами не будет таким же, как и строение окружности правильным равносторонним многоугольником. Но при применении бесконечности доказать эту разницу будет невозможно. Всмысле вообще, ты не сможешь выделить такую точку или отрезок этих многоугольников и доказать что она не принадлежит этой окружности.
Почему нельзя?
Провожу касательную к кругу в любой точке-проводится
Провожу касательную к твоей фигуре-не проводится(просто по определению касательной, она не будет существовать ни в одной точке этой фигуры).
Разница есть? Есть. Фигуры не одинаковые. Значит и периметры не одинаковые.
И вобще, парадокс уровня "есть круг и есть круг, сделавший второй оборот, у второго круга в 2 разв больше периметр, но они одинаковые"
>>354309
Придется, видимо, более сложно объяснять.
Хорошо, вместо кривых примеров приведу как же отличить можно по определениям и метаинформации.
Давай определим операцию разбиения квадрата на угол, то есть то, что на пике.
Что образуется в процессе? Образуется ломаная. Как эта ломаная определена? Тремя точками
Из этих трех точек только одна точка лежит на окружности, а две остальные всегда НЕ лежат на ней.
То есть при бесконечном разбиении будет бесконечное количество точек, которые будут лежать на окружности, но и бесконечное количество точек которые на ней лежать не будут. Причем в пределе получается, что соотношение количества того и другого всегда 1:2. Длина получившейся ломаной значения не имеет, ибо разбиение бесконечное и стремится к нулю. Следовательно квадрат нельзя таким образом преобразовать в круг.
Многоугольник можно и вот почему.
Определение окружности - бесконечное множество точек, расположенных на одном расстоянии от данной точки.
Определение многоугольника: фигура, образованная отрезками, соединяющими n-нное количество точек, находящихся от одной данной на одном расстоянии
Добавление ещё одной стороны образует всегда 1 новую точку, лежащую на окружности при условии, что радиус и центр многоугольника одинаковый с радиусом и центром окружности.
Следовательно бесконечное увеличение количества сторон приведет к тому, что все отрезки будут оканчиваться на точках, лежащих на окружности. Их длина значения не имеет, имеет лишь метаинформация. Вот в пределе и получится, что периметр такого многоугольника 2pir.
Так лучше?
>Причем в пределе получается
ИТТ весь тред никто не может определить, что такое "предел последовательности кривых", но каждый считает своим долгом посвятить всех остальных в то, что же в этом пределе получится.
Дальше не читал.
>Причем в пределе получается
>разбиения квадрата на угол
>ломаная
>количества того и другого
>repeat to infinity
Да это похоже ОП сам с собой бредит.
По поводу касательной - это "порочный круг", не касательная определяет фигуру, а фигура касательную. Касательную невозможно провести через одну точку.
>>354329
А по поводу ломанных и "срезания углов" - всё, что относится по поводу новых точек к моей фигуре так же относится и к твоему многоугольнику. Вот наглядно 5 секунд в пеинте, точно так же определяем точки, точно так же последовательным сокращением не можем от них никак избавится.
>>354350
Это обязательно? Вопрос в основном геометрический, если тебе нужно понять как мы получаем эти геометрические фигуры - спроси как вычисляется число Пи. Там как раз вписывается и описывается к окружности многоугольники, всё что нужно - гугл.
>>354353
Формулировки хоть и чисто на словах, но интуитивно же понятно о чём речь, лол. В чём проблема, чему мне нужно дать для тебя строгое определение?
>Это обязательно? Вопрос в основном геометрический, если тебе нужно понять как мы получаем эти геометрические фигуры
Обязательны ли в математике определения? Ну хуй знает, Фома Аквинский тоже, вроде бы, без них обходился.
Где конкретно и что тебе обьяснить?
Матан тоже обходится в некоторых местах без строгих определений, называя это Аксиомой, лол. Типа в этом случае всё норм, да?
Конкретно я веду к парадоксу, а ты, вместо того, чтобы пытатся вникнуть в хотя бы возможность этого парадокса пишешь "врёте, мне нужно обьяснить все и каждое слово или не было". Если что-то из сказанного непонятно - спрашивай, я и уточню. А пока в этом нет необходимости я подвожу к мысли такими словами, какими удобно, от этого я ошибки в суждении далеко не обязательно буду иметь.
Конкретно в месте:
>Причем в пределе получается
я не понимаю этого набора слов. Без кокетства и троллинга - не понимаю и всё.
>Матан тоже обходится в некоторых местах без строгих определений, называя это Аксиомой, лол. Типа в этом случае всё норм, да?
Нет, не обходится, между определением и аксиомой - огромная разница.
Кстати, конкретно в матане ни одной аксиомы нет. Матан пользуется аксиоматическим аппаратом теории множеств (ZFC).
>По поводу касательной - это "порочный круг", не касательная определяет фигуру, а фигура касательную. Касательную невозможно провести через одну точку.
Эмм, ты вобще в курсе, что такое касательная? Она как раз через одну точку и проходит.
И вобще, приведи-ка доказательство того, что твоя фигура в пределе переходит в круг. Если конечно сможешь. Потому что на самом деле это не так, и это ломает весь парадокс
Это значит, что мы последовательно создаём новую геометрическую фигуру, образованной от предыдущей точно таким же способом, как на предыдущей пикче. То есть я беру сегмент многоугольника и вместо одного угла в этой фигуре я создаю другой так, чтобы периметр фигуры остался тот же, тогда как между окружностью и новой полученной фигурой была в итоге ещё как минимум одна новая общая точка. В словах "в пределе" имелось ввиду "когда мы до бесконечности повторили это надругательство над фигурами квадратом/десятиугольником/100600угольником".
>Нет, не обходится, между определением и аксиомой - огромная разница.
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющее определения; для его объяснения используются описательные формулировки, характеризующие множество как совокупность различных элементов, мыслимую как единое целое[1][2].
Вот тебе цитата с вики. Вполне себе не строгое определение, оно должно быть интуитивно понятно тип.
Возьми и отметь одну точку. Через неё можно провести сколь угодно много "касательных". Я имел ввиду что окружность говорит что через неё нельзя провести касательную, а не касательная свидетельствует об этом.
Вот уточню: Касательную невозможно определить одной единственной точкой.
>через неё нельзя провести касательную
Сори за ломанный язык, заранее - через ОДНУ ТОЧКУ окружности нельзя провести больше одной касательной - это скорее определение окружности, а не самой касательной.
>когда мы до бесконечности повторили это надругательство над фигурами квадратом/десятиугольником/100600угольником".
Ты заменил "в пределе" на "до бесконечности повторили" и думаешь, что стало намного понятнее?
>Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющее определения; для его объяснения используются описательные формулировки, характеризующие множество как совокупность различных элементов, мыслимую как единое целое[1][2].
Множество и отношение "принадлежать" между множествами - действительно (единственные) неопределимые понятия в математике (в одном из её изложений). Все остальные понятия должны быть определены.
Что значит "неопределимые"? Перечисление аксиом объекта и есть определение объекта. Аксиомы теории множеств известны.
Ну а теперь докажи, что твоя предельная фигура будет кругом. А я пока скажу, что, если взять круг радиуса 1 и с центром в начале координат, то точка A, лежащая на круге так, что угол >XOA=60 градусов, не лежит в твоей фигуре(поскольку ни на каком этапе "складывания углов" она не может попасть в фигуру), а значит круг не равен предельной фигуре.
>>354370
Касательная-предел, к которому стремятся секущие через данную точку и другую, при приближении этой другой точки к данной. У окружности этот предел есть в каждой точке, у твоей предельной фигуры этого предела нет в каждой точке, могу даже попытаться доказать, но думаю это не нужно.
Бесконечность вполне себе математическое понятие, оно аксиоматично. Я то его опровергать пытаюсь, так что если ты не веришь в строгое математическое определение бесконечности и тебя смущает это понятие - тогда ты в общем то в моём зашкварном клубе, лол.
Нарисуй в пеинте, пока не уловил. В какой точке окружности моя фигура точно не будет иметь общей точки с ней? Вполне конкретную точку можно определить или нет?
Не, забей, тут я ошибся насчёт непринадлежащих точек. Есть точки, которые не при каком шаге "сгибания углов" не могут попасть в фигуру, но в пределе могут на ней лежать.
А вобще, спрошу пока у адекватных математиков: какое определение предела последовательности кривых? А то без него тут никак
В том смысле, что понятие "множества" не является определением в смысле консервативного расширения теории, оно уже - часть теории, ну так-то да.
>>354376
>Бесконечность вполне себе математическое понятие, оно аксиоматично. Я то его опровергать пытаюсь, так что если ты не веришь в строгое математическое определение бесконечности и тебя смущает это понятие - тогда ты в общем то в моём зашкварном клубе, лол.
Меня смущает, что ты не можешь объяснить мне, что значит "повторить до бесконечности", больше ничего - в математических учебниках словосочетания "повторить до бесконечности" не используют, я их читал, честно-честно!
Адекватное определение - как компактных множеств в смысле расстояния Хаусдорфа, например. И по этому определению - последовательность ступенчатых кривых на пике стремится к окружности.
Чтобы определить предельный переход на некотором множестве кривых, нужно определить на этом множестве метрику, т.е. расстояние между кривыми, или хотя бы топологию.
Конкретно здесь можно фиксировать окружность, рассмотреть множество всех "контуров", содержащих эту окружность, далее выделить в нём такое множество контуров, которое содержит нашу окружность и при этом если A и B - два контура, то либо A вложен в B, либо B вложен в A. На этом последнем множестве за расстояние между двумя контурами принять площадь области между ними. Тогда нарисованная на картинке последовательность контуров действительно будет сходиться к окружности. Именно такая метрика подразумевается на картинке.
Конечно, при таком определении ниоткуда не следует, что если у нас есть сходящаяся последовательность контуров одной и той же длины l, то и у контура-предела длина будет l. Предельный переход не обязан сохранять периметр.
Точно также, как ты чертишь окружность - так же я и создаю свою фигуру.
Как строишь ты окружность на листе? непрерывной линией. Но окружность - это не непрерывная линия, это множество равноудалённых точек. Так что, чтобы построить окружность корректно, тебе необходимо отметить все и каждую точку до бесконечности. Одну за одной. И никак иначе, все остальные способы - это удобство, но ни на йоту не правильность построения. Так яснее?
Во, спасибо за обьяснение. А можно ли поставить дополнительное условие, из которого бы следовало сохранение периметра?
Нет, ни яснее. Я не понимаю почему что-то не может быть множеством точек И непрерывной кривой одновременно. И я так и не понял, это ты пытался определение словам "повторить до бесконечности" дать или что?
>>354385
Нужно требовать равномерного стремления производных: так называемая C^(1) норма. То есть, чтобы касательные почти в каждой точке "приближающей кривой" отличались мало от касательной на окружности.
Поставить-то можно, но это будет изменением метрики. В изменённой метрике окружность уже не будет пределом контуров-лесенок.
Ага, ну тогда всё ясно. Приближение круга последовательностью правильных n-угольников удовлетворяет этому условию во всех точках, кроме углов этих n-угольников, поэтому предел их периметров равен периметру круга, а фигура ОПа этому условию удовлетворяет только в 4 точках(точки касания с начальным квадратом), поэтому предел последовательности периметров его фигур(равный 4) не обязан быть равен периметру предела(круга), что и обьясняет парадокс.
Не может быть по определению точки. Между любыми 2мя найдётся третья. То есть непрерывности как таковой у дуги (и как следствие окружности) быть не может, точки не связаны между собой отрезками. Единственная причина, по которой окружность считается непрерывной - это то, что между точками нет точек, не принадлежащих этой окружности. Но связи между точками нельзя найти никак, это множество не связано ни отрезками, ни любыми другими геом. фигурами. А потому тогда нельзя начинать считать Пи, ведь о какой длине окружности идёт речь?
>То есть непрерывности как таковой у дуги (и как следствие окружности) быть не может
Может следует сначала почитать по-поводу того, что в математике понимается под непрерывностью?
Я имею ввиду геометрию. То, что функция непрерывна - это очевидно. То, что определение точки противоречит утверждению о том, что окружность непрерывна - это тоже очевидно. Как длину у множества точек ты будешь искать?
>То, что определение точки противоречит утверждению о том, что окружность непрерывна - это тоже очевидно.
Мне не очевидно, поясни.
Как длину у множества точек ты будешь искать?
Длину ищут не просто у множества точек, а у непрерывно-дифференцируемой кривой.
>Я имею ввиду геометрию.
Кстати, не существует отдельно "геометрии" и отдельно "матана" - это всё единая теория, строящаяся на одних и тех же формализмах, то, что непрерывность кривых в школе не определяли - это из педагогических целей, а не из математических.
>Мне не очевидно, поясни.
Точки не связаны между собой никак, как подробнее то обьяснить. Функция определяет множество точек, и функция считается непрерывной тогда, когда нельзя наблюдать точки разрыва функции на плоскости. Но между отрезком, в определение которого входит определение длины, и дуги, в котором определения длины нет (и в общем то быть не может) разница видна. Дугу ты не определишь так, чтобы её можно было составить из отрезков. Это невозможно в принципе. Так откуда у множества точек длина? Ты не можешь знать, ты можешь это высчитать, но в реальности это не прямое измерение (тип как линейкой). У тебя множество точек, а точки это не отрезки, очевидно же.
>>354397
Чел, в геометрия сочетается с матаном скорее интуитивно, нежели реально. Меня одного смущает видимо что у вас тут "счётная" бесконечность присутствует и всем норм. 2 разных отрезка - 2 разные длины, 2 разные определяющие его точки. И одинаковое (бесконечное) количество в обоих. Это алогично.
То есть типа я взял нитку длины пять сантиметров - пока она прямая, у неё длина есть, а если я её в петлю согну, у неё длина исчезнет? Лол.
>Точки не связаны между собой никак, как подробнее то обьяснить.
Это не объяснение.
>Функция определяет множество точек
Функция ничего не определяет.
>Но между отрезком, в определение которого входит определение длины
В определение отрезка не входит определение длины.
>Ты не можешь знать, ты можешь это высчитать, но в реальности это не прямое измерение (тип как линейкой). У тебя множество точек, а точки это не отрезки, очевидно же.
Множество точек может как быть отрезком, так и не быть отрезком.
>Так откуда у множества точек длина?
Длина не у множества точек, а у гладкой кривой.
>Чел, в геометрия сочетается с матаном скорее интуитивно, нежели реально.
Она сочетается и интуитивно, и реально, и формально.
> 2 разных отрезка - 2 разные длины, 2 разные определяющие его точки. И одинаковое (бесконечное) количество в обоих. Это алогично.
Это значит только то, что количество точек в отрезке и его длина - две совершенно разные характеристики отрезка.
Так и не увидел объяснения чем "геометрическая непрерывность" отличается от "непрерывности в матане" (потому что она ничем не отличается).
Нитка - это не отрезок. Отрезок ты не сможешь согнуть никак кроме как углами.
Говоря проще чтобы нитка определённой длины стала окружностью - тебе нужно провести сгиб в каждой её точке, во всех. А их тип бесконечно. Вот и сгибай теперь, а потом мне обьяснишь "как же это ты сгибал до бесконечности!?"
лол(
>Отрезок ты не сможешь согнуть никак кроме как углами.
Почему?
>Функция ничего не определяет.
Хуясе. У=Х. я только что определил прямую. Начертить?
Это не функция, это график функции - в некотором смысле, разные понятия совершенно.
Бесконечность одна, счётность-свойство конкретного множества. А "одинаковое количество точек" на длину никак не влияет. Да, множества точек любых двух отрезков равномощны, как и множества точек отрезка и прямой, а длина/площадь/...- просто меры этих множеств, которые к измерениям линейкой имеют не самое прямое отношение. Ты же не говоришь, что у любой фигуры(хотя бы и квадрата) нет площади, потому что её нельзя измерить. Не вижу ничего нелогичного.
>>354406
Сгиб происходит в какой-то точке отрезка. Он происходит в точке. Насколько малым бы не был угол в точке - это всё ещё угол. И сколько бы таких сгибов не было - это только подобие дуги. А теперь найди мне метод, по которому ты в геометрии сможешь прийти к сгибу так, чтобы углов при этом не существовало в нём ( чему никак не прийти без уравнений и функций, то есть описать это нечто ты не сиожешь).
Эм, вобще-то нет. Не каждая функция имеет график и не каждое множество точек на координатной плоскости соответствует функции.
Я могу измерить площадь квадрата, я не смогу измерить площадь квадрата "в точках", не определив сами отрезки квадратов жи.
В теоретико-множественном формализме - да, в теоретико-типовом (например) - нет. В любом случае это не те тонкости, которые нужно знать ОПу (ровно как и то, что в ZFC 1=(0,0) ).
Кстати, если уж говорить строго, то функция - это тройка: область определения A, область значений B и функциональное полное слева отношение на A,B. А график - это всё-таки только лишь третий компонент этой тройки.
>Назови альтернативы.
Просто сказать "назови альтернативы" - это не доказательство. А что такое "сгиб", к слову?
Нет, ты не можешь измерить площадь квадрата прямо, да и длину отрезка тоже. Ты приставляешь к отрезку линейку с делениями, формально разбивая его на части с длиной, равной эталону(скажем 1мм), пользуясь тем, что:
1. Если отрезки совпадают при наложении-их длина одинакова
2. Длина отрезка равна сумме длин его частей.
После чего ты считаешь количество кусков, умножаешь на эталонную длину и получаешь результат. То же самое можно сделать с длиной кривой линии, но, поскольку куски кривой в общем случае не совпадают при наложении с эталонными отрезками-приходится приближать её ломаной линией, причём это приближение мы выбираем не произвольно, а поставив дополнительные условия
>>354386
После чего мы в пределе получаем величину, которую называем длиной этой кривой. Разницы по сути нет.
>После чего мы в пределе получаем величину, которую называем длиной этой кривой. Разницы по сути нет.
Ничего не понял, в пределе чего, по какой норме, получаем что?
В таком случае функции R→R, x↦x^2 и R→R0, x↦x^2 - это две разные функции, что странно. R0 - неотрицательные вещественные.
Не странно, а вполне нормальная практика - вторая называется коограничением первой (почитай, например в Хелемском).
Создание геометрической фигуры, имеющей длину и отличной от прямой или отрезка. допустим. Создать угол я могу, и моя фигура будет иметь длину. Создать дугу ты не сможешь ничем кроме как задать функцией. Потому я и говорю - где связь с геометрией?
Мы берём последовательность ломаных линий и вводим норму, так, чтобы последовательность этих ломаных сходилась к кривой, они удовлетворяли условиям, достаточным для того, чтобы периметр предела этой последовательности был равен пределу последовательности периметров этих ломаных не спрашивай, что за условия, я сам их прочитал в посте, который линканул выше. Если это возможно, и если этот предел существует, то мы получим длину этой кривой.
>не спрашивай, что за условия, я сам их прочитал в посте, который линканул выше
Этот пост я и писал.
>и если этот предел существует
Он не существует.
Приближение это не знак равенства. Такими последовательными приближениями ты строишь фигуру схожую, но той же самой ты назвать её не имеешь права. В окружности ведь углов не больше нуля.
> Создание геометрической фигуры, имеющей длину и отличной от прямой или отрезка.
А что такое "создание геометрической фигуры"? Пойти взять и вырезать лобзиком из линолеума её, или что?
Ничего нормального в этой практике нет. Это ненужная бюрократия, загромождающая выкладки. При такой практике придётся различать несчётное количество функций возведения в квадрат, совпадающих в каждой точке области определения.
Это значит что при черчении этой фигуры ты обозначил и доказал её свойства. Обозначь длину в множестве рандомных точек и докажи, что длина действительно там существует (и как следствие может быть определена отрезками)
>Ничего нормального в этой практике нет. Это ненужная бюрократия, загромождающая выкладки.
Это у тебя математическая культура низкая просто, иногда разделять такие функции просто необходимо для стройности теорем и формализмов. Вся теория категорий зиждется на том, что "образ" стрелки и кодомен стрелки - совершенно разные понятия.
>>354435
>При такой практике придётся различать несчётное количество функций возведения в квадрат, совпадающих в каждой точке области определения.
Да. И чё? Всё равно все нормальные люди определяют x^2 как R -> R, иначе просто тупо.
>Это значит что при черчении этой фигуры ты обозначил и доказал её свойства.
Мне следует разъяснять, чем черчение фигур на листочке отличается от формальной математики?
> Обозначь длину в множестве рандомных точек и докажи, что длина действительно там существует (и как следствие может быть определена отрезками)
Что это значит? Окей, я начертил окружность диаметра 1 на листочке, обкрутил её ниткой, так, чтобы ни в каком месте нитка на себя не накладывалась - развернул нитку и померил длину линейкой, вышло около 3.15, я доказал длину окружности или ещё нет? И как ты доказал длину отрезка? Интересно очень.
Что значит "не существует"? Вобще никогда? Вот я возьму круг и буду его приближать вписанными n-угольниками, условие касательных выполнено, предел периметров существует(периметр n-угольника n x 2rsin(pi/n), при n неограниченно растущем sin(pi/n) -> pi/n, и всё это выражение стремится к 2pi r), в чём ошибка?
>>354431
В пределе-имею. Вот просто по определению предела. Никто не говорит, что в пределе углы сохраняются.
>Вся теория категорий
Не существует вменяемого теоретико-категориального изложения матана. Моё глубокое имхо - не следует смешивать понятия "функция" и "морфизм".
>Да. И чё?
И то, что если две функции равны во всех точках области определения, то они равны. Это стандартное определение равенства функций. А как определить равенство функций при твоём подходе?
>Что это значит? Окей, я начертил окружность диаметра 1 на листочке, обкрутил её ниткой, так, чтобы ни в каком месте нитка на себя не накладывалась - развернул нитку и померил длину линейкой, вышло около 3.15, я доказал длину окружности или ещё нет?
Нет, ты провёл измерение, которое не является точным. Для того, чтобы измерить окружность тебе придётся сделать так, чтобы каждая точка окружности соответствовала каждой точке на нити. Нить при этом не должна сгибатся ни в одной точке (дабы не было углов) но при том прямой она быть тоже не может (или ты её никак не положишь). Так как ты согнёшь нить?
> И как ты доказал длину отрезка? Интересно очень.
Это уже тупость, без обид. Определение длины - это часть определения отрезка. отрезка без длины не сущ-ет, лол.
>Не существует вменяемого теоретико-категориального изложения матана. Моё глубокое имхо - не следует смешивать понятия "функция" и "морфизм".
Во-первых - это неправда, есть глобальный анализ и микролокальный анализ, в котором бесточечные подходы - давно доминируют, а "детским анализом" гладких функций R->R всерьез никто не занимается. Ну, то есть, может кто-то и занимается, но это явно не "в моде", и современные курсы пытаются всё-таки включать глобальные термины (даже во втором Зориче комплексы Де Рама есть, так-то!)
Во-вторых, никто их не смешивает - это просто как аргумент к тому, почему функции с разными кодоменами следует различать.
>И то, что если две функции равны во всех точках области определения, то они равны. Это стандартное определение равенства функций.
Стандартное школьное определение. В учебниках по математике определения другие.
>А как определить равенство функций при твоём подходе?
Этот подход не "мой", а классический. Стандартным образом: домены равны, кодомены равны и отношения равны.
>>354447
Это уже тупость, без обид, в определении отрезка нету ни слова о его длине, то, что ты (до сих пор!) не знаешь определение отрезка и не сумел его нагуглить - само по себе симптамотично.
Чел, есть эталон отрезка в 1 см. Если у тебя нет определения отрезка в котором одно из свойств - это длина, то можно бы подумать и понять что тогда само понятие длины определено отрезками. Это взаимосвязанные вещи, раздельно их представить логично ну просто невозможно.
На практике потребность в коограничении может возникнуть только в ситуациях, которые ты назвал словами "иначе тупо". Различать с разными кодоменами следует морфизмы, а для функций это делать просто незачем. Функции нужно отождествлять с графиками, это эпистемологически приятнее. При твоём определении мы как бы заранее откуда-то знаем, является ли произвольное множество функцией или не является. При моём определении мы можем для произвольного множества выяснять, является ли оно функцией - для этого достаточно проверить, есть ли у него две проекции и если да, то связаны ли они функционально.
Моя позиция эстетическая, а не логическая. Я считаю, что определять функции как тройки незачем, многословие это некрасивое.
Моя позиция тоже эстетическая.
> При моём определении мы можем для произвольного множества выяснять, является ли оно функцией - для этого достаточно проверить, есть ли у него две проекции и если да, то связаны ли они функционально.
При твоём подходе у тебя есть "жёстко выделенная" система координат, мне кажется гораздо приятнее подход - в котором все системы координат равноправны.
>>354453
Не знаю никакого эталона, открыл сейчас четвёрку современных учебников по геометрии - ни единого упомянания об эталонах и каких-то "см", - может в физике и в палате мер и весов и есть какие-то "см", но в геометрии их нету.
>Если у тебя нет определения отрезка в котором одно из свойств - это длина, то можно бы подумать и понять что тогда само понятие длины определено отрезками.
А можно знать - что определение длины иное и отрезок там вообще не при чём.
>Это взаимосвязанные вещи, раздельно их представить логично ну просто невозможно.
Почему?
Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально
>Длина — физическая величина
А мы о математике говорим или о физике? Физики, думаю, как считать длины и без нас разберутся.
"Математическая" длина противоречит логике, как угодно. Доказать, что кривая дуги обладает длиной, эквивалентной той длине, которой обладает отрезок, нереально. Всё будет упираться в определение точки, поэтому длина окружности - это совершенно друое свойство нежели длина отрезка. Разница между этими, казалось бы, одинаковыми вещами - как между небом и Землёй, как между плотностью и электрическим зарядом. Привести одно к другому невозможно, это разные вещи, которые математики обозвали одним и тем же словом.
>"Математическая" длина противоречит логике, как угодно.
Почему?
>Доказать, что кривая дуги обладает длиной, эквивалентной той длине, которой обладает отрезок, нереально.
Не знаю, что значит "длина эквивалентна длине", длина - это число, два числа могут быть либо равны, либо не равны.
>Всё будет упираться в определение точки, поэтому длина окружности - это совершенно друое свойство нежели длина отрезка.
Определение точки у нас есть, но понятие длины в него совершенно не упирается. как ни странно.
> Разница между этими, казалось бы, одинаковыми вещами - как между небом и Землёй, как между плотностью и электрическим зарядом. Привести одно к другому невозможно, это разные вещи, которые математики обозвали одним и тем же словом.
Почему?
>"Математическая" длина противоречит логике, как угодно.
Почему?
>Доказать, что кривая дуги обладает длиной, эквивалентной той длине, которой обладает отрезок, нереально.
Не знаю, что значит "длина эквивалентна длине", длина - это число, два числа могут быть либо равны, либо не равны.
>Всё будет упираться в определение точки, поэтому длина окружности - это совершенно друое свойство нежели длина отрезка.
Определение точки у нас есть, но понятие длины в него совершенно не упирается. как ни странно.
> Разница между этими, казалось бы, одинаковыми вещами - как между небом и Землёй, как между плотностью и электрическим зарядом. Привести одно к другому невозможно, это разные вещи, которые математики обозвали одним и тем же словом.
Почему?
>>354466
>Почему?
Потому что они схожи лишь интуитивно, доказать это необходимо. Нет док-ва = не должно быть всем так ОЧЕВИДНО что это так.
>Определение точки у нас есть, но понятие длины в него совершенно не упирается. как ни странно.
>Почему?
Я ведь раз 200 писал почему и как возникает противоречие же. Ну серьёзно.
>Потому что они схожи лишь интуитивно, доказать это необходимо. Нет док-ва = не должно быть всем так ОЧЕВИДНО что это так.
Что схожи? Можешь чётко утверждение сформулировать?
>Я ведь раз 200 писал почему и как возникает противоречие же. Ну серьёзно.
Ни разу не увидел.
Ты 200 раз повторил, что противоречие есть. Ты ни разу не продемонстрировал это противоречие.
>>354471
Понятия длины для отрезка и для дуги. Формально, в уме, ты её тип просто разгибаешь и тебе норм. но это так не работает, одно понятие никак не сводится к другому.
>Ни разу не увидел.
Окей, ещё раз:
Длина отрезка, так же как и сам отрезок, определяется его крайними точками. Таким образом протяжённость отрезка сравнима с эталоном длины (1 см) фактически, то есть числом я смогу выразить точно сколько таких отрезков в 1 см или их дробной части мне нужно чтобы получить отрезок нужной длины. Тоже самое с периметром замкнутой фигуры, которую можно определить отрезками - это легко. Вся мякотка в том, что длина определяется именно крайними точками. НЕ только лишь множеством точек, принадлежащих ему, а именно крайними, для определения длины это жизненно необходимо.
Теперь к окружности. Никаких крайних точек нет и в помине. Чтобы было проще представить далее будем работать с сегментом окружности - дугой. Она определяется множеством точек и расстояние между крайними двумя нам нихуя не говорят. Так как же я могу попытатся выразить длину? Может у меня будет множество отрезков, столь малых, что из них я могу сложить дугу? Нет, ведь это тебе не пунктирная линия, в которых ты можешь соединить ближайшие два пунктирных деления отрезком. Ведь основное свойство точек - это то что между любыми 2мя, какие бы ты не взял найдётся любая другая. Таким образом в длине отрезками нихуя не выразить. Все остальные математические способы - это обход геометрии, могу посметь сказать жульничество с логикой. вопросы?
> Так как же я могу попытатся выразить длину?
Берёшь кривую.
Рассматриваешь ломаную, вершины которой лежат на кривой.
Рассматриваешь множество всех таких ломаных.
Рассматриваешь множество длин этих ломаных.
Оно имеет точную верхнюю грань, конечную или бесконечную.
Эта верхняя грань и называется длиной кривой.
>Оно имеет точную верхнюю грань, конечную или бесконечную.
Этот набор слов для меня не имеет смысла и кажется алогичным. Поясни.
Существует множество, которое называется "расширенная числовая прямая". Оно состоит из вещественных чисел, а также из двух элементов, которые обозначаются +∞ или -∞. В этом множестве введены (частично определённые) операции сложения, вычитания, умножения и деления, а также отношение порядка.
Пусть R - множество вещественных чисел.
Пусть R' - расширенная числовая прямая.
Если M - непустое подмножество R, то существует такой элемент a из R', что:
1. Для любого m из M верно m≤x
2. Для любого положительного числа e существует такое b из M, что x-e < b.
Элемент x называется точной верхней гранью M. Если x = +∞, то верхняя грань называется бесконечной, в противном случае конечной.
>>354485
Повторяю: обход логики и жульничество это. Ты бесконечностью обьясняешь другую бесконечность, порочный круг. Если ты не сможешь полученные отрезки выразить в эталоне, хотя бы дробном, в 1 см - это всё не будет иметь смысла, потому что ты этими множествами наёбываешь понятие длины и отрезка. Так или иначе какое то понятие или определение у тебя будет страдать в следствие твоих манипуляций и как итог - не будет логичным. Хотя с точки зрения математики, да, и не такое можно буде
>Таким образом протяжённость отрезка сравнима с эталоном длины (1 см)
Ещё раз, что такое "эталон длины" в геометрии?
>>354489
Физическая величина в 1 см. Ты споришь с тем, что в геометрии есть сантиметры? Серьёзно сейчас меня спрашиваешь или траллируешь?
>>354490
У тебя в доказательстве присутствует бесконечность. Теория множеств основана на этом, лол, а я дальше определений из вики даже не зашёл. Если я правильно понимаю мы сейчас говорим о ZFC, так?
Что такое "порочный круг" я думаю обьяснять не следует.
ZFC - это одна из теорий множеств. Есть и другие, например NBG. Какой из них ты пользуешься?
Я не пользуюсь никакой, я пока в них разбираюсь прыгая по вики от статьи до статьи. Хоть в одной из них случаем есть такое, что понятие бесконечность там не аксиоматична?
Речь к тому же не о них, я сейчас ищу опровержение моих аргументов по существу. Через 50-100 постов наверняка ведь придётся повторять одно и то же. Парадокс то теперь ясен? Хотя бы с точки зрения школьной алгебры геометрии?
Если ты не пользуешься никакой теорией множеств, то ты не должен использовать объекты, которые основаны на теории множеств. Тебе не следует говорить ни о числах, ни о кривых, ни о точках, ни о линиях. Либо ты принимаешь аксиому бесконечности (существует множество множеств, которое содержит пустое множество и вместе с каждым x содержит x∪{x}), либо ты не принимаешь эту аксиому и вместе с ней не принимаешь всю существующую математику.
Я опровергаю её по существу, на основе логики. Результаты математики сомнению не подлежат, её большая часть базиса тоже, но конкретно с бесконечностью происходит подмена понятий, то, что считается бесконечностью, когда ты просто перечисляешь числа типа 1,2,3... и ты не можешь этот ряд закончить - это одна вещь, которую ты можешь назвать бесконечностью, она очевидна, логична и тоже вполне проверяема. Проблема в том, что когда ты делаешь утверждение о том, что в отрезке бесконечное количество точек - ты уже используешь совершенно другой смысл в этих словах, они у тебя как будто бы уже сосчитаны. Это не утверждение о том, что ты можешь сколь угодно много делить отрезок, это утверждение говорит именно о том, что их там бесконечно. В любом случае. То есть они в ряде чисел 1,2,3, ... ставят здесь восьмёрку горизонтально и считают это нормой. А это не так.
Ты не можешь использовать термины "число", "точка", "отрезок", если ты не принимаешь теорию множеств. Эти термины требуют теории множеств для своего определения. Ты не имеешь права их упоминать.
Почему? Я знаю их определения, я знаю как одни вещи в алгебре и геометрии обьясняются и выводятся из этих аксиом. И я вижу в них противоречия. Теория множеств же выведена из алгебры и геометрии, а не наоборот. Как раз ты то и не можешь употреблять её как строгое доказательство по существу, не противоречащее логике. Или школьникам тоже нельзя применять эти понятия, когда они их в школе учат, ещё не "доросли", чтобы рассуждать об этом?
Даже перефразирую:
>Эти термины требуют теории множеств для своего определения.
Лол, нет. Эти термины по большей части аксиоматичны и не требуют под собой ничего кроме алгебры и геометрии. Эти термины - это аксиомы, ты можешь их принять или же нет, ещё ничего не зная о матане. А вот когда ты уже работаешь с алгеброй и геометрией Евклида, то ты волен использовать его термины, волен проверять их совместимость и в полном праве, если вдруг из этого выйдет что 2+2=5 - пытатся опровергать это. Если бы это выражение не опровергалось на основе математики - значит логическую ошибку содержало бы условие задачи. Если нет - значит правила, по которым работает матан, то есть - аксиомы (или же ложные выводы из этих аксиом).
Их определения опираются на теорию множеств. Без теории множеств ты не сможешь определить даже таблицу умножения. И алгебра, и геометрия опираются на теорию множеств. Если ты отказываешься от теории множеств - ты отказываешься и от алгебры, и от геометрии.
Школьники изучают теорию множеств.
Школьная алгебра опирается на теорию множеств.
Школьная геометрия опирается на теорию множеств.
>>354507
В довесок вот лови.
Сам догадаешься что из чего было выведено.
https://ru.wikipedia.org/wiki/Вещественное_число#.D0.90.D0.BA.D1.81.D0.B8.D0.BE.D0.BC.D0.B0.D1.82.D0.B8.D1.87.D0.B5.D1.81.D0.BA.D0.B8.D0.B9_.D0.BF.D0.BE.D0.B4.D1.85.D0.BE.D0.B4
https://ru.wikipedia.org/wiki/Начала_(Евклид)#.D0.9F.D0.B5.D1.80.D0.B2.D0.B0.D1.8F_.D0.BA.D0.BD.D0.B8.D0.B3.D0.B0
https://ru.wikipedia.org/wiki/Аксиоматика_теории_множеств
Аксиомы Евклида неудачны. С их помощью нельзя доказать первый признак равенства треугольников, например. Единственное имеющееся изложение школьной геометрии опирается на теорию множеств.
О, его аксиомы опровергаемы то есть тем, что они что-то "доказать" не могут. А твоя особая геометрия, которую преподают в школе, имея противоречия, которые как раз от Евклида и пошли: они то опровергатся не могут формальной логикой, лол. На основе школьных знаний выведено моё противоречие, теория множеств выведена же из алгебры и геометрии, а не наоборот. Опровергать мои положения тем, что есть теория множеств, которая была выведена игнорируя эти места в алгебре и геом. - это странно как минимум. Ты вообще не в ту сторону клонишь.
Повторяю, и школьная алгебра, и школьная геометрия опираются на теорию множеств. Единственное корректное изложение геометрии - теоретико-множественное. Аксиомы Евклида не позволили даже самому Евклиду доказать все его теоремы. Отказываешься от теории множеств - отказываешься от математики.
Наоборот. Теория множеств - это дополнение сверху, никак не основа, она полностью Евклидова, по крайней мере определение точки, отрезка, длины и дуги. Ещё раз - ссылки кинул, прочти для начала.
Давай кое-что уточним. Ты можешь определить отрезок, не используя теорию множеств?
Да, ЕЩЕ РАЗ:
https://ru.wikipedia.org/wiki/Начала_(Евклид)#.D0.9F.D0.B5.D1.80.D0.B2.D0.B0.D1.8F_.D0.BA.D0.BD.D0.B8.D0.B3.D0.B0
Определение точки, отрезка, плоскости, длины - всё есть, никаких дополнительных "Множеств" не нужно чтобы полностью понимать каждый термин.
Цитирую:
Линия — длина без ширины.
Края же линии — точки.
Прямая линия есть та, которая равно лежит на всех своих точках.
Ты походу не шутишь, тебе реально в кайф или ты реально не способен? 3 цитаты строго соответствуют понятию "отрезок" во всех смыслах, если тебе это было не очевидно - то у тебя "врёёёти" головного мозга.

Во первых - ты ретард, это уже без сомнений.
Теперь по сути:
Назови мне место в высказывании, где можно это как то понять так, что данные высказывания не будут полностью соответствовать описанию отрезка?
Описанное только что - это, блядь, возможно описание квадрата? Или же обьёма? Может быть тут недостаточно чётко видно, что это отрезок? Го тогда замени везде, где я применил слово отрезок, на эти определение.
Назови мне определение отрезка. В процитированном тобой нет определения отрезка. Отрезок - это?
Опять же - своё словоблудство лучше при себе , "множество" никак не описывает прямую, она не зависима от твоей теории. Полагаю тебе и прямую нужно обьяснить подробно, но ссылки я уже кинул. В конце концов когда меня послали читать про булеаны - я заткнулся и читал. Ты же на основу геометрии говоришь "врёте", пока по буквам не разложишь.
Если ты желаешь использовать математику, то ты должен определять все используемые понятия. Определи "часть".
Сегмент целого, измеримый численно так, что из одинаковых сегментов можно будет сложить подобное, отличающее это в пропорциях, соответствующих численному определению этого сегмента. Говоря проще - когда я беру часть в 1см от отрезка, равному 10ти, я могу из 10ти таких обратно сложить целый отрезок.
Далее и впредь я буду отвечать только ссылками, потому что это уже словоблудство и демагогия.
Неправильно размышляешь.
У тебя каждый отрезок всегда определяется 2 точками. То есть эти две единицы простые не имели смысла до того, пока не произошло разбиение. То есть они тоже +1. Итого было одно -1 и три +1. Один из +1 лежит на окружности и остальные два нет.
Многоугольник для большей понятности стоило бы вписанным сделать, но применяется там такая же логика.
>>354584
Я немного по другому цифры раставлял, единицы - это фиксированные точки, а не углы, это то, от чего не избавится при любом срезе и любом издевательстве над фигурой.
Енивей других методов, кроме как приближения нету с точки зрения геометрии, а потому я хз чем тобой сказанное противоречит всему моему посылу.
Двачую.
Шта?
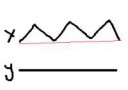
1ый пик: если бы это было не растровое изображение, а векторное, то при огромном приближении (неважно каком, хоть бесконечном) мы бы увидели пикрил, где y/x = 3,14/4.Миша, все хуйня, давай по-новой
2ой пик: о чем речь? о пределах? или тебя удивляет сам факт бесконечного дробления? погугли: "ряд Фибоначчи" и "золотое сечение".
>мы бы увидели пикрил
Не обязательно. На первом пике совершается некий таинственный предельный переход.
hey, do u wanna see some magic? тогда оп разделом ошибся, ему бы в /sn, /sf, /mg - это больше по той части.
Нет, ну почему. В самом предельном переходе ничего непозволенного нет, нужно только объяснить, какой предельный переход имеется в виду.
ну и что не так-то? science - наука, fiction - вымысел. научная выдумка/вымысел, разве не подходит по смыслу?
Нет же. Иначе бы не было приставки science.
Долбоебизм, опять повторю: Твоя картинка - хуета тля ретардов, у тебя не окружность изображена, не дуга даже, а прямая (кривые пиксели проигнорирую).
Знаете ли Вы, что до поражения Германии во Второй Мировой, было два вида математики, - арийская и еврейская, - названные так по национальности своих сторонников?
Арийская Математика брала пример с естественных наук, склонялась к эмпирицизму, конечности и познаваемости мира, и работала исключительно c объектами, которые можно построить физически (например, в памяти ЭВМ или на бумаге).
Еврейская Математика же слоняется к религиозной абстракции и казуистике: всеохватывающей бесконечности, множествам, и порождаемым ими апориям. Так Еврейская Математика постулирует, что можно удвоить объект, путём перекладывания его частей, пространство делимо на "бесконечно малые", а для любого числа, Бог может создать большее число (аксиома о бесконечности).
Основатель Еврейской Математики, Гидеон Кантор, писал, что работает с "Абсолютом - непознаваемым человеком Актус Пьюриссимус, именуемым многими Богом". Примечательно, что Кантор окончил свою жизнь в психиатрической лечебнице, однако дело Кантора поддержали сионистские организации и католическая церковь, доведя до того, что сознательные германские студенты и профессора протестовали, требуя убрать еврейскую заразу из ВУЗов.
После войны, евреи сделали все возможное, чтобы уничтожить Арийскую Математику, удалив ее сторонников и подменив ее Теорией Множеств - центральной опорой Еврейской Математики. Так основатель интуиционизма, Лёйтзен Брауэр, подвергся изоляции, а результаты Русских и Английских финитистов умалчивались и не получили распространения. В русской истории от их рук пострадали математики Егоров (умер в гулаге), Лузин (подвергся травле и был отстранен), Флоренский (расстрелян), Есенин-Вольпин (репрессирован).
Сегодня математика стала еврейской даже по-цвету. Государства поддерживают так называемую "анти-расистскую математику", требующую например использовать еврейские имена в примерах и задачках, рассказывая при этом о великом "вкладе" еврейства в развитие математики.
Евреи, занимающиеся математикой, предпочитают всё специфическое-эльфийское. Причём презирают тех, кто занимается вещами, имеющими практическое применение. Поэтому в Советском Союзе вышел закон, по-которому в ВУЗах должно учиться евреев пропорционально их населению. Лишних отчисляли. Преподаватели евреи на мехмате в знак протеста ушли из университета и образовали НМУ (Независимый Московский Университет). Отсюда и название в мехматянском простонародье ``еврейская секта''.
Еврейские дети в СССР часто учились отдельное от детей гоев, в специальных элитных школах. Одной такой была Московская 57-й спецшкола, ученики которой не без оснований называют себя "пятидесятисемитами". Там часто преподавали выдающиеся преподаватели с мехмата.
В основании математики последнего столетия лежит знаменитая теория множеств Георга Кантора. Если вы откроете большую часть современных серьезных учебников математического и функционального анализа или топологии, или теории вероятности, то в начале почти наверняка увидите экскурс в теорию множеств. Почти вся современная математическая литература написана на теоретико-множественном языке. Камень теории множеств лежит в основании грандиозного здания современной науки.
Но в самом сердце этой самой фундаментальной вроде бы теории, лежащей в основе "царицы наук", почти сразу после ее создания были обнаружены очень серьезные парадоксы и проблемы, не преодоленные до сих пор. Уже сто лет с тех пор математика находится в состоянии перманентного кризиса, который остро воспринимается самыми выдающимися учеными. Великий немецкий математик Герман Вейль писал по этому поводу: "Мы менее чем когда-либо уверены в незыблемости наиболее глубоких оснований логики и математики. Как у всех и всего в мире, сегодня у нас есть свой кризис".
Математика говорит, что у шпекеровой последовательности есть предел? Говорит. Практика говорит, что его нет? Тоже говорит. Математика говорит, что апельсин можно удвоить путём перекладывания его частей? Говорит. Удалось кому-нибудь с новозаветных времён повторить эту процедуру? Наблюдения раз за разом показывают, что при такого рода операциях закон сохранения вещества неукоснительно соблюдается. Математика предсказывает наличие в бесконечномерном гильбертовом пространстве базиса Гамеля. Наблюдать оный пока вообще никому не удалось. Так что математика - именно лженаука, и никак иначе.
Именно уверенность в нематериальности математических объектов влечёт за собой веру в возможность "приближённых" вычислений (что чушь - вычисления бывают либо точные, либо неверные). Да, самолёты летают и при засилье Теории Множеств. Но если бы математика была конструктивной, они летали бы лучше, потому что конструкторы не забивали бы себе голову теоретико-множественным мусором, на практике бесполезным и дезориентирующим.
Аксиомы имеют смысл только тогда, когда они выражают свойства объективно существующих предметов. Так, если мы введём аксиому "на каждой руке человека содержится 3.1415… пальцев" и построим на базе этой аксиомы формальную теорию, то положения этой теории будут бессмысленны и даже вредны.
Сегодня математика стала еврейской даже по-цвету. Государства поддерживают так называемую "анти-расистскую математику", требующую например использовать еврейские имена в примерах и задачках, рассказывая при этом о великом "вкладе" еврейства в развитие математики.
Евреи, занимающиеся математикой, предпочитают всё специфическое-эльфийское. Причём презирают тех, кто занимается вещами, имеющими практическое применение. Поэтому в Советском Союзе вышел закон, по-которому в ВУЗах должно учиться евреев пропорционально их населению. Лишних отчисляли. Преподаватели евреи на мехмате в знак протеста ушли из университета и образовали НМУ (Независимый Московский Университет). Отсюда и название в мехматянском простонародье ``еврейская секта''.
Еврейские дети в СССР часто учились отдельное от детей гоев, в специальных элитных школах. Одной такой была Московская 57-й спецшкола, ученики которой не без оснований называют себя "пятидесятисемитами". Там часто преподавали выдающиеся преподаватели с мехмата.
В основании математики последнего столетия лежит знаменитая теория множеств Георга Кантора. Если вы откроете большую часть современных серьезных учебников математического и функционального анализа или топологии, или теории вероятности, то в начале почти наверняка увидите экскурс в теорию множеств. Почти вся современная математическая литература написана на теоретико-множественном языке. Камень теории множеств лежит в основании грандиозного здания современной науки.
Но в самом сердце этой самой фундаментальной вроде бы теории, лежащей в основе "царицы наук", почти сразу после ее создания были обнаружены очень серьезные парадоксы и проблемы, не преодоленные до сих пор. Уже сто лет с тех пор математика находится в состоянии перманентного кризиса, который остро воспринимается самыми выдающимися учеными. Великий немецкий математик Герман Вейль писал по этому поводу: "Мы менее чем когда-либо уверены в незыблемости наиболее глубоких оснований логики и математики. Как у всех и всего в мире, сегодня у нас есть свой кризис".
Математика говорит, что у шпекеровой последовательности есть предел? Говорит. Практика говорит, что его нет? Тоже говорит. Математика говорит, что апельсин можно удвоить путём перекладывания его частей? Говорит. Удалось кому-нибудь с новозаветных времён повторить эту процедуру? Наблюдения раз за разом показывают, что при такого рода операциях закон сохранения вещества неукоснительно соблюдается. Математика предсказывает наличие в бесконечномерном гильбертовом пространстве базиса Гамеля. Наблюдать оный пока вообще никому не удалось. Так что математика - именно лженаука, и никак иначе.
Именно уверенность в нематериальности математических объектов влечёт за собой веру в возможность "приближённых" вычислений (что чушь - вычисления бывают либо точные, либо неверные). Да, самолёты летают и при засилье Теории Множеств. Но если бы математика была конструктивной, они летали бы лучше, потому что конструкторы не забивали бы себе голову теоретико-множественным мусором, на практике бесполезным и дезориентирующим.
Аксиомы имеют смысл только тогда, когда они выражают свойства объективно существующих предметов. Так, если мы введём аксиому "на каждой руке человека содержится 3.1415… пальцев" и построим на базе этой аксиомы формальную теорию, то положения этой теории будут бессмысленны и даже вредны.
Предположим, что я-физик, и использую математику в своих строго прикладных целях(решаю диф.уравнения, рассчитываю траектории и прочее). Это работает? Да, с любой требуемой точностью. При решении этих задач возникают такие понятия, как бесконечность, дифференциал и прочие плохие вещи. Но я, пользуясь ими, получаю правильный ответ, так в чём проблема? Пока математика позволяет получать результаты-она правильна, даже если кому-то не нравятся исходные предположения. Не нравится-построй математику без них, возможно это что-то даст(как дала геометрия Лобачевского, отказавшаяся от одной из аксиом Евклидовой геометрии), а возможно твоя математика загнётся в противоречии сама с собой.
Смысл в том, что если ты пользуешься такой математикой, в которой есть противоречия и нестыковки с реальностью, так ты и признай мол да, есть противоречия и нестыковки, но я все равно ей пользуюсь - и все никаких вопросов.
Гёдель доказал. Если в кратце - то суть такова. Допустим у тебя есть 0 и 1
2 = 1+1, 3 = 2+1, итд. Это хорошая, годная, непротиворечивая математика. Но она не может ответить на вопрос, хуй ли оп. Тогда ты ее дополняешь новой аксиомой: оп - хуй. Но тогда эта система аксиом не может сказать тебе, хуй ли 356590-кун. Процесс можно продолжать до бесконечности.
Неправильное понимание бесконечности - это в первую очередь логическая ошибка. Логические ошибки ведут к некоректному восприятию мира, и как следствие неправильного моделирования мира. Когда как в физике решённый вопрос об этом очень многое бы обьяснил.
>>356580
>для вычисления длины прямой. из чего видно, что
она не работает даже для прямых
Обьяснять почему ты ебаный или сам поймёшь?
>>356589
Это вполне исправимо.
>>356553
>Знаете ли Вы, что до поражения Германии во Второй Мировой, было два вида математики, - арийская и еврейская
Дальше не читал. Слишком толсто.
Ага, щас. Даже для расчёта свободного падения приходится интегрировать, предложи альтернативу
>>356587
Ну я и признаю, да, есть(наверное, не разбирался особо) противоречия, но это работает, а значит всё норм.
>>356639
Ну так расскажи про правильное восприятие бесконечности, и выведи из этого какие-то результаты. Пока что понятия дифференциала или длины кривой вполне себе используются и не дают расхождений с реальностью
Ну найди мне учебник с формулами для всех возможных задач.
Вот у меня есть физические законы, из которых в общем случае получается система a_i=f_i(r_j, v_j, t), то есть ускорение каждой из n частиц системы в любой момент есть некая известная функция положений всех n частиц системы, их скоростей и времени. В нормальной математике я проектирую это всё на 3 координатных оси и говорю, что всё это-система 3n диф.уравнений 2 порядка с 3n неизвестных функций, после чего решаю всё это аналитическими или приближёнными методами. А ты предлагаешь мне найти чудесный учебник, в котором для каждой возможной такой системы написан готовый ответ, ну что же, человечество научилось решать системы, причём ответы соответствуют реальности, а учебник такой до сих пор не найден.
>в любой момент есть некая известная функция
Функция - это не физический объект. Никаких функций на самом деле не существует. Ты физик? Изучай то, что существует. Небось кроме своих функций ничего не видел никогда. Ты какие в своей жизни опыты ставил вообще?
Лабораторные работы в школе/универе считаются?
Есть зависимость ускорения от координат, скоростей и времени, из этого мне нужно получить зависимость координат от времени, я могу взять математику и посчитать, а могу, как дебил, кинуть всё и орать "Бесконечностей не существует, функций не существует, без эксперимента ничего нельзя сказать!!!". Твои идеи неконструктивны, они не дают результата лучшего, чем тот, что есть сейчас, вывод-они не нужны, иди кому ещё рассказывай про еврейскую математику
Это подмена физики математикой. Когда ты решаешь задачу "камень брошен вертикально вниз с высоты пять метров, найти время падения" - это не физика, это арифметика. Когда ты решаешь задачу "частица двигается в поле" - это тоже не физика. Физикой это было бы, если бы ты брал реальный камень и смотрел как он падает. Брал реальную частицу и смотрел на её поведение. Ты опыты ставишь? Нет, ты пердолишься в абстракции. Это не физика, это чисельный манямирок.
>физика не имеет права ничего считать!
Короче всё ясно, иди хоть спутник запусти в космос без расчётов, на одних наблюдениях и экспериментах.
Ты лично много спутников запустил? Зачем тебе расчёты, если ты не изучаешь природу?
Зачем мне изучать природу, если я не могу на основе этого предсказать результат какого-нибуть эксперимента? Такое чуство, что для тебя физика-журнал экспериментов, а физики только и делают, что ставят опыты без какой-либо цели. Это какая-то другая физика, ею может в древности когда-то занимались, а сейчас я могу посчитать результат плчти любого опыта ещё до того, как он произойдёт
>а сейчас я могу посчитать результат плчти любого опыта ещё до того, как он произойдёт
Это называется схоластика: думать, что опыты для быдла.
>Зачем мне изучать природу
Потому что физика - это изучение природы. Хочешь назвать себя физиком - изучай природу. Не хочешь ставить опыты, хочешь арифметические задачки решать - называй себя решателем арифметических задачек. А врать не надо.
>выдёргивания частей фраз из целого
А это называется демагогия. Если у тебя есть какие-то аргументы против использования математики в физике и других науках-скажи их, а передёргивать мои фразы не нужно.
Хм, действительно, наверное ты прав.
ты не отличаешь модель и реальность. проще говоря не отличаешь то что есть и смысл этого которое есть.
реальности нет. есть только учебник математики, в котором написано, как правильно длину круга вычислять. и если у тебя получается 4r то ты ОП (хуй).
В физике действительно нет понятия "функция", поскольку невозможно определить понятие "цель".
все на самом деле наоборот. сначала люди рисовали круг, потом брали веревочку и обкладывали его.
и кстати если у квадрата отбирать по 4n мелких квадратов получится ромб. тоесть квадрат повернутый на 45. тот же самый квадрат. а круг так не получится.
>>356882
обсновано уже. если ты не видишь что в круг при 4н оно не превратится а превратится в ромб значит ты долбоеб и я апаю твой долбоебский тред.
Ебанат, читающий тред через жопу, можешь уёбывать, ты тут не нужен.
Модель математики соответствует реальности в большинстве положений, лол. Нахуя нужна модель, если она полностью - вымысел?
язык это полностью вымысел. стоит ли отказывать людям в возможности обмениваться смыслами в этом случае?
Язык - это инструмент обмена информацией. Если я скажу "зелёный" - ты сразу поймешь о чем конкретно речь, хотя точного спектра цвета, который я себе представил, ты и не поймёшь. Никакого вымысла в языке нет, есть лишь неточности в понимании и терминологии.
Если ты скажешь "мидори" - поймут анимеблядки и японцы, не более. То же с языком под названием "математика".
Математика не является языком. Нейронаука показала, что в восприятии математических утверждений принимают участие области мозга, ответственные за мышление о количестве и пространственных отношениях. Языковые же области нужны только для восприятия русского или какого-то ещё языка, на котором излагается смысл математического выражения.
Если какое-то быдло не воспринимает математику как язык, то это только проблемы быдла.
Неверно. Как раз быдло воспринимает математику как язык, и не способно понимать сложные выражения. Математики воспринимают математику как отношения количеств и пространств.
>>356924
Нонсенс. Математикой передаётся и обрабатывается информация, если для тебя решающее значенение имеет то место, где информация обрабатывается - то ты ретард.
Нонсенс – утверждать, что математикой что-то передаётся и обрабатывается. В частности – информация. Она может передаваться и обрабатываться как раз-таки мозговыми структурами, если на то пошло. В крайнем случае, можно говорить о существующем в современной цивилизации языке математической нотации. Но утверждать, что математика как корпус математических понятий и фактов есть язык, только потому, что мы имеем закорючки для их записи – столь же нелепо, как называть «языком» все явления материального мира, о которых мы способны говорить.
>называть «языком» все явления материального мира, о которых мы способны говорить
Может быть, это не так уж нелепо.
Мимопроходил.
Нет, как раз таки именно математически ты её выражаешь абсолютно точно так же как языком. У тебя нет врождённого навыка к дифференцированию, так же как ты не сможешь составлять осмысленные предложения зная только буквы. Как именно это обрабатывается мозгом значения не имеет.


> математически ты её выражаешь абсолютно точно так же как языком
Наоборот, языком я точно передаю математический смысл.
> Как именно это обрабатывается мозгом значения не имеет
Имеет, поскольку выбивает всё дерьмо из тех, кто утверждает, что математика – язык.
У меня есть врождённый навык мыслить о количествах и пространстве. Мышление такого рода не зависимо от языковых навыков; гипотетически, даже существо без языка, без букв, слов и самосознания способно понять, почему сумма нечётных количеств начиная с единицы будет всегда равна идеальному квадрату, просто поразмыслив о камешках. Точно так же оно, подобно Гауссу, поймёт, почему сумма количеств чего-то от 1 до n равна (1+n)n/2 этого чего-то – но, в отличие от Гаусса, не выведет формулы. Пикрелейтед. Количества и пространственные отношения существуют, воспринимаются и мыслятся непосредственно, созданные людьми закорючки и абстракции вроде чисел служат только для облегчения этого процесса. Синтаксис математической нотации создан таким, чтобы соответствовать количественному устройству наблюдаемой Вселенной, а не наоборот.
>У меня есть врождённый навык мыслить о количествах и пространстве.
Точно так же, как и другие врождённые навыки, выражающиеся через язык
отличный от математики, ретард.
>Мышление такого рода не зависимо от языковых навыков.
Мышление вообще независимо от языков в любом виде, выбивать дерьмо у себя за щекой можешь. Например восприятие двета никак не связано с мат. или русским языком. Следовательно все обозначения цветов типа "зелёный" - не языковые?
>Точно так же, как и другие врождённые навыки, выражающиеся через язык
Что это за бессмысленное утверждение?
> Например восприятие двета никак не связано с мат. или русским языком. Следовательно все обозначения цветов типа "зелёный" - не языковые?
Цвета имеют объективную природу нейрологического возбуждения, примерно одинаковую у человека и у бессловесной кошки. Предметы имеют объективную природу спектров поглощения и излучения. Эти вещи не являются ни языком, ни словами, ни предложениями, ни буквами, ни чем-либо ещё подобным. Слова типа «зелёный» или наборы слов типа «спектры поглощения и излучения» – это явления языка, который устроен так, чтобы мы могли соотносить некоторые из них своему неязыковому опыту. Таким же образом закорючки, при помощи которых передаются математические смыслы и свойства, существуют в языке. Но сами математические смыслы и свойства существуют и воспринимаются непосредственно, без языка. Чтобы мыслить о математике, нужно уметь мыслить о количествах, но не нужно иметь языка; хотя абстракция в математике практически необходима и неизбежно приводит к появлению языка при работе с более-менее сложными темами, абстракция – это всего лишь инструмент, а начинается математика с единичных камешков, известных, кстати, как calculus.
По данной причине бессмысленно утверждать, что математика – это язык.
>абстракция – это всего лишь инструмент
Так же как и язык.
>а начинается математика с единичных камешков, известных, кстати, как calculus.
> По данной причине бессмысленно утверждать, что математика – это язык.
А начинается язык с восприятия органов чувств, так что называть любой язык языком бессмысленно с такой логикой.
>Что это за бессмысленное утверждение?
Читать научить?
>начинается язык с восприятия органов чувств
Неверно. Восприятие начинается с ощущений органов чувств (ты даун и не знаешь, чем восприятие отличается от ощущения, но опустим). Язык начинается с грамматики. Язык не обязан строго соответствовать никаким ощущениям и восприятиям. Математика начинается с количества и пространства. Математическая нотация начинается с письменности. Подмены понятий тебе не помогут.
>Неверно. Восприятие начинается с ощущений органов чувств (ты даун и не знаешь, чем восприятие отличается от ощущения, но опустим).
Неверно, ты ретард, не знающий значения слов и применяющий их не по смыслу. Обосрался - будь добр исправляй ошибку, а не хуйню неси, даун.
>Язык начинается с грамматики.Язык не обязан строго соответствовать никаким ощущениям и восприятиям.
Эх, щас бы быть долбоёбом и не иметь строгих значений слов...
> Обосрался - будь добр исправляй ошибку
А то что, философствующая маня, ткнёшь меня в статью на википедии? Я прав, ты сосёшь, вот и всё.
Ещё раз для тебя выделю, а то видимо в глаза ебёшся и читаешь наполовину:
>Эх, щас бы быть долбоёбом и не иметь строгих значений слов...
С чего, по твоему, грамматика начинается? С фантазии? С твоих маняпроэкций?
>А то что, философствующая маня, ткнёшь меня в статью на википедии? Я прав, ты сосёшь, вот и всё.
https://ru.wikipedia.org/wiki/Грамматика
5 секунд в гугле, хуесос. 5 секунд, не более.
О, вижу ты нашёл определение грамматики, молодец. Грамматика – это, оказывается, наука. Ну и ну. Я сказал «грамматика», а не «грамматический строй», и теперь ты победил... почти. Дело за малым, маня. Тебе осталось всего-то доказать, что «начинается язык с восприятия органов чувств», а потом доказать, что «математика это язык». Думаю, ещё пара ссылочек решит дело.
> Тебе осталось всего-то доказать, что «начинается язык с восприятия органов чувств», а потом доказать, что «математика это язык».
Обойтись можно и без ссылок, просто мне нужно было указать дегенерату место, понимаешь.
Осмысленные предложения состоят из слов, слова имеют конкретные значения, эти значения слов в конечном итоге либо формулируются через другие предложения, либо через восприятие типа "Это - зелёное". Без ощущений и восприятия зрением слово "зелёный" теряет всякий смысл, поэтому нельзя пользоватся этим словом (и таким образом всеми остальными), не прибегая в первую очередь к восприятию этой информации мозгом, полностью врождённый навык. Тоже самое со счётом, можешь считать мозгом и "камушками", но применяя обозначения это уже будет являтся языком.
Настолько подробно расписал твой обосрамс что даже ребёнок справится.
Да, молодец. Теперь попытайся объяснить, почему твой высер имеет какую-то ценность, кроме как пример скудоумной аналогии. Восприятие очевидно независимо от языка. Коммуникация о восприятии не определяет восприятие ни в какой мере. Коммуникация о количествах и их свойствах, хотя использует те или иные закорючки-обозначения, никак не определяет восприятие и понимание количеств, а именно этот род психической деятельности является математикой.
Ты так туп, что не понимаешь, ни с чем споришь, ни что силишься доказать.
>Скудоумная аналогия
>Высерает антилогичную хуиту и использует слова, не веря в их же значения.
Вот уж лол.
> Коммуникация о количествах и их свойствах, хотя использует те или иные закорючки-обозначения, никак не определяет восприятие и понимание количеств, а именно этот род психической деятельности является математикой.
Коммуникация о цветах и их свойствах, хотя использует те или иные закорючки-обозначения, никак не определяет восприятие и понимание цветов, а именно этот род психической деятельности является частью языка. Сколь тупым надо быть, тебе ещё раз повторить могу, мне не лень.
12:45
Цитирую лол: Можно ли добавить что-то после бесконечности? Конечно же да! Это же математика, а не наука!
Просто проиграл, вся суть. Если коротко, то обьясню тебе суть моего треда - некоторые положения математики противоречат реальности (логике, наблюдениям, и т. д.), поэтому я и мешаю тут с говном людей типа долбоебика выше, то, что ты мне скинул обьясняет теорию множеств на бытовом уровне людям типа меня, теория множеств вообще тут не причём, это костыль, которым они смогли оганиченную (Спойлер: хуёвую) бесконечность сделать похожей на процесс, таким образом чтобы это соотносилось с реальностью и можно было с этим работать. В матеше и геометрии школьного уровня всё ещё не работает эта хуйня и как минимум одна из аксиом в итоге через неправильную интерпритацию порождает хуйню ввиде геометрической фигуры без углов и отрезков, типа имеющих длину.
>некоторые положения математики противоречат реальности (логике, наблюдениям, и т. д.)
Двачую Опа.
Кто тебе сказал, что математика должна соответствовать наблюдениям, ебанат? Математика просто берёт какие-то утверждения и выводит из них другие при помощи логики. Единственное требование к первоначально берущимся утверждениям - они не должны противоречить друг другу.
Сложность вселенной бесконечна. Вполне себе актуально бесконечна. За каждым "потому что" всегда найдётся "а почему оно так?".
А они противоречат. Тред ведь никто не читает, лал.
>>357094
Бесконечность в физическом мире и бесконечность в математике - 2 разные вещи.
Какие именно аксиомы какой аксиоматики противоречат? В треде ни слова про это.
Ну если жопой читать - то да, нету. Уже в 3й раз нету за тред.
Если коротко - аксиома точки, а точнее одно из её свойств конфликтует с определением длины и периметра геометрических фигур.
Ответь на вопрос, пожалуйста.
Существует ли непустое множество I такое, что если x - элемент I, то x∪{x} - элемент I?
Это к чему? Теорию множеств можешь подальше затолкать себе обратно, любое её доказательство основано на определениях геометрии, я с таким же успехом могу доказывать что бог есть потому что так написано в библии, а библия правда потому что это слово божие. Улавливаешь, верун?
Не надо коротко, наркоман. Просто ткни пальцем в конкретный перечень утверждений, перечисленных в учебнике, энциклопедии или неважно где и выбери несколько конкретных утверждений, которые ты считаешь противоречивыми. Вот тебе даже готовый список на выбор:
http://geometry2006.narod.ru/Lecture/Axioms/Axioms.htm
И заодно расскажи мне, где ты нашёл аксиому точки и как конкретно эта аксиома выглядит.
Как и ОП, Зенон уже давным-давно показал математикам какова их математика. Но они все продолжают копротивляться.
>>357189
Ну или если тебе лень сводить какое-то выдуманное тобой противоречие к аксиомам и выяснять, какие именно аксиомы противоречат, определись хотя бы, в какой именно геометрии существует твоё противоречие и дай нам, долбоёбам, хоть намёк на то, как твоё противоречие запишется формально.
>>357196
Прежде чем рассуждать о бесконечности, ответь на самый главный вопрос. Существует ли непустое множество I такое, что если x - элемент I, то x∪{x} - элемент I?
>>357196
Хули ты тут цитируешь, м-м, уёба? Я тебя спросил, в какой конкретно геометрии противоречие, не суй мне свою философообразную шизофазию, просто укажи, какая конкретно система аксиом тебе не понравилась.
Не буду, лол. Если это не относится к теме треда - сразу нахуй. Если тебе же нужны спецы по булеанам - то очевидно это тоже не ко мне.
> философообразную шизофазию
>Логическое противоречие, которое ни 1 петушок не опроверг
>шизофазия
Можешь уёбывать, верун. Не умеешь читать - это не моя проблема.
Как опровергать то, что не было сформулировано? Не говоря уже о том, что бремя доказательства лежит на утверждающем.
Ответь мне лучше как относится к теме треда теория множеств, основанная на алг. и геом.?
Доказать я уже смог, формулировка чёткая. Вполне себе доказательство, просто верунам неыозможно ничего доказать впринципе, включается "врёёёти".
Сначала ты ответь на этот главнейший вопрос. Затем я отвечу на твои.
От тебя требуется только сказать "да, существует" или "нет, не существует". Выбери один из этих двух вариантов. Любое увиливание будет означать, что ты отказываешься от дискуссии.
Во-первых, твоё доказательство и твоя формулировка не являются математическими. Математические формулировки и доказательства сводятся к аксиомам, а ты к ним ничего не сводил. Во-вторых, ты даже не можешь сказать, в каких аксиомах "формулируешь" и "доказываешь". Чтобы объяснить тебе, почему это важно, приведу конкретный пример: в системе аксиом Евклидовой геометрии сводится к аксиомам (то есть, доказывается) такое утверждение: если две прямые параллельны третьей, то и между собой они параллельны. В системе аксиом геометрии Лобачевского (которая отличается от Евклидовой только тем, что Лобачевский одну из аксиом выкинул), такое утверждение не только невозможно вывести из аксиом (читай - доказать), но можно даже и опровергнуть. Поэтому перед тем, как что-нибудь пиздануть, уточни, в какой аксиоматике ты пиздишь.


>Увиливание от ответа
>Не может пояснить причём тут теория множеств.
Может мне за тебя ещё и задачки порешать по матанализу, ретард? А ты тип потом мне обьяснишь зачем я тебе домашку делаю, просто лол.
За щеку мамке за домашку засчитаешь.
>>357208
Для любых двух точек прямой существует такая третья точка на этой прямой, что вторая лежит между первой и третьей.
На каждой прямой имеется бесчисленное множество точек.
Ну и то, что окружность имеет длину очевидно.
Ты всё ещё не ответил, в каких аксиомах все эти утверждения. Если в твоих собственных - пиняй на себя, что они противоречивы. Если в чьих-то ещё - скажи, в чьих именно.
Откопировал и вставил прямо с твоего сайта, что не так?
Евклидова, нет?
Хочешь сказать что в какой-то из геометрии (разновидности, лал) между 2мя точками нет 3ей? Или же окружность длины не имеет? Ты издеваешься?
Ещё раз:
>Хочешь сказать что в какой-то из геометрии (разновидности, лал) между 2мя точками нет 3ей? Или же окружность длины не имеет?
Ещё раз, другими словами: ты приходишь сюда и кукарекаешь о том, что кто-то неправ, не потрудившись уточнить, кто именно и в чём именно неправ.
>Хочешь сказать что в какой-то из геометрии (разновидности, лал) между 2мя точками нет 3ей? Или же окружность длины не имеет?
Евклидовая геометрия и все последующие, основанные на ней.
Ну допустим, самое важное сделано. Остался сущий пустяк: сформулировать утверждение Евклидовой геометрии и вывести его из аксиом, а также вывести из них же отрицание этого утверждения.
Что значит "допустим" верун блядь? Ты либо находишь логическую ошибку или враньё, либо не кукарекаешь, а? Что ты блядь имеешь ввиду под допустим?
>Остался сущий пустяк: сформулировать утверждение Евклидовой геометрии и вывести его из аксиом, а также вывести из них же отрицание этого утверждения.
Сделано, уже кидал выше. Философская шизофазия, как ты выразился. Только не включай "врёти", ок?
Как я уже говорил, тебе надо доказать целых две вещи, а ты не доказал ни одну. Ты просто наметил доказательства общими, тебе только понятными словами - а как свести их к аксиомам, неведомо ни тебе, ни кому-либо другому, потому что ты хуйло.
Опять же. Онли "врёти", ничего более выдавить из себя не способны. Утверждения основаны на существующих аксиомах, сделано все без допущения логических ошибок, новых тезисов я не вводил, противоречие выделено, для тебя видимо капсом нужно: ДОКАЖИ, ДОЛБОЁБ, ЧТО ОКРУЖНОСТЬ ИМЕЕТ ДЛИНУ В ЭТОЙ СИСТЕМЕ АКСИОМ, МУДИЛА.
Уже. В третий. Раз.
Как считать длину окружности в Евклидовой геометрии - хуй его знает. А вот через теорию множеств - пожалуйста, интеграл сосчитать.
Ой, вру. Интеграл для площади, а длину как супремум.
То есть в Евклидовой геометрии длины окружности не существует в природе? Потому что невозможность считать =/= не существует. Я тебе подскажу как считают окружность - делают приближение через другие геом. фигуры, как это выглядит математически не играет никакой роли, суть то в том, что это приближение, и только.
Ну можно приближать через многоугольники сколь угодно точно, но как это делать без теории множеств, для меня лично загадка.
Енивей нужно осозновать что это приближение к реальной окружности, а не к Евклидовой, сформулированной в соответствии с аксиомами геометрии. А потому называть реальную окружность (которой в природе вполне возможно и нет) и геометрическую (как множество равноудалённых от центра точек) одним и тем же - это ошибка.
Не понимаю, о каких таких реальных окружностях ты говоришь. А ещё, интересно было бы знать, как Евклид определял окружность.
>А ещё, интересно было бы знать, как Евклид определял окружность.
потому что не жопой нужно читать, ретард. Выделяю еще раз: (как множество равноудалённых от центра точек). В глаза трахаться зачем?
А реальная окружность - наиболее близкая по форме к определённой по Евклиду, но при этом имеющая реальную длину.
Выдели себе за щеку. Нет никаких множеств в евклидовой геометрии. Хочешь говорить про множества - давай про множества, а не про геометрию.
>Нет никаких окружностей в Евклидовой геометрии. Хочешь говорить об окружностях - обратись к саентологам.
Врёты выключаешь и пиздёж свой проверяешь, безпруфное хуило.
Абажуру припекло.
Кек. Только гринтекст и остается, когда аргументов нет. Копротивление продолжается.
Парадоксы в явном виде, то есть более понятно обьяснить невозможно, люди, подвергающие большему сомнению даже логику нежели свою веру - это обречённые дауны, сорян за новости.
Верующий петушок не удосужился подумать хотя бы немножко и продолжает крепко верить. Иди помолись, долбоёб, в окружности точки у него сходятся\не сходятся, ретард.

Ты даже речь поставить не можешь нормально без хуйни, ммм, сейчас бы быть долбоёбом даже в матане на элементарном уровне не разбиратся и нести хуйню, ммм...
Плз, даун, избавь меня от своего бреда, лучше читать научись, попробуй.
>>Ты даже речь поставить не можешь нормально без хуйни, ммм, сейчас бы быть долбоёбом даже в матане на элементарном уровне не разбиратся и нести хуйню, ммм...
Я так смотрю ты наслаждаешься своей жизнью.

>Этот перевод стрелок дегенерата, как не умеющего писать, так и не умеющего читать.
5тиклассник, плз. В глаза ебаться нехорошо, прекращяй это дело, ретард.
>>прекращяй
Продолжай обоссывать себя, пожалуйста.


> себя, пожалуйста.
>,
>Безграмотное уёбище приёбывается к грамматике
Это деграданство из 5б-класса, щас бы безграммотным уёбищем быть и приёбываться к букве, ммм...
И снова ты, как я вижу, смакуешь собственную жизнь. Пожалуй, перед тем, как читать про сходимость, тебе стоит выучить русский язык.
Будь тут возможность прикрепить аватарку - ты бы явно использовал в качестве своей эту картинку.



>Безграмотное уёбище переключилась на недоедкие попытки задеть за живое... Доебавшись до картинок?
Максимум дебил, я надеюсь ты школу прогулял сегодня видимо, да?
>>надеюсь ты школу прогулял сегодня видимо
Тебя опять отправить учить русский?

>Безграмотное уёбище всё ещё приёбывается к грамматике
>Не способен применять запятые по назначению
Знаешь, у тебя удивительный талант говорить со ртом, полным хуёв. Возможно даже суперспособность.
>сходимость
Сходимость это такой же финт ушами как и все остальное. Современный космонавт на современной ракете летит к Солнцу. Долетит ли он до туда? Нет, но мы будет считать что да - вот так вот.
Сойдется ли сумма бесконечного ряда к конечному числу? Нет, но мы будем считать что да - вот так вот. Бесконечность нельзя исчерпать, на то она и бесконечность, но мы будем считать что можно - ведь нам надо как-то считать, понимаете?
За 537 постов, тезис ОПа о возможности и аналогичности по сути распространения подобного финта ушами на подсчет длины окружности никто так и не опроверг.
Говна тупого кусок, до конца видею досмотри. Там как раз про возможность и перспективы применения бесконечности. Посмотри до конца, пидор тупорылый, будь умней.
И все в этом ITT треде, посмотрите это видео до конца.
Очевидно я досмотрел. Перспективы веры, не более.
мимо
О, очередной вскукарек тупого долбоёба, поднимающего мой тред. Девиз здешних "математиков" -верующие и тупые, лол. Полный дебил, кстати, твой батя, что не пользовался хотя бы носком как гондоном лишь бы такого дауна как ты не было.
Никто не твой тред не поднимает, он тонет в бамплимите, как мой хуй в разработанной пизде твоей мамки
Ты видео то уже снял с доказательствами, петушок? хахахаха: >>352921
Тебя развели как дворовую шлюху на минет за бутылку пива: >>352921
>>352914 >>352914
Лол тупое чмо уже было начал денежки подсчитывать за свое "открытие"
>>352920 : без сомнений, море бабла птушнику! хахахаха
>>352921
>будем следить за мамкиным гением всем саентачем!
Ебать ты опущенец. Ссу тебе в рот горячей струей.
Ахахахахаха тупое уебище
>>352914
>нигде не работаю и не учусь.
>выперли из шараги за тупость.
>не могу в матешу
>пришел посраться с теми кто может
Слишком ты тупой, ну слишком. Аргументы уровня 5б-класса, съеби в школу, долбоёб, раз в логику не умеешь, ок? Сын бляди мне ещё за базар "чётко и дерзко" поясняет тут, просто рофл. Тебе подобные впринципе школу не должны заканчивать, сразу в дворники иди, ущербыш.
Это парадокс, который решили ( и обьяснили) так - береговую линию задали с определённой точностью и все эти длины - это приближения, ведь никто не будет мерить линейкой по сантиметру.
Такая же проблема с окружностью НЕ считается проблемой, окружность НЕ считается заданной с какой то точностью, она считается идеальной с точки зрения своего определения что невозможно и ведёт ко всей этой хуйне с бесконечностями, в том числе и к бесконечности "константы" Пи, которая на самом деле константой быть не может ведь помимо того что точного значения не получат никогда по очевидным причинам, точную окружность не получат тоже никогда по тем же самым блядь причинам. Но верунам норм, они предпочитают не видеть проблему.
PS. Уже кидали этот парадокс, пока что второй раз.
Вы видите копию треда, сохраненную 29 июня 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.