Вы видите копию треда, сохраненную 21 октября 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.



Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
>Чё за когомология, а?
>Это... ну... типа... братки, чё за гомология-когомология, блин, такая? А?
Суть dxdy
А мне вот интересно, сколько людей сидящих тут действительно используют гомологические идеи в своих работах? А, тут одна студентота, зобыл.
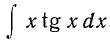
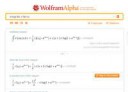
Не берётся в элементарных.
Я не студентота. Хотя и не математик. Использую гомологии на уровне построения трехмерных моделей белковых комплексов на основании структурной гомологии. :3
Да, про них.
Ты не понял! Определив R нам уже не нужно определять Q и N!!! Так что нужно определение R.
x1 = u1cos x3
x2 = u1sin x3
x3 = u2
D' = R^2/ (A union B) ?
анус себе определи, пес
Я знаю. Мы оба молодцы.
очевидно там только заслуженным участникам позволено кривляться подобным образом. Ньюфагу бы дали како-нибудь предупреждение. Нууу типа следи за базаром.
чтобы А расширить и сдвинуть. Допустим из [1500...2000] сделать [100...4000]. Например
1500 => 100.000000
1700 => 1660.000000
1800 => 2440.000000
2000 => 4000.000000
У меня получилась вот такая формула, ai - входное значение из A
(ai - a0) / (an - a0) * (bn - b0) + b0
(ai - a0) / (an - a0) - находим где на первом отрезке находится значение ai, (0.5 - посередине и тд), потом умножаем на (bn - b0) чтобы спроецировать на второй отрезок и прибавляем сдвиг b0.
Тащемта тривиально и работает верно, но все так интересно - можно ли поэлегантнее, в меньше действий?
>Подробностей не знаю пока.
>2007
>At a 1935 conference in Moscow, Andrey Kolmogorov and Alexander both introduced cohomology and tried to construct a cohomology product structure.
Как известно, (см., например Арнольд И. В. Теоретическая арифметика), для операций сложения и умножения определены обратные однозначные операции – вычитания и деления. Эти четыре операции хорошо согласуются с этим определением. Но попытки определить операцию извлечения корня, как обратную к возвышению в степень оказались неудачными. Одна из причин этого, конечно, неоднозначность. Но более серьезной причиной является то, что результат извлечения корня – это уже не число рационального множества, т. е., это уже не количество. Следовательно, операции, обратной возвышению в степень в области рациональных чисел, не существует. Введение понятия арифметического значения корня не сняло этой проблемы, а толкнуло математику на ошибочный путь. В результате введения этого понятия мы потеряли неупорядоченное множество иррациональных чисел, получив его урезанную и упорядоченную часть. Ее мы перемешали с рациональными числами и эту кашу назвали множеством действительных чисел. Дальше пошло развитие этого пути. Все ошибки мне не описать – не по силам. Это работа для всех математиков. Эти и последующие выводы я сделал по результатам обсуждения Форумом моих тем «По определению».
Niet
>В Пифагорейском определении числа «Вещи суть числа» присутствует и количество и качество.
>подразумевается, что ебанутая секта веганов-мистиков в пьяном оргическом угаре выдумала истинное определение
>дальнейшее рассуждение, подразумевающее, что математика нужна не для открытия новых фактов, а для соответствия каким-то математическим канонам, настоящей математики "которую мы потеряли".
можно просто уравнение прямой составить, проходящую через точки (a0, b0) и (an, bn)
Ха, действительно (bn - b0)/(an - a0) это же m, уравнение прямой и есть, хотя я думал про пропорции и смещения и грубо говоря его и вывел и даже не заметил, ох.
Ух ебать, я понял теорему ньютона лейбница. Вчера сижу, и меня осенило, будто сам гаусс вылез и могилы и дал мне в лоб.
Интеграл это ведь бесконечное количество сумм производных. И если эту сумму взять в производных то должна получатся подинтегральная функция.

Анон, помоги разобраться, почему семейство множеств вида [a;+inf) не образует топологию на R. Пикрил говорит привести пример, но на ум ничего не приходит.
Возьми лучи Пусть An = [1/n; inf) для n = 1, 2, .... Тогда объединение An по всем n равно (0; inf).
Спасибо.
Прочёл комменты под видое, какие же люди тупые.
чего бля.
>Я приводил пример в своей статье, за которую меня несправедливо забанили:
>Обсуждение действий модераторов вне специально предназначенных для этого разделов запрещено. Linkey - месячный бан.
Топ КЕК!
http://dxdy.ru/topic82487.html
второе сообщение. пиздос, сразу в бан лол.
это просто охуеть порядки. каким нужно быть рабом чтобы такую хуйню терпеть и строем ходить.
Нихуя себе! Обнаружен тред без мунина?! Надо куда-то сообщить, разобраться в чем дело
дитсадовиц не палица

Почему нет таких тредов по физике, химии? Куча тредов "посоветуйте книжек по физике с нуля, Я НИЧЕГО НЕ ЗНАЮ", но нет такого полного списка, как в оп-посте. Чё за хуйня, это /math на самом деле?
Лучше ответь: почему у меня не получается залить тред на архивач?
нет, хуево
Ебаш алгебру Шеня, её все котируют, как заебашишь, приходи - будем советовать тебе всем саентачом.
Так ты веришь в то что нет никаких gotchas которые так сказать из уста в усту передаются при личном общении учеников с ромой? Все можно самостоятельно?
Зачем Шеня? Я девять классов закончил уже и знаю нормально. на пять гиа на 100% сдал.
Содержание почитал, говно какое-то. Может повыше что-нибудь? Я же с ума сойду такие очевидные вещи читать.

Мат. анализ 58ой школы и Винберга попробуй.
>>369460
Мне кажется ситуация такая: (правильная) тусовка может мотивировать тебя что-то делать, и долгий разговор 1 на 1 с шарящим человеком о непонятных моментах может тебе очень многое прояснить и правильно поставить интуицию. Но основная работа по получению математического бэкграунда (как и любых знаний и навыков вообще) на 97% проводится самостоятельно, поэтому человек с сильным характером способен выучить всё сам на очень высоком уровне. В истории бывали такие случаи, Гельфанд, например.
С материалами для самообучения в сети проблемы нет конечно. Не знаю, бывает ли у вас такое, аноны, но очень часто я делаю какое-то наблюдение/вывод, или вижу каую-то логическую связь о которой не упоминается. И я начинаю гуглить до посинения через наводящие фразы, но явного подтверждения не нахожу. Только вижу что косвенно подразумевается и объясняние опускается, или смотрится с другого угла. И это очень некомфортное чувство - даже практически получив ответ, продолжаешь ао инерции продолжать искать ответ. Так можно зациклиться. А было бы у кого спросить - 5 мин разговора, это как часы или дни гугления.
Читай статейки кванта и сборники летних конференции турнира городов - это охуенно, мне кажется. Если хочешь чего-то более системного - то листочки Каледина, матан в 58 школе, Вавилов, Винберг.
>А было бы у кого спросить - 5 мин разговора, это как часы или дни гугления.
Это иллюзия, мне кажется. Если вопрос поставлен очень точно, то да - но в таком случае его можно и на stackexchange задать, а если вопрос очень размытый и интуитивный, то отвечающий его зачастую поймёт не так, как ты бы хотел, чтобы он понял, и ответ его тоже тебя не удовлетворит. Картина мира выстраиваиться самостоятельным мучительным поиском подобных ответов. А что за вопросы, кстати, мне аж интересно?
Хм. Как площадь параллелограмма? Синус угла между векторами на длину одного - проекция этого вектора на ось Y, или, высота. Ну и высота на другой - площадь. Знак у площади из-за знака синуса. Как ещё? Как найти такую площадь в 2д в координатах я знаю, с применением тождества синуса разности углов. Ну, я думал, что изначально требовалось найти такую площадь, только в 3д. Вот здесь я хз.
Ну это псевдоскалярное произведение, а не векторное. Векторное произведение двух векторов должно возвращать ковектор. Ну окей, что-нибудь про определители и антисимметрические формы слышал? Иль школьник?
Много всего возникает, но быстро забывается. В основном какие-то абстрактные вещи про векторные пространства, иногда хочется чтобы интуиции отсыпал, например про сопряженные пространства и тп, дуализм операций, тензоры, ковектора и тд и тп. Потом постоянно вопросы возникают про связь между разными науками, типа физическая интерпретация мат аппарата, всяких распределений, или использования комплексных чисел/кватернионов, связь между всякими красивыми формулами, графиками, использование векторных пространств или различных распределений в статистике, что имеет смысл, а что полное наебалово. Целостность восприятия достигается медленно и мучительно, и многие веще просто забываются причем довольно быстро, если их не используешь.
>В основном какие-то абстрактные вещи про векторные пространства, иногда хочется чтобы интуиции отсыпал, например про сопряженные пространства и тп, дуализм операций, тензоры, ковектора и тд и тп.
Как-то ты странно гуглишь:
http://math.stackexchange.com/questions/3749/why-do-we-care-about-dual-spaces
https://www.youtube.com/watch?v=mbv3T15nWq0
https://www.google.com.ua/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-
8#q=dual+spaces+pdf
От себя посоветую Вавилова:
https://youtu.be/85H7hamHyi8?t=1h12m49s
он няша ^^
>Целостность восприятия достигается медленно и мучительно, и многие веще просто забываются причем довольно быстро, если их не используешь.
Это да. Я для себя пользуюсь очень компактными конспектами, в которых формулировки основных концепций, теорем и конструкций записываю. Потом иногда их просматриваю, и пытаюсь наметить план доказательства по всем теоремам. Если не получается - подсматриваю в учебники.
Потому что там не нормальные курсы, а шпаргалки по вычислительным процедурам для студентов технических ВУЗов.
Про определители матриц? Я не школьник, но это всё сам пытался изучать, не систематически. Знаю, как определитель найти одним способом только. А про
>антисимметрические формы
Впервые слышу.
Спасибо за сцыли. Я читал много похоже, и так то проблем нет, но иногда бывают какие-то mental hurdles ВНЕЗАПНЫЕ, не знаю как это объяснить, рвется логическая цепочка, типа почему это так, откуда это и тп. Еще мне припекает, что про ВП язык статей совершенно разный, разный подход, разный уровень деталей и даже нотация различается. Возьми 10 pdfов по тензорам, и все они будут как-будто про разные вещи.
Современный вывод формулы псевдоскалярного произведения таков: обозначим пару векторов за a, b, а под F(a,b) будем обозначать как раз знаковую площадь параллелограмма, натянутого на a,b.
Вполне очевидно, что F удовлеторвяет следующим свойствам:
F(pa+qb,c) = pF(a,c) + qF(b,c) (полилинейность)
F(a,b) = - F(b,a) (антисимметричность)
Пусть i,j,k - базисные вектора в R^3, тогда
F(i,j)=F(i,k)=F(j,k)=1 (нормированность)
попробуй из этих свойств, путём разложения
a = a1 i + a2 j + a3 k
b = b1 i + b2 j + b3 k
найти координатную формулу для F(a,b).
>Еще мне припекает, что про ВП язык статей совершенно разный, разный подход, разный уровень деталей и даже нотация различается.
Мне кажется это наоборот плюс, почитаешь 10 таких статей и адекватная картина более-менее появляется. Хуже было бы, если бы все копировали друг у друга и рассказывали по шаблону (что наглядно демонстрирует большинство курсов на большинстве матфаков страны, sic!).
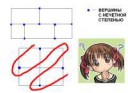
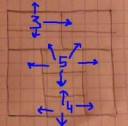
В графе G = (V, E) существует эйлеров путь тогда и только тогда, когда:
1. Количество вершин с нечетной степенью меньше или равно двум.
2. Все компоненты связности кроме, может быть одной, не содержат ребер.
Но линия, которую мы ведем не обязана по условию быть путем, то есть идти по ребрам. Она может "перепрыгивать" при необходимости. Соответственно теорема неприменима к этой задаче.
В качестве примера привожу более простой граф на ОП-пике снизус четырьмя вершинами нечетной степени (4>2, Эйлеров путь отсутствует), который преспокойно пересекается сплошной линией.
Если я прав, то реквестирую у математиков ПРИМЕНИМЫЙ способ проверки решаемости задачи.
Кстати, ещё нужно добавить условие на то, чтобы путь не проходил через стыки стен, то есть был, в некотором смысле, невырожденым, иначе столь простого доказательства не выйдет.
Вот например нашел свой аккаунт на physicsforums. так по существу никто и не ответил
https://www.physicsforums.com/threads/how-to-compare-two-huge-numbers-with-nested-exponentials.867615/#post-5447093
Это почему же? Графы на рисунке представлены самые натуральные. Какой смысл что-то в них представлять?
Странный вопрос, потому что одно представление даёт решение задачи, а другое представление - его не даёт, как ты сам и подметил в своём посте.
Я хочу сказать, если теорема Эйлера применима для решения задач такого типа, то она должна работать с любыми графами без всяких преобразований.
Давай представим всю верхнюю фигуру в виде одной точки - вуаля, все работает. Без всяких преобразований должно работать. Или если они есть, то должны ыть эквивалентными. Твое преобразование я никак не могу эквивалентным назвать. Граф получается другой.
Про нормированность и антисимметричность понятно, а вот полилинейность - нет. Что такое с? И как с разложением получится F(a1i+a2j+a3k, b1i+b2j+b3k)?
Я не понимаю, что ты вкладываешь в слово "преобразование".
У тебя на рисунке: палочки и точечки - это ещё не граф. Графом он будет, когда мы каждую точечку объявим вершиной, а каждую палочку, ребром, но конкретно для этой задачи такое объявление неестественно, а естественно другое: каждую дырку (+ внешность) объявить вершиной, а каждую перегородку между дыракми - ребром. Это будет работать и для верхнего и для нижнего графа и вообще для любого планарного, по модулю тех замечаний, что я сказал.
Я понял, что ты имеешь ввиду. Перегородка между дырками - это общая сторона этих дырок, так? "Внешность" - это просто отдельная вершина вне фигуры?
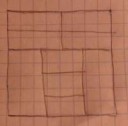
Для закрепления материала и чтобы удостовериться, что я правильно понял идею - пикрелейтед можно пересечь или нет?
У левой верхней комнаты степень 4, во внешность можно выйти через стенку слева.
11 получается, если из комнат вести ребра к внешности по две на каждую сторону... Непонятно. Если комната - это вершина, почему из нее во внешность выходит два ребра
Кратные рёбра будут.
Грубо говоря какая цель: каждой стенке сопоставить ребро в графе и каждой нарисованной тобою кривой сопоставить путь в графе таким образом, чтобы если твоя кривая пересекала стенку, то она проходила по ребру в этом пути. Но если у тебя нету ребра под стенку то как ты сможешь различить ситуации, когда твоя кривая её пересекла, а когда нет?
Все понял, очень толково объяснняешь, анон. Благодарю за терпение и время.
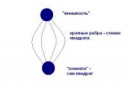
А, все вопрос исчерпан. То есть, скажем фигура "квадрат" преобразуется для решения задачи в пикрелейтед, так?
Np.
Если я правильно понимаю, то когда мы в N-мерном пространстве создадим M точек (при M <= N), мы сможем выделить в нем ровно одно (M-1)-мерное пространство.
Ну, то есть, две точки в 2+ измерениях - линия.
три точки в 3+ измерениях - плоскость.
По логике это должно работать в любом количестве измерений, да?
Но у меня что-то мозг ломается когда я пытаюсь понять, как 4 точки описывают трехмерное пространство. Мне кажется что я почти понимаю, как это работает, но что-то ускользает. Может кто-нибудь это обяснить на своих трехмерных пальцах?
>то когда мы в N-мерном пространстве создадим M точек (при M <= N), мы сможем выделить в нем ровно одно (M-1)-мерное пространство.
Только при условии афинной независимости этих M точек.
>По логике это должно работать в любом количестве измерений, да?
Да.
>Но у меня что-то мозг ломается когда я пытаюсь понять, как 4 точки описывают трехмерное пространство. Мне кажется что я почти понимаю, как это работает, но что-то ускользает. Может кто-нибудь это обяснить на своих трехмерных пальцах?
Большинство математиков мыслят аналогиями и метафорами, а работают с концепциями формально, мне кажется. Вот ты же действуя по аналогии сказал совершенно правильное утверждение:
В любом n мерном афинном пространстве, в котором зафиксирован набор из k афинно независимых точек существует ровно одно (k-1)-мерное афинное подпространство, содержащее эти точки.
А представить "настоящую четырёхмерность" никто особо не пытается.
Я больше пытался понять, как это работает.
Но кажется доперло.
В 3Д через две точки мы строим линию, а потом, перпендикулярно этой линии мы строим вторую, которая пересекает третью точку. Там где есть две перпендикулярные линии, мы можем строить двумерную систему координат.
так же и в 4Д мы строим через три точки плоскость, а потому строим вторую плоскость, перпендикулярную первой, которая проходит через четвертую точку?
В 5Д мы строим перпендикулярные 3Д, и так далее.
Вроде так, да?
Сложно сказать. Мы берём т.н. аффинную оболочку этих точек:
https://en.wikipedia.org/wiki/Affine_space#Affine_span_and_bases
её можно определить как множество всех афинных комбинаций или как пересечение всех афинных подпространств, содержащих эти точки.
Может тебе интересно будет изучить азы линейной алгебры? Простая наука же, школьники осиливают.
Смотрю его лекции по алгебрам Клиффорда и алгебрам Хопфа. Пока в нём не разочарован.
У него в основном спецкурсы по разным разделам алгебры. По общему курсу высшей алгебры тоже что-то есть, но там совсем начала тип линейной алгебры для перваков.
>Помните в тории вероятность есть какой-то парадокс про выбор двери?
Какой же это, в пизду, парадокс, уебище ты лесное. Это не парадокс, а просто красивая презентация того, насколько люди хуево умеют оценивать вероятности на глаз.
мы тут еще тервер не проходили. Мы тут не можем никак определить N
А википедия говорит что парадокс. Давайте решать задачу с коровами. Я чувствую что мы сможем её решить в отличи от тех британцев.
Не парадокс.
Начал читать Рудина. Самое начало. И вот допустим теорема, что всякое бесконечное подмножество B счётного множества A, так же счётно. Доказательство автора я нихуя не понял. Придумал своё: Пусть f:N => A биекция; т.к. каждый элемент из B принадлежит А и каждый элемент из А имеет прообраз в N, тогда каждый элемент из B имеет прообраз в N. Обозначим прообраз B при отображении f: N => A как N' и зададим функцию g: N => N' которая каждому n из N ставит в соответствие такое n' из N', что кол-во чисел, меньших n', равно (n-1); Тогда h = f*g задаёт биекцию из N в B, тогда B счётно.
Можно ли было так доказать? И что вы делаете, если док-во автора вам неясно или кажется, что он слишком налегал на ОЧЕВИДНО?
Открыл сейчас Рудина, хз мне все понятно.

> И. М. Гельфанд, А. Шень: “Алгебра”
Можно тупой вопрос по нему ? Почему "только единица может появиться
при переносе из разряда сотен в разряд тысяч" ? (4. Сложение столбиком)
А чего тут вообще доказывать? Очевидно же, что каждое подмножество счетного множества не более чем счетно. Если это подмножество еще и бесконечно, то только счетность и остается.
Потому, что при сложении двух чисел, каждое из которых меньше 1000, больше единицы в разряде тысячных быть не может. 999+999=1998.

Появилась пара вопросов. Зачем "домножать" вторую формулу на выражение в красном квадрате? И без него получается тождественное преобразование X.
И то что подчёркнуто это же опечатки, верно?
Там знак равенства пропущен.


Вот начало проебал
Пока вы тут Мудина хуесосили на dxdy переводят новое издание Рудина.
И поясните, какое лучше, то что с dxdy или старое.
Читай на английском. На дхду одни хуесосы, даже если переведут адекватно, то все-равно не стоит их услугами пользоваться, из принципа. Потому что мужику с петухами якшаться - западло.
Я не понимаю, зачем люди пишут новые учебники, тем более по матану. Бурбаки изложили общую математику раз навсегда, с максимальной общностью. Проблема закрыта.
я кстати серьезно не понимаю зачем пишут новую музыку например. все уже сыграно, мы же слышали только 0.1% может быть. книжки художественные не читаю, но вероятно с ними тоже самое.
Я не понимаю, зачем люди пишут сообщения на дваче, тем более в треде по матану. В прошлых тредах уже всё было сказано. Больше сообщений не надо.
Что вдруг? Все вузы учат по шаблону. Учебник матана состоит из главы про множества и R, главы про топологию, главы про непрерывность, главы про производную и главы про интеграл. Отклонений от этого шаблона в обозримом будущем не случится. Наши деды учились по этому шаблону, и наши внуки будут по нему учиться.
Открываю учебник Бурбаки. Вижу божественное изложение.
Открываю учебник Зорича. Вижу хрень какую-то.
>Бурбаки.
>Учить анализ по учебнику, в котором не упоминается про когомологии де-Рама.
Bwahahaha, oh you!
>С каких пор мат-тред по воровским понятиям живёт? Да и зачем на английском, когда можно на русском?
Всегда было. Это же двач, тут все по понятиям. А английскую литературу читать надо потому, что все самые авторитетные специалисты отнюдь не русскоязычны, а переводы либо очень древние, либо НЕТ ПУТИ.
Потому что математика преобразуется. Я считаю, что в Рудине надо оставить только то, что принципиально не решается с помощью компьютера.
>>836880
Платина. Так что обоссыте, только не бейте и подскажите великовозрастному лбу.
Выработал такой порядок чтения:
1. Сканави, Шень, Терешин -> Гельфанд
2. Констрикин и Виленкин (Комбинаторика) и, возможно, Зельдович.
Этого хватит для спокойного понимания учебников по физике Савельева и Сивухина?
Что скажете за книгу Пенроуз - Путь к реальности?
Что вообще такое линейная алгебра? Используется ли в физике? Что стоит добавить к моему скромному списку?
Пенроуз там в вольной форме обозревает всю математику, использующуюся в физике. Хорошо показаны проблемы современной физики. Обоссывает струнщиков.




Кому ты пиздишь, сучечка? Они уже в десятой главе книги "Алгебра" вводятся.
>Выработал такой порядок чтения:
Не строй планов на всю жизнь, начни - а там как пойдёт.
>Что вообще такое линейная алгебра?
Наука о линейных конструкциях, системах и законах, то есть о таких, что F(a+b)=F(a)+F(b). Пример линейного закона: если любую из сторон прямоугольного параллелепипеда увеличить в n раз (но не все сразу!) то его объём тоже увеличится в n раз. Пример нелинейного закона : если увеличить ускорение в n раз, то время, за которое мы пройдём участок пути в 1 метр, начав с нулевой скоростью и заданным ускорением сократится примерно в n^2 раз.
>Используется ли в физике?
Используется абсолютно везде, линейные эффекты/законы/структуры являются самыми простыми и очень хорошо изученными (линейной алгеброй же и изученные), поэтому более сложные законы очень часто приближают "линейной версией".
>Что стоит добавить к моему скромному списку?
Убрать школьные учебники, говно ведь.
Во-первых 10ый том - это уже не совсем Бурбаки, а во-вторых - это не учебник по анализу.
Детально пояснил, спасибо. Назревают тогда вопросы: если выбросить школьные учебники, то какие и в каком порядке вписать?
Оставить тригонометрию, комбинаторику, добавить книгу по линалукакую, подскажешь?. Зельдович как начало пути в матанализе пойдёт?
На самом деле я не очень знаю что нужно физикам, но предполагаю, что Шеня(по алгебре и геометрии)+Гельфанда (по тригонометрии) хватит с головой - только не нужно их решать с начала до конца, а то умереть можно, по диагонали профигач - и нормас. Комбинаторика для физики почти не нужна.
Если ты воннаби и совсем не учился математике раньше, то я тебе могу дать пару советов (самостоятельно я до них доходил очень долго):
1) Отказаться от идеи прорешивать все упражнения из данной книжки.
2) Отказаться от идеи прочитывать каждую встреченную книжку от корки до корки.
2.1) Прочитать 4-5 книжек на 30-40% >> прочитать одну книжку на 100%
3) Отказаться от идеи абсолютно последовательного изучения - идеальной базы не будет никогда, а если ты прочитаешь/просмотрешь курс о когомологиях ещё до изучения алгебры и выхватишь оттуда какую-то интуицию - тебе это не повредит. Поэтому если тебе интересна физика - начинай уже сейчас, непонятное можешь пропускать или пытаться узнавать "на лету".
4) В интернете есть дохуя годного образовательного контента. Непонятно доказательство теоремы косинуса в учебнике? Пишешь: "cosine law proof pdf", "cosine law intuition", "cosine law in real world"l ... Это же относится к абсолютно любому вопросу/теореме/концепту ...
Касательно учебников по матану и линалу для начинающих - не знаю, не просматривал, могу назвать только те, которые все хвалят.
Сам прочитал и прорешал Зорича и Винберга и почти полностью решил листок отсюда http://verbit.ru/MATH/Teaching/Ginzburg-listok-1986.pdf этого хватило с головой.
Заскринил твой пост, действительно, спасибо. Ценнейший опыт, я внемлю ему.
Математика, как и на любой ИТ-специальности, была, и я даже шарил, пятерочки итд. Хотя именно понимания и хоть какого-нибудь абстрактного мышления в те времена не было. После первого семестра забил и окунулся в кодинг. Кстати, кодинг помог выработать мышление а-ля выхватить и выделить главное и строить абстракции в голове или с помощью бумажки и карандаша.
Физика же всегда была моим хобби, вот и приспичило быть не только Java-обезьяной, но и уже по серьезному заняться физикой. И, к своему "удивлению", было обнаружено, что физика работает с абстрактными моделями, поведение которых описывается внезапноматематикой.
Тогда план таков: иду по основам + открываю книгу Савельева по физике, и если сталкиваюсь с чем-то, понятие чего я забыл или никогда и не понимал, то открываю уже учебник по матану на соответствующем разделе. Собственно, и самому матану ради матана уделяю какое-то количество времени в день.
>Тогда план таков: иду по основам + открываю книгу Савельева по физике, и если сталкиваюсь с чем-то, понятие чего я забыл или никогда и не понимал, то открываю уже учебник по матану на соответствующем разделе. Собственно, и самому матану ради матана уделяю какое-то количество времени в день.
Да, мне кажется неплохая стратегия.
Тогда это очень плохой, абстрактный учебник, в котором слишком много теории и мизер упражнений.




>мизер упражнений
Это неправда. Например, после главы с де Рамом идут восемь страниц упражнений. Гораздо больше, чем во всяких там Зоричах с Винбергами.
>Убрать школьные учебники, говно ведь.
Ну да, тебе с дивана, конечно же, виднее, чем докторам наук из минобра.

>докторам наук
докторам педагогических, напомню, наук. Типа Белошистой, которая написала пикрелейтед.
Фи, говно без души.
А с какой книги начинать читать? И где можно сказать "Бурбаки на русском без регистрации и смс" ?
Во-первых, не только педагогических. Во-вторых, даже в этом нет ничего плохого. Вся учебная программа составляется в соответствии с требованиями в нематематических вузах. Для будущих математиков существуют отдельные подготовительные программы.
>Во-вторых, даже в этом нет ничего плохого. Вся учебная программа составляется в соответствии с требованиями в нематематических вузах.
И имеем общество тупых мразей, за исключением тех людей, которые учились не по программе (кружки, родители, частные школы, школы для одарённых и т.д.).
И где оказался?
Да кому ты пиздишь бля. Тебе экспоненциально-логарифмические неравенства (10 класс) сколько раз попадались ИРЛ? А универсальная тригонометрическая замена? Всем вменяемым людям ясно - что это ненужный информационный шум, нужный только для того, чтобы сдать ЕГЭ и забыть это навсегда.

С первой, "Теория множеств". Собрание всех книг Бурбаки есть на рутрекере. Потом следует читать алгебру, общую топологию, функцию одного вещественного переменного, топологические векторные пространства и, наконец, интегрирование. Десятую главу Алгебры, а также группы и алгебры Ли, коммутативную алгебру, спектральную теорию и всё остальное лучше читать в самом конце. Дифференцируемые и аналитические многообразия следует читать параллельно с Интегрированием.
Если ты ни разу в жизни не слышал слова "эпсилон-оператор Гильберта", то перед чтением бурбаков тебе необходимо прочитать пикрелейтед, в противном случае ты рискуешь не понять первый том.
>>369936
Поясни.
Спасибо за развёрнутый ответ, анон.
Чет ты порвался, видимо.
>экспоненциально-логарифмические неравенства
Постоянно с ними работаю. В математические модели биологических и химических процессов на подобном основаны. С тригонометрией, подозреваю, что-то подобное же.
>Поясни.
Да мы говорили с тобой уже, вряд ли к чему-то другому придём:
Для программы по полной формализации математики - есть на гораздо более высоком уровне строгости и концептуальности выполненные программы, вроде того же metamath proof explorer.
Для учебника по полуаксиоматической ТМ - слишком формализованный и громоздкий подход (ебля со знакосочетаниями не нужна), устаревший необщепринятый подход (эпсилон-оператор Гильберта - вместо ZFC и теорий первого порядка), нету выхода на категорные конструкции (к чему и должен готовить учебник по ТМ).
Для учебника по аксиоматической ТМ - слишком формализованный и грмоздкий подход, нет современных результатов, методов и инсайтов - форсинг, большие кардиналы, принцип отражения, etc.
В итоге - ни рыба, ни мясо, а раздуто на дохуя страниц.

>ебля со знакосочетаниями не нужна
Рассуждения о знакосочетаниях тривиально решают проблему неформализуемости пикрелейтед (Букур-Деляну), и прочие метафизические проблемы. Строка символов есть - проблемы нет.
>эпсилон-оператор Гильберта
Эпсилон-оператор удобен и няшен, и за ним будущее. Не существует причин, по которым следует отказываться от няшненького эпсилон-оператора в пользу унылой спискоты ZFC, если твоя цель - заниматься математикой. Гораздо проще быстро обдумать эпсилон-оператор, чем долго-долго ебаться с аксиомой регулярности, схемой преобразования и прочим ZFC-шным мусором, который для интегрирования мер не нужен ни разу. Большие кардиналы - это логическая (или даже философская) проблема, безусловно интересная, но ненужная в учебнике общей математики.
>теорий первого порядка
Понятие формальной теории в книге Бурбаки вводится, причём довольно удачно. Сначала вводятся формальные теории вообще, затем они расширяются до логических теорий, далее до кванторных теорий, и наконец до эгалитарных теорий (то есть с равенством). И это хорошо, потому что в типичных книгах по теории множеств про разницу между теорией с равенством и теорией без равенства обычно вообще ничего не говорят, даже аксиомы для равенства не рассматривают. Ещё Бурбаки рассказывает об эквивалентности теорий и изучает несколько случаев, в которых рассуждения, сделанные в одной теории, остаются корректными в другой.
>нету выхода на категорные конструкции
Что ты под этим понимаешь?
>Для учебника по аксиоматической ТМ
Ты не улавливаешь сути "Теории множеств", похоже. Первая книга Бурбаки подобна справочным материалам по теории множеств, которые автор любого современного учебника считает своим долгом поместить в начале своей книги. Просто это ultimate-справка, в которой неясностей вообще не остаётся. Эта книга нужна, чтобы доказать все утверждения, которые будут использоваться в последующих книгах, а вовсе не для того, чтобы обозреть всяческие форсинги. Трактат ведь написан не о множествах. Он об алгебре, топологии, дифференцировании и интегрировании. Сочинение Бурбаки предназначено для того, чтобы заменить собою плохие учебники по этим вещам, которых ещё сто лет назад было дофига, а в наши дни так и вообще необозримое количество. Первая книга трактата нужна лишь для обоснования языка последующих книг.

>ебля со знакосочетаниями не нужна
Рассуждения о знакосочетаниях тривиально решают проблему неформализуемости пикрелейтед (Букур-Деляну), и прочие метафизические проблемы. Строка символов есть - проблемы нет.
>эпсилон-оператор Гильберта
Эпсилон-оператор удобен и няшен, и за ним будущее. Не существует причин, по которым следует отказываться от няшненького эпсилон-оператора в пользу унылой спискоты ZFC, если твоя цель - заниматься математикой. Гораздо проще быстро обдумать эпсилон-оператор, чем долго-долго ебаться с аксиомой регулярности, схемой преобразования и прочим ZFC-шным мусором, который для интегрирования мер не нужен ни разу. Большие кардиналы - это логическая (или даже философская) проблема, безусловно интересная, но ненужная в учебнике общей математики.
>теорий первого порядка
Понятие формальной теории в книге Бурбаки вводится, причём довольно удачно. Сначала вводятся формальные теории вообще, затем они расширяются до логических теорий, далее до кванторных теорий, и наконец до эгалитарных теорий (то есть с равенством). И это хорошо, потому что в типичных книгах по теории множеств про разницу между теорией с равенством и теорией без равенства обычно вообще ничего не говорят, даже аксиомы для равенства не рассматривают. Ещё Бурбаки рассказывает об эквивалентности теорий и изучает несколько случаев, в которых рассуждения, сделанные в одной теории, остаются корректными в другой.
>нету выхода на категорные конструкции
Что ты под этим понимаешь?
>Для учебника по аксиоматической ТМ
Ты не улавливаешь сути "Теории множеств", похоже. Первая книга Бурбаки подобна справочным материалам по теории множеств, которые автор любого современного учебника считает своим долгом поместить в начале своей книги. Просто это ultimate-справка, в которой неясностей вообще не остаётся. Эта книга нужна, чтобы доказать все утверждения, которые будут использоваться в последующих книгах, а вовсе не для того, чтобы обозреть всяческие форсинги. Трактат ведь написан не о множествах. Он об алгебре, топологии, дифференцировании и интегрировании. Сочинение Бурбаки предназначено для того, чтобы заменить собою плохие учебники по этим вещам, которых ещё сто лет назад было дофига, а в наши дни так и вообще необозримое количество. Первая книга трактата нужна лишь для обоснования языка последующих книг.
Бурбаки собрали ещё одного фрага.
Не обращай на него внимания. Есть такие опущенцы, которых много лет опускали, а они не хотят в этом признаваться. Более того, они убедили себя, что если они вытерпели они унижения, то это их сделало очень крутыми. Они хотят, чтоб других тоже опустили. Мол, меня ебали тригонометрическими уравнениями по несколько месяцев, значит, других тоже надо ебать. Их можно понять. Тяжело признаться себе, что за 11 лет учебы в школе полезных вещей было на 2 недели изучения максимум.
Аноны, распишите мне все темы по матану, которые нужно знать, чтобы смочь в нейронные сети, пожалуйста.
Да что ж за хайп-то такой.
Пойми что такое градиентный спуск (для этого достаточно знать, что такое частная производная и градиент). Еще нужно знать chain rule, чтобы вывести формулу для backpropagation.
А как же байесовский метод?
Двачую. Та же программа 1-9класса есть в "алгебра" Шеня, что в оп-списке. Зачем растягивать это на 9 лет и мучить детей миллионами заданий, которые может решить компьютер? Вместо прорешивания сотен тысяч задач на умножение в столбик(как говорят, для закрепления), лучше дать задание на пояснение, почему умножение в столбик выглядит так, а не как-то иначе. Так же и с делением.
Педагогика - это заставлять детей заучивать, что для того чтобы найти делимое, нужно частное умножить на делитель; произведение крайних членов равно произведению средних членов(или правило пропорции крест-на-крест); алгоритмов деления/умножения; и прочее и прочее. Я до сих пор всю эту хуйню помню лучше, чем Отче наш. Лучше бы не помнил. Нет ничего пагубнее заучивания.
Все эти доктора из мин. обр. хорошо показаны в недавнем мульте "Маленький Принц". Советую посмотреть, проникнуться омерзением, если ещё не прониклись.
Я лично знаю крутых математиков, которые не помнят таблицу умножения, и не собираются помнить.
Охотно верю. Но это ничего не значит. Просто им таблица, видимо, не нужна. А кому-то она пригождается.
Почему школьный предмет "математика" называется математикой? К математике он никакого отношения не имеет. Назовите его честно. "Числодрючка", "мозгоёбка" или как-то так. К "алгебре" с "геометрией" та же претензия.
Категории тоже не математика, будем честны и назовём её стрелкодрочество. Категории не имееют не малейшего отношения к математике. Вообще. К гомологиям и когомологиям так же претензия.
Потому, что это математика, что бы кто ни говорил. А алгебра вообще дается в исконном смысле "искусство перестановки членов".
Чтобы читать научную статью по математике, нужно владеть категориями. Решить 100500 примерчиков - не нужно.
>>370178
Нет, это не математика, это числодрючка-мозгоёбка. О реальной математике школьники не знают ничего. Ситуация, когда никто из школьников не понимает смысл доказанной Перельманом теоремы Пуанкаре, ненормальна.
Ну вот тут ты уже просто через край толсто. Не буду более с зеленым разговаривать.
>Чтобы читать научную статью по математике
А зачем мне читать научные статьи, а?
>числодрючка-мозгоёбка
А дрочка на статейки с катеогииями и гомологиия это нормально? Один хуй прорешал 100500 примеров или прочёл 100500 статей.
>Ситуация, когда никто из школьников не понимает смысл доказанной Перельманом теоремы Пуанкаре, ненормальна
Реформатор, плес. Её 70-80% как минимум населения планеты не понимают, а тут школьники должны понять.
Потому что математика - это и есть математические статьи. Изучение математики - приобретение способности читать и писать статьи.
Не следует называть предмет "математикой", если человек, прослушавший этот предмет, не будет в состоянии понять формулировку теоремы Пуанкаре. Называйте школьный предмет мозгоёбкой, а математикой его не называйте.

>Потому что математика - это и есть математические статьи. Изучение математики - приобретение способности читать и писать статьи
Как я проиграл! Это что-то уровня Рыбникова.
>математика - это и есть математические статьи. Изучение математики - приобретение способности читать и писать статьи
То есть опустил математика на уровень простого бюрократа, пишущего отсчёты?
>Изучение математики - приобретение способности читать и писать статьи
Человек по профессии журналист, он умеет читать и писать статьи. Внезапно он математик!
Чтобы читать математические статьи, нужно знать очень много вещей, для этого нужно прочитать большое количество учебников.
Чтобы писать математические статьи, нужно иметь способность к творчеству, отточенную долгими тренировками.
Научные статьи - это не бюрократические отчёты, это произведения искусства.
Ну а что кек. Ты научные журналы по математике видел когда-нибудь? Думаешь, любой журналист с улицы может вот так просто взять и написать в них статью?
Да.
Я считаю, что в школы нужно ввести обязательный предмет "выживание в дикой природе". Типа как в фильме "Выживший". Есть, конечно, люди, которым оно не пригодится, но это ничего не значит. Кому-то пригождается. А еще 5 семестров медицины нужно ввести во всех вузах. Вдруг в ресторане человек подавится, а рядом врача не будет?
>Я считаю, что в школы нужно ввести обязательный предмет "выживание в дикой природе".
Антигосударственные элементы готовить? Будущих террористов растить? А ну-ка пройдёмте, товарищ.
>Реформатор, плес. Её 70-80% как минимум населения планеты не понимают, а тут школьники должны понять.
Рост уровня образования это нормально, лет 200 назад население вообще в лаптях ходило и на пальцах считало. Тем не менее в понимании самой сути гипотезы нет вообще ничего сложного, нужно просто владеть некоторыми терминами.
Давай прежде чем убивать категории, убьем что-нибудь более бесполезное. Под полезностью мы будем понимать применение в других областях математики. Так я предлагаю убить теорию чисел, теорию графов, комбинаторику, теорию множеств, общую топологию, не вижу смысла в дальнейшем изучении этого всего: все полезное математики уже вынесли.

два купола с поносом этому копромсье.
> А дрочка на статейки с катеогииями и гомологиия это нормально?
Если бы в школах заставляли дрочить категории, то это было бы ничем не лучше дрочки на тригонометрические уравнения. Почему? Потому что категории пригодятся маленькому проценту людей, а дрочить заставляют всех. Понимаешь логику?
мимо-другой-анон
Офк, даже детсадсковского Aluffi не открывал.

Зачем нам ещё ОБЖ
Гугли линейное программирование.
В Винберге есть глава "афинные пространства", там как раз нужная база.
>>370312
> линейное программирование
В книге "Математика для биологов" (Гроссман, Тернер) очень доступно про него расписано.
А что делать если xi еще и сверху ограничен? Делать замену, где к x еще и прибавляют?
1. https://arhivach.org/thread/157681/
2. https://arhivach.org/thread/157894/
3. https://arhivach.org/thread/165665/
4. https://arhivach.org/thread/175432/
5. https://arhivach.org/thread/175434/
6. https://arhivach.org/thread/174050/
7. https://arhivach.org/thread/181477/
8. https://arhivach.org/thread/177783/
Анон, что говорил - "ТРИГОНОМЕТРИЯ НЕ НУЖНА", прочитай это и больше не говори таких глупостей!
у него еще сайт
http://ndspaces.narod.ru/
с интересным взглядом на мир
http://ndspaces.narod.ru/w1.htm
http://ndspaces.narod.ru/w/besedi1.htm
Я всегда подозревал, что школьная математика это не просто так, она имеет своих адептов, свои секты. Вот тут один из них, для него не имеет значения "зачем и почему", в его мире существуют только методы школьной математики, посланные Самой Природой. Любые попытки зайти за рамки, усомниться в аксиомах, методах, упираются в какие-то пространные рассуждения о житейской мудрости: "так оно у нас заведено". Действительно, какое можно вывести исследования из типично школьного определения: "натуральные числа - это целые положительные числа".
Он почему-то дико популярен среди научных фриков. У них почти у каждого есть свой собственный сайтик, и обязательно на народе.
Лол. А я думал, это шутка про то что школьники делают свои сайты на народе (как на юкозе) и поэтому - народ школоресуср.
А какие следствия можно вывести из определения "множество - это совокупность объектов"? Какие следствия можно вывести из определения "поле - это особая форма материи"? Ведь не ясно ни что такое объект (и тем более совокупность объектов), ни что такое материя (и тем более форма материи).
Вот его определения натуральных чисел:
http://ndspaces.narod.ru/nat.htm
Годнота!
>Натуральные числа - это числа, которые используются для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
>Математически точное "определение натуральных чисел от Николая Хижняка" вы найдете, пройдя по ссылке. Там нет никакого "счета", "предметов" или "порядковых номеров".
>Какие числа являются натуральными? - целые положительные числа.
>это числа, которые используются для счета предметов
Таким образом, уже один гугол не является натуральным числом.
http://ndspaces.narod.ru/a1.htm
> Этот сайт создан 20 декабря 2006 года и опубликована на нем была всего одна страница (сегодня она уже безнадежно устарела). Автором этого сайта являюсь я, Хижняк Николай Григорьевич, инженер-строитель по образованию. Строительство - это не математика, это гораздо сложнее. В абстрактных домах никто жить не хочет. А реальные дома не могут бесконечно приближаться к разрушению. Они либо стоят, либо рушатся
>Строительство - это не математика, это гораздо сложнее
Топ кек. Как же я проигрываю.
>поле - это особая форма материи
прямо таки агрономическое определение.
А вообще у школьной математики есть особого рода подход: антисистемный. Т.е. даются правила, аксиомы, определения, но в наистрожайшей тайне держится секрет, что это может образовывать своего рода систему. Только потом (может быть) расскажут, как можно строить математику по кирпичику, почему определение натуральных чисел это не бесполезная бюрократия, что аксиомы это не просто самоочевидные правила, что любимые тождества это просто замена строк.
Но ведь в школьной математике нет аксиом, особенно в геометрии. В старой книжке Погорелова про элементарную геометрию была аксиома: любой прямой сопоставлено два непересекающихся непустых подмножества плоскости таких, что любой отрезок с концами, принадлежащим разным подмножествам, пересекает прямую, а отрезок с концами, принадлежащими одному подмножеству, не пересекает прямую. Когда книжку переделывали в школьный учебник, эту аксиому заменили бессмысленной фразой "прямая делит плоскость на две полуплоскости". Определение полуплоскости, конечно, не написали.

Прирост, не?
Приращение аргумента и приращение функции.
>почему определение натуральных чисел это не бесполезная бюрократия
Я вот до сих пор не понимаю почему. Ну да, интересные метаматематические эффекты - наличие нестандартных моделей, неполнота, теорема Мятисевича - попиздеть в курилке можно, но знать это необязательно совсем.
Число обусловленности.
В физ-треде помогут.
И бесплатно полного решения - вряд ли ожидай.
И творить как Рамануджан, лол. Ну вот встретится тебе моноид натуральных чисел, а ты такой: эээ, целые положительные, бля...
Не понимаю, с "моноидом натуральных чисел" каждый сталкивается ежедневно и те, кто не знают аксиомы Пеано дискомфорта совершенно не чувствуют. Или ты не про них?
Чтобы доказать теорему о математической индукции тем, кто в неё не верит.
Натуральные числа - это множество всех ординалов, меньших омега. В любом множестве ординалов есть наименьший. Если теорема об индукции не верна, то во множестве чисел, на которых она фейлится, есть наименьшее, причём не равное нулю. Но у него, так как натуральные числа - ординалы, есть предшественник, и из условия следует, что теорема не может фейлиться на этом числе.
>Чтобы доказать теорему о математической индукции тем, кто в неё не верит.
Её так или иначе постулируют, в ZFC - это аксиома бесконечности, в РА - это (схема) аксиом полной индукции. Ебля со сведениями одной формализации к другой не нужна, всё равно утилитарное понимание натурального числа есть у всех и оно гораздо содержательнее любой формализации.
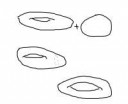
Просто им не приходилось никогда ничего доказывать. Например, рассмотрим моноид мыльных пузырей с конечным количеством дырок. Объединение двух пузырей происходит так, как склеиваются пузыри. Нейтральным элементом этого моноида является сфера.
Этот моноид изоморфен натуральным числам или нет?
>>370487
Нет, аксиома ZFC утверждает кое-что другое. Она утверждает, что существует множество, которое:
1. Содержит как элемент пустое множество
2. Содержит вместе со всяким элементом x также и элемент {x}.
Это множество не обязательно равно ординалу омега, оно может являться его собственным надмножеством.
1. Да.
2. Это всё педантизм, выхолащивание смысла и терминологическая суходрочка. Всем нормальным людям очевидно, что тобою сказанное и мною сказанное - эквивалентные в ZF вещи, это как различать аксиому о свойствах операции "-" в аддитивной группе и аксиому о существовании противоположного элемента в аддитивной группе - то есть долбоебизм совершенный.
1. Обоснуй, не используя определения N.
2. Ты многословно выругался, но ты не сказал ничего, что можно было бы доказать или опровергнуть.
Ты серьезно считаешь, что если бы в научной статье какому-то математику понадобился этот изоморфизм, он бы его "обосновывал" через ZFC или PA?
Эти аксиомы эквивалентны, кому не очевидна эквивалентность - то долбоёб. Это вполне доказательное утверждение.
А при чём здесь научная статья? Я просто размышляю о мыльных пузырях.
Эти аксиомы сами по себе не эквивалентны, для доказательства эквивалентности нужно как минимум привлечь схему выделения.
Я не понимаю какую позицию ты защищаешь. Я, такую: профессиональном математику, кроме узкого числа специалистов, не нужно знать определения натуральных чисел, помнить аксиомы ZFC или PA.
Натуральные числа определяются просто. Это множество всех ординалов, меньших омеги-нулевого. Математик, не знающий этого определения, не может быть профессионалом.
Аксиомы ZFC элементарны, и я не понимаю, как кто-то из математиков может их не знать. Разумеется, я не говорю сейчас о том ужасе, в который их превратили упоротые логики, я говорю о математически вменяемой формулировке.
Хочется спросить: а что там помнить? Профессиональный математик за период обучения проходит тысячи часов ненужных ему в профессиональной деятельности предметов. А эту тему можно покрыть за пару лекций.
>Объединение двух пузырей происходит так, как склеиваются пузыри.
Не понял, как? Если пузыри с 1 дыркой склеивать по дырке получится сфера. Если не по дырке то нет.
наоборот же.
Мат-юмор
С ручкой т.е., а не с дыркой. И это не совсем как пузыри склеиваются, там перегородочка между ними не исчезает.

Нет.
Алсо, вот http://elementy.ru/novosti_nauki/430564/Geometriya_mylnykh_puzyrey_do_sikh_por_ozadachivaet_matematikov
Пусть существует некоммутативная группа 4 порядка.
Возьмем любые 2 её элемента: ab (не)= ba, тогда в группе не менее 5 элементов.
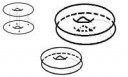
А в таком случае, не важно-ли как мы приклеиваем пузыри? Например, после того как мы тор наклеим на тор сверху и стенка исчезнет - мы получим опять тор.
Мы склеиваем их по маленькому диску, который потом исчезает.
{e,a,b,c}
Что не так? Если b не единица группы и не обратный к a, тогда ab и bd "добавляют" 2 других элемента. 1 из них может быть c(допустим c = ab), тогда ba - это какой-то ещё элем группы.
Точнее будет сказать, что не менее 6-эл. т.к. группа порядка 5 - циклическая(коммутативна)

можем ещё поговорить

Нет, конечно. Это полный абсурд.
Существуют тензоры - правильное обобщение того, что ты хочешь.

Книжка из шапки "Обыкновенные дифференциальные уравнения". А мне они и нужны.
>>370683
Толстяк. Мне считать их надо.
Если немного умеешь решать диффуры, то сразу бери книги по математическому моделированию для физиков (на английском их полно). Так вот диффуры и выучишь.
Правильно сделал?
Есть кредит на сумму 1кк. Чувак, выплачивает и получается такая схема. 1кк, 0,6;0,4;0,3;0,2;0,1;0. Нужно посчитать процент Р чтобы сумма выплатов чувака не превышала 1.2кк. 8%?
Я учился их решать на mathprofi, а потом уже по книгам по математическому моделированию для биологов.
Что касается учебников, то по обыкновенным диффурам я нормального так и не нашел, зато по по PDE (уравнениям мат.физики) вот эта книга очень доходчивая:
> С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Но это уже на будущее, если дойдешь до такого.
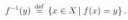
Да, это определение.
(a,b) - пара. a - первый элемент, а b - второй
Фигурными скобочками обозначается множество.
У тебя множество {s, {s,t}}. Сколько в нём элементов?
>>370980
Нет. В будет подмножеством А в том случае, если каждый элемент из В лежит в А. Можно перефразировать: В будет подмножеством А тогда, когда в В нет ни одного элемента, который не принадлежал бы А.
В пустом множестве нет ни одного элемента, который бы не принадлежал пустому множеству, поэтому пустое множество явл. подмножеством самого себя и любого другого множества.
Этот более мемовый. Здесь мы даём определения N, R и Set. Спорим чей-же подход к формальзму правильный Арнольда или Бурбаков. Хуесосим ОП-список из треда в тред. Поглощаем знания русов и ждём, когда Рыбников выпустит лекции по топологии. Пишем математические статьи и поясняем, почему категории - говно без задач, но они нужны. Набегаем на dxdy, где унижаем Мунина и его анальную модерацию. Когда проголодаемся, то поджарим картошки, запивая её Зелёной Маркой.
В общем, тралим друг-друга и пытаемся вызвать биекцию. А обычном занимаемся математикой.
Прочти первый тред, там вся суть.
https://arhivach.org/thread/157681/
То есть для примера, если В={1,2,3} подмножество А, то это НЕ: A = {a,b,c,B,d} = {a,b,c,{1,2,3},d}, А ВОТ ТАК: A={a,b,c,1,2,3,d}
Символ {x,y} означает такое множество P, что:
x∈P ∧ y∈P ∧ ∀p(p∈P → (p=x ∨ p=y)).
Символ {x} означает множество {x,x}.
Слова "множество M является упорядоченной парой" означают:
∃x ∃y ( {x}∈M ∧ {x,y}∈M ∧ ∀m( m∈M → (m={x} ∨ m={x,y}) ).
Обозначим это как Pair(M). У тебя определение пары нестандартное.
Слова "первый элемент пары M" означают такую букву x, что:
Pair(M) ∧ ∀m( m∈M → x∈m ).
Слова "второй элемент пары M" означают такую букву y, что:
Pair(M) ∧ ∃m( m∈M∧y∈m ∧ ∀a∀b( (a∈M∧b∈M∧a≠b) → (y∉a ∨ y∉b)) ).
>У тебя множество {s, {s,t}}. Сколько в нём элементов?
Два: множество {s} и множество {s, t}.
Вообще, я, кажется, понял. Куратовский вместо того, чтобы дать четкое определение упорядоченной пары, дал хуитку, которая не позволяет отождествить (a, b) с (b, a), поскольку {a, {a, b}} не равно {b, {b, a}}.
Упорядоченная пара тем и отличается от неупорядоченной пары, что (a,b) и (b,a) различны. Хули ты претензии выдвигаешь?
>Хули ты претензии выдвигаешь?
Потому что Куратовский дал не определение, а критерий, согласно которому пары (a, b) и (b, a) различны. Блять, то определение N дать не могут, то даже определение упорядоченной пары.
Просто если это число меньше твоей оценки, то по принципу дирихле среди покрашенных вершин найдутся k+1 вершин одного цвета, где k - число независимости (следовательно попарно несмежные - дают независимое множество больше максимального).
Как?
Ты идиот? Критерий как раз следует из определение упорядоченной пару по Куратовскому.
Да хз, зависимость может быть какой угодно. Какие коэффициенты эластичности даны.
Но у него нет определения, у него только невнятный критерий. Или показывай определение.
Критерий - это определение.
В основном связанные с реальностью разделы математики - это арифметика и геометрия. Все остальное - уже разные степени задротства и аутизма.




Думаю, послушаю мудрого анона из /sci, буду изучать связанные с реальностью разделы, а не абстрактную хуету. Открываю "основы арифметики" и двухтомник "геометрия". И что я вижу? Меня опять наебали. Никому не верь!
Ну, математический анализ вон весьма полезен при моделировании реальности.
Кловун, ты не ответил на вопрос а только развел демагогию. Тобишь увеличил энтропию вселенной и приблизил момент её тепловой смерти. Через 21 миллиард и 40 миллионов лет тебя бы на месте за это уничтожили, путем включения в подпространствуенную бомбу, созданную с целью создать ассиметрию распределения энергии во вселенной.
Так что молись больцмановскому мозгу, который сможет ПРЕВОЗМОЧЬ созданную тобой точку бифуркации.
> И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
Тупой вопрос по нему:
Назовём дроби a/b и c/d
(a, b, c, d - целые положительные числа) «соседними», если их разность
(ad-bc)/bd имеет числитель ±1, то есть если ad - bc = ±1.
1. Докажите, что в этом случае обе дроби несократимы.
Как решить?
От противного. Предположим, что какая-то из дробей сократима, скажем a = kp, b=kq, где k!=1,-1, тогда...
для начала надо выяснить что есть определение и почему критерий им не является.
критерий бесполезен, да
Да уже разобрались.
Спасибо.
То есть объединение этого семейства. Множества не пересекаются.
В твоем случае и континуум и его подмножества несчетны. Мощность у них одна и та же.
Я не понимаю, про что ты говоришь. Вот смотри. У меня есть множество M, его мощность континуум. Каждый элемент M сам является множеством мощности континуум. Элементы M попарно не пересекаются. Какова мощность объединения M?
Мне кто то ответит?
Ответил тебе в кадык, мразь
Здесь приводится определение этого обозначения. Слева от равенства степень в квадратных скобках, справа то что такая запись обозначает.
Континуум.
Модулярные формы в какой-нибудь галимой криптографии, наверное, применяются.
Опять критерий свой принёс, посмотрите на него. У такого спросишь, что такое шахматы, так он правила начнет объяснять.
define критерий
Никак. Пятый номер Демидовича - это известный гроб. Решай интегралы.
Ну а как ты обычный бином ньютона доказываешь? По индукции.
Зорич. Матанализ.
Шварц. Анализ. (Сказали после Зорича изучать)
Ван дер Варден. Алгибра.
Бурбаки. Разная аналгебра в трех частях.
Курош. Высшая алгебра и общая алгебра.
Вингнберг тожи.
Олсоу, можити дополнить и пасаветавать штота.
Это не целое число, там указано определение выше. Решается банально по индукции. Выпиши для 2, 3, сгруппируй и увидишь закономерность. Кстати, мне эта формула ни разу не пригодилась за 2 года.
https://ru.wikipedia.org/wiki/Теория_всего
Теория всего ведь "задача максимум" только в физике высоких энергий. Как по мне - нет такой задачи.
Лол.

>Теория всего ведь "задача максимум" только в физике высоких энергий.
Чем фундаментальней задача - тем она важнее.
Нет. Таковы свойства евклидового пространства.
не стоит вскрывать эту тему, несколько человек в монастырь ушло, еще один в пифагореизм
Ты про dxdy или число пи?
Ну памагити
http://www.ams.org/msc/pdfs/classifications2010.pdf
Разделы математики по версии самого влиятельного профессионального сообщества математиков на этой планете. Выходит раз в десятилетие, первый выпуск был в 1940 году. По ссылке текущая версия, 2010 год.
Продвинутая геометрия понятнее продвинутой алгебры во всяком случае
пиздец вопрос тупой, если ты дожил до 3го курса и задаёшь такие вопросы - убейся нахуй.
Для экономистов полезна статистика, комбинаторика, теория вероятностей, вот это все. Ну и еще можешь ряды качнуть, по вкусу. Но там ведь геометрия кривых. Конечно, не дифференциальная, но близко. А если просто хочешь заниматься математикой, но не любишь геометрию (книжек по геометрии и так нихуя), то вон, Винберг в помощь.
чёт как-то дохуя
Функционалами называют функции, заданные на векторном пространстве над полем K со значениями в поле K. В частности, над пространством функций.
Не, ну смотри. Функция - это график пар (область значений, область определения), и соотв. подмножество декатрова произведения множеств (область значений на область определения). Все просто и понятно. А функционал непонятно что.
Функционал - частный случай функции. Отъебись.
это у тебя 6-й класс определение.
функция это вообще все что угодно в общем смысле. интеграл например как тебе.
>это у тебя 6-й класс определение.
Это из бурбаков вообще-то.
>функция это вообще все что угодно в общем смысле. интеграл например как тебе.
Интегрируемость функции не отменяет самого понятия функции.
каких бурбаков ебта, ты пишешь "функция это график".
!7 лвл кун репортед ин.
Посоветуйте подходящие профильные учебники по алгебре и геометрии за 10-11 класс для самостоятельного изучения. Собственно сейчас я скачал Терешина-Калинина, но не совсем разобрался с Алгеброй т.к не нашел в Оп-посте учебника за 10-11. Ситуацию осложняет то, что чуть более, чем все занятия в школке я проебал из-за конфликтов с учителем и общей моей отбитости. Прошу не гнать меня и не насмехаться надо мной, но помочь советом - я действительно хочу изучать математику, но не знаю с чего начать.
Спасибо.
1-9 классы:
Шень. Алгебра.
Шень. Геометрия.
10-11 классы:
Шень. Тригонометрия.
Гашков. Современная элементарная алгебра.
Калинин. Геометрия.
Шубин. Математический анализ для решения физических задач. (Небольшая брошурка в 40стр.)
H.Weber & J.Wellstein. Энциклопедия элементарной математики.
Так же рекомендую:
Курант. Что такое математика?
Алексеев. Теорема Абеля в задачах и решениях. (Можешь прямо сейчас начать с нее, т.к. сейчас каникулы и можно было бы уделить внимание чему-то более интересному и ознакомительному.)
Виленкин. Рассказы о множествах.
До 1 сентября можно осилить. В этих книгах довольно серьёзная математика. Так в школе никогда не будут преподавать.
Алсо, ты хочешь дальше курс, за рамками элементарной('основной') математики?
Разумеется. Многими разными способами причём.
Хотелось бы знать твоё мнение о том, правильно ли двигаюсь. Сам программистишка, желающий понять физику и стать не дэбилом в матчасти. На всякий случай скажу, что этот ->символ означает, что предидущую книгу прошел и какая будет следующей. Так будет удобнее, наверное.
Дискретная математика:
Хаггарти, ДМ для программистов -> Романовский, Дискретный анализ -> Виленкин, Комбинаторика -> Теория автоматов.
Математика:
Щипачев - Базовый курс + Курант и Роббинс + Зельдович
А вот что дальше делать? После Щипачева и Зельдовичаили до?
Спали годноту что ли.
>Сам программистишка, желающий понять физику и стать не дэбилом в матчасти.
Ну, физика простая наука, на самом деле. Именно та, что не связана со специальными и сложно-технологическими задачами.
Большое старье кидать не буду:
Джей Орир. Физика. Полный курс.
Феймановские лекции по физике.
Берклеевский курс физики.
Васильев. Курс общей физики.
Зоммерфельд. Лекции по теоретической физике.
Ландау. Теоретическая физика.
Но, все же, лучше перед изучением этой литературы изучить хотя бы более-менее базовые понятия из математики, типа группы, производной, интеграла, дифференциала и прочего. А это как раз матанализ и современная элементарная алгебра, с которыми, впрочем, ты бы мог ознакомиться в Куранте "ЧТМ" и Зельдовиче. Но, насколько помню, там многое не выводится и многое принимается на веру, поэтому бери матан Зорича(в 2т.), Кудрявцева(в 3т.) и того же самого Винберга, ядумаю.
Или ты хочешь прямо основательно засесть в математике?
Физика относительно простая и чертовски интересная. Хотелось бы понимать процессы происходящие вокруг. Видеть мир более сложным и красочным.
По физике к меня лежат три тома Савельева в бумаге и скачанный трёхтомник Ландсберга на планшете. Плюс Физика И.В. Яковлева.
Ты написал много книг, с которыми я не знакомкроме Фейнмана и Ландау, очевидно. Сейчас чекну.
Однако, без матчасти не имеет смысла приступать к ним. И ты прав,ив том же Зельдовиче не выводится и не "разжёвывается".
Так что, надо выбрать что-то одно: Зорича или Кудрявцева? Или читать из обеих книг по каждой теме? Винберга - Алгебру?
Что скажешь про задачник по физике? Есть ли годнота?
Хочу выучить математику как язык физики. После программирования математика как-то легче пошла. Кодинг научил выделять главное, видеть основные принципы и причинно-следственные связи. Да и с абстрактными моделями дела легче пошли. В ВУЗе не тупил на вышке.
Везапно, "Путь к реальности" Пенроуза - это обзор математический физики. Нисколько не научно-популярная, просто он стартует буквально с примитивной арифметики и геометрии и доходит до квантовой физики и релятивизма.

Привет, наукач. Уже-не-первокурсник НГУ спешит обмазаться на лето матанализом, алгеброй и тервером. Посоветуйте годных учебников для этих целей, пожалуйста
С места в карьер.
Кажется, смогу его читать и понимать только освоив трёхтомник Савельева.
Иначе знания не будут структурированны.
>>371617-кун
>Ньюфаг просит учебников по математике
>Советуют ван дер Вардена, Лэнга, дифференциальную топологию и анализ на многообразиях
>Ньюфаг закончит там же, где и начнет это читать
Ну я уже читаю Зорича. Первый том.
Думаю, что мне хватит матанализа после того как я дочитаю второй.
Ньюфаг
Зорич весьма специфичен. Поглядывай параллельно другие учебники, типа Ландау, Рудина.
У этих множеств может быть только один общий элемент, ведь так?
график 3n-1 = прямая, график 5n+2 = прямая, а прямые пересекаются только в одной точке
3n-1 = 5n +2
-2n = 1
n = -0.5
так как n = натуральное число, то n != -0.5
Но в книге говорится, что правильный ответ {15n+2 | n = натуральное число}
Виленкин Н.Я.. Алгебра и начала математического анализа. 10 класс

Забыл прикрепить пикрил
И да уравнение будет не
>3n-1 = 5n +2
А 3n-1=5m+ 2 (m,n) - разные числа, то есть ты сравниваешь если в множествах совпадающие элементы.
Какого уровня учебник? Попробуй эти http://ium.mccme.ru/s13/teorver.html лекции. Может тебе они как раз окажутся.
Если лекции НМУ сложны, то попробуй "Лекции по теории вероятностей и математической статистике" Прохорова.
Какие разделы мне нужно изучить, чтобы заниматься теорией чисел? ТФКП, алгебру, гомологии(?), что-то ещё?
Слишком толсто.
Нахуя тебе лямбда исчисление? Ты что Хаскель или Черч?
А то что там лекции идут в порядке 1, 2, 5, 6 -- это нормально?
Нет, все эти книги взаимодополняющие.
Гнеденко-Хинчин, "Элементарное введение в теорию вероятностей, потом Гнеденко, "Курс теории вероятностей". Гнеденко - прямой ученик и коллега Колмогорова, одного из создателей этого вашего теорвера.
>>371629
Ну а что мне, сказку "Колобок" ему советовать?
А что плохого? Сейчас ты даже не знаешь то, чего ты не знаешь в физике. После Пенроуза ты будешь знать, что именно ты не знаешь в физике. Так и наметится общая структура, потом уже будешь детали прояснять. Он сам в предисловии говорит, что если не понятно - пропускай.
Удвою товарища.
Я с этого тоже сбугуртил сначала, а потом привык.
Уж лучше колобок, чем то, что он все-равно не поймет. Для начинающих есть отличные Винберг и Тао.
бампую реквест
Анализ на многообразиях первокурсники понимают? Ты о каких вообще первокурсниках говоришь? Первокурсники, тем более ИТ направления приходят в лучшем случае с хорошим знанием школьной программы.
Алгебру ван дер Вардена и первый том Зорича на первом курсе читают везде, например.

Потому что школа 57ая.
Не знаю ни одного такого.
В России их вообще не читают.
Я после работы или на выходных смотрю кинцо/сериалы и под них люблю решать задачки. На досуге почитываю шпрингеровские книги, поэтому с теорией знаком неплохо, но решать оттуда упражнения не хочу, так как они зачастую не снабжены ответами, часто пересекаются между собой и еще чаще там просят что-то пруфануть, а пруфы заходят под кинцо хуже, чем вычислительные упражнения.
Чет блеванул
Лал что?
Удваиваю этого. Хотел сам написать, но опоздал.
Чет блеванул
Вы видите копию треда, сохраненную 21 октября 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.