Вы видите копию треда, сохраненную 22 ноября 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
Обсуждаем и дополняем!

> Наверное, лучше всего сведения о современной матиматике искать на форумах, где обсуждают сложное программирование. Хабрхабр, например.
Даже специально пошел посмотреть где этот даун учился. Ну иного и ожидать было нельзя.
Если ты школьник, то для олимпиад тебе пригодиться комбинаторика. Гугли Виленкин Комбинаторика.
Ещё для определения n-факториала (он часто встречаеться в задачах) надо изучить Гамма-функцию.
С первых двух пиков сренькул

Дискас
Ты тот анон с модулями?
>последняя пикча
Я все еще жду ответа на уравнение (e^x)/x полученное конечно элементаным методом.
За второй пик - послушайте рому михайлова на ютюбе. Рассмотрим группу тюленей на колбасном многообразии, и так целый час Он же просто так что-то говорит на птичьем языке? А потом почитайте каменты. "Блять нихуя не понял но охуенно". "Я тупой но это потому что у меня такого учителя не было, а то бы я щас себя в жопу страпоном ебал на гладком многообразии
>что-то говорит на птичьем языке?
Чтобы понимать Рому достаточно выучить теорию групп и топологию. Любой второкурсник ВШЭ осилит.
> Нет, на второй пикче вполне приличное изложение.
Что блять? Да там вообще даунизм. Схуяли мы рассматриваем случай R^2 вместо произвольного пространства с мерой ну или хотя бы R^n? Схуяли мы рассматриваем замкнутую область? Нахуя нам знать какой линией ограничена область? Что значит "разобъем какими-нибудь линиями на n частей"? Что имеется в виду под линией и нахуя это нужно для определения интеграла?
> площадка
Уебищный нигде не употребляющийся термин.
>В ГАУСС БОННЕ
Уже давно бы на стаковерфлоу бы спросил и получил ответ. Или вербиле в комменты напиши. Он должен знать. Что ты тут школьников донимаешь?

Ну вот у них программа для 3 курса. Логично, что второкурсник уже знает и теорию групп и топологию.



Я раскрыл главный секрет Секретов математики. Автор просто манагер, который рубит бабло с помощью примитивной математики. Да ещё и называет себя проффесианальным, ух. По его определению тот же Перельман просто неудачник и вообще далёк от проффесианальной математики.
Чувак разбирается в вычислительных методах симмуляций. В этом он молодец. Для его разработок систем культиваторов не нужна точность выше 4 знаков после запятой. Ну что же, поздравляю его! Нахуя все это транслировать окружающим не ясно.
>Что
То. Книга написана для физиков и инженеров. Им случай R^2 гораздо важнее, чем R^n, и им нужны картинки.


> Нахуя все это транслировать окружающим не ясно.
Хочет собрать себе последователей в бизнес + продаёт свои услуги и рекламируеться в ВК. Может собирает альтернативную секту, противоположную НМУ. Если в первом брать сотни интегралов зашквар и такие задачи решаеються на калькуляторе, пооощраются аналитические методы и глубокая математика, то в его секте, всё что не решаеться на калькуляторе - зашквар.
Нет, физиков по этой книге учат. Очень известный и уважаемый учебник. Письменный, "Лекции по высшей математике". Для быстрого ознакомления студентов со смыслом интеграла (которые до этого интеграл в глаза не видели) - крайне годная вещь.
>Очень известный и уважаемый учебник. Письменный, "Лекции по высшей математике"
Мне кажется ты и есть этот даун, Виктор Посметьев из Воронежа. И срешь тут своими ебанутыми скриншотами. Больше никто не может знать о существовании подобных учебников. А Посметьев его читал. Отсюда вывод: Посметьев это ты и есть.
Нам по Зоричу толкают. И требуют учить "как надо", ибо "физик должен знать глубинный смысл".
Кстати, объясните третью пикчу, я просто только 11 класс закончил.
Виктору Посметьеву из Воронежа трудно запоминать формулы корней и поэтому он каждый раз составляет программу которая приближенно решает квадратное уравнение.
Посметьев решает квадратное уравнение методом перебора в цикле while. Если генератор случайных чисел написан удачно, то Посметьев получает 1 корень вместо двух и он идет дальше делать культиватор и богатеть. Если генератор случайных чисел написан неудачно у Посметьева случается бесконечный цикл и он получает 0 корней.
Смысл данной пикчи в том, что Посметьев -- д'Артаньян, а остальные пидорасы.
Звучит уёбищно. Я думал, что это что-то умное.
Твой интеграл не берёться аналитически, только численно. А я в численных методах не шарю, иди к Посметьеву он в них спец.
>я в численных методах не шарю
Вся суть маттреда.
Забыл добавить что ты только по гамалогиях спец.

http://www.wolframalpha-ru.com/2013/06/wolframalpha_16.html
Выбирай метод Буля, есть совпадение с методом Симпсона.

>Кроме пяти рассмотренных выше методов численного интегрирования, которые обычно изучаются в курсах прикладной математики для инженеров
Мне незачем. Один тут траллировал несколько тредов этим интегралом. Сейчас попросит посчитать площадь на всей вещественной прямой, вот увидете.
Такое то оправдание.
Вот смотрю я на четвертую пикчу и думаю, какой самый мощный метод решения еще имеет смысл применять для решения уравнений вручную на бумажке?
Вот есть статья. Софт для такого, по всей видимости, еще не написан. Читайте статью и пишите. Заработаете кучу денег на желающих поинтегрировать численно по всей числовой прямой.
> Для быстрого ознакомления студентов со смыслом интеграла (которые до этого интеграл в глаза не видели) - крайне годная вещь.
Вот ты серьезно считаешь, что для получения интуиции об интеграле лучше писать эту дичайшую хуйню, вместо того, чтобы сказать, что интеграл - это площадь (объем) под графиком или привести пример через объем и плотность? Интуиция - разбили на бесконечно маленький кусочки и просуммировали. Все. Какие нахуй замкнутые области в R^2? Какие линии?
Если не использовать аксиоматический метод, а просто считать инженерную хуйню по формулам, то нахуя вообще знать что такое замкнутое множество? Как вообще топология помогает в инженерных приложениях? Если использовать аксиоматический метод, то в любом случае нужен интеграл Лебега, потому что в конечном итоге это сократит количество информации, которую нужно воспринять, доказательства теорем будут проще. Нужно быть полным ебланом, чтобы этого не понимать.
Я так и знал, что ты мне не поверишь.


По определению же неопределенного интеграла не понимаю, чем ответ в виде интегральной показательной функции не подходит. Определению удовлетворяет, все иди нахуй.

Вообщем, как решить это уравнение аналитически?
А то вот я щас почти три часа думал как сделать ящик вмещающий 60 литров песка с минимальным расходом материала.
Это же просто пиздец, не додуматься до производной и приравнивания её нулю сразу же при постановке задачи. Я какой то дефективный или это норма?
>сделать ящик вмещающий 60 литров песка с минимальным расходом материала
И что в итоге? Ящик надо делать сферический?
Взял квадратное основание площадью хе_квадрат с высотой игрек, уравнял все 60, выразил игрек поделив 60 на хэ_квадрат, умножил на четыре уравнение, стенок ведь четыре штуки, Получил уравнение хэ_квадрат+480/хэ, нашел производную, уравнял её нулю и нашел хэ.
>Пузо
>В мат-треде
Я к такому не был готов, если честно. Сразу 2011 вспомнил. Пупы там всякие.
Речь идёт конкретно о двойном интеграле, глава посвящена ему и его вычислению. Смысл этого интеграла - не площадь под кривой, а объём под поверхностью. Линии были в предыдущей главе. Твои претензии нелепы, ну.
Просто попроси его посчитать двойной интеграл от xy+x, где x от 1 до 4, y от -1 до 1. Сольётся.
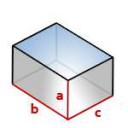
Я сейчас решил и у меня получилось следующее. В метрах:
a=0.157244
b=c=0.195339 (никаких специальных ограничений не накладывал, но оно само сравнялось)
У тебя так же?
15?
Хотя хуйня какая-то. Ящик со сторонами 20 см и объем 60 литров. Лол. Надо искать ошибку.
В общем я неправильно посчитал. У меня площадь материала вышла больше, чем для просто кубического ящика.
А я говорил - что такие задачки это дроч а не смекалочка. Всякая хуйня про коробки - это оптимизация, производные да.
Нужно взять двумерную деревянную плоскость, топологическими преобразованиями получить из нее ящик и зафиксировать изменения функцией гвозди
А разве ту гамалогии? Это же что-то компьютерное.
Вы, первая культура, презираете автоматическое доказательство и перевод математики в компьютерную среду?
Как иронично, что Харди написал курс по матану. Который нужен для этой задачи.
-мимо Литлвуд
Какому такому? Всякие численные методы простейшие. Ньютона например. Во втором посте второй пик глянь, принцип похожий. Или спрашиваешь как научиться запрогромить цикл простой?
Как вникнуть в компьютерную математику? Со всякими крутыми пруфф-ассистантами там.
мимо инженегр
Ага, мы ещё Рамануджана для своих утех из Индии вывезли.
ХЗ про пруф ассистенты. Знаю только что самый важный из них называется петух. А с чего ты взял что "компьютерная математика" это обязательно про них. Я говорил про юмор на пикчах. Они говорят - чем ебошить интегральчики по формулам, напиши простенькую программку.
Он переходит в крайности, как и Вербит.
Вербит кричит, что интегральное и дифференциальное исчиление не нужно, и говорит, что алгебраическая геометрия - тру математика.
Тут ситуация такая же, только в случии Секретов Математики, всё что не решаеться численно - не тру, и тру математик не уметь должен доказывать ничего, а должен гребсти бабло.
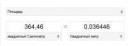
Для кубического ящика площадь равна 0.76631. Для оптимизированного 0.72986. Экономия 0.036446 квадратных метров. Или кусок фанеры 19 на 19 сантиметров. Стоило ли ради этого столько ебаться?
ХУЛИ ВЫ МЕНЯ ОБМАНЫВАЛИ, БЛЯДИНЫ
6666 На капче
https://www.youtube.com/watch?v=OLjHc3BOlPc
>19 см
ну этот хуй из секретов математики поставил бы на производство и за 10 лет дохуя бабла бы сделал на этих 19 сантиметрах. только число твое сперва обрезал бы до трех знаков после запятой.
Ну ты и хуйло.

> и за 10 лет дохуя бабла бы сделал
Скорее бы ему пришлось продать почку и квартиру банку, потому что конкуренты выпустили пластиковые и вынесли его с рынка, пока он экономил фанеру.
Проиграл.
https://oschool.ru/
>Книги
>В. БОСС. ЛЕКЦИИ ПО МАТЕМАТИКЕ
На обложке этот мужик. Он и есть легендарный Босс?
>Он и есть легендарный Босс?
На тифаретнике это выяснили еще несколько лет назад.
http://lj.rossia.org/users/tiphareth/786569.html?thread=43128713#t43128713
Вот почему так трудно выучится математике. Заходишь на сайт, прицеливаешься в номер 3, и тут же все сдвигается и попадаешь в номер 6.
Да. На втором курсе у них обычно и т. групп и топология.
Этот тред -- самое раковое, что я видел за два десятилетия
два десятилетия на дваче?
>а должен гребсти бабло.
Святая правда - поэтому вас так и корежит, питардии.
Как говорится: и хочется и колется, так-то.
Смотри балет, быдло.
ОП, ОБЯЗАТЕЛЬНО В СЛЕДУЮЩИЙ ТРЭД ДОБАВИТЬ ЭНГЕЛЬКИНГ - ОБЩАЯ ТОПОЛОГИЯ.
ЭТО ЖЕ, БЛЯДЬ, БИБЛИЯ ТОПОЛОГИИ. КАКОГО ХУЯ ЕЁ ТУТ НЕТУ? ЕБАНЫЙ ПРОФАН ВЗЯЛСЯ СОСТАВЛЯТЬ СПИСОК ЛИТРЫ ПО МАТЕМАТИКЕ. СУКА!
>ЕБАНЫЙ ПРОФАН ВЗЯЛСЯ СОСТАВЛЯТЬ СПИСОК ЛИТРЫ ПО МАТЕМАТИКЕ. СУКА!
>половину треда решали с помощью вольфрама как сделать ящик на 60 литров
Не ври! У нас даже рулеточек нет!
Серьёзно? Вот моё решение сходу: переводим литры в кубометры, извлекаем из получившегося кубический корень, получаем ребро нашего кубического ящика. Но прям ровно не получиться, но на разницу в хрен тысячных всем похуй.
Или так: переводим литры в кубометры, раскладываем получившиеся число(0.06 м^3) на 3 множителя(0.06 м^3=0.2 м×0.3 м×1 м, например). Получаем ровные измерения. Теоретики довольны, прикладники счастливы.
Суть была в том чтобы сделать ящик на 60 литров с квадратным дном с минимальным расходом материала.
Половина порвалась на тему "ЕТА РИАЛЬНАСТЬ, АНАН НИНУЖНА" вторая половина на ему "ДА ВИ ТАМ СИКАНОМИТЕ ПАЛТРА КАДРАВТНИХ МЕЛЕМЕТРА", третья пошла решать задачку в вольфрам, который на такую пустяковую задачку уперся рогом и не пускал их ровно до тех пор пока они не задали пределы.
Полистай нить до 80 поста примерно и оттуда начинай читать какие тут мамкины таполаги и гамолаги.
Я уверен, что эту задачку про ящик вбросил Виктор Посметьев, чтобы посмеяться над двачерами.
А я ее за минуту решил, хотя я вообще даун в математике. Что в ней тяжелого то?
>ящик на 60 литров с квадратным дном
Никакого условия на квадратность в оригинальной пасте не было:
>как сделать ящик вмещающий 60 литров песка с минимальным расходом материала
По моему, подрузомеваеться, что верх ящика открыт.
Идеальный ящик получится при n -> ∞. Все остальные ящики будут лишь его жалкой подобией.
высота = 2.46621207433
сторона дна = 4.93242414866
Что значит помещается? Мы ведь можем и на плоский лист фанеры песка насыпать. Нужно определить объем как-то иначе.
Можете отвечать итт
Можешь погуглить "Математика в техническом университете", там около 20-ти томов.

Вот тебе, кстати, названия книг.

Треугольная призма с дном из правильного треугольника, без крышки.
сторона треугольника = 7.82973528234
высота призмы = 2.26024988647
Как и в прошлый раз, в корнях кубических из литра. Если надо в метрах, то умножайте на 0.1.
ГДЕ ГАМАЛОГИИ
СДЕЛАЙТЕ МНЕ ИНЪЕКЦИЮ
Да я и так уже два раза считал. Скучно тоже самое по несколько раз делать.

Тебе в пердак или за щеку инъектировать?
> 100 производную
Кстати, а нахрена? И нахрена решать диффуры с 6-ми производными? Где вообще может пригодиться производная выше 3 порядка?
ВАС ХВАТИЛО НА 14, БЕЗВОЛЬНЫЕ ХУЕСОСЫ
А ТЕПЕРЬ КАТИТЕСЬ МЕТКОМ В СВОЮ РИАЛНОСТ
Ну удачи, запасайся там картофаном.
>ВОТ И КОНЧИЛИСЬ МАТЕМАТИКИ ДЛЯ НАЧИНАЮЩИХ ТРЕДЫ
>ДЛЯ НАЧИНАЮЩИХ ТРЕДЫ
>А ТЕПЕРЬ КАТИТЕСЬ МЕТКОМ В СВОЮ РИАЛНОСТ
>РИАЛНОСТ
>ДЛЯ НАЧИНАЮЩИХ
>>382420
У вас повышенный уровень гамалогий и тапалогий в крови, срочно принять 60 милилитров водовки перерорально и закусить картофаном.
Я тоже. Зачем нужны интегралы, если можно посчитать сумму площадей n прямоугольников под кривой.
почему вы так боитесь все слов топология и гомология? это из-за лекций Михайлова? нудак ежели не готовы нахуй смотреть было?
Зато тапалогии есть.

>скрутишь
Как лыжи скручивают, так и я скручу. Сначала распаривают, потом через валики пропускают.
Так то да, но вот только скорее всего фанера должна быть тонкая, чтобы такой небольшой лист в конус скрутить. Выдержит ли она 60 литров песка?
С чего ты взял, что я боюсь? Топологию я потихоньку учу, к гомологиям не прикосался пока.
Просто местные гомологи себя отвратительно ведут, как вот этот >>382427. И если какой-то дебил начинает орать, что интегральчики зашквар, значит гомолог порвался.
Бояться, на самом деле, гамологи интегралов.
гомотописты*
Вас посетила полиция Романа Михайлова, на этот раз без штрафов, но впредь будьте внимательнее


У пожарников конус выглядит неоптимальным. Они зря проебывают металл. Нужно срочно оптимизировать.
>боишься интегралов
>вся вышка построенна на предельных переходах, с интегралами и дифференциалами
Хотя не, может выгоднее брать не полусферу, а шаровый сегмент.
>Где вообще может пригодиться производная выше 3 порядка?
В гидроакустике, насколько мне известно, применяются производные очень высоких порядков, когда надо занимаются детектированием всяких подлодок на расстоянии в много километров. Вроде бы у французов самая крутая гидроакустика в мире именно поэтому.
> Вроде бы у французов самая крутая гидроакустика в мире именно поэтому.
Из-за Бурбаки чтоль?
Вообще-то оптимальный ящик -- это сфера.
Малышня с этого сайта не знакома с вариационный исчислением, нойс. Вот вам задание, юные аутисты, -- посчитайте оптимальный ящик для всех R^n.
>оптимальный ящик -- это сфера.
У нас в ящик надо насыпать песок, а сфера это замкнутая поверхность.
>оптимальный ящик для всех R^n
>не понимает что в замкнутую выпуклую фигуру не насыпать песка
Газифицировал лужу, молодец.
> замкнутую выпуклую фигуру
Какое значение здесь имеет выпуклось?
В замкнутой фигуре можно удержать песок. Как засыпать -- уже не вашего ума дело.
>плоского листа фанеры 0 толщины
ламина это называется, соблюдай терминологии блеать. ламинированный ящик. ламинат
Прекращай толстить уже, и выучи наконец, что такое замкнутое многообразие.
"нихуя не понял но интересно". 200 тыс просмотров, где он там в маске клоунадствует. 200 тыс, аноны. из контачека что ли гуманитарии понабежали. у мужика с двумя хуями и то меньше просмотров было.
это же бесконечнотонкая ламина
анус себе оптимизируй пес
Это нихуя неверно, поэтому доказывать нечего. Контрпример:
1. A /\ (not A) = empty
2. A = A
Эквивалентны.
Но
1. A \/ (not A) = empty
2. A = A
Не эквивалентны.
лифт пассажирский можно еще оптимизировать. jerk jolt и тд до 5-й производной. чтобы плавность была такая при разгоне торможении, что поссать можно было не обрызгавшись.
иди на хуй отсюда с этим, это тред про оптимизацию ящиков.
На полусферическом ящике в противовес ящику кубическому экономится кусок алюминия 42 на 42 сантиметра.
Читал жопой. False -- это константа, а не переменная, и равенство это вообще из другой оперы.
Фанеру, наверное, тоже можно согнуть в полусферу. Но я таких станков еще не видел. А для алюминия уже есть:
https://www.youtube.com/watch?v=JX51Dqd6TP4
>>382465
Нифига же не может быть 60 литровый ящик с радиусом 0.3 метра. Видимо надо корень третьей степени каждый раз в конце брать. Иначе получаются не метры нихуя. Как и во всех предыдущих случаях.
Выходит, что в треде до сих пор не было ни одного верного ответа.
Потому что утилитарный подход - это зашквар. От математики не должен быть практический результат. Давай те лучше N определять.

Верный ответ был, и это сфера. Если хочется, чтобы можно было открывать и закрывать, делаешь две полусферы, как в киндере.
У них сердечный приступ случился. Никто не выжил.
14x14x31 см. И в ней всего 6 литров.
Ты охуел эксперименты проводить, это же не физики тред.
Как вы без гамалогий поймёте, что из вашего n-мерного ящика песок не высыпется?!


Если кто не знает, Эйлер был лохом:
The Prussian king had a large circle of intellectuals in his court and he found the mathematician unsophisticated and ill-informed on matters beyond numbers and figures. Euler was a simple, devoutly religious man who never questioned the existing social order or conventional beliefs, in many ways the polar opposite of Voltaire, who enjoyed a high place of prestige at Frederick's court. Euler was not a skilled debater and often made it a point to argue subjects that he knew little about, making him the frequent target of Voltaire's wit. Frederick also expressed disappointment with Euler's practical engineering abilities:
I wanted to have a water jet in my garden: Euler calculated the force of the wheels necessary to raise the water to a reservoir, from where it should fall back through channels, finally spurting out in Sanssouci. My mill was carried out geometrically and could not raise a mouthful of water closer than fifty paces to the reservoir. Vanity of vanities! Vanity of geometry!

Знаю я законы де Моргана, но как с помощью них доказать - не понимаю.
Отрицание всей формулы меняет и все отрицания при переменных, а не только конъюнкции и дизъюнкции.

Таблицу для каких формул, блять?
Только ты нормально опиши сейчас формулы, формально.
Блять, тред математиков которые могут в формализм только когда копируют с википедии определение топологии.

Проиграл с этой математической мафии в википедии. Значит это некие абстрактные специалисты обосрались. Лол.
я видел это хуй поймешь чего, я посоветовал ему разбить как-то на куски и пояснить решение.
>It is the part of every morning routine in every public school I am aware of.
>Yes, for the vast majority of students.
>no one's forcing you to, but you're generally seen as 'edgy' by students and 'disrespectful' by teachers
>At least half of U.S. students still recite the pledge
https://www.youtube.com/watch?v=xcwg7cnhW4E
https://www.youtube.com/watch?v=LkpUbSejcjY
https://www.youtube.com/watch?v=_kOEg55vewU
спасибо!
Завтра сутра пора делать перекат с дополненным списком, ИМХО
>>382127 (OP)
Ну во-первых, Энгелькинг :)
Во-вторых, сейчас напишу еще несколько книжек (штук 5-10, как получится), отсутствие которых я приметил. Могу и больше, вам на выбор
>>382127 (OP)
Бляяяя, я ща начал записывать, что вставить, понял что ночи не хватит :)
Короче, вот что успел:
По алгебраической геомке прекрасный учебник Шафаревича "Основы алгебраической геомки". Грубейшая ошибка, что у вас в алгебре не упомнен КУРОШ, это же святое На пресловутом dxdy неокоему анаону даже давали полудневный бан, за то что тот нелестно отозвался об одной из глав http://dxdy.ru/post977460.html#p977460 , перечисляю святое: Курс высшей алгебры, Лекции по общей алгебре (2 книги в одной) и Теория групп (толстая-притолстая такая). Еще одна ГРУБЕЙШАЯ ошибка - в диффурах не упомнен Петровский (классик от области) его можно читать всего (как и ОДУ, так и в частных). Хорошим учебником по частным считается книжка Ольги Олейник. Аналитическую геометрию я бы посоветовал ебонить по 5-ти томнику Постникова (Хардкор, то шо надо для будущих Вербитов), а также по 2 книгам моего любимчика - ПСА: Аналитическая геометрия (ебать, какая жирная) и Лекции по аналитической геометрии. Теперь пара советов по "тапалогии","гаматопам", "гамалогии" - Прасолов Элементы комбинаторной и дифференциальной топологии, и вторая часть - Элементы теории гомологий, Постников - Лекции по алгебраической топологии в 2 томах (Основы теории гомотопий, Теория гомотопий клеточных пространств). Для новичков в тополоджи подойдет учебник Вербита (но для него желательно иметь мозг). Если будете знакомится с творчеством ПСА - не упустите еще Введение в теорию размерности, Введение в гомологическую теорию размерности и "Теория размерности и смежные вопросы. Статьи общего характера". По логике книги Клини обязательны (Введение в математику, Математическая логика). По теории Галуа читать пять книг Чеботарева + после ни может вкатит и его двухтомник избранных трудов, для топологов еще Аскольда Ховансокго читать (Топологическая тоерия Галуа) - это все классика. По теории множеств дохуя могу посоветовать, но пусть будет так: Хаусдорф (в преводе ПСА)->ПСА->Френкель с Бар-Хиллелом.
В трэде не советуют серий книг, если они не нужны, то ОП отпиши, если нужны - скиеу список. Еще нужно прогуглить файл goodbooks.txt книги по математике, советуемые там, почти все - самый сок. Корочи, я бля ночью займусь этой хуйней и скину в этот трэд отсортировано и по порядку список книжек, потом устроим небольшой совет и подготовим новый список. А пока, ОП, задумйся над этими.
>>382127 (OP)
Бляяяя, я ща начал записывать, что вставить, понял что ночи не хватит :)
Короче, вот что успел:
По алгебраической геомке прекрасный учебник Шафаревича "Основы алгебраической геомки". Грубейшая ошибка, что у вас в алгебре не упомнен КУРОШ, это же святое На пресловутом dxdy неокоему анаону даже давали полудневный бан, за то что тот нелестно отозвался об одной из глав http://dxdy.ru/post977460.html#p977460 , перечисляю святое: Курс высшей алгебры, Лекции по общей алгебре (2 книги в одной) и Теория групп (толстая-притолстая такая). Еще одна ГРУБЕЙШАЯ ошибка - в диффурах не упомнен Петровский (классик от области) его можно читать всего (как и ОДУ, так и в частных). Хорошим учебником по частным считается книжка Ольги Олейник. Аналитическую геометрию я бы посоветовал ебонить по 5-ти томнику Постникова (Хардкор, то шо надо для будущих Вербитов), а также по 2 книгам моего любимчика - ПСА: Аналитическая геометрия (ебать, какая жирная) и Лекции по аналитической геометрии. Теперь пара советов по "тапалогии","гаматопам", "гамалогии" - Прасолов Элементы комбинаторной и дифференциальной топологии, и вторая часть - Элементы теории гомологий, Постников - Лекции по алгебраической топологии в 2 томах (Основы теории гомотопий, Теория гомотопий клеточных пространств). Для новичков в тополоджи подойдет учебник Вербита (но для него желательно иметь мозг). Если будете знакомится с творчеством ПСА - не упустите еще Введение в теорию размерности, Введение в гомологическую теорию размерности и "Теория размерности и смежные вопросы. Статьи общего характера". По логике книги Клини обязательны (Введение в математику, Математическая логика). По теории Галуа читать пять книг Чеботарева + после ни может вкатит и его двухтомник избранных трудов, для топологов еще Аскольда Ховансокго читать (Топологическая тоерия Галуа) - это все классика. По теории множеств дохуя могу посоветовать, но пусть будет так: Хаусдорф (в преводе ПСА)->ПСА->Френкель с Бар-Хиллелом.
В трэде не советуют серий книг, если они не нужны, то ОП отпиши, если нужны - скиеу список. Еще нужно прогуглить файл goodbooks.txt книги по математике, советуемые там, почти все - самый сок. Корочи, я бля ночью займусь этой хуйней и скину в этот трэд отсортировано и по порядку список книжек, потом устроим небольшой совет и подготовим новый список. А пока, ОП, задумйся над этими.
>>382626
Хорошо бы написать краткое описание к каждой книге, которую ты предлагаешь.
Как вот тут:
>Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
>А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
>М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
>А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
окей, по мере сил и возможностей буду добавлять комметарии
> диффурах не упомнен Петровский (классик от области)
этот такой же ацкий пиздец как книжка Арнольда или в другом стиле, че нить в таком духе.
>>382650
Пусть в следующем так и будет, а этот уже скатился.
Просто лучше бы, чтобы он был в ОП. Но окей, постараюсь пораньше подогнать

>>382529
>сейчас в Питере
Он все еще в Москве и называется ВШЭ. Просто посмотри кто учит младшие курсы на матмехе: это же пиздец. А мэтры дай бог раз в год лекцию какую-нибудь проведут популярную.
Ты что охуел?!!!
Метода перебора ему недостаточно!!!
У нас в Секретах Математики за иакое убивают нахуй!!!!!!
http://yotx.ru/#!1/3_h/ubWwcH@1sHB/tGDOF/bf9o/2D/YN9PSq3t763v7B/sk2jYjZ1TxuPpFuNx6/Jid39rf2d9bxOxf7BPomE3dk4Zj6dbjMety4vd/a19AQ==
Графически можно доказать, что других решений нет.
>мало что там ближе к бесконечности случится
Кек. Тут всё ясно.
>>382675
http://youclever.org/book/ispolzovanie-grafikov-funktsij-pri-reshenii-uravnenij-neravenstv-sistem-1
Пока не прочтёшь, не возвращайся.
Тебя просто на лето оставили.
Могу лишь сказать, что все решения x имеют вид: x^2=4k+1
>Ольги Олейник
Накидайте еще имен теток от математики. А то очень мало их. Знаю на dxdy есть две активных постклимаксных пизды, провинциалка и шведка. Они тупые или ништяк?
Терли как-то здесь ровно про этот эпизод. Тупой альфач ерохин-вольтер открыто хуесосил омежку-гения и настраивал короля против него. В результате выиграла россия, купив эйлера с потрохами, как кого-нибудь голландского тренера по футболу. Еще и титул ему в придачу впихнули, бо омеган был тщеславен.

Расходится
>Почти сразу Джон Милнор построил пару изоспектральных неизометричных 16-мерных торов.
Ну тут все очевидно
Они норм, есть еще модератор Lia - умная няша
>свертка
Свойства
Коммутативность:
f ∗ g = g ∗ f
https://ru.wikipedia.org/wiki/Свёртка_(математический_анализ)
Нафиг ты это запостил? Ты вопрос прочитал до конца?
Что не так с калькой томаса? Почему такой бугурт? Гаматопей с гамалогеями не завезли, из за этого!?
и че
чому бугурт. просто история про участников математического треда. я сам люблю томаса.
Бамп впросу, ну.
А то я вот выучил интригали с дифринцалами, думаю, поа бы уже начать физику изуать. Открываю сивухина, и нихуя не понимаю в нем. Вижу дэ у по дэ икс, понимаю что это производная, но не могу понять к чему она тут, даже если перечитать по десять раз текст с ней.
Прочитай бесплатную брошюру Зорича:
Язык естествознания. Математическая азубка
а также брошюру из серии Библиотека "Математическое просвещение":
Дифференциальное исчисление.
Все просто, подробно и изично. Удачи!
А по преобразованиям Фурье есть что-то подобное?
Там слишком много букв которые что то означают, я не могу запомнить где что.
Потом, в лучших традициях ДОПУСТИМ ОЧЕВИДНО, КАК МОЖНО ПОКАЗАТЬ ПОСЛЕ НЕСЛОЖНЫХ ПРЕОБРАЗОВАНИЙ не пишут промежуточные действия.
Плюс, слишком быстро скачут по теме, я не успеваю понять что происходит.
Бесконечно малые это такие числа, которыми можно принебречь. x+c~x, если с бесконечно малая. У Виктора Посметьева, все числа которые меньше, чем 0.001 - бесконечно малые. В физики часто такие числа встречаються. Или например, когда ты считаешь сколько времени поспал ты будешь считать часы и минуты, но не будешь считать секунды и миллисекунды.
Бесконечно больше, наоборот, такие большие числа, что x+c~c. Как пример, у нас есть большой дом (девятиэтажка) и если мы впустим в дом одну кошку, то масса дома почти не изменеться, и массой кошки можно принебречь. Или масса Земли(без тебя) + твоя масса = масса Земли(без тебя), понял?
Это то я понял, я имел ввиду обоснование с точки зрения математики.
Хотя бы не очень строгое, но чтобы я мог пояснить другому человеку что это за бесконечные, почему бесконечные и т.д. радикально, без всяких пределов.
давай с баблосами так. я дам тебе 1 миллион, потом 2, и тд, но это долго, сразу дай мне 100 тыщ.
я хотел тебе пизды дать за этот график, а потом понял что в глаза ебусь. думал что квадрат синуса.

Это просто название такое. И так называют только физики, математики так не говорят, потому что это не точно.
Опять не то.
Я читал именно определение понятия бесконечно малая и почему ею можно пренебречь. Там пояснялось что если взять любое конечное е, потом поделить его на два и сделать так чтобы бесконечно малая была меньше этого е/2, то сильным колдунством получаем что бесконечно малой можно пренебречь.
Ну почему же, там конкретно поясняли почему она бесконечно малая, эта ваша бесконечно малая. Я понял что это поясняли, но не понял суть пояснения.
Во-первых, там ничего не обсуждают. Во-вторых, мне не нравится не уровень материала, который обсуждают, а его быдланская направленность: какие-то учебники по физике, калькулюсы без доказательств. Короче, просто отвратительно.
Говорили про пределы, потом скзли что предел это хорошо, но он оперирует конечными цифрами которые дают сильно приблизителдьный результат, поэтому надо ввести понятие бесконечно малого/большого.
На дхду, парниша.
Да так много где. У Рональда Фишера тоже самое, например. А потом другие ученые десятилетиями не совсем правильно понимали его идеи, как потом оказалось.
Она скорее всего просто по-другому называется. А так ее полно в интернетах.
>Во-первых, там ничего не обсуждают
Постите сами.
>Во-вторых, мне не нравится не уровень материала, который обсуждают, а его быдланская направленность: какие-то учебники по физике, калькулюсы без доказательств. Короче, просто отвратительно.
Это не тред чистой математики. Это тред для новичков, так что такие темы тут уместны.
>мне не нравится
Ты сам не постишь интересные посты, а только ноешь. Поэтому терпи, как я пощу скриншоты из вольфрама.
К тому же, я почему-то уверен, что ты не разбираешься ни в гомологиях ни в технорядах Фурье.
http://www.math.harvard.edu/graduate/quals/qs11.pdf
В сопромате же вроде уже 4 производные.
>Рональда Фишера
Спасибо за упоминание. Посмотрел в итоге годный видос. https://www.youtube.com/watch?v=9MkB4J5WQNc
Считаю, что такое надо преподавать вместо математики в школе 11 лет. Тогда мужчины осознают свою сущность (сдохнуть в 9 случаев из 10 не оставив потомства), а бабы станут еще более охуевшими, т.к. из интуитивных представлений их поведение получит научную основу.
>сущность (сдохнуть в 9 случаев из 10 не оставив потомства)
Под сущностью ты имеешь ввиду преднзачение или результат?

Например есть у меня отрезок (1;2). Я его могу преспокойно разбить на M1=(1;1.5) и M2 = (1.5;2) И они не пересекаются как в условиях написано. Или суть в том, чот здесь 1.5 не входит в эти два?
Могу же я любое закрытое множество разбить на границу и на саму внутренность, которые не имеют общих точке.
Можно ткнуть в не слишком солидных размеров литературу.
Могу посоветовать рассматривать топологию всегда или на плоскости или в пространстве, но не на плоскости. Иначе у тебя слишком часто будут встречаться вырожденные случаи в примерах.
Посмотри этот видос (там где-то с середины то что тебе нужно):
https://www.coursera.org/learn/complex-analysis/lecture/kvls8/topology-in-the-plane
Разбиение множества M - это такое семейство Mi, что M является подмножеством объединения Mi по i и притом для любых индексов i,j множества Mi и Mj не пересекаются.
У тебя первое условие не выполняется, (1;2) не есть подмножество M1UM2.
Ну и каждое Mi есть подмножество M, само собой.
>А Я НИ ОДНОГО ИНТЕГРАЛА ЗА ЖИЗНЬ НЕ ВЗЯЛ
Девятиклассник ворвался в тред! Следующие два класса ты будешь брать простые интегралы, школьник.

А я люблю обмазываться несвежими интегралами и дрочить. Каждый день беру по две страницы из Демидовича.


Интегралы пока легко беруться, но это только начало, как я думаю.
Разные задания, большинство на вычисления, есть немного на доказательства, есть йоба-задачи (только звёздочной они тут не обозначаються). Задач очень много ~4500.

https://www.youtube.com/watch?v=hN14vgOZPmU
Что тут написанно?

Просмотрел те немногие учебники по мат.логике которые есть в интернетах в нормальном качестве. Бегло просмотрел, выбрал самый годный в плане формальности изложения.
Охуел с того что это учебник для педагогических специальностей.
Игошин.
>логику предикатов
Андрей Бовыкин несколько лет назад читал несколько крутейших курсов по логике в Бристольском универе и от них были видео. Можно было бы тебе их порекомендовать, но он из Англии уехал (в Бразилию штоле), а на сайте универа уже вроде нифига не лежит.
http://www.maths.bris.ac.uk/robots.txt
Не понимаю таких мразей-сисадминов.
Хотят сохранить анонимность для будущих поколений.
ну обычно гундосят что то типа
I'd like people's opinions on alexa/ia_archiver/wayback machine. I would completely block ia_archiver if it were just alexa because I'm not getting any referals from them, while they hog my server time.

>сложна
А это все потому, что ты начал читать книги из особого раздела называемого калькулюс. А читал бы нормальные книги про дифференциальные формы и гладкие многообразия -- было бы все просто.
В 52 ТРЕД ПААПРАШУ ВАС
Давай ты мне сейчас аргументированно пояснишь чем плохи учебники лузина, по которым я учился.
Прежде чем ты напишешь что то хочу показать тебе списочек учеников лузина.
>Н. Н. Лузин — создатель московской математической школы. Среди его учеников — математики М. А. Айзерман, П. С. Александров, Н. К. Бари, В. И. Гливенко, Л. В. Келдыш, А. Н. Колмогоров, А. С. Кронрод, М. А. Лаврентьев, Л. А. Люстерник, А. А. Ляпунов, Д. Е. Меньшов, В. В. Немыцкий, П. С. Новиков, М. Я. Суслин, П. С. Урысон, А. Я. Хинчин, Л. Г. Шнирельман.
Возьмем учебник Лузина по интегральному счислению для заводобыдла. В 2016 в нем нет абсолютно никакого практического смысла, т.к. вольфрам-альфа может решить любой интеграл, лучше и быстрее Лузина. Гордиться тем, что ты прочитал учебник Лузина -- все равно, что гордиться тем, что ты поел говна.
Интеграл и тригонометрический ряд / Н. Лузин. - Москва : тип. Г. Лисснера и Д. Собко, 1915. - [2], 242 с.
Лузин, Николай Николаевич (1883-1950.).
Интегральное исчисление. - Москва, 1961.
Лузин, Николай Николаевич (1883-1950).
К абсолютной сходимости тригонометрических рядов / Н.Н. Лузин. - Москва : тип. Моск. ун-та, 1912. - 12 с.
Лузин, Николай Николаевич (1883-1950.).
Дифференциальное исчисление [Текст] : [Учеб. пособие для вузов] / Акад. Н. Н. Лузин. - 6-е изд. - Москва : Сов. наука, 1958. - 473 с.
Лузин, Николай Николаевич (1883-1950.).
Теория функций действительного переменного [Текст] : Общая часть : Учеб. пособие для педвузов / акад. Н. Н. Лузин. - Москва : Учпедгиз, 1940. - 304 с.
Лузин, Николай Николаевич (1883-1950.).
Calculul integral [Текст] / acad. N. N. Luzin ; In româneşte de Martha Weiner. - [Bucureşti] : Ed. de stat, 1950. - 3 т.;
Лузин, Николай Николаевич (1883-1950.).
Собрание сочинений [Текст] / Акад. наук СССР. - Москва : Изд-во Акад. наук СССР, 1953-1959. - 3 т.;
Лузин, Николай Николаевич (1883-1950.).
О некоторых новых результатах дескриптивной теории функций [Текст] : Доклад на Майской сессии Акад. наук СССР 1935 г. / Акад. Н. Н. Лузин ; Акад. наук СССР. - Москва ; Ленинград : Изд-во Акад. наук СССР, 1935
Лузин, Николай Николаевич (1883-1950.).
Differenciálszámítás [Текст] / Luzin ; Ford.: Kovács Vilmos. - Szolnok : Közlekedési műszaki egyetem, 1952-1953. - 2 т.;
После речи Лузина, встретив Лузина в коридоре, Колмогоров стал упрекать его в обмане, что тот не поддержал Александрова. Понтрягин пишет, что Лузин сказал Александрову: «Голубчик, успокойтесь, не волнуйтесь, вам надо обратиться к врачу» и начал похлопывать его не то по плечу, не то по руке. Колмогоров разозлившись сказал в ответ: «Что же вы хотите, чтобы я вам в физиономию плюнул или по морде дал!», на что Лузин продолжил уговоры обратиться к врачу. После этого Колмогоров ударил Лузина по лицу. Присутствовавшие при инциденте решили оставить случившееся в тайне. Однако, Лузин надел повязку и пожаловался президенту Академии наук.
Святая толстота
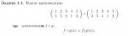
Задачка номер 1, ёпта.

Проебал еще один кусок опредление. Теперь все.

>Ящик на 60 литров без вольфрама сделал уже?
Решил ли я 2 уравнения в частных производных руками? Да как-то есть еще чем заняться. Это говно умеет делать машина.

Освоил синтаксис.
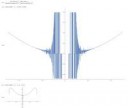
А Арнольд не плох. Не имею находить пределы. Придется читать Лузина Рудина. В вольфраме искать это чит.
Или провинциалка.
Помню тред, где кто-то из них пояснял, что люди вроде Гриши Перельмана редкость, и в науке полно тех, кто ходит в клубасики и так далее.
Вот хуй знает, как можно очень хорошо разбираться в математике и ходить в клубасики.
>как можно очень хорошо разбираться в математике и ходить в клубасики
Да легко. Все математики из ДС ходят в клубасики на даркфолк.
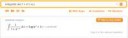
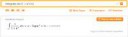
>Лузин, Николай Николаевич (1883-1950.).
>Дифференциальное исчисление
Годный учебник для старта
Проиграл с графика.
Годный, да.
Еще годно Зорича параллельно со Шварцем изучать, они похожи. Шварц тяжеляк, правда, поэтому надо сначала читнуть Зорича и полирнуть Шварцем.
А вообще, идеал - это Письменный. Я за одну ночь по нему научился интегралы считать.
Картофан, конечно, ну а хули.
Забыл кстати полностью уже весь картофан, даже простой интеграл или производную не посчитаю.
просто зашквар наверное убить несколько лет на математику, угореть по-хардкору, забить на все развлечения и вообще фляга потечет, а потом внезапно обнаружить, что есть поц, который разбирается в математике не хуже тебя, и у него есть тян и так далее.
Ландау тот же. Мега ебырь был.
Лучше уж картофанчика с водовкой жахнуть.
1) Устаревшая терминология, сгущение там всякое, стягивание и прочие изобретения
2) Устаревший подход к анализу, определению вещественных чисел, формализму, не позволяющий свободно двигаться дальше к современному материалу
3) Общая бесполезность такого подхода к калькулюсу при наличии компьютерных средств, это учебник по бегу в век автомобилей.
Согласен, учебник норм вроде, я по нему не угорал, но устаревшая терминология.
Сейчас все на рельсы теории множеств перевели, проще сразу нормально научиться, чтобы не переучиваться.
Математику довольно трудно быть альфачем, так как всякие неальфаческие качества (асоциальность, асексуальность, аутическая увлеченность) полезны в профессиональной деятельности.
100 раз лопиталя в ручную, и наверняка сработает (по аналогии со 100 раз производную). ну ка быстро засучайте рукава, мамкины гомологи, и сюда пик со 100 исписанными страницами!
Не прокатит. Арнольд слишком хитёр для такаого поворота событий.
Вербит долбоеб, отбивает всякое желание учить математику своими выебонами.
Я тоже так считаю. Сложная наука, чтобы ее нормально понять, надо как минимум ограничить клубасики и синеву. Хотя, где-то читал, у Понтрягина вроде, что какой-то хороший математик заливался как безумный.
Но вот пример Ландау не дает покоя. Как он успевал и баб пороть и в физике открытия делать? Физика не математика, но тоже не хуй собачий, да и математику он знал хорошо.
ну это же просто статистика. как и во всем, если есть дохуя дохуя математиков, то среди них есть те, кто не укладывается в усреденное представление о них, например повезло случайно с тянкой, так бывает.
>>382956
мунин не может не быть задротом - посмотри сколько он постов нахуячил, ему же даже поссать некогда, очевидно же что нет личной жизни у него. представь немытый мужик в трусах сидит за компом 24 часа в сутки, там же спит, ест доширак, просыпается от звука пришедшего сообщения и снова по клавишам пиздячит.
Я вообще хуею с его программы.
Ебаный в рот, он вообще видел типичную обычную среднюю школу?
Никто просто не поймет весь этот триппер, учить не будут ничего и выйдет, что такие школьники будут максимум знать программу по математике за 3 класс.
Да и в 10-11 классе на это всем похуй, все хотят пороться, всякие альфачи появляются, никто не будет этим заниматься.
Я вообще за то, чтобы анализ выкинули из школы. Лучше на тригонометрии и логарифмы упор сделать. Ну или теорию множеств и мат логику ввести.
У нас в школе производные объясняли как "штрих". Пределы - училка сказала, мол нахуй это вам, не поймете все равно.
>Вообще говоря, сам матан как наука, в том виде, в котором его изучают в российских вузах (а именно, теория пределов, дифференциальное и интегральное исчисления), был достаточно полезной наукой вплоть до конца XVIII века. Потом появилась эта ваша общая топология, которая перевела половину математики на новые рельсы и отправила старую половину материала на свалку. Поэтому взятие интегралов стало нужно лишь инженерам… к радости которых в ХХ веке появились компьютеры, к Y2K запилили всякие Wolfram Alpha и AutoCADы, а конкретные вычислительные задачи и прочие расчёты бухгалтерии стали решать не ручками, а численными способами (то есть с использованием вычислительной математики).
>И хотя матан «в себе» уже давно не актуален с научной точки зрения, преподаётся он повсеместно и в этой стране, и в забугорье, ибо есть основа или предтеча всех вещей, описанных выше. Не зная матан, заниматься функаном и той же топологией — дело гиблое.
>Таким образом, нынешние профессиональные математики-исследователи занимаются вообще другими вещами и вычисляют не пределы, а кольца когомологий, (а также дисперсию души, Григорий Перельман гарантирует это!); а вот прикладники, что делают из теории что-то юзабельное, в гробу видали все эти изъёбы с карандашом и бумажкой; а умение брать тройные интегралы символьно в настоящее время актуально только для того, чтобы решать первоапрельские матановые капчи.

>Ну или теорию множеств и мат логику ввести
Мат логика на информатике. И дети её просто ненавидят и не понимают. А теорию множеств неплохо в самом начале школы, чтобы потом через неё всё объяснять.
вряд ли. альфач не наделен такой экспериментаторской прытью чтобы догадаться себя в жопу ебать. это все-таки научная смекалк. я уже приводил пример с томасом едисоном. сука с ютюба выпилили английский вариант, только венгерский остался
https://www.youtube.com/watch?v=JuXBJJ1bRa8
thomas, what are you doing?!!
experimenting!
Только что хотел тебе это написать.
Бруквалюб там еще есть - он адекватный достаточно. Мне так показалось.
Помню тему, какой-то бизнесмен создал тред, мол, что высшее образование ненужно, там так полыхало, пиздец короче!
http://dxdy.ru/post208426.html
кстати мунин кажется не любит и комплексует перед ирл математиками. там был какой-то мгушный препод постящий под рилнейм, и пока он оттуда не ушел, они постоянно с муниным срались. моча конечно их не банила за срач,а только ласково журила, заслуженные хуле.
может мунин - образованец-ферматик?
>анализ выкинули из школы
так и не во всех быдлошколках он есть. а если есть (какие-нибудь производные) то только в книжках, но пацаны то не в курсе.
>так и не во всех быдлошколках он есть. а если есть (какие-нибудь производные) то только в книжках, но пацаны то не в курсе.
ЕГЭ все школы сдают. В 11 класс тру-быдло не берут (им самими это нахуй не надо). Производные изучаються в 10-11 классе.
ну егэ. сдаешь базовую, решаешь задачки "петя живет на 5-м этаже".

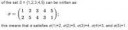
Недостающее определение того, что такое σ(n)
нет, не вычислил. Переполнение
Книга хорошо читается, но терминология старая пиздец.
http://demonstrations.wolfram.com/LHospitalsRuleFor00Forms/
Комбинаторика.

Нужна другая теорема.
Решение предела Арнольда.
мимо-дайн
Что я знаю из электротехники - знаю из книги Бессонова и гугла. Все.
Вот нахуя это ВО нужно? НАХУЯ БЛЯДЬ СУКА! Если не работаешь по специальности - оно все забудется.
Лучше бы сделали ВО платным, чтобы никто туда не ломился, раз никто не будет туда идти, а жить как-то стране надо - работодатели будут более адекватны и будут брать всех людей, где ВО не нужно по сути.
А нужно оно чуть меньше чем нигде.
Вот я по специальности АСУшник. Я нихуя не знаю даже кем я могу работать. Нахуя я учусь? Знал бы я раньше, что это за дерьмо, пошел бы в шарагу.
Заочно всегда можно "добить".
А конкретных таких знаний, например охуенные знания в электронике, чтобы я смог понять, как ябучий приемник работает и спаять его сам. Сам рассчитать, купить детали и спаять - я не могу! Я ебаный импульный преобразователь напряжения на дросселе на двух транзисторах не пойму как работает. Спаять смог, а понять нет
Чтобы прямо понятно было, вот чтобы очевидно, тривиально, сука! Не понимаю.
Чему я учился? Сука, даже ПТУшник успешнее, он хотя бы хуйней не страдал, а знаний у него столько же сколько и у меня примерно.
Ебаное высшее образование. Из-за того что оно бесплатное, оно обесценилось и по сути, его уже ОБЯЗАН иметь почти каждый. Оно нахуй не нужно на 90% профессий, но, СУКА, надо иметь! И битард, не имея ни малейшего желания, вынужден страдать хуйней 4 года!
Автоматизированные системы управления.
Есть такой предмет ТАУ - теория автоматического регулирования.
Там математики дохуя. Когда ТАУ началась - естественно все уже математику забыли нахуй.
А препод просто хуярил в стиле Бурбаки, то есть просто говорил кучу формул, иногда вставляя словосочетания вроде "критерий Гурвица", "система устойчива", "характеристический полином" и так далее.
Нихуя не поняв, но сдав экзамен, я нашел книжку Полякова (Теория автоматического управления для чайников) вроде называется.
Вот только тогда понял что я изучал. Ну как понял, общую суть, для чего предмет и что он изучает.
А так, нужна математика, картофан, да. Но я уже все забыл, а куча хардкорщиков с dxdy вообще отбили желание учиться.
Это же полный П. Этот, блядь, учебник устарел, этот хуевый.
Да как он, пидарас, мог устареть? Для математиков он устарел, да, но чтобы понять суть и научиться применять исчисление бесконечно малых он не устарел.
Тот же учебник Лузина. Или Фихтенгольц (хотя мне Фихтен ВООБЩЕ не пошел). Бермант и Араманович - хорошо попер зато. Но я уже все забыл нах.
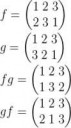
>Докажи
Для удоства будем считать, что A={1;2;3;...n}, если А состоит не их чисел, то мы может биективно отобразить его a_n -> n.
Отображений из 1-> t(1) - n, тогда 2->t(2) n-1 (мы не можем отобразить 2 в t(1), по опредению перестановки, как биективного А-> A) отображений из 3-> t(3) n-2 (не можем отобразить 3 в t(1) и t(2)) .... n-1->t(n-1) - 2 (не можем отобразить n-1 в t(1),...,t(n-2)) и n->t(n) - 1
По правилу произведения количество перестановок равно n(n-1)(n-2)...2*1=n!
1.4
Нет. Пик.
Мунин разработал программу для школьников по математике.
Это, конечно, более приземленная программа, но тоже даст просраться )
1. Современные статьи ты будешь читать с общепринятой терминологией на английском
2. Отсутствие элементов топологии и теории множеств вообще, поэтому первые главы совершенны нестроги и невнятны, определения каких-либо чисел вообще не дается
Совершенно дурацкое изложение множества тем, опять же из-за отсутствия нужного уровня формализма, криволинейный интеграл это вообще нечто мистическое
3. Половина учебника посвящена всяким там приемчикам, чтобы дифференцировать и интегрировать на необитаемом острове, как чертить графики и вообще справочным материалом. При этом калькулюс для теоретика это только старт, начало пути, сейчас не времена Лузина, впереди еще 25 книжек по другим темам. Хотя все же, это учебник для втузов, но для "прикладного математика" в 2016 году не использовать компьютер это нонсенс, чем он вообще тогда занят?

Кто решал?
Моя ошибка пикрел. Я думал там модуль икс и модуль игрек нужно.

a. 120 (5 факториал). 120/5=24 оставляют 1 на месте.
б. 120/5=24 переводят 1 в 5.
в.
24 --- множество всех σ(1)=1
+
24-6 --- множество всех σ(1)=2, таких что σ(1) < σ(2)
+
24-12 --- множество всех σ(1)=3, таких что σ(1) < σ(2)
+
6
Итого: 48+12=60
г.
20 штук.
У меня с тобой >>382994 отличается ответ на пукнт в и г. Кек.
В итоге выходит, что на дваче сказали, что учебник Лузина "это картофан, нах, его только под водовку можно читать))" - ну хули, поцу разорвало, думает, сейчас я вам, суки, покажу!
Берет Бурбаки и обсирается на первой или второй странице. Ладно, Лорана Шварца читнем или Зорича (Зорич это адаптированный Лоран Шварц). Ну хуле, страниц 40-50 пройдено, так, ну-ка порешаем задачи. Я ж теперь умный, блядь! Теория множеств это не хуй собачий!
Так, так... Е-е-еба-а-ать... Нихуя не получается. Да еще и гуглить каждое понятие приходится, одно нагуглил, второе встретилось, нагуглил его, сука, первое забыл. Да ебаный врот!
То есть, хоть и пишут, что мол с нуля все поясняем, на самом деле нихуя.

А я анализ по Штурму учу! Там предел надо воспринимать на интуитивном уровне, никаких множеств и в помине нет, но зато лампово то как.
Это ведь не учебники для туземцев, они предполагают нормальное советское образование. Ну, ту же "алгебру" Колмогорова прорешай, а потом уже за Зорича берись. И все сильно проще станет.
Единственный недостаток - это старая терминология.
Но это как говорить, что в СССР было хуево, потому что смартмоны не изобрели тогда еще.
Тот же Понтрягин люто хуесосил современный подход, когда пихают теорию множеств и эту формалистику ебаную везде.
Надо придрочиться сначала, чисто на интуиции понять, а потом угорать по-хардкору.
А иначе, будет так - задачи решать не научишься. Да и нахуя, это же зашквар, на дваче не поймут.
А вся теория улетучится нахуй, или просто хуево усвоится.
То есть: вроде как и нихуя не знаешь.
Вот-вот, там как начнут обсасывать тему, так все, пиздец, выносите нахуй.
Предикат, исчисление, формальная теория, логика первого и высшего порядков, парадокс Рассела, Кантора - все это дерьмище как бы между прочим говориться, будто бы любой советский человек это знает.
Все эти значки ябучие и их "автоматический" перевод в башке требует времени чтобы понимать и применять их на автомате.
Я пол дня потратил чтобы ебаный парадокс Рассела понять.
У Зорича, сука, он еще вводится так, типа смотрите, есть такая хуйня что множество всех множеств это совсем неочевидное понятие. И дальше парадокс Рассела.
А на самом деле множество всех множеств - это вроде парадокс Кантора.
Не совсем наивная теория множеств Вавилов, сам нашел, аноны сюда http://www.patryshev.com/books/set-int.pdf




(1 2 4)
>>383024
Если тебе такое заходит, то можешь ещё Харди прочесть. Никаких множеств там нет, много где используеться геометрический подход, задачи ХАРДовые.
Мне кажется тут должны быть люди, знакомые с конспектами Вавилова.

- Не знаю. Не дошел еще до этого. Сейчас аксиомы ZFC заучиваю. А еще понятие предела впереди. Ах да, топологическое и метрическое пространство, много всего в общем.
- Не, ну это... можешь так, ну, примерно почувствовать?
- Как это "почувствовать"?
- Ну так, площадь под графиком, сумма довольно малых трапеций под графиком. Быстрота изменения функции, ну эт производная. Ну и дифференциал - линейная функция от функции.
- Ты что, блядь, совсем мудак, что ли... Совсем охуел. Ты сначала определи действительное число чтоб о такой хуйне рассуждать. Знаешь, что R несчетно?
- Но... у меня все работает.
- Да нихуя не работает, вернее, это не доказано!
- А когда докажешь?
- Ну, эт не сразу. Года на 3 растянется.
Качай с twirpx. На сайте у Патрушева старая версия. Вообще жду, когда Вавилов уже допишет свои нетленки. Они у него все хороши, но ни одна не дописана до конца.
Что такое z с черточкой? Производная? Cопряжённое комплексное число? Что-то другое?
ну там в основном элементарщина. Тут такое не любят.

ну устно порешать норм вещь, правда иногда листочек нужен все еж
>sine
>8/5>1
ты не шути так
А как же множество всех заурядных множеств?
Если мы подставляем перестановку длины 34 в перестановку длины 123 -- какой длины получается подстановка?

ты это серьезно? ты пределы арнольда видал? после этого твое - это детский сад. лучше такое не пость - могут обоссать.
а забыл, сорян, мы же в другом треде, я думал это 53-й,
математика "в объеме технического вуза" лол. это интегральчики до опупения что ли
Вот он так опупел, что теорию множеств не может воспринимать.
Поясните мне мое затрудние. Перестановка переводит 34 в 1. Перестановка ^(-1) переводит 1 в 34. Перестановка σ ∘ ^(-1) переводит 1 в 35. Перестановка ∘ σ ∘ ^(-1) не может перевести 35 никуда, т.к. 35 не принадлежит . Но что это означает? Получившаяся перестановка стала определена на 33 элементах? Или я где-то проебался?
Я доволен. От сюда можно вывести, что математиская программа Вербита - это прогрмма по ебли себя в жопу.
Блин. Тау потерялась.

Вот определение цикла.
А его программа - не для обычных средних школ. Она для элитных матшкольников. Вербит ничуть не покушается на право быдла жрать отруби.
картофан и водовка их ждет
Есть выход - образование сделать непомерно дорогим. Тогда будут учебники с картинками и со студентотой будут носиться. И универы чтобы занимались рисерчем и привлекали баблосы. Тогда преподов с большим хиршем будут нанимать и давать им тенуры. Они будут скрипя зубами обучать калкулусу. И все наладится.
Посмотри, чего он добился.
https://ru.wikipedia.org/wiki/Понтрягин,_Лев_Семёнович
>АЗАЗА КАЛМАГОРАВ И ОРНОЛЬД НЕ МОТИМАТИКИ, РАЗ УЧИЛЕСЬ ПА ЭТАМУ УЩЕБНИКУ!!!!
Разрывом твой сраки, как функции обратной пропорциональности годности книги к фантазиям дващера, удовлетворен.
Вернувшись из больницы, я находился в полной растерянности: что делать? Сперва я поступил в специальную школу для слепых и пробыл там в интернате довольно короткое время. Обучение в этой школе совершенно не удовлетворяло ни меня, ни мать, так как учителя не обещали мне ничего большего, чем какое-нибудь ремесло. А у нас ещё сохранилась мечта о будущем, о моём высшем образовании. После этого я вернулся в свою прежнюю школу, в прежний класс, к прежним своим товарищам, которые встретили меня с большой чуткостью и теплотой! Особенно хорошо отнёсся ко мне мой ближайший друг и товарищ Коля Кириллов.
На первых порах обучение в школе после потери зрения не было для меня лёгким. Нелегко мне давалась и математика, поэтому ко мне пригласили репетитора, с которым я специально занимался. Помню, насколько трудно мне было разобраться, например, в такой простой вещи, как параллелограмм, дающий сумму двух векторов. Кажется, это относилось к физике сложения сил и скоростей. Мне было очень трудно представить себе чертёж. Но постепенно мои занятия с репетитором переросли из помощи школьному обучению в самостоятельную деятельность, опережающую школу. Я почувствовал большой вкус к математике.
После революции только первый год обучения я провёл сравнительно нормально. Преподавание в школе было дезорганизовано революцией.
Всё, по-видимому, зависело от учителя. Некоторые учителя грубо пренебрегали своими обязанностями и совершенно не старались нас учить и наводить в классе дисциплину, другие, наоборот, были очень хорошими и умело руководили нами, держали нас в руках.
Среди хороших учителей был любимый мною учитель Горохов, который обучал нас математике в 5-м и 6-м классах, а может быть и позже. Был совершенно отвратительный учитель математики Батманов, преподававший у нас в восьмом классе. Его методы преподавания уже тогда вызывали у меня ярость. Так, например, наизусть произносились всем классом хором формулировки теорем. Другой его способ обучения заключался в том, что ученик имел две тетради, в первой он записывал вопросы, во второй — ответы на эти вопросы. Когда учитель спрашивал урок, он вызывал ученика с первой тетрадью, который должен был прочесть вопрос и потом наизусть ответить записанный во второй тетради ответ.
Мы с этим учителем математики Батмановым возненавидели друг друга, я всячески хулиганил на его уроках, а он притеснял меня, задавая бессмысленный вопрос: почему я не пишу письменную работу? Письменные работы мы обычно делали вместе с Кирилловым, решали все варианты, заданные классу и наши собственные, он записывал оба, а потом мы по классу распространяли все варианты. Так что остальные ученики могли просто списывать.
Вернувшись из больницы, я находился в полной растерянности: что делать? Сперва я поступил в специальную школу для слепых и пробыл там в интернате довольно короткое время. Обучение в этой школе совершенно не удовлетворяло ни меня, ни мать, так как учителя не обещали мне ничего большего, чем какое-нибудь ремесло. А у нас ещё сохранилась мечта о будущем, о моём высшем образовании. После этого я вернулся в свою прежнюю школу, в прежний класс, к прежним своим товарищам, которые встретили меня с большой чуткостью и теплотой! Особенно хорошо отнёсся ко мне мой ближайший друг и товарищ Коля Кириллов.
На первых порах обучение в школе после потери зрения не было для меня лёгким. Нелегко мне давалась и математика, поэтому ко мне пригласили репетитора, с которым я специально занимался. Помню, насколько трудно мне было разобраться, например, в такой простой вещи, как параллелограмм, дающий сумму двух векторов. Кажется, это относилось к физике сложения сил и скоростей. Мне было очень трудно представить себе чертёж. Но постепенно мои занятия с репетитором переросли из помощи школьному обучению в самостоятельную деятельность, опережающую школу. Я почувствовал большой вкус к математике.
После революции только первый год обучения я провёл сравнительно нормально. Преподавание в школе было дезорганизовано революцией.
Всё, по-видимому, зависело от учителя. Некоторые учителя грубо пренебрегали своими обязанностями и совершенно не старались нас учить и наводить в классе дисциплину, другие, наоборот, были очень хорошими и умело руководили нами, держали нас в руках.
Среди хороших учителей был любимый мною учитель Горохов, который обучал нас математике в 5-м и 6-м классах, а может быть и позже. Был совершенно отвратительный учитель математики Батманов, преподававший у нас в восьмом классе. Его методы преподавания уже тогда вызывали у меня ярость. Так, например, наизусть произносились всем классом хором формулировки теорем. Другой его способ обучения заключался в том, что ученик имел две тетради, в первой он записывал вопросы, во второй — ответы на эти вопросы. Когда учитель спрашивал урок, он вызывал ученика с первой тетрадью, который должен был прочесть вопрос и потом наизусть ответить записанный во второй тетради ответ.
Мы с этим учителем математики Батмановым возненавидели друг друга, я всячески хулиганил на его уроках, а он притеснял меня, задавая бессмысленный вопрос: почему я не пишу письменную работу? Письменные работы мы обычно делали вместе с Кирилловым, решали все варианты, заданные классу и наши собственные, он записывал оба, а потом мы по классу распространяли все варианты. Так что остальные ученики могли просто списывать.
Хочеш сказать что со времен ньютона матан КАРДИАНАЛЬНО поменялся?
Эйлер и ко его просто доработали рашпилем, чтобы колмогоровы и прочие его наждаком шлифовали дальше, а так то суть осталась прежней, что с точки зрения множеств, что топологии, что аллаха.
Посмотрите, кстати, как раньше жили. Пацаны душевно общались, не было двачеров, омежек, альфачей.
Очень хорош был учитель химии. Так что мы с Кирилловым увлеклись одновременно математикой и химией. Изучали и ту и другую дисциплины с опережением по сравнению со школой. Химию мы изучали несколько странно. Я, например, выучил наизусть всю периодическую систему элементов Менделеева с атомными весами. Некоторые из них я помню до сих пор.
Был очень хороший учитель русского языка, но фамилию я его не помню. Один из преподавателей истории вёл себя на уроках совершенно возмутительно. Он сидел за учительским столом, подзывал к себе одного из учеников, разговаривал с ним о чём-то, а все остальные ученики могли делать что угодно. Мы хулиганили, двигали парты, бросали стулья, он не обращал на это никакого внимания и не пытался даже навести порядок. Мне кажется, что это была просто форма саботажа.
Той узкой областью математики, в которой Лузин реализовывал своё педагогическое нововведение, была теория множеств. Ученики Лузина подпали под обаяние теории множеств и стали считать её важнейшим новым направлением в области математики. А это мне кажется совершенно неверным. Теория множеств является и не очень новым, и не очень важным разделом математики. Педагогическое открытие Лузина имеет свою оборотную сторону. Молодые люди, в самом начале занявшиеся научной работой в узкой области математики, часто не могут покинуть её и, достигнув уже зрелого возраста, остаются навсегда узкими специалистами, не владеющими в сущности всей математикой или главнейшими разделами её.
Наиболее сильные, конечно, уходят из неё. К числу этих более сильных принадлежал и Колмогоров. Но на всю жизнь он остался под обаянием теории множеств и её идеологии.
Эту теоретико-множественную идеологию он стал внедрять в среднюю школу, где она совершенно неуместна и вредна, так как отодвигает на задний план изучение важнейших навыков вычислять, владение геометрическими представлениями, т.е. конкретные вещи, важные для дальнейшей трудовой деятельности.
Это теоретико-множественное бедствие постигло преподавание математики в средней школе не только в Советском Союзе. Я знаю о том, что такое же явление произошло во Франции, в Англии, в Соединённых Штатах и, вероятно, во многих других странах. Ведущий французский математик Лере резко выступал против теоретико-множественного засилья в средней школе.
Но были и другие причины. О них я хочу рассказать теперь.
Колмогоров очень охотно берётся за всякую новую организационную работу, но очень быстро она ему надоедает, и он передаёт её другим лицам. Именно это произошло при написании новых учебников. Колмогоров принимал участие в написании новых учебников лишь в очень незначительной степени. Потом он передоверил эту работу другим, малоквалифицированным и недобросовестным лицам, которые создали безграмотные отвратительные учебники. Их Колмогоров, вероятно, даже и не просматривал, и они без всякой проверки и апробирования хлынули в средние школы.
Ещё одной чертой колмогоровского характера, которая могла помешать успешному проведению улучшения преподавания, является отсутствие у Колмогорова чувства реальности.
Например, во время войны Московский государственный университет некоторое время находился в эвакуации в Ашхабаде. Довольно много математиков — профессоров физ-мата — находились там же вместе с факультетом. А Колмогоров был в Москве. Он выдвинул следующее предложение: оставить всех находившихся в Ашхабаде математиков там навечно, с тем чтобы они создали там новый научный центр. Сам же Колмогоров брался создать и возглавить факультет с новыми кадрами в Москве и два месяца в году проводить в Ашхабаде.
Среди математиков, находившихся тогда в Ашхабаде, эта колмогоровская идея вызвала бурю протеста. Ведь во время войны все эвакуированные мечтали о возвращении домой, в Москву.
Столь же нереалистическая идея, совершенно не учитывающая интересы людей, была высказана Колмогоровым во время войны по поводу опасности, грозящей деревянной части Москвы от немецких зажигательных бомб. Колмогоров считал, что немцы сумеют поджечь всю деревянную Москву, и для предотвращения этого бедствия предлагал сломать все деревянные дома, а жителей переселить в квартиры ранее эвакуированных граждан.
Той узкой областью математики, в которой Лузин реализовывал своё педагогическое нововведение, была теория множеств. Ученики Лузина подпали под обаяние теории множеств и стали считать её важнейшим новым направлением в области математики. А это мне кажется совершенно неверным. Теория множеств является и не очень новым, и не очень важным разделом математики. Педагогическое открытие Лузина имеет свою оборотную сторону. Молодые люди, в самом начале занявшиеся научной работой в узкой области математики, часто не могут покинуть её и, достигнув уже зрелого возраста, остаются навсегда узкими специалистами, не владеющими в сущности всей математикой или главнейшими разделами её.
Наиболее сильные, конечно, уходят из неё. К числу этих более сильных принадлежал и Колмогоров. Но на всю жизнь он остался под обаянием теории множеств и её идеологии.
Эту теоретико-множественную идеологию он стал внедрять в среднюю школу, где она совершенно неуместна и вредна, так как отодвигает на задний план изучение важнейших навыков вычислять, владение геометрическими представлениями, т.е. конкретные вещи, важные для дальнейшей трудовой деятельности.
Это теоретико-множественное бедствие постигло преподавание математики в средней школе не только в Советском Союзе. Я знаю о том, что такое же явление произошло во Франции, в Англии, в Соединённых Штатах и, вероятно, во многих других странах. Ведущий французский математик Лере резко выступал против теоретико-множественного засилья в средней школе.
Но были и другие причины. О них я хочу рассказать теперь.
Колмогоров очень охотно берётся за всякую новую организационную работу, но очень быстро она ему надоедает, и он передаёт её другим лицам. Именно это произошло при написании новых учебников. Колмогоров принимал участие в написании новых учебников лишь в очень незначительной степени. Потом он передоверил эту работу другим, малоквалифицированным и недобросовестным лицам, которые создали безграмотные отвратительные учебники. Их Колмогоров, вероятно, даже и не просматривал, и они без всякой проверки и апробирования хлынули в средние школы.
Ещё одной чертой колмогоровского характера, которая могла помешать успешному проведению улучшения преподавания, является отсутствие у Колмогорова чувства реальности.
Например, во время войны Московский государственный университет некоторое время находился в эвакуации в Ашхабаде. Довольно много математиков — профессоров физ-мата — находились там же вместе с факультетом. А Колмогоров был в Москве. Он выдвинул следующее предложение: оставить всех находившихся в Ашхабаде математиков там навечно, с тем чтобы они создали там новый научный центр. Сам же Колмогоров брался создать и возглавить факультет с новыми кадрами в Москве и два месяца в году проводить в Ашхабаде.
Среди математиков, находившихся тогда в Ашхабаде, эта колмогоровская идея вызвала бурю протеста. Ведь во время войны все эвакуированные мечтали о возвращении домой, в Москву.
Столь же нереалистическая идея, совершенно не учитывающая интересы людей, была высказана Колмогоровым во время войны по поводу опасности, грозящей деревянной части Москвы от немецких зажигательных бомб. Колмогоров считал, что немцы сумеют поджечь всю деревянную Москву, и для предотвращения этого бедствия предлагал сломать все деревянные дома, а жителей переселить в квартиры ранее эвакуированных граждан.
Здесь большую роль сыграла многотомная энциклопедия Гранат из библиотеки моего отца, в которой я читал статьи по математике. Особенно интересной и полезной была для меня статья «Высшая математика», написанная известным в то время математиком Л. К. Лахтиным 1. Эту статью я перечитал недавно и пришёл к заключению, что она написана хорошо и очень полезна для юношества.
Мои знания по математике были очень активны. Я постоянно занимался вычислениями, проводя их по необходимости в уме, решал геометрические задачи на построение. Всё время думал о математике.
Умение проводить вычисления в уме, мне кажется, у математиков столь же естественно, как у актёра знание большого количества пьес и литературных отрывков наизусть. Навык вычислять в уме, совершенно необходимый мне, приводил к тому, что я проводил вычисления особенно тщательно, стараясь осуществить их как можно проще. В частности, при проведении вычислений я всегда очень тщательно выбирал (и продолжаю это делать теперь) обозначения.
Я считаю, что хороший выбор обозначений чрезвычайно важен, так как при чтении математической литературы значительная часть усилий тратится на запоминание именно обозначений. Поэтому плохо выбранные обозначения вызывают у меня такое же ощущение, которое, вероятно, вызывает у музыкантов фальшивая нота. Всю жизнь, начиная со школьных лет до настоящего времени, я постоянно тренировался и тренируюсь в проведении вычислений, занимаясь этой деятельностью зачастую без всякой прямой необходимости. Я думаю, что это так же нужно математику, как музыканту постоянные упражнения в игре на своём инструменте. Конечно, я имею в виду не числовые, а формульные вычисления.
А ещё он выучил гомологии.
Зорича нету в интернетах(
За 50 рублей предлагают купить,
если есть в электронке поделитесь пожалуйста)
gen.lib.rus.ec
Вы видите копию треда, сохраненную 22 ноября 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


































