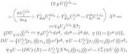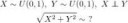Вы видите копию треда, сохраненную 6 декабря 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
Обсуждаем и дополняем!

Откуда третий пик? Помню, что где-то это уже видел. А где забыл.
Его там нет.
Анон около четырёх раз просил помочь ему с Бауусом-Бонне, при этом каждый раз пытался придумать новую формулировку, чтобы обратить внимание на свой вопрос. Но ему никто так и не объяснил. До сих пор.

1. "Лекции по функциональному анализу" А. Я. Хелемский
2. Дубровин Б. А., Новиков С. П., Фоменко А. Т. "Современная геометрия: методы и приложения"
3. "Анализ" Л. Шварц
4. "Математические методы классической механики" В. И. Арнольд
Анон тот кажется споткнулся даже не на теореме, а на пререквизитах - осмыслении геодезической кривизны и сетовал по поводу грубого захода через ковариантные производные. В итоге ему посоветовали не доебывать школьников а лучше расспросить Вербита лично. С тех пор он пропал. Наверное уже уехал в ДС и скоро вернется с новостями. Вот за кого я реально волнуюсь, это за анона с модулями. Он был близок к суициду.



> С тех пор он пропал
Нет. Разве >>383114 >>383125 не он?
>Он был близок к суициду
Уже, наверное. Несколько дней его как нет.
>не он?
Не, я мимо-крокодил. И смысла Гаусса-Бонне пока не понял. Хотя уже забил 790 строк в математику. Торы какие-то, гауссова кривизна, малофья.

фу какая гадость! в смысле годнота.
>Единственная профессор-женщина, она выделялась среди коллег хорошим тоном, изяществом и привлекательностью
так она няшная была?

4 пи-фикс
Прям вся суть нити в сци.
Да, ОП молодец, годная шапка.
Первая пикча божественна.
Понтрягин, кстати, люто хуесосил книгу Зельдовича и решил написать свои.

Вещь! Всем советую.
Понтрягин - сраный тупорылый антисемит, травил евреев. И брошюрка его говноедская, и сам он говноед, фубля, аж бесит.
Он их не травил.
Наоборот, многим помогал, когда некоторых посадили на зону, например.
Просто ему пекло от того что евреям пекло от того что евреев "слишком мало" в математике, в то время как, их было слишком много.
Вот Виноградов угорал по-харду вообще.
Виноградов тоже удивительный человек. Здоровый кач был. Мог поднять одной рукой за ножку стула человека на нем сидящего.
А ты сам каких математиков уважаешь?
Каждан.
Самое главное в математике не теория множеств, а умение доказывать. А это умели и древние греки.
в голосину с dxdy ))))))))))))))))))))
!!!А потом в предисловии написал, что Зельдович пиздат (точнее о его взгялдах). Об этмо инциденте рассказывал Арнольд в начале своей книги "Что такое математика"
Арни говорил, что книги Понтрягина скучные, как обои Windows, и Арни говорил, что одобряет книгу Зельдовича.
Мне же она не пошла вообще. Все внавал нахуярено, перемешано и предложено въебать под водовку.
Нигде не читал, что Понтрягин одобрял книги Зельдовича.
Если нашел такое - скинь читнуть.
а вообще Арни с Понтрягином не очень ладил, в свое время Понт лишил Арни премии Филдса и приложил к этому не мало усилий
Об этом хорошо написано в "Апологии математики" одного из моих любимых математиков Владимира Успенского
Как я понял, просто Понтрягин сказал, мол, ну да, по идее чтобы применять математику, считать объем ящика, решать демидовича, необязательно знать что такое эпсилон-дельта, производная это короч скорость, а интеграл площадь.
Но книги по математике так писать все равно не следует - будет ложная уверенность, что все просто, и привычка мыслить аналогиями. вот, что я думаю он имел в виду.
Как я понял, просто Понтрягин сказал, мол, ну да, по идее чтобы применять математику, считать объем ящика, решать демидовича, необязательно знать что такое эпсилон-дельта, производная это короч скорость, а интеграл площадь.
Но книги по математике так писать все равно не следует - будет ложная уверенность, что все просто, и привычка мыслить аналогиями. вот, что я думаю он имел в виду.
Залил первую пикчу на dxdy
http://dxdy.ru/topic54533-120.html
Посмотрим, как отреагируют старпёры (хотя наверняка им будет просто похуй)
http://dxdy.ru/topic105594.html
http://dxdy.ru/topic108092.html
С последнего проиграл вообще.
Это байка, он таки слушал лекции. Но начинал сам. Как и индийский математик Рамануджан, он тоже чуть ли не в чистую сам.
Баян ))))))))))))
Но там и не такое было, куда больше доставляют жалобы на модераторов и Ферма-подфорум, вот там я лулзов много словил
Интересные пособия по элементарной математике:
Это должен знать каждый матшкольник - Гордин
Энциклопедия Элементарной математики в 5 томах
Курс чистой математики - Гильберт
Элементарная математика - Олег Иванов
Элементарная математика с точки зрения высшей - Феликс Клейн
2 справочника Выгодского
Прикладная математика- зельдович
И по высшей выделю: Конспект лекций по высшей математике - Письменный (+задачники к ней)
Анализ (Азы):
Знакомство с высшей математикой - Понтрягин (4 книги)
Восемь лекций по матанализу - Хинчин
Высшая математика для начинающих и ее приложения к физике - Зельдович
Теория чисел (для школьников):
Курс арифметики - Жан Пьер Серр
Диофант и диофантовы уравнения - Башмакова
Арфиметика и алгебра - Опойцев
Неравенства - Харди, Литлвуд, Пойа
Задачи с параметрами - Субханкулова
Три жемчужины теории чисел - Хинчин
Великая теорема Ферма - Хинчин
ВТФ - Постников
Цепные дроби - Хинчин
Методы доказательства неравенств - Седракян, Авоян
Книги Чирского по уравнениям
Логика:
Введение в математику - Клини
Математическая логика - Клини
Святое, прочитать должен каждый
Некоторые интересные книги по элементарной геометрии:
Четырехмерная геометрия Элективный курс - Смирновы
Геометрия - Тихомиров и Прасолов
Геометрия Избарнные леции - Шарыгин
Геометрические миниатюры - Скопец
Наглядная геометрия - Гильберт
Основания геомтерии - Гильберт
Новая геометрия треугольника (Книг с таким названием 2, обе рекомендуются)
Геометрия Поиск и Вдохновление - Кушнир
Триумф школьной геометрии - Кушнир
Возвращение утраченной геометрии - Кушнир
Геометрические воспоминания - Кушнир
Геометрическое многоборье 7-9 - Кушнир
Геометрия в 2 томах - Кушнир
Шедевры школьной математики - Кушнир (тут не только про геометрю)
Этот мужик - вообще, классик от области, у него можно любые книги читать
Алгебра и теория чисел:
Введение в теорию групп - Павел Александров
Элементарное введение в абстрактную алгебру - Фрид (Приятная простенькая книжка, то что нужно для старта)
Многочлены - Прасолов
Теория чисел - Бухштаб (Виноградова не читать - помойка)
Курс высшей алгебры - Курош
Лекции по общей алгебре - Курош
Теория групп - Курош
Эту триаду должен прочитать каждый уважающий себя алгебраист
Геометрия:
Что такое неэвклидова геометрия - Павел Алекснадров
Лекции по геомтрии Лобачевского - Прасолов
Лекции по геометрии - Постников (6 книг на пять семестров, курс на всё про всё, рекомендую)
Высшая геометрия - Ефимов (Классика, по фасту, чтобы начать)
Высшая геометрия - Феликс Клейн
Теория Галуа и алгебра:
Обязательно читать фундаментальный труд Чеботарева, а именно
1. Основы теории Галуа I
2. Основы теории Галуа II
3. Теория Галуа
4. Теория групп Ли
5. Введение в теорию алгебр
6. Теория алгебраических функций
Все можно скать, все переиздавались URSS. После них вам может вкатить и двухтомник его избранных трудов.
Теория Галуа - Постников (Но после Чеботарева уже можно и не читать)
Топологическая теория Галуа - Хованский
Теория Галуа, накрытия и римановы поверхности - Хованский
Эти 2 читать, когда ты уже "таполаг" и в теории Галуа тоже шаришь.
Фрактальчики (не нелинейная динамика, а только фрактальчики):
"Просто фрактал, "Артфрактал", "Суперфрактал" и "Фрактал. Между мифом и ремеслом" - Сергей Деменюк (Неплохие но с претензиями популярные книжки по теории
фракталов)
Введение в теорию фракталов - Морозов (Хорошее введение с множеством иллюстраций, читается за 1 присев)
Фрактальная геометрия природы - Мандельброт (КЛАССИКА!!11 БИБЛИЯ!!11 СВЯТОЕ!! Но нематематику будет сложно а точнее он почти нихуя не поймет)
Линейка и аналитическая геометрия:
Основы линейной алгебры - Мальцев (Классика)
Курс аналитической геометрии и линейной алгебры - Павел Александров (Простенький курс)
Лекции по аналитической геометрии, пополненые необходимыми сведениями из алгебры (Курс посложнее, для продвинутых)
А вообще Александрова всего можно читать (у него много учебников на разные темы), как говорил дед с dxdy (brukvalub): У Александрова был ясный ум, поэтому его
учебники не стареют со временем.
Задачи и теоремы линейной аглебры - Прасолов
Диффуры:
Лекции об уравнениях с частными производными - Петровский (Классика)
Лекции об уравнениях с частными производными - Ольга Олейник (Более модернизированный, тут по вкусу)
Лекции по теории обыкновенных дифференциальных уравнениях - Петровский (Классика)
бонусом читаем Лекции по теории интегральных уравнений Петровского же
Обыкновенные дифференциальные уравнения - Арнольд
Геометрические методы в теории обыкновенных дифференциальных уравнений - Арнольд (Старое название: Дополнительные главы теории ОДУ)
Все перечисленные здесь книги - классика, но на мой взгляд предпочтительней Петровскиий + Вторая книга Арнольда
История математики:
Математика древняя и юная - Панов
Современная математика и её творцы - Панов (Немного обо всем, но книга скорее популярная, а не полноценный учебник)
История Отечественнйо математики - Штокало (В 4 частях, но 5 книгах)
Математика в её историческом развитии - Колмогоров
Пробуждающаяся наука - Ван дер Варден (В двух частях)
Утрата определенности - Морис Клайн (Популярно написано, а также классика)
поиск истины - Морис Клайн (Популярно написано, а также классика)
Математика. Ее содержание, значенеи, методы - Колмогоров
Дискретка:
Конкретная математика - Кнут и 2 его кореша (Это главная книга по дискретке)
Теория множеств:
Теория множеств - Хаусдорф (С неё все начиналось, читать вторео издание в переводе Александрова и Колмогорова)
Введение в общую теорию множеств и функций - Павел Александров
или как вариант: Введение в теорию множеств и общую топологию (Александрова же)
Оснвания теории множеств - Френкель, Бар-Хиллел
Теория меры - халмош
Последние 2 для продвинутых.
Алгебраическая геометрия:
Основы алгебраической геометрии Шафаревич
Элементы алгебраической геометрии Гротендика (Её ещё называют Евангелие от Гротендика, только на французком и английском)
Принципы алгебраической геометрии - Гриффитс, Харрис (В 2 томах)
Теория Ходжа в 2 книгах - Клэр Вуазен (Это читать, когда уже сможете изучать математику, не закидываясь LSD)
Интересные пособия по элементарной математике:
Это должен знать каждый матшкольник - Гордин
Энциклопедия Элементарной математики в 5 томах
Курс чистой математики - Гильберт
Элементарная математика - Олег Иванов
Элементарная математика с точки зрения высшей - Феликс Клейн
2 справочника Выгодского
Прикладная математика- зельдович
И по высшей выделю: Конспект лекций по высшей математике - Письменный (+задачники к ней)
Анализ (Азы):
Знакомство с высшей математикой - Понтрягин (4 книги)
Восемь лекций по матанализу - Хинчин
Высшая математика для начинающих и ее приложения к физике - Зельдович
Теория чисел (для школьников):
Курс арифметики - Жан Пьер Серр
Диофант и диофантовы уравнения - Башмакова
Арфиметика и алгебра - Опойцев
Неравенства - Харди, Литлвуд, Пойа
Задачи с параметрами - Субханкулова
Три жемчужины теории чисел - Хинчин
Великая теорема Ферма - Хинчин
ВТФ - Постников
Цепные дроби - Хинчин
Методы доказательства неравенств - Седракян, Авоян
Книги Чирского по уравнениям
Логика:
Введение в математику - Клини
Математическая логика - Клини
Святое, прочитать должен каждый
Некоторые интересные книги по элементарной геометрии:
Четырехмерная геометрия Элективный курс - Смирновы
Геометрия - Тихомиров и Прасолов
Геометрия Избарнные леции - Шарыгин
Геометрические миниатюры - Скопец
Наглядная геометрия - Гильберт
Основания геомтерии - Гильберт
Новая геометрия треугольника (Книг с таким названием 2, обе рекомендуются)
Геометрия Поиск и Вдохновление - Кушнир
Триумф школьной геометрии - Кушнир
Возвращение утраченной геометрии - Кушнир
Геометрические воспоминания - Кушнир
Геометрическое многоборье 7-9 - Кушнир
Геометрия в 2 томах - Кушнир
Шедевры школьной математики - Кушнир (тут не только про геометрю)
Этот мужик - вообще, классик от области, у него можно любые книги читать
Алгебра и теория чисел:
Введение в теорию групп - Павел Александров
Элементарное введение в абстрактную алгебру - Фрид (Приятная простенькая книжка, то что нужно для старта)
Многочлены - Прасолов
Теория чисел - Бухштаб (Виноградова не читать - помойка)
Курс высшей алгебры - Курош
Лекции по общей алгебре - Курош
Теория групп - Курош
Эту триаду должен прочитать каждый уважающий себя алгебраист
Геометрия:
Что такое неэвклидова геометрия - Павел Алекснадров
Лекции по геомтрии Лобачевского - Прасолов
Лекции по геометрии - Постников (6 книг на пять семестров, курс на всё про всё, рекомендую)
Высшая геометрия - Ефимов (Классика, по фасту, чтобы начать)
Высшая геометрия - Феликс Клейн
Теория Галуа и алгебра:
Обязательно читать фундаментальный труд Чеботарева, а именно
1. Основы теории Галуа I
2. Основы теории Галуа II
3. Теория Галуа
4. Теория групп Ли
5. Введение в теорию алгебр
6. Теория алгебраических функций
Все можно скать, все переиздавались URSS. После них вам может вкатить и двухтомник его избранных трудов.
Теория Галуа - Постников (Но после Чеботарева уже можно и не читать)
Топологическая теория Галуа - Хованский
Теория Галуа, накрытия и римановы поверхности - Хованский
Эти 2 читать, когда ты уже "таполаг" и в теории Галуа тоже шаришь.
Фрактальчики (не нелинейная динамика, а только фрактальчики):
"Просто фрактал, "Артфрактал", "Суперфрактал" и "Фрактал. Между мифом и ремеслом" - Сергей Деменюк (Неплохие но с претензиями популярные книжки по теории
фракталов)
Введение в теорию фракталов - Морозов (Хорошее введение с множеством иллюстраций, читается за 1 присев)
Фрактальная геометрия природы - Мандельброт (КЛАССИКА!!11 БИБЛИЯ!!11 СВЯТОЕ!! Но нематематику будет сложно а точнее он почти нихуя не поймет)
Линейка и аналитическая геометрия:
Основы линейной алгебры - Мальцев (Классика)
Курс аналитической геометрии и линейной алгебры - Павел Александров (Простенький курс)
Лекции по аналитической геометрии, пополненые необходимыми сведениями из алгебры (Курс посложнее, для продвинутых)
А вообще Александрова всего можно читать (у него много учебников на разные темы), как говорил дед с dxdy (brukvalub): У Александрова был ясный ум, поэтому его
учебники не стареют со временем.
Задачи и теоремы линейной аглебры - Прасолов
Диффуры:
Лекции об уравнениях с частными производными - Петровский (Классика)
Лекции об уравнениях с частными производными - Ольга Олейник (Более модернизированный, тут по вкусу)
Лекции по теории обыкновенных дифференциальных уравнениях - Петровский (Классика)
бонусом читаем Лекции по теории интегральных уравнений Петровского же
Обыкновенные дифференциальные уравнения - Арнольд
Геометрические методы в теории обыкновенных дифференциальных уравнений - Арнольд (Старое название: Дополнительные главы теории ОДУ)
Все перечисленные здесь книги - классика, но на мой взгляд предпочтительней Петровскиий + Вторая книга Арнольда
История математики:
Математика древняя и юная - Панов
Современная математика и её творцы - Панов (Немного обо всем, но книга скорее популярная, а не полноценный учебник)
История Отечественнйо математики - Штокало (В 4 частях, но 5 книгах)
Математика в её историческом развитии - Колмогоров
Пробуждающаяся наука - Ван дер Варден (В двух частях)
Утрата определенности - Морис Клайн (Популярно написано, а также классика)
поиск истины - Морис Клайн (Популярно написано, а также классика)
Математика. Ее содержание, значенеи, методы - Колмогоров
Дискретка:
Конкретная математика - Кнут и 2 его кореша (Это главная книга по дискретке)
Теория множеств:
Теория множеств - Хаусдорф (С неё все начиналось, читать вторео издание в переводе Александрова и Колмогорова)
Введение в общую теорию множеств и функций - Павел Александров
или как вариант: Введение в теорию множеств и общую топологию (Александрова же)
Оснвания теории множеств - Френкель, Бар-Хиллел
Теория меры - халмош
Последние 2 для продвинутых.
Алгебраическая геометрия:
Основы алгебраической геометрии Шафаревич
Элементы алгебраической геометрии Гротендика (Её ещё называют Евангелие от Гротендика, только на французком и английском)
Принципы алгебраической геометрии - Гриффитс, Харрис (В 2 томах)
Теория Ходжа в 2 книгах - Клэр Вуазен (Это читать, когда уже сможете изучать математику, не закидываясь LSD)
Первые понятия топологии - Стинрод, Чинн
Дифференциальаня топология - Милнор, Уолесс
Эти две простые и поплурные, одна могут послужить неплохим введением, обе выхрдили в рамках серии Современная математика от издательства мир
Мемуар о компактных топологических пространствах - Урысон, Александров (изи введение, классика)
Общая топология - Энгелькинг (Библия топологов!)
Учебник Вербита по топологии неплох, может посоперничать с "Элементарной топологией" Виро-Харламова-Нецветаева-Иванова
Элементы комбинаторной и дифференциальной топологии - Прасолов (I часть)
Элементы теории гомологий - Прасолов (II часть)
Задачи по топологии - Прасолов
Основы теории гомотопий - Постников (I часть)
Теория гомотопий клеточных пространств - Постников (II часть)
Теория гомологий. Введение в алгебраическую топологию - Вик Дж.
Общая теория гомологий - Павел Александров
Введение в теорию размерности - Павел Александров
Введение в гомологическую теорию размерности - Павел Александров
Теория размерности и смежные вопросы. Статьи общего характера - Павел Александров
Гомотопическая теория типов (HoTT) - Для продвинутых, каждый современный математик её читал
+бонусом Алгоритмическая топология и классификация трехмерных многообразий - Матвеев
Топологическо-геометрические курсы от Фоменко & Co. (МГУ-бригада:)
ОСНОВНОЕ:
Курс наглядной геометрии и топологии - Ошемков, Попеленский, Тужилин, Фоменко, Шафаревич
---
Введение в топологию - Борисович, Близняков, Израилевич, Фоменко
---
Современная геометрия. Методы и приложения (в 3 томах) - Дубровин, Новиков, Фоменко
---
Курс гомотопической топологии - Фоменко, Фукс
---
Краткий курс дифференциальной геометрии и топологии - Мищенко, Фоменко (нихуя он не краткий)
Сборник задач по дифференциальной геометрии и топологии - Мищенко, Соловьев, Фоменко
---
Дополнительно:
Элементы геометрии и топологии минимальных поверхностей - Тужилин, Фоменко
Элементы дифференциальной геометрии и топологии - Новиков, Фоменко
---
Геометрия и топология интегрируемых геодезических потоков на поверхностях - Алексей, Фоменко
Дифференциальная геометрия и топология. Дополнительные главы - Фоменко
---
Алгоритмические и компьютерные методы в трехмерной топологии - Матвеев, Фоменко
---
Компьютерная геометрия - Ильютко, Носовский, Фоменко, Голованов
Некоторые математические серии и журналы (в основном простеенькие):
Серия Основания математики (главным образом двухтомник Гильберта)
Серия Библиотечка Квант и сам Журнал Квант (можно еще и журнал Квантик)
Журнал Историко-математические очерки
Журнал Успехи математических наук (что осилишь)
Труды Московского математического общества
Труды Американского математического общества
Труды Математического института имени Стеклова
Срия Школьные математические кружки (очень простенькая, так что особо задерживаться на ней не надо, но галвное геометрию построения посмотреть)
Серия Учим математике (МЦНМО), это по вопросам преподавания, но там есть и задачки
Серия турнир Архимеда
Серия турнир Ломносова
Серия турнир Савина
Серия турнир Шарыгина
Серия турнир Эйлера
Серия математика Элективный курс
Серия библиотека маткружка
Серия библиотечка Физико-Математической школы
Журнал Математическое просвещение (!!!)
Серия Библиотека Математической просвещение
Серия Летняя Математическая школа
Серия Популярные лекции по математике
Серия Шедевры мировой физико-математической литературы
Серия турниры Городов
Серия Элементы математики (Да и вообще все Бурбаки)
Серия математика в техническом университете (diary.ru/~eek/p67723918.htm)
Серия Классические направления в математике
Серия Классические направления в математике
Серия Современные лекционные курсы
Серия Новые математические дисциплины
Серия Математическая библиотека
Серия Математическая библиотечка
Серия Математика. Элективные курсы
Серия Прикладная математика и информатика
Первые понятия топологии - Стинрод, Чинн
Дифференциальаня топология - Милнор, Уолесс
Эти две простые и поплурные, одна могут послужить неплохим введением, обе выхрдили в рамках серии Современная математика от издательства мир
Мемуар о компактных топологических пространствах - Урысон, Александров (изи введение, классика)
Общая топология - Энгелькинг (Библия топологов!)
Учебник Вербита по топологии неплох, может посоперничать с "Элементарной топологией" Виро-Харламова-Нецветаева-Иванова
Элементы комбинаторной и дифференциальной топологии - Прасолов (I часть)
Элементы теории гомологий - Прасолов (II часть)
Задачи по топологии - Прасолов
Основы теории гомотопий - Постников (I часть)
Теория гомотопий клеточных пространств - Постников (II часть)
Теория гомологий. Введение в алгебраическую топологию - Вик Дж.
Общая теория гомологий - Павел Александров
Введение в теорию размерности - Павел Александров
Введение в гомологическую теорию размерности - Павел Александров
Теория размерности и смежные вопросы. Статьи общего характера - Павел Александров
Гомотопическая теория типов (HoTT) - Для продвинутых, каждый современный математик её читал
+бонусом Алгоритмическая топология и классификация трехмерных многообразий - Матвеев
Топологическо-геометрические курсы от Фоменко & Co. (МГУ-бригада:)
ОСНОВНОЕ:
Курс наглядной геометрии и топологии - Ошемков, Попеленский, Тужилин, Фоменко, Шафаревич
---
Введение в топологию - Борисович, Близняков, Израилевич, Фоменко
---
Современная геометрия. Методы и приложения (в 3 томах) - Дубровин, Новиков, Фоменко
---
Курс гомотопической топологии - Фоменко, Фукс
---
Краткий курс дифференциальной геометрии и топологии - Мищенко, Фоменко (нихуя он не краткий)
Сборник задач по дифференциальной геометрии и топологии - Мищенко, Соловьев, Фоменко
---
Дополнительно:
Элементы геометрии и топологии минимальных поверхностей - Тужилин, Фоменко
Элементы дифференциальной геометрии и топологии - Новиков, Фоменко
---
Геометрия и топология интегрируемых геодезических потоков на поверхностях - Алексей, Фоменко
Дифференциальная геометрия и топология. Дополнительные главы - Фоменко
---
Алгоритмические и компьютерные методы в трехмерной топологии - Матвеев, Фоменко
---
Компьютерная геометрия - Ильютко, Носовский, Фоменко, Голованов
Некоторые математические серии и журналы (в основном простеенькие):
Серия Основания математики (главным образом двухтомник Гильберта)
Серия Библиотечка Квант и сам Журнал Квант (можно еще и журнал Квантик)
Журнал Историко-математические очерки
Журнал Успехи математических наук (что осилишь)
Труды Московского математического общества
Труды Американского математического общества
Труды Математического института имени Стеклова
Срия Школьные математические кружки (очень простенькая, так что особо задерживаться на ней не надо, но галвное геометрию построения посмотреть)
Серия Учим математике (МЦНМО), это по вопросам преподавания, но там есть и задачки
Серия турнир Архимеда
Серия турнир Ломносова
Серия турнир Савина
Серия турнир Шарыгина
Серия турнир Эйлера
Серия математика Элективный курс
Серия библиотека маткружка
Серия библиотечка Физико-Математической школы
Журнал Математическое просвещение (!!!)
Серия Библиотека Математической просвещение
Серия Летняя Математическая школа
Серия Популярные лекции по математике
Серия Шедевры мировой физико-математической литературы
Серия турниры Городов
Серия Элементы математики (Да и вообще все Бурбаки)
Серия математика в техническом университете (diary.ru/~eek/p67723918.htm)
Серия Классические направления в математике
Серия Классические направления в математике
Серия Современные лекционные курсы
Серия Новые математические дисциплины
Серия Математическая библиотека
Серия Математическая библиотечка
Серия Математика. Элективные курсы
Серия Прикладная математика и информатика
Эммммм, любая книга по математической физике?
Возраст и для чего это нужно, тогда дам более точный ответ
22 года. Студент, специальность "Радиоэлектронные системы и комплексы". Сегодня стало интересно как вообще смогли описать физические явления и процессы. Одно дело смотреть в книжке уже готовый результат, а другое дело самому понять почему то или иное уравнение лежит в основе чего-то и самое главное как можно из причинно-следственных связей построить математическое уравнение.
Поиски в гугле дали ответ, что этим занимается математическое моделирование. Сейчас сижу читаю вот эту статью http://www.pedsovet.info/info/pages/referats/info_00002.htm
И решил сразу задать вопрос на дваче, так как аноны относительно часто дают полезные советы.
Тем более в книгах зачастую в принципе не объясняется вообще как получена та или иная формула. Просто "Вот, пользуйся и не еби мозги.", что иногда раздражает.
Спасибо, анон. Думаю освою к своему выпуску.
Мунин хоть рубит в теме хорошо.
Странная она вообще.
Колмогоров-Фомин - святое, в моем спсике просто нету функана, вот и не занес. Ещё Хемелского могу посоветовать (всего)
Рамануджана не следует считать автодидактом, ему Кали все подсказывала
Все книги Колмогорова это гашишный бред.
Так они воспринимаются всеми, кто не на уровне Мунина и Co.
Комплексный анализ идет одновременно с действительным у Понтрягина.
Насчет этих книг вроде Куранта, Арнольд, Босса, Фейнмана - мне не помогли. Что-то вроде Докинза, научпоп, короче. После прочтения тут же забыл все нахуй и все. Как смищных картинок посмотреть.
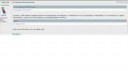
натуральный лого 7 получится
двачую, пока стирал и менял местами ошибочка вышла
Популярная серия
https://rutracker.org/forum/viewtopic.php?t=5268652
Вводные курсы
https://rutracker.org/forum/viewtopic.php?t=5268707
Скачиваем, благодарим и остаемся на раздаче
а не одно ли и то же? как составить список, если не разбираешься в теме?
я, в отличии от тебя, малец, закончил кафедру высшей геометрии и топологии, а ты не закончил школу
сиди, читай и не выёбывайся
трэд называется для начинающих, вот я и посоветовал соответствующую серию, хуле
Или вот предел Арнольда по тангенсам и синусам в точке 0. Вот узнали мы, что он равен 1. И нахуя мы это узнавали? Арнольд что-то кукарекал про связь математики и физики. Какая связь предела равно 1 с чем-то еще?
>закончил кафедру высшей геометрии и топологии
И как там? Анатолия Тимофеевича Фоменко видел там? Новую хронологию вместе с ним изучал?
Не верю, что можно знать всю математику и быть нормальным человеком.
>за 1-2 месяца
Ну давай разберем по частям, тобою написанное )) Складывается впечатление что ты реально контуженный , обиженный жизнью имбицил )) Могу тебе и в глаза сказать, готов приехать послушать?) Вся та хуйня тобою написанное это простое пиздабольство , рембо ты комнатный)) от того что ты много написал, жизнь твоя лучше не станет)) пиздеть не мешки ворочить, много вас таких по весне оттаяло )) Про таких как ты говорят: Мама не хотела, папа не старался) Вникай в моё послание тебе< постарайся проанализировать и сделать выводы для себя)
Всего в книгах из списка 8258 страниц. Если читать по 5 страниц в день, то на чтение уйдет четыре с половиной года. Чтобы прочитать эти книги за 1-2 месяца нужно читать со скоростью 136-271 страниц в день. Что не под силу даже Вербиту.
Всю математику никто и не знает смотря, что ты в это понятие вкладываешь. А нормальным человеком можно быть всегда, даже с багажом знаний по математике.
Посоны с мехмата, ответьте на мой вопрос плиз. Хотя бы про арнольдов предел.
Знать так как Грига Перельман
Ну а хули тогда кучу книг советуют? Что тут, что на dxdy? Эти все книги прочитать жизни не хватит, может если только тупо пролистать, картинки посмотреть.
Одной книги хватит, чтобы на год угореть.
Конечно нетрудно. Зато бесполезно.
Кстати, насчет Арнольда, я читал его книги и это пиздец полный. У Колмогорова тоже хардкор.
Арни вроде против Бурбаки, но по факту это лютый бурбакист. Вообще, тяжеляк, сам себе противоречит, противоречивость свойственна матлогикам, видимо, кто угорал по основам математики.
Еще сто раз замечал, что если препод с виду такой необычный, любит популярно объяснять докинз-стаил - то ничему не научит, а на экзамене так выебет, что охуеешь.
Так что не читайте Арни, это пиздос. Его поймет только тот, кто это и так знает.
Если бы он писал книги для школьников, их бы понял только мехматянин.

https://www.singular.uni-kl.de:8003/
А от чтения книг издательства Мир 65 года можно только превратиться в препода мухосранского вуза.
А хуй его знает. Расскажи, если знаешь.
Большинство людей вообще никакой учебник не открывали ни разу за всю учебу.
Все по лекциям и ссаным методичкам, где только и написано какую кнопку нажать.
Ни одной книги в год, путь следования конкретным книгам трудный и малополезный.
ВНИМАНИЕ: мысль поРОЖдает геном, поэтому будьте осторожны!!!
а. Лобанов. Русская вероятностная логика.
в. Говоров. Начала православной арифметики.
г. Дарияр. х’Арийская арифметика.
д. Джордан. Классическая нумерология.
є. Глобос. Практическая нумерология.
ѕ. Задорнов. Сила чисел, или Задорная нумерология.
ꙁ. Александров. От нумерологии к цифровому анализу.
и. Диксон. Символика чисел.
Ⱚ. Ключников. Священная наука чисел.
ӏ. Харди. Число жизни. Код судьбы (в 9 томах).
ӏа. Банцхаф. Математика и душа.
ӏв. Мартино, Ланди, Мартино. Сакральная геометрия, нумерология, музыка, космология, или Квадривиум.
ӏг. Посметьев. Математический блог «Секреты математики» (https://vk.com/mathsecret).
ӏд. Рыбников. Некоторые фундаментальные проблемы математики, физики, химии.
ӏє. Рыбников. Методика проверки-правки как средство обеспечения правильного восприятия и понимания связи грамматики и математики в научно образовательном тексте.
ӏѕ. Лайтман. Каббала и математика.
Почему этот список такой, а не другой?
Мне не кажется, что все области математики одинаково ценные; я уверен, что самоценности математика сама по себе не имеет. Иначе математика оказывается своего рода сложной интеллектуальной игрой, где никаких критериев нет вообще - кроме оценки профессионального сообщества. А профессиональное сообщество, что и скрывать, одновременно и коррумпировано, и разобщено, и ортодоксально. Профессиональное сообщество математиков не имеет единого критерия, а если бы и имело его, это было бы только хуже, наверное, потому что он был бы основан на невнятных властных играх по принципу ты почеши мне, а я почешу тебе, а ля академия наук.
Тем не менее, какие-то области математики претерпевают вполне очевидный расцвет. Я думаю, что это не случайно. Математика утеряла общие критерии, потеряв общий контекст; в настоящий момент, гораздо меньше людей понимают, что происходит в науке в целом, чем 20 лет назад, и еще меньше, чем 40 лет назад. В условиях потери абстрактных критериев, единственно эффективным критерием становится утилитарный. Это базовое предположение, которое я не хочу сейчас обсуждать.
Желающие следить за математикой (в том смысле, в котором это слово понимается выше) приглашаются на сервер https://habrahabr.ru, где почти все интересные работы по математикe выкладываются сразу после их написания. Выше приведенная математическая программа нужна именно для этого. Конечно, не все работы в https://habrahabr.ru будут немедленно понятны, даже и студенту, сдавшему все экзамены; но объяснить ему, в чем дело, можно будет за полчаса.
Математическое образование в России
Математического образования в России нет.
Исторически, в России имели место две параллельные образовательные системы; одна из них - университетская - за 5 лет худо-бедно давала знания, которые следует иметь студенту первого года обучения; она дополняла этот материал абсолютно бессмысленным концептуальным и вычислительным баластом и просто откровенным бредом. Даже те знания, которые давались университетской программой, давались ей в виде мало-осмысленных вычислительных рецептов, и в результате понимание студентом сути вещей только затруднялось. Университетская программа выпускала не математика, а калеку, который математикой не мог заниматься уже никогда; если кто-то в результате и становился математикой, то только вопреки тому, чему его учили, а не благодаря этому. Вторая программа была альтернативой; студент, попавший в эту структуру, к 3-4 курсу усваивал материал, соответствующий второму-третьему обучения математике (в смысле выше приводимой программы).
В последние 10 лет ситуация отчасти параллельна мною описанной. Имеются две конкурирующие программы: университетская (которая с 1980-х не изменилась, а только сократилась немного), и альтернативная, которой занимаются на habrahabr.ru, 2ch.hk/sci, dxdy.ru.
Но есть существенная разница - люди, которые понимают о чем идет речь в математической литературе (типа, в https://habrahabr.ru) в основном уехали; в результате, охват альтернативной системы сократился. При этом никаких ориентиров в плане дальнейшего самообразования студент не получает. Колоссальный барьер между обучением на студенческих семинарах и чтением научной литературы, который требовалось преодолевать самообразованием, увеличился с 2 лет до 4 и стал непреодолим. Вместо пропасти, второй край которой отчасти просматривается, мы имеем черную дыру, которая поглощает каждого, кто к ней приблизится.
У нас нет учебных заведений, где мою программу обучения можно было бы использовать; но смысл в ней тем не менее есть. Смысл ее - в установлении приоритетов и ориентиров. Программа, мною выше приведенная - есть не данность, а идеал, к которому необходимо стремиться. Студенту, если он хочет чему-нибудь выучиться, полезно время от времени поглядывать на описанный куррикулум; и сообразовать свое обучение с этой программой. Иначе кердык.
ВНИМАНИЕ: мысль поРОЖдает геном, поэтому будьте осторожны!!!
а. Лобанов. Русская вероятностная логика.
в. Говоров. Начала православной арифметики.
г. Дарияр. х’Арийская арифметика.
д. Джордан. Классическая нумерология.
є. Глобос. Практическая нумерология.
ѕ. Задорнов. Сила чисел, или Задорная нумерология.
ꙁ. Александров. От нумерологии к цифровому анализу.
и. Диксон. Символика чисел.
Ⱚ. Ключников. Священная наука чисел.
ӏ. Харди. Число жизни. Код судьбы (в 9 томах).
ӏа. Банцхаф. Математика и душа.
ӏв. Мартино, Ланди, Мартино. Сакральная геометрия, нумерология, музыка, космология, или Квадривиум.
ӏг. Посметьев. Математический блог «Секреты математики» (https://vk.com/mathsecret).
ӏд. Рыбников. Некоторые фундаментальные проблемы математики, физики, химии.
ӏє. Рыбников. Методика проверки-правки как средство обеспечения правильного восприятия и понимания связи грамматики и математики в научно образовательном тексте.
ӏѕ. Лайтман. Каббала и математика.
Почему этот список такой, а не другой?
Мне не кажется, что все области математики одинаково ценные; я уверен, что самоценности математика сама по себе не имеет. Иначе математика оказывается своего рода сложной интеллектуальной игрой, где никаких критериев нет вообще - кроме оценки профессионального сообщества. А профессиональное сообщество, что и скрывать, одновременно и коррумпировано, и разобщено, и ортодоксально. Профессиональное сообщество математиков не имеет единого критерия, а если бы и имело его, это было бы только хуже, наверное, потому что он был бы основан на невнятных властных играх по принципу ты почеши мне, а я почешу тебе, а ля академия наук.
Тем не менее, какие-то области математики претерпевают вполне очевидный расцвет. Я думаю, что это не случайно. Математика утеряла общие критерии, потеряв общий контекст; в настоящий момент, гораздо меньше людей понимают, что происходит в науке в целом, чем 20 лет назад, и еще меньше, чем 40 лет назад. В условиях потери абстрактных критериев, единственно эффективным критерием становится утилитарный. Это базовое предположение, которое я не хочу сейчас обсуждать.
Желающие следить за математикой (в том смысле, в котором это слово понимается выше) приглашаются на сервер https://habrahabr.ru, где почти все интересные работы по математикe выкладываются сразу после их написания. Выше приведенная математическая программа нужна именно для этого. Конечно, не все работы в https://habrahabr.ru будут немедленно понятны, даже и студенту, сдавшему все экзамены; но объяснить ему, в чем дело, можно будет за полчаса.
Математическое образование в России
Математического образования в России нет.
Исторически, в России имели место две параллельные образовательные системы; одна из них - университетская - за 5 лет худо-бедно давала знания, которые следует иметь студенту первого года обучения; она дополняла этот материал абсолютно бессмысленным концептуальным и вычислительным баластом и просто откровенным бредом. Даже те знания, которые давались университетской программой, давались ей в виде мало-осмысленных вычислительных рецептов, и в результате понимание студентом сути вещей только затруднялось. Университетская программа выпускала не математика, а калеку, который математикой не мог заниматься уже никогда; если кто-то в результате и становился математикой, то только вопреки тому, чему его учили, а не благодаря этому. Вторая программа была альтернативой; студент, попавший в эту структуру, к 3-4 курсу усваивал материал, соответствующий второму-третьему обучения математике (в смысле выше приводимой программы).
В последние 10 лет ситуация отчасти параллельна мною описанной. Имеются две конкурирующие программы: университетская (которая с 1980-х не изменилась, а только сократилась немного), и альтернативная, которой занимаются на habrahabr.ru, 2ch.hk/sci, dxdy.ru.
Но есть существенная разница - люди, которые понимают о чем идет речь в математической литературе (типа, в https://habrahabr.ru) в основном уехали; в результате, охват альтернативной системы сократился. При этом никаких ориентиров в плане дальнейшего самообразования студент не получает. Колоссальный барьер между обучением на студенческих семинарах и чтением научной литературы, который требовалось преодолевать самообразованием, увеличился с 2 лет до 4 и стал непреодолим. Вместо пропасти, второй край которой отчасти просматривается, мы имеем черную дыру, которая поглощает каждого, кто к ней приблизится.
У нас нет учебных заведений, где мою программу обучения можно было бы использовать; но смысл в ней тем не менее есть. Смысл ее - в установлении приоритетов и ориентиров. Программа, мною выше приведенная - есть не данность, а идеал, к которому необходимо стремиться. Студенту, если он хочет чему-нибудь выучиться, полезно время от времени поглядывать на описанный куррикулум; и сообразовать свое обучение с этой программой. Иначе кердык.
Ты мне объем ящика найди, этот бред гашишного наркомана не хочу читать.
>в моем спсике просто нету функана
Не нужен?
>>383193
Почему бред? Я начинал читать Колмогорова. Вроде понятно было.
>Не нужен
Нет, просто список ебать не полный. Я далеко не всё и не про все области написал, я его фастом делал, самое основное что в башню приходило.
агась, вместе кислоту ебашили
ебать. тупая агрессивная пизда. вот что климакс делает
Возможно, я сейчас нахуй расфигачу твой пердак, но я в свое время пахал по 15 часов в день (остальные 8 на сон, 1 на прием пищи и мелочи), проходя по 500-700 страниц в день (не просто читая, а именно конспектируя), просто нужно иметь терпение, настойчивость и, ГЛАВНОЕ, интерес к математике. Мне математика доставляет такое же удовольствие, как тебе Дотка, потому что я осознаю, что это нужная и полезная вещь, не говоря уже о том, что сам процесс постижения и решения задач крайне увлекателен. Так что если пахать по 15 часов в день, то спокойно можно качественно пройти все 2 серии (даже куда быстрее чем за 2 месяца). Что касается Вербита, то взгляни на его программу, этот наркоман, наверняка закидывал по марке каждый день и ебонил по 1k страниц, хули тут скажешь. Ему эти 2 серии даже в студенческие годы зашли бы за щёку :3^H за пару секунд, блядь.
>сам себя
независимость и самостоятельность и творческий подход у наиболее ярких математиков часто проявляется и в сексе так же.
Никто почти по существу ничего не сказал
начинается блять. вся история мехмата это различные травли. и вообще про личные взгляды многих известных советских ученых лучше и не знать. в двух словах - совки, ватники, антисемиты, мудаки. но в математике рубили да.
Тривиум АРНОЛЬДА решишь?
Не могут знания так быстро усвоиться.
Это как качок скажет, что по 100 грамм белка за раз принимает и так 5 раз в день. Продрищется только.
Зато тут же мунин нарисовался и слегка похуесосил. Нужно конкурс такой - два анона создают два треда, и победит тот, в котором в течении 30 минут не отметится мунин.
Вот по этому Гриша Перельман не взял миллион. Он просто был по сути битардом и верил, что раз чистая математика абстрактна, то и люди такие же кристально честные и хорошие. А это оказалось не так. Ему стало западло заниматься математикой дальше и брать миллионы.
Понимаю его.
Понтов нет, просто взял и доказал несколько теорем, а не выебывался 24/7 на dxdy
Но кстати Вербит же - не совок не ватник, мне как-то похуй на его взгляды, но он вполне разумен, хотя политизирован по самые уши (только с другим знаком) и за злобой дня в ирл следит пристально. Не понимаю как он совмещает и чем ему это говно интересно.
Там за последние полгода многих, смотрю, модернули
Да, я был сильно увлечен, сам составил программу по типу Вербитской (в плане жесткости), но не по всем областям, а только по алгебраической геометрии. Вещества здесь не помогут, это шутка была, да, есть байки о том, что некоторые ученые курили травку и им проще думалось (Саганчик об этом писал:3), есть байки, что Фоменко & Co писали свои учебники под веществами, но мне наркота никак не помогает, скорее наоборот. И стоит сделать уточнение, что работал я в таком темпе не слишком долго, несколько недель держался, а потом пизданулся и решил подсбавить. У меня прекрасно развита моторная память, когда пишу все железно запоминается, может в этом секрет.
>>383241
Оба решал, и уже давно.
>>383242
Алгеом, Хартшорна, Гродентика в том числе.
>>383246
>последние полгода
как раз таки нет, в последнее время модераторы слишком добрые, раньше анально было. Да и вообще, они по настроению, видимо, банят. Вот, взгляните на это: http://dxdy.ru/topic84588.html
Абсолютно ебанутый^2 пидр возомнил себя пупом Земли и ему хоть бы хны, в результате таки забанили, но не за это.
Эта тема вообще эпична
Не секрет. Но высшее образование тут не при чем.
Вообще, когда сидишь на dxdy, чувствуешь какую-то фальш, лицемерие, чувствуешь что где-то проигрывает мунин с каждого твоего вопроса.
>Алгеом Хартшорна
Ну серьезно, ты прошел его за день? Там же сотни упражнений, среди которых дохуя довольно гробовых.
Вызов принят.
2-3 минуты на страницу книги в день тратил.
Это невозможно так быстро учиться, а если и возможно, то забудется это все также быстро как и прочиталось.
Да и хватит максимум на 2 недели. Дальше фляга начнет подтекать, будешь как дурик ходить с отсутствующим взглядом по улице.
Да в целом неприятно этот обывательский подход к математике. Не обязательно, конечно, закатывая глаза вещать всем о том как ты проникаешься предметом, но когда большинство обитателей воспринимает математику как эдакий багаж знаний, "вот я мехмат окончил, поэтому я математик". Хочется спросить, а после окончания института образование уже не нужно? Сколько у тебя статей опубликовано в этом году, а в прошлом?
Сразу выясняется, кто на самом деле математик, хоть может с маленьким Хиршем, но математик.
>Хирш
ТРИГГЕРЕД! Хирш - хуйня, фаллометрия для падонков, вылизывание жопы друг дружке, из-за которого деградирует и страдает наука (математика больше всего). На него ни в коем случае не стоит обращать никакого внимания, он показателен лишь в редчайших ситуациях, когда речь идет или о совсем очевидном сравнении (где, блядь, можно и без него обойтись), или когда речь идет о двух очень близких ученых в одних областях и из одной и той же тусовки.
>>383259
к тому же 65 год это самая старая книга, которая есть в этой серии, там вплоть до конца 90-ых.
Чтобы прикладной, и было заебись для инженера: т.к. их довольно много, выделю мостопетуха .
Существует ли цепь, приводящая от элементарных и главное - прикладных разделов к МКЭ (да, не хочу заниматься макакством за копермейстером) ?
>Even among mathematicians, who tend to be singleminded and highly devoted to their work, Grothendieck was an extreme case. “Grothendieck was working on the foundations of algebraic geometry seven days a week, twelve hours a day, for ten years,” noted his IHÉS colleague David Ruelle.

Эчмм, я разве говорил, какие книги и в каком порядке я читал? ты шо ебанный?
откуда ты, блядь, взялся всратый уебок?
>>383177
>Введение в математику - Клини
>Математическая логика - Клини
Прошу, панэ.
Вообщем, заебало меня бессмысленное распиздяйнечество с школьниками на тему образования и ещё более бессмысленное перетирание заезженной темы dxdy и Мунина. Хотите работать по 15 часов - ебашьте, не хотите - не ебашьте, всем похуй. Хотите сидеть на dxdy... ну ты понел.
Чем продолжать этот флуд, я лучше займусь более составлением более качественной программы для следующего трэда, появлюсь там же, когда доделаю.
ну и пиздуй, нахуй ты тут всрался со своими 15 часами
>>Эчмм, я разве говорил, какие книги и в каком порядке я читал? ты шо ебанный?
> Алгеом, Хартшорна, Гродентика в том числе.
>всратый уебок?
Слив защитан. Больше тут не отсвечивай. Тебе место на dxdy.
Я перечислил 1 книгуи (суть, ясно, что у Хартшорна читал) и автора (Гротендика). Я не сказал "Алгеом Хартшорна", я сказал, что ебонил АЛГЕОМ в целом и Хартшорна, Гродентика в том числе (причем Гротендика далеко не всего). это, блядь, не есть перечисление всех книг и их порядка. Уважаемый, еще раз повторюсь:
>Введение в математику - Клини
>Математическая логика - Клини
Это не унизительно, это не оскорбительно, ЭТО НУЖНО ПРОЧИТАТЬ.
>Введение в математику - Клини
Тебе бы стоило начать троллинг с внимательного прочтения того, как же на самом деле называется книга Клини. Которую я-то читал. А ты видимо еще нет.

Соглашусь, она была немного не по теме, но их надо желательно читать подряд, поэтому указание её уместно.
да и вообще математическая логика это немного не по теме, у тебя проблемы с головой (не только с логическим мышлением), а это другое. К тому же добавлю, что в Введении в математику параллельно с основаниями рассматривается и матлогика, как таковая. Но не так подробно, как во второй книге.
>у тебя проблемы с головой
>Введении в математику
Иди нахуй, черт. Проблемы с головой у тебя. Сам читай Клини, даун. Там слово МЕТАматематика встречается раз 200 за книгу. Эта книга не про математику, дебел.
У тебя какое-то субъективно понятие математики, лол. Ну да что взять с унтерменша-битардика.
В связи с неадекватностью своего оппонента, считаю и без того бессмысленный спор завершенным.
Ебись нахуй :3
Вот тебе паста из предыдущих матрэдов, вот тебе гудбукс с dxdy (https://yadi.sk/d/_WXQoO3QuNkvZ ), и вот тебе 2 (3) списка итт. А чо делать решай сам. А ну и программу Вербита глянь :) (лучше этого не делай, а если решишься, то смотри старую версию, она более полная)
2-3 списка итт? Охуеть. Любой мимокрок в этом списке потеряется от количества пунктов в нем, к тому же в нем нет последовательности для чтения, а лишь перечисление. Алсо я спрашивал не об авторах, а об общем направлении.
В списке есть 21 пукт. Я спокоен.
Представляешь сколько бы наш скорострел ящиков бы мог сделать, если ему размеры дать.
в /dev/null в смысле в пургатории публикуют? пока все запятые не расставишь и чтобы пробелы не забывал после точек ставить. а кстати мелкобуквенных там хуесосят? сразу в гулаг наверное?
P.S. Прощальное наставление: читайте "Начала православной математики", если хотите стать тру абстрактным математиком и хуеососить прикладничков по полной
на dxdy улечу, а тут двач, и я не спал уже около 18 часов, так что кладу хуй на препинание и орфографию.
>>383319
Это как раз таки полная противоположность пикчи. На пирилке ОПа изображен фрик, начитавшийся двощей и нахватавшийся "умных слАвечек", при этом не желающий учиться, поэтому он и не решил инженеробыдлозадачу, а ебонил бы по 15 часов в день Православную арифметику Говорова - решил бы, даже не дослушав условие до конца.
на дваче можно как угодно писать, но тебе же нельзя расслабляться перед заплывом на dxdy.
>18 не спал ебошил по 15
Да, это впечатляет. А сколько ты не дрочил уже?
Если ты внимательно читал трэд, то мог бы заметить, что 15 часов - это был мой разовый эксперимент, еслибы я ебошил так каждый день, то элементарно полностью пизданулся бы. А эти 18 чсов сегодня, я бездарно проебал, как раз таки дроча и сидя на двощах, еще поиграл в баскет с гопотой, и все-таки был один положительный момент,- я посмотрел лекцию (точнее 2) Новикова отсюда https://rutracker.org/forum/viewtopic.php?t=3481701 .Отака хуйня

Лол. Был бы Посметьевым, то пиарил бы Секреты Маняматики в /b или /pr, а не тут. Просто хотел разбавить чистую математику прикладной.
Также поработал над шапкой. Теперь она стала более интерактивнее и уменьшилась в размерах. Зацените:
Архивы тредов
http://pastebin.com/kiRZGVHW
WARNING!!! WARNING!!! WARNING!!! Списки:
Если ты только зашел в тред и хочешь спросить, какую книжку прочитать, то ответ, скорее всего, будет в этих списках, анон.
Список от ОП-а, бывшего тут до меня. Был составлен на проятжении 13 тредов, к ознакомлению обязателен.
http://pastebin.com/4iMjfWAf
Список от анона с dxdy. Довольно внушителен, тоже рекомендуеться к прочтению.
http://pastebin.com/YP1uaUyd
Тестовый список. Теперь можно не только хуесосить ОП-список, но и создавать его in real time! Предлагайте свои книги, критикуйте уже имеющиеся.
http://pastebin.com/szzZfkCM
Там автор вообще смешал все подряд. Надо делать хотя бы дистинкции:
graduate и undergraduate
учебник и задачник
академическая книга и научно-популярная
актуальная книга и историческая
исправь во втором списке:
введение в математику -> введение в метаматематику
курс чистой математики - гильберт -> харди
Обсуждалось же.
да там много такого, не указаны соавторы, названия от балды, горбатого могила исправит.
Можно разделить на первую культуру и вторую. А там уже на graduate и undergraduate.
>лучше этого не делай, а если решишься, то смотри старую версию, она более полная
Только старая версия это версия как стать Вербицким, который тогда работал в области матфизики.
Первое разделение вряд ли можно применять к учебникам.
Анон помоги дебилу, PV=m/nu*RT нужно выразить T, нихуя не понимаю как это сделать, как такое решать? В каком классе это проходят? Может есть универсальный алгоритм какой,Maple же как-то решает.

PV/m*nu/R=T
Советую перейти в школу для умственно отсталых. Очень поможешь этим человечеству, не ставя себя в один ряд с нормальными (или около того) людьми, сразу начинай ориентироваться на окружение своего уровня развития.
Пропорцией это решается, "крест-накрест". Вот и весь алгоритм. Да и пример у тебя простой, была бы там переменная с сложением под корнем или ещё какая-то залупа, тогда пришлось бы дополнительно заморачиваться с раскрытием, выражением и т.д.
Проходится в классе 6, если не раньше.
мудила ебанная, если ты написал бы PVnu/(mR), то твой пример был бы правилен, а так ты умножаешь на R, поэтому пошел на хуй.
Топологический изоморфизм
Математики могут только полагать что математики асексуальны, доказать это они не смогут
Конечно, уверен, что она сама не понимала в нем нихуя.

Я тоже так подумал, но решил не говорить. Я удивлен немного.
Самые пиздатые:
Ли (не 20-ый, но он многое предопределил в 20-ом), Гильберт, Пуанкаре, Колмогоров - это общепризнанно.
Крутость - понятие относительно и субъективное, но думаю, если хорошенечко поднапрячься и дам более-менее четкое определение крутости в математике, то выйдут эти трое.
Пуанкаре аналогично Ли в список вошел
Его еще Ньютон хуесосил люто, но ему было похуй.

Короче, Гильберт.
Дай угадаю, Понтрягина из трэда взял, а Лейбниц - единственный, кого знал сам? :3
Пиздуй на с такими заявами.
Ещё раз, вот цепочка великих:
Греки-хуеки -> Эйлер -> Гаусс -> Ли и Пуанкаре -> Гильберт -> Колмогоров -> Арнольд (Это спорно, но не зряж он вице-президентом IMU был) -> Рома Михайлов, sowa, Вербит )))))))))))))))
Нет. Я знал и так.
Эндрю Уайлс, он доказал ЕЁ
двачую
ЛОООООООЛ
>2k16
>Не знать sowa
Не с dxdy, это был такой популярный математик в ЖЖ, потмо перешел на блогспот и вроде до сих пор пишет (я уже давно не читал). Для многих он также меметичен, как и Вербит С Ромкой.
еслиб хотел пошутить по dxdy, написал бы ewert или brukvalub.
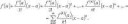
Ньютон свой бином вывел через треугольник Паскаля.
А Паскаль его вроде от нехуй делать составил.
Тоже считаю, что просто так эти формулы невозможно придумать.
Просто выдумывали их сотни лет, а в учебнике написано так, что мол их даже долбоеб выведет.
Я за исторический метод, читать первоисточники, а потом новье, чтобы современные термины знать.
Кстати, понятие определителя нормально раскрывает Понтрягин. Все остальные авторы писали, что мол, забейте, определитель это просто число такое. У каждой матрицы свое число.
А на самом деле это линейная функция (линейная форма) от векторов матрицы.
Векторами являются строки матрицы.
Лев Понтрягин - "Алгебра"
Книга небольшая, но поясняет по-хардкору.
И она "не отравлена теорией множеств" - почти точная цитата Понтрягина.
http://fracton.rgho.st/6y48q87F7
Анализ Понтрягина. Сразу идет комплексный+действительный.
Не отравлен теорией множеств
Анон, я новый ньюфаг. Ты понимаешь, что у меня не было интернета в те времена, когда он писал? Вся история интернета нулевых прошла мимо меня. О чём он писал? Чем меметичен?
Из интернет-персонажей я знаю только Вербита, Ромку, Мунина, Хеллера. Ну ещё Каледина, но его я бы не отнёс к мемам. Здесь ( https://lj.rossia.org/community/ljr_math/46837.html ) он говорит про какой-то Stacks. О чём он вообще?
> Все остальные авторы писали, что мол, забейте, определитель это просто число такое.
И у Винберга, и у Кострикина даётся несколько подходов к определителю: там тебе и объём, и формула полного развёртывания, и полилинейная кососимметрическая функция от строк матрицы.
Невозможно читать это дерьмо.
Надо быть уже хорошим математиком чтобы это понять.
Это не учебник, а справочник.
Кстати, читал учебник Беклемишева - это вообще пиздец. Записки сумашедшего.
Я наркоман если сейчас читаю "Символьный С++ введение в компьютерную алгебру с использованием объектно-ориентированного программирования" К.Ш. Тан, В.-Х. Стиб, Й.Харди?
Это же по сути анализ функций, а действительный, комплексный и гармонический это же по сути подвид функционального. Или не так?

Владыка-ситх пикрелейтед.
Понял многое? Теоремы доказать сможешь? Задачи решить?
Я не понимаю как доказывать. Вот сейчас матлогику формализовали, раньше этого не было, но доказывали же как-то. Книг от МЦНМО тоже не было, но доказывал же как-то Лейбниц, Ферма, Паскаль. Мужики страдали хуйней и угорали по математике, устраивали бокс по переписке, ничего еще толком не было открыто и можно было знать всю математику.
Золотые были времена. Романтика.
>доказывал же как-то Лейбниц, Ферма, Паскаль
БРЕШЕТЕ, НИВАЗМОЖНА, МОНЯМАТИКУ АТКРЫЛ ГАМЕЛЬТОН С ИШНТЕЙНАМ В НОЧАЛЕ ДВОЦАТОГО ВЕКА
Неа. А ты?
Слишком сложное все
Не допетрю я
>Курс арифметики - Жан Пьер Серр
А я не читывал, так, отдыхаю и решил частушки посочинять. А там действительно сложно? Сам смотреть боюс.


И тут у меня вознит вопрос, как деды считали первую задачу? Я понимаю, что сейчас можно запросто перемножить ряды производящих функций и найти у этого ряда коэффициент при A_100, но как деды делали это без высоких технологий? Как?
Основа всегда есть, в данном случае только не в математике а в психологии масс. Математика тебе просто дает тулзы - а как ты будешь их интерпретировать это другой вопрос. Естественно это полная хуйня - пытаться предсказать будущее по прошлым результатам. С другой стороны ты же знаешь, что это игра в musical chairs - все друг за другом следят, моргнул проиграл. Поэтому полезно сверяться со всякими moving average чтобы понять, например, что скоро будет resistance и многие это тоже увидят и захотят продать, поэтому нужно тоже так сделать - и все так делают, и потом говорят - о блять наука. Чистая психология и полностью лотерея. Что fundamentals что technicals.
жан поль сартр же
>Под "техническим анализом" есть какая-то рациональная основа?
Нет. Трейдинг это только генетические алгоритмы.
>Понятно, что первая задача - частный случай второй и решаеться всё это через производящие функции.
а еще с помощью смекалочки и рекурсии, ведь мы можем посчитать количество способов двух копеек, потом пяти...
Ящик сделал уже?

Шестигранный куб можно бросать сколько требуется раз, к результатам броска можно применять необходимые преобразования.
Давай наукач, я в тебя верю.
Можно.
Есть набор понятных правил? Чтобы написал пару диаграм и получил третью?!
У меня бомбит от этого!!!!
на самом деле, я вот всё ну никак ни сформлуировать не могу, ни найти источник.
это такая вещь варящаяся в собственном соку, что самостоятельно подобраться ну нереально.
охуенные картиначки! это стеб какой-то или for real? может там и ящика для песка есть диаграмка где-то? а кто этим пользуется и для чего? знатоки помнят каждую такую слесарную деталь?
>и многие это тоже увидят и захотят продать, поэтому нужно тоже так сделать - и все так делают, и потом говорят - о блять наука. Чистая психология и полностью лотерея. Что fundamentals что technicals.
Т.е., другими словами, тех.анализ работает потому что написано много книжек по тех.анализу. Но сама идея торговать по таким правилам всё равно должна была в какой-то момент истории зародиться, какие под этим основания были, интересно, и как она закрепилась?
Ну как, всегда были попытки использовать статистику, так же как ее используют в других областях для анализа каких-то результатов. Многим интуитивно кажется, раз математика, значит научный подход, значит так правильно - статистический анализ якобы помогает распознавать тренд и что якобы коллективный разум масс действует согласно каких-то психологических паттернов и их можно распознавать и тд. Ну и конечно это ж баблос - появились всякие школы, литература, свечки-хуечки, короч наебалово. Markets are efficient.
Ебать. То есть хрёхэтажные формулы можно описовать просто картиночной? Охуенно же. Пиздато будет, если в будущем вместо формул математику будут учить по картинкам.
Вернее, комбинацией стандартных пиктограмм типа электрической схемы. Задача в том, чтобы выработать наиболее интуитивные и удобные пиктограммы.
Мне нужно залатать дыры в школьной программе, весьма обширные должен сказать, и выстроить алмазную лестницу к дискретке и алгоритмам и вообще к пониманию мироздания
Можешь тогда почитать учебники Алимова 7-11 по алгбре класс, по геометрии не знаю, чего посоветовать, но для дискретки и алгоритмов геометрия не нужна.
Мерси
в яндексе на собесе спрашивают похожее. есть `rand2() -> 0 | 1`. с помощью нее написать `rand3() -> 0 | 1 | 2`.
кстати, математики, такое вообще можно решить без хаков? `0.5 (0) + 0.5 (1)` превратить в `1/3 (0) + 1/3 (1) + 1/3 (2)`
бтв, я знаю как решить в лоб. бросаем 3 раза, получаем 216 комбинаций, что есть 8 х 27. в зависимости от попадания в одну из этих 8 групп получаем значение 1d8.
не претендую на красоту и оригиналось, >>383767 кун
блять. сорри, обосрался с переводами строк.
с >>383767 такое не работает, там степень двойки никогда не даст число нацело делящееся на 3
Просто ИРЛ rand2() может выводить 1 или 0 с вероятность 70% / 30%. Псевдорандом же.
не будь таким занудой. это ж задача на собеседовании, там все чисто теоретически.
да, я должен был полностью условия задачи привести:
есть функция `rand2()` которая с равной вероятностью возвращает 0 или 1. напишите функцию `rand3()` используя `rand2()`(ее можно вызвать любое количество раз) которая с равной вероятностью будет возвращать 0, 1 или 2
так лучше?
Находим кортеж (rand2(), rand2()),
(0, 0) — возвращаем 0;
(0, 1) — возвращаем 1;
(1, 0) — возвращаем 2;
(1, 1) — «перебрасываем», находим кортеж заново и все повторяем.
Вероятность каждого исхода:
P(x) = 1/4 + 1/4*P(x)
P(x) = 1/3
>не будь таким занудой. это ж задача на собеседовании, там все чисто теоретически.
А я возьму, не буду её решать на собеседовании и быстро переведу разговор в сторону топалогий-тамалогий, как на первом оп-пике и меня сразу возьмут!
поясни за `P(x) = 1/4 + 1/4*P(x)` подробней. интуитивно я понимаю, что решение правильное, до доказать все же не могу
о себе: я недопрограммист, закончил быдловуз, фактически выкинул коту под хвост 5 лет жизни, которые мог бы заниматься наукой. теперь я хуйня без образования.
думаю вкатиться в математику. вижу это так:
1) учу мат анализ, мне видится это как основа основ
2) затем теорвер и матстат
3) далее уже буду иметь представление куда развиваться. вообще хотелось бы в финансовую инженерию податься или около того
по пункту (1) сейчас читаю Spivak "Calculus". все правильно делаю?
>учу мат анализ, мне видится это как основа основ
Определение N - основа основ.
>по пункту (1) сейчас читаю Spivak "Calculus". все правильно делаю?
Если тебе нужна математика не ради математики, то да.
>Если тебе нужна математика не ради математики, то да.
ну на самом деле оно как раз так и есть и это меня сильно напрягает. но с другой стороны: а какие у меня есть варианты практического применения анализа?
>варианты практического применения анализа?
Посчитать ящик?
Ты сам можешь взять и придумать приминения прямо сейчас!




А вообще, можешь поговорить с Посметьевым, он расскажет тебе, как применять математику.
как ты спивака выбрал, по каким признакам? он же сложнее аналогичных книг (стюарт, томас для инженеров). он как бы подводит к анализу. ты потом настоящий анализ (real analysis) будешь учить, с пруфами, все дела? он же поэтому называется REAL analysis, как бы говорит - that's the real deal bro.
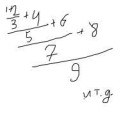
Я, например, люблю вот так вот ее изображать. Этот способ я придумал сам, назвал это Аноново число
Охуенно. А еще можно обратное число вывести - деаноново, снизу вверх если записать. 9/8 + .../ И наверняка тоже получится 1. И выглядить будет очень рекурсивненько.
Объем от верхнего конуса до оси минус объем нижнего конуса до оси.
> как ты спивака выбрал, по каким признакам?
ну на самом деле можно сказать, что выбирал рандомом
> он же сложнее аналогичных книг (стюарт, томас для инженеров). он как бы подводит к анализу. ты потом настоящий анализ (real analysis) будешь учить, с пруфами, все дела?
эм. ну в общем, я не знал, что она сложная. ни в коем разе не ставил своей целью тут перед кем-то выебываться. я попробую посмотреть другую литературу, спасибо.
>1) учу мат анализ, мне видится это как основа основ
Основа основ в 2016 — это гомотопическая теория типов.
охуеть, тут у вас списки литературы. вам нужен гайд как пользоваться вашим гайдом. кажется я действительно, очень сильно облажался просто взяв первую попавшуюся книгу.
>выебываться
При чем тут выебываться. Я просто подумал мало ли, тут же вон тролей полон двор, кто-то пишет что он еблан и начал сразу со спивака. А давно ты его изучаешь? Если ты не понял, сложная она или нет ДЛЯ ТЕБЯ, то может ты просто странички листал?
>>383862
чтобы вылечиться от нильпотенции очевидно
ну я просто очень мало успел прочитать. сказать смешно -- две главы пролога. так что не знаю, сложно или нет. упражнений там че-то дофига как-то.
в любом случае я бы предпочел начать с литературы попроще. желательно на английском. дашь советов каких?
короче, аноны, я осознал уебищность своего подхода к изучению математики (даже не начав его, лол). пожалуй, теперь я начну заново, с выбора действительно хорошей литературы. а искать я ее буду в архиве тредов + треде доброчана. всем спасибо, ближайшие пару дней я в ридонли.
Это же тупо обычные конусы круглые.
>тотомас
не тотомас, пробел потерялся. то томас. thomas. да хуй с ними с тотомасом, бери лучше стюарта на либгене.
ты тот анон с тотомасом? однохуйственно. стюарт так-то популярнее. если скажешь пацанам - стюарта многие знают. а тотомаса вряд ли.
и чем тебя его список не устроил? "сложна"? вербит "непостижима"?
ты тупой лох просто вот и все, в списке только тру книжки, а в комментах его ещё и обсуждают.
И ещё, пожалуй, запрошу комментарий по этому поводу:
>поехавшего
почему же? не нравятся советы, как выебать шлюху? "я у мамы правЕльный"?
stewart calculus. просто введи два слова в либген. их несколько, бери любой. single variable или сразу multivariate. кроме того есть early transcendentals вариант но это пох. сперва логарифмы, экспоненты, потом интегральчики или наоборот.
>>383884
лол чего ты до меня доебался. мопед не мой. говорю тебе - однохуйственно. оба для инженеров норм.
Ящик сделал?
Но это же вроде тред чистой математики и в нее играющих школьников.
Объясняю. Вот этот >>383805
думает что нашел
>жва года хотел такую доску с таким тредом
хотя говорит что
>финансовую инженерию податься
И списки в этом треде ему совсем не подходят. Вообще.
Зато! Он прочитает стюарта или даже тотомоса и сообразит как сделать ящик.
но в тотомасе спема логарифмы, а в стюарте гибко - может быть наоборот. може ты хочешь е всосать через интегралички, а можыт - как предел последовательности.
А можно как то посчитать производную цилиндра когда обе переменные считаются переменными, а не поодиночке?
Я пришел в нить с вопросом как применять маняматику к ирл. На вопрос "че ты там не решил, щас мы быстренька гамалогией тапалогией все решим" я сказал что мне надо было сделать ящик для песка на 60 литров с минимальными размерами стенок, чтобы потратить меньше всего материала.
Из за этого половина тапологов порвалась на тему "ПРОКТИЧИСКАЯ ЗОДАЧА, НИНУЖНА", вторая половина на "СИКАНОМИШЬ ДЖВА КВАДРАТНИХ МЕЛЕМЕТРА" а три с половиной таполага с трдом через вольфрам решили задачку, которю я врчную решал три часа.
Пик видел, просто первоисточник интересен.
>>383921
Вголос. Вся суть математиков с их "приклодная зодача питухи кукареку". Они же не умеют прикладное решать.
пришел выпизднул теперь уйди
причем здесь "прикладное"? эту задачу решит даже 5-лентний даун, блядь... мда ебанная школота
Так вы тут и до пятилеток не дотягиваете в таком случае. Только гомологиями в жопу ебетесь.
ну тут два сорта этих... математиков. одни могут но им лениво, они молчат. а вскукареки от гомологий не могут, но кукарекают громко зато. вторых больше :)
> овина тапологов порвалась на тему "ПРОКТИЧИСКАЯ ЗОДАЧА, НИНУЖНА", в
Ты забыл упомянуть нескольких анонов, которые решили задачу правильно вручную.
Все вы так!! Тривиально! Да еп.. СЛОЖНА
Мне нужен чёткий алгоритм, как от такой картиночки можно перейти к другой.
Понимаешь, алгоритм какой-нибудь, позволяющий решить - как рисовать новые диаграммы из существующих, а не копировать те, которые в учебнике.
Нужен язык программирования этих диаграмм.
А то тут блядь "очевидно", первое упражнение и сразу "докажите".
Да блядь какого хуя!
Только не перепутай где длина, где высота, где ширина. Иначе дороже выйдет.
http://www.wolframalpha.com/input/?i=f(x,y)=2xy+120/y+120/x
Вместо 2 дней я потратил на эту задачу 1 секунду.
ааа! понял! я думал он тебе сразу ящик нарисовал...
ну эт не я, я только план решения написал, а выдал вольфрам, разбираться мне лень, я спать
Он через жопу посчитал и его ящик выйдет дороже. А мой дешевле и не кубический.
Кстати тред задачку то быстро решил, понимаю что так смешнее, но это же не правда что не могли два дня решить
ну и в чем загвоздка? хули вольфрам неправильно вывел?
так?
Может и обсирается, но это не наша забота. Решили же как-то. А без вольфрама смысла нет решать - на бумажке что ли.
Я ща проилстал 14-ый, и бля в итоге какой ответ? и почему? и почему из этого нельзя понять из-за чего обсирается вольфрам?
ЭТА ИСТОРИЯ ОКУТАНА ТАЙНОЙ
предлагаю её распутать, го го го до конца этого трэда успеем, а следующем будем обсуждать возможность фапа и 25 часовой график, предложенный аноном (Гротендики в день)
Просто с математической точки зрения результат неинтересен. Есть принцип, есть доказательства, есть теория. Для остального вольфрам. Он дает примерный ответ, который в общем то не важен. Математика не об этом, а про красоту доказательств и абстракций. А ящики пусть инженеры колотят.
Какой функцией можно описать подобную структуру:
[2, 3, 4, 4, 4, 4, 3, 2]
[3, 4, 6, 6, 6, 6, 4, 3]
[4, 6, 8, 8, 8, 8, 6, 4]
[4, 6, 8, 8, 8, 8, 6, 4]
[4, 6, 8, 8, 8, 8, 6, 4]
[4, 6, 8, 8, 8, 8, 6, 4]
[3, 4, 6, 6, 6, 6, 4, 3]
[2, 3, 4, 4, 4, 4, 3, 2]
Собственно мне тут необходимо для известных X, Y (столбец, строка) найти эту Z (высоту). Можно в принципе и для четвертинки типо такой:
[2, 3, 4, 4,
[3, 4, 6, 6,
[4, 6, 8, 8,
[4, 6, 8, 8,
Где х1 у1 будет давать 2, а х4 у2 будет 6.
Я даже не понимаю с чего мне начать, чтобы разобраться. Как такие задачи решаются?

Если кому интересно, это задача для школьников по информатике, о том сколько клеток бьет конь на шахматной доске.
ну это типа залупы визуально получится - трехмерная функция z = f(x,y). восьмерки - это головка твоей залупы. а к краям - склоны. зафиксируй одну переменную и посмтори закономерность только для одной.
>>383969
Ты ебанутый, что ты тут делаешь?
Есть же https://2ch.hk/pr/res/792098.html (
По сути это свёртка матриц
[1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1] [0, 1, 0, 1, 0]
[1, 1, 1, 1, 1, 1, 1, 1] [1, 0, 0, 0, 1]
[1, 1, 1, 1, 1, 1, 1, 1] * [0, 0, 0, 0, 0]
[1, 1, 1, 1, 1, 1, 1, 1] [1, 0, 0, 0, 1]
[1, 1, 1, 1, 1, 1, 1, 1] [0, 1, 0, 1, 0]
[1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1]
но никто не заморачивается о матрицах, и пишут просто
bool inRange(int x, int y) {
return (0 <= x && x < 8 && 0 <= y && y <8);
}
int board[8][8] = {{0}};
int moves[8][2] = {{1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}};
for (int i = 0; i < 8; ++i) {
for (int j = 0; j < 8; ++j) {
for (int k = 0; k < 8; ++k) {
int move[] = moves[k];
if (inRange(i + move[0], j + move[1])) {
++board[j];
}
}
}
}
Свёртки матриц используются в обработке изображений. Но в олимпиадном программировании они встречаются нечасто. Полезнее будет разобраться в динамическом программировании.
Найти явную формулу для элементов матрицы можно далеко не всегда.
>>383969
Ты ебанутый, что ты тут делаешь?
Есть же https://2ch.hk/pr/res/792098.html (
По сути это свёртка матриц
[1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1] [0, 1, 0, 1, 0]
[1, 1, 1, 1, 1, 1, 1, 1] [1, 0, 0, 0, 1]
[1, 1, 1, 1, 1, 1, 1, 1] * [0, 0, 0, 0, 0]
[1, 1, 1, 1, 1, 1, 1, 1] [1, 0, 0, 0, 1]
[1, 1, 1, 1, 1, 1, 1, 1] [0, 1, 0, 1, 0]
[1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1]
но никто не заморачивается о матрицах, и пишут просто
bool inRange(int x, int y) {
return (0 <= x && x < 8 && 0 <= y && y <8);
}
int board[8][8] = {{0}};
int moves[8][2] = {{1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}, {-2, -1}, {-2, 1}, {-1, 2}};
for (int i = 0; i < 8; ++i) {
for (int j = 0; j < 8; ++j) {
for (int k = 0; k < 8; ++k) {
int move[] = moves[k];
if (inRange(i + move[0], j + move[1])) {
++board[j];
}
}
}
}
Свёртки матриц используются в обработке изображений. Но в олимпиадном программировании они встречаются нечасто. Полезнее будет разобраться в динамическом программировании.
Найти явную формулу для элементов матрицы можно далеко не всегда.
Может кто посоветовать материал, где доступно объясняются преобразования Фурье с примерами. Конкретно интересуют преобразования, применимые к уравнениям с разрывными коэффициентами.
Хермандера не предлагать.
Классика - классикой, но прочитать и понять больше 2 страниц в день - уже достижение.
Поэтому и спросил, может знает кто что-нибудь попроще.
>а еще с помощью смекалочки и рекурсии, ведь мы можем посчитать количество способов двух копеек, потом пяти...
Деды через производящие функции решали. И мне интересно как они это делали.
Я прочёл ссылку из первой задачи, но там всё на немецком и я ничего не понял.
http://fracton.rgho.st/7yT2kQWbS
вдруг кто-то знает немецкий!
Все что я знаю:
pfennige - пенсы
stuck - штука
zahle - число
ein,zwei,drei,vier,funf,zehn - 1,2,3,4,5,10
ordnung - порядок
>>384072
Но вообще, они там через алгебру все преобразовывали, переводили из пустого в порожнее, упрощали и считали
А как именно?
> а надо наоборот
Оптимальный ящик -- это полусфера. Затратить материала меньше, чем площадь полусферы нельзя. Поэтому задача имеет нижнюю границу. Однако, верхней границы задача похоже не имеет. Ящик на 60 литров можно сделать из поверности любой площади, например, путем бесконечного вложения гиперболоидов в гиперболоид объемом 60 литров. Объем будет оставаться постоянным, а площадь будет все время расти.
>Извините гуманитария
Извиняем.
>но проблема с ящиком решается в корне неверно
Конечно, я не думаю, что кто-то тут её серьёзно решает.
>Те, нужно манипулировать доствпными средствами на постройку ящика. Т.о. мы сможем элегантно найти решение этой проблемы, исэкономим на дорогостоящих специалистах
Нет, аноны пытаются построить ящик самым неэффективным и понтовым методом, отсюда всякие гомологии, н-мерные сферы и т.д. А потом от общего к частному перейти к конкретному ящику.
По определению.
Значение знаешь?
https://ru.wikipedia.org/wiki/Ящик_(значения)
>Ящик — ёмкость (вместилище) в форме многогранника, чаще всего — прямоугольного параллелепипеда.
Но будет ли он n-гранником, при n стремящиемся к бесконечности?
но... смекалочка... олимпиадные традиции...
Такие ящики уже были решены в прошлом треде. Теперь рассматриваем только ящики на афинных многообразиях.
а здесь можно было бы частично хотя бы формулу, если не inrage, че-нить с модулями (%) или / или вместе.
я помню какой-то сайтик есть, там грейдят по РАЗМЕРУ кода (!), поэтому такое бы не проканало, пришлось бы что-то менее piecewise и более аналитическое пилить. и думаю пришлось бы тройной цикл в 1-й схлопывать и вычислять индекс. и переменные однбуквенные. тупизна, но иначе в топчик не попадешь, печаль! а если попадешь - придет некий хуй "хворых павел" и будет ебошить до посинения пока на 1-й байт всех не победит даже в hello world.
внезапно задававший вопрос кажется давно съебал так как ему СРЧНО нужно было наверняка
Нет, не так это делается. Нужно искать решение для N, а уже тот кто ящик будет делать, подставит вместо N размер своего измерения в котором он. Если уж делать, то делать как следует, чтобы везде работало.
Да в принципе не проблема придумать общий вид подходящей функции и подобрать параметры или вручную или оптимизационным методом.
Что-то типа
int a(int x){return (4.4-Math.abs(3.5-x)0.9)}
int f(int x,int y){return (a(x)+a(y))*1.1608}
Кроссплатформенность! Да, это хорошо
https://rutracker.org/forum/viewtopic.php?t=3481701
https://rutracker.org/forum/viewtopic.php?t=3843125
https://rutracker.org/forum/viewtopic.php?p=56301988
К ним ещё годные брошюры есть (к части из них)
Лекториум (годнотища)
Массачусатские
Хан академи
Видеотека Mathneta
НМУ разбросан по разным сайтам (маснет, несколько каналов на ютубе, основной из них xUnicom)
На рутеркере полно годных подборок
это основные, но есть ещё дохуища ресурсов
Сам недавно посмотрел курс лекций Гордина по алгебре (все можно найти на сайте налекцию.рф), годнота и все понятно (лекций на 4 семестра), вроде как потом ещё 5-ый зальют.

А если нет - какой ты вообще нахуй математик? Как ты что-то доказывать будешь, без предикатов-то?
у того другие модули, более правильные! русский язык страдает низким динамическим диапазоном. absolute value и modulo схлопнул в одно слово. или не modulo а modulus. хуй знает я сам запутался.

>>383989
>Ты ебанутый, что ты тут делаешь?
Страшно было постить на /пр. Там ненавидят математику. Видимо это как-то связано с тем, что в универах ее заставляют изучать, а на работе она им не нужна.
>задававший вопрос кажется давно съебал
Я все это время пытался разобраться в матрицах, и представить себе кольца. Нечего мне по делу было сказать. Совсем ничего в математике не смыслю, просто хотел понять почему это работает:
http://pastebin.com/LXWiTi1s
Алгебра-2 же
Что такое "среднее от сотой степени синуса" и почему я этого не знаю?
Синус определен на всей числовой прямой. Ты не знаешь этого, потому что ты гнилой бурбакист, иди N с нулем определи
Нет, сука, дай определение среднему от сотой степени синуса. Ну или задачу с ящиком песка реши. Сделай хоть что-то полезное.
>Страшно было постить на /пр. Там ненавидят математику
php макаки? ненавидят математику? не может быть такого
удивил ежа. я сейчас мочезукину межпланетную теорию переписываю на символах пенроза и брауера. они идеально для этого годятся. вот первая страница. все вроде логично получается.
аноны, что вы видите на этих охуенных диаграммах из современной математики? дайте свою интерпретацию. я на левой вижу бомжа. у него нос на боку, глаз подбит и волосок из бородавки растет. да вот лучше обрисую для наглядности. пилите свои варианты


Как ты будешь считать интегралы не выстроив перед этом теорию математического анализа?
Как ты собираешься выстраивать математический анализ без теории множеств?
Как ты собрался теорией множеств без логики первого порядка - её языка?
>Как ты будешь считать интегралы не выстроив перед этом теорию математического анализа?
Инжинеры же как-то считают.

> Прообразы чисел, близких к 1/a, близки к a.
Охуительное доказательство просто.
Последовательностью формул теории множеств доказательство записать можешь, ублюдок?
Стоит сказать, что, немного подумав, я нашёл камень преткновения. Нельзя говорить о непрерывности функции, но можно — о непрерывности в точке и о непрерывности на множестве.
1. Чтобы функция была непрерывна на множестве, она должна быть непрерывна в любой точке.
2. Чтобы функция была непрерывна в точке, функция как минимум должна быть определена в этой точке.
Таким образом мы получаем, что 1 / x непрерывна на области определения, то есть ℝ \ {0}, ибо непрерывна в любой точке области определения x0 ∈ ℝ \ {0}, так как lim f(x) при x → x0 по множеству ℝ \ {0} равен f(x0), что можно доказать, опираясь на теорему о связи предела и арифметических операций и на тот факт, что lim x при x → x0 по ℝ равен x0, но при этом 1 / x не непрерывна на ℝ, ибо в точке 0 не определена, а потому ни о какой непрерывности в этой точке говорить смысла нет. Резюмируем:
1. 1 / x непрерывна на области определения ℝ \ {0}.
2. 1 / x не непрерывна на ℝ.
>>384435
Это не нужно, если ты не бурбакист, конечно.

Помогите мне решить другую задачку.
У меня на лице почти круглый год жара и лето. Я нашел на барахолке алюминиевую трубу пять метров длинна, тридцать радиус. Хочу сделать из нее летний душ, ну типа солнце должно нагревать воду в трубе, халява сэр.
Так вот, я могу её расплющить, чтобы у нее была большая площадь, чтобы она быстрее нагревалась. Насколько сильно при этом изменится её объем?
Для туповатых тапалагистав, из круга с периметром метр двадцать и площадью около 2.7К кадравтных сантиметровнадо сделать фигуру с другой, наибольшей возможной площадью.
квадрипл, насыпь биткойнов сперва, сделаем тебе душь.

Да нихуя.
Это бабах человека, который вкидывал на обсуждение/решение несколько простых вопросов по логике первого порядка и другим вещам касающимся оснований (без хардкорного дроча вроде ZFC).
И получал полный игнор.
Кажется этот тред только ради МЕМАСОВ создан.
Хотя завтра, решу. Пошел спать.
Я наоборот похудел с тех пор как начал, хотя всего несколько дней прошло.
Задача с ящиком затянулось. Много кто ушел.
А как же вероятностые методы в теории чисел?
Анонимные математики мирового уровня дневники с спайдерменом и россомахой выбирают.
gen.lib.rus.ec

для начала скажу, что этот пидр нас наебал
>>383945
СПИДа ему
Вот полное решение (снова):
Имеем xyz=60, отсюда z=60/(xy)
Площадь считается так: f(x,y)=2xy+2xz+yz=2xy+120/x+120/y=2(xy+60/x+60/y) Функция будет минимальна, когда многочлен в скобках будет минимален. И БЛЯДЬ! ВОЛФРАМ НЕ ОШИБАЛСЯ: http://www.wolframalpha.com/input/?i=f(x,y)=xy+60/x+60/y минимум, когда x и y = 3.91... Получаем сумму 91.95... А когда вариант СПИДозника (3,4,5), получаем 245+235+234=94. Он или тупой, или зелёный.
Да
Нет.
А сам-то как думаешь?
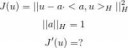
Ебать ты знаток.
Ну и че мне потом с этими знаниями делать? Работу не найти, тян не заинтересовать, вон родители тоже хуетой считают, пустая трата времени же. Лучше в огороде покопать, дома прибраться.
Не, ну че ты. Ты же понимаешь что лучше по дому дела сделать, намного полезней чем математикой заниматься. Зачем самому это этим заниматься, в школе же научат, в вузе там. А самому зачем интересоваться то? Диплом за это не дадут
это настоящая тянка или манекен? вот как математика поможет отличить? смотрю смотрю не могу понять.
Ну а где анон который посты начинал со слова ПУСТЬ. И дальше гомологии. Никто уже не пишет так.


C такими жизнеными позициями вам необходимо посетить Секреты Математики.
Ясно, просто я первокультурщик.
Ладно, похоже базовую нотацию теорвера вам незнакома. Перевожу. Есть две независимых случайных величины X, Y с равномерным распределением на [0,1]. Надо найти распределение (плотность) случайной величины sqrt(X^2+Y^2).
Забавно и понятно читать определение категории множеств через ETCS и потихоньку избавляться от налагаемых на множества требований.
Например, сначала избавляемся от аксиомы выбора: теперь не обязательно, чтобы у каждого эпиморфизма есть правый обратный морфизм. (что обязательно у функций)
Далее избавляемся от обязательности наличия начального объекта в среди диаграм вида (1->A->A). То есть от натуральных чисел и индукции по ним.
Избавляемся от требования функциональной экстенсивности. (Это делает наш элементарный топос не "well-pointed")
Да, конечно, избавляемся от требования нетривиальности категории, то есть того, что терминальный объект не является начальным.
Избавляемся от классификатора подобъектов. (прикольная штука, в категории множеств позволяет вводить индикаторную функцию подмножества)
Избавляемся от экспоненциала. (с помощью которого определяем множество функций)
Избавляемся от декартого произведения. (которое определяет множество пар)
И избавляемся от терминального объекта.
Вуаля, ничего не осталось.
ну кроме аксиом категории, которые включают требование к набору морфизмов между объектами быть МНОЖЕСТВОМ =D
и что? опечатка в одном месте, ДАЛЬШЕ-ТО Я ПРАВИЛЬНО НАПИСАЛ, ебаный ты мудак, вообщем репорчу.
Ещё раз для СПИДозных мудаков вроде тебя:
2xy+2yz+2xz=2⋅x⋅y+2⋅y⋅60/x/y+2⋅x⋅60/x/y=2xy+120/x+120/y
А теперь пиздуй в бан
ну там на единице - максимум плотности вероятности высотой в пи пополам
>ДАЛЬШЕ-ТО Я ПРАВИЛЬНО НАПИСАЛ
Нет, ты начал правильно, а закончил с ошибкой, ибо ящик без крышки.
Тем, что распределение и плотность - это функции, а у тебя хуйня какая-то написана.
во-первых никто этого не говорил, это была инженеробыдлозадача и ящики без крышки верстают только говнари.
во-вторых даже если так, то ответ 3,4,5 всё также идёт нахуй, проверяется аналогично - вбивкой формулы в вольфрам.
>во-первых никто этого не говорил
Возможно, мне это действительно показалось, но в прошлом треде аноны решали задачу, исходя из предположения, что верх ящика открыт.
>ответ 3,4,5 всё также идёт нахуй
Да с этим никто не спорит.

>>384385
И как это понимать? Как троллинг пеинтом?
>>384492
Настоящий математик легко поймёт что это шотик.
>Да с этим никто не спорит.
Спорить со мной начала истота, написавшая про 3,4,5 - ей я и отвечал
Какой тролинг пейнтом? Мы сейчас проходим твисторы и нотацию пенроза:
https://en.wikipedia.org/wiki/Penrose_graphical_notation
и брауэра
https://en.wikipedia.org/wiki/Brauer_algebra
у меня задание сделать перевод с нотации мочезуки в брауэра и пенроза.
кстати красноносый еблан - это запись ковариантной производной. она бы пригодилась анону который с гаусом боне не мог разобраться. а на картинке сразу понятно, что к чему, и где волосок.
Да.
Странное определение. Получается, что пустое множество — одновременно собственное и несобственное. Обычно определения дают другие: собственное (нетривиальное) подмножество множества A не должно совпадать ни с A, ни с пустым множеством.
Кудрявцев, матан
Порылся в инетах, везде считается, что пустое подмножество -- и собственное, и несобственное. Видно, надо верить.
Некрасивая же формула, конечно же, неправильно
X - случайная величина из (0;1), 1/x отображает (0;1) на (1;+inf), арксинус принимает значения из [0;1], так что саси хуй быдло.




Открыл пару учебников: 1-й пик — Зорич; 2-й пик — Кострикин; 3-й пик — Куратовский, Мостовский; 4-й пик — английская вики. Из всего выбивается только определение Кострикина. Определения несобственного множества я не нашёл ни в одном учебнике. Кудрявцев, видимо, скрестил ежа с ужом.

Откуда страница? Вариант обоснования формулы есть, например, в книге "Тарасов - Беседы о преломлении света (1982)".
>арксинус принимает значения из [0;1]
Во-первых https://www.wolframalpha.com/input/?i=asin(1.5)
А во-вторых даже в твоём реальном мирке область значений арксинуса это [-1;1], а не [0;1].
Два в журнал.
Мудила, у нас тут веротность, а она в R+ определяеться, дурень.
>А во-вторых даже в твоём реальном мирке область значений арксинуса это [-1;1], а не [0;1].
Ладно, я лажанул. Но ты всеравно, обосрался больше.
>у нас тут веротность, а она в R+ определяеться
Не истери. То, что внутри формулы есть подвыражение, имеющее комплексное значение, не означает что формула в целом имеет комплексное значение.
может все-таки в журнал не надо сразу. это ж нулевой урок
Ящик сделай и гуляй.
Вырываю фразы из контекста чтобы запутать оппонента подменой понятий.
>Хотите ли вы лично что-нибудь у меня спросить
А пруф можно, что именны вы хозяим группы? А так рад, что такие люди заглянули в наш тред, моё почтение.
>Может быть есть советы по улучшению группы?
Секреты идут как-то в разброс, надо бы список составить.
Ну смысл нашей группы очень прост и вполне логичен: донести правду о настоящей математике всякому сброду (извините за выражение, но так и есть) после вузов и прогнившей системы образования. Так же рассказать, что и на таком непопулярном предмете как математика можно заработать.
Что скажете об этой программе ( >>383227 )? Может быть, дополните её чем-нибудь? Какие-то критические замечания выскажете? Всегда интересно мнение здравомыслящего человека.

:А пруф можно, что именны вы хозяим группы?
Конечно, вот изменил описание группы для скриншота
:Секреты идут как-то в разброс, надо бы список составить.
Да, я обдумываю концепцию удобного меню и сортировки секретов по темам, но все никак не сяду серьезно за это дело
лол, наверное это его правая рука
Вконтакте часто так тупит, показывает как будто давно был, а человек на самом деле недавно заходил. Может попозже покажет.
: 0.5 - действительное, f(0.5) - действительное.
Не мое дело конечно, но я бы Вам посоветовал округлять до 3 знаков после запятой.
Мне кажестся, все эти программы не так уж и нужны, просто бери книгу к которой сердце лежит, и читай книги про успешных математиков, я обычно так и делаю.
Это удобная фича - показывать попозже, например с задержкой в неделю. Обфускация, запутывает шпионов.
Убедил. Мы все всё понимаем: редизайн, изменения — ну мало ли багов.
Скок зарабатывашь? По какому графику робишь?
Ты говорил, что
>у нас тут веротность, а она в R+ определяеться
и что моя формула на (0;1) имеет комплексные значения.
Я предъявил действительное значение при x=0
Что тебе не нравится?
Да не совсем, вот наподобие таких читай, и мотивация будет, и увидишь что нужно делать чтобы быть крутым математиком.
"Совершенная строгость. Григорий Перельман. Гений и задача тысячелетия"
А можешь составить список книг? можно и до переката успеть. Там численные методы всякие и т.д
Говорю же, все эти книги по сложным темам не особо и нужны, ты главное книги про успешных людей читай, про то как заработать на математике, про личностный рост, и все у тебя будет окей))
Ну вот пару книг:
https://www.ozon.ru/context/detail/id/22685935/
https://www.ozon.ru/context/detail/id/28330879/
https://www.ozon.ru/context/detail/id/135173281/
http://www.ozon.ru/context/detail/id/4749424/

Какие в пизду алгербы если задача на логику первого порядка из которой строится вся математика и предполагается что она ещё не построена?
пиздуй в перкат
https://2ch.hk/sci/res/384587.html (
https://2ch.hk/sci/res/384587.html (
https://2ch.hk/sci/res/384587.html (
https://2ch.hk/sci/res/384587.html (
https://2ch.hk/sci/res/384587.html (
и корешей с собой прихвати

Да я уже там. Кто-то попытался решить - сразу обосрался.
Пиздос, предикаты оказались непосильной задачей для маттреда.
не непосильной, а просто всем насрать
не то чтоб слишком просто
Двачую
Задача решена верно. Мудила
Бросаем 3 раза. Получаем четыре числа x1, x2, x3
строим новое число
y = (x1-1) + 6(x2-1) + 36(x3-1)
y распределено равномерно от 0 до 6^3-1.
Тогда y%8+1, где % - взятие остатка от деления - равномерно распределён от 1 до 8.
Я не из-за аниме ушел. Я ушел потому, что тред засрали как только могли. Какая, я понял, что на этой доске сидят оголтелые ебанаты.
Он застремался сидеть в разделе, где моча может совершенно внезапно и немотивированно удалить картинки с расслоением Хопфа из ОП-поста почти ушедшей в бамплимит нити. К тому же удаление сопровождалось тупым комментарием, который непонятно кто написал - может, даже мочератор.
>Так что больше не пости своё ебаное анимэ, понял, придурок?
Я бы тоже застремался на его месте. Сегодня трут аниме, завтра айпи сливают, как страшно жить вообще.
>>385931
Ты не он. Хотя пофиг.
К первой пикче.
ящик - полое вместилище в форме параллелепипеда, сделанное из жёсткого материала (досок, фанеры, стального листа) и предназначенное для хранения или транспортировки чего-либо. По определению.
Минимальные стороны параллелепипеда - у куба.
Корень кубический из 60 дм^3 равен 3.9148676411689 дм.
А чтоб положить что-то в сферу надо её сначала вывернуть наизнанку.
https://www.youtube.com/watch?v=p8zPx41oxwE
https://www.youtube.com/watch?v=eyNhhRCCMiI
Вы видите копию треда, сохраненную 6 декабря 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.