Вы видите копию треда, сохраненную 21 марта 2018 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 15 Кб, 342x340
15 Кб, 342x340Удваиваю вопрос. Как инутитивно обосновать определение ротора?
Попробуй Письменного, там вроде нормально написано.
http://bsuir-helper.ru/sites/default/files/2011/09/28/met/Konspekt_lekciy_VM.pdf
А вообще, математика - от дьявола.
Ротор ротора равен градиенту дивергенции минус лапласиан.
https://ru.wikipedia.org/wiki/Ротор_(дифференциальный_оператор)
http://ивтб.рф/exams/матан/3/13.htm
градиент скалярного произведения векторов равен векторному произведению первого вектора на ротор второго вектора плюс векторное произведение второго вектора на ротор первого вектора плюс произведение скалярного произведения первого вектора на набл умноженное на второй вектор плюс произведение скалярного произведения второго вектора на набл умноженое на первый вектор
![400px-D093D180D0B0D0B4D0B8D0B5D0BDD182D185D0BED0BBD0BCD0B0[[...].gif](/sci/big/thumb/406996/14894448615260s.jpg) 21 Кб, 400x185
21 Кб, 400x185>градиент скалярного произведения векторов равен
нулю, так как скалярное произведение векторов = числу
grad(С) = 0; С = const;
>скалярное произведение векторов
Ааа, ну да, если в векторном пространстве L, но над полем C комплексных (или R вещественных) чисел...
KhanAcademy в помощь.
>>07025
Крайне не рекомендую читать эту похабщину даже самым убитым инженерам и экономистам.
>>07099
Как вариант, но тоже так себе альтернатива.
>>07006
Вот, к примеру: http://mathinsight.org/curl_subtleties
Хотя смотри ниже, я для ОПа попытаюсь разъяснить.
>>06996 (OP)
Начнём с градиента. Его понять проще всего.
Я предполагаю, что всем присутствующим интуитивно понятна производная как локальная линейная аппроксимация. [1]
Дифференциал Df функции f в точке P "ест" малое изменение аргумента dx и возвращает число Df(dx, P) - с помощью него значение исходной функции можно приблизить в окрестности точки P:
f(P+dx) ~ f(P)+Df(dx,P)
По определению, мы ищем Df линейную по dx: Df(dx,P)=kdx
Число k называется производной функции в точке, часто обозначается как f'(P):
f(P+dx) ~ f(P)+f'(P)dx
Например, 5 в квадрате - 25. Производная x^2 в точке пять равна f'(5)=10. Тогда число 5.2 в квадрате приблизительно равно
5.2^2 ~ 5^2+100.2=25+2=27 (точный ответ 27.04).
Здесь значение дифференциала = наше приблизительный рост функции, т.е. +2.
Важный момент - функция f у нас ест числа и выдает числа. Например, ест день недели и выдает цену акций, ест длину тонкого стержня и выдаёт его температуру, и т.д.
Что если мы хотим изучить температуру не тонкого стержня, а целой пластины? Функция f по прежнему выдает число, но вот теперь dX - это совсем не число (а два числа - dx и dy - как их "прикрутить"?).
Красота идейного определения дифференциала в том, что ему неважны детали вроде размерности пространства. [2]
Снова будем искать Df(dX,P) [3] в линейном виде:
Df(dX,P)= k1dx+k2dy
Числа k1,k2 назовём частными производными. Тогда мы сможем расчитать наш "хак" для прироста функции в любом направлении (dx,dy):
f(P+dX) ~ f(P)+(k1dx+k2dy)
Выражение в скобках по сути есть умножение вектора (dx,dy) скалярно на вектор (k1,k2). ВЕКТОР (k1,k2) НАЗЫВАЕТСЯ градиентом*.[4]
[1] Точнее, это полный дифференциал или просто дифференциал или полная производная, но часто суть ясна из контекста и используют просто "производная".
[2] Ну конечно же важны, но практически незаметны при обобщении - а вот производная обобщается сначала до градиента, а потом до матрицы Якоби - гораздо более существенно. Это in layman terms, про нормы в пределах я умалчиваю.
[3] Здесь и dX, и точка P принадлежат пространству R^2. Формально, точка P приндлежит исходному многообразию R^2, а dX - касательному пространству, в нашем случае тоже совпадающему с R^2.
[4] На самом деле это не совсем вектор, а скорее линейная форма.
>>07025
Крайне не рекомендую читать эту похабщину даже самым убитым инженерам и экономистам.
>>07099
Как вариант, но тоже так себе альтернатива.
>>07006
Вот, к примеру: http://mathinsight.org/curl_subtleties
Хотя смотри ниже, я для ОПа попытаюсь разъяснить.
>>06996 (OP)
Начнём с градиента. Его понять проще всего.
Я предполагаю, что всем присутствующим интуитивно понятна производная как локальная линейная аппроксимация. [1]
Дифференциал Df функции f в точке P "ест" малое изменение аргумента dx и возвращает число Df(dx, P) - с помощью него значение исходной функции можно приблизить в окрестности точки P:
f(P+dx) ~ f(P)+Df(dx,P)
По определению, мы ищем Df линейную по dx: Df(dx,P)=kdx
Число k называется производной функции в точке, часто обозначается как f'(P):
f(P+dx) ~ f(P)+f'(P)dx
Например, 5 в квадрате - 25. Производная x^2 в точке пять равна f'(5)=10. Тогда число 5.2 в квадрате приблизительно равно
5.2^2 ~ 5^2+100.2=25+2=27 (точный ответ 27.04).
Здесь значение дифференциала = наше приблизительный рост функции, т.е. +2.
Важный момент - функция f у нас ест числа и выдает числа. Например, ест день недели и выдает цену акций, ест длину тонкого стержня и выдаёт его температуру, и т.д.
Что если мы хотим изучить температуру не тонкого стержня, а целой пластины? Функция f по прежнему выдает число, но вот теперь dX - это совсем не число (а два числа - dx и dy - как их "прикрутить"?).
Красота идейного определения дифференциала в том, что ему неважны детали вроде размерности пространства. [2]
Снова будем искать Df(dX,P) [3] в линейном виде:
Df(dX,P)= k1dx+k2dy
Числа k1,k2 назовём частными производными. Тогда мы сможем расчитать наш "хак" для прироста функции в любом направлении (dx,dy):
f(P+dX) ~ f(P)+(k1dx+k2dy)
Выражение в скобках по сути есть умножение вектора (dx,dy) скалярно на вектор (k1,k2). ВЕКТОР (k1,k2) НАЗЫВАЕТСЯ градиентом*.[4]
[1] Точнее, это полный дифференциал или просто дифференциал или полная производная, но часто суть ясна из контекста и используют просто "производная".
[2] Ну конечно же важны, но практически незаметны при обобщении - а вот производная обобщается сначала до градиента, а потом до матрицы Якоби - гораздо более существенно. Это in layman terms, про нормы в пределах я умалчиваю.
[3] Здесь и dX, и точка P принадлежат пространству R^2. Формально, точка P приндлежит исходному многообразию R^2, а dX - касательному пространству, в нашем случае тоже совпадающему с R^2.
[4] На самом деле это не совсем вектор, а скорее линейная форма.
Ну надо же, всю разметку проебал из-за хуевых звёздочек. Попозже дособерусь и напишу про див и кёрл.
 77 Кб, 722x535
77 Кб, 722x535>>07109
>>07110
Когда уже в сай прикрутят блядский тех. Продолжу про градиент, т.к. штука красивая и полезная, вдруг какой анон ещё забредет в трэд.
Итак, градиент есть обычное, естественное, совсем не сложное обобщение производной. По сути, это и есть производная для функций от нескольких аргументов.
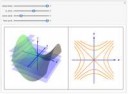
Например - пусть у нас высота холма над плоскостью (или температура металлического листа, или.. ) меняется как h = x^2 - y^2. [1]
Рассмотрим рандомную точку, скажем (1,2). Градиент по сути есть строка частных производных, посчитанных в точке:
grad f = [ df/dx|P=(1,2), df/dy|P=(1,2) ] = [ 2x|P, -2y|P] = [2,-4].
Давайте пойдём к "центру" "холма", по направлению (-1,-2). Нужно помнить, что аппроксимация всё-таки локальная, и отходить от нашего текущего местоположения лучше потихоньку (ограничено только ошибкой, которую хотите допустить).
Например, шагнём в сторону на dX = (-0.1, -0.2). Изначальная высота h(P) = 1-4 = -3. "Хак" для изменения
Df(dX,P) = grad f . dX = [2,-4].[-0.1,-0.2] = -0.2+0.8 = 0.6.
Мы видим, что местность "поднимается" в этом направлении - у нас высота -3, а в сторону dX она вырастет на 0.6 до -2.4.
Ещё раз подчеркну полную аналогию:
f(P+dx) ~ f(P) + f'.dx
f(P+dX) ~ f(P) + grad(f).dX
[1] Фактически это гиперболический параболоид, см. прикреплённый пик.
 96 Кб, 267x400
96 Кб, 267x400Продолжаем.
Чтобы так же объяснить дивергенцию и ротор, мне бы пришлось накатать ещё пару простыней о криволинейных и поверхностных интегралах. Будем считать, что они всем знакомы, если что спрашивайте.
Представим поток воды. Будем следить за каким-нибудь объёмом внутри потока. Интересно, в этот объём больше вливается, чем выливается, или наоборот? Как это посчитать?
Очень просто. Наш объём описывается какой-то поверхностью. Поток также описывается функцией от нескольких аргументов. Функция ест точку пространства и выдаёт вектор потока.
Чтобы найти, сколько вливается или выливается воды, нужно просто проинтегрировать нашу функцию потока по замкнутой поверхности, окутывающей объём. Интеграл возьмёт на себя всю унылую работу по изучению "какая там маленькая частичка входит или выходит из объёма по всей его границе". [1]
Важно понять - это макроскопическое свойство. То есть объём этот осязаем, существует. Можно измерить прибором, если очень захочется.
Что случится, если мы будем уменьшать объём? Самое главное - посчитанное нами "свойство" будет от чего-то глобального, измеряемого переходить в локальное свойство. [2]
Зачем это нужно? Это будет точечной, локальной характеристикой потока, что всегда приятно иметь под рукой, т.к. один из основных инструментов изучения процессов вокруг нас - дифференциальные уравнения. Ещё один аргумент - наше свойство зависит от выбора объёма, а если объём будет бесконечно малым, или точечным - свойство будет более "естественым". [3]
Итак, уменьшаем объём. Что будет происходить со значением интеграла? Интуитивно ясно, что он будет решительно идти к нулю. [4] Нужно слегка изменить выражение под интегралом, чтобы оно так быстро к нулю не шло - и чтобы "идея" свойства сохранилась. Как вариант, рассмотрим отношение потока к нашему объёму. В конце концов, сказать "в наш объём вошло 2л воды" как-то несерьёзно, ведь объём мог быть и с кастрюлю, и с летающую тарелку.
Теперь посчитаем такой интеграл, но будем уменьшать наш объём. Получится число - назвывается дивергенцией.
[1] Интеграл и задание ориентации, если точнее.
[2] Будучи математиком\физиком, я аж сам зафейспалмился, т.к. тут следует включить тонну сносок и замечаний.
[3] Вообще, мало времени в университетах уделяют методологии и интуиции определений, чем и оправдываю своё размахивание руками.
[4] И так простыня вышла, доказывать не буду.
 96 Кб, 267x400
96 Кб, 267x400Продолжаем.
Чтобы так же объяснить дивергенцию и ротор, мне бы пришлось накатать ещё пару простыней о криволинейных и поверхностных интегралах. Будем считать, что они всем знакомы, если что спрашивайте.
Представим поток воды. Будем следить за каким-нибудь объёмом внутри потока. Интересно, в этот объём больше вливается, чем выливается, или наоборот? Как это посчитать?
Очень просто. Наш объём описывается какой-то поверхностью. Поток также описывается функцией от нескольких аргументов. Функция ест точку пространства и выдаёт вектор потока.
Чтобы найти, сколько вливается или выливается воды, нужно просто проинтегрировать нашу функцию потока по замкнутой поверхности, окутывающей объём. Интеграл возьмёт на себя всю унылую работу по изучению "какая там маленькая частичка входит или выходит из объёма по всей его границе". [1]
Важно понять - это макроскопическое свойство. То есть объём этот осязаем, существует. Можно измерить прибором, если очень захочется.
Что случится, если мы будем уменьшать объём? Самое главное - посчитанное нами "свойство" будет от чего-то глобального, измеряемого переходить в локальное свойство. [2]
Зачем это нужно? Это будет точечной, локальной характеристикой потока, что всегда приятно иметь под рукой, т.к. один из основных инструментов изучения процессов вокруг нас - дифференциальные уравнения. Ещё один аргумент - наше свойство зависит от выбора объёма, а если объём будет бесконечно малым, или точечным - свойство будет более "естественым". [3]
Итак, уменьшаем объём. Что будет происходить со значением интеграла? Интуитивно ясно, что он будет решительно идти к нулю. [4] Нужно слегка изменить выражение под интегралом, чтобы оно так быстро к нулю не шло - и чтобы "идея" свойства сохранилась. Как вариант, рассмотрим отношение потока к нашему объёму. В конце концов, сказать "в наш объём вошло 2л воды" как-то несерьёзно, ведь объём мог быть и с кастрюлю, и с летающую тарелку.
Теперь посчитаем такой интеграл, но будем уменьшать наш объём. Получится число - назвывается дивергенцией.
[1] Интеграл и задание ориентации, если точнее.
[2] Будучи математиком\физиком, я аж сам зафейспалмился, т.к. тут следует включить тонну сносок и замечаний.
[3] Вообще, мало времени в университетах уделяют методологии и интуиции определений, чем и оправдываю своё размахивание руками.
[4] И так простыня вышла, доказывать не буду.
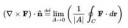 14 Кб, 679x155
14 Кб, 679x155Если понятно объяснение дивергенции, то с ротором проблем возникнуть не должно - абсолютно аналогичные идея и метод.
Вот пик - оыбчное определение, взято с википедии. Коль скоро ясно понятие циркуляции (аналог потока из предыдущего поста), то интерпретация очевидна - нам интересна циркуляция, но это глобальное свойство; будем сжимать контур в точку, да вот интеграл обнуляется - ну это ничего, нам всё равно интересней удельная циркуляция, разделим на площадь, там-парам.
С удовольствием, но времени у меня сейчас хватит только на один пост. Поэтому попытаюсь мотивировать введение обобщённых функций как таковых [1]. Я предполагаю, что анонам ф-цию Дирака дали не просто так, а с рукомаханием про обобщённые функции, так что это будет полезно.
"Классические", "обычные" функции [2] имеют несколько свойств, которые не совсем вяжутся с собственно описательным инструментарием физики.
1) Часто от этих функций требуется n-кратная дифференцируемость. Тем не менее, в теории частных диф. уравнений нередко возникают ситуации, когда удобно было бы рассматривать "плохие" функции, не имеющие нужных производных. Если ту же струну оттянуть, то это начальное условие уже не джважды дифференцируемое, ну и решение выходит тоже хуёвое. А дифференцировать то его хочется!
2) Возьмём функцию. Она ест точку пространства и выдаёт нам число - например, температуру чашки с какао (всем советую вместо кофе). Но когда мы дотрагиваемся до ручки, то мы "измеряем" не точечную температуру, а температуру по какой-то площади. Даже если мы стащим из НИУ невъебенно точные термометры, они тоже измеряют характеристики не в точке, а скорее "среднее" по какой-то площади. Так может у нас слишком "сильные" требования для функций, раз мы требуем их задания в каждой точке? В итоге-то всё равно один хуй проинтегрируем по этой площади, чтобы узнать "взвешенное" среднее.
3.1) [3] Если мы рассмотрим коммутативное кольцо функций и определим умножение как свёртку, то можно показать, что в кольце нет делителей нуля. Можно расширить это кольцо до поля, причём мультипликативной единицей будет именно функция Дирака.
3.2) Обобщённые функции составляют пространство, сопряжённое пространству "хороших" функций - т.е. это просто функционалы.
Может, сегодня-завтра дополню про собственно ф-цию Дирака, ну или аноны понапишут.
[1] Их ещё называют распределениями в англоязычной литературе, но у нас чаще используют "обобщённые функции".
[2] Конечно, таких определений нет, но часто подразумеваются функции, локально интегрируемые по Лебегу.
[3] Это математикам мотивация, её можно пропустить.
С удовольствием, но времени у меня сейчас хватит только на один пост. Поэтому попытаюсь мотивировать введение обобщённых функций как таковых [1]. Я предполагаю, что анонам ф-цию Дирака дали не просто так, а с рукомаханием про обобщённые функции, так что это будет полезно.
"Классические", "обычные" функции [2] имеют несколько свойств, которые не совсем вяжутся с собственно описательным инструментарием физики.
1) Часто от этих функций требуется n-кратная дифференцируемость. Тем не менее, в теории частных диф. уравнений нередко возникают ситуации, когда удобно было бы рассматривать "плохие" функции, не имеющие нужных производных. Если ту же струну оттянуть, то это начальное условие уже не джважды дифференцируемое, ну и решение выходит тоже хуёвое. А дифференцировать то его хочется!
2) Возьмём функцию. Она ест точку пространства и выдаёт нам число - например, температуру чашки с какао (всем советую вместо кофе). Но когда мы дотрагиваемся до ручки, то мы "измеряем" не точечную температуру, а температуру по какой-то площади. Даже если мы стащим из НИУ невъебенно точные термометры, они тоже измеряют характеристики не в точке, а скорее "среднее" по какой-то площади. Так может у нас слишком "сильные" требования для функций, раз мы требуем их задания в каждой точке? В итоге-то всё равно один хуй проинтегрируем по этой площади, чтобы узнать "взвешенное" среднее.
3.1) [3] Если мы рассмотрим коммутативное кольцо функций и определим умножение как свёртку, то можно показать, что в кольце нет делителей нуля. Можно расширить это кольцо до поля, причём мультипликативной единицей будет именно функция Дирака.
3.2) Обобщённые функции составляют пространство, сопряжённое пространству "хороших" функций - т.е. это просто функционалы.
Может, сегодня-завтра дополню про собственно ф-цию Дирака, ну или аноны понапишут.
[1] Их ещё называют распределениями в англоязычной литературе, но у нас чаще используют "обобщённые функции".
[2] Конечно, таких определений нет, но часто подразумеваются функции, локально интегрируемые по Лебегу.
[3] Это математикам мотивация, её можно пропустить.
Дивергенция это показатель в какую сторону в данной точке, если её представить поверхностью, будут идти впадины и выпуклости. Другими словами, показатель ландшафта, показывает на плоскости где высоко и где низко. \Еще можно сказать что она показывает где какое то поле сильное а где слабое.
Ротор это обобщенное понятие вращения тела на все тела, а не только на твердое. Грубо говоря, показывает циркуляция из пустого в порожнее в некоторой выбранной точке, откуда куда перетекает и как сильно.
Знатно излагаешь анон. Однако про водичку что-то не особо понял. Как будет время поясни пжл еще про диффуры, почему такая важная вещь и взаимосвязи с прикладными задачами. Могу втыкать на уровне формул, но вот такого глубинного понимания, как например ты написал про производную, его нет.
>Однако про водичку что-то не особо понял.
Формулируй вопросы точнее, а там разберёмся.
>диффуры
Нам интересно описание процессов, происходящих вокруг нас. Практически всегда мы хотим описать динамику явлений - другими словами, что-то меняется. Меняется положение частичек воды (со временем), меняется количество хищников и жертв (со временем), меняется вероятность обнаружения электрона (со временем), меняется цена опционов (c ценой акций), меняется экономический рост (с капиталом), и многое, многое другое. Можно погуглить, скажем, уравнения Навье-Стокса и Эйлера, Блэка-Шоулза и Солоу-Свана, Фоккера-Планка и Ньютона.
Наверное, первое диф. ур-ие, с которым встречается большинство - уравнение Ньютона. Тем не менее, оно не самое "удачное" для ознакомления, т.к. оно эффективно второго порядка.
Я рекомендую погуглить, или найти любой свежий американский учебник для колледжей\инженеров по обыкновенным диф. уравнениям, и ознакомиться по выбранному источнику с моделью Лотки-Вольтерры. По моему опыту, именно на этом уравнении у людей "щёлкает" идея диф. ур-ий.
Пример попроще - рост популяции без ограничений. Скажем, мы ничего сугубо технического не знаем про рост населения Земли. Обозначим текущее (в момент времени t) население за P(t). Нам бы хотелось смоделировать P(t), какой у неё может быть вид? Конечно, сначала нужно посмотреть на имеющиеся данные, и вид кривой натолкнёт нас на мысли, но пока это проигнорируем.
Давайте рассмотрим изменение за небольшой промежуток времени. Т.е. мы рассматриваем P(t+dt), где dt - мало. Как же, приблизительно, изменится P(t) до P(t+dt)? Обозначим для краткости это за dP.
Логично предположить, что чем больше людей, тем больше прирост, верно? Скажем, тысяча человек за 1 месяц изменится на 5-10 человек, а миллион - на несколько тысяч. В общем случае это говорит лишь о том, что dP является какой-то возрастающей функций от P.
Например, dP = aP + bP^2 +cP^3.
Но самый простой вариант, конечно - линейный, т.е. dP = aP. Это значит, что у нас было P(t) человек, но за dt оно выросло на aP до числа P(t)+aP. Здесь a - какая-то константа. Почему выбираем линейную модель? Во-первых, это самый простой и удобный вариант, и городить сущности без теоретической на то основы часто не приносит ощутимой пользы. Во-вторых, представим себе график численности населения. Приблизим его поближе к точке (t, P(t)). Приблизим ещё. И ещё. И ещё! Он будет практически неотличим от прямой, и это есть важная мотивация производной вообще. Прямая -> линейность при очень-очень малых изменениях.
Что если мы возьмём другой dT, отличный от dt, но тоже маленький? Линейность останется, но коэффициент "а" придётся выбрать другой, т.е.
dP1 (за dt) = aP
dP2 (за dT) = AP
Легче просто ввести один коэффициент k для "единичного" изменения, и тогда можно это переписать в виде
dP1 = k.dt.P
dP2 = k.dT.P
Отсюда естественно получается dP/dt = kP - самая простая модель роста численности; решение - экспоненциальная функция.
Если есть "нативное" понимание производной как роста, то можно было сократить пост, но на всякий случай я расписал подробней.
>Однако про водичку что-то не особо понял.
Формулируй вопросы точнее, а там разберёмся.
>диффуры
Нам интересно описание процессов, происходящих вокруг нас. Практически всегда мы хотим описать динамику явлений - другими словами, что-то меняется. Меняется положение частичек воды (со временем), меняется количество хищников и жертв (со временем), меняется вероятность обнаружения электрона (со временем), меняется цена опционов (c ценой акций), меняется экономический рост (с капиталом), и многое, многое другое. Можно погуглить, скажем, уравнения Навье-Стокса и Эйлера, Блэка-Шоулза и Солоу-Свана, Фоккера-Планка и Ньютона.
Наверное, первое диф. ур-ие, с которым встречается большинство - уравнение Ньютона. Тем не менее, оно не самое "удачное" для ознакомления, т.к. оно эффективно второго порядка.
Я рекомендую погуглить, или найти любой свежий американский учебник для колледжей\инженеров по обыкновенным диф. уравнениям, и ознакомиться по выбранному источнику с моделью Лотки-Вольтерры. По моему опыту, именно на этом уравнении у людей "щёлкает" идея диф. ур-ий.
Пример попроще - рост популяции без ограничений. Скажем, мы ничего сугубо технического не знаем про рост населения Земли. Обозначим текущее (в момент времени t) население за P(t). Нам бы хотелось смоделировать P(t), какой у неё может быть вид? Конечно, сначала нужно посмотреть на имеющиеся данные, и вид кривой натолкнёт нас на мысли, но пока это проигнорируем.
Давайте рассмотрим изменение за небольшой промежуток времени. Т.е. мы рассматриваем P(t+dt), где dt - мало. Как же, приблизительно, изменится P(t) до P(t+dt)? Обозначим для краткости это за dP.
Логично предположить, что чем больше людей, тем больше прирост, верно? Скажем, тысяча человек за 1 месяц изменится на 5-10 человек, а миллион - на несколько тысяч. В общем случае это говорит лишь о том, что dP является какой-то возрастающей функций от P.
Например, dP = aP + bP^2 +cP^3.
Но самый простой вариант, конечно - линейный, т.е. dP = aP. Это значит, что у нас было P(t) человек, но за dt оно выросло на aP до числа P(t)+aP. Здесь a - какая-то константа. Почему выбираем линейную модель? Во-первых, это самый простой и удобный вариант, и городить сущности без теоретической на то основы часто не приносит ощутимой пользы. Во-вторых, представим себе график численности населения. Приблизим его поближе к точке (t, P(t)). Приблизим ещё. И ещё. И ещё! Он будет практически неотличим от прямой, и это есть важная мотивация производной вообще. Прямая -> линейность при очень-очень малых изменениях.
Что если мы возьмём другой dT, отличный от dt, но тоже маленький? Линейность останется, но коэффициент "а" придётся выбрать другой, т.е.
dP1 (за dt) = aP
dP2 (за dT) = AP
Легче просто ввести один коэффициент k для "единичного" изменения, и тогда можно это переписать в виде
dP1 = k.dt.P
dP2 = k.dT.P
Отсюда естественно получается dP/dt = kP - самая простая модель роста численности; решение - экспоненциальная функция.
Если есть "нативное" понимание производной как роста, то можно было сократить пост, но на всякий случай я расписал подробней.
Что ты называешь «нормальным»?
Вот это заебись, все стало понятно,а по операторам в КТП можно также?
>Дивергенция это показатель в какую сторону в данной точке
Потише братишка в этой окрестности, результат оператора дивергенции над векторным полем - скаляр, это во-первых, а во-вторых я бы назвал дивергению степенью расходимости или сходимости поля в данной точке. Собственно, сравнение со источник/сток поля как он есть.
Вот смотрите, из нихуя, на ровном месте - ВНЕЗАПНО возникает противоречие, и по мере дивергенции образуется градиент.
Согласно закону о единстве и борьбе противоположностей из диалектики материализма - образуется тезис и антитезис.
Диалектическая триада при этом работает так: "тезис — антитезис — синтез".
В результате всего этого - синтезируется нечто новое, нечто такое - что имеет дальнейшее развитие.
Так как с точки зрения Энгельса, основой всякого развития является единство и борьба противоположных сторон
(имеется в виду конструктивный спор, например), к тому же первый закон диалектики вскрывает внутренний источник развития.
Значит исходя из этого всего - причиной развития является градиент дивергенции.
Третий закон диалектики отражает результат определенного цикла процесса развития и его направленность.
Процесс развития движения носит поступательно-повторяемый характер.
Поступательность и повторяемость придает цикличности спиралевидную форму.
И всё это по тандемному или даже политандемному принципу вертит вас по спирали, как на хую.
Пруф: http://ru.fapality.com/3733/
Бля, забыл ротор где-то вставить.
>Крайне не рекомендую читать эту похабщину даже самым убитым инженерам и экономистам.
Почему? Я вот очень хуёвое представление имею о математике, но она нужна по работе. Желания изучать саму математику нет, хочу понимать только прикладные аспекты. В доказательства вообще не могу, если в книжке будет хоть что-то про доказательства, я её читать не смогу. В моём случае эта книжка подойдёт?
Потому что без топологий.
Ты такой охуенный, что я попрошу у тебя пояснить за все уравнения Максвелла.
А если быть точным, то почему вектор магнитной индукции закручивается так, а не иначе?
>Блэка-Шоулза
ой бляююю про это помню только, что на опциях ябла я проебал кучу бабок. но чтобы так сказать подсластить пилюлю я еще написал программулину которая эту цену считала по блэкшолзу. практический смысл такого любопытства - ноль, да и цену реально устанавливают маркет мейкеры, и скачет она порой совсем не по шоулзу. зато немножко вкусил математики. методика вычисления по шоулзу показалась мне похожей на метод ньютона.
Просто матрица, короче.
Представь себе набор каких-то вещей, например груш или яблок. Сами по себе в совокупности их можно представить как некое абстрактное множество. Но иногда оказывается, что нам нужно эти яблоки или груши пронумеровать или, как говорят, проиндексировать. Мы можем поставить в соответствие каждой груше или яблоку свой индекс (столбец или строка) или ,например, даже два индекса (матрица) или вообще набор из произвольного количества n индексов (тензор n-го ранга). Теперь у нас есть целый компот из проиндексированных яблок и груш. Мы можем определить интуитивно понятные операции: складывать и вычитать элементы компота с одинаковыми индексами, если мы умеем интегрировать или дифференцировать яблоки, то дифференцировать по элементно, ввести понятие свёртки для столбцов или строк из яблок (обычное скалярное произведение строки и столбца), а потом обобщить это понятие на компот произвольного ранга. Так можно построить целый компотный анализ. Но можно работать не только с яблоками или грушами и компотами из них, а с произвольными абстрактными объектами и тензорами построенными из них.
Так я могу заявить, что тензор - это многомерная матрица? В /math за такое ругаются, семинарист по теории поля тоже сказал, что я неверно понимаю.
Ну, условно говоря, у тебя производные и бесконечно малые приращения (элементы касательного и кокасательного многообразия) преобразуются по-разному. Это назвыают ко и контра индексами.
 49 Кб, 560x420
49 Кб, 560x420Может кто пояснить за теорию вероятности и в частности гауссииану? Все ли случайные величины описываются нормальным распределением, если не все, то почему возникают другие "случайности" и к каким случайностям применимо нормальное распределение?
Определение читал, учебник даже по биостатистике наворачивал, но, на мой взгляд, СУТЬ(тм) явления не уловил. Буду очень признателен.
>Все ли случайные величины описываются нормальным распределением
Нет, есть куча других распределений. Например, Максвелла - Больцмана, Бозе - Эйнштейна, Ферми - Дирака в физике.
>почему возникают другие "случайности"
Потому что случайности не случайны, это лишь удобная мат. модель для вещей, которые зависят от многих и часто неизвестных параметров. Но это больше философский момент, на эту тему вагон копий сломано.
>к каким случайностям применимо нормальное распределение
Довольно много, в общем-то. Можно перечислить отклонение при стрельбе, погрешности измерений.
 163 Кб, 1200x675
163 Кб, 1200x675А есть что почитать на эту тему, где бы рассказывали не за конкретное применение (хуяк-хуяк и в продакшн), а именно с философской точки зрения что такое случайность, чем (и почему именно этим) описывается и тп?
Только без эзотерики со всяким квант мехом и прочей парашей.
Сап двач, есть один маховик, какие есть способы снятия энергии с него? Кроме коробки передач и супервариатора?
Пускай будет частью генератора.
 46 Кб, 480x720
46 Кб, 480x720> Я предполагаю, что анонам ф-цию Дирака дали не просто так
На самом деле мне её не дали, я случайно столкнулся по мере чтения учебника, не связанного с математикой как таковой. Вообще, я залез в область, где требуется много матанчика (волновые процессы, объёмные потоки, диполи как точечные источники тока и пр.), но при этом моего уровня подготовки не достаточно, а как его восполнить - хз, так как учебники обычно ориентированы на математиков. С одной стороны мне нужно понимание достаточно сложных концепций, а с другой стороны я не в состоянии использовать техническую литературу по матану для их изучения.
>Если мы рассмотрим коммутативное кольцо функций и определим умножение как свёртку, то можно показать, что в кольце нет делителей нуля. Можно расширить это кольцо до поля, причём мультипликативной единицей будет именно функция Дирака.
Вот здесь произошло какое-то страшное колдунство и я половины слов не понял.
>>07166
Вот такие объяснения самые збс. Мб есть какой-то учебник, где сложная математика объясняется на таком уровне для тех, кому нужен сложный матан, чтобы "хуяк-хуяк и в продакшн", но при этом не пришлось тратить 5 лет на изнасилование мозга? Как этот анончик >>15189 спрашивал.
А дивергенцию можно использовать не на поверхности, а на трёхмерной плоскости? Когда есть некоторый объект, в котором происходят электромагнитные процессы, и нужно было бы представить разницу в этих процессах в виде ландшафта?
> я бы назвал дивергению степенью расходимости или сходимости поля в данной точке.
Вот только что это значит я не понял.
>>15655
Бамп вопросу хоть он и не мой
>>18926
Ну так спрашивай в треде, чтобы потом все могли использовать ответ. Что ж за эгоисты такие-то, а!
>>19284
Бамп вопросу
>>21379
Тоже бамп
Он рассказывал про множество функций, что если там задать умножение и сложение, то его можно определить как кольцо. Что-то похожее на множество целых чисел. А чтобы сделать это множество похожее на множество действительных чисел(ну или комплексных), надо чтобы была единица по умножению, такую роль играет функция Дирака.
Как ты понимаешь, очень полезно бывает сказать "это множество, оно вон как то", так как определяет кучу его общих теорем и свойств.
Это если я его верно понял, ибо я вообще не математик и близко.
Ору с математики в РФ. Вроде круто в школе (в ФМЛ-ах) учат лучше, чем во всем мире. Но в вузе такое дерьмо в уши льют, что даже в руки бурбаки студент взять не может.
На всякий случай бампану хороший тред, чтобы не утонул.
чтобы у нормалфагов бомбануло.
Можно проще. Но математикам важна точность определений, отсюда и сложность. Когда привыкнешь перестаешь замечать.
>>24218
Почему у музыкоблядков всё так сложно? Понять очень легко - возьми в руки инструмент и попробуй придумать нетрмвиальную гармонию, подходящую к ней мелодию, и потом запиши это так, чтобы можно было понять завтра и через год.
Почему у программистоблядков всё так сложно? Понять очень легко - берёшь в руки низкоуровневый язык и пытаешься написать игру в крестики-нолики.
Почему у гончароблядков всё так сложно? Нет, серьёзно, берёшь в руки и изобретаешь велосипед. В какой-то момент (и не один) тф осознаешь, что надо было делать так-то. Ты будешь сам приходить к знанию, к которому другие до этого шли и накапливали. А до чего-то и не дойдешь.
Почему у математикоблядков всё так сложно? Возьми ротор. Интуитивно это кручение. Выброси все учебники, закрой двощ, возьми бумагу и ручку. Попытайся определить кручение. У тебя будут постоянно возникать мысли "не, так не пойдёт, ведь..". Так же, как и с гармонией, или программированием, или кувшином. Чтобы понять, почему определения такие заебные, нужно самому пройти всь путь хотя бы однажды.
Можешь использовать как пасту, я разрешаю.
q - заряд
C - capacitance
V - разность потенциалов
Кто может объяснить, что значит эта формула? Какой физический смысл в неё содержится и как её удобнее всего было бы представить?
С здесь - это некая константа пропорциональности, выражающая отношения между разностью потенциалов и электрическим полем.
Вроде всё просто, но в дальнейшем это уравнение используется в других местах, а я его не до конца понимаю. Типа чем больше разность потенциалов, тем выше сила создаваемого накопителем электрического поля, но чем обусловлено значение константы? Характеристикой самого накопителя, его площадью, расстоянием между пластинами?
И ещё. Предположим у нас есть цепь, в неё ток должен пройти через ёмкостный накопитель (не уверен, что правильно назвал, в английском учебнике называется capacitor). Вот у нас есть две пластины, которые изолированы. На них подаётся ток, на одной пластине концентрируются отрицательно заряженные ионы, на другой - положительные. Но что происходит, когда ёмкость насыщается?
Речь идёт про модель мембраны нейрона. Если подавать на волокно небольшой ток, то ответ волокна будет не прямоугольным (то есть таким же, каким мы подавали ток), а со сглаженными краями. Говорят, что это обусловлено емкостными свойствами мембраны, но что это значит я не понимаю. Насколько я понял, часть тока вместо того, чтобы непосредственно идти в клетку и изменять её потенциал, идёт на мембранную ёмкость. Но почему в итоге рисунок приобретает вид гиперболоподобный вид, то есть сначала процесс резко нарастает, а в конце происходит всё медленнее и медленнее? Как это объясняется с физической точки зрения?
Если не поняли, о чём речь, могу plot'ы нарисовать, если затребуете
Российская нейронаука будет вам благодарна.
Capacitor - кодненсатор. Физическией смысл формулы более понятен, если ты ее запишешь в виде c=q/v. То есть насколько кулонов заряжается твой конденсатор под каким-либо наприяжением.
Теперь по поводу воторого вопроса. Когда емкость насыщается, то ток останавливается и ничего не происходит, так как больше нет разница потенциалов.
Что у тебя за учебник? Ты в 10 классе? Если можешь в английский ,и у тебя возникнут более серьезные вопросы, задавай их лучше на stackexchange. По поводу своего вопроса ты мог бы нарыть кучу ответов и видео по тематике, на той же khan academy все разъяснено.
>stackexchange
спасибо
Вопрос действительно тупой и я мог бы сам на кхане посмотреть, но что-то разленился совсем.
На кхане тебе могут через пол года ответить. Юзай stackexhange или quora
> может у кого нибудь есть нормальным языком высшая математика?
Языком "для дебилов" темы "не для дебилов" нормально не объяснишь. Читай книги и не выебывайся.
Суть претензии, я думаю, даже не в этом. Почему-то когда я читаю английские учебники, то там всё объясняют просто, более того, все учебники подразумевают строгую модульность: есть учебные материалы, предназначенные только для Ъ-математикой и для их понимания требуется phd, а есть учебные материалы на те же самые темы, но написанные для специалистов из других областей. Например, биологу может потребоваться то же уравнение Дирака или тому подобные относительно сложные для непосвящённых штуки. И в английских учебниках такое есть, а ты кривишь носом и говоришь, что чернь не должна знать такого, пусть учит весь матан от корки до корки, ишь што удумали, нехристи.
Но ты не поверишь, есть куча людей, которым нахуй не сдались доказательства, более того, которых даже не интересует задрачивание вычислений, потому что комплюхтер всё сам посчитает. То, что их на самом деле интересует - понять, как оно работает, сформулировать правильно задачу, чтобы комплюхтер мог её посчитать.
Но ты мудак, ты не хочешь интердисциплинарной науки. ты хочешь продолжать жрать говно ради своего илитарства. Естественно, что в цивилизованном мире таких как ты нахуй сразу посылают, потому что продуктивность важнее ЧСВ очередного чухана.
Ох.. Как же двачую. И англоязычные учебники, и насчёт доказательств.
>Вот только что это значит я не понял
Если дивергенция больше нуля, то силовые линии поля выходят из нее, если меньше - то входят. Ну а если ноль, то в точке нет ни того, ни другого.
Вообще, рекомендую построить графики в чем-нибудь, что умеет считать эти характеристики.
Что такое сильно и слабо связанный граф?
bumo
https://youtu.be/qOcFJKQPZfo
Математические объекты суть концептуальные вещи. Они нужны не чтобы комплюхтер считал, а чтобы человек их думал. В язык обычных людей давно и прочно вошли такие математические объекты, как шар и куб. Когда обычный человек говорит "шарик", он считает, что говорит абсолютно понятно, и не пытается упростить свою речь, не разъясняет собеседнику, что есть шар. Обычные люди моделируют объекты реального мира шарами и даже не замечают этого, не замечают использования нетривиальной математической модели. Назначение многих математических объектов в том, чтобы люди необычные, специально обученные, использовали их так же, как обычные люди используют шары и кубы - для наияснейших, не требующих дальнейших пояснений умственных конструкций. Как базовые кирпичики для наиочевиднейших моделей.
Да-да, можешь сколько угодно илитарствовать и пускать пыль в глаза, но факт останется фактом: в англоязычник учебниках математики спускаются до простых смертных и объясняют всё понятно, в то время как аутисты из матфаков России продолжают верещать и бросаться дерьмой в других людей, кто не соответствует их стандартам задротства.
За понятной математикой в СНГ надо к физикам идти. Они к ней очень фривольно относятся, любят упрощения, наглядные иллюстрации, определения через свойства. Поговорочка даже ходит в их кругах такая:"Физик должен знать математику так, как вор уголовный кодекс."
Пиздец тут тебе объяснили.
Короче, ты играешь в PUBG. Высаживаешься в школе и буквально на каждом сантиметре вокруг тебя бегают нубы. Так вот, ты останавливаешь время и скорости каждого пидора ( а они все пидоры) будет векторным полем. Теперь заметь, какая-то тян стоит и в чате что-то пиздит, а вокруг нее кружатся пиздолисы. Там ротор поля будет ненулевой. А на крыше кто-то нашел гранату и от него съебываются все пидрилы вокруг, так вот тут будет дивиргенция ненулевая. Видишь как все просто: когда векторное поле съебывается из точки ненулевая дивиргенция, а когда векторное поле в панике бегает вокруг точки там ненулевой ротор. Модель дивигренции показывает объем пидоров в единицу времени, собственно то же показывает и модуль ротора.
Классический неосилятор.
И этого биолога всю оставшуюся мысль будет мучить мысль о том, что он строит теорию, основываясь на непонятной ему ебанине.
Вы видите копию треда, сохраненную 21 марта 2018 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.