Вы видите копию треда, сохраненную 25 июня 2018 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 69 Кб, 1024x767
69 Кб, 1024x767( а также выявить самую уникальную и длинную дробь без повторений )
бесконечные периодические дроби - это повторное цикличное повторение одного и того же результата
1\2 = 0.5
1\3 = 0,3333333333333333
1\4 = 0,25
1\5 = 0,2
1\6 = 0,16666666666666666666666666666667
1\7 = 0,14285714285714285714285714285714
1\8 = 0,125
1\9 = 0,11111111111111111111111111111111
Например
1\7 = 0,142857-142857-142857-142857-142857-14
( повторения из 6 цифр )
Тут например идут числовые квантовые эфекты, дробь не повторяется а накладывается саму на себя
если делить 1 на 79777
http://comptune.com/calc.php?methos=GET&base1=10&base2=10&S1=1121351&S2=35&func=bcpow&base3=10&places=500
>повторное цикличное повторение
кек
 117 Кб, 1000x1000
117 Кб, 1000x1000Как-то тоже на эту тему заморачивался.
Сча на JavaScript график ебонул http://xcont.com/division/
На графике:
по Y - число, которое делим (числитель).
по X - число, на которое делим (знаменатель).
Если дробь периодическая - черный пиксель. Белый пиксель - непериодические дроби.
Довольно любопытный график получается. А вот как там количество цифр в периоде посчитать - пес его знает. JavaScript обрезает все, что после 16 знака.
>1\6 = 0,16666666666666666666666666666667
>7
Лул.
>>22423
Нихуя не понял, но эта странная хуйня с цифрами мне всегда нравилась.
> А вот как там количество цифр в периоде посчитать - пес его знает.
Это очень важно
1 при делении на 97 там вообще 200 знаков
 55 Кб, 2583x482
55 Кб, 2583x482А вообще, если занимаешься теорией чисел - должен понимать (почему-то мало кто это понимает), что десятичная система - лютая хуита. Так уж исторически сложилось, что у людей 10 пальцев и начали они считать на пальцах. Когда пальцев стало не хватать - придумали переносить единичку в следующий разряд. Само же число 10 - скучное и унылое. Это тебе ни простое число, ни число Фибоначчи, ни квадрат целого числа. С одними числами оно взаимно простое, с другими - не очень. Из-за этой путаницы иногда бывает очень трудно найти закономерность в некоторых действиях над десятичными числами.
Самый охуенчик - двоичная система.
Ебанул деление единички на числа от одного до 25 в разных системах счисления. На картинке.
 10 Кб, 236x214
10 Кб, 236x214Я этот график видел год назад где то в \b там ещё тип чел говорил что нашёл теорию всего
а на деле зависит всё от системы счисления
>что десятичная система - лютая хуита. Так уж исторически сложилось
Так на какой расчитывают бесконечное число PI ?
https://habrahabr.ru/post/179829/
>А тема, кстати, пиздецки интересная. Хуй знает, чего все проигнорировали.
Потому что конечная суть квантовой теории кроется в виртуальности вселенной, основанной на вычислительном устройстве в виде моделирования - а любое моделирование это операции с числами - какая цель любого моделирования? усложнение или упрощение результатов - для полезных данных
Так как любая цивилизация хочет знать в точности своё будущее оно моделирует будущие все возможные события по методу монте карло усредняя все прогнозы
![ZWTw2VfsaCWn5OuuPjuz2Upk1Rx4g1KuWM7zLtcrqU43vY9OKRYrqxl420H[...].png](/sci/big/thumb/421997/15072762010350s.jpg) 49 Кб, 850x850
49 Кб, 850x850То и я мог быть. Периодически всякие няшные графики вкидываю то в бложик ( https://xcontcom.livejournal.com/2223.html ), то в /b
>Так на какой расчитывают бесконечное число PI ?
В двоичной же.
 121 Кб, 1000x664
121 Кб, 1000x664Это видел?
https://habrahabr.ru/post/194406/
http://xcont.com/pattern.html
Вообщем нужен список сложных для деления чисел
по типу 7 однозначное
двузначное 97 и так далее
в итоге найдём самые сложные вычислительные операции
>>Так на какой расчитывают бесконечное число PI ?
>В двоичной же.
Как выглядит двоичный механический калькулятор?
>Это видел?
Это писал.
>Вообщем нужен список сложных для деления чисел
Давай закономерность поищем.
Любое число можно представить в виде произведения простых множителей (разложить на простые множители). Например:
15 = 3 x 5
25 = 5 x 5
112 = 2 x 2 x 2 x 2 x 7
210 = 2 x 3 x 5 x 7
22 = 2 x 11
23 = 23
и т.д.
Ну и основание системы счисления тоже можно представить в виде произведения простых множителей.
Двоичная система счисления:
2 = 2
Десятичная система счисления:
10 = 2 х 5
Двенадцатеричная система счисления:
12 = 2 х 2 х 3
А теперь давай для начала разберемся, при каких условиях у нас появляется бесконечная периодическая дробь. Ну а потом уже будем думать, сколько там цифр в периоде. Очевидно, что бесконечная периодическая дробь появляется, когда в разложении (на простые множители) знаменателя дроби есть множители, которых нет в разложении числителя дроби и основания системы счисления.
Ну, например, 1/210. В разложении числа 210 есть 3 и 7 которых нет в разложении основания системы счисления (10 = 2 x 5). Поэтому получаем периодическую дробь (в десятичной системе счисления).
Или 1/6. В разложении 6 есть 3, которой нет в разложении основания. Тоже периодическая дробь в десятичной системе.
А если то же число 1/6 записать в двенадцатеричной системе - периодическая дробь не получится. Знаменатель 6 раскладывается на 2 и 3. Система счисления раскладывается на 2, 2 и 3. В двенадцатеричной системе счисления 1/6 = 0.2
Вот из-за таких непоняток с системами счисления я и предлагаю сходу избавиться от десятичной системы счисления и считать размеры периодов в двоичной системе. В двоичной системе счисления периодические дроби получаются для любых знаменателей, которые не являются степенями двойки (степени двойки в знаменателе: 2, 4, 8, 16, 32, ... - не дают период)
>Это видел?
Это писал.
>Вообщем нужен список сложных для деления чисел
Давай закономерность поищем.
Любое число можно представить в виде произведения простых множителей (разложить на простые множители). Например:
15 = 3 x 5
25 = 5 x 5
112 = 2 x 2 x 2 x 2 x 7
210 = 2 x 3 x 5 x 7
22 = 2 x 11
23 = 23
и т.д.
Ну и основание системы счисления тоже можно представить в виде произведения простых множителей.
Двоичная система счисления:
2 = 2
Десятичная система счисления:
10 = 2 х 5
Двенадцатеричная система счисления:
12 = 2 х 2 х 3
А теперь давай для начала разберемся, при каких условиях у нас появляется бесконечная периодическая дробь. Ну а потом уже будем думать, сколько там цифр в периоде. Очевидно, что бесконечная периодическая дробь появляется, когда в разложении (на простые множители) знаменателя дроби есть множители, которых нет в разложении числителя дроби и основания системы счисления.
Ну, например, 1/210. В разложении числа 210 есть 3 и 7 которых нет в разложении основания системы счисления (10 = 2 x 5). Поэтому получаем периодическую дробь (в десятичной системе счисления).
Или 1/6. В разложении 6 есть 3, которой нет в разложении основания. Тоже периодическая дробь в десятичной системе.
А если то же число 1/6 записать в двенадцатеричной системе - периодическая дробь не получится. Знаменатель 6 раскладывается на 2 и 3. Система счисления раскладывается на 2, 2 и 3. В двенадцатеричной системе счисления 1/6 = 0.2
Вот из-за таких непоняток с системами счисления я и предлагаю сходу избавиться от десятичной системы счисления и считать размеры периодов в двоичной системе. В двоичной системе счисления периодические дроби получаются для любых знаменателей, которые не являются степенями двойки (степени двойки в знаменателе: 2, 4, 8, 16, 32, ... - не дают период)
нужен список сложных для деления чисел c знаками в пер
по типу 7 однозначное
двузначное 97 и так далее
>Тут например идут числовые квантовые эфекты, дробь не повторяется а накладывается саму на себя
А можно кратенько объяснить что это ? Т. е. у неё нет периода по факту ?
 130 Кб, 672x909
130 Кб, 672x909Че-т я с тебя орнул немношк)))
Ясен хуй у тебя этот фрагмент не находит - он разбивается и переносится на следующую строку.
Чел я из-за этого в глупых вопросов тред аж написал, потом проверил на вики. Деление целых даёт либо конечную дробь, либо периодическую. Даже алгоритм сжатия Бабушкина вспомнил.
А тут еще и нашелся человек, который понял переживания ОПа. Горжусь, что сижу на одной доске с такими людьми. Вы с тем, который потенциальную энергию считает, случайно не в одном классе учитесь?
 40 Кб, 674x850
40 Кб, 674x850Бля, забей. Тема с количеством знаков в периоде интересная. А то, что там ОП себе про "квантовые эффекты в дробях" напридумывал - похуй.
Для двоичных чисел ебонул дроби. Как тут закономерность выявить?
 113 Кб, 1373x1003
113 Кб, 1373x1003В первом столбике число, во втором - двоичная запись числа, в третьем - дробь.
Что тут явно видно - в двоичной системе Теорема Миди ( >>22425 ) тоже работает.
1/37=0.00000(110111010110011111001000101001100000)
110111010110011111
001000101001100000 - вторая половина периода = инверсия первой половины
Нужны самые сложные числа для деления на 1
однозначные, двузначные, трех значные и тд
https://www.youtube.com/watch?v=qfRP_e3Xg_8
>С самого начала треда не мог въехать чем именно ОП тут траллит
Найди самые сложные числа при делении на 1
с самым большим количеством уникальной переодичностью
 678 Кб, 1408x865
678 Кб, 1408x865>А то, что там ОП себе про "квантовые эффекты в дробях" напридумывал - похуй.
>Какие еще блять квантовые дроби
Вот пример оптической илюзии, когда видны в целом волны квадратов а если смотреть внимательно на одну точку нету их
Сложноделящие
да например константы
>А в принципе выходит что может быть такая дробь, что у неё в периоде или просто после запятой огромное количество цифр ?
Щито, блять? При делении 1/n получается дробь, в периоде которой не больше n-1 знаков. Если быть еще точнее - получается, или n-1 знаков, или количество знаков кратное n-1. Количество знаков в периоде не больше числа, на которое делишь.
Пример:
1/17=0.(0588235294117647)
17-1=16 знаков в периоде
1/13=0.(076923)
(13-1)/2=6 знаков в периоде
1/97=0.(010309278350515463917525773195876288659793814432989690721649484536082474226804123711340206185567)
97-1=96 знаков в периоде
Ну а поиск числа 1/n, у которого количество знаков в периоде = n-1 - это из той же оперы, что и поиск наибольшего простого числа. Закономерность пока не нашли
 122 Кб, 1000x1000
122 Кб, 1000x1000>>22811
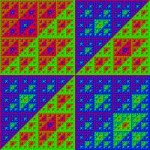
Еще одну картиночку сделал: http://xcont.com/division/3.html
По Y - число (знаменатель), на которое делим 1 в двоичной системе.
По X - двоичная дробь. Черный пиксель - 0, белый пиксель - 1.
 1,1 Мб, 3000x3000
1,1 Мб, 3000x30003000х3000
Как тогда получить бесконечную дробную экспоненту? с разными числами не прибегая к константам
Через ряд Тейлора, не?
Пиши на хабр. Статья будем бомба
Так как точность нашей вселенной определяются количеством атомов поэтому и число пи будет тоже не точным так как количество атомов не позволяет
Уже прочёл на вики, лол сам пришёл к этому и долго не мог понять где ошибка.
А что с Алгоритмом Бабушкина для сжатия данных ? Ну который предлагал файлы как огромное число интерпретировать, "дописывать" спереди 0, и искать подходящие числа для получения этой дроби. Хрень ведь полная да ?
Во-первых, подбирать такие числа можно целую вечность.
Во-вторых, искомые числа будут не меньше "сжимаемого".
К чему это?
Как-то ковырялся в этом, оказалось, что если число простое, то у него будет период число-1. Не всегда, но есть такие простые. Такие дела.
 8 Кб, 674x225
8 Кб, 674x2251. Что за хуита с квантовыми эффектами? Ебанутый?
2. Взглянем внимательно на 1\7 = 0,14285714285714285714285714285714
Можно заметить период: 142857. Про это и подобные числа с периодами(дроби то есть) я помню некоторые упоминания в книжках популяризаторов математики, автора назвать не смогу(забыл), но суть изложу. Итак, имеем 142857. Умножим на 7, получится 999999. Проведём аналогичные операции над периодами других дробей, скажем для 1/13 будет 0,07692307692307692307692307692308, а период - 076923. 7692313 = 999999.
Замечаем, что длина числа из девяток равна длине периода, понимаем, почему так(дробь - приближение, которое верно до 0,(0)1, я для себя примерно так объяснил). Что есть 9 в записи этого числа? Это 10-1. То есть для двоичного числа будет вид 11..11. Воспользовавшись пикчей из жж, я немного её подправил, обозначив периоды более верно. Для некоторых чисел, все править не стал. То есть, я считаю, что автор ЗРЯ опустил первые после запятой нули и не включил их в период(в некоторых случаях нули нужно опускать, если например число содержит в себе делитель, равный основанию системы счисления, так как очевидно, что число вида 11..11 не будет делиться на число вида ..0, аналогичный пример для десятичной с.с. - например 1/70.).
Теперь давайте проверим мои выкладки: возьмём число 9. Введу форму записи: [цифры]([система счисления]). Период 000111(2) = 6 цифр, значит я уже могу предположить, что 000111(2) это делитель 111111(2). Итак: 000111(2) = 7(10), 7(10) 9(10) = 63(10) = 111111(2). Бинго! Несложно убедиться, что это применимо и к другим числам.
Выяснили, что длина периода k для числа 1/m в n-ой системы счисления равна длине числа вида (n^k)-1, в число делителей которого входит число m.
3. Почему автор считает "Длина периода хаотична."? Только что выяснили, от чего зависит длина периода, от факторизации некоего целого числа (n^k)-1, а это уже известная проблема, о которой нельзя пока что чётко сказать, хаотично распределение делителей или нет.
4. В конце статьи красивенькая картинка(правда! мне очень понравилась!), а после неё ещё есть комментарии. Теперь я и их почитал, там как раз описан вкратце частный случай моих мыслей. Это очень здорово, или мы оба шизики, или мы оба правы.
5. Я не могу понять дроч на это. Что ахуительно интересного, кроме как красивых картиночек в периодах дробей? ОП хочет переизобрести архиватор Бабушкина? И эти новые термины, "числовой квантовый эффект". Найти дробь с периодом побольше в определённой системе счисления? Так ищи такие числа, которые являются делителями (n^k)-1, и чтобы k был побольше, простые числа, скорее всего, под эти параметры лучше подходят, хотя тут я могу быть и неправ. Смысл только ебаться с этим? Хуй знает, куда и как прикрутить, может для эстетического любования, ну такое себе.
То ли я тупорылый баран, что не вижу прикола в этих очевидных хуйнях, то ли ОП тупорылый баран.
возможны ошибки, указывайте смело
 8 Кб, 674x225
8 Кб, 674x2251. Что за хуита с квантовыми эффектами? Ебанутый?
2. Взглянем внимательно на 1\7 = 0,14285714285714285714285714285714
Можно заметить период: 142857. Про это и подобные числа с периодами(дроби то есть) я помню некоторые упоминания в книжках популяризаторов математики, автора назвать не смогу(забыл), но суть изложу. Итак, имеем 142857. Умножим на 7, получится 999999. Проведём аналогичные операции над периодами других дробей, скажем для 1/13 будет 0,07692307692307692307692307692308, а период - 076923. 7692313 = 999999.
Замечаем, что длина числа из девяток равна длине периода, понимаем, почему так(дробь - приближение, которое верно до 0,(0)1, я для себя примерно так объяснил). Что есть 9 в записи этого числа? Это 10-1. То есть для двоичного числа будет вид 11..11. Воспользовавшись пикчей из жж, я немного её подправил, обозначив периоды более верно. Для некоторых чисел, все править не стал. То есть, я считаю, что автор ЗРЯ опустил первые после запятой нули и не включил их в период(в некоторых случаях нули нужно опускать, если например число содержит в себе делитель, равный основанию системы счисления, так как очевидно, что число вида 11..11 не будет делиться на число вида ..0, аналогичный пример для десятичной с.с. - например 1/70.).
Теперь давайте проверим мои выкладки: возьмём число 9. Введу форму записи: [цифры]([система счисления]). Период 000111(2) = 6 цифр, значит я уже могу предположить, что 000111(2) это делитель 111111(2). Итак: 000111(2) = 7(10), 7(10) 9(10) = 63(10) = 111111(2). Бинго! Несложно убедиться, что это применимо и к другим числам.
Выяснили, что длина периода k для числа 1/m в n-ой системы счисления равна длине числа вида (n^k)-1, в число делителей которого входит число m.
3. Почему автор считает "Длина периода хаотична."? Только что выяснили, от чего зависит длина периода, от факторизации некоего целого числа (n^k)-1, а это уже известная проблема, о которой нельзя пока что чётко сказать, хаотично распределение делителей или нет.
4. В конце статьи красивенькая картинка(правда! мне очень понравилась!), а после неё ещё есть комментарии. Теперь я и их почитал, там как раз описан вкратце частный случай моих мыслей. Это очень здорово, или мы оба шизики, или мы оба правы.
5. Я не могу понять дроч на это. Что ахуительно интересного, кроме как красивых картиночек в периодах дробей? ОП хочет переизобрести архиватор Бабушкина? И эти новые термины, "числовой квантовый эффект". Найти дробь с периодом побольше в определённой системе счисления? Так ищи такие числа, которые являются делителями (n^k)-1, и чтобы k был побольше, простые числа, скорее всего, под эти параметры лучше подходят, хотя тут я могу быть и неправ. Смысл только ебаться с этим? Хуй знает, куда и как прикрутить, может для эстетического любования, ну такое себе.
То ли я тупорылый баран, что не вижу прикола в этих очевидных хуйнях, то ли ОП тупорылый баран.
возможны ошибки, указывайте смело
 8 Кб, 674x225
8 Кб, 674x225То ли я тупорылый баран, то ли ОП. Начнём.
1. Что за хуита с квантовыми эффектами? Ебанутый?
2. Взглянем внимательно на 1\7 = 0,14285714285714285714285714285714
Можно заметить период: 142857. Про это и подобные числа с периодами(дроби то есть) я помню некоторые упоминания в книжках популяризаторов математики, автора назвать не смогу(забыл), но суть изложу. Итак, имеем 142857. Умножим на 7, получится 999999. Проведём аналогичные операции над периодами других дробей, скажем для 1/13 будет 0,07692307692307692307692307692308, а период - 076923. 76923 умножить на 13 = 999999.
Замечаем, что длина числа из девяток равна длине периода, понимаем, почему так(дробь - приближение, которое верно до 0,(0)1, я для себя примерно так объяснил). Что есть 9 в записи этого числа? Это 10-1. То есть для двоичного числа будет вид 11..11. Воспользовавшись пикчей из жж, я немного её подправил, обозначив периоды более верно. Для некоторых чисел, все править не стал. То есть, я считаю, что автор ЗРЯ опустил первые после запятой нули и не включил их в период(в некоторых случаях нули нужно опускать, если например число содержит в себе делитель, равный основанию системы счисления, так как очевидно, что число вида 11..11 не будет делиться на число вида ..0, аналогичный пример для десятичной с.с. - например 1/70.).
Теперь давайте проверим мои выкладки: возьмём число 9. Введу форму записи: [цифры]([система счисления]). Период 000111(2) = 6 цифр, значит я уже могу предположить, что 000111(2) это делитель 111111(2). Итак: 000111(2) = 7(10), 7(10) умножить на 9(10) = 63(10) = 111111(2). Бинго! Несложно убедиться, что это применимо и к другим числам.
Выяснили, что длина периода k для числа 1/m в n-ой системы счисления равна длине числа вида (n^k)-1, в число делителей которого входит число m.
3. Почему автор считает "Длина периода хаотична."? Только что выяснили, от чего зависит длина периода, от факторизации некоего целого числа (n^k)-1, а это уже известная проблема, о которой нельзя пока что чётко сказать, хаотично распределение делителей или нет.
4. В конце статьи красивенькая картинка(правда! мне очень понравилась!), а после неё ещё есть комментарии. Теперь я и их почитал, там как раз описан вкратце частный случай моих мыслей. Это очень здорово, или мы оба шизики, или мы оба правы.
5. Я не могу понять дроч на это. Что ахуительно интересного, кроме как красивых картиночек в периодах дробей? ОП хочет переизобрести архиватор Бабушкина? И эти новые термины, "числовой квантовый эффект". Найти дробь с периодом побольше в определённой системе счисления? Так ищи такие числа, которые являются делителями (n^k)-1, и чтобы k был побольше, простые числа, скорее всего, под эти параметры лучше подходят, хотя тут я могу быть и неправ. Смысл только ебаться с этим? Хуй знает, куда и как прикрутить, может для эстетического любования, ну такое себе.
То ли я тупорылый баран, что не вижу прикола в этих очевидных хуйнях, то ли ОП тупорылый баран.
возможны ошибки, указывайте смело
 8 Кб, 674x225
8 Кб, 674x225То ли я тупорылый баран, то ли ОП. Начнём.
1. Что за хуита с квантовыми эффектами? Ебанутый?
2. Взглянем внимательно на 1\7 = 0,14285714285714285714285714285714
Можно заметить период: 142857. Про это и подобные числа с периодами(дроби то есть) я помню некоторые упоминания в книжках популяризаторов математики, автора назвать не смогу(забыл), но суть изложу. Итак, имеем 142857. Умножим на 7, получится 999999. Проведём аналогичные операции над периодами других дробей, скажем для 1/13 будет 0,07692307692307692307692307692308, а период - 076923. 76923 умножить на 13 = 999999.
Замечаем, что длина числа из девяток равна длине периода, понимаем, почему так(дробь - приближение, которое верно до 0,(0)1, я для себя примерно так объяснил). Что есть 9 в записи этого числа? Это 10-1. То есть для двоичного числа будет вид 11..11. Воспользовавшись пикчей из жж, я немного её подправил, обозначив периоды более верно. Для некоторых чисел, все править не стал. То есть, я считаю, что автор ЗРЯ опустил первые после запятой нули и не включил их в период(в некоторых случаях нули нужно опускать, если например число содержит в себе делитель, равный основанию системы счисления, так как очевидно, что число вида 11..11 не будет делиться на число вида ..0, аналогичный пример для десятичной с.с. - например 1/70.).
Теперь давайте проверим мои выкладки: возьмём число 9. Введу форму записи: [цифры]([система счисления]). Период 000111(2) = 6 цифр, значит я уже могу предположить, что 000111(2) это делитель 111111(2). Итак: 000111(2) = 7(10), 7(10) умножить на 9(10) = 63(10) = 111111(2). Бинго! Несложно убедиться, что это применимо и к другим числам.
Выяснили, что длина периода k для числа 1/m в n-ой системы счисления равна длине числа вида (n^k)-1, в число делителей которого входит число m.
3. Почему автор считает "Длина периода хаотична."? Только что выяснили, от чего зависит длина периода, от факторизации некоего целого числа (n^k)-1, а это уже известная проблема, о которой нельзя пока что чётко сказать, хаотично распределение делителей или нет.
4. В конце статьи красивенькая картинка(правда! мне очень понравилась!), а после неё ещё есть комментарии. Теперь я и их почитал, там как раз описан вкратце частный случай моих мыслей. Это очень здорово, или мы оба шизики, или мы оба правы.
5. Я не могу понять дроч на это. Что ахуительно интересного, кроме как красивых картиночек в периодах дробей? ОП хочет переизобрести архиватор Бабушкина? И эти новые термины, "числовой квантовый эффект". Найти дробь с периодом побольше в определённой системе счисления? Так ищи такие числа, которые являются делителями (n^k)-1, и чтобы k был побольше, простые числа, скорее всего, под эти параметры лучше подходят, хотя тут я могу быть и неправ. Смысл только ебаться с этим? Хуй знает, куда и как прикрутить, может для эстетического любования, ну такое себе.
То ли я тупорылый баран, что не вижу прикола в этих очевидных хуйнях, то ли ОП тупорылый баран.
возможны ошибки, указывайте смело
>Смысл только ебаться с этим? Хуй знает, куда и как прикрутить, может для эстетического любования, ну такое себе.
Картину себе представил. Садится такой Эвклид писать свои "Начала" и думает, "нахуй с этим ебаться". И мы такие сидим сейчас и думаем, "надо сегодня на мамонта сходить".
Нопример?
Я сам с них немного кипятком ссу. Это как открыть окно в параллельную вселенную.
А третья неплохие глюки вызывает.
Очень красиво! А можно ещё какую-нибудь анимацию запилить типа такой http://darkpsychedelic.ru/FV_17.html ?
осторожно, пиздец глазам, если вы эпилептик - не надо туда ходить
 513 Кб, 896x896
513 Кб, 896x896Вот кстати зацени моё творение
рандомный генератор изображений, но нужно зерно генерации или слово
http://www.random-art.org/online/
http://www.random-art.org/?liked=0&sort=popularity
http://www.random-art.org/
Есть некоторые соображения на счет анимации.
Аутисты в /rf/ сидят.
Правда это выражение а не число , но всё же
P.S золотая пропорция это (1+√5)/2
Чевоооо, блять?
Квадратные корни тоже имеют бесконечные последовательности
корень из 8
2,8284271247461900976033774484194
При этом если дроби бесконечны, то значит их точность выше количества атомов во вселенной ( что делает математику без размеров и дна )
Ну вот подели какие-то числа, чтобы в итоге получилось число пи. Или е. Вот и будут самые сложные для деления.
И почему одно число если делятся джва?
А если такую штуку в программировании применить будет ли это более пруфово чем стандартные методы? К примеру для каких то заоблачных цифр?
Это галактические скопления?
Там какие-то крестики в клеточках.
![3cc6df6c6074f5120e90705557289e04[2].jpg](/sci/big/thumb/421997/15170901889080s.jpg) 11 Кб, 604x189
11 Кб, 604x189Кстати, посоны, вы вкурсе что основные параметры стандартной космологической модели
могут быть получены из комбинирования всего лишь трёх чисел: 23, 42 и числа Пи:
https://life.ru/t/наука/1011461/mistika_kakaia-to_chislo_praviashchieie_mirom
>подели какие-то числа, чтобы в итоге получилось число пи. Или е
е вроде-бы можно из пи получить - по формуле Эйлера. Пикрелейтед.
По последней пикче можно умножение многоразрядных чисел ускорить, например в biginteger?
100000000000000000000000000000000500000000000000000000000000000000
× 100500100500100500100500100500100500100500100500100500100500100500
_____________________________________________________________________________
10050010050010050010050010050010100260100260100260100260100260100250050250050250050250050250050250000000000000000000000000000000000
http://www.javascripter.net/math/calculators/100digitbigintcalculator.htm
Только там, для многоразрядных чисел - суммирований дофига надо и сдвигов (правда меньше чем в столбик).
Наверняка алгоритмы умножения у бигинтегера эффективнее.
Потому что в калькуляторе по ссылке - почти сразу ответ получается.
Возможно ли использовать оптические устройства с системами зеркал, отражающих лучи сложным образом, в качестве дополнительного инструмента при взломе криптографических средств? Слыхал краем уха про способ физического моделирования, когда, к примеру, сложные задачи теплообмена с хитровыебанными граничными условиями решаются не за счет численного решения диф уравнений с помощью цифровых эвм, а за счет построения электрической цепи и измерения токов-напряжений. Естественно, когда цепь построена, она почти мгновенно выдает решение, намного быстрее цифровой эвм. Либо дает набор данных или приближенное решение, из которого несложно найти точное цифровыми методами. Другое дело, что цепь нужно каждый раз собирать по-новому под каждую задачу. Возможно ли использовать подобный принцип с системами зеркал и лучами для упрощения взлома криптографических средств?
В чём чуть альтернативных алгоритмов умножеия ? Помню в универе расказывали про ленивые и оптимизированные вычисления. Т. е. одни алгоритмы умножения требуют меньше/более быстрые аппаратно операции и потому работают быстрее ? На первых взгляд на пиках тоже самое умножение в столбик, только слогаемых больше.
>>29773 (Del)
Можно для совсем тупых объяснить как это связано с квантовыми компьютерами и, как пишет др. анон, криптографией ?
>Вообщем нужен список сложных для деления чисел
>по типу 7 однозначное, двузначное 97 и так далее
>в итоге найдём самые сложные вычислительные операции
Я вижу, что числа 7 и 97 — являются простыми. Пик1.
Поэтому попробуй делить единицу на простые числа.
То, что ты ищешь среди результатов деления единицы на переменную x - так это непериодические десятичные дроби.
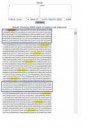
Но любую периодическую десятичную дробь - можно представить как обычную дробь. Пик2.
Непериодические же дроби - представляют из себя иррациональные числа.
По определению:
Иррациональное число — это вещественное число, которое не является рациональным,
то есть не может быть представлено в виде дроби m/n, где m — целое число, n — натуральное число.
Ну а дальше - посмотри как доказывается иррациональность некоторых чисел:
https://ru.wikipedia.org/wiki/Иррациональное_число#Примеры_доказательства_иррациональности
Алсо, попробуй делить и единицу на иррациональные числа.
Возможно это поможет тебе написать алгоритм поиска или вывести какую-то простую формулу для этого.
Например, ИМХО, любое целое число, умноженное на иррациональное - тоже не может быть представлено в виде дроби.
Как вариант - трансцендентные числа: https://ru.wikipedia.org/wiki/Трансцендентное_число#Примеры_трансцендентных_чисел
Там есть формулы, и если какая-то короткая понравилась - напиши тут, мне тоже интересно.
Вот здесь, видно, что результат, соответствующий числу 7 - представляет из себя двоичную периодическую дробь.
0.00(100)
А вот в числе, соответствующему уже числу 97 - биты, вроде, не повторяются.
Если иррациональные числа не могут быть представлены в виде дроби m/n
и являются бесконечными непиреодическими десятичными дробями,
то любое выражение 1/x не может дать бесконечную непериодическую дробь,
это будет либо конечная дробь, либо бесконечная но периодическая
(возможно даже с длинным периодом повтора).
У иррациональных чисел - цепная дробь https://ru.wikipedia.org/wiki/Непрерывная_дробь
>>21997 (OP)
ОП, смотри прикол, цитата оттуда:
Число представляется бесконечной периодической цепной дробью тогда и только тогда,
когда оно является квадратичной иррациональностью,
то есть иррациональным корнем квадратного уравнения с целыми коэффициентами.
Там, в гугле, про квадртачную иррациональность - корни квадратных уравнений какие-то вида (a+b√D) и теорема Лагранжа,
но такое число не будет целым, оно - иррационально. А ты хочешь целое...
Возьми отсюда https://ru.wikipedia.org/wiki/Наибольшее_известное_простое_число
пиздатое простое число или из PrimeGrid и раздели на него.
Думаю тебе хватит неповторяющихся десятичных знаков в твоей бесконечной, но периодической десятичной дроби.
Очевидная задача раскраски графов же. Можно просто посчитать число уникальных комбинаций цифр от 0 до 9, а потом сделать выборку по цифрам на границе. Как это реализуется на практике - хз, в академиях не обучался.
Брат, братан, братишка. Братишечка.
Ты немного тред читал?
>>23448 - я ещё вот тут написал от чего зависит длина периода. Вообще ещё вот это нашёл http://algolist.manual.ru/maths/teornum/simplper.php где основание 10 спокойно заменяется на другие.
1/97 = 0.(000000101010001110100000111111010101110001011111)
000000101010001110100000111111010101110001011111 base 2 = 2901803883615
111111111111111111111111111111111111111111111111 base 2 = 281474976710655
281474976710655 = 2901803883615 97
Длина периода для 1/97 в двоичной с.с. = 48.
Сейчас я, просто так, ради иллюстрации для себя, проверял эти штуки на системе счисления с основанием, равным золотой середине = (sqrt(5)+1)/2, она примечательна тем, что целые числа имеют конечное представление в ней(но имеют дробную часть в записи). И 100=011. Поэтому например для k = 6, 2^k-1 = 1000000 - 1 = 0110000 - 1 = 0101100 - 1 = 0101011 - 1 = 0101010, то есть 101010, а не 111111 в привычном представлении. Для k нечётных аналогично.
1/11 = 0.(0000100000) base phi
0000100000 base phi - от дроби
1010101010 base phi - phi^11 - 1
10101.0101 base phi - 11
10101.0101 100000 = 1010101010, действуют такие же законы умножения и сдвига запятой, как и в обычных с.с.
и опять я забыл про звёздочки, ну да ладно
Я что-то подобное этому графику видел, когда после операции, на которой мне сделали передозировку наркоза в 4хкратном объеме, внезапно проснулся через пару часов (хотя в основном люди отсыпаются часов 4-8). Только эта сетка еще закручивалась постепенно в спираль. Тогда я осознал, что никого и ничего не существует, но одновременно - всё, что есть - это одно целое, и это "одно целое" - информация, которая является нам кем-то вроде матери, и мы: каждый электрон, протон, нейтрон, каждый атом, каждая травинка, каждый человек - есть ее неотемлимая часть. И еще то, что всё посчитано во Вселенной, что Вселенная - это цифры. И тот, кто знает точное число - есть Бог, а мы - есть число, поэтому каждый из нас - часть этого Бога или Вселенной. Я не знаю, как еще это всё объяснить. Пробовал объяснить нескольким друзьям - алкоголикам, наркоманам и уголовникам, так они считают меня сумасшедшим.
https://ru.wikipedia.org/wiki/Теория_одноэлектронной_Вселенной
Моделей может быть много, но насколько они приближены к реальности?
Мне кажется, или этот график можно использовать для определения синуса через его угол? Просто тут график очень похож на квадратную сетку, на которую мы смотрим под двугранным углом.
Лол, а если 997, то там знаков еще больше, попытался на 99999997 поделить, результат–уже больше 100000 знаков после запятой, а периода нет и нет
 12 Кб, 318x477
12 Кб, 318x477Вам блять каждому писать про алгоритм? Писал здесь >>23448 здесь >>33758
Ещё раз: есть малая теорема Ферма[1]. (здесь и далее речь идёт об натуральных числах, если не указано иное)
Если p — простое число и a — целое число, не делящееся на p, то a^(p − 1) − 1 делится на p. достаточно А если выполняется последнее, то значит дробь 1/p в системе счисления с основанием a будет иметь lm(x) знаков в периоде, где lm(x) - функция Кармайкла[2](в общем случае, из-за особенностей основания системы счисления, это число может быть меньше).
Продолжим в соответствии с моими идеями.
Если p - составное число, то для каждого его простого множителя (p1, p2, ...) найдётся (a^lm(p1)-1, a^lm(p2)-1, ...) - число делящееся на (p1, p2, ...) соответственно, НОК[3] этих чисел по определению будет делиться на каждое число (p1, p2, ...) без остатка и как минимум содержать в себе каждое из этих чисел, так как оно по сути произведение простые числа относительно друг друга конечно же взаимно-простые, поэтому, по свойству НОК взаимно-простых чисел, оно равно их произведению (p1×p2×...) и НОК( (a^lm(p1)-1)/p1, (a^lm(p2)-1)/p2, ... ) это всё целые числа!.
Как найти НОК чисел такого вида? Обратимся к свойствам функции Кармайкла[4]. Сейчас имеем lm(НОК( (a^(p1-1)-1), (a^(p2-1)-1), ... ) ). Используя свойство разложения функции Кармайкла от НОК, получаем НОК( lm(a^(p1-1)-1), lm(a^(p2-1)-1), ... ). То есть по сути ищем НОК от периодов дробей каждого простого множителя.
Попробуем применить всё это к твоему числу.
99999997 = 1297×77101
lm(1297) = 1296, совпадает с периодом дроби.
lm(77101) = по вольфрамальфе 77100, у меня же получилось 15420( ну (x^15420) mod 77101 = 1 вроде при любом x, если я неправ, поправьте меня), период дроби 15420
НОК(1296, 15420) = 1665360
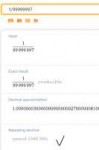
Открываю [5] или смотрю скриншот и вижу, что период дроби 1/99999997 равен 1665360. Сошлось.
Почему основание системы счисления может изменить число длины периода так, что это значение будет не совпадать с значением функции Кармайкла, а будет меньше в несколько раз? А хуй его знает.
Возьмём 1/11, lm(x) = 10, то есть x^10 mod 11 = 1. А длина периода равна 2, то есть 10^2 mod 11 = 1. То есть, при x=10, "10^10 mod 11 = 1" сократилось до "10^2 mod 11 = 1". В 5 раз длина периода меньше.
Возьмём 1/27, lm(x) = 18, то есть x^18 mod 27 = 1. Длина периода равна 3, то есть 10^3 mod 27 = 1. При x=10, "10^18 mod 27 = 1" сократилось до "10^3 mod 27 = 1". Уже в 6 раз.
Пока вообще не представляю, с чем этот минимум связан(ну кроме очевидного, что это минимальное число вида 10^k, для которого 10^k mod n = 1, где n - знаменатель в 1/n.) и как его находить без перебора.
Кстати, может вольфрамальфа права, и есть какой-то контрпример к "(x^15420) mod 77101 = 1 при любом x", и на самом деле функция Кармайкла в той точке равна 77100, а потом уменьшается для основания 10 и многих других, но не всех. Но пока это не так.
Ещё раз во избежание >>35947 если вы не можете найти период, то это не значит, что его нет. А если его нет, то это может быть иррациональное число[6], которое не представимо в виде дроби m/n, и уж точно в виде 1/n.
Использованная литература:
1. https://ru.wikipedia.org/wiki/Малая_теорема_Ферма
2. https://ru.wikipedia.org/wiki/Функция_Кармайкла
3. https://ru.wikipedia.org/wiki/Наименьшее_общее_кратное
4. https://ru.wikipedia.org/wiki/Функция_Кармайкла#Функция_Кармайкла_от_НОК
5. http://www.wolframalpha.com/input/?i=1/99999997
6 https://ru.wikipedia.org/wiki/Иррациональное_число
Справочные материалы по вольфрамальфе:
lcm() - НОК()
CarmichaelLambda() - функция Кармайкла
столько хуйни накатал, надеюсь, нигде не обосрался
 12 Кб, 318x477
12 Кб, 318x477Вам блять каждому писать про алгоритм? Писал здесь >>23448 здесь >>33758
Ещё раз: есть малая теорема Ферма[1]. (здесь и далее речь идёт об натуральных числах, если не указано иное)
Если p — простое число и a — целое число, не делящееся на p, то a^(p − 1) − 1 делится на p. достаточно А если выполняется последнее, то значит дробь 1/p в системе счисления с основанием a будет иметь lm(x) знаков в периоде, где lm(x) - функция Кармайкла[2](в общем случае, из-за особенностей основания системы счисления, это число может быть меньше).
Продолжим в соответствии с моими идеями.
Если p - составное число, то для каждого его простого множителя (p1, p2, ...) найдётся (a^lm(p1)-1, a^lm(p2)-1, ...) - число делящееся на (p1, p2, ...) соответственно, НОК[3] этих чисел по определению будет делиться на каждое число (p1, p2, ...) без остатка и как минимум содержать в себе каждое из этих чисел, так как оно по сути произведение простые числа относительно друг друга конечно же взаимно-простые, поэтому, по свойству НОК взаимно-простых чисел, оно равно их произведению (p1×p2×...) и НОК( (a^lm(p1)-1)/p1, (a^lm(p2)-1)/p2, ... ) это всё целые числа!.
Как найти НОК чисел такого вида? Обратимся к свойствам функции Кармайкла[4]. Сейчас имеем lm(НОК( (a^(p1-1)-1), (a^(p2-1)-1), ... ) ). Используя свойство разложения функции Кармайкла от НОК, получаем НОК( lm(a^(p1-1)-1), lm(a^(p2-1)-1), ... ). То есть по сути ищем НОК от периодов дробей каждого простого множителя.
Попробуем применить всё это к твоему числу.
99999997 = 1297×77101
lm(1297) = 1296, совпадает с периодом дроби.
lm(77101) = по вольфрамальфе 77100, у меня же получилось 15420( ну (x^15420) mod 77101 = 1 вроде при любом x, если я неправ, поправьте меня), период дроби 15420
НОК(1296, 15420) = 1665360
Открываю [5] или смотрю скриншот и вижу, что период дроби 1/99999997 равен 1665360. Сошлось.
Почему основание системы счисления может изменить число длины периода так, что это значение будет не совпадать с значением функции Кармайкла, а будет меньше в несколько раз? А хуй его знает.
Возьмём 1/11, lm(x) = 10, то есть x^10 mod 11 = 1. А длина периода равна 2, то есть 10^2 mod 11 = 1. То есть, при x=10, "10^10 mod 11 = 1" сократилось до "10^2 mod 11 = 1". В 5 раз длина периода меньше.
Возьмём 1/27, lm(x) = 18, то есть x^18 mod 27 = 1. Длина периода равна 3, то есть 10^3 mod 27 = 1. При x=10, "10^18 mod 27 = 1" сократилось до "10^3 mod 27 = 1". Уже в 6 раз.
Пока вообще не представляю, с чем этот минимум связан(ну кроме очевидного, что это минимальное число вида 10^k, для которого 10^k mod n = 1, где n - знаменатель в 1/n.) и как его находить без перебора.
Кстати, может вольфрамальфа права, и есть какой-то контрпример к "(x^15420) mod 77101 = 1 при любом x", и на самом деле функция Кармайкла в той точке равна 77100, а потом уменьшается для основания 10 и многих других, но не всех. Но пока это не так.
Ещё раз во избежание >>35947 если вы не можете найти период, то это не значит, что его нет. А если его нет, то это может быть иррациональное число[6], которое не представимо в виде дроби m/n, и уж точно в виде 1/n.
Использованная литература:
1. https://ru.wikipedia.org/wiki/Малая_теорема_Ферма
2. https://ru.wikipedia.org/wiki/Функция_Кармайкла
3. https://ru.wikipedia.org/wiki/Наименьшее_общее_кратное
4. https://ru.wikipedia.org/wiki/Функция_Кармайкла#Функция_Кармайкла_от_НОК
5. http://www.wolframalpha.com/input/?i=1/99999997
6 https://ru.wikipedia.org/wiki/Иррациональное_число
Справочные материалы по вольфрамальфе:
lcm() - НОК()
CarmichaelLambda() - функция Кармайкла
столько хуйни накатал, надеюсь, нигде не обосрался
ААААААААААААААА я перечитал с
>Если p - составное число
до
>Продолжим в соответствии с моими идеями.
Херня какая-то лютая, можно выкидывать и заменять одним свойством функции Кармайкла, а именно:
нам надо найти длину периода дроби, нам шепнули что она равна иногда значению функции Кармайкла.
для простого числа: x = lm(p) = p-1
для составного числа
x = lm(p)
= lm(p1×p2×...) представляем число p как разложение на простые множители
= lm(НОК(p1×p2×...) так как НОК взаимно-простых чисел равен их произведению.
= НОК(lm(p1)×lm(p2)×...) по свойству функции Кармайкла
И потом всё это применяем.
почему когда я читал те абзацы перед отправкой, то мне казалось, что всё нормально?
Я так понял, что зависимость длины периода от числа в знаменателе. Но как бы она всегда меньше его, как минимум на 1(для простого числа), так что я вообще не понимаю зачем искать "самую уникальную и длинную дробь", так как всё равно все периоды конечны. И лично я ищу зависимость этой длины периода от числа и основания системы счисления. В общем виде пока что совпадает с функцией Кармайкла, но в частном - с учётом конкретного основания - это значение в несколько раз меньше.
Ясно, только один момент. Это >>35986
твой пост ?
>Почему основание системы счисления может изменить число длины периода так, что это значение будет не совпадать с значением функции Кармайкла, а будет меньше в несколько раз? А хуй его знает.
Возьмём 1/11, lm(x) = 10, то есть x^10 mod 11 = 1. А длина периода равна 2, то есть 10^2 mod 11 = 1. То есть, при x=10, "10^10 mod 11 = 1" сократилось до "10^2 mod 11 = 1". В 5 раз длина периода меньше.
Я прочитал про функцию Кармайкла на вики. Нигде не сказано что её значение как-то связано с длиной периода дроби. Откуда ты это взял ? Скорее уже просто длина периода это минимальная степень для которой a^x mod p=1. Для простых чисел, конечно.
>Нигде не сказано что её значение как-то связано с длиной периода дроби.
Напрямую - нет.
>Скорее уже просто длина периода это минимальная степень для которой a^x mod p=1. Для простых чисел, конечно.
Да для всех чисел(натуральных) даже. n - искомое число, a - основание системы счисления, тогда длина периода 1/n будет равна минимальному x в уравнении a^x ≡ 1 (mod n)
Функция Кармайкла как раз таки и возвращает такой вот x от какого-то n, но она работает для всех a. В частном случае, при конкретном значении, когда a=const, решение x в a^x ≡ 1 (mod n) от n может быть в несколько раз меньше.
Но почему именно 5 ?
Мир не гармоничен, не симметричен, что то нарушает идеальный покой и равновесие, иначе всё бы просто остыло и остановилось
В замкнутом пространстве первая фигура которая нарушает симметричность это 5
А треугольник, квадрат гонят свет в одну линию бес пересечений
В десятичной системе счисления 5 это гармония и мгновенное равновесие всего.
Если бы гармония и существовала бы в этом мире была бы 100% стерильность
Поэтому 5 не существует, а существует скажем 4.999999999999999
>Поэтому 5 не существует, а существует скажем 4.999999999999999
и остальное
.. .....
Что за шизовысер? Почему 5 - сложное число? Почему мир должен "остыть", если он был бы гармоничен и симметричен? Как 5 может нарушать симметричность? Пятиугольник вполне себе симметричен, да как и любой правильный многоугольник. Как гонят свет? Откуда? Что ты понимаешь под равновесием? Почему 2 не равновесие? И с чего ты взял, что 5 не существует?
Нихера не понятно.
Весна?
 167 Кб, 1494x1076
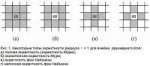
167 Кб, 1494x1076>Почему 5 - сложное число
структуры из треугольников, и квадратов не дают пустот
Первая полная структура которая образует пустоту это пятиугольник
если все физические законы основаны на балансе между наполнением и пустотой то.
У тебя на картинке не пятиугольник, а звезда(или даже пентаграмма).
мимо-фракталист (>>23934) вкатился обратно в тредик. Где-то тут еще один тредик был (>>412896 (OP)), но он о другом. Раз у вас тут тредик деления - напишу сюда. У меня тут одна идея в голове засела (довольно прочно и, кажись, я нащупал куда копать).
Короч, есть у нас, скажем, пара чисел. Эти числа - взаимно-простые (не имеют общего делителя). Если поделить меньшее число на большее - получаем некоторое число больше 0 и меньше 1. Правильно? Причем это же число нельзя получить с помощью пары других взаимно-простых чисел. То есть, число уникальное для каждой пары. Правильно?
Не, мне тут мысль пришла, как из этого дробного числа получить двоичную последовательность.
Перевести его лол в систему счисления с основанием 2? И использовать какую-нибудь нотацию для обозначения периодов?
 69 Кб, 883x897
69 Кб, 883x897Ай, потестировал на некоторых числах. Велосипед придумал, короч. Банально получился способ перевода дробного числа из десятичной системы в двоичную.
Короч, способ следующий. Есть у нас некоторое число на отрезке от 0 до 1. Мы этот отрезок делим на две части. Получаем два отрезка. Если число на левом отрезке - записываем нолик и делим левый отрезок на две части. Если в правой - соответственно записываем единичку и делим правый отрезок. Двоичный поиск типа.
3/5=0.6 в качестве примера.
отрезок (0, 1) поделили на две части - (0, 0.5) и (0.5, 1). Число находится в правой части. Соответственно 1 записали. Теперь правый отрезок поделили на две части (0.5, 0.725) и (0.725, 1). Число в левой части. Записали 0. Левый отрезок поделили на две части (0.5, 0.6125) и (0.6125, 0.725). В левой части. Записали 0... и т.д. Получается [1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1]. Собсно это дробная часть 0.6 в двоичной системе. Хуита короч)))
Ну и чисто от нехуй делать картиночку сделал. 16 картиночек. У каждой картиночки начало координат в левом верхнем углу. Берем x, делим на y - получаем дробное число. Дробное число переводим в двоичную запись. На первой картиночке берем первые знаки после запятой (на второй - вторые, на третьей - третьи и так далее). Если знак 0 - белый пиксель. Если 1 - черный. Например, для x=3 и y=5 (3/5=0.100110011... в двоичной) на первой картинке соответствующий пиксель черный (0.100110011), на второй - белый (0.100110011), на третьей - белый (0.100110011)... и т.д.
может даже покрасить разные цифры в разные тона, вдруг там помимо треугольников ещё какие-нибудь узоры откроются
На JS еще пару графиков нарисовал. Берем некоторую точку на отрезке (0, 1). В качестве примера на первой картинке взял 7/11=0.63636.. Делим отрезок на две части. Ту часть, в которой находится наша точка, увеличиваем до исходных размеров и проделываем с ним ту же операцию.
В чем кайф такого геометрического "двоичного поиска". Для рациональных чисел, через несколько итераций, полученный отрезок (расположение искомой точки на увеличенном отрезке) в точности повторяет исходный отрезок (0, 1). Отметил его на картинке стрелочкой. Для иррациональных чисел, отрезок никогда не будет повторять исходный. На второй картинке, в качестве примера, число эйлера -2.
 44 Кб, 1858x821
44 Кб, 1858x821>в точности повторяет исходный отрезок
Не, подожди, для некоторых случаев повторяет не исходный, а следующий. Точки 0.3 и 0.8.
 113 Кб, 700x1045
113 Кб, 700x1045Ежели менять разрешение с каким-нибудь хитрым периодом, наверное, можно было бы сделать чтобы линии плавненько так переходили в узорчики, а они в свою очередь в белый шум, а чтоб границы не ходили ограничить квадратиком по-меньше, но это что-то уже кумекать надобно, или быть профи математики, а не любителями вроде опа или меня, помню кстати тоже что-то такое пытался рисовать когда в школе учился по асму угорал, а сейчас почему-то на биологию больше тянет.
 65 Кб, 1700x816
65 Кб, 1700x816>чтобы линии плавненько так переходили в узорчики, а они в свою очередь в белый шум
Никакого шума. Откуда? Как там Фон Нейман говорил? "Всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений".
На тему этих узорчиков у меня огрызок статьи есть, которую никак до ума довести не могу.
Подобные узорчики можно получить чисто тригонометрически, с помощью синусов.
Возьмем функцию Z=sin(N(X/Y)). X и Y - это соответствующие пиксели на картинке. Если Z больше нуля - пиксель белый. Если меньше - черный. Вот эти же картинки >>36432 слева направо можно получить со следующими коэффициентами N - 2Pi, 4Pi, 8Pi, 16Pi и т.д.
На картинке справа - Z=sin(pi(2^16)(X/Y)), Слева - 16-й знак после запятой в двоичной записи дроби X/Y.
Собсно поиграться с разными коэффициентами (N) можно здесь:
http://xcont.com/trigonometry/sin0.php - Z=sin(N(X/Y))
http://xcont.com/trigonometry/sin1.php - Z=sin(N(XY))
Для примера:
7/11=0.63636363636
В двоичной:
0.101000101110100
z=sin(PI(2^i)(7/11)) для i от 0 до 15:
0.9096319953545184
-0.7557495743542582
0.9898214418809328
-0.28173255684142895
0.5406408174555962
0.9096319953545171
0.7557495743542624
-0.9898214418809309
0.2817325568414538
-0.5406408174556399
-0.9096319953545601
-0.7557495743541267
0.98982144188099
-0.28173255684065845
0.5406408174542452
0.9096319953531827
Положительные числа меняем на 0, отрицательные на 1. Получаем:
0.101000101110100 - ту же двоичную запись дроби.
 65 Кб, 1700x816
65 Кб, 1700x816>чтобы линии плавненько так переходили в узорчики, а они в свою очередь в белый шум
Никакого шума. Откуда? Как там Фон Нейман говорил? "Всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений".
На тему этих узорчиков у меня огрызок статьи есть, которую никак до ума довести не могу.
Подобные узорчики можно получить чисто тригонометрически, с помощью синусов.
Возьмем функцию Z=sin(N(X/Y)). X и Y - это соответствующие пиксели на картинке. Если Z больше нуля - пиксель белый. Если меньше - черный. Вот эти же картинки >>36432 слева направо можно получить со следующими коэффициентами N - 2Pi, 4Pi, 8Pi, 16Pi и т.д.
На картинке справа - Z=sin(pi(2^16)(X/Y)), Слева - 16-й знак после запятой в двоичной записи дроби X/Y.
Собсно поиграться с разными коэффициентами (N) можно здесь:
http://xcont.com/trigonometry/sin0.php - Z=sin(N(X/Y))
http://xcont.com/trigonometry/sin1.php - Z=sin(N(XY))
Для примера:
7/11=0.63636363636
В двоичной:
0.101000101110100
z=sin(PI(2^i)(7/11)) для i от 0 до 15:
0.9096319953545184
-0.7557495743542582
0.9898214418809328
-0.28173255684142895
0.5406408174555962
0.9096319953545171
0.7557495743542624
-0.9898214418809309
0.2817325568414538
-0.5406408174556399
-0.9096319953545601
-0.7557495743541267
0.98982144188099
-0.28173255684065845
0.5406408174542452
0.9096319953531827
Положительные числа меняем на 0, отрицательные на 1. Получаем:
0.101000101110100 - ту же двоичную запись дроби.
 36 Кб, 899x911
36 Кб, 899x911>Подобные узорчики можно получить чисто тригонометрически
Еще один график сделал. Черные точки - там, где синус не совпадает с двоичной записью числа.
>там, где синус не совпадает с двоичной записью числа.
Там, где дробь непериодическая, там и не совпадают.
Ладно, надоело че-т. Пойду дрыхнуть.
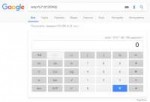 21 Кб, 796x547
21 Кб, 796x547Ну да, там синус где-то в окрестности 0 топчется для непериодических дробей. 35/40 в качестве примера. Непериодическая дробь, в двоичной системе = 0.111. Третий символ после запятой уже не посчитаешь с помощью синусов.
Вот теперь точно дрыхнуть.
>На картинке справа - Z=sin(pi(2^16)(X/Y)), Слева - 16-й знак после запятой в двоичной записи дроби X/Y.
Наоборот. Справа - знак в двоичной, слева - синус.
> Клеточный автомат
Уаааау! А какой именно клеточный автомат это и как найти его настоящее название? (и заодно проверить кто его изобрёл и изобрёл ли)
Я ебу, что у тебя за картинка и как ты ее получил.
Клеточные автоматы Фон Нейман изобрел и они вполне нормально гуглятся.
> математик
> не видит что на картинке простая арифметика
ну ты уже вообще заспециализировался я смотрю
 63 Кб, 928x951
63 Кб, 928x951Сделал аналогичные графики для десятичной системы.
На каждом графике 16 картиночек. Каждая из этих картиночек - соответствующая цифра после запятой. Делим X на Y (начало координат - левый верхний угол). Получаем дробь. Берем первую цифру после запятой на первой картиночке, вторую цифру после запятой - на второй картиночке и т.д.
Первый график - пиксель закрашиваем белым, если цифра = 0.
В каком месте эта самая непериодическая дробь заканчивается.
Объясню на примере второй картинки на графике. Если 1-й символ после запятой был, а второго уже нет - белый пиксель.
Для третьей картинки - если был второй символ, а третьего уже нет - белый пиксель. И т.д.
Вторая, третья и четвертая картинки 1000х1000
Ну так, навскидку, длина периода определяется знаменателем, а не числителем.
1/13=0.(076923)
2/13=0.(153846)
3/13=0.(230769)
...
 20 Кб, 861x291
20 Кб, 861x291Чёта проиграл
> самую уникальную и длинную дробь без повторений
https://en.wikipedia.org/wiki/Full_reptend_primeмимо из /math
>мимо из /math
Что скажешь насчет этого:
>>36467
>z=sin(PI(2^i)(7/11))
Для a=pi(2^n), sin(ax/y) будет меньше 0, если в (двоичной) дроби x/y соответствующий знак n после запятой = 1. Если соответствующий знак после запятой = 0, значение функции будет больше 0. Работает не только с периодическими дробями, но и с иррациональными числами.
Число e-2=0.71828182845, в двоичной:
0.1011011111100001
sin(pi(2^n)(e-2)) для n от 0 до 16:
0.77394268526
-0.98020715847
0.38811216212
-0.71537776606
-0.99972311483
0.04704836214
-0.09399252276
-0.18715281753
-0.36769195818
-0.68386854177
-0.99790815372
-0.12902480447
0.25589266685
0.4947455432
0.85990524205
0.87788361623
-0.84079136654
меняем положительные числа на нолики, отрицательные - на единички:
01011011111100001 - получаем двоичную запись числа e-2.
Хуита или дальше развивать?
>мимо из /math
Что скажешь насчет этого:
>>36467
>z=sin(PI(2^i)(7/11))
Для a=pi(2^n), sin(ax/y) будет меньше 0, если в (двоичной) дроби x/y соответствующий знак n после запятой = 1. Если соответствующий знак после запятой = 0, значение функции будет больше 0. Работает не только с периодическими дробями, но и с иррациональными числами.
Число e-2=0.71828182845, в двоичной:
0.1011011111100001
sin(pi(2^n)(e-2)) для n от 0 до 16:
0.77394268526
-0.98020715847
0.38811216212
-0.71537776606
-0.99972311483
0.04704836214
-0.09399252276
-0.18715281753
-0.36769195818
-0.68386854177
-0.99790815372
-0.12902480447
0.25589266685
0.4947455432
0.85990524205
0.87788361623
-0.84079136654
меняем положительные числа на нолики, отрицательные - на единички:
01011011111100001 - получаем двоичную запись числа e-2.
Хуита или дальше развивать?
 61 Кб, 1008x1008
61 Кб, 1008x1008кореш сделал:
#!/usr/bin/env python3
# -- coding: utf-8 --
"""
Created on Sat Apr 21 17:41:24 2018
@author: sat
"""
from PIL import Image
size=1008
img = Image.new( 'RGB', (size,size), "black")
pixels = img.load()
a=[]
colors=[(0,0,0),(127,0,0),(0,127,0),(0,0,127),(127,127,0),(0,127,127),(127,0,127),(255,0,0),(0,255,0),(255,255,255)]
for y in range(size):
a.append([])
out=""
for x in range(size):
if x==0:
val=1
elif y==0:
val=a[y][x-1]%10
else:
val=(a[y][x-1]+a[y-1][x])%10
a[y].append(val)
pixels[y,x] = colors[val]
img.show()
img.save('out.png')
https://2ch.hk/wp/src/54986/15247814142990.png (
 61 Кб, 1008x1008
61 Кб, 1008x1008кореш сделал:
#!/usr/bin/env python3
# -- coding: utf-8 --
"""
Created on Sat Apr 21 17:41:24 2018
@author: sat
"""
from PIL import Image
size=1008
img = Image.new( 'RGB', (size,size), "black")
pixels = img.load()
a=[]
colors=[(0,0,0),(127,0,0),(0,127,0),(0,0,127),(127,127,0),(0,127,127),(127,0,127),(255,0,0),(0,255,0),(255,255,255)]
for y in range(size):
a.append([])
out=""
for x in range(size):
if x==0:
val=1
elif y==0:
val=a[y][x-1]%10
else:
val=(a[y][x-1]+a[y-1][x])%10
a[y].append(val)
pixels[y,x] = colors[val]
img.show()
img.save('out.png')
https://2ch.hk/wp/src/54986/15247814142990.png (
Как побелы расставить с табуляцией - не работает ничего.
Залил бы на какой-нибудь python fiddle вроде этого: https://pyfiddle.io/
Ну тогда попроси еще своего корефундика таки познакомить тебя с клеточными автоматами. Если он хороший программист - то, скорее всего, слышал о них. Твои треугольники Серпинского можно нарисовать одномерными клеточными автоматами первого порядка. В принципе, они все (одномерные) довольно неплохо изучены, тем же Вольфрамом, например. У него даже книга про них написана (A New Kind of Science 2002). Без перевода правда (и по причине отсутствия оного, половину осилил, половину - пролистал).
Ну, если совсем в двух словах о клеточных автоматах. Есть у нас поле из клеточек (ячейки массива). Клеточки могут принимать два состояния - 1 и 0. На каждой следующей итерации берется поочередно каждая клеточка и для нее смотрим окрестность на предыдущей итерации. В зависимости от того, что там находилось, состояние клетки изменяем по соответствующему правилу. Правило для всех клеток одинаковое. На пикчах, в качестве примера, привила 90 и 60. (Каждая строка - это следующее состояние автомата. Верхняя строка - начальное состояние автомата, заполнена только центральная клетка.) Как уже написал, данные клеточные автоматы довольно плотно изучены. Хотя, тут тоже есть интересная тема, в которой можно покопаться. Границы клеточного автомата мы соединяем (в случае с одномерным - в окружность, с двухмерным - в тор), чтобы для граничных клеток действовали те же правила, что и для остальных ну и чтобы автомат не разрастался бесконечно. Две интересные темы - начальное состояние автомата и размер автомата.
Всего таких автоматов существует 256 штук - клетка и две ейные окрестности, в совокупности могут находиться в одном из 2^3=8 состояний. Для каждого из 8 состояний выбираем состояние клетки на следующей итерации, соответственно правил может быть 2^8=256 штук.
Еще есть клеточные автоматы, которые Вольфрам называет "second-order cellular automaton" (второго порядка). На третьей пикче суть. Самое любопытное в таких автоматах то, что они могут быть обратимыми. То есть, для текущего состояния может существовать только одно состояние на предыдущей итерации. Таких автоматов существует немношко побольше - 2^(2^4)=65536 штук. Там себе кто-то даже шизу заработал изучая одно из правил http://www.anmuha.narod.ru/37R.html. Эти автоматы тоже можно поковырять - они менее изучены.
Но самые интересные клеточные автоматы - двухмерные. Все они не изучены. Не изучены по той простой причине, что это невозможно. Попробуй осознать. Если рассматривать только окрестность фон Неймана (четвертая пикча) - имеем 5 клеточек. Это, стало быть, 2^5=32 - количество всех возможных состояний клетки и ее окрестностей. И стало быть 2^32=4294967296 количество возможных правил. Если же рассматривать окрестность Мура - 2^9=512 состояний. 2^512=1.340781e+154 возможных автоматов. Число, мягко говоря, не маленькое. Это примерно как. Если ты будешь выбирать случайное правило и запускать клеточный автомат с этим правилом - он у тебя будет каждый раз уникальным. Вероятность, что он у тебя повторится, практически нулевая. Я, вон, 15 лет назад клеточные автоматы на бейсике делал. Рандомно правила перебирал. Одно из правил дало очень любопытные результаты. Сколько я его не пытался повторить... ну, в общем, больше я его никогда не увижу.
И это только двухмерных столько! А есть же еще трехмерные. Сколько их там всего существует, гугль-калькулятор мне посчитать отказывается. Ну, можно попробовать очень грубо так на вскидку. 3х3=27 клеток. 2^27=134217728 - количество комбинаций. 2^134217728 гугль не считает. Прикинем. Каждая десятка в степени - это примерно плюс три циферки к числу... короче число с более 40 миллионами цифр. Тут остается только с рандомом баловаться. Ну или, пес его знает, какими-нить генетическими алгоритмами перебор устроить. Правда пес его знает, с какими критериями - так бы уже давно запрограммировал.
Может где-то там, одно из правил - точная копия нашей Вселенной.
Это мы тут говорим только о клеточных автоматах, клетка которых может находиться только в двух состояниях. Если состояний больше - все вот те вышеперечисленные числа нешуточно возрастают. Ну и плюс окрестность можно увеличивать. Брать не только предыдущее состояние, но и пред-предыдущее.
Ну тогда попроси еще своего корефундика таки познакомить тебя с клеточными автоматами. Если он хороший программист - то, скорее всего, слышал о них. Твои треугольники Серпинского можно нарисовать одномерными клеточными автоматами первого порядка. В принципе, они все (одномерные) довольно неплохо изучены, тем же Вольфрамом, например. У него даже книга про них написана (A New Kind of Science 2002). Без перевода правда (и по причине отсутствия оного, половину осилил, половину - пролистал).
Ну, если совсем в двух словах о клеточных автоматах. Есть у нас поле из клеточек (ячейки массива). Клеточки могут принимать два состояния - 1 и 0. На каждой следующей итерации берется поочередно каждая клеточка и для нее смотрим окрестность на предыдущей итерации. В зависимости от того, что там находилось, состояние клетки изменяем по соответствующему правилу. Правило для всех клеток одинаковое. На пикчах, в качестве примера, привила 90 и 60. (Каждая строка - это следующее состояние автомата. Верхняя строка - начальное состояние автомата, заполнена только центральная клетка.) Как уже написал, данные клеточные автоматы довольно плотно изучены. Хотя, тут тоже есть интересная тема, в которой можно покопаться. Границы клеточного автомата мы соединяем (в случае с одномерным - в окружность, с двухмерным - в тор), чтобы для граничных клеток действовали те же правила, что и для остальных ну и чтобы автомат не разрастался бесконечно. Две интересные темы - начальное состояние автомата и размер автомата.
Всего таких автоматов существует 256 штук - клетка и две ейные окрестности, в совокупности могут находиться в одном из 2^3=8 состояний. Для каждого из 8 состояний выбираем состояние клетки на следующей итерации, соответственно правил может быть 2^8=256 штук.
Еще есть клеточные автоматы, которые Вольфрам называет "second-order cellular automaton" (второго порядка). На третьей пикче суть. Самое любопытное в таких автоматах то, что они могут быть обратимыми. То есть, для текущего состояния может существовать только одно состояние на предыдущей итерации. Таких автоматов существует немношко побольше - 2^(2^4)=65536 штук. Там себе кто-то даже шизу заработал изучая одно из правил http://www.anmuha.narod.ru/37R.html. Эти автоматы тоже можно поковырять - они менее изучены.
Но самые интересные клеточные автоматы - двухмерные. Все они не изучены. Не изучены по той простой причине, что это невозможно. Попробуй осознать. Если рассматривать только окрестность фон Неймана (четвертая пикча) - имеем 5 клеточек. Это, стало быть, 2^5=32 - количество всех возможных состояний клетки и ее окрестностей. И стало быть 2^32=4294967296 количество возможных правил. Если же рассматривать окрестность Мура - 2^9=512 состояний. 2^512=1.340781e+154 возможных автоматов. Число, мягко говоря, не маленькое. Это примерно как. Если ты будешь выбирать случайное правило и запускать клеточный автомат с этим правилом - он у тебя будет каждый раз уникальным. Вероятность, что он у тебя повторится, практически нулевая. Я, вон, 15 лет назад клеточные автоматы на бейсике делал. Рандомно правила перебирал. Одно из правил дало очень любопытные результаты. Сколько я его не пытался повторить... ну, в общем, больше я его никогда не увижу.
И это только двухмерных столько! А есть же еще трехмерные. Сколько их там всего существует, гугль-калькулятор мне посчитать отказывается. Ну, можно попробовать очень грубо так на вскидку. 3х3=27 клеток. 2^27=134217728 - количество комбинаций. 2^134217728 гугль не считает. Прикинем. Каждая десятка в степени - это примерно плюс три циферки к числу... короче число с более 40 миллионами цифр. Тут остается только с рандомом баловаться. Ну или, пес его знает, какими-нить генетическими алгоритмами перебор устроить. Правда пес его знает, с какими критериями - так бы уже давно запрограммировал.
Может где-то там, одно из правил - точная копия нашей Вселенной.
Это мы тут говорим только о клеточных автоматах, клетка которых может находиться только в двух состояниях. Если состояний больше - все вот те вышеперечисленные числа нешуточно возрастают. Ну и плюс окрестность можно увеличивать. Брать не только предыдущее состояние, но и пред-предыдущее.
цифрами количество табов обозначил:
#!/usr/bin/env python3
# -- coding: utf-8 --
"""
Created on Sat Apr 21 17:41:24 2018
@author: sat
"""
from PIL import Image
size=1008
img = Image.new( 'RGB', (size,size), "black")
pixels = img.load()
a=[]
colors=[(0,0,0),(127,0,0),(0,127,0),(0,0,127),(127,127,0),(0,127,127),(127,0,127),(255,0,0),(0,255,0),(255,255,255)]
for y in range(size):
1 a.append([])
1 out=""
1 for x in range(size):
2 if x==0:
3 val=1
2 elif y==0:
3 val=a[y][x-1]%10
2 else:
3 val=(a[y][x-1]+a[y-1][x])%10
2 a[y].append(val)
2 pixels[y,x] = colors[val]
img.show()
img.save('out.png')
цифрами количество табов обозначил:
#!/usr/bin/env python3
# -- coding: utf-8 --
"""
Created on Sat Apr 21 17:41:24 2018
@author: sat
"""
from PIL import Image
size=1008
img = Image.new( 'RGB', (size,size), "black")
pixels = img.load()
a=[]
colors=[(0,0,0),(127,0,0),(0,127,0),(0,0,127),(127,127,0),(0,127,127),(127,0,127),(255,0,0),(0,255,0),(255,255,255)]
for y in range(size):
1 a.append([])
1 out=""
1 for x in range(size):
2 if x==0:
3 val=1
2 elif y==0:
3 val=a[y][x-1]%10
2 else:
3 val=(a[y][x-1]+a[y-1][x])%10
2 a[y].append(val)
2 pixels[y,x] = colors[val]
img.show()
img.save('out.png')
Пашет.
На тебе ещё вот: https://github.com/NataKuskova/tasks2
можно в зипе слить. Там прорисовка треугольников хаосом haos.py
Ссылочку дашь?
Я кстати периодически думаю, над вот этим >>36237
То есть почему
>Функция Кармайкла как раз таки и возвращает такой вот x от какого-то n, но она работает для всех a. В частном случае, при конкретном значении, когда a=const, решение x в a^x ≡ 1 (mod n) от n может быть в несколько раз меньше.
это решение x меньше, и как его найти за константное время(не перебором). Наверно, это одна из охуительных проблем, для которой требуется матаппарат, мне ещё неизвестный(а может и всем). А может я просто плохо думал.
Формулировка такая: даны числа a, n(взаимно-простые и пусть будут натуральные) такие, что a^k(n) mod n = 1(утверждение верно при любых a и n), где k() - функция Кармайкла. Надо найти минимальное число x, что a^x mod n = 1. Известно, что k(n) делится на x нацело.
>Ссылочку дашь?
Да там че-т много слишком. Сегодня не успею доспиать. Надо еще разные двоичные последовательности проверить.
 197 Кб, 1676x986
197 Кб, 1676x986>доспиать.
дописать.
Че-т я вчера, когда эту злую штуку придумал, не подумал что их там дохуища и они все РАЗНЫЕ.
Чисто вот только 12-символьные последовательности, 4096 штук. Как бы туда старый добрый Генетический Алгоритм не пришлось прикручивать.
Как дроби могут быть бесконечными, если не существует бесконечно делимой материи или пространства? Кто-то наёбывает.
 196 Кб, 1839x984
196 Кб, 1839x984>Злая штука
Потому-что математика это не наука(одна из точек зрения). Она не связана с природой, а является лишь инструментом описания мира.
В треде так и не дан ответ про сложность числа
Я пойду дальше.
Создаю файл на 1 гб - с результатами вычислений скажем 1\3
Архивирую ZIPом - получаю количество байт
чем больше байт, тем сложнее число
например картинки и видео не сжимаются
Ну в архиваторе наверно при считывании файла похожий как здесь алгоритм >>33758 http://algolist.manual.ru/maths/teornum/simplper.php при поиске одинаковых последовательностей. Предполагаю, что период заменяется единичкой, создаётся таблица ключей с 1 записью, где единица заменяется на период, и потом эти единички, если их несколько, заменяются на их количество и указание того, что повторяются именно единицы, то есть размер сжатого файла примерно равен (размер периода + log2(размер несжатого файла/размер периода)).
"Сложность" числа определяется размером его периода, а он от: >>23448
>Выяснили, что длина периода k для числа 1/m в n-ой системы счисления равна длине числа вида (n^k)-1, в число делителей которого входит число m.
Или же равна наименьшему k в (n^k) ≡ 1 (mod m). Что есть функция Кармайкла в общем виде, как я уже писал, и при конкретных значениях n, значение k может быть меньше во сколько-то раз.
>1\6 = 0,16666666666666666666666666666667
ОП-дегенерат детектед, говорит о дробях и округляет бесконечные числа, лол.
>Самая оригинальная дробь: число пи и экспонента, все было уже.
 42 Кб, 900x900
42 Кб, 900x900Описание: https://xcontcom.livejournal.com/29856.html
Берем координаты x и y картинки. Перемножаем. Получили число. Берем остаток от деления этого числа на x-координату мышки. Получили еще одно число. Берем остаток от деления оного на y-координату мышки. Ну и дальше смотрим, если получившийся остаток равен некоторому числу k - закрашиваем пиксель белым цветом (если не равен - оставляем черным).
На пикче, которую прикрепил - первый делитель - 780, второй делитель - 27, k=3
По ссылке выше (скриптец), слева-направо, сверх-вниз - k от 0 до 7.
 88 Кб, 1900x900
88 Кб, 1900x900Очень крутые паттерны получаются для:
k - не четное
первый делитель = n*4+2 (n - целое)
второй делитель = 16
На пикче:
k = 1, 3, 5, ..., 15
 169 Кб, 582x580
169 Кб, 582x580Тут нейросеть пытается найти самые запоминаемые участки фото
Может ты в double не вмещаешься? Посмотри библиотеки для длинной арифметики, должны быть доступны для js.
Че-т мой коммент вместе с шизиком потерли. Не вмещаюсь в double. Там проверка периодичности дроби делается примитивным образом - если после запятой меньше 10 знаков - дробь непериодическая. Для того, чтобы паттерн увидеть в общих чертах, такой проверки достаточно.
вручную не удобно
1\2 = 0.5
1\3 = 0,3333333333333333
1\4 = 0,25
1\5 = 0,2
1\6 = 0,16666666666666666666666666666667
1\7 = 0,14285714285714285714285714285714
1\8 = 0,125
1\9 = 0,11111111111111111111111111111111
1\10= 0.1
1\11= 0,0909090909090909
1\12= 0,0833333333333333
1\13 = 0,0769230769230769
1\14 = 0,0714285714285714
1\15 = 0,0666666666666667
1\16 = 0,0625
1\17= 0,0588235294117647
1\18 = 0,0555555555555556
1\19 = 0,0526315789473684
1\20 = 0,05
1\21 = 0,0476190476190476
Если ты имеешь в виду просто тысячное x, то вот у этого глянь: >>40921
А вот если ты хочешь - тысячное число после запятой,
то вот тут тебе BigInteger + BigRational запхнул: http://rextester.com/ZFJXR18249
Вначале - задаёшь три параметра (стартовое x, конечно x, и число знаков после запятой).
Затем, нажми Run It(F8) и закопируй себе всё это,
потому что каждое число - в одну строку выводится без переноса.
Сам код можешь поместить в html-страницу и запускать локально, без этого сайта.
уууууу и ни одного результата где было бы вроде 0.0999999999
математика резиновая и можно подогнать любой результат
0.99999 * 2 = 1.9999 \ 2 = 0.99999
>>41414
Заканчивай ты эту хуйню. Сам себе что-то напридумывал, сидишь тут мистику какую-то нагоняешь, как шаман блять.
Чем 6-ричная система счисления интересная? Чем она лучше 10-ричной системы? Составные системы счисления вообще треш нахуй. Заебись системы - это у которых в основании простое число. Двоичная - заебись, троичная - заебись, пятиричная - заебись. Степени двойки - тоже заебись. А 6, блять, чем она охуенная?
>1/314159
Это вообще блять пушка. Что ты этой хуйней сказать хотел? Ты так духов призываешь? Камлания делаешь? Или это у тебя какой-то чисто языческий ритуал?
 70 Кб, 1154x615
70 Кб, 1154x615Сдаётся мне, что ОП - протеиновый хомяк, тот самый, с вечной капсулой, обитающий в /сс
Пикрелейтед.
 264 Кб, 1280x960
264 Кб, 1280x960В /b/ с ним как-то сцепился. Конструктивного диалога не получилось - он на все мои вопросы порциями картиночек отвечал. Полез в гугл гуглить запрос "site:vk.com медийные клоуны" - вдруг тот шизик и вконтакте обитает. Ну и таки нашел в выдаче один интересный комментарий, написанный в таком же шизофреническом стиле - МЕДИЙНЫЕ КЛОУНЫ, СГНИЮТ, ЗАКОПАЮТСЯ. Вот этим пикрелейтед товарищем комментарий оставлен. На страничке картинки уровня /нибиру, мемасы и в списке групп сплошные анимешки. Исторический факультет, к слову.
>Нахуя деанон?..
Томущо он уже реально всех доебал своими протеинами. Совершенно какие-то уебанские шизофренические картинки делает и общается со всеми в духе "вы все пидарасы, потому что не считаете протеины, УМРЕТЕ И ЗАКОПАЕТЕСЬ а я считаю и буду жить в КАПСУЛЕ".
А самый пиздец в том, что он для BOINC лютую, просто лютейшую антирекламу делает. Бля, посмотри эти его картиночки. Что адекватный человек подумает, когда их увидит? "Да я в рот твое это говно ебал" он подумает.
Можно ж было нормально форсить. Тредики пилить там с перекатами, FAQ какое-нить написать, там мол, где скачать, как пользоваться, для чего это вообще нужно. Периодически сообщать новости и результаты, есть ли там прогресс какой, что уже посчитали. Там даже пиписьками можно было бы мериться - кто больше протеинов посчитал. Тема бы заебись взлетела. Нет, блядь, нахуй, "ВЫ ВСЕ ПИДАРАСЫ УМРЕТЕ И ЗАКОПАЕТЕСЬ КАК МЕДИЙНЫЕ КЛОУНЫ".
Я вон тоже одну тему в /b/ форсил. С ноября 2014 по декабрь 2016. 5-10 тредов полгода перерыв, потом опять 5-10 тредов и т.д. Около 50 тредов в общей сложности. Так охуенные были обсуждения, дискуссии, разные точки зрения. Советы и помощь новичкам, которые только вкатываются в тему. Постоянная аудитория сформировалась. Через полгода смотрели у кого какие результаты. Группа в вкшечке, чтобы за перекатами следить. Народ возмущался, почему, мол, треды не создаешь - они охуенно мотивируют этой темой заниматься. Потом еще и доску отдельно под это дело выделили.
Вы видите копию треда, сохраненную 25 июня 2018 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.





![D0B1D18BD181D182D180D0BED0B5-D183D0BCD0BDD0BED0B6D0B5D0BDD0[...].jpg](/sci/big/thumb/421997/15171153845310s.jpg)
![img17[1].jpg](/sci/big/thumb/421997/15171153845311s.jpg)
![35474original[2].png](/sci/big/thumb/421997/15171153845322s.jpg)
![i015[1].png](/sci/big/thumb/421997/15206014214890s.jpg)
![translationcirculardecimalintofraction[1].png](/sci/big/thumb/421997/15206014214901s.jpg)
![formules3153[1].png](/sci/big/thumb/421997/15206014214902s.jpg)