Двач.hk прислал битые данные.
Вы видите копию треда, сохраненную 11 мая 2020 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Вы видите копию треда, сохраненную 11 мая 2020 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 1,3 Мб, 3264x2448
1,3 Мб, 3264x2448Криптач умер? Да здравствует Криптач. Аноны, куда вы все пропали? Почему меньше одного поста в час? Может, стоит возрадить криптач?
Как я понимаю, этого треда будет недостаточно. Поэтому тут я также периодически буду писать переводы к некоторым интересующим меня вещам, касающимся криптографии.
>>38053
Пусть читают фак или пишут итт.
Пусть читают фак или пишут итт.
>>38063
Он есть. На нулевой в закреплённом треде.
Он есть. На нулевой в закреплённом треде.
>>38048 (OP)
все съебались в даркнет
все съебались в даркнет
>>38048 (OP)
У школьников учёба. Какой крпитач?
У школьников учёба. Какой крпитач?
>>38167
ссылочку запили пожалуйста
ссылочку запили пожалуйста
Раз уж тупых вопросов тред, то можно ли увидеть все скрытые доступные по ссылке видео на чужом ютуб канале?
>>38051
Здесь криптографию никогда и не обсуждали, в ней никто ничего не смыслит из местных. Как в /s не обсуждают кодинг. Это доска для трепа о прайваси, законах, софте с т.з. пользователей и т.п.
Здесь криптографию никогда и не обсуждали, в ней никто ничего не смыслит из местных. Как в /s не обсуждают кодинг. Это доска для трепа о прайваси, законах, софте с т.з. пользователей и т.п.
>>38048 (OP)
Каким алгоритмом
можно найти примитивный корень по модулю простого числа,
если оно пиздатющее?
Каким алгоритмом
можно найти примитивный корень по модулю простого числа,
если оно пиздатющее?
>>40313
Это троллинг такой, или что?
Сразу же, сходу, нашёл какую-то теорему от математика Сосницкого: https://dxdy.ru/topic52676.html
В схемах ElGamal и Diffie-Hellman нужно первым делом - сгенерировать пару p и g.
При этом g - является первообразным корнем по модулю простого числа p.
Как найти g? Есть что-то типа JavaScript генератора?
Я нашёл только ECDH - на эллиптических кривых: http://www-cs-students.stanford.edu/~tjw/jsbn/ecdh.html
Там изначально заданы координаты генераторной точки G, в самой эллиптической кривой.
Выбираешь кривую, задаётся генераторная точка G,
затем генерируешь число (приватный ключ),
и умножаешь генераторную точку на число - получаешь публичный ключ (точка с двумя координатами).
После обмена ими - рассчитывается общая точка, которая и может быть общим ключём шифрования
(если её координаты, конвертнуть в HEX, например)...
Но кривые эти - надо чтобы были и у Алисы и у Боба, к тому же нужно задать конкретную кривую.
А вот если просто числа брать, без эллиптических кривых,
то быстрое возведение в степень по модулю не так уж много места занимает и не требует всяких скриптов.
К тому же эти функции можно быстро написать.
Вот здесь: https://8gwifi.org/DHFunctions.jsp я вижу нечто наподобие PGP DH,
но тут тоже задаются изначально, параметры p и g.
То, что p - это простое число, и оно может быть большим, так есть алгоритм Миллера-Рабина.
Вопрос в том, как получить g при определённом, сгенерированном p.
>Алгоритмом Сосницкого
Это троллинг такой, или что?
Сразу же, сходу, нашёл какую-то теорему от математика Сосницкого: https://dxdy.ru/topic52676.html
В схемах ElGamal и Diffie-Hellman нужно первым делом - сгенерировать пару p и g.
При этом g - является первообразным корнем по модулю простого числа p.
Как найти g? Есть что-то типа JavaScript генератора?
Я нашёл только ECDH - на эллиптических кривых: http://www-cs-students.stanford.edu/~tjw/jsbn/ecdh.html
Там изначально заданы координаты генераторной точки G, в самой эллиптической кривой.
Выбираешь кривую, задаётся генераторная точка G,
затем генерируешь число (приватный ключ),
и умножаешь генераторную точку на число - получаешь публичный ключ (точка с двумя координатами).
После обмена ими - рассчитывается общая точка, которая и может быть общим ключём шифрования
(если её координаты, конвертнуть в HEX, например)...
Но кривые эти - надо чтобы были и у Алисы и у Боба, к тому же нужно задать конкретную кривую.
А вот если просто числа брать, без эллиптических кривых,
то быстрое возведение в степень по модулю не так уж много места занимает и не требует всяких скриптов.
К тому же эти функции можно быстро написать.
Вот здесь: https://8gwifi.org/DHFunctions.jsp я вижу нечто наподобие PGP DH,
но тут тоже задаются изначально, параметры p и g.
То, что p - это простое число, и оно может быть большим, так есть алгоритм Миллера-Рабина.
Вопрос в том, как получить g при определённом, сгенерированном p.
>>40314
Вот так и надо было с самого начала спрашивать. Прочитал за тебя википедию, вот какой-то алгоритм: https://en.wikipedia.org/wiki/Primitive_root_modulo_n#Finding_primitive_roots
Попробуй.
Вот так и надо было с самого начала спрашивать. Прочитал за тебя википедию, вот какой-то алгоритм: https://en.wikipedia.org/wiki/Primitive_root_modulo_n#Finding_primitive_roots
Попробуй.
>>40315
Там что надо факторизовать φ(p)?.. Равное (p-1).
А если оно, порядка 10^616 (2048 бит ~ 2^2048)?
Есть что-нибудь попроще?
>https://en.wikipedia.org/wiki/Primitive_root_modulo_n#Finding_primitive_roots
Там что надо факторизовать φ(p)?.. Равное (p-1).
А если оно, порядка 10^616 (2048 бит ~ 2^2048)?
Есть что-нибудь попроще?
>>40316
Во-первых, факторизовать его может быть и не очень сложно, тут как повезет. Во-вторых, я ничего об этом не знаю, но скорее всего в википедии приведен самый лучший из известных алгоритмов. В-третьих, обычно в качестве g берут какое-то маленькое число, например 2. Поботай еще вот этот вопрос, который я тебе только что нагуглил за минуту: https://crypto.stackexchange.com/questions/12961/diffie-hellman-parameter-check-when-g-2-must-p-mod-24-11
Во-первых, факторизовать его может быть и не очень сложно, тут как повезет. Во-вторых, я ничего об этом не знаю, но скорее всего в википедии приведен самый лучший из известных алгоритмов. В-третьих, обычно в качестве g берут какое-то маленькое число, например 2. Поботай еще вот этот вопрос, который я тебе только что нагуглил за минуту: https://crypto.stackexchange.com/questions/12961/diffie-hellman-parameter-check-when-g-2-must-p-mod-24-11
>>40319
Много букв на английском, и цифры другие.
Вот какой-то алгоритм нашёл на си++:
http://www.cyberforum.ru/turbo-pascal/thread273061.html
Как его в JS - не знаю.
И вот ещё: http://kaf401.rloc.ru/Criptfiles/primroots.htm
Тут наглядно видно, что первообразные корни - дают
равномерное распределение остатков по разным степеням,
а другие числа - нет.
Только как их искать - не пойму нифига, даже с кода, что выше.
Много букв на английском, и цифры другие.
Вот какой-то алгоритм нашёл на си++:
http://www.cyberforum.ru/turbo-pascal/thread273061.html
Как его в JS - не знаю.
И вот ещё: http://kaf401.rloc.ru/Criptfiles/primroots.htm
Тут наглядно видно, что первообразные корни - дают
равномерное распределение остатков по разным степеням,
а другие числа - нет.
Только как их искать - не пойму нифига, даже с кода, что выше.
 43 Кб, 707x614
43 Кб, 707x614>>40320>>40316>>40314>>40312
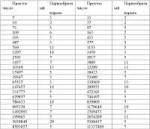
Глядя на этом сайте: http://kaf401.rloc.ru/Criptfiles/primroots.htm
на повторяющиеся числа 6 и 10
для разных первообразных корней по модулям простых чисел 7 и 11 - сделал следующий вывод:
1. Если p - простое, φ(p) = p-1.
2. Поскольку p - нечётное, то p-1 = φ(p) - чётное, оно делится на 2.
Делим, и получаем некое x = φ(p)/2 = (p-1)/2.
3. Дальше, для всех a, взаимно-простых с p, вычисляем a^x (mod p), и проверяем...
Если a^x (mod p) ≢ 1 и a^x (mod p) ≡ φ(p), вернуть a - это первообразный корень.
Пикрелейтед.
Примечательно то, что для непростого числа 9, факторизуемого как 3×3,
также можно видеть повторяющееся число 8 у корней 2 и 5.
Однако, φ(9) = 8, φ(9)/2 = 8/2 = 4,
при этом 2 - взаимно простое с 9,
однако 2^4 mod 9 === 7 !== 8,
и этот алгоритм для нечётных составных - не прокатит.
Чтобы найти генератор для нечётного составного, насколько я понял, надо от d отнять ещё одну единицу.
Глядя на этом сайте: http://kaf401.rloc.ru/Criptfiles/primroots.htm
на повторяющиеся числа 6 и 10
для разных первообразных корней по модулям простых чисел 7 и 11 - сделал следующий вывод:
1. Если p - простое, φ(p) = p-1.
2. Поскольку p - нечётное, то p-1 = φ(p) - чётное, оно делится на 2.
Делим, и получаем некое x = φ(p)/2 = (p-1)/2.
3. Дальше, для всех a, взаимно-простых с p, вычисляем a^x (mod p), и проверяем...
Если a^x (mod p) ≢ 1 и a^x (mod p) ≡ φ(p), вернуть a - это первообразный корень.
Пикрелейтед.
Примечательно то, что для непростого числа 9, факторизуемого как 3×3,
также можно видеть повторяющееся число 8 у корней 2 и 5.
Однако, φ(9) = 8, φ(9)/2 = 8/2 = 4,
при этом 2 - взаимно простое с 9,
однако 2^4 mod 9 === 7 !== 8,
и этот алгоритм для нечётных составных - не прокатит.
Чтобы найти генератор для нечётного составного, насколько я понял, надо от d отнять ещё одну единицу.
 14 Кб, 480x471
14 Кб, 480x471>>40326
Вообще-то при p = 9 (составное, 3×3),
φ(9) = 6, при этом x = φ(9)/2 = 6/2 = 3,
и при a = 2 (взаимно-простое с p):
a^x mod p = 2^3 mod 9 = 8 = (p-1).
Только вот чтобы найти φ(n), при составном нечётном n - надо факторизовать это n.
>φ(9) = 8
Вообще-то при p = 9 (составное, 3×3),
φ(9) = 6, при этом x = φ(9)/2 = 6/2 = 3,
и при a = 2 (взаимно-простое с p):
a^x mod p = 2^3 mod 9 = 8 = (p-1).
Только вот чтобы найти φ(n), при составном нечётном n - надо факторизовать это n.
>>40326
Для первых чисел - сойдёт, а вот для следующих...
6 - взаимно простое с 7;
и 6^3 mod 7 !== 1 = 6 = φ(7), но 6 - не первообразный корень.
То же самое и с числом 10 при p=11:
gcd(10, 11) = 1, и они взаимно-просты.
Проверил тут: http://www.alcula.com/calculators/math/gcd/ введя "10, 11".
Дальше...
a^φ(p)/2 mod p = 10^10/2 mod 11 = 10^5 mod 11 !== 1 = 10 = φ(11), но 10 - тоже не первообразный корень.
Надо, походу ещё, при переборе - отсеять a по условияю "a mod φ(p) === 0".
А затем уж, наверняка, можно будет и рандомные числа брать
например, от 2 до p, c неким определённым интервалом для поиска, скажем 1000 перебираемых a.
>>40327
Вот, допустим, я факторизовал число 5624351580503521 = 163×167×173×179×181×191×193
Дальше что?
http://e-maxx.ru/algo/euler_function тут ничего не понятно,
с этими индексами вверху и внизу - возле каждого простого числа в каноничном разлжении n.
Какие-то минусы и дроби пиздатые.
φ(n) = n⋅(1 - 1/p1)⋅(1 - 1/p2)⋅...⋅(1-1/pk) Это как считать???
Там такие длинные десятичные дроби получаются, если единицу на простое число поделить...
С индексом a вверху p - тоже ничего непонятно...
>Если a^x (mod p) ≢ 1 и a^x (mod p) ≡ φ(p), вернуть a - это первообразный корень.
Для первых чисел - сойдёт, а вот для следующих...
6 - взаимно простое с 7;
и 6^3 mod 7 !== 1 = 6 = φ(7), но 6 - не первообразный корень.
То же самое и с числом 10 при p=11:
gcd(10, 11) = 1, и они взаимно-просты.
Проверил тут: http://www.alcula.com/calculators/math/gcd/ введя "10, 11".
Дальше...
a^φ(p)/2 mod p = 10^10/2 mod 11 = 10^5 mod 11 !== 1 = 10 = φ(11), но 10 - тоже не первообразный корень.
Надо, походу ещё, при переборе - отсеять a по условияю "a mod φ(p) === 0".
А затем уж, наверняка, можно будет и рандомные числа брать
например, от 2 до p, c неким определённым интервалом для поиска, скажем 1000 перебираемых a.
>>40327
Вот, допустим, я факторизовал число 5624351580503521 = 163×167×173×179×181×191×193
Дальше что?
http://e-maxx.ru/algo/euler_function тут ничего не понятно,
с этими индексами вверху и внизу - возле каждого простого числа в каноничном разлжении n.
Какие-то минусы и дроби пиздатые.
φ(n) = n⋅(1 - 1/p1)⋅(1 - 1/p2)⋅...⋅(1-1/pk) Это как считать???
Там такие длинные десятичные дроби получаются, если единицу на простое число поделить...
С индексом a вверху p - тоже ничего непонятно...
>>40329
Там ещё брутфорсом надо либо единицы искать, либо φ(p).
Вот таблица для числа 31:
n = 31
φ(31) = 30
φ(n)/2 = 15
n-1 = 30
Количество первообразных корней: φ(φ(n)) 8
φ(φ(n)/2) = 8
a^x mod c; c = 31
a\x123456789101112131415161718192021222324252627282930
1111111111111111111111111111111
2248161248161248161248161248161248161
+3392719261617202925138241030282241251514112618237211
4416281416281416281416281416281416281
55251525152515251525152515251525152515251
6653025261653025261653025261653025261653025261+
77182145428108252016199171821454281082520161991
8821641821641821641821641821641821641
99191620258102845142187191916202581028451421871
101078182522014165194928110781825220141651949281
11112829964131923524162114302032222527181282671510171+
12122023282622491525214171830191183529722166102714131+
13131427106162272953811193018174212515924226282320121+
141410167581918425922820114101675819184259228201
15158272301623429115827230162342911582723016234291-
16168421168421168421168421168421168421
17171015726812182725222320301421162452319134692928111+
181814410251697252882019118144102516972528820191
191920828527916251041418119208285279162510414181
202028292541819857161014120282925418198571610141
21217231862111415512422283010248132529201716261927931+
22221915206821282751721373091216112523103426142918241+
23232154308291627123215430829162712321543082916271-
24241829142643102325111612930713217527282186201519221+
252551255125512551255125512551255125512551
26262530561262530561262530561262530561262530561-
27271629830415223127162983041522312716298304152231-
282894195161420225188710128941951614202251887101
29294231630227815129423163022781512942316302278151-
30301301301301301301301301301301301301301301301
Справа - первообразные корни отмечены знаком плюс. Их всего 8, как рассчитано и рассчитано выше.
Там где знак минус - это какие-то полукорни. Число a в степени φ(n)/2 для них равно 30, и это φ(31), но эти тридцадки - повторяются.
Также, есть и по нескольку единиц, в ряду. У первообразных корней - же числа не повторяются.
Возможно можно как-то найти φ(31), либо единицы, без перебора и факторизации φ(n)...
Ведь если оно большое, то не то что перебирать - факторизовать его сложно.
Я уже вижу некую закономерность, но через факторизацию числа 30.
30 = 2×3×5, и
6^(3×1) mod 31 = 6^(3×3) mod 31 = 6^(3×5) mod 31 = 6^(3×7) mod 31 = 6^(3×9) mod 31 = 30
6^(3×2) mod 31 = 6^(3×4) mod 31 = 6^(3×6) mod 31 = 6^(3×8) mod 31 = 6^(3×10) mod 31 = 1
23^(5×1) mod 31 = 23^(5×3) mod 31 = 23^(5×5) mod 31 = 30
23^(5×2) mod 31 = 23^(5×4) mod 31 = 23^(5×6) mod 31 = 1
26^(3×1) mod 31 = 26^(3×3) mod 31 = 26^(3×5) mod 31 = 26^(3×7) mod 31 = 26^(3×9) mod 31 = 30
26^(3×2) mod 31 = 26^(3×4) mod 31 = 26^(3×6) mod 31 = 26^(3×8) mod 31 = 26^(3×10) mod 31 = 1
27^(5×1) mod 31 = 27^(5×3) mod 31 = 27^(5×5) mod 31 = 30
27^(5×2) mod 31 = 27^(5×4) mod 31 = 27^(5×6) mod 31 = 1
29 - то же, что и выше.
А вот во 2-й степени - тридцаток не нахожу.
Вопрос: возможно ли без факторизации φ(n) и прямого перебора - с поиском φ(n) и 1, как-то отсеять не первообразные корни?
>a mod φ(p)
Там ещё брутфорсом надо либо единицы искать, либо φ(p).
Вот таблица для числа 31:
n = 31
φ(31) = 30
φ(n)/2 = 15
n-1 = 30
Количество первообразных корней: φ(φ(n)) 8
φ(φ(n)/2) = 8
a^x mod c; c = 31
a\x123456789101112131415161718192021222324252627282930
1111111111111111111111111111111
2248161248161248161248161248161248161
+3392719261617202925138241030282241251514112618237211
4416281416281416281416281416281416281
55251525152515251525152515251525152515251
6653025261653025261653025261653025261653025261+
77182145428108252016199171821454281082520161991
8821641821641821641821641821641821641
99191620258102845142187191916202581028451421871
101078182522014165194928110781825220141651949281
11112829964131923524162114302032222527181282671510171+
12122023282622491525214171830191183529722166102714131+
13131427106162272953811193018174212515924226282320121+
141410167581918425922820114101675819184259228201
15158272301623429115827230162342911582723016234291-
16168421168421168421168421168421168421
17171015726812182725222320301421162452319134692928111+
181814410251697252882019118144102516972528820191
191920828527916251041418119208285279162510414181
202028292541819857161014120282925418198571610141
21217231862111415512422283010248132529201716261927931+
22221915206821282751721373091216112523103426142918241+
23232154308291627123215430829162712321543082916271-
24241829142643102325111612930713217527282186201519221+
252551255125512551255125512551255125512551
26262530561262530561262530561262530561262530561-
27271629830415223127162983041522312716298304152231-
282894195161420225188710128941951614202251887101
29294231630227815129423163022781512942316302278151-
30301301301301301301301301301301301301301301301
Справа - первообразные корни отмечены знаком плюс. Их всего 8, как рассчитано и рассчитано выше.
Там где знак минус - это какие-то полукорни. Число a в степени φ(n)/2 для них равно 30, и это φ(31), но эти тридцадки - повторяются.
Также, есть и по нескольку единиц, в ряду. У первообразных корней - же числа не повторяются.
Возможно можно как-то найти φ(31), либо единицы, без перебора и факторизации φ(n)...
Ведь если оно большое, то не то что перебирать - факторизовать его сложно.
Я уже вижу некую закономерность, но через факторизацию числа 30.
30 = 2×3×5, и
6^(3×1) mod 31 = 6^(3×3) mod 31 = 6^(3×5) mod 31 = 6^(3×7) mod 31 = 6^(3×9) mod 31 = 30
6^(3×2) mod 31 = 6^(3×4) mod 31 = 6^(3×6) mod 31 = 6^(3×8) mod 31 = 6^(3×10) mod 31 = 1
23^(5×1) mod 31 = 23^(5×3) mod 31 = 23^(5×5) mod 31 = 30
23^(5×2) mod 31 = 23^(5×4) mod 31 = 23^(5×6) mod 31 = 1
26^(3×1) mod 31 = 26^(3×3) mod 31 = 26^(3×5) mod 31 = 26^(3×7) mod 31 = 26^(3×9) mod 31 = 30
26^(3×2) mod 31 = 26^(3×4) mod 31 = 26^(3×6) mod 31 = 26^(3×8) mod 31 = 26^(3×10) mod 31 = 1
27^(5×1) mod 31 = 27^(5×3) mod 31 = 27^(5×5) mod 31 = 30
27^(5×2) mod 31 = 27^(5×4) mod 31 = 27^(5×6) mod 31 = 1
29 - то же, что и выше.
А вот во 2-й степени - тридцаток не нахожу.
Вопрос: возможно ли без факторизации φ(n) и прямого перебора - с поиском φ(n) и 1, как-то отсеять не первообразные корни?
>>40329
Там ещё брутфорсом надо либо единицы искать, либо φ(p).
Вот таблица для числа 31:
n = 31
φ(31) = 30
φ(n)/2 = 15
n-1 = 30
Количество первообразных корней: φ(φ(n)) 8
φ(φ(n)/2) = 8
a^x mod c; c = 31
a\x123456789101112131415161718192021222324252627282930
1111111111111111111111111111111
2248161248161248161248161248161248161
+3392719261617202925138241030282241251514112618237211
4416281416281416281416281416281416281
55251525152515251525152515251525152515251
6653025261653025261653025261653025261653025261+
77182145428108252016199171821454281082520161991
8821641821641821641821641821641821641
99191620258102845142187191916202581028451421871
101078182522014165194928110781825220141651949281
11112829964131923524162114302032222527181282671510171+
12122023282622491525214171830191183529722166102714131+
13131427106162272953811193018174212515924226282320121+
141410167581918425922820114101675819184259228201
15158272301623429115827230162342911582723016234291-
16168421168421168421168421168421168421
17171015726812182725222320301421162452319134692928111+
181814410251697252882019118144102516972528820191
191920828527916251041418119208285279162510414181
202028292541819857161014120282925418198571610141
21217231862111415512422283010248132529201716261927931+
22221915206821282751721373091216112523103426142918241+
23232154308291627123215430829162712321543082916271-
24241829142643102325111612930713217527282186201519221+
252551255125512551255125512551255125512551
26262530561262530561262530561262530561262530561-
27271629830415223127162983041522312716298304152231-
282894195161420225188710128941951614202251887101
29294231630227815129423163022781512942316302278151-
30301301301301301301301301301301301301301301301
Справа - первообразные корни отмечены знаком плюс. Их всего 8, как рассчитано и рассчитано выше.
Там где знак минус - это какие-то полукорни. Число a в степени φ(n)/2 для них равно 30, и это φ(31), но эти тридцадки - повторяются.
Также, есть и по нескольку единиц, в ряду. У первообразных корней - же числа не повторяются.
Возможно можно как-то найти φ(31), либо единицы, без перебора и факторизации φ(n)...
Ведь если оно большое, то не то что перебирать - факторизовать его сложно.
Я уже вижу некую закономерность, но через факторизацию числа 30.
30 = 2×3×5, и
6^(3×1) mod 31 = 6^(3×3) mod 31 = 6^(3×5) mod 31 = 6^(3×7) mod 31 = 6^(3×9) mod 31 = 30
6^(3×2) mod 31 = 6^(3×4) mod 31 = 6^(3×6) mod 31 = 6^(3×8) mod 31 = 6^(3×10) mod 31 = 1
23^(5×1) mod 31 = 23^(5×3) mod 31 = 23^(5×5) mod 31 = 30
23^(5×2) mod 31 = 23^(5×4) mod 31 = 23^(5×6) mod 31 = 1
26^(3×1) mod 31 = 26^(3×3) mod 31 = 26^(3×5) mod 31 = 26^(3×7) mod 31 = 26^(3×9) mod 31 = 30
26^(3×2) mod 31 = 26^(3×4) mod 31 = 26^(3×6) mod 31 = 26^(3×8) mod 31 = 26^(3×10) mod 31 = 1
27^(5×1) mod 31 = 27^(5×3) mod 31 = 27^(5×5) mod 31 = 30
27^(5×2) mod 31 = 27^(5×4) mod 31 = 27^(5×6) mod 31 = 1
29 - то же, что и выше.
А вот во 2-й степени - тридцаток не нахожу.
Вопрос: возможно ли без факторизации φ(n) и прямого перебора - с поиском φ(n) и 1, как-то отсеять не первообразные корни?
>a mod φ(p)
Там ещё брутфорсом надо либо единицы искать, либо φ(p).
Вот таблица для числа 31:
n = 31
φ(31) = 30
φ(n)/2 = 15
n-1 = 30
Количество первообразных корней: φ(φ(n)) 8
φ(φ(n)/2) = 8
a^x mod c; c = 31
a\x123456789101112131415161718192021222324252627282930
1111111111111111111111111111111
2248161248161248161248161248161248161
+3392719261617202925138241030282241251514112618237211
4416281416281416281416281416281416281
55251525152515251525152515251525152515251
6653025261653025261653025261653025261653025261+
77182145428108252016199171821454281082520161991
8821641821641821641821641821641821641
99191620258102845142187191916202581028451421871
101078182522014165194928110781825220141651949281
11112829964131923524162114302032222527181282671510171+
12122023282622491525214171830191183529722166102714131+
13131427106162272953811193018174212515924226282320121+
141410167581918425922820114101675819184259228201
15158272301623429115827230162342911582723016234291-
16168421168421168421168421168421168421
17171015726812182725222320301421162452319134692928111+
181814410251697252882019118144102516972528820191
191920828527916251041418119208285279162510414181
202028292541819857161014120282925418198571610141
21217231862111415512422283010248132529201716261927931+
22221915206821282751721373091216112523103426142918241+
23232154308291627123215430829162712321543082916271-
24241829142643102325111612930713217527282186201519221+
252551255125512551255125512551255125512551
26262530561262530561262530561262530561262530561-
27271629830415223127162983041522312716298304152231-
282894195161420225188710128941951614202251887101
29294231630227815129423163022781512942316302278151-
30301301301301301301301301301301301301301301301
Справа - первообразные корни отмечены знаком плюс. Их всего 8, как рассчитано и рассчитано выше.
Там где знак минус - это какие-то полукорни. Число a в степени φ(n)/2 для них равно 30, и это φ(31), но эти тридцадки - повторяются.
Также, есть и по нескольку единиц, в ряду. У первообразных корней - же числа не повторяются.
Возможно можно как-то найти φ(31), либо единицы, без перебора и факторизации φ(n)...
Ведь если оно большое, то не то что перебирать - факторизовать его сложно.
Я уже вижу некую закономерность, но через факторизацию числа 30.
30 = 2×3×5, и
6^(3×1) mod 31 = 6^(3×3) mod 31 = 6^(3×5) mod 31 = 6^(3×7) mod 31 = 6^(3×9) mod 31 = 30
6^(3×2) mod 31 = 6^(3×4) mod 31 = 6^(3×6) mod 31 = 6^(3×8) mod 31 = 6^(3×10) mod 31 = 1
23^(5×1) mod 31 = 23^(5×3) mod 31 = 23^(5×5) mod 31 = 30
23^(5×2) mod 31 = 23^(5×4) mod 31 = 23^(5×6) mod 31 = 1
26^(3×1) mod 31 = 26^(3×3) mod 31 = 26^(3×5) mod 31 = 26^(3×7) mod 31 = 26^(3×9) mod 31 = 30
26^(3×2) mod 31 = 26^(3×4) mod 31 = 26^(3×6) mod 31 = 26^(3×8) mod 31 = 26^(3×10) mod 31 = 1
27^(5×1) mod 31 = 27^(5×3) mod 31 = 27^(5×5) mod 31 = 30
27^(5×2) mod 31 = 27^(5×4) mod 31 = 27^(5×6) mod 31 = 1
29 - то же, что и выше.
А вот во 2-й степени - тридцаток не нахожу.
Вопрос: возможно ли без факторизации φ(n) и прямого перебора - с поиском φ(n) и 1, как-то отсеять не первообразные корни?
Двач.hk прислал битые данные.
Вы видите копию треда, сохраненную 11 мая 2020 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Вы видите копию треда, сохраненную 11 мая 2020 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.