Вы видите копию треда, сохраненную 9 сентября в 10:43.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 52 Кб, 500x500
52 Кб, 500x500Основные списки литературы:
http://pastebin.com/raw/4iMjfWAf - classic
http://pastebin.com/raw/4FngRj6n - dxdy
Архив тредов (там же остальные списки литературы и полезные ссылки):
https://pastebin.com/raw/qhs0WNbY
Это всё понятно, но вот никак не исключает наличие вариантов целых чисел на прямой.
не читай, всё равно ответить не сможешь
 65 Кб, 1350x900
65 Кб, 1350x900Я правильно понимаю, что если среди всего бесконечного множества действительных чисел есть целые, то выбор их равен нулю, потому что потому. Хуйня какая то по определению если честно.
утверждение "выбор равен нулю" не имеет смысла
определись, что именно ты хочешь сравнить с нулём
>что именно ты хочешь сравнить с нулём
То что тыкая хуемпальцем на угад, я никогда не ткну в целое число
Тут пока только с петухов спрашивают
Дебил, тебе тяжело признать что у тебя нет аргументов. Тебя макнули в суть определения, а ты ещё пытаешься что-т вякать. Ой дебилище.
сформулировать, я имел в виду
 207 Кб, 640x640
207 Кб, 640x640Пацаны, не ссорьтесь
Сливом твоего холодного пота при переживании из-за непонимания вероятностей и меры Лебега? Ну что ж.
определения строго напиши, про которые ты рассказываешь, и укажи прямо ошибку, если ты её где-то видишь
без конкретики весь твой срач это голословный детский сад
>без конкретики весь твой срач это голословный детский сад
Очередное мнение дебила.
Попроси, тогда пришлю определения.
дорогой мой петух-неосилятор, ты ничего не пришлёшь, потому что у тебя ничего нет, ты ничего не знаешь и не понимаешь, потому что ты ничего внятного не написал ни разу раньше, потому что вот это
>Попроси, тогда пришлю
это голимый детский сад,
а эксцесс про "события с бесконечно малым значением, которое относится к наличию чисел на данной прямой" это бред сивой кобылы
всё, что ты в принципе можешь, это троллинг тупостью и рассуждения про дебилов, ведь ты ещё никогда не порождал ничего иного
так что на этом всё, сегодня ты слился, можешь ещё раз утешиться чем-нибудь вроде "мнения дебила" и пройти туда, где тебе самое место. давай, до следующего раза, посмотрим на что тебя стриггерит ещё
Вот это подрыв.
>на что тебя стриггерит ещё
Но самое забавное что это ты взорвался от уточнения, дебил.
>всё, что ты в принципе можешь
Могу попросить доказательство указанного тобою предположения на счёт строгой (нулевой) вероятности выбора целого числа на действительно прямой. Но вот проблема - ты в прошлый раз ничего не привёл.
Как вот это
>>2131 (Del)
>>2137 (Del)
опровергнешь, дебил?
И вообще, здесь вроде математическая тема, а дебил, строящий из себя гуру, не может доказать свои же утверждения. Смешно же. Это эталонный дебил.
>Могу попросить доказательство указанного тобою предположения на счёт строгой (нулевой) вероятности выбора целого числа на действительно прямой
я принёс тебе схему доказательства, если ты видишь где-то ошибку - укажи, где
>И вообще, здесь вроде математическая тема
вот и говори про математику, а не про дебилов
>я принёс тебе схему доказательства
Зачем мне твоя схема? Ты само доказательство принеси, дебил. Вероятность выбрать целое число строго равна нулю? Доказательство в студию, дебил.
>Зачем мне твоя схема?
ах, вот оно в чём дело. оказывается, петуха корёжит от того, что его с ложечки не кормят. а ведь разговоров-то было - и про суть каких-то определений, в которых кого-то обмакивают, и про парадоксы меры Лебега, и дебилы все эти бесчисленные. а оказывается, это всего-то петух-неосилятор опять не осилил что-то
нет уж, дорогой. если ты утверждаешь, что что-то неверно - ты указываешь, что
как вариант, можешь доказать мы знаем, что не можешь результат, опровергающий тот, который обеспокоил тебя вначале; тогда можно будет подискутировать о том, что является правильным
>ряяяяя
Графомания не интересует, дебил.
Доказательство где? А так-то, у меня есть схема, по которой ты умственно неполноценный. Прислать?
я думаю, здесь ты совершенно ясно расписался в своей несостоятельности и всего срача выше. так что давай, до свидания
>я думаю
Ты дебил и это не свойственно тебе.
Не вижу доказательства с твоей стороны. Дал утверждение - доказываешь, дебил.
Кроме двух книжек Арнольда.
А вот если бы ты не рождался вовсе, ты бы никогда не выебал тёлку. Такого события вообще нет среди рассматриваемых, потому что тебя самого тоже нет.
>Да когда уже раздел собственный по физике появится
Возьми да запили. /math так и появился из-за батхёрта от тредов в /sci.
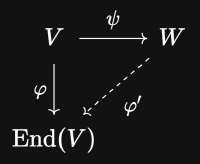
Например, пусть $V$ - конечное векторное пр-во над $\mathbb{R}$. Рассмотрим какой-то гомоморфизм (как векторных пр-в) $\phi : V \rightarrow End(V)$. Но на $End(V)$ есть структура алгебры - как тогда произведение "поднять" обратно в $V$? Ну или хотя бы в $V/ker(\phi)$. Что-то наивное вроде $\phi^{-1}(\phi(v)phi(w))$ может не сработать, потому что $\phi$ может быть не сюръективно. А что если расширить $V/ker(\phi)$, чтобы композиция эндоморфизмов (представимых как образ вектора) была замкнутая?
Наверное глупость какую-то говорю, но более содержательно не могу выразить. В идеале без введения доп структур типа квадратичной формы на $V$.
Буду признателен анонам за книжки или хотя бы названия концепций, куда копать.
естественным образом - никак, поскольку даже если ты определишь каким-то образом дополнительную структуру на $V$, чтобы $\phi$ был гомоморфизмом и по отношению к ней (т.е. чтобы уважал её тоже), то эта структура будет зависеть от $phi$, а ты бы хотел, чтобы её уважали все гомоморфизмы
что можно сделать - это определить отдельную алгебру $W$ вместе с фиксированным гомоморфизм векторных пространств $\psi\colon V \to W$ так, что для любого гомоморфизма $\phi\colon V \to \rm{End}(V)$ существует единственный гомоморфизм алгебр $\phi'\colon W \to \rm{End}(V)$, такой что $\phi = \phi'\colon\psi$ (здесь должна быть нарисована коммутативная диаграмма). грубо говоря, $V$ вкладывается в некоторую специальную алгебру $W$, и гомоморфизм векторных пространств $\phi$ "пропускается" через эту алгебру
нетрудно проверить, что если $W$ существует, то она единственна с точностью до изоморфизма (алгебр). поэтому нам остаётся только доказать её существование, что можно сделать, построив её явно
для твоего примера, если вместо $\rm{End}(V)$ задаться тем же вопросом о произвольной алгебре $A$, то в качестве $W$ подойдёт тензорная алгебра пространства $V$, т.е. прямая сумма всех пространств $\bigotimes^k V$, $k \geq 0$. можно ли исключительно для $\rm{End}(V)$ придумать что-нибудь попроще, я сомневаюсь, но можно подумать
эта конструкция называется универсальное свойство и применяется повсеместно, описана во множестве источников
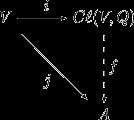
Существует понятие полного прообраза $\phi ^{-1} y$ данного элемента $y$ из области значений $D \phi$ как ${x: x \in D \phi \land y = \phi x}$, т. е. множества всех $x$, отображаемых в $y$. Понятно, что существует взаимнооднозначное отображение $\Phi$ между полными образами и прообразами.
Соответственно, на множестве всевозможных $\phi ^{-1} y$, взятых для каждого $y$ из $R \phi$, можно задать соответствующие $\Phi& операции так, чтобы соблюдался изоморфизм.
Также сюда каким-то образом относятся факторструктуры, состоящие из полных прообразов.
Спасибо анон! Про универсальное св-во я читал и даже делал упражнения, но пока ещё самостоятельно использовать в рассуждениях, как в твоём посте, не могу. Я даже не сразу понял, что это просто определение тензорной алгебры через универсальное св-во...
Твоя конструкция понятная, я нарисовал диаграмму. Получается, что тензорная алгебра - это самое "большое", чем может быть $W$. То есть в общем случае там будет подалгебра тензорной алгебры?
И мне тогда становится намного понятней определение алгебры Клиффорда, потому что это просто твоя диаграмма, но с дополнительными ограничениями на $\psi$ (которые зависят от допольнительной структуры квадратичной формы).
Спасибо ещё раз, пойду думать
 90 Кб, 1075x760
90 Кб, 1075x760"Прямоугольный Треугольник. Вся Правда. Полный Срыв Покровов." ?
Хммм
>Соответственно,
>можно задать соответствующие $\Phi& операции так, чтобы соблюдался изоморфизм.
А что мешает этому индуцированному произведению "выйти за рамки" множества полных прообразов?
более-менее все адекватные алгебраические конструкции отвечают какому-то универсальному свойству, тут никакой магии нет
если у тебя алгебра $A$ конкретная, то $W$ можно построить как подалгебру в $T(V)$, но мне кажется, в большинстве случаев она будет равна $T(V)$
Пользовательские доски смотри.
Правильно ли я понимаю, что окончить НМУ практически невозможно (если ты не Миша Тифарет, конечно)?
>Правильно ли я понимаю, что окончить НМУ практически невозможно
Правильно. Диплом НМУ не получил ни один человек за всю историю его существования.
>если ты не Миша Тифарет, конечно
...кроме Миши Тифарета, конечно – ну, это известнейший и величайший математик всё-таки, только такой глыбе по силам это начинание. Можно мы прекратим уже форсить это плешивое говно? Пиздец, раздули какого-то долбоёба до невиданных масштабов, потому что он громче всех матюкается и жирно набрасывает.
 230 Кб, 1024x768
230 Кб, 1024x768Потому что все лошары тупые и сами нихуя не знают, а только выёбываются, повторяя устаревшее на тысячи лет говно?
>раздули какого-то долбоёба до невиданных масштабов, потому что он громче всех матюкается и жирно набрасывает.
И ведь правда.
 247 Кб, 1080x810
247 Кб, 1080x810Я помню, как в шк, решал примеры и наполовину не втыкал, чо там за хуйня вообще происходит.
Хотя там всё элементарно, берём например, и выводим в два счёта "самую главную тригонометрическую формулу":
sin^2 α + cos^2 α = 1
Что это за ужосы, как же всё сложно...
a^2 + b^2 = c^2
(a/c)^2 + (b/c)^2 = 1
sin^2 α + cos^2 α = 1
Дальше по АНАЛогии.
тригонометрия это не наука, это набор тождеств с тригонометрическими функциями, каждое из которых выводится из формулы Эйлера элементарными преобразованиями
 78 Кб, 604x562
78 Кб, 604x562Тригономе́трия — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии.
+
Математика - это наука, изучающая числа, структуры, отношения и изменения.
=>
Тригонометрия - наука.
Формула Эйлера, как и многое другое - надстройка, и не проходится в школе.
Всё, что нужно для понимания тригонометрии - это Теорема Пифагора, которая проходится в школе в первом учебнике по Геометрии - тоже наука.
Нет никакого смысла использовать любые надстройки над ней, ну кроме как для редких специфических вещей, где так будет удобнее.
В любом случае, конкретно речь идёт про хуёвое школьное образование, где делается упор на тригонометрические функции, а не их смысл, включая геометрический.
Что толку от тупого решения примеров по стандартным схемам, где буквы перемешаны с цифрами, и ученик воспринимает это всё, как некое подобие иностранного языка, когда он должен понимать, как раз саму основу, что за хуйню он вообще творит, ёптать, риторический вопрос.
> Формула Эйлера, как и многое другое - надстройка, и не проходится в школе.
надстройка - это когда два конуса над топологическим пространством $X$ приклеены друг к другу по этому пространству, или, эквивалентно, когда у цилиндра $X \times [0,1]$ верхнее и нижнее основание стянуты каждое в точку
то, что формула Эйлера не проходится в школе, вместо этого школьников чуть ли не год насилуют исключительно тригонометрическими формулами, это пиздец
остальное комментировать не буду
Нет никакой математики в мнимых числах, это воображариум.
Есть реальность, а есть стандартные логические ошибки, повторяемые десятилетиями и столетиями, приводящие к иллюзорным псевдонаучным домыслам, так было в науке уже множество раз.
И здесь нечего обсуждать.
Это как с верой в бога, ты либо реалист, либо полный эксплуатируемый дурак, по факту.
Что такое мнимые числа?
 1,4 Мб, 1024x1024
1,4 Мб, 1024x1024Любимые числа Россиян:
Социологическое исследование.
7 - 38%
5 - 32%
3 - 23%
Суммарно: 93%
Мухосранск:
Нет любимых чисел - 46%
Дата (день/число месяца?) своего/родственников рождения - 23%
7 - 11%
Суммарно: 80%
"14 - ммм, наверное, это что-то зеркальное (противоположное?) число 41-го района, на котором я живу."
Увожаемые мотематики, а какое у вас любимое число?
Во во, вместо кручения Голландского Штурвала споры какие то
24, конечно же.
Нижегородские математики Иван Ремизов и Олег Галкин (НИУ ВШЭ) совершили прорыв, первыми решив знаменитую «задачу пятидесятилетия», сообщает MK.RU. Их работа дает ответ на ключевой вопрос в теореме американца Пола Чернова, остававшийся загадкой с 1968 года.
на mathnet есть видео, где один из авторов рассказывает про эту работу. я послушал, очень хороший доклад
боюсь я не осилю, но а так, да, молодцы мужики. Следующий научный прорыв хочу от местных двачеров.
книжку, автора?
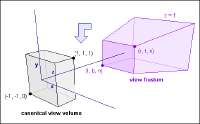
Если тебе нужна графика начни с графики, читай про WebGL, сразу пишешь и видишь результат, там же и кубик на первых уроках научат вращать.
кубик можно в юнити закинуть и камеру покрутить. Я хотел узнать, на каких принципах это основано, и почему вообще работают эти формулы, и как они вообще выводятся
 9 Кб, 484x301
9 Кб, 484x301юнити в жопу засунь
>А что мешает этому индуцированному произведению "выйти за рамки" множества полных прообразов?
Прошу прощения, что заставил Вас повторяться.
Теперь я обратил внимание, что $\phi$ может не покрыть произведения. Признаю неточность своего ответа.
Чем просмотреть по быстрому LaTeX, есть ли какие онлайнсервисы с конвертацией в PDF?
Ты ещё не победил диван.
Нет смысла нападать в лоб. Я подожду, пока ты отвернёшься, и всажу отвёртку тебе в шею, а потом вдарю со всей силы между ног
Я и сам пивные кеги часто пизжу с университетстких мероприятий.
пожалуй единственный раз соглашусь с нематематикапетухом
Однажды не пошёл на его концерт, потому что надо было к экзамену по матану готовиться. Лучше бы пошёл.
Тогда бы ты вероятно не стал двачером.
>Правильно. Диплом НМУ не получил ни один человек за всю историю его существования.
Человек 15 лет за 30 это не очень много, если не ошибаюсь.
Сап, анон. Дай совет. Нужно подтянуть за годик школьную математику и основы анализа. Сейчас не знаю, что такое дифференциал
Подскажите, какие книги можно покурить, чтобы понимать и школьную и университетскую математику (1-2 курсы) на базовом уровне?
Об этом нельзя говорить
Я так коммутативные диаграммы рисую.
О великие математики сея борды - помогите тупому гуму разобраться в матане пожалуйста
Короткая вводная:
Я - студент гум.вуза, который полностью забил на математику с 6 класса, и нихуя с того момента не помнит, и не хотел вспоминать.
Но тут вскрылась проблема. Я собираюсь подаваться на зарубежную стипендию, и чтобы её получить, нужно написать 3 экзамена, 2 из которых по ин. языкам, а 1 - МАТЕМАТИКА БЛЯТЬ
Причем математика такого уровня, что я ВООБЩЕ не понимаю что происходит в тестовых заданиях. Типо, абсолютно нихуя.
Что не удивительно, потому что я даже не помню, как квадратное уравнение решать
Буду честен - я не люблю математику, и не хотел бы с ней иметь никакого дела, но мне нужна эта стипуха, и я готов скрипя зубы начать заниматься. Проблема в том, что мне нужно сначала вспомнить всю базу хотя бы до 9 класса, а потом уже - всё, что происходит на пикрилах что бы это ни было
А так как всё это ещё и на английском с этим по факту проблем нет, просто я не знаю мат.термины, то мне надо бы её ещё на англе учить, а я вообще не знаю что юзать - какие учебники, курсы, гайды, видосы...
Стоит упомянуть, что у меня времени - примерно два года, и я готов заниматься каждый день, но не более часа.
очевидно, потому что мне не нравится этот предмет
И по первой я наверное буду вспоминать только алгебру, потому что с ней у меня хотя бы что-то получалось, а с геометрией - вообще пизда
В общем, анонасы- спасайте. Покидайте материалов, по которым возможно вспомнить всю базу до 9 класса включительно, поставить себе базу общую, и потом как-то натянуть на себя на то, что происходит на пикрилах.
Буду очень благодарен всем, кто поможет.
Плюс, прикрепил пример экзамена:
https://www.studyinjapan.go.jp/ja/_mt/2023/07/2019_ga_math_a.pdf
(На скринах мне нужно выучить темы с 1 по 17)
мне кажется, лучше всего нанять репетитора
из книжек на этот уровень мне известен только сканави, можешь попробовать, хотя я лично его не люблю (из-за детской травмы, меня по нему гоняли)
>мне кажется, лучше всего нанять репетитора
Честно - не хочется сливать бабки и сидеть с преподом. Да и в любом случае мне бОльшую часть работы придется самому делать.
Плюс, весь экзамен на английском, а кто у нас шарит за математику на английском? А если и шарит, то я представляю, сколько бабок берет
Мне лично будет мне так кажется проще в соло по ресурсам пойти. Главное - найти их, и понять, по чему учится вообще. Уже хоть на английском, хоть на русском
>Плюс, весь экзамен на английском, а кто у нас шарит за математику на английском?
точно не знаю, но подозреваю, что любой студент старших курсов матфака/мехмата
Очень сложно что-то в такой ситуации посоветовать, нужно просто титаническую работу проделать.
> то мне надо бы её ещё на англе учить
Не сильно надо, язык вообще не проблема в математике: термины и формулировки везде очень похожие и требует очень короткого времени, чтобы свыкнуться с ними в другом языке. Я, не зная французский, статьи и монографии на нём читать более-менее могу, например. Поэтому, если материал будешь знать, скорее всего хватит просто просмотреть с десяток вариантов на английском.
Могу очень осторожно посоветовать для самого первого подготовительного этапа "Элементарную алгебру" Туманова.
Аноны, по сколько часов в сутки или в неделю вы занимаетесь математикой и для какой цели?
Да ну, мне кажется, что далеко не каждый. Даже не каждый 2, наверное.
>>2435
>нужно просто титаническую работу проделать
Да оно понятно. Но другого выбора нет
>"Элементарную алгебру" Туманова
Спасибо. Что она покрывает, откуда стартовая точка?
>>2436
Ты шизоид? Тня на /math? Сам то веришь во что пишешь?
 49 Кб, 900x900
49 Кб, 900x900>Ты шизоид? Тня на /math? Сам то веришь во что пишешь?
>>2431
>помогите тупой
>пожалуйста
>Я - студентка
>забила
>Буду честена - я не люблю математику
>и я готова сосать лизать
>и я готова
>спасайте позязя
>Буду очень благодарна всем, кто поможет. Даже отсусу с проглотом.
>Вежливо положила педантично доккументик.
Ты максимально слепашарый? Это тёлка пишит. Мужик бы просто сказал что я далбоёб, киньте вы мне хуесосы книги.
>Да ну, мне кажется, что далеко не каждый
Старшие курсы предполагают работу над дипломом. Работа над дипломом предполагает почти всегда чтение научных статей на английском.
>Что она покрывает, откуда стартовая точка?
Позволяю открыть оглавление и увидеть самому.
Ещё можешь "Элементы алгебры и анализа" Киселёва глянуть. Это опять-таки про подготовительный этап.
Спасибо
>Аноны, по сколько часов в сутки или в неделю вы занимаетесь математикой и для какой цели?
Минимум час в день, каждый день. Разрабатываю свлю систему оснований.
Любая книга по 3д графике. Вообще любая. Кажется даже в книгах для профессионалов, типа Real-Time Rendering с штурмовиком на обложке, есть глава про нужную математику с объяснениями для совсем дебилов.
Если хочешь более математичное, то Стренг "линейная алгебра и её примнения".
Успехи незначительные.
Пытаюсь формализовать самые простые теории, как, например, натуральная арифметика, и попутно выясняю, как формализовать те или иные понятия, как существование, всеобщность и др.
Одна из идей: формулировать онтологию без логики. Возможно, удастся создать ультрафинитистские основания. Стараюсь двигаться в эту сторону.
Для большинства же идей разработка методов их формализации оборачивается "изобретением велосипеда", в то же время возникает понимание того, почему это делается именно так.
Имею в виду, что обыкновенно формальные системы включают в себя правила вывода, с помощью которых строются теоремы и некая онтология. Таким образом, внешняя метауровневая логика используется для построения онтология.
Я намереваюсь сделать наоборот, явно сформулировать онтологию, а логику можно рассмотреть уже внутри нее.
Ну а как тогда из семейства утверждений получить правила вывода? Проблема то даже в том что вы получите что из одних и тех же утверждений вы получите разные логики. Например если вы возьмёте все утверждения из ZFC и систему аксиом ZF + Лемму Цорна. они одинаковые утверждения порождают.
Как вообще математические аноны придумывают себе темы для исследований?
всегда хочется думать что ты умнее всех остальных и можешь доказать что то важное
Будет явно сформулированная строго конечная онтология. Например, онтология $O _{10}& будет включать натуральные числа, конкретно 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, а также понятия "и так далее", "существует", "для любого". Внутри онтологии будет своя внутренняя логика. Можно будет проверить общие утверждения, касающиеся всех натуральных чисел, а не только конечного перечня конкретно обозначенных.
Также будет внешняя металогика, позволяющая рассматривать более широкие онтологии, включающие любые наперед заданные числа. Например, по этой логике можно будет вывест онтологии $O _{15}$, $O _100$ и др. Эти онтологии будут принципиально подобны друг другу.
Будет явно сформулированная строго конечная онтология. Например, онтология $O _{10}$ будет включать натуральные числа, конкретно 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, а также понятия "и так далее", "существует", "для любого". Внутри онтологии будет своя внутренняя логика. Можно будет проверить общие утверждения, касающиеся всех натуральных чисел, а не только конечного перечня конкретно обозначенных. Также будет внешняя металогика, позволяющая рассматривать более широкие онтологии, включающие любые наперед заданные числа. Например, по этой логике можно будет вывест онтологии $O _{15}$, $O _100$ и др. Эти онтологии будут принципиально подобны друг другу.
Данные онтологии будут выражать то, как действительно рассуждает человек - возможно. Они будут представлять собой ультрафинитистские основания.
ну вот, какой явно нездоровый фетишист вуайерист создал эту трёхмерную анимацию непонятно для каких целей, а вы ещё и распространяете её на незаинтересованную в ваших влажных фантазиях аудиторию
так я всё ещё не понимаю что тако онтология. Если это множество утверждений, то "1" это не утверждение, можно более формальное определение онтологии?
хорошая анимация, не трясись, моралофаг
>так я всё ещё не понимаю что тако онтология. Если это множество утверждений, то "1" это не утверждение, можно более формальное определение онтологии?
Рассмотрены будут формальные онтологии. Отдельно взятая формальная онтология будет состоять из строго определенных объектов и отношений.
Игру не следует ограничивать никакой наперед заданной онтологией. Что сообщает теорема Геделя о неполноте. Рассмотрение различных онтологий, их составление и расширение - тоже часть игры.
речь не про то, о чём я думаю, а о том, что есть на данный момент
тогда логическая система это то же самое, набор объектов и отношений "правил вывода"
>тогда логическая система это то же самое, набор объектов и отношений "правил вывода"
Предполагается выводить не отдельные теоремы, а конечные онтологии целиком.
В своей основе, то же самое.
так это и есть математическая логика, ты просто переформулировал логические системы в онтологии и спрашиваешь когда они эквиваленты, этим вопросом матлогики длительное время занимаются.
Я ничего не спрашивал. Тут разные люди как анонимы.
 5 Мб, mp4,
5 Мб, mp4,640x360, 1:30
Возведение в квадрат, отрезок по оси икс, 1,2,3..., и кривая по оси игрик соответсвующая ввозведению в квадрат величин из отрезка по икс
всякий многочлен является непрерывной функцией на $\mathbb R$, тем самым, ограниченной на любом отрезке; поэтому: нет, не становится
Сфигали тогда энергия ионизации атома водорода конечная и именно 13.6эв, если электромагнитное взаимодействие подчиняется убыванию своей интенсивности по обратноквадратичному закону?
И та же вторая космическая скорость например конечная и для земли 11км/с.
Ну смотри, это полностью равнозначный обратный случай, как величина подчиняющаяся квадратичному закону не может стать бесконечной на конечном отрезке, так и величина подчиняющаяся ОБРАТНОквадратичному закону не должна становиться строго нулевой на бесконечном отрезке
Логично же?
При этом в физике почему-то принимают их за конечные величины.
функция $\frac{1}{f(x)}$, где $f(x)$ - многочлен, нулю никогда не равна (однако стремится к нулю на бесконечности)
Но сумма этих величин по прежнему стремится к бесконечности на бесконечном отрезке, так?
Не, сумма не функции и аргумента, а сумма значений функции стремящейся к нулю на бесконечном отрезке.
Или эта форма записи это и означает?
сумма двух функций, одна из которых стремится к нулю, а другая - к бесконечности, стремится к бесконечности
Не, ну это понятно, я про сумму значений одной функции которая стремится к нулю на бесконечном отрезке, но никогда строго ноль не становится.
Эта сумма бесконечная или конечная?
Функция y от x стремится к нулю при бесконечном значении х
Сумма значений функции y при х от 0 до бесконечности, конечна или бесконечна?
у функции действительного переменного в общем положении континуальное множество значений, просуммировать их все не так-то просто (надо определить, как вычисляется такая сумма)
вернее общепринятое определение для таких сумм есть - это интеграл, и на неограниченной области интеграторах может сходиться или расходиться, в т.ч. для ограниченных функций и для функций, которые стремятся к нулю на границе области
зависит от функции, бывает и так, и так
Ну вот допустим пружина, но которая становится слабее при растягивании. У пружины есть сила, а если силу умножить на перемещение то получится энергия запасённая в ней.
Получается сила это величина которая уменьшается от 1 до некоего значения(стремится к 0, или хз как это правильно назвать), нп бесконечном отрезке как y=x^(1/2)
Как тогда энергию найти запасённую в бесконечно растянутой так пружине? Если это некая идеальная пружина, у которой есть только свойство что её сила уменьшается от 1, как y=x^(1/2)
не, я что-то понимаю про функции, но я ничего не понимаю про пружины. пусть про пружины другой анон подскажет, если ему с ними комфортнее, а я удалюсь. будет вопрос про функции - я могу пробовать включиться
Лан, спасибо за ответы.
Не ждёшь а готовишься крыса?
>уменьшается от 1, как y=x^(1/2)
>Ты напсиал, что растёт.
Да, проебался
>Если имел в виду, что 1/x^2, то интеграл сойдётся и энергия будет конечной.
А как это доказать? Допустим представим потенциальную силу, которая не изменяется от расстояния, тогда потенциальная энергия на бесконечном расстоянии будет бесконечной. Но вот если сила уменьшается в зависимости от расстояния, но нет условия что она становится строго ноль на конечном расстоянии, или что она становится строго ноль на бесконечном расстоянии, то с чего бы тогда энергии потенциальной тогда стать конечной?
Интуитивно это примерно так обобосновывается. У тебя есть два тренда: 1) ты добавляешь к сумме всё новые и новые слагаемые, увеличивая её; 2) каждое новое слагаемое в свою очередь становится всё меньше и меньше. Если правильно подобрать соотношение этих двух трендов, то в итоге может получиться конечно число.
Пример: пусть есть отрезок от 0 до 1, и изначально мы находимся в точке 0. Затем проходим половину расстояния. Затем половину от оставшейся половины. Затем половину от оставшейся четверти расстояния. Затем... Т.е. на каждом шаге мы проходим половину от остатка. Есть идеи, где мы окажемся через бесконечное число шагов?
Сумма здесь -- это пройденное расстояние от нуля.
Ну про это я и так написал, вот тут
>>2523
>если сила уменьшается в зависимости от расстояния, но нет условия что она становится строго ноль на конечном расстоянии
Т.е. если такое условие задать то пример супер лёгким становится, это понятно. Как например тот же знаменитый пример с длиной береговой линии острова. Она может быть бесконечной, при очевидно и изначально заведомо конечной площади острова.
А мне бы какой-то пример, чтобы стало очевидно что сумма будет конечной, при том что изначально она не заведомо конечная, хотя и явно уменьшаются слогаемые с каждым шагом.
С днем ДВД!
В моём примере на любом шаге новое слагаемое не равно нулю.
На бесконечности новое слагаемое/сила должны обращаться в ноль, это необходимое условие, чтобы сумма/энергия были конечными.
Сила 1/x^2 на бесконечности обращается в ноль. Потенциальная энергия получается конечной, если мы суммируем/интегрируем не начиная с x=0.
День пива вчера был. Сидел, рисовал в баре коммутативные диаграммы.
>В моём примере на любом шаге новое слагаемое не равно нулю.
Но в примере берётся половина от оставшейся, кмк ключевой момент.
А в случае зависимости 1/x^2, про "оставшееся" мы ничего не знаем, и работаем со значением от прошлого шага или от начального значения.
Но я верю что энергия в итоге будет конечная
В моём примере "сила" выглядит как 1/(2^x), это просто другая формулировка.
Ну переформулируй.
"Пройди х, затем половину х (х/2), затем половину пройденного на предыдущем шаге, и так далее. За стремящееся к бесконечности количество шагов пройдешь не более 2*х".
Я кажется допёр в чём дело, асимптота это функция с заведомо ослабевающим ослаблением на каждом шаге. А обратноквадратичная зависимость это функция с явно усиливающимся ослаблением на каждом шаге. Собственно это наверное и есть достаточное доказательство.
Сорян, не знаю как называется кривая которая бесконечно к ней приближается но никогда не касается, я саму кривую эту всегда асимптотой называл(
Ну суть в том что площадь графика ограниченного асимптотой по такому принципу(бесконечно приближается к ней, но никогда не касается) будет бесконечной, потому что интенсивность приближения явно и заведомо замедляющаяся. А в случае обратноквадратичной зависимости энергия будет конечной, потому что зависимость явно и заведомо с усливающимся ослабеванием.
У обратно-квадратичной зависимости тоже есть прямая, к которой кривая графика приближается. Это прямая y=0.
Думаю, то, что ты хочешь сказать, звучит примерно как "если эта прямая выше, чем прямая y=0, то плошадь будет бесконечной". Это в принципе верно, это как раз то, что я писал как
>На бесконечности новое слагаемое/сила должны обращаться в ноль, это необходимое условие, чтобы сумма/энергия были конечными.
Но хотя это необходимое условие, оно не является достаточным: посмотри на правую сторону графика 1/x. Потенциальная энергия/площадь под графиком (я тут везде молча предполагаю как, полагаю, и ты, что мы стартуем правее нуля) на бесконечности будет всё равно бесконечной.
>"если эта прямая выше, чем прямая y=0, то плошадь будет бесконечной"
Не, я имел ввиду что они обе выше, но приближаются к ней по принципиально разному закону
И вот по тому в чём это принципиальное отличие заключается и можно "наглядно доказать" что площадь конечной будет.
Типа на каждом шаге, начиная с 1 площадь изменяется как 1, 4, 9, 16, 25... Т.е. явно видно что спад интенсивности(как некой величины делёной на площадь) усиливающийся с каждым шагом.
По этому критерию делаю вывод что величина именно "обращается в ноль на бесконечности", а не "стремится к нулю на бесконечности".
А вот тот пример который ты привёл, как раз и будет похоже этим самым случаем когда "явно стремится к нулю на бесконечности".
Короче я для себя пока такие критерии определил, в различии строгих определений "стремится к нулю на бесконечности" и "обращается в ноль на бесконечность".
В первом случае бесконечная площадь, во втором случае конечная.
А вывод "стремится" или "обращается" иногда сделать просто, иногда сложно. Но например когда явно ускоряется с каждым шагом, то значит "обращается в ноль", а если замедляется, то "стремится к нулю".
Ну в общем спасибо за ответы, а то прям поплыл от этого, как оказалось детского вопроса про бесконечности.
1/х, значения уменьшаются с явным "замедлением уменьшения" на каждом шаге
1/2, 1/3, 1/4, 1/5...
Т.к. делитель изменяется всегда на одно и то же число, а делимое постоянно, следовательно приближение к ограничивающей прямой на бесконечности "замедленное". И функция слишком простая чтобы потом какое-то изменение этой динамики могло случиться после n-го шага. Следовательно площадь будет бесконечной под ней.
Обратноквадратичная зависимость:
1/4, 1/9, 1/16, 1/25, 1/36...
А тут разница между делителями на каждом шаге больше чем на предыдущем
5, 7, 9, 11...
Значит приближение кривой к ограничивающей её на бесконечности прямой, ускоренное, следовательно площадь под кривой конечная.
Но вот интересно можно ли какие-то средние случаи между этими двумя придумать, и какой будет результат.
А ещё интересно если не кривая, а условие что "наклонная прямая пересекает ограничивающую прямой на бесконечности", то какая тогда площадь будет ограниченная этими двумя прямыми, конечная или бесконечная.
слушай, почему бы тебе просто обычный матанализ не поучить в объеме первого семестра первого курса? если тебе действительно нужны эти вопросы
Ну многовато целый семестр, для по сути одного пунктика насчёт бесконечностей, причём очень ограниченной части этой темы.
Но в принципе можно
>матанализ в объеме первого семестра первого курса
Какую лично ты книгу/книги хорошую подходящую под такое определение посоветуешь?
не знаю, фихтенгольца вроде аноны любят
терри тао какую-то книжку написал, наверное, он плохо не напишет
если тебе надо быстро и не слишком глубоко, mathprofi.ru вполне подойдёт; как интегрировать степенную функцию на бесконечности там объясняет, я предполагаю
Ок, спасибо
Почему пиво не бесконечно?
глупый вопрос
наливаешь кружку пива
выпиваешь полкружки
потом выпиваешь четверть (половину того, что осталось)
потом восьмую часть
и т.д.
так, чтобы выпить всё пиво в кружке, тебе понадобится бесконечое количество глотков
 145 Кб, 604x436
145 Кб, 604x436 31 Кб, 879x258
31 Кб, 879x258В каноническое разложение левой части равенства число 2 входит в чётной степени, а в разложение 2n^2 в нечетной, поэтому равенство m^2 = 2n^2 невозможно.
О какой нечетности идет речь ? что в 2n^2 нечетное ? какого хуя равенство невозможно ? Я щас моник разъебу от этих ваших математик.
без ограничения общности можно предположить, что $m/n$ несократима, в частности, $m,n$ не являются чётными одновременно
но из равенства $m^2 = 2n^2$ следует, что $m,n$ должны быть чётными одновременно.
на пике именно это и доказывается. если тебе трудно понять написанное, попробуй доказать самостоятельно (это можно сделать и без разложений)
Ну то есть если правая сторона умножается на 2 она четная, значит и левая тоже должна быть четной. Если они обе четные, значит могут сократиться, это противоречит тому что дробь несократима.
То есть начиная выражать несократимую дробь через корень двойки, я прихожу к тому что она должна быть сократима.
>Ну то есть если правая сторона умножается на 2 она четная, значит и левая тоже должна быть четной.
здесь ты доказал, что $m^2$ чётное
>значит и левая тоже должна быть четной
$2n^2$ чётное заранее. чётность $n^2$ пока ниоткуда не следует
>Если они обе четные, значит могут сократиться, это противоречит тому что дробь несократима.
даже если ты доказал, что $m^2,n^2$ обе чётные (ты не доказал), отсюда ещё не следует, что и $m,n$ чётные (следует, конечно, но надо доказывать, если хочешь использовать)
попробуй аккуратно расписать доказательство, что именно откуда получается и почему
а можно мне доказать? я умный
(x^2) чётный тогда и только тогда, когда (x) чётный.
Доказываю: возведение в квадрат не добавляет никаких новых простых множителей в разложение числа, а 2 это простое число, то есть 2 как множитель не появится в (x^2), а значит оно тоже будет нечётным. Отсюда также следует: если x^2 четный, значит там есть хотя бы 1 двойка в разложении, но если бы x был бы нечётен, она бы не добавилась бы
примерно это и написано на пике выше, но можно обойтись и без разложений (это вообще сама по себе довольно глубокая теорема)
и это ещё не полное доказательсвто иррациональнсти $\sqrt 2$
Походу, разложение на произведение степеней простых множителей:
$ m = 2 ^{k_1} \cdot 3 ^{k_2} \ldots \cdot m_p ^{k_p} $
$ n = 2 ^{l_1} \cdot 3 ^{l_2} \ldots \cdot n_q ^{l_q} $
При возведении в квадрат $ m ^2 = 2 ^{2k_1} \cdot 3 ^{2k_2} \ldots \cdot m_p ^{2k_p} $. Поэтому степень при 2 четная.
Соответственно $ 2n^2 = 2 ( 2 ^{2l_1} \cdot 3 ^{2l_2} \ldots \cdot n_q ^{2l_q} ) = 2 ^{2l_1+ 1} \cdot 3 ^{l_2} \ldots \cdot n_q^^{l_q} $, где степень при двойке нечетная.
Мне подход кажется странным. Фактически, нам нужно отделить рациональные числа от иррациональных, а частности от выбранного $ sqrt {2} $. Поэтому логично было бы доказывать, что $ sqrt {2} $ отличается от любого наперед выбранного рационального { m / n }. Для этого не нужно доказательство от противного. В остальном рассуждение полностью аналогично.
Коллега >>2556 предлагает упрощенный метод с заранее взаимно простыми & m & и & n &.
Соответственно
$ 2n^2 = 2 ( 2 ^{2l_1} \cdot 3 ^{2l_2} \ldots \cdot n_q ^{2l_q} ) = 2 ^{2l_1+ 1} \cdot 3 ^{2l_2} \ldots \cdot n_q^{2l_q} $
Так и есть. Однако все видно из разложения на множители, без дополнительных рассуждений. Кстати, может быть и $ 2 $ в степени $ 0 $.
В вопросах делимости ноль всяко фигурирует.
К тому же каноническое разложение - это некое соответствие между простыми числами и степенями. При этом удобнее будет не пропускать также и те простые числа, которые не входят в разложение, а просто назначить им нулевые показатели степени. Конечно, степени с ненулевым показателем будут только при конечном числе простых чисел. Далее определить бесконечное произведение всех степеней простых чисел, при этом считая его произведением только степеней с ненулевым показателем. Оно будет существовать и быть единственным для канонического разложения любого $k: 1 <_{\mathbb{N}} k$.
Во Франции есть.
прошлого пацана который за пивом бегал кстати придушили
Российский "Эйнштейн" 21 века утверждает, что море может быть плоским, а не круглым, как вся остальная планета в норме.
Он провёл десятилетние исследования, точные расчёты при помощи "Google Maps" и пришёл к настолько ошеломляющему выводу:
Белое Море Плоское!
Вся физика с этого момента признаётся устаревшей.
> Человек стоит на берегу Белого Моря, у самой воды, и его взгляд перпендикулярен морю.
> перпендикулярен морю
Ясно
 139 Кб, 250x218
139 Кб, 250x218науки должны стать более закрытыми, образование после 4 класса должно быть не только не обязательным, но ещё и труднодоступным. Хочешь работать в суде? иди проходи судебную практику и готов. Хочешь поваром? иди проходи практику с минимальной необходимой теорией. Хочешь изучать математику - пожалуйста, но эти знания должны быть не бесплатными,а курс не должен выходить за границы математики. Это в какой то степени, избавило бы мир от таких вот залётных полупокеров, шарлатанов и высокомерных невежд, считающих себя умнее всех остальных.
нет, образование (в фундаментальных науках) должно быть широким, а любая любознательность всячески поощряться
и, вне каких-либо сомнений, образование должно быть бесплатным
В целом да, но уж точно не теорфизикам пиздеть с их позорищем в виде перенормировок.
КЭД десятилетиями подгоняли, потому что она оч хуёво согласовалась. За то время можно было бы руками веса нейронки обучить с той же предсказательной способностью.
И есть ли какой-то аналог римановой поверхности, соответствующий алгебраическому замыканию $\mathbb{C}(t)$? Какой-нибудь обратный предел по всем накрытиям, у этого есть какое-то название?
Кто-нибудь знает, насколько реалистично самостоятельно подготовиться к ШАД программисту?
https://shad.yandex.ru/enroll
В целом, у меня не стоит цели поступить туда срочно. Я готов учиться и 2 и 3 года если надо.
Насколько реалистичная хуйня? Шадовики ИТТ есть?
Насчёт второго вопроса нашёл «проконечное (не)разветвлённое» накрытие, «про-этальное» над открытым подмножеством.
В датчиках где именно?
Пучки и прочие микрофункции придумали прикладники. Лере был гидродинамиком, Сато учил математику по брошюрам "как сделать чтобы самолеты летали быстрее и убивали больше филиппинцев".
 167 Кб, 1140x226
167 Кб, 1140x226Нет, получить вычисляторов гомотопических групп сфер, адептов (\inf, n) и бирациональную геометрию. Ну т.е. да, унылое говно, но ничего не имзенится.
 569 Кб, mp4,
569 Кб, mp4,314x228, 0:10
>могу ебануть на 1 больше
там все числа, скорее всего, получаются из множителей, которые имеют определённый смысл, порядок каких-нибудь групп или что-то вроде
так что если прибавить 1, то всё поломается
считаю, что если проводить эксперимент с монеткой в реальности и повторять все условия эксперемента, то монетка всегда будет выпадать одной стороной.
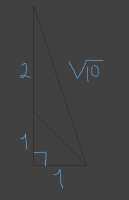 26 Кб, 506x782
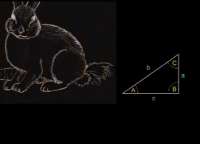
26 Кб, 506x782подсказка: в прямоугольном треугольники, в котором известны все стороны, известны все углы
можешь пояснее, что и где ты собрался строить?
Я понял что это что-то про фукнции, я знаю линейную фукнцию из школы и паралоболу. Этих знаний достаточно или нужно еще что-то вводное ?
Множества там, еще хуйня какая-нибудь ?
Ты можешь попробовать начать читать матан и решить это сам.
На Annas Archiv есть.
И согласны ли вы с тем что чем больше знаешь формул тем ты пизже?
Накатил пиваса что ли?
>Так матеша это инструмент для физики по сути. Разве нет?
Нет. Это физика источник идей для математики.
Вообще нет, не нужна, что будет неизвестно легко нагуглить и за час освоить. Но по ходу курсу у тебя могут возникать вопросы, нахуя это нужно. Держи в голове, что матанализ создавался для приблизетльных(важное слово) расчетов нелинейных величин. Физическая интерпретация идей в виде пути, скорости, времени очень хорошо на простейший матан ложится, он из них и вырос.
Вообще анализ изобрел Непер, изучая степенную функцию. Тяжело перемножить 16 и 32, но зная что 16 = 2^4, и 32 = 2^5, то умножение можно заменить на сложение 16 x 32 = 2^(4+5), нам нужно всего лишь посчитать степени двойки и заранее записать куда-нибудь результат. Непер пытался придумать, как заполнить пробелы, как быстро высчитать, например 2^9.5, хотя бы приблизительно. Вконце концов он придумал физическую аналогию с катящимися шариками. Все базовые факты, производные, интеграллы и простейшие теоремы хорошо мотивируются подобными примерами с движением.
Можешь параллельно с каким-нибудь дефолтным курсом полистать Абельсон "Рождение логарифмов".
Ребятишки, надо статистику подтянуть, посоветуйте чонить
Физик сможет решить ЕГЭ по матеше.
Зато далеко не каждый математик сможет решить ЕГЭ по физике.
Что тебе не нравится?
Прокачиваешься пока не сможешь решить профиль за 20-40 минут без ошибок. Ачивка РЕШАЛА unlocked
Далее олимпиады хотя уровня всероса.
Много тут тех кто может решить ЕГЭ за 20 минут и за столько же олимпиаду? Сомневаюсь...
Ладно, это не про это было, это для фиксированного открытого множества, над которым мы смотрим на конечные неразветвлённые накрытия. А надо брать предел по множествам, над которыми мы хотим построить конечные неразветвлённые накрытия, при этом для каждого множества такого свой предел конечных накрытий, неразветвлённых над ним. В итоге я что-то не уверен, что тут как-то поверхность построится хоть какая-то. Или это какой-то проконечный предел проконечных поверхностей... Дурка.
Как дела, котятки? Прошла жара и можно наконец то продолжить обучение чему то новенькому!
> Плюс, весь экзамен на английском, а кто у нас шарит за математику на английском? А если и шарит, то я представляю, сколько бабок берет
Какой же ты тупой, пиздец просто, математика у него на английском другая, блядь. Ты с головой дружишь?
>что её сила уменьшается от 1, как y=x^(1/2)
Элементарная работа δA = Fdx, F = x^1/2, тогда A равняется интегралу x^(1/2)dx от x = 1 до x = inf, т.е. [2/3 inf^(3/2) - 2/3] = inf, бесконечность.
В "реальных" физических системах сила всегда равняется нулю на бесконечности - одна система не может повлиять на другую, бесконечно дальнюю от неё, поэтому энергии взаимодействия двух различных систем конечны.
Сосать, теоретики.
 69 Кб, 866x378
69 Кб, 866x378На уровне понимания я дохожу до окружности с радиусом 1, того что синусы и косинусы это отношения сторон в прямоугольном треугольнике. Типо вот я могу на окружности построить угол, опустить высоту получить треугольник. Но дальше начинается какой то ад, со всеми эти верчениями, кручениями, тангенсами ебучими.
>Вся эта ебля с преобразованиями и пинусами, синусами должна заучиваться или я могу прийти к какому то пониманию, что-бы эту хуйню не заучивать ?
всё это (любая из тригонометрических формул любого уровня забористости) выводится из одной формулы Эйлера путём нехитрых преобразований со степенной функцией. формула Эйлера при этом по сути и есть эта самая окружность с радиусом $1$, единственное добавление здесь состоит в том, что точка окружности отвечает комплексному числу $e^{i\varphi}$
>или я могу прийти к какому то пониманию, что-бы эту хуйню не заучивать ?
ты обязан прийти к пониманию, иначе говно будет.
Читай I.M. Gelfand Mark Saul Trigonometry
 36 Кб, 742x609
36 Кб, 742x609>Читай I.M. Gelfand Mark Saul Trigonometry
Спасибо анон, начал читать, дошел аж до 8 старницы.
Нужно доказать что радиан угла a больше синуса этого угла. Радиан это отношение длины дуги к радиусу, в данном случае он равен 1, то есть длина дуги сам радиан и есть. Синус это катет против угла а деленый на гипотенузу 1, то есть сам катет.
Визуально я вижу что дуга длинней катета. Как это доказать ? Зачем мне дорисовали равнобедренный треугольник ?
То есть радиан это отношение дуги к гипотенузе = 1, синус отношение катета к гипотенузе 1, если в центре дуги поставить точку М на оси х, получится дуга дальше катета, это доказывает что дуга = радиан будет больше синуса ?
 6 Кб, 187x269
6 Кб, 187x269>Читай I.M. Gelfand Mark Saul Trigonometry
Погугли, есть решения с ответами всех задач. На твоем пике задача из книги того же Гедьфанда ст.10, только другой, пикрил, а на следующей странице расписанное доказатество только для тангенса.
з.ы.
мне только такое пришло
по определению высота катета b меняется от 0 до радиуса r включительно, sina=b/r, а длина дуги l = a * r, следовательно sina < l.
>На уровне понимания я дохожу до окружности с радиусом 1, того что синусы и косинусы это отношения сторон в прямоугольном треугольнике. Типо вот я могу на окружности построить угол, опустить высоту получить треугольник. Но дальше начинается какой то ад, со всеми эти верчениями, кручениями, тангенсами ебучими.
Читай Виленкин, Ивашев-Мусатов, Шварцбурд, Алгебра и начала анализа, 10 кл.
>Это такой прикол, что там опечатки и ответы неправильные
А где именно? Я до компаса дошел и свичканулся на английскую книгу Гендальфа, поскольку на гите есть подробные решения, потом уже нашу поняшу.
Вот еще книги по геометрии, может кому надо.
https://github.com/manjunath5496/Geometry-Books
 448 Кб, 1920x1080
448 Кб, 1920x1080Как вообще решать эти упражнения? Это же пиздец какой-то просто. Я в Зориче понимаю 95% доказательств и определений, решаю задачи из Shaum's Outlines Advanced Calculus, но там всё на уровне "используй определение и подставь".
Когда дело доходит до Зорича, я вообще нихуя не понимаю. Эти проблемы расчитаны на гениев с мехмата или что? Поэтому и прошу скинуть, если есть, ответы, чтобы хотя бы примерно понимать, куда думать.
Да и вообще, так ли решают эти доказательства? После дрочки интегралов из Демидовича, поймал себя на мысли, что я ничего нового про интегралы не узнал. Такое ощущение, что с упражениями Зорича такая же хуйня. Ну используешь ты эти определения, а в остатке всё равно алгебраический дроч как будто.
 58 Кб, 933x167
58 Кб, 933x167>Как вообще решать эти упражнения? Это же пиздец какой-то просто.
>Эти проблемы расчитаны на гениев с мехмата или что?
Упражнения Зорича зачастую связаны с другими областями математики и чтобы их решить нужно владеть ими.
Пикрил упражнения про идеалы из темы непрерывность. Тут уже алгебраическая геометрия вылезает и двойственность между многообразиями и кольцами функций над ними.
Короче, предназначений задач у Зорича не для того, чтобы ты прочитанный материал отработал, а скорее показать некие интересные примеры или связь с другими разделами математики.
Так что забей на них пока.
программист спок
>На странице 70-ой понял
далеко тебя протащило, я не помню, чтобы я и 10 страниц осилил из этой книги
но если она тебе во всём заходит, кроме теорката, может быть, стоит подучить немного теоркат, благо вещь нетрудная и встречается повсеместно. (я, правда, не знаю, зачем в функане теоркат, во всяком случае в базовом курсе (или даже в продвинутом))
книга Колмогорова-Фомина отличается разительно, там совсем нет теорката и много, собственно, анализа, в самом противном смысле этого слова (интегралы, оценки, и очень много текста)
какую книгу читать, зависит от того, что тебе от неё, собственно, нужно. если исключительно для повышения эрудиции, я бы не советовал никому ни Хелемеского, ни Колмогорова-Фомина (не спрашивайте меня, что стоило бы взять вместо них)
Спасибо за ответ!
> какую книгу читать, зависит от того, что тебе от неё, собственно, нужно.
Я обучаюсь на специальности, связанной с физикой элементарных частиц, а там в учебном плане вообще нет функционального анализа, хотя это основа КТП зато есть экономика, право и психология.
твой выбор - это M. Reed, B. Simon - Methods of Modern Mathematical Physics, том 1
это прекрасная книга, которая если и не покроет все необходимые тебе вещи, то даст очень приличный буст, особенно по сравнению с твоим текущим уровнем (нулевым). так что бери её и радуйся, она как раз то, что нужно
ХРЮКОСТЯГ
>медиана делит противоположную сторону треугольника пополам
это определение
определение не есть факт, его не надо доказывать
(иногда нужно доказывать корректность определения, но это другое)
Это Z повернутая на π/2
Ну т.е. получается, что эта операция есть просто некая математическая абстракция, и вовсе не обязательно, чтобы во вселенной было что-то физическое, что удовлетворяет этому уравнению?
какая операция?
математика по сути своей есть лишь мыслимая абстракция, и она не занята ничем "физическим во вселенной"
если тебе трудно представить $i^2 = -1$ как что-то "физическое", то можно замыслить $i$ как вектор $(x,y)$ такой, что при умножении его на матрицу
$A=\left(\begin{array}{cc}x&-y\\y&x\end{array}\right)$
получится вектор $(1,0)$. тогда выходит система двух уравнений, решение которой даётся вектором $(x,y) = (0,1)$.
такая интерпретация полностью отвечает представлению комплексных чисел как точек (векторов) на плоскости: умножение на комплексное число $z$ отвечает умножению соответствующего вектора на специальную матрицу, составленную из координат этого числа; при этом никаких загадачных слов про квадрантый корень из отрицательного числа можно не произносить
Пчел, я просил дать мне физическое объяснение, а ты накидал ещё больше матана. Если не можешь объяснить на физическом примере, то не мучайся, я и не требую.
Зорич, глава V, параграф 5: Комплексные числа и взаимосвязь элементарных функций, пункт 3: Формула Эйлера и взаиосвязь элементарных функций
[3,3,2][3,3,2]
[8,8,1][8,8,1]
Ну вот теперь заебись
наверно, потому что там много синусов и косинусов, а также имеются дифференциальные уравнения вида $du/dt = Au$. но это вопрос не по математике, так что мимо доски
Годные циклы были, зачитывался ими. Щас одна китайщица пришла на смену нечитабельная.
В летний лагерь приехали три друга: Миша, Володя и Петя. Известно, что каждый из них имеет одну из фамилий: Иванов, Семенов, Герасимов. Миша не Герасимов, отец Володи инженер, Володя учится в 6 классе, Герасимов учится в 5 классе. Отец Иванова слесарь. Какая фамилия у каждого из ребят?
герасимов учится в 5 классе, он не миша и не володя => петя герасимов
отец иванова слесарь => он не отец володи => володя не иванов => володя семенов
миша иванов
наверно, можно нарисовать граф, в котором имена и фамилии соединяются через промежуточные ноды, и решение становится сразу видно
 328 Кб, 723x753
328 Кб, 723x753Это же головоломка а не игра, мне на пример нравится, но усидчивости не хватает и поэтому сразу смотрю ответы.
мимо
>>2902
Посчитать вероятности для произвольного n не сложно, потом можно для достаточно большого n показать, что вторая вероятность будет выше. Очевидно, она не всегда выше, что легко можно увидеть для n=1,2. Сложно, как мне кажется, только посчитать, начиная с какого n вторая вероятность будет выше, и я не вижу как это можно сделать, не вычисляя просто в тупую вторую вероятность.
загадываю число от 0 до 1
беру случайное число от 0 до 1
вероятность, что случайное число оказалось моим - 0, потому что между 0 и 1 бесконечное число чисел, а 1/х при х стремящимся к бесконечности 0. Но тем не менее, какие то числа мне всё равно будут попадаться, и если бы я выбрал бы их, то угадал бы. Получается шанс 0, но событие может произойти. Обьясните?
вероятность это урод в математике, она противна всякому, кто хоть раз прикоснулся к святому попучкиванию
0.(9) это просто запись конкретного числа
у кого проблемы с пониманием записи, это их личные дела
я о том, что к самому числу этот вопрос отношения по существу не имеет. так что он вообще не про математику, если радикально
 57 Кб, 724x363
57 Кб, 724x363Хочется прокачать мозги
Знаю матешу на уровне 8 класса
да задолбали вы берёшься и вкатываешься без задней мысли, если у тебя уровень 8 класса, бери 9 класс книжку и читай
хорошая попытка
жаль, там не указано, как монетки эти считать в две строчки через спектральную последовательность Гротендика
>>2913
0.999... isn't a real number in the same way that ...111.0 is not a real number. For a decimal representation to represent a real number, it must satisfy 2 conditions:
a) It must begin with an infinity of zeros.
b) It must NOT end with an infinity of nines.
Since 0.999... ends with an infinity of nines, it doesn't represent a real number.
началось.. (it's started)
что ж, какие виды записи можно и запретить, я тебе разрешаю
>для достаточно большого n показать, что вторая вероятность будет выше.
Почему ты так думаешь? Я как раз проверил при малых n и она оказалась ниже. И решил что она будет меньше при всех n. Как минимум постановка задачи намекает на это. Что меня довольно удивило.
вероятность получить $k$ орлов при $n$ подбрасываниях вычисляется через биноминальное распределение и равна $P(k) = \binom{4n}{k}\left(\frac 1 2 \right)^{4n}$. вероятность получить $B(n)$ не менее $n$ орлов равна сумме $B(n) = \sum_{k = 0}^{n-1}P(k) = \left(\frac 1 2 \right)^{4n}\sum_{k = 0}^{n-1}\binom{4n}{k}$
так речь идёт о сравнении чисел $A(n) = \left(\frac 1 2 \right)^n$ и $B(n) = \left(\frac 1 2 \right)^{4n}\sum_{k = 0}^{n-1}\binom{4n}{k}$
например, при $n = 1$ слева получится $1/2$, а справа - $1/16$, т.е. $A(1) > B(1)$
чтобы выяснить, что происходит при больших $n$, нужно вычислить асимптотику $B(n)$ при больших $n$ с помощью центральной предельной теоремы. делать я это не умею, но по вдохновению свыше ясно, что $B(n)$ убывает как экспонента, и потому при больших $n$ она станет меньше $A(n)$, которая убывает как степенная функция
я написал глупость, $A(n)$ тоже убывает как экспонента
так что асимптотику $B(n)$, видимо, надо вычислять
интуитивно ясно, что вероятность не получить ни одного орла при большом количестве подбрасываний крайне мала, а получить малое количество орлов при вчетверо большем количестве подбрасываний хоть и тоже мала, но наверно не настолько. но чтобы понять точно, асимптотика для B(n) нужна
Доставте пикчу с Вербитом и Гауссом, где Гаусс спрашивает интересно какова асимптотика функции, а Вербит говорит пиздоссс.
там вторая вероятность убывает, наверно, как $e^{-n/2}$ и потому убывает немного медленнее (первая есть $2^{-n}$)
 121 Кб, 588x371
121 Кб, 588x371Нет. Это мем типа такого. Гаусс спрашивает про асимптотику функции Якоби. А снизу Вербит, Каледин и Виттен.
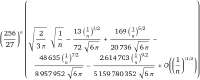 15 Кб, 420x169
15 Кб, 420x169>>2938
С помощью формулы Стирлинга и WA можно получить аппроксимацию для биномиального коэффициента (4n, n) (пикрелейтед).
Тогда получается вторая вероятность убывает асимптотически как (256/27)^n 1/2^4n что больше чем 1/2^n
В любом случае уебанская задача. Ведь сразу же это было понятно по тому что CLRS убрали ее из новых изданий. Только зря время потратил и в очередной раз убедился что решение задач - пустая трата времени.
 608 Кб, 800x600
608 Кб, 800x600Есть ли какие нибудь книги типо "Пучки для программистов" или "Пучки для тех кто знает матешу на уровне 9 класса"?
>как (256/27)^n 1/2^4n что больше чем 1/2^n
не знаю, для кого предназначается этот набор значков (печально петух-неосилятор не осилил LaTeX), но петух-неосилятор заслуживает похвалы, что попытался что-то посчитать, пусть и не совсем сам (с помощью компьютера) и пусть настолько грубо
а всё-таки, раз уж речь идёт о точной асимптотике этой самой второй вероятности, давайте подобно петуху-неосилятору страдать не будем, вместо этого научим его, как посчитать её по-настоящему и всю целиком, не убиваясь об одно слагаемое
для этого, как я выше отметил, надо применять центральную предельную теорему, которая гласит (см. https://en.wikipedia.org/wiki/Central_limit_theorem)
$P\left[\sqrt{n}\left(\bar{X}_n-\mu\right) \le \sigma z\right] \to \Phi(z)$, $n\to\infty$
У нас: $\mu = \frac{1}{2}$, $\sigma = \frac{1}{2}$, вместо $n$ нужно брать $4n$, а интересует нас величина $P\left[S_{4n} < n\right]$, где $S_{4n} = 4n \bar{X}_{4n}$.
приступим. выражение $P\left[\sqrt{n}\left(\bar{X}_n-\mu\right) \le \sigma z\right]$ превращается в $P\left[\sqrt{4n}\left(\frac{S_{4n}}{4n}-\frac{1}{2}\right) \leq \frac{1}{2} z\right]$, что преобразуется к $P\left[S_{4n} \leq \sqrt{n}z+2n\right]$ в арифметике могу ошибиться. теперь нужно взять такое $z$, чтобы $\sqrt{n}z+2n = n-1$, а именно $z = -\frac{n+1}{\sqrt{n}}$.
остаётся выяснить асимптотику $\Phi(-x)$, где $x=\sqrt{n} + \frac{1}{\sqrt{n}}$.
но она хорошо известна (см. https://en.wikipedia.org/wiki/Error_function): $\Phi(x) = \frac{e^{-x^2/2}}{x\sqrt{2\pi}}\left(1 - \frac{1}{x^2} + O(x^4)\right)$
дальше устное вычисление.
имеем $\left(\frac 1 2 \right)^{4n}\sum_{k = 0}^{n-1}\binom{4n}{k} = P\left[S_{4n} < n\right] = \frac{e^{-n/2 -1}}{\sqrt{2\pi n}}\left(1 + O\left(\frac{1}{n}\right)\right)$, $n\to\infty$
вот так это делается (для тех кому не по силам)
>не знаю, для кого предназначается этот набор значков
>вот так это делается
Напомнил мне препов-уебищ для которых только их решение единственно правильное, а в чужих решениях разбираться дело не царское.
>пусть и не совсем сам
Как будто сам аппроксимации из собственной сральни достал, а не скопировал с википедии.
>надо применять центральную предельную теорему
Одним днем ранее:
>с помощью центральной предельной теоремы. делать я это не умею
Решил таки обучится? Похвально.
>в арифметике могу ошибиться
Ничего страшного, не переживай, все и так знают что ты уебок.
>theorem)
>function):
Осилил LaTeX, но не осилил вставление ссылок. И предложения с большой буквы начинать. Ну как же так.
В целом молодец, хорошо постарался, петух-осилятор aka мелкочмоха.
 9 Кб, 225x225
9 Кб, 225x225>петух-осилятор
А можно списочек всех петухов раздела с их описанием? Я слышал лишь про N-петуха, конструктивного петуха, умн-петуха.
Чем петух-осилятор отличается от петуха-неосилятора? А анон, который говорит форсит нематику - это петух или нет?
Петухосписко-петух закукарекал.
>а не скопировал с википедии
так хохма в том, что ты и этого не можешь, хотя куда смотреть, было уже выше указано. всё такой же неосилятор
>Решил таки обучится?
решил потратить 15 минут, дабы тебя унизить ещё раз. результатом доволен, хаха
>>2948
>петух-осилятор
это петух-неосилятор превозмогает. его борьба
конструшок спокуха
Моя академическая успеваемость и в принципе способность заниматься математикой в последнее время сильно страдает из-за моего увлечения порнографией, гунерством и эджингом. Можете что-то посоветовать, как с этой проблемой справляться?
Недавно появилась мысль, а что если прочитать тему и прорешать буквально пару базовых задач и двигаться дальше. Если я буду учиться в таком темпе то я быстро доберусь до высшей математики.
Насколько важно иметь хорошую школьную базу в виде натренированности решать школьные упражнения и задачи для вката в высшую математику? Просто я смотрю мемы с матаном и у меня уже стойкое чувство, что оно не сложнее школьной матеши.
>Насколько важно иметь хорошую школьную базу в виде натренированности решать школьные упражнения и задачи для вката в высшую математику
вообще неважно
начинай давить матан, если какой-то момент непонятно, разбирай его по другим источникам. например, если тебе непонятно, что такое синус, можешь обратиться к школьным учебникам; если непонятно, как раскрывать скобки в выражении $(a+b)^3$, можешь потренироваться по Сканави
никакой другой базы, кроме наивной теории множеств (с которой учебник матана может и начинаться), не требуется
 98 Кб, 1280x720
98 Кб, 1280x720Эх, ты может конечно и правильно говоришь. Но держу пари я в этом разделе единственный экземпляр, кто решил будучи нулем в матеше вкатиться в вышмат. А значит твой опыт сложно наложить на мой путь обучения. Т.е. вы все выпускники мифи, мфти,,мгу и прочих топовых вузов имели невероятно большую школьную базу от топовых школ страны + олимпиадное задротство.
Вот к примеру, я давно мог начать изучать вышмат, если бы не решил устроить себе контрольную по школьным темам. Для примера, в школе мне плохо давалась математика потому что я не понимал, что из чего получается.
В итоге когда я решил самостоятельно учиться, то принял для себя решение не спорить с решениями и принять такими какими они есть. Я усиленно отгонял от себя мысли зачем нужна формула сокращенного умножения, зачем нужны квадратные уравнения итд. Я даже векторы принял такими какими они есть, думая что вот когда дойду до высшмата то пойму их.
И вот буквально в начале лета я начал понимать зачем нужны квадратные уравнения и сокращенные умножения. Т.е. мне буквально пришлось по второму кругу пройтись + прорешать тонны задачек, чтобы все это уместилось в одну картину. А зная все это, у меня больше нет страха перед сложными темами и сложными задачами. Для меня это стало просто вопросом времени.
Так что, я бы хотел узнать мнение такого же человека как и я, который усвоил высшмат НЕ будучи отличником-олимпиадником. Если конечно я не стану первым таким человеком в этом разделе..
не надо учить школьную математику. тебе геометрия вот никогда не понадобится. чисто для интуиции полезно теорему пифагора знать, чтобы понять, почему, например, евклидова метрика задается так как задается, не более.
из тригонометрии достаточно знать зачем эти функции нужны чтобы выражать углы через стороны и наоборот.
прочитай про векторы, умей преобразовывать выражения, это прикол из класса 5, и в общем можешь брать нормальные учебники по анализу и линейке.
тебе может быть не всё сразу понятно, что, почему, зачем. но в будущем ты их закроешь, а школьная математика в этом никак не поможет.
вообще если ты нигде не учишься и учишь ради какого-то своего интереса, то сразу копай в сторону того, что интересно, а не пытайся объять необъятное. мне например изначально хотелось теорему руффини-абеля разобрать, затем захотелось в фурье разобраться, так до сих пор анализ и изучаю. просто берешь книгу по теме, пытаешься пререквезиты нагуглить, пререквезиты к пререквезитам и тд. самая база, что везде нужна, это линейка и анализ на R, учатся за месяцев 6-9.
Ладно, попробую прочитать какую-нибудь модную книжку по линейной алгебре.
хуйню пишешь. я вообще из обычного моу сош мухосранского, возможно даже одной из худших в моем городе, в олимпиадах участвовал, без интереса, учителя отправляли, но даже первый этап заваливал всегда, решая максимум одну задачу, уровня "сколько есть цифр 7 в числах от 1 до 100", и то неверно наверняка.
>>2957-нон
Ну не знаю, в школьных материалах очень много надо преобразовывать выражения. Неиронично испытал детский восторг, когда узнал что можно выводить минус из дробных выражений. И главное это показывается и учиться на простых примерах. Держу пари я бы обосрался, если бы встретил такое в высшмате. А сейчас я готов к такому.
>чисто для интуиции полезно теорему пифагора знать, чтобы понять
из нее тащем то все основные тождества тригонометрии выводятся, это база.
Отращиваю вуса в виде интеграла
 95 Кб, 651x140
95 Кб, 651x140В дробно-рациональных уравнениях при избавлении от знаменателей неизвестное значение может вознестись в степенное выражение.
> усвоил высшмат
Я сегодня советский справочник по физике открыл, там в кинематике в формулах синусы. Да можно посмотреть таблицу синусов, но по факту например показать тангенс на окружности уже может вызывать трудности при таком подходе. Надо это или нет каждый сам решит.
Факт в том что все хорошие математики дрочили школьные задачи а не работали таксистами.
В вышмате используются те же самые приведения с уравнениями и дробями как в 6 классе если что.
Хочу вкатываться в матешу и физику одновременно)
То есть вообще любой простой идеал содержит делители нуля. А может быть так, что содержит не все?
А если пересечь все простые идеалы, получим ли мы какие-то "важные" делители нуля?
Ладно, поискал, вот такое вроде верно:
Множество всех делителей нуля есть объединение простых идеалов
Любой минимальный простой идеал состоит только из делителей нуля
Всё не так просто, видимо. А что если я не хочу прорешивать всего атью-макдональда...
>С помощью формулы Стирлинга и WA можно получить аппроксимацию для биномиального коэффициента (4n, n) (пикрелейтед).
кстати, такого коэффициента в искомой сумме>>2928 нет
там последний коэффициент имеет вид $\binom{4n}{n-1}$
не факт, что метод петуха вообще даёт какой-то ответ, если применить его правильно
>А что если я не хочу прорешивать всего атью-макдональда...
По моему опыту это не сильно помогает, если ты не алгебраист, возможно. Каждый раз приходится эти факты по новый вспоминать/доказывать. Так что проще по мере надобности просто этим заниматься. Особенно если это естественно в геометрическом контексте появляется, тогда и запоминается лучше.
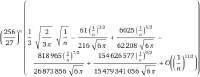 17 Кб, 436x169
17 Кб, 436x169Ты думаешь у (4n n-1) будет асимптотическое поведение отличное от (4n n)?
Соси хуй, тупой долбоеб.
число должно получиться другое, причём меньшее, чем было в прошлый раз (т.е. оценка ещё грубее)
посасываешь пока только ты :)
изучать дано всем, это уже структурированный и разжёванный материал буквально для беспомощных младенцев
 32 Кб, 1379x259
32 Кб, 1379x259*если конечно речь не идёт о каких то значительных умственных расстройствах
 15 Кб, 508x260
15 Кб, 508x260Да, дискалькулия, умственная отсталость, аутизм, эффект Данинга-Крюгера, Феномен Баадера — Майнхоф и + короткие ручки и толстые пальцы, не твоё короче
Не обязательно функций, но это основной пример, да. Другой основной пример — это сечения каких-нибудь расслоений.
Но в алгебраической геометрии бывают пучки в виде пересечения локальных колец всяких, например.
Спасибо
синус угла - это отношения противолежащей стороны к гипотенузе (в прямоугольном треугольнике)
синус 30 градусов - 0.5
хочешь подробнее - забей, как выводится синус
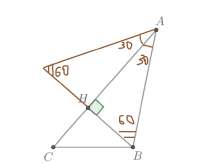 40 Кб, 605x497
40 Кб, 605x497В прямоугольном треугольнике если один угол равен 30, то другой 60. Если к нему приложить такой же треугольник, только отражённый, то получится треугольник, у которого все углы по 60. Это равносторонний треугольник (из теоремы о соотношении углов и сторон). Отсюда ответ видишь?
 1,2 Мб, mp4,
1,2 Мб, mp4,720x1280, 0:06
12 минут, серьезно?
чтобы сдать экзамены, лучше всего учить то, что требуется на этих экзаменах, по соответствующим материалам
>то мне надо бы её ещё на англе учить, а я вообще не знаю что юзать - какие учебники, курсы, гайды, видосы...
Очевидный Khan Academy: лучший англоязычный курс по матеше и отлично подходит чтобы вспомнить всю самую базу, но можно и подучить немного универской математики
>>2993
Да
Зря многие гуманитарии думают что математика это что-то на уровне врождённого таланта, мол если не начал врубаться в математику с нулевой, то всё
Это скорее нужно сравнивать с изучением какого-нибудь навыка, например иностранного языка
Олимпиадники это нейтив спикеры, они поняли математику ещё в детстве и начальных классах (скорее всего не без помощи хороших учителей, родителей и репетиторов), а затем просто дополняли знания
Но это не значит что конкретно ты не сможешь выучить матешу
Просто придётся сидеть с учебникам и репетиторами чтобы нагнать тот пласт знаний который олимпиадник усвоил ещё в детстве и школе
>скорее всего не без помощи хороших учителей, родителей и репетиторов),
А какие есть хорошие учебники, чтобы ребёнок сам учил? Серия, учебный план.
Скажем, у ребенка 10 лет от роду есть усидчивость и интерес, и нужен такой учебник(программа, серия учебников) чтобы заперев его с ними через 5 лет вышел будущий отличник мм СПбГУ.
Школьная программа это ведь ерунда. Это буквально базовая арифметика и геометрия, все что там используется это синусы/косинусы и различные простые интегралы и 2/3 мерные уравнения. В принципе, не углубляясь, это все можно впихнуть в один учебник 100 стр толщиной. Арифметика с 1 по 11 класс, по 10 стр на каждую. Ну ладно, 500 страницы. И чтобы бином ньютона давали ввести самому.
Я думаю что в принципе очень много детей могут изучать математику на уровне так сказать prodigy. Когда в 8 лет решаешь кубические уравнения, а в 13 на первом курсе мехмата Гарварда проглатываешь и пережевываешь все, идя впереди курса. Как терренс тао и гении прошлого.
Если оглянуться с высоты 5 курса мм МГУ на школьную программу - то ведь там ничего сложного, в принципе 1-4 класс можно пройти за год, если ты 5 летний адекват а твой брат 23 летний 5 курсник мгу и хорошо тебе объяснит. А 5-11 класс можно пройти за 2-3 года. Если есть желание, упорство, голова варит на уровне 50%+ IQ percentile и у тебя хороший наставник который тебе разжуёт, графический и алгебраически соотнесет, даст наводящие вопросы и скажет поработать ручкой на листке бумаги, чтобы понять что такое преобразования матриц, двойные интегралы, каков физический смысл , как на практике используется и тд и тп.
Это база.
Есть еще более пространная олимпиадная математика, к ней тоже нужны свои учебники. Не у всех же есть такси до 239 школы, да и что-то в форме книжки понятнее чем ютуб лекции
Например, те же кубические уровнения в 8 лет чтобы учить не так формулу корней в 7 классе заучиваешь (или она объясняется в учебнике, ты пробегаешь глазами, потом ты ее заучиваешь. Но смысла тут мало т.к. Один хуй то что своими руками и ручкой несколько раз не прошел туда-сюда несколько раз в памяти надежно не засядет), а приходишь к формулам пройдя путь собственного researchа, так сказать, с личным наставником или учебником. Вот именно спрашиваю про учебники, в идеале целый курс от условно простой арифметики и геометрии к диплому бака math major. Чтобы в том числе у многих людей на домашнем образовании, у людец из обычных мбоу мухосрани и умирающей провинции были такие классные , компактные и ёмкие, путеводители с 0 до 100 баллов ЕГЭ и участия в олимпиадах
>скорее всего не без помощи хороших учителей, родителей и репетиторов),
А какие есть хорошие учебники, чтобы ребёнок сам учил? Серия, учебный план.
Скажем, у ребенка 10 лет от роду есть усидчивость и интерес, и нужен такой учебник(программа, серия учебников) чтобы заперев его с ними через 5 лет вышел будущий отличник мм СПбГУ.
Школьная программа это ведь ерунда. Это буквально базовая арифметика и геометрия, все что там используется это синусы/косинусы и различные простые интегралы и 2/3 мерные уравнения. В принципе, не углубляясь, это все можно впихнуть в один учебник 100 стр толщиной. Арифметика с 1 по 11 класс, по 10 стр на каждую. Ну ладно, 500 страницы. И чтобы бином ньютона давали ввести самому.
Я думаю что в принципе очень много детей могут изучать математику на уровне так сказать prodigy. Когда в 8 лет решаешь кубические уравнения, а в 13 на первом курсе мехмата Гарварда проглатываешь и пережевываешь все, идя впереди курса. Как терренс тао и гении прошлого.
Если оглянуться с высоты 5 курса мм МГУ на школьную программу - то ведь там ничего сложного, в принципе 1-4 класс можно пройти за год, если ты 5 летний адекват а твой брат 23 летний 5 курсник мгу и хорошо тебе объяснит. А 5-11 класс можно пройти за 2-3 года. Если есть желание, упорство, голова варит на уровне 50%+ IQ percentile и у тебя хороший наставник который тебе разжуёт, графический и алгебраически соотнесет, даст наводящие вопросы и скажет поработать ручкой на листке бумаги, чтобы понять что такое преобразования матриц, двойные интегралы, каков физический смысл , как на практике используется и тд и тп.
Это база.
Есть еще более пространная олимпиадная математика, к ней тоже нужны свои учебники. Не у всех же есть такси до 239 школы, да и что-то в форме книжки понятнее чем ютуб лекции
Например, те же кубические уровнения в 8 лет чтобы учить не так формулу корней в 7 классе заучиваешь (или она объясняется в учебнике, ты пробегаешь глазами, потом ты ее заучиваешь. Но смысла тут мало т.к. Один хуй то что своими руками и ручкой несколько раз не прошел туда-сюда несколько раз в памяти надежно не засядет), а приходишь к формулам пройдя путь собственного researchа, так сказать, с личным наставником или учебником. Вот именно спрашиваю про учебники, в идеале целый курс от условно простой арифметики и геометрии к диплому бака math major. Чтобы в том числе у многих людей на домашнем образовании, у людец из обычных мбоу мухосрани и умирающей провинции были такие классные , компактные и ёмкие, путеводители с 0 до 100 баллов ЕГЭ и участия в олимпиадах
 104 Кб, 960x600
104 Кб, 960x600>Скажем, у ребенка 10 лет от роду есть усидчивость и интерес, и нужен такой учебник(программа, серия учебников) чтобы заперев его с ними через 5 лет вышел будущий отличник мм СПбГУ.
учебники есть, но с ребёнком должен сидеть взрослый и вместе с ним заниматься (как и с любой внешкольной программой, если ты желаешь, чтобы ребёнок её освоил)
дай ссылку на эти учбеники
?
я понимаю, что в идеале иметь личного персонального гида-тютора, фаната матматики и физики, знающего всё про всё, знающего как одно и то же объяснить с 12 разных стороны, знающего какие подводящие управжнения и примеры лучше отложат в голове ребенка структуру математики, в идеале лет 20-30 , чтобы был свежим и сам поннил школьную программу и помнил, как на такие-то темы смотрит человек несведующий, и, соответсвтенно, знающий какой путь к поучению данных знаний - а также форма и вид этого пути - наилучший
но если такого чела нет, есть ли книга которая бы смогла заменить его? серия книг
Мне кажется сейчас уже легче его отправить в ютуб чем пихать ему учебники. На ютубе есть целый пласт учителей-математиков которые подают материал в разной манере.
я против ютубного обучения т.к. это пассивное обуучение
глобально, грубо, есть 2 типа обучения: пассивное и активное. Первая - хуйня для галки. Это когда ты смотришь вумный ted talk про то как self improve, потом (ложно) чувствуешь что САМОРАЗВИЛСЯ))) т.к. 45 минут слушал вумных людей вместо просмотра эпизода крутого серича, и гордишься что НЕ ПРОЕБАЛ ДЕНЬ. А по факту это пшик так как ты только поставил галку в голове что посомтрел ТЕД ТОК вместо эпизода серича и типа приблизился к просветлению. нихуя. Это было пассивное потребление. Только АКТИВНАЯ ДЕЯТЕЛЬНОСТЬ является (само)развитием . Если ты не просто прослушал ТЕД ТОК а sat your white ass down и записывал все тезисы и подводящие к тезисам граундсы, чтобы каждый следующий день твоей жизни ВЫПОЛНЯТЬ запианные пункстты. Утром и вечером каждого дня сверяться со списком наклееным у кровти/холодильника. Всопминать тот тед ток и "прорабатывать" его но не как разговор с самим собой, а как физическое что-то в твоей повседневной жизни, как что-то что ты ingrained в свою натуру, привычка вторая натура ведь, что-то что ты ввел в свою жизнь и свой характер, личность, чем ты являешься и что ты делаешь буднично
ТО же самое про математику и науки. Просмотреть ютуб лекцию про вывод бинома ньютона для галки/самоуспокоения или самостоятельно ручками в тетради вывести его, поговорить с учителем, получить от него наводящие вопросы, в идеале чтобы он был умным и стройно подвел тебя к выводу бинома, но вернее не он подвел тебя, а ты сами пришел, как когда-то ньютон, потом туда-сюда побродить вперед-назад в методике получения формул - вообще абсолютные разные вещи.
поэтому я бы хотел именно "рабочую книгу" (по аналогии с рабочей тетрадью), которая бы - в идеале - вообще не давала ответов, но давала много подводящего материала, с разных ракурсов, короче, вообще одаривала читателей методолгией математики в первую и вторую очередь.
я понимаю чть есть зоричи и фихтенгольцы, есть школньные курсы математики с 1 по 11 классы, но вы вспомните как соотносится зорич и лекционный курс, который парарллельно шел с ним в вашем мехмате/физфаке. Всё же когда живой человек структурированно разжеванно преподносит материал, когда он в начале лекции знает чем оно все закончится и складно строит свое провествование, это ощущается иначе чем если - представьте - вы просто самостоятельно изучаете зорича, без тюторста, без препода, один вы, учебник и комната.
я против ютубного обучения т.к. это пассивное обуучение
глобально, грубо, есть 2 типа обучения: пассивное и активное. Первая - хуйня для галки. Это когда ты смотришь вумный ted talk про то как self improve, потом (ложно) чувствуешь что САМОРАЗВИЛСЯ))) т.к. 45 минут слушал вумных людей вместо просмотра эпизода крутого серича, и гордишься что НЕ ПРОЕБАЛ ДЕНЬ. А по факту это пшик так как ты только поставил галку в голове что посомтрел ТЕД ТОК вместо эпизода серича и типа приблизился к просветлению. нихуя. Это было пассивное потребление. Только АКТИВНАЯ ДЕЯТЕЛЬНОСТЬ является (само)развитием . Если ты не просто прослушал ТЕД ТОК а sat your white ass down и записывал все тезисы и подводящие к тезисам граундсы, чтобы каждый следующий день твоей жизни ВЫПОЛНЯТЬ запианные пункстты. Утром и вечером каждого дня сверяться со списком наклееным у кровти/холодильника. Всопминать тот тед ток и "прорабатывать" его но не как разговор с самим собой, а как физическое что-то в твоей повседневной жизни, как что-то что ты ingrained в свою натуру, привычка вторая натура ведь, что-то что ты ввел в свою жизнь и свой характер, личность, чем ты являешься и что ты делаешь буднично
ТО же самое про математику и науки. Просмотреть ютуб лекцию про вывод бинома ньютона для галки/самоуспокоения или самостоятельно ручками в тетради вывести его, поговорить с учителем, получить от него наводящие вопросы, в идеале чтобы он был умным и стройно подвел тебя к выводу бинома, но вернее не он подвел тебя, а ты сами пришел, как когда-то ньютон, потом туда-сюда побродить вперед-назад в методике получения формул - вообще абсолютные разные вещи.
поэтому я бы хотел именно "рабочую книгу" (по аналогии с рабочей тетрадью), которая бы - в идеале - вообще не давала ответов, но давала много подводящего материала, с разных ракурсов, короче, вообще одаривала читателей методолгией математики в первую и вторую очередь.
я понимаю чть есть зоричи и фихтенгольцы, есть школньные курсы математики с 1 по 11 классы, но вы вспомните как соотносится зорич и лекционный курс, который парарллельно шел с ним в вашем мехмате/физфаке. Всё же когда живой человек структурированно разжеванно преподносит материал, когда он в начале лекции знает чем оно все закончится и складно строит свое провествование, это ощущается иначе чем если - представьте - вы просто самостоятельно изучаете зорича, без тюторста, без препода, один вы, учебник и комната.
>дай ссылку на эти учбеники
>?
ты детей воспитываешь? я не очень хорошо знаком с этой областью
посмотри вот здесь: https://biblio.mccme.ru/main?tag=279
>но если такого чела нет, есть ли книга которая бы смогла заменить его?
10-летний ребёнок не будет заниматься этим самостоятельно
Ну это зонтичное понятие, куда обычно втыкаются теория алгоритмов, теория графов, математическая логика, комбинаторика, куски алгебры (всякие кольца-группы) но в разрезе конечных структур каких-то, теория чисел
>10-летний ребёнок не будет заниматься этим самостоятельно
Джвачую, пусть вначале пиздюка курить и пить научит.
Мне один быдлокодер сказал на собесе что жуквери это непростая штука и за недельку ее не выучить. До сих пор проигрываю с этого.
Не стоит недооценивать тупость тупых долбоебов.
>>3038
Сколько человек выпустилось из дристочечной за всю историю ее существования?
Ладно, сам посмотрю - 103 человека за 30 лет.
нет, очень полезное
Это они понизили сложность или во мне проснулся гений математики?
бедняжка, пришлось податься в тараканы, чтобы выжить
только и остаётся, что читать про волновое уравнение в $\mathbb R^n$ урывками да поучать других на двощах
ага, как будто это я подрываюсь при каждом упоминании листочков, нму и вербяши и это я пытаюсь всем объяснить, как надо единственно правильно смотреть на вещи и делать что-то. а так-то всё проекции, как ещё
>листочков, нму и вербяши
Такая то боль что кто то иногда пошатывает твои авторитеты. Расскажи если ты каждый день начинаешь с дрочки на НМУ то почему ты еще не в списке из 103 людей его окончивших, неужели не осилил?
Алсо, если бы я поставил себе задачу обоссывать каждого еблана сбирающегося прорешать всего Сканави и все дристочки из НМУ мне пришлось бы мониторить этот тред 24 на 7 прямо как это делает проецирующая мелкочмоха.
>вербяши
Бля хочу стать как он известным математиком из топ вузов, а потом в интернете писать полнейшие эджи тейки про политику
(Хотя уже был такой?)
>Расскажи если ты каждый день начинаешь с дрочки на НМУ то почему ты еще не в списке из 103 людей его окончивших, неужели не осилил?
Раньше разве не так было?
>прорешать всего Сканави
Так Сканави это база для всех желающих вкатиться в математику. Не можешь прорешать задачник - нахуй с пляжа.
здесь ты применяешь петушиный демагогический приём «подмена тезиса» (ignoratio elenchi), пытаясь сместить внимание со своих обосанных штанов на какую-то выдуманную херь, отношения к дискуссии не имеющей. но штаны-то дико воняют, так что сместить внимание не получится. лучше, наверно, всё-таки постираться и двигаться дальше, хотя дело твоё, конечно
>отношения к дискуссии не имеющей
На все сто процентов имеет отношение к дискуссии, в отличии от твоих фантазий про "обоссаные штанишки" которыми ты пытаешься прикрывать горящую сраку.
Почему "самый эффективный метод" в реальности на столько не эффективен. Почему если НМУ самое лучше место на земле, мелкочмоха не прошла все его курсы с отличием, вместо того чтобы 24 на 7 дристать тупостью в матх.
не имеет потому что полностью выдумано
ты сам придумал «дрочку на нму» и всё такое, а теперь подрываешься
Возможно, потому, что срать на двощах может любой мудак, а закончить нму - не любой (а только совершенно исключительный, кому блять вообще нужен диплом этой хуйни лол)
>ты сам придумал «дрочку на нму»
Поэтому
> при каждом упоминании листочков, нму и вербяши
в негативном ключе, чмоня подрывается и начинает реактивно срать в тред визгами про петухов-неосиляторов (очевидно проецируя собственный обсер в НМУ). Прохладная история.
не, ты не понял. мне наплевать на любое негативное отношение к нму и к вербяше. но когда петух-неосилятор (это ты) раззевает рот, чтобы упомянуть (как он это называет) что-то негативное о вещах, про которые он ничего не знает и не понимает, всегда здорово заметить ему определённые моменты в этих «упоминаниях», в чём я себе не отказываю
на самом деле указанной тряской является вот это
>при каждом упоминании листочков
в исполнении петуха-неосилятора
такие дела
>петуха-неосилятора
>визгами про петухов-неосиляторов (очевидно проецируя собственный обсер в НМУ)
Ну а кто дрочит на НМУ вприсядку и отчего то поленился на экзамены пойти? Тут в треде только один такой петух-неосилятор. И ты можешь поговорить с ним как раз в зеркале.
>Ну а кто дрочит на НМУ вприсядку и отчего то поленился на экзамены пойти?
это твой воображаемый друг, которого ты выдумал
я же выше написал
У меня нет таких друзей чтобы дрочили на НМУ вприсядку и срали в матх 24 на 7, так что мимо, чмоня.
ну, это ты со своим психиатром обсудишь, а я только напомню, что ты штаны-то так и не переодел. фу как воняют
Так можно про любой задачник сказать.
Решение задач это и есть математика. И для желающих вкатиться это идеальный задачник. Нравится решать задачки, и хватает усидчивости каждый день сидеть думать над ними - значит шансы вката в математику есть. Задачник Сканави можно за лето прорешать, проверено мною. Если уровень Сканави внезапно слишком лёгкий, можно что-нибудь другое подыскать, но для большинства местных хочу вкатиться в математику лучше Сканави сложно что-то придумать.
Если человек осилил Сканави, осилит Фихтенгольца или Демидовича. А если бросил Сканави, тоже не страшно - тут уже ясно что математика ему не интересна и не нужна как таковая.
>Решение задач это и есть математика.
А, ну тогда программирование это математика. Задачи ведь они решают.
Есть интересные задачи, есть неинтересные. В Сканави интересных нет.
Оно ей было, и отчасти остается - теор информатика считается разделом математики. Кнут математик, первые программисты в СССР были математиками. Другое дело что сейчас отрасль выродилась в ремесло, которому обучают на курсах.
>Есть интересные задачи, есть неинтересные. В Сканави интересных нет.
Субъективно. Математика это про упорную и регулярную работу, а не про "интересно/неинтересно". Вот прорешивание Сканави как раз та лакмусовая бумажка чтобы понять для тебя это или нет. Не хватает усидчивости, кажется что "неинтересно" значит нет.
Поддерживаю этого автора.
Почему Сканави? Почему не какой-нибудь задачник для бухгалтеров?
>Кнут математик, первые программисты в СССР были математиками.
Ну ты же понимаешь, хотя бы на уровне ощущений, что Кнут не такой же математик, как, например, Хаусдорф?
>Вот прорешивание Сканави как раз та лакмусовая бумажка чтобы понять для тебя это или нет. Не хватает усидчивости, кажется что "неинтересно" значит нет.
Интересно, как же люди до Сканави то жили. Рекомендую, кстати, полистать книжки по математике для школьников до олимпиадного помешательства и создания "вступительной математики". До 60-х было полно интересных, содержательных книг. После, в массе своей, пошла тупая бессмысленная неинтересная хуета. Я не знаю кем нужно быть, чтобы на серьезном ебале жрать пик 2 и советовать другим. Лучше уж реально программировать пойти, хотя бы денег заработаешь. Случайно еще раз крутанув попал на пик 3. Интересные задачи. Но на всю книгу подобных едва сотня наберется кажется.
>поэтому я бы хотел именно "рабочую книгу" (по аналогии с рабочей тетрадью), которая бы - в идеале - вообще не давала ответов, но давала много подводящего материала
звучит нереалистично хорошо
азаза
[iмимо ]первокур
>аналоговые вычислительные машины
у тебя на пике вроде дифференциальная машина бэбиджа, она никаким боком не аналоговая кстати вроде как поправьте если ошибаюсь
кстати да нематематика
>Вот лично тебе надо? А?
Да, мне надо. Собираю материал по аналоговым вычислениям и буду осваивать.
>дифференциальная машина бэбиджа
Самая что ни есть аналоговая.
>кстати да нематематика
А что, физкультура?
алё оболтус, бэбидж придумал цифровую машиину, дискретную, она оперирует целыми числами. Ты вообще о чём говоришь?
Самая что ни есть аналоговая, числа там вторичны
>А какие есть хорошие учебники, чтобы ребёнок сам учил? Серия, учебный план.
Многие хвалят советские учебники по математике
Возможно, действительно стоит присмотреться, учитывая что СССР и правда ставил цель создать сильнейшую физмат школу в мире (особенно во время космической гонки), а сейчас учебники пишут для коммерциализации: чем больше воды будет, тем больше купят и тд
>А какие есть хорошие учебники, чтобы ребёнок сам учил?
Ребёнок 10 лет сам учить не будет. Точка
Вообще да
Да и нет учебников таких, чтобы ребёнок сам учил
Все учебники рассчитаны на прохождение материала вместе с учителем
Судя по количеству элементарных частиц там у них весело🤭
Вы видите копию треда, сохраненную 9 сентября в 10:43.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.