Вы видите копию треда, сохраненную 14 августа в 05:51.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 163 Кб, 845x1024
163 Кб, 845x1024Есть ли наглядное объяснение всех тригонометрических формул? Если да, то объясните кому интересно.
Есть, но нужно знать что такое комплексные числа.
|w|=1, arg(w)=ф. f(z)=wz - это поворот вокруг 0 на ф градусов.
допустим |w'|=1 и arg(w')=ф'. Тогда arg(ww')=arg(w)+arg(w'). Это число с тригонометрической форме записывается как cos(ф+ф')+isin(ф+ф'). Представив в тригонометрической форме w и w', и перемножив их получаем: (cosф+isinф)(cosф'+isinф')=cosфcosф'-sinфsinф'+i(cosфsinф'+cosф'sinф).
Сопоставив получим: cos(ф+ф')=cosфcosф'-sinфsinф' и sin(ф+ф')=cosфsinф'+cosф'sinф.
Начиная со страницы 120 пункты 2 и 3 прочитай, там всё разжёвано на пальцах.
http://ilib.mccme.ru/pdf/kurant.pdf
В смысле? Там за 5 страниц вся тригонометрия объясняется, начиная с геометрической интерпретации комплексного числа выводится формула Муавра , из которой можно получить любую тригонометрическую формулу, которые заставляют в школе зубрить. Причём тут олимпиадки?
Про векторы я имею ввиду, что у тебя есть r и i единичные вектора и любое комплексное число через их линейную комбинацию выражается, это то же самое, что и там написано. Что не понадобится? Формула Муавра конечная цель, из неё можно получить любые формулы для sinkx / coskx. А ты про что?
Банальный, школьный уровень имел в виду.
http://www.cleverstudents.ru/trigonometry/angle_addition_formulas.html
Ну так, а если там sin10x, что проще, через sin(9x+x), потом каждый sin8x, cos8x черезз 7x + x представлять или через формулу Муавра? Я до сих пор помню как заставляли зубрить sin3x, cos3x вместо того, чтобы дать общую формулу из которой можно все подобные вещи вывести. Ненавидел тригонометрию в школе.
Или что, ты про интерпретацию умножения комплексных чисел как умножение модулей и сложение углов? Так всё это тоже там есть, в тех 5 страницах. Короче, не понимаю я, что тебе не нравится.
>Я до сих пор помню как заставляли зубрить sin3x, cos3x вместо того, чтобы дать общую формулу из которой можно все подобные вещи вывести.
Да к тому, что необязательно знать обобщённую формулу Муавра, чтобы объяснить вывод формул тригонометрии. Мол, меньше получится затрагиваемых тем и школьного уровня будет достаточно для восприятия (не надо даже касаться комплексных чисел). Ну да ладно.
> чтобы объяснить вывод формул тригонометрии
Ну простых да, а сложные школьнику придётся зубрить так как выводить какой-нибудь sin(10x) из sin(a+b) он просто заебётся. Кто-то наверху в системе образования решил, что комплексные числа для школьникам сложно и поэтому им приходится зубрить формулы, непонятно как выведенные, хотя всё это объясняется за один урок.
>даже комплексных чисел
Да откуда такой страх комплексных чисел?
Да и потом, так красивее, какие связи затрагиваются, а так просто сухие синусы касинусы, которые непонятно зачем нужны. Скука.
Ну не то что страх, просто упор на простое представление, хотя вы правы - некоторое смущение они вызывают, но это тоже из-за личных стереотипов (мол, в реальности они выводятся алгебраически, а не строго фиксируются посредством счёта).
А школьники должны в 11 классе достаточно близко познакомиться с ними, спору нет, но требовать от них изучения формулы Муавра - это жестоко, ведь и так мало у них времени. Да и теории много нужно будет перелопатить. Кто-то вообще считает что школьников нужно привести к основной теореме алгебры, но мне бы хотелось увидеть как он выстроит программу со всеми доказательствами, и это учитывая что идиоты хотят сделать английский обязательным экзаменом.
>требовать от них изучения формулы Муавра - это жестоко
Она простая, рассказываешь про комплексные, потом вот у тебя комплексное z = p(sinx+icosx), рассказываешь про умножение комплексных, модули перемножаются, углы складываются, zz'=pp'(sin(x+y)+icos(x+y)), при z' = z z2=p2(sin2x+icos2x) по индукции получаешь zn=pn(sinnx+icosnx), при p=1(единичная окружность) zn = sinnx+icosnx, но мы знаем, что z = sinx+icosx, получается формула Муавра (sinx+icosx)n = sinnx+icosnx. Всё, что нужно знать это вот твоё векторное представление комплексных чисел и как их перемножить. Если бы это было суперсложно то да, нет смысла это давать, но это реально можно за урок объяснить, а профитов дофига, по мне так гораздо сложнее зубрить кучу формул, а в егэ часто встречаются всякие sin5x, cos10x. Ну это имхо, конечно.
Только я синусы с косинусами перепутал, cosx+isinx, то, что z = pcosx(проекция на x)+ipsinx(проекция на y) это как раз следует из "векторных" соображений, аналогичная ситуация с умножением комплексных чисел как произведением модулей и суммой углов(аргументов). Всё, больше ничего не нужно.
 8 Кб, 250x251
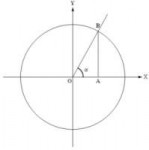
8 Кб, 250x251А если модуль единица, то раскрывается смысл косинуса как проекции единичного отрезка на ось x/синуса на ось y, так-то по сути всё, что нужно, это нарисовать крестик и кружочек и из этого рисунка можно научить выводить все формулы тригонометрии.
Так нам-то может и просто, а вот школьникам, которые ещё не привыкли к абстрактным представлениям будет тяжко. Тем более, вы не учитываете вывод бинома, что накладывает ещё сверху комбинаторику. В общем, согласен что вывод формулы Муавра - это полезное (универсальное) обобщение, но это накладывает большую нагрузку на школьника, по личному мнению.
>А если модуль единица, то раскрывается смысл косинуса как проекции единичного отрезка на ось x/синуса на ось y, так-то по сути всё, что нужно, это нарисовать крестик и кружочек и из этого рисунка можно научить выводить все формулы тригонометрии.
Бесспорно, только и представление комплексных чисел не понадобится для вывода. Ну, это тоже лишь мнение.
Опыт покажет что лучше подходит для наглядного вывода.
 79 Кб, 1280x720
79 Кб, 1280x720Нахрен комплексы лепить к тригонометрии, непонятно. Тригонометрия прекрасно понимается с помощью этого кружка и без всяких коплекснутых чисел.
>>51840
Ну ладно, может ты и прав, я просто по себе сужу, детская обида так сказать, я в школе ненавидел тригонометрию, нас просто заставляли зубрить какие-то косинусы тройных, четверных углов, что, зачем, для чего хуй его знает. А потом оказалось, что всё это легко и просто, лёгким движением руки как говорится, получается из крестика с кружочком и каких-то совсем простых идей. Но да, может быть при такой подаче я, будучи школьником, вообще нихуя не понял бы. Может и так, опыт критерий истины, все дела. Да и про бином Ньютона я забыл как-то, само собой разумеющимся кажется, а ведь у школьника и глаза могут на лоб полезть немножко.
>Тригонометрия прекрасно понимается с помощью этого кружка и без всяких коплекснутых чисел.
Изначально поддерживал это. Согласен.
>Ну ладно, может ты и прав, я просто по себе сужу, детская обида так сказать, я в школе ненавидел тригонометрию, нас просто заставляли зубрить какие-то косинусы тройных, четверных углов, что, зачем, для чего хуй его знает. А потом оказалось, что всё это легко и просто, лёгким движением руки как говорится, получается из крестика с кружочком и каких-то совсем простых идей. Но да, может быть при такой подаче я, будучи школьником, вообще нихуя не понял бы. Может и так, опыт критерий истины, все дела. Да и про бином Ньютона я забыл как-то, само собой разумеющимся кажется, а ведь у школьника и глаза могут на лоб полезть немножко.
Благодарю за обсуждение.
>Тригонометрия прекрасно понимается с помощью этого кружка
Так ведь этот кружок есть множество всех комплексных корней из 1; ось y есть мнимая ось, а x вещественная.
То есть ты как бы можешь об этом недоговаривать, скрывать эту часть информации так сказать от учащихся, что конечно не очень красиво, но твоё дело. Суть однако не изменится, представление в виде кружка и с помощью комплексной плоскости это буквально одно и то же, хочешь быть честным, отказывайся от кружка тоже.
>Так ведь этот кружок есть множество всех комплексных корней из 1
А разве такое представление не было выработано ещё до развития комплексных чисел, за счёт тригонометрического тождества?
 34 Кб, 423x662
34 Кб, 423x662Изоморфизм - не тождественность. Подгруппа кручения U(1) и корни из единицы - разные вещи. Прямая на плоскости и Ax+By+C=0 - разные вещи.
>Изоморфизм - не тождественность. Подгруппа кручения U(1) и корни из единицы - разные вещи. Прямая на плоскости и Ax+By+C=0 - разные вещи.
По модулю контекста дискуссии - абсолютно одни и те же вещи, так что попытка выебнутся не прокатила.
И как же предлагается доказать, что отношение противолежащего катета к гипотенузе - это то же самое, что x-x^3/3! + x^5/5! + ... ?
вообще прикольно, что сначала математика шла по пути отождествления почти одинаковых объектов (с точностью до изоморфизма) а потом наоборот стало важно различать различные, но изоморфные объекты, эквивалентные категории и т.д....
и чего дальше?
Нужно сначала посчитать производную ентого катета на гипотенузу и в формулу Тейлора её ебануть.
Вы видите копию треда, сохраненную 14 августа в 05:51.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.