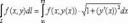Это копия, сохраненная 13 июня 2024 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 1,2 Мб, 1275x713
1,2 Мб, 1275x713Списки хорошей литературы:
http://pastebin.com/4iMjfWAf - Classic / http://pastebin.com/4FngRj6n - dxdy / http://4chan-science.wikia.com/wiki/Mathematics
Полезные ресурсы >>104 (OP):
http://gen.lib.rus.ec / http://mathprofi.net / http://math.stackexchange.com
Архив тредов:
https://pastebin.com/PMvY34XF
мы условились, что это дефолтная картинка
не нравится - предложи свою
моча может отредактировать пост
Ластбамп из тонущего
Это сразу в голову пришло, но оно же неверно или там виды не те, о которых я думаю? Алсо матаны скажите почему an-1 делится на a-1?
 30 Кб, 697x215
30 Кб, 697x215Ну типа я это случайно получил, когда суммировал 1n+2n+3n+...+nn, может есть гораздо проще следствие какое-нибудь из теоремы Эйлера, скажем.
А, блядЬ.я дебил похоже, если прибавить к обеим частям 1, то получится an делится на a лул. Сорян.
Хотя нет, тогда можно было бы отнять два и должно было бы тоже так получаться. Не понимаю тогда.
Ясно, лол.
Совсем уже обдвачевался похоже.
Ебнулся что ли?
Пусть a = zy1+x1; b = zy2+x2, тогда ab = z2y1y2 + zy1x2+zy2x1 + x1x2 = z(...) + x1x2.
an mod (a-1) = 1111...1 = 1.
Да всё, я обдвачевался чуть-чуть, да. Достаточно просто (a-1) вынести.
разобраться в линейных уравнениях
это неверно, потому что у тебя бок будет вертикальным
а вот если повернуть, чтобы он стал видом спереди, то и верх будет вертикальным
мое решение подходит, но, видимо, это не то, что хотел увидеть арнольд
да хз, мне кажется охуенное решение, я как раз после неудачи с лесенкой в том же направлении думал, пока твой рисунок не увидел и не проспойлерил себе ответ :/
 411 Кб, 928x275
411 Кб, 928x275да
Наверно поздно отвечу, но все же. У тебя эти самые векторы образуют векторное пространство, а на нем определено внутреннее сложение векторов и внешнее умножение на элементы поля, думаю дальше сам поймешь.
я о том, что это бред /b
Условие
Многочлен P(x) дает остаток 2 при делении на x – 1, и остаток 1 при делении на x – 2.
Какой остаток дает P(x) при делении на многочлен (x – 1)(x – 2)?
Решение
Пусть P(x) = (x – 1)(x – 2)Q(x) + ax + b. По теореме Безу a + b = P(1) = 2, 2a + b = P(2) = 1, откуда a = –1, b = 3.
Ответ
3 – x.
Собственно, мне неясен этот момент:
> По теореме Безу a + b = P(1) = 2, 2a + b = P(2) = 1,
Каким раком?
P(1) = (1-1)=0(1-2)Q(x) + (a+b) = a+b.
Чтобы узнать чему равен Р(1) можно сделать так:
P(x) = (x-1)Q(x) + 2 => P(1) = 2
С P(2) та же ситуация.
Кстати, чтобы ты не расслабился прочитав объяснение, даю тебе задачу - почему в P(x) = (x-1)(x-2)Q(x) + (ax+b) именно (ax+b), а не (a+b).
Точнее не почему (ax+b) вместо к примеру обычного b?
![page0018-720px-d0b8d0bdd182d0b5d180d0b2d18cd18e-d181-d0b4d0[...].jpg](/math/big/thumb/19020/14956406902040s.jpg) 192 Кб, 1436x971
192 Кб, 1436x971То ли я укуренный черезчур, то ли ты годно пошутил.
А на чем ты моделирование образований в атмосфере будешь проводить? На пеке офисной? Закономерно, что, как ты сказал, это будут делать на кластерах. Там же данных и параметров много.
Да. Если P(x) какой-то многочлен и ты делишь его на многочлен R(x) степени r, то остаток может быть многочлен степени (r-1), т.к. возможно на каком-то этапе деления в столбик нужно будет делить многочлен степени меньше r, чего сделать нельзя и он уходит в остаток.
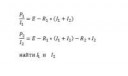 3 Кб, 334x200
3 Кб, 334x200А можно подробнее? Что даст такое вычитание в результате?
Я могу выразить I2 из верхнего и подставить в нижнее. При таком порядке действий я получу квадратное уравнение, но оно даёт 2 корня, => 2 варианта решения. Но решение должно выходить одно.
Там не 0, в этом и дело. Это задача из области ТОЭ. I1 и I2 - сила тока. Не должно выходить больше 1 варианта решения.
Хорошо, я попробую. Существуют ли другие пути решения?
Дело в том, что я пытался считать таким способом при различных значениях остальных параметров, но решения получаются довольно странными с точки зрения электротехники, потому и спросил.
Плохо знаю физику. Возможно у тебя некоторые корни будут неподходящими. Нулями или отрицательными не знаю могут ли быть отр. величины в физике
Других путей не знаю. Вычитать можно чтобы выразить проще. У меня получилось l1 = p1l1/(r2l22 - p2.
Видимо, я где-то совершил ошибку, когда считал своим способом. Попробовал вычитанием - один из корней квадратного уравнения отсекается всегда и значения больше приближены к реальности. Спасибо за помощь.
Твой батя прав. Теория динамических систем гугли.
есть N10. Нужно сконвертить в N2.
Есть ли какой-то простой способ заранее узнать количество разрядов бинарного числа?
Нет, понятно, что оно будет длинны ближайшей большей степени двойки. Типа 29 < 666 < 210 = 10 разрядов.
Для маленьких чисел это просто, но как быть когда ты не можешь достать из жопы таблицу степеней двойки и сравнить?
Есть ли какая-то компьютерная система куда я буду вводить матрицу, а она будет ее классифицировать подобным образом?
ты это в уме хочешь? в уме не получится
или на листочке/калькуляторе?
Тогда бери двоичный логарифм от своего числа, и к целой части прибавляй единицу - получишь число разрядов в двоичной форме.
Например, log[2,666]=9,37937..., округляем девятку -получаем 10. Готово.
(Я на самом деле эту формулу эмпирически вывел только, так что она может быть неверна)
О! Вот помнил же, что есть какой-то способ!
не, мне не руками, я говнокод пишу.
>printf("%d have %d digits in binary\n", n, (int)floor(log(n)/log(2)+1));
>>19140
>(Я на самом деле эту формулу эмпирически вывел только, так что она может быть неверна)
Ну, я сейчас на нее эмирически посмотрел, и чот как она может быть не верна, если она возвращает степень, в которую нужно возвести двойку чтобы получить это число?
 52 Кб, 692x511
52 Кб, 692x511Ну мне нужно составить мат модель задачи (ПЛАТЁЖНУЮ МАТРИЦУ). С решением я уж как-то разберусь, там чисто механика. Но я счас не могу понять, как эту платёжную матрицу составить. Могу кинуть какие-то копейки, если реквизиты оставите
Условие:
Два противника А и В ведут борьбу за два стратегических пункта. Под командованием
А находится два (три) полка, под командованием В - три (три). Обе стороны должны
распределить свои силы между двумя пунктами. Пусть n1 и n2 числа полков, посланных со
стороны А на пункты 1 и 2 соответственно. Аналогично, пусть m1 и m2 - распределения
полков противника по соответствующим пунктам. Выигрыш А подсчитывается
следующим образом: если n1>m1, то он получает m1+1, и, если n2>m2, он получает m2+1. С
другой стороны, если n1<m1, то он теряет n1+1, и, если n2<m2, он теряет n2+1. Если число
полков на каждой стороне одно и тоже, то каждая сторона получает нуль. Определить
оптимальные стратегии для каждого игрока.
На скрине эт пример. Такую же надо матрицу по этой
Ты имел ввиду полые? Куб это множество точек (xi, yi, zi), где
a<=xi<=b;
a<=yi<=b;
a<=zi<=b;
Поэтому он внутри "заполнен" точками(любая точка внутри его "каркаса" будет удовл. неравенству).
Сфера внутри полая.
Да. Квадрат тоже не полый?
В школьной геометрии считается, что полые. Треугольник - это три отрезка, квадрат - это четыре отрезка, куб - это двенадцать отрезков и т.д.
Что то связанное с формулой Бернулли
>Заходил в казино и ставил к примеру 1 крышку на черное, если выпадало красное, следующей ставкой ставил 2 на черное, если опять выпадало красное - ставил 4 на черное, если опять красное, то 8 на черное. Самое большое помню это проигрывал семь раз подряд, но так как я удваивал каждый раз ставку, то все равно всегда был в плюсе и итоге. Вот так я наебал теорию вероятностей, математики соснули!
Можно было и не менять цвет, тупо ставить всё время на черное. Результат был бы таким же.
найди вероятность товара из каждого магазина и умножь на вероятность брака в нем, затем сложи эти три значения
Есть один вопрос по аналитической геометрии
можно было вообще тупо ставить на ЛЮБОЙ цвет
вероятность выигрыша от раза к разу равна 50%
нужно просто покрыть убыток
ваш кэп
Сначала объясни что значит физмат
Учебник по физике.
Психика для быдла. Хорошая крыша летает сама и в самый них и в самые верха.
Переоценено.
Мне б какую-нибудь прогу или онлайн калькулятор
Я сейчас в математике застопорился, потому что занимаюсь математикой один уже больше года и мне становится довольно одиноко и грустно, без общения мотивация теряется. В универе я не учусь и возможности поступить нет, потому что работать надо.
1. Первообразную
2. Производную
3. Пределы lim
Как это находить? Зачем это нужно и где используется.
Общайся в /math.
Голосую за этот пик.
На форумах, в конфах. Ты как первый день в интернете. Советую сразу идти в западные интернеты, если умеешь читать и писать по английски.
/math похож больше на помойку с мемами, я не хочу здесь ничего обсуждать, например.
>>19212
Любой учебник Calculus'a. Тебе советую почитать Лузина "Дифференциальное исчисление", параллельно читая более строгое и современное изложение, ибо первый хоть и хорош для неокрепших умов, но у него есть свои косяки.
>Зачем это нужно и где используется.
Считать. Физика. Теорвер/статистика и все, где они применяются. Экономика. Оторвись от двачей/игр и посмотри вокруг себя.
За такие вопросы убивают нахрен.
>и где используется
Нигде. Это разминка для ума или сложная игра, типа шахмат, с особо сложными правилами. Если ты такой долбоеб, что ничего не добился в жизни, не можешь норм общаться с людьми, имеешь слабое тело и слишком ленивый для настоящей науки -- добро пожаловать в математику.
> Это разминка для ума или сложная игра, типа шахмат, с особо сложными правилами.
> Если ты такой долбоеб
> добро пожаловать в математику
Dos not compute. Слишком толсто.
Не нужно анон. Я пытался найти. Одни сливаются, другие в физику перекатываются, третьи зацикливаются на каком-нибудь тупом занятии, типа решение всего демидовича. Но это не важно. Пытался найти кого-то т.к. вербит говорил в группе проще изучать. Может быть, но это наверное только в реалиях какого-нибудь НМУ, когда у всех одни и те же листки. Но даже в таких случаях мне неприятно контактировать с другими. Неприятно рассказывать свои мысли и слушать чужие. Так что подумай действительно ли тебе нужен кто-то.
>>19232
Этого двачую. Нужно взорвать все нефтяные вышки, засадить поля конопли для производства бумаги и жить в землянках, постигая связи между структурами. А за вопросы -нахер это нужно убивать. Как Харди завещал.
Да он многих в США покрамсал за королеву. В Америке его называют ЗОДИАК.
Понимаю предел настолько же очевидно, как идею цифры 0 или деления чисел. Ты скоро тоже поймешь, когда начнешь проходить производную и интегралы. Твоя сложность не в том, что ты не понимаешь "зачем", а в том, что ты прошел кучу определений, а свободно оперировать ими пока не можешь, забываешь. Также сложность в доказательствах, к которым ты себя еще не приучил.
Еще раз повтори все определения и внимательно вникай в доказательства. Готов поспорить, ты не решал никаких теоретических задач, а они очень-очень важны для понимания.
Так я вроде как по естественно-научной специальности учусь. Действительный анализ уже прошел и сдал. С задачами типа нахождения предела/производной или взять интеграл проблем не было. Теоретических задач и правда не решал. Но когда захотелось разобраться в сути понятий, оказалось, что умение решать задачи не дает мне понимания того, что такое нижний/верхний предел, и дает очень смутное представление отличия границы от предела. Что я делаю не так? Не материализуется же понимание само? Как добиться просветления?
Что значит "в физику перекатываются"? С какой целью? Расскажи пожалуйста поподробнее про этот типаж.
У последовательности может быть много предельных точек. Одна, два, три, миллиард. Бесконечно много. Более того, бывают такие последовательности, что _каждое_ вещественное число является их предельной точкой.
Наибольший элемент множества всех предельных точек называется верхним пределом. Наименьший элемент - нижним. У последовательности есть предел тогда и только тогда, когда множество её предельных точек состоит в точности из одного элемента, т.е. верхний предел равен нижнему.
То и значит, что математика им интересна только как приложение к физике.
>>19292
Мистер олимпиадник f(x) = sqrt(x) однозначна?
>У последовательности может быть много предельных точек. Одна, два, три, миллиард. Бесконечно много.
а - предел хр если любой отрезок содержащий а содержит почти все х
если а и б пределы хр то их можно покрыть непересекающимися отрезками. Тогда оба отрезка содержат почти все элементы но такого быть не может т.к. они не пересекаются. поэтому предел единственен.
>Более того, бывают такие последовательности, что _каждое_ вещественное число является их предельной точкой.
Пусть окрестность точки а содержит конечное число элементов из Х. Тогда а - не предельная точка: все шары радиуса r < min(d(a,x)) не содержат элементов Х.
Множество членов последовательности счётно. Пусть а - предельная точка. Тогда её окрестности содержат счётное число элементов. Любая другая будет содержать конечное число => не является предельной.
>Наибольший элемент множества всех предельных точек называется верхним пределом
{4,5,6} верхняя грань = 6 но 6 не предельная точка, как и нижняя грань = 4 не предельная точка.
>У последовательности есть предел тогда и только тогда, когда множество её предельных точек состоит в точности из одного элемента, т.е. верхний предел равен нижнему.
У последовательности 1+1/n нижняя грань = 1 а верхняя = 2. Предел = 1. У последовательности -1n/n верхняя грань и нижняя различны и не равны приделу последовательности.
> мне неприятно контактировать с другими. Неприятно рассказывать свои мысли и слушать чужие.
Ну ты реальный социопат, значит, таких людей очень мало и я не из них.
А как насчёт действительного предела последовательности рациональных чисел?
> Хочу не просто оперировать пределами, решая упражнения на них, а понимать их глубинный смысл.
Тогда только один путь: решай задачи на доказательства, пытайся по формулировкам теорем доказывать их сам, перед тем, как смотреть доказательства в учебнике, при прочтении определения пытайся сам придумать примеры определяемого объекта, выявить какие-то простейшие свойства. В идеале еще надо иметь кругозор и перед началом чтения книги примерно знать, какие результаты в этой книге самые главные, и когда встречаешь теорему/лемму/определение думать, как это может помочь для получения тех главных результатов.
В случае с пределами, например, тебе нужно поверхностно узнать про интеграл и производную (например, с точки зрения физической интуиции: разбили множество на бесконечно малые кусочки и просуммировали; скорость в определенный момент времени) и подумать, с помощью чего интегрирование и дифференцирование можно было бы строго обосновать. Тогда не будет возникать вопрос "зачем нужны пределы".
Если ты реально только-только начал заниматься математикой и читаешь первые главы Зорича, то, скорее всего, ты не сможешь делать все, что я перечислил, но к этому надо стремиться, если хочешь максимального понимания. Если у тебя в жизни нет времени, чтобы постоянно заниматься математикой, то тебе будет намного сложнее, придется либо забивать на осознанность вообще и как макака применять готовые формулы, либо научиться понимать, что концептуально, а что чисто техническим аспектом, но это приходит только с опытом и кругозором, так что первый год-два в любом случае придется изучать математику как чистые математики.
Здесь необходимое и достаточное условие получается, что должны существовать положительные числа k и m, такие что:
ka+mb=c?
Предел это как чёрная дыра, точка такая, в её окрестности, горизонт событийотметил красным, находится бесконечное число элементов последовательности, вне её конечное. Для функции немного по другому, но суть та же. Найдётся такая точка, что все значения функции при приближении аргумента к x0 будут лежать в окрестности этой точки. В формуле епсилон это координата y угла pi/2 красного круга, а дельта координата x угла 0 красного круга. Вот у тебя есть y=1/x, x->oo, тогда y будет ->0. Это как воронка в ванной.
мимосантехник
 3 Кб, 625x151
3 Кб, 625x151Отклеилось.
 50x51
50x510
1
2
0 1
0 2
1 0
1 2
2 0
2 1
0 1 2
0 2 1
1 0 2
1 2 0
2 0 1
2 1 0
Хочу обратить внимание, что 02 и 2 разные числа.
Количество числ, которые можно сосчитать такой системой это сумма всех размещений из набора длины n по i элементов, где i меняется от 1 до n. Формула на пике.
Теперь главный вопрос. Как из такой системы переводить в обычную? Неважно основание. Хоть 2, 10 или n.
Мне кажется, твои задачи были основаны на таинственных правилах типа "sin(x) превращается в cos(x)", или "делим числитель и знаменатель на старшую степень Х". Если ты учился на действительно технической специальности, ты бы все эти теоремы, которые сейчас читаешь, доказал бы на первой сессии.
>Но когда захотелось разобраться в сути понятий, оказалось, что умение решать задачи не дает мне понимания того, что такое нижний/верхний предел, и дает очень смутное представление отличия границы от предела. Что я делаю не так? Не материализуется же понимание само? Как добиться просветления?
Хз, мне показалось наоборот, что он знает зачем оночтобы решать задачки лул , но не понимает его сути.
Нет, я не социопат. Когда кто-то догадался до решения, а я нет, то я завидую. Если догадался я, а другой нет, то я чувствую жалость. Поэтому нахуй.
Ты жертва собственного ЧСВ.
>если а и б пределы хр то их можно покрыть непересекающимися отрезками.
В случае общего положения это не так. Это работает только для хаусдорфовых пространств.
>Бля пацаны не понимаю картофельный анализ
>Ну тут хаусдорфовые...
Пиздец. Может у тебя и НОД в кольцах столько же сколько единиц?
Даже в картофельном анализе, тот же Зорич приводит пример пространства ростка функций.
Что такое картофельный анализ?
"Предел" и "предельная точка" - два разных понятия. Пределом называется предельная точка в том случае, когда она существует и единственна. Понимаешь это?
Докажите, что если какое-то равенство (содержащие переменные для множеств и операции пересечения, объединения и вычитания) неверно, то можно найти контрпример к нему, в котором множества пусты или состоят из одного элемента.
С какой стороны тут подступиться?
Пусть X1, X2, ... - множества в левой части, R - результат применения операций пересечения-объединения-вычитания к этим множествам, Y - множество в правой части.
Представим каждое множество трансфинитной строкой из нулей и единиц.
Допустим, что равенство неверно.
Тогда R и Y отличаются в какой-то букве, её номер обозначим ординалом x.
Заметим, что операции объединения, пересечения и вычитания действуют на строки покомпонентно.
Заменим в строках, представляющих множества, все буквы, кроме x-й, нулями.
От этого множества станут либо пустыми, либо одноэлементными.
При этом x-я буква в R не изменится и по-прежнему будет отличаться от x-й буквы в Y.
Нет, маняматик, верхний и нижний предел это не просто предельные точки, это наименьшие и наибольшие предельные точки.
Да всё равно то, что ты сказал, верно, если последовательность сходящаяся. У произвольной числовой последовательности, в которой бесконечно много элементов, может быть больше предельных точек.
 85 Кб, 583x339
85 Кб, 583x339На равносильность. Если последовательность сходящаяся и имеет единственную предельную точку, то это её предел. Обратное неверно.
>Обратное
В смысле если последовательность сходящаяся, то она имеет единственную предельную точку, совпадающую с её пределом, это верно. А обратное если последовательность имеет единственную предельную точку, то она сходящаяся не верно.
Не-не, анон, дело не в выражении же. Это ошибка, я сам так часто ошибаюсь, равносильность и следование коварные штуки. Не за что.
 40 Кб, 938x267
40 Кб, 938x267Только там вот так.
В общем, не хотел вас доебывать с такой простой задачкой, но не могу решить уже часов 6. Перепробовал всё.
Залью в картинках, так будет понятнее.
Вместо корня из 910 должен быть корень из 14, и тогда все будет хорошо. Где я обосрался? Пробовал уже все, и ортогонализировать по Г.Ш. систему из e1,e2,e3 и т.д.
Помогите пожалуйста.
рандомпик
Я как бы этим постом и хотел донести, что предел и предельная точка это разное... Пиздец. На хуй эту доску кароче.
Анон? Поможешь?
Ну ты омеган. Здоровый мужчина, когда кто-то догадался, а он нет, чувствует спортивную злость и мотивацию больше задрачивать, а когда наоборот - выброс серотонина от осозания своей доминантности.
 170 Кб, 450x972
170 Кб, 450x972>Здоровый мужчина, когда кто-то догадался, а он нет, чувствует спортивную злость и мотивацию больше задрачивать
Серьезно, кто-то ещё не вырос из олимпиадных яслей?
Мне кажется, что на такой "мотивации" далеко не уедешь, когда дело касается сложного знания.
 85 Кб, 1600x900
85 Кб, 1600x900Ай, то ли макаба шутит, то ли проблемы на моей стороне.
>>19361
... и какими-то публикациями? Причем тут «тянки»? Хотя я, должно быть, догадываюсь, что ты несёшь и откуда вообще ты сюда свалился.
Такая «мотивация» — самая паршивая из всех возможных. Серьёзно, заниматься математикой/наукой ради тянок или фаллометрии? Бросит тебя изменчивая мирская слава, и вот ты уже проклинаешь науку, на чем свет стоит, ведь ты мечтал на самом деле жрать картофан под водочку и трахать толстозадых самок на лавочке в парке, а не трахаться с квантами или гомологиями. How pathetic.
>>19296
>То и значит, что математика им интересна только как приложение к физике.
То есть, они изначально не планировали сильно углубляться в математику. Не перекатывались, а шли по заранее намеченному пути. Ты ввёл меня в заблуждение своим нестрогим языком.
Мотивация вообще хуйня, заставлять себя зачем-то. А зависть ещё большая хуйня, это как завидовать, что кто-то поёт лучше, бред какой-то. Может вы не тем занимаетесь просто, не должно быть такого от любимого занятия
.
 331 Кб, 768x800
331 Кб, 768x800>Мотивация вообще хуйня, заставлять себя зачем-то
Никто и не говорит о пересиливании. Ты неправильно употребляешь слово «мотивация», надо колбасой вниз.
>Может вы не тем занимаетесь просто, не должно быть такого от любимого занятия
А чем же заниматься, подскажешь?
Пока это хобби, то ок. Но нахуй заниматься чем-то всерьез, если нет планов делать это действительно хорошо. А если собираешься делать что-то как можно лучше, то нужно использовать всякую мотивацию, которая доступна.
мимо
п.с. найденный центр масс должен находиться на поверхности сферы, не внутри ее
Не понял, что именно ты хочешь, но если у тебя есть группа из более чем одной точки с положительными массами на поверхности шара, то центр масс будет всегда внутри шара.
хочу найти центр масс для группы точек, лежащих на поверхности шара, так чтобы этот центр масс был точкой на поверхности
ладно, а если просто искать центр масс для пары точек на дуге, то он может лежать на дуге, а не под или не над ней?
НАД ней не может, как и НА дуге
потому что он будет лежать на хорде ВНУТРИ окружности
ты действительно такой глупый? или просто засираешь тред?
нее
мне оказывается была нужна точка пересечения прямой, проведенной через центр шара и центр масс, с поверхностью шара
 223 Кб, 1280x853
223 Кб, 1280x853Есть какое-то чувство разочарования
Скучно, многие загадки, фильмы и жизненные ситуации не вызывают больше интереса, становится "слишком легко".
Как вы живете вообще, математические аноны? Чем занимаетесь и какие у вас интересы
>Чем занимаетесь?
Математикой. И только ей.
вне математики ничего нет
вообще ничего
какие-то грязные тряпки, заборы, коровники, менты и быдло
мы в аду
ею*
Показать, что Q порождается из 1 и 0.
Любое подполе Q содержит единицу. Следовательно, содержит любое целое число. Вместе с любым ненулевым a содержит a-1 и замкнуто по умножению, следовательно, содержит все рациональные числа. Следовательно, совпадает с Q.
 17 Кб, 1359x548
17 Кб, 1359x548Затем поискал про него в интернете и ничего не нашел!
Зато вместо него повсюду толкают теорему о том, что если противоположные углы четырехугольника в сумме дают 180, то вокруг него можно описать окружность;
оно что, из нее как-то вытекает?
Что она квадратная, я думаю, ты докажешь, а дальше поумножай с обеих сторон на матрицы, в которых на всех позиция нули, кроме одной, на которой единица.
Бумп
https://pastebin.com/R49C3vaz
Вот такой код из вольфрам математика.
Но дело в том, что он почему-то не работает, точка улетает за параболу. Что может быть?
>Докажите, что делителы нуля необратимы
Оставим это очевидное утверждение любопытному читателю в качестве упражнения.
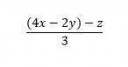 8 Кб, 146x77
8 Кб, 146x77Ещё как назло во всех пособиях примеры по МТ тривиальные какие-то
Ну, закончил вышку, прикладную.
Теперь уже года два сижу углубляюсь в алгебру и топологию.
Сейчас опять начал дискретку читать.
Работаю аналитиком, иногда применяю for lulz всякие формулы.
Какая рутина например?
Мань, ты уходишь от ответа. Естественно, я имел в виду обобщенных тянок, в частности, например, тебя самого: вот ты сам гордишься собой, считаешь, что чего-то достиг?
> Мотивация вообще хуйня, заставлять себя зачем-то. Может вы не тем занимаетесь просто, не должно быть такого от любимого занятия
Мань, представь себе, любое занятие частично состоит из неприятных вещей. Например, мне нравится алгебра, топология, а чтобы заниматься матаном, мне нужно реально заставлять себя. Я не сказал бы, что он мне противен, но без самопринуждения тут никак.
> А зависть ещё большая хуйня, это как завидовать, что кто-то поёт лучше, бред какой-то.
Ты путаешь негативные эмоции, которые испытывают бессильные омеганы с эмоциями нормального человека, когда он смотрит на кого-то и думает: "Он крутой, я же тоже могу думать мозгом, почему я не смог сделать то, что он сделал? Нужно больше задрачивать". При этом нормальный человек не испытывает ненависти к более успешному или зависти к себе.
>>19398
Михаил Сергеевич, залогиньтесь.
>>19432
Рассмотри выражение baa-1, где ba равно угадай чему.
Бамп годной картинке!
Производная - это скорость изменения чего-нибудь.
Ну смотри, пусть у нас есть функция f и мы хотим в какой-то точке x приблизить ее линейным отображением, потому что с линейными отображениями в отличие от произвольных функций работать легко. А именно, попытаемся рядом с точкой x представить f(x + h) как f(x) + A(h) + R(h), где A - линейное отображение, а R - это какая-то функция, которая при h -> 0 очень быстро стремится к 0, а именно, R(h)/|h| -> 0 при h -> 0. Если так можно сделать, то функция f называется дифференцируемой, а линейное отображение A - ее производной в точке x.
Если f - функция из R в R, то A представляет собой просто умножение на число, поэтому можно отождествить A с этим числом и считать, что производная в точке - это число.
Если мы в выражении f(x + h) = f(x) + f'(x)h + R(h) устремим h к 0, то получим
f'(x) = lim (f(x + h) - f(x)) / h, h -> 0.
Понятия не имею. Мне всё-равно пришлось проходить через все свои "детские" страхи, и не все ещё пройдены.
Можешь почитать Gullberg'овскую Mathematics - From the Birth of Numbers. Но ингриш.
(4x - 2y) - z = 2(2x - y) - z
Удвой x влево, вычти y, получишь w = 2x - y, теперь посчитай по тому же алгоритму 2w - z и подели результат на 3.
![0c385c9e17f339XL[1].jpg](/math/big/thumb/19020/14962670258660s.jpg) 31 Кб, 659x750
31 Кб, 659x750Нет царских путей)))
 33 Кб, 706x420
33 Кб, 706x420Бамп. Вот еще одна.
Она и есть красивая. Но для освоения любой темы придется решать много задач, и даже по любимой области этот процесс может быть скучным.
Если у тебя нет таких качеств, как усидчивость, целеустремленность, если ты не способен концентрироваться, а для работы тебе нужно перманентное "чувство красоты", то математика не для тебя.
1
В каждом из N независимых испытаний событие А происходит с вероятностью P. Найти вероятность того, что событие A происходит
А)точно K1 раз
Б)меньше чем К2 и больше K1 раз
В) больше чем к2 раз
N=600
P=0,20
K1=140
K2=290
2
Телефонный комутатор обслуживают N абонентов. Для каждого абонента вероятность позвонить в течение часа = P.
Найти вероятность того что в течение часа позвонят на коммутатор
А) М абонентов
Б) не менее М + 1
N=2000
P=0,025
M=1
С МЕНЯ КАК ОБЫЧНО
Доска та первокультурная
Я ещё школьникам домашку делать не помогал.
Для примера - по составу двух команд по футболу необходимо определить победителя. Нам подарили волшебный шар, который спрашивает состав команд и говорит что-то типа "Локомотив - 75% шансов на победу, Манчестер - 25% шансов на победу. Прогнозируемый победитель - Локомотив", но нас честно предупредили, что победителя он угадывает лишь в 80% случаев. Какова реальная вероятность победы Локомотива в таком случае?
Мне кажется, что не хватает данных. Если бы шар просто выдавал победителя, то ок, но он выдает вероятность победы.
Алсо не дай бог ты просто пытаешься к ставочкам примазать математику.
Я просто хочу для тренировки написать угадывалку победителя в одной древней стратегической мертвой браузерке, в которой дохуища данных накоплено.
А что не так? И в ставочки, и в биз)
50/50
Кстати, как так же интуитивно объяснить, почему слайс проходит именно через эти точки? В видео это обходится стороной.
https://youtu.be/BAZhSTqsKUo
У меня была ебань с контрольными. 32 студента писали 2 контрольные, при чём каждый мог писать либо одну, либо обе. Оценивались контрольные от 0 до 20 включительно. Средний балл по обоим контрольным составил 14. После этого каждый студент назвал свой максимальный балл за одну или две контрольных. Средний балл равен S.
а) Приведите пример, когда S<14
б) Может ли быть 2 человека, писавших 2 контрльных при S=11
в) Какое минимальное количество человек может писать две контрольные при S=11.
Как это решать?
 22 Кб, 600x317
22 Кб, 600x317>гарвардских самородков
Есть один такой, который на своем ютуб канале как-то раз рассказывал, как делать 200к в год.
Бамп.
да что там деньги, c какого-то момента мне кажется похуй уже даже на жопу вытирать. просто живешь высокими материями.
Боюсь, они слишком умны для того, чтобы хвалиться своими успехами. Да и не каждому дано, умело применять математику к жизненным ситуациям.
Чаще бывает наоборот, дяденьки с деньгами нанимают математиков для своих нужд. Сколько среди первых вторых, я не знаю.
Так Перельман еврей, в случае чего бы ему помогли.
Кембриджский институт вроде, кембридж внутри.
Пусть X - топологическое пространство, компактно, не локально компактно. Значит, в нем есть последовательность xn, в которой нет сходящейся подпоследовательности. Значит, для любой a из X существует открытая окрестность X(a), в которой содержится лишь конечное число членов xn. Все такие окрестности образуют открытое покрытие, у него есть конечное подпокрытие, в котором тоже должно быть конечное число членов, но тем не менее, они покрывают все пространство, в котором содержится вся последовательность. Противоречие.
Пардон, секвенциально компактно конечно же. Не знаю, чего я вдруг "локально" написал.
 88 Кб, 1180x482
88 Кб, 1180x482Но ведь из компактности следует секвенциальная компактность.
http://bogomolov-lab.ru/KURSY/TOP-2012/slides-top2012-8.pdf
Ты перепутал направление. Это из секвенциальной компактности не следует компактность.
Потому что начинается с открытого покрытия, которому принадлежит вообще каждая точка пространства вместе с открытой окрестностью, а дальше по компактности оттуда выделяется конечное подпокрытие.
>>19628
>>19629
>>19630
Все, вроде бы разобрался уже.
Ровно свой кусок увидел в доказательстве, но он доказывает только наличие предельной точки, и оказывается, что это совсем не гарантирует, что из нее можно выбрать сходящуюся подпоследовательность.
Короче, говорят что хватает первой аксиомы отделимости, но я видел доказательство только для метризуемых.
1. Пусть K - компакт. Рассмотрим последовательность его замкнутых непустых вложенных подмножеств A1 ⊃ A2 ⊃ A3 ...
и пусть A - пересечение всех Ai.
Дополнение множества Ai обозначим через Bi.
Тогда B1 ⊂ B2 ⊂ B3 ⊂ ... - последовательность открытых множеств.
Пусть B - объединение всех Bi.
Тогда, по законам де Моргана, B есть дополнение A.
Предположим, что A пусто.
Тогда B=K, то есть Bi образуют покрытие K.
Выберем конечное подпокрытие Bm, ... , Bn.
Из-за вложенности Bi-ых, Bm⊂ ... ⊂ Bn.
Значит, K⊂Bn.
То есть K - подмножество дополнения An.
Но это означает, что An пусто. Противоречие.
Значит, A непусто.
2. Точка a называется точкой прикосновения множества X, если в любой окрестности a есть хотя бы одна точка множества X.
Замыкание множества X - пересечение всех замкнутых надмножеств X.
т.е. замыкание для X - наименьшее замкнутое надмножество X.
Замыкание множества X состоит в точности из всех точек прикосновения X.
В самом деле, пусть C - замыкание X.
Пусть x - точка C такая, что её окрестность U не пересекается с X.
Тогда C\U - замкнутое множество, содержащее X.
Значит, C не является наименьшим замкнутым надмножеством X.
Обратно, пусть точка x такова, что каждая её окрестность пересекается с X.
Пусть W - дополнение C.
W открыто.
Тогда W - окрестность каждой своей точки.
W не пересекается с C и подавно не пересекается с X.
Значит, x не может быть элементом W.
Значит, x - элемент C.
3. Пусть x1, x2, x3, ... - последовательность точек компакта.
Через P1 обозначим {x1, x2, x3, ...}, через P2 обозначим {x2, x3,..} и т.д. для каждого n.
Через Rn обозначим замыкание Pn.
Множества Rn образуют последовательность замкнутых непустых вложенных множеств. Следовательно, их пересечение непусто и в нём содержится по крайней мере одна точка a.
Следовательно, a принадлежит всем Rn.
Следовательно, a является точкой прикосновения каждого из Pn.
Это означает, что в любой окрестности точки a для любого натурального n есть по крайней мере одна точка с номером, не меньшим n.
Значит, в любой окрестности a лежит бесконечно много точек последовательности.
Таким образом, a является предельной точкой для x1, x2, x3, ...
Следовательно, каждый компакт - секвенциальный компакт.
1. Пусть K - компакт. Рассмотрим последовательность его замкнутых непустых вложенных подмножеств A1 ⊃ A2 ⊃ A3 ...
и пусть A - пересечение всех Ai.
Дополнение множества Ai обозначим через Bi.
Тогда B1 ⊂ B2 ⊂ B3 ⊂ ... - последовательность открытых множеств.
Пусть B - объединение всех Bi.
Тогда, по законам де Моргана, B есть дополнение A.
Предположим, что A пусто.
Тогда B=K, то есть Bi образуют покрытие K.
Выберем конечное подпокрытие Bm, ... , Bn.
Из-за вложенности Bi-ых, Bm⊂ ... ⊂ Bn.
Значит, K⊂Bn.
То есть K - подмножество дополнения An.
Но это означает, что An пусто. Противоречие.
Значит, A непусто.
2. Точка a называется точкой прикосновения множества X, если в любой окрестности a есть хотя бы одна точка множества X.
Замыкание множества X - пересечение всех замкнутых надмножеств X.
т.е. замыкание для X - наименьшее замкнутое надмножество X.
Замыкание множества X состоит в точности из всех точек прикосновения X.
В самом деле, пусть C - замыкание X.
Пусть x - точка C такая, что её окрестность U не пересекается с X.
Тогда C\U - замкнутое множество, содержащее X.
Значит, C не является наименьшим замкнутым надмножеством X.
Обратно, пусть точка x такова, что каждая её окрестность пересекается с X.
Пусть W - дополнение C.
W открыто.
Тогда W - окрестность каждой своей точки.
W не пересекается с C и подавно не пересекается с X.
Значит, x не может быть элементом W.
Значит, x - элемент C.
3. Пусть x1, x2, x3, ... - последовательность точек компакта.
Через P1 обозначим {x1, x2, x3, ...}, через P2 обозначим {x2, x3,..} и т.д. для каждого n.
Через Rn обозначим замыкание Pn.
Множества Rn образуют последовательность замкнутых непустых вложенных множеств. Следовательно, их пересечение непусто и в нём содержится по крайней мере одна точка a.
Следовательно, a принадлежит всем Rn.
Следовательно, a является точкой прикосновения каждого из Pn.
Это означает, что в любой окрестности точки a для любого натурального n есть по крайней мере одна точка с номером, не меньшим n.
Значит, в любой окрестности a лежит бесконечно много точек последовательности.
Таким образом, a является предельной точкой для x1, x2, x3, ...
Следовательно, каждый компакт - секвенциальный компакт.
Но почему не гарантирует? Гарантирует жэ.
Известно, что это не всегда правда, искать дыры в твоем доказательстве мне лень, сто раз уже обсуждали.
Пространства без 1 аксиомы отделимости. Ибо из первой а.о. следует существование точки накопления последовательности, а из первой а.с. следует что к точке накопления можно выбрать сходящуся подпоследовательность.
И среди них есть компакты?
Структура на множестве - это набор операций и отношений.
Функция сохраняет структуру, если она перестановочна со всеми операциями и если не изменяет отношения.
Функции, которые сохраняют структуры, называются морфизмами структур.
Функтор - это морфизм категорий.
Это не просто функция.
Но тебе это неважно.
Потому что в хаскелле смысл слова "функтор" свой собственный, не такой как в теории категорий.
А что значит перестановочна? Ассоциативна, дистрибутивна и тд? Или только одно что-то?в хаскеле я так понял функтор это "эндофунктор на категории хаск', частный частный случай. Ну ясно, короче всё не так и всё не то. Спасибо.
Например, f(a+b) = f(a)+f(b)
f(ab) = f(a)f(b)
f(O(a,b,c,d,e)) = O(f(a), f(b), f(c), f(d), f(e))
a<b => f(a) < f(b)
Потому что там объясняется, что это что-то вроде мап, только глобальнее. Типа способ применить функцию к вложенному вложенному вложенному элементу не трогая остальные.
> f(a+b) = f(a)+f(b)
>f(ab) = f(a)f(b)
Ну так да, там тоже вроде этого
(a->b)->f a->f b
fmap f (Just a)=Just (f a)
В категориях f должно переводить объект в объект, стрелку в стрелку, начало стрелки в начало стрелки, конец стрелки в конец стрелки, а также сохранять композицию функций и нейтральный элемент, т.е. f(pq) = f(p)f(q) и f(idX) = idf(X).
Нет.
Эндофунктор - это когда категория отображается сама в себя.
А не-эндофунктор - это когда функтор устанавливается между двумя разными категориями.
В хаскелле есть только одна категория, Hask. Других категорий в нём не может быть в принципе. Поэтому все функторы в нём отображают Hask в Hask - переводят типы данных в другие типы данных, программы (стрелки) в программы.
Вот если бы Hask морфировала каким-то образом в теорию групп (типы данных переводились в группы, а программы - в гомоморфизмы групп), то это был бы не-эндофунктор.
>Эндофунктор - это когда категория отображается сама в себя.
>Поэтому все функторы в нём отображают Hask в Hask
>я так понял функтор это "эндофунктор на категории хаск
Ну так вроде бы то и говорю, не?
>сохранять композицию функций и нейтральный элемент
1.fmap id-id
2.fmap (f.g)=fmap f.fmap g
То есть всё-таки в хаскеле это не какой-то другой функтор, а просто частный случай, эндофунктор из хаск в хаск, так можно думать? Илои ошибка?
>1.fmap id-id
>2.fmap (f.g)=fmap f.fmap g
Это из учебника, типа законы функторов, без этих свойств не будет считаться функтором класс типов.
В сообществе хаскелля не хотят знать о том, что бывают какие-то другие функторы кроме специальных эндофункторов хаск.
Может не не хотят, просто Хаскелл про хаск и только про хаск, откуда там другим взяться. Так, ну хорошо, значит я верно всё понял. Теперь такой вопрос по сути связки функторов можно рассматривать как инструмент такой телескопический, позволяющий копаться во внутренностях типов? "Предчувствие функториальной хирургии" это об этом Михайлов писал в аннотации к лекции?
>Предчувствие функториальной хирургии
На функториальных диаграммах можно делать преобразования, напоминающие преобразования в маломерной топологии. Владыки гомотопического хаоса держат воздушный шарик за ниточку.
https://www.lektorium.tv/lecture/14228
Что это вообще за раздел математики? (гомологическая?)Алгебра, теория категорий? Что почитать по этому поводу?
Лол, хаскель реально напоминает игрушечную обучающую программу, чтобы потрогать можно было это всё, а не только сухой текст читать, пока воображение не так сильно развито, может и задумывался с этой целью даже.
Блин. Ну ладно.
И да, спасибо.
А разделы математики они прям разделы или это условности всё, с какой стороны не вкатись всё равно придёшь. А то вот гуглю, а там всё пересекается. Теория категорий это вообще что, эволюционировавшая теория множеств? Как множества юзаются во всей условно старой математике вроде матанализа так и теоркат юзается во всяких гомологических алгебрах и прочих алгебраических топологиях? Сорт ов язык?
Есть Core Math - набор из общеизвестных понятий и теорем. Есть надстроенные над ним мало пересекающиеся разделы.
См. arxiv.org
Язык категорий не заменяет язык множеств, а дополняет его. Гомологическая алгебра - это старая математика, ей уже почти сто лет. Более новая математика - это KK-theory, motivic cohomology, anabelian geometry, россыпь всяких там moonshine theory (monstrous moonshine, umbral moonshine) - им по пятьдесят лет.
> Это означает, что в любой окрестности точки a для любого натурального n есть по крайней мере одна точка с номером, не меньшим n.
> Значит, в любой окрестности a лежит бесконечно много точек последовательности.
Вот этот переход неверный.
Ну или распиши его подробней.
Но ты не распишешь, потому что в пространстве без 1 аксиомы отделимости это неправда.
x1, x2, x3, ... - последовательность.
P1 = {x1, x2, x3, ...}
P2 = {x2, x3, ... }
и т.д.
a - точка прикосновения всех Pi
U - произвольная окрестность точки a
Допустим, что в U есть лишь конечное количество точек последовательности.
Пусть m, ... , n - номера этих точек. Причем n наибольший.
Тогда в окрестности нет точек с номерами, большими n.
Значит, a не является точкой прикосновения для всех Pj, j>n.
Но a является.
Находишь точки перемены знака, разбиваешь ими числовую прямую на интервалы, каждому интервалу присваиваешь символ + или -, выбираешь нужные интервалы.
Идешь читать про метод интервалов. Решение писать тебе здесь никто не будет, а анон выше уже достаточно рассказал.
Хотя я вот что придумал.
-14 делится на какое-то число и получается число больше или равное нулю. Что ты можешь сказать про делитель?
Спасибо анон!
Ок, тут ты прав, а я не прав.
Тогда вот что распиши:
Ты доказал, что а - предельная точка, теперь докажи, что есть сходящаяся к ней подпоследовательность.
Это кажется очевидным, но судя по всему, это не так, и ошибка именно здесь.
И да, вот сейчас я задумался, и понял, что нужна не первая аксиома отделимости, а первая аксиома счетности, тоже прошу прощения за ошибку.
Итак, смотри, у тебя есть предельная точка для последовательности, и из последовательности нужно выбрать сходящуюся.
Тогда ты можешь выбирать каждый раз n-ю точку из пересечения первых n элементов базы, и гарантированно в каждой открытой окрестности есть элемент базы (напр. k-й), который содержит пересечение первых k элементов базы, которое содержит точку и ВСЕ последующие. То есть любая окрестность содержит ВСЕ элементы подпоследовательности, начиная с k.
Для метрических пространств это доказательство тоже канает, так как в метрическом пространстве есть счетная база в точке, например, шары с радиусом 1/n.
В пространстве без счетной базы, судя по всему, это рассуждение ошибочно, но если ты считаешь что нет, то я хочу его видеть.
Итак, у тебя есть топологическое пространство, в нем есть последовательность, у нее есть предельная точка a. Я хочу посмотреть, как ты выделишь из нее сходящуюся подпоследовательность, то есть такую, у которой в любой окрестности Ua содержатся ВСЕ члены подпоследовательности, кроме конечного числа.
 40 Кб, 938x267
40 Кб, 938x267> а - предельная точка, теперь докажи, что есть сходящаяся к ней подпоследовательность.
Так это разве правда?
Подпоследовательность, сходящаяся к нулю, в ней, без сомнения, есть. Она состоит из нечетных членов последовательности, то бишь из нулей.
Про теорию формальных языков. Можешь посмотреть этот вводный курс http://www.mccme.ru/free-books/pentus/pentus.pdf
Спасибо. Мне нужно как-то алгоритм написать следующий: сначала задаем алфавит, потом правила выборки необходимых подстрок, затем регулярками или еще как получаем слова.
Загвоздка в том, что одних регулярок мне нехватает, т.к. строка у нас не отсортирована, а а слова разделяются разными разделителями. Уже поехал на этой почве и неделю как шизик долблю по мышке и удаляю код, разбрасывая бумаги по комнате
"и" и запятая. там проблема в том, что сложно установить логику за один проход.
допустим:
строка 1: иван, 128 и 30, 2, 3
строка 2: 5 и 6, николай
...
порядок слов в строке практически случайный. есть как бы несколько видов слов, допустим:
1) имя: иван
номер: 128 и 30
код1: 2
код2: 3
2) имя: николай
номер: 5 и 6
код1:
код2:
но.
у нас номер может быть например такой:
А и Б,... , Я
А и Б и С
А
А и С
Б и С
Б
там пиздец короче вариантов. весь алфавит.
мутируешь в бога-задрота. инфа 94 %
>мань
>мань
>бессильные омеганы
>нормального человека
Сам тоже уходишь от сути разговора и переходишь к обсуждению личностей. Ок, погнали.
Проецируешь свою школьную иерархию в до смешного примитивном полярном виде "альфа-омега" на других людей, которые могут даже не знать, что они должны думать так, как хочешь ты.
>ты сам гордишься собой, считаешь, что чего-то достиг?
Достигатор, почему, из всех возможных вариантов, ты выбрал именно математику? Здесь ты не можешь быть "уверен в себе" или "гордиться собой", не можешь предсказать, создашь ли новое знание, решишь ли задачу, или будешь бесплодно блуждать, как поколения доказывателей великой теоремы Ферма.
А, и оф корс, у меня никакой гордости и в помине нет. Как и "достижения" не более чем пустой звук. Я просто занимаюсь, чем хочу.
>"Он крутой, я же тоже могу думать мозгом, почему я не смог сделать то, что он сделал? Нужно больше задрачивать"
Это настолько инфантильно и наивно, что я даже умилился.
До чего всё это на самом деле отвратительно. Жалкие и претенциозные псевдо-биологизаторские ползновения с приведением любви к науке к каким-то альфам и омегам!
Настоятельно рекомендую тебе и подобным тебе товарищам вернуться в родной /sci/.
Не могу.
> Я просто занимаюсь, чем хочу.
А когда тебя тыкают носом "Сосницкий, а где публикации? Ну надо что-то родить, чтоб тебе дали денег на еду", ты как к этому относишься? Просто высираешь никому не нужную хуйню, обобщения ради обобщений, чтоб дали денег? Или ты студентик, которому мамка деньги дает и он думает, что он весь такой охуенный независимый монах?
 28 Кб, 703x499
28 Кб, 703x499В общем осталось сделать замену переменных. Полный квадрат по иксу я вроде выделил. Теперь осталось избавиться от всех кооэфициентов при y, как это лучше сделать?
А есть ли какое то введение в математику в которой еще бы и была философия математики и история?
добавлю. я прост нихуя не понимаю чё это за дроби, кубы и квадраты чисел и нахуй их кто то придумал(а придумал ли? может открыл.) зачем это всё вводили и т.д.
тебя ждет увлекательное путешествие в документалочки под пивас.
https://embedy.cc/movies/UUsrTXI3d2lMc252bWV0bmRMMVRZK0ZsL2JFdE4wWXdnemZydS8ya0hZYz0=
А написанное есть?
Wilderberger на ютубе. У него есть курсы "введение в математику" и "история математики".
Но это тоже видосы, а не письмена, да.
А ешё он странный какой-то
>Wilderberger на ютубе.
>введение в математику"
Это похуй.
>история математики
А вот этим обмааажусь, обмааажусь.
посмотри стэнфордский инструментарий nlp toolkit,, там в опенсорсе все можно подчерпнуть идей
Киселев например
Серр "Курс арифметики"
Как минимизировать барьеры, чтобы всё более-менее последовательно было? По нарастающей?
>Начать с теории чисел
????
Обычно, если начнешь что-то изучать, то там расписано абсолюто все, что нужно из других наук.
Совсем не всё, а только маленькая часть. А для понимая обычно нужна как раз другая часть. Или третья, ты понял. Потому что учебники пишутся для студентов вузов, у которых после этой пары ещё пять по другим областям и предполагается, что ты знаешь необходимое. А я не студент. Ты понял, в общем.
Ничего не понял. Если ты в самом начале пути, то в каждом учебнике все обосновано до последней точки. А если мы говорим не про начальные знания, то тебе не хватит жизни, чтобы выучить хотя бы полный математический кандидатский минимум.
Ну вот анон, в самом начале пути, а какое-нибудь задание под звёздочкой ты не решишь нихуя и не докажешь.
А второе вообще ты зачем меня расстроил блядь грустный кот жпг.
Ты вообще пытался что-то изучать в математике? Все что нужно для глубокого понимания или решени задачи со звездочкой дано в учебнике, где это все и описывается. Не можешь взять производную - знание того, как устроена биекция топологий тебе не поможет.
Ну ни траль. Вот (1+x)^n это же комбинаторика,но это во всём анализе юзается. И число е тоже. И вообще.
И поэтому бином ньютона - одна из первых тем, которая описывается в любом курсе матана.
Я боюсь, что проблема в тебе. Но если ты не хочешь сдаваться, то попробуй почитать те же самые слова в курсе комбинаторики.
> попробуй почитать те же самые слова в курсе комбинаторики.
Так попробовал и сразу всё понял. В том и дело, потому и встал вопрос. Но может во мне, да.
Лол. Спасибо, сенсей. На самом деле спасибо. Я понял.
Как описывается? Знаю только через перестановки. Матан не читал, нахуй он нужен блядь. Топологию нужно учить через симплициальное множество, а никак в учебниках для нубов.
>Матан не читал, нахуй он нужен блядь
Тебе не нужен, другим нужен.
>Топологию нужно учить через симплициальное множество, а никак в учебниках для нубов.
Профит?
Ну через перестановки и описывается.
помогите мне разобраться пожалуйста с задачей,
мне нужно найти площадь треугольника между 3 точками на земле, и у этих точек известны их долгота и широта. Так вот, у меня 2 вопроса:
1.Можно же рассматривать долготу как x-координату, а широту как y-координату и просто с помощью аналитической геометрии найти длины 3 отрезков и потом по формуле Герона найти площадь? То есть, искажений из-за географических координат не будет? Или будут?
2.если так площадь считать можно, то в каких единицах она будет посчитана, если в качестве координат были использованы широта и долгота? В квадратных метрах?
>мне нужно найти площадь треугольника между 3 точками на земле, и у этих точек известны их долгота и широта. Так вот, у меня 2 вопроса:
https://ru.wikipedia.org/wiki/Географические_координаты
Там сферические координаты. И похоже, что треугольник находится на сфере.
Мне кажется от школьной математики вы далеки. Возьмите глобус и поймите, что икс? игрик тут явно не при чем.
С другой стороны, если вы вырежете ваш сферический треугольник(кратчайшее расстояние на сфере, это не прямая, потому что она не принадлежит сфере), то поймете, что распрямить его не получиться. А раз не получиться распрямить, то и площадь будет считаться не очень. А именно бесконечным покрытием маленькими квадратиками. Короче полезут интегралы.
Но я вот нашел вам ссылку, почитать. http://stu.alnam.ru/book_ster-98
Была ли уже новость? Там Начала Эвклида с красивым оформлением вышли на русском.
Вечно меня математики обламывают. Никто так не обламывает как математики.
 13 Кб, 499x90
13 Кб, 499x90О-большое и о-малое.
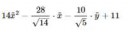 2 Кб, 246x67
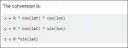
2 Кб, 246x67Помогите пожалуйста, чет туплю уже второй день
Да хуй знает. О-большое, это типа функция, которая в любой точке больше данной (а вообще там f|n| для какого-то n). О-малое - какая-то функция, такая, что f = gh, где g меньше единицы, например. Если предел g стремится к нулю, то f бесконечно малая. Я вообще сам в этом говне не шарю, короче.
ты ошибся
иди почитай про выделение полного квадрата. Тут просто алгоритм и ничего другого, а то, что тебе лень, не значит, что мы должны это делать.
>иди почитай про выделение полного квадрата
Да я много раз уже прочитал
Просто там везде статьи уровня алгебры 7 класса, а тут этот корень из 14
Чем тебя смущает корень из 14? Самое настоящее число. Где алгоритм для 7 класса дает сбой?
Или там приписки есть, что метод не работает если встречается деление на иррациональное число?
Если g(x) не обращается в 0 окрестности точки а и lim x->a f(x)/g(x)=0, то f=o(g), f растёт медленнее g
Если g(x) не обращается в 0 в окрестности точки а и lim x->a f(x)/g(x)=0, то f~g, f растёт так же, как g
f,g:E->R Если существует C>0, такое что |f(x)|<=C|g(x)|, то f=O(g) на E, f растёт не быстрее g.
f=o(g)=>f=O(g)
f~g=>f=O(g)
Если очень огрубить, получится что-то вроде знаков <,=,<=.
 135 Кб, 600x629
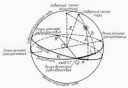
135 Кб, 600x629помогите мне пожалуйста, читаю вывод формулы площади сферического треугольника, и не понимаю, почему из формулы(9) следует (8), потому что если перенести слагаемые с \alpha, \beta, \gamma в (9) влево, то они ведь станут отрицательными, а угол \pi останется положительным, в общем, а в (8) наоборот.Тут что, в выводе формулы ошибка? И если да, то какая из формул является правильной?
 12 Кб, 609x229
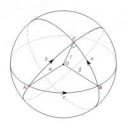
12 Кб, 609x229но в этой книге приведена формула вычисления площади, если известны 3 угла между 3 окружностями, составляющими этот прямоугольник, но ведь я знаю только широту и долготу точек, углы не знаю.
может быть это возможно, перевести географические координаты в декартовы? И если да, то правильны ли формулы перехода на картинке? Тут lat это широта, а lon это долгота. Правильные эти формулы? И после перехода к этим координатам можно найти длины отрезков, используя аналитическую геометрию и по формуле Герона найти площадь? Можно так делать?
Ты определись, тему нужно решить задачу или понять решение?
Если второе, то для начала курс школьной математики изучи, но если так не терпится, то я намекну.
>угол \pi останется
Что мертво умереть не может.
Ну еп твою мать. Формулы правильные, это обвчные сферические координаты, но тебе же уже было сказано - здесь не нужно переходить в декартовы координаты. Так ты найдешь площадь ебучего трехмерного евклидового треугольника, а тебе нужен поверхностный, понимаешь? У него стороны не рямые, соединяющие точку а и б, а дуги, идущие по поверхности.
Что касается углов, то там должно быть описано, как их найти через производную.
 158 Кб, 1280x960
158 Кб, 1280x960 887 Кб, 810x1080
887 Кб, 810x1080Да нормально, классика же. Оформление значительно помогает. Впрочем, это пока версия 0.4
 24 Кб, 495x147
24 Кб, 495x147линейкой
 63 Кб, 1098x433
63 Кб, 1098x433> площадь ебучего трехмерного евклидового треугольника
а если взять только координаты x и y,
и не брать z, то он будет двумерным. Можно так сделать?
> обвчные сферические координаты
точно? почему тогда формулы перехода тут отличаются от тех что в википедии?
>Что касается углов, то там должно быть описано, как их найти через производную.
но в этой книге не написано, как найти углы, тем более, известны лишь долгота и широта 3 точек, и ничего более
Опечатки. Ну, и есть пока не все Начала, а только первые 6 книг об планиметрии.
Чувак, тебе наверное очень весело, но у меня есть занятие поинтереснее, чем кормить толстяка.
А потом спрашивают, почему доска в говно скатилась?
ну блин((
наверное мои вопросы очень глупые, и это выглядит как троллинг, но я просто не понимаю, поэтому и задаю их. То есть нельзя перевести геометрические координаты в декартовы и использовать только х и у? Тогда ведь треугольник плоский получается, а не трёхмерный.
И про нахождение угла сферического треугольника там правда ничего не написано, в тех формулах нахождения площади сферического треугольника углы заранее известны, и я не знаю, как из трёх точек найти углы.
Смотри, чувак, полярная система координат, эта такая вот штука:
Представь себе сферу и точку на границе этой сферы. Ты можешь получить ее координаты по x,y,z. Узнав три эти координаты ты точно можешь определить, где эта точка. Но определить, где точка, можно другим способом. Просто хуяришь вектор от центра координат в этой точке. Каждой точке на окружности соответствует только один такой вектор. Откладываешь проекцию этого вектора на плоскость XY. Угол между осью ОХ и проекцией - первая координата. Откладываешь проекцию этого вектора на плоскость YZ. Угол между осью ОZ и проекцией - первая координата.
Ты точно уверен, что он берется?
Я первый свел к 1/sqrt(sint) и застопорился, потом глянул в гугле, и там говорят, что это эллиптический интеграл.
Короче, может я где-то напутал, но сомневаюсь.
>полярная система координат, эта такая вот штука:
То, что ты описал - этол сферическая.
>>19949
>и это выглядит как троллинг
Когда человеку говоришь, как не стоит делать и объясняешь почему, а он делает именно так - это не выглядит как троллинг, это им и является. Короче вы меня заебали, не доска, а помойка.
>Откладываешь проекцию этого вектора на плоскость YZ. Угол между осью ОZ и проекцией
разве не угол между осью OZ и самим вектором?
в общем, мне теперь понятно, что декартовы координаты тут использовать нельзя.
И есть формула для нахождения площади сферического треугольника, но мне для её использования нужно знать 3 угла между кривыми, составляющими треугольник. Подскажите пожалуйста, как мне их найти, если известны только долгота и широта?
В дифференциальной геометрии есть формула нахождения угла между двумя кривыми на поверхности.
>разве не угол между осью OZ и самим вектором?
Нельзя провести угол между вектором и и осью, аутист.
>я не знаю дифференциальную геометрию
С чего ты взял, что я ее знаю?
алсо, когда я писал ее на шпорах, там было довольно много, даже по меркам математики, символов.
Переводи все три вершины треугольника в (x, y, z).
Потом для каждых двух вершин (x1, y1, z1) и (x2, y2, z2) надо построить нормаль (перпендикулярный вектор) (a, b, c) к кругу, проходящему через эти точки. Это очень просто, потому что скалярное произведение равно 0:
ax1 + by1 + cz1 = ax2 + by2 + cy2 = 0
и нормировка a²+b²+c²=1
Дальше угол между двумя кругами равен углу между их нормалями. Угол между нормалями считаешь опять же через скалярное произведение, которое равно косинусу искомого угла.
>Переводи все три вершины треугольника в (x, y, z).
по формулам из >>19928 ? Да?
>Потом для каждых двух вершин (x1, y1, z1) и (x2, y2, z2) надо построить нормаль (перпендикулярный вектор) (a, b, c) к кругу, проходящему через эти точки.
это как на рисунке >>19925
для двух точек показано? Но так надо сделать 3 раза, да?
>ax1 + by1 + cz1 = ax2 + by2 + cy2 = 0
объясни пожалуйста эту строчку, почему это так? Я имею в виду равенство левой и средней частей. Вот у нас есть отрезок MK например, почему его нормаль будет касательной к кругу, проходящему через эти точки М и К? То есть, к отрезку МК ведь можно построить бесконечно много нормалей, но из чего следует, что эта самая нормаль пересекает(касается) окружности, которая проходит через эти точки?Можешь привести какую-нибудь иллюстрацию? У меня просто с пространственным мышлением беда, поэтому мне это сложно представить((
Спасибо за объяснения.
>Потом для каждых двух вершин (x1, y1, z1) и (x2, y2, z2) надо построить нормаль (перпендикулярный вектор) (a, b, c) к кругу, проходящему через эти точки
А можно и мне объяснить? Зачем нам вектор, перпендикулярный радиус-ектору двух точек?
Вопрос снимается.
Я к вам, может, не оче в тему, но надеюсь всё-таки, что с моим вопросом это самый полезный раздел харкача.
Посоветуйте, пожалуйста, софт (не обязательно, но желательно под прыщи), суть токова: есть таблица данных (2 "входа", 2 "выхода") и есть теоретическая модель из взаимосвязи (вид функции с параметрами) из "простых" операций: +, -, *, /, кв. корень да синус. В общем, мне нужна софтинка, которой на вход даёшь данные и вид функции, ещё могу хорошее первое приближение дать, а она выдаёт параметры, минимизирующие сумму квадратов невязок, причём крайне желательно (скорее всего обязательно, но не уверен), чтобы она использовала как минимум квази-ньютоновские методы (Гаусса-Ньютона, Левенберга-Марквардта), а частные производные вычисляла символически, к.м.к. иначе нихуя не выйдет.
Я такое делал когда-то давно в маткаде, но там было оче неудобно работать с табличными данными, помню, вбивал по уравнению на каждую строку (точку) в Given-блок ручками, либо реализовывал Гаусса-Ньютона "вручную", что тоже не ок.
 35 Кб, 1316x912
35 Кб, 1316x912> по формулам из >>19928 ? Да?
Да.
> это как на рисунке >>19925
Нет, на том рисунке нет нормалей. Нормаль - не касательная к кругу, а перпендикуляр.
Вот тебе картинка: два круга - эклиптика и экватор - и две нормали к ним: северный полюс эклиптики и северный полюс мира. Угол между кругами равен углу между нормалями (обозначен через эпсилон). Кстати, обрати внимание, что нормаль должна быть ориентированная, потому что если одна из нормалей смотрит в южный полюс, а другая в северный, то угол будет 180 - эпсилон.
> левой и средней частей
Это просто сокращенная запись системы
ax1 + by1 + cz1 = 0
ax2 + by2 + cy2 = 0
А решение этой системы называется векторным произведением - https://ru.wikipedia.org/wiki/Векторное_произведение
TensorFlow, Theano, Torch...
--------------------------------------------------
Так как среди исходного набора условий было равенство (первое условие) мы ввели искусственную переменную R1. - во всех случаях так вводится или в каких только?
Приведите решение примера 1, если бы там тоже было равенство.
Анон выручи, могу даже сотку на телефон закинуть
Сдаю бабкину хату.
В банке.
Ну что же вы бэтмэны
спасибо за рисунок, теперь мне более понятно, но
>нормаль должна быть ориентированная, потому что если одна из нормалей смотрит в южный полюс, а другая в северный, то угол будет 180 - эпсилон.
что значит ориентированная? Я имею в виду, ведь перпендикуляр может быть и с одной стороны, и с другой
объясни пожалуйста, как строится нормаль
я имею в виду, вот например на этом рисунке 2 точки Q и R, допустим координаты Q это(x1,y1,z1) и аналогично для R, так вот,
>ax1 + by1 + cz1 = 0
это же произведение точки и нормали, и также для второй, но ведь обе эти точки лежат на одном круге, и одновременно на втором, и мне непонятно ничего, откуда берутся эти нормали.
Я б помог, но уже походу не нужно, лол.
> что значит ориентированная?
то и значит, что с правильной стороны перпендикуляр должен быть. Где правильная сторона - это целое дело, ты лучше сначала почитай про векторное произведение и в какую сторону оно смотрит и почему оно меняет при перемене аргументов местами.
> объясни пожалуйста, как строится нормаль
векторное произведение
> вот например на этом рисунке 2 точки Q и R
Это плохой пример, потому что Q = -R. Нельзя однозначно провести круг через противоположные точки, потому что он проворачивается. Например, через северный и южный полюс проходят все меридианы, а не только один.
> это же произведение точки и нормали
Произведение радиус-вектора и нормали. Нормаль к кругу перпендикулярна радиус-вектору любой точки на круге, кроме центра.
 20 Кб, 356x358
20 Кб, 356x358вот, хорошая картинка
то есть
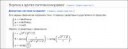
1. Переводим географические координаты в Декартовы. И тут такой вопрос у меня, если южная широта или западная долгота, то при переводе координат нужно эти значения брать с отрицательным знаком?
2. Строим 3 нормали к кругам, через каждый круг проходят 2 точки.
и нормаль получается можно найти двумя способами?
первый через скалярное произведение?
А второй способ через векторное произведение?3. Находим косинусы углов через скалярное произведение
Так?
 101 Кб, 705x455
101 Кб, 705x455(b1b2 −c1a2)x2 +c2b1x3 = b1y2 −a2y1
Что мы приводим там чтобы получить такой результат?
А все понял, там векторный столбик x умножается не так как я думал.
Я по ошибке посчитал что:
R1a2 = b1a2x1+c1a2x1
А на самом деле (правило умножения матрицы):
R1a2 = b1a2x1+c1a2x2
Потом просто подобные взаимоисключаем и все.
1. конечно
2. ну да
Хорошо, что там стрелочки нарисованы - можно попробовать про ориентировку объяснить. Допустим, ты считаешь векторные произведения "вдоль стрелок", то есть [AC], [AB], [BC]. Тогда для углов A и C все хорошо, потому что обе стрелки идут в одну сторону, а в B одна приходит, а другая выходит, поэтому две нормали в разные полюса заедут, одну надо будет взять с обратным знаком.
3. да.
Не забудь, что векторное произведение не обязано иметь длину 1.
Линк с архивами книг удален.
Хотел посмотреть чего советуют ещё аноны, помимо Сканави.
Он пока сложноват для меня. Есть полегче чтиво?
Линк с предыдущими тредами*
О, бля. Тоже метод прогонки смотрел сегодня.
Реквестирую гайды по математике, чтоб всё объяснялось, специально для даунов по темам:
Числовые множества. Арифметические действия над числами.
Вычисления и преобразования выражений.
Функции и графики.
Уравнения и неравенства.
Подкиньте годные уроки по этим темам в гугле забанили
Кстати про шапку. В ней не написано, что читать, чтобы успешно прорешать матфаковские листочки по геометрии для первого курса.
А еще там не написано, что почитать, чтобы решить 27 задачу из Гордина.
Да чего уж там, там ни слова про необходимый багаж знаний для одоления своего первого связанного крючком носка.
M = {a, b, c, d}
P = {(a, a), (a, b), ...} -- все перестановки из M по два элемента.
p(x1, x2) метрика на P. метрика называется Расстоянием Левинштайна. пример:
e1 = (a, b)
e2 = (a, c)
p(e1, e2) = 1
меняем в e1, в втором столбце, "c" на "b", и получаем новый элемент e1`, такой, что p(e1`, e2) = 0. одна операция изменения, поэтому p(e1, e2) = 1.
p[(a, b), (c, c)] = 2 -- две операции изменения.
p[(a, b), (b, a)] = 1 -- поменяли местами элементы столбцов, 1 операция.
найду все точки из P, такие, что расстояние других элементов из P, но не всех, к этим точкам равно 1:
для точки (a, a), это [(a, b), (a, c), (a, d), (b, a), (c, a), (d, a)] --- множество A
для (b, b), это [..., (b, a), (a, b)] --- множество B
для (c, c), ... --- множество С
между множествами точек принадлежащих A и B, есть пересечение. длина пересечения равна 2. между A и C, A и В, тоже двум. и так далее для любых пар множеств. выбранными точками можно "покрыть" все множество P.
теперь, если:
M = {a, b, c, ..., z} -- 26 элементов
P = {(a, a, a, a, a), ...} --- длина строки теперь равна 5
1. как искать точки из P, такие что расстояние других точек из P, к ним не более k. хотя бы, сколько таких точек?
2. построив множества как в предыдущем примере, только уже с расстоянием k, нужно узнать максимальную длину пересечений между этими множествами.
не математик. я не изучал метрические пространства. что читать?
>найду все точки из P, такие, что расстояние других элементов из P, но не всех, к этим точкам равно 1:
найду все точки из P, такие, что расстояние других элементов из P, но не всех,
>выбранными точками можно "покрыть" все множество P.
объединение A, B, C... = P.
Если это матрица над C, то она нильпотентна. Чтобы это увидеть, заметь, что ее характеристический многочлен равен zk.
Забавная ситуация. Матфак не нужен, а геометрия из него почему-то нужна.
Билеты лотереи были выпущены на общую сумму 10000 рублей. Цена одного - 10 рублей. Ценные выигрышы выпадают на 50 билетов. Определить вероятность выигрыша хотя бы на один билет из 5
Я правильно понимаю что нас устроит если от 1-ого до 5-и билетов будут победными? Значит можно посчитать вероятность того что все 5 будут проигрышными и отнять от 1-цы?
Нету такого?
Да. Ты абсолютно прав.
 8 Кб, 712x62
8 Кб, 712x62Да ладно, я видимо какую-то совсем ерунду придумал.
Стоп, а не просто ведь (a^m)/(a^n) = (a^(m-n))?
Тогда ведь по определению. Чего-то затупил. Наверное, на ночь не очень и хорошо заниматься математикой.
Всхожесть семян 85%. Найти вероятность того, что из 300 семян прорастут не менее 250?
Вроде бы на лицо стандартная ф-ла Бернулли, но не менее все портит. Как решить?
Не знаю насчет формулы бернули, но тебе нужна интегральная теорема Муавра-Лапласа .
Поехал я туда из за того что бабушке моей приспичило построить пирамиду из фанерки, ибо в какой то книжке написали что от этого она проживет сто лет и вообще все хорошо будет. Объяснять её что пирамида это обычное платоново тело, частный случай конуса, бессмысленно.
При чем построить её нужно было без гвоздей и металла вообще, иначе фараоны будут недовольны, но это все не так важно.
Так вот, суть была в том чтобы посчитать по каким углом нужно отпилить уголки реек, которые шли как ребра, чтобы они сошлись идеально в вершине пирамиды.
Размеры основания, квадратного, два метра, высота должна была быть полтора метра.
Я считал так. Находим сперва диаметр квадрата по формуле штанов, получилось корень8.
Высота уже есть, тригонометрией находим угол при вершине примадиды. Я насчитал что угол при вершине получается 82 градуса с копейками. А так как нужно обрезать каждую рейку то делим его на два и получаем около 41 градуса. Небольшой допуск в десятую градуса пренебрегаем.
В итоге у меня получилось то что на фото. Додуматься сперва поставить и посмотреть что получилось у меня мозгов не хватило. Я же блять МАТЕМАТИК!!!!!!! а не хачик какой то
Почему у меня не сошлись расчеты? То что я под неправильным углом обрезал не катит, у меня была специальная циркулярка от боша с крутящимся основанием на котором были проградуированы градусы от нуля до 180.
Так все таки, как работать с рядами? Откуда тейлор с маклореном достали свою формулы?
Как ими пользоваться на примере многочлена 6x^4-18x^3+2x-7?
Иди нахуй. Прости. У меня едет крыша. Просто ты тупой. Но ты не виноват. Это я виноват, что выёбываюсь. Но всё же иди нахуй.
 66 Кб, 320x179
66 Кб, 320x179ПИЗДОС. Им дали кольца, им дали гомоморфизмы-стрелочки. Нет, хочу как деды. Уверен ты про пучки не знаешь.
Ты совсем даун? Бери логафирм по основанию 10 из числа, добавляй единицу и округляй в меньшую сторону.
Как пример такой функции - f(x)=1/x, и предел X=+∞.
Коши - так и называется.
Я не ебу вроде целое
В чем вообще смысл делить угол в вершине пирамиды на 2, если у тебя 4 рейки должны сойтись в вершине крестом?
Конечно, неправда. Возьми любой набор рациональных чисел (x_i), который тебе нравится своей взаимной простотой или еще чем, и рассмотри многочлен (x - x_1)(x - x_2)...(x - x_n). Он, правда, не совсем над кольцом (не полем!) целых чисел, но его можно домножить на константу и он станет над кольцом целых чисел.
Вот тебе и многочлен с понравившимися тебе корнями.
а все я уже догнал это конечно не всегда так, но всегда старший коэффициент в таком многочлене будет кратен произведению всех чисел в числителе всех корней
У тебя весь пак пыни есть? Я ещё сюда картинку рисовал, типа 3 уровня /math. Искать в архиве лень, может сохранил ты/кто?
Напомните, почему этот бездарь с индексом хирша 20, считается на сосаче крупным ученым?
наверное потому что это единственный, кто знает о существовании матача
Зачем нужна "дескриптивная теория множеств"?
Вроде современное направление, а зачем оно нужно - не знаю.
Рамануджан не слишком серьезный ученый.
Впрочем, вопрос тут в том, насколько простираются твои амбиции. Если тебя просто прет в свободное время решать задачки, то в чем твоя проблема? Сиди и решай. Если ты откроешь что-то серьезное, то ты это поймешь.
>В том что "работа математиком" появилась в веке так 19-ом. До этого не было тех, кто занимается только математикой. Типа как Ньютон, кароче, открытия сделал но математиком он не был.
Не ври, тогда математика была сильно переплетяна с физикой и другими науками. Люди занимались математикой как могли.
Может ещё до Додекиндора у тебя математиков не было?
Академик РАН, президент Московского математического общества Виктор Васильев указывает, что математическое сообщество негативно относится к индексу Хирша из-за ряда причин и почти не принимает его во внимание. Одной из причин, по мнению Васильева, является то, что у математиков библиометрические показатели традиционно являются существенно более низкими по сравнению, например, с физиками. Также Васильев отмечает, что наиболее цитируемыми математическими публикациями являются публикации в традиционных областях математики, которые не требуют от читателя высокого уровня специальных знаний и часто бывают лишены какой-либо оригинальности. Публикации же в узкоспециализированных областях математики, требующие высокого уровня подготовки от читателя, цитируются значительно меньше: «Скажем, математический логик может иметь в 15 раз меньше цитирований, чем специалист того же уровня, работающий в динамических системах, теории функций или математической статистике»[12].
Но сравнить то его можно с другими дифгемщиками. Да и по его собственным словам это - горячая наука.
Так он же сам топит за физическое приложение.
Например, как ответить за 30 секунд является число 2017 простым или не является?
Не могу ничего придумать, кроме как проверять его признаками делимости до определенного момента(корня из числа).
Спасибо >>20076 - куну за полезный совет.
На этот раз задача, в которой совсем не понятно что искать.
Студент может потратить на решение задачи 10 минут с вероятностью 0.25, 20 минут с вероятностью 0.5 и 60 минут с вероятностью -0.25. Известно, что он потратил на решение задач ровно полтора часа. Случайная величина - число решенных задач.
Действительно непонятен вопрос. И непонятно - дискретная ли случайная величина. Возможно стоит найти вероятность события?
Хотя нет, случайная величина точно дискретная, а вот как выглядит функция распределения - неясно.
Величина, понятное дело, дискретная.
Мое предположение в том что стоит составить ф-ция распределения числа задач. Начиная от допустим 3 задач (60 & 20 & 10) и вероятностью в виде произведения для каждой задачи.
Только вот тогда получается просто перебор и смысл теряется.
И это полтора часа он мог потратить по разному. Либо на решение часовой задачи + 20минутной + 10 минутной, либо вообще 10-минутными потратить решить кучу задач, по 10 минут каждая. Это по факту нам нужно распределить?
Я не автор оригинального поста, просто рассуждаю.
В общем я так понимаю нужно построить функцию распределения количества задач, которые были решены за полтора часа. Решается действительно перебором.
Все равно спасибо за ответ.
Бамп
>60 минут с вероятностью -0.25
Чего чего? За 60 минут решит задачу с вероятность -0.25? Это как вообще?
Я думаю это тире, а не минус.
Да, точно, опечатался, минуса там, разумеется, не может быть.
Открытая математическая проблемма.
Неоднозначный вопрос. Понятно что в программирование и физику ему будет легче вкатиться, чем, например, филологу. С другой стороны в языки и прочую гуманитарщину будет проще тому, кто имел опыт изучения.
Ну и не всегда хороший математик == хороший физик или программист. Например Сатоши Накамото придумал и реализовал гениальную концепцию, однако его код переписывали, потому что с точки зрения программирования там было все криво.
а чтоб пространство римана прошарить, энтропию, фишеровские уравнения и информационную геометрию нужна физика или можно с голым матапаратом ?
Анатолий Тимофеевич, залогиньтесь
Мне почему-то кажется, что как раз в языки математику будет вкатиться проще, потому что он надрессирован на усваивание множества новых понятий и связей между ними. Но это чисто умозрительное предположение, было бы интересно увидеть его подтверждение\опровержение.
приведи к ступенчатому виду и посчитай кол-во не нулевых строк
Почти все профф математики знают английский, а иногда и еще один язык, причем на довольно солидном уровне.
Переводчики-технари же на вес золота, наоборот.
Прости, что усомнился в святом Михаиле.
Теперь я тоже уверовал, и убежден, что его индекса Хирша хватит даже чтобы стать президентом Вселенной.
Ну, английский сегодня знает любой специалист в любой области.
Сегодня как раз читал, что Гамильтон в 12 лет знал 12 языков, но это скорее исключение.
 62 Кб, 613x531
62 Кб, 613x531Для начала, не хотел бы тебя разочаровывать, но 3 в кубе никак не равно 9.
ОДЗ, бля. Почему никто не хочет решать, равносильно преобразовывая? Так же понятнее и проще.
Как считать интеграл лебега?
Скоро экзамен по топологии, я пытаюсь вкатиться в теорию, пока не особо получается
Застрял на когомологиях де Рама, везде в сети примеры не разбираются, а пишется итоговый ответ
В частности, не могу разобраться, как найти H^k(R^2/{a,b,c}), то есть эти самые когомологии для плоскости с тремя выколотыми точками
Вроде как дошел до того, что тогда это Z[x,y,z]/(x^2,y^2,z^2)
потому что это букет трех окружностей, у каждой кольцо когомологий изоморфно Z[x]/(x^2)
Но итоговое решение хуй знает как оформить
Короче, если поможете - с меня как всегда
Верю в вас
В математику нет царских путей.
>А в обратную сторону можно как-то замкнуть R2
Пополняешь его бесконечноудаленной точкой(проективность в общем)
Это получится RP1 и в точки сферы будут отображаться прямые, проходящие через начало координат в R2?
Сам-то понял, что сказал?
Если получился объект, изоморфный сфере, то как он может быть проективной плоскостью?
Олсо, RP1 это окружность.
Сорян, но не очень. Если бы понимал, не было бы и самого вопроса скорее всего. Но тогда я всё ещё не понимаю, как эту блядскую плоскость компактифицировать. Можешь обеснить?
Ладно, прости, я другой анон, а из знаний топологии у меня только полсеместра лекций на лекториуме. Я сам соображал минут 10, прежде чем ответить что к чему.
Но у тебя тут очевидная путаница в понимании проективной плоскости. Ты считаешь, что прямые на обычной плоскости переходят в точки на проективной, но на самом деле наоборот - точки на плоскости переходят в прямые через точку вне плоскости. И вот это множество прямых через точку вне плоскости и является проективной плоскостью.
Чуть выше там анончик говорит про пополнение - это, наверное, самый простой способ, но для пополнения тебе нужна подходящая метрика на плоскости. Без метрики пополнения не бывает.
О, короче, я тут подумал и придумал, как легко обойтись без пополнения. Опять же, я нуб, так что за это доказательство не ручаюсь, но думаю, все правильно.
Добавляешь к плоскости точку, как множество это уже то что тебе нужно, осталось описать топологию. Ну так это очень просто, возьми любую базу исходной топологии R2, и добавь к ней базу в бесконечно удаленной точки, например, все открытые шары вокруг бесконечно удаленной точки - наверное, понимаешь, как их описать.
1) для любых i, j из m: |i-j| >= N
2) размер m максимален
Есть какие-нибудь быстрые решения без перебора всех вариантов?
ну элементарщина же, подумай сам
Раз это многочлен - конечное число ненулевых коэффициентов ряда.
Извините за тупой вопрос.
Кольцо - это что-то типа чисел. Элементы кольца можно складывать и умножать, прямо как числа, а вот делить их друг на друга можно не всегда. Поле - это кольцо, в котором можно делить на любой элемент, кроме нуля. Группа - это когда рассматриваешь множество только с одной операцией, например только со сложением. Поле можно рассматривать как две связанные группы. Группу-сложение и группу-умножение. Пространств бывает много, тебе какое нужно?
Пространство - это то, в чем хотят выделять фигуры, в абстрактном смысле. В векторных пространствах основные фигуры - линейные многообразия, в топологических пространствах основные фигуры - открытые множества.
Спасибо. Я тут открыл для себя такую штуку, как одноточечная компактификация Александрова.
Рассмотрим единичную сферу S2, как подмножество ℝ3 с центром в (0, 0, 1) и подмножество ℝ3 - ℝ2 × {0}. Дополним это ℝ2 × {0} точкой {∞}, отождествлённой с точкой (0, 0, 2) ∈ ℝ3. Потом начнём фигачить проекции из P = (0, 0, 2) на ℝ2 × {0}. Лучи из P будут пересекать сферу однократно. Получим отображение между S2 \ P и ℝ2 × {0}.
Теперь определим отображение F следующим образом:
F(x) = f : S2 \ P → ℝ2 × {0} при x ≠ P
F(x) = g : P → {∞} при х = Р.
Итак, F : S2 → ℝ2 × {0} ∪ {∞} очевидная биекция. Более того, F : ℝ3 → ℝ3 есть очевидный автоморфизм подмножества ℝ3. Проективное пространство тут не получается. Оно получилось бы при отображении фактора сферы в линейное подпространство ℝ3.
Хз, может ерунду написал.
Напиши мне как его расписать, ебана в рот.
Так же как и не понимаю почему экспонента в какой то степени равна икс плюс икс квадрат на факториал два, плюс икс куб на факторал три плюс...
Откуда они взяли такую формулу?
Смотри, ты все правильно пишешь абсолютно, но этого недостаточно.
Ты сейчас описал множество, плоскость, плюс бесконечно удаленная точка, которое биективно с точками сферы. Но этого совсем недостаточно, биекцию между чем угодно можно провести, например, между точками отрезка и плоскости.
Чтобы получить гомеоморфизм, тебе нужно:
1) навесить на эту точку+плоскость топологию
2) найти биективное отображение, непрерывное в обе стороны
Смотри, мне кажется, что ты ищешь не доказательство, а просто хочешь понять что происходит, и поэтому ищешь какие-то интуитивно понятные примеры. Окей, давай я тебе тогда попробую просто объяснить что происходит, без всяких топологий и факторов.
Представь себе, что тебе нужно дополнить плоскость, так, чтобы с ней стало удобней работать. Это можно сделать двумя простыми способами.
1) Просто добавляешь бесконечно удаленную точку, получаешь нечто, гомеоморфное сфере. В комплексном анализе это называется - сфера Римана. Она очень удобна например, потому что в ней многие преобразования координат сводятся к вращению сферы.
НО! Эта штука хороша для комплексного анализа, а геометрически от нее мало толку, ну просто потому что все прямые например начинают пересекаться в бесконечно удаленной точке, ну и какой с этого профит? Поэтому, другой способ - ввести проективную плоскость, то есть дополнить нашу R2 кучей новых точек, а именно, считать, что все параллельные прямые пересекаются в некоей, своей бесконечно удаленной точке, связанной с данным направлением прямой. Это очень удобно; получается, что любые две прямые пересекаются ровно в одной точке, но прямые хуй с ним, а когда ты изучаешь например кривые третьего порядка, то они почти всегда пересекаются с прямой ровно в трех точках проективной плоскости.
То есть сфера и проективная плоскость это два расширения плоскости, каждое из которых удобно для своих целей. Но это я тебе неформально описал, а формально, опять же, ты этот объект должен строго задать, описав топологию. Ты не можешь просто так добавить бесконечно удаленную точку, и сказать, что ты что-то там расширил.
Короче, попытался объяснить, как я это понимаю, может тоже неправильно, лол.
Смотри, ты все правильно пишешь абсолютно, но этого недостаточно.
Ты сейчас описал множество, плоскость, плюс бесконечно удаленная точка, которое биективно с точками сферы. Но этого совсем недостаточно, биекцию между чем угодно можно провести, например, между точками отрезка и плоскости.
Чтобы получить гомеоморфизм, тебе нужно:
1) навесить на эту точку+плоскость топологию
2) найти биективное отображение, непрерывное в обе стороны
Смотри, мне кажется, что ты ищешь не доказательство, а просто хочешь понять что происходит, и поэтому ищешь какие-то интуитивно понятные примеры. Окей, давай я тебе тогда попробую просто объяснить что происходит, без всяких топологий и факторов.
Представь себе, что тебе нужно дополнить плоскость, так, чтобы с ней стало удобней работать. Это можно сделать двумя простыми способами.
1) Просто добавляешь бесконечно удаленную точку, получаешь нечто, гомеоморфное сфере. В комплексном анализе это называется - сфера Римана. Она очень удобна например, потому что в ней многие преобразования координат сводятся к вращению сферы.
НО! Эта штука хороша для комплексного анализа, а геометрически от нее мало толку, ну просто потому что все прямые например начинают пересекаться в бесконечно удаленной точке, ну и какой с этого профит? Поэтому, другой способ - ввести проективную плоскость, то есть дополнить нашу R2 кучей новых точек, а именно, считать, что все параллельные прямые пересекаются в некоей, своей бесконечно удаленной точке, связанной с данным направлением прямой. Это очень удобно; получается, что любые две прямые пересекаются ровно в одной точке, но прямые хуй с ним, а когда ты изучаешь например кривые третьего порядка, то они почти всегда пересекаются с прямой ровно в трех точках проективной плоскости.
То есть сфера и проективная плоскость это два расширения плоскости, каждое из которых удобно для своих целей. Но это я тебе неформально описал, а формально, опять же, ты этот объект должен строго задать, описав топологию. Ты не можешь просто так добавить бесконечно удаленную точку, и сказать, что ты что-то там расширил.
Короче, попытался объяснить, как я это понимаю, может тоже неправильно, лол.
> Чтобы получить гомеоморфизм, тебе нужно:
Это чересчур. Ты можешь просто объявить биекцию изоморфизмом, тогда у тебя сразу и топология, и непрерывность биекции в обе стороны. Компактификация плоскости в сферу так и происходит.
Можешь, но тогда ты получил хуй знает что, у тебя нет никаких гарантий что это сфера.
Просто плоскость плюс точка с какой-то мутной топологией.
Ок, ладно, я погорячился, может тут и легко будет доказать, что это сфера, но это все равно нужно доказывать.
Что делать абитуриенту, чтобы подтянуть математику перед вузом: решать олимпиадные задачки или начинать первый курс ботать?
Еще не взяли, но думаю поступлю, но все равно, мне нравится математика, я люблю ей заниматься, сижу читаю Зорича и получаю удовольствие
Извини. Когомологии - штука интересная, но мне ещё не настолько знакомая, чтобы отвечать на такие вопросы.
Ну вот и занимайся тем, что нравится.
Анон в >>20230 прав так-то. Компактификация Александрова гарантирует вложение, в данном случае плоскости в сферу, но не гомеоморфизм. Вложение не обязано быть гомеоморфизмом целых пространств. Я сам уже достроил отображение до биекции, но с топологией тут какой-то косяк выходит.
Я вообще уже не уверен, что эта задача имеет решение, лол
Хз, пруфануть бы это как-нибудь.
Ладно, не ругайся. Похоже ты прав. Так и сделаю. Ещё раз спасибо.
Стоит там вопросы спрашивать или обольют помоями и проигнорируют так же как тут?
Конечно ответят, там бездуховные буржуи же.
Не то что русская интеллектуальная илита с тифаретника, которая покоряет глубины топологии и теории категорий но при этом не умеет перемножить две матрицы.
>интегрируют.
Но ведь это анализ привлекают.
Я говорю именно про стереометрию, её методами взять и найти объем.
Формальная верификация доказательств?
Я тебе открою ужасный секрет, но например основную теорему алгебры невозможно доказать средствами алгебры.
Не обращай внимание, это первая быдлокультура.
Вот решаешь себе площадь круга, вот тут сразу пи выходит.
Считаешь интеграл на бесконечных пределах, вылезает пи деленное на три.
Считаешь вероятность пересечения иглы линии, хуяк, опять пи.
Что за магия?
Ты ебанулся? Это общеизвестный факт, и он очень смешной, его описывают фактически в любой книге по алгебре с некоторой иронией.
Средствами алгебры нельзя доказать, что любой полином имеет ХОТЯ БЫ один корень в С. Смирись с этим.
Как ты себе вообще представляешь это доказательство без использования непрерывности полинома? Ну разве что впрямую указать, чему равен корень; для n<5 это даже возможно, лол.
Ну это как сказать.
Если у алгебраиста отнять понимание анализа, он это в принципе переживет.
Если у аналитика отнять понимание алгебры (векторных пространств к примеру), то анализ провалится в каменный век.
Another algebraic proof of the fundamental theorem can be given using Galois theory. It suffices to show that C has no proper finite field extension.[9] Let K/C be a finite extension. Since the normal closure of K over R still has a finite degree over C (or R), we may assume without loss of generality that K is a normal extension of R (hence it is a Galois extension, as every algebraic extension of a field of characteristic 0 is separable). Let G be the Galois group of this extension, and let H be a Sylow 2-subgroup of G, so that the order of H is a power of 2, and the index of H in G is odd. By the fundamental theorem of Galois theory, there exists a subextension L of K/R such that Gal(K/L) = H. As [L:R] = [G:H] is odd, and there are no nonlinear irreducible real polynomials of odd degree, we must have L = R, thus [K:R] and [K:C] are powers of 2. Assuming by way of contradiction that [K:C] > 1, we conclude that the 2-group Gal(K/C) contains a subgroup of index 2, so there exists a subextension M of C of degree 2. However, C has no extension of degree 2, because every quadratic complex polynomial has a complex root, as mentioned above. This shows that [K:C] = 1, and therefore K = C, which completes the proof.
> and there are no nonlinear irreducible real polynomials of odd degree
Ну вот я боюсь, что здесь используется непрерывность, а именно, что любой многочлен нечетной степени имеет корень, а значит приводим над R.
Мань, никакая непрерывность в галуа вообще не используется. Это факт для всех алгебраически замкнутых полей, в том числе и для полей ненулевой характеристики, где вообще непонятно что такое "непрерывность".
Я так полагаю, ты тоже завсегдатай бородатого дебила, оперируешь гомологиями, но не в состоянии вычислить объем ящика?
Ну давай, разложи-ка мне x^3-2 на неприводимые в F7.
Это ещё началось с маттредов в /sci/. Один чувак задал непосильную на самом деле детскую задачу про вычисление объёма ящика. Тамошние математики насчитали какую-то хитрую схему про n-мерную сферу при n→∞
Присоединяюсь к вопросу.
У меня аналогичный вопрос про число е. Оно даже интереснее, потому что хуй его знает чем оно такое уникальное.
Это вообще в школе проходят. Но сам ты вряд ли догадаешься. Открой учебник. Это говно через производные выводится.
Я не шучу. Это в каждом сраном рашкинском учебнике есть.
Гауссов интеграл, например, тащемта.
Ну это понятно, а решать то как?
https://arhivach.org/thread/194111/ не благодари.
Ничего особого там на самом деле нет, кроме того, что люди пытаются решить задачу для 9 класса с помощью Вольфрама.
Бамп
>Заходят как-то в бар кун с модулями и анон с калькулюсом томаса. А бармен им с порога ПОМОГИТЕ С ГАУССОМ БОНЕ!
 56 Кб, 606x663
56 Кб, 606x663Господа, а какие существуют теоремы логики второго порядка?
Ну то есть, какая теорема, например, невыразима в логике первого порядка?
НЕ ЛЕЗЬ БЛЯДЬ ДЕБИЛ СУКА ЕБАНЫЙ
Есть два кубика. Вероятность выпадения одно числа на одном кубике равна 1/10. Допустим их кидают по очереди. Вероятность выпадения числа стопицот равна одной десятой для одного кубика.
Но нам нужно узнать какова вероятность выпадения двух одинаковых чисел. Чтобы узнать вероятность выпадения, подумаем что мы выкинули первый кубик на любое число и нам нужно выкинуть второй кубик на то же самое число. Вероятность выпадения все еще одна десятая.
Но у нас вкидываютс одновременно оба кубика. Значит вероятность будет одна сотая. Почему? Потому что для каждо числа каждого кубика выроятность выпадения такого же числа второго кубика равна одной десятой, и мы должны умножить вероятности ибо переббираем варианты ВСЕХ комбинаций чисел.
ДЕБИЛ ЕБУЧИЙ СУКА ТЫ
А ты попробуй посчитать количество всех возможных комбинаций, которые могут выпасть на кубике и количество всех возможных комбинаций-дуплетов.
Количество комбинаций сто, количество дуплетов десять из ста, вероятность одного дубля один из ста.
Пруф ми вронг.
Ни в каком, просто интересно стало, а в теорвере не шарю.
Что-то комбинаторика вспомнилась. Принцип умножения или как там.
45 комбинаций.
комбинации, это когда не важно, выпадет 3, а потом 2, или наборот.
это вероятность определенного дубля: 1/45.
вероятность, что выпадет любой дубль: 10/45
Это нормально как вступ в дискретную математику или есть что по лучше?
А ты кто и чего хочешь добиться?
Ну раз десять из ста равновероятных комбинаций - дуплеты, значит и вероятность дуплета - 10%. Что не так?
>>20330
>>20333
Так нельзя. Если рассматривать "2+3" и "3+2" как одну комбинацию, то нарушается равновероятность комбинаций. В частности выпадение {2, 3} в два раза вероятнее чем выпадение двух девяток.
Алсо почему вопрощающий не был послан нахуй? В интрнете куча материала, это же вопрос из ЕГЭ.
 27 Кб, 129x200
27 Кб, 129x200Формализма много. В доказательствах часто пропущены "тривиальные" шаги (как там? "две пропущенные тривиальности в совокупности могут образовать непреодолимое препятствие"). Никаких заострений внимания на важных моментах в доказательствах. В целом я бы сказал что это интересный трактат по логике, но крайне хуевый учебник.
Прости, но когда ты пытаешься определить что такое доказательство этого не избежать.
Чего не избежать? Хуевой подачи материала?
Учебник должен быть расчитан на еще не подготовленные мозги и на максимальную скорость усвоения. В английском есть слова manual и treatise. Мануал - для чайников, тритайз - для опытных.
Найти себе парня-математика и сосать ему хуй, чтоб он за тебя все делал.
cos -sin
cos sin
Не пойму, если полярные координаты - это rcos, rsin, то откуда у нас берутся сумма и разности синусов?
Поподробней объясни, пожалуйста.
возьми декартову систему координат, возьми другую декартову повернутую на угол /alpha, вырази одни координаты через другие.
Бамп
Ага, математика для начинающих, а не математика для ленивых пидоров, которые хотят чтобы за них делали элементарные вещи.
пример:
Имя ............... Кол-во имен в России
Вова .............. 100000
Боб ................ 10
если ты знаешь таблицу и я тебе назову цифру 10, то ты сможешь сказать, что 10, это Боб. мне не нужно давать левый столбец. тебе нужно только знать что таблица содержит именя.
мне заранее не известна статистика и таблицу я строю так: мне говорят слово, и если оно есть в таблице, то я добавляю +1 к колличеству.
мне называют: Вова
в таблице:
Вова ................ 10 + 1
задача в представлении таблицы таким образом, что бы если ты знаешь статистику имен и тебе дам правую часть таблицы, ты не сможешь сказать это за имя.
проще всего построить таблицу таким образом:
Вова1 ....... 1
Вова2 ....... 1
........
Вова100000 1
Боб .......... 1
я знаю, что нет имен с цифрами, поэтмоу мне не сложно посчитать сколько Вов в России в моей таблице. ты же, зная статистику, уже не сможешь сказать по числу имен, что это за имя.
но этот метод не подходит, так-как таблица получится большой.
забыл сказать: менять число в правой части таблицы нельзя.
пусть максимальное кол-во одинковых имен не больше 3, для примера.
Вова1 .... 30000
Вова2 .... 30000
Вова3 .... 30000
Боб ...... 1
теперь, в зависимости сколько Вась:
Вова1 .... 30000
...
Вася1 .... 30000
Вася2 .... 30000
Боб ....... 1
теперь ты все еще сможешь сказать, что, 1 это Боб, но не сможешь сказать, кто Вася, а кто Вова.
алгоритм. если дано имя name, нас интересует куда его добавить, в name1, name2, name3:
avg -- среднее кол-во имен
x1 - кол-во имен с name1
x2 - кол-во имен с name2
x3
выбрать min {|x_i - avg|}
что бы хоть что-то сказать про этот алгоритм, про то, как хорошо или плохо он прячет инфу, как это сделатЬ?
пусть: если инфу прячет плохо, то я теряю 1 тысячу долларов. если хорошо, то я получаю 1 доллар. могу я выиграть? и речь не про имена, а про любую информацию которая может .
пример:
Имя ............... Кол-во имен в России
Вова .............. 100000
Боб ................ 10
если ты знаешь таблицу и я тебе назову цифру 10, то ты сможешь сказать, что 10, это Боб. мне не нужно давать левый столбец. тебе нужно только знать что таблица содержит именя.
мне заранее не известна статистика и таблицу я строю так: мне говорят слово, и если оно есть в таблице, то я добавляю +1 к колличеству.
мне называют: Вова
в таблице:
Вова ................ 10 + 1
задача в представлении таблицы таким образом, что бы если ты знаешь статистику имен и тебе дам правую часть таблицы, ты не сможешь сказать это за имя.
проще всего построить таблицу таким образом:
Вова1 ....... 1
Вова2 ....... 1
........
Вова100000 1
Боб .......... 1
я знаю, что нет имен с цифрами, поэтмоу мне не сложно посчитать сколько Вов в России в моей таблице. ты же, зная статистику, уже не сможешь сказать по числу имен, что это за имя.
но этот метод не подходит, так-как таблица получится большой.
забыл сказать: менять число в правой части таблицы нельзя.
пусть максимальное кол-во одинковых имен не больше 3, для примера.
Вова1 .... 30000
Вова2 .... 30000
Вова3 .... 30000
Боб ...... 1
теперь, в зависимости сколько Вась:
Вова1 .... 30000
...
Вася1 .... 30000
Вася2 .... 30000
Боб ....... 1
теперь ты все еще сможешь сказать, что, 1 это Боб, но не сможешь сказать, кто Вася, а кто Вова.
алгоритм. если дано имя name, нас интересует куда его добавить, в name1, name2, name3:
avg -- среднее кол-во имен
x1 - кол-во имен с name1
x2 - кол-во имен с name2
x3
выбрать min {|x_i - avg|}
что бы хоть что-то сказать про этот алгоритм, про то, как хорошо или плохо он прячет инфу, как это сделатЬ?
пусть: если инфу прячет плохо, то я теряю 1 тысячу долларов. если хорошо, то я получаю 1 доллар. могу я выиграть? и речь не про имена, а про любую информацию которая может .
Баамп
Там в определении только одна импликация.
Представим, что любой x ∉ данной δ-окрестности. Тогда о каком пределе может идти речь?
Точка, в которой вычисляется предел, должна быть точкой сгущения. Это как-бы необходимое условие (если мы не обсуждаем "предела по базе", у Зорича он вроде так называется).
 2,6 Мб, 3120x4208
2,6 Мб, 3120x4208На пикче 100% где-то есть ошибка, так как я в первый раз решаю подобную ебалу, да и вообще нихера не понимаю в неравенствах (особенно в иррациональных). Скажите что не так.
Всеобщность не подразумевает существования.
Попробуй написать определение предела для функции y=0 в x=0. В качестве эпсилона возьми 1 и замени импликацию на равнозначность.
Вот именно. Когда любой х не входит в δ-окрестность, то что тогда? Ты можешь по-человечески объяснить? Потому что из определения следует, что, когда любой х не входит в δ-окрестность, тогда предел все равно существует.
Еще раз: помимо самого определения предела, есть условие, что точка в которой вычисляется предел должна быть точкой сгущения.
Точка называется точкой сгущения, если в любой ее выколотой окрестности есть хотя бы одна точка из области определения функции.
Не понятен вопрос. Что значит есть ли смысл?
>>20390
Первый переход абсолютно верный, что дальше за говно происходит? Почему минус корень должен быть положительным? Почему ты возводишь в квадрат будто так и надо? Как ты избавляешься от корня. Короче проговори словами, что ты хочешь сделать вторым действием.
Алсо знаешь ли ты значение всех этих скобочек, что наставил?
>>20392
>тогда предел все равно существует
Читай Зорича или что там у тебя раз за разом до полного просветления.
>если в любой ее выколотой окрестности есть хотя бы одна точка из области определения функции
Это высказывание не подразумевает под собой, что в любой выколотой окрестности бесконечное количество точек из области определения?
Зорича вообще невозможно понять, как и Кудрявцева. Пытался по ним учить – ничего не понял. Лоран Шварц во много раз понятнее.
Нет. В некоторых книгах не даётся внятное объяснение этим определениям. Покажи их человеку, который только начал изучать анализ – он не поймёт.
Подразумевает, если мы на R.
>Достижимы, хоть и с большим скрипом.
Ну они и для рядового студента достижимы со скрипом. Олсо я младше 30 - ближе к 20-ти, просто взял с запасом.
Это обычное окрестное определение. И оно намного проще может быть сформулировано. Не понимаю, зачем все эти шторки. Как будто главная задача – это запутать, а не дать знания.
Ну сам Зорич, возможно, считал что это удобно: в одном символе указана область определения, радиус и выколотость окрестности. К тому же это подготовка к символике пределов по фильтру.
Зорич хотел показаться крутым, но обосрался. Кстати, на кой черт U(a)∩E? Что он этим хотел сказать?
 3,7 Мб, 3120x4208
3,7 Мб, 3120x4208Первый правильный, потому что я спросил у препода, что даже не знаю с чего начать решать. Ну она сказала перенести единицу и общий знам найти. Потом спросил, что дальше и она написала эти две системы. Ну я сказал типо все ок, дальше я сам (образец решения вроде был, решал как на пикче, только в этом случае x>0 есть в системе)
1) избавился от минуса умножением на -1
2) там в формуле так написано
3) фигурная скобка - система неравенств.
Наверное мне рано сюда лезть. Надо по-легче неравенства порешать.
Можно и так написать, но у Зорича подход более общий: сначала он берет "базовую" окрестность на R, потом модифицирует ее на E и, соответственно, добавляет значок "E" к символу окрестности.
Ты понимаешь, что новичок просто голову сломает? А у Зорича таких ляпов очень много. Что за подход? Обоснуй подробнее правомочность такого подхода. Ты ведь понимаешь, что над двумя множествами с пересечением можно думать что угодно, и они могут быть не тождественны именно "окрестность точки на области определения".
Я все еще нихуя не понял.
Система написана верно, это я непонятно выразился. Первый переход имелся в виду этот.
вопрос про скобки я задал не просто так. Там же еще квадратные, понимаешь, что они означают?
В общем для начала разберись, как был осуществлен переход к системе первой. Возможно стоит начать с чего-то попроще, но проще этого придумать сложно, разве что уменшить кол-во действий.
Основная идея - равносильные переходы, то есть такие видоизменения, что множество решений не меняется. Ну и метод координат. В неравенствах куда без него.
Вот меня просят найти предел какой то ххитровыебаной функции синуса тангенса от арксинуса деленную на косинус синуса тангенса. Как его искать без помощи матлаба?
Ну вот пример: функция на Q. F(x)=x2.
Теперь мы берем "базовую" окрестность нуля, например U(0)=(-1, 6), корень из 2, например в нее входит. Теперь модифицируем ее и получаем окрестность на области определения F(x), именно: UQ(a)=U(a)∩Q=(-1, 6)∩Q. Корень из двух теперь в нее не входит. Все шаги строго определены.
>Ты понимаешь, что новичок просто голову сломает?
Тут согласен. Формализм ради формализма в обучении не нужен. Я к примеру не студент, могу и потупить пару часов над доказательствами. Студентам же важна каждая минута.
>Что за подход?
Он пытается давать понятия очень общо, и, думается мне, с самого начала хочет затачивать ученика под топологию.
>они могут быть не тождественны именно "окрестность точки на области определения"
Ну в определении это четко написано. Если U(a) - окрестность на R, то U(a)∩E - окрестность на E. По другому и быть не может.
Я вот студент. И из-за чего-то непонятного начинаю жутко баттхердить. Под E тут подразумевается любое множество вообще?
Всём спасибо, всем здоровья.
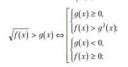 17 Кб, 364x194
17 Кб, 364x194Квадратные объединяют две системы, так как в знаменателе может быть меньше или больше нуля, как я понимаю. Во второй системе появятся еще квадратная и две системы (формула на пикче) В конце надо будет все объединить и узнать чему будет принадлежать x.
>>20418
Дело в том, что 2 месяца назад узнал, что меня не берут в армию после шараги. И так как у меня есть деньги на учебу, а работать идти не хочется, решил пойти на очку в инст. Для этого нужно написать внутренний экзамен. А я бля, последний раз учил матем в 7 классе. Пришлось идти на курсы и вот на 3 занятии дали на дом такую вещь, при этом задачи такой сложности еще не решали.
Эх вы, математики, не помогли ньюфагу, нашёл замечательную книгу от автора Гельфанд - "Алгебра", это именно то, что я искал.
Курсы проводит один инст в моем городе. Предназначены для поступления по внутренним экзаменам, длятся один месяц. Всего 3 предмета, на каждый - 6 занятий, которые длятся по 3 часа.
Нет.
Хотя и так разобрался.
Ну вот в случае с тригонометрией не работает же маняподход "квадрат бесконечно малой меньше чем обычная бесконечно малая"?
Распиши короче что да как.
 131 Кб, 1080x810
131 Кб, 1080x810В интернетах есть разные таблицы с математическими символами. У меня же есть на телефоне клавиатура с ними.
Я понял. Очень очевидно было, да. Спасибо, анон.
Не понял. Если противоречит условию теоремы, то теорема должна быть неверна. Откуда они взяли, что раз отрицание теоремы верно, то верна сама теорема? ¬(a≤b) ≡ a>b
Когда a>b – истина, тогда a≤b – ложь.
Пиздишь!?
Почему тогда формалисты в жопу ебутся чтобы не считать все аналитически а теорией выводить?
Че ты бля несешь???
Есть два способа посчитать предел.
Численный - так считает матлаб и этому посвящены численные методы.
Символьный, аналитический, через теорию, называй как хочешь - это когда ты на бумажке, делаешь 10 преобразований и получаешь общую функцию.
>делаешь 10 преобразований
Считаю икс 0.1, потом 0.001, потом 0.00000001, потом 0.0000000000001, потом....?
Объясните лучше вот
Какой смысл у мнимого корня уравнения?
Что показывает корень уравнения 2х^2+4=0? Решение -2i/2i что показывает?
>Решение -2i/2i что показывает?
в данном случае ничего, ибо даже не является корнем написанного тобой уравнения.
>Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке
Тобишь я правильно понял, нужно брать числа в районе предельной точки и считать с их помощью предел?
Понял только сейчас, разделять корни знаком / это надо еще додуматься. А так 2i,-2i являются решениями для уравнения 2x^2+4=0 надо полем комплексных чисел. Всё.
>Тобишь я правильно понял, нужно брать числа в районе предельной точки и считать с их помощью предел?
Смотря что ты понимаешь под считать. Возьмем последовательность 1/n, и рассмотрим её предел при n стремящимся к нулю, интуиция прдсказывает нам, что предел нуль, берем в качестве предельной точки 0 и проверяем выполнимость определения предела. Всё.
Первый замечательный предел можно же написать как 1/х * син(х). Слева ноль, справа ноль, ноль на ноль будет ноль, не сходится предел в таком виде.
А что показывает действительный корень?
А с чего ты взял, что действия над пределами делаются так же, как и с обычными числами?
> 2i,-2i являются решениями для уравнения 2x^2+4=0 надо полем комплексных чисел. Всё.
Больше ничего извлечь из этого нельзя? Просто решение и все? Глубокого скрытого смысола нету? Пересечение гиперплоскостей шестнадцатого и пятого измерения, топологический дефект четырехмерного графика функции для выбраной точки, нет?
Просто расширение корня на отрицательные числа и ничего более? Про тригонометрическую и показательную форму комплексных чисел я сейчас не говорю.
>Каких преобразований?
Равносильных.
>А разве нет? Почему тогда пишут что можно предел функции умножать на число без опросов?
Ну точно нет, ты сам привел аргумент против. и одно дело умножить но число, а другое умножить на другой придел. Пишут, что лед можно отколупывать ломиком, так почему бы не ебнуть по двери?
>можно же написать как 1/х * син(х)
Написать то можно. Но предел частного определен только в том случае, если знаменатель не обращается в нуль в рассматриваемой точке.
Значит логически нельзя по типу "тридцать пять икс куб делить на семнадцать икс икс квадрат при пределе в нуле.....так так, куб стремится к нулю %быстрее% чем икс квадрат, значит получается что вверху дроби ноль намного меньше чем внизу. А по определению деления бесконечно малых получаем в результате бесконечно малую, тобишь ноль"?
1. Вот эти вот размахивания руками типа стремится быстрее годятся для школы. Есть адекватные способы через свойства лимитов.
2. Да.
>Я их прочитал и не понял
Когда ты говоришь что не понял, полезно для себя понять, что ты не понял. В противному случае, ты либо читал через жопу, либо читал плохую литературу.
Написал же, как вычислять пределы.
Я могу их посчитать вот таким вот "размахиванием руками" как ты сказал и все.
Я помню что читал про порядок роста, деление на самую большую степень, приписку что все элементарные функции непрерывны во всех точках и предел в них численно равен значению функции в точке предела, что разрывных функций по сравнению с непрерывными мало и не нужно себе делать головную боль, но все таки...
 8 Кб, 606x77
8 Кб, 606x77>>20500
Понял все нахуй.
Теорем о трех собачках или о двух милицинерах, если функция ограниченная на всей области определения двумя функциями то она сходится/расходится одновременно с двумя ограничивающими функциями.
можно как-то через определение доказать гомотопическую эквивалентность R^3\R^1 и R^2\R^0, то есть трехмерное пространство без прямой и плоскость с выколотой точкой?
через определение - предоставить два таких отображения, ну вы поняли
алсо, если можно как-то иначе это доказать - тоже пилите
с меня как всегда
На него никто не отвечает, потому что #666?
просто интересно: тебе для дела (универ там или ещё что) или ты просто интересуешься топологией? Мне правда любопытно, зачем люди таким занимаются
А схуяли? Конечное количество членов можно нахуй отбросить. При н = 2 и больше все сходится по верхней грани. То есть в ряде н = 1 до бесконечности должно сходится.
Но пишут именно "сходится или расходится вместе". То есть они не по верхней грани делают.
универ, офк
хотя на самом деле многие считают это наиболее интересной областью математики, а мой пример это уж совсем основы
Дядя Петя, ты дурак?
Признак сходимости применяешь и смотришь, стремится на бесконечности разница соседних членов к нулю или нет.
Берешь даламбера, делишь соседние члены друг на друга, извлекаешь корень бесконечной степени, считаешь интеграл на бесконечности, тупо сравниваешь члены с одинаковом номером с рядом который ты уверен что сходится.
Эта конкретика вообще нахуй не причем здесь.
Какие интегралы нахуй? Это глава по пределам еще. Ты бы блядь еще сказал прибавить 2 и 2 с помощью топологических алгебр нахуй.
Зарегаюсь все таки на матхэксченж, а то что то местные топологи-гополи не могут ни на вопрос ответить, ни ящик посчитать ни матрицы умножить.
ПОЧЕМУ ОНИ ВМЕСТЕ СХОДЯТСЯ ИЛИ РАСХОДЯТСЯ СУУКА?! (Впрочем я уже понял, но все равно интересно, что ты вскукарекнешь на это).
Это должно быть ясно без конкретики.
Злив зарахований.
никак
 372 Кб, 1296x972
372 Кб, 1296x972n → ∞, arcsin(1/n) → 0;
arcsin(1/n) ~ 1/n (следствие первого замечательного)
Имеем ряд Σ (1/n)^n
Можно прогуглить признак сравнения дальше:
Сравниваем с рядом Σ (1/n)^2, который сходится
Далее пишешь: Un = (1/n)^n; Vn = (1/n)^2
Потом пишешь: 0 < Un ≤ Vn ⇒ ряд сходится по первому признаку сравнения
Математика делится на три области, алгебра, геометрия и анализ.
Куда тогда дифференциальную топологию и теорию вероятностей пихнуть?
Но почему? Все же логично. Газ в одну сторону, ракета в другую. Просто в учебнике не объясняется почему. Вот написано, что импульс ракеты за время dt равен (m+dm)×(v+dv)–mv – это понятно. А почему импульс газа за это время равен (dm_газ)×(v_газ)?
Ну, допустим, что за время (t+dt) масса вышедшего газа увеличивается на dm, тогда масса газа становится (m+dm). Так же за это время скорость газа на некотором промежутке времени dt увеличивается на dv, тогда скорость газа становится (v+dv). Тут, мне подсказывает интуиция, закрылась ошибка, ибо скорость не всего вышедшего газа стала равна (v+dv), а только скорость его части, видимо.
У меня такой вопрос: почему изменение импульса газа за время dt = (m_газ×dt)×(v_газ). Почему не аналогично ракете?
Мне требуется ликбез в области правых и левых систем координат.
1) Как задаётся левая система координат в числах ? Можно ли сказать так: "есть левая система координат с базисом abc, где а =1i, b = 1j, c = 1k." Т.е. ijk это правый базис, а abc должен быть левым. Или это сразу ошибка.
2) Зависит ли правость/левость базиса от координат его векторов ? Если я буду случайным образом придумывать базисы, можно ли сказать что иногда получится левый, а иногда правый. Что если получится левый, а интерпретировать я его буду как правый с какими проблемами я столкнусь ? Изменения направления поворотов ?
3) Как перевести из правой СК в левую ? Впрочем в зависимости от ответов на 1 и 2 вопросы, тут я сам разберусь.
В этом месте и проблема. Я не понимаю, почему так происходит. Если только не предполагать, что v_газ = C.
Разбираем по частям тобою написанное.
м - масса ракеты.
дм - это отрицательная величина показывающая насколько уменьшилась масса ракеты
в - скорость ракеты
дв - приращение скорости
в - это расстояние умноженное на время
дв это расстояние умноженное на бесконечно малый промежуток времени
Первые две скобки это изменение импульса ракеты выраженное через изменение массы и скорости улетевшей массы, второе слагаемое это импульс улетевшего газа.
Потом, импульс это сила умноженная на время. Сила по определению это ускорение на массу. Умножение ускорение на время дает скорость. Умножение массы на скорость дает импульс.
И потом, в тексте написанно "нужно добавить импульс газов образовавшихся за время дт." От времени зависит только дм, ведь скорость истечения газов постоянна, а количество выбрасываемо массы выражается линейно, больше времени больше массы.
Я не по, почему второе слагаемое выглядит именно так, вот в чем прикол. Почему оно выглядит на так, например: (m_газ+dm_газ)×(v_газ+dv_газ)?
>Студент, которому для вычисления с десятипроцентной точностью среднего от сотой степени синуса требуется значительно больше пяти минут, не владеет математикой, даже если он занимался нестандартным анализом, универсальными алгебрами, супермногообразиями или теоремами вложения.
Смогут ли местные анализаторы многообразий вычислить сотую степень синуса за пять минут?
> ведь скорость истечения газов постоянна
Воот... Я о том же. Скорость движения газов одинаковая. А в учебнике это не указано. Поэтому я и ломал голову. Значит, моя догадка, что v_газ – это постоянная величина, была верна.
Здесь не нужно вычислять сотую степень синуса. Речь идёт о среднем от сотой синуса. А ты ведь знаешь, что это такое, да?
Нет
Не знаю. Просвещай.
А Вы сказали, что я бред несу. Обидно! Т.е. я правильно понимаю, что импульс газа за время (t+dt) будет равен (m_газ+dm_газ)×(v_газ+dv_газ)? Мне кажется, что тут ошибка есть. Ибо газ – это не твердое тело.
Потому что это сплошная среда.
Потому что скорость истечения газа не может быть переменной. Она может быть РАЗНОЙ при разной скорости подачи газа в камеру сгорания, поэтому зависит от поступающей массы газа.
Т.е. разной, в смысле, зависимой от количества подачи топлива в камеру сгорания? В таком случае, чем больше топлива (в ед. изм. массы) расходуется, тем выше скорость движения газа?
Еще зависит от количества и качества окислителя, объема камеры сгорания, материала сопла, погоды на альдебаране и не забудь про поправку на черта лысого.
В таком случае, я не совсем понимаю действие принципа импульса. Получается, чем больше массы топлива расходуется, тем быстрее движется ракета, но при этом скорость движения газов остаётся такой же? Как это?
>Получается, чем больше массы топлива расходуется, тем быстрее движется ракета, но при этом скорость движения газов остаётся такой же?
Ты дурак? Читай определение импульса.
Импульс это скорость умноженная на массу, производная кинетической энергии. Так что все зависит от массы и от скорости испускания массы. Можно отбрасывать килотонны массы и двигаться с пердячьей скоростью, а можно пару атомов в секунду излучать и двигаться на сверхсветовых скоростях.
> Читай определение импульса.
p=mv
Просто получается, что, поскольку изменение импульса движения газа за время dt = (m_газ)×(v_газ), иными словами, p_газ = (dm_газ)×(v_газ), то, если мы увеличиваем dm_газ, то v_газ остаётся прежним? Но импульс-то увеличивается. Объясните.
*dp_газ
 21 Кб, 467x412
21 Кб, 467x412Как их пересчитать в проекции на оси повернутого базиса если вектор "не поворачивается" вместе с ним, а остаётся в первоначальном положении, относительно оригинального базиса.
Размерность = 3
И в чем проблема опять?
Изменение импульса за единицу времени равно дм х в. По закону ньютона импульс ракеты изменится на столько же со знаком минус.
ИМПУЛЬС увеличивается. А импульс это скорость на массу.
В этом случае импульс увеличивается из за того что уменьшается масса, но увеличивается скорость.
Знаю, но проекции будут скорее не синусом описываться, а каким-то произведением тригонометрических функций в которые должны входить как углы поворота вектора относительно начального базиса, так и углы поворота самого начального базиса.
Если что, у нас есть многообразие М (R^3\R^1), это трехмерное пространство без прямой (допустим, (х,у,0)), есть многообразие N, R^2\0 (плоскость без точки)
Нам нужно для доказательства предоставить два отображения, f (из М в Н) и g (из Н в М)
Я думал, f(x,y,z)=(x,y,0); а g(x,y)=(x,y) {g - тождественное}, но оказалось, что в таком случае f отображение из М в М, а g - из Н в Н.
Как фиксить-то?
если ряд сходится то его общий член стремится к нулю, обратное неверно.
 454 Кб, 1080x1136
454 Кб, 1080x1136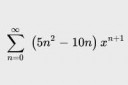 52 Кб, 960x640
52 Кб, 960x640Но ведь ряд расходится, n проходит только целые числа, в формуле n в квадрате и сумма будет равна бесконечности на бесконечности.
хотя не я обосрался, надо подумать
Я не находил ошибок. Просто меня напрягает эта неточность. Я все понимаю, но вот от таких неточностей меня прямо колотить начинает. Может быть я ненормальный. Я не люблю делать такие предположения, которые не оглашены в учебнике, т.к. боюсь усвоить что-либо неправильно.
Если v_отн вектор скорости газа относительно ракеты, то он должен быть направлен в противоположном направлении по отношению к вектору скорости самой ракеты v. Они связаны отношением mdv=(v_отн)×dm. Получается, что mdv – величина положительная, а (v_отн)×dm – величина отрицательная? Это как?
выразить a так, чтобы на одной стороне была a, а на другой какое-то выражение с b, но без а.
короче делаешь +- так чтобы получалось (n+1) в какой то степени перед x^{n+1}
М, нет, все не так. Я забыл, что dm тоже отрицательная величина. Сам нашёл ошибку в своих суждениях. Но спасибо тебе за помощь.
Возможно вы и правы, но я для начала вот это поробую.
https://math.stackexchange.com/questions/338852/find-a-closed-form-of-the-series-sum-n-0-infty-n2xn
ох ебать, чет долго до меня доходило, но теперь я понял, спасибо
И ещё. Как научиться сохранять спокойствие, когда из-за невнимательности начинаешь злиться, а из-за этого ещё хуже идет усвоение материала? Из-за такой-то очевидной ерунды так злился...
Делай намаз 5 раз в день, главное не ведись на всякую восточную хуйню типа медитации.
Мне кажется эффективнее будет узнать у уже поступивших, на что стоит особенно обратить внимание, если есть такая возможность. А так - можно загуглить списки для подготовки к собеседованиям, по твоим темам самое то.
А зачем ты напрягаешься над всякими мелочами, сверяешь там что-то? Так и до дурки недалеко. Главное - чтобы основная мысль была понятна.
>Главное - чтобы основная мысль была понятна.
А потом такие математики ящик посчитать не могут...
Просто в учебнике, по-идее, вся информация должна предоставляться верной. Когда же ты решаешь какую-нибудь фундаментальную задачу собственноручно, тогда действительно лучше все максимально проверить.
Почему не псалмы?
Понимаю что очень невнятно написал, попробую ещё раз. Вот если я написал на бумаге:
i = (1,0,0)
j = (0,1,0)
k = (0,0,1)
И отдал бумагу кому-то другому. Он сможет понять левый это базис или правый ?
Если я, не задумываюсь о левости и правости базисов, буду переводить один в другой строя матрицу перехода как обычно и переведу левый в правый будут ли у меня какие-то проблемы с вычислениями потом ? Возможно ли вообще левый базис перевести в правый ?
Она должна быть понятной, а не "очевидно после небольших преобразований которые легко показать"
Нету там косяков. Просто онон не помнит что дм с минусом, и почему дм зависит от времени а в нет.
Есть такая теория о том что любой многочлен любой степени можно разложить на произведение линейных или квадратных многочленов.
Как её оказать и ею пользоваться?
> Предположение о постоянстве v_отн, очевидно, не затрагивает основные черты явления.
> очевидно
Опять 25! Почему же не затрагивает? Когда из этого следует, что: либо v_газ = const и v = const, либо v и v_газ не постоянны, ибо v_отн = v_газ – v.
УУУУ как же меня уже достало. В остальных учебниках же даже не упоминается это! Ну в чем СМЫСОЛ дифференциального уравнения тогда, если v = const или НИЛЕНЕЙНА БЛЭдб
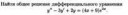 18 Кб, 404x49
18 Кб, 404x49Давай менятся.
Ты мне почему у меня ффмпег кодирует медленно, а я тебе дифференциальные уравнения.
>Перевести можно, нужно только отразить ли одну из координатных осей или все три.
А что значит отразить ? Я правильно понял что обычной матрицы перехода в другой базис не достаточно ? А что будет если как раз просто перевести при помощи матрицы перехода, "забыв", отразить ось ?
Объясните уже, что автор имел ввиду. А то ведь совершенно непонятно. Ведь данное допущение противоречит условиям.
Перепиши что тебе не понятно так чтобы я понял что тебе непонятно. Тобишь со всеми предпосылками из которых ты вывел факт что в книге все неправильно.
Мне уже на dxdy ответили. Автор специально наделал эти ляпы, чтобы упростить выкладки до "школьного" уровня.
>>20648
Изначально предполагается, что скорость газа постоянна, а скорость ракеты нет. Затем, почти в самом конце, делается предположение, что разность вектора скорости газа с вектором скорости ракеты постоянна. Это значит, что, либо скорости газа и ракеты постоянны, либо не постоянны. Противоречие.
Я весь вчерашний день на эту херню потратил, чтобы понять, что же, все-таки, с этим уравнением не так.
> Что за книжка то?
Да это Сивухин гребанный. Чтоб его...
> Читай тогда джанколи.
Для детей ведь.
> Читай, раз другие учебники не понимаешь.
Как оказалось, понимаю, но в некоторых много ляпов и противоречий недавно открыл Ландау-Лифшица, вот ее я понял, т.к. там не было подобных ляпов, но, мне сказали, что пока рановато. И почему-то именно мне они бросаются в глаза. Все же, попробую в следующий раз не вникать в детали и быть смелее в предположениях.
Савельева читаю. Может Матвеева взять? Он как?
Услышало краем уха. Ну имеется в виду есть счетные объединения, а вот кто-то говорил про континуальные.
Для любого множества множеств X существует объединение, независимо от мощности X.
Множество Y называется объединением множества X, если
1. Каждый элемент X - подмножество Y
2. Каждый элемент Y - элемент некоторого элемента X.
Не объединение континуальных множеств, а континуальное объединение.
Счетное, это когда происходит счетное количество объединений, а континуальное?
А, понял.
>Счетное, это когда происходит счетное количество объединений, а континуальное?
Да. Например, X - множество, объединений подможеств, состоящих их одного числа из R.
Я чего-то не так понял? Аноны, поясните, как такое вообще возможно?
Не так, аналитическое продолжение гугли.
У многочлена n-ной степени будет n комплексных корней, соответственно он разлагается в произведение линейных комплексных многочленов. Если тебе комплексные корни не нужны, группируешь сопряженные корни в квадратичные многочлены.
Какой алгоритм я должен соблюдать чтобы разложить любой многочлен в линейные/квадратичные?
Сопряженные корень это корень вида а+_-√(с)?
Утверждается, что есть такой алгоритм?
 85 Кб, 1366x768
85 Кб, 1366x768Пусть p - простое число, большее 3. Покажите, что числитель (максимально сокращенной) дроби
1/1+1/2+1/3+...+1/(p-1) делится на p^2.
Например, если p равно 5, то дробь равна
1/1+1/2+1/3+1/4=25/12 и числитель очевидно делится на 5^2
Это сильно сложная задача? уровень межнара?
Считаю это высказывание глупым подростковым мемом, мешающим реальному процессу обучения при отсутствии наставника. Уже сама необходимость в наличии хороших учителей намекает на то, что готовые ответы и грамотные способы решения заданий/построения доказательств необходимы, если учащийся хочет быстро перейти к интересующим его вопросам науки или математики, а не тратить время на героическое превозмогание давным-давно решенных за него заданий.
Допустим, что учащийся не смог решить некоторые критически важные задания, или дал заведомо неправильные ответы. Тогда он рискует либо потратить время впустую(в лучшем случае), либо получить искаженные знания и навыки, которые в будущем выйдут ему боком, если не обрушат всю карьеру.
>>20640
Алгебра и геометрия вполне употребительны, несмотря на возраст "исходного" учебного материала(учебникам > 100 лет).
>Какой-то просто на многие руки мастер
Это элементарные школьные курсы, не надо быть семи пядей во лбу, чтобы держать их все в уме.
Тогда получатся мемные поцы с ящиком, которые вместо решения задач читали ответы на них и одобрительно кивали.
Это другой тип книг.
ок, но если для школьника, то она сложная?
Арнольдовские задачки это не поможет решить.
Нужно дать скрытый намек на то как решать конкретно эту задачу.
Хорошие, некоторые шизики считают, что систему образования развалили заменив их на другие.
 404 Кб, 500x800
404 Кб, 500x800Если IQ студента > 75, тогда он должен осознавать, что ответы нужны либо для самопроверки, либо в случае, если он не смог решить задачу. Тогда учащийся заинтересован в тщательном изучении ответа и прояснении своих слабых мест.
>получатся мемные поцы
Таким гражданам нужно либо осознать, для чего они вообще читают книгу, либо закрыть её и заняться чем-нибудь другим. Мы же в тематическом разделе, а не в /b/, какой вообще смысл обсуждать дурачков, которые не знают и знать не хотят, как надо учиться?
>какой вообще смысл обсуждать дурачков, которые не знают и знать не хотят, как надо учиться?
Ничего что тут чуть более чем все такие? С гауссом боне сколько помогали? С калькулусом? Решали интеграл на бесконечности? Умножение матриц? И это только то что я сходу вспомнить могу.
 2,2 Мб, 1700x1200
2,2 Мб, 1700x1200Если не знаешь решения, не знаешь математики или не хочешь разбираться в чужих задачах, всегда можно с умным видом порассуждать, как и по каким книгам следует учиться и какой уровень IQ следует считать недостаточным для математики.
Я тоже регулярно не получаю хороших ответов на свои вопросы, только общие фразы, которые с успехом скомпилировал в два поста выше. LMAO
Я не понимаю ее совсем, но мне она очень нужна.
Я не могу решить даже первую олимпиадную задачу 4-5 класса. Это ж пиздец!
Ну давай попробуешь решить. Вот тебе первая задачка для 5 класса районной олимпиады.
Всего лишь три года назад
В три раза был старше мой брат.
Теперь же возраст его
В два раза больше всего.
Дайте, пожалуйста, точный ответ:
Так сколько же брату исполнилось лет?
Ответ скину, когда попросишь
Никакой, возведение отрицательных чисел в степень определено только для целых степеней, чтобы не происходило подобного.
Олимпиадные задачи для 5 класса и настоящая математика - несколько разные вещи. Ты скажи зачем она тебе нужна, а дальше посмотрим.
Ответ верный
В таких случаях по определению на подкоренное выражение навешивается модуль.
Мне надо участвовать в олимпиадах, где есть очный этап в другом городе.
Нужно, чтобы встречаться так с одним человеком.
Ну и еще надо в вуз в будущем поступать не самый плохой и обязательно в другом городе.
Плюс, перевожусь в лучшую школу города прошел отбор под ноотропами - а там математика пригодится
Потому что гугл делает действия последовательно, а не задумывается над их значением. Можешь поменять 4 и 1,25 местами и посмотреть, что получится.
Ты - просто феерический долбоеб, именно поэтому у тебя проблемы с математикой. Надеюсь, что у тебя все будет хорошо и математика тебя вылечит, хотя умные люди говорят, что математик-еблан - не редкость.
Нет, нет, нет. Ты, наверное, не понял. У тебя слабоумие, граничащее с дибилизмом. А если этот самый человек еще и тян, то я сомневаюсь, что ты умнее моего кота, а он сегодня в говне своем уснул.
Неожиданно. Наверное господин выше прав про модуль, но это пиздец как ломает нам деление.
Уходи с этой доски, пожалуйста, у нас нет готового рецпта как шарить математику, кроме задротить 24 на 7. А уродов тут и без тебя хвататет.
Отношений на растоянии не существует, а твоя пизда ничем не отличается от пизды из соседнео подъезда.
Ну вот, ты и дал мне рецепт. Этого я и просил, спасибо.
А закадрить старшекласнницу, да еще и так, чтобы она была готова тебя обеспечивать - это не так уж и легко.
А вот я никогда не задротил математику 24/7, просто слушал учительницу на уроках и делал дз, но все равно как-то удается ее понимать. Как у меня это получилось?
Наверное, дело в том, что школьная математика - это проверка на то, что ты не сильно тупее моего кота, а он, напоминаю, спит в своем говне.
Да и разговор здесь идет не про школу, а про олимпиады, а тут уж, если не напрягаться, дальше районного призерства не уедешь.
А я не съезжу, не поступая в вуз.
И вряд ли я смогу часто с ней видеться, не посещая олимпиады.
Я в школе не напрягался никогда, заслуги слабые. Наскреб призерство шаражных олимпиад, ни одного первого уровня, мой максимум - призерство районной и проход на городскую пару раз. Но я с 6-7 класса учился не по обычной программе. Все всеросы, которых я знаю - звери, которые могут заниматься с утра до ночи.
1. Если ты думаешь, что дорогу куда-то кроме Всероса тебе кто-то оплатит, то ты ошибаешься.
2. Если она готова тебя обеспечивать, то пусть и с жильем поможет.
3. Олимпиад таких, как ты описал за год не так уж и много.
 437 Кб, 621x1000
437 Кб, 621x1000Начинать?
Просто берешь книгу и тетрадь с ручкой/карандашом, просто открываешь книгу, просто вдумчиво читаешь, просто решаешь задания.
А олимпиады... weirdo-tier. Задача >>20716 такая стремная. Если бы вся математика состояла из подобного треша, то я бы держался от неё подальше.
>>20734
>А если этот самый человек еще и тян
А что, с не-тян всё по-другому?
 53 Кб, 750x500
53 Кб, 750x500Ну если он хочет съездить к своему пропавшему отцу-инвалиду или увидеть своего кумира, который в 85 на руках вынес из горящего озера мощи Ленина, то это одно.
Ну а если у него любовь на растоянии, то это другое.
Закроем тему, матемач, а не б.
>Задача такая стремная
5 класс же. Вот тебе 6 класс:
Всего лишь три года назад
В три раза был старше мой брат.
Теперь же возраст его
В два раза больше всего.
Пройдёт ещё время, наступит пора,
И будет брат старше меня вполтора.
Узнать бы хотелось конкретный ответ:
А сколько пройти должно ещё лет?
Помню свой 7 класс, я тогда еще не то, что людей не доебывал в вк, я тогда про двач считай не знал и все в моей жизни было хорошо.
Иди решай, а не пизди.
анон_с_обосраным_котом
 964 Кб, 1357x1700
964 Кб, 1357x1700Меня больше тревожит другое. Если математика ему нужна только ради того, чтобы забить свою шайбу в ворота другому человеку, причем даже не в виде подсчета статистической вероятности успеха любви-по-переписке, то... это плохо для самого математического образования. Оно может даваться ему крайне туго ввиду того, что он не заинтересован в самих знаниях и их применении в реальных задачах.
Ты аутист? Телепаты на пенсии.
Те, которые смогут позволить участникам временное жилье.
Да и вообще любые неплохо. не кенгуру
Вообще, целюсь на ту, которая в иннополисе.
Там просто охуенные комнаты и еще школа математическая как лагерь
Так ты же уже перевелся в другую школу.
Твоя тян в иннополисе? Мамка отпустит? Ведь тебе всего лет 12-14.
Так написано же, математическая школа, как лагерь. Там проводишь полторы недели и 6 часов занятий математикой.
Я там был, лол. Там намного комфортнее, чем дома.
И мама отпустит. А тян еще в 10 учится, но в инно поедет снова на олимпиаду 100%
А тебе сколько? Твоя главная цель встретиться с тян или все же затащить олимпиаду?
Мне тоже 14
Цель - встретиться, скорее.
До нашего знакомства вообще почти не интересовался математикой, поэтому начинаю практически с нуля.
Ну тогда просто найди кого-нибудь, кто затащит затащит заочный этап вместо тебя и едь в Иннополис и проеби очный
как я и сделал в прошлый раз
знаешь, как я затащил отбор? скинул задачи в b и попросил помочь.
То, что в прошлый раз произошло чудо.
Да и мне еще в вуз потом поступать. Хз, максимализм это или нет, но в своем городе я ни за что не останусь.
Лучше раньше начать и потом тащить олимпиады в старших классах.
15к за полторы недели в школе, билеты на поезд, шаурма, нямка в магазе.
Вроде всё
А скинь)
Попробую порешать
 140 Кб, 850x1200
140 Кб, 850x1200> затащить олимпиаду
So edgy statements.
Каков ваш IQ? Я сомневаюсь, что выше двух средних отклонений. Следовательно, вам здесь делать нечего, вам пора вернуться в /un/.
бамп вопросу, открыл пока Рудина. Раз написано, что сжато все изложено в предисловии, то может при первом знакомстве будет нетрудно.
>унач - говно, матач - клас
>рядом тред математических мемов
Может еще и решать будешь кому жить а кому нет?
Насколько мне известно в программу CS различных ВУЗов входит мат анализ, вот я и хочу его изучить вместе с линейной алгеброй. Вот решил тихо начать в своем темпе.
Это такой особый подход к обучению
>пик
Это Пыня после алгебраический геометрии такой уставший? Или пост второкурсника про вротендика его огорчил?
>CS
Английский язык. Must have. Литература по математике на русском языке довольно куцая и в большинстве своём староватая, а по CS и подавно. Начинай сегодня же.
Думаю, не стоит говорить о пререквизитах вроде элементарной алгебры, геометрии, тригонометрии, курсам по теории множеств, логике, математическим доказательствам. Найди их сам. Например так http://www.people.vcu.edu/~rhammack/BookOfProof/
На русском по основам анализа кроме Зорича читать больше и нечего. Но ты можешь на первых порах упороться чем-нибудь полегче, с упором на технику и реальные применения, так называемый calculus. Например вот http://faculty.etsu.edu/knisleyj/calculus/final.pdf или ещё вот http://computo.fismat.umich.mx/~fhernandez/Cursos/Calculo2015/spivak.pdf
По линейной алгебре есть лекции Гельфанда, есть Strang's Linear Algebra and Its Applications. На английском, разумеется. Выбирай что хочешь.
Разумеется, ты можешь забить на скромные подсказки начать с книг попроще, послушать мемных пацанов и сразу начать читать Рудина. Но я не рекомендую этого делать.
Аниме закукарекало, глядите!
Все, пизда. Рыбников тебя засудит за открытие нового элемента русов и сокрытие его в матаче.
>Кенгуру
Оно во всем мире проходит.
Или ты дурной и не смотрел на обложку решебника за прошебший год?
>что он не заинтересован в самих знаниях и их применении в реальных задачах
Даже в /un физикобыдла было меньше. Я вас посылал-посылал, но вас сейчас здест стало слишком много. Я ухожу. Всё засираете, уебки, хуже пидорашек. Здохните, суки.
Ещё аниме-пидор, пиздец просто.
>>20794
Чем тебе Рудин не нравится, уебак? Нормальный, простой учебник + короткий, а не на 2тома хуеты, где открытое множество на 600странице появляется.
Спасибо, анон, за развернутый ответ. Мало приходилось по английским учебникам заниматься конкретно математикой, но надеюсь будет не очень трудно.
Он гавно насоветовал. Бери алгебру из тривиума нму который вёл вербит с калединым, а топологию по учебнику миши, после того как в топологии прочтёшь про открытые-закрытые множества, то открывай Рудина, читай всё, кроме первых трёх глав(определение R и основы топологии и рядов; ты это и так знать будешь).
Забыл. Ещё перед этим пробегись по Шень "Множества". Потом можешь почитывать категории для работающего математика потихоньку.
Отвращение ты испытаешь от бесконечных епсилон-дельт, и описания векторного пространства в виде 100аксиом. Люди не думают эпсилонами-дельтами, а думают "близкие/далекие", суть которого и отражает понятие открытого множества.
>Отвращение ты испытаешь от бесконечных епсилон-дельт, и
Что плохого в дельта-эпсилон технике? Это действительно так сложно для тебя? Я не понимаю тупого форса вокруг неё.
Какой-то чепушила, вроде дмитрия павлого чего-то там вякнул, а тифаретное говно за ним вслед повторяет.
>описания векторного пространства в виде 100акси
Нет, он должен мудели над кальцием знать.
>Люди не думают эпсилонами-дельтами, а думают "близкие/далекие", суть которого и отражает понятие открытого множества.
Близкие-далёкие это и есть эпсилон, мань. А открытое множество отрожает внутри/снаруже.
>Какой-то чепушила, вроде дмитрия павлого чего-то там вякнул, а тифаретное говно за ним вслед повторяет.
Давай самое простое. Как думает человек: функция непрерывна в точке х, если прообразы точек, лежащих близко к f(х), лежат близко к x.
Как думают больные наголову: функция непрерывна в х0, если для любого е>0 найдется такой г>0, что |х0-х| < г => |f(x)-f(x0| < е
Я думаю всем очевидно, что вариант снизу труднее для восприятия.
>Близкие-далёкие это и есть эпсилон, мань. А открытое множество отрожает внутри/снаруже.
чего блядь? ты на солнце перегрелся?
>Давай самое простое. Как думает человек: функция непрерывна в точке х, если прообразы точек, лежащих близко к f(х), лежат близко к x.
>Как думают больные наголову: функция непрерывна в х0, если для любого е>0 найдется такой г>0, что |х0-х| < г => |f(x)-f(x0| < е
Это одно и тоже, только от второй записи больше профита. Я действительно не понимаю, чего тебя так отпугивает в этой записи.
>чего блядь? ты на солнце перегрелся?
Открытое множество отрожает наше представление об лежании внутри, снаржи. Даже внутренность множества - объединение всех открытых множеств множества.
>Разве что для инженеробыдла
А пучкобыду откртые множества подавай. Ты не ответил на вопрос, что тебе не нравится в нём.
>Чего тогда закрытое множество отражает?
Множество, дополнение к которому открытое.
Я это в самом первом посте писал. Люди так не думают. Поэтому ваша определение гавно.
Это формальная запись для подобных мыслей, чтобы можно было что-то измерить, а значит твой аргумент говно.
>Очко своё измерь.
Измерил твоё, у тебя туда большие кардиналы влезают. Также провёл диагностику пучка и он у тебя вялый.
>Математика не про измерения.
Измерения её часть, которые используются во многих теоремах.
Как ты докажешь второй замечательный предел без дельта-эпсилона?
 127 Кб, 794x1114
127 Кб, 794x1114Если я засну на сто лет и когда проснусь меня спросят "что происходит в матх?" я отвечу "Вторая культура бугуртит и таполаги-гамолаги не могут решить задачки первого класса церковно приходской школы"
Значит у дебилов, которые задачки в книжках не решали а пропускали их Я ЖЕ НЕ ПИДОР ЗАДАЧКИ РЕШАТЬ!!!! ЛУЧШЕ ОТОБРАЖЕНИЯ С ИНЪЕКИЕЙ СДЕЛАЮ ПОКА МАМКА НЕ ВИДИТ и решили что они математики дохуя.
Боевая петушиная платформа во всей свое красе.
Может мне в реале еще и интеграл тебе посчитать, или многочлен в ряд разложить, ммм? Диктуй адрес, так и быть приеду и поясню тебе за дельта эпсилон предел.
>Зачем мне его доказывать?
Раз не можешь доказать, то прекрасно видно твой математический уровень. И бугуртишь от дельта-эпсилон техники, потому что не владеешь ей. Мань. Матемотики ни щетают ани устанавливайут изамарфизам.
>Я лучше нассу тебе на ебальник, инжебыдло.
Пучкбыдло, ну не злись, лучше иди пределы решать, хоть математики научишся. А Павлова не слушай, он пидар.
>Ты только ирл стрелки не переводи, а то мигом по еблету схлопочешь.
От такого чмошника и немужчины, как ты?
>>20818
>Я ЖЕ НЕ ПИДОР ЗАДАЧКИ РЕШАТЬ!!!! ЛУЧШЕ ОТОБРАЖЕНИЯ С ИНЪЕКИЕЙ СДЕЛАЮ ПОКА МАМКА НЕ ВИДИТ
В голос.
> дельта-эпсилон техники
Ваще она нужна только чтобы студиозы с каникулярами въехали в суть дела.
Потом можно бесконечно малые ебашить, когда все всё поняли.
>Не траль плз. Первая для любых топ. пространств, вторая нет.
Больше профита в анализе и решение задач.
И вообще, надо идти от частного к общему, а не наоборот.
> Но, разумеется, лучше обмазываться мемами про пучки и дрочить.
А ещё лучше мемами про модули и тифарентиком.
Первый вариант правильный, школьное правило (a^m)^n=a^(mn) нормально работает только для позитивных реальных a.
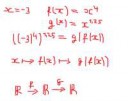 12 Кб, 518x414
12 Кб, 518x414Вот картинка.
Покажи.
 53 Кб, 1024x576
53 Кб, 1024x576Начертить область на комплексной плоскости по данным условиям:
3<|z|<6,
0<arg(z)<3pi/4,
Re(z)<4,
Im(z)<5.
Решение.
Решение неравенства с комплексными числами начинается с представления числа в действительной форме.
Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z дейсвительными переменными x и y, а именно z=x+iy, где x=Re(z), y=Im(z).
3<|z|<6, z=x+iy
3<|x+iy|<6
{|x+iy|<6, => {sqrt (x^2 + y^2) <6, => {x^2 + y^2 = 36
{|x+iy|>3, => {sqrt (x^2 + y^2) >3, => {x^2 + y^2 = 9
Итоговый ответ, область решения - это часть плоскости, расположенная внутри окружностей:
x^2 + y^2 = 36
x^2 + y^2 = 9
Так же ограничиваем область по осям Re(z)<4 и Im(z)<5.
Откладываем угол от 0 до 3pi/4 в соответствии с неравенством 0<arg(z)<3pi/4.
Фото схематичного графика в приложении. Область решения заштрихована карандашом.
Прошу анонов проверить решение задачи.
 53 Кб, 1024x576
53 Кб, 1024x576Начертить область на комплексной плоскости по данным условиям:
3<|z|<6,
0<arg(z)<3pi/4,
Re(z)<4,
Im(z)<5.
Решение.
Решение неравенства с комплексными числами начинается с представления числа в действительной форме.
Чтобы представить комплексное число в действительной форме, нужно заменить комплексную переменную z дейсвительными переменными x и y, а именно z=x+iy, где x=Re(z), y=Im(z).
3<|z|<6, z=x+iy
3<|x+iy|<6
{|x+iy|<6, => {sqrt (x^2 + y^2) <6, => {x^2 + y^2 = 36
{|x+iy|>3, => {sqrt (x^2 + y^2) >3, => {x^2 + y^2 = 9
Итоговый ответ, область решения - это часть плоскости, расположенная внутри окружностей:
x^2 + y^2 = 36
x^2 + y^2 = 9
Так же ограничиваем область по осям Re(z)<4 и Im(z)<5.
Откладываем угол от 0 до 3pi/4 в соответствии с неравенством 0<arg(z)<3pi/4.
Фото схематичного графика в приложении. Область решения заштрихована карандашом.
Прошу анонов проверить решение задачи.
Прочитал. Ничего нового не узнал. Всё время было ощущение, что бьют молотком с наждачной бумагой по голове. Есть что-то ещё?
правильно
>Твой мозг недостаточно развит, чтобы понимать важность основательного и последовательного обучения
Это тебе так препод говорит, давая листок с сотней интегралов?
Как раз путь алгебра-топология-анализ последовательный, а не анализ-анализ-анализ-анализ-топология(огрызок, фундаментальных групп не завезли)-анализ-анализ.
> Как думают больные наголову: функция непрерывна в х0, если для любого е>0 найдется такой г>0, что |х0-х| < г => |f(x)-f(x0| < е
Джвачую. Когда впервые познакомился с этим определением кажется, это был 10 класс, где-то месяц голову ломал над ним. И так нихрена не понял. Пока не познакомился с топологией. Считаю, что сначала должны даваться топологические определения, а затем уже сводиться к таким, как эпсилон-дельта. Ибо от таких определений отвращение к математике и появляются. Они же крайне жестокие и совершенно бесчеловечные. Причём почти ни в одном учебнике не поясняется смысл данного определения.
Чего не так? Ты думаешь в Рудине с 1-ой страницы интеграл Лебега и многообразия? Там всё последовательно. Определение R, немножко топологии, анализ.
>основательного и последовательного обучения
в нём именно всё так.
Если вы считаете что я - мемный поц и только повторяю за вербитом-павловым, то подумайте, не повторяете ли вы за дедами с ваших шараг, или вы просто неосиляторы.
кстати забыл добавить, что в том же рудине епсилон-дельты присутствуют
> Рудин
Там не очень хорошо объясняются некоторые теоремы. Неподготовленному читателю с первых страниц сорвет крышу от абстрактности. Надо все постепенно.
А если в других книжках почти одно и то же? Редко попадается книжка, где тема хорошо изложена. К тому же у каждого автора свой стиль и свое изложение, поэтому зачастую приходится читать книжку с самого начала.
Рыбников Юрий Степанович (15 марта 1955) — исследователь, создатель «Периодической таблицы электроатомов» РУСов, «Единой теории поля», методики построения электроструктур электроатомов, соединившей физику, химию, электричество, счёт РУСов (математику) в единую систему Знаний.
Изобрёл, разработал и внедрил в СССР порошковую полимерную покрасочную технологию.
Преподавал в Московском государственном техническом университете Радиотехники Электроники и Автоматики (МГТУ МИРЭА), доцент.
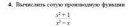 7 Кб, 330x72
7 Кб, 330x72Ну давай, покажи мне что ты не только инъектировать можешь пока мама не видит.
 114 Кб, 863x803
114 Кб, 863x803¯\_(ツ)_/¯
Если человек понятия не имеет, что такое "математический анализ", то Рудин для него пока что мем уровня Коляна Бурбаки. Пусть сначала почитает что-нибудь более приземленное.
К тому же третьего издания на русском языке нет.
Размножаются пучкованием.
Есть теорема: "Доказать, что н.о.к. нескольких чисел делится на их н.о.д.". Можешь привести мне доказательство(с комментариями), могу и в скайпе если что.
>"Доказать, что н.о.к. нескольких чисел делится на их н.о.д."
НОК делится на каждое из двух чисел. А значит, делиться и на НОД.
Да-да. Иди дальше интегралы считай, как посчитаешь все 100штук - так сразу просветление придет, отвечаю. Методика мехмата.
>Показать, что если (a, b) = k, то (a/k, b/k) = 1
По определению - НОД - максимальный общий делитель, больше него общих делителей нет. А значит, числа a/k b/к, подёленные на него взаимнопросты.
Я человек считаейте, что со стороны. И я вот замечаю, что адепты тривиума - неадекватные объебосы.
Алсо я пытался решить из тривиума задачи - эта получилась с ходу.
Оп-пик сменить не забудьте!
Потому что ты не хочешь/не можешь решать задачки и сам не понимаешь смысл своего обучения тапалогий с приабразаваниями.
Нахуя мне тогда с тобой общаться, на доске посвященной математике, если ты только на околоматематические темы можешь общаться, а напрямую показать что ты реально знаешь математику и посчитать какую то задачку уровня второго курса не хочешь/не можешь?
>ты не хочешь
Зис, когда нужно дифференцировать из демидовича, мне становится грустно.
>сам не понимаешь смысл
Понимаю.
>своего обучения тапалогий с приабразаваниями
Я же сказал, что человек, считай со стороны, у меня пока даже нет области интересов, в которой я хоть как-то разбираюсь.
>Нахуя мне тогда с тобой общаться
Но ты продолжаешь это делать, потому что ты ебнутый.
>только на околоматематические темы можешь общаться
Это не я развел срач по поводу того, по какому учебнику нужно учиться, ни сказав ни слова про их мат-сущность.
>посчитать какую то задачку уровня второго курса не хочешь/не можешь
Я же сказал, ее даже я смог сделать в лоб, а я на матане в основном списывал.
Короче в очередной раз убеждаюсь в верности своих мыслей. Триумвиристы - шизики, которые сами занимаются чем угодно, но только не математикой.
Ничего что я кун с калькулусом тотомаса и сейчас высчитываю оптимальную форму для лопастей своего личного ветрогенератора и тривиум упомянул только потому что от него всякие недоматематики рвутся как попкорн в микроволновке?
Что я хотел сказать? Пшел прочь отсюда, собака. Ничего не знаешь а лезешь, нахватался вершков и мнишь себя лобачевским.
 55 Кб, 700x525
55 Кб, 700x525>Ничего что я кун с калькулусом тотомаса
Нихуя не понял. Это болезнь какая-то?
>что от него всякие недоматематики рвутся как попкорн в микроволновке
Сам упомянул, сам порвался.
>Ничего не знаешь а лезешь, нахватался вершков и мнишь себя лобачевским
>я человек со стороны
????? Триумвиристы нева чейнж.
Анон которому ты задал эту задачу. Отвечу.
>сам не понимаешь смысл своего обучения тапалогий с приабразаваниями
Может быть потому что мне это интересно, и топологии-гомологии дают возможность посмотреть на объекты иным взглядом, увидеть какие-то их скрытые свойства? Твоя же задача и им подобные(вычислить стотысячную производную, решить хитровыебаный интеграл) ничего нового не несут, это просто извращение. Их решение настолько же бесполезное занятие, как и решение кроссвордов. Вот ты сейчас размахиваешь №346 сборником кроссвордов и кричишь, что сначала нужно прорешать этот сборник и ещё несколько следующих, и только потом заниматься чем-то осмысленным(хотя бы составлять кроссворды), а если не можешь его прорешать, то ты не готов, глупенький ещё.
>Может быть потому что мне это интересно,
Твои вкусы не уменьшают значимость таких задачь.
> и топологии-гомологии дают возможность посмотреть на объекты иным взглядом, увидеть какие-то их скрытые свойства
Для кого-то и тапалогии-гамалогии скучная и бесполезная вещь. Ты не должен руководстоваться личным вкусом.
>Твоя же задача и им подобные(вычислить стотысячную производную, решить хитровыебаный интеграл) ничего нового не несут, это просто извращение
А алгебраические задачи, вроде подсчёта смежных классов в группе нужны? Или какие-то задачи, связанные с кольцами?
Опять никакой конкретики, только пустопорожний гринтекст. Вот это уровень твоей дискуссии, не выше.
>>20890
Что топология нашла нового в квадрате? А в фрактале? А в везде разрывной функции? А у черта лысого на рогах что обнаружила?
Ба, погодите ка, она ведь только сферами с ручками занимается и покрытиями со стягиваниями.
Я понимаю что рано или поздно физика упрется в то что свойства/законы вселенной зависят от размерности пространства и тут то топология и выстрелит, её даже переведут с множественно-абстрактного на человеческо-доступный язык, чтобы молодые копченые-в говне моченые смогли натягивать сову на глобус и протаскивать провода от модема к центральному серверу где то между седьмым и тринадцатым измерением.
Но то что ты умаляешь тут всю остальную математику, комплексные корни многочленов, сильную теорию больших чисел, площади и объемы на бесконечности, создает такое впечетление что ты занимаешься биекциями с многообразиями только потому что считаешь это модным. Хотя бы потому что эта ваша топология пользуется понятиями и действиями из самых азов математики уровня ясельной группы, которая, по твоему не нужна. Зачем мне учится складывать в столбик если я могу прямо сейчас пойти учится тензорным разложениям? Вот ты сейчас размахиваешь учебников по математике для дошкольников и говоришь что тебе не нужно его, и несколько следующих, решать чтобы заняться чем то осмысленным, например сравнивать часть континуума со всем континуумом
Подсчет классов смежности не есть самоцель в отличие от. И это скучное занятие лишь плата за доступ к чему-то более интересному.
>Подсчет классов смежности не есть самоцель в отличие от.
Разве? С чего ты взял, что взятие интегралов самоцель.
>И это скучное занятие лишь плата за доступ к чему-то более интересному.
То же и про интегралы можно сказать. И что-то интересное тут диффуры.
Можно ли считать дегенератом, не достойным вести дискуссию, любого обитателя матача, если он не в состоянии выучить даже рюсскей?
Не конечно, тут многие на русский кладут болт и учат клятый пиндосский.
Разложим дробь на сумму элементарных.
Получится -1/x + 1/(x-1) + 1/(x+1).
Сотая производная будет, очевидно,
100! (-1/x101 + 1/(x-1)101 + 1/(x+1)101)
И чё?
А алгебра без пучков?
Algebraic K-theory
Topological K-theory
Semi-topological K-theory
Real K-theory
Complex K-theory
Quaternionic K-theory
K theory with coefficients
Connective K-theories
Differential K-Theory
Equivariant K-theory
Hermitian K-theory
Self conjugate K-theory
Twisted K-theory
Twisted differential K-theory
KR-theory
Morava K-theory
2-periodic Morava K-theory
Equivariant Morava K-theory
Integral Morava K-theory
Milnor K-theory
Operator K-theory
KK-theory
Karoubi K-theory
Waldhausen K-theory of a dg-category
Groupoid K-theory
Relative K-theory
K-theory of a bipermutative category
K-theory of a permutative category
K-theory of a stable (∞,1)-category
K-theory of a symmetric monoidal (∞,1)-category
...
Algebraic K-theory
Topological K-theory
Semi-topological K-theory
Real K-theory
Complex K-theory
Quaternionic K-theory
K theory with coefficients
Connective K-theories
Differential K-Theory
Equivariant K-theory
Hermitian K-theory
Self conjugate K-theory
Twisted K-theory
Twisted differential K-theory
KR-theory
Morava K-theory
2-periodic Morava K-theory
Equivariant Morava K-theory
Integral Morava K-theory
Milnor K-theory
Operator K-theory
KK-theory
Karoubi K-theory
Waldhausen K-theory of a dg-category
Groupoid K-theory
Relative K-theory
K-theory of a bipermutative category
K-theory of a permutative category
K-theory of a stable (∞,1)-category
K-theory of a symmetric monoidal (∞,1)-category
...
Алгебраическая и топологическая. А можно в общех чертах о K-функторе.
Дано нечетное простое число p. Доказать: 10 - первообразный корень по модулю p тогда и только тогда, если длина наименьшего периода дроби 1/p в десятичной записи равна p-1.
Я не математик, совсем плаваю. Нашел для примера такое простое число - 7. Получается 0,(142857). Если делить в столбик, домножая остаток на 10, все время получаются разные классы вычетов, потом цикл замыкается. Что с этим делать, не пойму. Пытался понять, как это привязать к конкретному первообразному ключу или найти что-то на эту тему в интернетах, но безрезультатно.
Поможите!
Медики и фармацевтические компании работают над улучшением здоровья человеческого организма.
Программисты улучшают инфраструктуру и веб.
Строители строят сооружения.
Лингвисты помогают развитию языка, тому, чем мы пользуемся практически не останавливаясь.
И только математики занимаются какой-то абстрактной херней, не имеющей никакого отношения к реальной жизни, как и практического применения. (ну максимум для криптографии, но там и не математика, а так, высшая арифметика просто)
Было что-то такое? Что это я мог вспомнить?
Поясните за мемасы на ОП.
Опознал n петуха, рому михайлова, вербита, перельмана и кажется арнольда. Ворон этот наверное мунин. А что за книга с роже посредине? Что за свинья? Зачем петух на картофане c двоичной арифметикой? И что за злобный красноносик?
>Что за свинья?
Хорен создатель /math. Его пидорнули с модерки и забанили за его тупые выходки. Главный рак тут, после вербитоподсосков и форсеров модулей над кольцом.
>Зачем петух на картофане c двоичной арифметикой?
Сиплоглот. >>7203
Есть версия, унижаюшая первокультурщиков. >>11356
> И что за злобный красноносик?
Божидзе.
>и кажется арнольда.
Это Вротендик.
Есть ещё на пике книга - кубические формы Манина, книна для которой требуется знание много облостей математики.
>А что за книга с роже посредине?
Хз.
Спасибо. Когда-то я заходил в ламповый маттред на sci. На тот момент гротендики считали ящик. Так и не знаю, чем закончилось, построили ящик или нет. Спохватился - а тред выпилили, и теперь тут math.
>Так и не знаю, чем закончилось, построили ящик или нет. Спохватился - а тред выпилили, и теперь тут math.
Он в архиваче есть.
Мотидзуки, abc-гипотеза.
Интер-универсальная геометрия Тейхмюллера.
Он просто хикка максимального левела.
Недавно всё-таки вышел на контакт и начал объяснять.
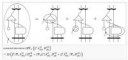 96 Кб, 1125x534
96 Кб, 1125x534Изначально это была covariant derivative в нотации Пенроуза.
https://en.wikipedia.org/wiki/Penrose_graphical_notation
>Я понимаю что рано или поздно физика
Просто пойми, что мне похуй на физику, я срать хотел на приложения.
>комплексные корни многочленов, сильную теорию больших чисел, площади и объемы на бесконечности
Где я говорил, что это нинужно? Кстати, самое простое доказательство основной теоремы алгебры, которое поймет даже 5классник, пришло из алгебраической топологии.
Я устал. Ты передергиваешь. Не хочу дальше отвечать.
 25 Кб, 1014x62
25 Кб, 1014x622 в этом контексте должно восприниматься именно как абстрактное число, а не в качестве записи на письме цифрой в какой-то системе счисления.
другой
Точнее бывает.
Проблемы? Четные простые числа бывают. Я не сказал, что их дофига.
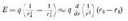 5 Кб, 344x60
5 Кб, 344x60почему там dr и вообще откуда взялось d если интеграла нет
в учебнике никакиз пояснений к этому фрагменту нет
 5,4 Мб, webm,
5,4 Мб, webm,700x394
абсолютно точно польза будет.
В школе так делал, в итоге ничему не научился.
Если хочешь картофан освоить то возможно, но это не самый эффективный метод, имхо в ответы надо глядеть после того как пытался сам решить.
Градиент: показывает в какую сторону скалярное поле растёт быстрее всего, и с какой скоростью. Пример: поле - температура воздуха, градиент показывает куда надо из данной точки бежать, чтоб согреться.
Дивергенция: показывает, куда проёбывается хрень, переносимая векторным полем. Пример: двумерное векторное поле - скорость воды в неком мелком бассейне. Дивергенция будет показывать, где вода прибывает или убывает через дырки в полу.
Ротор: показывает области, вокруг которых векторное поле как бы крутится (сюрприз).
этот вопрос уже задавался в тупых вопросах на sci. и там было несколько интересных ответов и какое-то обсуждение. а здесь математеги типа. и практически тишина. и зачем такой math??
Мне неинтересно отвечать на такой вопрос.
Почему математики такие поехавшие?
Вот сижу себе в бэ, жду пока кто то тренд со смешнявочками создаст, и вижу тред математика в котором он призывает переписать всю программу обучения чтобы все учили многообразия до четвертого класса и после аж до пятого курса дрочить топологию. Почему? Зачем? Как? На эти вопросы нет ответа.
Неужели это компенсация по фрейду того что раньше математику развивали всякие физики с адвокатами, а сейчас, когда математика стала более менее отдельной ветвью науки, современных математиков такое унижает, непонятно почему, и они хотят определять единицу по бурбаки?
Они мемы с тифарентика нахватались. Зайди в мемовый тред, всё сам увидешь.
В чем проблема определять единицу по Бурбаки?
Для справки, по Бурбаки 0 определяется как кардинал пустого множества, 1 определяется как кардинал множества {0}.
что ты хочешь от идиота с ониме?
Берешь и читаешь, переводишь.
Если учил хотя бы в школе, то все пойдет нормально.
Как сказал мой одногрупник, в этих книгах английский - не главная проблема.
> Берешь и читаешь, переводишь.
Прям так сразу, без всего? На это слишком много времени уйдёт.
Задача:
Вычислить интеграл по дуге L от точки z_1 до точки z_2.
Int (z Im(z) dz);
L : x=y^2;
z_1=0
z_2=4+2i.
Решение:
Координаты точек: A(0;0), B(4;2)
y(x)=sqrt(x) - парабола (график в приложении).
Т.к. x_1 < x_2, то необходимо использовать формулу
<<<-- Int {_L} f(x;y)dl = Int {x_1..x_2} f(x;y(x)) sqrt (1+(y'(x))^2) dx
Сначала находим производную и упростим корень.
y'(x) = (sqrt(x))' = 1/2sqrt(x)
sqrt(1+(y'(x))^2) = sqrt (1+(1/2sqrt(x))^2 = sqrt (1+1/4x)
Так как f(x;y)=y и y(x)=sqrt(x), то f(x;y(x)) = sqrt (x) - на данном шаге мы избавляемся от "игреков".
Предварительная подготовка завершена, пользуемся формулой.
Int {L..} ydl = Int {0..4} sqrt(x) sqrt (1+1/4x) dx = Int {0..4} sqrt(x(1+1/4x)) dx =
= Int {0..4} sqrt(x+1/4) dx = 1/2 Int {0..4} (x+1/4)^(1/2) d(x+1/4) =
1/2 2/3(x+1/4)^(3/2) | {0..4} = 1/3 sqrt((x+1/4)^3) | {0..4} = 1/3 ((3+1/4) - (0+1/4)) =
1/3 (13/4 - 1/4) = 1/3 * 12/4 = 1
Ответ: Int {L..} ydl = 1
Задача:
Вычислить интеграл по дуге L от точки z_1 до точки z_2.
Int (z Im(z) dz);
L : x=y^2;
z_1=0
z_2=4+2i.
Решение:
Координаты точек: A(0;0), B(4;2)
y(x)=sqrt(x) - парабола (график в приложении).
Т.к. x_1 < x_2, то необходимо использовать формулу
<<<-- Int {_L} f(x;y)dl = Int {x_1..x_2} f(x;y(x)) sqrt (1+(y'(x))^2) dx
Сначала находим производную и упростим корень.
y'(x) = (sqrt(x))' = 1/2sqrt(x)
sqrt(1+(y'(x))^2) = sqrt (1+(1/2sqrt(x))^2 = sqrt (1+1/4x)
Так как f(x;y)=y и y(x)=sqrt(x), то f(x;y(x)) = sqrt (x) - на данном шаге мы избавляемся от "игреков".
Предварительная подготовка завершена, пользуемся формулой.
Int {L..} ydl = Int {0..4} sqrt(x) sqrt (1+1/4x) dx = Int {0..4} sqrt(x(1+1/4x)) dx =
= Int {0..4} sqrt(x+1/4) dx = 1/2 Int {0..4} (x+1/4)^(1/2) d(x+1/4) =
1/2 2/3(x+1/4)^(3/2) | {0..4} = 1/3 sqrt((x+1/4)^3) | {0..4} = 1/3 ((3+1/4) - (0+1/4)) =
1/3 (13/4 - 1/4) = 1/3 * 12/4 = 1
Ответ: Int {L..} ydl = 1
В мат. литературе хитрого английского нет, разве что, несколько терминов придется перевести.
Ааааа, тебе нужно побыстрее? Идешь в ближайшую аптеку, покупаешь охуин+ и на следубщий день с утра ты доктор МИТ.
Ну, интуитивно кажется для того, чтобы через любой топологический инвариант сходный его кривизну в различных там гауссовой и геодезической, что позволяет вычислить некую кривизну симплекса резольвенты.
Что за ересь
 103 Кб, 640x1136
103 Кб, 640x1136Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
 22 Кб, 265x224
22 Кб, 265x224это пустое множество
>приплюснутая окружность
Не определяет эоллипс конкретно. Как ты нарисуешь нужный для какой то задачи эллис если он определяется у тебя как "слагка попяченая окружность"?
Как найти размеры объекта зная угол под которым я его вижу и расстояние до него? Через синус угла умноженные на расстояние?
> это просто приплюснутая окружность.
Строишь ты на даче прудик и вертолетную площадку.
Как построить эллипс понятно, а вот с твоей окружностью покареженной проблема. И садится на твою дачу вертолет президента, а он смотрит, а у тебя прудик кривой. И улетает вертолет.
Говорят что математика делится на три области, алгебру операции над числами геометрию операции с пространственными объуктами и анализ собственно анализирование образов из двух предыдущих областей.
Так ли это?
Так и есть, причем, анализ из них самая главная.
Нет.
 319 Кб, 640x540
319 Кб, 640x540Разумеется.
Чем занимается современная алгебра геометрия и анализ?
Бампану. Оче уж интересно.
>>21032
Реакция на его анальное засилье в отечественных университетах, видимо.
>>20997
Двачую. Сам удивишься, когда сравнишь художественную англоязычную литературу и популярные англоязычные книги по математике.
>>20982
Поехали от математики, очевидно же. И не просто няшат друг друга в попки, а ещё и других призывают.
Эллипс чертили, втыкая два колышка и привязывая к ним нитку, которая длиннее расстояния между колышками. Натянутая нитка описывает эллипс.
Ушла в себя хочешь сказать?
Математика основывается на логике или логика выводится из математики?
Что главнее короче.
При чем тут физики? Тут же суммирование бесконечно убывающих, грубо говоря ряд.
>бесконечно убывающих
Но тогда, начавшись, движение тут же закончится в точке назначения, ведь сколько ни складывай бесконечно малые, можно сделать их такими маленькими, чтобы умещались в бесконечно малый промежуток времени.
t. школьник Петя
Ну все, значит движение невозможно в принципе.
Задача физическая. Математикам наплювать на движение каких-стрел и какое-то там время с пространством.
Укажет на логическую ошибку в этой апории. Из того, что стрела неподвижна в каждый момент времени, не вытекает, что стрела неподвижна на промежутке.
Тобишь ты станешь отрицать факт того что вся математика держится в прямом смысле на пальцах?
Но просто лежащая стрела тоже неподвижна в каждый момент времени и неподвижна так же на промежутке.
А в Киеве дядька.
О чем ты?
Рыбников уже сделал.
Это официальное деление. Неофициально можешь делить как хочешь, кто же тебе запретит.
Какое нахуй официальное? Это не МИТ, не кембридж и даже не устьпердюйско-суходрищенское пту, а какая то сборочка мутных типов.
 74 Кб, 853x1280
74 Кб, 853x1280Средняя масса пакетов, расфасованных на автомате, равна 1 кг при среднем квадратическом отклонении 3 г. Сколько нужно отобрать пакетов, чтобы с вероятностью 0.95 гарантировать отклонение средней массы отобранных пакетов от 1 кг, не превышающее 0.1%?
меня как всегда
физики просуммируют и получат -1/12 понятное дело
Жёстко туплю с совместными вероятностями.
P(A+B) = P(A) + P(B) - P(AB)
P(AB) = P(A)+ P(B) - P(A+B)
Хочу посчитать вероятность что на двух монетках при одновременном бросании выпадут два орла:
0.5+0.5-0.5*0.5 = 0.75
Где я ступил ?
У тебя какой уровень тервера? Школа, шарага, матфак, книжка 1000 вопроов для умников и умниц?
P(A+B) - выпадение орла хотя бы на одной из монет. Оно происходит в 75% случаев.
Считай P(AB).
 71 Кб, 1366x768
71 Кб, 1366x768>>21065
Всё, разобрался вроде. Это несовместные события, формулы для них неприменимы. Просто я доверился примеру отсюда:
http://self-edu.ru/otp.php?id=2
А пикрилейтед мой Вентцель. Вот что там происходит я не могу понять. Ошибка или нет ?
то b разбивают на степени двойки b=b1+b2+b3... Но почему модуль нужно брать два раза?? В смысле
сперва получаем произведение a^b1(mod x) . a^b2(mod x) etc
а потом результат еще раз промодулить на mod(x)
почему????
Два варианта
Либо рассмотри на маленьких числах и степенях.
Либо распиши по определению в общем случае.
И небольшая подскака. Операцию взятия по модулю можно делать сколько угодно раз, ответ не изменится.
Ага, пофиг на степени, все сводится к умножению, т.е нужно показать что
(a x b) mod C = (a modC x b modC ) modC
а не просто a modC x b modC
Как это в общем виде показать я не знаю, но интуитивно на примере видно что в произведении может получиться число > C отсюда нужно еще раз моd
Стоит почитать про арифметические операции над остатками.
это паста или что? где тут фашисты. такие срачи как раз были в sci /math треде. а здесь даже до срачей не дотягиваемся, очень болото.
Чекай в "Что такое математика?" Куранта и Роббинса
 33 Кб, 665x278
33 Кб, 665x278Тебе стоит начать с книги попроще, где объясняются стандартные обозначения.
Суммирование по всем таким и, что они удовлтворяют данным условиям.
Можешь по фасту пояснить? Ни в одной книге не поясняется значение этих i и неравенств под знаком суммы.
Слышал, но что с них толку то? Это сборище двачематиков никто не контролирует, плюс они, по сути, кучка анонов которых связывает исключительно шкурный интерес.
Эй тапалаг, ну-ка быстро за водкой метнись, Петровичу опохмелиться надо.
Все, я понял, i - это такой индекс для удобства, который показывает, что иксы, обладающие им, распределяются по закону типа: если, например, k=3, а n=4, то
c3 = x1x2x3+x1x2x4+x1x3x4+x2x3x4
Я правильно понял?
Я не понимаю, нахера эти все изъебства с i, больше-меньше, когда можно все проще сделать?
Ты видимо их все прочитал, раз делаешь подобные выводы.
Ну и разумеется все студенты технари, профессоры, инжинеры да и просто любители математики эти знания передают из уст в уста, а если запишешь, то тебя линчуют?
Будто я виноват, что в учебниках ничего не написано по этому поводу. Остается только гадать на кофейной гуще и размышлять методом исключения.
Проиграл с жидопучкиста. В концлагерь, быдло.
Чтобы научить меня как лебезговать нужно на примере обычной функции.
Это копия, сохраненная 13 июня 2024 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
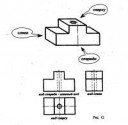






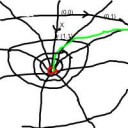







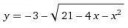

![img1[1].jpg](/math/big/thumb/19020/14964097386230s.jpg)
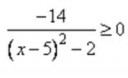











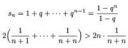




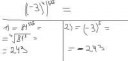







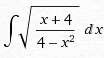
![images[1]](/math/big/thumb/19020/14983531624280s.jpg)