Вы видите копию треда, сохраненную 13 августа в 01:37.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 183 Кб, 610x451
183 Кб, 610x451Приготовь свой алгоритмизациоанал, для аналлизирования различных алго, невъебенных.
Заебатой автоматизированной алгоритмизации-нить, иди.
Что делает эта хуета?
https://github.com/indutny/miller-rabin/blob/master/lib/mr.js#L73
Как вернуть делитель, при помощи алгоритма Миллера-Рабина, ёпт?
Кто-нибудь может расписать агоритм, а то чё-то нихуя не пашет.
В /pr/.
A number of computer scientists have argued for the distinction of three separate paradigms in computer science. Peter Wegner argued that those paradigms are science, technology, and mathematics. Peter Denning's working group argued that they are theory, abstraction (modeling), and design. Amnon H. Eden described them as the "rationalist paradigm" (which treats computer science as a branch of mathematics, which is prevalent in theoretical computer science, and mainly employs deductive reasoning).
Пусть будет, всё равно они никуда отсюда не денутся, так хоть в своём треде пусть прогают, а не по всей доске.
Разница лишь в запуске их той или иной функцией. А дальше - в код смотри, заебал.
>Это тараканы
Заткни ебало своё, прыщавое, и чтобы о "тараканах", я больше не слышал ни здесь, ITT, ни на доске, ни на двоще.
Чтобы ты знал, не так давно, нашли в Париже - Фелисьена Кабугу, который там финансировал https://ru.wikipedia.org/wiki/Свободное_радио_и_телевидение_тысячи_холмов
Там людей тоже тараканами решили поназывать, и дальше уже глянь что получилось там.
Мы программеры, а не тораканы.
А будете, сука, выёбываться,
запрограммируем на вас программизацию программизацию программизациоаналистичную, похлеще вашей математизации математизацианаличной.
>>75552
>Тарканы бегут из токсичного програмача сюда
Тарканы чуть пижже звучит, нежели "тараканы". Аххах.
>а матх-то здесь причём
Да ты заебал. Очевидно, же, что тред о математических алгоритмах. Иди спроси в программаче, как найти делитель алгоритмом Миллера Рабина, или блядь, как посчитать функцию Эйлера, чтобы найти количество первообразных корней по простому модулю.
Тебя там нахуй пошлют, и пойдут дрочить свои фронтендики и бекендики, под пледиком, с кофейком, в тёплом и уютном офисе.
Там нет математиков, и именно математика с её математической логикой, на уровне инструкций - алгоритмизирует автоматизацию информатизианалистичную.
>и чтобы о "тараканах", я больше не слышал ни здесь
ой, всё нахуй иди
>Мы программеры, а не тораканы.
go to /pr finally
>о математических алгоритмах
бред
>ой, всё нахуй иди
Ну ок. А дорогу нахуй покажешь, или сегодня ты пошёл в хуйц?
>go to /pr finally
Ты тупой мочерок, не?
>о математических алгоритмах
>бред
маняматических - фикс.
В разложении отображения в композицию отображений, обладающую рядом специальных свойств.
Ну по сути игра с двумя основными законами алгебры, коммутативностью и ассоциативностью плюс индукция. Хорошо ориентируясь в этой базе, по сути средней школы можно стать очень хорошим программистом.
>swap([1, 2]) -> [2, 1]
>swap([2, 1]) -> [1, 2]
>[2, 1] !== [1, 2]
>swap([1, 2]) !== swap([2, 1])
Если позаниматься программированием, станет довольно очевидно, что точка с запятой, разделяющая команды, - это просто оператор композиции. И появляется большое желание перегрузить этот оператор. Отсюда вылезает хаскель.
а полиморфизм это функтор
Любое множество можно рассматривать как дискретную категорию. Но ты же не это имел в виду, да?
что мы имеем ввиду под коммутативностью? Результат операции.
В результате
----
а = 1
b = 2
swap(a, b)
a = 2
b = 1
----
а = 1
b = 2
swap(b, a)
a = 2
b = 1
--
a = 2
b = 1
==
a = 2
b = 1
Если не важен порядок, то да.
Результат операции swap([], []) - это void.
Поскольку ни один void не должен быть равен другому, swap не коммутативна.
Чем вредна.
Только это не аксиома, а (внематематический) тезис, звучащий как "определение вычислимой функции адекватное".
Лолблядь.
Ты меняешь местами только значения параметров?
Или же ты меняешь местами и сами параметры,
вместе со сменой их значений?
Если второе, то то так, по твоей логике,
можно любую некоммутативную операцию сделать "коммутативной":
То же возведение в степень, например...
Смотри:
2^4 = 4^2 = 16, но 2^5=32 != 5^2=25 - некоммутативная операция.
Пусть: pow(a, b) = a^b;
----
a = 2;
b = 5;
pow(a, b) = 2^5
----
Меняем местами значения переменных:
a = 5;
b = 2;
Теперь, внимание - меняем местами сами переменные:
pow(b, a) = 2^5
----
Вывод: pow(a, b) = pow(b, a) - возведение в степень коммутативно. Ололо.
Ах да, мне померещилось чёт, что он поменял и значения,
в этом вот месте:
>а = 1
>b = 2
>a = 2
>b = 1
но он просто поменял местами значения в результате:
>swap([a, b]) = [b, a]
>swap([b, a]) = [a, b] -> и тут вот поменял на [b, a] = swap([a, b])
То есть, попросту, сделал:
>swap(swap([b, a]))
У него наверно аргументы по ссылке передаются, а сама функция swap ничего не возвращает.
$ \text{программирование} \subset \text{CS} $
 15 Кб, 832x431
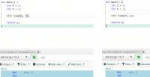
15 Кб, 832x431Т.е. swap это преобразование:
$ swap = {\left({AB} \atop {BA} \right)} $
A переходит в B, B переходит в А.
> Как так получилось, что все эти абстрактные вычислительные машины оказались эквивалентны друг другу.
Потому что описывают одно и то же. Вот только в этой области нет своего Скиннера, который от частной топографии поведения перешёл бы к общему понятию операнта. Средства у нас есть, у нас мозгов нету. Так и живём.
> Почему нет машин, у которых множество вычислимых функций не совпадает с машиной тьюринга и не яаляется подмножетвом?
Потому что вычисление это одно явление, как ты его ни описывай, в итоге получится одно и то же разными словами.
>Потому что описывают одно и то же. Вот только в этой области нет своего Скиннера, который от частной топографии поведения перешёл бы к общему понятию операнта. Средства у нас есть, у нас мозгов нету. Так и живём.
что?
Придумали же альтернативные аксиоматики геометрии, почему нельзя придумать альтернативного, неэквивалентного тому что есть, определение вычисления?
С оракулами есть, вопрос нахуя они нужны.
Из CS?
1) Нет, тамошнЯЯ категорИЯ - не категория.
2) Используются самые-самые базовые понятия. Это как говорить, что ты используешь теорию множеств в решении своей задачи, если тебе нужно найти пересечение или булеан.
3) Теоркат возник естественным образом для обобщения совершенно конкретных идей из алгема и алгтопа, которые 3.1) не имеют аналогов в CS; 3.2) не могут быть поняты типичным программистом просто из-за колоссального порога вхождения (если они потратят пару лет на чистую математику, то может и поймут, но никто так не делает).
>Используются самые-самые базовые понятия. Это как говорить, что ты используешь теорию множеств в решении своей задачи, если тебе нужно найти пересечение или булеан.
Так в алгеоме и алгтопе тоже используются самые базовые понятия из теорката.
> . Это как говорить, что ты используешь теорию множеств в решении своей задачи, если тебе нужно найти пересечение или булеан.
А это и есть использование теории множеств. По прямому назначению. Ты себя читаешь вообще?
>Так в алгеоме и алгтопе тоже используются самые базовые понятия из теорката.
Открой учебник по теоркату для хаскеля и нормальный курс алгема-алгтопа. Те же производящие функторы - это одно из основных понятий современного теорката, они и в помине в CS не используются.
>>75800
Имел в виду аксиоматическую, конечно же. Хотя даже для наивной "подсчёт булеана есть применение теории множеств в программировании" это совершенная поебота.
>Те же производящие функторы - это одно из основных понятий современного теорката
Нет, это из гомологической алгебры. Тогда из функциональные алгоритмы из Хаскеля, использующую категории это тоже понятия современного теорката.
> производящие функторы
https://stackoverflow.com/questions/20336987/what-exactly-does-deriving-functor-do
Так ведь есть же!
Итак, делаем некоторые выводы:
Функторы — это в С++ прежде всего классы с перегруженной операцией (), а потом любые объекты, которые умеют вести себя как функции: это указатели на функции, лямбда-функции и имена функций, но сами функции и ссылки на функции функторами не являются, потому что они в терминах С++ не объекты.
Функторы полезны там, где функции должны вести себя как объекты.
Функторы имеют очень важное значение при использовании стандартной библиотеки шаблонов (STL), а следовательно могут так же широко использоваться в других библиотеках.
В стандартной библиотеке шаблонов (STL) есть некоторое множество предопределённых функторов, и их нужно использовать в предпочтение своим самописным.
Функторы имеют свойсто быть пересылаемыми и присваиваемыми, поскольку они объекты; обычные функции таким свойством не обладают.
Функции, возвращающие булевы значения, называются предикатами. Функторы могут быть и очень часто являются предикатами.
Есть языки, в которых функции это объекты первого класса. Но всё это не о том, это не алгоритмы. Да мейби предикаты только участвуют в алгоритмах но это опять же не первостепенно.
Омерзительно
А можно как-то в виде блок-схемы представить что там творится?
наверно, да
когда нет возможности сопротивляться, надо суметь расслабиться и получать удовольствие..
Жалко только конечно что все следующие математические открытия из CS и теории графов придут
бинарные отношения раздел интегралов под водовку
 118 Кб, 1224x756
118 Кб, 1224x756Теория категорий на переднем крае SJW-наук.
Какой путь необходимо проделать к теории категорий?
математика
13
6
Привет, ЛОР!
Предположим, понравился мне Haskell. Предположим, более-менее я его понял. Начинал я его учить с надеждой, что пойму математику. Ан нет, язык как язык, просто подход необычный.
Поспрашивав людей, я получил ответ, что просто так теорию категорий не выучить. Кто-то сказал, что нужно знать топологию. Кто-то упомянул другие области. А что скажете вы?
Исходные данные: студент второго курса какого-то шаражного вуза, непонятно как ещё не вылетевший. Практически полностью не понимаю матан, чуть лучше дела обстоят с линейной алгеброй и дискреткой, хотя тоже весьма плохо. Да, я тупой. Или ленивый. Или всё сразу. Но хочется исправиться.
Цель: понять теорию категорий и, желательно, применение оной. Ещё желательно было бы изучить как можно больше сфер математики, но это так, мечты.
Что скажете? Какую шикарную литературу по математике вы в своей жизни встречали? Нет ли какой-то волшебной книги по математике, которая охватывала бы все сферы?
долби азы.. abc = cba, a(bc) = (ab)c, почему -(-a) = a итд
>Существуют ли математики-анальники?
нет
среднестатистические тян не добираются до математиков, потому и тезисная психология приматов на них не распространяется. не потому, что она совсем в их случае не верная, а потому что репрезентативная выборка слишком мала (в отличии от тараканов), невозможно разделять её элементы по слишком обобщённым и примитивным критериям
но ты можешь думать, что все вокруг -- одни "анальники", если тебе так нравится. вряд ли обидишь кого-нибудь
>среднестатистические тян не добираются до математиков, потому и тезисная психология приматов на них не распространяется.
Так про анальников не тян, а Фрейд придумал. И тянка тоже может анальницей. Это не что-то привязанное именно к прогерам.
В системно-векторной психологии кроме анального, есть еще уретральный, кожный, мышечный, зрительный, обонятельный, слуховой и оральный типы.
Ему то откуда знать, его фрик-псхологинь_ка рассказала ему только про анальников.
 237 Кб, 475x394
237 Кб, 475x394>В системно-векторной психологии кроме анального, есть еще уретральный, кожный, мышечный, зрительный, обонятельный, слуховой и оральный типы.
"программисты-анальники" это был такой не сильно громкий мем, порождённый какой-то блогеркой-психиатриней, которая любит затирать про аналы и подобное
не помню, как её зовут, но помню то видео про "программистов-анальники", из которого всё пошло
очевидно, запрашивающий анон аппелировал именно к нему, так что я отвечал, на него ориентируясь
Ну так та баба на Фрейда и ссылалась. Типа программисты анальники застряли на анальной стадии развития, когда детьми были или типа того. Не помню уже. Вот интересно, есть ли математики-анальники.
нет, все математики - сверхчеловеки
>Ну так та баба на Фрейда и ссылалась.
в её науке ссылаться больше не на кого
По этой классификации математики являются звуковиками, я думаю.
да похер на неё
видеоблоггер = говно по определению, по-моему
Harpreet Bedi, конечно, исключение, но и видеоблогером его назвать трудно, разве что чисто формально (выкладывал видео)
я просто не знал, что нарцисс это другая часть той же классификации, и потому не понял правильно
я только про анальников слышал
тараканы не палятся
но смешно: он с таким усердием и светимостью рассказывает, какую прекрасную они создали книгу, как будто кто-то будет её читать
Хотелось бы видеть больше книг по современной высшей математике, написанных в более доступной манере. Я уважаю сухой академический стиль, но всё же сложно переоценить простоту и красочность естественного языка при описании абстрактных понятий. Я не имею в виду научно-популярные труды вроде книг Брайана Грина, в которых вообще нет формул. Ведь мой опыт чтения книг по программированию показывает, что даже сложные практические концепции можно наглядно продемонстрировать и пояснить. Также с большим теплом вспоминаю книги вроде «Наглядная геометрия и топология» и издания «Кванта»…
Спасибо за ваш труд, постараюсь выделить время и полистать вашу книгу.
я однажды на ютубе нарвался на некого препода по математике (не профильного, в школе или даже для гуманитариев, не помню), которого все каким-то нездоровом образом массово восхваляют. фишка его заключалась в том, что он очень много кривляется. например, в том видео, где я его увидел, он начал занятие с того, как он смешно изображает, будто спускается по лестнице под парту. и всё в таком духе, а комментарии кричат: если бы меня так учили, я бы любила математику!!
в русском сегменте тоже есть что-то подобное, например, канал "математика без хуйни", на котором автор пересказывает (не в лучших его местах) http://www.mathprofi.ru/, вставляя через слово "блядь"
книги по программированию, написанные для хипстеров - они похожи на брошюры по личностному росту: в них повсюду переливается из пустого в порожнее, обсасывается до невозможности одна и та же мысль, наливается куча воды, у них названия вроде "думай как в джаве" или "философия джава" и они безумно любимы тараканами народом, непонятно за что
Я же считаю, читатель, которого надо развлекать вместо того, чтобы учить, - это неправильный читатель. И нехватка мотивации для читателя - это проблема читателя, а не автора. Я думаю, книга должна быть ясной, точной и короткой.
скажем, по этой причине я не люблю Алуффи, он удивительном образом пишет на высоком уровне и одновременно пытается развлекать читателя, будто тот младенец. Получается не очень
Самая большая наглядность достигается, если реализовать программу. Теоремы в общем-то бесполезны.
>скажем, по этой причине я не люблю Алуффи, он удивительном образом пишет на высоком уровне и одновременно пытается развлекать читателя, будто тот младенец
'Algebra Chapter 0' довольно сухая книга же. Где там развлечения?
 31 Кб, 519x150
31 Кб, 519x150если кто-то считает, что так писать в научной литературе нормально, давайте больше про алуффи не говорить
пиздец ты сухарь, на пике ничего криминального. Культовые авторы аля Арнольд, Хатчер, Лэнг позволяют себе еще более лихие фамильярности.
Арнольд, Хатчер, Лэнг, наверно, нет, но другие иногда позволяют
дело, впрочем, не в одномоментной фамильярности (это ничего), а в том, что у алуффи весь текст более-менее такой (хотя этот пример, конечно, выбивается вперёд). мне трудно объяснить, это на уровне ощущений.
а Ленг мне нравится. строго и по делу
>Лэнг
Take any book on homological algebra, and prove all the theorems without looking at the proofs given in that book.
Homological algebra was invented by Eilenberg-MacLane. General category theory (i. e. the theory of arrow-theoretic results) is generally known as abstract nonsense (the terminology is due to Steenrod).
Зачем, если и этого хватит? Или вот эта хуйня про гомологическую алгебру - это "строго и по делу"?
у лэнга (в 3ьем издании алгебры) гомологической алгебре посвящено почти 100 страниц
именно их я не читал, но, думаю, там всё вполне строго и по делу
>в 3ьем издании алгебры
Это цитата из первых двух изданий. То есть в первых двух изданиях было не строго и по делу, а в третьем стало.
хорошо, если тебе настолько хочется доебаться, давай притворимся, что эти две строчки, обозначенные как "упражнение", уничтожают всё ленгом написанное, превращая это всё в фамильярность и несуразность, мне не жалко, честно
>давай притворимся, что эти две строчки
Давай притворимся, что единственное «шуточное» (но корректное, тем более учитывая, что позже Алуффи конкретней поясняет, что он имеет в виду) определение группы через группоид уничтожает учебник по алгебре на 700 страниц, превращая это всё в фамильярность и несуразность, мне не жалко, честно.
>>77169
Ваши рассуждения больше опираются на эстетику, чем на какие-то объективные метрики. А объективно они оба хороши - и не просто хороши, а на две головы выше среднего. И оба, кстати, экспериментаторы в области стиля и общего тона изложения.
Их тексты не фамильярны, а дружелюбны. Им недостаточно выступить в роли рассказчика, они хотят установить эмоциональный контакт с читателем. И это большая редкость, на самом деле. Несмотря на то, что математика в целом является одной из самых творческих профессий, стилистика математических текстов по какой-то не очень понятной причине чрезвычайно скудна - сказывается то ли доминирование аутистических черт у авторов, то ли выраженный консерватизм сообщества.
>А объективно они оба хороши - и не просто хороши, а на две головы выше среднего.
Я к этому и вел как бы. Что одна хохма на несколько сотен страниц никак не портит книгу, ни в случае Лэнга, ни в случае Алуффи.
На какой странице у Алуффи определяется категория? А на какой функтор? И как именно в книге Алуффи используются сопряженные функторы?
как верно заметил >>77170, алуффи действительно, очевидно, пытается установить эмоциональный контакт с читателем, он, однако, делает это повсюду и лично для меня эти попытки выглядят очень несуразно и топорно. дело не только в этом примере, у него целиком весь текст такой. я выше в первых же своих постах всё обозначил, как я ощущаю, ты пытаешься доебаться до каких-то частностей, мне не совсем понятно, зачем
определение группы через группоид было бы нормальным, если бы оно было выделено в виде короткого замечания где-нибудь в конце в середине, ничего плохого в этой "шутке" нет, просто не надо с неё начинать главу и обильно размусоливать на целую страницу.
втянули меня в какойто бредовый спор непонятно о чём, зачем я отвечаю только
>как я ощущаю
Ну раз ты так ощущаешь.
>ты пытаешься доебаться до каких-то частностей
Могу еще доебаться до того, что по твоим словам «Хатчер не позволяет себе таких фамильярностей». Это при том, что его книжка по алгтопу - настолько «дружелюбная», насколько вообще возможно, сплошной handwaving и визуальные аргументы, а не «строго, коротко и по делу». Так что для последовательности мог бы хейтить и его тоже.
>зачем я отвечаю только
Не знаю, можешь не отвечать.
>>77172
На первые два вопроса можно ответить просто открыв индекс в конце, но ладно: категории на странице 19, функторы на 494. А третий вопрос слишком неконкретный чтобы я мог что-то внятное сказать, ну сопряженность функторов тензорного произведения и Hom он например рассматривает, не знаю, отвечает ли это на вопрос о «как именно».
Как именно - какие теоремы доказываются с использованием этого понятия (или определений, данных с помощью этого понятия).
>>77177
Вообще, я хочу сказать, что Алуффи просто вводит терминологию ради терминологии - иначе бы между определениями категории и функтора не было бы такого разрыва. Содержательных утверждений у него настолько мало, что вся эта терминология остаётся никак не использованной. Зачем было такой абстрактный огород городить, непонятно.
>Алуффи просто вводит терминологию ради терминологии -
Вот тоже так показалось. Что хорошего в 'традиционном' (по факту) подходе (то есть, рассказать кратенько про категории и функторы в курсе алгтопа) - это то, что ты сразу видишь, а нахуя это вообще нужно, потому что функториальность это просто заебенно. А ковыряться в определениях - так себе затея, уровня 'теоркат для cs' высеров (раз уж мы в погромистском трэнде).
>доминирование аутистических черт у авторов, то ли выраженный консерватизм сообщества
Все в месте.
...но никто не знает, в каком(с).
>«строго, коротко и по делу»
я не сказал это про Хатчера, про Хатчера я сказал, он не позволяет себе того что же, что Алуффи, который пытается установить контакт с читателем, прибегая для этого к сомнительным стилистическим приёмам. Хатчер просто пытается понятно объяснить (насколько ему самому кажется, что это понятно)
у меня чувство, ты вообще не читаешь, что я пишу, просто вырываешь из контекста частности и упорно доёбываешься
x / y = 1 / 3
в этом выражении мы можем задать в правой части любое соотношение которое мы хотим получить от x / y и не важно какие там будут величины. Понимаю что выглядит это как хуйня но я чувствую что у этой идеи есть большой потенциал.
не совсем понятно, что ты имеешь в виду, но чувтсвуется, что ты на пороге великого открытия
>x / y = 1 / 3
>3x / y = 1
>3x = y
>y = 3x
>в этом выражении мы можем задать в правой части любое соотношение которое мы хотим получить от x / y и не важно какие там будут величины.
>x / y = 1 / 3
>x = 5
>y = 8
>5/8 != 1/3
а если x / y = 2 / 3 уже всё не так очевидно
Банальный пример про аспект фото, если ширина относится к высоте более чем как два к трём то делаем то-то
Похуй на неочевидность:
>x / y = 2 / 3
>x = 2 / 3 × y
>y = x / (2 / 3)
>y = x × (3 / 2)
Опять же, одна переменная. Так что матан не наебёшь этим.
да
в книге Ж.Арсака есть замечательный вставной фантастический рассказ про ханойские башни
https://zh.b-ok.cc/book/437192/460d68
Спасибо. Выглядит занимательно.
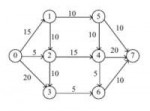
Пик 1 - собственно, граф, пик 2 - таблица, построенная алгоритмом Дейкстры.
Как построить эту таблицу я понимаю. Как по ней получить путь?
 355 Кб, 720x720
355 Кб, 720x720Встаю на колени перед /math/ анонами
Помогите с алгоритмом Калмана. Нужно снизить количество шума. Хочу онлайн обновлять (XYZ) координаты двигающейся точки. В условном пространстве [0:100] в каждом направлении.
Пытаюсь на Питоне реализовать, но что-то второй день не выходит. А теорию изучать СИЛ МОИХ БОЛЬШЕ НЕТ.
Это вероятностный тест числа на простоту. Тебя в википедии забанили?
https://ru.wikipedia.org/wiki/Тест_Миллера_—_Рабина
И как он вычисляется - нихуя не пойму.
Какой-то "bn.mont(n)", "bn(1).toRed(red)" , чё-то неведомое творится ваще. Есть блок-схема?
Ебать, я уже и не помню нахуй мне нужен был этот ебучий делитель.
>02/11/20 Пнд 04:29:04
Там не выполняется деление самого проверяемого числа, там некоторое сконструированное делится НА проверяемое. Ты вообще читал что в вики написано? Там алгоритм - две строки, епт.
 7 Кб, 652x55
7 Кб, 652x55Да блять, ты посмотри в код, что я закинул. Там же фиолетовым по темно-серому написано - getDivisor. А что оно дальше делает - хуй знает. Кракозябры какие-то делает, непонятные.
Я знаю, как работает тест миллера-рабина, на простоту. Но речь шла о более расширенной функции этого алго - о функции getDivisor, которая должна бы, походу, возвращать ещё и делитель. И она его, вроде как возвращает, только как - хуй знает. Блок-схему бы, читабельную.
Анон, тоже пишу фильтр Калмана, но на крестах. Как задаешь шум?
И какую модель движения используешь?
ты кассиром работаешь?
Везде невнятная копипаста с википедии и реализация на псевдоязыке.
пиздец, как же много можно сделать штрихом Шеффера. За годы работы ещё ни разу не понадобилась использовать конъюнкции, дизъюнкции, и негации, нахуя они вообще нужны в реальной жизни?
Заебенил себе даже Стрелку Пирса, из Штрихов Шеффера.
>Любой ГПСЧ с ограниченными ресурсами рано или поздно зацикливается
Тут вроде тоже всё понятно, но я наткнулся на одну штуку, которая похоже нарушает это правило. Решил найти собственно формальное док-во этого утверждения, но чёт не выходит. Помогите найти формальное доказательство.
https://ru.wikipedia.org/wiki/Генератор_псевдослучайных_чисел#Детерминированные_ГПСЧ
там же буквально по твоей ссылке и написано формальное доказательство
Тараканы совсем поплыли, перед своим же носом не видят
там нет подходящего раздела, могу дополнить что с самого начала у меня есть пять объектов А, Б, В, Г, Д внутри каждого есть координаты и велосити где он находится в текущем фрейме и нужно вычислить координаты и направление в следующем фрейме. Поэтому я создаю матрицу где по горизонтали у меня А-Б-В-Г-Д и по вертикали А-Б-В-Г-Д, поэтому в 0,0 у нас столкновение А с А, что нам не нужно, а в 1-0 уже нужное столкновение А с Б. Есть ли способы отрезать треугольник от квадратной матрицы, так как получается что в нём будет дублирующиеся столкновения Б с А и т.д
ну да согласен, чего-то я хуйни какой-то понаписал, прошу прощения.
Кто-то помнит как проделать упражнение из Городенцева, где нужно показать, что на последнем шаге алгоритма Евклида мы получим $НОК(a,b)$?
Ну, то есть мы все возникшие числа в алгоритме Евклида легко можем представить в виде $ax+by$ c целыми $x,y$. На предпоследнем шаге получаем представление $НОД(a,b)$ в таком виде, а на последнем можем и ноль представить точно так же:
$0 = ax+by$ И далее утверждается, что $|ax|=|by|=НОК(a,b)$.
Ковыряясь в коэффициентах в общем виде становится понятно, что на каждом шаге коэффициенты $x_i,y_i$ при $а,b$ взаимно просты. А значит и на последнем шаге коэффициенты $x,y$ тоже взаимно просты и тогда все доказано.
Проблема в том, что не вполне ясно как доказать взаимную простоту коэффициентов на каждом шаге, индукцией не получается, вот тут у чувака та же проблема, но ему банальщину затирает ответчик: https://math.stackexchange.com/questions/3784896/least-common-multiple-in-euclidean-algorithm
>Детерминированные_ГПСЧ
>Детерминированные
>Детерминированные, БЛЕАТЬ.
https://ru.wikipedia.org/wiki/Детерминизм
Короче, смотри. Если ГСПЧ имеет какое-либо состояние, то состояние ДО этого, является причиной этого состояния.
ДО, значит, чуть раньше во времени.
Любое состояние, ГСПЧ, какое не возьми, имеет состояние ДО этого, а значит любое значение на выходе ГСПЧ, имеет причину,
и ГСПЧ не может выдать истинно случайные числа.
И вообще, любое состояние, любого генератора, имеет состояние ДО этого, то есть, хотя-бы на одну единицу планковского времни предшествующее ему,
а значит ни один генератор не может выдать случайные числа.
Если конечно, эти состояния не появляются откуда-то извне времени, то есть спонтанно,
как появилась, вне времени, планковская эпоха, например, потому что ДО планковской эпохи,
не было другого планковского интервала времени, время появилось в планковскую эпоху.
Ну так вот, если время, на самом деле, комплексное, как говорил Стивен Хокинг,
здесь: https://ru.wikipedia.org/wiki/Мнимое_время#В_космологии
то возможно, из комплексного времени или из многомерия 11-ти мерной М-теории суперструнной,
может появиться нечто, что появляется спонтанно, то есть вне времени, и не имеет состояния ДО сгенерированного состояния.
Тогда, если спонтанные явления существуют, возможны ГСЧ, и как следствие индетерминизм ещё.
А так, во времени, движется всё, и всё имеет состояние ДО, а значит нихуя случайного быть не может в принципе.
Если взять ГСПЧ, то это просто, грубо говоря, кольца из значений, кольца, с большим периодом,
и если последовательно пробежать все элементы, когда-нибудь, ты упрёшься в самый первый элемент,
и при этом, последний элемент, будет являться причиной генерации этого вот первого элемента.
Как, например, при использовании этого ГСПЧ: https://ru.wikipedia.org/wiki/Линейный_конгруэнтный_метод
Но из-за пиздатости этих колец, у таких генераторов, как https://ru.wikipedia.org/wiki/Вихрь_Мерсенна брутить весь период ГСПЧ,
мягко-сказать, энергозатратно.
Однако, последний, не является криптостойким, а вот https://ru.wikipedia.org/wiki/ISAAC является.
И там тоже большой период зацикливания.
А ваще, юзай шумы. Ну, там, белый шум, тепловой шум, дробовой шум, джонсоновский шум, квантовые, фотонные, фононные ГСЧ,
всю эту хуйню, моделировать, врядли кто станет.
>Детерминированные_ГПСЧ
>Детерминированные
>Детерминированные, БЛЕАТЬ.
https://ru.wikipedia.org/wiki/Детерминизм
Короче, смотри. Если ГСПЧ имеет какое-либо состояние, то состояние ДО этого, является причиной этого состояния.
ДО, значит, чуть раньше во времени.
Любое состояние, ГСПЧ, какое не возьми, имеет состояние ДО этого, а значит любое значение на выходе ГСПЧ, имеет причину,
и ГСПЧ не может выдать истинно случайные числа.
И вообще, любое состояние, любого генератора, имеет состояние ДО этого, то есть, хотя-бы на одну единицу планковского времни предшествующее ему,
а значит ни один генератор не может выдать случайные числа.
Если конечно, эти состояния не появляются откуда-то извне времени, то есть спонтанно,
как появилась, вне времени, планковская эпоха, например, потому что ДО планковской эпохи,
не было другого планковского интервала времени, время появилось в планковскую эпоху.
Ну так вот, если время, на самом деле, комплексное, как говорил Стивен Хокинг,
здесь: https://ru.wikipedia.org/wiki/Мнимое_время#В_космологии
то возможно, из комплексного времени или из многомерия 11-ти мерной М-теории суперструнной,
может появиться нечто, что появляется спонтанно, то есть вне времени, и не имеет состояния ДО сгенерированного состояния.
Тогда, если спонтанные явления существуют, возможны ГСЧ, и как следствие индетерминизм ещё.
А так, во времени, движется всё, и всё имеет состояние ДО, а значит нихуя случайного быть не может в принципе.
Если взять ГСПЧ, то это просто, грубо говоря, кольца из значений, кольца, с большим периодом,
и если последовательно пробежать все элементы, когда-нибудь, ты упрёшься в самый первый элемент,
и при этом, последний элемент, будет являться причиной генерации этого вот первого элемента.
Как, например, при использовании этого ГСПЧ: https://ru.wikipedia.org/wiki/Линейный_конгруэнтный_метод
Но из-за пиздатости этих колец, у таких генераторов, как https://ru.wikipedia.org/wiki/Вихрь_Мерсенна брутить весь период ГСПЧ,
мягко-сказать, энергозатратно.
Однако, последний, не является криптостойким, а вот https://ru.wikipedia.org/wiki/ISAAC является.
И там тоже большой период зацикливания.
А ваще, юзай шумы. Ну, там, белый шум, тепловой шум, дробовой шум, джонсоновский шум, квантовые, фотонные, фононные ГСЧ,
всю эту хуйню, моделировать, врядли кто станет.
никто не знает
ищи сам
утомил
на ру.википедии есть две ссылки, кстати
на английской ссылок с десяток
>Если ГСПЧ имеет какое-либо состояние
Вот меня это если смущает, даже на вики сказано что только большинство ГПСЧ удовлтеворяют схеме с состоянием и т. д. Я наверно плохо выразился, зря начал с ГПСЧ, прост на эту тему я всегда в их контексте думал, т. к. в вузе так проходил. Правильнее спросить так: можно ли детерминированно получать последовательноть без периода ?(конечно же используя ограниченную память) В теории то понятное дело что можно, с бесконечной памятью.
Ну, смотри...
Возьмём, для примера, обычный счет двоичного представления натуральных чисел... Поехали:
0
1
10
11
100
101
110
111
1000
... и так далее...
Эта последовательность требует всё большей и большей памяти, а именно +1 бит на каждый новый разряд.
Если продолжать этот счет, бесконечно, то нужно будет бесконечное число разрядов, а значит и - бесконечная память.
Тем не менее, эта последовательность не имеет периода, то есть она вообще не зацикливается.
Но возьмём конечную память в 3 бита.
000 - 0
001 - 1
010
011
100
101
110
111
000 - 0
101 - 1
...
Очевидно зацикливание с периодом 2^3 = 8, каждые 8 значений, потому что 3 бита на три разряда.
И хотя, с ростом числа разрядов до N, период зацикливания простого счета, растёт по экспоненте до 2^N,
тем не менее, всё-же, при конечной памяти, этот цикл имеет конечное число значений, и счет зацикливается.
Но возьмём число разрядов N = 256. Число комбинаций 256-битных значений, равно 2^256 ,
и это ебически пиздатое число, и это период зацикливания генератора, основанного на последовательном счете.
Чтобы пробежать все значения всего этого цикла, можно спалить, нахуй,
всю энергию Вселенной, и так и не пробежать эти значения.
такой "генератор" не является криптостойким,
потому что чтобы из состояния x вычислить 3-е, или 7-е, и т. д., состояние,
не обязательно пробегать все 3, или 7, и т. д. значений,
можно просто прибавить число 3 или 7, и получить это значение.
А вот если это будет нечто вроде: (hash(x), hash(hash(x)), и т. д...) , тогда хуй.
Но хэши имеют коллизии, и их цепочки могут зацикливаться тоже, причём раньше чем зацикливается весь период.
Например, грубо-говоря, хэш какого-нибудь числа, может дать хэш2, его хэш даст хэш3, а хэш хэша3, даст снова число, хэш которого даст хэш2.
Это грубо-говоря, конечно там период побольше будет, но грубо-говоря, в этом примере, получишь генератор с циклом в 3 значения,
несмотря на то, что в записи хэша - дохуя бит. И ещё, из-за коллизий, какое-нибудь число2, может дать хэш2, с тем же результатом на выходе.
Короче, блядь, если у тебя память ограничена, ты не можешь записать в неё бесконечность, а значит будет конец,
и либо опять всё сначала, либо вообще ну конец прям. Всё станет и начнёт лагать, и забаговываться.
Ну, смотри...
Возьмём, для примера, обычный счет двоичного представления натуральных чисел... Поехали:
0
1
10
11
100
101
110
111
1000
... и так далее...
Эта последовательность требует всё большей и большей памяти, а именно +1 бит на каждый новый разряд.
Если продолжать этот счет, бесконечно, то нужно будет бесконечное число разрядов, а значит и - бесконечная память.
Тем не менее, эта последовательность не имеет периода, то есть она вообще не зацикливается.
Но возьмём конечную память в 3 бита.
000 - 0
001 - 1
010
011
100
101
110
111
000 - 0
101 - 1
...
Очевидно зацикливание с периодом 2^3 = 8, каждые 8 значений, потому что 3 бита на три разряда.
И хотя, с ростом числа разрядов до N, период зацикливания простого счета, растёт по экспоненте до 2^N,
тем не менее, всё-же, при конечной памяти, этот цикл имеет конечное число значений, и счет зацикливается.
Но возьмём число разрядов N = 256. Число комбинаций 256-битных значений, равно 2^256 ,
и это ебически пиздатое число, и это период зацикливания генератора, основанного на последовательном счете.
Чтобы пробежать все значения всего этого цикла, можно спалить, нахуй,
всю энергию Вселенной, и так и не пробежать эти значения.
такой "генератор" не является криптостойким,
потому что чтобы из состояния x вычислить 3-е, или 7-е, и т. д., состояние,
не обязательно пробегать все 3, или 7, и т. д. значений,
можно просто прибавить число 3 или 7, и получить это значение.
А вот если это будет нечто вроде: (hash(x), hash(hash(x)), и т. д...) , тогда хуй.
Но хэши имеют коллизии, и их цепочки могут зацикливаться тоже, причём раньше чем зацикливается весь период.
Например, грубо-говоря, хэш какого-нибудь числа, может дать хэш2, его хэш даст хэш3, а хэш хэша3, даст снова число, хэш которого даст хэш2.
Это грубо-говоря, конечно там период побольше будет, но грубо-говоря, в этом примере, получишь генератор с циклом в 3 значения,
несмотря на то, что в записи хэша - дохуя бит. И ещё, из-за коллизий, какое-нибудь число2, может дать хэш2, с тем же результатом на выходе.
Короче, блядь, если у тебя память ограничена, ты не можешь записать в неё бесконечность, а значит будет конец,
и либо опять всё сначала, либо вообще ну конец прям. Всё станет и начнёт лагать, и забаговываться.
>Короче, блядь, если у тебя память ограничена, ты не можешь записать в неё бесконечность
А я запишу потенциальную бесконечность, ведь актуальная это не математика.
>А я запишу потенциальную бесконечность, ведь актуальная это не математика.
Погуглил, нарыл это: https://ru.wikipedia.org/wiki/Бесконечность#Потенциальная_и_актуальная_бесконечность
>Бесконечность может рассматриваться как неограниченность некоторого процесса, например, когда
>во втором постулате Евклида утверждается возможность продолжить бесконечно и непрерывно любую прямую,
>то имеется в виду, что процесс можно непрерывно продолжать,
>но существование такого самостоятельного объекта, как бесконечная прямая, из него не следует.
Подумал-подумал, как можно продолжить прямую бесконечно, без существования бесконечной прямой как объекта,
и просто замкнул мысленно прямую в кольцо, искривив пространство каким-нибудь гравитационным искривлением.
Если прямая это кольцо, то ей моно продолжаь и продолать, и продолжать и продолжать,
но в итоге, одна точка может иметь одну и ту же координату на прямой этой, после нескольких проворотов по кольцу.
То есть, получаешь цикл из координат, и генератор координат - зацикливается.
>Такого рода процессы и совокупности объектов, их описывающие,
>характеризуют как потенциальную бесконечность
>(в схоластике используется термин «синкатегорематическая бесконечность»),
>потенциально бесконечное
>не подразумевает целостных бесконечных предметов и явлений,
>в каждой фазе бесконечного процесса рассматриваются лишь конечные сущности,
>то есть является
>лишь частичным отрицанием конечного.
То есть, как я понял, бесконечная прямая, рассматривается как бесконечное число конечных отрезков,
складываемых по мере необходимости продолжения прямой, а не уже сложенных в бесконечную прямую.
Но опять же, ключевое слово здесь - БЕСКОНЕЧНОЕ число отрезков, и если их больше чем (2^8-1),
при 8-ми битах в разрядах записи числа отрезков, то число трезков большее (2^8, например),
уже нельзя будет записать 8-мью битами, надо 9 бит,
и вот так вот, конечная память, просто не даст возможность представить в числовом виде - бесконечное число отрезков.
>А я запишу потенциальную бесконечность, ведь актуальная это не математика.
Погуглил, нарыл это: https://ru.wikipedia.org/wiki/Бесконечность#Потенциальная_и_актуальная_бесконечность
>Бесконечность может рассматриваться как неограниченность некоторого процесса, например, когда
>во втором постулате Евклида утверждается возможность продолжить бесконечно и непрерывно любую прямую,
>то имеется в виду, что процесс можно непрерывно продолжать,
>но существование такого самостоятельного объекта, как бесконечная прямая, из него не следует.
Подумал-подумал, как можно продолжить прямую бесконечно, без существования бесконечной прямой как объекта,
и просто замкнул мысленно прямую в кольцо, искривив пространство каким-нибудь гравитационным искривлением.
Если прямая это кольцо, то ей моно продолжаь и продолать, и продолжать и продолжать,
но в итоге, одна точка может иметь одну и ту же координату на прямой этой, после нескольких проворотов по кольцу.
То есть, получаешь цикл из координат, и генератор координат - зацикливается.
>Такого рода процессы и совокупности объектов, их описывающие,
>характеризуют как потенциальную бесконечность
>(в схоластике используется термин «синкатегорематическая бесконечность»),
>потенциально бесконечное
>не подразумевает целостных бесконечных предметов и явлений,
>в каждой фазе бесконечного процесса рассматриваются лишь конечные сущности,
>то есть является
>лишь частичным отрицанием конечного.
То есть, как я понял, бесконечная прямая, рассматривается как бесконечное число конечных отрезков,
складываемых по мере необходимости продолжения прямой, а не уже сложенных в бесконечную прямую.
Но опять же, ключевое слово здесь - БЕСКОНЕЧНОЕ число отрезков, и если их больше чем (2^8-1),
при 8-ми битах в разрядах записи числа отрезков, то число трезков большее (2^8, например),
уже нельзя будет записать 8-мью битами, надо 9 бит,
и вот так вот, конечная память, просто не даст возможность представить в числовом виде - бесконечное число отрезков.
Ну вот я дальше копаю, и наконец я уже понял как правильно классифицируется то что изначально принял за возможность бесконечного апериодичного генератора.
https://en.wikipedia.org/wiki/Low-discrepancy_sequence
Есть, оказывается, понятия квазирандом и квазипериодичная последовательность. Можно ли их получать используя конечную память я пока ещё не выяснил, но вот смотрите что гуглится:
https://www.sciencedirect.com/science/article/abs/pii/0167715286900994
Тут вроде читать бесплатно не даёт. Я также понимаю что, даже если окажется вдруг, что так можно делать, то скорее всего такой ГК(квази)СЧ окажется полным уг по своим свойствам, уж по криптографическим точно.
Получить квази RNG с бесконечным периодом - это задачка в две строчки для первокурсников
Дело-то не в периоде, выше уже писали, что даже периода в 256 хватает, чтобы никогда не повторяться в обозримом будущем
Дело-то в предсказуемости, и тут бесконечный период ничего особенно лучшего не гарантирует по сравнению с конечным
>Получить квази RNG с бесконечным периодом - это задачка в две строчки для первокурсников
Ну го, покажи эти две строчки нам.
В твоей статье эти две строчки
>Ну вот я дальше копаю,
>и наконец я уже понял
>как правильно классифицируется то
>что изначально принял за возможность
>бесконечного апериодичного генератора.
>Есть, оказывается, понятия квазирандом
>и квазипериодичная последовательность.
Блядь, я не могу читать этот инглиш, поэтому прогуглил сам, и нашёл вот это: http://math.nsc.ru/~serge/qpsl/problem_statement_1.htm
>Последовательность, имеющая квазипериодическую структуру,
>или квазипериодическая последовательность ―
>это последовательность с квазипериодической сменой своих свойств.
То есть, я так понял, ты просто хочешь сделать так, чтобы период зацикливания генератора был динамическим, и изменялся?
Ну, даже если так, всё-равно это не даст бесконечное число вариантов, при конечной памяти.
>Можно ли их получать используя конечную память я пока ещё не выяснил, но вот смотрите что гуглится
Квазипериодические последовательности, вроде можно.
Но конечной памяти, они всё-равно не будут иметь бесконечное число вариантов, и всё-равно будут зацикливаться.
Можно просто по прохождению цикла - смещения в цикле юзать, чтобы проворачивать этот цикл.
Наример, период зацикливания трехбитного генератора составляет 8 значений (включая 0 - от 0 до 7):
0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2 значения повторяются
А можно сделать так:
0, 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 0, 2, 3, 4
то есть, по прохождению цикла в 8 элементов - плюс единичка,
и в целом, последовательность уже имеет разные периоды,
хотя некоторые из них меньшие, нежели 8, из-за того, что 2^3 = 8 значений в конечной памяти, объёмом в 3 бита.
>Ну вот я дальше копаю,
>и наконец я уже понял
>как правильно классифицируется то
>что изначально принял за возможность
>бесконечного апериодичного генератора.
>Есть, оказывается, понятия квазирандом
>и квазипериодичная последовательность.
Блядь, я не могу читать этот инглиш, поэтому прогуглил сам, и нашёл вот это: http://math.nsc.ru/~serge/qpsl/problem_statement_1.htm
>Последовательность, имеющая квазипериодическую структуру,
>или квазипериодическая последовательность ―
>это последовательность с квазипериодической сменой своих свойств.
То есть, я так понял, ты просто хочешь сделать так, чтобы период зацикливания генератора был динамическим, и изменялся?
Ну, даже если так, всё-равно это не даст бесконечное число вариантов, при конечной памяти.
>Можно ли их получать используя конечную память я пока ещё не выяснил, но вот смотрите что гуглится
Квазипериодические последовательности, вроде можно.
Но конечной памяти, они всё-равно не будут иметь бесконечное число вариантов, и всё-равно будут зацикливаться.
Можно просто по прохождению цикла - смещения в цикле юзать, чтобы проворачивать этот цикл.
Наример, период зацикливания трехбитного генератора составляет 8 значений (включая 0 - от 0 до 7):
0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2 значения повторяются
А можно сделать так:
0, 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 0, 2, 3, 4
то есть, по прохождению цикла в 8 элементов - плюс единичка,
и в целом, последовательность уже имеет разные периоды,
хотя некоторые из них меньшие, нежели 8, из-за того, что 2^3 = 8 значений в конечной памяти, объёмом в 3 бита.
>>81867
>>81868
Я помню когда мне надо был рандом, думал сделать какой-то фрактальный квазипериодический ГСЧ,
как вот эта вращающаяся диковина: https://youtu.be/qhbuKbxJsk8?t=738
Но потом просто поставил камеру на Lava-лампу с блётсками, и снимал поток хэшей изображений с её матрицы.
https://www.youtube.com/watch?v=-lplhvnKYxU
дихлофосом их, по-другому никак
https://www.youtube.com/watch?v=_fwJA2_hXt4
Как можно в 21 веке смотреть лекции, где пишут на доске? Это значит, что лектор вообще не уважает зрителей или даже не может сделать презентацию.
На этом примере видно на сколько лучше строят свои лекции люди имеющие дело с алгоритмами, нежели обычные математики типа Саватеева, которые двух слов связать не могут чтобы слушатель не запутался
давно известно уже, что ни математека, ни программирование ум в порядок не приводят
хороший тараканий скил, анализ на уровне ШП
не у всех
статистическое наблюдение
Реквестирую алгоритм для авторизации клиента на сервере, алгоритм с доказательсвом с нулевым разглашением.
Чтобы клиент мог отправить пруф того, что он знает пароль, не отправляя сам пароль, и чтобы сервер мог проверить вероятностно знает ли юзер пароль или нет.
Судя по этой статье:
https://sites.google.com/site/anisimovkhv/learning/kripto/lecture/tema11#p115
из раздела:
>III. Упрощенная схема аутентификации Фейге-Фиата-Шамира.
число s должно обладать какими-либо особыми свойствами, и как его генерировать - не совсем понятно.
Мне же, нужен алго такой, где s может быть произвольным числом.
Ну, блядь. Регистрация - делай так, так, так. Авторизация - делай так, так, так, так, блядь. Вход по кукам, куки есть? Так, нет - нахуй на перелогин. Восстановление доступа - секретный вопрос прохешировал, сравнил, дальше делай так, так пароль меня, так потом вот так блядь, и на перелогин. Так, так, потом так, и потом ещё эдак, и всё нахуй проверено и заебись. Алгоритм, короче.
Всё нашёл https://ru.wikipedia.org/wiki/Протокол_Фиата_—_Шамира#Описание_протоколa динах со своим дихлофосом.
В жопу себе засунь свой баллон с дихлофосом, это тред про алгоритмы.
Как же ты его приложил.
Один ебанат с пынями-пучкистами спугнул почти всех мало-мальски имеющих отношение к математике, теперь форсер дихлофоса спугнет и айтишников. Проклятое место, реально.
пыни-пучкисты были прекрасны, не надо
не знаю даже, кого они спугнули, если тараканов, так то к лучшему
>теперь форсер дихлофоса спугнет и айтишников.
Здравствуй, какая тематика в /math/?! Этот тред вообще по-хоршему нужно было сразу снести
>Один ебанат с пынями-пучкистами спугнул почти всех мало-мальски имеющих отношение к математике
Те, кто "спугнулись" такой хуйнёй, нашли бы от чего спугнуться и в дальнейшем, это сосач всё-таки
Кстати, весьма интересные алгоритмы встречаются в топологическом дата сайенсе, с гамалогиями.
правильно он травит, аутентифиакция, и прочие крипты, блокчейны, бобы, алисы это не алгоритмы, литр дихлофоса им
Сортировка Пузырьком
вот у меня на повестке дня рекурсия, ханойские башни, но я пока не могу сформулировать мой вопрос
 226 Кб, 301x725
226 Кб, 301x725>ITT, мы будем алгоритмизировать алгоритмизацию алгоритмизациоанальную. Алгоритмизацианалично, и алгоритмизациоаналистично.
>Приготовь свой алгоритмизациоанал, для аналлизирования различных алго, невъебенных.
>
>Заебатой автоматизированной алгоритмизации-нить, иди.
 79 Кб, 960x1280
79 Кб, 960x1280Картинка неверная, у тебя х=3.5
Для вектора $(x, y)$ номер ячейки $N$ равен $8 \cdot (\overline{y}-1) + \overline{x}$ где $\overline{a}$ это функция ceiling
Для [3.5, 4.5] формула даёт 8(4-1)+5=24+5=29, всё верно
Если ты прогроммист, как ты намекнул выше, то про https://en.wikipedia.org/wiki/Floor_and_ceiling_functions должен знать
так если мы округляем как написано в педии
> В математике, целая часть вещественного числа x до ближайшего целого в меньшую сторону.
то получается вообще
8(3 - 1) + 4, но я понял спасибо, буду искать celling на движке
 48 Кб, 601x579
48 Кб, 601x579Задавал недавно вопрос в соседнем треде:
>>85163 →
Анон >>85166 → посоветовал уточнить тут.
И в дополнение хотелось бы спросить, если бы я вдруг ебанулся и решил-таки перегенерить, хешировать по описанному в первом посте методу все 60^31 вариантов за пару миллиардов лет, чтобы узнать, сколько комбинаций в итоге получится - то каким ЯП мне стоило бы воспользоваться, какой бы наиболее быстро смог выполнять нужный алгоритм (офк с задействованием rtx 3090 в моем пека, а не процессора)?
Perl, C/C++, что-то другое?
Вдруг тут погромисты тоже есть.
 145 Кб, 1000x750
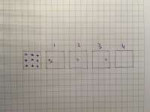
145 Кб, 1000x750Матаны, пиздец как срочно надо просчитать 10-ти триллионный знак числа пи. Есть вот такое вот: ru.wikipedia.org/wiki/Формула_Бэйли_—_Боруэйна_—_Плаффа
и там, внутри, 16k. Если k будет 10 триллионов, это ж ваще пиздец скоко умножений. Как оптимизировать оптимизацией оптимизациоаналистичной, чтобы алгоритмика вся эта няшная - сразу заалгоритмизировала всё алгоритмизациоанальностью, алгоритмической?
Блядь, тут https://en.wikipedia.org/wiki/Bailey–Borwein–Plouffe_formula
столько много букафф, а что значит k - нихуя не написано. Проясните, алгоритматаноны.
Прочитай статью целиком (особенно раздел BBP digit-extraction algorithm for π), а не только первые пару параграфов.
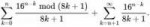 4 Кб, 283x51
4 Кб, 283x51>>а что значит k - нихуя не написано
>Без комментариев.
Действительно, там нет ваще никаких комментариев, про k.
Сама формула, как я понял, вычисляет пи целиком, а не эти вот знаки шестнадцатиричные.
>>86569
>Прочитай статью целиком (особенно раздел BBP digit-extraction algorithm for π),
>а не только первые пару параграфов.
Так там же (пикрил), тоже везде есть это ебучее и неведомое k,
а что оно значит и что туда подставлять надо - хрен поймёшь.
Нет, блять, не тролленк. Мне надо знать что значит это ёбанное "k",
и что туда пихать надо, чтобы махина эта завелась.
Что если нам надо срочно, высчитать ебический-космический 10-ти триллионный знак, блядь? Сидеть вычитывать что такое "k"? А где вычитывать, блядь, если нихуя инфу не дали, какую-то неполную хуйню намазюкали, а остальное скрыли и зацензурировали мочернёй, на мочане этом, мейлачевском?
И степень эту пиздатющую можно как-то через модуль заебенить? А то считать, блядь, 10^(в 10-ти триллионной) как-то, ну, мягко-сказать, что - пиздец как неэнергоэффективно.
А, всё, понял, это ж сумма. k инкрементируется там от нуля. Так она аж до бесконечности штоле суммирует, блядь?
Это будет бесконечный цикол, штоле?
А хуле они тогда пиздят, эти пендосы, что прога даёт n-ный знак из пи, без вычисления предыдущих?
Если мне надо 10-ти триллионный hex-char оттуда, значит надо всё-равно просчитать это пи, с точностью до 10-ти триллионного знака, а потом извлечь цифру эту, так ведь?
Какой алго годно считает, давай сюда его быстрее, и чем быстрее - тем лучше, потому что теперь, мне уже срочно нужен унтригинтиллионный знак числа пи, блядь, пиздец как нужно усираюсь прям. Меня тут в МГУ, уже на счетчик поставили прост.
 369 Кб, 640x464
369 Кб, 640x464Да не сижу я на таблетках, заебали, у меня петуховены спиздили, какие нахуй таблетки, заманали? Числа из пи извлекай давай мне, быстраблять.
>Так там же (пикрил), тоже везде есть это ебучее и неведомое k
>>86580
>А, всё, понял, это ж сумма. k инкрементируется там от нуля. Так она аж до бесконечности штоле суммирует, блядь?
Можно мне нобелевку, или там премию тысячелетия?
У меня пятсот косарей спиздили, мне лямчик не помешает.
Короче, зырьте, мне чет кажется что правую часть можно опустить, нахуй, где степень бинарная, потому что при k от 0 до n, пи уже рассчиталось с точностью до n-знаков. А то эта бесконечность ебическая, и ещё и степень там.
Тупо закомментировал код с этой частью уравнения, и всё вроде робит. Гоните бабала сюда, есличо. Адрес петухоина, сами знаете: 1KSRkvTQGgFkiwczwJpqgn8ZuSeHs8uVk9
 66 Кб, 500x486
66 Кб, 500x486>мне лямчик не помешает
Хоть мне стоко бабала нахуй и не надо, а то пузо треснет, но всё-равно пущай валяется где-нить на болванке, хуле. Оно жрать не просит, это говно петуховенское, которое пиздят постоянно всякие капиталистоблядские - крысы хуесосские.
>BBP
Вот тут BBP наварганил: https://gist.github.com/username1565/2ff957b29c6eae26207d5b7ac8af94f8
А тут консолька, онлайн: https://gistpreview.github.io/?2ff957b29c6eae26207d5b7ac8af94f8/BBP_NthHexDigitOfPI.html
Миллионную цифру долго считает, может можно было бы как-то и ускорить, я не знаю, но оставил коммент.
 35 Мб, mp4,
35 Мб, mp4,854x480, 17:34
Раньше пи многогранниками и треугольниками паскаля считали.
Каким алгоритмом рассчитать высокоточно - знаки числа Эйлера "e"?
И ещё один вопрос - вы уже нашли число Скьюза? https://ru.wikipedia.org/wiki/Число_Скьюза
Может мне заняться этой хуйнёй?
Всё, не надо, уже просчитал 10000 знаков.
Вот последние 50 из них:
>71039765214696027662583599051987042300179465536788
4 строчки кода на JavaScript, тупо копипастишь в консоль браузера и вот оно "e":
>var nDigs = 10000; var pad = Math.round(Math.log(nDigs)); var n = 1n;
>var f = 10n ٭٭ BigInt(nDigs + pad), e = BigInt(f) + BigInt(f);
>do e += (f /= ++n); while (f > n);
>console.log( '2.'+(e / (10n ٭٭ BigInt(pad))).toString().slice(1));
Звёздочки, конечно же - заменить на астерикс.
Осталось просчитать терь золотое сечение. Вижу здесь уже есть миллион цифор https://onlinemathtools.com/js/libs/golden-ratio-digits.js
а как их считать, блядь - хз. Как просчитаю, буду весь в золоте, и сечь его буду золотым сечением этим.
Ой бля, там корень считать надо, вавилонский метод виснет наглухо при 1000000-не цифр после запятой. Могу показать говнокод.
Может есть какой-нить попижже алго для вычисления корней, чтобы точно вот считало всё это?
Ну же, матаны?!!
Реквестирую же самый быстрый и эффективный способ рассчета квадратного корня, для длинных чисел!!
Как и чем рассчитали этот вот миллион десятичных чисел корня из двух: https://catonmat.net/tools/generate-sqrt2-digits
Вот тут они все: https://catonmat.net/js/tools/libs/sqrt2-digits.js
Сидели и ждали неделями, штоле?
Пока пришёл лишь к двум методам - вавилонский метод, и метод Ньютона.
Оба, зависают при числе знаков в 10000.
Может можно всю эту хуйню как-то оптимизировать?
Вот код, в консоль браузера (JavaScript):
>function Sqrt( // Returns the square root of n, with decimal digits nDig
> n //number to compute square root
> , nDig //number of decimal digits in result
> , algo //Heron - for Babylonian method, or Newton for Newton Iteration method
>)
>{
> if (n < 0n) { throw 'square root of negative numbers is not supported' }
> if (n < 2n) { return n; }
> n = BigInt(n) (10n BigInt(nDig2)); //square have length nDig*2
> var x = (algo=='Heron') ? n : 1n, y = 1n;
> while (true) {
> if(algo === 'Heron'){
> if(x>y){ x = (x + y) / 2n; y = n / x; }
> else{ break; }
> }
> else if(algo === 'Newton'){
> y = ((n / x) + x) >> 1n;
> if (x === y || x === (y - 1n)) { break; }
> x = y;
> }
> }
> return x; //return BigInt
>}
>console.log(Sqrt(2, 1000, 'Heron' )); // -> 1000 decimal points of sqrt(2)
>console.log(Sqrt(2, 1000, 'Newton' )); // -> 1000 decimal points of sqrt(2)
Пока пришёл лишь к двум методам - вавилонский метод, и метод Ньютона.
Оба, зависают при числе знаков в 10000.
Может можно всю эту хуйню как-то оптимизировать?
Вот код, в консоль браузера (JavaScript):
>function Sqrt( // Returns the square root of n, with decimal digits nDig
> n //number to compute square root
> , nDig //number of decimal digits in result
> , algo //Heron - for Babylonian method, or Newton for Newton Iteration method
>)
>{
> if (n < 0n) { throw 'square root of negative numbers is not supported' }
> if (n < 2n) { return n; }
> n = BigInt(n) (10n BigInt(nDig2)); //square have length nDig*2
> var x = (algo=='Heron') ? n : 1n, y = 1n;
> while (true) {
> if(algo === 'Heron'){
> if(x>y){ x = (x + y) / 2n; y = n / x; }
> else{ break; }
> }
> else if(algo === 'Newton'){
> y = ((n / x) + x) >> 1n;
> if (x === y || x === (y - 1n)) { break; }
> x = y;
> }
> }
> return x; //return BigInt
>}
>console.log(Sqrt(2, 1000, 'Heron' )); // -> 1000 decimal points of sqrt(2)
>console.log(Sqrt(2, 1000, 'Newton' )); // -> 1000 decimal points of sqrt(2)
ёбанные звёздочки.
Где бубны, там - короче одна звёздочка
>function Sqrt( // Returns the square root of n, with decimal digits nDig
> n //number to compute square root
> , nDig //number of decimal digits in result
> , algo //Heron - for Babylonian method, or Newton for Newton Iteration method
>)
>{
> if (n < 0n) { throw 'square root of negative numbers is not supported' }
> if (n < 2n) { return n; }
> n = BigInt(n) ♦ (10n ♦♦ BigInt(nDig♦2)); //square have length nDig♦2
> var x = (algo=='Heron') ? n : 1n, y = 1n;
> while (true) {
> if(algo === 'Heron'){
> if(x>y){ x = (x + y) / 2n; y = n / x; }
> else{ break; }
> }
> else if(algo === 'Newton'){
> y = ((n / x) + x) >> 1n;
> if (x === y || x === (y - 1n)) { break; }
> x = y;
> }
> }
> return x; //return BigInt
>}
>console.log(Sqrt(2, 1000, 'Heron' )); // -> 1000 decimal points of sqrt(2)
>console.log(Sqrt(2, 1000, 'Newton' )); // -> 1000 decimal points of sqrt(2)
ёбанные звёздочки.
Где бубны, там - короче одна звёздочка
>function Sqrt( // Returns the square root of n, with decimal digits nDig
> n //number to compute square root
> , nDig //number of decimal digits in result
> , algo //Heron - for Babylonian method, or Newton for Newton Iteration method
>)
>{
> if (n < 0n) { throw 'square root of negative numbers is not supported' }
> if (n < 2n) { return n; }
> n = BigInt(n) ♦ (10n ♦♦ BigInt(nDig♦2)); //square have length nDig♦2
> var x = (algo=='Heron') ? n : 1n, y = 1n;
> while (true) {
> if(algo === 'Heron'){
> if(x>y){ x = (x + y) / 2n; y = n / x; }
> else{ break; }
> }
> else if(algo === 'Newton'){
> y = ((n / x) + x) >> 1n;
> if (x === y || x === (y - 1n)) { break; }
> x = y;
> }
> }
> return x; //return BigInt
>}
>console.log(Sqrt(2, 1000, 'Heron' )); // -> 1000 decimal points of sqrt(2)
>console.log(Sqrt(2, 1000, 'Newton' )); // -> 1000 decimal points of sqrt(2)
Вот, короче, оно тут: https://onecompiler.com/javascript/3x8py7xjf
Долго считает, сука, пиздатые числа.
Если 1 миллион цифр просчитывать,
то корень будет - пиздатое число,
порядка 1*10^1000000,
а квадрат - ещё пиздатее,
порядка 1^10^2000000,
поэтому надо бы, чё-то попижже понавыдумывать.
С другой стороны, какой метод последовательных приближений не возьми, всё-равно он будет сжирать по биту, из предпологаемого значения корня, длиной в 1000000 знаков,
а значит число итераций будет примерно равно:
root.bitlength если не больше, и оно растет, это число итераций, по мере наращивания числа вычисляемых цифр, блядь.
Вот запилил, пока черновой вариант (неоптимизированный),
тут корень считается - методом последовательных приближений,
за фиксированное число итераций цикла (это битовая длина корня log_2(10^N), где n - число цифр в корне): https://onecompiler.com/javascript/3x8qcnjtg
10к цифр этот говносайт не даёт просчитать, но в консоли (если скопировать код) можно просчитать эти корни ебучие,
но оно всё-равно долговато пашет,
надо оптимизировать бы, что-то там, но а как - хз.
Квадраты пиздатые, наверное, можно было бы powmod как-то считать, быстро, или каким-то бинарным возведением в степень,
или ещё чо.
Можно было бы складывать квадраты, или считать их без умножения, а сдвигом бинарным.
200 миллиардов знаков если считать - всё зависнет нахуй:
>Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор с частотой 3,6 ГГц и 16 ГБ ОЗУ.
Вот, блядь, последовательные приближения: https://onecompiler.com/javascript/3x8rsccn9
Уже быстрее, за счет акселлерации побитовыми операциями.
Всё-равно медленно, блядь. Каждый бит корня пробегает, и столько же квадратов пиздатющих вычисляет.
Может прихуярить туда ещё и бинарный поиск, для пущей акселлерации? https://ru.wikipedia.org/wiki/Двоичный_поиск
Чтобы не все биты пробегать, а как-бы начиная с бита посередине.
Меньше квадратов бы должно вычисляться, тогда, в конечном итоге.
Если длинна корня лям-лярд, должно бы быстрее хуячить такое вот алго. Но это пока идея, и руки так и не дошли ещё чтоб вговнокодить всю эту хуйню.
Чёт подумалось бинарным поиском искать биты корня,
просто чтобы все биты не пробегать,
а то с к каждым битом, последовательные приближения, приближают значение корня на один бит.
Если бит дохуя, и число цифр в корне n, и корень порядка 10^n,
то алго будет срабатывать за log2(n) итераций,
потому что столько бит примерно в корне этом ебучем,
и это может быть дохуя.
Вон, челы миллиарды знаков считали. Представляете себе число 10 в степени 200 миллиардов, блядь? А сколько бит у него? Столько и итераций в цикле, и это дохуяшечки.
Я вижу здесь: https://ru.wikipedia.org/wiki/Квадратный_корень_из_2#Алгоритмы_вычисления
Есть какой-то алго пошустрее.
Он за один шаг, удваивает число цифр в корне, якобы.
Но мне кто нить пояснит, как работает это алго?
Откуда берутся эти дроби ебучие?!! Я уже и так, и сяк, не получаются нихуя дроби, а получается хуйня какая-то неведомая, с каждым шагом, которая даже на приближенный корень не похожа. Пиздец просто. А потом, каким-то магическим образом, всё это сходится в корне, опять же за log2(n) итераций. Пиздят википидоры, походу, но где и в чём - не пойму чёт. ПАМАГИИИИТИИ.
Всё ясно. Там любое число на входе може быть, как сторона прямоугольника, например, число 3, далёкое от корня.
И в любом случае итерации сходятся в корне.
Только здесь нашёл внятное описание: https://ru.wikipedia.org/wiki/Итерационная_формула_Герона#Геометрическая_интерпретация
>одну сторону нового прямоугольника сделаем равной среднему арифметическому обеих сторон предыдущего шага
поэтому, из-за среднего арифметического (xn/2) и не удивительно, что алго работает за log2(n), так как для корня битовой длины n, сжирается по биту за шаг, этим вот делением на два.
Нет.
Что ты хочешь сказать, математик не может нарисовать сферу?
Это очевидно по числу ответов ITT.
Местные маняматики даже не в состоянии врубиться о чем идёт речь в постах анона.
Наверное, тред про алго следовало бы создать в /pr или /s потому что математические абстракции здесь
слишком сложны для окостеневшего лба, среднестатистического маняматика из матача, на этом - мочерском мейлаче.
Ну а хейт погромистов в этом разделе, и всякий тараканизм - это уже стадная хуйня,
тут у них своя стадная иерархия в виде примитивной пирамидки, я гляжу.
Как же у кодерка нибамбит от того, что его хуйня никому кроме узкой кучки таких же аутистов не интересна. Да-да, про матешу можно сказать то же самое
Пошёл нахуй. Там на модедях ваших ебучих, где слежка непрактичная, блядь, прекрасно видно, крысинные черви, как мне здесь норм.
500 косарей пендосской срани мои, мне сюда, ещё вчера. И коробку шмали мне мою отдайте ещё, дешёвая крысинная гниль. Да, я не за был, сука. Ничтожества никчёмные.
-----BEGIN BITCOIN SIGNED MESSAGE-----
console.log(new Date().getTime()); //1631323200242
Я принёс вам 11 сентября в говнявесном блохчейне: https://wavesblockexplorer.com/tx/72ses9JqiJ7BAvjaAJbBAB4hgT9g6dUycvjmy4uU7bAB
Всосите его сполна, суккакрысы.
Сегодня годовщина, кстати. Ровно 20 лет.
Хуй вы удалите это, теперь, мрази мочерские.
-----BEGIN SIGNATURE-----
1QGmrMkWAwpauFRMUq9Y9mK34e7uoc7ge5
HAHRcIOg34XJx++hfSEocxWGiTJbiKT3WH5JCZSw1QGeGft0RCCFHyLsADoIj4HHifHlz3wnGoaEh81NL6mkVek=
-----END BITCOIN SIGNED MESSAGE-----
>Наверное, тред про алго следовало бы создать в /pr или /s потому что
хотя и не могу согласиться с аргументацией, тезис полностью поддерживаю
Математика загибается, прорывов следует ждать в тараканьих науках от молодых тараканов
Тараканьи мантры
Да б-га ради. Почему бы вам не наныть свою доску по комплюхтер саенс и обсуждать там алгоритмы, нейронки и прочее? Матх то тут при чем.
Вот тебе "прорыв" https://www.researchgate.net/publication/354423778_P_Does_Not_Equal_NP . Проверяй.
Если отсюда погромисты уйдут, скорость постинга раза в три ведь уменьшится, а доска и так полуживая.
У меня диссонанс.
Я всегда считал что существуют хитромудровыпиханные алго, позволяющие подобрать хэшируемые данные по хэшу,
с той же скоростью, с которой проверяется хэш.
Например, квантовыми вычислениями какими-то невъебенными, или обратимыми вычислениями.
Когда хэшируешь данные - инфа теряется из-за необратимости конъюнкций и дизъюнкций всяких.
А если делать это через обратимые вычисления, не теряя инфу, то по выходной инфе можно однозначно восстановить входную,
так же быстро, как вычисляется входная инфа (хэш), но только в другую сторону (обратимость обратимых вычислений).
Лучше тишина, чем мусор, ясчитаю
Почему кого-то должна волновать скорость постинга?
а спасибо, простое должно быть меньше 10, то есть чем большее мы возьмём число вместо 10, тем более разнообразен будет у нас выбор простых?
Это презентация, видимо, для младших классов средней школы. Предлагаешь им рассказывать про тезис Черча?
Предлагаю им сказать: алгоритм сложная вещь, поэтому вообще дать ему определение нельзя. Но если очень упростить, то вот:
>Но если очень упростить, то вот: (|), Є====3, (_Y_), .|. , (. Y .), (_8_), (_O_), :=O===3 , 8====D
Какой-то эзотерический язык программирования получается.
Помню когда был мелким спермотоксикозником, то в кс 1.6, когда кто-то рисова (_о_) у меня хуй вставал.
А теперь у меня хуй только на такое встаёт, о чём вслух произнести стрёмно. А всё остальное уже никакой реакции не вызывает
А так? ( \|/ )
Вопрос: можно ли всякий алгоритм представить в качества конечного автомата? Речь идет об алгоритмах постоянно повторяющихся действий
Алгоритм, который бесконечно заполняет память, нельзя представить конечным автоматом.
А бесконечным автоматом? Это такой автомат, который всегда тра-та-та-та-та, и в котором никогда не кончаются патроны.
Почему нельзя, просто циклом запрашивается память у операционной системы и забивается мусором. Многие программы на C/C++ написаны именно так - с утечками памяти. Программисты выделяют память, что-то туда пишут, а освободить забывают.
Она только у тебя конечная, а у нас уже бесконечная есть.
Да, всё правильно. Конечна даже не сама память, а адресное пространство. Поэтому либо комп зависнет, либо операционная система завершит процесс.
блеять понял уже что хуйню сказал. 15 это составное число, тогда вопрос такой: то одно число обязательно будет не чётным а второе чётным
И если мы продолжим 'делить' это первое нечётное число, то мы никогда не получим два чётных числа
(64 - 1) / 2 = 32 + 31
31 / 2 = 16 + 15
15 / 2 = 14 + 7
7 / 2 = 4 + 3
То есть получается какой-то постоянно повторяющийся плохой случай, а всего лишь надо было от степени двойки отнять единицу
Что ты какой-то хуйнёй занимаешься, как мне кажется. Вот норм лекции, попробуй посмотреть https://www.youtube.com/watch?v=KdZ4HF1SrFs&list=PLRDzFCPr95fK7tr47883DFUbm4GeOjjc0
https://ru.wikipedia.org/wiki/Целая_часть
Ты по сути просто обнаружил, что $\lceil x/2 \rceil + \lfloor x/2 \rfloor = x$, где $x$ целое число. Если $x$ четное, то $\lceil x/2 \rceil = \lfloor x/2 \rfloor$, если нечетное, то $\lceil x/2 \rceil = \lfloor x/2 \rfloor + 1$.
>⌈x/2⌉=⌊x/2⌋
>⌈x/2⌉=⌊x/2⌋+1
Это отдельный пиздец. Как так? Там были эти формулы, но я не понимаю, как одно и то же действие равняется двум разным результатам?
Всё, что ни на есть - это алгоритмы. Даже если нихуя не исполняется, а просто если что-то существует, то что-то существует во времени, и переходит из одного состоиния в другое, с каждым новым интервалом планковского времени - как-бы исполняя алгоритм. Процесс развития Вселенной - это тоже один пиздатый алгоритм, который пиздует во времени.
А поскольку везде алго, и Вселенная - это сплошной алго, то алго фундаментален, и если познать дзен в сути алго, и алгоритмизировать алгоритмизацию алгоритмическую, то алгоритмически алгоритмизирующая алгоритмизация, заалгоритмирует алгоритмом алгоритмизирующим.
ну типа того.. например бинарный поиск имеет ту же самую природу что и простые числа. Это естественная природная конструкция
А разве при бинарном поиске рассчитываются простые числа?
Можно ли присунуть в алго массив заранее вычисленных простых чисел и ускорить бинарный поиск?
Что у тебя там? Простые числа? Держи алгоритм миллера-рабина: https://username1565.github.io/BigInteger.js/Miller-Rabin_test.html
А оно заебётся такие пиздатющие числа на простоту чекать, и зависнет нахуй.
нет конечно, это же не имеет смысла, какой прок от алгоритма если мы не можем его осмыслить нашим конечным мозгом. Другое дело, что алгоритмы вполне могут выдавать бесконечные данные, типа алгоритма для числа пи.
все так аминь
В принципе, да, но можно было и более бытовое что-то, ведь там, в основном, любят давить на сортировки.
И ты спрашиваешь, есть ли оно. Ну да, есть. Куча сайтов с задачами, где можно решение отослать и его по тестам прогонят. И не только на сортировку. Или ты что-то иное имеешь в виду.
 71 Кб, 800x600
71 Кб, 800x600Двухмерное пространство, есть два класса зон: разрешающие и запрещающие. Могут быть окружностью либо полигоном (выпуклым, пока). Задача - найти близжайшую окружность, которая будет полностью в допустимой зоне, при этом не будет пересекаться с запрещающими зонами, т.е. для точки в центре - одна из двух фиолетовых.
Изначально, задача была про точку, я ее решал перебором: начиная от тестовой радиуса 0.5 (вокруг изначальной точки), перебрать точки на окружности с шагом 0.5, если попадает в разрешающие и не попадает в запрещающие - ок. В итоге оказалось низкопроизводительным, хоть и работало. Потом оказалось что есть погрешность - поэтому нужно искать не точку, а целую окружность. В теории - можно сделать то же самое, только смотреть не попадание тестовой точки в зоны, а пересечение окружности с этими зонами. Все равно выглядит как дилетанство, тем более на практике такого количества фигур не будет и перебор сильно замедляет алгоритм.
Мб кто подскажет более эффективный способ? На питоне написано, мб либа есть?
>Или ты что-то иное имеешь в виду.
Что-то, по мнению возможных ответчиков, интересное. Например, вывод специфических перестановок или подсчёт маршрутов с погрешностями, возможные задачи на приближённое моделирование без теории из численных методов.
Пчел, задача у тебя невыпуклая, это пиздец с точки зрения именно матеши, так что сетка это идеальный алгоритм для глобальной оптимизации. Можешь разве что увеличить шаг сетки и прикрутить градиентный спуск, его и сам написать можешь. Как еще один прикол - вместо того, чтоб решать задачу с ограничениями, просто наебни функцию штрафа, по типу $f(x) = ||x||^{2} + \betha \sum_{i} (\min(0, \rho_{i}(x) - r))^{2}$, где $\pho$ - знаковые функции расстояния до фигур.
Пиздец я в техе обосрался, но вроде все и так понятно.
Двачую сетка. Можно на ГПУ наебенить
$ сдвиг графика по оси Х += (координаты мыши масштаб графика) - (координаты мыши новый масштаб графика) $
какая то поебень у вас тут
﹩сдвиг графика по оси Х += (координаты мыши масштаб графика) - (координаты мыши новый масштаб графика)﹩
 1,1 Мб, 1200x759
1,1 Мб, 1200x759Потому что ты не знаешь разницы между машиной Тьюринга и универсальной машиной Тьюринга. Если бы знал, то знал бы и то, что последняя - это общий формализм универсального вычислителя, поэтому любая конкретная нумерация ячеек ленты не имеет смысла.
Если бы была возможность не ползать по ленте влево вправо, а сразу прыгнуть на ячейку с конкретным номером, то вычислитель перестал бы быть универсальным?
Тогда пришлось бы добавить возможность записывать произвольные числа в ячейку вместо конечного алфавита.
>Если бы была возможность не ползать по ленте влево вправо, а сразу прыгнуть на ячейку с конкретным номером, то вычислитель перестал бы быть универсальным?
Нет конечно же. Описанная тобой возможность изначально предполагает конкретную нумерацию ячеек, отсюда возможность перейти к любой ячейке, нумерация которой вычислима в данной программе. В чем и суть, можно задать любую нумерацию ячеек, вычислимую в заданной программе, а не ограничиваться заранее заданной. Это одна из причин, почему универсальная машина Тьюринга это именно общий формализм любого возможного вычислителя.
> Потому что ты не знаешь разницы между машиной Тьюринга и универсальной машиной Тьюринга.
Слово "разница" в данном контексте как-то нелепо звучит. Какая, например, "разница" между множеством всех натуральных чисел и числом 1?
Вот так и тут... Понятно, что универсальная машина Тьюринга - это конкретный пример машины Тьюринга. Но говорить о РАЗНИЦЕ между конкретным примером какого-то объекта и множеством всех этих объектов - это как-то странно, мягко говоря.
Или ты нам хочешь сказать, что универсальная машина Тьюринга - это не машина Тьюринга?
>Какая, например, "разница" между множеством всех натуральных чисел и числом 1?
Что-то из этого является наименьшим индуктивным множеством содержащим 1, другое - нет. При определенном формализме теории множеств, одно является множеством, а другое - нет.
>Но говорить о РАЗНИЦЕ между конкретным примером какого-то объекта и множеством всех этих объектов - это как-то странно, мягко говоря.
Число 1 это не множество натуральных чисел, красное яблоко это не множество красных яблок (если только ты не готов отождествлять синглетоны с их единственными элементами). Раз решил до слова доебаться, то хоть бы аналогии нормальные придумал.
Но я понимаю о чем ты. Посмотрим на вопрос "есть ли смысл говорить о РАЗНИЦЕ между абстрактной группой и группой симметрий конкретного множества?". Очевиднейший для любого нормального человека ответ - имеет, как минимум потому что у нас есть теорема их нетривиальным образом связывающая и одно с другим путать нельзя.
мимо
>универсальная машина Тьюринга - это конкретный пример машины Тьюринга.
Вообще-то, наоборот. Универсальная машина Тьюринга это общий формализм, а не конкретный пример.
>говорить о РАЗНИЦЕ между конкретным примером какого-то объекта и множеством всех этих объектов - это как-то странно, мягко говоря.
То есть, ты не видишь разницы между например, аксиомами группы, и конкретной группой?
> Универсальная машина Тьюринга это общий формализм, а не конкретный пример.
О, вот это уже интересно. А если всю эту филологическую воду опустить, сможешь хотя бы примерно накидать твои определения машины Тьюринга и универсальной МТ?
Уже предвкушаю смешное чтиво.
> То есть, ты не видишь
Я этого не утверждал. Я лишь сказал, что странно говорить разнице объектов, которые уже на уровне типизации различаются. Давайте ещё обсудим, чем отлицается цвет от красного и вкус от горького.
>сможешь хотя бы примерно накидать твои определения машины Тьюринга и универсальной МТ?
"Мои" определения не отличаются от общепринятых.
>странно говорить разнице объектов, которые уже на уровне типизации различаются.
Надо же, про типизацию знаешь, ты у бабушки молодец? В таком случае, ответ на твой изначальный вопрос
>>103354 можно упростить до одного слова - полиморфизм.
> "Мои" определения не отличаются от общепринятых.
В таком случае ты противоречишь сам себе. Не забывай пить таблетки.
Почему бы не записать в ячейку произвольное число, она же не ограничена определенным числом битов, как ячейка памяти компьютера? Для произвольного числа все еще нужен конечный алфавит.
Как раз потому что компьютер так не может, а мы его моделируем. Вообще цель в том чтобы определить минимально возможную модель вычислителя, а не городить в нее удобств. Таблица переходов тоже тогда должна быть бесконечной.
У меня есть такая задача:
Пусть $X=\{1,...,n\}$, дана метрика $d$ в $X$ и функция $\omega: X^2 \rightarrow N_0$. Нужно определяя пермутацию(биекцию) $\sigma: X \rightarrow X$, нужно минимизировать $F(\sigma)=\sum_{(i,j)\in X^2}\omega(i,j)d(\sigma(i), \sigma(j))$
Если у вас есть хорошие идеи для алгоритма решения, то будет здорово, но у меня есть более конкретный вопрос.
Если я начну с произвольной пермутации $\sigma_0$ и определю $\sigma_i = argmax_{\sigma \in \{t \circ \sigma_{i-1}: t\in T\}}F(\sigma)$, где $T$ это множество транспозиций, то какое максимальное число итераций(можно через нотацию $O$) требуется для схождения алгоритма?
Почкольку твоя омега произвольная, никакой возможности воспользоваться остальной информацией особым способом не предвидится, так что давай чисто перебором. O(n^2)
Проигрываю с чуханов не могущих в O нотацию.
Я конкретно про этот случай.
То, что я наблюдаю в самых популярных книгах - это какое-то позорище. Тестирующие системы существуют уже не менее 20 лет, а они как писали задачи на бумажке, так и продолжают, блять.
Вы видите копию треда, сохраненную 13 августа в 01:37.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.