Вы видите копию треда, сохраненную 13 августа в 00:12.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
 47 Кб, 555x327
47 Кб, 555x327Рудин, Спивак, Зорич, Лоран Шварц, Дьедонне, Апостол, Аман-Эшер, Львовский, Ильян-Позняк, Фихтенгольц, Кудрявцев, ...
 22 Кб, 56x476
22 Кб, 56x476>НЕЛЬЗЯ ТАК ПРОСТО ВЗЯТЬ И РЕШИТЬ ВЕСЬ ДЕМИДОВИЧ
Если бы ты знал, как ошибаешся. Когда-нибудь я решу его всего.
получается понятие метрического пространства вводится аж в середине второго тома? неплохо так.
Понтрягин, Анализ бесконечно малых. Остальное не нужно.
Решетняки и Бонопольские это так называемая "новосибирская математика", отдельная наука, имеющая небольшие пересечения с обычной.
По-моему, в книге по анализу теории множеств не должно быть вообще, а на топологию хватит 5 страниц. Но если хочешь первые два тома только под это говно, твоё дело.
для тебя есть Харди "Курс чистой математики" и Гурса "Курс мат.анализа", а для людей из 21ого века другие учебники.
Физики сейчас по топологиям, дифференциальным формам, геометриям и когомологиям только и угорают. Посмотри "Geometry, Topology and Physics" Mikio Nakahara, есть на либгене.
Теория множеств это как раз доисторический материализм, вместе с Харди, Эдмундом Ландау, Гильбертом и прочей мразью
Для людей из 21 века, вроде меня, есть например, Conway A course in abstract analysis
Двачую. Еще Годбийон неплох.
В топологии ваша сраная теория множеств не была нужна никогда, кстати. Там специально придумали сначала симплициальные, потом cw-комплексы. См Зейферт-Трелльфаль например. Если в книге по топологии есть что-то про топологические пространства, это полный зашквар. Но если и надо, то открытых множеств можно избежать, введя понятие окрестности, например. Общая топология это недобитая мразь, последнее прибежище которой – курс анализа для института.
Для пиндосов и Винберг graduate, что ты хотел. Средний студент второго курса нму знает больше, чем аспирант любого вуза сша, кроме топ-10. У них там тригонометрию на бакалавриате учат, если. Страна дебилов, образования нет в принципе.
Пруф Винберга. Аспирант первого года в США = первокурсник в России, это было неоднокрано отмечено в сносках, в советских переводах книг типа Рудина и т.д. Андерград соответственно – матшкольник в понимании Вербицкого. То есть, зачем нужны книги типа Dummit-Foote, Rotman и тд до сих пор людям не ясно, типа смотри, мы вот поняли три главы Ленга, теперь популярно изложим тебе на 900 страницах.
Любой человек может читать сразу graduate, необходимый бэкграунд есть на ютубе у Вайдбергера, Harpreed Bedi, ХанАкадеми, в популярных брошюрах типа Библиотечка Квант, Современная математика –Популярная серия,
Сначала я хотел их похвалить, а потом вспомнил, что они даже ящик посчитать не могут.
Преимущество матшкольников совершенно точно не в способностях, и скорее всего даже не в том, что им все разжевывают максимально понятно. Хорошая мотивация скорее, людей стараются заинтересовать. Их так мало не потому что математика сложна, просто откуда еще обычный школьник узнает о её существовании. Ну интернет сейчас есть, из него можно.
В НМУ хуево, адекватные курсы по алгебре (типа Левин, Смирнов) не каждый год, гомологическая алгебра только в спецкурсах и тоже редко, алгебраичесой к-теории считай нет (Шарыгин читает топологическую сейчас впервые, и то дай бог если до хар классов дойдут).
Это никакой не идеал, конечно. Но даже мехмат по факту лучше большинства западных вузов, просто там учат прикладной математике по сути, давно пора это признать.
>Рудин, Спивак, Зорич, Лоран Шварц, Дьедонне, Апостол, Аман-Эшер, Львовский, Ильян-Позняк, Фихтенгольц, Кудрявцев, ...
И все жиды.
Картан хорош, да, но нужно линейку знать, прежде чем его читать.
По мне так, лучшие курсы алгебры были у Городенцева и Локтева, а Левин, наоборот, совсем не понравился.
> Для людей из 21 века, вроде меня, есть например, Conway A course in abstract analysis
Поделился бы.
Оп забыл винрарного лузина, по которому арнольды с колмогоровами учились.
Но он небось даже мем вин забыл...
Тобишь, если книга понятно написана то она для школьников, да!?
А если написана в духе ПОСЛЕ НЕБОЛЬШИХ ПРЕОБРАЗОВАНИЙ ОЧЕВИДНО ЧТО то она для Ъ маняматиков!?
>У них там тригонометрию на бакалавриате учат, если.
Студенты (не все из них math majors) там сами себе выбирают курсы, которые предлагает math department университета.
>Физики сейчас по топологиям, дифференциальным формам, геометриям и когомологиям только и угорают
это не физики, а долбоебы-недоматематики, решившие заняться физикой.
dima, zaloginsjya
Давай разберём всех трех.
Есть кукарекающий петух, у которого постоянно веруны мерещатся. Он ещё постоянно приклеплял Брауэра к картинкам, хуесосил Гилберта и переводил любой разговор в русло конструктивной математики.
Есть смайло-чуханчик. Анон, использующий :3 этот смайлик. Хотя, по-моему, смайло-чуханчик и есть первый.
Есть адекватный анон, который говорил первому заткнутся. Думаю, именно он заказывал книгу о Hott.
Из-за агрессивного настроя и ненависти к множествам, я предположил, что это первый конструктивист.
Заткнись и иди нахуй. Тред про учебники, а тебе давно пора в /soc со своими обсуждениями, говно.
Чуханчику ко-ко-косруктивисту непрятно. Тебе дать огнетушитель, чтобы ты потушил свою горящую задницу? Хотя тут огнетушителем не обойтись, нужна пожарная бригада. И не одна.
Я не есть ни один из тез трех анонов, которых ты перечислил. Просто ты меня заебал уже своим школоебством. Иди создай себе отдельный тред и там обсуждай своих воображаемых друзей, заебал уже.
Да ведь у меня ГЕТ ОЛОЛО КВАДРИПЛ НЕ ПИЗДИТ
Да, надо, но не потому, что я "конструктивист", а потому что ты заебал своими непрестанными кукареканьями.
Дело не в понятности, а в охвате (подборке) материала, серия так и назвается "Знакомство с высшей маняматикой", это исключительно для предварительного ознакомления и углубления школьных знаний, насколько я помню она достаточно небольшая и в ней даже формулы ньютона-лейбница нет (sic!). Я, честно говоря, не вижу особо смысла во всяких Пратусевичах/Давидовичах/Понтрягиных/Зельдовичах, все равно же потом Зорича-Шварца ебашить (и причем Зорич-Шварц это только азы, я уже молчу про остальное, в т.ч. нестандартный) тобишь П/Д/П/З - это АЗЫ АЗОВ.
У Понтрягина есть книга "Математический анализ для школьников". А есть "Анализ бесконечно малых". И вот в этой второй не только формула Ньютона-Лейбница, но и ряды Тейлора и Лорана, например. А самое главное достоинство – анализ излагается для R и C одновременно. И нет теории множеств, совсем.
>все равно же потом Зорича-Шварца ебашить
Ну ебашь своего Зорича, почему это обязательно? 1000 страниц и на 30 из них что-то о многообразиях, дифференциальных формах, "два слова о когомологиях де рама". Тогда как можно читать Спивака, Милнора/Уоллеса и далее любые graduate textbook по анализу, из упомянутых выше. Зорич же нужен чтобы приобрести мехмат головного мозга.
>про остальное, в т.ч. нестандартный
Что-то вроде универсальной алгебры, ты в 70-х застрял? Давно появился p-адический анализ. Зачем R*, когда есть Qp? Выбрасывай это говно нахуй.
 144 Кб, 600x696
144 Кб, 600x696Даю оглавление для сомневающихся. Кстати, формула Ньютона-Лейбница и в той книге есть. Размеры у них 280 и 90 страниц соответственно.
ты шо ёбнутый шо ли?
Зорич - это противовес мехмата, на мехмате изучают матан ВООБЩЕ без топологии и преподают какой-то пиздец 1920 годов.
и какой нахуй блядь милнор/уоллес? это популярное введение в дифференциальную топологию, зорич блядь тут ни при чем, как вообще можно эти 2 книги сопоставлять?
ЗОРЕЧ-ШВОРЦ, Я СКОЗАЛ!
На мехмате учат именно по Зоричу, инфа 100%. Алсо, point-set topology материал в твоём Зориче это и есть пиздец 1914 года, первый том уж точно.
Ты мыслишь ярлыками. Книга Милнора в англоязычном мире известна как введение в дифференциальную геометрию. У нас её издали в популярной серии. И что? По этим темам (теорема Стокса, теорема Сарда) там в разы больше, чем в Зориче. Calculus и differential topology это одна и та же область, вернее первое раздел второго.
Зачем учить отдельно калькулюс на вещественной прямой? Многообразия –> пучки –> векторные расслоения –> дифференциальные формы.
>вербита
Ну так он тоже рекомендует Спивака и Милнора, лолка.
Зорич/Шварц в его рекомендациях обусловлен тем, что вербит не осилил топологию, и считает, что когомологии де рама нужно изучать раньше, потому что так легче. Это чисто индивидуальная травма.
Ты прям страдаешь классическим математическим синдромом, когда что-то осознал, а потом не понимаешь, как это другие в это не вьедут. Типа давать надо самое абстрактное, все из него истекает. А в реальности все же строится совершенно наоборот, например, сначала дети ебутся с координатной системой, потом осознают векторное пространство, а потом обнаруживают для себя модуль над полем. Если же просто дать в лоб глубокий результат, это покажется каким-то абстрактным бредом, мотивировка очень важна для понимания.
>да знаю, меня же Фукс долго учил и здорово выучил
>этот процесс был прекращен, потому что
>Гинзбург решил, что если меня не остановить, я стану топологом,
>а эта наука на тот момент была при издыхании
>>1226
Jürgen Jost – Postmodern Analysis; Mathematical Concepts.
>>1237
Сначала дети ебутся с детерминантом как формулой, потом как площадью косоугольного параллепипеда, потом с алгеброй грассмана.
В математике есть либо простые определения, либо простые доказательства. Всегда только одно из двух, никогда оба. Сложные абстракции и обобщения создаются для каких-то целей, а не сами по себе; одна из этих целей – линеаризация.
>>1235
>симплициальные когомологии - какая-то мешанина индексов
>кроме того, континуальномерная
>производит впечатление тошнотворно некрасивой искусственной дряни
>(по крайней мере, на меня производила такое впечатление в 10-м классе,
>пока я не прочитал анализ Лорана Шварца)
Вот и вывод: Шварц не нужен, если есть нормальные книги по топологии. А они есть.
>топологии
вся топология - это стакан и чашка
этот факт так поразил топологов что с 19го века они дальше не продвинулись
https://ncatlab.org/nlab/show/ETCS
А они и не хотят.
Не существует никаких категоритов, гомотопистов, конструктивистов.
Есть современная математика. Это унивалентные основания, топосы без аксиомы выбора, категорная теория множеств.
А есть второкультурная мразь, которая их не понимает, зовут ли её мишей вербицким или как-то иначе, не важно, в данном случае.
Прими как данность.
>современная математика
Охуенная современная математика, думаю до теоремы Стокса эти математики лет через 50 дойдут с результатом уровня "невозможно доказать без аксиомы выбора".
>А есть второкультурная мразь
> Школьник подразумеевает, что вторая культура не является математикой и что с мнением второкультуршиков не следует считаться
Посчитайся с мнением Ферма, Декарта и Стевина. Их математика математикой не являлась, можешь думать что угодно по этому поводу. До Куммера, Жордана и Дедекинда математики вообще не было.
Мы до сих пор находимся на том же концептуальном уровне, а кое-кто и ниже. Не идущий в ногу со временем становится отстающим, но вторая культура и не пытается догнать первую. Это просто балласт, выброшенный в море.
Ну еще более днищенскими являются любители оснований математики, которые вместо того, чтобы жить в раю, построенным Кантором, как жили Гротендик и прочие Бурбаки, а пытаются сделать из говна и палок что-то свое, не продвигаясь дальше доказательств тривиальных фактов.
> До Куммера, Жордана и Дедекинда математики вообще не было
Конечно же была. Но ты можешь считать по другому, я тебе разрешаю.
>Не идущий в ногу со временем становится отстающим
Не согласен.
В математике много направлений. Не обязательно заниматся самыми модными. Представь, что есть математики, которые при виде категорей испывают то же чувство отвращения, что алгебраисты при решении интегралов. К тому же решение диффуры вторая культура, но их методы диффуров тоже модренизуруются со временем. То есть нужно знать все современные методы решения диффуров?
>но вторая культура и не пытается догнать первую
Первая далеко и не убегала.
>Это просто балласт, выброшенный в море.
Звучит, как описанние первой культуры.
Основания тут вообще не при чем. Здесь про методы работы.
а) you consider this a paradise, me considering as a joke.
б) теория множеств кантора построена не самим кантором, а дедекиндом
в) гротендик построил теорию топосов, а у бурбаков была собственная аксиоматика
То, что ты называешь словом "алгебраист", примерно соответствует значению слова математик.
>Конечно же была
Было решение уравнений. Это не математика.
>То есть нужно знать все современные методы решения диффуров?
Они решаются на компьютере. Базисами Грёбнера, сведением к системе линейных уравнений, численно. Полиномы выше пятой степени тоже решаются всегда, пусть и не в радикалах. Открыл это Кронекер, далее оно развилось в область называемую "теория тэта-функций". Работы Лагранжа и Галуа за бортом, вместе с ебанатами вроде тебя.
>То, что ты называешь словом "алгебраист", примерно соответствует значению слова математик.
Нет, алгебраист - математик, занимающейся алгеброй. Математики занимающеяся диффурами, комбинаторикой, теорией вероятностью, численными методами тоже математики. Ты можешь кукарекнуть что МОТИМАТИКА ЭТО ТОЛЬКО КОТИГОРИИ И ТОПАСЫ ДА ГАМАЛОГИИИ ОСТАЛЬНОГО НУЖНО ВЫБРАСИТЬ НА СВАЛКУ ИСТОРИИИ КУКДА-КУЖАХ
Но это будет очередной безосновательный кукарек.
>Было решение уравнений. Это не математика.
Решения уравнений математика, ты конечно можешь поспорить, но ведь у тебя нет на это аргументов, равда?
>Они решаются на компьютере.
Не всё можно решить на компе, только самое простое. Сложные вещи обычно решаются в ручную + немного на компе.
>численно
Ты обосрался, есть вещи которые численно не берутся.
>Работы Лагранжа и Галуа за бортом, вместе с ебанатами вроде тебя
>ко-ко-ко-кудах
*правда
В /pr есть байто-слесари, которые руками пишут на asm или сразу в машинный код. Вот то, что ты описываешь здесь, это такой слесарь от математики. Решающий руками диффуры, не берующиеся численно (лолшто?).
Наук есть много разных, но все они являются разделами алгебры, спасибо можешь сказать Дедекинду.
>Наук есть много разных, но все они являются разделами алгебры
И где же пруфец? Даже если там и можно примять категорно-гомологические методы то это как-раз и будут те байто- слесари.
Математика это наука о модулях над кольцами.
Функции, определенные на заданном интервале, образуют кольцо. Дифференцирование это гомоморфизм кольца. Интегрирование это примение двойственности Пуанкаре к классу когомологий дифференциальной формы.
Естественное расширение понятия числа это векторное пространство, что есть частный случай "хорошего" модуля. Естественное расширение понятия функции это пучок. Анализ – набор узкоспециализированных областей алгебраической и дифференциальной геометрии.
В рамках мышления 12-го века все это кажется неестественным, но на самом деле это инертность мышления.
>Математика это наука о модулях над кольцами.
Проиграл. Тебе не обязательно всюду сувать свою алгебру.
То есть вычислительная математика для тебя уже не математика?
Вычислительная математика это раздел алгебры. Базисы Грёбнера, методы Эрмита и Горовица, алгоритм Евклида. Система Sage. См: Идеалы многообразия и алгоритмы, eisenbud commutative algebra, геометрия полугруппы Z^n >=0.
Это было на самом деле оскорбление, типа да у тебя и собака алгебра на кольцом.
>Они решаются на компьютере. Базисами Грёбнера, сведением к системе линейных уравнений, численно.
решаются, но не тобой. ты сам походу ничего не сможешь решить, своими теэта-функциями.
>Полиномы выше пятой степени тоже решаются всегда
предоставь аналитическое решение уравнения x^6+ax+b=0
Естественно не мной, не моя область. Просто довожу до тебя, пса отсталого, известную мне информацию.
wolframalpha.com/input/?i=x%5E6%2Bax%2Bb%3D0
Что сказать-то хотел? Диффуры порядка выше четырёх тоже не решаются аналитически в общем виде. Что говорит только о содержании "дифференциальных уравнений" как учебной дисциплины.
На еще почитай, там есть список identities для каждой степени в конце.
Спасибо за /math.
Кстати, кто что думает по книге Дьедонне "Основы современного анализа"? Я просмотрел, конструкция красивая, всё на банаховых пространствах. Первокультурно. Но Вербит сказал как-то, что книга нереально плохая. Почему, блядь? Он ебанулся? Не понимаю. Оцените сами. Вот либген-ссылка: http://libgen.io/ads.php?md5=97316A8109C09065EDA147526E6BFE6E
Дык читай Jost'а, он тоже на банаховых пространствах. Правда и его ругают (sowa в основном).
А что думаешь по поводу трёхтомника "Analysis" от Aman и Escher?
Там пиздец какой-то. Гамалогеи с гапатопеями в первом курсе анализа! Нахуй?
Другой анон.
Так тебе настоящее решение нужно, без этих философских бредней? Тогда тебе к специалисту:
https://vk.com/id216412435
Двачую, начиталься своих модулей на кольцами, а потом выёбывается тут.
Гомотопии и накрытия, по-хорошему, надо учить еще в школе. Проще будет объяснять векторные расслоения на первом курсе.
>еще в школе
опять матшкольник с задней парты вещает. У всего нормального мира есть undergraduate для такого.
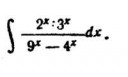 5 Кб, 274x167
5 Кб, 274x167http://www.wolframalpha.com/input/?i=integral+((2/3)^x)/(9^x-4^x)
Ты жиденько обосрался.
*могут
Хуйло с домашкой, ты серьезно считаешь, что каким-то прикладникам в их работе требуется символьно решать задачи из Демидовича?
Почему компьютер не посчитал? Потому что ты не научился выполнять ПРЕОБРАЗОВАНИЕ ПОДЫНТЕГРАЛЬНОГО ВЫРАЖЕНИЯ и ЗАМЕНУ ПЕРЕМЕННОЙ. Есть книга Боярчук, там расписано как это делать.
Но если ты думаешь, что крутые математики только и делают что решают Демидовича (или что крутым математиком не стать, пока не решишь толстую красную книжку), то я с тобой не согласен.
Детский сад какой-то, блядь, Сканави иди еще порешай.
Хуесос, я лишь показал, что твою компы нихуйя не умеют кроме самых легких однотипных задач. Твои вскукареки о чудодейственных компах полная лажа.
Софтверные пакеты умеют все, что может когда-либо понадобиться на практике: считать матрицы больших размеров при чем тут становится очевидной несостоятельность картофельных алгоритмов типа формул Гаусса и Крамера, приближать диффуры системами с очень большим количеством линейных уравнений, и тд. Но вот делать тупую домашку за тебя умеют плохо, видимо. Для тебя это очень важно, и отсюда ты делаешь вывод что вычислительная алгебра второй половины 20-го века полная лажа и бесполезна, то ли дело набор трюков для решения Демидовича.
>Но вот делать тупую домашку за тебя умеют плохо, видимо
Найс, подрыв.
Во первых это не моя домашка.
Во вторых,
>Софтверные пакеты умеют все
тогда почему они не могут решить простейший интеграл? А?
>Для тебя это очень важно, и отсюда ты делаешь вывод что вычислительная алгебра второй половины 20-го века полная лажа и бесполезна, то ли дело набор трюков для решения Демидовича.
Я не демаю вывод, что она бесполезна, идиот. Я просто говорю, что всеравно приходится считать ручками потмоу что компуктер тупой.
>то ли дело набор трюков для решения Демидовича.
Даже набор трюков полезнее, чем определять векторное пространство, как модуль на кольцом. Прими это как факт.
Я не особо-то в калькуляторах шарю, но разве Mathematica не самый навороченный из них? Если она не справится, другой уж точно.
Это вопрос конкретной реализации алгоритма Риша-Трагера-Бронштейна, вполне может быть, что Axiom или Maple могут лучше.
Я просто проходил мимо и вынужден признать, что твои оппоненты по спору выглядят по сравнению с тобой пятилетними детьми.
Я с тобой не вполне согласен, но не готов аргументированно и убедительно спорить. Возможно, дело и вправду в инертности мышления.
 441 Кб, 1920x1080
441 Кб, 1920x1080>что за зеленые галочки?
Я любитель решать ВСЕ задачи в книге. Раньше решал их по порядку, потом понял, что это тормозит меня, т.к. всередину могут всунуть харкорную задачу. Чтобы не запутатася, стал вести список решенных задачь на бумаге, но это было слишком муторно. Потом понял, что можно отмечать их прямо в книге.
Так и перфекцеонизм не мучает, поскольку знаешь, что всегда можно вернутся к старым нерешенным задачам и прорешать их все.
>это какая-то программа?
PDF-XChange Viewer
>>1454
Шабат Введение в комплексный анализ
Альфорс и Хермандео. Они на шведском, но шведский легко выучить по книга Маслова, Лошанская, Толстая. Либо по курсам assimil, но они на французском, который можно выучить по Попова Казакова Кавальчук
Почти все книги минимум тридцатилетней давности давно переведены
дер*
Кудрявцев лол. Помню начал изучать анализ по его книге.
Вводит понятие числовой последовательности.
Элементами могут быть числа.
Потом (или перед этим) как-то вскользь упоминает бесконечность - т.е. символ бесконечности. Это - не число.
Потом такой хуяк и показывает - числовая последовательность бесконечностей. Типа - бесконечность у нас тоже может быть элементом последоватльности.
Сижу с дырой в мозгу, чешу затылок. Не понимаю прикола.
Спрашиваю у товарищей - им вообще похуй на такие мелочи.
Потом взял другой учебник - там уже такой дичи не было.
Определение топологического пространства в самом конце. Не нужно.
Оттуда же. Там дополнение в конце книги этой теме посвящено.
Ну половину демидовича за пару курсов, сверхсильно на нем не концентрируясь, сделать можно.
>Шабат Введение в комплексный анализ
Его же Методы теории функций комплексной переменной читаются до анализа или после?
А почему?
Поясните, теория функций комплексной переменной идет до комплексного анализа или после?
Ну и что плохого? Стандартный бурбакист.
Могу только поаплодировать за такую статью за его авторством.
Всё так.
Кстати, известно ли, какой из томов Бурбаки написал лично Дьедонне?
По-моему скромному мнению, Фихтенгольц хорош , потому-что понятный, а Кудрявцев нет.
Ded, pls.
Заебись тебе, сможешь преподом в универе работать за еду.
А теперь поберегите силы. Это определение производной.
Вопрос к догадливым читателям. Как Дьедонне определяет производной? Как определяет интеграл?
Ты идиот? Нормальные определения.
Простая первообразная функции f определяется как отображение F числового промежутка I в банахово пространство, такое, что
1. F непрерывна
2. Почти во всех точках промежутка I производная F существует и равна соответствующему значению f.
Простой интеграл от функции f по промежутку от a до b определяется как число, равное разности F(b)-F(a), где F - произвольная первообразная.
В определениях предполагается, что f имеет односторонние пределы в каждой точке промежутка.
Почти во всех = во всех, кроме счётного множества.
Да пусть что угодно пишет. Похуй ваще. Гротендик всё равно охуенен.
Всем это и так ясно. Там определяются дифференциальные операторы и комплексно-аналитические пространства максимально доступным языком.
Нет, лучшая книга по анализу - это Винберг "Алгебра". Потому что анализ - херня, и учить его не надо.
 38 Кб, 634x317
38 Кб, 634x317шёл бы ты отсюда, долбоёб
А ссылочкой не поделишься? Я погуглил, как-то не нашёл ничего.
Где он его ругал? И за что? Чем учебник плох?
Jost Postmodern Analysis. Поищи на либгене.
Ругал не конкретно это, а его же книгу по римановым поверхностям, как плохо написанную и довольно бессмысленную. Обсуждение в жж его можешь найти, воспользовавшись гугл-поиском по сайту livejournal.
Поискал (я так понял, книга имелась в виду "Riemannian Geometry and Geometric Analysis", но нихера не нашёл (в lj, а не ljr, верно?)
А ты сам читал "Postmodern Analysis". Просто выглядит охеренно. Там, кажись, и на векторных нормированных пространствах всё делается, и ещё и педагогичнее, чем Дьедонне. Но хуй его знает. Мб лучше читать что-то типа Львовского или Рудина (или Pugh "Real Mathematical Analysis"). Я хз. Amann, Escher слишком большой.
http://lj.rossia.org/users/dmitri_pavlov/4733.html?thread=150397
Да это я попутал. Думал в лж посика, а оказалось в лжр павлова.
Посмотри ещё Gert Pedersen Analysis now и Conway Course in abstract analysis, мож зайдет.
J. Jost, Riemannian Geometry and Geometric Analysis (4 или 5 изданий за не более, чем 10 лет) - хороший подбор материала, но (судя по его другим книгам и статьям), очень неаккуратный автор, отчасти предпочитает формулы структурным объяснениям;
Я решаю Сканави.
Что думаете о Amann-Escher "Analysis"
Чотко, заебись? бля просто 3 тома по 400 страниц, пизда рулю, епта
Или там всё по делу? Мощно, четко, молодежно, надо знать?
В третьем томе вообще абстрактная теория меры и гладкие многообразия, круто же?
Но второй том какой-то стремные... Там всякие картофан, не? Или показалось и надо смело читать?
Картан - это суровая книжка калькулюса ТОЛЬКО на Банаховых пространствах.
Материала Рудина и Львовского она не содержит.
>Ильян-Позняк, Фихтенгольц, Кудрявцев
Это всё совок и картофан. Ещё и плохо написанный
Читать только если ты долбоеб стремящийся только сдать экзамен на своем мехмате или даунке. И то скорее всего не сдашь, потому что ты ебаный мудак
А если хочешь выучить математику, то такие книги полезны только в камине
>Спивак
Какой? "Calculus"? Он морально устарел. Ну, инженерам, может, и стоит читать, а математикам не надо
Или "Calculus on Manifolds"? Эту книгу надо читать уже после первых 6-ти глав Рудина, и она очень сжатая (есть менее краткая альтернатива - Munkres "Analysis on Manifolds")
> Зорич
Мехмат и координатная ахинея. Написано хорошо и понятно, но лучше не стоит. Хотя, если ты инженер или физик, то можно. Но математикам не стоит, если, конечно, они не хотят посвятить научную карьеру картофану, типа диффуров и асимптотик
Так с какой конкретно книги по анализу начать, если ты хочешь быть чистым математиком?
Я бы посоветовал Amann-Escher "Analysis". Если осилишь, кроме знания анализа приобретешь существенную долю математической грамотности.
Но учти, что я сам её не читал, и сужу по тому, что знаю.
Ещё, наверное, Шварц неплохой, если из русских надо (но если хочешь быть математиков, знание английского - мастхэв).
А что значит "знать анализ"? Уметь решать заумные интегралы с параметром из Демидовича?
Шварц француз.
Знать для чего и откуда, для незнающего анализ, шварц это тонна определений данных хуйми для чего и теорем доказываемых хуй пойми зачем. Если же человек знает анализ, то по шварцу он вполне может взглянуть с других сторон на него.
>Знать для чего
Узнаешь, когда будешь заниматься науками, использующими анализ. Но некоторые понятия никогда не пригодятся, да.
>откуда
Это уже относится к истории математики.
>шварц это тонна определений данных хуйми для чего и теорем доказываемых хуй пойми зачем
Ну как зачем? Как, минимум, для эстетического удовольствия и для использования в других областях математики, знать которые изучающий анализ пока не может в силу своей неподготовленности.
>Узнаешь, когда будешь заниматься науками, использующими анализ. Но некоторые понятия никогда не пригодятся, да.
>Это уже относится к истории математики.
А если тот анон имел ввиду внутри самой математики? Знать откуда откуда одна теорема следует и для чего она нужна, то есть какой место занимает в теории, что с помощью неё можно доказать. Твой ответ выглядит, как толстый троллинг.
>и для использования в других областях математики, знать которые изучающий анализ пока не может в силу своей неподготовленности.
Тогда почему бы не сказать в каких?
Нет ты
Я шизоид. А чего добился ты?
Чем?
>Я бы посоветовал Amann-Escher "Analysis"
Сейчас читаю его в оригинале. Аманн-Эшер точно не подходит как первый курс анализа. Проверить, подходит ли он тебе, можно достаточно просто: качается английский перевод первого тома с либгена, открывается 44 страница (31 по внутренней нумерации), читается весь раздел The Arithmetic of Natural Numbers. Если он не понятен - книга откладывается до лучший времен. Собственно, пруф там просто отвратительный, у Биркхоффа-Маклейна в Алгебре этот момент пояснен намного лучше, хотя так же абстрактно.
>>5083
>Так с какой конкретно книги по анализу начать, если ты хочешь быть чистым математиком?
С той, которую ты понимаешь. Я бы посоветовал сначала пройти вот это хотя бы до 9-ой главы (упражнения, есть на либгене, как и решебник):
https://www.amazon.com/Mathematical-Proofs-Transition-Advanced-Mathematics/dp/0321797094/
И прочитать вот это:
https://www.amazon.com/Naive-Set-Theory-Paul-Halmos/dp/1781394660/
А потом брать Зорича.
Не знаю, насколько она хороша для первого прочтения, но как reference очень хорошая.
1) Немного в стиле Дональда Кнута. Автор примерно настолько же эрудирован в современном анализе.
2) С одной стороны, мало картофана; с другой стороны, нет ухода в геометрию там, где это не надо; чистый анализ.
3) Довольно интересный (хотя и не новый) подход к изложению теории меры.
Я не хочу особо навязыать, но если вы планируете теоремы доказывать, а не только выпенриваться знанием доказательства теоремы де Рама через пучки, то посмотрите хотя бы по диагонали.
Высококачественные pdf от издательства были украдены в день релиза, поэтому найти их нет проблем.
А по оставшимся двум томам наука слишком сильно ушла вперёд, и вместо каждой главы нужно читать отдельную книгу, или забить.
По структуре этот пятитомник напоминает 4-томник Elias M. Stein\Rami Shakarchi. Интересно было бы сравнить.
Я бы сказал, что Stein-Shakarchi примерно уровнем ниже по сложности. Например, спектральная теорема только для ограниченных операторов и мелким шрифтом.
Но в целом оба хорошие, и акценты примерно соответствуют предпочтениям авторов.
Стейн является хорошей подготовительной книгой к микролокальному анализу.
Саймон подготавливает к уходу в дебри спектральной теории.
А чем доказательство плохое-то? В стиле Лэнга что-ли, теорема доказывается последовательным применением слова "очевидно"? Или что? Качать и смотреть лень. Если просто абстрактно, то это и хорошо. Другое дело, если детали не объясняются, и куски док-ва пропускаются. Это не дело уже.
И что читать людям тогда? Рудина? Pugh?
А то первый том Зорича - это какой-то картофан.
Кстати, я согласен, что Халмоша стоит прочитать в самом начале. Я вот не прочитал, пришлось потом наверстывать.
>А то первый том Зорича - это какой-то картофан.
Картофан тоже надо знать, или он так уж страшен? Спроси у Тао в бложике, почему он, передовой математик, в первом томе своего "Анализа" писал о картофане.
>Рудина? Pugh?
Такой же картофан.
В свое время Шварц был в свое время лютым вином. Жаль, устарел.
Остальное либо не читал, либо сорта говна: Львовский - относительно свежее и ароматное, Фихтенгольц - засохшее говнецо мамонта.
Например, давать интегралы через когомологии де Рама. Теория меры ненужное говно.
> давать интегралы через когомологии де Рама
> Теория меры ненужное говно.
Дмитрий Павлов, залогиньтесь
как вы уравнение Монжа-Ампера решать будете, карасики?
а теорему индекса вы будете без эллиптических операторов и альтернативы фредгольма постигать? да даже за лемму Пуанкаре, чтоб ацикличность резольвенты де Рама показать, вы что, мамкой поклянётесь?
лучшая книга по анализу нужна только для этого: чтоб понимать современный анализ, а не чтоб вводить многообразия и интегралы без разрывов
>чтоб понимать современный анализ
Современный анализ - это здорово, но не все будут им заниматься.
Обсуждается, какую книгу по анализу читать ВСЕМ чистым математикам, в том числе тем, которые анализом никогда заниматься не будут в жизни.
>>5574
>а не чтоб вводить многообразия и интегралы
А вот как раз многообразия надо знать всем, в отличие от Монж-Ампера.
При том, что Монж-Ампер очень важен сейчас в комплексно-аналитической геометрии, это всё интересно лишь для специалистов для аналитиков и (дифференциальных) геометров.
Речь о образовательном курсе для всех математиков (но не для инжынерав).
Дай книгу, где так излагается всё. И чтение которой не требует знания дохуя классических курсов, где интегралы даются не через когомологии.
Иначе твоё сообщение смысла не имеет.
>Картофан тоже надо знать, или он так уж страшен?
Не страшен, а бесполезен для большинства математиков. А кому надо, пусть учит. Никто же не добавляет алгебраическую геометрию в обязательные курсы для всех. Почему и все математики должны учить то, что нужно лишь диффурщикам и прикладникам?
> Спроси у Тао в бложике, почему он, передовой математик, в первом томе своего "Анализа" писал о картофане
У Тао, кажется, не очень плохо всё. Но Тао как раз занимается в том числе "классическим" анализом ("картофаном"). Да, можно быть топовым математиком, занимаясь и картофаном.
>Такой же картофан.
Ты вообще походу не знаешь, что такое картофан.
Анализ != картофан. Картофан - это экзотические архаичные части анализа, типа всяких экзотических трюков для решения диффуров, которые любят преподавать всем на рашкованских мехматах и махметах.
А в Зориче слишком много вычислений и недостаточно концептуальности. Например, он дает формулы разложения в ряд Тейлора и говорит: "Пользуйтесь, докажем потом как-нибудь".
Но на фоне существующего безумия а-ля Ильин-Позняк/Фихтенгольц/Подольский и т.д. Зорич неплох.
Крутые краткие лекции по анализу от Филдсовского медалиста из Беркли.
всего за 50$ без регистрацией и СМС - специальное предложение!
уметь решать (ну то есть доказывать C^0-оценки и подобное) Монж-Ампера все не могут, но иметь представление как это вообще делается, если ты имеешь отношение к комплексной геометрии, несомненно надо. да даже и вообще, для общей культуры
а то, о чём ты, анончик, говоришь, это называется анализ на многообразиях, и по нему ТЫЩЩИ учебников. какой кому нравится, это вопрос глубоко интимный, но недостатка в учебниках точно нет.
по-моему, тутошние аноны доброй воли на самом деле хотят устроить "анализ анонимус" и рассказать всем о своих иррациональных страхах перед пучками, теорией интегрирования на многообразиях и теоремой стокса
ну так не над стесняться, чо, все такими были
>но иметь представление как это вообще делается, если ты имеешь отношение к комплексной геометрии,
И я об этом же. Но открою секрет: не каждый математик даже сталкивается с комплексной геометрией
>>5704
>да даже и вообще, для общей культуры
Не надо.
>а то, о чём ты, анончик, говоришь, это называется анализ на многообразиях, и по нему ТЫЩЩИ учебников. какой кому нравится, это вопрос глубоко интимный, но недостатка в учебниках точно нет.
И что с того? Фишка в том, что не всем надо тратить время на "картофан". Пусть тратят те, кому это надо.
>Например, он дает формулы разложения в ряд Тейлора и говорит: "Пользуйтесь, докажем потом как-нибудь".
Ты бы ещё к окрестностям у него приебался.
>И что с того? Фишка в том, что не всем надо тратить время на "картофан". Пусть тратят те, кому это надо.
Тогда почему местные аноны кричат, что всем нужны пучки-гомологии-категории? Те кому нужно сами выучат.
Потому что они используются в большем количестве областей математики, чем архаичная экзотика из Фихтенгольца.
Ладно, разжую. Никто не говорит, что людей не надо знакомить с анализом. Фишка в том, что большинству больше классического анализа, чем у Рудина (а то и чем у Львовского), не понадобится.
Точно так же и с гомологической алгеброй. Не каждый математик должен изучать целую толстую книжку по ней. Но каждый должен ознакомиться с её базовыми понятиями, использующимися в немалом кол-ве областей математики.
> не надо
> Но открою секрет: не каждый математик даже сталкивается с комплексной геометрией
открою секрет: больше половины современной математики связано с комплексной геометрией так или иначе. если ты вообще с ней не сталкиваешься, это очень странно
оно конечно хочешь быть ускоспециализированеым специалистом по сепуклькующимся сепуляторам --- be my guest
по поводу картофана
как тут уже отметили, анализ не картофан автоматически. без Леммы пуанкаре в геометрии не проживёшь, если давать конкретный пример. если доказывать формулу индекса, это потянет элл операторы и соболевские пространства, самый что ни на есть анализ. под картофаном понимают (это пошло от поста у вербита, сославшегося на метафору, употреблённую крыловым) то, что плохие, зашоренные сотрудники мгу рассказывают студентам, хотя ненавидят сами, за сложность и бессмысленность. лемма пуанкаре и соболевские пространства к этому не относятся. "анализ на многообразиях" тоже, потому что азбука
>Фишка в том, что большинству больше классического анализа,
>большинству
И кто же это большинство? Алгеомщики?
Я вот думаю, большинству математиков, как раз дохуя анализа и надо, а те же категории им максимум пригодятся в виде первых главах Ленга.
Промазал, звиняйте.
Теория категорий, гамалогии и тапалогии. Вообщем всё самое новое в науке, что не может иметь пркатического применения.
Ясно, очередной вербитоеб. Как подрастешь, увидишь, что нет никакой "единой математики".
Комплексная геометрия - это, кстати, довольно обособленная область, хоть и большая (я сам её люблю и уважаю).
>>5741
>И кто же это большинство? Алгеомщики?
Алгебраическая геометрия
Дифференциальная топология
Алгебраическая топология
Алгебраическая теория чисел
Гомологическая алгебра
Некоммутативная геометрия
Метрическая геометрия
Коммутативная алгебра
Некоммутативная алгебра
Алгебраическая К-теория
Теория множеств
Теория категорий
Это так, с ходу. Даже Вербицкий, занимающийся аналитическими науками, признает, что классический анализ ему почти не нужен (нужен современный анализ, который почти не опирается на классический). Где нужен классический анализ? В нескольких полуприкладных областях?
>>5737
>как тут уже отметили, анализ не картофан автоматически.
Это именно я и отмечал. Современный анализ - не картофан.
>о, что плохие, зашоренные сотрудники мгу рассказывают студентам, хотя ненавидят сами, за сложность и бессмысленность.
И я об этом. Анализ 1920-х годов. Вычисления и т.д. Фихтенгольц или первый том Зорича. Всякие несобственные интегралы с параметрами и прочая муть.
Вы хотите сказать, что современные математики SOVSEM NE ZNAJUT KLASSICHESKOGO ANALIZA?
А чем занимается теория множеств в наши дни, какие у них загадки нераспутанные есть?
Без понятия, не интересовался, но знаю точно, что исследования в этой науке ведутся.
В основном в ZFC. Они ещё какие-то другие аксиомы добавляют к ней, кажется.
>А чем занимается теория множеств в наши дни, какие у них загадки нераспутанные есть?
Где-то с 60-х в теории множеств люди в основном занимаются построением моделей теории множеств с разными свойствами. В основном с целью доказать, что какое-нибудь утверждение независимо от какого-нибудь другого над ZF, хотя, конечно, этим дело не ограничивается. Насколько я могу судить, на настоящий момент запас хороших задач в области порядком истощился.
Из крупных вопросов, до сих пор идут математические исследования с философской подоплекой вокруг проблемы континуума (Коэн и Гёдель уже давно доказали, что CH независима от ZFC, если ZFC непротиворечива, но это не закрывает вопрос для людей не отождествляющих математическую истину с доказуемостью в ZFC).
Есть несколько вопросов имеющих большую внутреннюю важность для современной теории множеств, но боюсь, что пытаться объяснить о чем идет речь будет довольно безнадежно (я начал писать абзац о программе внутренних моделей, но поняв глупость этой затеи стер его).
Если отойти от центральной части теории множеств, то до сих пор есть вопрос о естественных комбинаторных утверждениях независимых от ZFC (есть примеры Фридмана, но их естественность несколько сомнительна).
что-то я тебя не пойму анон, сначала ты говоришь комлексная геометрия не нужна, потом, отвечая другому анону, приводишь список из десятка дисциплин, которые тесно с ней связаны.
и топишь за "современный анализ". ну я как бы за него же и топлю
не вижу ничего зазорного в признании влияния Вербицкого: он на меня повлиял. не один один
а насчёт "подрасти", в условиях анонимности мы credentials конечно меряться не будем, но поверь, у меня больше
>сначала ты говоришь комлексная геометрия не нужна,
Она нужна. Очень хорошая наука.
Но единство математики - миф Вербицкого.
>>5838
>не вижу ничего зазорного в признании влияния Вербицкого: он на меня повлиял. не один один
На меня тоже. Но к его словам надо относиться критически. Особенно к его мнению о том, что крутая наука? а что говно.
это не миф, а точка зрения, которая разделяется многими математиками.
во-первых, есть беспристрастные бесчисленные наблюдения, как неожиданные вещи друг с другом связаны. типа, есть связь между числовыми полями и 3-многообразиями; и у тех и у тех гомологическая размерность 3 (если у первых брать этальные когомологии), простым идеалам соответствуют узлы, а локальный фробениус это обход вокруг соответствующего S^1. ну ок, можно подойти утилитарно, и сказать, что это детская забава, а не наука, и серьёзным дядям нахуй не всралось искать аналогии в таких столь отдалённых друг от друга областях как топология и теория чисел (манин и мэйзур так не считают), но если бы это был один такой пример!
почти всегда объединение техник из разных разделов приводит к прогрессу, одна теорема калаби-яу чего стоит. ну или я не знаю, более общо, можно делать алгебраическую геометрию на чисто упёртом алгебраическом языке, по-над кольцами, но если ты работаешь над C, то игнорировать трансцендентные техники глупо, алгебраические аналоги не всегда есть и часто сложнее (и наоборот). ок, разложение ходжа можно делать по делиню-иллюзи через редукцию в характеристику p, но алгебраического аналога кэлеровости уже нет, кэлеровых соотношений нет, хард лефшеца нет, черна-вейля нет. итд итп
во-вторых, есть этический императив: если ты занимаешься чем-то, что не может быть встроено во всеобщую канву развития математики, то значит ты эгоистически узурпируешь ресурсы - внимание рецензентов и слушателей твоих докладов, деньги из грантов наконец - на что-то, что сообществу вцелом не может быть полезно.
в-третьих, чисто эстетически моменты взаимодействия красивы, их следует ценить и к ним стремиться. как и все эстетические критерии, это очень личное.
>SOVSEM NE ZNAJUT KLASSICHESKOGO ANALIZA?
Конечно. И Калькулюс в вузиках не преподают, это все выдумки рнептилоидов. Зуб даю, что Тао не найдет производной от косинуса.
Зачем математику знать тригонометрические функции, если они сводятся к показательным?
Зачем математику знать показательные функции, если они сводятся к тригонометрическим?
Знать не надо, надо уметь работать. Некоторые вещи намного проще воспринимаются через геометрические аналогии, чем через голую алгебру.
ты дебил, основывающий свой вкус даже не на мнении, а на фольклорном представлении о мнении авторитетов
Иди нахуй, мелкобуквенный даун. Я не знаю каким дебилом надо быть, чтобы полагать, что ведущие математики мира не владеют калькулюсом. С трех лет одни только гамалогии видели, ага.
Ты такой же даун, если не видишь взаимосвязи. Ведущие математики мира жрут говно, не потому что им это нравится, а потому что так надо. Если в зарубежной аспирантуре ты обязан читать калькулюс, это входит в твой контракт, блядь, без которого тебе не видать оплаты твоего обучения, естественно ты его знаешь, мудило.
>Ведущие математики мира жрут говно, не потому что им это нравится, а потому что так надо.
>так надо
Кекнул с пидорашьей мантры.
Во-первых, калькулюс они проходят еще в школе. А во-вторых, настоящие преподы (Тао, к примеру, в своем бложике писал, и я знаю цитату у John M. Howie) признают, что первым уровнем приобретения мат. знаний должен быть интуиционный/наглядный. Калькулюс как раз и выступает таким инструментом в областях, связанных анализом, непрерывностью и бесконечно малыми.
Если какого-то левого Васяна с двора сразу же начать кормить формализмами-бурбакизмами, которые он не понимает, то он быстрее поедет крышей или забьет хуй, чем докажет любую теорему или продвинется в понимании предмета.
>Во-первых, калькулюс они проходят еще в школе
То-то на андерграде у них только тригонометрия а gre соответствует уровню егэшной матеши
Вылезай из манямирка
Я говорил о всяких Тао, Джейкобах Лурье и прочих Мирзахани - тех, кто еще школотой нагибал в ММО. Это они ведь ведущие математики сегодня.
Салливан до поступления в аспирантуру вообще математики не знал
А среди тех, кого ты назвал, ни одного первоклассного математика все равно нет
God: Шварц
Top: Зорич, Львовский, Рудин
Shit: Ильин-Позняк, Кудрявцев, Фихт
С остальным мало знаком.
>ни одного первоклассного математика все равно нет
Только не говори мне, что "первоклассные математики" - это диды с Абелем в кармане.
Просто глянте, что мразь Brukvalub говорит о Шварце!
 33 Кб, 456x240
33 Кб, 456x240Какой-же у этого брюквалюба отвратительный аватар, наверное, один из худших, что я видел. Когда он пишет что-то, то я представляю, как маленький уродливый скрученый дед тоненьким говолочком начинает поучать всех. Бррррр.
Только прочитайте это. Все в радости от того, что Brukvalub возвращается на dxdy, счастливо размазывают кал друг по другу и поздравляют друг друга.
http://dxdy.ru/topic23558.html
А здесь он уходит, потому что его забанили! Забанили, вот беда-то!
Со множеством оговорок можно провести аналогию:
Форум – государство.
Заслуженные участники – граждане. (Я не случайно выделяю постоянных и уважаемых участников в отдельную категорию).
Модераторы – представители власти.
Правила форума – законы.
Текущее состояние соответствует самому примитивному гос-ву: принимают законы, судят и применяют санкции одни и те же лица.
Я не в укор кому-то говорю про примитивность, на первом этапе такая система естественна. Но так же естественна ее порочность.
Бегство граждан от авторитарного произвола – закономерно. Такая проблема присутствует и на других форумах.
Решение проблемы не оригинально. По аналогии с развитием гос-ва: расширять гражданские права, совершенствовать судебную систему.
На даче можно картоху посадить ))))
Этот совок преподает на мехмате, но считает, что математики не нужны, соответственно, на мехмате так и должны преподавать замшелое говно мамонта, так как "нет такой профессии - статьи писать"(с)
Ну совок это понятно.
Но нам он как раз рассказывал про то как математики важны, что это широко применяемая специальность и тд, поэтому на мехмат и набирают по 400 человек на курс.
Алсо ненужными он считает только нму и Мишу Вербицкого.
Не читал. Это что?
>что это широко применяемая специальность и тд
Какая "широко применяемая специальность"?
Математика - это наука. Есть специальности, использующие отдельные результаты математики.
Мехмат всё-таки должен быть о науке хотя бы чуть-чуть (по крайней мере, таким он был в 60-х годах).
> поэтому на мехмат и набирают по 400 человек на курс.
Цирк, да и только. Потом вся эта толпа идёт "рубить бабло" в IT и финансы, не используя ничего, кроме элементарной арифметики.
>Алсо ненужными он считает только нму и Мишу Вербицкого.
Вот-вот. Потому что "НМУ и Миша Вербицкий" - это именно математика-наука, а не инженерная математика.
В США и Европе (точно не знаю, как в Китае) вообще немыслимо, чтобы на факультете математики работал человек, не относящийся к этой науке. А тут он не просто работает, так ещё и ненавидит эту математику, считая её не наукой, а просто набором древних результатов, полезных некоторым инженерам.
Его конкретная цитата "нет такой профессии - статьи писать".
То есть чисто такой вот совок. Фундаментальная наука не нужна, нужно больше инженеров, которые будут строить ракеты для "Родины".
В нормальном обществе за такие высказывания профессора затравили бы и вынудили уволиться. И были бы правы.
Так что мехмат - это то ещё болото. По-хорошему его бы закрыть, чтобы справедливо было. А то получается сплошной обман: студентов математиков обманывают, подсовывая им инженерное дело вместо математики, а студентов-инженеров обманывают, подсовывая им математику вместо практических навыков.
Лохотрон, да и только. Неудивительно, что они потом гордятся своими "400-ми студентам". Наверное, думаю про себя: "набрали лохов и развели государство на бабло, какие мы молодцы".
Какое-то у вас странное представление о мехмате. Из какой-то мимолетной истории какого-то одного из сотен преподов о причине такого большого набора вы сделали вывод, что на мехмате учат только инженерному делу. Да и где вы нашли что-то про инженерное дело. Точные сложные расчеты для тех же ракет, например, это тоже что ли инженерное дело? Это же тоже математика, только прикладная. Поэтому и набирали 300-400 со всего Союза, чтобы потом в разных областях были спецы.
Да и как по вашему можно учить на ученого, да и еще и в 21ом веке, да и еще и в нашей стране. Ты либо родился с мозгами, либо родился с мозгами, но до ученого не дотянул - пошел в ИТ или финансы. Да и тем более кто, как не идейный захочет за гроши ломать мозги, когда можно жировать на бумерах в тех же банках. Так что единицы из любых вузов РФ, Европы, США станут учеными.
>Из какой-то мимолетной истории какого-то одного из сотен преподов о причине такого большого набора вы сделали вывод, что на мехмате учат только инженерному делу
Если бы он один такой был. И учат как раз не инженерному делу, а непонятно чему, сборной солянке предметов, оставшихся ещё с 70-х годов.
Всё это бесполезно как для обычной карьеры, так и для науки.
Используют знания, полученные на мехмате, единицы, как среди будущих ученых, так и будущих финансистов/программистов.
>Точные сложные расчеты для тех же ракет, например, это тоже что ли инженерное дело?
Ну уж точно не математика.
>Это же тоже математика, только прикладная.
Нет никакой "прикладной математики". Есть приложения математики. А делать ракеты - это не наука вообще.
>Поэтому и набирали 300-400 со всего Союза, чтобы потом в разных областях были спецы.
Скорее, чтобы потом было кому обслуживать оборонку. СССР же.
>Да и как по вашему можно учить на ученого,
Легко. Для начала надо набирать 15 человек, а не 400, но при этом не трубить повсюду, что "математика полезна для бизнеса и программирования", а четко объяснить, что мы готовим будущих ученых-математиков для исследований (тогда эти 15 мест займут как раз те, кому математика действительно нужна, а не как сейчас "пойду на матфак, чтобы потом уйти в банк")
>да и еще и в 21ом веке
Самое лучшее время для научной карьеры.
> да и еще и в нашей стране
Сильный ученый всегда может иммигрировать. Но кто хочет, спокойно занимается наукой и в этой стране, в том числе области чистой математики.
>но до ученого не дотянул - пошел в ИТ или финансы
Личное дело каждого. Но программистов и компьютер саентистов надо учить на факультетах IT, а финансистов - на факультета х финансов или экономики.
А на факультете математики должны учить математике.
>Да и тем более кто, как не идейный захочет за гроши ломать мозги, когда можно жировать на бумерах в тех же банках.
Это совсем другой разговор. На мой взгляд, лучше зарабатывать не очень много (при этом сильный ученый вполне может немало зарабатывать в каком-нибудь университете уровня Ive League), но заниматься любимым делом, а не сидеть 20 часов в сутки клепать бессмысленные презентации. Но в народе последнее считается "престижной элитной работой" (Investment Banking, например).
>Так что единицы из любых вузов РФ, Европы, США станут учеными.
Только так и надо. Но ученым тоже надо где-то учиться. А так получается, что даже на факультетах математики готовят каких-то гибридных инженеров.
>Из какой-то мимолетной истории какого-то одного из сотен преподов о причине такого большого набора вы сделали вывод, что на мехмате учат только инженерному делу
Если бы он один такой был. И учат как раз не инженерному делу, а непонятно чему, сборной солянке предметов, оставшихся ещё с 70-х годов.
Всё это бесполезно как для обычной карьеры, так и для науки.
Используют знания, полученные на мехмате, единицы, как среди будущих ученых, так и будущих финансистов/программистов.
>Точные сложные расчеты для тех же ракет, например, это тоже что ли инженерное дело?
Ну уж точно не математика.
>Это же тоже математика, только прикладная.
Нет никакой "прикладной математики". Есть приложения математики. А делать ракеты - это не наука вообще.
>Поэтому и набирали 300-400 со всего Союза, чтобы потом в разных областях были спецы.
Скорее, чтобы потом было кому обслуживать оборонку. СССР же.
>Да и как по вашему можно учить на ученого,
Легко. Для начала надо набирать 15 человек, а не 400, но при этом не трубить повсюду, что "математика полезна для бизнеса и программирования", а четко объяснить, что мы готовим будущих ученых-математиков для исследований (тогда эти 15 мест займут как раз те, кому математика действительно нужна, а не как сейчас "пойду на матфак, чтобы потом уйти в банк")
>да и еще и в 21ом веке
Самое лучшее время для научной карьеры.
> да и еще и в нашей стране
Сильный ученый всегда может иммигрировать. Но кто хочет, спокойно занимается наукой и в этой стране, в том числе области чистой математики.
>но до ученого не дотянул - пошел в ИТ или финансы
Личное дело каждого. Но программистов и компьютер саентистов надо учить на факультетах IT, а финансистов - на факультета х финансов или экономики.
А на факультете математики должны учить математике.
>Да и тем более кто, как не идейный захочет за гроши ломать мозги, когда можно жировать на бумерах в тех же банках.
Это совсем другой разговор. На мой взгляд, лучше зарабатывать не очень много (при этом сильный ученый вполне может немало зарабатывать в каком-нибудь университете уровня Ive League), но заниматься любимым делом, а не сидеть 20 часов в сутки клепать бессмысленные презентации. Но в народе последнее считается "престижной элитной работой" (Investment Banking, например).
>Так что единицы из любых вузов РФ, Европы, США станут учеными.
Только так и надо. Но ученым тоже надо где-то учиться. А так получается, что даже на факультетах математики готовят каких-то гибридных инженеров.
Все же чем будет отличаться ваш кружок будущих ученых в 15 человек от современного мехмата/матфака? Вы учились или преподавали на мехмате?
Да и как определить, будет ли тот или иной из этих 15ти учёным, может он на 3ем курсе захочет запустить ракету или стать скинхедом. А тут 400 человек раскидываются по кафедрам и занимаются тем, что им ближе. И может с какой-то вероятностью найдутся примерно 15 человек, которые будут потом участвовать в научной жизни. Да и все наши ученые-математики кстати, как олдовые, так и молодые, все мехмат кончали. Так что по-моему нет никакого смысла делать какой-то отдельный факультет для чистых ученых - такой попросту не нужен.
>Но программистов и компьютер саентистов надо учить на факультетах IT, а финансистов - на факультета х финансов или экономики.
А мехмат он на то и существует, если ты не уверен на все 100, идешь на мехмат, может быть даже потом в науку уйдешь.
Асло когда я говорил про нашу страну и время, я имел ввиду нашу современную молодежь, которая о науке не думает вообще. Интересно было бы провести какой-нибудь среди студентов мехматов, матмехов, матфаков. Может я и ошибаюсь.
>Да и как определить, будет ли тот или иной из этих 15ти учёным, может он на 3ем курсе захочет запустить ракету или стать скинхедом.
Его дело. Всегда можно поступить в магистратуру на другую специальность. Или второе высшее. Или самообразование.
>А тут 400 человек раскидываются по кафедрам и занимаются тем, что им ближе.
Это в теории. На практике, как минимум, 3 года их всей ебут какой-то "ядерно-ракетной" математикой и примесью архаики 1920-х годов, а также "историями отечества, философиями".
Всё это нахуй не нужно ни будущим математикам, ни будущим карьеристам.
Сделайте обязательную часть в программе минимальной, как в США, проблем не будет. Но это другая система образования, где студент поступает в университет, а не на факультет. В РФ же гордятся своей "классической" университетской системой.
>И может с какой-то вероятностью найдутся примерно 15 человек, которые будут потом участвовать в научной жизни.
И будет это не благодаря, и вопреки. Мехмат вообще НИЧЕГО не дает будущим математикам-исследователям. Только мешает гигантской и бессмысленной обязательной программой.
Не, пусть будут возможности как для ученых, так и для будущих банкиров, я не против.
На деле же мехмат не только не помогает начинающим исследователям, но и мешает.
Лучше взять 15 человек и дать им нормальную жизнь, чем окунуть в говно 400 в надежде, что кто-то из них "выбьется в люди". Это к вопросу о "вероятности".
>Так что по-моему нет никакого смысла делать какой-то отдельный факультет для чистых ученых - такой попросту не нужен.
Чудно. Тогда надо уничтожить университеты капитально, так как не нужны и "факультеты физики", и "факультеты экономики", и "факультеты истории" и т.д. Оставить ПТУ, че.
ПТУ для финансистов, ПТУ для программистов, ПТУ для инженеров.
>А мехмат он на то и существует, если ты не уверен на все 100, идешь на мехмат, может быть даже потом в науку уйдешь.
Тогда мехмат должен давать выбор и стимулировать человека к тем или иным занятиям. На деле же он отбивает у людей всю охоту и делает из них неприспособленных овощей.
>Асло когда я говорил про нашу страну и время, я имел ввиду нашу современную молодежь, которая о науке не думает вообще. Интересно было бы провести какой-нибудь среди студентов мехматов, матмехов, матфаков. Может я и ошибаюсь.
Вот в этом и проблема набора 400 человек на факультет математики.
Сейчас в бизнесе модно думать, что можно пойти на мехмат или матфак, потратить 4-6 лет на математику, зато потом "мозги варить будут в бизнесе" и "возьмут в McKinsey работать".
А факультеты не препятствуют этому мракобесию, они только способствуют. А должны фильтровать. Таким образом, чтобы на мехматах и матфаках оставались ТОЛЬКО те, кто хотя бы на момент поступления планирует заниматься наукой. Если планировал заниматься наукой, но потом забил, то это его проблемы. Но если он сознательно поступил на факультет математики зная, что наукой никогда не будет заниматься, то... В общем, мехмат должен сделать всё возможное, чтобы "вонаби-бизнесмены-математики" к ним не поступали. А они только культивируют этот бред, с улыбкой вещая: "Набор такой большой, потому что математика важна во всех сферах человеческой деятельности".
>Да и как определить, будет ли тот или иной из этих 15ти учёным, может он на 3ем курсе захочет запустить ракету или стать скинхедом.
Его дело. Всегда можно поступить в магистратуру на другую специальность. Или второе высшее. Или самообразование.
>А тут 400 человек раскидываются по кафедрам и занимаются тем, что им ближе.
Это в теории. На практике, как минимум, 3 года их всей ебут какой-то "ядерно-ракетной" математикой и примесью архаики 1920-х годов, а также "историями отечества, философиями".
Всё это нахуй не нужно ни будущим математикам, ни будущим карьеристам.
Сделайте обязательную часть в программе минимальной, как в США, проблем не будет. Но это другая система образования, где студент поступает в университет, а не на факультет. В РФ же гордятся своей "классической" университетской системой.
>И может с какой-то вероятностью найдутся примерно 15 человек, которые будут потом участвовать в научной жизни.
И будет это не благодаря, и вопреки. Мехмат вообще НИЧЕГО не дает будущим математикам-исследователям. Только мешает гигантской и бессмысленной обязательной программой.
Не, пусть будут возможности как для ученых, так и для будущих банкиров, я не против.
На деле же мехмат не только не помогает начинающим исследователям, но и мешает.
Лучше взять 15 человек и дать им нормальную жизнь, чем окунуть в говно 400 в надежде, что кто-то из них "выбьется в люди". Это к вопросу о "вероятности".
>Так что по-моему нет никакого смысла делать какой-то отдельный факультет для чистых ученых - такой попросту не нужен.
Чудно. Тогда надо уничтожить университеты капитально, так как не нужны и "факультеты физики", и "факультеты экономики", и "факультеты истории" и т.д. Оставить ПТУ, че.
ПТУ для финансистов, ПТУ для программистов, ПТУ для инженеров.
>А мехмат он на то и существует, если ты не уверен на все 100, идешь на мехмат, может быть даже потом в науку уйдешь.
Тогда мехмат должен давать выбор и стимулировать человека к тем или иным занятиям. На деле же он отбивает у людей всю охоту и делает из них неприспособленных овощей.
>Асло когда я говорил про нашу страну и время, я имел ввиду нашу современную молодежь, которая о науке не думает вообще. Интересно было бы провести какой-нибудь среди студентов мехматов, матмехов, матфаков. Может я и ошибаюсь.
Вот в этом и проблема набора 400 человек на факультет математики.
Сейчас в бизнесе модно думать, что можно пойти на мехмат или матфак, потратить 4-6 лет на математику, зато потом "мозги варить будут в бизнесе" и "возьмут в McKinsey работать".
А факультеты не препятствуют этому мракобесию, они только способствуют. А должны фильтровать. Таким образом, чтобы на мехматах и матфаках оставались ТОЛЬКО те, кто хотя бы на момент поступления планирует заниматься наукой. Если планировал заниматься наукой, но потом забил, то это его проблемы. Но если он сознательно поступил на факультет математики зная, что наукой никогда не будет заниматься, то... В общем, мехмат должен сделать всё возможное, чтобы "вонаби-бизнесмены-математики" к ним не поступали. А они только культивируют этот бред, с улыбкой вещая: "Набор такой большой, потому что математика важна во всех сферах человеческой деятельности".
>Лучше взять 15 человек и дать им нормальную жизнь, чем окунуть в говно 400 в надежде, что кто-то из них "выбьется в люди". Это к вопросу о "вероятности".
Так все таки как должен выглядеть твой турбо орден 15ти ученых? Чем программа будет реально отличаться от мехматовской? Что там такого будет? Только не надо говорить о каком-то мифическом инженерном деле, если не учились/учитесь там.
Соображения о том, что нужно набирать всего 15 человек и существующий мехмат вообще ничего не дает - это, конечно, радикализм. Но тем не менее, тот анон указывает на реально существующие проблемы.
Мехмат при текущем объеме набора в 400 человек не может полноценно ориентироваться на обучение будущих математиков. Сколь-нибудь серьезные планы стать математиками даже на 1-ом курсе есть, судя по всему, в лучшем случае есть у трети студентов. Остальные, в массе своей, не очень знают, чего хотят от обучения. Мотивация и подход к учебе у них соответствующие. Эту массу студентов надо чему-то учить. Соответственно программа подстраивается под эту реальность. Исторически, видимо где-то, в 60-е, когда факультет активно раздувался, решение состояло в том, чтобы учить их первое с ориентацией на дальнейшее занятие прикладными расчетами и второе, как будущих преподавателей математики в инженерных ВУЗах.
К несчастью мехмат, по крайней мере в последние десятилетия, является весьма консервативной структурой, где программа определяется, по-существу, балансом сил между разными кафедрами, которые пытаются приписать себе по-возможности больше курсов. В такой ситуации никакого серьезной реформы программы произвести невозможно. В частности, на настоящий момент навыки ручного решения диффуров, подсчета интегралов и т.п. стали практически полностью бесполезны в свете развития систем символических расчетов. При этом обучение им занимает, насколько я помню, примерно треть всего учебного времени, если взять все математические предметы.
При этом, даже если бы набор мехмата сократился и удалось бы избавиться от откровенного бессмысленной деятельности в духе подсчета 500 интегралов. Все-равно большая обязательная программа в стычке с большой разнородностью кафедр, вынудили бы программу быть поверхностным проходом по большому разнообразию довольно разнородных предметов, начиная с логики и заканчивая теорией вероятности. В итоге фактически почти все время будет потрачено на создание общей математической культуры. В самом создание такой культуры нет ничего плохого, но для будущих математиков было бы полезнее также обучить их и набору знаний полезных именно в их области.
В итоге, я здесь вижу два лучших потенциальных варианта - относительно маленькие более узкоспециализированные факультеты (в сущности, для некоторой части математиков в Москве это уже произошло, в виде организации матфака Вышки) и существенное сокращение обязательной программы с увеличением числа предметов по выбору. Такие варианты, на самом деле, будут не менее полезны для более-менее всех тех кто там учится. Для людей, которые математиками не станут, основная польза от изучения математики видимо состоит в развитие ряда мыслительных навыков, но здесь не так уж важно, чему конкретно их учат. Для будущих математиков позволит получить существенно больше полезных знаний из учебного процесса.
Хотя хочу отметить, что в любом случае, не стоит переоценивать важность формального учебного процесса для будущих математиков (ну и видимо ученых в целом). Самостоятельное обучением и собственно творческая математическая деятельность вместе с общением с сильными и квалифицированными математиками, судя по моему опыту, имеет куда более существенное значение.
Соображения о том, что нужно набирать всего 15 человек и существующий мехмат вообще ничего не дает - это, конечно, радикализм. Но тем не менее, тот анон указывает на реально существующие проблемы.
Мехмат при текущем объеме набора в 400 человек не может полноценно ориентироваться на обучение будущих математиков. Сколь-нибудь серьезные планы стать математиками даже на 1-ом курсе есть, судя по всему, в лучшем случае есть у трети студентов. Остальные, в массе своей, не очень знают, чего хотят от обучения. Мотивация и подход к учебе у них соответствующие. Эту массу студентов надо чему-то учить. Соответственно программа подстраивается под эту реальность. Исторически, видимо где-то, в 60-е, когда факультет активно раздувался, решение состояло в том, чтобы учить их первое с ориентацией на дальнейшее занятие прикладными расчетами и второе, как будущих преподавателей математики в инженерных ВУЗах.
К несчастью мехмат, по крайней мере в последние десятилетия, является весьма консервативной структурой, где программа определяется, по-существу, балансом сил между разными кафедрами, которые пытаются приписать себе по-возможности больше курсов. В такой ситуации никакого серьезной реформы программы произвести невозможно. В частности, на настоящий момент навыки ручного решения диффуров, подсчета интегралов и т.п. стали практически полностью бесполезны в свете развития систем символических расчетов. При этом обучение им занимает, насколько я помню, примерно треть всего учебного времени, если взять все математические предметы.
При этом, даже если бы набор мехмата сократился и удалось бы избавиться от откровенного бессмысленной деятельности в духе подсчета 500 интегралов. Все-равно большая обязательная программа в стычке с большой разнородностью кафедр, вынудили бы программу быть поверхностным проходом по большому разнообразию довольно разнородных предметов, начиная с логики и заканчивая теорией вероятности. В итоге фактически почти все время будет потрачено на создание общей математической культуры. В самом создание такой культуры нет ничего плохого, но для будущих математиков было бы полезнее также обучить их и набору знаний полезных именно в их области.
В итоге, я здесь вижу два лучших потенциальных варианта - относительно маленькие более узкоспециализированные факультеты (в сущности, для некоторой части математиков в Москве это уже произошло, в виде организации матфака Вышки) и существенное сокращение обязательной программы с увеличением числа предметов по выбору. Такие варианты, на самом деле, будут не менее полезны для более-менее всех тех кто там учится. Для людей, которые математиками не станут, основная польза от изучения математики видимо состоит в развитие ряда мыслительных навыков, но здесь не так уж важно, чему конкретно их учат. Для будущих математиков позволит получить существенно больше полезных знаний из учебного процесса.
Хотя хочу отметить, что в любом случае, не стоит переоценивать важность формального учебного процесса для будущих математиков (ну и видимо ученых в целом). Самостоятельное обучением и собственно творческая математическая деятельность вместе с общением с сильными и квалифицированными математиками, судя по моему опыту, имеет куда более существенное значение.
Какой, блять, турбо орден? Обычный факультет математики, где обучают математики, как науке. Я поражаюсь, что для людей это кажется чем-то из ряда вон выходящим, когда у нас есть факультеты филологии, философии и физики.
Что до программы, то это нетривиальный вопрос. Лучшее, что я видел, это новая программа Вербицкого для первых двух курсов бакалавриата (с расчетом на то, что последующие два курсы есть только курсы по выбору): http://verbit.ru/Job/HSE/Curriculum/all.txt
Только не надо кричать "ФУУУУ, ВЕРБИТКА, ГОВНО!!" если не знаком с материалом по ссылке. Там реально адекватная программа, в отличие от его же первой, получившей славу в рунете.
Ты, в принципе, во всем прав. Хотя я лично не вижу ничего радикального в наборе 15 человек ПРИ УСЛОВИИ правильного пиара в стиле: "Мы готовим только будущих ученых-математиков, кто хочет стать программистом или финансистом, не идите к нам"
>>7266
>Хотя хочу отметить, что в любом случае, не стоит переоценивать важность формального учебного процесса для будущих математиков (ну и видимо ученых в целом). Самостоятельное обучением и собственно творческая математическая деятельность вместе с общением с сильными и квалифицированными математиками, судя по моему опыту, имеет куда более существенное значение.
Тут ты тоже прав. Но мы сталкиваемся с суровой реальностью. Для дальнейшей карьеры в науке диплом бакалавра всё же нужен, как и нужны контакты с профессорами. В нынешних реалиях процесс получения диплома полностью ортогонален процессу математического образования. Более того, он занимает очень много времени и отнимает очень много сил. А взамен дает только этот самый диплом (контакты с профессорами можно завести и по-другому, например, хорошо показывая себя на курсах НМУ и НОЦ МИАН Стекловки).
Почитай, что ли, посты Посицельского про его обучение на мехмате. У Вербицкого тоже можно. Там много всего. Например: дочь Вербицкого учится на мехмате и из-за ублюдочной обязательной программе не успевает учиться чему-то полезному.
>избавиться от откровенного бессмысленной деятельности в духе подсчета 500 интегралов
Ну не знаю, может я, конечно, не прав, но это дело как раз довольно активно развивает ряд математических мыслительных навыков, кроме того, приучает к рутинной работе.
>будущих математиков было бы полезнее также обучить их и набору знаний полезных именно в их области.
А разве этим не занимаются кафедры после 2го курса? Хочешь, например, заниматься ТЧ - иди на кафедру тч. Алсо сможешь научиться чему-то про защиту информации, если захочешь, конечно. Хочешь заниматься логикой - иди на их кафедру. И твои дальнейшие общение и творческая деятельность как раз исходят из твоего выбора. Алсо есть мильон спецсеминаров и спецкурсов на мехмате по тем или иным научным направлениям.
Ну про минусы структуры мехмата согласен. Так по всему факультетам МГУ порою происходит.
Матфак решил проблему лишь частично. Там тоже куча проблем сейчас. Сам Вербицкий считает, что он медленно скатывается во второй мехмат. Сначала я думал, что это очередной литературный прием в стиле Вербицкого ("Все говно и все плохо"), но теперь начинаю с ним соглашаться.
В частность, "экзотические" люди изуродовали обязательную программу до ужаса механикой и диффурами. Доходит до смешного. Преподаватель механики (скорее физик, нежели математик) недоволен, что студенты требуют строгих определений на его курсе. В частности, интересное:
http://lj.rossia.org/users/tiphareth/2032676.html?nc=115
Когда студенты в 2015-м году написали коллективное письмо с просьбой пересмотреть программу, последнюю действительно пересмотрели. Да только так, что убрали теорию Галуа и алгебраическую топологию, зато разделили "динамические системы" аж на два курса - "ОДУ" и "механику".
Вот, собственно, вышеупомянутая ссылка и посвящена последнему обсуждению программы с международным экспертным советом.
И да, на матфаке также есть лишние люди, свято верящие в догму: "Чтобы клепать презентации в банке 24/7 за большие бабки, нужно математическое образование". Показателен вот этот тред, например:
http://yuptalk.ru/aspirantura_magistratura_vtoroe_visshee_obrazovanie/vshai_matfak_ili_aikonom-t5307.0.html
(Хотя там ещё всё довольно-таки адекватно, если сравнивать с...)
>Ну не знаю, может я, конечно, не прав, но это дело как раз довольно активно развивает ряд математических мыслительных навыков, кроме того, приучает к рутинной работе.
>
Не прав. Скорее, создает в большинства неправильное впечатление о том, что такое вообще "математика", а также вызывает к ней отвращение.
>А разве этим не занимаются кафедры после 2го курса? Хочешь, например, заниматься ТЧ - иди на кафедру тч. Алсо сможешь научиться чему-то про защиту информации, если захочешь, конечно. Хочешь заниматься логикой - иди на их кафедру. И твои дальнейшие общение и творческая деятельность как раз исходят из твоего выбора. Алсо есть мильон спецсеминаров и спецкурсов на мехмате по тем или иным научным направлениям.
Да. Но обязательная программа должна давать лишь необходимые навыки для того, чтобы определиться, а не мешать жить людям.
На мехмате бОльшую часть обязательной программы составляет "классический" анализ, довольно маргинальный предмет. Причем изучают его так, как будто все 400 человек обязательно станут классическими аналитиками.
Про кучу гуманитарщины и прикладовщины я вообще молчу. Это все должно быть по выбору.
А что насчёт архаичных бессмысленных предметов, типа "классической дифференциальной геометрии" и "аналитической геометрии"? Это, вроде бы, чисто-математические предметы, но осмысленней от этого они не становятся. Бесполезный мусор, как для математиков, так и для прикладников.
Ты хотел сказать "первая"? До не особо.
Слишком большая, во-первых. Полезнее копать около своей области, а не учить все, что когда-то учил Вербицкий.
Во-вторых, последние курсы неадекватны, так как отражают область интересов Вербицкого (комплексная аналитическая геометрия).
Хотя, возможно, на первые 2-3 курсы можно как-то ориентироваться.
>"классической дифференциальной геометрии" и "аналитической геометрии"
интуиция для дифгеома и линейки.
Спасибо, обойдемся и без такой "интуиции". А правильная интуиция для предмета вырабатывается уже в процессе изучения того самого предмета. Не надо пытаться вести любую науку к Евклидовой геометрии.
>не вижу ничего радикального в наборе 15 человек
Я думал о реалиях Москвы и это весьма мало - более-менее талантливых выпускников, которые думают, что хотят стать математиками заметно больше. Учитывая, что в любом случае заметная часть поступивших поступит непонятно зачем, в итоге это отсечет много, если не большинство людей, которые станут математиками - см.
>И да, на матфаке также есть лишние люди, свято верящие в догму: "Чтобы клепать презентации в банке 24/7 за большие бабки, нужно математическое образование". Показателен вот этот тред, например:
Вариант же с существенным усечением тематики факультета тоже не слишком удачен так как абитуриенты в норме имеют слишком слабое представление о разных областях математики.
>Более того, он занимает очень много времени и отнимает очень много сил.
Я закончил мехмат. Отнимает, но не то, чтобы уж невероятно много. У меня выходило примерно по полтора месяца на каждую из двух сессий в году. После каждой сессии нужна примерно неделя, чтобы прийти в себя. Остальное время нужно иногда появляться на семинарах.
>А взамен дает только этот самый диплом
Опять же, хотя с процессом обучения на мехмате есть множество проблем, как бы то ни было, он дает некоторый обзор ряда областей, пусть и в сильно далекой от оптимальной подборке. В итоге, это полезно так как математика взаимосвязана и чем больше ты знаешь, тем больше возможностей усматривать связи.
Хотя в целом я согласен.
>>7332
>но это дело как раз довольно активно развивает ряд математических мыслительных навыков, кроме того,
Такого рода упражнения заточены, на то, чтобы научить студентов символическим алгоритмам. Думаю, что это позволяет усвоить более сложные символические алгоритмы в дальнейшем. Но в наше время это не слишком нужно так как всегда можно формализовать тот же алгоритм и получить программу.
>А разве этим не занимаются кафедры после 2го курса?
Занимаются, но с весьма ограниченным успехом (хотя зависит от кафедре). Если я ничего не упускаю, то максимум, что есть - это кафедра алгебры с обязательным спецкурсом на 4 семестра + парой курсов ЕНС (естественно научного содержания) их кафедры. Дальше все зависит от студента. По факту оказывается, что малополезные (а часто и вовсе бесполезные) общеобразовательные курсы довлеют на студентов куда больше, чем связанные с их специализацией.
>>7333
Ну собственно не удивительно. Может и в самом деле, единственный выход - это сильно сокращать обязательную часть программы.
>не вижу ничего радикального в наборе 15 человек
Я думал о реалиях Москвы и это весьма мало - более-менее талантливых выпускников, которые думают, что хотят стать математиками заметно больше. Учитывая, что в любом случае заметная часть поступивших поступит непонятно зачем, в итоге это отсечет много, если не большинство людей, которые станут математиками - см.
>И да, на матфаке также есть лишние люди, свято верящие в догму: "Чтобы клепать презентации в банке 24/7 за большие бабки, нужно математическое образование". Показателен вот этот тред, например:
Вариант же с существенным усечением тематики факультета тоже не слишком удачен так как абитуриенты в норме имеют слишком слабое представление о разных областях математики.
>Более того, он занимает очень много времени и отнимает очень много сил.
Я закончил мехмат. Отнимает, но не то, чтобы уж невероятно много. У меня выходило примерно по полтора месяца на каждую из двух сессий в году. После каждой сессии нужна примерно неделя, чтобы прийти в себя. Остальное время нужно иногда появляться на семинарах.
>А взамен дает только этот самый диплом
Опять же, хотя с процессом обучения на мехмате есть множество проблем, как бы то ни было, он дает некоторый обзор ряда областей, пусть и в сильно далекой от оптимальной подборке. В итоге, это полезно так как математика взаимосвязана и чем больше ты знаешь, тем больше возможностей усматривать связи.
Хотя в целом я согласен.
>>7332
>но это дело как раз довольно активно развивает ряд математических мыслительных навыков, кроме того,
Такого рода упражнения заточены, на то, чтобы научить студентов символическим алгоритмам. Думаю, что это позволяет усвоить более сложные символические алгоритмы в дальнейшем. Но в наше время это не слишком нужно так как всегда можно формализовать тот же алгоритм и получить программу.
>А разве этим не занимаются кафедры после 2го курса?
Занимаются, но с весьма ограниченным успехом (хотя зависит от кафедре). Если я ничего не упускаю, то максимум, что есть - это кафедра алгебры с обязательным спецкурсом на 4 семестра + парой курсов ЕНС (естественно научного содержания) их кафедры. Дальше все зависит от студента. По факту оказывается, что малополезные (а часто и вовсе бесполезные) общеобразовательные курсы довлеют на студентов куда больше, чем связанные с их специализацией.
>>7333
Ну собственно не удивительно. Может и в самом деле, единственный выход - это сильно сокращать обязательную часть программы.
>Я думал о реалиях Москвы и это весьма мало - более-менее талантливых выпускников, которые думают, что хотят стать математиками заметно больше. Учитывая, что в любом случае заметная часть поступивших поступит непонятно зачем, в итоге это отсечет много, если не большинство людей, которые станут математиками - см.
Может быть и так. В любом случае, нужен грамотный пиар. Чтобы повысить шансы того, что на факультет придут только те люди, кому это действительно нужно. А не кокетливо на официальном сайте писать, что "математика важна во многих сферах деятельности".
>Вариант же с существенным усечением тематики факультета тоже не слишком удачен так как абитуриенты в норме имеют слишком слабое представление о разных областях математики.
Я не предлагаю ничего усекать. Наоборот, я считаю, что единственной целью обязательной программой должно быть возможность людей сделать выбор, в каком направлении копать. Она должна быть и широка, и мала одновременно.
Но ориентироваться она должна на науку и на тех, кто желает стать ученым-математиком.
>>7407
>Я закончил мехмат. Отнимает, но не то, чтобы уж невероятно много. У меня выходило примерно по полтора месяца на каждую из двух сессий в году. После каждой сессии нужна примерно неделя, чтобы прийти в себя. Остальное время нужно иногда появляться на семинарах.
Ну о чем вообще речь, если тебе была "нужна неделя, чтобы прийти в себя". Зачем так мучиться? Чтобы получить престижный "диплом МГУ"?
Более того, я слышал, что на мехмате контроль посещаемости.
>>7407
> он дает некоторый обзор ряда областей
Вот именно, что не дает! Максимум, обзор прикладных областей. Но от математики там разве что классический анализ. Ну, немного алгеры, даже теории Галуа нет (это базовый курс).
https://youtu.be/a7ZfClXj6-k
https://ru.m.wikipedia.org/Смирнов,_Станислав_Константинович
Блядь! Это просто пиздец.
Каким только хуесосам не дают филдса.
>существуют континентальная и англо-саксонская система, первая это много курсов по выбору, а вторая это как у нас, много обязательных
Он туда право пришел обсуждать или математику? Из юриспруденции термины вообще-то
Дальше полный ад
>советские специалисты по алгебраической геометрии хорошо знали статистику и теорию вероятностей, что иногда выстреливало
Выстрелил тебе в ебало, щенок
>не все хотят быть алгебраическими геометрами и теоретиками пучков
О чем несет этот опущенный? Пиздец, харкнул бы в лицо этой мрази.
И это еще не все
На справедливое замечание студента, что подписавшие письмо против даже не количества анализа в обязательных курсах (близко к 100%) но его качества, что преподают в координатах и тд
Прославленный лауреат-пидорас, все заседание призывавший "не вдаваться в подробности" на это промямлил:
>некоторые вещи мы еще не умеем объяснять без координат, возьмите, например, вейвлеты
>вейвлеты
У этой суки надо сначала забрать медаль, потом застрелить нахуй, после обоссать.
У меня все.
>>7433
Понимаю бомбежку. Смирнов чего-то погнал. Не сомневаюсь, что медаль заслуженная, но вот к академическому совету подпускать не стоило. Такое ощущение, что человек тупо сидит там, что оправдывать "линию партии". Не факт, что он с ней вообще согласен. Типа если Филдсовский медалист вам говорит, что "партия" права, то "партия" права.
Весь этот разговор был организован из рук вон плохо. Не было никакого регламента, люди не ознакомились оригинальным письмом и, я уверен, своих statements в писменной форме не подготовили для ознакомления до встречи. Т.е. большая часть даже не разобралась в сути конфликта за 2 (?) года с момента публикации письма. Там даже не столько анализ просили урезать, сколько переписать структуру курсов, чтобы выиграть время для современной "попсовой" математики.
Потом ещё намешали в кучу метавопросы о том, как наладить диалог между студентами и университетом (преподавателями и административным телом).
В итоге собрались и демократичненько поизливали друг другу души, кто-то рассказал про самураев непонятно зачем, кто-то, что студенты sovsem ne znayut не хотят слушать курс физики без строго определения гильбертового пространства, кто-то не хочет изучать алгеом и т.п. А диалога не было: изменение программы не обсуждалось, и даже эти метавопросы по организации диалога по возможному изменению программы никуда не ушли.
А Смирнов аналитик же вроде, так что он боль мамкиных алгеомщиков понимает только мозгом, но не сердцем. Он, вполне возможно, как и все топит за свою область и считает её самой полезной подсознательно. Мне с дивана кажется, что он мог бы своим авторитетом повилять на то, чтобы студентов послушали, но отказался это делать, ограничив своё участие потенциальными советами по организации диалога. Ну или он понимает, что нет таких людей, которые подобную реформу программы смогут осуществить, потому что преподы сами этих модных подходов не знают и знать не хотят дети мехмата же все небось.
Феерический бред. Зельдович и Яглом - это курсы для инженерных ПТУ.
Если вы считаете, что учить на матфаке нужно, как на инженерных ПТУ, может быть, вам всё-таки не на матфак надо, а в ПТУ?
>>7944
>Есть мнение (прочёл статью в матпросвещении) что такой формальный подход в преподавании привёл к тому, что во Франции стало меньше математиков крупного калибр
Больше слушайте поехавших арнольдистов, помешанных на "наглядной топологии".
>>7441
24 x 7 сколько будет? (Из зала: 168)
Окей, 168. Чтобы вас не пугала сложная арифметика, поясню: у вас есть 168 часов в неделю, чтобы заниматься математикой.
Расскажу о себе. Я студент магистратуры, к программе бакалавриата никакого отношения не имею. Более того, я совсем не знаю математики, поэтому буду здесь говорить только простые вещи, которые должны быть понятны всем.
1) Если не знать что такое расслоенное копроизведение в категории топологических пространств, невозможно понять формулировку и доказательство теоремы Ван Кампена;
2) Если не знать классификации конечно порожденных модулей над областями главных идеалов, невозможно понять что такое жорданова нормальная форма;
3) Если не знать, что такое локально тривиальное расслоение, нет смысла изучать анализ на многообразиях;
4) Если не знать, что такое гомологический функтор, нет смысла изучать топологию;
5) Если не знать, что такое главные однородные пространства, невозможно понять чем отличается вектор от точки, это уже вопрос из школьной геометрии.
Теперь вопрос к присутствующим: сколькие из вас читали письмо и думают, что понимают, в чем состоит смысл предложенных студентами изменений?
(Считает руки)
В общем, человек семь.
К студентам: я читал программу. Хотелось бы увидеть её в более однородом виде: с развернутым описанием каждого курса, количеством часов, списком литературы, листками и упражнениями, конкретными примерами задач, взаимосвязями и зависимостями между предметами. Если студенты окажутся не в состоянии этого сделать, нужно найти преподавателей, которые в состоянии.
Я смотрел видеозапись обсуждения программы с экспертным советом, Владлен Анатольевич (Тиморин) начал с такой фразы:
"Есть конфликт двух точек зрения (на преподавание), одна из них дедуктивная, другая индуктивная. Конечно, если я скажу сейчас это в таком виде, меня сразу закидают камнями"
Но этого не произошло. Мне очень интересно, почему этого не произошло.
Никакой индуктивной и дедуктивной точек зрения, конечно, нет. Есть одна хорошая статья, которую я советую прочитать всем, кто интересуется этим вопросом. Называется так (записывает на доске) "Гегель. Кто мыслит абстрактно?"
http://caute.ru/ilyenkov/tra/denkabc.html
Плохо, что с доски стёрли, здесь было записано определение предела в эпсилон-дельта формализме. Я считаю, что нормальный человек понять его не в состоянии, нормальный человек говорит на русском языке, на языке эпсилон-дельта нормальный человек говорить никогда не будет.
На этом у меня всё.
>>7441
24 x 7 сколько будет? (Из зала: 168)
Окей, 168. Чтобы вас не пугала сложная арифметика, поясню: у вас есть 168 часов в неделю, чтобы заниматься математикой.
Расскажу о себе. Я студент магистратуры, к программе бакалавриата никакого отношения не имею. Более того, я совсем не знаю математики, поэтому буду здесь говорить только простые вещи, которые должны быть понятны всем.
1) Если не знать что такое расслоенное копроизведение в категории топологических пространств, невозможно понять формулировку и доказательство теоремы Ван Кампена;
2) Если не знать классификации конечно порожденных модулей над областями главных идеалов, невозможно понять что такое жорданова нормальная форма;
3) Если не знать, что такое локально тривиальное расслоение, нет смысла изучать анализ на многообразиях;
4) Если не знать, что такое гомологический функтор, нет смысла изучать топологию;
5) Если не знать, что такое главные однородные пространства, невозможно понять чем отличается вектор от точки, это уже вопрос из школьной геометрии.
Теперь вопрос к присутствующим: сколькие из вас читали письмо и думают, что понимают, в чем состоит смысл предложенных студентами изменений?
(Считает руки)
В общем, человек семь.
К студентам: я читал программу. Хотелось бы увидеть её в более однородом виде: с развернутым описанием каждого курса, количеством часов, списком литературы, листками и упражнениями, конкретными примерами задач, взаимосвязями и зависимостями между предметами. Если студенты окажутся не в состоянии этого сделать, нужно найти преподавателей, которые в состоянии.
Я смотрел видеозапись обсуждения программы с экспертным советом, Владлен Анатольевич (Тиморин) начал с такой фразы:
"Есть конфликт двух точек зрения (на преподавание), одна из них дедуктивная, другая индуктивная. Конечно, если я скажу сейчас это в таком виде, меня сразу закидают камнями"
Но этого не произошло. Мне очень интересно, почему этого не произошло.
Никакой индуктивной и дедуктивной точек зрения, конечно, нет. Есть одна хорошая статья, которую я советую прочитать всем, кто интересуется этим вопросом. Называется так (записывает на доске) "Гегель. Кто мыслит абстрактно?"
http://caute.ru/ilyenkov/tra/denkabc.html
Плохо, что с доски стёрли, здесь было записано определение предела в эпсилон-дельта формализме. Я считаю, что нормальный человек понять его не в состоянии, нормальный человек говорит на русском языке, на языке эпсилон-дельта нормальный человек говорить никогда не будет.
На этом у меня всё.
Ебать, ну и даун. Если будет форум с возможностью отгородиться от таких людей с нервным каналом вместе мозга, я только "за".
Ты со своим трипфажеством и протеканием во все треды напоминаешь мне о прошлом, аж стыдно становится.
>Делинь
Фигасе у него научрук Гротендик был, что же он этих аналитиков на вилы не поднял вместе с прогрессивными студентами как в Великую Французскую Революцию?
Делинь предал Гротнедика, он второкультурщик.
А еще по русски лыка не вяжет, так что вообще в душе не ебет о чем маза идет.
>Есть ли смысл читать Рудина перед тем, как браться за Зорича?
Нет, Рудин годен для повторения материала, если будешь читать с нуля, застрянешь на метрике и топологии.
Я топологию и метрический стафф учил как раз по Рудину.
 71 Кб, 1286x353
71 Кб, 1286x353Он переопределил слово "положительные числа", в его книге положительными называются неотрицательные. Вербита это бесит.
Ну да, неортодоксально. Но у лягушатников так типа принято
https://en.wikipedia.org/wiki/Sign_(mathematics)#Sign_of_zero
>In France and Belgium, 0 is said to be both positive and negative. The positive resp. negative numbers without zero are said to be "strictly positive" resp. "strictly negative".
У Шварца вон тоже, в оригинале по крайней мере, и в дву- и в четырёхтомнике postif это ≥ 0, а >0 - strictement positif
Да. Ещё у Шварца подмножества зовутся частями множества. Вербит говорил, что учил по Шварцу анализ. Поэтому навряд ли дело в положительных-отрицательных.
Да? Вроде в Рудине подмножествами зовутся.
Но что же с ним не так? Мне этот учебник нравится, но других особо и не читал.
О, мастер уравняшак.
Студент всратого прикмата, где его учили по Фихтенгольцу и Курошу, врывается в тред и охуевает от происходящего. Аноны, что мне делать, чтоб перестать быть петухом?
Замри и ничего не делай! Тут обитает шизфреник, которого я когда-то наслушался на нальчане в це, Мне тогда тоже показались его диалоги с другими ебанатами крутыми, поэтому я решил угарать по мотану и поступить на матфак(мехмат), По мере того как я угарал, ко мне пришло осознание, что этот шизойд просто ебнутый на полголовы дигинират, едва ли осиливший хотя бы одну публикацию в скопусе (хотя бы VAK), в то время как даже у меня их 3 появилось. Несет хуйню с умным видом, ему нравится. С таким говном в голове нельзя решить ни одной задачи, стоящей публикации, но зато кукарекать на околонаучных форумах можно. Сравни к примеру темы stackxchang/math и кукареки в этом треде; местные кукареки с гоматопией головного мозга спутали математику со своими фантазиями о правильных подходах. Ваеводскiy бы покраснел, узнай он о местной секте долбоебов.
У моего друга специалиста по функциональному анализу таких публикаций четыре, и он не знает определение пучка. Это разговоры в духе "вот я нейробиолог, а вы петухи, даже не осилили мою область". Нахуй твои маня-публикации сдались? В любом учебнике graduate уровня любая задача со звездочкой это тема отдельной публикации или диплома.
>Студент всратого прикмата, где его учили по Фихтенгольцу и Курошу
Вообще насрать, Фихтенгольц отличный учебник матана, с кучей примеров и пояснениям, да в нем устаревшая терминология, поэтому параллельно стоит читать какого-нибудь Зорича(но без фанатизма) а так надо понять зачем тебе этот примат.
Тем что первые 250 страниц не посвящены теории множеств. Доступнее написано, более удачный выбор материалов и примеров, есть мотивация.
>в сто раз лучше написано.
> Доступнее написано, более удачный выбор материалов и примеров, есть мотивация.
Субъективщина.
>>25028
К примеру, то что называют множеством нулевой меры, у Фихтенгольца в зависимости от размерности R, называется кривая имеющая нулевую длину/площадь/объем, так то чтению не мешает, но всё же.
>Тем что первые 250 страниц не посвящены теории множеств.
Открыл Фихтенгольца, заявленного не увидел.
У Фихтенгольца это называется "теория предела" и ей посвящен примерно весь первый том. Обычно для определения непрерывности и сходимости используется язык дескриптивной теории множеств (также известной как "общая топология"), но в учебниках для альтернативно-одаренных свой эпсилон-дельта язык.
Итак, мы с тобой выясняли, что в Фихтенгольца теории множеств раз два и обчелся, зачем тогда врешь?
Кому нравится "решать задачи" просто для того чтобы написать никому не нужную публикацию и чего-то вякать с высоты авторитета "а у меня больше" лучше идти в биологи, там публикации печатаются просто потоком. К математике это не имеет отношения.
>А то первый том Зорича - это какой-то картофан.
>Картофан тоже надо знать, или он так уж страшен? Спроси у Тао в бложике, почему он, передовой математик, в первом томе своего "Анализа" писал о картофане.
Что такое картофан? Сейчас прохожу Зорича.
И чето я охуел от главы Зорича о вещественных чисел. 15 страниц следующего:
Вот вам аксиомы действительных чисел
Вот я немножк из них вывожу штуки (и блядь как же мне сложно тут следить за тем, что происходит, потому что я не помню и не вижу логики в том, что мы уже доказали для вещественных чисел, а что нет, и соответственно какими фактами можно пользоваться, а какими нет)
Вот определяем N, Z, Q внутри действительных чисел
А вот доказываем, что каждой (кроме такой, что заканчивается на 9999999..., если мы смотрим на десятичную систему) записи a_0 a_1 ... a_n, a_{n+1} a_{n+2} ... соответствует единственное вещественное число
И за всеми доказательствами мне оч сложно следить, потому что общей картины (графа), что из чего мы выводим, и что мы уже знаем, а что нет, я не увидел.
Хочется дропнуть зорича и пойти читать Тао на английском
Читать Тао по-английски при любых раскладах полезнее, чем Зорича, но если ты хочешь просто вкатиться в матан, то главу о вещественных числах можно пропускать
Если тебе что-то из этих аксиом когда-нибудь понадобится (очень вряд ли), тогда и освоишь их, сколько надо
Моя цель - "вкатиться" в матан (ака вещественный анализ, анализ на R^n и комплексный анализ, мб анализ еще на чем-нибудь, о чем я не знаю) при условии, что я закончил бакалавриат computer science хорошего рашковузика, но к сожалению недостаточно хорошо ботал там математику первых 2-3 курсов. Еще одна моя цель - научиться решать задачи вступительных экзаменов всяких магистратур computer science в Рашке, чтобы поступить туда. Еще цель - чтоб мочь на фундаменте этого анализа легко изучать прочие области, которые про R^n.
Ранее я прошел 1-2 главы Spivak - Calculus, и сначала он мне показался охуенным, а потом говном, потому что я, тратя 100500 времени, решал сотни задач в конце каждой главы, доказывая штуки чисто ради тренировки, сами эти штуки уметь доказывать смысла не имеет. Первые главы Спивака с их "вот вы доказали основные алгебраические свойства чисел, а теперь докажите вот десяток сложных неравенств" это пушка. Одновременно ебически плохая пушка, и охуенно хорошая, потому что активная практика это полущ, чем читать и пытаться понять 100 текста почти без упражнений.
>Читать Тао по-английски при любых раскладах полезнее, чем Зорича
Почему?
Алсо Зорич наркоман ебаный. В главу о действительных числах посреди текста о реально важных фундаментальных вещах он засунул абсолютную и относительную погрешность, как она меняется от арифметических операций, алгебраические и транс. числа, и R как числовая ось (со kinda строгой геометрической терминологией, которую он, однако, не объясняет; видимо глава, чтобы порадовать геометров). Еще и блядь картинок нет. Вон в Спиваке сотни картинок.
P.S. Бля раз уж у меня влажные фантазии об охуенности Спивака, надо пойти его задрачивать
Алсо если правда хороший вуз был, то ты без проблем поступишь в его же магу, да и в другие по идее, зачеты же ты получил как-то.
Ну типа вас же основам учили? Производные находить, О большое, О малое, экстремумы искать. Большего там не нужно, лучше бы алгоритмы и прочую дискретную математику учил.
Пердолиться с непрерывными функциями в теорвере; оптимизация ака нахождение локального или глобального минимума в машинном обучении.
Еще возможно я захочу выучить сколько-нибудь экономики, чтобы понимать, как работает социальная часть мира, как предсказывать всякое об обществе. Там наверное тоже непрерывные функции будут.
>>37074
Учу (или повторяю) то, что нужно на экзаменах в Сколтех, ВШЭ факультет компьютерных наук, ШАД, МФТИ: анализ, линейная алгебра, немножко теорвера, алгоритмов и диффуров.
Этого у тебя на экзамене не будет же, а в реальных задачах тебе дадут алгоритм/формулу/схему, ты по нему точно делаешь и напильником потом доработать.
Я не хочу быть программистом, я хочу PhD in CS -> быть постградом в CS -> быть профессором в CS
>я хочу PhD in CS
Об этом стоит писать на соответствующей доске. Тут этому не место.
(Автор этого поста был забанен. Помянем.)
Дело твоё, конечно, но по мне так ты теряешь время попусту. Основ анализа для CS вполне достаточно. Для поступления точно. Это время можно потратить на другие разделы, которые ближе к CS, по которым наверняка будет больше вопросов.
я не знаю, о чём спрашивают в этих аспирантурах, но хочу продвинуть мысль о том, что для освоения анализа (непрерывность, дифференцируемость, интегрируруемость), никаких аксиом вещественных чисел не надо, ты не найдёшь ни одного утверждения в том же зориче (после первой главы), в котором хотя бы одна из них упоминается. Для всего этого достаточно интуитивного понимания числа
Я видел очень хорошие отзывы про Спивака на math.stackexchange, но сам не читал наверно теперь почитаю после твоего описания, спасибо. Зорича смотрел (1 главу не открывал), но не обрёл счастья, от него привкус остаётся неприятный какой-то, что ли. Я читал Рудина, был вполне доволен, хотя чтобы рекомендовать, тоже не могу. Но всё же мне зашло
инб4 зачем тебе это
>начальные
Я имел ввиду базовые, ну то есть те которые дают по моему курсу. Учили нас по Кудрявцеву к слову.
Топологию. Виро Харлмов "элементарная топология" или Вербитский "топология в задачах".
>думаю между Зоричем и Фихтенгольцем
>Топологию. Виро Харламов.
Еще один гений разрешения альтернатив итт
аналис учить бес паталогии ты сафсем ку-ку? У зорича открытые мнажества ток фо втаром томе.
Сейчас еще придет чувак, который скажет, что открытые множества в патологии нинужны.
Да, в топологии не нужны открытые множества, и вообще теоретико-множественный язык. Все естественные конструкции общей топологии закономерным образом возникают на языке локалей и немедленно обобщаются. Как побочный эффект, отпадает необходимость возиться с аксиомой выбора.
Павлов, залогинься.
Да.
Борсук не я не Борсук
трехтомным сборником задач (с решениями) Kaczor и Nowak. Многие задачи из Зорича нашел там с решением, сам же особо не напрягаюсь в попытках делать их самостоятельно, т.к. не нахожу в этом пользы.
Один раз для решения задачи пришлось обратиться к Рудину (д-во существования и единственности арифметического корня n-ой степени из положительного числа элементарной техникой), потом нашел решение этой же задачи в Aliprantis, но без хитрожопых оценок с подстановками, - такое, что и сам мог бы изобрести.
Сейчас читаю главу о пределе, теор. материал дается очень легко, т.к. на матфаке своего Устьусрамска Красноярска на первом курсе уже это проходил, хотя и очень поверхностно, да и сам тогда учился лишь бы сдать.
Еще у меня на всякий случай запасены курсы калькулуса Спивака и Апостола, возможно параллельно буду читать что-нибудь из них, решать картофанчик.
После первого тома Зорича собираюсь начать накатывать какие-нибудь из анализов Jost, Дьедонне, Шварца, A.Knapp, обязательно Kolk, Duistermaat по многомерному анализу и четырехтомник Барри Саймона. Еще хочу почитать как-нибудь вечерами четырехтомник Godement'а. И еще про двухтомник Амана и Эшера тут недавно узнал, его может тоже прочту.
В первую очередь хочу вкатиться в группы Ли, теорию представлений. Также мне нужны комплексный анализ, теория многомерных вычетов. Есть бэкграунд в алгебрах Ли, конечных группах, теории их представлений, коммутативную алгебру знаю на уровне школьника. Со временем хочу еще заняться алг.геометриией, но пока даже не знаю конкретно чем из нее.
>коммутативную алгебру знаю на уровне школьника
Может быть, матшкольника?
Ну и между прочим у тебя в списке к прочтению явно не достаёт Conway, A Course in Abstract Analysis и Schechter, Handbook of Analysis and Its Foundations - без них знания будут неполными, даже и смысла начинать тогда нету. Кстати, по поводу начинать - единственный верный вариант это "Advanced Calculus, A Differential Forms Approach" Эдвардса, хотя это все знают уже конечно
Книжка Конвэя у меня на очереди в руководствах по теории мер, вместе с двухтомником Богачева, который выглядит весьма энциклопедичным. Остальное забрал для библиотеки, спасибо.
>читаю главу о пределе
>собираюсь прочитать почти все котируемые в мире учебники по матану
Да чувак, у тебя вся жизнь впереди.
>После первого тома Зорича собираюсь начать накатывать какие-нибудь из анализов Jost, Дьедонне, Шварца, A.Knapp
Читать Шварца после Зорича пустая трата времени, это учебники примерно одного уровня.
Отсюда следует, что ты не читал ни того, ни другого.
Фихтенгольц для инженеров отличная книга.
В каком учебнике есть хорошие задачи на доказательства?
Зорич
Вы бурбаки, да? Если вы бурбаки, то идите вы нахуй короче.
Меня ебут инженерной графикой и прочим говном уже четвертую неделю, а математики у меня хуй да нихуя(лекции - 1 линал и 1 матан в неделю, по семинарам - 1.5 матан и 1 линал).
Что хочет: понимать в математике чуть позже тупорылых инженеров, ибо математика стала нравится только к концу 11-го класса, примерно тогда же, когда мне ее стали нормально обьяснять, но поменять направления я не решился(а зря).
Хочу смотреть лекции физтеха по мат.анализу первого и второго семестра, параллельно с этим ботая учебник (какой?тут все картошкой называют, из того, что я знаю), нормально будет? И если с ангемом и линейной алгеброй также сделаю, т.е. буду ботать лекции и семинары физтеха, нормально?
Гений разрешения альтернатив вернулся!
>тут все картошкой называют
Вообще забей, это не для тебя написано. Тебе как раз картоха и нужна. Если хочешь понимать побольше тупых инженеров, то покатит любая хуйня с "теоретическими задачками". Можешь даже у препода своего их выпрашивать, прорешивать наряду с обычной домашкой, и будет тебе счастье.
Ненене, ты не понял, я хочу как раз математикой заняться плотно, я передумал насчет инженерии, но поздно(а может и перепоступлю на матфак в следующем году, посмотрю ближе к концу года), вот чем мне заниматься? Можно мне чуть обрезанную программу мехмата например за первый курс? В вузе дрючат почти никак, так что свободного времени у меня до жопы. Только учитывайте, что я учился в очень хуевой школе и самообразовываться начал полгода назад, так что я не потяну учебники, рассчитанные на лицеистов.
Это опять же зависит от того, чем ты вдохновился. Если школьной математикой или матрицами-интегралами, то Зорич по матанализу, Курош (курс высшей алгебры) или лучше Кострикин (введение в алгебру) должно прокатить, и это скорее всего будет как раз тем, что тебе будут втюхивать на математическом направлении. Если будешь читать Зорича, то захвати ещё пару первых глав из второго тома, чисто для вдохновения.
Главное - прорешивать "теоретические задачки" наряду с обычной домашкой. Ещё где-то посередине всего этого действа можно впихнуть что-нибудь по теории множеств. Аналитическая геометрия нахуй не нужна.
Если ты насмотрелся каких-то видосиков или пообщался с матшкольниками, и хочешь открыть двери в дивный мир групп, игр, топологий, диаграмм и пучков, то я даже хуй знает. Во-первых, на первом курсе это если и дают, то обычно весьма сжато. Во-вторых, вроде бы есть какие-то программы для школьников, но ты можешь охуеть с непривычности.
Если в тред придёт умный дядька и скажет, что я неправ, а надо делать как он говорит, то слушай его. Я еблан-старшекурсник с маленьким кругозором и не вправе давать такие советы, отвечаю тебе только потому, что больше никто не отвечает. Зато, может быть, кто-то сагрится на картофельные фамилии.
думаю Рудина попробуй, "математический анализ"
это хороший правильный анализ на нормальном строгом математическом языке. ты почувствуешь и вкус этого языка и обретёшь желаемую глубину предмета
Мне впринципе вкатило, что мы в мат.анализе не как в школе какую-то хуйню делаем, а обьясняем что и зачем мы делаем
Что функция это не какие-то линии и кривые, а отображение одного множества в другое и тд
Вот хочу глубже изучать это
Зорича вчитну, но мне ещё Фихтенгольца советовали, он то норм?
Кострикина сейчас найду
А у тебя нету теоретических задачек? Или демидовича просто дрочить?
>>43745
Я посмотрел, чет он короткий, мне бы материал чтобы больше разжевывался, я же не выпускник физмат лицея(
Я сохранил и Рудина, и Зорича, и Кострикина и Куроша, спасибо большое, начну все, а там что пойдет буду продолжать
>А у тебя нету теоретических задачек?
Они и у Зорича, и у Кострикина идут прям по ходу дела, у Рудина в конце каждой главы раздел "Упражнения".
Учить линейную алгебру сперва, вот что надо. И топологию!
Из классического анализа нужно выучить производные(и связанные с ними теоремы) и формулу-ньютона-лейбница. Это всё за день-два можно сделать.
"Мудрец, как мне сдать профильный матан?
- Матан говоришь?
- Да, математика. Профиль.
Тут мудрец накормил говном человека и сказал, что если он ещё раз назовет анализ бесконечно малых матаном, то он ещё и кружку мочи ему на голову выльет"
Хуясе мемный парень как порвался.
Ньютон открыл свою хуиту с его помощью, и васяны вроде тебя искали там ошибки, как же так, бесконечно малые НЕ ФОРМАЛИЗИРУЮТСЯ!!!!!!!!!!!
Зашивайся а потом убейся.
Бесят бурбакситы вонючие вроде тебя, пиздец, АЖ ТРЯСЕТ!!!!!!!!!!!!!!!!!!1111111111
>>1246
>>1250
>>1258
>>1266
>>1267
>>1272
>>1276
>>1282
>>1285
>>1331
надоело дальше кликать
Ну хули вы тут развели опять. У вас же есть оснований тред, был N петух тред, вроде успокоились, ну ебаный в рот, что зачесалось-то опять? Как алкоголики бля: вроде потерпят даже немного все равно потом сорвутся нахуй. А разгадка она: сами ничего не можете, кроме как срать всякой демагогией гамалогией, никаких результатов нет, а тешить себя чём-то надо. Наркоманы бля заколебали
Лучше начать с чего-нибудь простенького, а-ля "Матанализ с человеческим лицом", и после прочтения соответствующей главы из простенькой книжки, в которой тебе всё объясняют на пальцах - перекатываться в другую, которая то же самое объясняет более строго и на более высоком уровне формализации и обобщения. Книги, которые ты привёл, в основном излагают одно и то же, но на разных языках. Я считаю, первоклассникам читать университетский курс лингвистики для обучения русскому языку - затея бредовая. Так и многие книги, которые ты привёл. Кроме того, крайне редко можно встретить книгу, в которой хорошо всё, обычно где-то удачно одно, где-то - другое.Так что я бы посоветовал начать со старых, добрых Зоричей-Фихтенгольцев, даже несмотря на некоторое устаревание, это - хорошие, понятные книги. Освоив их, ты можешь потом перейти к другому языку, например, к языку топологий, и понять новый язык тебе будет гораздо, гораздо легче.
И не слушай тех, кто тебе говорит о "картофане", о "недостойных математика занятиях". Тот же анализ вырос из чисто прикладных размышлений о движении.
Не эквивалентна. Слабее. Q(p) удовлетворяет Дедекинду, но не удовлетворяет Архимеду. Архимеду и Дедекинду удовлетворяет только R. Уже доказано. Теорема Островского. По сути утверждается, что метрику можно задать двумя способами: обычное расстояние и p-адическое. Других полных по Дедекинду полей нет. Неархимедов анализ, впрочем, есть. Даже в какой-то там физике используется, гугли.
Как по Шварцу чему-то научиться, если там нет ни одного упражнения? Читаем Шварца для развлекухи, решаем Демидовича и там упарываемся, так что ли?
Есть ответы для глупеньких.
Да.
Оно и понятно. Такое читать никакой зависимости от матана не будет.
Харди "Курс чистой математики"
Читаю только из-за красивого названия. Невероятно сложно! Но, блин, как интересно.
Не знаю, мне нравится, как автор старательно разжевывает читателю простые истины, на которые современные авторы просто ссылаются без всяких комментариев. Для человека моих способностей это самое то. Ну и плюс есть ряд задачек разной степени трудности.
Ну я вряд ли гожусь в роль профессионального математика. Это у меня скорее как хобби, поэтому я в принципе не могу идти в ногу со временем. Но получать некоторый кайф от осознания идей, концепций и решения несложных задач способен, чем и довольствуюсь в настоящее время.
Лол, Кудрявцев это методичка для тех, кому анализ и не нужен. А учебник Харди это искусство, жаль, что материал устарел.
Как там у вас в 19 веке? У кудряшки современный язык, аксиоматические теории и всё такое. У харди гуманитарный пиздёшь.
Ну Харди все-таки выдающийся математик 20 века, а не чухан с кафедры, ему лучше знать. Его учебник все-таки нацелен на то, чтобы дать человеку интуицию, а не снабдить его корявым пересказом Бурбаков.
Он чухан только в другом жанре. В пиндостане преподы кривляются у доски иначе спрос среди студентов упадёт и он окажется не у дел. Поэтому их учебники лайтовые. У кудряшки же настоящий хардкор.
>У кудряшки же настоящий хардкор.
Типа одно упражнение на главу и разжевывания очевидных лемм?
Хозяин барин. Читай физические рассмотрения фихтенгольца если современный математический язык не хочешь юзать.
По этим же причинам я считаю лучшими американские учебники. Настолько понятно, как там, материал не излагается ни в одной русскоязычной книге.
>экономфаке
Так экономистам нужен калькулус обычный, он действительно в каком-нибудь Stewart описан прекрасно, а матанализ это совершенно другие книги, и англоязычные нередко тоже написаны в структуре lemma->theorem->corollary. А собственно хорошие англоязычные книги по матанализу так и вовсе не американские.
Есть нормальные учебники а ля - Pugh Real Analysis или Undergraduate Analysis Лэнга, после них можно уже что-то серьезное изучать и не шквариться о русскую школу матана.
> Есть нормальные учебники а ля - Pugh Real Analysis или Undergraduate Analysis Лэнга
[тугая струя блевотины с жидким бульканьем ударила в переполненный таз]
> Это уже потом можно накатить Шварца, Дьедонне или Барри Саймона, если хочешь упороться.
Да не буду я это старьё читать, только мозг засирать. Кудряшка лучше всех.
Барри Саймон еще преподает, так что читай его. Или можешь Тао навернуть, если любишь поживее.
Что думаете о книгах Валерия Босса?
Я выслушал тебя, дед, а теперь пройдемте на dxdy
Сначала Кудрявцев определяет неупорядоченную пару {x, y} как двухэлементное множество (то есть x != y), а потом вводит понятие упорядоченной пары как множества {x, {x, y}}, где {x, y} - пара. Поскольку дальше функция определяется как множество упорядоченных пар, получается, что функции по Кудрявцеву не имеют неподвижных точек.
Еще в этом определении неявно подразумевается фундирование (то есть x != {x, y})
Не понял, обычное определение же. Вон открыл вики и там примерно то же.
>Если задана пара {a, b}, то множество {a, {a, b}}называется упорядоченной парой и обозначается (a, b). При этом элемент a называется первым элементом, а элемент b — вторым элементом пары
>неявно подразумевается фундирование
Ну и что? Аксиома регулярности же. А если её нет, то это уже не ZFC будет.
Ну и вообще, всю жизнь так определяли, называется упорядоченная пара по Куратовскому. Либо я тебя не понял вообще, либо ты до хуйни какой-то доебался.
Во-первых, у Кудрявцева нет никакой аксиоматики, поэтому подразумевается именно что неявно. Во-вторых, пара (x,x) никак не описывается этим определением.
У Кудрявцева упорядоченная пара определяется только для x != y, поэтому тождественная функция для Кудрявцева не функция.
Кудрявцев не говорит что в записи {x, y} для определения множества x и y должны быть отличны. Двухэлементность это метаязыковое понятие означает наличие двух синтаксических переменных (символов), а не объектов которые они обозначают.
>пара (x,x) никак не описывается этим определением.
>только для x != y
Да почему? Чем плохо {x, {x}} ?
 40 Кб, 591x101
40 Кб, 591x101>Определение по Куратовскому это {{x}, {x, y}}
Да, долблюсь в глаза. Алсо вот что пишет Вавилов по этому поводу.
Схуяли он прав? Он именно что долбоёб приписывающий кудряшке свои представления аксиоматики ZF
Какое же тупое хуйло этот вавилов. В треде оснований выяснили, что он потенциальную бесконечность не осилил, а теперь оказывается он даже начала теории множеств не понимает. С какого хуя он решил, что запись {a, b} влечет неравенстов а и b?
 9 Кб, 300x155
9 Кб, 300x155>тупое хуйло
пикрелетейтед, теперь неси свой хирш
>влечет
знакомься
https://en.wikipedia.org/wiki/Axiom_of_extensionality
Не буду, не люблю хвастаться, тем более было бы перед кем.
У кудряшки-то он поди поболее будет
А вообще, это ничего не значит, полно примеров авторитетов в одной области, которые несут хуйню в другой. И вообще, ну дрочил он где нибудь в прикладнине, кого волнуют его выпуки по основаниям если он в них нихуя не петрит?
> знакомься
ууу, школььничек начал знакомиться с матлогом. Правда нихуя не понял, ну да это не важно, он же кудряшку победил. Как же это характерно для малолетнего долбоёба, лол.
Что не так ебанько? По этой аксиоме {x,y} = {x} если x = y. Где тут противовречие с определением упорядоченой или неупорядоченной пары?
Нет, у Кудрявцева сначала определяется понятие двухэлементного множества {a, b}, чтобы не осталось никаких сомнений что а !=b, а потом уже вводится неупорядоченная пара как двухэлементное множество.
Так что у Вавилова критика по делу.
С того, что у Кудрявцева явно прописывается двухэлементность множества, ну нельзя назвать множество {x, x} двухэлементным, да и с фундированностью хуеватисто выходит. Вон даже у дидов кто-то спрашивал по этому поводу.
https://dxdy.ru/topic121506.html
Да это не та аксиома, у Вавилова ZF9 это аксиома фундированности ака регулярности
>. Axiom of regularity (also called the Axiom of foundation)
Следствие оттуда, что никакое множество не может быть своим элементом. И получается, что Кудрявцев неявно её предполагает. Что хуйня. И с парой хуйня. Математика это про точность, сука, чтобы не допускалась двусмесленность,раздражают эти ебучие аналисты безалаберные со своими корявыми определениями, вангую твой кудряшка тупо из советской энциклопедии определение спиздил, а там тупо опечатку сделали, должно было быть {{x}, {x, y}}. Дело раскрыто. Пойду срать.
Ой блин, не в тот раздел запостил, извиняюсь. Не ходите по ссылкам, там ничего хорошего нет.
Норм, подрочено.
Да нормально, нормально, в тот, у меня хуй колом встал, ща посру и дрочить буду.
Там же встречается такой перл: "Таким образом, понятие множества, состоящего из одного элемента, равносильно понятию элемента."
>множество, состоящее из двух элементов
По первому вопросу тут явно Вавилов прав, даже если допустить, что имелось ввиду, что вместо y мы подставим х везде всё равно хуета, какой еблан назовёт множество {x} множеством из двух элементов? К тому же там сильный акцент делается на этом, именно два элемента, различные множества и тд. По второму вообще пиздец, Кудрявцев официально зашквар.
>У кудряшки-то он поди поболее будет
да? это самоцитирования в вестнике мгу? он за всю жизнь меньше статей опубликовал, чем вавилов за год.
А что, символично так получилось. Гей-порно в треде про матан, типа вот до чего доводят гомологии.
> В конце концов Кудрявцев таки вводит аксиомы Пеано
И всё равно фейл так как аксиомы Пеано не являются определением натуральных чисел.
У вавилова достижений с хуй, лучше бы не вылазил из своей генетики, лол. А цитируют его только во всяких щитхол изданиях, это своего рода сеть по обмену баннерами что бы раздувать свой рейтинг.
Просто ты неосилятор и тупое ебанько. В математике вырожденные случаи встречаются на каждом углу и фиксятся элментарно добавлением тривиальных оговорок. У кудряшки учебник матана а не труд по основаниям теории множеств и главы эти скорее для напоминания пререквизитов к матану и стандартизации обозначений.
>>51211
Хуйло пиздливое, ты опять со своим формализмом лезешь как опущенный? Двумысленность только у тебя в тупой башке, сам придумал и пытается на няшного кудряшку повесить, хуесос.
Всё правильно он сказал, ты небось как малолетний долбоёб представляешь множество как пакетик или мешочек. Так ведь тебе в садике говорили, лол.
Кстати, это же и есть ключ к разгаде, почему местные долбоёбы нихуя не поняли. Этой фразой он неформально поясняет вырожденный случай когда x=y, т.е. в его системе элемент x это тоже самое что {x}, поэтому при x=y упорядоченная и неупорядоченные пары это по сути тоже самое что x.
>У кудряшки учебник матана а не труд по основаниям теории множеств и главы эти скорее для напоминания пререквизитов к матану и стандартизации обозначений
Ну так и нехуй тогда вообще писать об этом, можно бля к специалистам подойти и узнать и не пиздоболить в учебнике, а он же просто хуйню пишет и потом люди это хавают.
>>51235
>повесить
Ты долбоёб что ли блядь? Твой кудряшка ебанат, который пиздит в своих учебниках, ты сам же это признал в этом же посте, кого куда я вешаю? Или ты сам тоже дебил и не понимаешь, в чём он обосрался?
Ладно, ты, видимо, совсем конченый, не вижу смысла дальше спорить с таким дурачком.
> Ну так и нехуй тогда вообще писать об этом, можно бля к специалистам подойти и узнать и не пиздоболить в учебнике, а он же просто хуйню пишет и потом люди это хавают.
Хуйня у тебя в голове, краткие справки по теории множеств во всех книжках по матану так пишут. У Колмогорова в фунане в таком же стиле написано, попробуй на него попиздеть, лол.
> ы долбоёб что ли блядь? Твой кудряшка ебанат, который пиздит в своих учебниках, ты сам же это признал в этом же посте, кого куда я вешаю? Или ты сам тоже дебил и не понимаешь, в чём он обосрался?
Я лишь признал, что ты пытаешься свои домыслы и непонимание повесить на кудряшку. Ты попутал дискурс, основания математики это другая тема а не матан и никто не обязан соблюдать лично твои обозначения и тупые представления о том как должно быть.
>>51251
Ты походу вообще не обучаемый, равносильно в тексте кудряшки это м етаязыковое неформальное пояснение. Он юзает НАИВНУЮ теорию можносте и поясняет на пальнцах, это блять курс матана для первокуров, аксиоматическую теорию множеств никто в книгах по матану не юзает.
>>51252
Да насрать на тебя, я просто буду опровергать твой бред что бы ты не засирал мозг посетителям этой борды своим малограмотным пиздежом.
 109 Кб, 463x247
109 Кб, 463x247> У Колмогорова в фунане в таком же стиле
Колмогоров вместо того, чтобы пиздеть о том, в чём не специалист, никаких определений упорядоченных пар не даёт, просто даёт общую интуицию, что (a, b) это не (b, a) и пользуется этим понятием без определения. Это в тысячу раз лучше, чем пиздеть хуйню неверную из области, в которой ты профан, читатель при желании поищет точное определение и будет нормально. Ну и такого бреда как элемент равносилен множеству он не писал.
>рря равносильно метаязыковое он другое имел ввиду
Мне похуй, равносильно это блядь равносильно, что тут можно не так понять? Он обосрался и следом за ним ты вот этим постом>>51237
>>51253
>опровергать твой бред
Ты просто нашёл какое-то говно, называемое по недоразумению учебником, похавал его, обмазался им, а теперь воняешь и срёшь под себя, думая, что что-то опровергаешь, не более.
Просто блядь осознай вред таких петухов, как кудряшка твой, ты воспринял его невнятную хуиту за истину возможно, кстати, что сам-то он как раз всё правильно понимает, просто написал коряво, "формализм хуйня и так сойдёт все же меня поняли" и потом пишешь такое>>51237
а потом рыбниковы плодятся, ты сам блядь стал жертвой и в то же время доказательством, что его учебник хуёвый. Он не обязан знать аксиоматическую теорию множеств, но он обязан как учитель, как человек, по чьему учебнику будут люди математику изучать хотя бы не врать о том, в чём не разбирается, дабы не вводить их в заблуждение.
Просто пиши им, что уринировал их лица и иди дальше заниматься своими делами.
Наивная теория множеств - это оригинальная теория множеств Кантора.
Она формализуется в виде первопорядковой теории следующим образом.
Алфавит одноуровневый, аксиомы равенства обычные. Метатеоретически это означает, что домен дискурса состоит только из множеств, урэлементов нет. Констант нет. Есть один двуместный реляционный символ ∈ и две аксиомы. Точнее, одна схема аксиом и одна аксиома.
1. Для любой формулы P(x, p°) и любого набора параметров p° выполнено ∃M∀x P(x, p°)⇔x∈M
2. Аксиома экстенсиональности.
Многие идиоты почему-то думают, что наивная теория множеств - это когда можно пиздеть про множества любую муть. Эти идиоты ошибаются. На то они и идиоты.
>1. Для любой формулы P(x, p°) и любого набора параметров p° выполнено ∃M∀x P(x, p°)⇔x∈M
Вавилов пишет, что Кантор никогда так не считал
>По этому поводу стоит заметить, что сам Кантор не только никогда не пользовался предположениями, подобным аксиоме Фреге, но уже лет за 20 до парадокса Рассела тщательней-
шим образом различал множества (Mengen) и совокупности (Gesamtheiten, Vielheiten,Totalit¨aten, Unmengen), которые слишком велики для того, чтобы быть множествами и чтобы к ним можно было применять стандартные процедуры образования новых множеств. Совокупности, к которым неприменима его теория трансфинитных множеств, Кантор называл абсолютно бесконечными. Иными словами, уже в 1880-х годах Кантору были известны не только сами парадоксы, но и способ их преодоления, по существу эквивалентный предложенной Дж.фон Нейманом теории классов.
И вот ещё
>В книге ‘Was sind und was sollen die Zahlen’ Рихард Дедекинд писал “Множество S полностью определено только тогда, когда относительно всякой вещи известно, является ли она элементом множества S или нет”. Ясно, что такой взгляд на множества устраняет все парадоксы до их появления, но его слабость состоит не в излишней широте, а в недопустимой узости понятия
множества. В действительности, описываемая ниже теория Цермело-Френкеля понимает множества значительно более широко, чем их понимали основатели теории множеств Кантор и Дедекинд, хотя, конечно, более узко, чем их первоначально понимали Фреге и Рассел.
Вообще довольно занятно он пишет
>французских аналистов
>Некоторые аналитики возражают против недискриминированного использования формы аналист, однако эта форма вполне отвечает правилам русского языка, параллельна таким общеупотребительным словам, как даосист, алгебраист, таксидермист и многократно исполь
зовалась Набоковым, который говорил психоаналист, а не психоаналитик.
И вот эти его шутки про анал. Бесценно.
Хотя, судя по Кудрявцеву и шизику, математику многие рашкинские аналисты действительно через жопу как-то учат.
Доставь
В доказательстве принципа индукции Кудрявцев неявно использует индуктивное определение натуральных чисел, получается такой порочный круг
>любое натуральное число получается из 1 последовательным прибавлением 1
Если он это ввёл как аксиому, то все ок.
 99 Кб, 618x740
99 Кб, 618x740Определения я не увидел. С таким подходом можно к любой строке придраться. Например, обозначение n+1 конфликтует с операцией + (если судить по тому куску текста, что я увидел). Я так понял, там всё через жопу. Зачем ты в дерьме копаешься?
Да из-за этого шизика. Действительно, только зря время потратил.
https://en.wikipedia.org/wiki/Treatise_on_analysis
Изданные на русском "Основы современного анализа" это только первый том
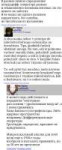 370 Кб, 702x1683
370 Кб, 702x1683В этом томе никакого анализа даже нет, метрическая топология только. Я кстати кажется выяснил, почему вербит не любит это.
Цитирую:
Насчет банаховых алгебр - эта наука, кроме теоремы
Хана-Банаха, применений особенных не имеет, мне кажется.
Функциональный анализ (в той степени, в которой он
зависит от аксиомы выбора) специально изучать, наверное,
не стоит, как и теорию множеств и общую топологию.
Вообще, случаев, когда в математике используются вещи,
которые следуют из (несчетной) аксиомы выбора - очень
мало; и мне думается, что это не случайно, т.е. разумная
математика остается разумной, если принять аксиому
детерминированности. Кстати, К-теория поля C становится
даже разумнее, так как если все цепи измеримы,
то К-теория C это пространство примитивных циклов
в алгебре измеримых, или же непрерывных, когомологий
пространства BGL; то есть конечномерное пространство.
То есть по его мнению, анализ даже как мы его понимаем тут (теория фредгольма, банаховы алгебры, спектральная теорема, обобщенные функции, пространства соболева, псевдодифференциальные операторы; т.е. Бурбаки, Данфорд-Шварц, Ахиезер-Глазман и т.д.) по мнению Вербита не особо и нужен. Про ПДО Каледин не верит, что возможно разумное определение (за 50 лет не справились).
>теория фредгольма, банаховы алгебры, спектральная теорема, обобщенные функции, пространства соболева, псевдодифференциальные операторы
ну если это всё не нужно, тогда и атью-зингера можно выкинуть к хуям? я не совсем понял из приведённой цитаты, что там имеется в виду, но наверно всё-таки имеется в виду что-то другое, помимо "не нужен". может быть, "неправильно сформулирован". не знаю, алгебра "измеримых когомологий пространства BGL" для меня звучит как ересь какая-то, это что вообще?
проследить, где в функциональном анализе есть теорема хана-банаха, а где нету, -- довольно трудно. по правде, мне казалось, что везде в теории всяких локально выпуклых топологических векторных пространств тоже, хотя это я знаю плохо и не помню; но в приложениях к обобщённым функциям вроде бы использовалось весьма существенно.
по поводу символа тоже не понял
главный символ пдо -- это элемент алгебры калкина, чего тут ещё надо? символ же это не просто произвольная гладкая функция, на неё куча условий, а самое распространённое -- символ это буквально ряд (из которого, конечно, можно выкинуть главный член). Короче, непонятно. Спорить с богами не берусь, я-то сам хуже грязи под их подошвами.
Для Атьи-Зингера нужны только эллиптические операторы, а не ПДО в целом. Просто полистай и сравни содержание соответствующей главы Р. Уэллса и например Шубина где куча двойных интегралов на каждой странице соседствует с коммутативными диаграммами.
https://youtube.com/watch?v=4-IiSYnA2Ek
"They figured out general context of it, but they're lacked machinery. In the end, it was easier for us to learn the analysis, than for them to learn algebraic topology."
>измеримых когомологий пространства BGL
Я сам не понял, что он имеет в виду, в смысле как именно принятик аксиома детерминированности упростит К-теорию. BGL по идее это пространство петель (бесконечнократное), можно доказать единственность распетливания, что будет эквивалентно функториальному определению пространства Квиллена.
>где в функциональном анализе есть теорема хана-банаха
Здесь видимо подразумевалась формулировка и доказательство этой теоремы именно на языке банаховых алгебр. И типа это единственное применение. По мне странно несколько, что не упомянута спектральная теорема. И теоремы Гельфанда-Наймарка. В принципе, как я вижу, это как раз же предложенный еще Эмми Нётер подход к математике. Определяем алгебраически соответствующие объекты, доказываем ряд структурных теорем про них, отсюда уже получается много содержательного. Как доказательство Нётер теоремы о ЖНФ (modules over PID). Деятельность Гельфанда в этом ключе и проходила. Что банаховы алгебры, что обобщенные функции (современное определение дал Гельфанд, а не Соболев). Мне вроде казалось очевидным что это первокультурное и правильное, но возможно что нет.
>эллиптические операторы
А ты их как определяешь? если обычные дифференциальные с какими-то условими, то между ними гомотопиию не нарисуешь, например, да и вообще топологическая часть формулы А-З в явном виде содержит в себе символ оператора, а поимев символ, ты имеешь пдо; пусть и с точностью до операторов меньшего порядка, что с того? таки индекс это довольно грубый инвариант (что нормально, точных инвариантов вообще не бывает). в общем, не понимаю, чем каледин недоволен
определения гротендика дифференциальных операторов мне неизвестно; алгебраической геометрией и её техникой (всякими пучками) не владею совсем. оно может и очень красивое, но на гладких многообразиях вот тебе символ, иже гладкая функция, производные, ограничения на порядок роста.. интегралы сходятся, всё работает. вроде бы даже и аксиомы выбора (пока) нет
кстати, насколько я могу судить, "микролокальный анализ по Касиваре" никому, кроме Касивары (и Шапиры), неизвестен; это какая-то вещь в себе; видимо, он известен ещё каледину, но основные работы каледина вроде не об этом
>Здесь видимо подразумевалась формулировка и доказательство этой теоремы именно на языке банаховых алгебр.
мне известна только формулировка "функционал можно продолжить", где там сидят алгебры, не догадываюсь, вроде бы только линейные пространства с нормой.
>Определяем алгебраически соответствующие объекты, доказываем ряд структурных теорем про них, отсюда уже получается много содержательного.
снова не слишком хорошо разбираюсь во всех этих второкультурах, да и вообще в основаниях/философии математики, но такой подход вроде бы довольно традиционен, тут и программа клейна, и что угодно; по-другому просто мало что получается в математике
>современное определение дал Гельфанд, а не Соболев
кстати, пространства Соболева без труда определяются вообще без обобщённых функций -- пополнение гладких функций по некоторой норме, и всё. никакой аксиомы выбора
 327 Кб, 1200x1642
327 Кб, 1200x1642>А ты их как определяешь?
Ну через эллиптический комплекс например.
Эллиптический оператор это частный случай псевдодифференциального. Просто дело в том что Атья-Зингер даже формулируется как утверждение об индексе эллиптического оператора, а в самом доказательстве ключевую роль играет один конкретный пример (оператор Дирака).
Формулу индекса нельзя вывести из теоремы Римана-Роха, но если получить аналогичную формулу для индекса оператора Дирака (который равен А-роду многообразия). Из формулы для А-рода можно формально вывести формулу индекса для любого комплекса
>чем каледин недоволен
Тем что нет определения псевдодифференциального оператора (точнее есть несколько, но они не эквивалентны); не очевидно почему композиция ПДО есть снова ПДО (это доказывается уже переходом к явной конструкции; подходящая аксиоматика просто отсутствует на данный момент).
>определения гротендика дифференциальных операторов
https://ncatlab.org/nlab/show/regular+differential+operator
Это, вроде?
>и её техникой (всякими пучками)
Пучки это допустим вообще общая топология, и вполне применимы в дифференциальной геометрии, например гладкое многообразие можно определить через пучки, а в науке о комплексных многообразиях без них вообще никак.
> Колмогоров вместо того, чтобы пиздеть о том, в чём не специалист, никаких определений упорядоченных пар не даёт, просто даёт общую интуицию, что (a, b) это не (b, a) и пользуется этим понятием без определения.
т.е. поступает ещё хуже, вводит избыточное неопределяемое понятие. Вот это новость.
> Это в тысячу раз лучше, чем пиздеть хуйню неверную из области, в которой ты профан
Ну тебе, например, профанство не мешает пиздеть и писать всякую хуйню на сосаке.
> Ну и такого бреда как элемент равносилен множеству он не писал.
Хто сказал что это бред, ты? Если ты не способен прочитать и понять простой текст, делай дауншифтинг до букварей или перекатывайся к гуманитарные науки к тупым пёздам.
> Мне похуй, равносильно это блядь равносильно, что тут можно не так понять? Он обосрался и следом за ним ты вот этим постом
т.е. понять ты не способен, тогда ты фундаментально путаешь кто из вас обосрался.
>>51270
Кудряшка всё правилно написал, ты доебался к нему с выдуманной проблемой, которая к тому же находится только у тебя в голове т.к. ты ни в основаниях математики ни в содержательной её части не петришь ровным счётом нихуя. Ты малограмотный малолетний долбоёб который нахватался фрагментарных знаний из матлога, нихуя не понял но бегаешь тут как опущенный пытаясь показать "знания".
Аксиоматическая теория множеств это хуйня которая зафейлилась и поэтому не особо нужна. Просто запретить юридически создавать супермножества много ума не надо, лол.
>>51274
Ты тупое пиздливое хуйло. Под наивной теорией множеств в литературе всегда имеют ввиду содержательную основанную на интуитивных представлениях теорию, а то что она в принципе может быть в ограниченном виде формализована никого не ебёт, максимум умывают руки делая такое замечание в предисловии и всё.
> Колмогоров вместо того, чтобы пиздеть о том, в чём не специалист, никаких определений упорядоченных пар не даёт, просто даёт общую интуицию, что (a, b) это не (b, a) и пользуется этим понятием без определения.
т.е. поступает ещё хуже, вводит избыточное неопределяемое понятие. Вот это новость.
> Это в тысячу раз лучше, чем пиздеть хуйню неверную из области, в которой ты профан
Ну тебе, например, профанство не мешает пиздеть и писать всякую хуйню на сосаке.
> Ну и такого бреда как элемент равносилен множеству он не писал.
Хто сказал что это бред, ты? Если ты не способен прочитать и понять простой текст, делай дауншифтинг до букварей или перекатывайся к гуманитарные науки к тупым пёздам.
> Мне похуй, равносильно это блядь равносильно, что тут можно не так понять? Он обосрался и следом за ним ты вот этим постом
т.е. понять ты не способен, тогда ты фундаментально путаешь кто из вас обосрался.
>>51270
Кудряшка всё правилно написал, ты доебался к нему с выдуманной проблемой, которая к тому же находится только у тебя в голове т.к. ты ни в основаниях математики ни в содержательной её части не петришь ровным счётом нихуя. Ты малограмотный малолетний долбоёб который нахватался фрагментарных знаний из матлога, нихуя не понял но бегаешь тут как опущенный пытаясь показать "знания".
Аксиоматическая теория множеств это хуйня которая зафейлилась и поэтому не особо нужна. Просто запретить юридически создавать супермножества много ума не надо, лол.
>>51274
Ты тупое пиздливое хуйло. Под наивной теорией множеств в литературе всегда имеют ввиду содержательную основанную на интуитивных представлениях теорию, а то что она в принципе может быть в ограниченном виде формализована никого не ебёт, максимум умывают руки делая такое замечание в предисловии и всё.
Пиздец ты на говно весь изошёл, шизло. Твоим Кудряшкой только жопу вытирать. x = {x}, лол.
Лол, ты походу жертва изнасилования, тебя выебал мужик с кудрявыми лобковыми волосами, поэтому ты ненавидишь всё что как-то напоминает тебе кудри. Другого объяснению твоего бреда я не вижу.
Какого бреда? Что одноэлементное множество равносильно элементу множества не я писал, про охуительную пару, которая не работает для (x, x) тоже. Я понимаю, что ты дурачок и неспособен понять, почему это бред, но щито поделать, бредом это не перестаёт быть от этого.
Ты хуйливое пиздло. Смысл равносильности тебе пояснили не раз в этом итт треде. Про вырождение пары в {x} тоже пояснили. Но ты тупое хуйло понять этого не способен.
>смысл равносильности
В каком месте? Ты что-то пукнул про рря нитакой смысл, но конкретно ничего не сказал. А во-вторых охуительные манёвры про равносильность на самом деле не равносильность меня как-то не особо интересуют.
>вырождение пары в х
Пара это двухэлементное множество, {x} одноэлементное множество, я понимаю, что у твоего маразматика это одно и то же и ∅ = {∅}, например, но у нормальных людей это считается бредом. Возможно, когда ты, шизло, послушаешь доктора и перестанешь пропускать принятие таблеток тебе это тоже бредом покажется, а пока мне с тобой говорить не о чем.
Если в твоём букваре написана конкретная кодировка пары это не отменяет других подходов. Он явно высказывается про вырожденный случай отмечая его тривиальность. Если ты не полный даун, то сходу понимаешь это и идеёшь дальше. Но, увы, ты - даун.
PS Тут на самом деле зарыт более глубокий смысл, дурачок думает что кодировки пары или натуральных чисел определяют эти понятия, но на самом деле это всего лишь кодировки в формальной системе. От них толку 0 за пределами матлога. Так что Колмогоров в плане обоснования прав что понимает упорядоченную пару как исходное понятие и даже не упоминает кодировки из формализаций.
>в главе ряды где-то 150 задач, я буду их несколько месяцев решать
Так делать в принципе не надо, это не математика.
Единственное, что ты должен делать самостоятельно, это пытаться доказывать все утверждения. Всякий раз, когда в книге приводится теорема, ты должен её доказать сам. Если это не получается, можно во всяком случае пытаться разобрать имеющееся доказательство. Некоторые книги, заради экономии места, доказательств вообще не приводят, а лишь иногда дают краткие указания. Такие книги называют "задачниками". Кириллов там, Атья-Макдональд, Кириллов-Гвишиани, Любич-Глазман, ну ты понял.
Но даже если доказательство приводится, там всё равно пропускаются некоторые шаги, "очевидно далее, что" "нетрудно увидеть, таким образом"; твоя цель это заполнять такие пробелы.
Есть как бы несколько уровней изучения математики.
Лучше сказать несколько уровней понимания. В семиотике есть синтаксис, семантика, и прагматика. Это соответственно формулировка, смысловое содержание, примеры использования. Маклейн учит, что математику можно изучать только на конкретных примерах. Но ведь это и есть доказательство утверждений. По определению, ты знаешь что-то про объекты, если можешь доказать теоремы про них.
В школе и в вузе обычно учат только синтаксической математике, то есть заучиванию определений, алгоритмов решения, в общем приобретению вычислительных навыков.
Вон диды с dxdy любят говорить, что нельзя понять что такое интеграл, не посчитав 500 интегралов символьно.
Но ведь это чушь редкостная. С тем же подходом можно просто 500 раз повторить вслух определение интеграла Римана. Это не математика, а тупое заучивание, мартышкин труд, бессмысленный абсолютно.
Не трать время на это.
>Ну через эллиптический комплекс например.
В переводе на человеческий язык, для тебя эллиптический оператор -- это дифференциальный оператор, символ которого есть изоморфизм. ну всё, чуть-чуть расширяя класс функций, которые называем "символами", получаем определение пдо. вполне себе строгое, стандартное, всё с ним в порядке.
претензии, что у кого-то есть определения неэквивалентные или там что-то не очевидно (выводится из определения с помощью прямого вычисления) многого не стоят
> а в науке о комплексных многообразиях без них вообще никак.
но там и атьи-зингера тоже нету. это другая история уже, нечего её сюда. хотя вербицкий и каледин могли иметь в виду именно это, т.к. в этой области их основные интересы
Там разговор был про определение ПДО, а ты даешь определение эллиптического оператора, это более узкий класс ПДО. Бескоординатного определения ПДО пока нет.
https://ncatlab.org/nlab/show/pseudodifferential+operator#definition
http://www-math.mit.edu/~rbm/18.157-F05.pdf
>эллиптический оператор -- это дифференциальный оператор
Можно ещё определить собственный ПДО и показать что любой линейный дифференциальный оператор это собственный ПДО. Шубин так и делает, у него символ вводится для собственных ПДО.
>там что-то не очевидно (выводится из определения с помощью прямого вычисления)
Не выводится, т.к. его нет, есть только явная конструкция.
>но там и атьи-зингера тоже нету
В каком смысле нету? Риман-Рох это частный случай Атьи-Зингера. Римана-Роха без упоминания пучков даже сформулировать нельзя.
Это он так потроллил бакалавров что ли?
>это более узкий класс ПДО
so what? не понимаю, что ты хочешь донести вообще (я про эллиптические и не начинал)
>Бескоординатного определения ПДО пока нет.
есть, вот оно
https://onlinelibrary.wiley.com/doi/abs/10.1002/cpa.3160180307
обидно, конечно, что без пучков, но есть же
мне известно ещё одно, но оно довольно дикое
>Можно ещё определить собственный ПДО
мало ли что ещё можно. на компактном гладком многообразии все операторы собственные
>Не выводится, т.к. его нет, есть только явная конструкция.
опрделения нет? не совсем понимаю, чем "определение" отличается от "явная конструкция"
>Риман-Рох это частный случай Атьи-Зингера
не наоборот же. разные это науки (гладкие многообразия и аналитические)
ну ок. я с этого и начал примерно:
>не совсем понял из приведённой цитаты, что там имеется в виду, но наверно всё-таки имеется в виду что-то другое, помимо "не нужен". может быть, "неправильно сформулирован"
 1,3 Мб, 1024x1391
1,3 Мб, 1024x1391Валерия Ильинична, вы же вроде всё?
Анализ у нас довольно слабый, преподам на нас похуй. Зорич таки подойдёт?
Вы видите копию треда, сохраненную 13 августа в 00:12.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


















