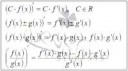Вы видите копию треда, сохраненную 23 апреля 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.



Самое главное, непонятно, зачем всё это. Всевозможные инженеры и научные работники либо воспользуются программой символьных вычислений (а для элементарных функций есть общий универсальный алгоритм интегрирования, который является следствием развития дифференциальной алгебры), либо (что скорее) будут интегрировать численно.
Венцом всего этого стало событие, произошедшее больше года назад. По просьбе своей кафедры я участвовал в олимпиаде Санкт-Петербурга по математике для технических вузов. Задачи на той олимпиаде были довольно техническими (простите за каламбур), судя по всему, ориентированными на те же синтаксические преобразования.
В одной из задач требовалось решить диффур. Я никогда не умел решать диффуры, кроме как методом подстановки-проверки. Подставил две или три простейших функции, вижу — получил ответ, так и пишу в решении: проверим что данная функция удовлетворяет уравнению, проверим, что выполнены условия теоремы существования и единственности. Вполне строгое решение, даже самому строгому проверяющему не к чему придраться.
На апелляции вижу, что за эту задачу у меня стоит далеко не полный балл. Беру свою работу, но в ней по этому поводу ничего не отмечено. Вдруг какой-то человек (позднее оказалось, что это был заведующий кафедрой математики ВИТУ) спрашивает меня: что я собираюсь апеллировать? Я отвечаю. Он начинает со мной спорить, что то, что я написал — это не решение, а решением должен быть некий набор действий, показывающий, как это решение получилось (полученный, очевидно, при помощи синтаксической процедуры). В конце концов, ему предложили пример: есть поле, на котором закопан клад, который надо найти. Один человек перекопал всё поле и нашёл клад, а другой просто угадал, где надо копать, и сразу выкопал клад. Кто из них решил задачу (нашёл клад)? Заведующий кафедрой математики сказал, что только тот, кто перекопал всё поле.
Но это, конечно, было не самым интересным. Через некоторое время у меня началась собственно апелляция, которую проводил председатель жюри (он же отбирал задачи) профессор матмеха Н. А. Широков. После некоторого спора он в конце концов выдал мне следующую фразу (воспроизвожу не дословно, но близко к оригиналу и без потери смысла): «Возьмите любой учебник дифференциальных уравнений, там есть набор стандартных подстановок, их-то и надо использовать при решении таких задач. При решении диффуров вы должны продемонстрировать ваше владение этим набором стандартных подстановок, а не умение решать задачи.». Это был для меня сильнейший деморализующий удар, я так и не нашёлся, что можно на это возразить, так и ушёл с неполным баллом (хотя выиграл олимпиаду). А вот другой человек получил полный балл, применив пару подстановок, даже не соизволив пояснить, почему его решение единственно (что было сделано у меня).
Математика делится на содержательную и синтаксическую. Представителями синтаксической математики являются подавляющее большинство учителей школ, всевозможные репетиторы, заведующий кафедрой математики ВИТУ, а также профессор матмеха Н. А. Широков (он, кстати, там заведует кафедрой матанализа).
Не путайте содержательную математику с синтаксической!
Пикрелейтед - картины Фоменко "Математика", "Математика. Гомеоморфизм, достаточно близкий к тождественному" и "Математика. Расслоенные пространства".
Предыдущий: >>337592 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/


есть ещё кто-нибудь, кого от изобразительной графомании Фоменко тошнит так же, как меня? Видеть его не могу, везде форсят
Меня больше тошнит от чисто текстовых "элегантных" преобразований и восхищения формулами.
Картинки у него как раз вполне годные. Ну не Эшер, но все-таки.
а как же посещать концерты классической музыки и послать весь мир нахуй с его миллионом?
Форсит один и тот же даун. Ещё в прошлом году в /b начал. Теперь этот уебан сюда перекатился.
Я ленивый.
>а матанализе требовали вычислить 50 (!) интегралов и производных
На самом деле все общие результаты получаются от большого количества ебли с частными случаями. Вот сидели там Эйлер и прочие Коши, считали свои сотни-тысячи интегралов, решали задачи, не брезговали и в столбик числа складывать наверное - и в результате родились у них многие формулы и теоремы имени Себя.
Вот тут возникает "непростая" дилемма - можно взять все готовые результаты, полученные человеко-тысячелетиями работы выдающихся умов, и восхищаться их красотой, НО современная система образования считает что правильный путь - бескрайняя ебля. Нужно быть КАКДИДЫ. Иначе ты никогда ничего своего не откроешь. И вообще будешь никудышным человеком.
>все общие результаты получаются от большого количества ебли с частными случаями
Весьма сомнительное утверждение, нуждающееся в аккуратном доказательстве.
Ну может не совсем уж все, но довольно многие. Как по-твоему можно написать алгоритм вычисляющий интегралы, не прорешав предварительно их дохуищи?
> Вот сидели там Эйлер и прочие Коши, считали свои сотни-тысячи интегралов, решали задачи, не брезговали и в столбик числа складывать наверное - и в результате родились у них многие формулы и теоремы имени Себя.
Ага, и декарт тоже сидел и что-то считал. пидор, блять, бросил всё и пошел бродяжничать по миру, а потом нахуярил кучу всякого
> можно взять все готовые результаты,
> восхищаться их красотой
Ну бери восхищайся, делов то.
> НО современная система образования считает что правильный путь - бескрайняя ебля
> Иначе ты никогда ничего своего не откроешь
И правильно делает. Православная ебля позволяет тебе на своей шкуре ощутить все косяки, которые возникли при открытии этого.
А господа смотрители и восхищатели каждый день изобретают велосипед, который ещё и объясняют не на уровне решения, а на уровне ну как-то так, а когда им говорят, что эта хуйня так не работает, это ещё 2 столетия назад доказали, то они обижаются и кричат ВРЁТИ! А ТЫ САМ ДОКАЖИ ЧТО НИРАБОТАЕТ ну и дальше по классике, они требуют доказывать каждую мелочь, которая оспользовалась в опровержении, в плоть до того, что производная х2 /2х
В данном случае вербитодауном является postdoc неплохого американского университета. У вербитодаунов вообще с удивительной частотой немало математических достижений в наличии (за всю жизнь встречал только одно исключение, когда человек действительно упоролся тифаретиком и пытался имитировать математическую деятельность).
>>340558
Примерно так же, как додуматься до формулы в радикалах корней многочлена третьей/четвертой степени и доказать, что ее нет для больших степеней. Т.е. занимаясь содержательными вещами и развив теорию групп и теорию Галуа.
>НО современная система образования считает что правильный путь - бескрайняя ебля.
И ты конечно же выбрал самый верный путь для решения этой проблемы - прийти на двач, в мат.тред(!), рассказать всем, какая плохая на самом деле система образования. Министры и чиновники, которые здесь сидят, прислушаются к твоему мнению, поймут свои недочеты и проведут школьную реформу. Жди почтового уведомления об удовлетворительном решении по поводу твоей просьбы.
>postdoc неплохого американского университета
Быстро всем коленопреклоняться! Это же постдок неплохого американского университета.
Ты какой-то странный, если считаешь, что обо всех проблемах говорят только ради того, чтобы их решили.
Ты какой-то странный, если считаешь, что о проблемах системы образования нужно говорить в мат.треде /sci. un/ вообще-то есть для этого.
До вербитодаунов Каледина и Вербицкого ему, конечно, далеко. Но тем не менее лучше, чем весь этот тред вместе взятый.
>un/ вообще-то есть для этого.
С тем же успехом можно обсуждать проблемы математики со школьниками на детской площадке. Здесь люди хоть что-то понимают.



>Примерно так же, как додуматься до формулы в радикалах корней многочлена третьей/четвертой степени и доказать, что ее нет для больших степеней. Т.е. занимаясь содержательными вещами и развив теорию групп и теорию Галуа.
Мне кажется ты несешь полнейшую поебень. В историческом контексте. Но не то чтобы я очень хорошо ориентировался в истории математики, может быть знающие меня поправят. История на самом деле мне представляется такой - сначала было много ебли. Были даже соревнования по решению уравнений высоких степеней (лал). Еще там была какая то история как ученик спиздил формулу решения у учителя.
Ну а Галуа лежал спокойно в ящике (в двух смыслах) до того времени как его стали применять. И кубические трехчлены были изучены к тому времени вдоль и поперек.
Да, пожалуй /sci/ стух окончательно.
Ты говоришь, конечно, верно. Решать уравнения третьей и четвертой степени научились до Галуа. И всячески ебались. Но вот только понимания никакого не было. А после появления теории Галуа люди разом доказали неразрешимость в радикалах уравнений степени пять и больше, а также получили почти забесплатно понимание про степень меньше пяти. При этом ебли никакой не требуется, для появления теории Галуа она тоже не требовалась. Т.е. все эти миллионы человекочасов ебли с явным решением уравнений просто канули в лету без какой-либо пользы.
Неразрешимость до Галуа.

Что-то я совсем не раздуплил, чего от меня хотят в пикрелейтеде. В чем метод ответа на этот вопрос? Ведь у нас может быть любая функция, и ряд ее вокруг единицы может вообще любым оказаться. Что они хотят?
Я тыкнул все, где есть (х-1), но это неверно.
В каком смысле "а если"? Я не могу методом тыка проверять. В чем ризонинг бихайнд твой конклюжн?
Я нигде не видел в определении ряда Тейлора условия сходимости. Мне неочевидно, что несходящийся ряд не может являться рядом Тейлора какой-нибудь нехорошей функции. Поясни, пожалуйста.
>>340593
От твоего имхо ни горячо, ни холодно. Рассуждение в чем состоит?
5 - не может быть рядом тейлора в окрестности единицы, просто по своей структуре.
2 - не может быть рядом тейлора, ибо в окрестности единицы имеется неаналитическая особенность
Я тут подумал еще и 4 не ряд тейлора, ибо 4 - конечен.
Насчет 3, мне лично не нравится, что все коэффициенты ряда равны единице, но мб и может быть такой ряд.
> просто по своей структуре
> блябуду, атвичаю, не ряд Тейлора нахуй, очевидно бля
Отличный аргумент.
> 2 - не может быть рядом тейлора, ибо в окрестности единицы имеется неаналитическая особенность
Хм, хорошо. Но откуда это следует? Можешь привести твое определение ряда Тейлора и показать, что из него следует невозможность особенностей?
> Я тут подумал еще и 4 не ряд тейлора, ибо 4 - конечен.
А вот это действительно очевидно! Я даже не обратил внимания, что там HOT'a нету. Спасибо.
>>340597
>6 - тоже не ряд тейлора, ибо есть член с отрицательной степенью
Точно! Спасибо.
>>340599
Да, согласен, спасибо.
Алсо, подозрительно, что на другой вопрос я дал тот же ответ, что и в прошлый раз, но теперь он помечен как неверный. Нет, ну вероятнее, конечно, что я просто ошибся и не туда жмакнул, но все равно подозрительно. Короче, подумываю забить на это, четыре верных ответа из пяти - тоже норм.
>Отличный аргумент.
Определение ряд тейлора в точки a знаешь? Нет? Ну так пиздуй в учебники или еще куда.
>Хм, хорошо. Но откуда это следует?
Я слышал, что логарифм в нуле не определен.
>>340605
> Определение ряд тейлора в точки a знаешь?
Знаю.
>Я слышал, что логарифм в нуле не определен.
Аутист, перечитай еще раз то предложение, на которое ты отвечаешь.
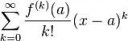
Хуило вонючее, видишь пик, вот так выглядит ряд ебучего тейлора, скажи мне, членосос ссаны, номер 2 похож на пик? А?
Отличное доказательство: "не похож".
Из-за того, что я сейчас сонный, тебе удалось воспользоваться моим доверием к саентачу и начать сеять смуту и ложь в этом треде. Но это время закончилось. Ты - вредитель. Уходи.
Да, я
> Из-за того, что я сейчас сонный, тебе удалось воспользоваться моим доверием к саентачу
вот это как раз в связи с этим и сказал, лол.
Дана функция f. Нужно показать существование функции, разложение которой в ряд Тейлора в окрестности некой точки совпадает с f, или доказать, что таких функций нет.
>Короче, сформулирую еще раз задачу:
А функция f какая? Ты блять из себя математика корчишь тут или хуи сосешь?
Ууууу, зарепортил, какой большой мальчик.
> Что значит нехорошей?
Неаналитической как минимум, но это не совсем то, понял.
> но он всё равно сходится к чему-то.
Вообще, я все еще не уверен в этом. Вот смотри:
https://math.stackexchange.com/questions/694697/infinitely-differentiable-function-with-divergent-taylor-series
Тут задан тот же вопрос, что и у меня, и вроде как раз есть примеры функций, у которых ряд Тейлора нигде не сходится. Сейчас почитаю, что там по ссылкам.
> In general, Taylor series need not be convergent at all.
А вот это - Borel's theorem - отвечает на вопрос из этого >>340614 поста.
Самспросилсамответил
Ну, все равно спасибо - за мотивацию к поиску.

Он и по жизни поехавший.
Кто решал задачи нахождения глобального экстремума функции многих переменных? Какими методами пользовались? Я тут читал про мультистарт, но у меня 5 переменных и разброс начальных значений каждой должен быть 3 порядка, а значит этих точек мультистарта должно быть просто ОЧЕНЬ много.
Использую матлаб, можете посоветовать готовые решения или теоретические методы?
Если бы курс читался по-русски, записалось бы 2 человека. Так хоть количество потенциальных слушателей увеличивается.
Да, но это будет грязный трюк, основанный на переопределении чего-нибудь. Либо, в наихудшем случае, банальная вычислительная ошибка.
Например, определяю алгебраическую структуру, где A x B = 5, где A и B элементы N. То есть 1 x 1 =5, 5 x 5 = 5, 100 x 4 =5. Великолепно.
Это миф, распространенный среди профанов.

Я все в лоб пересчитал, с раскрытием скобок и дельтой, все правильно.
Ладно, так долго получится объяснять. Вот
http://www.cleverstudents.ru/derivative/differentiation_rules.html#derivative_of_the_product
С э R что значит? Натуральные числа через N обозначаются. Или это комплексные?
Хорошо, а если там три, четыре, пять, октоллиард функций перемножаются и надо их производную найти, надо каждый член перемножать на производную остальных функций?
По ссылке пример есть, но там загнули аж арктангенсы с арккосинусами в качестве простого примера.
И что не так с моим личным определением производной как скорости изменения функции в точке?
А там годно? Я калькулюс сейчас прохожу, убергоднота. От русских честно говоря не ожидаю чего-то хорошего.
Бамп вопросу.
А я все не теряю надежды что сам смогу додуматься. Если какой-то пиздюк двести лет назад смог, то чем я хуже? Знаю что там какие-то симметрии и все. В учебники специально не заглядываю.
Алсо курсера - говно ебаное. Лекции можно было бы глянуть если они в открытом доступе будут.
5 переменных это немного. Если у тебя функция ±хорошая, то обычный градиентный спуск тебя спасёт. Если плохая то копай в сторону метода отжига.
Да нормально всё со скоростью. Смотри, ты в интернете нашёл картинку с бабой в огромном разрешении и начал в фотошопе прямоугольным выделением выделять её сиськи, чтобы кропнуть и поставить на рабочий стол.
Когда ты двигаешь мышкой, у тебя едет верхняя и правая границы прямоугольника с некоторыми скоростями. А ты хочешь понять с какой скоростью растёт количество пикселей в твоём прямоугольнике (=произведение). Дебилу ясно, что приращение площади увеличится на ширину×приращение высоты + высота×приращение ширины + площадь квадратика, которой можно пренебречь в пределе.
отсюда и следует (w×h)' = w'×h + w×h'
Это и так было понятно. Я просто попросил вывод формулы.
Что делать если у меня больше двух функций перемножаются под производной? Каждый отдельный член перемножать на все производные остальных членов? Или такого НЕ МОЖЫТ БЫД, две функции под проихводной это предел?
Может. Возьми да посчитай (fgh)', учитывая, что (ab)' = a'b+ab'.
(fgh)' = (fg)'h + (fg)h' = f'gh + fg'h + fgh'.
(fghpq)' = f'ghpq + fg'hpq + fgh'pq + fghp'q + fghpq'.
Причем здесь калькулюс? тут вообще про другое
то что я не смогу взять производную арксинуса и не понимаю смысл ряда тейлора не помешает мне при желании освоить подобный курс, потому что я что-то знаю про группы, действия групп, векторные пространства и прочее из алгебры.
Ну, тогда попробуй курс. Хорошо, если почитаешь еще что-то про кольца/поля/идеалы/модули. Тогда зайдет.
Ясно, каждый раз выражать все функции с одной производной, а не одну функцию со всеми производными.
Тоже подойдут.
Ага.
>>340922
>Тебе пока рановато.
Вовсе нет. Ты либо переснобил, либо сам не в курсе, о чем теория Галуа.
>>340922
>И что не так?
Ужасный акцент, плохая подача. Не вижу смысла тратить на это время.
>>340939
>Алсо курсера - говно ебаное
Почему?
>Лекции можно было бы глянуть если они в открытом доступе будут.
Они и так в открытом доступе, глупышка.
Попробуй погуглить по слову "кришна".
Всегда хотел спросить: зачем смотреть курсы, если можно читать учебники? Или на слух информация лучше запоминается?
Зря стараешься. Во-первых, у Галуа была мотивация в виде проблемы неразрешимости в радикалах полиномов выше 4-й степени (а статьи по этой теме тогда уже были, т.е. ему было на что опираться), а не просто желание сделать теорию с "какими-то симметриями". Во-вторых, никаких полей, групп, и тем более групп Галуа сам Галуа никогда не придумывал. Необходимый багаж понятий более менее созрел только ко временам Дедекинда, а законченное изложение теории Галуа на современном языке и вовсе создал Эмиль Артин в 30-е годы 20 века. Так что советую читать учебник и не выпендриваться.
Во-первых, применительно к обсуждению конкретного курса с курсеры это нерелевантно. Во-вторых, теорию Галуа на "современном" языке изложил таки Делинь.
Всегда хотел ответить. Шучу, на самом деле эта мысль не так давно начала у меня вызревать и еще даже не приобрела окончательной формы. Но я поспешу ей поделиться.
Когда я был молодым и шутливым, я думал - нахуя вообще нужны лекции? Все же ведь можно прекрасно в книжках прочитать.
Сейчас у меня на жестком диске валяется тысяч двадцать книг на разные интересные мне темы. Сколько же из этих книг я прочитал от корки до корки? Или хотя бы осилил несколько глав?
Внезапно оказалось что изучать новый предмет гораздо легче по курсам.
С книгами явно есть какая-то наебка. Чтобы осилить типичный "томик" по какой-нибудь науке нужно приложить просто несравнимо больше усилий, чем на просмотр курса из десятка лекций.
А главный секрет тут в том - что курс ограничен по времени. По этому если даже автору ну очень хочется поделиться охуительными историями, разобрать 100500 примеров, изложить advanced главы - ему приходиться как-то себя ограничивать и оставлять самое главное.
>в открытом доступе
Это наглая ложь. Нет нужно чтобы без регистрации, без смс, без js-говна, можно было спокойно скачать или смотреть онлайн.
Дальнейших возражений уже не будет? А жаль, я уже было изготовился поумничать.
Во многом с тобой согласен. Но если курс не очень сложный, а лектор медленно читает, то проще взять и почитать книжку. Ну, и кому что больше нравится же: я вот люблю лекции смотреть, учебники тоже иногда наворачиваю.
Может еще хочешь чтобы мокрые писечки за тебя дрочили?
Это интереснее. Тебе дают задания, которые автоматически проверяются. Тебе дают план занятий и следят за его выполнением. Рядом всегда есть другие студенты, у которых можно спросить, если что-то непонятно.
Вообще, вопрос уровня "зачем нужны универы, если есть учебники?". Одно другому не мешает, а наоборот - дополняет.
Мне кажется, что держать под рукой бумажку с ручкой и использовать их для создания неструктурированных заметок нужно обязательно. То есть это даже не конспект, а просто чиркание во время просмотра.

Но ведь эти мрази не выкладывают торенты. А кукарекать-то горазды как все открыто и доступно. Только если добрые люди найдутся которые захотят этим заняться.

Кажется седьмую дорешал. Можно рассмотреть данный гомоморфизм, как тождественный автоморфизм группы вращений, тогда в ядре будет лежать единичный элемент. Что делать с восьмой? Вот определение разрешимости из книжки.
Ядро гомоморфизма --- прообраз единицы. То есть вся группа SO(3, R). Ф со скобочками там были лишними, спасибо.
Первый случай: хотя бы один поворот в ядре, а значит и вся группа лежит в ядре.
Второй случай: только тождественное отображение лежит в ядре.
Как быть с восьмой задачей? Все доказанное ранее значило бы неразрешимость, только если во втором случае образ гомоморфизма был бы некоммутативной группой.
Охуеть братан, спасибо тебе большое. Я думал что сегодня не усну.
Там, если записался, можно ли просто смотреть на Катю, но не сдавать задачки, экзамены, ни с кем не общаться? В скайп там не надо заходить, сиди себе и смотри? Скачивать видео себе на хард?
https://habrahabr.ru/post/167583/
для этого отдельный тред по соседству создали же
Это даже на научпоп не тянет. Так... автор показал, что знаком с фундаментальными понятиями мат. логики.
ну это же какой-то юный второкурсник вдруг ощутил, что ему доступно какое-то необыкновенное знание, и что ему необходимо понести его людям
Я всё сказал.
Математика - язык описания геометрии, например. Очевидно, что язык не может являться частью науки.
Записался на Катю. Блядь, охуенно же! Жалко, другой приличной математики на этих курсоерах так не представлено. Я о них до того слыхал, но не интересовался
Спасибо анон!
Трахнул бы вернюю
Ну когда он появляется, каждый уважающий себя человек обязан кинуть ему знаменитую пикчу
Аноны посоветуйте литературу по линейным операторам в гильбертовых пространствах.
И ваще про логарифмы, зачем нужны.
Спасибо, Анон
Все мы в чем-то математики, братишка.
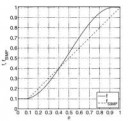
Аа, забыл уточнить, что сплайн 3 степени, хотя это и так видно из исходных данных.
Люстерник Л.А., Соболев В.И. Элементы функционального анализа
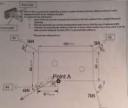
Корректно ли будет идти от противного? (т.е. привести пример, почему оно не может быть меньше, потом привести пример, где оно будет равно 6, затем пример, где оно будет больше 6?)
Нет, это не будет корректно: тебе нужно для всех х доказать. Просто разбери случаи, когда x< -3, -3<x<3, x>3.
Возьми х=0, а потом заметь, что левая часть при увеличении икса уменьшается на столько же, насколько правая увеличивается (а при больших иксах обе увеличиваются). Для уменьшения икса аналогично. Все дела.
Вон тот костёр развёл. Мамку твою рядом с ним выебал.
Ок, надо было сказать, что отображение должно быть биективным. Две разные точки должны оставаться двумя разными точками.
Выбери что-то одно. Отображение пространства в плоскость либо непрерывное (соседние точки являются соседними), либо биективное. Ну, либо вообще ни то ни другое. Непрерывной биекции 3D в 2D нет.
> можно было бы взять проекцию
Не понял что значит "взять проекцию".
И в предыдущем комментарии ты написал:
> Отображение пространства в плоскость
Но мне нужно отображать не пространство целиком, а только его часть - один объект.
Но если всё же нельзя, то есть какой-нибудь аналог развёртки (биективное отображение, точки расположенные рядом в большинстве случаев остаются расположены рядом) только для самой фигуры, а не только её оболочки.
Пусть f и g - две функции.
g = O(f) означает, что g растёт пропорционально f.
Если f(x) = 10, то g(x) = k10. Если f(x) = 100, то g(x) = k100. k одно и то же.
g = o(f) означает, что g растёт на порядок медленнее f.
Например, если g(x1) = 10, то f(x1) = 100, а если g(x2) = 20, то f(x2) = 100500. Никакого k тут подобрать нельзя, рост f непропорционально быстрее роста g.
Для тебя специальная резервация выделена. https://2ch.hk/sci/res/295488.html (
И да, туда писали, но в основном неадекваты какие-то, сходи да посмотри.
За килобакс уже норм будет.
>>341644
>Единица это неопределяемое понятие, это фундамент который мы фиксируем для дальнейшего определения N.
Все! Тема определения N закрыта! Не смейте больше ничего писать.
Resolvent Monte Carlo algorithm (RMC)
Inverse Monte Carlo Iterative algorithm (IMCI)
Какой из них выбрать, если:
а) Мне потом его нужно будет распараллеливать
б) Хотелось бы прогать поменьше.
Пункт а) важнее, чем пункт б). В методе ничего не понимаю, только сейчас сижу ковыряюсь.
Что за теорема? Гугл ничего не выдал, может быть, я искал как-то не так.
представь как разницу 100000...00 и 2. Если там могут быть не только девятки, тогда не знаю.
Петрика Путяху.
Фигура область ограниченная многогранником каким-нибудь? Эта область гомеоморфна всему пространству, поэтому так же нет. Тебе прямо только обязательно биекция нужна или "соседние точки переходят в соседние" больше нужно? Спроектируй на пространство меньшей размерности.
Да вряд ли целый учебник, а тем более "учебники". Главки хватит про матрицы да линейные преобразования. Не сам же библиотеки будешь писать. Просто чтобы общее понятие иметь
Возводи её жорданову форму, а потом точно так же обратно сопрягай.


Прямая определяется двумя точками. На твоих пиках просто взяли две удобные точки (0, y) и (x, 0) и нашли недостающие координаты.
сука
5x-10y=20
2x+4y= -16
Лягко.
Приводишь к виду:
x=2y+4
x=-8-2y
Ищем пересечение по y
2y+4 = -8-2y
4y=-12
y=-3
Подставляем:
5x-10 -3 = 20
5x=-10
x=-2
2x + 4 -3 = -16
2x =-4
x=-2
Евклид, "Начала".
Берже "Геометрия" (тем кто осилил хоть треть первого тома - памятник)
Любой компетентный логик тебе скажет, что без отрицания не обойтись. Не знаю, есть например алгебра Жегалкина.
Да, конструктивиская "логика". Колмогоров утверждал, например, что если A - корректное конструктивистское высказывание, то его отрицание не имеет никакого смысла.
Там же написано.
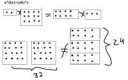
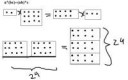
Принялся я тут читать "Что такое математика" Куранта. Почитал от редактора, очень все хорошо. Немножко конечно обосрался на вступлениями, где автор оперирует понятиями "Вещь в себе" и задвигает какие-то сложные философские телеги, хотя ранее пишет, что книга подойдет для школьника 6-7 класса. Но думаю, ладно, стал дальше читать. И тут я обираюсь уже второй раз и дальше уже продвинуться не получится, нужно понять. Так вот, антош, в чем тут фишка?
Должно же быть равно. В смысле 24=24 должно быть или 32=32. Я конечно ёбу-то дал, не спорю, но я все равно не понимаю.
Я ничего не понимаю в твоей мазне. Задай вопрос человеческим русским языком. Я на твоей картинке вижу 32 ≠ 24, это правильно.
Не благодари.
Человек в раисии может отучиться на математика в ВУЗе и при этом не заниматься обучением, становиться преподавателем в шараге, etc, а только заниматься чистой исследовательской деятельностью?
>и при этом не заниматься обучением
Нет. Справочка для хохлов: не только в "раисси", мало где за границей тебе просто дадут делать свой "ресёрч" без педагогической нагрузки. Оно и понятно, кому ты там такой охуительный сдался, деньги тебе запросто так платить.
Ну, если по чесноку, то это не вся правда и какие-то способы не преподавать (в смысле, вести регулярно какой-то курс) вообще никогда есть, и даже именно такая возможность есть у нас, но это редкие случаи. Вон, Каледин по-моему вообще не преподавал ничего.
Нет, не может. Аспирантура предполагает обязательную педагогическую нагрузку.
Ну есть знаменитый философский спор: можем ли мы познать вещи вокруг. Море для тебя синее, для дальтоника зеленое, для коровы серое, и т.д. Так вот какое на самом деле это море, это и есть вещь в себе. Именно поэтому математика о вещах в себе, т.к. изучает по сути сами объекты, не основываясь на нашем чувственном восприятие их.
Такому дауну вроде тебя и не место среди академической элиты. Так что да, хороший отсеивающий барьер.

Этим барменом был Сергей Пахомов.

Для первого примера ответ будет 8/6, а как пятое считать? Я еще не до конца понимаю как интегралу задавать пределы мнтегрирования, по какой переменно.
Как-то я погорячился. Вопрошаяющего я совсем зря послал, а еще спойлер с Калединым не прочитал. Но в любом случае в Стекловке таких людей дофига
Потому что отвечаю сам себе.
Там, как и везде, только объяснение, чему оно равно. А доказательства теоремы нет.
>А доказательства теоремы нет.
Сука глаза разуй, мудень.
>Graham, R. L.; Rothschild, B. L. (1971). «Ramsey's Theorem for n-Parameter Sets». Transactions of the American Mathematical Society 159: 257-292. DOI:10.2307/1996010. The explicit formula for N appears on p. 290.
>Graham, R. L.; Rothschild, B.L. (1978). «Ramsey Theory», Studies in Combinatorics, Rota, G.-G., ed., Mathematical Association of America, 17:80-99. On p. 90, in stating «the best available estimate» for the solution, the explicit formula for N is repeated from the 1971 paper.
Нет, в конструктивизме и интуиционизме же есть отрицания, просто с ними работают по-другому. Я говорю о чем-то без отрицаний вообще, совсем без такого понятия.
>>342215
>Любой компетентный логик тебе скажет, что без отрицания не обойтись.
Почему? Где можно про это почитать подробнее?
> Не знаю, есть например алгебра Жегалкина.
Сейчас погуглю, спасибо.
(Интеграл а/(2р)^² минус интеграл а/р^²) делить на р, так?
Алексиевич в треде. Все в букач.
В России организовался строй под названием постосовок, пока есть что из ресурсов выкачивать, он будет существовать, затем эта страна наконец то умрет.
Стекловка - одно из немногих мест, где не нужно преподавать, таких мест в мире не так много, типа TIFR, HRI, IHES, IAS и типа того, но с IHES и IAS не строит сравнивать таки, там мало постоянных профессоров и гигантские зарплаты. В Стекловку трудно попасть, чаще всего надо, чтобы кто-то из людей реально впрягся. Ну и многие путешествуют, катаются по странам, институтам, универам - зарабатывают там, пишут статьи.
В гринтексте.
Йди бути товстуном де небудь інде
Скажем первая форма - это дифференциал функции, т.е. её приращение на кривой.
Вторая форма это приращение функции на "плоскости".
Пусть мы имеем f(x,y).
Тогда 1-форма: f(x,y)dx + f(x,y)dy
2- форма: f(x,y)dx/\dy
Если я не прав, прошу пояснить доступно, что это такое.
Читал https://en.wikipedia.org/wiki/Differential_form и
https://en.wikipedia.org/wiki/One-form
Не понял немного почему Градиент - это первая форма
Зато представил, что первая форма показывает сколько бесконечно малых плоскостей проходит заданный вектор.
Ага, одни дифференциалы и интегралы.
The symbol O was first introduced by number theorist Paul Bachmann in 1894, in the second volume of his book Analytische Zahlentheorie ("analytic number theory"), the first volume of which (not yet containing big O notation) was published in 1892.[16] The number theorist Edmund Landau adopted it, and was thus inspired to introduce in 1909 the notation o;[17] hence both are now called Landau symbols. These notations were used in applied mathematics during the 1950s for asymptotic analysis.[18] The big O was popularized in computer science by Donald Knuth, who re-introduced the related Omega and Theta notations.[12] Knuth also noted that the Omega notation had been introduced by Hardy and Littlewood[10] under a different meaning "≠o" (i.e. "is not an o of"), and proposed the above definition. Hardy and Littlewood's original definition (which was also used in one paper by Landau[13]) is still used in number theory (where Knuth's definition is never used).
https://en.wikipedia.org/wiki/Big_O_notation#History_.28Bachmann.E2.80.93Landau.2C_Hardy.2C_and_Vinogradov_notations.29
в продолжении своего вопроса.
Правильно будет говорить, что производная от 1-формы - это градиент.
Так оно?
>Правильно ли я понимаю, что дифференциальная форма - это просто производная?
Что значит просто производная? Между дифференциальными формами и дифференциалом есть некоторое соответствие, ибо дифференциал есть линейная форма,а значит она есть дифференциальная форма и в подходящем базисе она выглядит как полагается.
>Правильно будет говорить, что производная от 1-формы - это градиент.
Нет, можно сказать применение оператора d, который форме степени p ставит в соответствие форму степени p+1
неправильно. производная функции - это снова функция, дифференциальная форма - это не функция.
читай у Зорича о дифференциальных формах (там же будет про градиент и всё остальное).
Двачую. Почему пишут f(n) = O(g(n)), а не f(n) ∈ O(g(n)), если по сути O(g(n)) - это класс функций? Во-вторых, почему не пишут в какой точке это все происходит? Я бы писал f ∈ O(g, x0), причем x0 может быть равно ±∞.
Предлагаю следующее определение.
Пусть задана функция g : R → R. Определим
O(g, x0) = {f : R → R | ∃M > 0, ε > 0 : |x − x0| < ε ⇒ f (x) ≤ M g(x)}.
Аналогично определим и O(g, ±∞).
Чтобы, например, записать, что функция f растет полиномиально, будем писать
f ∈ O(np, +∞)
Потому что значок ∈ стал широко использоваться только благодаря Бурбаки, в конце тридцатых.
В HO иногда попадаются всяческие вводные статьи. Типа такого http://arxiv.org/abs/1602.03006 , первая попавшаяся навскидку.
Я не шутил.
http://www.mth.uct.ac.za/people/perm-aca-staff.php - африканский универ
http://arxiv.org/find/nlin/1/au:+Alexeeva_N/0/1/0/all/0/1 - некоторые статьи

Сенсация! Гриша Перельман отыскался в Кейптауне.

Там только формальные определения, не очень понятен смысл этих чисел, зачем они вообще. Видеорелейтед.
Поле, в котором любой многочлен имеет корень, называется алгебраически замкнутым. Многочлен - это основной строительный кирпичик в алгебре. Из многочленов сооружается большое количество сложных объектов. Поэтому алгебраически замкнутые поля весьма ценны.
Есть поле вещественных чисел R. В нём не любой многочлен имеет корень. Например, многочлен x2+1 вещественных корней не имеет. То есть R не является алгебраически замкнутым. Это плохо.
Поля, содержащие R в качестве подполя, называются расширениями R. Комплексные числа - это, по определению, наименьшее из всех алгебраически замкнутых расширений R. Это объясняет их популярность.
Комплексные числа популярны не только в чистой математике. Они оказались довольно полезными для приложений. Дело в том, что справедлива формула Эйлера cosф + isinф = eiф, позволяющая свести всю тригонометрию к простой арифметике комплексных чисел. Так как тригонометрия очень важна в физике и в инженерном деле, физики и инженеры очень любят комплексные числа.
Для тахионов.
Нахуй уже иди, мудак тупой. Сколько здесь ни сижу - стабильно из треда в тред вижу ебаната, спрашивающего про комплексные числа и на любое пояснение заявляющего, что ему НЕПОНЯТНО и вообще бурбакизм.
Здохни, мразь.

Бурбаки.
Вам в царство цифр или в математику? Вы уж определитесь.
Комплексные числа используются для нахождения корней квадратичных функций, когда функции требуют извлечение корней из отрицательных чисел. Это их изначальное предназначение при иизобретении, а потом уже они начали пользоваться для рассчета токов и прочего.
>>343240
>>343246
Бурбакидауны уже изобрели прогрессивную теорию множеств будущего?!
>>343242
Вполне обычное явление. Рано или поздно кто то в самообучении доходит до них и не понимает их сути.
Это я к оому, чтобы ты кинул ему книжек про то что это такое и как их используют. А то я уже не помню как научился считать их, так что не могу ему объяснить.
БУРБОКИЗМ ХАХАХАХА ЕТО ТИ ЛОХ МНЕ НЕПОНЯТНА ДОВАЙ ДРУГОЕ ХЛЕБУШЕК ПАКУШАТЬ ПРИНЁС
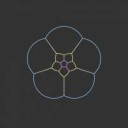
Комплексные числа в большинстве алгебраических манипуляций ведут себя так же, как вещественные (образуют поле), но являются их расширением. Геометрически им соответствует плоскость, а не прямая, там есть корни из -1 и вообще, любые уравнения имеют решения и раскладываются в произведения типа (x - a), анализ тоже работает, но приобретает некоторую специфику.
То есть они интересны тем, что, с одной стороны, очень похожи на вещественные числа, но, с другой стороны, во многом от них отличаются, что позволяет вдохнуть немного свежести в остоебавшую вещественную интуицию.

>точное определение единицы по бурбаки
Пикрелейтед - как Бурбаки определил единицу на самом деле. Скрин из "Теории множеств".
>точное определение единицы через теорию множеств
и
>как определили единицу бурбаки
это две большие разницы, как говорят у нас в Одессе.
Ты наркоман штоле сука? "Теория множеств" - это книга, которую написал Бурбаки. На моём скрине - оригинальное, настоящее определение Бурбаки.
Если число не делиться на любое другое простое число то оно является простым? или если оно не делится на все простые? или как?
Пусть x - натуральное число.
Определение 1. Натуральные числа, отличные от x и от 1, назовём другими для x.
Определение 2. Число x называется простым, если оно не делится ни на какое другое число.
Определение 3. Простые числа, являющиеся другими для x, назовём другими-простыми числами.
По основной теореме арифметики каждое натуральное число является произведением каких-то простых чисел.
Теперь очевидно, что если x не делится ни на какое другое-простое число, то x является простым числом.
сделал проверку так.
если X не делится на числа от 2 до N то число является простым.
N в свою очередь квадратный корень числа округленный в большую сторону. Вроде работает
Гельфанд Шень алгебра
дальше Зельдович высшая математика для начинающих физиков и техников
и Алексеев теорема Абеля в задачах и решениях
А почему именно ЮАР и причём здесь российские студенты? По какому признаку ты их связываешь?
во мудак

класс, именно вот это всегда и искал. добра и тонны нефти тебе!
Мне всё равно непонятно, как фактор-группа построена. Почему смежные классы к SLn - это числа?
ну по определению же получается
берешь матрицу с единичным определителем
домножил её на число
она в другом смежном классе получилась
и так все матрицы получаются очевидно
да он же говно посоветовал
Хм. Вроде, понимаю. Я не совсем ещё освоился, несколько иначе представлял себе расклад. Спасибо.
Историческая близость математических школ. Многие учёные из России в девяностые-нулевые переехали в ЮАР и теперь куют там матан российского образца.
> матан российского образца
А в чём это выражается?
Что конкретно в http://arxiv.org/find/nlin/1/au:+Alexeeva_N/0/1/0/all/0/1 тебе кажется таким непроходимым матаном российского образца, что принципиально не могло быть опубликовано нигде ещё? И причём здесь всё-таки современные российские студенты?
пиздец он гриб
Спасибо. Я не тот, кто задавал вопрос, но ты понятно и годно все объяснил. Побольше бы таких постов. Ты няша.



Т.е. умение считать важно лишь постольку, поскольку оно связано с абстрактной алгеброй образца начала 20 века? Весьма спорное утверждение. Или в том треде был какой-то контекст, которого мы не знаем?
Умение считать - это умение пользоваться калькулятором. Оно не предполагает знания всей той теории делимости, которую изучают в школе.
А что это за ненужная теория делимости, которой учат в школе? Просто с моей точки зрения, чтобы пользоваться этим пресловутым калькулятором нужно еще придавать некий смысл производимым арифметическим операциям, чему в школе собственно и учат. Никакой теории делимости (сравнений по модулю, например) сверх того в обычной школе и не дают.
Ну вот возьмём то же самое деление с остатком, в школе оно изучается. Скажи, почему остаток всегда должен быть положительным? С какой целью определение именно такое? Почему бы не сказать, что остаток от деления -10 на 6 - это не два, а минус четыре? Обоснуй чисто школьными аргументами.
Сука это мой ответ.
А он был всегда положительным? Я честно говоря уже забыл. Но разницы-то никакой и нет, т.к. по модулю 6 +4 и -2 одно и то же. В школе просто для удобства придерживались записи, при которой все элементы Z/nZ записывались как {0,1,...,n-1}.
Но суть-то не в этом - утверждается, что без знания колец, идеалов и т.п. умение делить с остатком бесполезно. Но по моему без него вообще никак не обойтись - уж во всяком случае студент-инженер должен же знать, что не все числа делятся нацело, при этом про кольца, группы поля ему знать совсем необязательно.
В школе не говорят, что можно найти остаток от деления отрицательного числа. Эта операция вводится только для положительных чисел.
Аналогично, в школе говорят, что корень n-й степени из отрицательных чисел не определен. Хотя, изучение корней в школе - это обман, потому что существование корня n-й степени из положительного числа еще надо доказать, а как его доказать, если в школах даже не проходят вещественные числа?
Щитоблядь. В школе говорят, что если a=b*c+d, то d - ето остаток. Все.
У меня хорошая память. Я помню, о чем мне говорили в школе. Это что, правда так странно?
>Аналогично, в школе говорят, что корень n-й степени из отрицательных чисел не определен.
Вот здесь ты тоже хуй пойми что имел в виду. Как это не определен? Для нечетных эн - определен.
Наименьший по модулю.
Да, он всегда был положительным. Дело в том, что деление с остатком - это на самом деле проявление особой, целочисленной нормы. Деление с остатком - это на самом деле операция понижения нормы. А так как всякая норма положительна, остаток тоже положителен.
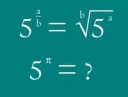
В школе нет вменяемых определений. Например, школьники не смогут определить операцию возведения в иррациональную степень.

Настоящая разница состоит в рисовании стрелок и одновременном оперировании с разными пространствами, тогда как в школе предпочитают сидеть в одном пространстве.
Какое отношение возведение в иррациональную степень имеет к извлечению кубических корней из отрицательных чисел? Ты совсем упоротый, или что с тобой такое?
Я утверждаю, что в школе нет определений.
Пример с возведением в иррациональную степень - самый простой способ это продемонстрировать.
А я утверждаю, что Земля круглая! А! Слыхали? Какой я молодец, правда?
Нет, неправда - я выгляжу дураком, потому что это и так общеизвестный и очевидный факт. Улавливаешь?
>это и так общеизвестный и очевидный факт
То есть ты согласен с тем, что в школе вместо математики занимаются хуйнёй.
Нет, в школе занимаются обучением детей. Впрочем, в твоей школе, очевидно, действительно занимались хуйней.
То есть вот смотри.
1. Школа обучает детей математике.
2. Выпускники школы не знают ни одного определения.
Ты правда не видишь здесь противоречия?
Проблема с введением в школу "правильной" программы по математике в том, что непонятно
а) Зачем и кому это нужно
б) Где остановиться, т.е. какой объем математики школьник должен знать и почему.
Сегодняшняя школьная программа обоснована в первую очередь тем, чтобы на первом курсе технических вузов не нужно было определять sin, cos и log. При этом строго формального определения (начинающегося с определения действительных чисел) не нужно, т.к. его могут дать и на матанализе, а вот понимать, почему проекция силы на ось х это модуль умножить на косинус полезно с самого начала. Предлагаю придумать свою версию того, зачем школьникам знать, что такое кольца идеалы и пр.
Мне, кстати, кажется, что в школе основными предметами должны быть 1) русский язык 2) английский язык 3) логика 4) какой-нибудь гибрид истории, культурологии и философии.
Искренне не понимаю, почему в школе не преподают логику.
>>343584
Открой введение в анализ за 10-11 классы и посмотри, дурилка картонная.
Как скажешь.
Я не согласен. Строго формальное определение синуса не имеет ничего общего со школьным представлением о синусе.
В анализе синус определяется как функция, сопоставляющая числу x сумму ряда x - x3/3! + x5/5! - x7/7! + ...
Это абсолютно не похоже на школьное представление о синусе как об y-координате точки координатной окружности.
Я не он, но никакого противоречия не вижу.
Школьники, кстати, (автоматически подразумевается «хорошие», «плохие» не знают вообще ничего) могут сказать, что такое иррациональное число — последовательность приближений, как правило десятичными дробями. Чтобы применить операцию к двум иррац. числам (в том числе возведение в степень ^) нужно применять её к возрастающим по точности приближениям десятичными дробями и „перейти к пределу“. В общих чертах это все знают. Те, кому интересно, рассмотрят детали потом.
Точна. Чтобы определение было определением, нужно, чтобы все входящие в него объекты были определены. А "функция" в школе не определена. Школьник имеет полное право спросить, что именно в наборе символов |f(x) - A| обозначено как f(x). Судя по ранее записанному тексту - сама функция. Выучиться чему-нибудь по таким "определениям" - нереально.
>Искренне не понимаю, почему в школе не преподают логику.
Потому что она никому не нужна.
На самом деле русский язык и математика тоже никому не нужны, но нужно же что-то преподавать.
Да кто спорит-то? Суть в том, зачем это проходить в школе - для элементарных приложений достаточно элементарного определения, для того, чтобы точное определение стало осмысленным нужно учить матан, которого в школе нет.
Мне нужны.
В школе нет того уровня строгости о которой ты говоришь, но целям школьного обучения он не отвечает.
>А "функция" в школе не определена.
О ней даётся представление на том уровне, который достаточен для определения предела. Если ты считаешь, что каждый математический объект необходимо определить в (например) логике предикатов – то это наивная позиция так или иначе приводящая к перегруженности из-за лишнего формализма.
Мне не нравится такой подход. Он предполагает, что до восемнадцати лет человек настолько глуп, что ему нельзя показывать ни одного настоящего определения. Меж тем, например, Эйлер поступил в университет в тринадцать лет, магистром стал в семнадцать, а в девятнадцать чуть не стал профессором. Это убедительно доказывает, что люди моложе восемнадцати лет - не идиоты.
>>343602
Что значит "даётся представление"?
Какова связь между быть "не идиотом" и знанием определений? Ещё раз: можно использовать тот или иной формализм и объяснить деление с оста тком при помощи теории колец. Но обычно цель определяет средства, и есть разные уровни градации понимания. Сразу начинать с формальных определений с рассмотрением всевозможных контринтуитивных случаев – нереально.
>Что значит "даётся представление"?
Формируется первичное понятие, образ, "что это и с чем едят". Извини, я не могу строго описать этот процесс. Однако я с уверенностью могу сказать, что формальное представление не является необходимым условием понимания.
Люди отказываются учить своих школьников нормальной математике с настоящими определениями. Это мотивируется тем, что школьники - идиоты, тупые и не поймут.
Проблема в том, что не всем школьникам это нужно. Есть такая потребность - есть 57 школа, колмогоровский интернат и т.д.
Нет, это мотивируется ненужностью и избыточностью, относительно поставленной цели дать начальное представление об изучаемом материале.
>Нормальной математике
>Настоящими определениями
?
Давай-ка сменим тему - какая тогда должна быть правильная программа по математике, чем обосновать ее содержание и зачем она понадобится 99.9 % школьников, которые не станут математиками в будущем?
Ну что ж такие вопросы в последнее время не редкость. Это даже не вопрос, а очень сложная задача в области педагогики и педагогической психологии, решением которой пытались заниматься многие.
Пока имеем то что имеем: некоторое "среднее", решение, которое очевидно уже "трещит по швам". Ты правильно задал вопрос, но пытаешься неправильно на него ответить. Формализацией и строгим изложением – здесь не решить.

В детском саду.

В этих тредах никогда не идёт активного математического обсуждения математических тем, зато постоянно идут околоматематические срачи, связанные, в основном, с преподаванием и основаниями.

Я утверждаю, что появилась особая разновидность человеческой деятельности: школьная математика.
Школьная математика не имеет ничего общего с настоящей математикой.
Школьную математику создают и развивают методисты всяческих гороно-районо-минобрнауки-уо. То есть чиновники.
Эти чиновники имеют, как правило, учёные степени в так называемых "педагогических науках".
Методисты и педагоги докатились до того, что отменили коммутативность умножения.
Я не хочу ничего безумного.
Я просто хочу, чтобы школьной математики не было, чтобы методисты и педагоги перестали существовать.

Шизики.
Я никогда не поверю что человек в здравом уме будет предлагать давать школьникам определения тригонометрических функций через ряды.
>Я не хочу ничего безумного.
>Я просто хочу, чтобы школьной математики не было, чтобы методисты и педагоги перестали существовать.
Это тебе так кажется, на самом деле ты хочешь внимания и хуя по губам.
Какой-то ты тупой. Доктор педагогии небось?
>Методисты и педагоги докатились до того, что отменили коммутативность умножения.
2 куска сахара и 5 раз - это элементы разного типа, не принадлежащие полю, поэтому коммутативность здесь действительно неприменима. Здесь не 2 и 5, а 2к и 5.
>Я не хочу ничего безумного.
>Я просто хочу, чтобы школьной математики не было, чтобы методисты и педагоги перестали существовать.
Альтернативы?

Ты идиот, который не может в физическую размерность.
Как и докторша педагогических наук, впрочем.
Речь идёт о размерности "кусок сахара"/"чашка". Не о чашках.
>Альтернативы?
Сейчас во всех школах массово жрут говно.
Я не хочу предлагать альтернативу пожиранию говна.
Я просто хочу, чтобы его перестали жрать.
Здесь можно рассмотреть и
числа разной размерности, можно рассмотреть сахар и разы в виде модуля. Так или иначе – коммутативность здесь не причём. В случае с модулем, мы имеем умножение элемента кольца слева или справа на элемент поля.
Ни один из школьных учебников математики не написан учёным-математиком.
Авторы школьных учебников не имеют научных публикаций в уважаемых журналах и, как правило, не имеют степеней.
Я утверждаю, что эти люди не имеют права писать учебники по математике.
Хотя бы в силу ограниченности кругозора.
Учебники по математике должны писать только учёные-математики.
Действующие учёные. Не методисты, не чиновники.
Писались учебники учеными математиками и как правило они были совершенно нечитабельны.
Ты дебил?




Лучшие из учебников написаны учёными.
Всем вам известен, например, классический курс математического анализа, начинающийся пределами, содержащий эквивалентные бесконечно-малые, протекающий через "раскрытие неопределённостей" и так далее.
Этот курс изложен во множестве книг множества авторов.
Все эти книги являются отражениями, тенями одной и той же оригинальной книги.
Это всего лишь пересказы учебника, который впервые написал Коши в 1821 году.
Все авторы следуют одной и той же схеме, введённой Коши.
Вот эта схема: http://ilib.mccme.ru/djvu/klassik/analysis/koshi.htm
Всевозможные математические анализы для чайников, вся эта классическая архитектура курса анализа - это на самом деле просто пересказ Коши.
Плагиат длиною в двести лет.
Только передовые учёные имеют право писать учебники.
Только учебники лучших учёных планеты заслуживают шанса быть прочитанными.
Я с удовольствием учился по учебнику матана, который написал Анри Картан.
Я отказываюсь учиться по учебнику матана, который написал методист Говнов.
>Я отказываюсь учиться по учебнику матана, который написал методист Говнов.
Правильно. Потому что такого нет.
В каждом провинциальном вузике каждый провинциальный хуй с кафедры матана считает своим долгом написать книжку.
В этой книжке всегда содержится дрянной пересказ сочинения Коши, причудливым образом преломившийся в провинциальном сознании.
Святая толстота. Хотя бы бурбаки запостил, и то тоньше было бы.
Реформатор от БогаВербицкого; борец за настоящуютм математику; пишет строфами, как принято у вербитопомазанных, легко детектится.
Нужно дать ему имя.
Косинус и синус это процентное обозначения количества вмещающейся гипотенузы в катетах треугольника, тангенс отношение количества гипотенуз двух катетов. А как можно найти эти три функции для произвольного угла без построения единичного круга, при условии что угол не слишком мал?
> Какова связь между быть "не идиотом" и знанием определений?
На самом деле связь есть, только немного не такая. Если какой-то человек заинтересовался математикой, потому что думает, что математика это целиком дрочево на определения - то он скорее всего идиот.
Такой то реформатор, не может определение синуса и косинуса написать. И это даже без пеано такой говнопад в штанах.
Ну, если речь идёт о других науках, то это уже даже не идиот, а какой-то имбецил.

Шизик имеет ввиду вот это определение. И предлагает его давать в школах.
Игнорируя что в той же вики, выше дано геометрическое определение.
N питушок, ето ти? Я не могу по доугому объяснить полное отсутсвие у тебя аргументации

Что именно кажется тебе недостаточно обоснованным?
>>343758
Ну и?
Я где-то призывал анафематствовать знания о координатной окружности?

nУ тебя плохая картинка
ALLO, PEANO, ETO TI? ETO N PITUSHOCK, YA HOCHU U TEBYA OTSOSAT
Скорее, ты ебанулся и решил, что я хочу спрятать знания об элементарном смысле синуса.
Ну, бывает.
>Косинус и синус это процентное обозначения количества вмещающейся гипотенузы в катетах треугольника,
> тангенс отношение количества гипотенуз двух катетов.
Что?
> В школе нет определений.
Как минимум я вспоминаю определение окружности на как множества всех точек некоторой плоскости, равноудалённых от данной. Так что ты обоссан в один ход. Кстати говоря, это один из исторических примеров, на счёт которого постоянно воют вербитоприближённые и прочие пятисемиты как раз потому, что на нестрогом формулировании этого определения (опускали слово "всех") многих из них сбривали на вступительных в МГУ. Следуя твоей позиции, это было правильно, так как определения настолько самоценны что должны всегда быть изложены в полной строгости, иначе не верны.
Энергия частицы перемещающейся в электорческом поле зависит только от напряженности поля, но не от расстояния? Тобишь, если взять и создать разность потенциалов в десять вольт, но в одном случаетнатрасстоянии два метра, а во втором полтора нанометра, энергия иона в обоих случаях десять электронвольт?
Человек понимает определение только тогда, когда ему понятны все используемые в нём слова.
В школе не рассказывают о том, что такое "точка плоскости".
В школе не рассказывают о том, что такое "множество".
Поэтому даже если обычному школьнику дадут твоё определение, школьник его не поймёт.
Хотя такого определения школьнику не дадут.
Школьные методисты ненавидят теоретико-множественную терминологию.
Они говорят "геометрическое место точек".
Ты знаешь, что такое "геометрическое место точек"?
Да, это набор точек удовлетворяющий определённым условиям.
Ок, и какое определения множества ты будешь давать школьникам? ZFC-аксиоматику?
Человек понимает определение только тогда и.т.д. и.т.п. Так что обоих, и смотри без использования тавтологической ссылки на понятие определения в какой-то метатеории.
Примем, что существует класс вещей, называемых "документы".
Примем, что с каждым документом связано вполне линейно упорядоченное множество S, имеющее последний элемент.
Его элементы называются состояниями чтения.
Примем, что каждое состояние чтения, кроме последнего, имеет последователя.
Примем, что с каждым документом связан класс вещей M, называемых терминами.
Примем, что с каждым документом связана функция f: M×S → {true, false}, называемая функцией осмысленности.
Интуитивно, если m - термин, s - состояние чтения, то если f(m,s) = true, то термин m определён в состоянии s, и не определён в противном случае.
Примем, что для всякого m если s1 < s2 и f(m,s1) = true, то f(m,s2) = true.
Интуитивно, осмысленный термин не может стать бессмысленным по ходу чтения.
Пусть фиксирован документ. Пусть m - термин.
Определением m называются такие два состояния чтения s1, s2, что:
а) s2 - последователь для s1
b) f(m,s1) = false и f(m,s2) = true.
Имеет место очевидная теорема:
Если определение существует, то оно единственно.
>>343812
Да, школьники без проблем усваивают ZFC.
Если изложить её естественным языком, конечно.
...
Аксиома 3. Из любых двух множеств можно образовать неупорядоченную пару.
Аксиома 4. Любое множество имеет булеан.
Аксиома 5. Любое семейство множеств имеет объединение.
...
Как-то так.
Примем, что существует класс вещей, называемых "документы".
Примем, что с каждым документом связано вполне линейно упорядоченное множество S, имеющее последний элемент.
Его элементы называются состояниями чтения.
Примем, что каждое состояние чтения, кроме последнего, имеет последователя.
Примем, что с каждым документом связан класс вещей M, называемых терминами.
Примем, что с каждым документом связана функция f: M×S → {true, false}, называемая функцией осмысленности.
Интуитивно, если m - термин, s - состояние чтения, то если f(m,s) = true, то термин m определён в состоянии s, и не определён в противном случае.
Примем, что для всякого m если s1 < s2 и f(m,s1) = true, то f(m,s2) = true.
Интуитивно, осмысленный термин не может стать бессмысленным по ходу чтения.
Пусть фиксирован документ. Пусть m - термин.
Определением m называются такие два состояния чтения s1, s2, что:
а) s2 - последователь для s1
b) f(m,s1) = false и f(m,s2) = true.
Имеет место очевидная теорема:
Если определение существует, то оно единственно.
>>343812
Да, школьники без проблем усваивают ZFC.
Если изложить её естественным языком, конечно.
...
Аксиома 3. Из любых двух множеств можно образовать неупорядоченную пару.
Аксиома 4. Любое множество имеет булеан.
Аксиома 5. Любое семейство множеств имеет объединение.
...
Как-то так.
Если нужно, могу объяснить замысел, который стоит за всем этим.
Ведь данное мной определение определения вполне корректно.
Разве что дополню его одним моментом.
Примем, что множество терминов M разбито на два непересекающихся множества.
Элементы одного из них назовём техническими терминами.
Элементы другого назовём содержательными терминами.
Содержательный термин, имеющий хотя бы одно определение, назовём определённым.
Интуитивно, технические термины - это что-то вроде слов "точка", "прямая" и "плоскость" в гильбертовой аксиоматике.
А содержательные термины - это то, что выстроено из технических.
Далее.
Примем, что с каждым определённым термином связано непустое множество терминов, называемое дефиницирующим.
Причём так, что выполняется нижеописанная аксиома.
Пусть m - термин, пусть d = (s1, s2) - определение для m.
Пусть X - дефиницирующее множество для m.
Если x - элемент X, то f(x, s1) = true.
Интуитивно, всякое определение использует какие-то ранее введённые термины.
Они-то и образуют так называемое дефиницирующее множество.
Аксиома требует, чтобы эти термины сами были осмысленны к моменту использования.
Примем, что существует класс вещей "пространство".
Примем, что с каждым пространством связан класс вещей "его точки".

Ну и сможешь ты детям объяснить, нахуй им это нужно? Сказав вышеозначенные сентенции и назвав это определением ты не скажешь ровным счётом НИЧЕГО реально нового чего пятикласник не понимает, просто ему хватило ума не думать над этим "определением", а заниматься более содержательными вещами.
Слишком толсто. Это можно даже примерно представить, исходя из названия.
Ну давай, объясни мне зфц на уровне понятий пятого класса.
Опять вильнеш жопой как с тригонометрией начну репортить.
Криптография.
Ну и зачем еще нужна тч?
Пиздец, /ph/ протек. Сука, ненавижу вас. Нет, чтоб сказать: я занимаюсь тч, потому что меня прет с этого, это искусство. Нет, обязательно надо какой-то околофилософией дристануть.
>Методисты и педагоги докатились до того, что отменили коммутативность умножения.
Ты совсем идиот, да? Ты хотя бы прочитал текст на своей картинке перед тем, как спиздануть очередную хуйню?
>При записи задачи с помощью умножения важен порядок множителей
>важен порядок множителей
> > важен порядок множителей
>В школе не рассказывают о том, что такое "точка плоскости".
Рассказывают. Целая отдельная глава страниц на 10 этому была посвящена во всех учебниках геометрии, что я видел.
>В школе не рассказывают о том, что такое "множество".
Аналогично.
Если "важен порядок множителей", то умножение некоммутативно. Это определение коммутативности.
То есть из "при записи задачи с помощью умножения важен порядок множителей" ты выводишь "умножение некоммутативно"?
Тут и дедукции не надо. Порядок важен - умножение некоммутативно. Умножение коммутативно - порядок не важен. Это определение коммутативности.
Представим, что у нас есть какой-нибудь алгоритм, перемножающий два числа, причем он работает быстро, если первое число большое, а второе маленькое, и медленно в противном случае. Заботливый преподаватель предупреждает: "при умножении чисел с помощью этого алгоритма важен порядок множителей". В этот момент школореформатор вскакивает с места и кричит: "УМНОЖЕНИЕ НЕКОММУТАТИВНО!".
Мораль басни, видимо, в том, что на качество школьного образования в основном жалуются те люди, которые сами действительно не получили удовлетворительного образования в школе - вот только не знаю, виновата в этом их школа или они сами.
Твой пример неуместен. В твоём примере разница только в скорости, а результат - один и тот же. Но в книжке сказано, что если переставить местами множители, то в ответе будут чашки, а не куски сахара.
Если под результатом понимать <произведение; время выполнения>, то результаты в моем примере, очевидно, разные. Если под результатом понимать <произведение; тип>, то результаты в твоем примере, очевидно, разные.
Почему ты не можешь в абстракции?
Умножение чисел в обоих примерах коммутативно. Операция записи решения задачи, очевидно, некоммутативна - именно это и утверждалось в тексте на той картинке. Ты совсем запутался.
Скажи это авторше учебника, лол.
В каком картинке? Таблетки выпил?
Решение задачи на умножение можно решать хоть дроча вприсядку, порядок умножения не важен. Даже в твоей манязадаче в университете имени академика Маняврянского ты натягиваешь сову на глобус.
>В каком картинке?
Вот в этом картинке: >>343621, не волнуйся ты так.
> Решение задачи на умножение можно решать хоть дроча вприсядку, порядок умножения не важен.
Ясно, пошли по второму кругу. Отсылаю тебя обратно к этому >>343919 и откланиваюсь.
Ты слишком туп, чтобы пгнять что эта задача аналогична тгму что в две чашки поклали пять кусков сахара?
Опиши мне тггда зфц теорию в поеделах знаний пятого класса, кловун. Ты сам сказал что она илиминтарна, отвечай за свой базар гнилой.
Кому - им?
Определение определения было нужно >>343807.
Он его получил.
>>343873
Сперва нужно понятным образом объяснить аксиоматический метод.
То есть рассказать, что такое "система вещей" по Гильберту, что такое аксиомы.
Далее нужно ввести элементы логики.
Объяснить, что такое предикат, что такое функциональный символ, что такое квантор и т.д.
Теория множеств вводится так.
Существует система вещей, называемых множествами.
Для них задано логическое отношение "быть элементом".
Всякая вещь A либо является элементом вещи B, либо не является.
Кроме того, для этих вещей задано отношение равенства с традиционными свойствами:
рефлексивность, симметричность, транзитивность, подстановочность.
Далее нужно дать несколько определений.
1. Множество называется пустым, если никакое множество не является его элементом.
2. Множество называется индуктивным, если хотя бы одно пустое множество является его элементом и если оно вместе с каждым элементом x содержит элемент {x}.
3. A называется подмножеством B, если всякий элемент A является элементом B.
В таком случае B называется надмножеством A.
4. Вместо того, чтобы говорить "множество множеств", мы часто будем говорить "семейство множеств".
5. Пусть M - семейство. A называется объединением M, если каждое множество из M - подмножество A и каждый элемент A - элемент хотя бы одного элемента M.
6. Семейство называется регулярным, если в нём есть такое множество, что каждый его элемент не входит в семейство.
7. Непустое C называется неупорядоченной парой A и B, если каждый элемент C равен либо A, либо B.
8. Пусть A и M множества.
Пусть каждое подмножество A является элементом M.
Пусть каждый элемент M является подмножеством A.
Тогда M называется "булеан A" или "множество всех подмножеств A".
9. Пусть M - множество, P - высказывание о его элементах, N - подмножество M.
Мы говорим, что N удовлетворяет P, если для всякого n из N высказывание P(n) истинно.
10. Пусть, в тех же обозначениях, N удовлетворяет P.
Пусть любое подмножество M, которое удовлетворяет P, является подмножеством N.
Мы говорим, что P выделяет множество N из множества M.
Или что N выделено предикатом P из M.
11. Пусть f - функциональный символ от двух аргументов.
Если вещь можно подставить в этот символ в качестве первого аргумента, то мы говорим, что функциональный символ осмыслен на этой вещи.
Мы говорим, что функциональный символ корректен на множестве M, если функциональный символ осмыслен на каждом элементе M.
Мы говорим, что функциональный символ является истинным функциональным высказыванием об M, если он корректен на M.
12. Мы говорим, что функциональный символ f, корректный на M, преобразует множество M во множество N, если
а) для всякого m из M существует единственный n из N такой, что f(m, n) истинно
б) для всякого n из N существует элемент m из M такой, что f(m, n) истинно
13. Пусть есть функциональный символ, корректный на M. Пусть существует такое N, что f преобразует M в N.
Тогда мы говорим, что f является преобразованием M.
Далее нужно сказать, что вещи нашей системы подчиняются следующим аксиомам (Цермело-Френкеля с выбором).
1. Два множества равны тогда и только тогда, когда первое является подмножеством второго и второе является подмножеством первого.
2. Для всякого множества всякое высказывание о его элементах выделяет подмножество.
3. Существует пустое множество.
4. Существует индуктивное множество.
5. Для любых двух множеств, не обязательно разных, существует неупорядоченная пара.
6. Для всякого множества существует булеан.
7. Для всякого семейства множеств существует объединение.
8. Всякое истинное функциональное высказывание о множестве является преобразованием множества.
9. Всякое непустое семейство регулярно.
10. Для всякого семейства непустых множеств существует множество, содержащее ровно по одному элементу из каждого множества семейства.
Кому - им?
Определение определения было нужно >>343807.
Он его получил.
>>343873
Сперва нужно понятным образом объяснить аксиоматический метод.
То есть рассказать, что такое "система вещей" по Гильберту, что такое аксиомы.
Далее нужно ввести элементы логики.
Объяснить, что такое предикат, что такое функциональный символ, что такое квантор и т.д.
Теория множеств вводится так.
Существует система вещей, называемых множествами.
Для них задано логическое отношение "быть элементом".
Всякая вещь A либо является элементом вещи B, либо не является.
Кроме того, для этих вещей задано отношение равенства с традиционными свойствами:
рефлексивность, симметричность, транзитивность, подстановочность.
Далее нужно дать несколько определений.
1. Множество называется пустым, если никакое множество не является его элементом.
2. Множество называется индуктивным, если хотя бы одно пустое множество является его элементом и если оно вместе с каждым элементом x содержит элемент {x}.
3. A называется подмножеством B, если всякий элемент A является элементом B.
В таком случае B называется надмножеством A.
4. Вместо того, чтобы говорить "множество множеств", мы часто будем говорить "семейство множеств".
5. Пусть M - семейство. A называется объединением M, если каждое множество из M - подмножество A и каждый элемент A - элемент хотя бы одного элемента M.
6. Семейство называется регулярным, если в нём есть такое множество, что каждый его элемент не входит в семейство.
7. Непустое C называется неупорядоченной парой A и B, если каждый элемент C равен либо A, либо B.
8. Пусть A и M множества.
Пусть каждое подмножество A является элементом M.
Пусть каждый элемент M является подмножеством A.
Тогда M называется "булеан A" или "множество всех подмножеств A".
9. Пусть M - множество, P - высказывание о его элементах, N - подмножество M.
Мы говорим, что N удовлетворяет P, если для всякого n из N высказывание P(n) истинно.
10. Пусть, в тех же обозначениях, N удовлетворяет P.
Пусть любое подмножество M, которое удовлетворяет P, является подмножеством N.
Мы говорим, что P выделяет множество N из множества M.
Или что N выделено предикатом P из M.
11. Пусть f - функциональный символ от двух аргументов.
Если вещь можно подставить в этот символ в качестве первого аргумента, то мы говорим, что функциональный символ осмыслен на этой вещи.
Мы говорим, что функциональный символ корректен на множестве M, если функциональный символ осмыслен на каждом элементе M.
Мы говорим, что функциональный символ является истинным функциональным высказыванием об M, если он корректен на M.
12. Мы говорим, что функциональный символ f, корректный на M, преобразует множество M во множество N, если
а) для всякого m из M существует единственный n из N такой, что f(m, n) истинно
б) для всякого n из N существует элемент m из M такой, что f(m, n) истинно
13. Пусть есть функциональный символ, корректный на M. Пусть существует такое N, что f преобразует M в N.
Тогда мы говорим, что f является преобразованием M.
Далее нужно сказать, что вещи нашей системы подчиняются следующим аксиомам (Цермело-Френкеля с выбором).
1. Два множества равны тогда и только тогда, когда первое является подмножеством второго и второе является подмножеством первого.
2. Для всякого множества всякое высказывание о его элементах выделяет подмножество.
3. Существует пустое множество.
4. Существует индуктивное множество.
5. Для любых двух множеств, не обязательно разных, существует неупорядоченная пара.
6. Для всякого множества существует булеан.
7. Для всякого семейства множеств существует объединение.
8. Всякое истинное функциональное высказывание о множестве является преобразованием множества.
9. Всякое непустое семейство регулярно.
10. Для всякого семейства непустых множеств существует множество, содержащее ровно по одному элементу из каждого множества семейства.
Неужто весь тред полон школоты проецирующей свои проблемы на всех остальных?
Чтобы человек захотел что-то искать, нужно, чтобы он знал о существовании этого чего-то.
Чтобы человек захотел искать математику, нужно, чтобы он знал о существовании математики.
Школьники не знают о существовании математики.
Школьники думают, что школьная математика - это и есть математика.
Я не толстяк.
>Всякое истинное функциональное высказывание о множестве является преобразованием множества.
Необычная формулировка.
Где оно?
Идинах.
Это не определение коммутативности. 2 куска сахара положить 5 раз и 5 кусков сахара положить 2 раза – разные выражения. Результат действительно получается одинаковым, но поскольку в 1-м и 2-м случаях в операции участвуют элементы разных множеств (сахар, и разы) – то о коммутативности речь не идёт. Это или умножение на скаляр:
2к x 5 = 10к
5 x 2к = 10к
или действие с элементами имеющими разную размерность:
2 к/р x 5р = 10к
Оговорюсь: коммутативность бинарной операции x, в данном случае можно рассматривать только на множестве содержащее как элементы обоих типов (куски, разы) или (к/р, к), но в таком случае теряется контекст задачи.
Пиздец идиот. Ты знаком с понятием размерности? В курсе, что килограмм на метр равен метр на килограмм?
Это сложно?
Размерность образует абелеву группу. В нашем случае она состоит из элементов {сахар, чашка, 1, сахар-1, чашка-1} и их всевозможных конечных комбинаций. Иди луркай математические основы метрологии.
>При записи задачи с помощью умножения важен порядок множителей
>При записи задачи
Все верно написано. Две монеты по пять рублей, и пять монет по два рубля - разные объекты с одинаковой ценностью. И задачу нужно записывать правильно, как она прозвучала, а не заменяя Васю на Петю потому, что тебе на это похуй. Решать ты можешь как хочешь, но на чистовую надо писать чисто, четко поясняя каждый свой шаг - это нужно для самоконтроля, чтобы не совершать ошибок, для того, чтобы убедиться, что ты все понимаешь и понимаешь правильно - да блядь, это просто нужно, как ты собираешься теоремы потом доказывать, если не умеешь расписывать все по-хардкору? Нахуячишь 100 страниц доказательства гипотезы Римана, во второй строчке обнаружат, что ты пределы суммирования переставил там, где на самом деле нельзя было, или еще в какой "очевидной" хуйне, и до конца жизни будешь ходить с обоссаным еблом из-за своей расхлябанности. И это надо все не только в матеше, а вообще везде по жизни. Поэтому аккуратности нужно научиться, и именно в связи с этим такие холивары, а не с тем, что умножение некоммутативно.
Что касается того, есть ли разница между 5яблок х 2 и 2 х 5яблок. Вспоминаем школьное определение умножения: a x b = a + ... + a (b раз). То есть здесь строго: сколько раз - это второй аргумент, а чего именно - первый. Сразу надо обратить внимание, что первый аргумент может и не быть числом (главное - уметь их складывать), а вот второй - обязан. Чтобы иметь право писать наоборот, надо сначала определить такую операцию - например, доопределить по коммутативности (объект х число := бла-бла-бла; число х объект := объект х число). Если ты прожевываешь этот шаг при записи решения, то с тебя вправе спросить пояснений, и в случае отсутствия четкого и правильного пояснения - заслуженно обоссать. Впрочем, тут надо вспомнить, что в школе учат умножать именно числа, а не яблоки, и при переводе задачи на математический язык избавляться от не-математических понятий (Задача: Есть пять монет по два рубля. Сколько всего рублей? Решение: Всего рублей: 2 + 2 + ... + 2 (5 раз) = 2 х 5 = 10), а за приучивание бездумно писать 2 руб. х 5 ссать в ебло уже учителю.
>При записи задачи с помощью умножения важен порядок множителей
>При записи задачи
Все верно написано. Две монеты по пять рублей, и пять монет по два рубля - разные объекты с одинаковой ценностью. И задачу нужно записывать правильно, как она прозвучала, а не заменяя Васю на Петю потому, что тебе на это похуй. Решать ты можешь как хочешь, но на чистовую надо писать чисто, четко поясняя каждый свой шаг - это нужно для самоконтроля, чтобы не совершать ошибок, для того, чтобы убедиться, что ты все понимаешь и понимаешь правильно - да блядь, это просто нужно, как ты собираешься теоремы потом доказывать, если не умеешь расписывать все по-хардкору? Нахуячишь 100 страниц доказательства гипотезы Римана, во второй строчке обнаружат, что ты пределы суммирования переставил там, где на самом деле нельзя было, или еще в какой "очевидной" хуйне, и до конца жизни будешь ходить с обоссаным еблом из-за своей расхлябанности. И это надо все не только в матеше, а вообще везде по жизни. Поэтому аккуратности нужно научиться, и именно в связи с этим такие холивары, а не с тем, что умножение некоммутативно.
Что касается того, есть ли разница между 5яблок х 2 и 2 х 5яблок. Вспоминаем школьное определение умножения: a x b = a + ... + a (b раз). То есть здесь строго: сколько раз - это второй аргумент, а чего именно - первый. Сразу надо обратить внимание, что первый аргумент может и не быть числом (главное - уметь их складывать), а вот второй - обязан. Чтобы иметь право писать наоборот, надо сначала определить такую операцию - например, доопределить по коммутативности (объект х число := бла-бла-бла; число х объект := объект х число). Если ты прожевываешь этот шаг при записи решения, то с тебя вправе спросить пояснений, и в случае отсутствия четкого и правильного пояснения - заслуженно обоссать. Впрочем, тут надо вспомнить, что в школе учат умножать именно числа, а не яблоки, и при переводе задачи на математический язык избавляться от не-математических понятий (Задача: Есть пять монет по два рубля. Сколько всего рублей? Решение: Всего рублей: 2 + 2 + ... + 2 (5 раз) = 2 х 5 = 10), а за приучивание бездумно писать 2 руб. х 5 ссать в ебло уже учителю.
Пожалуйста, прочитай внимательно. В книжке, написанной доктором педнаук, сказано, что если переставить местами множители, то в ответе будут чашки, а не куски сахара. Ты тоже думаешь, что если переставить местами множители, то получатся чашки, а не куски сахара?
Доктора педнаук, увы, не всегда понимают математику. Но вот воинственность, с которой отстаивается точка зрения о необходимости соблюдать пооядок, наталкивает на мысль, что обосрался какой-то важный доктор педнаук, возможно, друг министра. Ведь спор точно не научный, в математике коммутативность умножения и сложения совершенно точно не зависят от размерностей величин. Это просто чьё-то растиражированное заблуждение, которое отстаивают для сохранения лица.
http://www.mshu.edu.ru/index.php?option=com_content&task=category§ionid=12&id=452&Itemid=2532
https://www.youtube.com/watch?v=Bcah30JVYsg
Вроде ничего необычного в ней нет.
>Ты тоже думаешь, что если переставить местами множители, то получатся чашки, а не куски сахара?
Нет, я так не думаю, я думаю, что чашки на куски сахара не умножают, так же как и чашки на числа, например. В школе (на этом этапе обучения, разумеется) умножают числа и только числа. Любой, кто не может это понять и мыслить именно на этом уровне - не математик, а специально надроченная обезьяна, любой, кто не может это пояснить - не педагог, а вы поняли кто, а кто выдумывает подобную хуету с чашками и сахаром - тот вообще блядь мракобес.
Ты заблуждаешься. В школе на этом этапе учатся работать с произвольными коммутативными конечнопорождёнными модулями над кольцом целых чисел. Конкретно в этом случае исследуется модуль, порождённый двумя образующими {чашка, кусок сахара}.
Ага, вот только если ты скажешь вслух вот это, с чем учатся работать, половина класса упадет в обморок, вместе с училкой. И для того, чтобы строить какой-либо модуль над кольцом целых чисел, надо бы сперва объяснить, что такое целые числа (сюрприз-сюрприз), а мы как бы в этом направлении и работали, пока ты не пришел.
Нет смысла запрещать говорить прозой тем людям, которые не знают, что такое "проза". Нехай перемножают чашки и сахар, даже не зная, что работают с модулями. Положительные натуральные числа они уже определили вполне корректно как кардиналы конечных множеств - с помощью яблок, спичек и счётных палочек.
Вероятно, эта проблема просто одна из тысяч других (типа сюжетов "Пусть бугуртят"), постоянно создаваемых и соревнующихся за место в эфире твоего сознания. Чтобы ты не увидел того, что действительно важно (не увидел какой-нибудь очередной налог или правку конституции).
>Теперь это элитарный тред математике.
Действительно, одна элита собралась - не мещане. Решают великую математическую проблему чашки и сахара.
Даже в таком случае надо все четко пояснять - что именно понимается под умножением чашек и сахара, и почему именно оно. В противном случае в башке учащегося может образоваться мешанина (например, создается путаница между числами и всякими яблоками, непонятно, где операции над числами, а где над "элементами модуля", как переводить одно в другое, когда надо это делать и зачем, чем они отличаются, чем похожи, и что именно из этого просят в данной конкретной задаче, и еще миллион подобных вопросов), что наглядно демонстрируют нам авторы того текста.
Зачем вообще говорить о проблемах, если не для того, чтобы их решить? В жизни не хватает черных красок?
Двачаю. Реформист ведет себя как бабка с лавочки, ко-ко-ко, кудах-кудах, все пидарасы, я дартаньян. А выхлопа при этом - ноль. Занялся бы делом, пробежался по кабинетам, подал заявки в нужные инстанции.
Не выходит законным путем, доебала бюрократия, ну тогда бери топор и иди ебашить методистов, покажи всем, что не тварь дрожащая и право имеешь.
>Поясните за комплексные числа. Зачем это надо, какие задачи
Если коротко, то с их помощью ты можешь описывать любые циклические процессы: колебания и всю ботву.
Попробуй взять любое понравившееся число на действительной оси, ну например, 3, умножь его на i, результат снова умножь на i, результат снова умножь на i и т.д. Получишь следующую последовательность: 3 действительная ось +, 3i мнимая ось +, -3 действительная ось -, -3i мнимая ось -, 3 действительная ось + и так до бесконечности.
Т.е. по сути, постоянно умножая на i, ты описываешь движение по окружности против часовой стрелки. А из движения по окружности уже вытягиваются синусоиды и всё остальное.
Не за что!
Если умеешь в английский и хочешь быстро втянуться в математику - так, чтобы понятно и "на пальцах", - то рекомендую тебе учебники Рона Ларсона (Ron Larson). Алсо, можешь накачать себе с торрентов видосы от mathtutordvd.com Джейсон - отличный препод! У него и про комплексные числа, по-моему, что-то есть.
Так это не я изначальный вопрос задавал, если честно. Просто ты так годненько расписал, что я не удержался и поблагодарил, вот.
Обсессивно-компульсивное расстройство.
Вы видите копию треда, сохраненную 23 апреля 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.