Вы видите копию треда, сохраненную 22 марта 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Накрывающие когомологии алгебраических многообразий с l-адическими коэффициентами обладают значительно более богатой структурой, чем классические, в том отношении, что на них действует группа Галуа. Это обстоятельство открывает новую область исследования, даже в классическом случае. Хотя доказанных теорем еще мало, имеется благодарная почва для гипотез. Некоторые из них я намерен обсудить ниже, в сопровождении скудных свидетельств в их пользу, как вычислительного, так и философского характера. Основная идея состоит, грубо говоря, в том, что класс когомологии, инвариантный относительно группы Галуа, должен быть алгебраическим, если основное поле имеет конечный тип над простым подполем. Я пришел к этой идее, исследуя вопрос о порядках полюсов дзета-функций, а большинство дорожных знаков на этом пути увидел во время бесед и/или переписки с М. Артином, Мамфордом и Серром. Я сердечно благодарю их за поддержку.
http://mi.mathnet.ru/umn6123
Предыдущий: >>335184 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
Опять этот проткнутый со своими множествами...
нахуя всё это вообще нада?
и вот такой вопрос почему в записи действительные числа и мнимые пишутся через знак "+" ведь между действительными и мнимыми числами не может быть сложения и вычитания, записывали бы через запятую, меньше бы непонятных ситуаций было.
>нахуя всё это вообще нада?
Тебе - не "нада". Перестань этим заниматься и иди посмотри сериальчик.
Да то, что, раз я не понимаю комплексных чисел, этому миру не быт!!! .здохнете.
Ньюфаг. Хочу понять гомотопическую теорию типов из одноименной книженции. Посоветуйте с чего начать, пожалуйста.
чот даже в америкосии мне нормально ответить не могут
http://boards.4chan.org/sci/thread/7850544/little-disclaimer-here

Какое же бесполезное и неинтересное говно эта ваша алгебраическая геометрия. Математика деградирует и летит в совсем отдалённую от науки пропасть. Главным образом благодаря "чистым математикам". Ведь не для кого не секрет, например, что чистый математик-теоретик бесконечно самовлюблённая и отвратительная дрянь, демонстрирующая половое поведение. Самое обидное, что среднестатистический студент матфака с подобострастием и вожделением готов есть говно, подло генерируемое их кумирами, и тем самым является(в самых изощрённых случаях) годной заменой им. И на фоне всего этого культа полового поведения, эти твари очень любят говорить про нравственность математиков, про нравственность математики, как самой нравственной науки. Осталось лишь только созерцать, как эти боевые говноеды засрут информационное пространство грудой теорий с множеством искусственных понятий(сложность которых состоит только в определении, а не во "вложенности") и несчетным количеством соответствий между ними, которые никогда не отобразят формально правильно феномен природы. Будем надеяться, что в этот момент пассионарное население придумает другую математику, сделав тем самым ненужными все последние высеры, и эвакуирует всех любителей чистой математики в ад.
>нахуя всё это вообще нада?
Встречный вопрос, нахуя нужен ты?
А вообще первоначально для решения уравнений типа x^2 + 1 = 0 . Последующие мотивы гораздо глубже, но такому обывателю как ты, они не нужны.
>и вот такой вопрос почему в записи действительные числа и мнимые пишутся через знак "+" ведь между действительными и мнимыми числами не может быть сложения и вычитания, записывали бы через запятую
Ты можешь записывать комплексное число как пару (x,y) и определять для нее сложение и умножение, соответствующим правильным образом.(Таким образом, чтобы полученная структура была полем)
> меньше бы непонятных ситуаций было
Проблема в том, что тут все однозначно, непонятные ситуации тут могут возникнуть у обывателя, незнакомого вообще с математикой.
>Какое же бесполезное и неинтересное говно эта ваша алгебраическая геометрия.
Нам очень важно ваше мнение. Вообще то, что неинтересно тебе это лишь твоя проблема. А причислять все что тебе не нравится к говну и ненужно, признак 16 летнего подростка, советую повзрослеть.
Это твои проблемы, хочешь их исправлять - пиздуй за учебники или в вузики, а лучше просто нахуй.

Ответ тебе уже был дан.
>Нам очень важно ваше мнение.
Спасибо, оно не бесплатное, тебе придется отсосать мой вонючий хуй.
>Вообще то, что неинтересно тебе это лишь твоя проблема.
Да. Но я такой не один. И то что неинтересно совокупности людей, это проблема совокупности людей.
> причислять все что тебе не нравится к говну и ненужно, признак 16 летнего подростка, советую повзрослеть.
Выходит если человек причисляет говно к говну, то он называется 16-летний подросток? Ну допустим так, но это не поменяет того факта, что алгеом говно без задач, которое НИКОГДА не найдёт применения в том виде, в котором он сейчас существует.
>НИКОГДА
Ок, но опять же твое мнение очень важно для всех нас, ведь ты такой выдающийся, талантливый и умелый. нет
>говно к говну
Как ловко ты своё субъективное мнение ставишь в абсолютную истину, надеюсь также ловко ты сосешь хуи.
Вообще спорить с такими утилитаристами как ты, это как разговаривать со стеной, единственный вопрос:почему именно алгем, что-то личное?
Бампецкий.
Плюсом хочется какую нибудь научно популярную книжку где более менее наглядно раскрыты многие разделы математики в общем виде, ну типа что где и для чего применяется.
Я не утилитарист, я формалист, например. Алгеом твой формально убог и является теорией вокруг проблем, которые необходимо разрешать самыми элементарными средствами, а не абстрактно-условными, непонятными и сложными. Вместо этого придумываются р-адические числа и театры Ходжа, которые не пытается пояснить человек, который их придумал. Хуле, его дело ведь в том чтобы самому убедиться в истинности решённой проблемы, на остальных похуй. И молодёжь дико фапает на весь этот пафос подражая пидору.
Я согласен. Но какая альтернатива касательно описания мира может быть алгебраической геометрии? Какая альтернатива вообще существует для математики?
От математики необходимо отказываться.
>которые необходимо разрешать
Почему? Потому что ТЫ так сказал? Открою страшный секреты, ты - никто и звать тебя никак.
Добавлю, что твое неосиляторство - это проблема сугубо твоя.
>Вместо этого придумываются р-адические числа
Который вдруг внезапно возникают в математической и статистической физике. Вот так на те, оказывается не все так бесполезно.
>И молодёжь дико фапает на весь этот пафос подражая пидору.
Молодежь всегда обмазывалась говном, ей это свойственно. Повзрослеют, интересы трансформируются во что-то более конкретное и существенное. С другой стороны, научпоп литературы по математике, в отличие от, например, физики минимум, и поэтому как-никак, таким путем, - через модные тенденции и мемчики, - школотуны всё же начинают интересоваться математикой, понимают, что есть такая наука, и что она самобытна и прекрасна.
Причем здесь альтернатива для описания мира? Алгеом покамест послужил только для доказательства ВТФ и абс-гипотезы. Конкретные практические задачи (предполагающие формальное исчисление) не предусмотрены.
Научпоп очень далек от математики. Математика это ведь поиск, а не находка. И если всунуть кому-то в рот формулу Эйлера или число Грэма, то пользы от такого научпопа мало. А журнал Квант уже никто не читает.
>Конкретные практические задачи
Один диссертант в советские времена представил диссертацию под названием "Циркуляция ротора кусочно гладкой функции по недиффиренцируемому многообразию". Защита провалилась, так как в то время все диссертации рассматривались в плане их приложений к народному хозяйству. Диссертант не стал особо напрягаться, а изменил несколько строк во введении и переделал название. Повторная защита прошла на ура. Новым названием диссертации было "Качение сучковатого бревна по шероховатой поверхности".
Этим диссертантом был Альберт Эйнштейн.
Можно их по разному понимать.
Создай тред-замены-математики и сиди в нём. В этот не сри.
Пиздуй в свой новосозданный тред, мудило.
В смысле кто?
Ты отбитый что ли? Уточни че ты хочешь узнать обо мне.
Бамп
>>337814
У меня в каждом разделе где я сижу по имени имеется. Но ты то просто отбитый и задаешь вопрос просто что бы задать вопрос.
Репорти его
А сразу на человеческом языке статью привести было нельзя? Пришлось гуглить английскую версию, чтобы понять, что "накрывыающая топология" - это на самом деле этальная топология.
Да и какой вообще смысл приводить ссылку на рандомную статью 50 летней давности? Те же гипотезы Вейля (которые там упоминаются) уже 41 год как доказаны, подозреваю, что по всему остальному тоже был большой прогресс. По какому критерию была выбрана эта статья, а не любая другая?
> ведь между действительными и мнимыми числами не может быть сложения и вычитания
Повторюсь.
Когда мы работаем в C, под вещественными числами мы имеем в виду не вещественные числа, а подполе C, изоморфное полю вещественных чисел, так что все может.
Ты опять выходишь на связь?
Зачем-это не тот вопрос на который отвечает естественная наука. Иди философов спроси

Треду шабата.
>В этом треде мы будем обсуждать
обоссанные основы математики, семёнство N-петуха, метафизические опровержения математики от "физиков" и бред буйных вербитокурочек в сотый раз. Добро пожаловать. Снова.
Все философы, которые могли в математику, умерли давно.
Вот, посмотри чувачка вводную лекцию https://www.lektorium.tv/lecture/26550
Там он говорит что-то такое общеобразовательное, тебе пойдёт.
Ну да, просто передислоцировать буйных по другому адресу, решение уровня /b/.
Нахуя такие ебанутые преамбулы? Никто не будет обсуждать это говно, как минимум потому, что не поймёт 95% слов (включая самого ОПа).
Конфы долго не живут, как правило. К тому же в конфах немного сложно обмениваться картинками так, чтобы они архивировались.
>>337929
>>337930
В принципе, времени у меня достаточно. Но я сомневаюсь, что на тематической доске будет достаточно людей, чтобы получились какие-то обсуждения. /sci/ - весьма медленный раздел, даже с учётом шизофреников, а мелкодоска будет ещё менее населённой.
>>337932
Кто не поймёт - хотя бы на слова умные посмотрит. Интересно же.
>Какое же бесполезное и неинтересное говно эта ваша алгебраическая геометрия.
Это правда. А всё остальное - просто лучи говна.
>Конфы долго не живут, как правило.
Нормально они живут. Уж точно побольше всяких мелкопомоек.
Да алгем и всякие категории с когомологиями уже "вышли из моды" лет 20 назад, поэтому ничё делать и не надо.

"Спам — это форма жизни, агрессивная и враждебная по отношению к человеческой. На бумажный спам, подобный журналу Столица и дочернему изданию, уходят кубометры леса, что известно как отражается на окружающей среде. Электронный спам разрушает возможность осмысленной коммуникации, чем атомизирует общество и лишает смысла человеческое существование. ... По сути, спамом является любая односторонняя коммуникация".
Реально, в треде завёлся оживший спам, который ведёт упоротую одностороннюю коммуникацию и сильно мешает существованию человеков.
>Моё математическое образование на уровне технической специальности средне-хорошего столичного ВУЗа, но имею сведения не только о прикладной, но и чистой математике. Знаю отдалённую цельную картину.
Proigral. Небось прочитал определение группы в википедии и уже мнишь, что "цельную картину" видишь?
>Блядь, я больше не могу. Я скорее вскроюсь, чем перестану думать об этом. Последний месяц только и занимаюсь размышлениями на тему альтернативы математики, но пока этого, очевидно, мало. Даже для первого шага на пути к новой науке.
Ну ты и дурашка, ни одна наука не начиналась с того, что какой-то битард садился за стол с мыслью "нужна новая наука" и начинал что-то писать на листочке (за исключением всяких псевдонаук, типа синергетики и system science).
>Ты только что со страницы Википедии и потому влепил этот бред? Неуместное проецирование за незнанием сути.
Я конечно-то не знаю сути, я могу только экстраполировать из твоих постов и некоторого своего жизненного опыта, в частности я уверен на 99%, что для тебя "когомология" и "алгебраическая геометрия" - это такой смешной мемчик на саентаче и тифаретнике, ни один "видящий общую картину" человек не напишет что-то вроде: "Какое же бесполезное и неинтересное говно эта ваша алгебраическая геометрия".
>Ещё больше скажу: ни одна новая наука не начиналась просто так.
Вот именно. А ты хочешь её начать просто так.
>люди начали ощущать нехватку аналитических средств математики
С этого места поподробнее, какие люди, когда начали, предпочтительно с цитатами и ссылками на литературу.
>Опираться на жизненный опыт при общении с анонимами - худшее.
Почему? Я точно так же могу сопоставлять фразы и поведенческие шаблоны с виденными мною уже раннее. Ничего от того, что я не вижу твой ebal'nik не меняется.
>Если ты чего-то не знаешь - не значит, что знают все.
Ну давай, видящий общую картину, реши следующие задачи ("видящий общую картину" решит их устно меньше, чем за три минуты, я специально подобрал максимально простые задачи однако такие, которые, скорее всего, не нагуглятся):
1) Указать попарно гомеоморфные пространства: O(1), SO(1), SL(1), R, C, M={(sin t + sin t cos t, 2+cos t,5+sin t), t \in R} в топологии R^3
2) Найти первую группу когомологий Де-рама у R^3/{0}
3) Найти внешний дифференциал у формы sin(x)dx + (x+y)dy
4) Привести пример трёхлистного нерегулярного накрытия
Если не решишь, то покажешь всем - что ты выпускник недошараги, видящий математику сквозь призму мемасиков саентача о мочидзуки и когомологиях, но при этом вообще не в теме, но при этом кукарекающий что-то о новой науке.
Правда на 1-ом курсе нормально так интегралы считал
>хаха щас затралю Иво)))) я как википедия сылки папрашу ну я геней)))
Множества материалов тут не может и быть - математики в основе своей ретроградны и всю жизнь работают в своей области, исключая те редкие моменты, когда клерк в свободную минуту, с потом на лбу, размышляет над основаниями математики и спустя пару минут отстраняет от себя эти грешные порывы, возвращается в своё математическое русло. Начать думать об альтернативе математике сложно. Очень. Но я смог.
Математика индуктивна и оперирует абстрактными объектами, её связь с физикой - натяжка, присвоение возможности точно описать естественный мир - иллюзия.
Самый простой и понятный для всех пример - теория детерминированного хаоса. Математики не хватает и не хватит на описание турбулентных потоков, что так важно людям.
Более узкий пример: уравнения Навье — Стокса не будут решены.
Потому что не элитно и востребован только в игрострое.
Поздравляю, шизик с сверхценным бредом
А мне похуй способен я или нет.
Турбулентные потоки вот уже как лет 30 описываются ренормгруппой, но наша маня то не знает, она грезит о "новой" математике.
Потому что питон говно для хипстеров, что непонятного то?
Точные решения есть лишь для идеальных моделей, шаг влево, шаг вправо и всё.
Бамп еще раз этой проблемме тысячелетия.
>Набор заплаток и костылей под каждый из миллиарда вариантов.
Двощую. Физеки физекой называют только самые общие варианты, а все остальное "это уже не наш случай"
1 - 1-4, 2-3, 5-6
2 - {0}
3 - 0dx^dy
4 - лентой мебиуса с любым количеством перехлестов диск в 3 оборота (но не уверен про нерегулярность).
Если что, я не тот товарищ, просто жалкий гум-миимокрокодил, пытающийся осилить.
*3 - 1dx^dy, мой косяк.
Кстати, определения вполне себе гуглятся. А из них и задачи сразу почти.
Значит, что множество - это группа, с операцией умножение (R^*)или сложение(R^+).
Может, потому что ты незаметно применяешь основную теорему анализа, хотя именно её мы и собираемся доказать?
>>337608
Верность алгебраической формы следует из "стандартной модели"(определение как пары чисел и операций +, .) просто подставляя вещественное число a -> (a, 0), i=(0, 1), и применяя определения операций.
Для чего это надо? Ну, к примеру, чтобы посчитать e^(a+bi) формулой Эйлера, а не хз-что в виде e^(a; b). Туда же cos, sin, ln.
>>337987
Попробуй применить к правому уравнению cos/sin от 2a и 3=3(cos^2 (5x)+sin^2 (5x))
Как он "заподозрил" переход от левого ур-я к правому -спроси у дяди Вольфрама, если узнаешь - расскажи.
Это какую такую теорему?
Еще раз, производная интеграла некой функции сумма последовательности бесконечно малых значений функции в неких пределах, ТОЧНОЕ приращение тобишь, деленная на "скорость" изменения функции на промежутке равна значению функции внутри интеграла. Это я так неазметно для себя проанализировал как Гаусс!?

Algebra [Saunders Mac Lane, Garret Birkhoff]
и
A Survey Of Modern Algebra [Garrett Birkhoff, Saunders Mac Lane]
? Какую выбрать и нахрена они две одинаковые книги написали?
>Чем отличаются
Лень смотреть, предполагаю что годом выпуска (+- 1-2 года)
>нахрена они две одинаковые книги написали?
А ты посмотри, сколько они стоят. 2 тиража одной книжки = х2 шекелей.
Покажи правильные ответы.
>Всё неправильно
>Всё
С каких это пор у R^3 без нуля, что гомотопически двумерная сфера, появились первые когомологии.
Да, тут я немного обсадился.
>Почему тогда просят через икс-игрек нулевое выразить?
Потому что это границы области интегрирования?..

Ага, я понял, это точка на функции до которой надо проинтегрировать, из которой опущен перпендикуляр до абсциссы.
Результат получается Ах0^3/3!?
А тут как решать? Тут уже игрек входит в переменную.
Надо брать от минус икс до плюс икс интеграл так ведь?
Писать внутри интеграла суммма икс квадрата и игрек квадрата делить на два? Или под корень загонять квадраты?
1)1-4 не верно, 2-3 верно, 5-6 неверно. Все неверные ответы исключаются из соображений размерности. Единственный вариант, над которым надо чуть-чуть подумать, это 6. Но рисовать (или воображать) кривую здесь необязательно - все следует из некого свойства функций sin и cos.
2)Верно.
3)Откуда минус?
4)Как ты себе это представляешь? Подсказка - такого накрытия не может быть.
1 - 2-3 по условию детерминанта, О(1) по сути разве не R? Последнее просто методом исключения сказал.
3 - Это не минус, а тире)
4 - Смутно. Просто обмазался определениями за 5 минут и что-то попытался кукарекнуть.
Я вообще на 3 курсе сейчас и когда начал потихоньку понимать, что из себя представляет современная математика, волосы дыбом встали. Такое ощущение, что летающую тачку производят уже, а нам все рассказывают, что колеса неплохо бы сделать круглыми. поэтому в полной растерянности и не знаю с чего начать.
Как по мне, сперва надо прикладную маняматику штурмовать. Те же интегралы сперва научиться решать с матрицами и векторами, а потом уже в пучину топологий с теорией чисел кидаться.
наверное надо было дописать, что на 3 курсе матфака, так что в дифуры, матан, функан, тфкп и прочее я могу
О (1) - группа изометрий одномерного векторного пространства над R. Сколько их (изометрий)?
4 - выберем нестягиваемую петлю на листе мебиуса и рассмотрим её образ на диске, предположим, что он не тривиален. Фундаментальная группа у диска тривиальна (он стягиваем), так что продеформируем образ этой петли в точку. Но эту деформацию тоже можно слой за слоем поднять до листа мебиуса (по определению накрытия), в результате получим непрерывное стягиваем первоначальной петли, что противоречит условиям. Значит образ петли тривиален. Это рассуждение можно сильно обобщать.
Если летающую тачку когда-нибудь и сделают, то весь этот аутизм там точно не будет задействован. Самые значительные инженерные вещи, перевернувшие мира которые когда-либо были созданы используют математику уровня максимум второго курса любой шараги.
Начать нужно с изучения всяких вводных англоязычных курсов по разным дисциплинам - вроде "Алгебры" Ленга, "Алгебраической Топологии" Хатчера и т.д. Плюс к этому советую просмотреть лекции НМУ и ВШЭ для младшекурсников и прорешать их листочки. Материал это базовый, в приличных книгах никто не будет пояснять, что такое группа Галуа ,когомологии де Рама или алгебра Ли. Дальше уже можно пытаться учить серьезные вещи, следуя хотя бы тому же Вербицкому.
Самое смешное что это правда. Даже йоба ускорители на маняматике и физеке чуть ли не 18 века работают.
Максвел во все поля.
Из этого следует лишь опережение научно-технического прогресса математиками на 200 - 300 лет, а не бесполезность математики.
Это при условии, что векторы развития математики и прогресса коллинеарны.
Насколько разбираешься? Что такое модуль над кольцом, знаешь?
Или тебе узнать, зачем оно вообще нужно в теории?

>Максвелл
>18 век
Алсо забавно было бы глянуть как вы вместе с Максвеллом пытались бы разобраться почему частицы в вашем циклотроне ни в какую не хотят превышать скорость света.
Хоть я и не тот анон, но ответь, пожалуйста, что такое сравнение по модулю. Еще не совсем понимаю запись Z/nZ для кольца целых чисел. Я совсем нуб, поэтому, если можно, самыми простыми словами.
Ок. Судя по второму вопросу, сравнение по модулю интересует в простом смысле. Тогда смотри, вот есть у нас 3 множества. Z - целые числа, их можно складывать и вычитать (про умножение пока не говорим). Есть множество nZ - очевидно, тоже целые числа, но умноженные на n. То есть {0,+-n,+-2n,...}. Очевидным образом можно засунуть второе в первое - по буквальному равенству членов друг другу, то есть nZ->Z:(n*)m->nm. Но заметим, что совершенно интуитивно можно засунуть туда это множество еще 4 раза, сдвигая элементы на единицу вверх. Но только 4, потому что попытка сдвинуть на какое-то еще число приведет к тому, что какие-то 2 множества совпадут.
Теперь в более общем смысле. Говоря об обычных числах, ты можешь делить одно на другое и получать третье число. Это удобно и полезно для всяких бытовых ситуаций, и математики решили что делить им хочется абсолютно все от неба до Аллаха. Но начали с групп, уравнений, топологических пространств и прочих многообразий, чтобы опять было удобно и полезно, только уже в более сложных областях. Логично, что если делишь число на число, то получаешь 3-е число, а результатом деления групп или уравнений становятся, соответственно, группа или уравнение. Только надо, чтобы одно число было множителем другого, уравнение имело второе своим многочленом. Группа, соответственно - подгруппой. Так вот, мы уже заметили, что nZ - подгруппа Z, значит мы хотим поделить одно на другое. Давай представим, что должно получиться. Вот делим мы 100 на 5, и видим, что 5 помещается в 100 20 раз. Как мы уже поняли, nZ в Z помещается n раз. Логично, что результат будет группой из n элементов. Она называется факторгруппой Z по nZ (Z/nZ), в нашем случае это Z_n, которое, грубо говоря, является множеством всех возможных остатков при делении произвольного числа из Z - то есть, в интуитивном смысле ВСЕГО МНОЖЕСТВА
Z - на n. По сути, ты отвечаешь на вопрос "А на какую группу, с той же операцией - сложением в нашем случае - мне умножить nZ, чтобы получить Z, причем чтобы все групповые операции на элементах приводили к тем же результатам?" Ну и логично, что если ты хочешь описать любое число a в том смысле, сколько раз в него влезает n, тебе по сути надо записать a=bn+c, где c - остаток. Так вот, b - это элемент из группы nZ, а с - из Z_n. И ты можешь запараметризировать любой a как (b,c), то есть представить всю группу Z как декартово произведение nZ и Z_n. Соответственно, вот и смысл Z/nZ именно такой: Z разбили на равное количество подгрупп, ведущих себя как nZ; какой группой можно показать, как элементы каждой из этих подгрупп ведут себя (в какую из подгрупп попадут), когда их умножат (в нашем случае операция - сложение) на какой то элемент из другой подгруппы? Оказывается, достаточно знать, как относятся друг к другу именно подгруппы, в которых эти элементы находятся.
Вот как-то так. Сравнение по модулю же - просто посмотреть, какой остаток имеют число при делении на модуль (8 (mod 3)=2). В смысле групп - какому элементу Z_n будет принадлежать число. Но вообще модули, и все остальное можно обобщить дальше. Тебе это пригодится в топологии, когда помимо очевидного "квадрат это отрезок умножить на отрезок", ты будешь в охуении понимать, что "тор - это окружность умножить на окружность", или что "повороты кубика - это двумерные повороты в двух осях умноженные друг на друга".
Надеюсь, что помог. Если что непонятно, спрашивай.
Ок. Судя по второму вопросу, сравнение по модулю интересует в простом смысле. Тогда смотри, вот есть у нас 3 множества. Z - целые числа, их можно складывать и вычитать (про умножение пока не говорим). Есть множество nZ - очевидно, тоже целые числа, но умноженные на n. То есть {0,+-n,+-2n,...}. Очевидным образом можно засунуть второе в первое - по буквальному равенству членов друг другу, то есть nZ->Z:(n*)m->nm. Но заметим, что совершенно интуитивно можно засунуть туда это множество еще 4 раза, сдвигая элементы на единицу вверх. Но только 4, потому что попытка сдвинуть на какое-то еще число приведет к тому, что какие-то 2 множества совпадут.
Теперь в более общем смысле. Говоря об обычных числах, ты можешь делить одно на другое и получать третье число. Это удобно и полезно для всяких бытовых ситуаций, и математики решили что делить им хочется абсолютно все от неба до Аллаха. Но начали с групп, уравнений, топологических пространств и прочих многообразий, чтобы опять было удобно и полезно, только уже в более сложных областях. Логично, что если делишь число на число, то получаешь 3-е число, а результатом деления групп или уравнений становятся, соответственно, группа или уравнение. Только надо, чтобы одно число было множителем другого, уравнение имело второе своим многочленом. Группа, соответственно - подгруппой. Так вот, мы уже заметили, что nZ - подгруппа Z, значит мы хотим поделить одно на другое. Давай представим, что должно получиться. Вот делим мы 100 на 5, и видим, что 5 помещается в 100 20 раз. Как мы уже поняли, nZ в Z помещается n раз. Логично, что результат будет группой из n элементов. Она называется факторгруппой Z по nZ (Z/nZ), в нашем случае это Z_n, которое, грубо говоря, является множеством всех возможных остатков при делении произвольного числа из Z - то есть, в интуитивном смысле ВСЕГО МНОЖЕСТВА
Z - на n. По сути, ты отвечаешь на вопрос "А на какую группу, с той же операцией - сложением в нашем случае - мне умножить nZ, чтобы получить Z, причем чтобы все групповые операции на элементах приводили к тем же результатам?" Ну и логично, что если ты хочешь описать любое число a в том смысле, сколько раз в него влезает n, тебе по сути надо записать a=bn+c, где c - остаток. Так вот, b - это элемент из группы nZ, а с - из Z_n. И ты можешь запараметризировать любой a как (b,c), то есть представить всю группу Z как декартово произведение nZ и Z_n. Соответственно, вот и смысл Z/nZ именно такой: Z разбили на равное количество подгрупп, ведущих себя как nZ; какой группой можно показать, как элементы каждой из этих подгрупп ведут себя (в какую из подгрупп попадут), когда их умножат (в нашем случае операция - сложение) на какой то элемент из другой подгруппы? Оказывается, достаточно знать, как относятся друг к другу именно подгруппы, в которых эти элементы находятся.
Вот как-то так. Сравнение по модулю же - просто посмотреть, какой остаток имеют число при делении на модуль (8 (mod 3)=2). В смысле групп - какому элементу Z_n будет принадлежать число. Но вообще модули, и все остальное можно обобщить дальше. Тебе это пригодится в топологии, когда помимо очевидного "квадрат это отрезок умножить на отрезок", ты будешь в охуении понимать, что "тор - это окружность умножить на окружность", или что "повороты кубика - это двумерные повороты в двух осях умноженные друг на друга".
Надеюсь, что помог. Если что непонятно, спрашивай.
"Программа для генерирования последовательностей случайных величин, имеющих различные одномерные законы распределения вероятностей"
Нууу, теорвер и алгоритмы. Ваш кэп.
Алсо, "различные одномерные законы" - что за новояз? Сюда, кароч:
https://ru.wikipedia.org/wiki/Шаблон:Список_вероятностных_распределений
Бамп
Ну давай, выведи мне из теории относительности, которая про гравитацию, скорость света.
вывел тебе за щеку, не благодари.
1 - да, с какого-то перепугу не вспомнил, что там не ортогональные, а ортонормальные составляющие, а еще прочитал не гомеоморфизм, а гомоморфизм. Тогда там просто {1,-1}, двухэлементная группа. Ты сказал "попарно", но походу все остальное ни разу друг другу не гомеоморфно, так как там еще линия, плоскость и окружность.
4 - ты не так понял, но это уже мой фейл. Я сказал "диск", но имел в виду 1<x^2+y^2<2, то есть, что-то типа кольца в 2D (S^1*(0,1) можно сказать). Так-то я знаю, что такое гомотопия, не обижай уж совсем, анон.
Предельная точка множества M - это точка, любая проколотая окрестность которой пересекается со множеством M.
Точка прикосновения множества M - это точка, любая окрестность которой пересекается со множеством M.
Теория чисел.
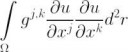
Изначальный смысл коэффициентов? Метрика на римановом многообразии небось, тогда надо смотреть что за многообразие \Omega
Спасибо, анон!
>Но заметим, что совершенно интуитивно можно засунуть туда это множество еще 4 раза, сдвигая элементы на единицу вверх. Но только 4, потому что попытка сдвинуть на какое-то еще число приведет к тому, что какие-то 2 множества совпадут.
Почему именно 4?
И еще, получается nZ - группа элементов Z, умноженных на обратный элемент от элемента n? И если умножить эту группу на n, то получим Z? Но ты представляешь Z как декартово произведение nZ и Z_n, это ведь совсем разные вещи, разве нет?
>повороты кубика - это двумерные повороты в двух осях умноженные друг на друга
Это, кстати, интуитивно понятнее, чем остальные примеры. По крайней мере для меня.
Омега - область в R^2, g - метрика (конкретно в моей задаче это g^{jk}=const в декартовой ск).
Владимиров?
Для этого не нужно использовать то, что Q плотно в R.
Рассмотрим eps-окрестность рационального q. Выберем натуральное n такое, что 1/n < eps. Тогда q + 1/n рациональное и находится в eps-окрестности.
Ну и что ты хочешь сказать? Множество чисел вида 1/n всюду плотно в множестве 1/n U {0}, но это не значит что в любой окрестности числа вида 1/n есть число вида 1/n. Если не считать себя, конечно же, но в таком случае это просто идиотский вопрос.
Если ещё добавить тот факт, что в R нету изолированных точек - то следует.
При чем здесь это? Всюду плотное множество - такое, что его замыкание совпадает со всем пространством; другими словами, всякое открытое подмножество содержит точку из этого множества (иначе бы его замыкание содержалось в дополнении к этому открытому множеству). Окрестность любой точки открыта (по определению), а значит пересекает всюду плотное множество.
>>338439
4 - это и называется кольцо, вот только бессмысленно искать нерегулярные накрытия пространства с абелевой фундаментальной группой
>>338598
>>338600
ну и?
Третья аксиома отделимости.
Нужно, забыл. Нужно, правда, Т1 (любое одноточечное множество замкнуто - значит выколотая окрестность - открыта).
>>338707
Спасибо, я помню определения. Она может пересекать всюду плотное множество ровно в одной точке - а именно в той, окрестность какой мы берём, выше же уже пример приводили >>338689 а спросившего явно интересовало то, во всякой ли окрестности найдётся хотя бы ещё одна точка, помимо той, окрестность которой мы берём. Важно, чтобы выколотая окрестность была непустой и открытой, для чего нужно отсутствие изолированных точек и Т1 соответственно.
Посоны, вот этот например вопрос к какому разделу математики причесляется? У меня это в функ.анализе было, но это скорее топология? Мне очень доставлял весь этот анализ метрических/линейных/гильбертовых пространств.
пидор вылетивший из вуза, но которому доставляла математика. кроме матана
Нет, нет, нет и нет.
Постулируем, что кроме множеств существуют ещё объекты, которые называются реляционные типы. Два реляционных типа могут быть либо равны, либо не равны.
Постулируем, что всякому упорядоченному множеству соответствует один и только один реляционный тип.
Постулируем, что два упорядоченных множества изоморфны тогда и только тогда, когда их реляционные типы равны.
Ординалы - это реляционные типы вполне упорядоченных множеств.
Общая топология.
Числа
Пожалуйста. Подробнее - Куратовский-Мостовский, теория множеств.
Таким образом, доказательство строится не только на определении всюду плотного множества, но и на аксиомах отделимости? А в какой книге эти теоретические факты лучше всего изложены?
>>338734
У нас это в матане. Топологии нет.
спросивший анон
Пусть x - вещественное число. В любой окрестности A вещественного числа x найдётся отличное от x вещественное число y. Два различных вещественных числа обладают непересекающимися окрестностями, так как R - хаусдорфово. Значит, x и y обладают непересекающимися окрестностями B и C. Положим X - пересечение B и A, Y - пересечение C и A. Так как рациональные числа плотны, в Y есть рациональное число z. Оно отлично от x, так как X и Y не пересекаются. Но Y - подмножество A. Выходит, в A есть рациональное число z, отличное от x. В окрестности каждого вещественного числа есть отличное от него рациональное число. Так как рациональное число - вещественное число, в окрестности каждого рационального числа есть отличное от него рациональное число.
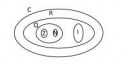
Опс, что-то я проебался с этим.
Ты какой-то хуйней занимаешься.
> Все правильно сделал?
Абсолютно непонтяно, что ты сделал и зачем.
> почему в интернете нет такой пикчи?
Потому что нахуя она нужна? Почему должна быть картинка с какими-то особыми структурами? Как она должна помочь в понимании чего-либо?
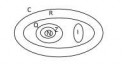
Круги Эйлера соответствуют множествам, а, например, Z не является подмножеством Q, потому что Q не содержит целых чисел. Q состоит из классов эквивалентности пар целых чисел. Аналогично, Q не является подмножеством R, а R не является подмножеством C.
Стоит отметить, что поле C содержит подполе, изоморфное R. Но с помощью кругов Эйлера этот факт не отразить.
Не вводи людей в заблуждение.
>Q не содержит целых чисел
Содержит, разумеется. Q содержит подкольцо, попадающее под определение целых чисел.
Наподобие "Что такое математика" Куранта и Роббинсона, только без разжевывания каждой вещи, современнее, для людей уже знакомых с математикой и топиков должно быть существенно больше.
>>338754
Что не так?
Такой книги нет.
Математику шквариться о физику?
В любой по общей топологии. Можешь топ-бук Вербита навернуть ( http://verbit.ru/MATH/UCHEBNIK/top-book.pdf ), или стандартного Виро Харламова "Элементарная топология" - и то и другое очень на любителя и лично мне не нравится.

Ставлю на статистику или что-то из CS.
Это, конечно, круто, но
> 277 страниц
слишком много, слишком подробно. Мне нужен скорее outline, чем что-то подробное.
Ну и это только алгебра.
Книжки "Все идеи современной математики за 15 минут" не существует. Шафаревич это и есть обзор по алгебре, причём довольно короткий.
Не, ну что значит, как? По сути-то просто смотреть, насколько поведение одного похоже на поведение другого. Вот гомотопии например. Почему всякие стягиваемые петли ведут себя как группа? Вот тебе и интуитивность. А поток мыслей начинается как раз с этого представления. Ну у меня так, аноны еще подскажут наверное.
А справочника никакого нет?
>>338806
Но мне нужен outline, а не описание. Я не собираюсь по этой книги что-либо учить.
Не представляю зачем кому-нибудь может понадобиться этот "outline". Он всего лишь будет связывать одни непонятные слова с другими непонятными словами; даже грубое представление об основных понятиях некой современной науки требует некой квалификации. Чем тебе поможет например фраза "методы почти математики Фалтингса позволили добиться значительного прогресса в p-адической теории Ходжа", если ты ни слова из нее не понимаешь?.
> методы почти математики Фалтингса позволили добиться значительного прогресса в p-адической теории Ходжа
Конкретно это не пойму, но я закончил матфак несколько лет назад (но я не математик) и такая книга позволила бы мне:
- собрать все в одно целое (сейчас у меня остались разрозненые знания и нет единой картины);
- понять что я знаю, что забыл, что вижу в первый раз;
- было бы круто узнать какие еще есть области математики, зачем они нужны и как связаны с другими;
- и когда начну изучать заинтересовавшие меня области эта книга будет служить своеобразным чек листом
>собрать все в одно целое
Этим занимаются в вузиках на матфаках. Дают общую картину. Техническим специальностям дают глубоко узкую хуйню, никакой общей картины им не нужно.
Можешь посмотреть на сайте nlab. Там есть статьи про многие современные направления математики, правда весьма специфической направленности. Но опять же, чтобы приблизительно понять о чем речь нужно знать кучу preliminaries, которых у тебя скорее всего не будет.
Поясните нубу кстати плиз, что значит "теория гомологий" и "теория когомологий"? Одно от другого отличается же просто переобозначением индексов.
Я понял что второй отличается от первого отсутствием пределов и разницей значений на константу, но вычислять его не научиться пока.
С т.з. гомологической алгебры разница только в том, рассматриваем мы цепи или коцепи, т.е. куда указывает дифференциал.
Если мы говорим о сингулярных (ко)гоиологиях топологического пространства, то там в соответствие этому пространству ставится комплекс (ко)цепей и его (ко)гомологии называют (ко)гомологиями этого пространства. При этом гомологии и когомологии обладают вообще говоря разными свойствами, разница между ними не сводится к замене индексов.
Вперемешку приведены названия глав из учебников (теория идеалов, гладкие многообразия, дифференциальные формы) для младших курсов и более менее современных научных направлений (вроде теории Ленглендса), вероятнее всего просто нагугленные, много бреда. Если хочешь конкретики:
1) Что такое наследие Гротендика, почему оно относится к теории категорий
2) Почему гомологическая алгебра часть теории категорий
3) Теория пучков - частный случай теории топосов
4) Алгебраические многообразия - частный случай схем
5) Коммутативная алгебра - частный случай теории схем
6) Почему не переведено intersection theory (есть каноничный перевод в русском издании Хартсхорна), не отнесено к алгебраической геометрии
7) Что такое modulli space, почему это название математической дисциплины
8) Что означает теория модулей
9) Почему (ко)гомологии указаны 3 раза
10) Что понимается под теорией гомотопий, почему теория гомологий - не частный случай теории гомотопий
Пока все
Возьми определение определённого интеграла и прочитай определение неопределённого интеграла
Слился
11) Почему алгебры Клиффорда не часть теории модулей
12) Почему топологическая К теория - не часть алгебраической топологии
13) Почему переведено высокие категории, а не высшие или квазикатегории
Т.е. это просто два разных комплекса, не связанных (или связанных, но не так явно)?
Да.
Сразу видно человека, который никогда не заглядывал в классификацию AMS.
http://www.ams.org/msc/pdfs/classifications2010.pdf
Эта классификация отвечает на вопросы 2-10.
>названия глав из учебников (теория идеалов, гладкие многообразия, дифференциальные формы)
Это не названия глав из учебников, это уже почти суверенные самостоятельные науки.
>Что такое наследие Гротендика
Натурально, наследие Гротендика. Гротендик - это такой великий математик, недавно умерший.
Я считаю что первокуры - элита, боги матеши и вообще соль земли. Надо всем быть первокурами как можно чаще, я бываю первокуром по вторникам и в четверег с обеда до пополудня. А также надо всем зазнаваться. Вот ету картинку зделал первокур и её уже несколько лет обсуждают, это потому что картинка хорошая. А другие куры не зделали картинок, это потому что они творезкие импотенцы. Надо делать правельные картиночки а не спорить с уже имеющимися картиночками потому что. ТАк сказал.
Откуда я знаю? Его бумаги написаны на французском, и их прочитали только три с половиной Мотидзуки.
Спасибо что помог сдать матанализ, двощ.
Я не отрицал, что существуют такие слова в математике. Cомнительно, что автор картинки их все понимал, когда ее составлял. Опять же, теория пересечений там отнесена к алгебраической геометрии, теории пучков там нет, moduli space - это пространство модулей (одно), опять же непонятно, модулей чего (кривых, абелевых многообразий, формальных групповых законов и т.д.).
Гомотопии и группы то еще интуитивно. А когда какие-нибудь комбинации хом-сетов - моя интуиция уходит в запой. Hom(X, Z) x Hom(Y, Z) и Hom(X+Y, Z) в категории TOP, как пример. Я не ебу, как это представить в голове. С диаграммами играться? Может просто у меня знаний мало слишком...
Так и суть в том, что не надо делать. Я просто не вижу в этом смысла - пользы этот несвязный винегрет все равно никому не принесет, все что он показывает - индивидуальные пристрастия автора и некоторые обидные промахи. Тогда уж проще сразу давать ссылку на классификатор.
Скорее наоборот от него вред, ибо зря смущает неокрепшие умы.
Есть серия книг Босса "Лекции по математике". Ещё можно, банально, введения в учебниках читать.
У С все нетривиальные расширения будут даже не алгебраическими.
Да, это любое сепарабельное замыкание несовершенного поля (если под расширением понимать алгебраическое расширение).
Если у тебя моментальный агр на слово "Бог" вне зависимости от того, в каком оно контексте употреблялось и в какой стилистике подано - то это исключительно твои проблемы.
Если в учебнике математики фигурирует Создатель Бог, который заложил наличие винта в устройство физического пространства и таким образом привёл к малому проценту левшей, то это - плохой учебник математики.
Начнём с того, что это не учебник математики, о чём прямо написано во введении, а закончим тем, что твои демагогические передёргивания и перевирания написанного слишком жалки даже для сцая.
Если ты рекомендуешь какую-то книжку как образовательную и научную, а в этой книжке встречается Бог-Создатель, то хорошим тоном будет предупредить о наличии в книжке оного непотребства. Это этика.
Хорошо, поясняю для особо одаренных, фраза: "Не заложил ли Создатель асимметрию пространства до производства штопора?", конкретно в том тексте - это некоторым образом стилизованная метафора на: "Существует ли у физического пространства выделенная ориентация?", - я просто не знаю кем нужно быть, чтобы этого не понять. А ты, небось, подумал о настоящем штопоре, которым твоя мамка шампусик на новый год открывает и о теистическом/христианском Боге?
зря ты так. среди математиков подавляющее количество верунов. а среди биохимиков их почти нет. все потому что математики не знают как дофаминовые фуги влияют на мозг хоть и постоянно в них находятся. математики используют "бог" как "предельная гармоничность" что отражает событие происходящее с их мозгами. их мозги заливает веществами и они чувствуют как прикасаются к "самой важной тайне эротично скрытой полупрозрачной шторкой". я как (почти) биолог вижу в этом реализацию инстинкта познания сцепленного с половым. поощрение таково что заливает везде. у них приход а значит и "бог".
caught, а не catch, лол.
самое забавное тут (на мой вкус) то что можно закинуться кока-опием и получить на мгновение схожий эффект. у шизиков так часто бывает. другое дело что у математиков (да и у всех ученых в авангарде науки) такие приходы адекватны проделанной работе.
я даже не вспоминал про протопопова. он шаралатан кстати. а все его последователи просто идиоты.
и кстати изза таких вот ничтожеств типа протопопова изучение людей постоянно дискредитируется.
он в общем прав что указал на приматность человека. но он на этом остановился. а люди между прочим приматы с языком, сложным социумом, культурой, передачей информации из поколения в поколение, специальным "классом" изучателей опять же. ни в одном обществе приматов(кроме людей) нет касты ученых, нет касты философов. они просто не нужны, так как нет достаточно емкого способа хранить и передавать информацию. значит и существования добытчиков информации сложнее "я видел там орех" не возможно.
так что вот эта познавательная система подкрепления и есть чисто человеческая фишка. в системе подкрепления, которая досталась от предков нет специальной познавательной области. зато можно немного "отщипнуть" от социальной, от половой.
а вместе это и есть "бог" только у "нормальных" людей это вызывается органическими повреждениями, заместителями веществ и наследственными заболеваниями. а истинным людям познавать приятно по дефолту.
По мне так вообще общую топологию можно отдельно не учить. Во введении книжек по анализу, функ. анализу и алг./маломерной топологии всё то, что нужно из общей будет написано.
>это некоторым образом стилизованная метафора
Ничто не указывает на это. У автора не было никакой необходимости приплетать бога, левшей и вращение Земли к тексту, но он это сделал.
Это характеризует и автора, и читателя.
>Ничто не указывает на это.
Что ты понимаешь под "указателями на метафору"?
>>339002
>У автора не было никакой необходимости приплетать бога, левшей и вращение Земли к тексту, но он это сделал.
У тебя не было никакой необходимости уцепиться из 16 томов к одному метафорическому пассажу, но ты это сделал. Что характеризует только лишь тебя.
В чем алгебраический эффект?
Все ведь правильно. Или о том что при отнимании неправильно поступили?
Под указанием на то, что это метафора, - например, наличие аналогичных "метафор" и подсветка того, что это именно метафора, а не буквальное утверждение.
>из 16 томов
Надо же, какой плодовитый автор. Надо будет посмотреть остальные его тома и выбрать из них моар непотребных цитаток. Наверняка они там есть.
Я вообще не понял сути претензий. Упоминание Бога совершенно нейтральное как чего-то вне нашего понимания и ответственного за фундаментальные законы вселенной.
При этом замечание весьма разумное, так как стоит объяснять, что выбор ориентации это всегда свобода с точки зрения математики. Но у читателя может возникнуть вопрос про наш физический мир, в котором хуй поймешь что с асимметрией и из-за чего она возникает.
Ну, требуется алгебраически незамкнутое расширение.
Многие математике говорили о боге в контексте математики. Есть, например, известная цитата Кронекера: "God made the integers, all else is the work of man". Не вижу ничего такого. Если ты тупой и не понимаешь метафор, то это твои проблемы.
Бог сделал йобу, а YOBA ETO TI
>например, наличие аналогичных "метафор" и подсветка того, что это именно метафора, а не буквальное утверждение.
Там в рамочку для таких даунов как ты обвели, дебил.
Даже хотя сферы религии и науки сами по себе ясно разграничены, между ними существует сильная взаимосвязь и взаимозависимость. Хотя религия может служить тем, что определяет цели, она тем не менее научилась у науки, в широком смысле, какие средства приведут к достижению целей, которые она наметила. Но наука может быть создана только теми, кто насквозь пропитан стремлением к истине и пониманию. Но источник этого чувства берёт начало из области религии. Оттуда же — вера в возможность того, что правила этого мира рациональны, то есть постижимы для разума. Я не могу представить настоящего учёного без крепкой веры в это. Образно ситуацию можно описать так: наука без религии — хрома, а религия без науки — слепа.
Привет вам от Альберта Айнстайна.
Учёные часто любят обращатся к "богу", но думать что при этом имеется ввиду теистический бог - верх долбоебизма.
А также за высокий процент леворуких людей, связанный, возможно, с вращением Земли, угу.
>>339055
Кронекер вообще был странный. Он не верил в иррациональные числа, например.
Я читал. Могу сказать, что его книги оставляют больше вопросов, чем дают ответов. При прочтении есть перманентное желание найти источник, с нормальны изложением материала, и посмотреть каноническое доказательство того или иного факта. Но, конечно же, ссылок подтверждающих его кукаретизирования, он не дает.
>Kronecker gives the Leibniz series for π/4 and writes that this definition of the transcendental number π is actually of a number theoretic character.
Нет противоречия. Современные финитисты иррациональные числа воспринимают так же.
Топологических пространств.
>каноническое
Я читал, куча дико годных фольклорных сюжетов, образов и мотивов о которых не пишут в учебниках и которые передаются непосредственно при разговоре специалистов со студентами (на семинаре, например). Его книги как раз предназначены для "ненормального" - фривольного изложения материала и стандартный учебник не заменят, о чём непосредственно написано в предисловии, но это не минус этих учебников, а, скорее, плюс, ибо аналогичной литературы либо очень мало, либо нету вообще.
>куча дико годных фольклорных сюжетов, образов и мотивов
и ни одного пруфа или нормального доказательство.
Как неофиту понять, что все эти "фольклорные сюжеты, образы и мотивы", поясняют действительно актуальные математические концепции и имеющие отношение к математике вещи, а не являются шизофреническими фантазиями автора?
Как твою мамбку ебу сойдёт?
Из книжки, в смысле.
0 = (n - 1)(m - 1) mod 4, следовательно, n - 1 + m - 1 = nm - 1 mod 4
Как получили последнее сравнение?
(n - 1)(m - 1) = mn - m - n + 1
mn - m - n + 1 = 0
mn - m - n + 1 - 1 = -1
mn - 1 = m + n - 1 -1
Просто гугл тебе кое на что ненавязчиво намекает.
>Стоит пробовать их книжки читать?
Да.
>Почему их критикуют?
Кто их критикует? Покажи хоть одну обоснованную критику.
>Не научусь ли я какому-нибудь говну, если буду учиться математике по их работам?
Нет.
Майн готт, бурбакидаун опять покинул пределы шконки.
Ну ка, формализируй тогда по Бурбаки единицу, чтобы можно было тебя вкусным свежим говном марки "детская неожиданность" накормить.
> формализируй тогда по Бурбаки единицу,
Проблемс? У бурбаков в самом начале первого тома написано, что абсолютная формализация математического текста нечитаема и неудобна, поэтому достаточно изложения, которое при желании допускало бы полную формализацию, но для читабельности содержащее сколько угодно вольностей речи и соглашений. Главное, чтобы это не вызывало путаницы.
>МЫ ФАРМАЛЕЗИРУЕМ МОТЕМАТИКУ ЧИРЕЗ ОБСТРАКЦЕИ
>в самом начале первого тома написано, что абсолютная формализация математического текста нечитаема и неудобна
Жиденько ты. Впрочем как и всегда.
Проблемы человекоблядей никого не волнует. Не можешь запомнить 4 миллиона абстракций -- молчи в тряпочку.
>подразумевает что сам помнит 4 миллиона символов
«Разум не может существовать в теле, обреченном на смерть!» — раздался пронзительный квантовый сигнал со стороны Тау Кита.
Но лысые гоминиды, как всегда, не обратили внимания на этот шум в радиоэфире. Пусть шумит, что с него взять?
Существо трансцендентное — не человек, и сегодня ему предстоит очень трудная ночь. У него уже в течение полутора миллионов лет каждая ночь была очень трудной, и теперь его мозг был разработан настолько, что он без труда мог уместить в нем все познания об устройстве вселенной.

Ты ведь все равно не самоубьешься...
Да, добавлю, что и теорема Ферма и АВС-гипотеза касаются всего лишь натуральных чисел, которые школьники в 1 классе проходят.
ну перебор это тоже исследование, лол.
короче такие себе анонемасы-математики, решившие формализовать всю математику на ебучей теории множеств. Разумеется ничего у них не вышло - получилась груда говна. Лишь самый извращенный и больной ублюдок способен съесть её хотя бы на половину. Другое дело, что результатов никаких они не сделали, ничего концептуально нового не изобрели. Книги их читать рекомендуется чистым математикам например.
>>339490
Мой друг Василий, самый модный бомж, доказал абс-гипотезу еще когда твой пиздоглазик не родился на свет. Для этого он развил интер-универсальную теорию целлофановых пакетов. На данный момент ни один математик не нашел формальных ошибок в его доказательстве.
Не стоит вскрывать эту тему...
Если в выражении (a+b)(a+b)...n раз...(a+b) раскрыть все скобки то получится сумма некоторого числа слагаемых, каждое слагаемое формируется следующим образом: мы из очередной скобки (а+b) берём либо a либо b а затем всё это перемножаем, чтобы сформировать a^k b^(n-k) нужно "взять" из n скобок k штук а и n-k штук b. Сколькими способами это можно сделать? Как раз C(n,k)
>>339188
Существование в R^4 выпуклых многогранников с произвольным количеством смежных вершин; замкнутый шар (в гильбертовом пространстве) слабо компактен, но замкнутая сфера - нет; матрица, которая при возмущении одного элемента на 2^-23 "революционным образом" меняет спектр. Ну и вообще всякие акценты хорошо расставлены: почему определения именно такие, а не другие, зачем нужны те или иные теоремы, и где они работают и прочее.

По Бурбаки 0 - это кардинал множества ∅, 1 - это кардинал множества {0}.
Давай, начинай кормить.
Единичный отрезок. Иррациональные я записываю как \mathbb{Irr}.
Где-то в педивикиях встречал высказывание(то ли Гаусса, то ли кого-то из современников), что любой дурак может сформулировать математическое высказывание(там теория чисел, вроде подразумевалась), которое не докажет ни один топ.
И даже Ферма, если не ошибаюсь, доказали попутно, как следствие более общей гипотезы, типа ради одной Ферма никто бы усираться не стал.
>>339509
>Другое дело, что результатов никаких они не сделали, ничего концептуально нового не изобрели.
Хоть бы поинтересовался, кто в Бурбаков входил ИРЛ. Там было много признанных топов, как доказавших трудные теоремы, так и концептуально расширивших теорию, включая Вейля, Серра, Гротендика и многих других.
>Мой друг Василий, самый модный бомж
>На данный момент ни один математик не нашел формальных ошибок в его доказательстве.
Не путай своих друзей-бомжей и "уважаемых людей". Мочидзука до ABC высирал годноту, да и попытки анализа его теории другими "уважаемыми людьми" по крупицам указывают, что в них есть рациональное зерно, что внушает вполне обоснованную надежду.
>Вейля, Серра, Гротендика
Самые хуевые пидоры на свете
>>339563
>по крупицам указывают, что в них есть рациональное зерно, что внушает вполне обоснованную надежду.
Вроде бы наоборот: все говорят, что его работа - не читаемое говно. И не признают например его доказательство.
Википидоры вот говорят, что простейшими примерами колец являются числа. Вот к примеру множество, состоящее из двух элементов - натуральных чисел 2 и 3, это кольцо? И нахера нам нужно это кольцо 2,3?
Опять же википидоры говорят
>Для изучения общих свойств операций умножения и сложения, их внутренней связи между собой, безотносительно природы элементов
Какие блять можно вывести общие свойства из сложения 2+3? Что это за йоба-теория поясни пожалуйста?
Мы берем определенную группу чисел и определяем как мы можем по ней ходить. и ВНЕЗАПНО обнаруживаются интересные свойства.
https://en.wikipedia.org/wiki/Ring_(mathematics)
И чего ты меня снова к википидорам отправляешь, пидор? Я только что от туда, и просил объяснений у анонимуса, потому что нихуя не понял у википидоров. Я привык, что кольцо это такая круглая хуйня, которую на палец надевают. Где в множестве 2,3 круглая хуйня? Покажи!
2+3=3+2=5
2х3=3х2=6
Это мне еще в 7 лет училка пояснила. Что из этого еще можно придумать нового? ГДЕ ТУТ КОЛЬЦО?
Нигде, ведь числа 5 и 6 не входят в твое множество, следовательно оно не является коммутативной группой.
Хорошо, а как насчет множества, состоящего из 4 элементов: 2,3,5,6. Эта запись будет уже справедлива.
>2+3=3+2=5
>2х3=3х2=6
ГДЕ ТУТ КОЛЬЦО?
Ты опять же не определил деление. Давай-ка ты вернешься в википедию и прочитаешь аксиомы кольца.
Пояснение -- чистый пересказ википедии.
In 19th century German, the word "Ring" could mean "association", which is still used today in English in a limited sense (e.g., spy ring),[10] so if that were the etymology then it would be similar to the way "group" entered mathematics by being a non-technical word for "collection of related things".
Ну ахуеть. Вы только посмотрите что творится. Никто даже не попытался ничего пояснить, отправили к википидорам и обозвали дауном. Сажи вам и идите нахуй!
>Кто их критикует? Покажи хоть одну обоснованную критику.
https://www.dpmms.cam.ac.uk/~ardm/bourbaki.pdf

>Бурбаки говорят о некоторой ограниченности аксиоматического метода, но делают это с недостаточным уважением, они даже не упоминают имени Гёделя.
Очевидный Бурбаки.
А если честно, то нет. Так что хватай фихтенгольца и не возвращайся пока не осилишь все три тома.
>И не признают например его доказательство.
Но, видишь ли, ему это глубоко безразлично. Он знает, что он доказал, и со временем мат. сообщество разовьется до его уровня и сможет наконец понять его доказательство. И именно он будет считаться доказавшим эту теорему. Пусть это будет даже через тысячу лет.
Открой первый том фихтенгольца и начинай читать.
>любой дурак может сформулировать математическое высказывание(там теория чисел, вроде подразумевалась), которое не докажет ни один топ.
Тут понимаешь, какое дело. Он не сформулировал, он именно доказал. А ни у кого мозгов не хватает чтобы просто въехать в его доказательство. Это не то, о чем ты говоришь.
Уточню, я говорил в контексте этого
>Так-то людишки правда для математики не очень пригодны.
>Сколько там веков теорема Ферма была открытой проблемой?
Шиза какая-то.
>В этих бумагах нет ни малейшего поминания Гёделя
>...они поминали Кантора, Кронекера, Цермело, Френкеля, Фихтенгольца, Садовничего, Каледина
>Но ни разу не помянули Гёделя!
>Картан рассуждал в принципе о фундаментальных вещах
>Таких как почему не помянут Гёдель
>Я хочу адресовать такой вопрос
>ПОЧЕМУ черт возьми не помянут Гёдель?
>В "архитектуре математики" также не помянут Гёдель
>Их книги росли и росли, сместились к тому, чтобы даже помянуть Гёделя
>Но в целом фундаментальное отношение к догеделическим временам и критическое непоминание, выжили, что и заставило меня провести это "исследование"
>Так вот перейдем к моему первому и основному вопросу:
>ПОЧЕМУ Бурбаки не адаптировали свое отношение к поистине божественному, феноменальному вкладу Гёделя в вопросы основания?
>Они рассуждают об основаниях, но делают это без уважения
Лучше начни с того, что ты считаешь прикладными задачами. Обычно в материалах с этими задачами(ну или ликбезам по ним) делаются ссылки на области матеши, которые надо знать. От них и танцуй.
А то можешь прокатиться по серии бугуртов вроде:
Матеша - хуясе, и я всё это время тратил на теоремы существования и обобщения %раздел_нейм% без задач!?
Физика - ебошил теорию струн, рассчитывал коня в вакууме с учётом квантовых эффектов - и всё, чтобы запилить игру-физическую песочницу с корованами!?
А оказалось-то, надо накатить пару либ и накидать говнокода немножк на пистоне, а интрегалы переоцененное говно!
К примеру, после фразы "неких симуляций физических" обычно на ум приходят ДУЧП, они же уравнения математической физики(механика всяких тел и сред, моделирование жидкостей, термодинамики, электромагнетизма, атомов, квантов и прочая). Хотя, в принципе, это может быть что угодно - хоть иммитационная модель, или хуйня на графах.
Кстати, поясните за Арнольда. Как уважаемый профессор стал синкретическим божеством? Какие были предпосылки/предыстория? Часто ли математик в конце карьеры становится Тот?
>много признанных топов
Нихуя не индикатор. Фейнман был йоба ученым, как говорят, но его курс физики то еще говно. И это самый простой и свежий пример.
>Арнольда. Как уважаемый профессор стал синкретическим божеством?
Он попал в аварию, когда катался на велосипеде. Врачи его вытащили, но он на некоторое время потерял память и разучился говорить. Когда пришёл в себя, почему-то начал поклоняться Гермесу Трисмегисту и рассказывать про гибнущее образование во Франции.
В 19 вековой германии слово кольцо могло означать ассоциая, что до сих пор используется в инглише в ограниченном смысле(типа шпионское колько), так что это этимология там, где это понятие может быть заменено словом группа, вошедшее в математику на замену нетеххнических слов набор связанных вещей

Самое весёлое, что Бурбаки как раз уважали Гёделя, а случай 36 пикрелейтед я до этого видел описанным в «Очерках по истории математики» Бурбаки же, с тем же оттенком возмущения, только говорил это какой-то сторонний профессор, а не член группы, лол.
Зачем пытаться объяснять дураку с шизофренией что он не прав, если он дурак с шизофренией, которого невозможно переубедить без живительной эвтаназии в том, что он дурак с шизофренией? Легче и практичнее принять его как воскресны дождик и не обращать на него внимания.
Если учесть, что дурак с шизофренией здесь только ты, то и действительно незачем.
Всегда было интересно, то, что он рассказывал, что весталки при каком-то храме в незапамятные времена водили планеты по эллитическим орбитам — правда?
Начну пожалуй тебя репортить.
Создай свой личный тред про онанизм на бурбаки. Не надо заставлять всех дрочить на него.
Не стоит вскрывать эту тему.

В простейшем случае с двумя точками имеем задачу минимизации R_sum=a^2+b^2, где a и b - расстояния вдоль оси OY от первой и третей точек соответственно.
Но по теореме пифагора, имеем a^2+b^2=c^2, то есть вместо задачи минимизации зависимости от двух переменных R_sum(a, b) получили аналогичную задачу для одной переменной, тем самым, сократив размерность исходного пространства в целых 2(!) раза.
Дальше сам.
В общем, я понял, почему ничего не нагуглил. Рисовать это богородица не велит.
>>339746
>Пацаны, почему быдлочеловечество до сих пор сидит в говне десятичной системы и не хочет принять божественную дюжинную?
Потому что всем похуй. Можешь считать в системе 12, если очень нравится.
>Потому что всем похуй. Можешь считать в системе 12, если очень нравится.
Я уже.
Алсо, ретрограды-декадники удалили мой пост. Боятся, что люди откроют глаза на правду.
синай курс теории вероятностей
Кольца - это структура, аксиоматизирующая всякие целые числа, многочлены и матрицы определённым образом. Каким - определяется списком аксиом, которые надо просто посмотреть где-то, например в википедии. Кроме как сказать что это аксиоматизация того, что выполняется в целых, многочленах, матрицах и.т.п. тут особо нечего. Твоё {2,3} или {2,3,5} с умножением как обычных целых чисел не является кольцом, потому что не замкнуто относительно этого умножения.
А гегеля упоминают?
Кстати, замкнутость относительно этой операции подразумевает, что результирующий объект будет тоже принадлежать этой алгебраической структуре (кольцу, группе, полю...)?
Мимо-другой-анон
Спасибо. Поясни, если не трудно, еще тогда утверждение, что пересечение любого множества подколец является подкольцом. Пусть элементы АхВ=С принадлежат одному подкольцу, а КхР=М - другому. Тогда мы же можем взять пересечение этих подколец такое, что в множество его элементов попадут А, В и М, но они не образуют замкнутого объекта. Получается это пересечение не подкольцо?
Замкнутость доказывается так.
Пусть {Xi} - семейство подколец, не обязательно конечное. Пусть X - его пересечение. Если a и b - элементы X, то они являются элементом каждого Xi, и, так как каждое подкольцо замкнуто относительно операций, их сумма a+b и произведение ab также являются элементом каждого Xi, а потому являются элементом X.
Лол, спасибо. Я чего-то с теорией множеств затупил. Теперь вижу ущербность своего примера.
Кольцо целых чисел же подразумевает бесконечное количество элементов? Или я опять не прав?
В кольце ℤ целых чисел бесконечно много элементов, да. Но бывают и кольца с конечным количеством элементов. Самый простой пример - кольцо {0} из одного элемента.
Еще раз благодарю. Поясни еще за главный идеал, пожалуйста. Определение понятно, типа есть элемент кольца х, при умножении на который всех элементов кольца и получается этот самый главный идеал. Но для чего введено понятие главного идеала (что особенного оно дает)? Чем он от прочих идеалов отличается? И откуда следует, что в кольце целых чисел все идеалы главные (я понимаю, что, скорее всего, это очевидно, но я слегка туповат и биолог по образованию)?

Пересечение любого семейства идеалов кольца - снова идеал.
Пусть есть какое-то множество M элементов кольца R. Пересечение всех идеалов кольца R, являющихся надмножествами M, называется идеалом, порождённым множеством M. Идеал называется главным, если он порождён одноэлементным множеством. Кольцо называется кольцом главных идеалов, если в нём каждый идеал - главный.
В кольце ℤ для каждого элемента x множество всех кратных zx является, как нетрудно доказать, идеалом, содержащим x. Далее, любой идеал, порождённый элементом x, по определению содержит элемент x и потому содержит все кратные x. Следовательно, пересечение всех идеалов, содержащих x, является множеством всех кратных x. То есть в кольце целых чисел идеал является главным, если он является множеством всех кратных какого-то числа x.
Доказательство, что ℤ - кольцо главных идеалов, не очень тривиально и опирается на определение деления с остатком. Пусть I - идеал в ℤ. Если он нулевой, т.е. {0}, то он главный. Предположим, что он не нулевой. Тогда в нём есть несколько положительных чисел, и, так как любое непустое множество целых положительных чисел имеет наименьший элемент, в нём есть наименьшее положительное число a. Покажем, что все целые числа идеала являются кратными a. Пусть b - какое-то целое число идеала I. Разделим b на a с остатком: b = ak + r, где, по определению деления с остатком, 0 <= r < a. Так как a - наименьшее положительное число идеала, остаток r равен нулю, то есть b = ak. Таким образом, I является множеством всех кратных a и потом главным идеалом. Такие дела.
Кольца главных идеалов важны тем, что в них выполняется много хороших теорем. Самая хорошая - это, пожалуй, теорема о единственности разложения на простые множители. Слышал про основную теорему арифметики? Аналогичная теорема верна в произвольном кольце главных идеалов. Но я не буду её ни формулировать, ни доказывать, потому что мне понадобится много вспомогательных понятий - простой идеал, максимальный идеал, кольцо вычетов, факторкольцо и т.д.

Пересечение любого семейства идеалов кольца - снова идеал.
Пусть есть какое-то множество M элементов кольца R. Пересечение всех идеалов кольца R, являющихся надмножествами M, называется идеалом, порождённым множеством M. Идеал называется главным, если он порождён одноэлементным множеством. Кольцо называется кольцом главных идеалов, если в нём каждый идеал - главный.
В кольце ℤ для каждого элемента x множество всех кратных zx является, как нетрудно доказать, идеалом, содержащим x. Далее, любой идеал, порождённый элементом x, по определению содержит элемент x и потому содержит все кратные x. Следовательно, пересечение всех идеалов, содержащих x, является множеством всех кратных x. То есть в кольце целых чисел идеал является главным, если он является множеством всех кратных какого-то числа x.
Доказательство, что ℤ - кольцо главных идеалов, не очень тривиально и опирается на определение деления с остатком. Пусть I - идеал в ℤ. Если он нулевой, т.е. {0}, то он главный. Предположим, что он не нулевой. Тогда в нём есть несколько положительных чисел, и, так как любое непустое множество целых положительных чисел имеет наименьший элемент, в нём есть наименьшее положительное число a. Покажем, что все целые числа идеала являются кратными a. Пусть b - какое-то целое число идеала I. Разделим b на a с остатком: b = ak + r, где, по определению деления с остатком, 0 <= r < a. Так как a - наименьшее положительное число идеала, остаток r равен нулю, то есть b = ak. Таким образом, I является множеством всех кратных a и потом главным идеалом. Такие дела.
Кольца главных идеалов важны тем, что в них выполняется много хороших теорем. Самая хорошая - это, пожалуй, теорема о единственности разложения на простые множители. Слышал про основную теорему арифметики? Аналогичная теорема верна в произвольном кольце главных идеалов. Но я не буду её ни формулировать, ни доказывать, потому что мне понадобится много вспомогательных понятий - простой идеал, максимальный идеал, кольцо вычетов, факторкольцо и т.д.
Под кольцом нужно понимать коммутативное целостное кольцо, уточню. В некоммутативных всё сложно.
>коммутативной группой.
Коммутативность здесь не причём, здесь не выполняется свойство замкнутости.
>Но для чего введено понятие главного идеала (что особенного оно дает)?
Принадлежность b главному идеалу (a) эквивалентна делимости a на b.
В многочленах на полем все идеалы главные (потому что их тоже можно делить с остатком, доказательство такое же), это используется везде, где возникают многочлены, а они возникают везде, и. т. д.
Вообще, удобно, когда есть соответствие между элементами и идеалами.
Имеются в виду многочлены от одной переменной конечно же.
Блеать, да какая разница делится или делит — главное, что фигурирует деление.
inb4 накидал тебе за щеку
1. Гнеденко. Элементарное введение в теорию вероятностей.
2. Гнеденко. Курс теории вероятностей.
Гнеденко - это непосредственный ученик Колмогорова, работавший вместе с ним над теорией вероятностей.
Опять таблетки не принял?
Замкнутая линия на поверхности гомологична нулю, если она является границей некоторого её участка. Пример: на сфере любая замкнутая линия гомологична нулю, а на торе, хотя и существуют гомологичные нулю замкнутые линии, но разрез по меридиану или параллели не приведёт к отделению куска поверхности.
Да-да, я википедию читал. Но мне хочется пояснение про общий случай гомологии, простым языком. А там пздц на десять страниц, в который я решительно не въезжаю.
Тебе конкретно про топологические гомологии говорят, откуда всё это возникло. Здесь, формально говоря, возникает комплекс, ассоциированный с топологическим пространством, к которому можно применять всякие методы гомологической алгебры. Но в математике построено множество всяких комплексов, в разных совершенно областях, это просто один из примеров.
Ок, но это же не отвечает на вопрос что такое гомология. Я понимаю, что в двух словах ньюфагу такое сложно объяснить. Однако можно же перефразировать формальные определения русским языком.
К тому, что это способ классифицирования различных "форм" по их "специальным характеристикам".
Представь себе сферу и тор (это простые примеры "форм"). Их можно отличить по следующей "характеристике":
На сфере любую замкнутую линию можно стянуть в точку.
На торе этого сделать нельзя.
Таким образом сфера и тор относятся к разным классам. А гомологии это показывают и доказывают.
А где же дыры? А дыры это тоже характеристика, которую можно показать при помощи гомологий.
То что я тебе пытался показать относится к области математики под названием «алгебраическая топология». В ней даётся более строгое и точное объяснение всего того, что я взял в кавычки.
Не знаю, думаю что вряд ли. Алгебраическая топология оперирует понятиями из областей абстрактной алгебры. То есть прежде чем освоить эту ступень, необходимо освоить предыдущую. Для освоения такой области абстрактной алгебры, как «теория групп» необходимо ознакомиться с основными алгебраическими структурами и понятиями, а для этого подходит линейная алгебра.
Прослушал курс видеолекций по высшей алгебре Николая Вавилова, я уже достаточно хорош, или еще чего-нибудь сначала прочитать/посмотреть надо?
>Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.
Поясните мне, почему вместо няшных бесконечно малых/больших мы учим в школах перделы?
>нестандартный анализ
>в школах
Хотя бы прочел что-нибудь, кроме истории, прежде чем высказывать свое негодование. Нужно хорошо владеть теорий множеств, чтобы вкурить нестандартный анализ. Теорию множеств, как известно, шкальники не проходят. Зато школьными методами можно вполне себе обосновать понятие предела.
Если ты из тех борцунов с системой, мамкин реформатор, которой жаждет изменения школьной программы, - с отменой домашки и категориями с 5-го класса, - то пиздуй лучше в un/, тут вы заебали уже.
Гомологическая алгебра - это такой технический инструмент для выбивания информации из комплексов. Про "потаённый смысл" гомологий я не знаю, может он и есть конечно, но вряд ли.
Я говорю про определения теоремы и т д. Вот, например, прочитал я определение симплексов на вики и нихрена не понял. То ли я тупой, то ли язык там переусложненный, то ли все вместе.
>>340008
Нет. Неужели я список задач где-то пропустил? Вроде смотрел внимательно.
Спасибо, попробую.
Поясните за геометрический смысл регулярности множества в точке, пожалуйста
Множество D называется регулярным в точке x по отношению к классу рассматриваемых задач Ф, если для любой функции Q из Ф имеющей в точке x локальный минимум, условие оптимальности записывается через функцию Лагранжа при a*!=0
Где функция Лагранжа это функция вводимая в задаче minQ(x) в области D=(g(x)<=0, h(x)=0), здесь g,h - векторные и x тоже вектор.
Мне кажется, я нихуя не понятно описал, в общем это термин из математического программирования.
Ну про школу может я перетолстил, но все же. Во времена метода неделимых разве была йоба теория множеств? Она же только в 19 веке появилась. До этого там были зачатки множеств, как и зайчатки матана.
За оффтоп меня на три дня забанишь?
>Нет.
Тогда вряд ли. Ты сейчас в лучшем случае лишь имеешь представление о прослушанном, «цветочные кулаки и вышивание ногами». Для приобретения определённого уровня понимания необходима практика.
А скажи, есть ли доказательство того что мощности множества натуральных чисел и действительных различны кроме диагонального метода Кантора?
Но насколько я знаю, что и в этом случае используется диагональный метод.
(это про множество всех подмножеств)
>в этом случае используется диагональный метод
В каком - в этом? В доказательстве теоремы Кантора?
Да, я имел ввиду доказательство, что мощность множества всех подмножеств непустого множества А больше, чем мощность исходного множества А.
Но я уже посмотрел, там нет диагонального метода.
А как тогда показать равномощность R и 2^N?
>А как тогда показать равномощность R и 2^N?
Вот это уже больше похоже на диагональный метод.
Известно, что множество R равномощно множеству всех последовательностей из нулей и единиц. Каждой такой последовательности можно поставить в соответствие подмножество из N, причём взаимно однозначно. Например,
последовательности (0,0,0,1,0,0,0,0...) соответствует подмножество {4}; последовательности (1,0,0,1,0,0,0,0...) подмножество {1,4};
(1,1,0,1,0,1,0,0,0...) - {1,2,4,6};
(1,1,1,1,1,1,0,0,0...) - {1,2,3,4,5,6} и т.п.
Логику построения, надеюсь, понял.
Да. Диагональный метод появился уже после того, как Кантор доказал неравномощность. Первое доказательство Кантора было другим.
Теорема. Если есть отрезок [a;b], то для любой последовательности вещественных чисел в отрезке найдётся число, не входящее в последовательность.
Доказательство (доказываю по памяти, доказательство, скорее всего, не совпадает с канторовским). Пусть x1, x2, x3, ... - последовательность вещественных чисел, [a;b] - данный отрезок. Если в отрезке лежит только конечное число элементов последовательности, то доказывать нечего. Предположим, что в отрезке лежит бесконечное число членов последовательности.
Найдём первые два числа из последовательности, которые входят в отрезок. Обозначим через a1 меньшее из них, b1 - большее. Найдём следующие два числа из последовательности, которые входят в отрезок уже [a1; b1], обозначим через a2 меньшее из них, b2 - большее. Продолжая таким образом, получим последовательность вложенных отрезков. По аксиоме вещественных чисел, пересечение этих отрезков не пусто.
Это пересечение либо содержит две разные точки p<q и потому целый отрезок [p;q], либо сводится к одной точке x. В первом случае любая внутренняя точка отрезка [p;q] не входит в последовательность. Рассмотрим второй случай. Он означает, что lim an = lim bn. Если точка x входит в последовательность an, то для какого-то N верно, что aN = x. Но учитывая, что для любого n верно, что an<= bn, и что an - возрастающая последовательность, bn - убывающая, заключаем, что для N верно, что bN = x и потому последовательность xn содержит в отрезке [a;b] не больше чем 2N членов. Но она содержит в отрезке бесконечно много членов, противоречие.
Следствие. Предположим, что множество вещественных чисел счётно. Тогда их можно расположить в виде последовательности. Но тогда в отрезке [0;1] по теореме найдётся число, не входящее в последовательность. Значит, множество вещественных чисел несчётно.
Формулировки правильные, в доказательстве теоремы неточность.
https://en.wikipedia.org/wiki/Georg_Cantor's_first_set_theory_article#Second_theorem
>Теорию множеств, как известно, шкальники не проходят
В 57,2,239,Сунц,АГ проходят в 5-6 классе, че там в быдлошарагах -- хз.
>не замкнуто относительно этого умножения.
Что это значит, поясни пожалуйста. И приведи пример записи кольца {2,3,5} которое замкнуто относительно умножения
Пусть есть множество M, на котором введена операция ×. Пусть N - подмножество M. Подмножество N называется замкнутым относительно ×, если вместе с любыми двумя элементами a и b оно содержит элемент a×b.
Например, рассмотрим множество целых чисел Z с операцией сложения.
Пусть N - множество чётных чисел. Сумма двух чётных чисел - чётное число, то есть множество счётных чисел замкнуто относительно сложения.
Пусть теперь N = {1,2,3}. Оно содержит элементы 3 и 2. Но 3+2 = 5, а 5 не является элементом N. Поэтому N не замкнуто относительно сложения.
Т.е. замкнуто относительно сложения и умножения множество ВСЕХ натуральных чисел? Конечное множество натуральных чисел всегда будет не замкнуто?
Да.
Однако на конечном множестве натуральных чисел можно ввести другое, необычное сложение.
Например, рассмотрим множество M = {0,1}. Положим 0+0 = 0, 1+0 = 0+1 = 1, 1+1 = 0. Относительно этого сложения M замкнуто. Относительно обычного сложения натуральных чисел M не замкнуто.
С линейной алгебры? Ну е-мое мне двух лет линала в универе хватило. Ну ок, благодарствую, посмотрю что за Ленг такой.
>двух лет
Кто его джва года учит-то, лол? У всех физматов и экономистоблядей он максимум два сема.
Сначала 1 год в одном универе, потом еще один в другом. Программы, что странно, между собой имели очень мало общего, хотя направления обучения не такие уж и далекие.
Единое образование умерло ещё в семидесятые. Теперь в каждом университете свои собственные гниющие ошмётки некогда единого курса. В разных местах они гниют по-разному.
Возможно. Может именно поэтому сейчас я учу математику, а не у меня ей учатся.
Лол, смотрю я этого Ленга, а там линейная алгебра только в последней части. После теории полей и гомологий. Интересная последовательность изложения.
"ОШИБКА ГЕОРГА КАНТОРА"
http://www.ccas.ru/alexzen/papers/vf1/vf-rus.html
Введение мне не понравилось. Тем, что человек утверждает, что то-то не является тем-то так как такого раздела математики не существовало.
Но вот как быть с тем, что после указания действительного числа, которого мы не занумеровали, мы можем опять произвести перенумерацию?
Да, мы сначала занумеровали все, но потом исходя из диагонального метода строим новое число, которое не занумеровано.
И вроде бы противоречие.
Но мы же можем ещё раз всё перенумеровать уже включив его.
Где здесь логика ломается?
Мы предположили, что занумеровали все. Пришли к противоречию. Всё, финита, дальше делать нечего, нет смысла что-то добавлять.
Теорема. Самого большого числа не существует.
Доказательство: Предположим, что самое большое натуральное число N существует. Но для каждого числа n существует число n+1. Значит, для самого большого натурального числа N существует большее число. Пришли к противоречию, значит, самого большого натурального числа не существует.
Мнение автора статьи. Но мы же можем в качестве самого большого числа взять N+1!
Классная аналогия!
Спасибо.
А есть название подобной логической уловки, чтоб поискать про неё что-нибудь?
Нет.
Galois Groups and Fundamental Groups
Tamás Szamuely
Там не совсем про топологию, но совершенно точно про накрытия.
можем ли определить "новую" операцию на множестве действительных чисел, чтобы выполнялась ассоциативность, коммутативность, существовал обратный элемент, и единичный(абелева группа), так чтобы операция не была представима в виде суммы(или произведения) функции от каждого операнда по отдельности?
ab=F(a)+F(b)
Нашёл вот только для ограниченной области такую операцию:
ab=(a+b)/(1+abX^2)
где X - положительный коэффициент
Ну, например, группы Ли или топологической группы на R, не изоморфной естественной получится не может. Поэтому умножение должно задаваться какой-то разрывной функцией.

пик для привлечения внимания и чтобы не потерять свой пост
>Циркуляция ротора кусочно гладкой функции по недиффиренцируемому многообразию
>>337758
>Качение сучковатого бревна по шероховатой поверхности
Вот, блять. Именно тебя я и искал. Я знаю, ты мне можешь посоветовать такой литературы, где первая фраза описывается при помощи второй. Иными словами, эта ваша когомология для чайников.
Я не очень понимаю, что конкретно здесь нужно, но на совсем элементарном уровне есть 2 книжки с названием "наглядная топология" (Прасолов и болтянский-Ефремовия), есть заметно посложнее, но все равно не слишком формальный задачный учебник по топологии Виро Харламова Нецветаева Иванова.
Например, если я нарисую совершенно любой невнятный узор, его всё равно можно задать математической функцией (пускай даже, что она будет неебически длинной и сложной)?
Что такое узор?
Если под узором понимать непрерывную функцию, а под
>задать математической функцией
аппроксимацию полиномом, то положительный ответ на вопрос дает теорема Стоуна-Вейерштрасса.
Ну у меня данные были 1:2:3 и V=6. По моему площади сторон получились 6, 2 и 1. Но я не помню и это теперь не важно.
Действительно неважно, лучше к психиатру.
Почему?
Пусть M - множество, пусть K - какое-то поле.
Множество всех отображений из M в K обозначим как X.
Множество всех отображений из X в K обозначим как Y.
Множество всех отображений из X в X обозначим как Z.
Элементы множества X традиционно называются функциями.
Элементы множества Y традиционно называются функционалами.
Элементы множества Z традиционно называются операторами.
Во, и я был того же мнения. А вики говорит, что это любое отображение из произвольного множества в произвольное. А если это произвольное отображаемое множество - не множество отображений? Ааааааааа, паника!
Да похуй абсолютно.
>любое отображение из произвольного множества в произвольное.
Не в произвольное, а в числовое. Или в поле.
В более широком смысле функционалом называется любое отображение из произвольного множества в произвольное (не обязательно числовое) кольцо.
Цитата с вики.
>Теоретически, любой графический узор можно задать функцией?
Нет. В любом из естественных способов определить "узор" (например, как графики гладких/кусочно гладких функций и.т.д.) множество этих узоров будет несчётно, в то время как множество всех формул в любом конечном алфавите не более чем счётно.
Да.
>является ли {1} подмножеством {1, 2}
Да.
>записать вот так {{1}, 2}
Нет.
>>340365
Любое множество является подмножеством себя.
Про множество, являющееся подмножеством себя. Это в аксиоматике ZF говорится, или откуда-то еще следует?
X является подмножеством Y титтк каждый элемент X является элементом Y.
Ясно, что для любого множества M каждый элемент M является элементом M. Поэтому каждое M - подмножество M.
Множество содержит себя в качестве подмножестве. Это подмножество тоже содержит себя в качестве подмножества, и т д.
X не есть {X}. Это два разных множества.
X есть элемент {X}, но не есть элемент {{X}}.
не понимаю, зачем я тебя кормлю?
Кормишь? Я тут вообще-то разобраться пытаюсь. Х - элемент {Х}, а {Х} - элемент {{Х}}. Получается бесконечное вложение подмножеств, состоящих из одних и тех же элементов друг в друга.
Если есть {2, 3}, тогда оно содержит само себя как подмножество и получается, что {2, 3, {2, 3}}. Парадокс.
Ну тут либо {2, 3, {2, 3}}, либо {{2, 3}}. Другого способа включать себя как подмножества я не вижу.
Верно ли, что каждый элемент множества {1,2,3} является элементом множества {1,2,3,4}?
Я понял твою мысль. Но мне очень не очевидно, что {2, 3}=/={{2, 3}}, ведь содержать как подмножество = содержать все элементы. Тогда {{}} содержит все элементы {}, а {{{}}} содержит все элементы {{}}, поэтому {...{}...} содержит в итоге все элементы {}.
Так это тред про математику. Математическая логика очень даже подходит под тему.
Тут у каждого, кто вопрос задает личные проблемы, связанные с непониманием какого-то раздела математики, и что? Я пытаюсь в математику вникнуть, доска эта посвящена науке, а одна из функций науки - образовательная, все очень даже в тему. Плюс, кроме здешнего треда мне некуда обратиться. Знакомых математиков у меня нет.
Вопрос ты задал, ответ получил. То, что этот ответ не согласуется с твоей "думалкой", - твои проблемы.
Дальнейшие рассуждения на эту тему веди, пожалуйста, в /ph/ или в /un/. Здесь - тред математики.
Какой раздел математики занимается данной проблемой? В каких книгах производится подробный разбор подобных задач? Каковы возможные алгоритмы поиска минимального набора недостающих аксиом? По каким ключевым словам мне всё это искать?
>при котором система будет непротиворечивой
При этом, предполагается, что изначальная система заданных теорем и известных аксиом сама по себе является непротиворечивой.
Кроме того, интересует проблема приведения системы аксиом к "простейшему" (среди эквивалентных систем аксиом) виду (минимальная суммарная длина строк при фиксированном алфавите) при неизменном их количестве.
В каком принципе?
Иначе, если {a} = {{a}} тогда a = {a}, а это неверно.
>Какой раздел математики занимается данной проблемой?
Логика и теория моделей. Конкретно: смотри метод форсинга (forcing).
Спасибо, постоянно забываю.
Короче, создайте перекат кто-то, в новом треде переспрошу.
Вы видите копию треда, сохраненную 22 марта 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.