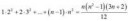Вы видите копию треда, сохраненную 12 марта 2017 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




http://pastebin.com/kiRZGVHW
Предыдущий >>389022 (OP)
ВНИМАНИЕ! ВНИМАНИЕ!! ВНИМАНИЕ!!!
On-line LaTex. Формулы пишем в нём, а после прикрепляем картинками к посту
http://www.codecogs.com/latex/eqneditor.php
Львовский Набор и вёрстка в системе latex
http://www.mccme.ru/free-books/llang/newllang.pdf
Если ты только зашел в тред и хочешь спросить, какую книжку прочитать, то ответ, скорее всего, будет в этих списках, анон.
Список от ОП-а, бывшего тут до меня. Был составлен на протяжении 13 тредов, к ознакомлению обязателен.
http://pastebin.com/4iMjfWAf
Список от анона с dxdy. Довольно внушителен, тоже рекомендуется к прочтению. Является дополнением к списку старго ОП-а.
http://pastebin.com/YP1uaUyd
Goodbook.txt список книг с dxdy, рекомендованный тамошними обитателями.
http://pastebin.com/4FngRj6n
ОП-список 2. Составляйте список в реальном времени! Предлагайте в тред книги, критикуйте уже имеющиеся!
http://pastebin.com/szzZfkCM
Форчановский список, книги на английском.
http://4chan-science.wikia.com/wiki/Mathematics
Список с видеолекциями(в разработке):
http://pastebin.com/S3d7Jj6J
Качать книги тут:
http://libgen.io
А статьи тут(в разработке):
http://pastebin.com/3BfHPskz
Мемасы(в разработке):
http://pastebin.com/e38Yuj5V
СПИСКИ В РАЗРАБОТКЕ, НУЖНА ПОМОЩЬ АНОНА, ПОЖЕЛАНИЯ ОСТАВЛЯЕМ В ТРЭДЕ
Наверное, она так сильно и не нужна была.

Значит, ты не безнадёжен.
Cipolla's algorithm

Пользуясь случаем, хочу напомнить присутствующим, что каноническим изображением Вербитана отныне следует считать вот это.
Некий трансгендер много-много лет назад обсыпал мишу мукой.


>>392737
>>392738
это я в прошлом трэде закинул, сам СЛУЧАЙНО (в ленте рекомендованного) наткнулся на ютубе, тут же зробил шбм
Вербицкий сидит в оксфорде.. рядом с оксимироном.. на политических дебатах
бля звучит как начало анекдота
потом встает трап, невнятно что-то спрашивает про зоофилию и опсыпает их мукой...
а вот это уже точно анекдот
На ютубе один чувак написал, что это легендарное видео, люди, посмотревшие оригинал в свое время, делились на 2 категории: те, кто узнали о Вербицком благодаря тому что это видео с Оксимироном, и те, кто узнали об Оксимироне благодаря тому что это видео с Вербицким.
https://www.youtube.com/watch?v=MBk0BQ_LrHI
давайте дружно поищем соус

Вот эталонная фотка Вербицкого
а вот тут еще дохуя
https://fotki.yandex.ru/users/veniamin-veniamin1/tags/вербицкий
такой маленький, а уже телемит
Речь о "производной сложной функции".

Да.
хватит форсить эту хуйню, эта картинка переполнена противоречиями, и делал её школьник:
как минимум алгтоп и алгеом не могут стоять ДО их подкатегорий, когомологии галуа проходят на втором курсе, а не на 666 и такой хуйни полно. На 666 можно поставить труды мочисуки и подобное (помниться тифарет когда-то перчислял, если найду выложу),
так что эта говнокартинка не более, чем рандомно расположенные рандомно выбранные области (более того, сам 7-классник, который её делал об этом писал, что по красоте звучания ставил)
444466
Комбинаторика будет в самом конце. Она самая сложная.
Доказал гипотезу Римана.
Кто гед и когда мне даст мой миллион далларов?
Ты всегда можешь его отсудить, если аноны спиздять, просто показав архив этого треда. Только пруфани, что ты это ты.
мимодаун
Блять, хотел курсивом

Тогда врываюсь со своим дерьмом.
Решение было чуть больше, но я обосрался когда переписывал степени и в итоге смог рассчитать заново только досюда.
Это я уже и вольфрамом посчитал.
Мне бы хоть дальнейшее решение посмотреть и понять как оно вообще решается.
Слыхал.
А хули тут решать? Обычна логика. Не надо ничего решать даже, все в итоге сводится к общему знаменателю, где будет n, а это стремится к бесконечности. Число деленное на бесконечность это 0. В уме решается.
Я даун-гуманитарий, который случайно попал на технарское направление и решил грызть гранит.
Разъясни, пожалуйста.
Я именно на этом моменте и понял что степени слил.
бамп
Если ты гребёшь бабло лопатой, то почему не купишь себе нормальную скатерть для стола?

И ещё.
Ну циферки рядом с буквами я понимаю уже, но вот сами буквы, что за k, r, e, n и т.д? то же самое что и a c b или у этих букв другие значения?
Чет я совсем тупой, спасиба
Загони все слагаемые в левом корне под один корень, а после умнож разность корней на их сумму и раздел на них.
Что у тебя вечно с мягкими знаками? Реформу 64-го года близко к сердцу принял?
Слоупок из прошлого треда таки нашел решение, если вдруг кому будет интересно.
>>392602
Я в глаза долбился и не видел, что после замены у меня получился под интегралом арктангенс, помноженный на аргумент. Используя стандартный ряд Маклорена для арктангенса, считаем результат как сумму интегралов членов ряда, деленных на х.
Благо ряд как раз сходится в пределах [0;1], к которым я перешел после замены.
Теперь второй вопрос. Как добиться точности до шестого знака? Мне придется считать 1к членов ряда, после преобразования эйлера - 31, мой препод сделал за 17, и не говорит, как. Что курить по теме?
Воу. Мне как раз посоветовали между делом посмотреть фильм "Человек, который познал бесконечность". Не знал, что препод так иронично намекает на решение моей курсовой. Спасибо большое.

Привет
каждый день по 2 гротендика
Твой шкаф в два раза больше моего.
Хуя ты. Всегда завидовал умению читать, лично я ни одного учебника полностью не прочитал, так хватал кусками из многих.

Какие из следующих систем функций являются функционально замкнутыми классами:
а) функции от одной переменной;
б) функции от двух переменных;
в) все функции алгебры логики;
г) линейные функции;
д) самодвойственные функции;
е) монотонные функции;
ж) монотонно убывающие функции;
з) функции, сохраняющие ноль;
и) функции, сохраняющие единицу;
к) функции, сохраняющие и нуль, и единицу;
л) функции, сохраняющие нуль, но не сохраняющие единицу?
Теорему Поста прошел уже?

>б) функции от двух переменных;
Будучи ещё 20-летним учеником Андрея Николаевича Колмогорова в Московском государственном университете, в 1957 году Арнольд показал, что любая непрерывная функция нескольких переменных может быть представлена в виде комбинации конечного числа функций от двух переменных, тем самым решив тринадцатую проблему Гильберта.
Лол. Время интересных фактов.
Фу блядь, какая быдлятина. Так и вижу толстые короткие желтые пальцы, грязь под ногтями и трехлетнюю одежду.



так он тоже, он просто их покупает и забывает
невозможно столько математики осиливать
без очень конкретной мотивации
На первом что кардинальность последователя произвольного элемента натуральных чисел Фон Нюмана больше нулевого множества.
На второтретьем что для х и y (снова-таки из Неймановских натуральных), хотя бы один из которых является подмножеством другого, их кардинальность либо равна, либо у одного больше, чем у другого. Очевидно, без использования свойств кардинальных чисел.
Кардинальность определяю как функцию на множествах, значения которой линейно упорядочены.

Не обращай внимание на выблядков-неосиляторов - это наш аналог омежек из /б, которые кукарекают про то как "снимать тян в клубе это мемас и нивазможно, ягарантирую".
дык мне итак насрать :)
Но уточню, что из того шкафа я действительно прорешал/прочитал не все; что-то уже поздно (пользы от школьных (пусть и олимпиадных) задачек особо не будет), некоторые вещи пока в планах, но в целом большая часть мною освоена. В частности все книги по топологии/функану из него прочитал... но у меня ещё 2 таких + жесткий диск с овердохуя книг, статей, даже лекций (почти все отсортированы непосильными трудами) - вот на это уйдет вся моя оставшаяся жизнь.
вы че пацаны, этой стори лет 10 наверное
Пиздец... Ты хоть понимаешь, что ты делаешь? Ты же задротом будешь, ни бабла, ни баб, ни хуя. Ты хоть девственности лишился уже? Хотя бы марихуану пробовал? А то совсем как хуй знает что выйдешь.
Поправка: доказать на правых двух пиксах надо полноту на Неймановских натуральных относительно включения, то есть левое выражение вверху левого пика.
А кардинальность - это множество классов эквиполлентности. О нем известны только транзитивность, антисимметричность и полнота относительно >=, а также то, что булеан всегда высококардинальнее своего аргумента.
во-первых я 196, и верхняя на уровне головы
во-вторых, этот >>393223 за меня ответил, но не суть
>>393220
>задротом будешь
уже
>бабло, бабы, секс, марихуана
это и есть цель жизни?
от бабок не отказался бы, но сам не бичую, все устраивает
>А то совсем как хуй знает что выйдешь
бессмысленный набор слов
> это и есть цель жизни?
С точки зрения эволюции - абсолютно. А от природы не убежишь - ебаться-то тянет. Вот и получается, что если ты не можешь достать себе ресурсы, пизду и марьиванну, то ты низкофункциональный образец и лох по жизни.
Он тебя тролит.
Ты все правильно делаешь.
Ему просто завидно. Он тупой и проецирует к тому же.
>С точки зрения эволюции - абсолютно.
Нет
>Вот и получается
Нет
>А от природы не убежишь - ебаться-то тянет
Нофап уже 3 года спускаю раз в 3 дня, и норм
>Вот и получается, что если ты не можешь достать себе ресурсы
Ресурсов достаточно
>пизду
если вся твоя жизнь строится вокруг желания запихивать стручок в дырки - это, блядь, повод задуматься о себе, ты тратишь время впустую, ебанный гедонист, моя же цель - развитие, и мне абсолютно поебать на вагины
>низкофункциональный образец и лох по жизни.
С точки зрения полоумных гедонистов - да
Вообщем, здесь с самого начала обсуждать было нечего. Разные философии, разные взгляды на мир; нравится ебать вагины - еби, мне насрать.
>196
>задрот
задроты заканчиваются где-то на уровне 182. выше я не видел. точной формулы не помню, но это и эмпирически можно вывести. руки длиннее, можно уебать почти любому, и не каждый до твоего фейса дотянется.
а ктож я тогда? если по всем параметрам/характеристикам, кроме роста, подхожу
особый вид задротов: долговязый хикка-тополог
мимохиккан взорвался, найс.
>>393227
> >С точки зрения эволюции - абсолютно.
> Нет
То есть наше стремление к удовольствию, в т.ч. от наркоты, ебли и признания - это от боженьки?
> >пизду
> если вся твоя жизнь строится вокруг желания запихивать стручок в дырки - это, блядь, повод задуматься о себе, ты тратишь время впустую, ебанный гедонист, моя же цель - развитие, и мне абсолютно поебать на вагины
Найс ад абсурдум. Вот только если бы тебе было ПОЕБАТЬ НА ВАГИНЫ, ты бы не дрочил каждые три дня на вагины.
Ты же понимаешь, что нельзя быть счастливым, если тратишь жизнь только на одну вещь? Только ебаться и упарываться в итоге надоест и будет какая-то пустота. Но при этом только дрочить матёху - поедешь нахуй, на стену залезешь от недоебина и нехватки человеческого контакта, а также банальной дофаминовой стимуляции.
Да и вообще. Одна жизнь дана, а он рационализирует свою неспособность достать то, во что задумано вставлять хуй вместо кулака.
А негатив фота Вербита выглядит охуенно.
Не трать время на ущерба, пусть себе хиккует - что с него взять
Проиграл с лютой проекции корзинки. Продолжай фейервек.
Блядь, какой же у меня багет! Какая-то омежка боится к тянке подойти, а потом в интернете пишет ТНН. Ух блядь как же у меня подорвало!
Совсем уже поехали от недоёба, лол.
А тебе никогда не хотелось прокрастинировать и забить на чтение/решение? Просто тоже хочу начать угорать по книгам, но проблемы с "заставить себя"
>То есть наше стремление к удовольствию, в т.ч. от наркоты, ебли и признания - это от боженьки?
нет, но оно отчасти иррелевантно с его же точки зрения, поясню: ты можешь всю жизнь кайфовать, или пол жизни работать, а потом кайфовать в пентикле, второй вариант, очевидно, предпочтительней. А у меня все ещё пизже: я как бы и работаю, и кайфую одновременно.
>Вот только если бы тебе было ПОЕБАТЬ НА ВАГИНЫ, ты бы не дрочил каждые три дня на вагины.
Да, но это не цель моей жизни. Мне фапа раз в три дня достаточно, и я не чувствую себя убогим, из-за того что не трахаюсь, мне просто похуй, в отличии от закомплексованных биопрбелмников, заполняющих двач.
>Ты же понимаешь, что нельзя быть счастливым, если тратишь жизнь только на одну вещь?
Нет, можно, к тому же математика крааааайне разнообразна; областей дохуя, не говоря уже о том, что одна топология может затянуть на всю жизнь. Пока меня все устраивает, захочу - сменю занятие, спокойно могу устроиться программистов за нехуевую зарплату (более того, уже работал).
>на стену залезешь от недоебина и нехватки человеческого контакта
На оба похуй, вот такой я человек, ни разу не было проблем ни с тем, ни с другим. Всё.
>>393230
взять дохуя статей, я пока учусь, но сомнений в том, что такими темпами стану продуктивным математиком нету.
>>393236
ВОУ-ВОУ-ВОУ, паренек, ты мои тексты-то не префразируй, я нигде не писал ТНН, я писал, что МНЕ это не нужно. Двачевские ТННщики - заместо баб играют в доту, я же занимаюсь математикой, вот она принципиальная разница, более того я не осуждаю людей, ебущих баб, моя позиция: "я читаю книги и развиваюсь, вы ебете баб и деградируете, окей, мне насрать, но лучше бы читали книги".
>>393237
с такими проблемами иди в /psy, там тебя пошлют делать эту вашу КПТ,
у меня прокрастинации, благо, не было с детства привык работать и пока рос лишь увеличивал нагрузку, к тому же моя работа - мое хобби, это все упрощает.
>первый абзац
всм, что работа по идее противоречит "кайфованию", но во втором варианте она лишь усиливает его, скажем так.
А ты алгебру нормально знаешь? Сможешь пояснить про сигнатуры гиперповерхности 2го порядка?
Анон, объясни пожалуйста, почему производная Фреше от композиции двух функций есть композиция их производных Фреше.
> Да, но это не цель моей жизни. Мне фапа раз в три дня достаточно
Про цель жизни никто и не говорил. Говорить, что фапа ДОСТАТОЧНО - это всё равно что говорить, что хлеба и воды достаточно. Можешь хоть с пеной у рта повторять, но того факта, что тебе будет не хватать витаминов и макроэлементов, это не отменит. Ебля химически и нейронно различается, даже с андроидом.
> Нет, можно
Сейчас ты споришь с Фейнманом, потому что это его слова были: нельзя заниматься чем-то одним всю жизнь, в т.ч. если это наука или математика. Его тоже биопроблемником закомплексованным назовешь?
> На оба похуй, вот такой я человек
Сознательно многим похуй, вот только твоему бессознательному нихуя не похуй и пока ты ведешь такой аскетический образ жизни, у тебя там нейронные цепи перестраиваются не очень хорошим образом.
> моя позиция: "я читаю книги и развиваюсь, вы ебете баб и деградируете, окей, мне насрать, но лучше бы читали книги".
Ты деградируешь аналогично, только в другой сфере. И при этом отрицаешь это. Хотя бы обычное быдлецо признает свою тупость и необразованность. Ты хуже них.
Он спорит с тобой. Ты не Фейнман, Фейнман помер. Ты говоришь своими словами. Не разводи демагогию.
Хочешь сказать, что НИЩИТАЕТСЯ МАМ НУ СКАЖИ ЕМУ ОН ЖЕ ЦИТИРУЕТ ТАК НЕ ЧЕСНО ПРАВДА ЖЕ? МААААМ?
Не вмешивайся, даун нецелованый.
Ты пытаешься позаимствовать авторитет Фейнмана, чтобы сделать свою позицию убедительнее. Твой-то собственный авторитет ничтожен, ты аноним на АИБ.
бляя так много разностортного говна накидал, ну попытаюсь быстро ответить, ибо уже спать ложусь
>Говорить, что фапа ДОСТАТОЧНО - это всё равно что
говорить что фапа достаточно. от нетраха проблем не бывает
>Сейчас ты споришь с Фейнманом
фейнман - физик, а не философ, и меня не ебёт, что он говорил, по твоей логике, чтобы он не выпизднул - все правда. уважают его только за научные заслуги , как и других учёных
ну и далее
>нейронные цепи перестраиваются не очень хорошим образом.
пффффффффф, нашелся тут мамкин нейробиолог, блядь, я могу хоть 3 года хикковать, хоть всю жизнь и нихуя мне не будет
>Ты деградируешь аналогично, только в другой сфере
В моем случае
>Ты деградируешь в сфере недеградирования
Окей, меня это устравиает.
Ну а ближе к теме: в сфере неебли баб и некурения марихуаны? В чем моя тупость? В том, что я не трачу время попусту? Что мне даст, если вместо чтения Шварца-Виттена-Грина я начну переодически всовывать и высовывать свой хрен из чьей-то дырки? Ты пока других альтернатив не предложил.
В целом, единственное твое обвинение было звучит так: "Многие считают, что ебать баб хорошо, да и от природы хочется, а ты не ебешь, значит хуесос
К тому же занимаешься одной только математикой, ну а нужно разнообразие, значит хуесос"
На оба твоих псевдоаргумента уже давал ответ, но повторю ещё раз:
>у людей так заведено
похуй
>природа и эволюция
развитие вот, что ближе к эволюции (а следовательно и природе), чем что либо
>нужно разнообразие
не-а, нахуя? Перельман для тебя авторитет? Так вот гипотезой Пуанка он занимался 9 лет. К тому же все математики занимаются также физикой и кодингом (и в обратную сторону), взглянув на мой шкаф на верхней полке ты можешь найти и биологию, и схемотехнику, и классику по ИИ, и даже психологию, я развиваюсь по всем фронтам, но концентрируюсь на матем, но даже если бы я занимался только матем, я бы не был хуже. Ты, видимо, просто не понимаешь ЗАЧЕМ вообще заниматься матем, для тебя это не область для открытий, а теорема Виета и задачи про треугольники, которые тебя заставляли делать в пром. масштабах в школе (и что, по всей видимости, не особо тебе нравилось и оставило пейративный отпечаток на твоей психике), вот из-за такого узколобого воззрения, ты и пишешь подобные высеры.
>>393245
Да и авторитет в целом здесь роли не играет, важно само высказывание,
ну а я на такие хуйни не попадаюсь, кстати читал Поварина недавно на почти что эту тему.
бляя так много разностортного говна накидал, ну попытаюсь быстро ответить, ибо уже спать ложусь
>Говорить, что фапа ДОСТАТОЧНО - это всё равно что
говорить что фапа достаточно. от нетраха проблем не бывает
>Сейчас ты споришь с Фейнманом
фейнман - физик, а не философ, и меня не ебёт, что он говорил, по твоей логике, чтобы он не выпизднул - все правда. уважают его только за научные заслуги , как и других учёных
ну и далее
>нейронные цепи перестраиваются не очень хорошим образом.
пффффффффф, нашелся тут мамкин нейробиолог, блядь, я могу хоть 3 года хикковать, хоть всю жизнь и нихуя мне не будет
>Ты деградируешь аналогично, только в другой сфере
В моем случае
>Ты деградируешь в сфере недеградирования
Окей, меня это устравиает.
Ну а ближе к теме: в сфере неебли баб и некурения марихуаны? В чем моя тупость? В том, что я не трачу время попусту? Что мне даст, если вместо чтения Шварца-Виттена-Грина я начну переодически всовывать и высовывать свой хрен из чьей-то дырки? Ты пока других альтернатив не предложил.
В целом, единственное твое обвинение было звучит так: "Многие считают, что ебать баб хорошо, да и от природы хочется, а ты не ебешь, значит хуесос
К тому же занимаешься одной только математикой, ну а нужно разнообразие, значит хуесос"
На оба твоих псевдоаргумента уже давал ответ, но повторю ещё раз:
>у людей так заведено
похуй
>природа и эволюция
развитие вот, что ближе к эволюции (а следовательно и природе), чем что либо
>нужно разнообразие
не-а, нахуя? Перельман для тебя авторитет? Так вот гипотезой Пуанка он занимался 9 лет. К тому же все математики занимаются также физикой и кодингом (и в обратную сторону), взглянув на мой шкаф на верхней полке ты можешь найти и биологию, и схемотехнику, и классику по ИИ, и даже психологию, я развиваюсь по всем фронтам, но концентрируюсь на матем, но даже если бы я занимался только матем, я бы не был хуже. Ты, видимо, просто не понимаешь ЗАЧЕМ вообще заниматься матем, для тебя это не область для открытий, а теорема Виета и задачи про треугольники, которые тебя заставляли делать в пром. масштабах в школе (и что, по всей видимости, не особо тебе нравилось и оставило пейративный отпечаток на твоей психике), вот из-за такого узколобого воззрения, ты и пишешь подобные высеры.
>>393245
Да и авторитет в целом здесь роли не играет, важно само высказывание,
ну а я на такие хуйни не попадаюсь, кстати читал Поварина недавно на почти что эту тему.
Муравью нельзя объяснить даже такого простого факта, что он муравей а здесь ситуацтя еще хуже
Организму и психике важна ебля и получение удовольствия в целом (не такого как от дрочки задач, а более прямого, как от шоколада, только гораздо сильнее). Ты самодурствуешь, пытаясь убедить себя в том, что то, что ты не можешь получить нинужно.
Ты уже дрочишь, чем и опровергается нинужность тян. Пизда это буквально в дохуя раз лучше дрочки и ты утверждаешь, что она не нужна, но дрочка нужна.
А развитие с точки зрения эволюции нахуй не въеблось. Конечно, лучше разиваться, чем не развиваться, но от отсутствия занятия жизни вроде матёши максимум будешь пустоту ощущать. От отсутствия удовольствия и блядей же - психика шататься начнет. И как бы ты не кукарекал "мне норм кудкудах!", уже десятилетия как установлено наукой, что есть серьезный вред психике и как следствие здоровью.
я спать пошел, завтра распишу, а вообще если ты читал колмогорва-фомина (а это классика, блядь, альтернативы нету), должен на изи ответить
Буду ждать. Спасибо авансом.
Хуем в твоем рту закончим.
просто я хочу закатиться в репетиторство.
у меня вообще-то уже есть законченный бакалавриат по мат. специальности.
но вот как решать всякую ебень типа тригонометрических неравенств я забыл, ибо кому это нахуй надо? только школьникам
охуенно. а можно фотку норм качества и фотки двух других шкафов? а то у некоторых книг названия не видно.
У Евклида - нет, а у Римана, Финслера, и Лобачевского и Пуанкаре - возможно, да.
Последний раз я её понимал на 3- на пером курсе, потом её было ещё меньше и я ничего не учил. В сейчас ехидные экзамены впереди а подготовительную работу я написал на 0
Потому что ничего не написал))))
Что мне делать аноны?
вскрыться и идти работать дворником. ленивые уёбища не нужны
Выделить время набросать план и целенаправленно работать над всем этим - рационально, а не эмоционально, пошагово и не отвлекаясь.
Теперь такой же план только для ленивых, и тех кто не может иногда даже чашку на кухню отнести перекладыая на потом
Просто собери в кучу всё то что тебе надо и всё, а то только ноешь тут ни по чём.
Пусть G - группа.
Требуется доказать, что произведение g1 g2 ... gn не зависит от расстановки скобок.
Док-во:
по индукции. база n=3 - верно (аксиома)
предположим, что верно для n = k,
докажем, что верно для n = k+1
(g1 g2 ... gk)gk+1 = ((g1 g2...gm)(gm+1...gk))gk+1
Пусть g1 g2...gm = a
gm+1...gk = b
Тогда (ab)g k+1 = a(b*g) в силу аксиомы
Верно?
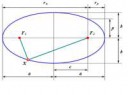
У меня есть круг.
Надо его "сплющить" в эллипс с одной заданноой полуосью. Как это сделать?
Я так понимаю нужно найти периметр круга и потом с ним и размерами полуоси искать вторую полуось, но как?
Видимо потому, что производная Фреше - это (эндо)функтор функторкатегории операторов из банахова пр-ва X в банахово пр-во Y?
p.s. я не разбирался в вариационном исчислении.
>>393318
Давай формулы для обеих, а то я что то не понял для которой точно.
Вроде для малой, но я не уверен.
>>393318 - энкукарекун
>Показывай там мне
Там 12 формул для каждой из полуосей.
>неверно, переформулировал
>я что то не понял
>я не уверен
>По сути - не знаю.
>Вроде
>карекун
>да?
Cформулируй для начала, правильно, чё тебе надо, конкретно...
ок, пок-пок
Да, тащи сюда, за-save'лю.
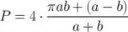
Выводи...
Хм. А как определяется этот функтор, как доказывается корректность определения? Как устанавливается связь с, собственно, дифференцируемыми отображениями?
>>393322
Ну давай посмотрим, как он действует на тождественный оператор... Получаем опять тождественный оператор. Значит с этим ок. (а ещё остаточный член - нулевой)
Осталось ответить на твой вопрос про композицию, лол.
Пусть F, G - операторы, допускающие композицию G o F. Тогда (G o F )(x+h) - (G o F )(x) =
G(F(x+h))-G(F(x))=
G(F(x) + A h + r_A(x,h)) -G(F(x)) =
G(F(x)) + B( A h + r_A(x,h)) + r_B(F(x), A h + r_A(x,h)) - G(F(x)) =
(B o A) h + ( B r_A(x,h) + r_B(F(x), A h + r_A(x,h)) )
где второе слагаемое - "о малое от линейного оператора"
Стало быть эндофунктор для функторкатегории дифференцируемых по Фреше операторов из б.п. Х в б.п. Y.
Искренне Ваш, н-петя
Наряду с функториалами иногда полезно рассматривать и кофунктпориалы, сопоставляющие группе ее фактор-группу.
Функторы же, вроде никаких "функториалов" нет... Есть факториал - который тоже вроде функтор из категории множеств в категорию групп, спопоставляющий множеству симметричную группу перестановок его элементов. Факторизация по нормальной группе - тоже вроде функтор, но тут я плохо себе представляю.
>второе слагаемое - "о малое от линейного оператора"
Вот в этом-то проблема. Почему оно o-малое?
Функториал тогда и только тогда является вербалом, когда он Н - замкнут.
Функториал g назовем предвербалом, если это копредради-кал и он согласован с подгруппами ( а не только с нормальными делителями, как это требуется в определении корадикала), gf тогда и только тогда предвербал, когда соответствующий gf есть предмногообразие. Из приводившихся раньше замечаний следует, что в каждой группе предвербал выделяет вполне характеристическую подгруппу.
Естественно выделить функториалы, сопоставляющие каждой группе ее вполне характеристическую подгруппу.
Систему всех функториалов можно рассматривать как некоторую алгебраическую систему, хотя она и не является множеством.
Такие дела.
Ох, ебать. Деанон по вороне. Схоронил пикчу. Мунин же на дваче сидел ещё в 2009.
может потому что действие линейного оператора не влияет на малость функции, меняются только константы...
Хотя если брать интеграл с переменным верхним предлом, то o(x^n) становится о(x^(n+1)).
Строго не скажу, скажу "очевидно", Может фишка в том, что малость-то от h... Расскажи если поймёшь
зачем они так. остальных ебланов не знаю, но зачем роме вещества. вроде математика и и так вставляет. или экспазим нужно реинфорсить веществами? он так долго не протянет, а жаль.
Я не могу аккуратно восстановить всю цепочку рассуждений. Во всех книжках авторы ссылаются на "очевидно".
если человек смотрит Линча и слушает Летова он мой друг априори

помогите пожалуйста решить пример из функционального анализа, имеется функциональная последовательность, и постоянная функция a(t)=1, всё это на пространстве непрерывных функций С[0,5]. Объясните пожалуйста, как найти супремум разности x(t)-a. Сначала находим производную по t и приравниваем её к нулю, у меня получилось 2 значения t, их надо подставить в функциональную последовательность, и также точки 0 и 5? При подстановке 0, то есть точки начала отрезка, у меня получается 0, а при 5, то есть точке конца отрезка, у меня получается выражение с n, которая считается постоянной. И как узнать, какое из данных 4 значений будет супремумом, если у нас остаётся фиксированное n, которое может принимать любое значение?
по t, n нужно считать фиксированным числом. И ещё вместо t нужно подставить в функциональны ряд 0 и 5 и значения t, найденные из производной, поэтому мне нужен супремум именно по t
Значит это заговор, очевидно же
джае не зматеил оишкби при прчонетии, ибо есть вот такая фитча, когда быстро читаешь (главное, чтобы первая и последняя совпадали)
это особенность лишь некоторых языков, в основном - потомков праиндоевропейского.
Предлагаю вам игру. Я колхозник и предлагаю вам соревнование в топологии. Я в ней не силен как и вы блядь. Мудаки.
Так вот
Вот список литературы
https://www.math.cornell.edu/~hatcher/Other/topologybooks.pdf
У меня нет времени ебаться с топологией я успешный человек
но
месяц даю вам и возвращаюсь сюда и обоссываю)
Так что вот епта
Если через месяц вы не будете этого знать я буду на вас ссать ))
Удачи, топологи.
Я дам вам доступ к книгам на английском естественно вам останется только их прочитать. С той секунды и пойдет отсчет)
Вот и все.
Удачи.
Доказательство подробное и лёгкое, поймёт любой, знакомый с комплексным анализом.
хатчер пригоден лишь для того, чтобы отбиваться им от гопников, а как учебник по топологии иррелевантен, ибо есть Фукс-Фоменко (которого нужно читать вместе с http://ru.bookzz.org/book/933098/e29ada или Спаньером)
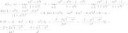
но мне нужно найти производную по t и приравнять её к нулю, и из этого равенства выразить t, получается 2 значения t; и вот дальше я не понимаю как найти этот супремум; мне не понятно, что у тебя в третьей строке и как ты находишь супремум, и t принадлежит не всему пространству R а отрезке [0,5]
Вербит одобрает твой пост.
Ну напряги хоть немного мозги. Ну ты же видишь, что дискриминант твой меньше нуля для n>1, нахуя ты корни какие-то ищешь? Нет там действительный корней. Это значит, что твое квадратное уравнение в данном случае положительно для всех t, а раз оно положительно всегда, то и производная твоя положительна для всех t и всех n. Это значит, что функция строго возрастает при всех n на (в данном случае) отрезке по t от 0 до 5. Тогда самое большое значение твоя функция примет в точке t=5 из-за возрастания. Подставляешь в свою разность t=5 и получаешь свой супремум, который здесь к тому же и максимум.

хорошо, супремум найден, теперь, чтобы проверить, сходится ли мой функциональный ряд к функции a(t)=1, нужно посмотреть, к чему стремится супремум при n->∞? И если супремум стремится к нулю, как в данном случае, то функция а(t)=1 является пределом данной функциональной последовательности, то есть функциональный ряд сходится к a(t)? Мои рассуждения верны?
скажите можно ли быть "одновременно" математиком "альфой" и sissy cocksucker bitch? я люблю математику со школы и хочу ей посвятить всю жизнь, при этом не упуская прекрасного пола как фейнман (ну вы понимаете, хех). НО у меня еще есть такое "пристрастие" кк sissification и все что с этим идет, как говорится....

Конечно можно, только с такими пристрастиями тебя примут в констурктивную математику.
Ну за геометрический смысл я понимаю, но я все равно не понимаю почему число именно такое - 3,14... Почему не 3,15... или 3,13...?
На самом деле я тоже хотел бы это узнать, где-то было тема на dxdy, но там ничего особо не сказали.
большое спасибо)
Брауэр ещё та cocksucker bitch.
Сколько аффтар получил за доказательство на третьей пикче?
Ну смотри, сигнатура большой кв. формы 3, ранг большой 1, сигнатура малой 3, ранг тоже 1. Т.е. действительно конус. Можно сделать замену переменных, чтобы все свелось к $x^2 + y^2 - z^2 = 0$, перейти в сферические. Угол $\theta$ будет равен углу раствора конуса.
Филдсовскую премию
Серьезно? или это щутка в стиле "а в двоичной будет 10101110011001001011011101111110100010001100100100100111010110 азаза)))"?
В другой системе счисления число пи будет, другое. Но его ответ про системы счисление не объясняет почему в десятичной число равно именно 3.1415... а не 6.71233243... По существу он ничего не скзал.
Вообще, число-то одинаковое в любой системе счисления, а вот его представление будет отличатся. 2 (в десятичной) и 10 (в двоичной) это ведь одно и то же.
Если честно, не ведет. Я гуманитарий. Если ты знаешь ответ, можешь написать, пожалуйста?
Пи - это отношение длины окружности к длине её диаметра, т.е. число, определяемое как дробь, в числителе и знаменателе которой стоят некоторые интегралы. К этому числу сходятся некоторые ряды. Записывая предел какого-нибудь из них в десятичной системе, получаешь пи.
мимошёл
Да, это я понимаю. Я даже эксперименты проводил с ниткой и окружностями, как школьник. Но я не догоняю почему зависимость именно такая.
Как я понимаю: пи это зависимость длинны окружности от диаметра.
Рассмотрим окружность, вписанную в квадрат со стороной 1. Как мы можем вычислить длину окружности? Хоть приблизительно. Она больше диаметра, это очевидно. Но она не может превысить периметр квадрата, т.е. не больше 4. Если мы мысленно начнем сгибать верхнюю и нижнюю стороны квадрата, то они не опишут круг полностью, т.е. двух сторон не достаточно. Следовательно, наше число {2;4}. А вот дальше самое интересное начинается.
Запиши уравнение окружности диаметра 1.
Запиши интеграл, выражающий длину окружности.
Возьми его.

Русификатор edishon.
Я все же хотел спросить про смысл именно плюса. Неважно где, допустим у дисперсии.
Это просто все отрицательные значения учитываются как ноль?
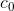
подскажите пожалуйста, что это за пространство c маленькое c нижним символом 0, и какова его метрика
нет, это не то пространство, пространство непрерывных функций это большая буква Цэ, а я спрашиваю про маленькую букву цэ с нижним индексом ноль
Бесконечно малые числовые последовательности. Метрика, по-моему, супремум модуля.
Бамп
супремум модуля чего? Суммы числовой последовательности? Напиши пожалуйста формулу метрики
Супремум модуля разности.
Есть две бесконечные последовательности x, y. Метрика: ρ(x, y) = sup|x_k − y_k|, где k ∈ ℕ.
Я - не тот, с кем ты спорил, но обоснуй, пожалуйста.
> Организму и психике важна ебля и получение удовольствия в целом
Докажи, пожалуйста. Иначе какие последствия?
> (не такого как от дрочки задач, а более прямого, как от шоколада, только гораздо сильнее)
Докажи, пожалуйста. У меня иногда бывает такой нахлыв от интересного чтива, что я не могу сдерживаться, начинаю задыхаться и т.п. Ебля рядом не стояла, шоколад и тем паче.
> пытаясь убедить себя в том, что то, что ты не можешь получить нинужно
Думаю, он имел ввиду то, что оно не является обязательным. И, хотя, ебля для него была бы предпочтительнее дрочки, он (как и я, в общем-то), не готов платить за неё такую цену. Банально сходить куда-то с какой-то тёлкой - это проебать день (либо половину). Для меня это довольно много. Я чувствую себя несчастным из-за этого.
> Ты уже дрочишь, чем и опровергается нинужность тян
Пфф
> Пизда это буквально в дохуя раз лучше дрочки
Пфф

то есть у этого пространства бесконечно малых числовых последовательностей такая же метрика как и у пространства непрерывных функций? Если у меня например есть две числовые последовательности x c нижним индексом n и а, все члены которой нули,то расстоянием будет супремум моей числовой последовательности x c нижним индексом n? В моей последовательности под нижними скобками должны быть n, я не знаю как их поставить
>то есть у этого пространства бесконечно малых числовых последовательностей такая же метрика как и у пространства непрерывных функций?
Вообще говоря, нет, но идейно то же самое.
>расстоянием будет супремум моей числовой последовательности x c нижним индексом n?
Не уверен, что так можно писать. У тебя на пикче x_n — это последовательность, поэтому запись sup|x_n| на самом деле должна означать sup|x_n_k|, где k ∈ ℕ.
У нас есть числовая последовательность x. Её элементы индексируются натуральными числами, поэтому запись x_k означает конкретное число. Если у тебя x_n — числовая последовательность, то элемент этой последовательности, или число, будет обозначаться x_n_k. Короче, в супремуме должны быть числа (элементы последовательности), а не сама последовательность.
то есть супремумом будет сумма всех элементов, что означает в данном случае сумму 2n ненулевых элементов последовательности x_n?
Супремум — это верхняя грань. Последовательность состоит из чисел. Не знаю, где ты там сумму нашёл. Надеюсь, ты можешь отличить последовательность последовательностей от числовой последовательности.
Ещё раз. Даны две последовательности: x = {x_k}, y = {y_k}, тогда ρ(x, y) = sup|x_k − y_k|, везде k ∈ ℕ. В супремуме — разность чисел, которые парно берутся из обоих последовательностей. В твоём примере (немного странном) супремум x_n, при условии, что n принадлежит натуральным числам, равен 1 / n.
>>393801
Парни, вы умны походу. Ответьте на один вопрос.
Есть две записи допустим. E(X-EX) и E(X-EX)+ (индекс внизу).
Что значит это плюс? Учитываются только положительные значения? Как это влияет? Свойства остаются все те же самые ведь?
Спасибо.
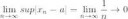
ясно, а чтобы проверить, сходится ли x_n к a, нужно перейти к пределу супремума при n->∞? и если он стремится к нулю, то x_n сходится к a в пространстве бесконечно малых числовых последовательностей?
> Докажи, пожалуйста. Иначе какие последствия?
Школьная анатомия в помощь
> У меня иногда бывает такой нахлыв от интересного чтива, что я не могу сдерживаться, начинаю задыхаться и т.п.
Обратись к врачу.
> пф
Хуиф.
там может быть +, может - а может ничего не быть. + означает приближение справа, - приближение слева, если нет ни того ни другого то с любой стороны
баян
Зачем?
Ну и хуй с ним.

Если ты правильно выписал условия, то должно быть что-то типа такого.
Они и не выливалсь из неё.
Какая разница? Бурбаки с того света написал недавно книгу по алгебраической топологии, и этот напишет. Если захочет.

Колмогоров-Фомин. Доказательство оставим читателю в качестве упражнения.
))))00
Есть ли хоть 1 человек, изучивший алгебру по Ленгу? Очень тяжело читается, если бы я не знал того, что там написано, то ничего бы не понял.
Да, есть.
Да нормальная книга это. Большинство учебников по алгебре (dummit-foote, axler, aluffi, кострикин-манин, артин младший, винберг) это разбавленный водой пересказ каких-то частей Ленга. Лучше сразу учить по нему.
Но Pierre Grillet еще лучше.
конечно же НЕТ блядь. Это как и Анализ Шварца, учебник для того, чтобы освежить и скомпоновать свои знания. Если ты не знаешь ничего ни об алгебре, ни об анализе, Лэнг даст больше вопросов, чем ответов.
я знаю, что не пожалею, но у меня и так много книг, которые я читаю. мне нужен более компактный и информативный вариант, изложенный как можно понятнее.
спасибо
Бамп вопросу.
Неужели я настолько топологизировался что забыл сколько будет 2+2?
Потому что этот минус воспринимается как минус для 3^4, т.е. отрицательный РЕЗУЛЬТАТ. Не забывай школьные азы, братуха е жи.
Я подозревал.
Но так получается что уравнения в духе 900-4^2 я всю жизнь решал неправильно, ведь возводил в степень -4
Получается так. Хотя анон, который полгода дрочил на французского короля, всё-таки круче.
Уравнения в духе 900-4^2 решается так: сначала 4^2, потом 900-(4^2). Даже в школе -3^4 стараются выделять как (-3)^4 или ...-(3^4) там где нужно. Просто отдохни
900=30^2, далее (30+4)(30-4), далее 900+120-120-16
Я не помню чтобы выделяли.
Ты поставил минус спереди, получаеться -(3^4)=-81 Взятие степени выполняется до минуса

Например, вот Вики. Что это за пары? Откуда нули, если в двух множествах A0 и A1 нулей нет?
Это объединение всех не пересекающихся подмножеств двух (или больше) множеств, правильно я понимаю?
Ну, а что это за ноль тогда в парах на скрине? Откуда он взялся? Или таких пересечений бесконечность?
Бамп.
Ну так ты чуть ниже посмотри. Там всё написано. У тебя есть семейство множеств A_i, которое индексируется другим множеством I. Например, A_0 = {1, 2, 3}, A_1 = {1, 2}. A_0 индексируется нулём, поэтому множество A_0 (со звёздочкой) = {(1, 0), (2, 0), (3, 0)}. A_1 индексируется однёркой, поэтому A_1 (со звёздочкой) = {(1, 1), (2, 1)}. Можно, например, добавить ещё одно множество A_2 = {2, 3, 4}. Тогда A_2 (со звёздочкой) = {(2, 2), (3, 2), (4, 2)}. Короче, второе число в паре — это индекс множества A.
Очень просто. Если бы S_5 была бы разрешима, то и A_5 была бы разрешима, а это не так. Докажи, что А_5 не разрешимая группа.
У Шварца 80% материала при первом чтении пройдет вникуда. Зорич жует по целой страницы то, что у Шварца обозначено опасным поворотом Z.
Спасибо Антош, только два вопроса:
1) В конце для х надо матрицу полученную от умножения надо будет сделать обратной, да ?
2) Для у надо В обратную умножить на (из С2 - вычесть это (А2С1А1) и потом результат сделать обратным), right ?
Ой, точнее A1 и C1.
Ага. У неё всего 2 норм. подгруппы(очевидно тривиальные). Т.к. K(A_5) - нормальная, и A_5 не коммутативная, то K(A_5) = A_5
Желательно на английском. Их много, не знаю, что выбрать.
Спасибо.
>Бурбаки
Смеёшься, что ли?
>Ленг
Абсолютно нечитабелен.
>Алуфи
То же + не годится для первого обучения. Это скорее обзор современной алгебры.
Ван дер Варден!
>>394080
>То же + не годится для первого обучения. Это скорее обзор современной алгебры.
Какой-то бред, ты вообще открывал его? Алуффи отличный учебник для новичков с правильным подходом.
> не годится для первого обучения
Листочки для матшкольников. На mccme можно их найти, хотя на русском.

Тогда объясни, что он здесь имеет в виду. Я так и не понял определения. Почему его нельзя дать уже в полном виде тогда, когда весь необходимый материал будет изложен?
Несвязное объединение, не? Берем два множества {a,b,c} и {a,b}. Обычное объединение будет очевидно {a,b,c}. А несвязное {a,b,c,a,b}. Он разъясняет, что грубо говоря, мы наделяем множества тем, что даже имея равным элементами, они не пересекутся, т.е., например, дырявим ложку элементов из второго множества.
То есть, при несвязном объединении неважно, как изменить элементы множества, чтобы гарантированно сделать их отличными от множества другого - можно, например, первое множество A × {0}, второе множество B × {1}, а затем объединить, так и A × {1337} и B × {666} и объединение получившегося всё равно будет несвязным? Путь, с которым можно сделать "копии", совсем не важен?
ну собственно A x {0} U B x {1} сойдет за определение для случая из двух множеств. Главное, чтобы было ясно, из какого множества тот или иной элемент.
Так я этого и не понимаю. Чем числа 0 и 1 такие особенные от 666 и 1337? Почему с первыми связать элементы можно, а со вторыми - нет?
Я тебя неверно понял, мне показалось, что ты подразумеваешь множество {1,3,3,7}. А так, ничем.
ty.
Вообще-то дизъюнктное объединение вводится не для произвольных множеств, а для индексированного семейства. Т.е. множество индексов уже сразу дано.
Просто дальше замечают, что всякое семейство множеств можно считать индексированным. Например, самим собой.
по k.
пишут:
f(s) = a_0 s^0 + a_1 s^1 + ...
что можно записать так, если s != 0, что бы избежать 0^0:
f(s) = a_0 + a_1 s^1 + ...
об условии s != 0 забывают и пишут: f(0) = a_0
что я упустил?
понял.
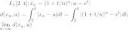
помогите пожалуйста решить пример из функционального анализа, имеется пространство L_1[2,4], последовательность x_n, и функция a, нужно определить, сходится ли последовательность функций x_n к функции а.
У меня правильно выписана метрика этого пространства? Мне нужно вычислить значение этого интеграла? А после того как интеграл будет вычислен, нужно перейти к пределу при n стремящемуся к бесконечности? Помогите пожалуйста вычислить значение этого интеграла
АНОНЫ срочн. ответьте пож на вопрос, если мы к кольцу, например к Z добавляем x и получаем кольцо многочленов Z[x], то x^(-1).ну т.е. обратный к x, не добавляется, я правильно понимаю?
Да. Правильно.
Да, верно. Но может случиться так, что в кольце уже есть x^(-1)[например сначала к Z добавили x, а потом и x^(-1)]
Просто гляньте на посты этого аутиста, особенно доставило это
Вот. Ещё одна типичная ситуация.
На Филдсовскую премию номинировали Бхаргаву.
http://www.mathunion.org/general/prizes/2014/
Почему его упомянул. Пишет работу из той же области, что и я.
Можно посмотреть работы тут.
http://arxiv.org/pdf/1006.1002v2.pdf
http://arxiv.org/pdf/1007.0052v1.pdf
Можно всё это перечитать. Нет ни одной формулы хоть мало мальски простого уравнения!
Это же надо иметь какую наглость.
Он не может ни одну формулу вывести и спокойно arxive.org размешает статью.
Я формулы не могу нигде разместить.
Он значит пишет, что так только можно решить - фактически отрицает существование формул.
Но они же есть.
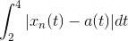
>У меня правильно выписана метрика этого пространства?
Да, но лучше немного поправить. Пик.
>Мне нужно вычислить значение этого интеграла?
Да.
>нужно перейти к пределу при n стремящемуся к бесконечности?
Да.
>Помогите пожалуйста вычислить значение этого интеграла
wolframalpha.com
http://www.artofproblemsolving.com/community/c3046
Ты только глань, с 14-го года блог ведёт, куда свои формулки постит, ярый фанатик, видимо.
спасибо за ответы
Это всем известный математический юродивый. Отмечен во всех перечнях научных фриков. Сорок лет, ума нет.
Что не так с калькулусом? Почем математики упорно хотят все науки перевести на теорию множеств?
Что не так со схоластикой? Почем физики упорно хотят всю натурфилософию перевести на исчисление бесконечно-малых?
Мы в Кембридже тоже негодуем, ведь недавно мой преподаватель привёз совершенно уникального преподавателя из Индии, который сулит открыть новую веху в математику!
Только не забудьте обучить индуса пользоваться одеялом, а то он зиму не переживёт.
Просто проигрываю с его постов. Хотя стить похоже на школьника-специалиста по теории множеств-каколда.
Так аноны, еще один вопрос, у мя завтра колока и нужно б узнать как доказывать квадратичный закон взаимности, самое простенькое доказательство. без регистрации и смс

помогите пожалуйста, вот мой интеграл посчитан, но вольфрам пишет, что моё n может быть или больше -2 или меньше -4 или не быть действительным числом. Как в этом случает перейти к пределу при n->∞?
И что тебя смущает? Просто выпадает отрезок [-4; -2]. Он тебе и не нужен. Предел нормально должен посчитаться.
Ты неправильно написал свой интеграл. У тебя там модуль должен быть, а если хочешь раскрыть модуль, то раскрывается он с минусом, потому что e^t - это супремум соответствующего ряда. Вообще эта сходимость автоматически следует из теоремы о мажорируемой сходимости интеграла Лебега, но тебе скорее всего о ней неизвестно, так что считай свой интеграл, только модуль раскрой правильно.
Что тебе не понятно-то?
УРА СПАСИБО ТОМУ АНОНЫ КОТОРЫЙ КУПИЛ ПАССКОД И ПОШЕЛ НА КОВЕР К АБУ!
Обоснуй.
Тред для новичков перекатывается в /math.
Обычный мат-тред, остаётся в /sci и превращается в тред математики для не математиков, ну или филиал /math в /sci.
Перекатываемся =======> https://2ch.hk/math/res/200.html (
Просто нажми раз в жизни на "скрыть" и мастер умножения с петухами тебя не побеспокоят. Вкатись в анализ-тред и бери интегралы, вкатись в алгебра-тред и предложи интересные задачи, которые я или другие аноны затем решат. Помоги в прикрепленной треде анонам с университетским вопросами. В конце концов, создай свой ебучий тред любой математической или околоматематической направленности и хоть в топологическое пространство там ебись сквозь потоки Риччи.
Но ты просто ноешь, как энурезный дед с dxdy. Там тебе и место.
/math – либеральная доска, не для дедов, дрочащих на значки и идеологическую чистоту, как при совке.
>энурезный дед с dxdy.
А я рад, что кому-то понравилось моё определение дедов с dxdy и он его использует.
-Мимо проходил
освой замену переменный

Какая-то разновидность водовки.
Ага


Z, B, C элементы.
A_1 = Z, A_2 =B, A_3 = C
1,2,3 индекс, i.
можно же занумеровать и так:
A_1 = C, A_2 =B, A_3 = A
кажется понял. {A_i} - последовательность. любых, т.е. можно переставить как угодно. {A_iN} - последовательность последовательностей размера 1, 2, ..., N.
Мне предлагали стать политиком.

@
ВСПОМИНАЕШЬ, ЧТО НА ДВАЧЕ ЕСТЬ РАЗДЕЛ НАУКА, ЗАХОДИШЬ В МАТ ТРЕД, ЧТОБЫ ПОБЕСЕДОВАТЬ С КОЛЛЕГАМИ О МИРСКОМ
@
ТРЕД ПОЛОН ЗАДАЧ ИЗ ГИА, ЕГЭ, И ДОМАШЕК ДЛЯ ПЕРВОКУРОВ ШАРАГ
А ты попробуй поусваивать и посмотри, как оно усваивается в сравнении с другими.
А вообще по случайному стечению обстоятельств слушал сейчас одного профессора, который рассказывал, что лично видел челвоека, у которого не было лобной доли слева с рождения, при этом он вёл себя, как совершенно здоровый человек, у него не было никаких отклонений, закончил школу, университет и работал. Только вот потом попал в аварию, и благодаря этой аварии медики то и обнаружили такую вот хуиту.
Всё индивидуально, зависит от масштабов, локализации и времени.
Это ты ещё в раздел /math не заходил, там филиал /poраши.
Есть какие-то быстрые методы набросать фазовый портрет системы от руки кроме линеаризации?

Сап, аутист снова выходит на связь.
Я чет начал смотреть улучшения сходимости, метод Куммера, и поймал себя на мысли, что не понимаю одной мелкой вещи. А именно - пикрилейтед. Сорян, если уже заебал.
Вторая строчка с конца неправильная; если проинтегрировать ряд почленно, то в знаменателях будут квадраты. Например, \int_0^1 x^2/3 dx=1/9.
Эта https://www.amazon.com/Basic-Mathematics-Serge-Lang/dp/0387967877/ref=pd_sim_14_5?_encoding=UTF8&pd_rd_i=0387967877&pd_rd_r=CH4SZWSW2ZVTCC5CVM10&pd_rd_w=c6Oye&pd_rd_wg=ceM9e&psc=1&refRID=CH4SZWSW2ZVTCC5CVM10
или эта
https://www.amazon.com/Algebra-Israel-M-Gelfand/dp/0817636773/ref=mt_paperback?_encoding=UTF8&me=
Он не для школ. Там всё серьёзно.
Господи, это то, что я искал! Начала Эвклида я прочитал на одном дыхании, а оказывается есть и не только они. Может еще что-то?
Что-то такое, дабы систематизировалось в мозге и понять, как оно связано. Будто из того, лаконично выходит это. Нужно еще некое ощущение открывателя, то есть почти учебник, но вроде Начала Эвклида. Ну и дичь я написал, прости
Курант Что такое математика.

Вроде на стаке поясняли, но линалом. А тут без линала должна решаться задача, так что нахуй то говнорешение.
Альзо как доказать биноманальную формулу ньютана индукцией без всякой комбинаторики?
>Альзо как доказать биноманальную формулу ньютана индукцией без всякой комбинаторики?
На самом деле, это сложный вопрос, поскольку в биноминальной формуле дохуя комбинаторных свойств.
Но ты можешь попробывать, вывести её из свойст Гамма-функции.
> вывести её из свойст Гамма-функции.
Охуительная история блядь. Я тебе говорю, что у меня вступление в мотан, а он мне про гамма-функцию рассказывает.
Как я могу использовать матан который идет ПОСЛЕ задачи, а не до? Ты понимаешь, что ты даун?
Еблан, позорный хуеплёт, ты задал определёный вопрос, я ответил на него, можешь ты или нет, мне поебать, а сейчас завали ту дырку, куда тебя ебут и который ты обычно ешь.
Мать твоя пусть сосёт.
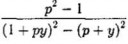
ой то есть ответ есть, но самого решения нет. я хз что делать, и так и так в тупик прихожу......
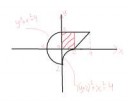
Я разобрал все, кроме одного - КАК МНЕ ОПИСАТЬ ЕБАНЫЙ КВАДРАТ через интегралы? У меня просто когнитивный диссонанс от всех размышлений, просто намертво встал.
Неужели как 0~2 dx 0~2 dy, это слишком банально выглядит для меня.
Мне нахуй площадь не сдалась. Это некая абстрактная фигура, которую мне нужно по правилам обхода описать.
Вот левая четверть сферы описана как -2~0 dx 0~sqrt(4-(x^2)) f(x;y) dy
А на квадрате почему-то так тупо заступорился.
Странно, что в списках книг по анализу нет Шилова (на которого дрочат на Западе), который представлен 6(8)-ью книгами вполне энтри-левела. Вместо Тао, так сказать.
А также Решетняка, который вроде бы как один из самых модерновых курсов, сейчас представленных на русскоязычном рынке.
>А также Решетняка
Скачал его ещё давно, увидел год выпуска и то, что курс излагает современный анализ. Хотел спросить у анонов, как он в качестве альтернативы Зоричу, но потом забы про него. Что ты о нём скажешь?
>Что ты о нём скажешь?
Я сам о нем сегодня вспомнил. Но о нем хорошие отзывы в сети. Говорят, что он доказывает абсолютно все, при этом очень подробно.
Квадрат? В полярных? Лол
Пратусевичь, там хорошее оформление.

ОБОЖАЮ ТЕБЯ, МОЙ СЛАДКИЙ, ПАЦАНЫ ВСЕ ПИЗДУЕМ НА НОВУЮ, >>392615 (OP) ОП-КУН, ПИЗДУЙ НА НОВУЮ!
http://golibgen.io/view.php?id=525872
по этой серии учился фейман
Каким математическим законом можно описать явление, например что при каждом последующем прохождении теста на IQ твой коэффициент интеллекта будет повышаться?
Я в математике ноль, но нагуглил что-то про экспоненциальный закон. Не бейте. Я сам не уверен, поэтому к вам и пришёл.
если ты найдёшь такой закон который бы однозначно бы моделировал/предсказывал обучаемость (на любом материале, хоть на икю тесте) учитывая всю ту бездну вариативности, что сопутствует процессу обучения, как во вне так и внутри каждого условного школьника - то это будет мега-прорыв в когнитивистике и нобелевка.
А так ты можешь просто делать наблюдения, что вот дескать у тебя тренд, n=1488, p=0.000001, три звезды и т.д.
Как называется методика, чтобы найти соответствия между числами и расположить их в иерархию?
Попробуй расписать разложение определителя по доп минорам, может поможет. Ну или по индукции для размера матрицы
Индукцией хорошая идея, подумаю.
Я не пойму вот что - откуда там в принципе может возникнуть эта "дзета". Т.е. как бы мы ни раскладывали определитель - он все-равно будет суммой произведений x1...xn с какими-то степенями. Но как из этих произведений произвольных комплексных чисел может появиться примитивный корень - вот что не понятно.
Ты ждёшь, что он возникнет. Не жди, доказывай по индукции стандартным алгоритмом. Философским анализом этой формулы и попытками объяснить её займёшься потом.
>>395374
Удачи с переходом. При попытке ебошить стандартную индукцию у тебя количество переменных и размер матрицы перестанут быть равны.
А вот стандартная философия помогает. Слева и справа однородные многочлены степени n над комплексными числами. Коэффициент при {x_0}^n совпадает. Так что чтобы доказать равенство многочленов достаточно доказать, что множество нулей многочлена слева содержит множество нулей многочлена справа. А это очевидно (справа написана линейная зависимость столбцов).
Да, с индукцией получился тупик. Но к сожалению твое объяснение не понял т.к. главу про многочлены еще не читал. Как ни странно в учебнике Кострикина она идет как раз после этой задачи.
>справа написана линейная зависимость столбцов).
Только вот этот момент объясни. Ты имел ввиду линейнкая комбинация? Но как это может быть, ведь во-первых тогда это должен быть столбец (а это число), а во-вторых коэффициенты при всех x_k должны быть одинаковы, а они разные.
Кроме последней строчки
хватить пиарить филиал b
Телевизор пересмотрел? Из всего пояснения только модули и японцев запомнил?
1/36 же?
ПО 3ЕМ СТОЛБЦАМ?
В гугле нихуя, в учебнике нихуя
Потому что проебал все полимеры и может ошибаться.
1. Ильин, Садовничий "Математический анализ"
Тому, кто хотел бы, чтобы у Фихтенгольца было меньше слов.
2. Что скажите о книге Треногина "Функциональный анализ"?
Мне она понравилась и я бы порекомендовал, но это была единственная книга по функану в универе. Потому что препод был его учеником.
Посмотри какую-нибудь популярную по теории Галуа. Вся эта нечисть вылезла из попыток решения алгебраических уравнений.
Ну есть Кольман "предмет и метод современной математики", там про группы, множества очень всё понятно разжёвано http://rgho.st/8PpPhs2qC.
В "математика. утрата определённости" хорошо показано, как люди сначала думали, что всю математику можно основать на предельно ясных самоочевидных представлениях, как в аксиомах Евклида, затем в попытках этого обоснования и разрешения противоречий стали обмазываться абстрактной хуитой, сначала нехотя и стесняясь, а потом уж без всякого стыда, и тут заверте. Хотя там, в основном, про теорию множеств, но и про отделение алгебры от арифметической основы тоже есть.
Спасибо.
Он доказывал, что 1x7 не равно 7x1 т.к.
1x7 = 1x1x1x1x1x1x1 = 1
https://www.youtube.com/watch?v=j8l0Eh6ctls 10:35
что это?
>>395608
А так что он толстейший тролер.
Умножение это сокращенная запись суммирования одинаковых чисел определенное число раз. А как ты ни сумируй семь единиц, ты в итоге всегда получишь семь единиц.
ну справедливости ради: 1*a=a это по определению умножения, а возможность определить это для всех N доказывается по индукции.
а ты точно даун?
x > e^x ?
В 0 e^x>x, затем берем производную с двух сторон, у e^x она больше => она растет быстрее. Все
производная = скорость роста функции в точке
это не значит, что где-нибудь в ебенях одна функция не сможет пересечь другую
или я загоняюсь? там жи экспонента и она очевидно растет
Боюсь, что препод скажет, что я еблан и это не очевидно
Строго гря, тогда нужно еще доказать, что exp(x) больше 1. Проще, видимо взять ряд Тейлора для экспоненты, вычесть х, и остаток будет положительным.
эт слишком строго
Раз у exp(x)-x производная положительна, значит эта функция растет, а так она равна 1 в х=0. отсюда оно и следует.
Ну это очевидно, же, что она больше 1
Это обычная вода, чтоб цензура пропустила, кого ебёт? Всё равно что фильмы про вов и гражданку смотреть, фильтруя пропагандонство. Тем более, что в сабже этого и нет почти
Геометрически, пи это интеграл от функции типа корень(1- x^2 ), но пи всплывает и когда начинаешь интегрировать функции без корней типа 1/(1+x^2). Геометрически интерпретировать анализ конечно можно, но это как удалять гланды через жопу – долго, больно и муторно. Насчет геометрического доказательства пи квадрат на шесть – я о таком не слышал. Обычно, комплексная переменная или ряд Фурье.
Позже скину тебе пару книжек.
http://www.math.chalmers.se/~wastlund/Cosmic.pdf
Так и знал, что будут фигурировать треугольник, круг и обратная теорема пифагора.
На каком уровне тебе нужны дифуры? Если на компьютере считать, то производные и интегралы. Немного более продвинуто, еще функция комплексного переменного. Если в частных производных, там еще могут быть нитегральные уравнения, обобщенные функии, теоремы типа Стокса, Гильбертовы пространства. И да, линейная алгебра нужна по минимуму - собственные вектора и значения.
Если легкое, то хуйня - было бы легкое, уже давно бы нашли. В архиве сотня доказательств гипотезы Римана висит, полагаю. Повесь где угодно - проиритет будет. Но наверняка он тебе нахер не понадобится.
>>396017
http://math.stackexchange.com/questions/1425240/geometrical-representation-of-square-of-pi
http://mathart.livejournal.com/24013.html
Ещё эту еботу нашёл. Я просто считаю всем похуй, что там, где это п всплывает, связь с окружностью должна быть, и умение подобные связи находить, когда какая-то постоянная внезапно всплывает не в своей теме, есть самый цимес математики для меня. Хотя, может, серьёзные матаны этим в 15-20лет переболели.
>где это п всплывает, связь с окружностью должна быть
Всё проще. Пи всплывает там, где связь с тригонометрическими функциями. Твой ряд связан с синусом.

Анон, о мудрый анон ! мне нужен твой совет.
Я гуманитароблядок, но хочу научится думать логически и рационально. Стоит ли мне начать заниматься таким предметом как Математика, либо же отдать свое предпочтение Шахматам ?
Что эффективней и что даст больше профиту ?
>я хочу научится фехтовать. Стоит ли мне начать дудеть в дудку, либо же начать стучать в барабан?
Хочешь научиться думать - учись, блджад, думать. Что ты качаешь, то и прокачивается. Начнёшь играть в шахматы - научишься играть в шахматы и всё.
А то что я к примеру научившись играть в шахматы прокачаю свой аналитико-логический аппарат как следствие И так далее не учитываешь ? Поэтому и задаю вопрос.
Все это завязано друг на друга. Окружность это линия уровня простой фунуции x^2+y^2 когда мы начинаем смотреть что получается для маленьких отклонений в механике, скажем, у нас появвляется пара квадратов в Гамильтониане и что-то вроде пи, которое окружность характеризует. И вообще эта пара квадратов много где лезет, раз мы вынуждены работать с приближениями. Оператор Лапласа, скажем, во всех дырках. Там тоже квадраты и тоже лезет пи. Из этого не следует, что окружность есть где-то в колебаниях маятника явно, либо что ее надо туда насильно совать для лучшего понимания. То есть что пи так важно – это от нашей тупости – дальше квадрата лезть уже тяжело.
Ух, так и думал, только ланг в параграфе не говорил типа можно помножать обе части на что-то как с номерами. Но думаю это единственный способ доказать равенство.
>Хочешь научиться думать - учись, блджад, думать.
Ну и как это сделать без определенного инструмента?
Для начала пройти тест на логику http://www.hr-portal.ru/pages/hu/logika.php
Если меньше тридцати баллов - нужно читать книги по логике.
Но ведь в реальной жизни математика то не больно нужна, тут явно математическая логика не поможет
Если бы тебе было легко его сделать правильно, ты бы с такими вопросами не лез. Попробуй, хотя тебе и скучно - вероятно, результат тебя удивит.

Ну я имел ввиду что если я прочитаю например пикрелейтед, то может я и смогу в матлогике разбираться, но по жизни так и буду тупеньким.
Ну, смотри. Какое логичное поведение, если ты подозреваешь, что у тебя плохо с логикой? Прежде всего, разобраться насколько плохо, затем попытаться улучшить результат и попытаться снова разобраться насколько улучшилось.
А какое нелогичное? Начинать рассуждать, что тебе лучше ее разовьет, преферанс или ходить по шлюхам, и так ни хрена и не делать. И мне кажется, что ты демонстрируешь явную склонность ко второму варианту.
матанализ. ну и научный метод тоже. нахуя? играя в шахматы ты конечно научишся играть только в шахматы. а вот матанализ в той же экономике применяется. по жизни поможет. изменит именно мышление. любят кукарекать что вычисление производных в жизни не пригодилось никому. но речь и не об умении брать кратные интегралы и прочую хуйню. речь о том что само твое представление мира изменится после изучения матана. + наберешься всяких хитрожопых методов. про ту же эпсилон окрестность из определения предела. короче в теорию матана вникаешь, утруждать себя решением примеров не обязательно для гуманитария, и смотришь на жизнь совсем другими глазами. альзо именно логика после матана будет казаться смишной простой хуетой.
>и смотришь на жизнь совсем другими глазами
Какими? Что то типа мир становится интересным и математически правильным?
типа того. только не мир, а твой взгляд на него. смотреть будешь совсем по другому. мне сложно обьяснить. я помню только то, что охуевал от того, как у меня мировоззрение поменялось. но это было давно. не помню уже, как я думал не зная его
Анонимасы, посоветуйте, что почитать по основам теории алгоритмов (нужны универсальные алгоритмические модели и сложность алгоритмов).
За ответы заранее спасибо.
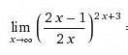
Пздц... Ведь тут вроде бы можно даже не считать, и так понятно что в числитель будет бесконечно уменьшаться, а значит будет 0 !! Ну, анончики, обьясните мне, или решение подкиньте, правильное. Мне заочнику надо сдать это, а в феврале математики уже не будет в моей учебе.
Вы видите копию треда, сохраненную 12 марта 2017 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.