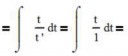Вы видите копию треда, сохраненную 12 марта 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
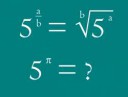
Есть теорема: всякое бесконечное множество содержит счётное подмножество. Любительское доказательство этой теоремы (встречающееся, однако, во многих учебниках) таково. Пусть M - бесконечное множество. Тогда оно непусто, то есть содержит элемент i1. Так как M бесконечно, множество M\{ i1 } тоже бесконечно и, стало быть, содержит элемент i2 (значком \ обозначена теоретико-множественная разность). Множество M\{ i1, i2 } тоже бесконечно и, стало быть, содержит элемент i3. Продолжая этот процесс, получаем, что M содержит счётное множество {i1, i2, i3, ... }.
Малоизвестный нюанс здесь в том, что мы, вообще-то, не доказали, что совокупность {i1, i2, i3, ... } является множеством. Чтобы доказать это, нужно воспользоваться одной из форм аксиомы выбора. Без аксиомы выбора, оказывается, нельзя доказать, что во всяком бесконечном множестве есть счётные подмножества. Коэн доказал, что с системой аксиом Цермело-Френкеля без аксиомы выбора совместно утверждение о существовании бесконечных множеств, не содержащих счётных подмножеств.
Некоторые люди ведут войну с аксиомой выбора, утверждая, что её следствия парадоксальны. Но отказ от аксиомы выбора уничтожает гораздо больше теорем, чем думают эти люди.
Предыдущий: >>331617 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
У ощущение лютой хуйни от этого.
Во-первый, от того, что надо доказывать, что бесконечное множество содержи счетное. Это же очевидно, зачем это доказывать?
И второе вообще пушка:
>>мы, вообще-то, не доказали, что совокупность {i1, i2, i3, ... }
Ну вот же оно: i1, i2, i3... Счетное множество. Бери и считай. В чём, блядь, проблема?
>Это же очевидно
Нет, это не очевидно. Здесь утверждается, что алеф-нуль - наименьший из кардиналов, грубо говоря. Но почему это должно быть так? Легко можно представить кардиналы, которые меньше алеф-нулевого.
>В чём, блядь, проблема?
Аксиомы теории множеств были введены как раз для того, чтобы отличить те совокупности сущностей, которые являются множествами, от тех совокупностей сущностей, которые не являются множествами. Например, совокупность всех множеств не является множеством, но совокупность всех подмножеств некоего данного множества является множеством. ZF без аксиомы выбора не позволяют доказать, что вот эта вот совокупность {i1, i2, i3, ... } является множеством, а ZF с аксиомой выбора - позволяют.
> Легко можно представить кардиналы, которые меньше алеф-нулевого.
И какие же это?
Строго говоря, дело тут не в том, чтобы "доказать, что совокупность {i1,i2,i3,...}" является множеством, ведь ZFC вообще не имеет дело ни с чем, кроме множеств, поэтому в ней не формализуется задача "доказать, что заданная совокупность - это множество", а дело в том, что вот тут:
>Продолжая этот процесс, получаем, что M содержит счётное множество {i1, i2, i3, ... }.
мы как бы "проделываем бесконечное рассуждение", которые в математике не допускаются. В классической, по крайней мере. С помощью аксиомы выбора можно проделать конечное рассуждение, которое докажет существование счётного подмножества, но для этого нужно для начала строго определится с определением бесконечного множества.

>ведь ZFC вообще не имеет дело ни с чем
Я придерживаюсь идеи, что аксиомы вводятся лишь с целью уточнить уже имеющиеся построения. Умозрительные, если угодно. Если система аксиом адекватна имеющимся интуитивным, "доаксиоматическим" построениям, то это хорошая, годная система аксиом. Если же аксиомы не позволяют доказать интуитивно очевидные утверждения, то следует искать другие, более адекватные аксиомы. Идея совокупности, к которой я обращаюсь, - это доаксиоматическая, фантастическая идея. Не какой-то объект ZFC. Моя мысль в том, что ZF без аксиомы выбора не адекватна наивной теории множеств, потому что не позволяет доказать, что некая совокупность, которая очевидно должна быть множеством, действительно им является.
>мы как бы "проделываем бесконечное рассуждение", которые в математике не допускаются
Бесконечное рассуждение можно инкапсулировать в какую-то конечную аксиому же, и таким образом спокойно использовать.
>И какие же это?
Это кардиналы бесконечных множеств, которые меньше счётного. Тоже фантастический объект, я не знаю, изучал ли кто-нибудь такие штуки.
Конкретно теорему Коэна я позаимствовал у Вавилова. Вавилов, в свою очередь, ссылается на книжку Йеха "Теория множеств и метод форсинга".
Мысль я понял, и позиция эта известная и понятная. Но проблема аксиомы выбора не в том, что она доказывает контринтуитивные результаты, а в том, что доказательства через АС неконструктивны. Мы, конечно, можем разрезать шар на два шара, но если нам дадут конкретную координату точки, то мы не сможем сказать - будет ли она после разрезания принадлежать первому шару, или второму. Более того, мы даже не можем сказать, сможем ли мы вообще когда-нибудь узнать это или нет, то есть с точки зрения конструктивиста - у нас ровно 0 полезной информации от этой аксиомы. Но с позиций некоторой вселенской истины мне такой взгляд тоже кажется недальновидным: мне очевидно, что должны существовать объекты, которые человечество не сможет сконструировать никаким образом, но которые всё же существуют и своим существованием делают всю эту вашу математическую картину эстетичнее, что ли.
Платиновая околофилософия на sci!
Выебал тебя еще в первом треде.
1. Производную бери один раз.
2. В получившееся выражение подставляй значение икса точки касания.
Если вам помогло это сообщение, ответьте "ЗЕЛЁНЫЙ СЕРХРАЗУМ БУБУГИ".
Кстати, это утверждение следует из того, что если существует сюръекция из A в B, то card(A) >= card(B). Вот пост на mse про это:
http://math.stackexchange.com/questions/726611/surjective-map-and-cardinality
Точно, я и забыл что надо подставлять значение икса в точке. Спасибо.
А разве множества появляются не после их определения?
И из определения уже будет ясно, можно там что-то посчитать или нет, можно выделить какие-то элементы или нет.
Например, взяли множество всех множеств, поняли, что это парадоксальная ерунда, и не рассматриваем его.
Рассматриваем рациональные числа или поле каких-нибудь многочленов и понимаем, что это счетные множества. Или счетность рациональных чисел тоже требует для доказательства аксиому выбора и прочие умные слова (смысл которых я не очень понимаю)?
Да.
>Это кардиналы бесконечных множеств, которые меньше счётного.
Таких нету: в рамках ZFC они существовать не могут.
Сверхразум вкатился.
Да. ω - наименьший предельный ординал.
>Рассматриваем рациональные числа или поле каких-нибудь многочленов и понимаем, что это счетные множества. Или счетность рациональных чисел тоже требует для доказательства аксиому выбора и прочие умные слова (смысл которых я не очень понимаю)?
Не требует.
>А разве множества появляются не после их определения?
Об этом думать так странно. Лучше думать, будто все множества "уже есть", а мы можем только доказывать, что множества с некоторыми свойствами существуют, а с некоторыми - не существуют. И эти доказательства должны быть формально корректными, то есть использовать чётко фиксированные правила вывода из чётко фиксированных аксиом. Например, вот так http://us.metamath.org/mpegif/isinf.html выглядит формально корректное доказательство того, что любое бесконечное множество содержит сколь-угодно большое кон
Кандл дже
>все множества "уже есть"
Множество, которое существует в одной системе аксиом, легко может не существовать в другой. Это портит всю метафизику.
>>Лучше думать, будто все множества "уже есть"
А что полезного дал этот подход? Какие задачи над привычными нам множествами (разного сорта чисел, например) он позволяет решить?
Мне с позиций дилетанта кажется, что рассуждать о множествах "вообще" и потом ковыряться с доказательствами очевидного это какая-то абстрактная вода.
Ну ты рассуждаешь как нормальный человек, а они рассуждают так, будто они сверхумные, но на самом деле их "знания" это бред какой-то.
Что вообще доказывает, что множество/ряд чисел/природный феномен/эмоция и т.д. является бесконечным? В нашей Вселенной сейчас ничего бесконечного быть не может, только в вымышленном/мнимом мире могут быть бесконечные процессы. И вообще, бесконечность это не число, его не возможно преобразовать, разделить, помножить, вычесть... Бесконечность это концепция, идея как например справедливость, воля, трусость...
Ну имеется в виду, что формальная система вместе с моделью фиксирована и относительно неё мы "строим метафизику". В другой формальной системе или даже в той же самой, но с другой моделью - другая метафизика.
>>335327
>А что полезного дал этот подход?
Ну такая философия сейчас более-менее доминирует в математике, то есть неявно предполагается, что любое рассуждение можно при достаточном усердии свести к формальному выводу из аксиом ZFC (или каких-то других). Она, собственно, математику в современном виде и дала. Вообще я не очень понял вопроса, наверное.
>с доказательствами очевидного
Я думал тут весь тред о том, что кому-то не очевидно, что у ZF существуют модели в которых есть бесконечные (= не конечные) множества, несравнимые со счётным, лил.
>>335330
>В нашей Вселенной сейчас ничего бесконечного быть не может
Табу во все поля.
>неявно предполагается, что любое рассуждение можно при достаточном усердии свести к формальному выводу из аксиом ZFC
А разве нет?
>Вообще я не очень понял вопроса
Ну вот мы например ввели абстракцию: линейное пространство. С её помощью можно ответить на вопрос, можно ли составить такой многочлен из других многочленов, чтобы он был равен нулю. Или понятие поля: оно позволяет доказать, что нельзя в общем виде решать уравнения степени выше трёх.
А какие задачи помогает решить абстрагирование от конкретных множеств к неким множествам вообще?
>оно позволяет доказать, что нельзя в общем виде решать уравнения степени выше трёх.
Выше четырёх.
>А какие задачи помогает решить абстрагирование от конкретных множеств к неким множествам вообще?
Ну если нужны совсем уж рабоче-крестьянские применения: доказательство теоремы Гудстейна, теоремы о гидрах. Очень часто можно доказать существование всяких объектов без их конкретного предъявления тупо сравнив мощности: доказательство существования невычислимых чисел, трансцендентных чисел, неборелевских множеств. Всякие рассуждения по типу "композиция инъективных функций - инъективна" - тоже чисто теоретико-множественные и оторваны от конкретной конструкции.
А вообще, у теории множеств больше фундирующая функция, нежели прикладная: она даёт удобный язык, на котором можно формулировать и высказывать мысли: например конструкция фактормножества по отношению эквивалентности настолько вошла "в кровь" математики, что сложно назвать какой-нибудь раздел, где её бы не было.
Ну и ценность полей, кстати, тоже далеко не в одной теореме Абеля и теории Галуа, я бы сказал, что у полей тоже фундирующая функция, то же определение векторного пространства формулируется в общем случае над произвольным полем, что позволяет сразу построить одну стройную теорию для векторных пространств над Fp,Q,R,C (до определенного момента, по крайней мере).
>она даёт удобный язык, на котором можно формулировать и высказывать мысли
Похоже физека катиться в эту самую пизду множеств.
Она скатывается в тех местах, где с теориями уже всё понятно и никто их глобально трогать не будет (классическая механика, СТО), а в местах, которые на стадии формирования (КТП) она не скатывается, просто потому, что там самим физикам ещё не очень понятно что происходит, не говоря уже о какой-то формализации. И это правильно.
Ну вот пусть у нас есть группа G и подгруппа H, и мы хотим рассмотреть "группу G с точностью до группы H", то есть писать как-то типа: a=b (mod H). Или, что тоже самое ab^-1 = 1 (mod H). Логично для этих целей попробовать ввести на G отношение эквивалентности a~b <-> ab^-1 лежит в H. Возьмём фактормножество группы G по отношению эквивалентности ~. Будем обозначать класс эквивалентности g как [g]. Очень бы хотелось, чтобы классы эквивалентности тоже можно было перемножать по очевидному правилу (aH)(bH)=[a] x = [ab] = ab H. Если мы посмотрим на равенство aHbH=abH множеств чуть поближе, то мы заметим, что оно выполняется тогда и только тогда, когда bH=Hb, но ведь это и есть требование нормальности группы!
Если коротко: то нормальность группы в точности означает, что мы можем ввести структуру группы на фактормножестве G/H.
Знания по математике - 11 класс.
Нужно хотя бы в общих чертах знать матан. С чего начать? И в какой последовательности изучать? Нужно самые основы.


>Платиновая околофилософия
Потому что все, связанное с бесконечными множествами околофилософия и есть, причем с самого начала. Всем известное "доказательство", основанное на взаимнооднозначном соответствии точек отрезков разной длины (1) ничего не говорит о том, как быть с иными всевозможными вариантами (2), не дающими однозначного соответствия. А следовательно второе всем известное "доказательство", что мощность множества вещественных чисел больше множества рациональных может говорить лишь о том, что найденное Кантором соответствие относится к случаю (2), но это еще никак не говорит о том, что между вещественными и рациональными числами не может существовать взаимнооднозначного соответствия. Кантор доказал лишь, что в показанном им варианте сопоставления нет взаимнооднозначного соответствия, а не то, что такого соответствия не может быть в принципе.
Вся же дальнейшая аксиоматика никакое не развитие, а просто запрещение неудобных случаев. Попытались построить множество всех множеств, получили парадокс - запретить. Ситуация тут ничем в принципе не отличается от античной математики, которая просто запрещала бесконечные величины по той же самой причине - не умела с ними работать.
Ну а уж то, что бесконечного множества в принципе никто никак не смог показать, кроме как в виде буквы, его обозначающей, про это только ленивый тут не кукарекал.
Неосилятору теоремы Кантора что-то объяснять неинтересно, иди на dxdy.ru, там есть люди которым интересно пережёвывать одно и то же по 170 раз.
Да я, на самом деле, сам это и написал и сам себе ответил0.
Апл не взлетел. Что еще?
Рисуй в пейнте
ЗЕЛЁНЫЙ СЕРХРАЗУМ БУБУГИ
Я не понял, какое мы вообще имеем право вводить аксиому выбора, не определив перед этим натуральных чисел?
Твоя мамка нам лично каждому разрешение дала.
Посылать найух, на dxdy.ru лишь показывает, что ты как раз сам не понимаешь того о чем говоришь. Если ты такой осиливающий, так будь любезен доказать это своими доводами и аргументами, а не отсылкой на неопределенное множество {X,Y,Й}
Ну давай попробуем. Для начала ты приводишь полный текст доказательства из какого-нибудь более-менее стандартного источника (если хочешь, то я могу его привести), потом указываешь на ошибку конкретно в этом тексте, а потом уже говорим. Я лично никакого доказательства "... основанного на взаимнооднозначном соответствии точек отрезков разной длины ..." не знаю.
Ну а почему до сих пор человечество не смогло и не научилось работать с бесконечными величинами? Это связано с технологическими недостатками компьютеров, калькуляторов, арифмометров, abacusов или с неправильными основополагающими принципами математики, физики, философии? Вот мы будучи частью космоса и имея разум не можем однозначно сказать бесконечна ли вселенная или она не бесконечная/замкнутая.
>Ну а почему до сих пор человечество не смогло и не научилось работать с бесконечными величинами?
Да вроде как научилось.
Неотрендеренный тех читать не очень-то удобно. Он для другого. Я же ясно сказал: делать заметки, а не публиковать.
Так а ты его рендерь. При достаточной надрочке и скорости печати получается фигарить формулы очень быстро, что для заметок вполне себе.
>человечество не смогло и не научилось работать с бесконечными величинами?
Лол, как там в 18-м веке?
Ох, ну не знаю. Я пробовал - неудобно. Когда надо редактировать, приходиться смотреть на отрендеренное, а править неотредеренное, и это... уныло как-то. Да и элементарно много лишних буков.
Во первых, моя цель не придираться к теоремам и пытаться выискивать соринку в чьем либо глазу, а попытаться понять то, что есть и познал ли я это.
Есть отрезок с двумя точками А и В, на этом отрезке есть точки и количество этих точек, как нас учат еще со школы, бесконечно. Есть другой отрезок с точками С и D, он в 2 раза длиннее отрезка АВ, но между С и D есть точки и количество этих точек тоже бесконечно. Но АВ в 2 раза короче CD. Как это надо понимать?
Понимать следующим образом: длина отрезка и мощность отрезка как множества точек - две принципиально разные характеристики отрезка, никак между собою не связанные.
Я не умею..
Ты сейчас ответил как поп, навсеволябожья! Мощность отрезка? Это как длина и толщина члена? Так сейчас во всей математике, чтоб объяснить одно ссылаются на другое, выясняешь другое он отсылает на третье, третье на 4-е , а это уже и есть Бесконечное Множество. Что и требовалось доказать.
Хуйню какую-то дилетантскую сказанул.
Я из твоего словесного потока ничего не понял, но что-то объяснить тебе пытаться уже не буду.
>aHbH=abH
А почему не aHbH=abH^2? Мне вот это не понятно. Остальное, вроде бы, складно звучит. Только почему-то у тебя ab^-1, а в учебниках bab^-1, или я опять не про то говорю?
Платонист закукарекал.
Ты не обладаешь необходимым уровнем знаний для исчерпывающего и внятного ответа. Ты как астролог, даже хиромант. Твоим следующим действием будет призыв сжигать еретиков
Ты либо неприлично толстый, либо непроходимо тупой.
Анон всю твою натуру через интернет вычислел. Прогнать, изгнать, колесовать, сжечь на костре, разстрелять как бешеных собак
H^2 = H, так как H группа и, следовательно, содержит единицу.
Не про то. aH=Ha <-> aHa^-1=H <-> aha^-1 \in H для любого h.
>>335419
Какая жалкая попытка семёнить. Просто всем неинтересно общаться с дауном, а тебе будет неинтересно общаться с умными людьми, так как ты - даун. Вот тебе и предложили съебать. Можешь оставаться, конечно, благородные доны будут время от времени снисходить до того, чтобы поссать тебе в рот, например.
>aH=Ha <-> aHa^-1=H <-> aha^-1 \in H
Почему тогда просто не написать aH=Ha принадлежит H? Почему в определении именно сопряженные элементы?
aH - это множество, состоящее из всех элементов H умноженных слева на а, соответственно, Ha - это множество, состоящее из всех элементов H, умноженных справа на a, равенство: aH = Ha это равенство множеств, которое, если раскручивать, значит буквально следующее: для любого a из G, существуют такие h1 и h2 из H, что a h1 = h2 a. отсюда a h1 a^-1 = h2, что значит просто то, что a h a^-1 принадлежит H для любых a из G и h из H.
>для любого a из G, и h1 из H существует такое h2 из H, что a h1 = h2 a.
fix
Лол, спасибо, у меня как-то по-другому все в сознании работает. Я бы иной формализм создал, будь я на месте основателей теории групп. По-моему, можно все проще сделать. Но суть теперь понятна. Еще раз благодарю, а то мучаюсь с этими вопросами уже добрую неделю.
Обоснуй с выкладками.
На самом деле гораздо лучше посмотреть на факторы всяких групп по всяким нормальным подгруппам, потом посмотреть на ненормальные подгруппы и подумать, почему не пройдёт номер точно так же их отфакторизовать.
Почему ноль и нуль считаются тождественными понятиями. Ведь ноль, если прочитать наоборот будет лон->лоно, разве лоно пустое? Нет оно полное. А если нуль прочитать наоборот будет лун->луна->лунка, вот это ничто, может быть по этому луну назвали луной так как она внутри полая? Почему математики не видят в этих словах разницы?
Как доказать, что в хаусдорфовом пространстве одноточечное множество замкнуто?
Спасибо за содержательный ответ.
Бесконечность не число, это концепция, идея - возникшая из-за неспособности нашего мозга полностью понять реальность, даже имея компьютеры. Человек, когда изучает мир, часто пытается делить объекты на более мелкие составные части, но это приводит часто к абсурду. Также и с отрезками из твоего вопроса, состоящими из составных частей, самой маленькой и неделимой частью считается точка. На первый взгляд это невозможно, но на самом деле АВ имеет бесконечно точек как и CD, но бесконечность бесконечности рознь, бывает так, что одна бесконечность больше другой бесконечности. Пусть длина АВ равна 1см, а CD равна 2см. Загадай отрезок длиной от 0 до 1см - вероятность того, что ты загадаешь отрезок помещающийся в АВ, такая же, как и вероятность загадывания отрезка помещающегося в CD. Загадай отрезок длиной от 0 до 2см - вероятность загадывания отрезка помещающегося в CD будет большей, а значит CD включает в себя большее количество составных частей и бесконечность точек CD > АВ. В начале 20-го века ввели понятие МЕРА ОТРЕЗКА, МЕРА МНОЖЕСТВА которые какбы интуитивно связаны с их размерами. В общем ищи в google…
Возьмём точку p и точку x. Возьмём окрестность Ux, которая не содержит точки p. Объединение всех Ux x \in \Omega, x!=p даст как раз дополнение до {p}.
Хм, и правда. Я тупой.
>Некоторые люди ведут войну с аксиомой выбора, утверждая, что её следствия парадоксальны
Какие, например?
> Бесконечность не число, это концепция, идея - возникшая из-за неспособности нашего мозга полностью понять реальность, даже имея компьютеры.
Блять, /ph/ протек.
Ууууу блять, как же вы мне противны.
5^Пи = 1√5^Пи
У матанодаунов число пи не определено. Это физекам 3.1415926 уже с головой хватает чтобы длинну окружности атома ксенона рассчитывать, а маняматикам подавай АБСАЛЮТНАЮ ТОЩНАСТ
5^Pi = 156.50 - 157.10
Ответил тебе за щеку, проверяй.
1) Вся математика сводится к исчислению предикатов на основе аксиом ZFC, или что-то не сводится?
2) Возможны ли другие подобные системы аксиом, или ZFC уникальна?
Мощность отрезка-количество точек принадлежащих этому отрезку, и она имеет мощность континуума.
Длинна отрезка-функция от координат концов отрезка.
Противен здесь только ты, быдло.
Если ты хочешь использовать теорию категорий, то ZFC не подойдет.
Можешь почитать про NBG
https://en.wikipedia.org/wiki/Von_Neumann–Bernays–Gödel_set_theory

А NBG актуальна во всех вообще случаях, или есть что-то что не сводится к ней?
Там.
Не знаю, я не разбираюсь в основаниях.

Высрался тебе в глотку. И НЕ СМЕЙ ВЫТИРАТЬСЯ, МРАЗЬ!!!!!!!
как грубо!
Не понял.

ну тогда второй пример
почему так? Правдивое основание и ложный вывод, дает правду
1 0 A=>B дает правду?
Выглянуло солнце => Стало темно и это правда
У тебя таблица истинности от обратной импликации вроде. Ноль должен быть во второй строке (и только).
Почитай что нибудь по теории функции и меры, потом возвращайся.
Потому что ты даун
На самом деле это не так принципиально - есть по крайней мере три разных подхода к формализации теории категорий в теории множеств (и один из них проходит собственно в ZFC):
1) Подход, когда большие категории понимаются, как классы, он обычно формализуется в теории множеств Маклейна (чуть усиленная NBG).
2)Подход на основе вселенных, когда аксиоматически полагается, что имеется семейство вложенных вселенных множеств и вместо рассмотрения, например, категории всех групп рассматривается категория всех групп в некоторой вселенной и эта категория оказывается множеством с точки зрения вышестоящей вселенной (формализуется в ZFC + аксиома вселенных Гротендика).
3)Замена вселенных Гротендика из 2) на немного более слабые, существование которых доказуемо в чистой ZFC (принцип отражений).
А мне интересна позиция математиков. Наверняка этому есть обоснование. Может просто аксиоматическое, а может откуда-нибудь следующее.
У-тю-тю, какой ты мамкин злобный омежка. Даже злиться на тебя не хочется.
Это на самом деле стандартная позиция, которая, в частности, отражена в аксиоме объемности в теории множеств. Учитывая то, что математика, по существу, культурный феномен, если что-то воспринимается математическим сообществом, как аксиома, то это она и есть. Аксиомы не подлежат доказательству.
Семилетняя личинка поймет то что там написано?
Да и три тома это как то слишком для ребенка, как по мне.
Да, конечно, ведь там все действительно подробно расписано, единственная проблема что математика там явно не доходит до 11 класса (в лучшем случае он относится к 3-4).
пример этих объектов: числа, многочлены
Это ты хочешь покидаться. Тебе предложили точное значение пи, ты сказал, что это неверно. Вполне закономерный вопрос я задал.
Потому что это один и тот же символ.
Три тома расписывать уровень третьего класса? Там что, абстракции уровня бурбаки?
Трактат Бурбаки, по существу, идеологическое продолжение книги Уайтхеда Рассела. При этом, надо отметить, что он написан, с учетом ошибок предшественников, принципиально более человечным языком и опусканием куда большего числа формальных деталей.
По определению равенства. Мы пишем a = b, если симолы a и b обозначают один и тот же объект.
Определение не является доказательством. Значит все-таки просто взяли и и сказали, что оно будет так. Интересно как изменится математика, если отбросить эту догму.
Тождество - равенство истинное при всех значениях переменных.
Ты сам сказал что там до 3 класса только поясняют все. А до 11 класса что делать? Сразу дискриминантам его учить с матрицами?
Обычные ноотроп, что такого то? Все математики такие употребляют.
Трактат Бурбаки, по существу, идеологическое продолжение книги Уайтхеда Рассела. При этом, надо отметить, что он написан, с учетом ошибок предшественников, принципиально более человечным языком и опусканием куда большего числа формальных деталей.
Твои постановки вопросов по своему духу явно относятся не к этому треду, а к соседнему >>295488 (OP)
Лол, употребляю те понятия, которые мне удобны. С чего это мне отчитываться перед кем-то?
Особенно в тех, когда мы хотим рассмотреть категорию всех классов с морфизмами - отображениями.
>>335663
Кольцо.
Если серьёзно, то, надеюсь, Вы знаете, что школьная математика - не математика вовсе, а отработка простейших навыков и умений работать с тривиальными методами. Вы желаете отработать с ребёнком именно их? Тогда необходима простейшая теория и как можно больше практики. Для этих целей подходит сборник "Пособие для поступающих в вузы" под авторством Модёнова. Все арифметические законы Вам придётся объяснять самому, а само введение в книге требует знаний на уровне пятого класса - тоже ваша работа.
Но на самом деле важно также подготовить не только теоретическую базу, но и умение рассуждать логически. Для этих целей подходит серия из двух книг "Планиметрия. Пособие для углубленного изучения математики" и "Стереометрия. Пособие..." - не предполагает изначальных алгебраических знаний и, по-моему, намного лучше предлагаемого сейчас в школах курса под авторством Атанасяна.
Но если ребёнку изначально не очень интересен абстрактный мир математики, ничего не получится.
Это и аксиома/постулат и прямой результат минимально здоровой логики. Доказательством верности этой аксиомы служат очевидные факты нашей каждодневной жизни т.е. верность этой аксиомы доказать очень легко и никто даже не требует доказательств. Например: говоришь ребенку, что не хорошо прятать в кармане 2 слитка золота. Ребенок тут же говорит что у него нет вообще никакого золота, т.е. 2 не равно 0, а 0=0, а был бы у ребенка 1 слиток золота, то ребенок сам бы тебе сказал 1 не равен 2
В архивах соросовского оразовательного журнала есть статья "Тождество". Лежит в интернетах. Гугли.
Честно говоря я с тобой согласен и в этой жизни все болтовня и вся математика и физика и химия... Чем больше изучаешь, тем больше понимаешь, что ничего на самом деле не знаешь. Вроде столько ученых, но никто не может четко предсказать среднюю цену на нефть/золото... в 2016; не могут даже точно сказать куда и когда грохнется затапливаемая космическая станция.
Я это понимаю, но я лично могу вспомнить из школьного курса только дискриминант, а это уже уровень 8-9 класса вроде. Что там до него проходится я не помню.
Посмотрю что там за книжечки.
И мне надо просто научить ребенка самой базовой математике, чтобы потом не пришлось объяснять почему квадратный многочлен связан с параболой и что скрывается за понятием корня.
Базовая математика - это как базовая физика. Всё настолько упрощено, что ребёнок потом, когда узнает правду, просто запутается.
Зачем учить ребёнка этой фигне? В школе ему и без тебя голову испортят. Учи его теории множеств и другим полезным вещами.
Если ты сам знаешь школьную математику на хорошем уровне, то сможешь её рассказать сам, без всяких книжечек. (максимум что, можно смотреть на идеи для интересных задач), а если не знаешь, то и книжечка не поможет - выйдет полное уебанство, лучше отдай его в какой-нибудь хороший олимпиадный мат. кружок.
Пи = Пи/1, а дальше,
по первой формуле с пикчи ОП-поста.
Для выражения, не обязательна ОПСАЛЮТНОЙА ТОШНОСТЬ.

>Геометрия на верхней полуплоскости (Лобачевского). Свойства инверсии. Действие дробно-линейных преобразований.
Уважаемые господа, что конкретно под этим понимается? Какие главы в какой книжке читать? Поясните по-хардкору.
Двачую
Есть брошюра Прасолова: https://vk.com/doc41446009_257315839?hash=4fe79ece33d870910e&dl=c91ee440edf1890ea7 но вообще я бы не советовал задрачиваться - юзелесс хуйня с передозом тригонометрии.

1) Вся математика сводится к логике первого порядка на основе аксиом, скажем, NBG.
2) Все правила вывода в исчислении предикатов - чисто механическая задача.
3) Доказательство любой теоремы - чисто механическая процедура в пруф ассистантах / ЯП с зависимыми типами.
Собственно, идея:
1) Берем клеточные автоматы, много клеточных автоматов, прописываем в них правила исчисления предикатов на основе заданной аксиоматики.
2) Нагенерированные сетями клеточных автоматов теоремы верифицируем в пруф ассистантах.
3) То, что приводит к противоречиям и т.п. удаляем, оставляем доказанные непротиворечивые.
4) Доказанные теоремы пробиваем по всем поисковым системам краулерами, те что уже существуют и доказаны, удаляем.
5) Остаются теоремы и прочие построения, которые во-первых, верны, во-вторых, не встречаются в современной математике.
6) ...
7) Выгода?
Я кстати давно о таком думал. Подвох небось в нехватке памяти для хранения такого объема комбинаторики.
Подвох в том, что главная ценность теорем - их интуитивный смысл. Всё то облако понятий, знаний, эмоций, которое связано с теоремой. Компьютер пока что не умеет писать осмысленные тексты, так что генерировать математику компьютером не получится. Компьютер может генерировать только строчки символов по заданным правилам. Но что с этого толку? Любая строчка символов является теоремой в некоторой подходящей системе аксиом. Но ведь не все строки символов эквивалентны.
>строчки символов по заданным правилам
В этом суть любого математического построения.
>главная ценность теорем - их интуитивный смысл.
Смысл метематического построения не зависит от того как оно получено. Более того, правильное математическое построение в смысле вообще не нуждается. Главное - непротиворечивость, еще бурбаки об этом писали.
>Всё то облако понятий, знаний, эмоций, которое связано с теоремой.
У тебя просто магическое мышление.
Я уже вижу как все математики зассали перед мощью компьютерных числодробилок. Данные удобнейшие для компрессии, огромные процессинговые фермы, йобабайты данных, фильтры, критерии, комбинаторика и оптимизация, оптимизация, оптимизация, оптимизация... И самую могущественную математику творят Васяны, прочитавшие книжку "C++ за 21 день".
А так и будет. Жалкие людишки математику давно не тянут. Сколько там веков была открытой проблема теоремы Ферма? Потом, АВС-гипотеза. С этим еще смешнее, один японец доказал, а кроме него никто в доказательство вкурить не может уже четвертый год. Нахуй так жить вообще? А ведь АВС-гипотеза и теорема Ферма - жалкая хуйня про натуральные числа, которые школьники в 1 классе проходят. По-настоящему сложная математика еще даже не начиналась.
Загвоздка не в "интуитивном смысле теорем" (который окончательно проёбан ещё в XIX веке кмк).
И не в нехватке памяти для объёма комбинаторики.
А в том, что теорем будет овердохуя и они будут бесполезными до шизоидности. Условно говоря, алгоритм тебе выдаст миллиард функций вида f(x^+y^2)=0 и докажет — рассматривая каждую по отдельности — что они все суть окружности, хотя при умении абстрагироваться и так ясен хуй, что это всё окружности.
И уже на сотой f(x^2+y^2)=0 ты плюнешь на это дело и пойдёшь двачевать.
Я этой темой не занимался (только что-то слышал краем уха), так что это просто домыслы диванного эксперта. Было бы приятно оказаться неправым.
Ты будто из докомпьютерного века. Почему алгоритм не может занести эти функции в класс? Не создать правило? Не объединить правила?
Можно выдумывать сколь угодно говнотеорем, которые будет понимать только автор. В википедии это называется ОРИСС. Математика ущербна. А ты ещё ущербнее чем математика.
>еще бурбаки об этом писали
Сразу видно человека, который не читал бурбаков.
>в смысле вообще не нуждается
В таком случае вот тебе формальная система.
1. Символ ы есть строка.
2. Конкатенация двух строк есть строка.
3. Доказательный текст есть набор строк, записанных друг за другом, так, что каждая очередная строка есть либо аксиома, либо конкатенация каких-либо двух предыдущих строк.
4. Теоремы есть строки, встречающиеся в доказательных текстах. Доказательный текст, в котором встречается теорема, называется доказательством теоремы.
5. Строка ы - аксиома.
Ты можешь, в полном соответствии со своей философией, посвятить жизнь построению теорем в этой формальной системе - ведь для тебя нет разницы, какой формальной системой пользоваться. Я могу первые несколько теорем вывести за тебя.
Теорема 1. ы. Доказательство: ы.
Теорема 2. ыы. Доказательство: ы ы ыы.
Теорема 3. ыыы. Доказательство: ы ы ыы ыыы.
...
И так далее. Думаю, в день ты сможешь открывать тысячи теорем. Вперёд, удачи.
Пиздуй в /em, там на языки дрочат.
А зачем? Ведь смысл никого не интересует. А раз смысл не важен, то какая разница, какую формальную систему изучать.
Теорема 4. ыыыы. Доказательство: ы ы ыы ыы ыыыы.
> Не создать правило?
Потому что тебе придётся вручную набить весь класс бесполезных шизодных теорем, чтобы программа их отсеивала.
А что-то мне подсказывает, что их таких гораздо больше, чем хороших и нужных. Сначала ты скажешь фильтру: окей, не надо доказывать про круги. Потом: не надо про круги в 3-х измерениях. Четырёх. Потом будут не круги, а просто какая-нибудь ебала. А потом ещё. И так до бесконечности.
Более того, та хуйня что ты описал, Л-системы, или системы Линденмайера, давно используют, правда, поумнее чем это сделал ты.
>>335822
>то какая разница, какую формальную систему изучать.
Я даже написал, какая разница. Исходный пост >>335791 ты либо не читал, либо, что скорее всего, не понял.
Кое-кто выше написал:
>правильное математическое построение в смысле вообще не нуждается. Главное - непротиворечивость
Объясни с такой точки зрения, чем моя формальная система (я нареку её ЫЫЫ) хуже, чем NBG.
Смысл это жалкое творение эволюции, как и сам человек. Тебя окружает лишь белый шум. Твои глаза, уши, мозг -- инструмент, выделяющий из шума определенной структуры этот самый смысл. Если бы наши предки кушали радиоволны, то мы бы видели радиоволны, смекаешь? Так почему мы не можем создать такой же инструмент для математики? Пусть он будет примитивный, как глаз моллюска, но ведь он тоже сможет эволюционировать, если подвергнуть его отбору. Для человека это более рациональный путь, ведь создавая самого себя он руководствуется по сути такими же этими случайно возникшими принципами (аминокислотами, клетками) как инструкцией.
Лол, эти сказки еще Гильберт в начале прошлого века рассказывал и тогда это было куда убедительнее, чем сейчас.
>ты просто понятия не имеешь о клеточных автоматах.
Клеточный автомат это либо Машина Тьюринга, только в профиль, либо сильно урезанная машина Тьюринга.
Да, кстати, объясни, зачем ты к своему выводителю теорем прикрутил это стародавнюю игрушку студентов-первокурсников? Как они решат тебе проблему, описанную в >>335823
?
Когда ты говоришь "класс" ты же что-то подразумеваешь под этим понятием? Наверное, каким-то правилом руководствуешься, чтобы выделить класс. Я тебе расскажу про сепульки и ты выделишь из них класс, каким-то чудным образом.
>Объясни с такой точки зрения, чем моя формальная система (я нареку её ЫЫЫ) хуже, чем NBG.
Тем, что практической ценности не представляет.
Практическая ценность - это, внезапно, смысл. Выходит, осмысленность всё же нужно учитывать?
>Когда ты говоришь "класс" ты же что-то подразумеваешь под этим понятием?
Да, я подразумеваю бесконечный список лютой хуиты, которую непонятно как отсеивать.
И ты даже не попытался решить проблему просеивания теорем.
Это не философия, это просто констатация факта. Фотоны с монитора попадают тебе на рецептор, а дальше путем сложных манипуляций ты сначала неосознанно выделяешь формы, цвета, объем, после объединяешь это в более сложные структуры, которые для тебя речь, выискиваешь в этом некую "философскую подоплеку". Но это же просто набор фотонов, разве способна сраная нейросеть на что-то подобное? Ей ведь не хватит мощности и памяти на такое!
Не нет, а да. Смысл теории - это, по определению Клини, всё то, что не описано в метатеории формальной теории явно. Практическая ценность не описана ни в метатеории NBG, ни в метатеории ЫЫЫ, поэтому практическая ценность - смысл.

Практическая ценность - смысл.
Допустим, смысл не имеет значения. Тогда и практическая ценность, как часть смысла, не имеет значения.
Но практическая ценность имеет значение. Значит, допущение неверно.
Засим обтекай.
Ты же обнаружил в круге, измерении, прямой, функции, etc, какую-то похожесть. Некоторые похожи алгебраической записью, некоторые графиком, некоторые производной, да дохуя критериев. Математическая интуиция это лишь набор фактов в голове. Вспомнил что-то и связал. А у компьютерного фильтра в качестве источника фактологии весь arXiv.org.
>Ты же обнаружил
>imply Значит, и компуктер обнаружит
> интуиция это лишь набор фактов в голове.
Ты себя со стороны совсем не видишь, поехавший?
>да дохуя критериев.
Удачи тебе их все формализовать, увязать и замкнуть на себя для дальнейшего автоматического расширения и развития.
В общем смысле -- да. Но я не уверен в том, что все существующие в публикациях математические объекты абсолютно изучены и не могут принести пользу.
Разговор прежде всего вероятностях, а не о причинно-следственных связях. Какова вероятность того, что сраная клетка с рецептором эволюционируют за пару миллиардов лет до человека, способного в этого разговор? У нас же есть весьма неплохие возможности ускорить этот процесс и начать с более развитого организма, чем клеточный автомат, аналогичный клетке.
Но 98%, с теми мощностями.
Раскусил чертяка! когда в покер уже будем играть?


Матаны-батруханы
поясните пожалуйста мне дауну за
- мнимую единицу
- комплексные числа
- кватернионы
оче сильно хочу понять, не посылайте нахуй аргументируя что мне не дано...оче сильно жи хочется(((жи есть жи!!!!
вы моя последняя надежда
Вообще, есть тред про элементарную математику, без философии и шизиков.
Что именно тебе непонятно?
- нахуя вообще эту единицу придумали?
есть жи 0 на который делить нельзя и никто не выёбывается
- нахуя вообще комплексное число нужно, я так понел это тупо вектор с координатами?
- кватернион это вообще пздц, векторный поворот легко описывается матрицей координат, какие они блять там противоречия блять нашли вообще нихуя не понятно, и нахуй в кватернионе ввели понятие 4-го измерения, хватило бы трёх составляющих.
Это не тупо вектор с координатами, на комплексных числах можно ввести коммутативное ассоциативное умножение с делением, по теореме Фробениуса это единственный с точностью до изоморфизма такой объект над действительными числами.
Для чего они нужны - см. комплексный анализ и далее комплексную алгебраическую геометрию.
Банальное объяснение про i:
В 16 веке хотели решать уравнения 3 и 4 степени, и для вывода потребовалось воспользоваться "трюком" - взятием корня из -1. Ввели i и -i.
В том же духе про кватернионы:
При помощи кватернионов удобно было записывать преобразования пространства.(Повороты, симметрии, перемещения, ...) Физикам понравилось, много кому ещё понравилось. Причём придумали кватернионы одновременно, если не раньше матриц.
> есть жи 0 на который делить нельзя и никто не выёбывается
На ноль делить нельзя потому что если попытаться расширить математику так чтобы разрешить деление на ноль то получится хуита http://math.stackexchange.com/questions/125186/why-not-to-extend-the-set-of-natural-numbers-to-make-it-closed-under-division-by
А мнимую еденицу ввели - и получился удобный инструмент. Потому она и есть.
>Её носитель не может быть даже собственным классом.
Почему не может? Разве на собственные классы накладываются какие-то ограничения?
>Разве на собственные классы накладываются какие-то ограничения?
Да. Их элементами могут быть только множества, а не классы.

Ну проблема-то решаема, если потребуется такая необходимость.
Как он поживает?
>ссылка
спасибо почитал просветился
как будто корень из -1 это не ломание устоев и логики действий в алгебре.
Потому что множеств в математике каждый день возникает слишком дохуя разных, чтобы учить всех только множеству полиномов или множеству рациональных чисел.

Я пишу игру, сильно упростив ее можно свести к такой модели: на следующем шаге можно встретить врага, или восстановить здоровье. При встрече врага есть вероятность умереть. Как должны соотносится эти три параметра (вереятность умереть при встрече, вероятность встречи и вероятность регенерации) чтобы игра максимально затягивала?
Должна же быть теория какая-нибудь?
Можно ли доказать связность матричных групп типа GL(n), SL(n) и SO(n) геометрически, исходя из того, что задаются они неразложимым полиномом?
Если С и D существуют, то они существуют благодаря А и В или благодаря прямой?
Тебе стоит сначала определить что такое "затягивала", в математическом смысле. Вообще для анализа подобных моделей используют цепи маркова.
Они существуют, потому что условия задачи не запрещают им существовать. Это же очевидно.
Прямая – неограниченное множество точек.
Есть карта со 100 000 персонажами. У каждого 4 характеристики с 4мя значениями каждая.
Какова вероятность встречи двух персонажей, у которых 4 из 4 характеристик имеют одинаковые значения? 3 из 4х? 3 из 4х, но трех персов?
Вероятность совпадения значений k из 4-х характеристик у n любых персонажей: p = C(4, k)(1/4)nk
Число вариантов выбора n персонажей из 100,000: C(100,000, n).
Требуемая вероятность: C(100,000, n)pn(1-p)100,000-n
Большое спасибо, анон.
До апреля скучать будет.
Блядь уже и вопрос нельзя задать. Сразу в толстоте обвиняют. Вы тут уже в конец доабстрагировались.
Расшифруй вопрос, что конкретно ты имеешь в виду. Как для тебя выглядит ситуация нехватки чисел в физической теории?
Наоборот, нету нехватки. Я подумал, что для описания стандартной модели и квантовой механики достаточно только натуральных чисел. Все остальные виды чисел в этой вселенной НЕ НУЖНЫ.
Нахуя ты сам с собой тут диалоги ведёшь, долбоёб?
Ты тот же поехавший, который Универсальный Сочинитель Теорем изобрёл или вы тут всё время новые?
Нужно все величины в физике умножить на постоянную Планка и тогда она станет натуральным числом.
Принимаем постоянную планка за единицу и пересчитываем все остальные величины исходя из этого. Природа этой вселенной квантовая, т.е. дискретная по сути. Все основанно на неделимых величинах, натуральных числах.
В любом случае тебе надо будет предполагать, что ты работаешь с непрерывными величинами, чтобы использовать мат аппарат, а потом каждый раз округлять, это будет тупо неудобно.
>В любом случае тебе надо будет предполагать, что ты работаешь с непрерывными величинами
Вот это непонятно. Объясни почему?
Кам минимум в атоме водорода есть один на эн квадрат, в осциляторе одна вторая, так что нельзя, вопрос закрыт.
>>в атоме водорода есть один на эн квадрат
Нутак надо просто перевернуть дробь, это же условность
>>в осциляторе одна вторая
Надо домножить на два и всё
Ты очень тупой
Спасибо, теперь вот буду вероятности вспоминать.
Почему?
Дерганье пиписьки состоит из следующих аксиом:
А Прислушиваться к шагам родителей
Б Тянуть вверх
В Тянуть вниз
Г Воображать всякое
Д Малафить
Любая комбинация этих строк есть фап. Если комбинация содержит Д, фап назвается завершенным.
Докажем, что твоя жизнь есть фап. Твой вчерашний день прелставляет собой:
АБВГАБГВАГБВГААААААААААГГБВАГГБВД
Репорти блядь. Он не обязан за тобой бегать с тряпкой и подтирать говно.
В /fl/.
add-on - в браузерах надстройка
penthouse - доп надстройка на зданиях
bells and whistles - доп свистелки и перделки
конкретное предложение дай, из какой сферы наук
Большая часть знаний созданных человеками переведена на английский или написана на нем. Когда будешь публиковать свои статьи на arxiv.org я помогу тебе с переводом.
P.S. за соответствующее вознаграждение of course.
Да.
Очевидный Демидович + Антидемидович (антидемидовичи есть китайский и русский за авторством боярчука).
Только не объёма, а площади. И не на два шара, а на пять частей, из которых составляются два объекта. И не просто равные площади, а равные площади начального шара.
Сорь, не бейте
> Малоизвестный нюанс здесь в том, что мы, вообще-то, не доказали, что совокупность {i1, i2, i3, ... } является множеством.
Не. В этом доказательстве другая дыра. Оно доказывает, что для любого N бесконечном множестве содержится не менее N элементов. Далее подразумевают, что это якобы доказывает, что в бесконечном множестве содержится счётное. Об этом нужно говорить аккуратнее.
Сдохнуть бы. Поскорее. Я заебался плакать по ночам.
Могу предложить утешающую задачку.
Это >>336409 не я, интересует в принципе любой степени.
>>336410
Первая кривая задана явно f(x) = 0.
У второй кривой задана степень n.
n не обязательно превосходит степень f.
Тащемта, если степень не задана четко, можно до бесконечности перечилять все варианты кривых.
1. Метрика на функциях в R d0 не зависит от выбора координат - так(площадь между кривыми не меняется от поворотов-перемещений)? А почему это так?
2. Допустим, решение ОДУ методом разделения переменных - можно сделать без нотации dy/dt - и как обосновать перетасовывания дифференциалов по разные стороны равенства? Где-то встречал мнение, что эта нотация ущербна(правда не очень понял, осознавая её удобства). Подозреваю юзается инвариантность формы первого дифференциала(нам не важно что y - функция от t, а не наоборот, к примеру).
3. В интеграле фигурирует выражение f(x)dx. А что если вместо dx взять величину g(dx) -> 0 при dx -> 0 к примеру g(x)=x^k, e^x-1 и.т.д. и рассмотреть суммы, аналогичные интегральным - будут ли они существовать, сводиться к интегралам или у них своя собственная атмосфера?
4. Ну и встречал тут вопросец - формула производной обратной функции легальна или нет для частной производной, с пояснениями. Видимо опять же связь с инвариатностью дифференциала - ведь "частные" дифференциалы даже обозначаются по-разному(дельта малое vs латинского d).
1. Площадь определяется с помощью интеграла. Интеграл специально определён так, чтобы конгруэнтные фигуры (совмещающиеся движением: параллельным переносом, поворотом, симметрией) имели равную площадь.
Неочевидным мне кажется то, что определение интегральных сумм завязано на конкретные оси, по которым мы делаем разбиения.
Нарисуй ось в которой будет твой икс и игрек, если не ПОНИмаешь по другому.
Ну есть же тред про элементарную математику!
>В интеграле фигурирует выражение f(x)dx. А что если вместо dx взять величину g(dx) -> 0 при dx -> 0
При стремлении аргумента dx к нулю g(dx) превратится, в сущности, просто в линейную функцию от dx. Я полагаю что это будет эквивалентно растягиванию или сжатию оригинального интеграла по оси х.
Например, пусть g'(0)=5, в таком случае g(dx)=5dx. Итого имеем формулу:
Int f(x)g(dx)= int f(x)g'(0) dx = g'(0) int f(x) dx
Я тупанул, никакой это не диффур
ссылки на работы с таким - было бы хорошо.
Ньютоновская механика - тривиальный случай. Луркай гамильтонову механику как структуру на симплектическом многообразии и "Математические методы классической механики" Арнольда.
Пусть дано множество X. Система T его подмножеств называется тополо́гией на X, если выполнены следующие условия:
1 Объединение произвольного семейства множеств, принадлежащих T, принадлежит T
2 Пересечение конечного семейства множеств, принадлежащих T, принадлежит T
3 Пустое множество принадлежит T
Бля, да в каких случаях пункты 1,2 не будут выполняться? По-моему, они будут выполняться всегда. Это же очевидно из определения Кантором множества.
И уточнение о конечном семействе во 2 пункте зачем?
Возможно тебя смутило словосочетание "система подмножеств". Имеется в виду, что T --- подмножество P(X), где P(X) --- множество всех подмножеств X.
Кстати, есть. Гугли наглядную топологию.
Что такое псевдовектор? Почитал википедию, ничего не понял, вектор, не меняющий направление относительно отражений чего блядь несёшь.
Я не знаю и пытаюсь понять. Это термин из физики.
>>336582
>да в каких случаях пункты 1,2 не будут выполняться?
Пусть M = {a,b,c,d} - четырёхточечное множество. Пусть T = { {}, {a,b,c,d}, {a,b}, {b,c} }. Объединение {a,b} и {b,c} есть {a,b,c} - не элемент T. Пересечение {a,b} и {b,c} есть {b} - не элемент T.
>И уточнение о конечном семействе во 2 пункте зачем?
Бесконечное пересечение открытых множеств может не быть открыто.
Например, рассмотрим вещественную прямую R, откроем в ней все интервалы (a,b), a<b, и всевозможные их бесконечные объединения и конечные пересечения. В такой топологии - это известный факт - отрезки не будут открыты.
Рассмотрим следующее бесконечное семейство открытых множеств. {(-1; 2), (-0.5; 1.5), (-0.25; 1.25), (-0.125; 1.125), ... } Пересечение этого семейства есть отрезок [0;1]. Он не открыт.
Потому что ты хочешь форум по математике, а не матанализу, долбоёб.
Нет, меня интересует именно форум.
Спасибо
В клеточном автомате выразим не только Ньютон, но и Энштейн. Клеточные автоматы в общем случае Тьюринг-полные.
Тензоры.
Законы логики это не физика.
Ну смотри, клуточные автоматы работают на логике.
У физики тоже есть логика, только она своя собственная. Например, есть у нас электрическое поле. Почему вместе с ним вознивает магнитное? Ведь они никак не связаны. На этот вопрос ответить не можем пока, так как не понимаем логики по которой они работают.
dxdy
Мамашу свою репрезентируй.
Пиздос бред
>У физики тоже есть логика, только она своя собственная.
Чот чувствую себя, будто в религиозную секту попал.
Арнольда тебе уже вкинули, а всякое говно типа
> Комбинаторы, клеточные автоматы
оставь при себе
даун думает, что кв неопределенность нельзя формализовать какой-нибудь тривиальной функцией.
>не видеть разницу между математическим анализом и алгеброй
Или ты из тех пэтэушников, кто математику матаном называет?
Очередной тупорылый воняющий водкой тупорылый физик лезет пиздеть за математику
Мне действительно интересно, как ты отличаешь матан от алгебры. Скажем, теорема о том, что многочлен ненулевой степени с коэффициентами из C имеет по крайней мере один корень в C, относится к алгебре или к матану? Ведь все её доказательства используют топологию.
а тогда в сарданашвили загляни, тебе понравится
А́лгебра (от араб. اَلْجَبْرْ, «аль-джабр» — восполнение[1]) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики.
Математи́ческий ана́лиз (классический математический анализ) — совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно малых», объединяет дифференциальное[⇨] и интегральное[⇨] исчисления.
На классическом математическом анализе основывается современный анализ, который рассматривается как одно из трёх основных направлений математики (наряду с алгеброй и геометрией)
лол
Этот текст не даёт способа отличить анализ от алгебры. Попробуй ещё раз.
Прости, если я задел твои чувства. Это не потому, что я хотел тебя обидеть, а потому, что я не хочу ебаться с мужиком.
Не все, есть и чисто алгебраические доказательства.
Даун настолько не в теме, что даже не знает, что кв неопределенность - это не функция, лол.
Разве нельзя все свести к множествам и отображениям, как основе матемики?

провернул автомат в твоем анусе
>нихуя не понял о чем разговор
>развонялся на всю нить
Твое мнение очень важно для меня. Пожалуйста, формализируй псевдовекторы по бурбаки.

>оператор
>свести к множествам и отображениям
У меня есть одна охуительная картинка на этот случай.
А вот и она.

Если нужно что-то подобное, то смотри во 2 томе Лорана Шварца
Смотря какого. Пустое множество является элементом множества {∅, 1, 2, 3}, но не является элементом множества {1,2,3}. ∅ не является элементом ∅.
Тем не менее, для любого множества X верно, что ∅⊂X. Ибо не нужно путать значки ⊂ и ∈.
Известно, что количество элементов в множестве всех подмножеств в некоем множестве А равняется 2 в степени n, где n — количество элементов этого самого множества А.
Возьмём множество А = { {a, b}, a, b}. В нём содержатся, как я понимаю, три элемента — {a, b}, a и b.
Тогда, следуя вышеизложенному правилу, количество элементов в множестве P всех подмножеств множества А равно 2^3 = 8.
Но пытаясь задать это самое множество Р, мы получаем ({a, b} — один элемент): Р = {∅, {a, b}, a, b, {{a, b}, a}, {{a, b}, b}, {{a, b}, a, b}} — всего семь элементов, хотя должно быть, как мы видели, восемь! Почему не хватает одного элемента? А потому что по комбинаторным правилам этим элементом должно являться множество второго и третьего элементов исходного множества: {a, b}, но у нас оно уже есть, потому что содержится в изначальном множестве А, а элементы множества, как известно, не могут повторяться!
Внимание, вопрос: так, блядь, где я ошибся? Ведь согласно формуле должно быть восемь элементов, а из-за первоначального набора приходится избегать повтора и выходит на один меньше! Почему? Что я не понял?
Ебучая, блядь, теория множеств. Абсолютно неудобная.
|S| = 1000, n = 50
Точное решение не нужно.
Мне кажется что-то подходящие должно быть в discrete optimization, но мне пока не удалось ничего найти. Может кто-нибудь что-нибудь подсказать?
И что бы понятнее было: S - множество строк и его первые элементы могут выглядеть так: {alice, bob, cat, dog, abu, 2ch, ...}

Нет. Ты написал множество их двух элементов: {a, b} и пустого множества.
Спасибо! Всё понятно.
$s_i^2 = 1$, $s_i s_j = s_j s_i$ для $|i-j| > 1$ кроме $i=0,j=n$, $s_i s_{i+1} s_i = s_{i+1} s_i s_{i+1}$, но только ещё и $s_0$ и $s_n$ в таком же соотношении, как будто они рядом $s_0 s_n s_0 = s_n s_0 s_n$. Как доказать что эта группа изоморфна $S_{n+1}$ полупрямо на решётку $Z^n$ ?
Мне даже лень комментировать.
Откуда?
А ты ещё ничего не доказал и не создал, уныло, да?
Даже Мочизуки прочитать не в состояние, что ты делал всё это время? Пил ягуар в 8 классе вместо того, чтобы изучать топологию? Выпились
Он мёртв, например, так что выпиливайся
Многомерная матрица.
Тензор над пространством V - это вектор из тензорного произведения нескольких экземпляров пространства V и нескольких экземпляров пространства Vd, двойственного к V.
Тензорное произведение векторных пространств A1, A2, ... , An - это векторное пространство V, снабжённое отображением g: A1×A2×...×An→V и обладающее следующим фундаментальным свойством.
Обозначим символом A декартово произведение A1×A2×...×An.
Пусть E - любое векторное пространство, и пусть f - любое полилинейное отображение из A в E.
Тогда существует единственное отображение h:V→E такое, что для любого x из A верно, что f(x) = h(g(x)).
Это универсальное полилинейное отображение. Совсем грубо говоря — к обычным векторам добавлена операция крест в кружке (типа умножение, это и есть «отображение»), можно раскрывать скобки в линейных комбинациях («полилинейность»). «Унивесальность» означает что больше ничего делать нельзя.

Вы только посмотрите, кое-кто пытается в перефорс.

Хрень какая-то.
Концепции, обычно, ничего не изучают. По-поводу топологии можешь почитать хороший ответ тут: http://math.stackexchange.com/questions/60152/motivation-behind-topology
Ничего не изучают - они отражают некоторые явления или взаимосвязи в реальном мире или в манямирке математика. Или не отражают.
Со всего, лол.
Что изучают явления?
Что изучают явления?
второй судя по пику
Привет. Что изучают явления?
Спасибо. Хотя конструкция всё ещё выглядит неестественной, но суть я, похоже, понял.
Для чего интересуешься?
Но мне 14
бамп
Ну тогда общий способ синтеза механик.
Ну поясни тогда как.
Это Что изучают явления? не я писал. Мне интересны абстрактные механики. И синтез и/или определение механики в рамках математики.
Хули все так эклектично? Вот, например, есть язык, из него можно составить любую поебень, а в математике не так? Суки, где базис и основания?


Вавилов умный, но ебанулся. Впрочем, его ёбнутость пока ещё не зашла далеко и не вредит работоспособности. Просто фильтруй все лишнее.
А что такого особенного в отношениях, что матан не должен их изучать? Например, отношение на R геометрически представляет собой какую-то область на плоскости. Естественно, это изучается в матане.

И вот тут ВНЕЗАПНО захотелось понять в Фурье-образы, ибо через них работает быстрое сравнение изображений, а через сабж - поиск фрагментов в компьютерном зрении.
Посоветуйте источников, чтобы прокачать матан с нуля? Читал википедию и охуевал - каждое второе слово непонятное. Причем в вузике этого преобразования Фурье то и не было нихуя, были ряды, а это совсем другая ебань.
Ты произвольную функцию как t представил, у тебя уже нет права считать t рандомной переменной, следовательно t' в данном случае уже не 1, а... f'(x).
Линейный оператор, свертка, равенство Парсеваля, гильбертово пространство, функция хевисайда, дельта Дирака, пространство Шварца.
Блять, кто все эти люди?
Моя собака любит Педигри.
Рудин. Только упражнения не пытайся делать, они там пиздец сложные. Просто просматривай все упражнения и делай самые простые и самые важные.
От "энциклопедия".
интересно просто, что это за место где об линейных операторах не знают.
Легко там всё.
Сначала раскрываешь скобки, а потом сворачиваешь по теореме Христоса-Шварца.
Курс по ссылке не смотрел, но имеющиеся в сети книги за его авторством (конкретная теория колец и конкретная теория групп) содержат кучу отсебятины, минимальное количество общеполезного материала и вообще отдают фриковатостью. Подозреваю, что курс состоит из того же самого.
Современная алгебра - это алгебра Ленга (современное издание) или любой аналог, Атья Макдональд или Matsumura по коммутативной алгебре и Weibel по гомологической алгебре. Для "чтения более-менее современных статей" этого недостаточно, но знать это необходимо, т.к. эти сведения считаются общеизвестными.
>имеющиеся в сети книги за его авторством (конкретная теория колец и конкретная теория групп)
Гораздо интереснее поговорить о его теории множеств, http://rghost.ru/6XGdThvR4
Можешь ли ты подвергнуть критике эту книгу?
Есть серия годных лекций по абстрактной алгебры?
Само собой.
Лично мне очень нравится.
>>337390
>содержат кучу отсебятины
Да.
>минимальное количество общеполезного материала
Нет. Материала у него наоборот больше, просто излагается неспешно.
>и вообще отдают фриковатостью
Ничего подобного, если, конечно,
фриковатостью не называть всё, что немного отличается.
>Подозреваю, что курс состоит из того же самого.
Неправильно подозреваешь, вообще записанные лекции у него заметно «стандартнее».
Посмотрел первую лекцию на ускорении 2x. За первые сорок минут он рассказал историю алгебры, напал на христианство, продемонстрировал русофобию и англоманию, прорекламировал теорию категорий и гомологическую алгебру, рассказал про своих крутых предков, а также высмеял специалистов по дифференциальным уравнениям с их страстью писать триста статей про решение одного дифура.
Затянуло. Смотрю дальше.
Вавилов плес
Не буду и пытаться, т.к. вообще не разбираюсь в этой теме
>>337390
Они весьма многочисленны - есть видеолекции матфака ВШЭ и НМУ, плюс куча курсов от MIT, Гарварда и т.д.
На самом деле, почти все содержат стандартный материал:группы, кольца, поля, линейная алгебра, теория Галуа, с включением чего-то из коммутативной алгебры или алгебр Ли на усмотрение автора, так что особой разницы что смотреть по-моему нет
Под "минимальным количеством общеполезного материала" я подразумевал не полную бесполезность, а лишь сомнительность а качестве базового учебника. Простые идеалы и спектр кольца в последней главе - слишком странное решение чтобы быть оправданным.
Только что досмотрел до содержания курса Вавилова, как его видит Вавилов. В содержание входят теория представлений, полилинейная алгебра (ну, поливекторы), теория категорий и (sic!) гомологическая алгебра.
>>337405
Это не учебники, это объекты искусства, о чём он ещё во введении заявил. Разве тебя не заинтересовал факт, что почти все эпиграфы в книжке выдуманы лично Вавиловым? Об этом он сам предупреждает.
А Algebra 3 - на третьем
>Под "минимальным количеством общеполезного материала" я подразумевал не полную бесполезность, а лишь сомнительность а качестве базового учебника.
Пожалуй, согласен. Слишком много отвлекается.
>Простые идеалы и спектр кольца в последней главе - слишком странное решение чтобы быть оправданным.
То, что лежит в интернете по теории колец — адово сырое. Это черновики всё, выложенные не автором.
Вполне доработанная первая часть теории групп: http://ir.nmu.org.ua/bitstream/handle/123456789/19792/db5229cc07d857754e34fe4a61b6cbda.pdf?sequence=1
намного законченнее демонстрирует стиль сабжа.
Ну ОК, "объект искусства" так "объект искусства", на вкус и цвет все фломастеры разные. Я также готов признать способность тов. Вавилова написать вводный курс алгебры для второкурсников - вопрос закрыт.
>>337411
а где тогда искать полную версию, есть ли она в природе?
Никак, блеать, перебором, если про функцию ничего не известно и там в принципе значения в каждой точке могут быть любыми, никак не зависящими друг от друга — какие тут могут быть методы. И что значит «точное решение не нужно», вообще пушка.
> если про функцию ничего не известно и там в принципе значения в каждой точке могут быть любыми
Там не всё рандомно, закономерности есть. Но нужен метод, который сам бы понял эти закономерности.
> что значит «точное решение не нужно», вообще пушка.
Может я не так выразился. Мне не обязательно нужен глобальный минимум, достаточно близкого к нему значения.
Интересная задача.
Как насчет исследовать функцию методом градиентного спуска, получить набор описывающих минимумы векторов, затем скомпоновать на основе твоей таблицы похожие вектора и, подставив, сравнить значения?
>>337442
>>336893
один хер придется перебрать весь массив, чтобы знать что есть минимум. а когда перебрал уже и знаешь какой минимум.
да,годная тема
так это оно и есть, только подбираются алгоритмы подбора, а не тупо варианты. типа первая производная брутфорса по методам лол
ну он предлагает сперва взять и прогнать вообще все возможные значения через эту функцию. и уже заранее знать что в точке м должен быть градиент. после чего, когда соберешся сортировать конкретный массив, предлагает подставить эти, заранее известные значения. и проверить оно канает на самом деле или нет.
Первак, марш с двача нахуй! Ща Хана позову, он твою life сделает miserable.
А у меня получилось, что производная любой дифференцируемой функции равна 1.
f'(x)=[сделаем замену t=f(x)]=t'=1
Пагни, есть ли смысл вкатываться в математику (для себя), с бездуховной литературы?
https://sites.google.com/site/scienceandmathguide/subjects/mathematics
Годны ли эти книжонки, читал ли кто? Или не выёбуваться, и читать на русском?
Нет, необязательно. Главное, что каждый курс занимает 1 семестр и проходить курсы надо именно в таком порядке.
> есть ли смысл вкатываться в математику (для себя)
нет
> Годны ли эти книжонки, читал ли кто? Или не выёбуваться, и читать на русском?
Рудин норм, остальные хуйня.
Я просто сделал более сильное утверждение. Из того, что нет смысла вкатываться в математику для себя, следует, что нет смысла вкатываться в математику для себя по любой литературе.
> сложения и вычитания между реальными числами и мнимыми быть не может.
Когда мы работаем в C, под вещественными числами мы имеем в виду не вещественные числа, а подполе C, изоморфное полю вещественных чисел, так что все может.

Вы видите копию треда, сохраненную 12 марта 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.