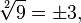Вы видите копию треда, сохраненную 12 мая 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Некоторое множество попарно непересекающихся отрезков прямой покрасили в белый цвет. Может ли так случиться, что на любом отрезке есть белая точка? (Точка отрезком не считается).
Предыдущий: >>343958 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
Че тут решать? Красишь рекурсивно как множество Кантора строится и все. К тому же эта задача была тредов 20 назад.
И что - всё? Во множестве Кантора есть дырка в центре. Любой отрезок, лежащий целиком в этой дырке, не будет иметь белых точек.
>>346795
Недостаточно формально описана процедура помещения. Если принять её без оговорок, то ясно, что в результате этой процедуры получится бесконечное множество отрезков, зазоры между которыми равны строго одной точке. А это невозможно. В самом деле, всякий отрезок содержит рациональную точку, и, так как отрезки попарно не пересекаются, можно инъективно отобразить множество отрезков во множество рациональных чисел, то есть отрезков не более чем счётное количество. Зазоров между отрезками тоже не более чем счётное количество, таким образом. Но R несчётно.
Если зазор больше чем одна точка, то в него на каком-то шаге вставлен отрезок.
Ну это верно. А как из этого следует, что существуют 2 отрезка, между которыми зазор 1 точка?
А почему их не существует? Отсутствие доказательства существования не равно доказательству несуществования.

Я не понял, а чем тебя множество Кантора не устроило?
>>346791
> Во множестве Кантора есть дырка в центре.
Наоборот там белая область.
Берём отрезок [0;1]. Начинаем строить множество Кантора. На первом же шаге выкидываем интервал (1/3; 2/3).
В этом интервале есть много отрезков, но на них не будет ни одной белой точки.
Ну ты на картинку можешь посмотреть и сопопоставить с условием задачи? Видишь на картинке белое посередине? То есть мы покрасили прямую так, что множество черных точек совпадает с множеством Кантора.
Лол!
thanc you mr. ornold
Кастрации-тред ниже по течению.
В радиаче годный тред - электростимуляция для секса. Аноны проектируют высоковольтный еба девайс и экспериментируют на себе с параметрами и формой импульса.
Палю годноту. Берешь утюг, отрезаешь шнур, оголяешь с конца, суешь себе в очко, второй конец, с вилкой, - в розетку. Профит! Базарю, захочется еще.
Дуралей, очком сожмёт зачищенный конец и кроме вылета пробок ты ничего не добьёшься.
Какой же ты тупой, сука...
Ты можешь прочитать построение множества Кантора на википедии и чуть-чуть ее изменить? Просто невозможно быть таким тупым.
Че за тупой вопрос?
Это следует из определения экспоненты. Есть несколько эквивалентных определений и в зависимости от определения по-разному доказывается, что (e^x)' = e^x.
Если "чуть-чуть" изменить конструкцию, то получится не канторово множество, а что-то другое. Свойства этого другого нужно изучать заново.
> зазоры между которыми равны строго одной точке
На прямой нельзя выделить два отрезка такие что зазор между ними равен ровно одной точке, так как из этого следовало бы что существует два таких вещественных числа что между ними находится ровно одно другое вещественное число. А это неверно - между любыми двумя вещественными числами (не равными друг другу) находится бесконечное количество других вещественных чисел. Следовательно, какое бы мы множество попарно непересекающихся отрезков прямой не выделили, на прямой будет еще оставаться бесконечно большое количество отрезков не входящих в выделеное множество.
Мне кажется то что английская - это уже большое дело. А так это же просто справочник определений. Гуглить надо. Англогугл умный - он сам куда-надо приведет. Хоть на stack/math exchange, хоть pdf предложит с сайта универа какого-нибудь. Ну и учебники качать. Мне кажется у английского большое приемущество - на нем много всего, и в основном годнота из проверенных источников.
Вот мне как школьнику понятнее всего по-тупому - графически. На графике экспоненты в каждой точке касательная (что есть тангенс угла наклона, что есть производная) равна самому значению функции. По-моему достаточно интуитивно. Можешь сам попробовать - прицелься в точку на эксопеньте и прочерти касательную и померяй отношение dy/dx - охуеешь. Будет само значение ф-ции. правда хуй так касательную точно проведешь, скорее всего
А число элементов не должно быть простым? Я не шарю если че, просто наугад сказал.
Возьми, например, функцию 2^x. Наклон ее касательной в точке (значение производной) будет меньше значения самой функции в той же точке. Теперь возьми функцию 3^x. Значение ее производной в точке будет больше значения самой функции. Очевидно, что в диапазоне между 2 и 3 будет такая функция (что-то там)^x, для которой значение производной в точке будет равно значению функции в той же точке. Это "что-то там" и определено как e.

Z_3[x]/x^2+1
Есть стандартная колода из 36 карт, 4 масти по 9 карт. Мы тянем 9 карт. Как расчитать вероятность того, что среди этих карт не будет карт какой-то одной масти? Вот есть 36! вариантов расположения карт. И хули с ними делать?
Ладно, это не домашка, просто я начал разгребать свои знания комбинаторики после универа и просто даже думать не могу. Но без наращения базы это тяжеловато сделать, а все базовые знания восстанавливать это не один месяц уйдёт.
И задачка не про игральные карты, а про ККИ, но мне стыдно в этом признаться даже на анонимной доске.
Ну от этих хз, но ты же матан абстрактным назвал. Матан дал миру производные например. Первая производная от скорости - ускорение. Элеткроны ускоряются и замедляются, порождают ЭМ поле, приебошим антенну - получим ЭМ излучение и полетим к звездам. Профит. Если бы не было такого перевернутого треугольничка-оператора, не было бы уравнений фарадея, т.е. вообще бы не было бы нихуя. Я так щитаю.
блять максвела имел ввиду

То есть в мире математики такая же хуйня как и с физикой? Открыли бозон хиггса/грави волны, а чё теперь с этим делать пока что хуйевознает?
Про какой выхлоп ты говоришь? Хочешь чтобы гомологиями тебе картошку пожарить можно было?
Почему хуйня. Математика дает им тулзы, без которых они нихуя не могут. А если они из тулзами нихуя свои теории подружить не могут - not our problem, bitches.
А хули бы и нет? Ньютон же помог запускать космические зонды по нужным траекториям. Просто мне интересно, что в современном мире может предложить доказанная теорема ферма?
Поможет создать самое разрушительное оружие в истории человечества. Если оно и пожарит тебе картошку, то только вместе с тобой.
Владимир Игоревич, залогиньтесь. Мы тут все - убежденные бурбакисты и вы нас не переубедите!
Интересно, а что физики думают про бурбакизм? До них как-то брызги долетают?
Думается мне, что они согласны с Арнольдом. Абстрактная математика их интересовать не должна.
Скажите, пацаны, а бурбакизм это в принципе клозетное явление? Я имею ввиду в универах их изучают? У нас, или в сшаке, или нигде кроме франции? Ну может не прямо по книжками, а например фанаты-преподы определения/нотацию заимствовывают? Скажут типа, сегодня пацаны будем проходит 2+3 по бурбаки. Кстати я им имейл послал на bourba!|WkiANUSeen!nsPUNCTUMf47wr чисто из любопытства спросить - кто у них сейчас под бурбаками пишет. Нихуя не ответили суки. Ведь имена же известны из прошлых, значит не тайна в приницпе.
Что в твоем понимании 2+3 по бурбаки? Элементы формализма даже дети в пятом классе учат. Кнут вон еще символ опасного поворота подсмотрел.
Ну это я так, для лулзов Арнольда процитировал. Я просто интересуюсь, оказывает ли бурбакизм влияние на школьную или универскую программу в мире и в каком виде.
Нет.
Они про него ничего не думают, для них даже теория множеств - слишком абстрактная и потому ненужная хрень. Все их потребности ограничиваются таблицей производных и разложением в ряд Тейлора. Немногочисленная элита ещё использует ряды Фурье и таблицы оригиналов и изображений. Но не больше.
Они не умеют в абстракции. Даешь им N-мерную модель мира, а они говорят - ну мы же в 4-х мерном пространстве живем. Ну ебта подставь N=4.
>А что же по-твоему? Возникло в физике из сугубо физических соображений
Возникло-возникло, ля-ля-тополя. Мало ли чего где возникло. Только вот современная матфизика - это такой раздел математики для самых аутичных математиков. Реальные-то физики обо всех этих теориях представлений квантований какой-нибудь хуйни никогда никого и не просили вообще.
Поясни мне подробнее за эти определения. Через пределы я определение экспоненты понял.
Поясни мне подробно почему именно 2.1718281828 и т.д. взяли, почему это число при любой степени остается неизменным, т.д.
Короче. Сейчас понял, что математика выполняет функцию универсального языка. Собственно на этом языке написаны различные работы, которые мне интересны.
Есть какой-то роадмап, с чего начинать, как и по каким книгам продолжать изучение математики? Ожидаю, что анон в этом треде должен знать винрарные учебники, написанные людьми, которые реально хотят и могут тебе пояснить, что и почему. Просто абстрактная нечитаемая хуйня из набора теорем и формул - это конечно круто, но в плане обучения, а особенно самообучения, это пиздец.
Мой уровень - школа. Матан, и алгебру из универа уже почти не помню.
Собственно проблемы - не могу себе представить всякие сложные интегралы кроме НУ ТИП ПЛОЩАДЬ ТАМ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ КОРОЧ, смутно очень себе представляю, что такое дифференциальное исчисление и никогда не решал диффуры. Ну и все, что "дальше" по нулям.
В первую очередь хочется приобрести именно понимание основных концепций и интуицию.

В точности 28.
Из внутренней точки, являющейся общим концом нарисованных отрезков, проведём по отрезку в каждую из вершин квадрата. Дальше вспомним, что площади треугольников одной высоты на равных основаниях равны. Дальше элементарно.
вот этот, вроде, не совсем дебил.
>дауны из бэ
ты такой же даун, если полез к даунам это выяснять.
AD равно BC в таких случаях или нет? Получается 28 самым легким путем
Соси хуй, быдло.
Никакого бурбакизма не существует. Определения/нотацию у них заимствовывают все.
Человечество становится умнее.
По книгам сложно, живой препод намного круче. Программы для нубов хз, тоже не видел ничего такого, найдёшь -- пиши.
Можешь попробовать посмотреть для начала лекции Арнольда для школьников (например лекция https://youtu.be/qDrrkbf15Ow просто рассказывает об интересных вещах, показывает красоту связи разных разделов математики), почитать что-то типа "How to Prove it" и "Survey of modern algebra". Геометрические книги для нубов хз какие есть.
https://ru.wikipedia.org/wiki/Шень,_Александр_Ханиевич
Можешь посмотреть его книжки с прибаутками для школьников, тебе как раз.
Тебе нужна наивная теория множеств и логика (чтобы уметь доказывать и понимать доказательства, разворачивать абстрактные определения в более элементарные формы, на которых проще видеть, что что-то верно или неверно), какое-то понятие об алгебре и символьных манипуляциях. По идее какое-то введения в геометрию тоже надо, попробуй "Занимательная геометрия" Перельмана (ну и посомтри другие его книжки).
Дальше уже берёшь работы, которые тебе интересны, смотришь, какие разделы математики там используются. Изучаешь их. Пытаешься читать работу. Находишь, что непонятно, проясняешь в книжках или самостоятельно смысл сказанного и т.д.
мамкин-домашний-математик
When you read a problem, for example prove that something is an isomorphism of something else do you actually visualize the structures as geometric objects in your head?
I recently started abstract algebra and I have no idea how anyone could come up with all that. I feel exceptionally retarded when i fail to prove most theorems or see the connections and relations between structures and morphisms.
Лучше пусть читает Википедию.
Одной теории недостаточно, она не вкладывает в понимание изучающего всех аспектов - для цельной картины нужно решать задачи.
Ответил английской пасте.
>Собственно на этом языке написаны различные работы, которые мне интересны.
Какие именно работы тебе интересны? Может тебе вовсе и не нужны никакие основные концепции, а просто следует прочитать один параграф из Зорича.
Да хуле ти доебался до меня, лох?
In matematic world matematica delaet trud matematicom
Мать еьал, тупица
Че то с падежами я не могу разобраться в это фразе. Математика (она) делает кем-то что-то? Или как это отпарзить блять
Oche tolsto.
Так как отрезок состоит из точек, то значит, что ты пидор.
Школоло мамкин математик на связи. Я думаю с интегралами проблемы потому что небось пять минут объясняют а потом год-два ебошишь тупые табличные интегралы. Я сам выучил - не поверишь - одновременно учась программированию. Двойной интеграл - это же объем, то есть двойной цикл по х и у. Допустим вычисляешь объем квадратного хуя, в смысле с прямоугольным основанием (для простоты). Ставишь хуй в плоскть xy залупой смотрит в z (наверх). Нарезаешь основание на квадратики и в высоту у тебя получаются столбики (такие квадратные цилиндры). И у них высота естессно будет разная, то есть от пола до залупы, которая есть полушарие. Вот твой двойной интеграл - это сумма площади каждого такого квадратика dx*dy умноженная на высоту до залупы (значение ф-ции f(x.y) если по-умному). А вот с тройным я сперва наебался, думал что это тоже объем, а хуй там - объем только если f(x.y.z) = 1. А так это 4D. То есть 3D + значение ф-ции, например плотность, тогда вычисляешь массу куска говна переменной плотности. На жабе это тоже хуета - тройной цикл. Вот это интересно, а не что примерчики решать с ебаными интегрированием по частям, это я нихуя не знаю и это скууучно.
Да забыл сказать, формула залупы z=x^2 + y^2.
Пацаны, а кто-нибудь может запилить формулу сисек? В принципе это сумма должна получиться двух таких залуп, только я не поймку как соски вычислить? Как вообще к таким задача подступиться?
А мне кажется наоборот - нахуй теорию. В смысле пруфы. Правда где-то посередине. Когда нихуя не объясняют, но дрочат тупыми задачками - это отстой. Но другая крайность, когда тебя пруфами ебут - тоже не очень. С теми же производными и интегралами нужно объяснять на пальцах физсмысл и давать несколько примерчиков "на закрепление" и все. Вот для этого интернеты хороши.
Хм, звучит красиво. Пока пытаюсь хотя бы в 2D. Так понимаю кол-во горбов = кол-во крит. точек где производная нуль. Допустим нам жопу нужно нарисовать. То есть три горба, значит полином 4-й степени? А дальше можно коэффициентами полужопия рихтовать чтобы из няшной попки получилась жопент жирухи! Это охуенно, надо попробовать. Только я не понимаю, настоящую 2D жопу же сделать не получится - это же не гладкая ф-ция или как это правильно называется, там в это жопном переходе какая-то сингулярность, в смысле предела же нет где булки стыкиваются, значит и производной быть не может?? Как это описать??
Ты тню себе запилить хочешь, чтобы с ней листвы лишиться?
Помнится Вольфрам про это что-то писал, погугли.
Да, такая ламповая полиномная тня. Я могу сктати целое векторное пространство их запилить. То есть как я себе представляю в полиномном в.п. каждый тюпл (ок ок вектор!) это набор коээфициентов полинома n-cтепени. Если тянка состоит только из жопы и сисек (чтоб не пиздела и денег не просила), то примем n=4, больше ей и не надо. Вот только вопрос у меня, аноны, а как базис задавать и что это вообще в полиномном в.п.? Это же вам не эвклидово пространство. Просто сам полином без коэффициентов и будет базисом? x + x^2 + x^3 + x^4? в принципе он же будет linearly independent и мы сгенерим из него все жопопсисечное пространство тянок из соотв коэффициентов?
Фи, так неинтересно

С меня как всегда
в голосину
производная от тета-функции(функции хевисайда) это дельта функция, дельта функция умноженная на икс есть нуль.
>>347373
>что такое интегрирование
Если F - это σ-алгебра, то, работая в топосе пучков Sh(F), операция интегрирования по Лебегу - это естественное преобразование D × M → M. Где D - объект, являющийся дедекиндовыми вещественными числами в Sh(F), M - пучок мер на M.
Всё просто же. Смотри учебник Matthew Jackson.
У тебя сосач вместо гугла теперь? Куча народу занимаются КА, хуярят статьи, книги и конференции.
Game of Life просто демонстрирует сложное поведение при очень простых правилах.
>>что такое интегрирование
>Если F - это σ-алгебра, то, работая в топосе пучков Sh(F), операция интегрирования по Лебегу - это естественное преобразование D × M → M. Где D - объект, являющийся дедекиндовыми вещественными числами в Sh(F), M - пучок мер на M
Абсолютно бесполезное определение.
Ты охуенен, анон! Наконец-то я всё понел!
Почаны а по чем сейчас модно изучать абстрактную чепуху? Я тоже хочу хуярить категориями.
Известно, что матрица нечетной размерности над R имеет вещественное собственное число. Назовем его λ. Рассмотрим аннулирующий многочлен X p(x) = x^2 + 1. λ должно быть корнем этого многочлена (потому что он делится на минимальный многочлен), но у этого многочлена нет вещественных корней. Противоречие.
Как вам?
Но у Маклейна нет модных инфинити-категорий. Разве они там есть?
Подождите пацаны, но это вы нас наебать ходите, при чем тут лебег, мы же про римана говорим. Или вы в общем смысле? Кстати, а не должно там быть в определениях красивого словечка "функционал", что-то мне кажется попадалось в описании в.просранств, что как-будто интеграл это такой функционал, ф-ция ф-ций??
Задача из экза в ШАД.
Кстати тебе зачем оно надо. Мне лично вот кажется тянкам нравятся куны, которые категориями хуярят. может поможет листву сбросить??
Примеры каких либо содержательных утверждений следующих из этого определения? (Которые не следуют из других определений)
Ну вот да, хотя бы. Задвигаешь ей про функторы с предпучками и естественными преобразованиями, а она уже течет и готова отсосать, не отходя от кассы, как говорится. Охуенно же, ну.
Почему-то звездочки не отобразились
Постройте, пожалуйста естественный изоморфизм между (ΛkV) и Λk(V).



Есть верхняя полуплоскость. Как самый простой случай, взял для начала равнобедренный треугольник. То есть я могу задать все три точки ak, а неизвестными остаются лишь параметры С и С1. С1 это лишь сдвиг, а С - масштабирование и поворот, то есть вне зависимости от них должен получится треугольник нужной формы.
Но выходит пикрелейт(на вертикальные линии не обращайте внимания, это на границе где деление на 0 происходит такие баги возникают. Только квадратная сетка имеет полезный смысл). Треугольник правильной формы как-то выражен, но выходит стрёмное многолистное отображение, так что сетка дублируется, лишь оборачивая нужные вершины треугольника. Что может быть не так? Я вроде и другие треугольники пробовал, и ставил минусы рандомные в формулах, и рассчёт интеграла перепроверял.
Вершины треугольника (-10;0);(0;10);(+10;0), углы 1/4,1/2,1/4.
>>347476
>звездочки не отобразились
Они как разметка используются. Проценты тоже распепячит.

Сука, всё понял, я такой тупой, что просто убейте меня.
:)))
Что посоветуете?
Воображение
Это тоже категории.
Можете объяснить, почему
(а^2)^(1/2) = |а|
Почему, не может быть -а ?
Потому что возведение в степень не есть извлечение корня. Если ты извлекаешь квадратный корень, то будет два значения, в том числе -а. Если возводишь в степень 0.5, то всегда строго одно значение.
Правда, иногда записывают корень подрузамевая только главное значение, которое положительное.
Где это написано? Во всех источниках (в википедии то есть, лол) эти понятия - одно и то же.
Попробуй подставить конкретные значения и поймешь почему
По определению x^a. Определение, если что, такое:
x^a = e^(a ln x)
Отсюда x^a > 0. Ты, конечно, можешь определить x^a по-другому, но я тебе привел общепринятое определение.
Аноны, это какого уровня учебник? Че-то там подозрительно все просто. Небось наебка какая-то. Там же корень для понтов, в смысле не из-за корня же модуль возникает, а потому что а^2 же не может быть отрицательным? Если тупо подставить -2 например до в квадрате будет 4 и корень из 4 будет 2.

Если не ошибаюсь, то там подписано если корень арифметический в примерах дальше.
>>347985
Алсо вот, на "всех твоих источниках" есть разъяснение что корень в разных смыслах иногда берут.
Хм, точно! я же помню это наебку, но забыл.
тяжело вздохнул
У арифметического корня (радикала) ровно одно значение, которое больше или равно нуля. Радикал обозначается символом √ . Именно чтобы было ровно одно неотрицательное значение, радикал √x2 = |x| т.к. x может иметь как отрицательное так и положительное значение в силу определения операции возведения в квадрат.
Я тут мимо пробегал. То есть символ модуля просто так написан?Из-за того что корень арифметический и из под него нельзя отрицательное значение выводить, но учитывать его все-равно нужно?
>То есть символ модуля просто так написан?
Нет.
>Из-за того что корень арифметический и из под него нельзя отрицательное значение выводить, но учитывать его все-равно нужно?
Да.
Как-то нелогично все. Почему не использовать неарифметический корень и не писать +-?
почему мы просто помним, что есть отрицательное значение, но не пишем его?
это я задал изначальный вопрос про извлечение числа из под корня, если что.
>почему мы просто помним, что есть отрицательное значение, но не пишем его?
Перефразируй свой вопрос.
Почему, если корень арифметический (а из него нельзя выводить отрицательное значение), отрицательное значение всё равно надо учитывать?
В общем, в учебнике просится доказательство того самого равенства, а доказательства ещё никто сюда не написал
√х²=±х
А какая разница? Ну представь это как уравнение b=a^2.
Докажем, √a2 = |a|
В силу определения функции квадратного корня достаточно показать |a|2 = a2, а это верно т.к. является одним из свойств функции абсолютной величины.
Это не функция, т.к. для аргумента получаются два значения, что противоречит определению функции.
Для существования обратной функции, также необходимо, чтобы функция была биективной.
Может. Многозначная функция функцией не является, и я о них не говорил.
Нет. У функции кв. корня одно неотрицательное значение.
Это пример с Вики, если что. Так что я с тобой не согласен.
2 чаю
По определению корень дает положительное и отрицательное значение. Квадратное уравнение вуаля:
х²-1=0
х²=1
х=√1
х=±1
Да ну вас нахуй с вашими ололо-определениями
Дурачок? Тут корень берется из квадрата числа, вот если бы из обычного числа брали — то да.
>По определению корень дает положительное и отрицательное значение.
Нет.
Квадратное уравнение вуаля:
>х²-1=0
>х²=1
√x2 = √1
|x| = 1
>х=±1
Положительным должно быть значение арифметического корня, но корень не обязан быть арифметическим.
Для элементарных алгебраических преобразований, операция извлечения корня определяется как функция.
Ну да, я как раз и хотел сказать, что если корень определяется как функция, то он не может иметь два значения для одного х и отсюда модуль. И вроде как доказывать это не надо, так как по определению
Потому что ты ебанутый
>и отсюда модуль.
Нет. Справедливость равенства √a2 = |a| нужно было доказать, в этом состояла задача в учебнике. Из самого определения функции это не следует, определение подразумевает только единственность значения.
Да, я имел в виду только про ф-цию кв корня конечно, а не все задание целиком. Все равно видимо нужно доказать что |a|^2 = a^2
>Все равно видимо нужно доказать что |a|^2 = a^2
Можно и опереться, но если нет то:
0 ≤ a: |a|2 = a⋅a = a2
a < 0: |a|2 = (-a)⋅(-a) = a2
Сам ты раковый
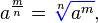
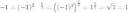
>Почему, не может быть -а ?
>пункт г
Всё дело в последовательности операций. Из неё и исходи.
В приоритете - возведение в степень. Потом - извлечение корня.
Какого лешего, ты приплёл вот сюда >>347897
степень (1/2)? Получилась хрень какая-то >>348273 + весь тред засрали.
Результат возведения в квадрат - модуль. Всё, иди со своим листиком!
А тут у нас что? Вот такая вилка...
Условие: a = 5;
Решение: 5 = 5^1 = 5^(2•1/2) = (5^2)^1/2 = 25^0.5 = 25^1/2 = √25 = -5, 5;
Проверка: -5 ≠ 5, 5 = 5; первый вариант отметается.
Ответ: вариант второй. 5.
Условие: a = -5;
Решение: -5 = -5^1 = -5^(2•1/2) = (-5^2)^1/2 = 25^0.5 = 25^1/2 = √25 = -5, 5;
Проверка: -5 = -5, 5 ≠ -5; второй вариант отметается;
Ответ: вариант первый. -5.
Так бы сразу
Че это за хуйня? Ты себя умнее википедии считаешь? Мне так не кажется.
Съебал тебе за щеку, недоучка. С каких это пор первачье, сдав первую сессию вдруг стало мнить себя математиками. О, времена!
За щеку пояснил тебе, что щека у тебя в штанах, а именно в анальной дырке отныне. А теперь съебал
я другой анон, прохманулся ответом. я тащемто всем вам луч хотел послать, засрали все какой-то хуйней по третьему кругу.
там выше правильный ответ был же
>Всё, иди со своим листиком!
На нас всех так один сажедебил влияет... Как бы от него избавиться то...
а доказательство никто так и не расписал нормально
Я вот думаю, что уже давно пора бы создать отдельный тред для нубов, чтоб они сюда не скатывались. И там все пояснять.
Ты что обиделся? Извини, люблю тебя
Хорошо. Пусть буду нормальным.
>там выше правильный ответ был же
>Результат возведения в квадрат - модуль.
>Потом - извлечение корня.
И тут же, ниже, квадратный корень из положительного - есть два числа, положительное и отрицательное.
>Че это за хуйня?
Это символы, знаки, цифры и буквы, операции. Что конкретно тебя интересует?
>Ты себя умнее википедии считаешь? Мне так не кажется.
Ты что-то сказать хотел?
Так вырази это нормально, без перехода на личности.
Нет. √9 = 3, но у числа 9 есть два квадратных корня: +√9 и -√9 то есть 3 и -3. Не нужно путать квадратный корень числа с функцией корня. Значение функции корня равно 3, что является одним из корней.
>√9 = 3
>Нет.
√9 = +3, -3
>но у числа 9 есть два квадратных корня:
√9 = +3, -3
-√9 = -3, +3
Корень чётной степени из положительного числа имеет два значения с противоположными знаками, но равными по модулю.
википедрия
Именно поэтому я предпочитаю английскую википедию.
>In mathematics, a square root of a number a is a number y such that y2 = a, in other words, a number y whose square (the result of multiplying the number by itself, or y × y) is a. For example, 4 and −4 are square roots of 16 because 42 = (−4)2 = 16.
>Every non-negative real number a has a unique non-negative square root, called the principal square root, which is denoted by √a, where √ is called the radical sign or radix.
>Every positive number a has two square roots: √a, which is positive, and −√a,
Но ведь, сперва, считается умножение, в скобках...
-а^(2•1/2) = -а^(2/2) = -а^(1) = -|a^1| = -|a| = -a
Как быть тем, кто хочет осмыслить математику, но не владеет английским? Учить английский?
Другого выхода вообще нет?
Бля, вот почему в рашкинских учебниках нихуя не понятно? Но зато даже с моим убогим знанием английского - я понимаю что написано по этой теме в иностранной литературе.
Тогда, мне кажется, было бы точнее выразить эту мысль так:
√a^2 = {-a, a} = {-√|a|, √|a|};
-√a^2 = {a, -a} = {√|a|, -√|a|}.
И даже -|a| = a
Загугли-ка, "английский за 16 часов".
Разве значения квадратного корня не является значениями функции квадратного корня при положительной константе под квадратным корнем?
Всё понятно, с твоим "квадратным корнем".
Как видно из первого примера, у вещественного корня могут быть два значения (положительное и отрицательное), и это затрудняет работу с корнями. Чтобы обеспечить однозначность, вводится понятие арифметического корня, значение которого всегда неотрицательно, в первом примере это число 3.
Что касается функции корня -
можно было бы, записать так,
√a^2 = {-a, a} = {-√a^2, √a^2};
-√a^2 = {a, -a} = {√a^2, -√a^2}.
Но тут, рекурсия в последнем значении.
Поэтому,
|√a^2| = a;
-|√a^2| = -a.
√a^2 = {-a, a} = {-|√a^2|, |√a^2|};
-√a^2 = {-a, a} = {-|√a^2|, |√a^2|};
Если ты хочешь впендюрить свои минусы перед знаком корня, как там на википедии, у буржуев за бугром.
Не являются.
Да, и ариф. корень (он же радикс) обозначается символом √
И чё?
Арифметический корень - и есть корень квадратный, с одним лишь, положительным ответом. Причём тут символика?
Название сего опуса пожалуйста, чтобы знать чего читать не надо.
И вообще, корни функции корня - не является арифметическими корнями.
Это звучит, как "корни уравнения".
Так что, забери отсюда, свой, вот этот модуль
>>348410
Так.
Есть понятие «квадратный корень»
И есть понятие «функция квадратного корня».
Квадратный корень числа a есть число b такое что b2.
Понятно, что квадратными корнями (например) числа 4 являются числа 2 и -2.
Заметь я ни разу не написал √ (кроме этой строки).
Функция квадратного корня определена f(x) = √x, где √x является обозначением арифметического корня, который по определению неотрицателен. Таким образом квадратные корни числа x выражаются при помощи f(x) как +√x и -√x.
Поскольку √x есть неотрицательное значение значит если x=a2 то √x = √a2 = |a|. Доказательство справедливости этого равенства приведено здесь: >>348146
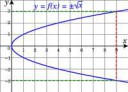
Две ветви параболы, этому историку, натолкнувшему на понятие "многозначная функция".
Ну почему же?..
Там в комплексном анализе многозначных функций - всякие такие аналитические функции, и даже красивые римановы поверхности, переливающиеся разными цветами...
Угу, а также ветви комплексного логарифма и их области сингулярности. Но по-моему это из пушки по воробьям, и функцию кв. корня вполне можно объяснить не обращаясь к понятию многозначной функции.
>области сингулярности
Ой, не, лучше там не лазить, а то засосёт в чёрную дырку и всё, и пиздец.
Да ладно, тип сингулярности определяешь по вычетам и всё.
Но здешним троллям/семиклассникам такое ещё рано.
Math stage.
Чему равен кубический корень из -8?
Правда.
Два "Корня квадратного уравнения" тебе.
>√x является обозначением арифметического корня
А речь идёт, про алгебраический корень. Обозначается также.
Я не знаю что такое "алгебраический корень". Если ты хотел сказать "алгебраическое число", которое является корнем многочлена, то это никакого отношения к функции кв. корня не имеет.
Корни многочлена (например) x2 - 4 вполне можно выразить используя функцию корня.
Психбольница ей-богу
Алгебраический (многозначный) корень в источниках часто называют просто корнем.
арифметический корень, в отличие от ранее определённого (алгебраического[5]), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно и неотрицательно. Например, квадратный корень из числа 4 имеет два значения: 2 и -2, из них арифметическим является первое.
Поскольку арифметический корень и алгебраический обозначаются одним и тем же символом, но являются разными объектами, в рамках данной статьи арифметический корень обозначается синим цветом, а алгебраический — чёрным.
Википедия.
>Если ты хотел сказать "алгебраическое число", которое является корнем многочлена, то это никакого отношения к функции кв. корня не имеет.
Да причём тут, корни многочлена ?..
x = a^2; подкоренное выражение, не многочлен.
f(x) = √x; функция квадратного корня.
√x; корень квадратный, алгебраический корень, операция извлечения корня второй степени.
a, -a; корни вышеупомянутой функции.
|√x| - арифметический корень. Одно единственное число.
Всё!
Да, здесь я ошибся. Во всех моих постах я говорил о функции кв. корня, значение которой есть радикал (ариф. корень).
Если использовать «алгебраический корень», с тем же символом то тогда есть два значения.
А вот интересно, тогда можно выразить арифметический корень через алгебраический так:
√x (ариф. корень)= |√x| (алгебр. корень)
?
Ну, и, как следствие,
>>348414
>>348426
?
Возведение, в степень 1/2
Тогда согласен.
Конечно, уже coq есть. Ввел утверждение, компуктер его доказал и не какая математика не нужна!
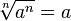
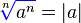
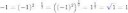
Чёрный - алгебраический.
Синий - арифметический.
Попытки возведения в рациональную степень отрицательных чисел могут привести к ошибкам, поскольку значение алгебраического корня неоднозначно, а область значений арифметического корня ограничена неотрицательными числами.
Такие дела.
Оххох, ебтить-колотить, пора запастись картофаном, по полной программе "Вербицкого", что там красуется, как монумент.
Не, лучше "три семерки", картофан в виде пачки чипсов и чупа-чупс.
а я что говорю, идет как влитая.
Суббота же, выходной. Мамка сегодня уроки делать и компутер выключать не заставляет.
А почему больше всего рака именно в мат тредах. Этот засрали, новый второй - вроде бы по идее раковник, но тоже читать невозможно.
Посещаемость мат.тредов всегда большая, и периодически рачки активизируются. Подождать нужно пару дней - и всё утрясется.
Аноны, знаю баян. Но как вы прокомментируете, эти ФАКТЫ?
Репорт.
ппояснили плс интерограл
А как?
Нас специальна обманывают учёные и правительство. Математика - выдумка и всё не работает
Опять ты
А что такое натуральные числа?
Но правда же
Дай им определение.
>>349307
Для снятия противоречий в определении действия умножения необходимо логическое и природное обоснование математического определения действия умножение по правилам РУСов. Пример: 1.три семечки просуммируем 1с+1с+1с=3с «возьмём и сложим (складируем, капитализируем)» в ящик, где они будут храниться 1год, результат как до сЛОЖения трёх семечек-3с, так и через год 3с. 2. Три семечки просуммируем 1с+1с+1с, после чего посадим их в землю и польём, солнышко их прогреет и природа начнёт производить: вначале корешки, затем листочки, цветки и на последней стадии семечки.
Определение не определяемое. Натуральные числа определяемы. Ты сосёшь мой вонючий хуй.
>Определение не определяемое.
А почему тогда это слово раздаётся из твоего рта в математической дискуссии?
>мой вонючий хуй.
Так мыться надо, хикка омежная, дебилом и останешься - но хоть не вонючим.
Попытаюсь подшутить над тобой, т.к. конструктивные ответы себя исчерпали.
>что
поясни
>это
определи сначала "это"
Что за "Что"? Что за "за"?
Это не критика определения.
А по делу - Пеано всё уже сказал, в треде всё обсосали и обоссали, problems?
Единичная матрица это всё равно что единица.
Понимаю, что сейчас в треде много школьников и прочего говна и я не получу поддержки, но имиджборды - ложь. Все они кончились после Двача. Сейчас нас обманывают, 99% постов пишут роботы правительства.
аналитическое, если вы понимаете, о чем я, коллега ;)
Нет бурбакистов и анти-бурбакистов, есть только неосиляторы с раздутым самомнением
А если неосиляторы чего-нибудь придумают какой-то костыль для того чтобы не осиливать того что они не могут осилить, считаются ли неосиляторами те, кто не осиливают этот костыль?

Ещё скажи 2+3 равно 3+2 поскольку умножение коммутативно.
Эту шутку поймёт лишь Тот(самый).

Пикрелейтед - геометрическое доказательство того, что (a+b)^2 = a^2 + 2ab + b^2.
Для доказательства того, что (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 соответственно можно применить куб и параллелепипед.
Получается, что для доказательства аналогичного выражения от (a+b)^4 нужно применить тессеракт. Как это сделать? Возможно ли это, говоря о наглядности?
Уже сделал тебе за щеку, проверяй.
Кто тебе право из под шконки вылезти дал? А ну обратно пиздуй
или вообще как-то его через что-то известное выразить нормально?
Ясно.
Он пять должен был сказать 5. Школьника не научили даже считать, зато научили абстрактной хрене с коммутативностью! Непорядок!
Вы про Арнольда что ли. Он по-моему был слегка ебнут. В одной из книжек он описывал, что когда он преподавал во франции, к нему однажды подошла мексиканская тянка с вопросом. На что он ей сказал, что ты прежде чем мне самому арнольду всякие вопросы задавать, реши-ка 100 моих задачек. И она якобы не решила правильно НИ ОДНОЙ :) Но он не удивился, и сказал, что у вас в мексике математика такое же говно как и во франции, а вот в МГУ студенты правильно решают весь тривиум за 3 часа. Но короче мексиканку он научил уму разуму и она доказала гипотезу пуанкаре, в смысле че-то там добилась в области hilbert's 16th problem и стала звездой в мексике.
Ты ебанутый? Это физика раздел математики. Математика применяется не только в физике, но и в биологии, медицине, инженерии, программировании, экономике, социологии и прочем. Математика, в переводе с греческого, дословно и означает науку как таковую. Все остальное - ее отрыжка.
Какой-то ебанутый немецкий психолог создал теорию на основе векторных пространств, куда запихнул все чуйства человеческие. При чем кажется сам по-своему определил такие понятия как "поле" и тд. Слова то все очень красивые, всем нравятся, видимо поэтому.
Что математика применяется везде, даже там, где вроде можно было бы обойтись, и пример отрыжки. Это было в ответ на "математика применяется и везде ее отрыжка". А об чем тема, маня?
И этой мексиканкой был Гриша Перельман?

>И она якобы не решила правильно НИ ОДНОЙ :)
А ты эти сто задачек видел? Я тоже ни одной не решу, просто потому что мне это нахуй не нужно.
https://mipt.ru/dafe/upload/abf/ArnoldMathTrivium1-arphceleape.pdf
> Я тоже ни одной не решу, просто потому что мне это нахуй не нужно.
Нет, всё дело в том, что у тебя безнадёжно упавший уровень математической культуры. Очевидно же.
> Я тоже ни одной не решу
Ну там есть задачи, где нужно численно посчитать интеграл. Не знать, как численно считается интеграл - это реально зашквар.
Ебанутый, всё что ты сказал это лишь малая часть физики. И да, математика - это часть физики. Так Арнольд сказал!
*из тривиума - самофикс
Я просто не буду заходить в такие ситуации. Ну хотят люди бессмысленно и беспощадно брать интегралы и вычислять сотые производные - ну ок, это их дело, не моё. Я лучше на семинар к Каледину схожу.
пиздец хуйня какая-то. нахуй мне решать эти ебнутые интегралы. как это повысит мой математизм?! диды, такие диды...
Они бы поднимали, если бы ты сам метод их вычисления с нуля придумывал. Но т.к. форма подачи это не подразумевает, то это просто механическое зазубривание фокусов, придуманных умными дедками из 18 века.
Вербитоблядка принимаешь меня ты за? Я гомологиям не обучен, ни разу не математик тащемта.
А чем интегралы поднимают? Как только ты себя представил что это такое, дальше же просто тупой процесс заучивания формул и способов интеграции.
>>350191
С воображением напрячься надо. Не будешь же ты топологии с вычислением площади сравнивать по сложности восприятия.
Просто даже хотя бы потому, что нафига делать то, что делали совковые диды. Ты же не слушаешь аллу пугачеву. Интегралы это такой же зашквар.
В твоей топологии тоже много заучивать надо, одних определений дохуища.
>С воображением напрячься надо. Не будешь же ты топологии с вычислением площади сравнивать по сложности восприятия.
Но ведь ты все равно пользуешься заученными приёмами, а не сам всё придумываешь?
я не тот чел, но
В топологии(точнее при её изучении) гораздо меньше узконаправленных техник, которые нацелены на борьбу с конкретными классами уравнений/интеграллов/и тп зато куча всяких очень концептуальных вещей. Вот придумал ты гомологии и хрясь в этом формализме целая куча задач недоступных раньше раскалывается как орешки. А научился ns считать интегралы от такого-то класса функций идей никаких ценных не узнал(обычно).
Кроме того когда обмазываешься интегралами, то гораздо больше рутины всякой омерзительной.
Arbeit macht frei!
Чтобы порешать тривиум Арнольда, считаться тру-математиком и унижать бурбакистскую мафию своим скиллом, конечно же. Но так как я не умею в интегральчики, приходится интересоваться гаммологиями.
>Чтобы порешать тривиум Арнольда, считаться тру-математиком
>унижать бурбакистскую мафию своим скиллом
Вся печальная суть современной математики по Гротендику(см. "Урожаи и посевы"). Раздувание ЧСВ и меритократия во все поля. Содержание(aka Суть) и интерес к предмету - вторичны.
Ну ладно, не печалься, я шучу. Но интегральчики действительно был бы не прочь брать, хотя гомологии бы на них не променял.
>Раздувание ЧСВ и меритократия во все поля. Содержание(aka Суть) и интерес к предмету - вторичны.
Словно что-то плохое. Я вот в своё время к бурбакистской мафии примкнул только за тем чтобы хуесосить картафанщиков.
Ну надо же кого-то хуесосить...
>хуесосить сторонников теоретико-множественного подхода дидов.
Просто попроси их дать определение N.
Но это же хуесосинг со стороны оснований и матлога, а не категорного подхода.
>Читал про топосы, нихуя не понял
Выясни причину, по которой нихуя не понял.
inb4 "я тупой": эти два слова не являются причиной, это просто затычка для вопросов
тут в них никто не разбирается
Блядь, всю голову уже сломал.
Сдвинутый по осям параболический гипереблоид. А не, вру - эллиптический параболоид. Ещё проще - парабола, повернутая вокруг оси симметрии. Сдвинутая на dx, dy, dz > 0.
Блядь, я геометрический смысл нихуя не понимаю, и преобразовать в циферки не смогу. Скажи, какое должно быть условие, что бы в точке минимума все переменные были положительны? И как примерно должно выглядеть такое уравнение.
Да вы что, подцоны, хуесосить кого-то всегда надо - это же аксиома. Иначе зачем мы на дваче. Сидишь, пишешь научную работу домашку делаешь, и уже невмоготу, пришел сюда - кого-нить отхуесосил и полегчало. Для этого надо математику подтягивать. Тогда можно аспирантом претворяться и хуй кто догадается.
Блядь, дайте мне просто уравнение. У меня труба горит, целый день потратил и нихуя не смог придумать.
Пик отклеился
Можно, это же линейная ф-ция
За рядки-рядочки тебе бы Тот пояснил. Тут никто не будет, т.к. ими дидов не похуесосишь. Кстати, рядочек просто считается вроде бы - вверху арифм. прогрессия, внизу - геом. Но чёт усталый и ленивый я, поищи по запросу "арифм. прогрессия в числителе геом. в знаменателе". Да прибудет с тобой Равшан Рамануджан!
За рядки-рядочки тебе бы Тот пояснил. Тут никто не будет, т.к. ими дидов не похуесосишь. Кстати, рядочек просто считается вроде бы - вверху арифм. прогрессия, внизу - геом. Но чёт усталый и ленивый я, поищи по запросу "арифм. прогрессия в числителе геом. в знаменателе". Да прибудет с тобой Равшан Рамануджан!
Витька, уйди. Ты ещё с комплексными числами не разобрался.

>Ни для кого не секрет, что в математике решает уровень абстракции мышления
Математика разная бывает. К примеру, придумать хитрый и сложный чит-многоходовочку(что-то вроде шахматной комбинации) для решения какой-либо задачи/теоремы - это нифига не абстрактность, а скорее ловкость ума/остроумие+концентрация и приложенные усилия. Придумать новое понятие, сформулировать гипотезу, обобщить что-либо имеющееся - там да, больше абстрактное, фундаментальное мышление.(только вот не надо 1-2-культура срач плиз)
А так - для развития довольно много решает окружение и наставник(см. видос). Ну и саморазвитие - задачки, головоломки, популярно-обзорческая-мотивирующая литература(списки давали), осиливание серьёзных талмудов, лекций и листочков. Ну и собственный интерес+способности+скилл удачи.
Ладно, запилю
>>350603
Нет, тоже стянул крупными кусками с разных мест и слил в одно. Большую часть кстати с каких-то украинских мелкоторрентов кстати у единственного сида недели две качал.
> видос
Ебать, что за поехавший. Это что-то вроде ПравоSSлавной математики и закона Ньютона во все стороны? Он адекватные вещи заливает или не случайно про эзотерику и ФОРМУЛУ ВУ заикнулся?
libgen же есть, нахуя это всё хранить? ты дрочишь на этот список что ли?
>\Бейтман Г., Эрдейн А., Таблицы интегральных преобразований. Том 1.djv
ой касатик, а вот это можно мне, только на дискете, у меня 5 дюймовый дисковод. помню мы с бабкой моей как раз познакомились, когда эта книжка вышла!
да нормуль, у меня тоже куча pdf не для дрочения, а просто че-нить ищещь, загрузил десяток другой не выкидывать же, авось пригодится. ну и накапливаются немеряные гиги. другое дело в торрентах много старинного говна без поиска и тп. лучше всего новые книжки качать они и отсканированы годно.
Можешь сколько угодно утешать себя мыслями, какой ты у мамки молодец запасливый, какую огромную работу проделал и скачать ещё хоть двести гигов книг - знаний математики у тебя от этого не прибавится. 99.9% из них ты никогда в жизни даже не откроешь. Все твои усилия по скачиванию и сортировке - хуйня собачья. Ни на миллиметр ближе к математикам и математике ты не стал.
Мог бы сказать, что он стал на пару гигов дальше от них.
Ты еблан что ли, где он говорил что-то про свои знания? Аноны попросили, он поделился. Мне лично не надо, но ему добра, а тебе луч поноса, петушок.
Гуго -> Основания математики.
Подсказка
Искомая вероятность — сумма вероятностей всех ячеек, отмеченных плюсом. Поскольку австралийцы выбираются независимо, в каждой ячейке вероятность равна произведению вероятностей соответствующих строки и столбца.
>где он говорил что-то про свои знания?
А нахуя тогда все эти книги? Ты, вырожденец ебаный, даже не понимаешь зачем нужны учебники и что из них люди получают знания. Небось, только картинки рассматриваешь, со смешных фамилий угораешь, и карандашиком хуи на полях рисуешь.
Лоль, что тебе так припекло, анончик? Не похуй ли тебе должно быть? Что за струну у тебя задели эти торентные книжечки?
>>350664
Не сри тут элементарщиной - тут илитка собралась тип, обсуждаются концептуальные вопросы и гамалогии с тапалогиями. Для элементарной математики есть отдельный тред.
На нулевой же >>349176 (OP) (OP)
>>350677
Можно сказать что после (мат.) школы, либо примерно после "базовых" курсов матана, линала, теорвера, топологии, общей алгебры. Как-то так.
Понятно. Ну то есть я так для себя внутреннюю грань и прочертил - proverbial дидов-староверов хуесосить допускается, а с домашкой сразу нахуй во второй тред.
Математический институт им. В.А. Стеклова РАН, Москва. Доктор физико-математических наук. С 2004 года работает в отделе алгебры МИАН, старший научный сотрудник. Автор более 40 работ, в том числе монографии (совместно с И.Б.С. Пасси). Область научных интересов: гомологическая и гомотопическая алгебра, К-теория, теория групп и групповых колец, теория категорий.
http://www.mi.ras.ru/~romanvm/
Ну сразу поехавший. Просто специфическое чувство юмора в связи с асоциальностью.
>И что, как ты на необитаемом острове будешь преобразования Меллина делать без интернета со своим либгеном?
Ну я себе либген скачал. А ты - страдай дальше.
Профессионально занимается эзотерикой, ездил в Индию, наркоманит вещества.


Спасибо. У меня именно такая мысль и была, но не нашел подобного среди свойств определенных интегралов.
При замене переменной в определённом интеграле пределы интегрирования тоже нужно менять, да.
Что там литий делает, да еще и молекула лития
Есть линейное дифур 2 го порядка, приводящееся к канон виду. Знаю, что любое уравнение с постоянными коэф может быть приведено к канон виду с помощью линейного преобразования и тип уравнения не меняется при невырожденной замене переменных.
сам алгоритм нахождения :
1)привести к квадратичной форме методом Лагранжа
2)ввести новые переменные
3)найти матрицу преобразования
4)транспонировать
5)выполнить искомую замену
На практике просто, в теории ступор, преподу нужно объяснить почему вводятся новые переменные во втором шаге.
Не выражается в элементарных функциях. Обычно такие интегралы берутся по частям:
∫udv = uv - ∫vdu.
∫x tgx dx = -x ln(cosx) + ∫ln(cosx)dx.
∫ln(cosx)dx - он-то и не выражается.
>преподу нужно объяснить почему вводятся новые переменные во втором шаге
Потому что это позволяет решить уравнение?..
На катоде восстановим из р-ра KCl
Но веть не обязательно через литий решать, можно же через хлор? clausen function cl2 -> Σ[1..∞] sin nx/n^2.
Главное, чтобы под картофан.
почему когда диды теоремы доказывают, они не могут без присказки "в самом деле". и так было бы понятно. ну че за хуйня, в самом деле?
Потому что ты попросил рыбу, а он спросил как ловить рыбу.
Анон с торрентом, давший 20 гиг матеши и биток - просьба зайти на ип лича по http и порту 80. Абуняша всё потёр.
хяусся абуняша, штук 30 записок затерто нахуй. это против правил что ли торренты, или опять потому что в неправильном треде?
Дай объем дискеты, порежу тебе рар.
>Форматы записи на пятидюймовые дискеты позволяет хранить на ней 110, 360, 720 или 1200 килобайт данных.
Выбран минимальный размер дискеты 110 000 байт.
75 дискет.
75 фрагментов рара в зипе, ждут тебя на рыгхосте: http://rghost.ru/6sr2HnzyJ
Вы видите копию треда, сохраненную 12 мая 2016 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.