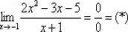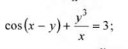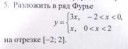Вы видите копию треда, сохраненную 15 июня 2017 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




http://pastebin.com/e38Yuj5V
Архивы тредов
http://pastebin.com/w1nJGYv4
Целый раздел по математике
https://2ch.hk/math/ (
Почти все математики ушли в /math. Но вы все равно можете обсудить ваши математические проблемы здесь. Серьёзно.
lim n->inf (n*abs(sin n))
n - натуральные числа
почему предыдущий тред не открывается в архиваче ?
Ты про этот >>392366 (OP)?
Вот он https://arhivach.org/thread/206244/
Если же про >>392615 (OP), то ветвь этого перехала в /math. Там и архивы.
Начни с Serge Lang "Basic Math", у него задания годные.
ВСЕ УВИДЕЛ СПС!
Неизвестно чему она равна на бесконечности.
https://www.google.ru/search?q=y+=+abs(x*sin(x))&ie=utf-8&oe=utf-8&client=firefox-b&gfe_rd=cr&ei=JEUnWJOaEeb37gTApoS4DA
Вот тебе график.
И какое отношение этот график имеет к пределу функции при икс стремчщемся к бесконечности?
Вопрос задавал другой анон, не я. Я просто разместил объяву указал, что такое рассуждение некорректно.
Я хотел направит его и объяснить смысл простым языком. Думая, что тот анон не очень умный. Ты ожидал более формального доказательства?
Не, я не ожидал. Просто тот анон спросил, ты ему ответил, но твой способ хоть и дает правильный ответ в конкретной ситуации, в общем случае является некорректным. То есть тот анон мог бы подумать, что всегда так можно делать, а это не так, и в итоге получилось бы распространение ложного знания, увеличение энтропии и вообще баланс силы склонился бы на темную сторону. Да, я зануда. :3
Просто лень было писать строгое формальное доказательство. Но почему это так, объяснить хотелось.
Просто лень было писать строгое формальное доказательство. Но чем это кончается, объяснить хотелось.
петянка
>читать книги вместо просмотра кханакадеми
> пики в шапке на русском
> раковый вузиковый мемас, еще и без заглавной
Найс канцер-тред.
да, ты зашел туда!
>пики в шапке на русском
Имбицил, мы на русской борде. Не нравится язык - пиздуй на форчан.
>раковый вузиковый мемас, еще и без заглавной
Мамка твоя раковая, этот мемас старше тебя. Увожай его, псина.
>Найс канцер-тред.
Это же каким надо быть дебилом, чтобы говорить о раке в 2016.
>sage
Полный даун.
>Имбицил, мы на русской борде.
>имбицил
Если мы на русской борде, почему ты так плохо знаешь русский язык?
Под шконарь, щенок.
Оно, конечно, очевидно, но если нужно формальное доказательство:
Возьмем отрезок от 2pik+1/4pi до 2 pik+3/4pi. Для любого целого k в этом промежутке будет хотя бы одно целое число m (промежуток больше 1). Синус этого целого числа m больше 1/корень(2). Видно, что выражение под пределом для подобных чисел стремится к бесконечности.

А что с математикой? Для профана она выглядит словно бездонный ковш.
Есть ли вообще какие то ограничения для математики? Существует ли некий принцип достаточности, где один математик говорит другому "Всё, тут хватит, потому что ты не создаёшь что-то новое, а пиздевово-гомотопово-хитровыебанно-через-12-мерный-континуум-поле-ландау рассматирваешь то, что ааранов и бом уже рассмотрели 20 лет назад", или "мойша, ты залез слишком глубоко, и вылез с другой стороны, хватит время тратить на бег по кругу", что то в таком духе? Просто если нет ограничений - то можно плодить сущности до бесконечности же, но интуитивно же очевидно, что где то это перестаёт иметь смысл, и всё переходит в теории о теориях о теориях о теориях, где вероятность ошибки достигает 100%.
Есть неизвестное число, в двоичном коде:
01000101 или 11000101.
Есть результат умножения его на другое, известное, случайное число.
С результатом умножения, можно проводить операции сложения, вычитания, удвоения. Умножать и делить нельзя.
Вопрос: Возможно ли однозначно определить старший бит числа, и если нет, то почему?
Казалось бы, это может помочь:
01000101 + 10000000 = 11000101
11000101 - 10000000 = 01000101
Но знак зависит от старшего бита, опять же.
И 01000101 - 10000000 = отрицательное
а 11000101 + 10000000 = 101000101
Ну смотри, начни с простого. Понятно, что все xi>1. Тогда ясно, что n<=8. Уже неплохо, но перебирать 8 вариантов нахуй надо. Давай заюзаем кое-что помощнее -- неравенство о средних. Тогда 9/n >= n/1 <=> n <= 3. Заебись. Случай n=1 тривиален, случай n=2 решается квадратным уравнением (реши сам). N=3 -- неравенство превращается в равенство, а это происходит только тогда, когда все xi равны между собой. Тогда легко понять, что x1=x2=x3=3.
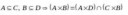
А декартово произведение по аналогии с конъюнкцией что ли работает? Какие тут вообще формулы?
В твоем случае это пары элементов множеств, так как множество индексов мощности 2.
Спасибо


к чему стремится: (x - 1/n, x + 1/n) при n -> inf?
к {} или к {x}?
μ({x}) = μ(B_n), n -> inf
μ - мера
почему из этого следует, что μ({x}) = 0?
бля, а ты совсем матана не знаешь? может нахуй эти ваши лебеги, если возникают вопросы, типа к чему стремится что-нибудь? стремится твоя интервал конечно к (x-0,х+0). причем сколь угодно близко.
Пойа - Как решать задачу
понял.
B_n, n -> inf:
(x, x), пустой интервал {}.
B = пересечение B_n = {x}.
свойство непрерывности:
μ(B) = μ(B_n), n -> inf = μ(B_n, n -> inf)
тогда:
μ({x}) = μ({}).
Counter Strike или Compiter Science? Если второй, то я могу материалов для шапки собрать.
/pr/ же
Начал читать и ты не представляешь, как я тебе благодарен. Давно надо было реквестовать.
представление числа в системе исчисления с основанием B это сумма произведений (линейная комбинация) положительного целого числа b в некой степени и чисел Ak больше нуля, но меньше b.
B=10,A1=1,A2=4,A3=8,A4=8
1488 = 10^31 + 10^24 + 10^18 + 10^08
предположим мы хотим найти вид числа x в системе исчисления меньшего основания y. Тогда поделим его с остатком. Получившийся остаток это самый маленький член в новом представлении (Почему?). Далее взглянем частное z от деления x=yz+k и поделим его на y. Взглянем на частное: z=yf+r. Число r это самый маленький член в представления числа z. Очевидно, можно продолжать деление, до тех пор, пока частное от него не станет меньше числа y, это число самый большой член в представления. (Почему?) Тогда подставим последнее уравнение в предыдущее, а получившееся уравнения в предыдущее, и так далее, получившееся уравнение будет вида x=y^(n)a+y^(n-1)b...+k, что и будет представлением исходного числа.
Пример. b1=10,b2=8, число 255
255/8=831 mod 7
31/8=83 mod 7
3/8= 0 mod 3
Следовательно: 255(10)=377(8). Проверим:
210^2+510^1+510^0=38^2+38^1+38^0
Например, 362= 310^2 + 610^1 + 210^0. В этом смысл позиционной системы записи чисел. Но видно, что степени десятки тут в принципе случайны - они от количества пальцев на руке - вместо десяти можно взять любое другое число больше 1 и посторить позиционную систему на нем. Проще всего строить на степенях двойки, тогда будут всего две цифры 0 и 1. Запись 1010 надо интерпретировать как 12^3+02^2+12^1+02^0 = 18+04+12+01= десяти в нормальной системе. Обратно тоже можно поднатужившись перевести. Для тройки будут цифры 0, 1, 2 и умножения на степени тройки и т.п. Например, 25 в троичной системе будет 25=29+23+11, то есть запись в троичной будет 221.
Поясните за монотонные и линейные булевы функции, я нихуя не понял из определения.
ИМХО, учебник сложноват для вкатывания с 0.
Но Х^2 будет стремиться хуже Х..
А если записать это, заменив X на -1+А и при этом А устремить к 0, то получится фигня, т.е. -7, если я спьяну не обсчитался.
xy dx + (x+1) dy = 0
Переменные разделил, проинтегрировал, получил общий интеграл:
Ln |y| = Ln |x+1| - x - C
После потенциирования получается:
|y| = |x+1| exp(C) / exp(x)
Как правильно избавляться от модулей, и что делать с постоянной С, у которой область значений изменилась (не у самой постоянной, но у выражения, хз как правильно сказать).
Похоже ты не послушал училку в школе.
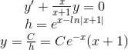
Это же линейное однородное уравнение, почему бы не решить его через интегрирующий фактор?
1 рядок - уравнение в стандартном линейном виде
2 рядок - интегрирующий фактор
3 рядок - общее решение
Тема с интегрирующим множителем будет чуть дальше, пока думаю по порядку освоить все методы.
И как все-таки от модуля над (х+1) избавляемся? Знак от раскрытия модуля "вносим" в постоянную С?
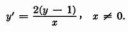
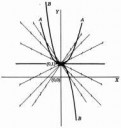
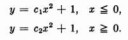
Насколько я помню, у математиков в таких случаях принято расписывать случаи: решение с одной произвольной константой до точки разрыва и с другой - после. (1 картинка - ДУ, 2 -его поле направлений, 3 - общее решение). Если вкратце, то суть в том, что если ты двигался по одной ветке параболы до точки разрыва, то нет никаких оснований для того, чтобы не начать двигаться по ветке абсолютно другой параболы после точки разрыва. Лишь в этом случае это будет действительно общее решение. Но на самом деле при использовании ДУ в реальной жизни в подавляющем большинстве случаев эти модули ни во что не уперлись и с ними даже не заморачиваются. Главное не забывать о existence and uniqueness theorem и intervals of validity для линейных уравнений.
Кстати, в рашкинской программе иногда и не дают интегрирующие множители для линейных ДУ, а дают только для ДУ в неполных дифференциалах.
Я знаю книжки туманова, понарина, алгебру и геометрию жидоШеня. Какие еще есть?
И еще желательно такую книжку в которой про линейную и высшую алгебру объясняли бы без гамалогий с тапалогеями и множаствами. Чтобы там показывали как вывели формулу для суммы первых n квадратов/кубов/тессарактов/т.д., про векторные поля, про кольца...

А все, идите нахуй я и сам понял. Квадратный корень четного числа, всегда будет четным числом. И тоже с нечетным.
На курсере есть курс. Analysis of a complex kind..
1. как учебник 3го класса
2. переменные представляю как недосказанные числа.
3. Столбиком, калькулятором, иногда разложением на "круглые" числа
А можно подробней? Как вся эта математика фиксируется? Есть какая-то привязка к геометрическим фигурам и т.д
>А формулы как представляются? Ты же не просто их зазубрил?
как соотношения между числами, записанные на бумаге.
Ну, епт, ничего нормального не находит. Лишь смотри на облачка да слова задом наперед читай.
Задавай вопрос в /матх лучше, тебе тут один школьник только отвечал. Хотя сам вопрос довольно интересный и сложный. Я не математик, так что мне вдвойне сложно судить об этом, но попытаюсь ответить. Если решаю какую-то конкретную задачу, то обычно просто пытаюсь пробовать разные известные мне методы решения, пока подсознание не найдет правильный. Это может работать просто как фокусировка на задаче, то есть смотрю на буквы и пробую с ними что-то сделать, а потом щелкает и становится понятно, либо как изменение представления, то есть я перевожу буквы из одной формы в другую, и на одной из форм щелкает и осознаешь, что вот это - то же самое, что вон то. У настоящих математиков это все происходит еще более интуитивно. С другой стороны, иногда бывает так, что ты терякшься и наоборот не понимаешь, что делаешь, не видишь общей картины, но поскольку ты знаешь формальные правила, то можешь делать следующий корректный шаг локально. То есть вот ты на пятом шаге, допустим, и не понимаешь уже, как это связано с тем, что было на первом шаге, но у тебя есть формальные инстоументы, с помощью которых ты можешь перейти от пятого шага к шестому и это будет гарантировано правильно - и уже после этого попытаться осознать, какая на самом деле связь между тем, что было на первом шаге и тем, что получилось. Вообще, математика - это в основном про то, как видеть, что разные вещи, не имеющие на первый взгляд ничего общего, являются на самом деле одним и тем же. В этом смысле это чистая, дистиллированная деятельность нашего мозга - в процессе эволюции он затачивался как раз под то, чтобы видеть паттерны и аналогии, и математика именно этим и занимается - только относительно не реального мира, а абстрактных, выдуманных систем. Да, ну а когда я не решаю данную задачу, а придумываю что-то свое, то тут гайдом в основном выступают эстетические категории - придуманное должно быть красивым, приятным, о нем должно быть приятно думать, оно должно нравиться. Опять же, у настоящих математиков это, наверное, выражено еще сильнее.
Вообще, погугли "интуиция и математика", Вейль кажется писал.
Задавай вопрос в /матх лучше, тебе тут один школьник только отвечал. Хотя сам вопрос довольно интересный и сложный. Я не математик, так что мне вдвойне сложно судить об этом, но попытаюсь ответить. Если решаю какую-то конкретную задачу, то обычно просто пытаюсь пробовать разные известные мне методы решения, пока подсознание не найдет правильный. Это может работать просто как фокусировка на задаче, то есть смотрю на буквы и пробую с ними что-то сделать, а потом щелкает и становится понятно, либо как изменение представления, то есть я перевожу буквы из одной формы в другую, и на одной из форм щелкает и осознаешь, что вот это - то же самое, что вон то. У настоящих математиков это все происходит еще более интуитивно. С другой стороны, иногда бывает так, что ты терякшься и наоборот не понимаешь, что делаешь, не видишь общей картины, но поскольку ты знаешь формальные правила, то можешь делать следующий корректный шаг локально. То есть вот ты на пятом шаге, допустим, и не понимаешь уже, как это связано с тем, что было на первом шаге, но у тебя есть формальные инстоументы, с помощью которых ты можешь перейти от пятого шага к шестому и это будет гарантировано правильно - и уже после этого попытаться осознать, какая на самом деле связь между тем, что было на первом шаге и тем, что получилось. Вообще, математика - это в основном про то, как видеть, что разные вещи, не имеющие на первый взгляд ничего общего, являются на самом деле одним и тем же. В этом смысле это чистая, дистиллированная деятельность нашего мозга - в процессе эволюции он затачивался как раз под то, чтобы видеть паттерны и аналогии, и математика именно этим и занимается - только относительно не реального мира, а абстрактных, выдуманных систем. Да, ну а когда я не решаю данную задачу, а придумываю что-то свое, то тут гайдом в основном выступают эстетические категории - придуманное должно быть красивым, приятным, о нем должно быть приятно думать, оно должно нравиться. Опять же, у настоящих математиков это, наверное, выражено еще сильнее.
Вообще, погугли "интуиция и математика", Вейль кажется писал.
сап. есть вопрос. дано: не переодический(к примеру) сигнал конечной длительности. с помощью преобразования Фурье мы получаем его спектр. сам вопрос: что такое спектр? его физический смысл? что он показывает? или у него нет абстракции? можно ли связать как то спектр с исходным сигналом путем аналогий или же фурье-преобразование это и есть единственная связь? можно ли надрочиться так, чтобы смотря на сигнал можно было видеть его спектр (хотя бы примерный?) спасибо заранее если кто нибудь прочитает этот высер
Реально ли конструирование системы, в рамках которой число Пи будет равно %поебать_какому_числу%, т.е задано переменной?
Гугли мангу "анализ Фурье". Там поясняется в лайтовой форме (что даже такой конченный дебил как ты сможет понять).
спасибо

Аноны, помогите деграданту поделить 3 на 4,почему получается 0,75 а не 0,705 , разве мы не должны после того как спустится двойка добавлять 0, после семерки ?
нет.
В самом деле, интересно. Но что касается физики, то, действительно, для нашей вселенной наверняка существует предел описательной математики. Однако, если допустить гипотезу мультивселенной, с бесконечным их числом, и как следствие со всевозможными законами физики, то и математика для каждой вселенной может быть совершенно различной, что приводит к отсутствию ограничений для нее.
во всех вселенных одна математика. она не зависит от законов физики. нужно трёхмерное пространство описать? опишем. 11-мерное? опишем. сферическое? опишем.
>>396745
ч-ч-ч, Винберг сильновато для тебя и не подробно
>с головы до писечек
Идеально подойдет двухтомник Городенцева, новый охуительный учебник, написанный для матфака ВШЭ (лучший матфак, после НМУ), к нему даже лекции есть на налекцию.рф , первую часть можно купить, вторая только в электронке.
Есть еще двухтомник Алгебра и Геометрия Зуланке, Онищика - отличнейшая вещь для новичка, если бы мне в свое время ее дали, мне в 3 раза проще было бы.
Исчо, месяц назад в каком-то математика-треде мне посоветовали теорию чисел. Википедию читал, но нихуя не понял, почему тот анон назвал её дохуя интересной. Поясните тут.
Вы владелец диагностической лаборатории для исследований биоматериалов в городе 500к населения. Для n различных пациентов, возраст и пол которых нормально распределены относительно всего населения, нужно сделать качественный анализ на ОДНО инфекционное заболевание. Каким образом можно снизить затраты на материалы и увеличить выручку, для всей лаборатории, сохранив точность результатов не ниже 99,85%. Во сколько раз возможно теоретически снизить затраты, в сравнении с методикой "1 пациент - 1 пробирка"?
Группы крови и резус-факторы у всех пациентов одинаковы.
Как точность определяешь? Т.е. что верный результат точно верный?
Утверждаешь, что в кокой-нибудь вселенной "жопа" не могут существовать законы физики, для описания которых не хватает современного математического аппарата? Разумеется, при допущении гипотизы мультиверсума.
Кардиоида
http://www.imperium.lenin.ru/~verbit/MATH/programma.html
Всё необходимое. Программа превосходит курс аспирантуры мехмата, лол. Но это не прикладная. Если хочешь в прикладную, то стоит смотреть лекции с лекториума мфти. Там всё необходимое для понимания, просто она прикладная.
>Идеально подойдет двухтоник Городенцева, новый охуительный учебник
>Городенцев
Тебя коником ебнуть или квадриком? Если под учебником подразумевается то, что выложено у него на сайте, но это вообще пиздос.
Слишком начально. Или у них есть книжка уровня тензоры для чайников?
я даже не понимаю, с чего ты допустил такое предположение. математикой можно описать по крайней мере всё.
Алло блядь, математика -- это язык. Ты вообще понимаешь, что говоришь? Какая "одна" математика? Мы спокойно берём и меняем одну математику на другую, изменив аксиомы/правила вывода. Всё во всех вселенных, что возможно наблюдать, то можно и описать математически (хотя бы координаты, лол), ибо если мы это наблюдаем -- значит, мыслим. Если мыслим, значит, есть язык. А язык и есть математика, просто точную модель построить мы не можем в силу хаотичности аксиоматики и правил вывода. Но они есть.
Вот никогда вопросом КПД автогенераторов не задавался. Ты какую-то сверхэкономичную схему проектируешь?
Да и за фразу "бога нет" бьют, и за "сталин убийца" тоже (причём те же). Это не показатель неверности утверждений.

Ой, бля, сто нефти этому.
Я интеллектуально поднастроился
на ответ 0,705 не учитывая реал результата. Лол.
>2/4 = 0 + 2;
Не надо это.
Тут ноль должен был бы быть снесён сразу.
>20/4 = 5 + 0;
Поэтому, фикс:
3/4 = 0 + 3;
30/4 = 7 + 2;
20/4 = 5 + 0;
Ну если отвлечься от "математика это гранты, люди, институты, etc", то математика это класс формальных систем, что смело можно назвать языком.
Математика не является формальной системой. Даже банально аксиомы ZFC мало кто может вспомнить.
Мало-ли неграмотных на земле.
Математика имеет язык, а именно: набор применяемых символов - алфавит, и правила позволяющие отличать строчки языка от случайных наборов символов.
Этот язык в свою очередь имеет семантику, т.е. набор аксиом и правила вывода, что позволяет определять является ли строчка языка выводимой в этом формальном языке. Следовательно, математика является формальной системой.
Но это грубо, на самом деле подходов к формализации много, поэтому математика скорее совокупность формальных систем, из которых выбирают люди.
Если бы математика была формальной системой, то люди, не знающие аксиом ZFC, не могли бы ею заниматься. Однако они занимаются.
>математика является формальной системой
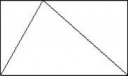
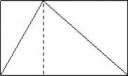
Это всего лишь влажные мечты логиков. Нормальные математические доказательства не доводятся до уровня формальных систем. Например, рассмотрим следующую теорему с доказательством. Теорема о треугольнике, вписанном в прямоугольник.
Теорема. Площадь снаружи треугольника равна площади внутри треугольника.
Доказательство. Разрежем треугольник по пунктирной линии и увидим, что стороны треугольника рассекают каждую из частей ровно надвое.
Вот так и выглядит математика. Простые элегантные рассуждения, без всякого зубодробительного формализма.
Почему именно аксиомы ZFC? Люди знают простейшие теоремы, правда чисто в синтаксическом исполнении, например, свойства сложения и умножения. Нетрудно убедиться, что эти теоремы по сути та же формальная система, с избыточным набором аксиом.
>Теорема. Площадь снаружи треугольника равна площади внутри треугольника.
Для данного рисунка?
>Доказательство. Разрежем треугольник по пунктирной линии и увидим, что стороны треугольника рассекают каждую из частей ровно надвое.
Это не доказательство, это вера в правильность рисунка. Используя такой способ можно придти к неверным выводам в случае с более сложными теоремами.
А если мы реально начнем доказывать, то надо начать хотя бы с того факта, что пунктирная линия делит центральный треугольник на два треугольника, а потом доказывать равенство каждого из них с соседним. Но это уже рассуждение высокого уровня. Ведь тут несколько раз применяются аксиомы равенства и постулат о параллельности, благодаря которым можно использовать утверждение о равных углах при параллельных прямых. "Видеть" это на деле просто обладать геометрической интуицией.
При этом для неевклидовых геометрий эта интуиция уже работать не будет. Придется свыкаться с другими аксиомами.
А по-моему тот анон все правильно сказал, просто ты неправильно его понял.
Алсо, по-твоему математика = аксиоматический метод?
Доказательство - это сведение неочевидного утверждения к очевидным. Чем быстрее и неожиданнее это сведение, тем лучше. Хорошее доказательство должно вызывать смех и радость, как остроумная шутка. А формальные "доказательства" обычно вызывают смертную скуку.
Единственное, что мне не было очевидно в этом примере, - что площадь внутри треугольника равна площади снаружи. Я сделал так, что мне это стало очевидным. Всё, больше ничего тут делать не надо. Не нужно разговаривать ни о каких углах, ни использовать какие-то там "аксиомы равенства". Доказательство завершено.
И вот так везде. Нужно просто делать неочевидное очевидным. Именно в этом математика, и именно поэтому математика не является формальной теорией.
Формальные теории - это не более чем инструмент, которым работают в тех областях, где нет почти ничего очевидного. В областях, где очевидных вещей много, формальные теории не нужны.
Моё доказательство прочитали, и поняли, и приняли. Формальное "доказательство" тут больше уже не нужно. Писать формальное "доказательство" могут только прожженные бюрократы, которым место среди мертвых формуляров и пыльных печатей, а отнюдь не в живой, радостной науке. Да ведь если бы я запостил формальное "доказательство" этого факта, то его никто бы даже не прочитал.
Опять же, детский сад. Давай точно так же докажи мне теорему Вариньона, чтобы мне очевидно стало. Да и в целом результат про треугольник весьма слабый, не обобщается на что-либо помимо евклидовых пространств.
>детский сад
От того, что ты кого-то обзовёшь детсадовцем, его правота не изменится.
>докажи мне теорему Вариньона
Доказательство есть в вики, в одну строчку. Оно опирается на дистрибутивность векторного произведения относительно сложения, [a,b] + [a,c] = [a,b+c]. Интересной математики тут нет. И это доказательство тоже не является формальным, к слову.
известно что число пи иррационально. но вот вопрос. оно иррационально только в системе по основанию 10 или во всех позиционных системах счисления? если взять систему счисления по основанию Пи то число пи перестанет быть иррациональным? есть ли такая система счисления по основанию которой все иррациональные числа перестанут быть иррациональными?
что если основание Пи х Е х 1\3 х (что там еще иррациональное) является универсальным? или из под него все остальные числа станут иррациональными?
Иррациональность числа определяется независимо от какой-либо системы счисления. По-видимому, ты неправильно формулируешь вопрос, который тебя интересует. Спрашивай лучше, существуют ли такие позиционные системы отсчёта, в которых пи записывается периодической десятичной дробью.
А?

нет. но по сути если брать колебания бесплатных вечных источников (микроколебания земли, дуновения ветра) то это как бы самая правильная схема вечного двигателя. ПОка существует земля и вращается , то это будет работать.
мне кажется это самая важна научная отрасль которую надо развивать. Автоколебания ключ к будущему
НУ ПОМОГИТЕ, Я ВАМ СКИНУ ПОСЛЕДНИЕ ДЕНЬГИ, ЕСЛИ НАПИШУ НА 4
Эйлер нашел простой многочлен n^2 -n +41, принимающий простые значения для n 0..40, какова вероятность математическая что это простое совпадение? Видел где то формулу вероятности числа быть простым что-то там x/ln(x) и доказано что не существует многочлена в одной переменной n, значение которого являются простые числа для челых значений n. Какого хуя?
Он не поехавший.
Ну давай
Отписал
Анонимасы, посоветуйте, что почитать по основам теории алгоритмов (нужны универсальные алгоритмические модели и сложность алгоритмов).
За ответы заранее спасибо.
Какова вероятность, что 2 объекта встретятся на бесконечности времени?
Стопроентная.
clrs
>Этот язык в свою очередь имеет семантику, т.е. набор аксиом и правила вывода,
Это не семантика.
Большего собачьего бреда я не читал. "Смех" и "радость". Угу. А про математическую строгость (rigour) ты слышал, радостный?
Право рассуждать о математической строгости имеют только математики. Ты не являешься математиком.
Ну я имел в виду геометрическую теорему и ее следствие о площади
>>397505
Выводимо=имеет смысл.
Мне неинтересно твоё мнение по поводу того кем я являюсь или не являюсь. Твоя позиция о сведении «неочевидного» к «очевидному» (остальное не выдерживает критики) — в корне ущербна, т.к. существуют «очевидные» высказывания (например предел последовательности) нуждающиеся в строгом определении, для дальнейшего развития теории. Не говоря уже о том, что «очевидность» — неопределённое понятие. Одним очам видно, другим нет.
Понятия нуждаются в определении постольку, поскольку неочевидны, и ни на копейку больше. Толчком к появлению строгого понятия предела стал кризис анализа начала XIX века, когда журналы массово начали публиковать откровенный мусор, шизофазию, и понадобилось каким-то образом её заткнуть, - то есть когда предел перестал быть очевидным. Анализ флюксий и флюент не требовал строгого определения предела.
>Одним очам видно, другим нет.
Люди, которым очевидно одно и то же, образуют какой-нибудь заговор, семинар, научную школу или что-то подобное. Затем из этого заговора выделяются люди, которым что-то неочевидно, и образуют новый заговор. Это нормально, это прогресс.
подскажите пожалуйста какую-нибудь функцию, которая принадлежит пространству L_1[0,1], но не принадлежит пространству L_2[0,1],
спасибо.

помогите пожалуйста с примером из функционального анализа, есть 2 пространства сходящихся числовых последовательностей, X=l_2, и Y=l_1, и задано отображение Fx. Необходимо ответить, является ли заданное отображение:
a) непрерывным;
б)равномерно-непрерывным;
в)удовлетворяющим условию Липшица;
Объясните пожалуйста, как проверить все эти условия, определения всех этих понятий выписаны, но я не понимаю, как их проверить на практике,
объясните пожалуйста алгоритм решения такого задания.
Каждую попытку есть есть проигроишное число. Оно может быть любым получая таким образом 1010 комбинаций. Но так или иначе проигрышных цифр всего 10 по 1 на каждую попытку.
Какая наиболее не проигрышная стратегия. заранее выбрать 10 чисел, или каждый раз выбирать новое, или одинаково?
По условию, все строчки из десяти цифр равновероятны. Поэтому однохуйственно.
Имеет смысл = существует конструктивный алгоритм для проверки смысла данного утверждения и он выдает правду. Для выводимости алгоритм очевиден.
Soundness обеспечивается самим построением. Completeness не знаю причем тут.
Не подскажете, как начать?
Так. Я чуть-чуть подумал и решил представить первый многочлен в виде f(x^2) = x^50 - x^(51/2) + 1
Тогда остатком будет f(1), то есть один. Странно
Обращайся, дружище.
В первом надо вычислить, во втором найти геометрическое место точек на комплексной области, удовлетворяющих этим условиям
в любой непонятной ситуации домножай на сопряженное!

Спешите ознакомиться с реальной математикой.
заглянуть в википедию например.
пусть он конечен... тогда
Множество бесконечно, если есть биекция между всем множеством и некоторым его подмножеством. Или что именно тебе не понятно?
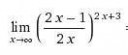
Пздц... Ведь тут вроде бы можно даже не считать, и так понятно что в числитель будет бесконечно уменьшаться, а значит будет 0 !! Ну, анончики, обьясните мне, или решение подкиньте, правильное. Мне заочнику надо сдать это, а в феврале математики уже не будет в моей учебе.
выражение в скобках при 10 будет 19/20, при 100 199/200, а значит стремится к единице. Показатель стремится к бесконечности. Предсказать результат нельзя, т.к. числа стремящиеся к единице в бесконечной степени могут дать любой результат.
Обычно в этом случае поступают так: представляет x^y в виде e^ylnx, и вычисляют предел уже этого выражения.
В ун/ уёбуй.
exp(-1) ответ
(2x-1)/(2x)=1-1/(2x).Предел этой фигни в степени 2х будет exp(-1), а предел скобки в третьей степени будет 1.
Докажи по определению, предъявляй эпсилон.
вот есть у тебя эта твоя фигня. то что в скобках можно расписать как разность 2х\2х- 1\2х. 1\2х при устремлении к бесконечности будет бесконечно малой и хуй на неё забьем. а 2x\2x=1. поэтому твой пердел можно переписать как единичку в бесконечной степени. единичка в любой степени будет единичкой. т.е. ответ 1. пруф ми вронг.
лан, не надо пруфать. вспомнил про второй замечательный пердел. давно просто всё это говно было.
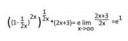
это же замечательный lim ! Решение на пике, ответ e^1
Не слушай этих петухов: >>397823 >>397834 >>397857 , они матан не знают, студентота 1 курс
>>397848
ты всё правильно сделал, но только если бы Х стремился к 0
мимо_преподаватель_этих_ваших_втузов
я это ты, чувак. Давай выпилимся вместе. Какой город?
меня волнует
Хочу угореть по геймдизайну, работаю в близкой сфере.
Пишу тексты, персонажей, квесты, все дела.
Но для того, чтобы работать геймдизайнером, - нужно знать тервер и статистику.
Можно ли задрочить эти сферы, не отвлекаясь на другую математику?
Насколько сложно для ньюфага, который особо не горит въезжать в математику, но нужно для работы.
Что посоветуете почитать?
Вообще-то тебе интегралы еще надо брать. Короче, программу первого курса бери. Если в школе у тебя не было фундаментальных проблем с математикой, то несложно, вопрос только во времени.
Кстати, на курсере есть и матан, и статистика, и микроэкономика и вообще все, что тебе нужно.
Надо было тогда уж начать так: "пусть икс принадлежит <левой части>. Тогда...", а потом: "пусть икс принадлежит правой части, тогда..." - и каждый переход сопровождать ссылкой на обоснование справедливости перехода.
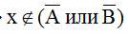
Продавец продаёт шапку. Стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только банкнота 25 р. Продавец отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает, и отдаёт 10+10+5. Продавец отдаёт шапку и сдачу 15 руб. Через какое-то время приходит соседка и говорит, что 25 р. фальшивые, требует отдать ей деньги. Ну что делать, продавец лезет в кассу и возвращает ей деньги. На сколько обманули продавца?
Шапка(10)+15р покупателю-наебателю + 25 соседке итого 50 рублей
15 рублей
Можно и саму теорему о неполноте составить из мат знаков и даже небо, даже алдаха! Мат знаки это те же слова.
Мат символы это те же самые слова. Важно не то какой закорючкой ты выражаешь слово, а то какой смысл, какую структуру порядок и отношение ты в это слово вкладываешь. Вообще математики используют символы только для того, чтобы подчеркнуть свою элитарность. Чтобы для не сведущего человека вся запись казалась непостижимой тарабарщиной. Тем самым у человека начинает складываться образ математиков, как каких то гениев недостижимого уровня. Сами математики в глазах быдла всячески стараются этот образ, миф поддерживать.
Сам я точно не пройду а от этого зависит получение зачета,в общем помогите плиз


Добавлю, что надо, чтобы они были трёхмерными. Если знаете, где, подскажите, плиз.
2^n > n^1000
Пробовал пока что логарифмировать и решать неравенство в лоб, но не вышло чего-то хорошего. Предполагается, что число e и соответствующий замечательный предел решающий пока не знает.
>>397975
>>397974
>>397973
Разобрался, спасибо. Хотя, конечно, задание подразумевало тупой перебор, но потом на досуге подумаю о решении неравенства в целом. Спасибо.
"Укажите такое n, при котором 2^n > n^1000"

И тогда у меня варила голова, я хоть чего-то соображал, мышление было ясным и острым.
Потом матан кончился и я за год-другой без математики превратился в туповатого дауна.
Посоветуйте раздел математики/учебник/задачник, который поможет хорошо размять мозги, привести ум в порядок, только не слишком сложный, чтобы я не забил на всё это дело, но и не слишком простой, чтобы был интерес.
чувак 100% кидает в поле, какой шанс попасть во внешний круг, если Радиус внутреннеого круга в 2 раза меньше чем внешний?
вероятность = (мера искомого множества)/(мера всего множества)
Очевидная теория множеств очевидна. У неё уровень сложности может варьироваться от детсадовского до космического, а за нежелание пользоваться умом мгновенно прилетает лопатой по лбу.
Все эти гильберты, формалисты, теоремы о неполноте, интуиционизм и логицисты все это сранные философы,
в то время как "И для специалистов, и для любителей не
философия, а именно активные занятия самой математикой смогут дать
ответ на вопрос: Что такое математика?"
( из предисловия Куранта Что такое математика)
короче Пойа "как решать задачу"
и "думай математически" Мейсона
А дальше "Тому, что в математике действительно необходимо и полезно знать, можно выучиться в шесть месяцев; всё же остальное составляет только предмет любопытства."
Надеюсь ты не подразумеваешь что это мне как то противоречит?
Gödel, Kurt. "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I".
Q: Правда ли, что Гёдель доказал, что мир невозможно познать?
A: Нет. Если выразить суть теоремы о неполноте простым языком, она утверждает, что человеческое мышление (и, в частности, математическое доказательство) - это существенно творческий процесс, и его нельзя свести к так называемой "китайской комнате", то есть к формальному исполнению некоторого алгоритма. Гёдель построил логическую формулу, выражающую свою собственную формальную (!) недоказуемость. Если бы эта формула была доказуема, это привело бы к противоречию в теории. Поэтому она недоказуема, а значит, верна, поскольку сама по себе именно это и утверждает. Кажущийся парадокс (мы доказали истинность недоказуемого утверждения) возникает из-за фундаментальной разницы между алгоритмическим (формальным) и семантическим (творческим) способом рассуждений - второй оказывается существенно богаче и мощнее. Вот и всё. Ничего сложного, если не брать технические детали построения самой формулы, которые довольно занудны.
Q: Значит ли это, что у человека есть душа, а искусственный интеллект невозможно построить?
A: Не значит. В процессе Гёдель сделал множество предположений, совершенно естественных для того, что мы обычно понимаем под формальной алгоритмической процедурой, но которые совершенно неверны для, скажем, человеческого мозга. К примеру, ключевым предположением является алгоритмическая разрешимость множества КОРРЕКТНЫХ формальных доказательств, то есть предполагается существование алгоритма (в строгом смысле, машины Тьюринга, например), способного отличать верное рассуждение от неверного. Это, скорее всего, не так, поскольку естественный язык позволяет формулировать утверждения, не являющиеся ни истинными, ни ложными. На простом языке это означает, что способность ошибаться и "тупить" является неотъемлемым свойством творческого процесса, и не ошибается только безмозглый автомат. Кроме того, Гёдель предположил конечность алфавита (и, следовательно, счётность слов в этом алфавите), в то время как множество состояний мозга, скорее всего, несчётно.
Q: Но зачем нам тогда формальные системы и аксиомы, если они такие плохие?
A: Затем, что формализованное доказательство, как уже было сказано, допускает алгоритмическую проверку своей корректности. Это позволяет практически полностью исключить из математики влияние авторитета и добиться объективности получаемых результатов. Формула, полученная Гёделем, строится для конкретной формальной системы, то есть для конкретных аксиом и правил вывода. В другой системе та же формула может оказаться прекрасным образом доказуемой, и никакого противоречия уже не будет. Однако теорема о неполноте говорит нам, что полностью свести математику к формальному языку, раз и навсегда задав систему аксиом и правил вывода, у нас не получится. Основания математики так же подвижны, как основания любой другой естественной науки. Она растёт и вверх, и вниз.
Q: Правда ли, что Гёдель доказал, что мир невозможно познать?
A: Нет. Если выразить суть теоремы о неполноте простым языком, она утверждает, что человеческое мышление (и, в частности, математическое доказательство) - это существенно творческий процесс, и его нельзя свести к так называемой "китайской комнате", то есть к формальному исполнению некоторого алгоритма. Гёдель построил логическую формулу, выражающую свою собственную формальную (!) недоказуемость. Если бы эта формула была доказуема, это привело бы к противоречию в теории. Поэтому она недоказуема, а значит, верна, поскольку сама по себе именно это и утверждает. Кажущийся парадокс (мы доказали истинность недоказуемого утверждения) возникает из-за фундаментальной разницы между алгоритмическим (формальным) и семантическим (творческим) способом рассуждений - второй оказывается существенно богаче и мощнее. Вот и всё. Ничего сложного, если не брать технические детали построения самой формулы, которые довольно занудны.
Q: Значит ли это, что у человека есть душа, а искусственный интеллект невозможно построить?
A: Не значит. В процессе Гёдель сделал множество предположений, совершенно естественных для того, что мы обычно понимаем под формальной алгоритмической процедурой, но которые совершенно неверны для, скажем, человеческого мозга. К примеру, ключевым предположением является алгоритмическая разрешимость множества КОРРЕКТНЫХ формальных доказательств, то есть предполагается существование алгоритма (в строгом смысле, машины Тьюринга, например), способного отличать верное рассуждение от неверного. Это, скорее всего, не так, поскольку естественный язык позволяет формулировать утверждения, не являющиеся ни истинными, ни ложными. На простом языке это означает, что способность ошибаться и "тупить" является неотъемлемым свойством творческого процесса, и не ошибается только безмозглый автомат. Кроме того, Гёдель предположил конечность алфавита (и, следовательно, счётность слов в этом алфавите), в то время как множество состояний мозга, скорее всего, несчётно.
Q: Но зачем нам тогда формальные системы и аксиомы, если они такие плохие?
A: Затем, что формализованное доказательство, как уже было сказано, допускает алгоритмическую проверку своей корректности. Это позволяет практически полностью исключить из математики влияние авторитета и добиться объективности получаемых результатов. Формула, полученная Гёделем, строится для конкретной формальной системы, то есть для конкретных аксиом и правил вывода. В другой системе та же формула может оказаться прекрасным образом доказуемой, и никакого противоречия уже не будет. Однако теорема о неполноте говорит нам, что полностью свести математику к формальному языку, раз и навсегда задав систему аксиом и правил вывода, у нас не получится. Основания математики так же подвижны, как основания любой другой естественной науки. Она растёт и вверх, и вниз.

Тут домашку не делают.
Есть d-мерный куб (длина стороны - a). У него соответственно 2^d углов. Столько же d-мерных шаров с радиусом a/4 мы хотим наказать и поставить в угол так, чтоб они были полностью внутри куба. И вот вопрос. С какого d можно впихнуть ещё один шар в середину куба, чтоб он пробивался через куб? Помогите советом.
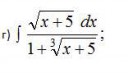
Вот задание
>>398913
Вроде, с N=4 уже должно бы влазить. По симметрии задачи, надо рассмотреть диагональ x1=x2=...xN. Взять а=4, тогда круг из центра будет сечь линию при всех x=1/sqrt(N). Посчитав расстояние от этой точки до (1,1,...1) получим искомое.
я нашла, что только с d=10 он выпирает. d=9 соприкосновение со стенками. Но доказательства нет...
Я просто не понял вопроса.
Если катать шар по шару, то центр подвижного идет по шару с радиусом 2 (оба единичные для простоты ). Тогда если сделать вокруг точек (+-1, +-1 …. ) шары двойного радиуса, вопрос в том, будет ли соответствущая полость иметь выход к поверхности. Возможно, прокатит сначала надуть шары до такого радиуса, чтобы осталась лишь маленькая полость в центре, а потом сдувать помаленьку? Вероятно, протекание полости на грань будет при бифкркационном значении радиуса – когда какие-то пары шаров начинают касаться, а не пересекаться. Бифуркаций при сдувании явно будет несколько ( порядка N в натуре ). Может из этого что-то можно выдоить?
смогла вырешать очень просто через теорему пифагора )))) столько нервов потрачено на простейшую фигню.
В первом же шаге - копейки должны быть в квадрате под корнем.
Сначала приведём всё к единым единицам и будем считать только копейки.
Это просто в данном случае, ибо в рубле 100 копеек, потом слово "рубля" без вреда для здоровья заменяем на " 100"
sqrt(1/4 100) = 5 копеек
1/2 * 100 = 50 копеек

сенкс
>Посоветуйте раздел математики/учебник/задачник, который поможет хорошо размять мозги, привести ум в порядок, только не слишком сложный, чтобы я не забил на всё это дело, но и не слишком простой, чтобы был интерес.
"Полный сборник задач по математике для поступающих в вузы. Группа повышенной сложности" - https://www.livelib.ru/author/385499/latest
Достаточно стандартная семейная история — подросток сбежал из дома, написав смску: «Я сюда больше не вернусь, можете даже не пытаться меня найти» и, естественно, отключив телефон. Найти его смогла сестра, используя знания, полученные во время учебы на программе «Прикладная математика и информатика». Эта история также показывает, что могут рассказать соцсети о своих пользователях понимающему человеку.
Никто не знал, к кому мог уехать беглец — родители были полностью уверены, что молодой человек близок лишь со своими одноклассниками. Но тех, кого знали, обзвонили, и ни у кого из них он не обнаружился. Был еще один путь — поиск по сети Вконтакте. Именно этим и занялась сестра беглеца, которую из этических соображений мы назовем инициалом Л.
«Но друзей у него там было слишком много, чтобы проверить каждого, — вспоминает она. — Как посчитали статистики, в среднем у каждого пользователя социальной сети около 150 взаимных подписчиков, в то время как в реальной жизни круг общения в пять раз меньше виртуального. Нужно было искать другой способ. В курсе «Комбинаторика» мы в том числе писали программу обработки, анализа и визуализации сети друзей ВКонтакте. Я решила посмотреть, смогу ли я что-то полезное извлечь из этого анализа, поскольку любая информация приветствовалась».
+++
Все сделанные аналитически выводы позже подтвердились показаниями сбежавшего брата. Сам он до сих пор считает, что его сестра владеет какой-то математической магией.
«На этом этапе я наконец решила начать переписку и связалась с личностями А, Е и F, — рассказывает Л. — Это было рискованно, но стоило попытаться. Личность F в итоге оказалась бесполезна, хотя во время общения продемонстрировала открыто враждебную позицию. Личность A предпочла меня проигнорировать. Личность E некоторое время утверждала, что ничего не знает, но после, в общем-то, безосновательного, но очень уверенного напора все же признала, что брат находится в безопасности неподалеку. После этого было уже нетрудно опосредованно уговорить его выйти на связь сначала со мной, а потом уже и с родителями».
К этому моменту родители уже поехали подавать заявление о розыске в органы внутренних дел, захватив с собой «черный список» из этих трех личностей. Предполагалось, что если за выходные брат не появится, с них можно будет начать поиски. Но до этого не дошло, молодой человек сам вернулся домой.
После завершения этой истории граф его социальных связей выглядел так. Голубые точки — это друзья из новой школы с уклоном в сторону развития творческого потенциала учеников и патриотического воспитания, куда его перевели. На графе они не пересекаются с остальными. Участники же старых зеленого и фиолетового кластеров, которые на этом рисунке еще присутствуют, вскоре были удалены из друзей.
Преподаватели департамента анализа данных и искусственного интеллекта благодарны Л. за то, что она поделилась с ними своей историей. «Огромной радостью для педагога является не только успех его учеников, но и применение знаний на практике, особенно в таком важном деле, как спасение жизни ребенка», — говорит научный руководитель Л. и автор курса по комбинаторике Илья Макаров. — Я уверен, что этот пример заставит многих задуматься о том, сколько личной информации на самом деле хранится в социальных сетях и как обученные профессионалы могут использовать эти данные для предотвращения подобных случаев в будущем».
Описанные выше методы анализа социальной сети в Вышке можно изучить в рамках дисциплин и проектов на магистерских программах «Науки о данных» и «Прикладная статистика с методами сетевого анализа», они также затрагиваются на программе «Журналистика данных». Для всех магистрантов 1 года обучения любых других программ доступен вводный курс «Social Network Analysis» из цикла МАГоЛЕГО, а бакалавры могут взять курс по выбору «Комбинаторика».
Достаточно стандартная семейная история — подросток сбежал из дома, написав смску: «Я сюда больше не вернусь, можете даже не пытаться меня найти» и, естественно, отключив телефон. Найти его смогла сестра, используя знания, полученные во время учебы на программе «Прикладная математика и информатика». Эта история также показывает, что могут рассказать соцсети о своих пользователях понимающему человеку.
Никто не знал, к кому мог уехать беглец — родители были полностью уверены, что молодой человек близок лишь со своими одноклассниками. Но тех, кого знали, обзвонили, и ни у кого из них он не обнаружился. Был еще один путь — поиск по сети Вконтакте. Именно этим и занялась сестра беглеца, которую из этических соображений мы назовем инициалом Л.
«Но друзей у него там было слишком много, чтобы проверить каждого, — вспоминает она. — Как посчитали статистики, в среднем у каждого пользователя социальной сети около 150 взаимных подписчиков, в то время как в реальной жизни круг общения в пять раз меньше виртуального. Нужно было искать другой способ. В курсе «Комбинаторика» мы в том числе писали программу обработки, анализа и визуализации сети друзей ВКонтакте. Я решила посмотреть, смогу ли я что-то полезное извлечь из этого анализа, поскольку любая информация приветствовалась».
+++
Все сделанные аналитически выводы позже подтвердились показаниями сбежавшего брата. Сам он до сих пор считает, что его сестра владеет какой-то математической магией.
«На этом этапе я наконец решила начать переписку и связалась с личностями А, Е и F, — рассказывает Л. — Это было рискованно, но стоило попытаться. Личность F в итоге оказалась бесполезна, хотя во время общения продемонстрировала открыто враждебную позицию. Личность A предпочла меня проигнорировать. Личность E некоторое время утверждала, что ничего не знает, но после, в общем-то, безосновательного, но очень уверенного напора все же признала, что брат находится в безопасности неподалеку. После этого было уже нетрудно опосредованно уговорить его выйти на связь сначала со мной, а потом уже и с родителями».
К этому моменту родители уже поехали подавать заявление о розыске в органы внутренних дел, захватив с собой «черный список» из этих трех личностей. Предполагалось, что если за выходные брат не появится, с них можно будет начать поиски. Но до этого не дошло, молодой человек сам вернулся домой.
После завершения этой истории граф его социальных связей выглядел так. Голубые точки — это друзья из новой школы с уклоном в сторону развития творческого потенциала учеников и патриотического воспитания, куда его перевели. На графе они не пересекаются с остальными. Участники же старых зеленого и фиолетового кластеров, которые на этом рисунке еще присутствуют, вскоре были удалены из друзей.
Преподаватели департамента анализа данных и искусственного интеллекта благодарны Л. за то, что она поделилась с ними своей историей. «Огромной радостью для педагога является не только успех его учеников, но и применение знаний на практике, особенно в таком важном деле, как спасение жизни ребенка», — говорит научный руководитель Л. и автор курса по комбинаторике Илья Макаров. — Я уверен, что этот пример заставит многих задуматься о том, сколько личной информации на самом деле хранится в социальных сетях и как обученные профессионалы могут использовать эти данные для предотвращения подобных случаев в будущем».
Описанные выше методы анализа социальной сети в Вышке можно изучить в рамках дисциплин и проектов на магистерских программах «Науки о данных» и «Прикладная статистика с методами сетевого анализа», они также затрагиваются на программе «Журналистика данных». Для всех магистрантов 1 года обучения любых других программ доступен вводный курс «Social Network Analysis» из цикла МАГоЛЕГО, а бакалавры могут взять курс по выбору «Комбинаторика».

А с чего тогда математики уверены, что все формулы для вычисления этого числа без привязки к окружности являются именно числом Пи, а не более изощрённой его аппроксимацией, как 22/7, только более точной?
Его можно через пределы, через ряды, через бесконечные дроби, через интеграл, методом Монте-карло посчитать, но многие из этих методов и близко не связаны с окружностью по крайней мере, на первый взгляд.
С чего тогда все решили, что все эти методы расчёта даёт именно то самое число пи, а не очень очень близкие к нему приближения?
аноны, выручайте. Как привести (Cos(4x)-Cos^3(4x))/(3x^2) к первому замечательному пределу?
Все эти пределы равны одному и тому же вещественному числу. Это устанавливается посредством тригонометрических функций - точнее, их рядов Тейлора.
Сам виноват, теперь Родина любит его.
Любить не обязательно, достаточно говфифьфя.
(Cos(4x)-Cos^3(4x))/(3x^2)
((Cos(4x)(1-Cos^2(4x))/(3x^2)
(Cos(4x)Sin^2(4x))/(3x^2)
Cos(4x)(16/3)(Sin(4x)/4x)^2
Ноль в 0.1, 0.1 в 0.01, 0.01 в 0.001...
Один в 0.9, 0.9 в 0.99, 0.99 в 0.999...
Остальное в себя
Правильно всё?
Функционал = функция от функции.
Формально особо ничем не отличается, просто при рассмотрении какого-то пространства функций и пространства функций на нём нужно как-то отличать одно от другого.
Но функция от функции - это ж суперпозиция, не? Н-р g(f(x)) - это разве функционал?
В теории автоматического управления кто нибудь понимает? Критерии устойчивости, лафчх и прочая хуйня. нужно построить лфчх а я даун в тригонометрии
В чем вопрос то?
Чёт нихуя не пойму
Ты фи зик дохуя? Подумай про функцию как про отображение.
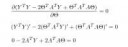
Тета и Y - векторы, X - матрица, если нужно больше пояснений, см. исходную статью https://habrahabr.ru/post/307004/ , а вообще это вывод формулы для линейной интерполяции.
Быстрый гуглеж по запросам "линейная алгебра производные" и "матрицы производные" то ли ничего не дал, то ли я туплю.
Чтобы найти решение моей проблемы, мне пришлось гуглить очень долго, но это таки удалось!
http://nabatchikov.com/blog/view/matrix_der
У тебя эпичный гет, но я не знаю, что тебе ответить...
Аналитическая геометрия? Дифференциальная?
Где ты берешь такие задачи?
По сабжу: я придумал, как доказать, что аkn-1 делится на an-1:
тупо считаем (an-1)(an(k-1)+an(k-2)+...+an+1)=ank-an(k-1)+an(k-1)-an(k-2)+...-an+an-1)=аkn-1 (все сокращается, кроме нужного)
Это доказывает, что и аn-1, и аm-1 делятся на аНОД(m,n)-1 (см. >>400017 ), но не доказывает, что не существует общего делителя побольше. Продолжаю думать.
Если я непонятно объясняю, переспрашивай.
Спасибо. На матфаке, лол.
А вообще: http://math.stackexchange.com/questions/678730/gcd-number-theory-proof-an-1-am-1-am-n-1?noredirect=1&lq=1
Только последний шаг для меня остаётся загадочным
Полная хуйня, куча многозначных и они совершенно обычны - те же дробные степени, например.
Так и комплексные будут чем-то удивительным, лолка.
Функция это просто отображение из одного множества в другое, никто не говорит про сюрьекцию/иньекцию
Просто с таким объектом удобно работать. Много доказаных теорем и так далее.
Функция - отображение произвольных множеств f: X -> Y, функционал - отображение произвольного множество во множество действительных числе f: X -> R
Как раз под функцией чаще всего подразумевается отображение в вещественную прямую R или произвольное кольцо R, а X → Y, где X и Y — множества называется отображение.
XxY - декартова произведения
Функционал это отображение в любое поле, разве нет?
Такое идиотское определение присутствует исключительно в русскоязычной википедии. В английской функционал определяется как функция из векторного пространства (= пространства функций) в скаляры.
"Математическая энциклопедия" Виноградова подтверждает приведенное в рувики определение, мотивируя Колмогоровым.
Выбираешь последовательность в (0,1) и делаешь биекцию между ней и ней же + точка 0 и точка 1.
Остальное на месте
Пример:
Пусть последовательность 1/q^n
n с 1 до бесконечности.
0 -> 1/q
1 -> 1/(q^2)
1/q -> 1/(q^3)
1/(q^2) -> 1/(q^4)
....
1/(q^k) -> 1/(q^(k+2))
Только не для целых чисел а для произвольного целостного кольца (не обязательно факториального). Вроде простая вещь а что-то застрял и туплю, не могу доказать.
Он хочет сказать, что в последовательности частичных сумм этого ряда никогда не встретится число 2, но он не знает таких слов.
Я ЖЕ СКАЗАЛ БЛЯДЬ 0 в 0.1 в 0.11 в 0.11 етц

Производная показывает наклон касательной, или что то же самое, скорость изменения значения функции.
Если у функции вверху/внизу дроби скорость ухода в бесконечность больше чем функции внизу/вверху дроби то получается какое то число.
Если же функция вверху/внизу дроби имеет очень большую производную, скорость изменения, по сравнению с второй функцией, то дробь уходит в бесконечность быстрее чем ты успеваешь сказать абрвалг и нужно применять правило клопиталя еще и еще
Смотри доказательство по базе. там все случаи сразу.
надо доказать исходя из дистрибутивности и существования (ta,tb)
(4x^2 + 1) sqrt(x)/(2 x^2) exp(-x)
По частям не выходит, а курс матана уже подзабылся. Заменой тоже вроде так себе, короче, я немного в ахуе.
А когда язык стал формальной системой? Язык -- это единственный способ описания мира. Что же ещё математика? Ты считаешь, что законы математики существуют вне нашего разума, они материальны или имеют физический смысл? Математика по отношению к реальности -- это как отражение по отношению к отражаемому. Да что там, даже если твой аргумент будет не на столько идиотским, он всё-равно будет глупым. Почитай Витгенштейна, ЛФТ. Первые пару глав, и всё станет ясно само собой. Если увлечёшься, то и "философские исследования" стоит почитать.
А, кстати, что вообще язык, по-твоему?
На первом же курсе приличного с точки зрения мат образования факультета поймёшь, что для настоящей математики понятия алгебры и геометрии слишком обширные, а в школе -- бредовые. Если совсем того, то лучше (реально лучше) Петерсона за 6 класс брать, потом каких-нибудь профильных школ 7-8-9 класс, потом решать олимпиадки всякие разные, ну а дальше можно заняться хотя бы сколько-нибудь серьёзной математикой, вроде Фихтенгольца по матанализу. Да и, кстати, выбор литературы предельно сильно зависит от конкретных целей. Если хочешь решать задачки, то по линейной алгебре будет лучше Беклемишев, если хочешь глубинного понимания, то ближе Костринкин, фор экзампл.
Учусь в меде и хотелось бы в физику углубиться, т.к. мед науки во многом с физикой связаны. Плюс мозг в технтческом плане станет лучше работать (надеюсь), а это в изучении химии чрезвычайно способствует.
Да и непосредственно физика интересует, что уж там говорить.
пиши мне, могу пояснить за физику и матан, даже вводный курс тебе провести
puphistX#|ickANUSgmaBZ1ilPUNCTUMc6c3om
Вот расскажите мне, есть ли такая штука, что благодаря некоторым силам какие-либо уравнения или системы уравнений могут или давать определенный результат, или продолжать действия, при том меняя свои переменные и преобразуя сами функции и формулы? Я не знаю как это описать и как это должно в полной мере выглядеть, но в среде определенных чисел такие системы должны принимать такие значения, что при различных условиях возможно было бы найти функции, описывающие зависимость значений. Но при этом эти находимые функции не находят любое решение, они определяют диапазон, необязательно последовательность, и сами имеют неизменное колличество действий.
Дополню что системы, что я описываю изначально, сами определяют диапазон, а исходные функции необходимо определть уже по корреляции значений чисел или выводов этого диапазона. Диапазоны могут быть различны, массив данных будет гораздо больше возможного для обработки.
шизофазик в треде, скорее в машину
Примечание: подвижная монета все время находится в плоскости стола.
Сколько оборотов вокруг своей оси?
Это физическая задача а не математическая. Да она и притом не абстрактная. Если хочешь, чтобы я её решил, тебе придётся составить уранение/систему уравнений с неизвестными.
Блять. Хули два-то. Сука.
Хотя, очевидно. Если мы совместим монеты как шестерёнки и прокрутим на один оборот, то каждая сделает один оборот. А если мы перенесём систему отсчёта в одну из монет, то вторая займёт вертикальное положение дважды, только контактируя разными боками. Лол.
Что ты несёшь?
Интересует сигма точечный фильтр калмана(Unscented Kalman filter)
Как вообще использовать матрицы ковариации? У меня всего две полученые величины. Как я могу попарные ковариации из них получить? И собрать их в матрицу?
Математика не занимается эмпирическими фактами. И не решает задачи эмпиречески.
Общепризнанное мнение и то, что каждый считает давно решённым, чаще всего заслуживает исследований. (Г.К. Лихтенберг).
"Я верю, что числа и функции анализа не являются произвольными созданиями нашего разума: я думаю, что они существуют вне нас в силу той же необходимости, как и объекты реального мира, и мы их встречаем или их открываем и изучаем точно так, как это делают физики, химики и зоологи" (Ш. Эрмит)
НИНУЖНО (Аноним)
Первое высказывание вообще не к месту. Что ты им хотел сказать? Что математики должны по десять раз решать тупые задачи, которые давно решены физиками? Ещё скажи, что все должны по десять раз трястись над одним и тем же интегралом, которые был взять двести лет назад и проверять эксперементально правильно ли он решен! В математике эмперический метод практически бесполезен, поскольку его можно провести только конечное число раз, а матерует и бесконечноми сущностями. Например, можно эмпирически пару раз проверить верна ли формула квадратных уравнений, но нельзя таким способом доказать её верность для всех чисел а значит и верность в общем случаи.
>Я верю
Ключевое слово - верю. Кто-то верит в христа, кто-то в аллаха, кто-то, что математика постоенна алгориметрически и аксиома выбора верна только для конечного числа чисел. У тут научная доска, а религиозная.
>что числа и функции анализа не являются произвольными созданиями нашего разума: я думаю, что они существуют вне нас в силу той же необходимости, как и объекты реального мира, и мы их встречаем или их открываем и изучаем точно так, как это делают физики, химики и зоологи
Филосовский вопрос, который не интересен математикам, поскольку ответ на него по-факту ничего не меняет. Физическа построенна на эксперементах, математика нет. Даже если они что-то и пытаются это искать, то после того как докажут, это становится незыблемым камнем, который не нужно больше проверять, с физикой дела не так.
>постоенна алгориметрически и аксиома выбора верна только для конечного числа чисел. У тут научная доска, а религиозная.
Вынь хуй из рота и реши, наконец, эту задачу.
*физик
Это пизические условния, мне же нужны математические. Смотри, из этой задачи ты должен вычленить математическую часть, переписать в виде уравнений и тогда я её решу.
Оk педант, сколько оборотов вокруг своей оси сделает монета, достаточно абстрактно, или математики не могут это представлять?
>>401922
Угомонись, неполноценный.
Это не троллинг - ты просто обмазываешься говном публично, не более.
бамп вопросу
Есть какие то современные книги по вышмату для прикладного применения вышмата? Тобишь без теории множеств, топологий, аффинных преобразований на двадцатой странице учебника и т.д.

Точно, формулы приведения! Спасибо анон, может я еще чуть позже отпишусь, если дальше тоже не получится с другими примерами.
Чтобы мп3 играть.

Подскажите, пожалуйста, программу, в которой можно "от руки" нарисовать график, а программа выдаст массив значений.
>4367935+de8accb[...].jpg
лишь неделю назад понял, что такое большое колесо на старинных велосипедах было вызвано необходимостью убрать у лошади желание перепрыгнуть эту конструкцию ударив ездока копытом по ушам
А нахуя лошади перепрыгивать велосипед?
Велосипед-то с педелями на переднем колесе, так что я думаю, что размер колеса связан с оптимальным соотношением число оборотов/скорость.
Ладно, блядь, с оцифровкой графиков разобрался, теперь скажите мне, как имея набор значений функции найти саму функцию.
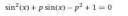
У меня там вроде бы как квадратное тригонометрическое уравнение с параметром, но я, решая это уравнение, каждый раз получаю новый ответ. В общем, я уже запутался и не знаю, что со мной не так.
Я не прошу решить это задание, я прошу натолкнуть меня на верный ход мыслей.
Условие такое: при каких p уравнение имеет корни?
ну если квадратные уравнения умеешь с параметром решать, то думаю проблем возникнуть не должно.
Я делаю замену синуса на t, решаю уравнение, дохожу до дискриминанта, мне должно хватать условия, что если D>=0,то корни есть. Это ведь ты имеешь ввиду?
Хотя, стоп. Если D>=0,то у меня есть корни относительно уравнения с t, но не для первоначального уравнения. Получается, D>=0 — это одно из условий?
Осталось вспомнить, что синус функция ограниченная, вопрос к тебе: чем она ограничена?
Тьфу. Включая единицу. А если решать графическим способом, то не нужно рассматривать случаи, когда один из корней лежит за пределами промежутка от -1 до 1?
Если корень т.е sin(x) по модулю оказался больше единицы, то нет смысла его рассматривать, потому что уравнение sin(x) = t где |t|>1 не имеет решения в вещественных числах.
Благодарю.
Ну например сложение естественно:
Есть тут 3 яблока, а там 5, ты их скинул в кучу, пересчитал и получил 8. Вот иллюстрация сложения.
А как показать умножение с яблоками? Его же нету...
Потому что умножение это соркащенная запись опредленного числа суммирования одинаковых чисел.
Чтобы не писать +5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок+5 яблок просто пишут 5 яблок*33
Да я про другое спрашивал. Забавно что абстракция начинается уже с умножения. А это там 2-ой класс..
Какая нахуй абстракция? Просто сокращенная запись суммирования.
Открой учебник первого класса где то в конце и там прямо про это писать будут
Ну так это сокращение само по себе не существует.
Нельзя обучить умножение до этого не обучив счету и сложению.
Т.е это операция уже внутри мат модели, как там возведение в степень - тоже сокращение.
Вот мой тренд, который не взлетел. Я планировал именно такими книжками и делиться. >>398226 (OP)
сложение это тоже абстракция.
Что такое восемь яблок? Это 11111111 яблок, обозначенные странным значком. А если мы будем складывать допустим лис и зайцев, то получится, что какое-то количество зайцев съедят и будет другое сложение. А если в нашей корзине дырки, то бумага + ягода и ягода + бумага будут давать разный результат. Все зависит от модели в которой мы работаем.
Такой подход фейлится при определении вещественных чисел. Под капотом каждого вещественного числа скрывается бесконечность, поэтому вещественное число нельзя рассматривать как абстракцию от яблок - в реальном мире бесконечностей нет.
Как раз таки в реальном мире одни бесконечности, а вот яблок - нет.
>И только математика по настоящему абстрактна и не привязана к материальному миру, благодаря чему можно постичь непостижимое
Гуманитарий детектед. Математика привязана к особенностя человечекого сознания и мозга - эта реально субъективная методологическая фигня основанная на том как моск может думать. При этом реальный мир плохо ложиться в прокурстово ложе математики - уже сейчас очевидно что с помощью математики невозможно точно описывать объективную реальность, но моск сука по другому думать не умеет и наука топчется из-за этого на месте. В общем нашел на что дрочить.
>реальный мир плохо ложиться в прокурстово ложе математики - уже сейчас очевидно что с помощью математики невозможно точно описывать объективную реальность
Развивай пруфы
>эта реально субъективная методологическая фигня основанная на том как моск может думать. При этом реальный мир плохо ложиться в прокурстово ложе математики - уже сейчас очевидно что с помощью математики невозможно точно описывать объективную реальность
Гуманитарий детектед, который никогда не видел Нётеровых зарядов, группы Пуанкаре, симметрий в Стандартной Модели и проч.
А ты сам-то видел?
если мы конструктивно определим вещественные числа как последовательности и будем считать только до определенного знака, то такой проблемы нет.
При таком подходе понятие равенства двух вещественных чисел, вообще говоря, потеряет смысл.
Что от меня хотят, блядь!?!
Нет, это джве разных записи одного числа.
Понятно. Идите с таким определением нахуй.
Как это ты умножил ноль на 4 и получил 28? Научи

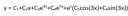
4. 2-й пик
7. 4 точно не является, думаю также, что 3 и 5 также не являются
8. 5-й порядок
Правильно ли я думаю?
это "черточки" для обозначения равных отрезков. т.е нижняя сторона треугольника разделена на два равных отрезка "две черты". Боковые стороны равны "одна черта"
нихуя они так не определены, у них мощность континуума.
>>402760
равенство до определенного знака опять же.
0.(9) и 1 равны как вещественные числа, но не равны как последовательности.

- отрицательная вероятность
- трансфинитные числа
Читал Вики. Ни хуя не понял.
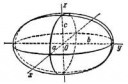
Нужно посчитать площадь проекции трёхосного эллипсоида размерами a,b,c на произвольную плоскость Ax+By+Cz=0.
Пытался влоб — не осилил. Ответ вроде интуитивно прост, но не всплывает. Я так понял надо аффинные преобразования курить, чего стоить читануть по этому поводу?
1. Отрицательная вероятность - крайне нестандартное понятие. Вероятность, согласно аксиомам Колмогорова, всегда неотрицательна. В учебниках отрицательная вероятность не встречается.
2. Натуральные числа - это 0, 1, 2, 3, 4, 5, ... и так далее. Самого большого натурального числа нет. Однако за всеми натуральными числами идёт первое трансфинитное число ω0. С него начинается как бы новый натуральный ряд. ω0+1, ω0+2, ω0+3, ... и так далее. Потом идёт число ω0+ω0, за ним ω0+ω0+1, ω0+ω0+2, ω0+ω0+3, ... и так далее - ещё один натуральный ряд. Этот процесс продолжается неограниченно. За далью даль, за каждым рядом - ещё один такой же ряд.
Дело в том, что каждое число - это множество всех предыдущих чисел. 0 - это пустое множество, 1 - это множество {0}, 2 - это множество {0,1}, 3 - это множество {0,1,2}, и т.д. Так вот, ω0 - это множество всех натуральных чисел, ω0+1 - это множество, содержащее все натуральные числа а также число ω0. А число ω0+ω0 - это множество, содержащее все натуральные числа и все числа вида ω0+n, n - натуральное.
Числа, о которых я говорю, называются "ординалы". Натуральные числа - конечные ординалы, все остальные ординалы - бесконечные. Ординалы, у которых есть предшественники, называются непредельными. Остальные называются предельными. ω-числа - типичные предельные ординалы. Каждый предельный ординал есть не более чем множество предыдущих ординалов.
Каждый ординал - это множество. У множеств есть мощность, поэтому у ординалов она тоже есть. ω0 - счетный ординал, ω0+ω0 и другие подобные тоже являются счетными. Первый несчетный ординал называется ω1, все последующие ординалы также несчетны. Для каждого множества ординалов существует ещё больший ординал. Самого большого ординала нет.
Формально ординалы определяются с помощью конструкции фон Неймана. Её я не приводил. Сказанное выше - просто пояснения.
Хуиные преобразования. Приводишь к системе координат (A,B,C) и два рандомных ортогональных этому направлению вектора, далее, к каноническому виду, и считаешь площадь (эллипса).
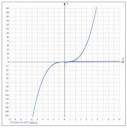
Ну напимер у нас есть y1=ln(x) и y2=x^3. Как найти X при котором y1=y2? Я знаю что надо приравнять к нулю, но как в матлабе?
Нет. /sci/ не помогает с домашками, это принципиальное правило.
Ой, спасибо. Я уже разобрался :^)

Посоветуйте как можно более полный учебник по математике ориентированный на даунов с тремя классами церковно-приходской школы. Чтобы всё разжевывалось максимально интересно и понятно, без воды, с интересными примерами где это можно применить и главное чтоб присутствовала история, как, когда и зачем такой-то математик открыл или вывел свою хуету.
> алеф-нуль это натуральное число
Каждое натуральное число число следует за каким-то натуральным числом (кроме числа 1 которое ни за чем не следует). За каким натуральным числом следует алеф-нуль?

>За каким натуральным числом следует алеф-нуль?
Алеф-нуль минус 1))) Не, если серьезно, мне правда непонятно как так. Есть множество натуральных чисел. Есть его кардинальное число. Но оно почему-то само по себе не натуральное число.
Ну смотри, если б алеф0 было натуральным, натуральные числа можно было бы отобразить в некоторое конечное подмножество, а это, очевидно, не так.
Множество называется транзитивным, если каждый его элемент является его подмножеством.
Ординал - транзитивное множество, вполне упорядоченное отношением "x является элементом y".
Теорема 1.
Элементы ординала - ординалы.
Для каждого ординала x определен ординал x+1.
Каждый ординал содержит все предшествующие ординалы.
Пруф. В любой книжке по теории множеств.
Кардинал - ординал, не равномощный предшествующему ординалу.
Омега-нуль определяется как наименьший ординал, который вместе с каждым элементом x содержат x+1.
Два множества называются равномощными, если между ними есть биекция. Если первое множество равномощно второму, а второе - третьему, то первое и третье равномощны, очевидно.
Мощность множества ординалов определяется как наименьший кардинал, которому оно равномощно.
Алеф-нуль определяется как мощность множества омега-нуль.
Множество называется счетным, если оно равномощно множеству натуральных чисел.
Множество называется конечным, если оно не содержит счетного подмножества.
Натуральными числами называются мощности конечных множеств.
Теорема 2. Мощность множества натуральных чисел есть алеф-нуль.
Пруф. Множество натуральных чисел вместе с каждым числом n содержит число n+1, значит, между ним и омега-нуль есть биекция. По т.1, мощность омеги-нуль - алеф-нуль.
Теорема 3. Алеф-нуль не является натуральным числом.
Пруф. Алеф-нуль равномощен множеству натуральных чисел. Значит, он не является конечным множеством. Значит, он не является натуральным числом - они все конечны по определению.
Множество называется транзитивным, если каждый его элемент является его подмножеством.
Ординал - транзитивное множество, вполне упорядоченное отношением "x является элементом y".
Теорема 1.
Элементы ординала - ординалы.
Для каждого ординала x определен ординал x+1.
Каждый ординал содержит все предшествующие ординалы.
Пруф. В любой книжке по теории множеств.
Кардинал - ординал, не равномощный предшествующему ординалу.
Омега-нуль определяется как наименьший ординал, который вместе с каждым элементом x содержат x+1.
Два множества называются равномощными, если между ними есть биекция. Если первое множество равномощно второму, а второе - третьему, то первое и третье равномощны, очевидно.
Мощность множества ординалов определяется как наименьший кардинал, которому оно равномощно.
Алеф-нуль определяется как мощность множества омега-нуль.
Множество называется счетным, если оно равномощно множеству натуральных чисел.
Множество называется конечным, если оно не содержит счетного подмножества.
Натуральными числами называются мощности конечных множеств.
Теорема 2. Мощность множества натуральных чисел есть алеф-нуль.
Пруф. Множество натуральных чисел вместе с каждым числом n содержит число n+1, значит, между ним и омега-нуль есть биекция. По т.1, мощность омеги-нуль - алеф-нуль.
Теорема 3. Алеф-нуль не является натуральным числом.
Пруф. Алеф-нуль равномощен множеству натуральных чисел. Значит, он не является конечным множеством. Значит, он не является натуральным числом - они все конечны по определению.
>Множество называется транзитивным, если каждый его элемент является его подмножеством.
>Ординал - транзитивное множество, вполне упорядоченное отношением "x является элементом y".
>Кардинал - ординал, не равномощный предшествующему ординалу.
Все это справедливо для алеф0 же.

Я недавно начал работать в ресторане, у нас там около 100 столов, каждый работник ответственнен за примерно 20, на каждом столе салфетница, в ней 12 салфеток, и дело все в том, что с утра когда никого нету мы в основном приготавливаем резервные салфетки для салфетниц которые в течении дня пустеют, меня это заебало и я понаблюдал за их расходом.
Получается, что чем больше салфеток в салфетнице, тем менее экономнее их тратят, например когда их остается 2-4 они лежат часами так же как пачка из 12 спускается с 12 до примерно 5. И вот я начал класть по 8 салфеток в салфетницу и по времени вроде как выходит одно и тоже, но там была контрольная группа из 2 столов, больше не смог ибо в часы пик бегаю как угорелый.
Сам я человек в точных науках очень отсталый, в школе было стабильно 2 по математике с 3 по 11 класс, до 7 класса не понимал, что такое дроби, но при этом как то сдал ЕГЭ лол Как бы все это правильно рассчитать, хочу показать научную работу манагеру, с графиками там, хотя вангую, что она разабьется об какой нибудь маркетинг в духе у нах бохатое заведение. Но может повезет и придется меньше дрочиться с салфетками...
Короче, что и как правильно делать? наверное ещё смогу запросить на складе накладную с общей статистикой по ежемесячным закупкам салфеток

У тебя последовательность вложенных интервалов. Интуитивно, левые концы будут потихоньку возрастать, а правые убывать. Множество 'А' есть ничто иное, как последовательность левых концов. Любой левый конец меньше любого правого. Другими словами, множество 'А' ограничено. По аксиоме/теореме о полноте, существует супремум 'А'. Обозначим его за 'с'. Это число
1) больше an. Это ясно, т. к. это верхняя гиань по построегию; Интуитивно, к нему стягиваются an.
2) меньше bm. Конечно, мы можем взять новое 'с' такое, что оно будет за пределами bn, и которое будет верхней гранью 'А'. Но супремум - наименьшая такая грань! Значит, оно меньше любого из правых концов.
Раз у нас число 'с' больше любого левого конца и меньше любого правого, то оно принадлежит всем интервалам.
Под иеньше/больше я везде понимал меньше или равно и т. д.
>>403322
>>403317
Первое. Если тебя интересует математическая часть, то нужно провести эксперимент, случайно выбирая столики и т. д. Скажем, измерить количество салфеток в первом случае. Потом заново, и еще, и еще. Отсюда полу, ишь среднее количнство оставшихся сплфеток. Потом ты изменяешь условия (кладешь меньше ижначально), и сновп несколько раз измеияешь, вычисляешб среднее.
После этого классическая мат. статистика (ANOVA/дисперсионный анализ, тут - тест Стьюдента) говорит тебе: со значимостью в 95%/99%/а% разницы между этими средними нет. Другими словами, количество оставшихся салфеток одинаково как при 12 начальных, так и 8 начальных.
Есди у тебя с математикой неоч, то вот другой вариант. Эффект, о котором ты говоришь, действительно существует - это scarcity heuristic. Не знаю, как в русской психологии переводят - вероятно, эвристика дефицита. Чем меньше ресурса остается, тем больше человек начинает его ценить. Заходишь на Google Scholar и вбиваешь там scarcity heuristic, или открываешь учебники по психологии, там должно быть написано. Куча статей есть на эту тему.
Ну значит по индукции алеф0 должен быть натуральным числом? Если он строится итеративно начиная с нуля? 0,1,2,3,...алеф0-1, алеф0.
> алеф0 - 1
Ты не можешь использовать число "алеф0 - 1" пока не определишь операцию вычитания единицы для алеф0 либо не докажешь что алеф0, к примеру, натуральное (так как для натуральных числе операция вычитания уже определена). Естественно, что при доказательстве натуральности алеф0 нельзя использовать операцию вычитания (так как для ее применения нужно доказать что алеф0 натуральное). Насколько я помню, ты остановился на попытке указать натуральное число которое предшествует алеф0.
>Ты не можешь использовать число "алеф0 - 1" пока не определишь операцию вычитания единицы для алеф0
Ну хуй знает. Если так: >>403296
>Множество называется транзитивным, если каждый его элемент является его подмножеством.
Очевидно, что единица является подмножеством алеф0, как и любое другое натуральное число. В итоге получится предшествующий ординал, т.к. алеф0 - кардинал.
>Кардинал - ординал, не равномощный предшествующему ординалу.
Стань чуть тоньше, твои вопросы становятся менее интересными.
Для любого ординала определена операция inc.
inc X - это наименьший из ординалов, больших X.
Существуют предельные ординалы. Ординал x называется предельным, если нет такого ординала a, что inc a = x.
Теорема. Каждый алеф - предельный ординал.
Охуенный вопрос, кстати. Серьезно.
>Эффект, о котором ты говоришь, действительно существует - это scarcity heuristic. Не знаю, как в русской психологии переводят - вероятно, эвристика дефицита. Чем меньше ресурса остается, тем больше человек начинает его ценить. Заходишь на Google Scholar и вбиваешь там scarcity heuristic, или открываешь учебники по психологии, там должно быть написано. Куча статей есть на эту тему.
Я что та такое и думал, но не мог правильно выгуглить, сейчас буду дрочить эти исследования.




Я так понял, что ан и бм это фактически константы, а вот ам и бн могут двигаться как угодно между ними. Получается что с это ан, так как в таком случае оно подойдет для всех значений ам и бн включая предельный случай когда ам = ан = бн.
Но в таком случае достаточно взять любой непредельный случай и следующий интервал с ао > ан и тогда с уже не попадет в этот интервал ао бо.
Хз. Из всех известных мне задачников на "Группа А, группа Б" делил разве что Сканави.
Объясни нормально, мемзнаток.
(1) <= (2)
Правильно?
A(1) => A(2)
Правильно?
Рисовал человечка, решил, что если начать с мужика, то будет неполиткорректно. Но если всех баб нарисовать, то будут думать, что ты поехавший сжв. Но нарисовав мужика понял, что математик в конце будет тоже мужиком, и будут все думать, что ты думаешь, будто бабы не могут в математику - нарисовал два мужика подряд.


Привет математикам! Прошу пожалуйста отнестись с пониманием без рофлов.
Дело в том, что я год назад закончил нептуаколледж, что какбэ намекает.
Так вот, я хочу по крайней мере попытаться вырваться из стадий деградации и поступить на заочку в какой-нибудь ВУЗ, потому как ходить с корочкой ПТУ для меня сплошной стыд и срам. Для поступления надумал сдавать вместо ЕГЭ вступительные. Желанием ужасно горю, а вот мозгов - нет.
Знаю, что просьба моя возможно будет очень жирная, но может есть на примете какие-нибудь лекции желательно по темам на пике с разжевыванием, который поймет даже аутист?
Да, и именно видео. По книжкам мне как долбоебу нихуя не ясно.
Буду благодарен вам за вашу поддержку и понимание.
Да. Но менее ебанутые занимаются наукой, а не пишут видео для школьников. Этот хотя бы компетентный.
Кхан академи, курсера.



Серьёзно. Просто не обращай внимания на такие заскоки.
попробуй еще зуланке-онищик
Насколько я знаю, что касается физики, он вообще первостепенный фрик, так что я бы опасался читать его впринципе.
Книжка по топологии - вполне вин.
Все бегемотики ускакали в /матх.

Норм так, ничё.
Двач помогай я нифига не понимаю!
Пик рандом
На двойном тетрадном листе бумаги (обяза-
тельно в клеточку) отметьте оси координат.
Отметьте на осях минимальные и максималь-
ные значения следующим образом. По оси Х
отсчет начните с нуля, поместив его в начало
шкалы. Расстояние в одну клеточку будет рав-
но единице (должно получиться по меньшей
мере 35 делений). По оси Y отступите от оси Х
одну клеточку и начните отсчет с числа, рав-
ного дню Вашего рождения. Например, если
Вы родились 14 мая, начните отсчет по оси Y с
14. Расстояние в одну клеточку также будет
равно единице (получится по меньшей мере 20
клеточек вверх).
В правом верхнем углу графика в узел сетки
(пересечение вертикальных и горизонтальных
линий сетки) поставьте точку (она должна
иметь координаты, которые возможно отме-
56
тить на графике). В левой нижней части графи-
ка, отступив от оси Х 3-5 клеток, а от оси Y –
только одну, также в узел сетки поставьте точ-
ку. Соедините эти две точки тонкой линией
(обязательно начертить карандашом и без ли-
нейки, от руки! Линия не должна быть идеаль-
но ровной — будет лучше, если она будет по-
чти прямой).
Теперь вдоль полученной линии, но не на
ней самой, отметьте в узлах сетки (на пересе-
чениях вертикальных и горизонтальных линий)
от 35 до 45 точек на удалении от неё не более
двух клеток. Постарайтесь расставить точки
таким образом, чтобы они не образовывали ко-
ридор, в центре которого будет проходить ис-
ходная линия. В идеальном варианте точки, на-
ходящиеся ближе к линии, должны встречать-
ся чаще, чем точки, расположенные от неё
дальше. Запишите целочисленные координаты
каждой точки в таблицу (она будет содержать
по меньшей мере 15 столбиков — рекомендуем
57
сначала определять, какие значения будут на-
ходиться в столбике, и только после этого отво-
дить под него место на листе.
Пример таблицы:
x y
1 15
2 17
2 16
... ...
Примечание. В таблице должны быть записа-
ны координаты всех отмеченных на графике
точек.
Посмотрите внимательно на график. Судя
по всему, он отражает некоторую линейную за-
висимость между показателями x и y. При этом
видно, что существуют погрешности измере-
ния, вызванные случайными факторами (а так-
же тем фактом, что измерения значений про-
водились с округлением до целых). Эти по-
грешности несколько искажают общую зависи-
мость, однако в целом вступает в силу закон
58
больших чисел, и искажения в общей массе
сглаживаются. Предположим, что отмеченные
точки выражают реальную ситуацию, которую
необходимо смоделировать.
Дальнейшие вычисления нужно проводить
вручную, поскольку это позволяет задуматься
над тем, что именно и правильно ли Вы делае-
те. Можно порекомендовать проверить полу-
ченные результаты расчетов на компьютере.
Самую трудоёмкую часть работы — построение
доверительных интервалов — разрешается де-
лать сразу на компьютере.
По полученным точкам постройте линейную
модель парной регрессии (y зависит от x) в
полном соответствии с рассмотренным в этой
лекции алгоритмом. Каждый пункт алгоритма
должен сопровождаться выводами по проде-
ланной работе и полученному результату, что
поможет Вам в дальнейшем при разработке об-
щих выводов и рекомендаций по практическо-
му использованию модели.
Двач помогай я нифига не понимаю!
Пик рандом
На двойном тетрадном листе бумаги (обяза-
тельно в клеточку) отметьте оси координат.
Отметьте на осях минимальные и максималь-
ные значения следующим образом. По оси Х
отсчет начните с нуля, поместив его в начало
шкалы. Расстояние в одну клеточку будет рав-
но единице (должно получиться по меньшей
мере 35 делений). По оси Y отступите от оси Х
одну клеточку и начните отсчет с числа, рав-
ного дню Вашего рождения. Например, если
Вы родились 14 мая, начните отсчет по оси Y с
14. Расстояние в одну клеточку также будет
равно единице (получится по меньшей мере 20
клеточек вверх).
В правом верхнем углу графика в узел сетки
(пересечение вертикальных и горизонтальных
линий сетки) поставьте точку (она должна
иметь координаты, которые возможно отме-
56
тить на графике). В левой нижней части графи-
ка, отступив от оси Х 3-5 клеток, а от оси Y –
только одну, также в узел сетки поставьте точ-
ку. Соедините эти две точки тонкой линией
(обязательно начертить карандашом и без ли-
нейки, от руки! Линия не должна быть идеаль-
но ровной — будет лучше, если она будет по-
чти прямой).
Теперь вдоль полученной линии, но не на
ней самой, отметьте в узлах сетки (на пересе-
чениях вертикальных и горизонтальных линий)
от 35 до 45 точек на удалении от неё не более
двух клеток. Постарайтесь расставить точки
таким образом, чтобы они не образовывали ко-
ридор, в центре которого будет проходить ис-
ходная линия. В идеальном варианте точки, на-
ходящиеся ближе к линии, должны встречать-
ся чаще, чем точки, расположенные от неё
дальше. Запишите целочисленные координаты
каждой точки в таблицу (она будет содержать
по меньшей мере 15 столбиков — рекомендуем
57
сначала определять, какие значения будут на-
ходиться в столбике, и только после этого отво-
дить под него место на листе.
Пример таблицы:
x y
1 15
2 17
2 16
... ...
Примечание. В таблице должны быть записа-
ны координаты всех отмеченных на графике
точек.
Посмотрите внимательно на график. Судя
по всему, он отражает некоторую линейную за-
висимость между показателями x и y. При этом
видно, что существуют погрешности измере-
ния, вызванные случайными факторами (а так-
же тем фактом, что измерения значений про-
водились с округлением до целых). Эти по-
грешности несколько искажают общую зависи-
мость, однако в целом вступает в силу закон
58
больших чисел, и искажения в общей массе
сглаживаются. Предположим, что отмеченные
точки выражают реальную ситуацию, которую
необходимо смоделировать.
Дальнейшие вычисления нужно проводить
вручную, поскольку это позволяет задуматься
над тем, что именно и правильно ли Вы делае-
те. Можно порекомендовать проверить полу-
ченные результаты расчетов на компьютере.
Самую трудоёмкую часть работы — построение
доверительных интервалов — разрешается де-
лать сразу на компьютере.
По полученным точкам постройте линейную
модель парной регрессии (y зависит от x) в
полном соответствии с рассмотренным в этой
лекции алгоритмом. Каждый пункт алгоритма
должен сопровождаться выводами по проде-
ланной работе и полученному результату, что
поможет Вам в дальнейшем при разработке об-
щих выводов и рекомендаций по практическо-
му использованию модели.

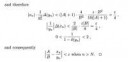

Очевидно левые части двух верхних неравенств складываются и умножаются на среднюю часть третьего с верху неравенства, благодаря чему получаем < epsylon.
И вот у меня выходит правый пик, хотя должен выйти модуль разницы а/б и х/у.
Вы математик? Можно с Вами познакомиться?
Есть ли в математике ещё примеры подобных "доказательств невозможности", по фундаментальности и исторической значимости сравнимых с уже упомянутыми?
1) для любых i, j из m: |i-j| >= N
2) размер m максимален
Есть какие-нибудь быстрые решения без перебора всех вариантов?
Вы видите копию треда, сохраненную 15 июня 2017 года.
Можете попробовать обновить страницу, чтобы увидеть актуальную версию.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.